Impact of Feature-Selection in a Data-Driven Method for Flow Curve Identification of Sheet Metal
Abstract
1. Introduction
2. Overview of Data-Driven Methods for Plastic Flow Identification
3. Materials and Methods
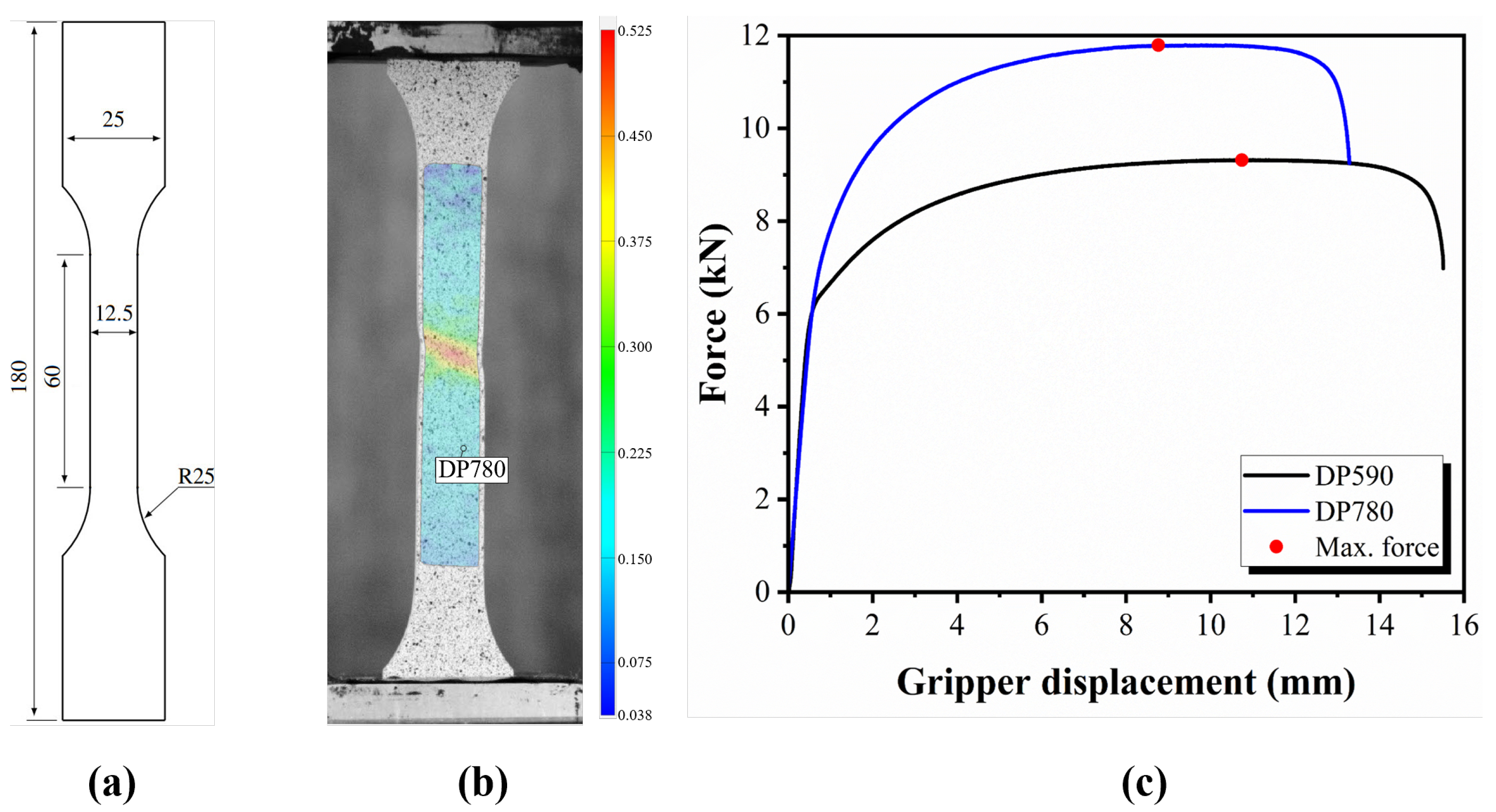
3.1. Uniaxial Tensile Test
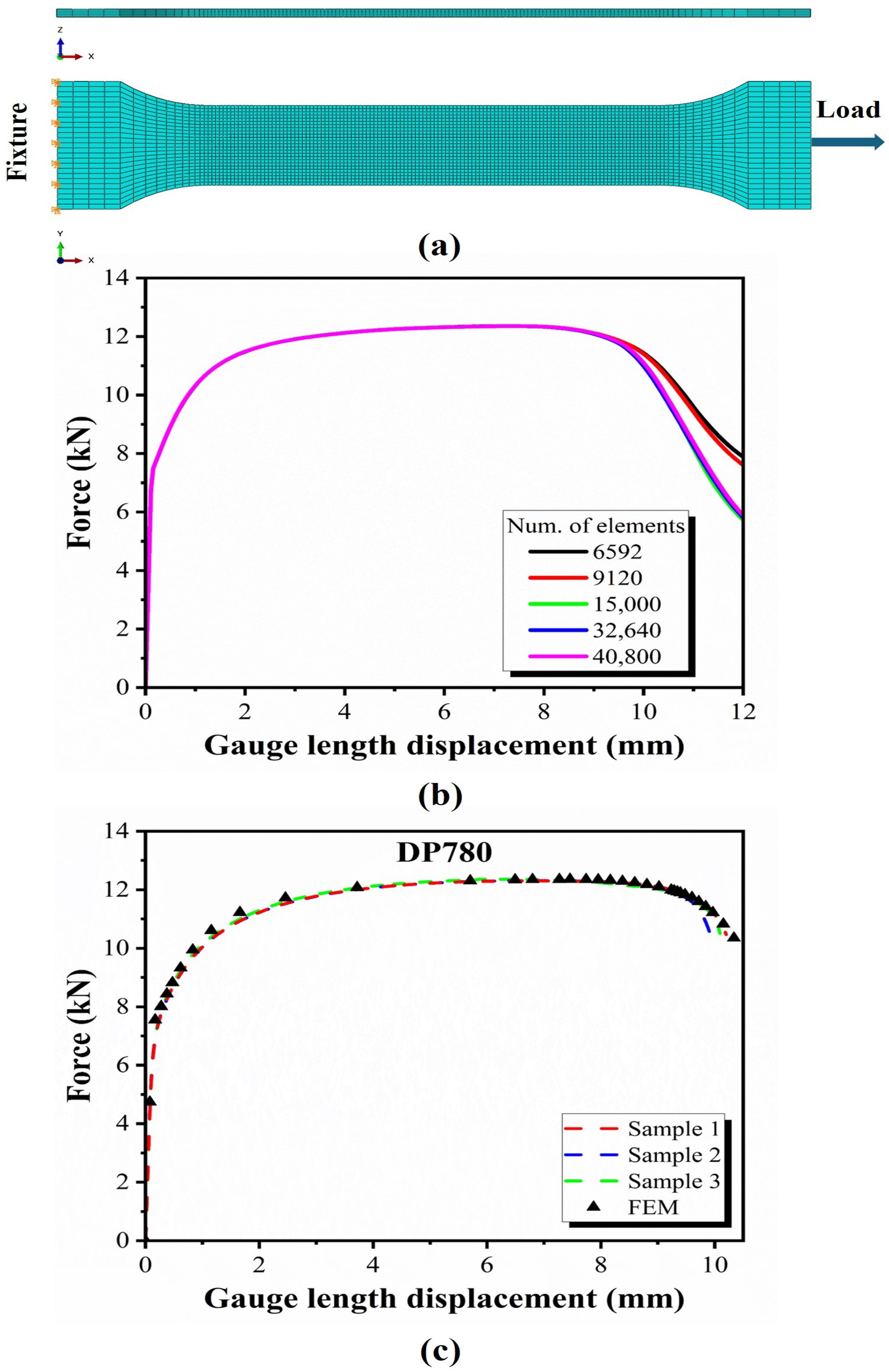
3.2. Finite Element Model
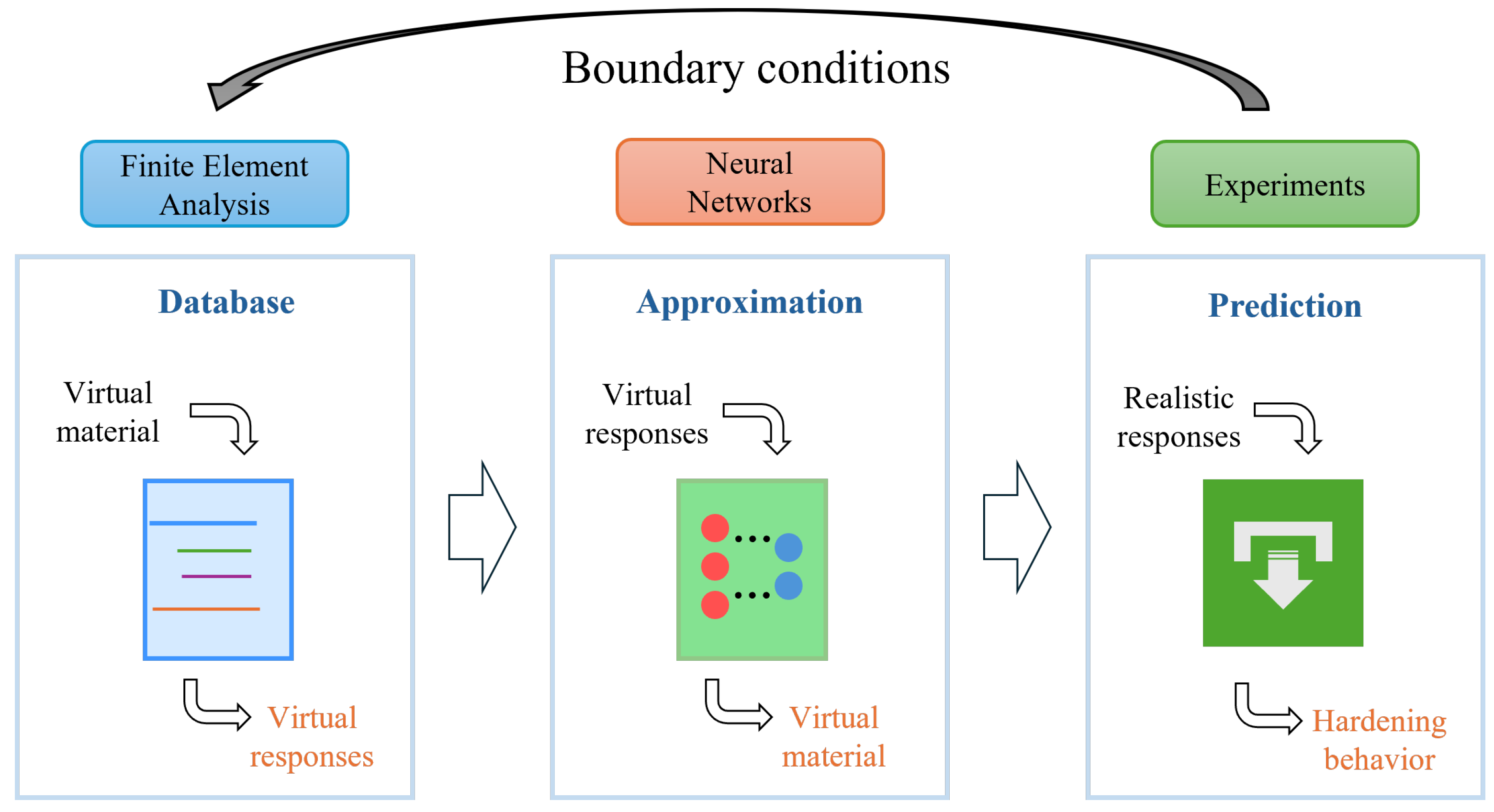
3.3. Surrogate Model
3.3.1. Data Acquisition
3.3.2. Feature Selection
3.3.3. Neural Network Architecture
3.4. Training and Validation
4. Application
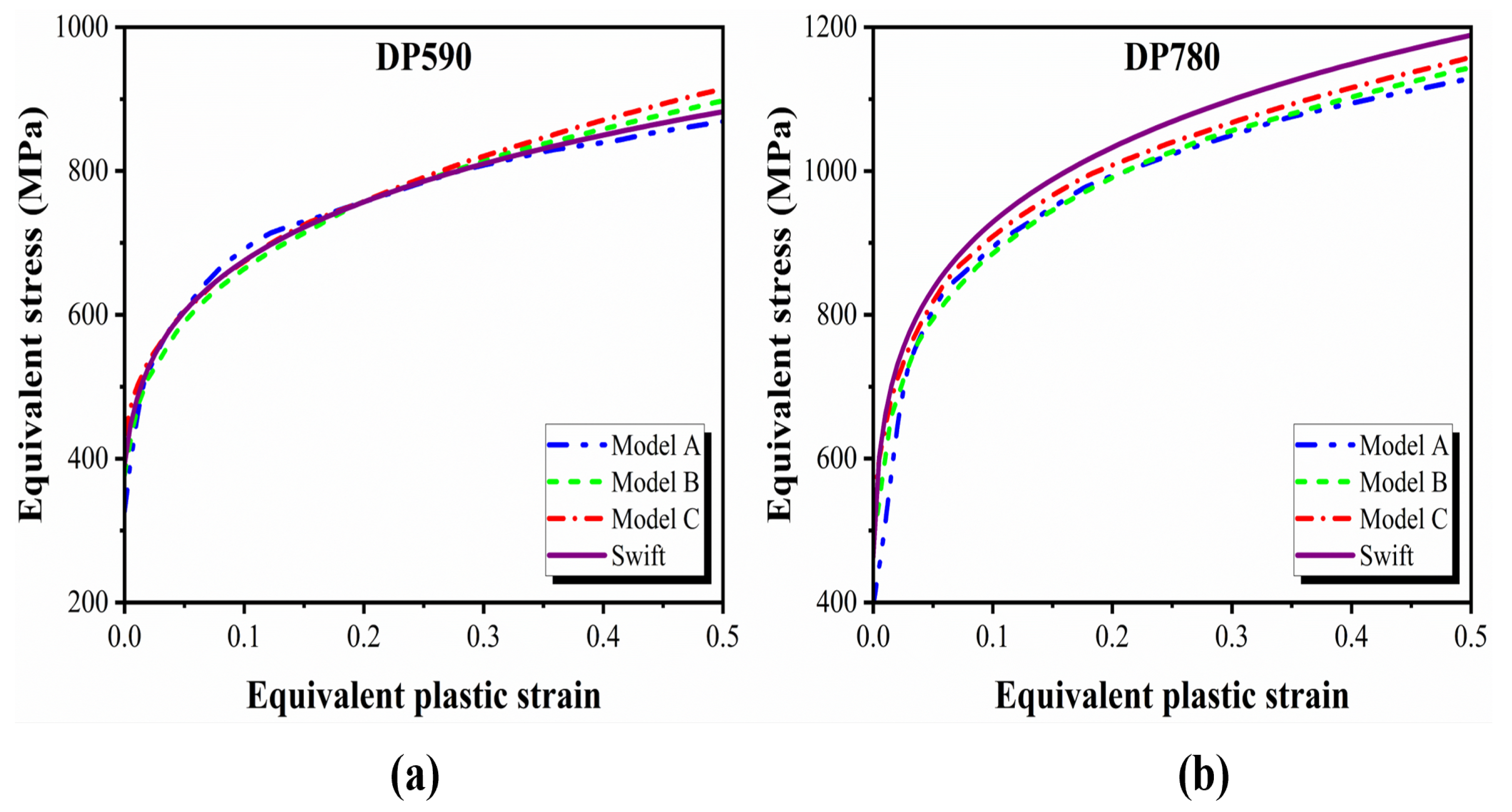
4.1. Flow Stress in the Pre-Necking Range
4.2. Flow Stress in the Post-Necking Range
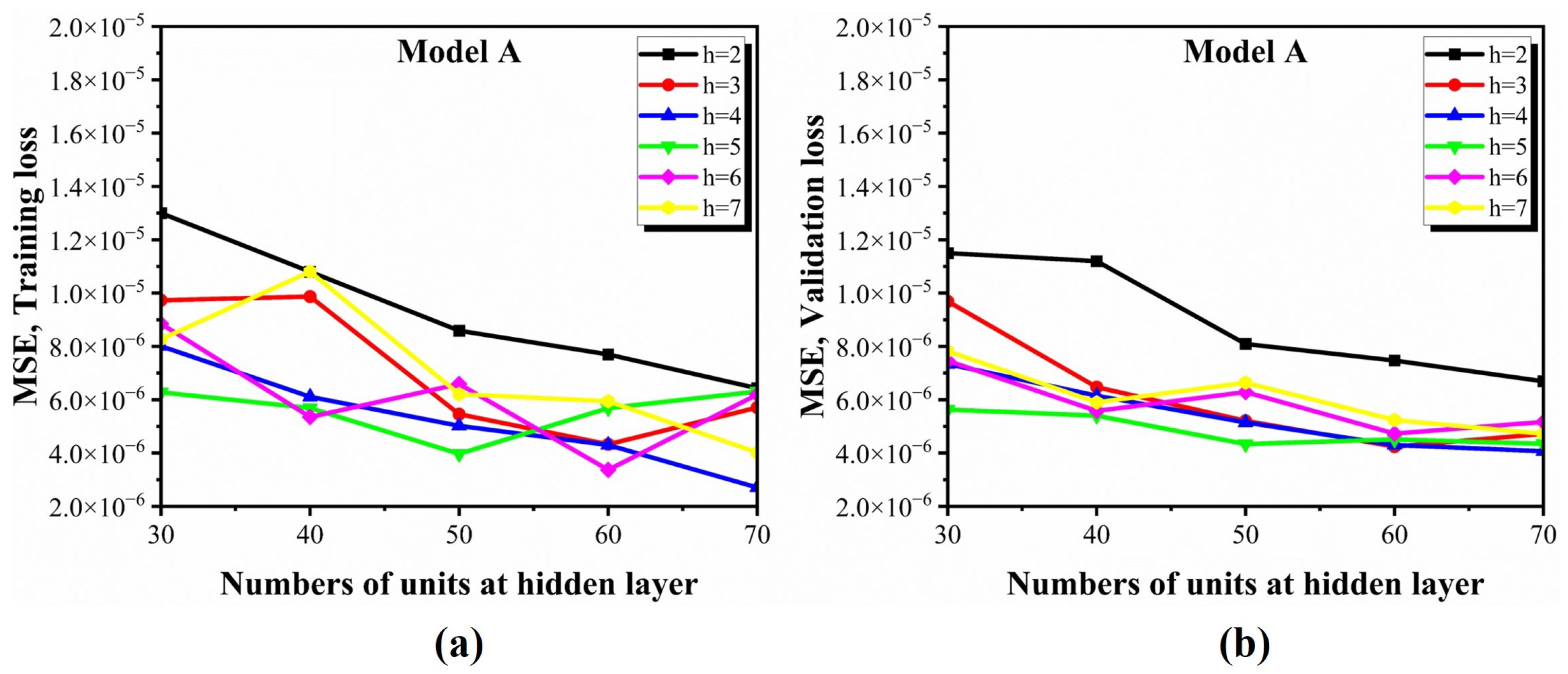
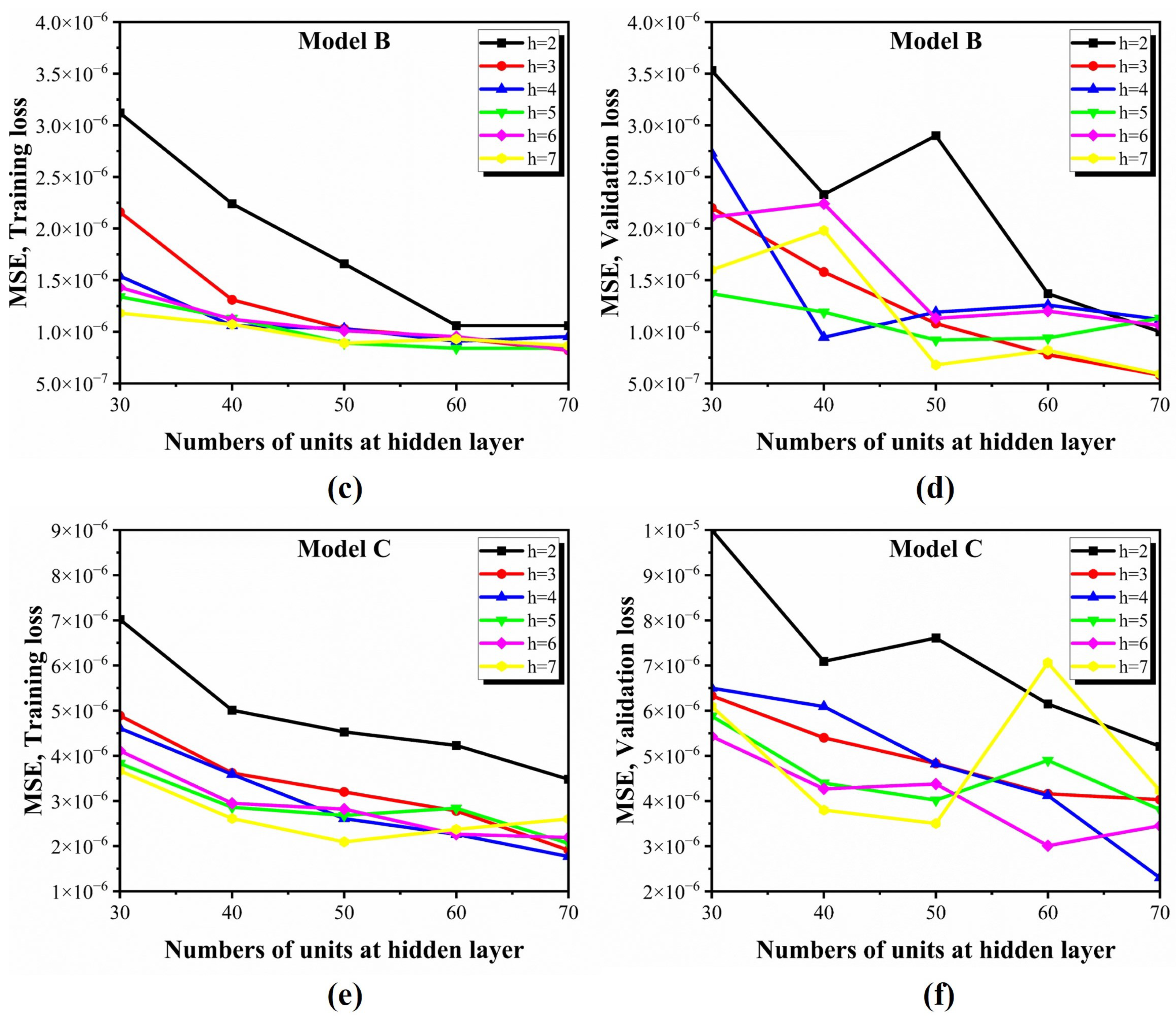
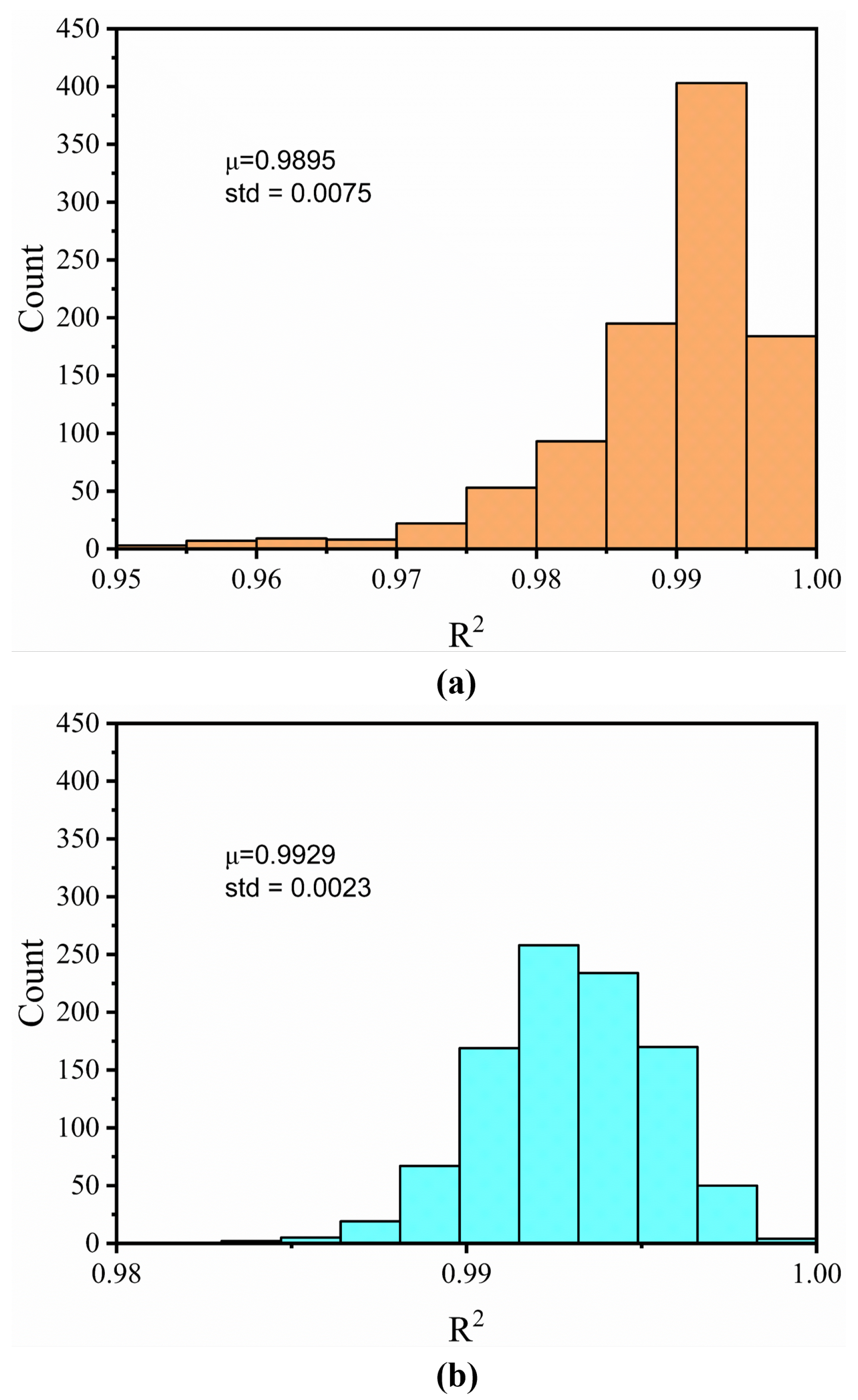
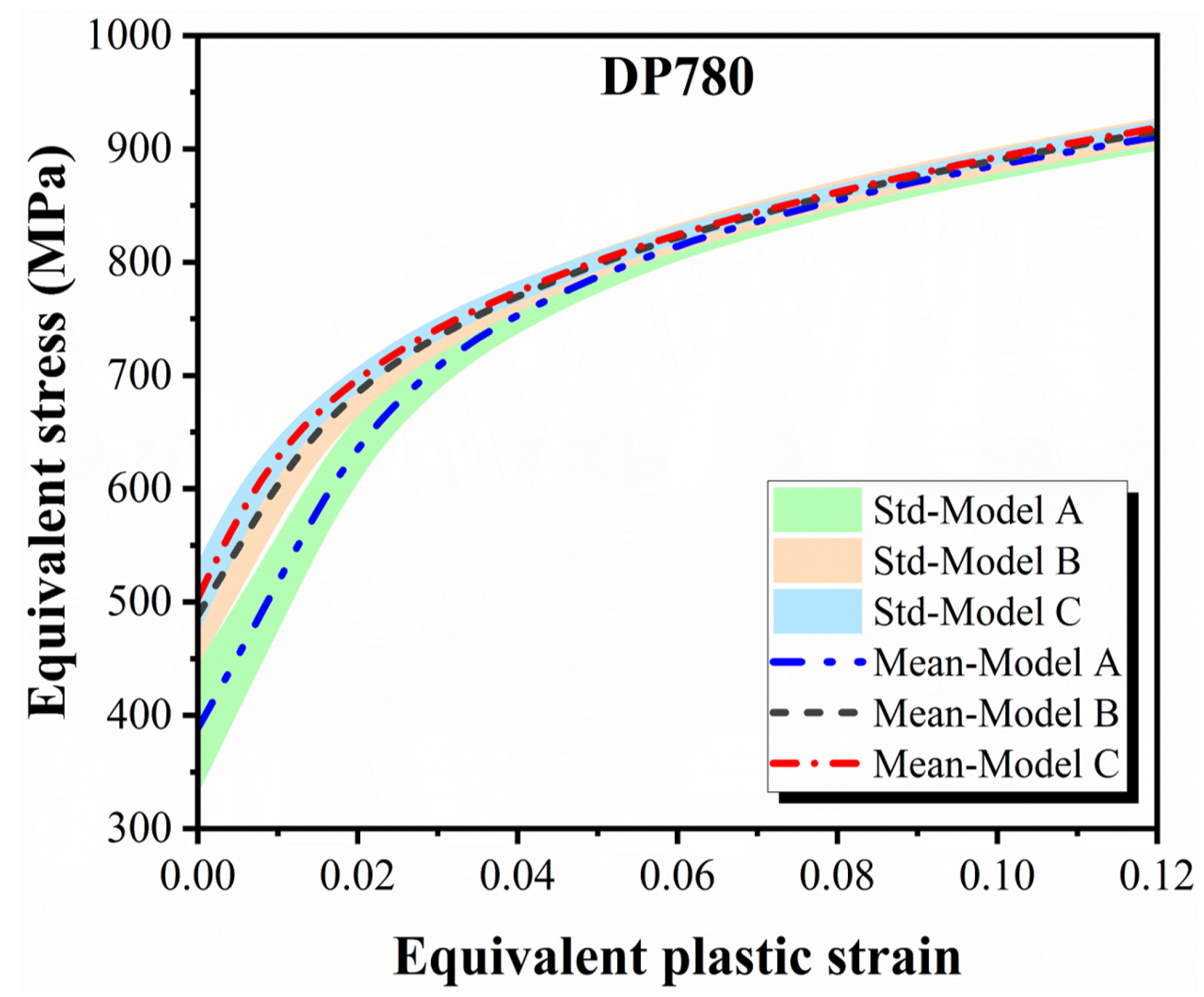
4.3. Repeatability of the Training Process
5. Validation
6. Conclusions and Discussion
6.1. Discussion
6.2. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Hyperparameter Tuning
References
- Stoughton, T.B. A non-associated flow rule for sheet metal forming. Int. J. Plast. 2002, 18, 687–714. [Google Scholar] [CrossRef]
- Groche, P.; Ringler, J.; Vucic, D. New forming processes for sheet metal with large plastic deformation. Key Eng. Mater. 2007, 344, 251–258. [Google Scholar] [CrossRef]
- Vegter, H.; ten Horn, C.H.; An, Y.; Atzema, E.H.; Pijlman, H.H.; van den Boogaard, T.H.; Huétink, H. Characterisation and modelling of the plastic material behaviour and its application in sheet metal forming simulation. In Proceedings of the 7th International Conference on Computational Plasticity, COMPLAS 2003, Barcelona, Spain, 7–10 April 2003; CIMNE Barcelona: Barcelona, Spain, 2003; pp. 777–780. [Google Scholar]
- Kessler, L.; Gese, H.; Metzmacher, G.; Werner, H. An approach to model sheet failure after onset of localized necking in industrial high strength steel stamping and crash simulations. SAE Int. J. Passeng. Cars-Mech. Syst. 2008, 1, 361–370. [Google Scholar] [CrossRef]
- Coppieters, S.; Zhang, H.; Xu, F.; Vandermeiren, N.; Breda, A.; Debruyne, D. Process-induced bottom defects in clinch forming: Simulation and effect on the structural integrity of single shear lap specimens. Mater. Des. 2017, 130, 336–348. [Google Scholar] [CrossRef]
- Do, V.C.; Pham, Q.T.; Kim, Y.S. Identification of forming limit curve at fracture in incremental sheet forming. Int. J. Adv. Manuf. Technol. 2017, 92, 4445–4455. [Google Scholar] [CrossRef]
- Gutscher, G.; Wu, H.C.; Ngaile, G.; Altan, T. Determination of flow stress for sheet metal forming using the viscous pressure bulge (VPB) test. J. Mater. Process. Technol. 2004, 146, 1–7. [Google Scholar] [CrossRef]
- Ranta-Eskola, A. Use of the hydraulic bulge test in biaxial tensile testing. Int. J. Mech. Sci. 1979, 21, 457–465. [Google Scholar] [CrossRef]
- Mulder, J.; Vegter, H.; Aretz, H.; Keller, S.; van den Boogaard, A.H. Accurate determination of flow curves using the bulge test with optical measuring systems. J. Mater. Process. Technol. 2015, 226, 169–187. [Google Scholar] [CrossRef]
- Koç, M.; Billur, E.; Cora, Ö.N. An experimental study on the comparative assessment of hydraulic bulge test analysis methods. Mater. Des. 2011, 32, 272–281. [Google Scholar] [CrossRef]
- Mei, H.; Lang, L.; Liu, K.; Yang, X. Evaluation study on iterative inverse modeling procedure for determining post-necking hardening behavior of sheet metal at elevated temperature. Metals 2018, 8, 1044. [Google Scholar] [CrossRef]
- Zhao, K.; Wang, L.; Chang, Y.; Yan, J. Identification of post-necking stress–strain curve for sheet metals by inverse method. Mech. Mater. 2016, 92, 107–118. [Google Scholar] [CrossRef]
- Do, N.D.; Nguyen, V.T.; Nguyen, D.T. A Comparison Study of a DIC and Extensometer on Stress-Strain Curve for AL5052 Aluminum Sheets and Its FEM Applications. In Advanced Materials: Proceedings of the International Conference on “Physics and Mechanics of New Materials and Their Applications”, PHENMA, Hanoi, Vietnam, 2019; Springer: Berlin/Heidelberg, Germany, 2020; pp. 461–474. [Google Scholar]
- Quanjin, M.; Rejab, M.; Halim, Q.; Merzuki, M.; Darus, M. Experimental investigation of the tensile test using digital image correlation (DIC) method. Mater. Today Proc. 2020, 27, 757–763. [Google Scholar]
- Pham, Q.T.; Lee, M.G.; Kim, Y.S. New procedure for determining the strain hardening behavior of sheet metals at large strains using the curve fitting method. Mech. Mater. 2021, 154, 103729. [Google Scholar]
- Van Tonder, J.D.; Venter, M.P.; Venter, G. A New Method for Improving Inverse Finite Element Method Material Characterization for the Mooney–Rivlin Material Model through Constrained Optimization. Math. Comput. Appl. 2023, 28, 78. [Google Scholar] [CrossRef]
- Nicholson, D.W. On finite element analysis of an inverse problem in elasticity. Inverse Probl. Sci. Eng. 2012, 20, 735–748. [Google Scholar]
- van Tonder, J.D.; Venter, M.P.; Venter, G. A novel method for resolving non-unique solutions observed in fitting parameters to the Mooney Rivlin material model. Finite Elem. Anal. Des. 2023, 225, 104006. [Google Scholar]
- Bastos, N.; Prates, P.A.; Andrade-Campos, A. Material parameter identification of elastoplastic constitutive models using machine learning approaches. Key Eng. Mater. 2022, 926, 2193–2200. [Google Scholar]
- Jeong, K.; Lee, H.; Kwon, O.M.; Jung, J.; Kwon, D.; Han, H.N. Prediction of uniaxial tensile flow using finite element-based indentation and optimized artificial neural networks. Mater. Des. 2020, 196, 109104. [Google Scholar]
- Pham, Q.T.; Le, H.S.; Nguyen, A.T.; Xiao, X.; Kim, Y.S.; Nguyen, V.D.; Tran, H.S.; Van Tran, X. A machine learning–based methodology for identification of the plastic flow in aluminum sheets during incremental sheet forming processes. Int. J. Adv. Manuf. Technol. 2022, 120, 3559–3584. [Google Scholar]
- Yamanaka, A.; Kamijyo, R.; Koenuma, K.; Watanabe, I.; Kuwabara, T. Deep neural network approach to estimate biaxial stress-strain curves of sheet metals. Mater. Des. 2020, 195, 108970. [Google Scholar] [CrossRef]
- Rao, K.; Prasad, Y. Neural network approach to flow stress evaluation in hot deformation. J. Mater. Process. Technol. 1995, 53, 552–566. [Google Scholar]
- Phaniraj, M.P.; Lahiri, A.K. The applicability of neural network model to predict flow stress for carbon steels. J. Mater. Process. Technol. 2003, 141, 219–227. [Google Scholar]
- Gupta, A.K.; Singh, S.K.; Reddy, S.; Hariharan, G. Prediction of flow stress in dynamic strain aging regime of austenitic stainless steel 316 using artificial neural network. Mater. Des. 2012, 35, 589–595. [Google Scholar]
- Zhu, Y.; Zeng, W.; Sun, Y.; Feng, F.; Zhou, Y. Artificial neural network approach to predict the flow stress in the isothermal compression of as-cast TC21 titanium alloy. Comput. Mater. Sci. 2011, 50, 1785–1790. [Google Scholar]
- El Mehtedi, M.; Forcellese, A.; Greco, L.; Pieralisi, M.; Simoncini, M. Flow curve prediction of ZAM100 magnesium alloy sheets using artificial neural network-based models. Procedia CIRP 2019, 79, 661–666. [Google Scholar]
- Cruz, D.J.; Barbosa, M.R.; Santos, A.D.; Amaral, R.L.; de Sa, J.C.; Fernandes, J.V. Recurrent Neural Networks and Three-Point Bending Test on the Identification of Material Hardening Parameters. Metals 2024, 14, 84. [Google Scholar] [CrossRef]
- Andrade-Campos, A.; Bastos, N.; Conde, M.; Gonçalves, M.; Henriques, J.; Lourenço, R.; Martins, J.; Oliveira, M.; Prates, P.; Rumor, L. On the inverse identification methods for forming plasticity models using full-field measurements. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2022; Volume 1238, p. 012059. [Google Scholar]
- Parreira, T.G.; Marques, A.E.; Sakharova, N.A.; Prates, P.A.; Pereira, A.F. Identification of Sheet Metal Constitutive Parameters Using Metamodeling of the Biaxial Tensile Test on a Cruciform Specimen. Metals 2024, 14, 212. [Google Scholar] [CrossRef]
- Singh, K.; Rajput, S.; Soota, T.; Verma, V.; Singh, D. Prediction of hot deformation behavior of high phosphorus steel using artificial neural network. In Proceedings of the IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 330, p. 012038. [Google Scholar]
- Dixit, M.C.; Srivastava, N.; Rajput, S. Modeling of flow stress of AA6061 under hot compression using artificial neural network. Mater. Today Proc. 2017, 4, 1964–1971. [Google Scholar]
- Li, X.; Roth, C.C.; Mohr, D. Machine-learning based temperature-and rate-dependent plasticity model: Application to analysis of fracture experiments on DP steel. Int. J. Plast. 2019, 118, 320–344. [Google Scholar]
- Zhang, Q.; Babuška, I.; Banerjee, U. Robustness in stable generalized finite element methods (SGFEM) applied to Poisson problems with crack singularities. Comput. Methods Appl. Mech. Eng. 2016, 311, 476–502. [Google Scholar]
- Thite, A.; Mace, B. Robust estimation of coupling loss factors from finite element analysis. J. Sound Vib. 2007, 303, 814–831. [Google Scholar] [CrossRef]
- Gawlikowski, J.; Tassi, C.R.N.; Ali, M.; Lee, J.; Humt, M.; Feng, J.; Kruspe, A.; Triebel, R.; Jung, P.; Roscher, R.; et al. A survey of uncertainty in deep neural networks. Artif. Intell. Rev. 2023, 56, 1513–1589. [Google Scholar] [CrossRef]
- Cao, J.; Bambach, M.; Merklein, M.; Mozaffar, M.; Xue, T. Artificial intelligence in metal forming. CIRP Ann. 2024, 73, 561–587. [Google Scholar] [CrossRef]
- Kubik, C.; Knauer, S.M.; Groche, P. Smart sheet metal forming: Importance of data acquisition, preprocessing and transformation on the performance of a multiclass support vector machine for predicting wear states during blanking. J. Intell. Manuf. 2022, 33, 259–282. [Google Scholar] [CrossRef]
- Coppieters, S.; Cooreman, S.; Sol, H.; Van Houtte, P.; Debruyne, D. Identification of the post-necking hardening behaviour of sheet metal by comparison of the internal and external work in the necking zone. J. Mater. Process. Technol. 2011, 211, 545–552. [Google Scholar] [CrossRef]
- Pham, Q.T.; Nguyen-Thoi, T.; Ha, J.; Kim, Y.S. Hybrid fitting-numerical method for determining strain-hardening behavior of sheet metals. Mech. Mater. 2021, 161, 104031. [Google Scholar] [CrossRef]
- Alharbi, M.; Kong, I.; Patel, V.I. Simulation of uniaxial stress–strain response of 3D-printed polylactic acid by nonlinear finite element analysis. Appl. Adhes. Sci. 2020, 8, 5. [Google Scholar] [CrossRef]
- Carvalho, C.P.; Baltar, J.P. Simulation of uniaxial tensile test through of finite element method. INOVAE-J. Eng. Archit. Technol. Innov. (ISSN 2357–7797) 2017, 5, 3–13. [Google Scholar]
- Huang, Y.; Young, B. Stress–strain relationship of cold-formed lean duplex stainless steel at elevated temperatures. J. Constr. Steel Res. 2014, 92, 103–113. [Google Scholar] [CrossRef]
- Dzioba, I.; Furmańczyk, P.; Lipiec, S. Determination of the fracture toughness characteristics of S355JR steel. Arch. Metall. Mater. 2018, 63, 497–503. [Google Scholar] [CrossRef]
- Yang, X.; Choi, C.; Sever, N.K.; Altan, T. Prediction of springback in air-bending of Advanced High Strength steel (DP780) considering Young’s modulus variation and with a piecewise hardening function. Int. J. Mech. Sci. 2016, 105, 266–272. [Google Scholar]
- ARYANPOUR, A.; Rodzik, M.; Green, D.; Van Tyne, C.; Rothleutner, L. Characterization of advanced high strength steel sheets in view of the numerical prediction of sidewall curl. SAE Int. J. Mater. Manuf. 2013, 6, 90–98. [Google Scholar]
- Chung, K.; Noh, W.; Yang, X.; Han, H.N.; Lee, M.G. Practical failure analysis of resistance spot welded advanced high-strength steel sheets. Int. J. Plast. 2017, 94, 122–147. [Google Scholar]
- Deng, D.; Kiyoshima, S. Numerical simulation of residual stresses induced by laser beam welding in a SUS316 stainless steel pipe with considering initial residual stress influences. Nucl. Eng. Des. 2010, 240, 688–696. [Google Scholar]
- Swift, H. Plastic instability under plane stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar]
- Butcher, C.; Khameneh, F.; Abedini, A.; Connolly, D.; Kurukuri, S. On the experimental characterization of sheet metal formability and the consistent calibration of the MK model for biaxial stretching in plane stress. J. Mater. Process. Technol. 2021, 287, 116887. [Google Scholar]
- Abedini, A.; Narayanan, A.; Butcher, C. An investigation into the characterization of the hardening response of sheet metals using tensile and shear tests with surface strain measurement. Forces Mech. 2022, 7, 100090. [Google Scholar]
- Bonatti, C.; Mohr, D. Neural network model predicting forming limits for Bi-linear strain paths. Int. J. Plast. 2021, 137, 102886. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Agarap, A.F. Deep learning using rectified linear units (relu). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems. 2015. Available online: https://www.tensorflow.org/ (accessed on 8 February 2025).
- Masters, D.; Luschi, C. Revisiting small batch training for deep neural networks. arXiv 2018, arXiv:1804.07612. [Google Scholar]
- Tu, S.; Ren, X.; He, J.; Zhang, Z. Stress–strain curves of metallic materials and post-necking strain hardening characterization: A review. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 3–19. [Google Scholar]
- Colaco, S.; Kumar, S.; Tamang, A.; Biju, V.G. A review on feature selection algorithms. In Emerging Research in Computing, Information, Communication and Applications: ERCICA 2018, Volume 2; Springer: Singapore, 2019; pp. 133–153. [Google Scholar]
- Qu, M.; Li, M.; Wen, Z.; He, W. Data-Driven Construction Method of Material Mechanical Behavior Model. Metals 2022, 12, 1086. [Google Scholar] [CrossRef]
- Kim, T.; Ryu, W.H.; Yoo, G.H.; Park, D.; Kim, J.Y.; Park, E.S.; Lee, D. Data-driven discovery of ultrahigh specific hardness alloys. J. Mater. Res. Technol. 2024, 33, 7753–7760. [Google Scholar] [CrossRef]
- Heider, Y.; Wang, K.; Sun, W. SO(3)-invariance of informed-graph-based deep neural network for anisotropic elastoplastic materials. Comput. Methods Appl. Mech. Eng. 2020, 363, 112875. [Google Scholar] [CrossRef]
- Abueidda, D.W.; Koric, S.; Sobh, N.A.; Sehitoglu, H. Deep learning for plasticity and thermo-viscoplasticity. Int. J. Plast. 2021, 136, 102852. [Google Scholar] [CrossRef]
- Ghavamian, F.; Simone, A. Accelerating multiscale finite element simulations of history-dependent materials using a recurrent neural network. Comput. Methods Appl. Mech. Eng. 2019, 357, 112594. [Google Scholar] [CrossRef]
- Gorji, M.B.; Mozaffar, M.; Heidenreich, J.N.; Cao, J.; Mohr, D. On the potential of recurrent neural networks for modeling path dependent plasticity. J. Mech. Phys. Solids 2020, 143, 103972. [Google Scholar] [CrossRef]
- Mozaffar, M.; Bostanabad, R.; Chen, W.; Ehmann, K.; Cao, J.; Bessa, M. Deep learning predicts path-dependent plasticity. Proc. Natl. Acad. Sci. USA 2019, 116, 26414–26420. [Google Scholar] [CrossRef]




| Group | Ref. | Testing Method | NN Architecture | Input | Output |
|---|---|---|---|---|---|
| Group 1 | [23] | Compression test | FFNN | ||
| [24] | Uniaxial tensile test | FFNN | |||
| [25] | Uniaxial tensile test | FFNN | |||
| [26] | Isothermal CT | FFNN | |||
| [27] | Uniaxial tensile test | FFNN | |||
| Group 2 | [21] | ISF | FFNN | Hardening parameters or | |
| [22] | Biaxial tensile test | CNN | Images | ||
| [28] | TPBT | RNN | F | Hardening parameters | |
| [29] | Uniaxial tensile test | Decision trees | Hardening parameters | ||
| [30] | Biaxial tensile test | GPR | Hardening parameters |
| Material Properties | DP590 | DP780 |
|---|---|---|
| Young modulus (GPa) | 206 | 206 |
| Initial yield stress (MPa) | 409 | 495 |
| Ultimate tensile strength (MPa) | 618 | 820 |
| Elongation at fracture (%) | 25.2 | 20.4 |
| Model | Input Feature | Description |
|---|---|---|
| Model A | Force at | |
| Force at | ||
| Force at | ||
| Forces at 19 consecutive displacements between and | ||
| Gripper displacement at | ||
| Examined | ||
| Model B | Force at | |
| Gripper displacement at | ||
| Force at | ||
| Gripper displacement at | ||
| Force at | ||
| Gripper displacement at | ||
| and | Coefficients a and b of | |
| and | Coefficients a and b of | |
| Examined | ||
| Model C | Force at | |
| Force at | ||
| Ratio between the gripper displacement at and the sample’s initial length | ||
| Ratio between the gripper displacement at and the gripper displacement at | ||
| Second derivative of | ||
| Second derivative of | ||
| Examined * |
| Model A | Model B | Model C | |
|---|---|---|---|
| Input layer | |||
| Target output | |||
| Architecture | 4 hidden layers, 70 nodes per each | 3 hidden layers, 70 nodes per each | 4 hidden layers, 70 nodes per each |
| Epoch | 1172 | 941 | 1227 |
| Training loss | |||
| Validation loss | |||
| Test dataset valuation | |||
| Training time | 17 min | 23 min | 30 min |
| CPU | CPU i7-12700F, 2.10 GHz, 48 GB RAM, Window 10 Pro | ||
| Model | DP590 | DP780 |
|---|---|---|
| A | 0.970 ± 0.028 | 0.448 ± 0.253 |
| B | 0.967 ± 0.030 | 0.775 ± 0.112 |
| C | 0.979 ± 0.014 | 0.838 ± 0.056 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoang, Q.N.; Park, H.; Lai, D.G.; Nguyen, S.-N.; Pham, Q.T.; Dinh, V.D. Impact of Feature-Selection in a Data-Driven Method for Flow Curve Identification of Sheet Metal. Metals 2025, 15, 392. https://doi.org/10.3390/met15040392
Hoang QN, Park H, Lai DG, Nguyen S-N, Pham QT, Dinh VD. Impact of Feature-Selection in a Data-Driven Method for Flow Curve Identification of Sheet Metal. Metals. 2025; 15(4):392. https://doi.org/10.3390/met15040392
Chicago/Turabian StyleHoang, Quang Ninh, Hyungbum Park, Dang Giang Lai, Sy-Ngoc Nguyen, Quoc Tuan Pham, and Van Duy Dinh. 2025. "Impact of Feature-Selection in a Data-Driven Method for Flow Curve Identification of Sheet Metal" Metals 15, no. 4: 392. https://doi.org/10.3390/met15040392
APA StyleHoang, Q. N., Park, H., Lai, D. G., Nguyen, S.-N., Pham, Q. T., & Dinh, V. D. (2025). Impact of Feature-Selection in a Data-Driven Method for Flow Curve Identification of Sheet Metal. Metals, 15(4), 392. https://doi.org/10.3390/met15040392






