Springback Angle Prediction for High-Strength Aluminum Alloy Bending via Multi-Stage Regression
Abstract
1. Introduction
2. Experimental Materials and Research Methods
2.1. Test Material
2.2. Finite Element Modeling
2.3. Orthogonal Experimental Design with Different Process Parameters
2.4. Prediction Method for Inner Wall Thinning, Outer Wall Thickening, and Springback
2.5. Transfer Learning
3. Results and Discussion
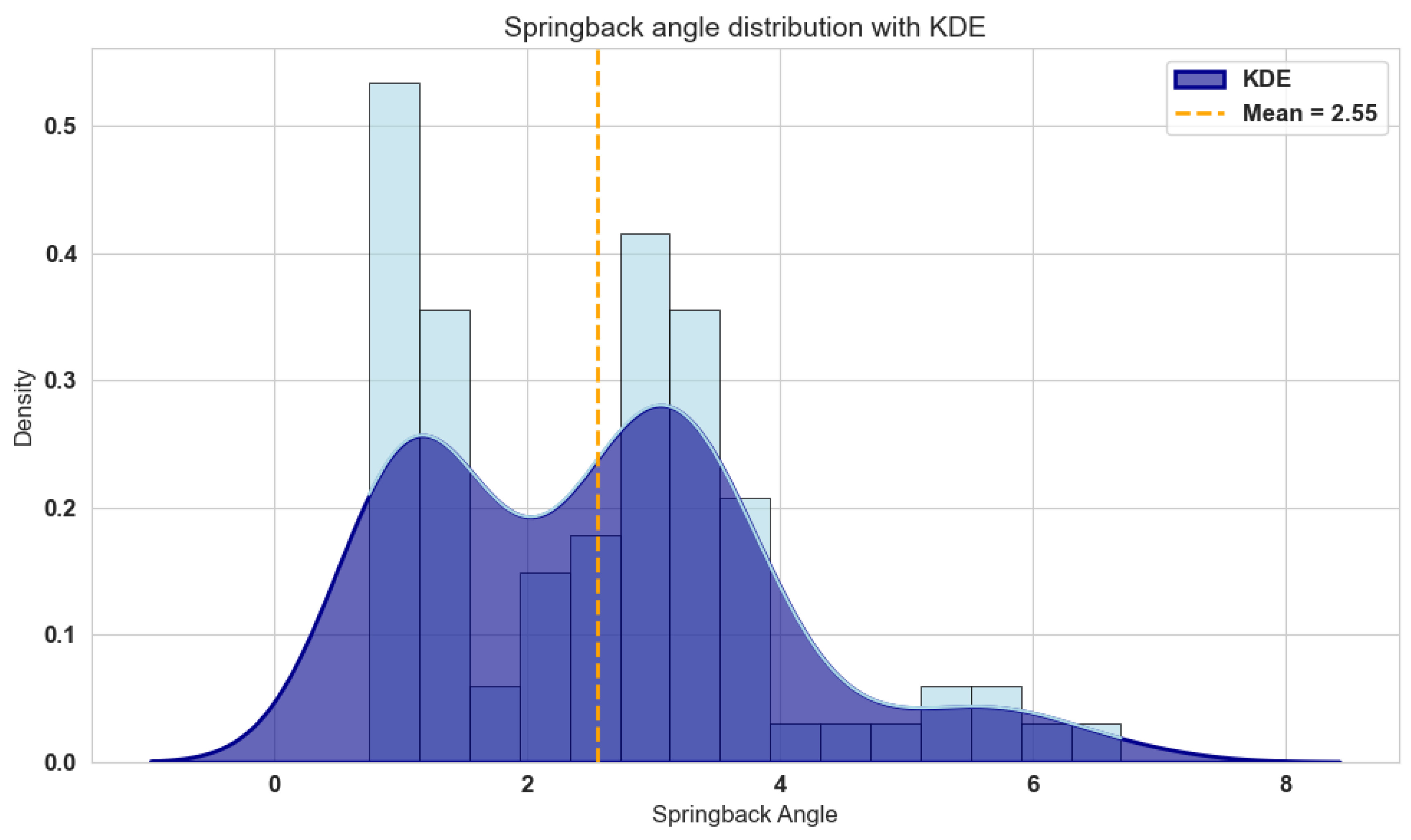
3.1. Experimental Results
3.2. Results of Finite Element Simulation Orthogonal Test Data
3.3. Machine Learning to Predict Springback Angle
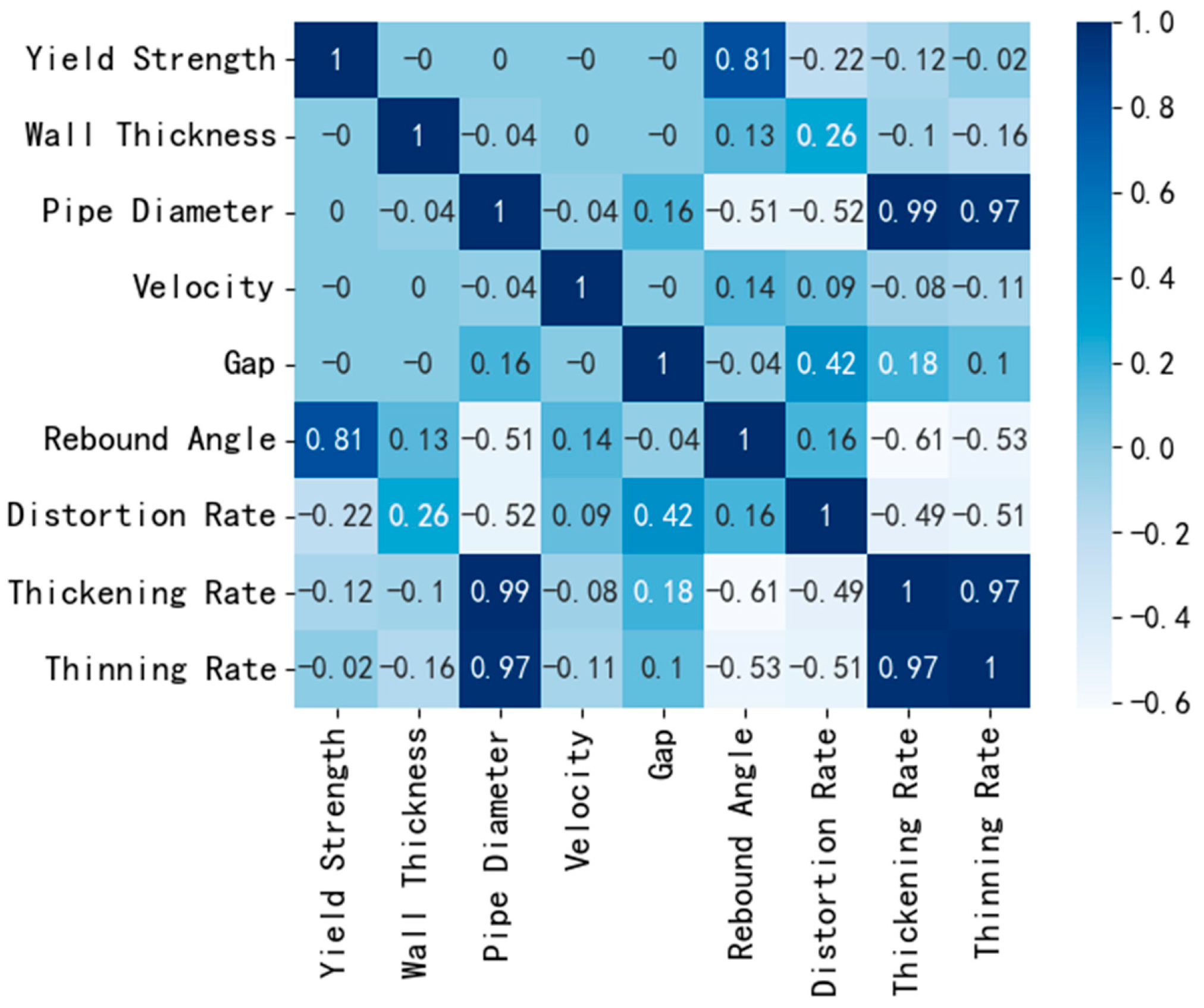
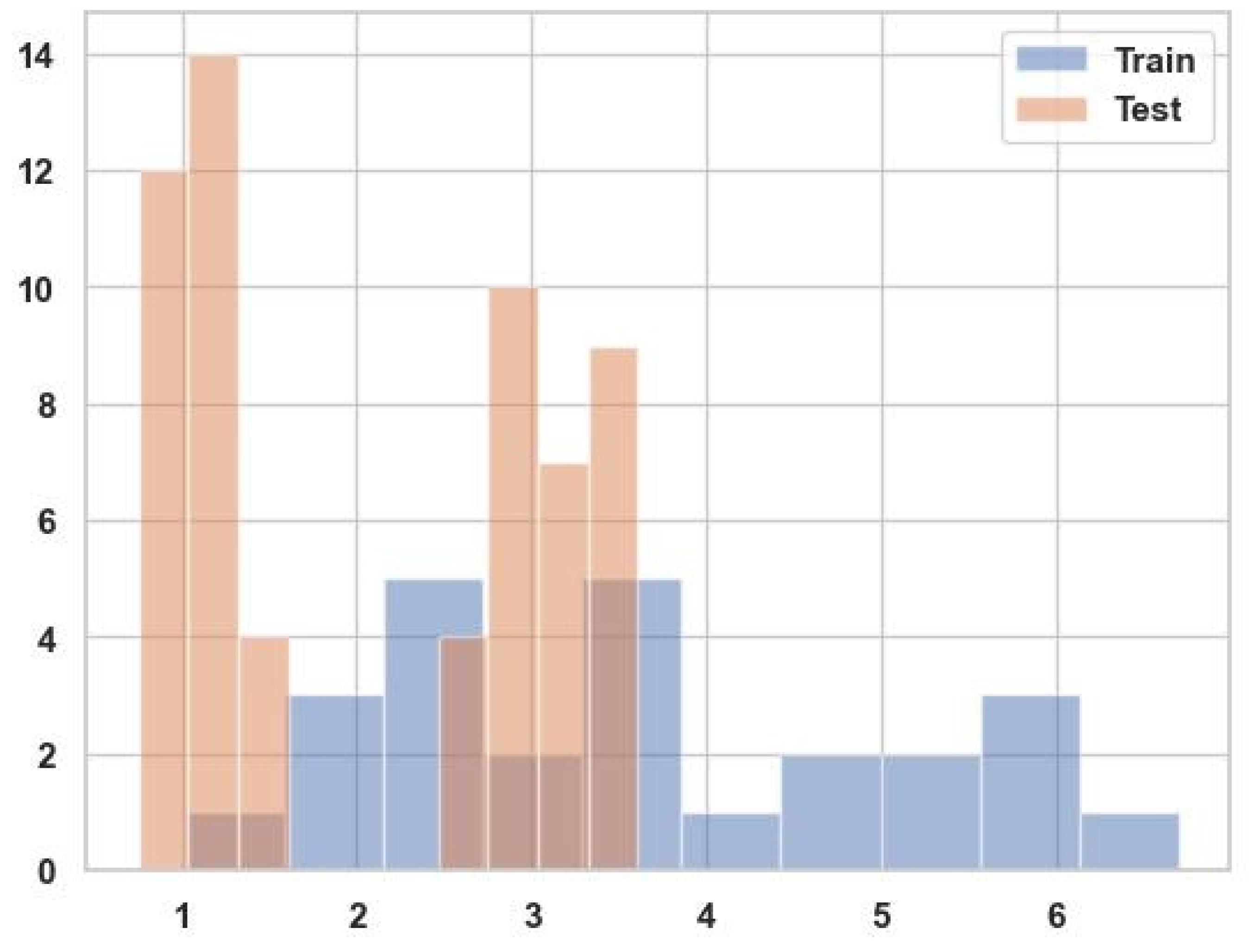
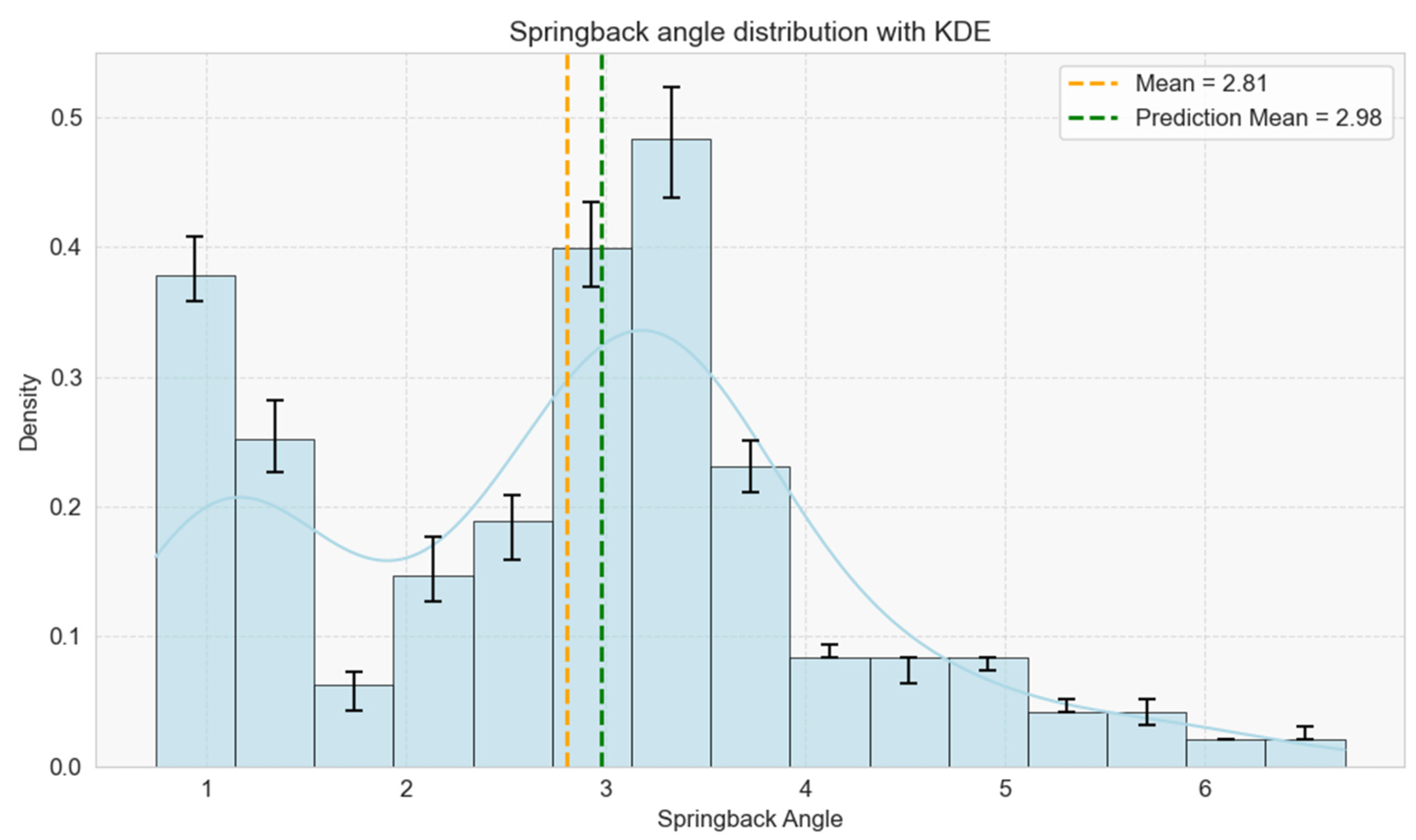
3.3.1. Dataset Description
3.3.2. Data Preprocessing
3.3.3. Evaluation Functions
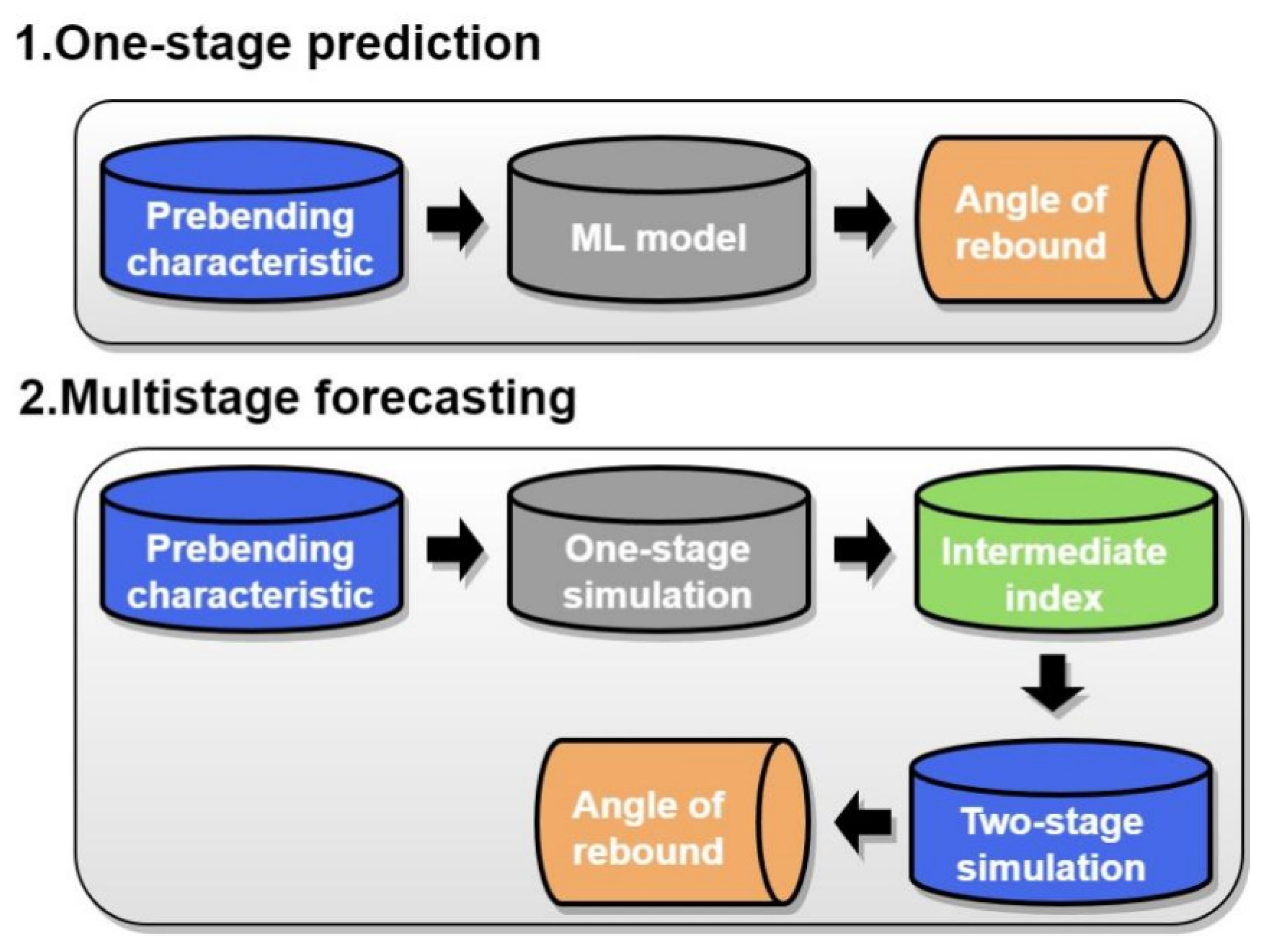
3.3.4. Multi-Stage Forecasting
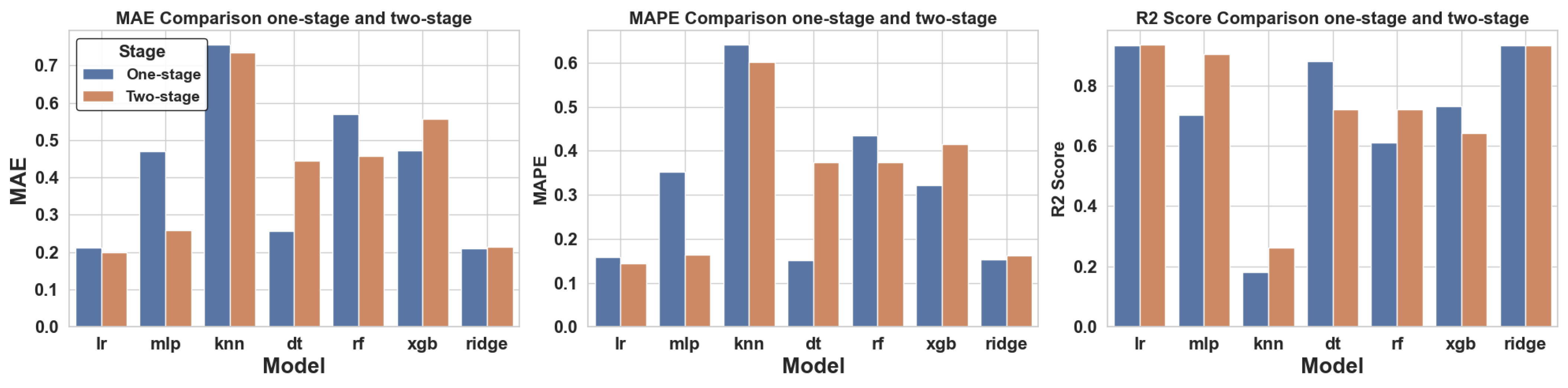
3.3.5. Multi-Stage Prediction Results
3.4. Experiments on Real Collection Data
3.4.1. Prediction of the Real Dataset Based on Transfer Learning
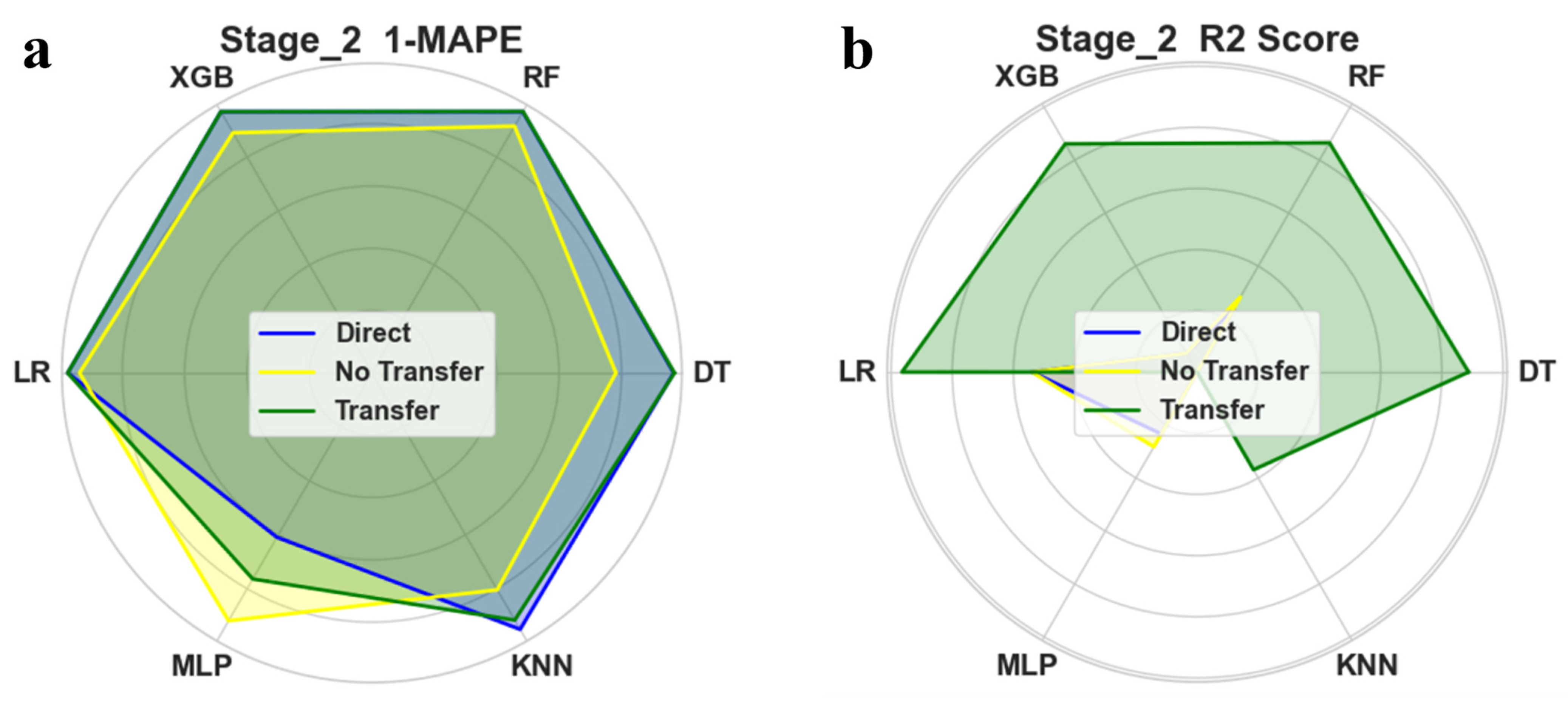
3.4.2. Transfer Learning Results
4. Conclusions
- Based on the entropy value method polar analysis and ANOVA on the comprehensive score of bending and forming defects, it is unanimously pointed out that the pipe diameter is the most significant influencing factor. The intuitive analysis of the single index springback angle shows that the material properties and pipe diameter have a significant effect, proving that orthogonal test eigenvalue screening is effective. It further verifies that the springback angle of large pipe diameter bending and forming has high research value.
- Using data enhancement techniques based on small samples greatly reduces the time required to collect simulation experimental samples. It avoids the finite element simulation for the high dependence on technical reserves, as well as in the large-scale or high complexity of the simulation of the computational inefficiency problem. Through the data enhancement technique, the distribution interval of the sample variables is greatly expanded, and the diversity of the samples is increased, which effectively improves the model’s ability to deal with small sample data and the model’s generalization ability.
- A multi-stage prediction model based on ridge regression is established and compared with common machine learning models, and the R2 correlation score on the final test set reaches 0.9669, which shows the higher prediction accuracy of the model and the universality of the prediction of pipe bending springback. The model can be integrated into a real pipe bending production system and trained using real-time production data, providing strong technical support for accurately forming high-strength aluminum alloy pipes.
- Analogous to the transfer learning pre-training approach, it takes the first pre-training on the simulated dataset. Subsequently, the pre-trained two-stage prediction model is trained on the experimental dataset for transfer learning. Compared with the two methods of direct prediction after training on the simulated dataset and direct training of prediction on the experimental dataset, the transfer learning approach achieves a more significant prediction accuracy.
- Due to the small amount of data that can be collected in the real production environment, there is a certain deviation between the data obtained by finite element simulation and the feedback of the real scene. The multi-stage prediction and transfer learning prediction methods proposed in this paper use simulation data for model pre-training and fine tuning and multi-stage prediction on real data, which can effectively reduce the impact of the deviation between simulation data and real data and significantly improve the prediction accuracy of the rebound angle in real production scenarios.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, J.; Zhan, Y.; Hon, G.B. Current Status and Development Plan of Military Helicopter Equipment in the World. Helicopter Tech. 2020, 3, 68–72. [Google Scholar]
- Canumalla, R.; Jayaraman, T.V. Decision science-driven assessment of Ti alloys for aircraft landing gear beams. Aerospace 2024, 11, 51. [Google Scholar] [CrossRef]
- Liang, T.; Yin, Y.; Yin, Q.; Nie, H.; Wei, X. Comparative research on landing and rollout characteristics of skid-equipped and wheeled aircraft. J. Aircr. 2025, 62, 34–47. [Google Scholar] [CrossRef]
- Taskesen, A.; Aksöz, S.; Özdemir, A.T. The effect of cryogenic treatment on ageing behaviour of B4C reinforced 7075 aluminium composites. Met. Mater. 2017, 55, 57–67. [Google Scholar] [CrossRef]
- Vikas, P.; Sudhakar, I.; MohanaRao, G.; Srinivas, B. Aging behaviour of hot deformed AA7075 aluminium alloy. Mater. Today Proc. 2020, 41, 1013–1017. [Google Scholar] [CrossRef]
- Aksöz, S.; Kaner, S.; Kaplan, Y. Tribological and aging behavior of hybrid Al 7075 composite reinforced with B4C, SiC, and TiB2. Sci. Sinter. 2021, 53, 311–321. [Google Scholar] [CrossRef]
- Kang, H.; Zhang, Y.; Zhang, N.; Wang, K.; Du, J.; Ma, K. Microstructure and Mechanical Properties of 7075 Al Alloy TIG-Welded Joint with 7075 Al Alloy Wire as Filler. Trans. Indian Inst. Met. 2024, 77, 2593–2599. [Google Scholar] [CrossRef]
- Zheng, K.; Dong, Y.; Zheng, D.; Lin, J.; Dean, T.A. An experimental investigation on the deformation and post-formed strength of heat-treatable aluminium alloys using different elevated temperature forming processes. J. Mech. Work. Technol. 2018, 268, 87–96. [Google Scholar] [CrossRef]
- Zheng, K.; Politis, D.J.; Wang, L.; Lin, J. A review on forming techniques for manufacturing lightweight complex—Shaped aluminium panel components. Int. J. Lightweight Mater. Manuf. 2018, 1, 55–80. [Google Scholar] [CrossRef]
- Lee, M.S.; Jin, C.K. Investigation of optimal solid solution heat treatment temperature and artificial aging time of Al7075 sheet. J. Mech. Sci. Technol. 2022, 36, 1783–1788. [Google Scholar] [CrossRef]
- Du, Z.; Han, Y.; Han, D.; Zhang, H.; Mao, X.; Zhang, Z.; Cui, X. Effect of heat treatment and electromagnetic forming on springback and related properties of 7075 aluminum alloy sheet. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 707. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, J.; He, D. Effects of contact body temperature and holding time on the microstructure and mechanical properties of 7075 aluminum alloy in contact solid solution treatment. J. Alloy. Compd. 2020, 823, 153919. [Google Scholar] [CrossRef]
- Liu, Q.; Chen, S.C.; Gu, R.Y.; Wang, W.R.; Wei, X.C. Effect of heat treatment conditions on mechanical properties and precipitates in sheet metal hot stamping of 7075 aluminum alloy. J. Mater. Eng. Perform. 2018, 27, 4423–4436. [Google Scholar]
- Kumar, M. AW-7075-T6 sheet for shock heat treatment forming process. Trans. Nonferrous Met. Soc. China 2017, 27, 2156–2162. [Google Scholar] [CrossRef]
- He, Y.; Li, H.; Zhiyong, Z.; Zhan, M.; Liu, J.; Li, G. Advances and trends on tube bending forming technologies. Chin. J. Aeronaut. 2012, 25, 1–12. [Google Scholar]
- Dakhore, M.; Kale, A. An overview of pipe bending methods and defects produced for the development of an improved pipe bending mechanism. Adv. Mater. Process. Technol. 2023, 10, 3393–3410. [Google Scholar]
- Tronvoll, S.A.; Ma, J.; Welo, T. Deformation behavior in tube bending: A comparative study of compression bending and rotary draw bending. Int. J. Adv. Manuf. Technol. 2022, 124, 801–816. [Google Scholar]
- Wenpei, Z.; Zhili, H.; Huanhuan, L.; Lin, H. Experimental and Numerical Investigation on Springback of Automotive Aluminum Alloy Sheet. Rare Met. Mater. Eng. 2019, 48, 2130–2137. [Google Scholar]
- Wang, Z.; Lin, Y.; Qiu, L.; Zhang, S.; Fang, D.; He, C.; Wang, L. Spatial variable curvature metallic tube bending springback numerical approximation prediction and compensation method considering cross-section distortion defect. Int. J. Adv. Manuf. Technol. 2021, 118, 1811–1827. [Google Scholar]
- Sun, C.; Wang, Z.; Zhang, S.; Liu, X.; Wang, L.; Tan, J. Toward axial accuracy prediction and optimization of metal tube bending forming: A novel gru-integrated pb-nsgaiii optimization framework. Eng. Appl. Artif. Intell. 2022, 114, 105193. [Google Scholar]
- Lee, H.-S.; Park, S.-G.; Hong, M.-P.; Kim, Y.-S. Process design of multi-stage cold forging with small size for ESC solenoid valve parts. J. Mech. Sci. Technol. 2022, 36, 359–370. [Google Scholar] [CrossRef]
- Ghobadnam, M.; Mosaddegh, P.; Rezaei Rejani, M.; Amirabadi, H.; Ghaei, A. Numerical and experimental analysis of hips sheets in thermoforming process. Int. J. Adv. Manuf. Technol. 2015, 76, 1079–1089. [Google Scholar] [CrossRef]
- Bock, F.E.; Aydin, R.C.; Cyron, C.J.; Huber, N.; Kalidindi, S.R.; Klusemann, B. A review of the application of machine learning and data mining approaches in continuum materials mechanics. Front. Mater. 2019, 6, 110. [Google Scholar] [CrossRef]
- Guo, K.; Yang, Z.; Yu, C.-H.; Buehler, M.J. Artificial intelligence and machine learning in design of mechanical materials. Mater. Horizons 2021, 8, 1153–1172. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Bai, R.; Lei, Z.; Jiang, H.; Liu, D.; Zou, J.; Yan, C. CPINet: Parameter identification of path-dependent constitutive model with automatic denoising based on CNN-LSTM. Eur. J. Mech.-A/Solids 2021, 90, 104327. [Google Scholar] [CrossRef]
- Huang, H.; Li, J.; Yang, H.; Wang, B.; Gao, R.; Luo, M.; Li, W.; Zhang, G.; Liu, L. Research on prediction methods of formation pore pressure based on machine learning. Energy Sci. Eng. 2022, 10, 1886–1901. [Google Scholar] [CrossRef]
- Wei, X.; van der Zwaag, S.; Jia, Z.; Wang, C.; Xu, W. On the use of transfer modeling to design new steels with excellent rotating bending fatigue resistance even in the case of very small calibration datasets. Acta Mater. 2022, 235, 118103. [Google Scholar] [CrossRef]
- Agrawal, A.; Choudhary, A. An online tool for predicting fatigue strength of steel alloys based on ensemble data mining. Int. J. Fatigue 2018, 113, 389–400. [Google Scholar] [CrossRef]
- Yang, P.; Wu, S.; Wu, H.; Lu, D.; Zou, W.; Chu, L.; Shao, Y.; Wu, S. Prediction of bending strength of Si3N4 using machine learning. Ceram. Int. 2021, 47, 23919–23926. [Google Scholar] [CrossRef]
- Shen, C.; Wang, C.; Wei, X.; Li, Y.; van der Zwaag, S.; Xu, W. Physical metallurgy-guided machine learning and artificial intelligent design of ultrahigh-strength stainless steel. Acta Mater. 2019, 179, 201–214. [Google Scholar] [CrossRef]
- Ye, Y.; Scharff, R.B.N.; Long, S.; Han, C.; Du, D. Modelling of soft fiber-reinforced bending actuators through transfer learning from a machine learning algorithm trained from FEM data. Sens. Actuators A Phys. 2024, 368, 115095. [Google Scholar]
- Yang, C.; Meng, K.; Yang, L.; Guo, W.; Xu, P.; Zhou, S. Transfer learning-based crashworthiness prediction for the composite structure of a subway vehicle. Int. J. Mech. Sci. 2023, 248, 108244. [Google Scholar]
- Nagarajan, L.; Mahalingam, S.K.; Vasudevan, B. Abrasive waterjet drilling process enhancement using machine learning and evolutionary algorithms. Mater. Manuf. Process. 2024, 39, 2166–2182. [Google Scholar]
- Zhao, W.P.; Li, J.; Zhao, J.; Zhao, D.; Lu, J.; Wang, X. XGB model: Research on evaporation duct height prediction based on XGBoost algorithm. Radioengineering 2020, 29, 81–93. [Google Scholar] [CrossRef]
- Bastl, P.; Chakraborti, N.; Valášek, M. Evolutionary algorithms in robot calibration. Mater. Manuf. Process. 2023, 38, 2051–2070. [Google Scholar]
- Paszkowicz, W. Increasing importance of genetic algorithms in science and technology: Linear trends over the period from year 1989 to 2022. Mater. Manuf. Process. 2023, 38, 2107–2126. [Google Scholar] [CrossRef]
- Guha, R.; Suresh, A.; DeFrain, J.; Deb, K. Virtual metrology in long batch processes using machine learning. Mater. Manuf. Process. 2023, 38, 1997–2008. [Google Scholar]
- Wolday, A.K.; Ramteke, M. Optimisation of methanol distillation using GA and neural network hybrid. Mater. Manuf. Process. 2023, 38, 1911–1921. [Google Scholar] [CrossRef]
- Song, F.; Yang, H.; Li, H.; Zhan, M.; Li, G. Springback prediction of thick-walled high-strength titanium tubebending. Chin. J. Aeronaut. 2013, 26, 1336–1345. [Google Scholar]
- Wang, J.; Liu, J.; Zhang, G.; Zhou, J.; Cen, K. Orthogonal design process optimization and single factor analysis for bimodal acoustic agglomeration. Powder Technol. 2011, 210, 315–322. [Google Scholar] [CrossRef]
- Chen, Y.; Sun, Z.-Q.; Zhang, X.-X.; Sun, Q.-Z.; Huang, S.; Han, X.-H. Effect of heat treatment process parameters on microstructure and properties of 7075 aluminum alloy in t6 state. J. Plast. Eng. 2021, 28, 145–149. [Google Scholar]
- Feng, Z.; Li, H.; Liu, Y.; Xie, J.; Mou, H.; Xi, X.; Shu, W. Comparison of Constitutive and Failure Models of 7075-T7351 Alloy at Intermediate and Low Strain Rates. Materlals Rep. 2020, 34, 12088–12093. [Google Scholar]
- Weiss, K.; Khoshgoftaar, T.M.; Wang, D.D. A survey of transfer learning. J. Big Data 2016, 3, 9. [Google Scholar]
- Cruz, D.J.; Barbosa, M.R.; Santos, A.D.; Miranda, S.S.; Amaral, R.L. Application of machine learning to bending processes and material identification. Metals 2021, 11, 1418. [Google Scholar] [CrossRef]
- Wang, A.; Xue, H.; Saud, S.; Yang, Y.; Wei, Y. Improvement of springback prediction accuracy for Z-section profiles in four-roll bending process considering neutral layer shift. J. Manuf. Process. 2019, 48, 218–227. [Google Scholar]
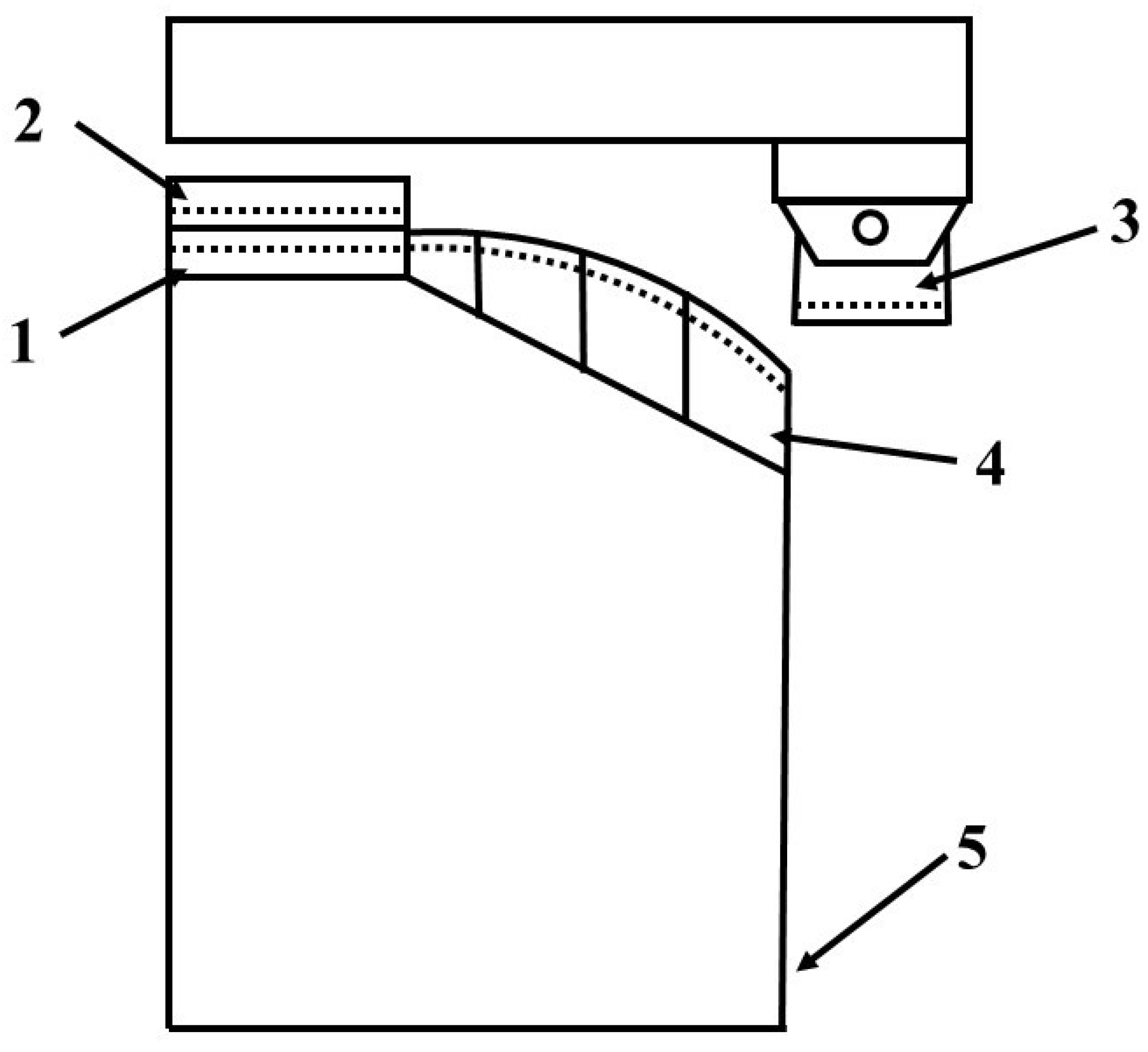
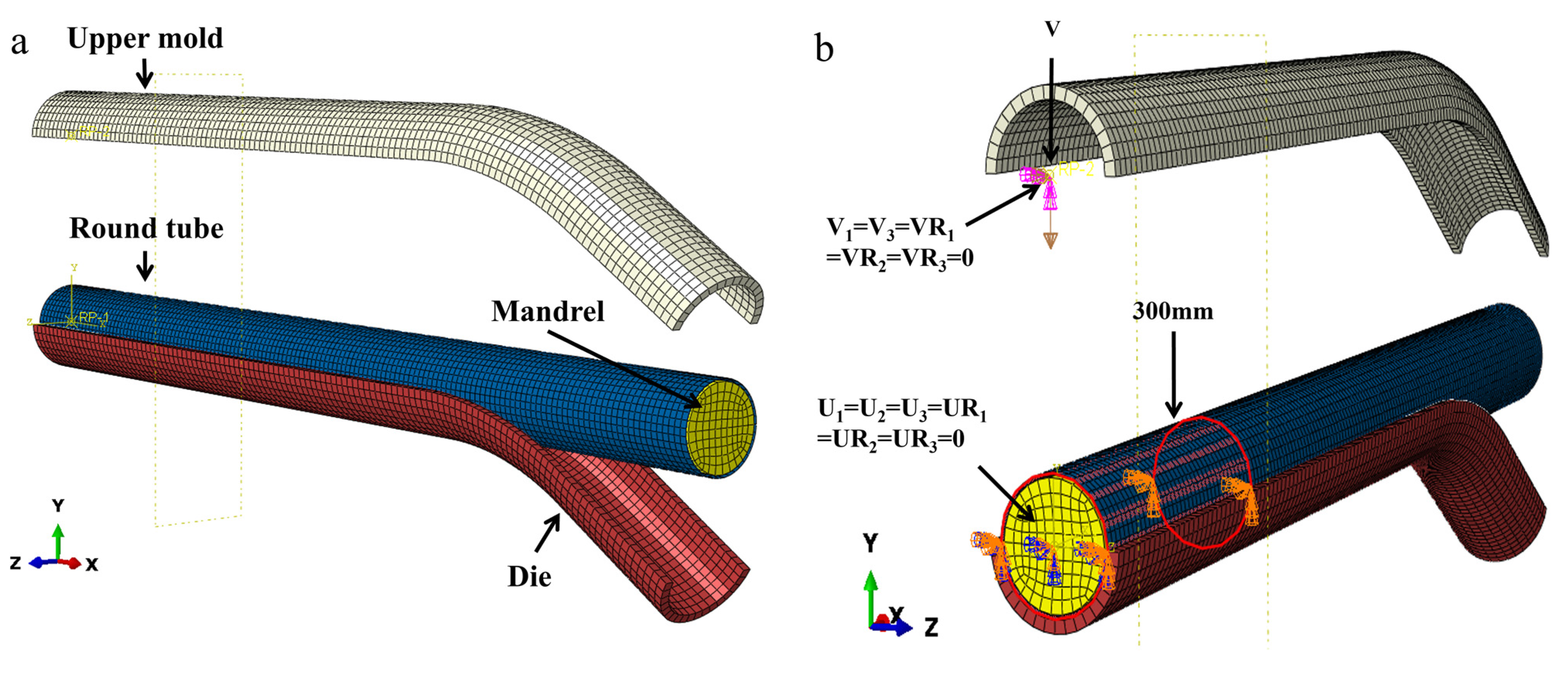
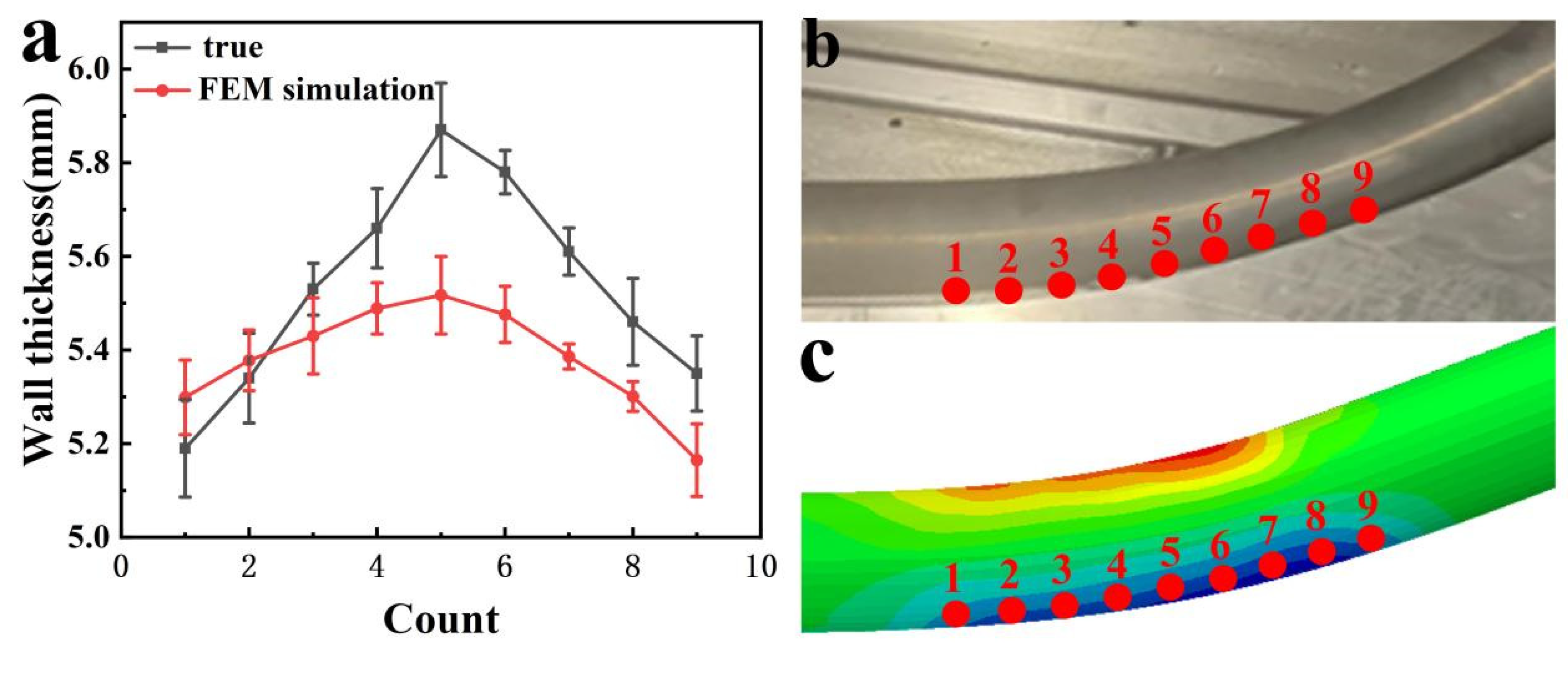


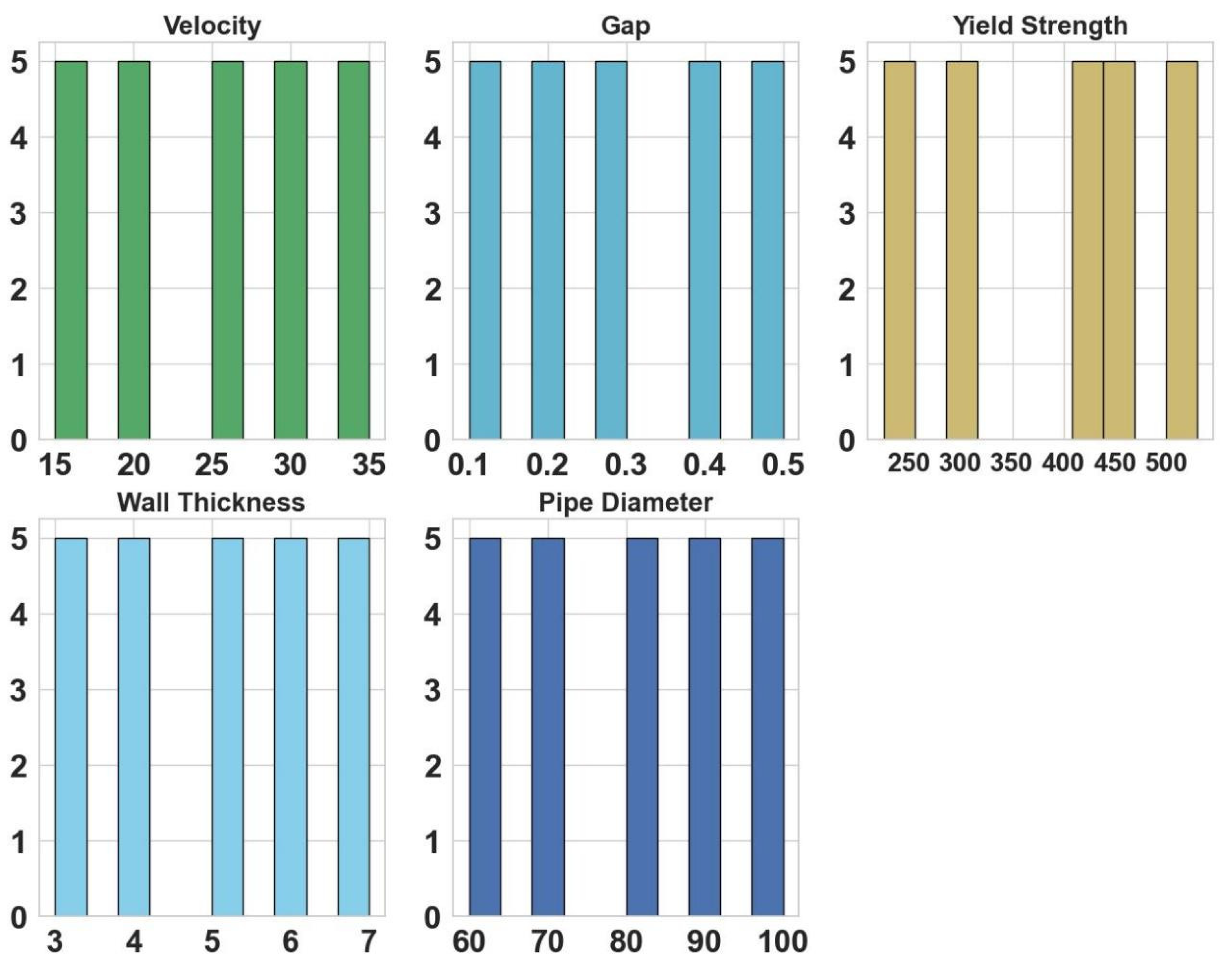




| Zn | Mg | Cu | Ti | Mn | Fe | Cr | Si | Al |
|---|---|---|---|---|---|---|---|---|
| 5.6 | 2.55 | 1.4 | 0.02 | 0.06 | 0.2 | 0.2 | 0.08 | Bal |
| Young’s Modulus (Mpa) | Densities (Kg/m3) | Yield Stress | Yield Strain | Poisson’s Ratio |
|---|---|---|---|---|
| 72,000 | 2180 | --- | 0.2 | 0.33 |
| Horizontal Factors | |||||
|---|---|---|---|---|---|
| A (Yield Strength) | B (Wall Thickness) | C (Pipe Diameter) | D (Speed) | E (Mandrel–Pipe Clearance) | |
| 1 | 225 | 3 | 60 | 15 | 0.1 |
| 2 | 293 | 4 | 70 | 20 | 0.2 |
| 3 | 426 | 5 | 80 | 25 | 0.3 |
| 4 | 440 | 6 | 90 | 30 | 0.4 |
| 5 | 530 | 7 | 100 | 35 | 0.5 |
| A | B | C | D | E | |
|---|---|---|---|---|---|
| K1 | 10.09 | 16.44 | 24.46 | 15.94 | 18.99 |
| K2 | 12.14 | 18.16 | 20.49 | 18.36 | 19.68 |
| K3 | 20.54 | 17.65 | 18.12 | 18.5 | 17.17 |
| K4 | 21.86 | 20.15 | 14.79 | 19.41 | 15.84 |
| K5 | 26.83 | 19.06 | 13.6 | 19.25 | 19.78 |
| K1 | 2.01 | 3.28 | 4.89 | 3.18 | 3.79 |
| K2 | 2.42 | 3.632 | 4.09 | 3.672 | 3.93 |
| K3 | 4.1 | 3.53 | 3.62 | 3.7 | 3.43 |
| K4 | 4.372 | 4.03 | 2.95 | 3.88 | 3.16 |
| K5 | 5.36 | 3.812 | 2.72 | 3.85 | 3.95 |
| R1 | 3.34 | 0.742 | 2.172 | 0.69 | 0.78 |
| Method | First Stage | Second Stage | ||||
|---|---|---|---|---|---|---|
| MAE | MAPE | R2 | MAE | MAPE | R2 | |
| Linear regression | 0.2876 | 0.4623 | 0.1876 | 0.1992 | 0.1444 | 0.9343 |
| Ridge regression | 0.2838 | 0.4261 | 0.1348 | 0.2141 | 0.1625 | 0.9316 |
| Multilayer perceptrons | 0.4112 | 0.3965 | −0.1598 | 0.2579 | 0.1644 | 0.9046 |
| K-nearest neighbor | 0.7438 | 0.7423 | −1.6376 | 0.7353 | 0.6016 | 0.2617 |
| Decision tree | 0.3134 | 0.318 | 0.2134 | 0.2378 | 0.14 | 0.8537 |
| Random forest | 0.3126 | 0.5211 | 0.3151 | 0.4409 | 0.3515 | 0.7478 |
| XGBoost | 0.4317 | 0.6768 | −0.338 | 0.5576 | 0.4147 | 0.6422 |
| Method | Direct | Learning Without Transfer | Transfer Learning | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | MAPE | R2 | MAE | MAPE | R2 | MAE | MAPE | R2 | |
| Decision Tree | 0.7993 | 0.1918 | −5.7497 | 0.1252 | 0.032 | 0.7769 | 0.1168 | 0.0299 | 0.797 |
| Random Forest | 0.3842 | 0.0928 | −0.5039 | 0.1287 | 0.0333 | 0.7619 | 0.1234 | 0.0318 | 0.7644 |
| XGB | 0.467 | 0.1099 | −1.7342 | 0.1256 | 0.0318 | 0.7672 | 0.1256 | 0.0318 | 0.7672 |
| Linear Regression | 0.2555 | 0.0628 | 0.2994 | 0.0948 | 0.0249 | 0.8791 | 0.0941 | 0.0247 | 0.8804 |
| MLP | 0.3375 | 0.0848 | −0.5363 | 1.7704 | 0.4867 | −112.11 | 1.0447 | 0.2716 | −11.72 |
| K-Nearest Neighbors | 0.8229 | 0.1959 | −6.8323 | 0.1925 | 0.0496 | 0.5573 | 0.3227 | 0.0837 | −0.0808 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, E.; Xue, D.; Li, Y. Springback Angle Prediction for High-Strength Aluminum Alloy Bending via Multi-Stage Regression. Metals 2025, 15, 358. https://doi.org/10.3390/met15040358
Gao E, Xue D, Li Y. Springback Angle Prediction for High-Strength Aluminum Alloy Bending via Multi-Stage Regression. Metals. 2025; 15(4):358. https://doi.org/10.3390/met15040358
Chicago/Turabian StyleGao, Enzhi, Di Xue, and Yiming Li. 2025. "Springback Angle Prediction for High-Strength Aluminum Alloy Bending via Multi-Stage Regression" Metals 15, no. 4: 358. https://doi.org/10.3390/met15040358
APA StyleGao, E., Xue, D., & Li, Y. (2025). Springback Angle Prediction for High-Strength Aluminum Alloy Bending via Multi-Stage Regression. Metals, 15(4), 358. https://doi.org/10.3390/met15040358





