Auxetic Meta-Biomaterials: Computer Simulation and Experimental Results
Abstract
1. Introduction
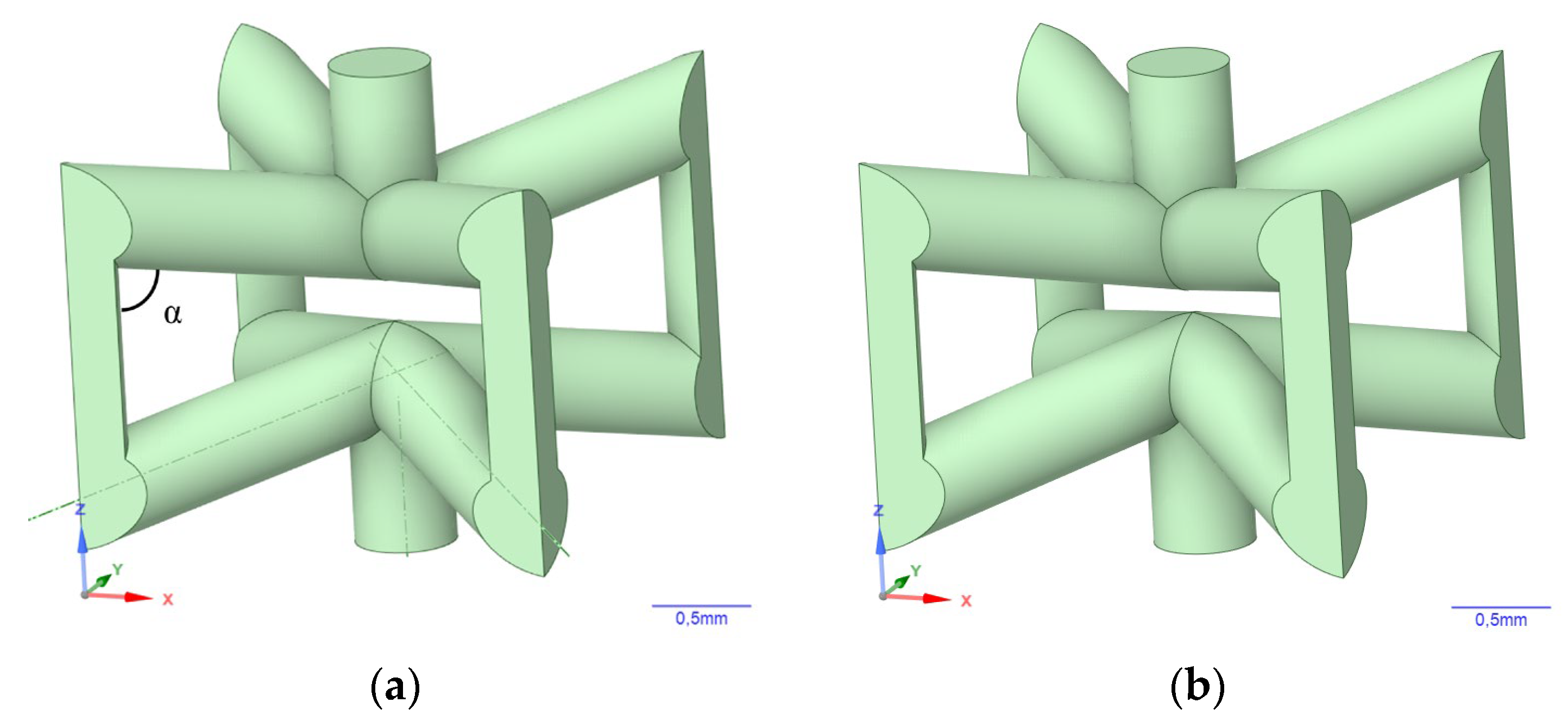
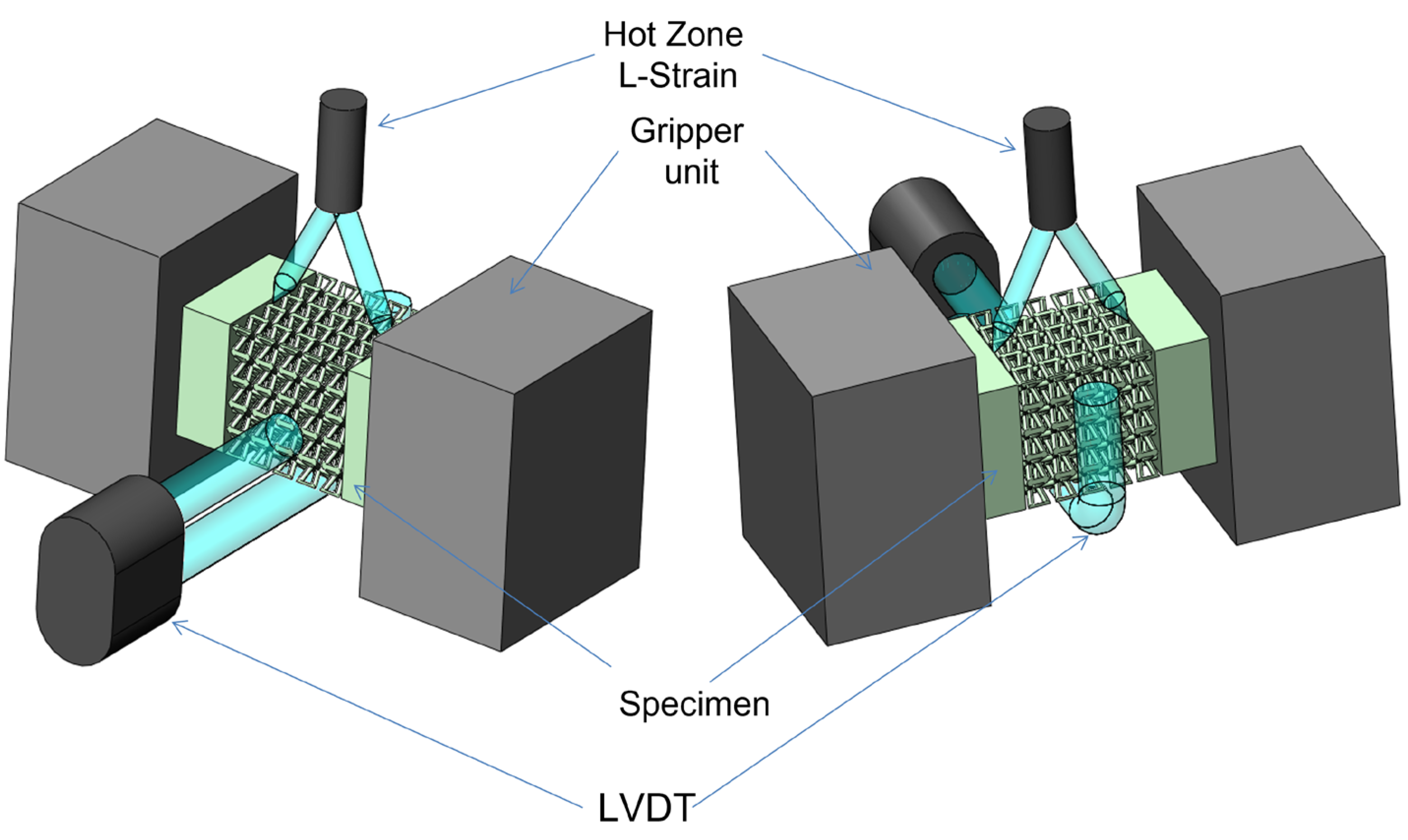
2. Materials and Methods
3. Results
3.1. Alloy Initial Properties
3.2. Simulation Results
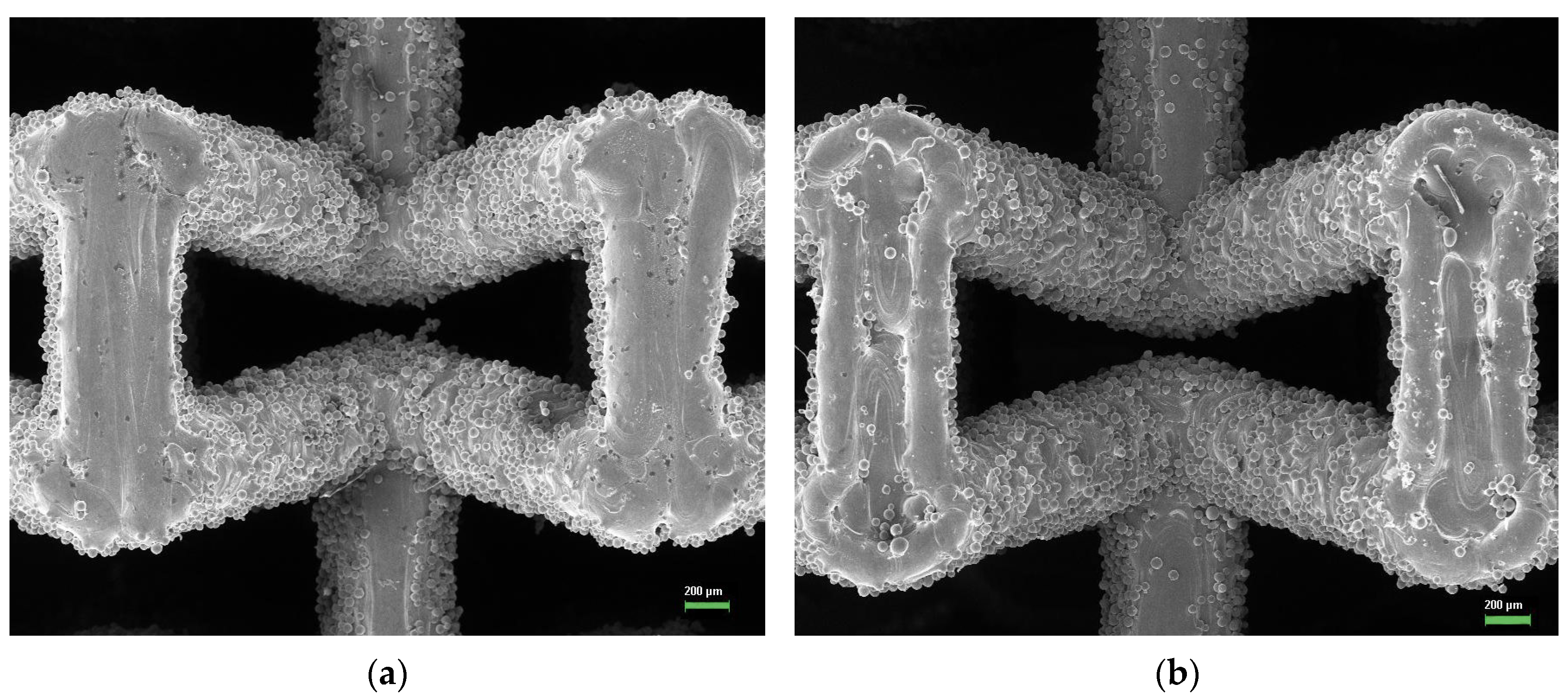
3.3. Fabricated Meta-Biomaterial Samples
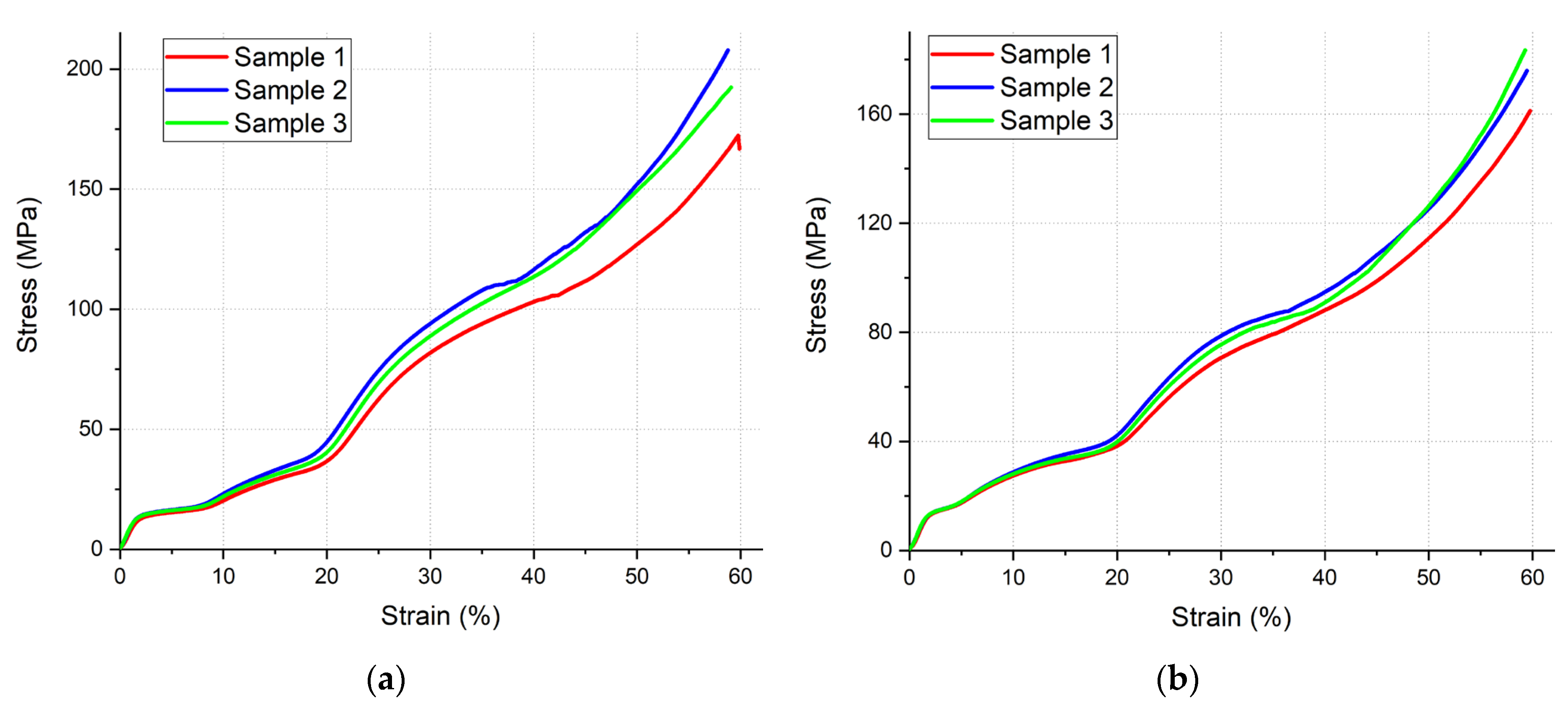
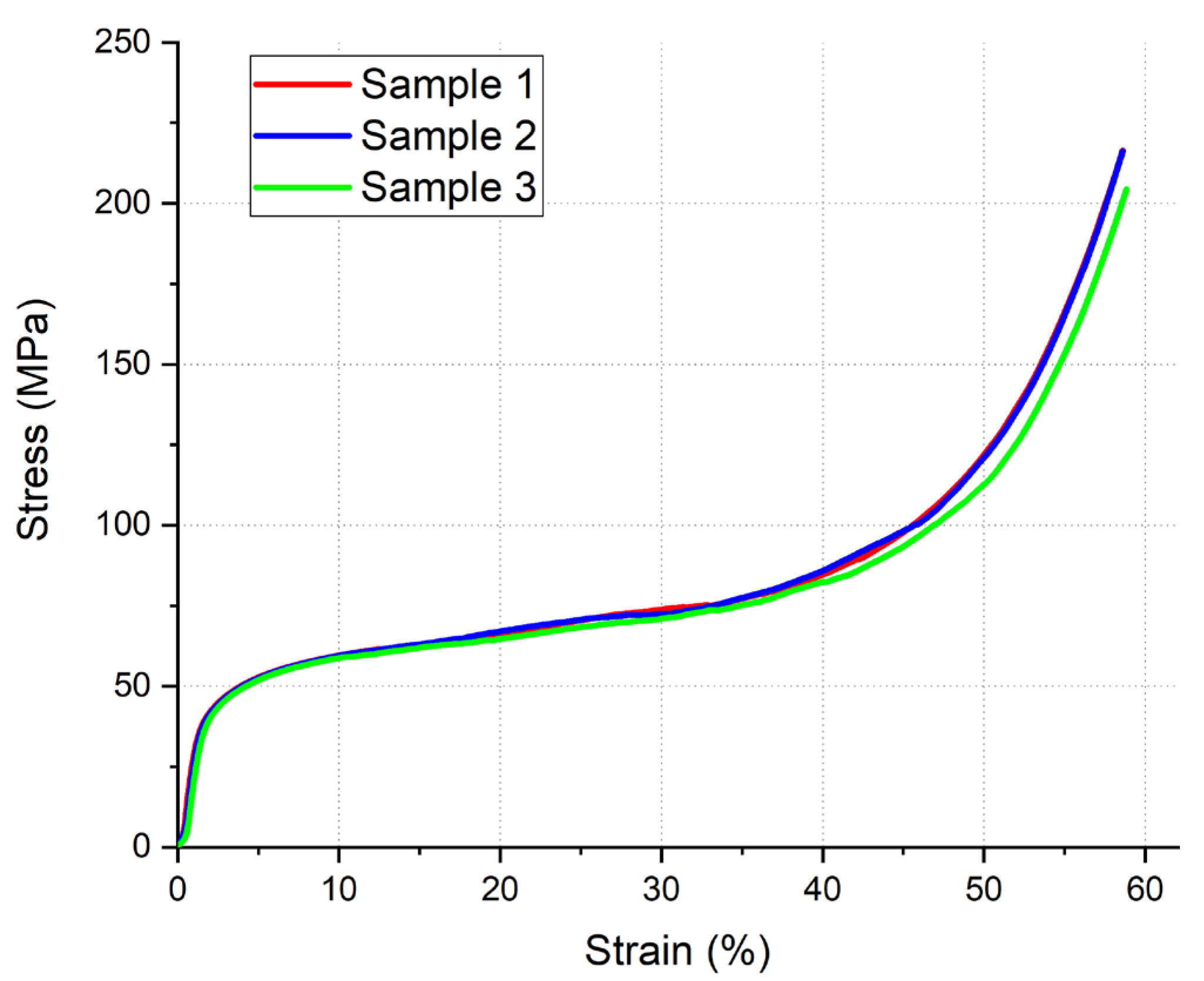
3.4. Compression Test
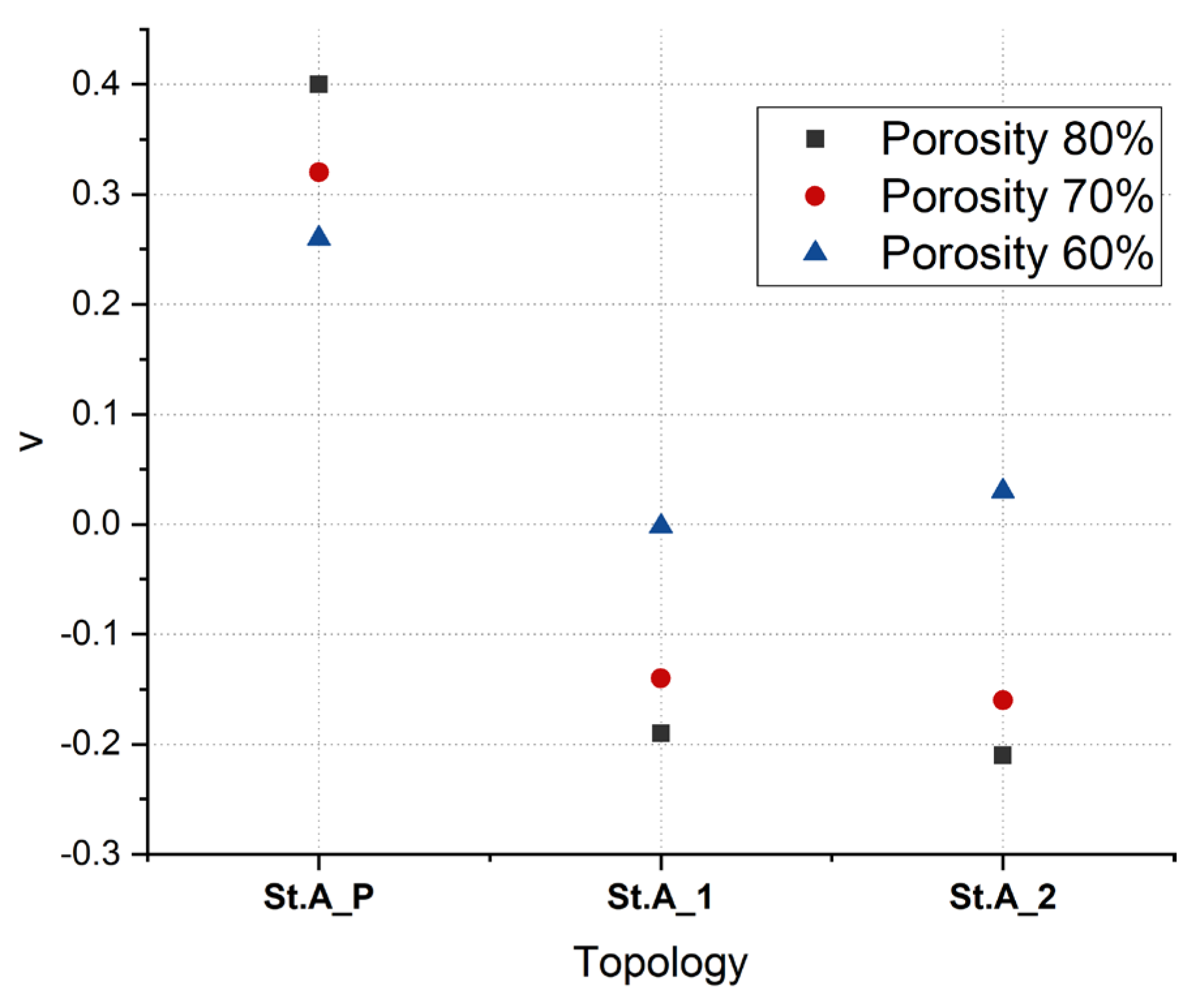
3.5. Poisson’s Ratio
4. Discussion
5. Conclusions
- Based on the topologies St.A_1 and St.A_2, auxetic meta-biomaterials with a negative Poisson’s ratio of −0.09 and −0.003, respectively, were obtained. The elastic modulus of the auxetic meta-biomaterials is within the range corresponding to the elastic modulus of a human trabecular bone, which generally indicates the possibility of using meta-biomaterials with these geometrical parameters as implants.
- The St.A_1 topology can be considered as the most promising for further research and practical application, as it has the highest negative value of Poisson’s ratio.
- No auxetic meta-biomaterials have been fabricated on the basis of St.A_P topology. At the same time, St.A_P topology is promising for application as well. Its characteristics suggest that this topology can be used as a meta-biomaterial with a different purpose. For example, this topology can be considered in further studies as a topology with a positive Poisson’s ratio for implants with a complex structure.
- Verification of the simulation results shows that the used technique is not accurate enough, as it does not take into account all specific features of the meta-biomaterials fabrication by SLM technique. Either other simulation techniques or additional processing of the fabricated meta-biomaterial samples, for example, by sandblasting, may be necessary to remove the stuck particles.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mirzaali, M.J.; Zadpoor, A.A. Orthopedic Meta-Implants. APL Bioeng. 2024, 8, 57–59. [Google Scholar] [CrossRef]
- Bobbert, F.S.L.; Janbaz, S.; Zadpoor, A.A. Towards Deployable Meta-Implants. J. Mater. Chem. B 2018, 6, 3449–3455. [Google Scholar] [CrossRef] [PubMed]
- Yarali, E.; Zadpoor, A.A.; Staufer, U.; Accardo, A.; Mirzaali, M.J. Auxeticity as a Mechanobiological Tool to Create Meta-Biomaterials. ACS Appl. Bio Mater. 2023, 6, 2562–2575. [Google Scholar] [CrossRef] [PubMed]
- Kolken, H.M.A.; Garcia, A.F.; Du Plessis, A.; Rans, C.; Mirzaali, M.J.; Zadpoor, A.A. Fatigue Performance of Auxetic Meta-Biomaterials. Acta Biomater. 2021, 126, 511–523. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Wang, L.; Fan, Y. Metallic Meta-Biomaterials: A Critical Review of Fatigue Behaviors. J. Sci. Adv. Mater. Devices 2023, 8, 100585. [Google Scholar] [CrossRef]
- Zadpoor, A.A.; Mirzaali, M.J.; Valdevit, L.; Hopkins, J.B. Design, Material, Function, and Fabrication of Metamaterials. APL Mater. 2023, 11, 020401. [Google Scholar] [CrossRef]
- Chen, M.; Fang, S.; Wang, G.; Xuan, Y.; Gao, D.; Zhang, M. Compressive and Flexural Behaviour of Engineered Cementitious Composites Based Auxetic Structures: An Experimental and Numerical Study. J. Build. Eng. 2024, 86, 108999. [Google Scholar] [CrossRef]
- Li, X.; Peng, W.; Wu, W.; Xiong, J.; Lu, Y. Auxetic Mechanical Metamaterials: From Soft to Stiff. Int. J. Extrem. Manuf. 2023, 5, 042003. [Google Scholar] [CrossRef]
- Yarali, E.; Klimopoulou, M.; David, K.; Boukany, P.E.; Staufer, U.; Fratila-Apachitei, L.E.; Zadpoor, A.A.; Accardo, A.; Mirzaali, M.J. Bone Cell Response to Additively Manufactured 3D Micro-Architectures with Controlled Poisson’s Ratio: Auxetic vs. Non-Auxetic Meta-Biomaterials. Acta Biomater. 2024, 177, 228–242. [Google Scholar] [CrossRef]
- Putra, N.E.; Zhou, J.; Zadpoor, A.A. Sustainable Sources of Raw Materials for Additive Manufacturing of Bone-Substituting Biomaterials. Adv. Healthc. Mater. 2024, 13, e2301837. [Google Scholar] [CrossRef]
- Zadpoor, A.A. Mechanical Performance of Additively Manufactured Meta-Biomaterials. Acta Biomater. 2019, 85, 41–59. [Google Scholar] [CrossRef] [PubMed]
- Kolken, H.M.A.; Janbaz, S.; Leeflang, S.M.A.; Lietaert, K.; Weinans, H.H.; Zadpoor, A.A. Rationally Designed Meta-Implants: A Combination of Auxetic and Conventional Meta-Biomaterials. Mater. Horiz. 2018, 5, 28–35. [Google Scholar] [CrossRef]
- Kolken, H.M.A.; Lietaert, K.; van der Sloten, T.; Pouran, B.; Meynen, A.; Van Loock, G.; Weinans, H.; Scheys, L.; Zadpoor, A.A. Mechanical Performance of Auxetic Meta-Biomaterials. J. Mech. Behav. Biomed. Mater. 2020, 104, 103658. [Google Scholar] [CrossRef] [PubMed]
- Safavi, M.S.; Bordbar-Khiabani, A.; Khalil-allafi, J.; Mozafari, M.; Visai, L. Additive Manufacturing: An Opportunity for The Fabrication of Near-Net-Shape NiTi Implants. J. Manuf. Mater. Process. 2022, 6, 65. [Google Scholar] [CrossRef]
- Nugroho, W.T.; Dong, Y.; Pramanik, A.; Chithirai Pon Selvan, M.; Zhang, Z.; Ramakrishna, S. Additive Manufacturing of Re-Entrant Structures: Well-Tailored Structures, Unique Properties, Modelling Approaches and Real Applications. Addit. Manuf. 2023, 78, 103829. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, C.; Xu, C.; Ren, J.; Zhong, J. Auxetic Meta-Materials and Their Engineering Applications: A Review. Eng. Res. Express 2023, 5, 042003. [Google Scholar] [CrossRef]
- Farber, E.; Orlov, A.; Borisov, E.; Repnin, A.; Kuzin, S.; Golubkov, N.; Popovich, A. TiNi Alloy Lattice Structures with Negative Poisson’s Ratio: Computer Simulation and Experimental Results. Metals 2022, 12, 1476. [Google Scholar] [CrossRef]
- Ghavidelnia, N.; Bodaghi, M.; Hedayati, R. Femur Auxetic Meta-Implants with Tuned Micromotion Distribution. Materials 2021, 14, 114. [Google Scholar] [CrossRef]
- Kumar, R.; Rezapourian, M.; Rahmani, R.; Maurya, H.S.; Kamboj, N.; Hussainova, I. Bioinspired and Multifunctional Tribological Materials for Sliding, Erosive, Machining, and Energy-Absorbing Conditions: A Review. Biomimetics 2024, 9, 209. [Google Scholar] [CrossRef]
- Wei, J.; Sun, B.H. Study on the Mechanical Properties of Cylindrical Mechanical Metamaterials with Biomimetic Honeycomb Units of the Diabolical Ironclad Beetle. Extrem. Mech. Lett. 2024, 67, 102127. [Google Scholar] [CrossRef]
- Shirzad, M.; Bodaghi, M.; Oh, D.; Yi, M.; Nam, S.Y. Design and Optimization of Bioinspired Auxetic Structure for Biomedical Applications. Eur. J. Mech. A/Solids 2024, 103, 105139. [Google Scholar] [CrossRef]
- Wang, P.; Yang, F.; Zheng, B.; Li, P.; Wang, R.; Li, Y.; Fan, H.; Li, X. Breaking the Tradeoffs between Different Mechanical Properties in Bioinspired Hierarchical Lattice Metamaterials. Adv. Funct. Mater. 2023, 33, 2305978. [Google Scholar] [CrossRef]
- Xu, C.; Li, Q.; Lu, Z.; Liu, Q.; Ren, L. Negative Poisson’s Ratio Metamaterial Structure with Bionic Structure. China CN116292712, 17 March 2023. [Google Scholar]
- Zhang, L.C.; Chen, L.Y. A Review on Biomedical Titanium Alloys: Recent Progress and Prospect. Adv. Eng. Mater. 2019, 21, 1801215. [Google Scholar] [CrossRef]
- Bordbar-Khiabani, A.; Gasik, M. Electrochemical Behavior of Additively Manufactured Patterned Titanium Alloys under Simulated Normal, Inflammatory, and Severe Inflammatory Conditions. J. Mater. Res. Technol. 2023, 26, 356–370. [Google Scholar] [CrossRef]
- Repnin, A.; Borisov, E.; Emelianov, A.; Popovich, A. Fracture Toughness of Ti6Al4V/Cp-Ti Multi-Material Produced via Selective Laser Melting. Metals 2023, 13, 1738. [Google Scholar] [CrossRef]
- Bartolomeu, F.; Costa, M.M.; Alves, N.; Miranda, G.; Silva, F.S. Additive Manufacturing of NiTi-Ti6Al4V Multi-Material Cellular Structures Targeting Orthopedic Implants. Opt. Lasers Eng. 2020, 134, 106208. [Google Scholar] [CrossRef]
- Farber, E.; Orlov, A.V.; Popovich, A.A. TiNi Alloy Lattice Structures with Negative Poisson Ratio: Computer Simulation. Key Eng. Mater. 2023, 944, 61–67. [Google Scholar] [CrossRef]
- Zhang, Y.; Attarilar, S.; Wang, L.; Lu, W.; Yang, J.; Fu, Y. A Review on Design and Mechanical Properties of Additively Manufactured NiTi Implants for Orthopedic Applications. Int. J. Bioprint. 2021, 7, 340. [Google Scholar] [CrossRef]
- Yuan, L.; Ding, S.; Wen, C. Additive Manufacturing Technology for Porous Metal Implant Applications and Triple Minimal Surface Structures: A Review. Bioact. Mater. 2019, 4, 56–70. [Google Scholar] [CrossRef]
- Ashby, M.; Shercliff, H.; Cebon, D. Materials. Engineering, Science, Processing and Design; Butterworth-Heinemann: Cambridge, UK, 2007; Volume 1, ISBN 9780750683913. [Google Scholar]
- Carvill, J. Mechanical Engineer’s Data Handbook; Butterworth-Heinemann: Cambridge, UK, 1994; ISBN 0750619600. [Google Scholar]
- De Witte, T.M.; Fratila-Apachitei, L.E.; Zadpoor, A.A.; Peppas, N.A. Bone Tissue Engineering via Growth Factor Delivery: From Scaffolds to Complex Matrices. Regen. Biomater. 2018, 5, 197–211. [Google Scholar] [CrossRef]
- Saedi, S.; Saghaian, S.E.; Jahadakbar, A.; Shayesteh Moghaddam, N.; Taheri Andani, M.; Saghaian, S.M.; Lu, Y.C.; Elahinia, M.; Karaca, H.E. Shape Memory Response of Porous NiTi Shape Memory Alloys Fabricated by Selective Laser Melting. J. Mater. Sci. Mater. Med. 2018, 29, 40. [Google Scholar] [CrossRef] [PubMed]
- Szczęsny, G.; Kopec, M.; Politis, D.J.; Kowalewski, Z.L.; Łazarski, A.; Szolc, T. A Review on Biomaterials for Orthopaedic Surgery and Traumatology: From Past to Present. Materials 2022, 15, 3622. [Google Scholar] [CrossRef] [PubMed]
- Morgan, E.F.; Unnikrisnan, G.U.; Hussein, A.I. Bone Mechanical Properties in Healthy and Diseased States. Annu. Rev. Biomed. Eng. 2018, 20, 119–143. [Google Scholar] [CrossRef] [PubMed]
- Jindal, S.; Manzoor, F.; Haslam, N.; Mancuso, E. 3D Printed Composite Materials for Craniofacial Implants: Current Concepts, Challenges and Future Directions. Int. J. Adv. Manuf. Technol. 2021, 112, 635–653. [Google Scholar] [CrossRef]
- Murr, L.E. Global Trends in the Development of Complex, Personalized, Biomedical, Surgical Implant Devices Using 3D Printing/Additive Manufacturing: A Review. Med. Devices Sens. 2020, 3, e10126. [Google Scholar] [CrossRef]
- Fard, M.G.; Sharifianjazi, F.; Kazemi, S.S.; Rostamani, H.; Bathaei, M.S. Laser-Based Additive Manufacturing of Magnesium Alloys for Bone Tissue Engineering Applications: From Chemistry to Clinic. J. Manuf. Mater. Process. 2022, 6, 158. [Google Scholar] [CrossRef]











| Ti | N | C | H | O | Fe | |
|---|---|---|---|---|---|---|
| Max. | Balance | 0.03 | 0.08 | 0.015 | 0.25 | 0.30 |
| Parameter | Value |
|---|---|
| Density, ρ, kg/m3 | 4500 ± 26.81 |
| Elastic modulus, E, GPa | 104.21 ± 0.84 |
| Shear modulus, G, GPa | 39.18 ± 0.23 |
| Poisson’s ratio, ν | 0.33 ± 0.002 |
| Parameter | Porosity | St.A_P | St.A_1 | St.A_2 |
|---|---|---|---|---|
| E, GPa | 80% | 2.93 | 0.79 | 0.77 |
| 70% | 8.07 | 1.88 | 1.83 | |
| 60% | 18.38 | 6.02 | 8.79 | |
| G, GPa | 80% | 0.97 | 0.24 | 0.21 |
| 70% | 2.59 | 0.66 | 0.60 | |
| 60% | 5.72 | 1.56 | 1.46 | |
| ν | 80% | 0.40 | −0.19 | −0.21 |
| 70% | 0.32 | −0.14 | −0.16 | |
| 60% | 0.26 | −0.002 | 0.03 | |
| T, µm | 80% | 335 | 519 | 516 |
| 70% | 441 | 653 | 649 | |
| 60% | 563 | 773 | 770 |
| Topology | Conditional Elastic Modulus, GPa | Conditional Yield Strength, MPa | |
|---|---|---|---|
| St.A_1 | Sample 1 | 0.90 | 11.56 |
| Sample 2 | 1.04 | 12.35 | |
| Sample 3 | 0.99 | 12.15 | |
| Average | 0.98 | 12.02 | |
| Standard deviation | 0.07 | 0.41 | |
| St.A_2 | Sample 1 | 0.88 | 12.30 |
| Sample 2 | 0.91 | 12.35 | |
| Sample 3 | 0.97 | 12.13 | |
| Average | 0.92 | 12.26 | |
| Standard deviation | 0.04 | 0.12 | |
| St.A_P | Sample 1 | 4.77 | 32.80 |
| Sample 2 | 4.65 | 33.95 | |
| Sample 3 | 4.52 | 34.40 | |
| Average | 4.65 | 33.72 | |
| Standard deviation | 0.12 | 0.83 |
| Topology | Elastic Modulus, GPa | Poisson’s Ratio | Porosity, % | Strut Thickness, µm | |
|---|---|---|---|---|---|
| St.A_1 | Simulation | 0.79 | −0.19 | 80.00 | 519.00 |
| Experiment | 0.98 | −0.09 | 76.35 | 597.60 | |
| Deviation, % | 23.59 | 52.63 | 3.65 | 15.14 | |
| St.A_2 | Simulation | 0.77 | −0.21 | 80.00 | 516.00 |
| Experiment | 0.92 | −0.003 | 74.52 | 606.35 | |
| Deviation, % | 19.24 | 98.57 | 5.48 | 17.51 | |
| St.A_P | Simulation | 2.93 | 0.40 | 80.00 | 335.00 |
| Experiment | 4.65 | 0.63 | 66.12 | 427.60 | |
| Deviation, % | 58.66 | 57.50 | 13.88 | 27.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farber, E.; Orlov, A.; Popovich, A. Auxetic Meta-Biomaterials: Computer Simulation and Experimental Results. Metals 2025, 15, 241. https://doi.org/10.3390/met15030241
Farber E, Orlov A, Popovich A. Auxetic Meta-Biomaterials: Computer Simulation and Experimental Results. Metals. 2025; 15(3):241. https://doi.org/10.3390/met15030241
Chicago/Turabian StyleFarber, Eduard, Alexey Orlov, and Anatoly Popovich. 2025. "Auxetic Meta-Biomaterials: Computer Simulation and Experimental Results" Metals 15, no. 3: 241. https://doi.org/10.3390/met15030241
APA StyleFarber, E., Orlov, A., & Popovich, A. (2025). Auxetic Meta-Biomaterials: Computer Simulation and Experimental Results. Metals, 15(3), 241. https://doi.org/10.3390/met15030241






