Abstract
The growing environmental impact of copper production necessitates innovative approaches for optimizing metallurgical processes and minimizing waste. This study addresses this challenge by leveraging advanced machine learning (ML) techniques to enhance the efficiency of pyrometallurgical operations such as slag optimization, composition prediction, and waste minimization. Using a combination of real-world and synthetic data, we developed models capable of both forward prediction, estimating slag and matte compositions from ore characteristics, and backward prediction, inferring ore compositions from output characteristics. Five ML algorithms were evaluated, with Gradient Boosting and Support Vector Regression demonstrating superior performance in capturing complex, non-linear relationships. Forward prediction achieved near-perfect accuracy, while backward prediction highlighted the inherent complexity of inverse modeling. This backward-driven strategy proposed in this research aims to determine optimal ore compositions to achieve desired outputs, reducing waste and energy consumption. By integrating ML models with a systematic hyperparameter optimization approach, this work advances the potential for sustainable and precise metallurgical processes. While challenges remain in refining backward predictions, the findings demonstrate the transformative potential of data-driven strategies in industrial metallurgy, paving the way for environmentally sustainable and economically efficient copper production practices.
1. Introduction
Copper production involves multiple stages, including mining, grinding, ore enrichment, smelting, refining, and waste management. As with any large and complex production facility, every stage of copper production generates waste that requires proper disposal. Unfortunately, before this waste is managed, it often leaves a significant impact on the planet’s ecology. Ashes, slags, and dusts, which are by-products of mining and metal processing, serve as sources of toxic metals like Cd, Pb, and As causing air, water, and soil pollution [1,2]. Addressing climate change has brought renewed focus on evaluating the environmental impact of metal production technologies [3]. With copper’s environmental impact expected to grow significantly from 2010 to 2050 due to its large supply, this issue needs to be taken seriously [4]. Some ways to address this issue include optimizing factory operations [5,6,7,8] or working directly with wastes. As an example, in Chile, where about 50 million tons of copper slag has been dumped throughout history, the government began to think about how to reduce the amount of slag [9]. Slags are a by-product of pyrometallurgical processing, an important waste product of metallurgy as they are produced in large volumes and contain significant concentrations of metallic elements. Because the slags contain a large amount of useful metals, it is important to look for ways to take the most useful metals out of them and thus reduce the amount of the slag [10,11,12].
Most of the methods used to extract metals include the following [13]:
- Pyrometallurgical [9,14,15,16,17,18,19,20,21,22,23,24,25];
- Hydrometallurgical [25,26,27,28];
- Physical Separation [19,29];
- Flotation [30,31,32];
- Combined [33].
Previous studies have explored both individual approaches and combinations of approaches to improve efficiency and minimize environmental impact. For example, the method with CaS [15] recovered up to 98.51% copper at less than 5% iron in the matte, with a temperature of 1450 °C and carbon addition. Also, one of the pyrometallurgical methods, sulfidation–reduction using pyrite, recovered 97.58% copper, 98.20% lead, and 89.91% zinc, reducing Fe3O4 in the slag from 19.50% to 2.97% [24].
On the other hand, hydrometallurgical methods such as sulfide roasting and leaching showed good efficiency in the extraction of valuable metals. Optimal conditions of the experiment made it possible to achieve recovery of copper up to 74.2%; nickel, 71.1%; and cobalt, 69.6%, while minimizing the recovery of iron (4.9%) and aluminum (17.6%) [27].
Previous works also mentioned using secondary slag after recovery as a method to reduce the amount of slag. Carbothermal reduction at high temperatures (approximately 1440 °C) enabled the recovery of most of the valuable metals, such as Fe, Cu, and Mo, into an iron-rich alloy suitable for use as feedstock in steel production. Meanwhile, the non-metallic residue, referred to as secondary slag, found potential applications in glass and ceramics [20]. In addition to recovering valuable metals through various extractive metallurgical methods, the by-products can be repurposed for producing materials such as cement, fillers, ballast, abrasives, aggregates, roofing granules, glass, and tiles [34]. Beyond traditional chemical and metallurgical methods, machine learning (ML) has emerged as a powerful tool for optimizing and predicting outcomes in copper recovery processes.
Recently, the advent of Artificial Intelligence (AI) has allowed the usage of earlier data to make predictions about the future. Therefore, many industries stand to benefit from this technology, and the copper mining industry is one of them. With the availability of digital data, machine learning methods, which are a subset of AI, have been proven to predict various process parameters reliably. Flores et al. have shown the effectiveness of Random Forest in predicting copper recovery [35]. In another study, they carried out a comparative analysis of three ML algorithms for copper recovery quality prediction in a leaching process. These models were Support Vector Machines, Random Forest, and Artificial Neural Networks (ANNs), and the study found that ANNs as the best-performing model, with class precision scores of more than 99.0 on the four datasets applied [36]. In addition to these methods, fuzzy logic and Model Predictive Control (MPC) have shown promise in optimizing mining processes and waste management [37]. However, challenges persist, including data scarcity, difficult sensor environments, and interoperability issues [38]. Hybrid geometallurgical approaches, combining historical data and deep learning, can accurately predict metallurgical responses, reducing costs and improving planning [39]. These approaches establish a comprehensive relationship between geological and mining characteristics and metallurgical parameters in a mineral processing plant. ML methods also accelerate alloy development, enabling rapid optimization of mechanical and electrical properties [40]. ANN-based models assist in forecasting production while managing energy consumption effectively [41]. Furthermore, ML-driven optimization of hydrodesulfurization processes helps reduce sulfur compounds, emissions, and costs, promoting environmental sustainability [42]. There is more challenging work to be completed, like using metallurgical optimization employing the Genetic Algorithm–Back Propagation (GA-BP) method to predict matte grade [43]. This approach combines the global search capability of Genetic Algorithms with the strong generalization ability of Back Propagation neural networks, improving the accuracy and reliability of matte grade predictions.
Building on such insights, this study suggests a unique approach. Instead of searching for ways to increase recovery from slag, which requires additional energy inputs and is accompanied by environmental risks, we aim to determine the optimal masses of different ores to ensure a given stable chemical composition of both matte and slag [44]. In other words, we work backward: starting from the desired result, we determine the most efficient feed strategy. This approach ensures homogeneity, quality, and waste reduction, which ultimately improves the efficiency of metallurgical production.
We will employ advanced machine learning [45] and AI models capable of handling the non-linear, interconnected factors in copper smelting. By seamlessly integrating predictions with evolutionary algorithms, our work moves beyond traditional optimization, driving more sustainable, consistent metallurgical processes, and helps to reduce ecological damage.
2. Materials and Methods
At the core of this study is an intelligent system designed to optimize metallurgical processes by leveraging machine learning techniques. The system follows a structured workflow comprising three main stages: synthetic dataset preparation, machine learning modeling, and prediction evaluation. Figure 1 provides an overview of this workflow. Initially, real-world data from the metallurgical process are used to generate synthetic data to create a comprehensive dataset. This dataset is then used to train regression models, with cross-validation and hyperparameter tuning applied to enhance performance. The software used in this study are Python (3.10.2) for scripting, NumPy (2.1.3) and Pandas (2.2.3) for synthetic data computation, and scikit-learn (1.4.2) for machine learning modelling.
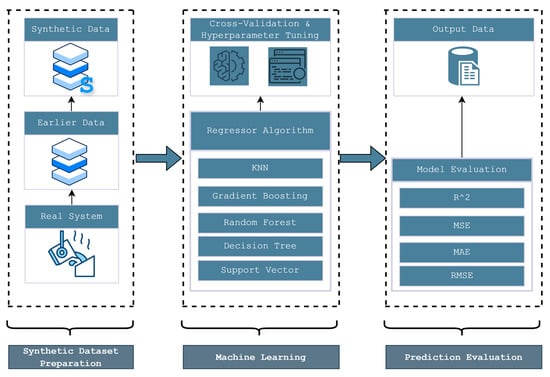
Figure 1.
Intelligent system for metallurgical process optimization.
The objective is to train models to first predict the resulting matte and slag compositions based on the ore composition, and secondly, to predict the ore composition from the resulting matte and slag compositions (reverse modeling). The trained models are then evaluated based on the test set using key performance metrics, including coefficient of determination, mean squared error, mean absolute error, and root mean squared error, to ensure accurate predictions of metallurgical outputs. This structured approach enables precise modeling of metallurgical processes, facilitating data-driven decision-making to improve efficiency and reduce waste.
This Methodology section further details the data collection process, synthetic data generation, model training procedures, evaluation metrics, and the overall approach used to develop and validate the predictive models.
2.1. Data Preparation
The data presented in this study were prepared by integrating real-world data with synthetic data generation techniques. The dataset is based on detailed records provided by the Institute of Metallurgy and Ore Beneficiation, a leading organization in Almaty, Kazakhstan, specializing in industrial pyrometallurgical processes. Due to confidentiality agreements, the data are available on request from the corresponding author. The original dataset includes critical information on the composition of various ores and the parameters associated with the pyrometallurgical smelting process.
Each ore sample in the dataset represents a complex mixture of metallic and non-metallic compounds. The primary parameters recorded for each ore included the weight and composition of specific elements. These elements were categorized into metals such as gold, silver, copper, and iron, and non-metallic compounds including silicon dioxide (SiO2), calcium oxide (CaO), aluminum oxide (Al2O3), sulfur, and arsenic. The concentrations of gold and silver were provided in units of grams per ton, while the other elements were expressed as percentages of the total ore weight. Additionally, constants related to the pyrometallurgical process, such as the combined weight of the melt (comprising both matte and slag), were included.
Given the constraints of real-world data availability, synthetic data were generated to expand the dataset and simulate a broader range of pyrometallurgical scenarios. The generation process involved sampling ore compositions from the original dataset to create a base distribution that reflects realistic variability. To ensure diversity while maintaining the integrity of the data, random perturbations were introduced to the concentrations of each element. These perturbations were carefully bounded to prevent unrealistic values, ensuring that the total elemental composition remained consistent, with percentages summing to 100%.
The synthetic data generation process also ensured that the distributions of element concentrations closely mirrored those found in industrial settings. For each synthetic sample, the total weight of the ore and the proportions of individual elements were adjusted to reflect plausible conditions under which the pyrometallurgical process operates. This approach facilitated the creation of a dataset that balances authenticity with variability, allowing for more generalized modeling and analysis.
The final dataset consists of 10,000 rows and 20 columns. The columns are divided into ore compositions as seen in Table 1, and pyrometallurgical process results, and described in Table 2. A detailed statistical description of the dataset can be found in Appendix A.1.

Table 1.
Ore composition.

Table 2.
Pyrometallurgical process results.
The data preparation process aligns closely with the principles of pyrometallurgical smelting, a method extensively used for extracting non-ferrous metals. In this process, ores are crushed and mixed to ensure uniform composition, followed by smelting in high-temperature furnaces with the addition of fluxes like lime and gases such as oxygen. The smelting process results in the formation of three distinct fractions: the matte, which contains the valuable metals and sulfur; the slag, which captures the oxides and impurities; and the sublimates, which are volatile compounds like sulfur and arsenic that can be captured or lost as waste.
In this research, we employ two prediction approaches using machine learning models: forward prediction and backward prediction. These approaches allow us to explore the relationships between ore composition and the resulting outputs of the pyrometallurgical process from different perspectives.
In forward prediction, we use the ore composition as the input features to predict the resulting matte and slag compositions. This approach models the traditional pyrometallurgical process, where the goal is to determine the output (composition of matte and slag) based on known input parameters (composition of the ores).
In backward prediction, we reverse the modeling process by using the matte and slag compositions as the input features to predict the ore composition. This approach is useful for scenarios where the characteristics of the resulting products are known, and we want to infer the properties of the original ore. Backward prediction can provide insights into the types of ores that may have produced specific outputs.
The dataset was divided into training and testing subsets. Specifically, 80% of the data were used for training the models, while 20% were reserved for testing. The data were randomly shuffled before splitting. This prevents any inherent order or patterns in the dataset from influencing the training or testing results. This ensures that the models are trained on one subset of the data and evaluated on a separate, unseen subset to assess their generalization performance. The same splitting strategy was applied to both forward and backward prediction tasks.
Since the features in the dataset vary widely in scale (e.g., ore weights in grams, element concentrations in percentages, or grams per ton), it was essential to standardize them. Standardization ensures that all features contribute equally to the model, preventing features with larger scales from dominating the learning process. The scaling was applied independently to the training and testing subsets to avoid data leakage, ensuring that the testing data remained unseen during training.
2.2. Machine Learning Modeling
Our approach for modeling the prediction involves testing a suite of machine learning algorithms, employing rigorous evaluation metrics, and optimizing model hyperparameters using cross-validation and grid search.
We selected five machine learning algorithms for this research, each with distinct characteristics and strengths. These models are well suited for multi-output regression tasks, which involve predicting multiple continuous outputs simultaneously. From a theoretical perspective, multi-output regression aims to model the relationships between input features and multiple dependent variables, leveraging shared structures or dependencies among outputs. By adapting algorithms originally designed for single-output tasks, this approach allows for simultaneous prediction of interrelated target variables, enhancing efficiency and predictive accuracy in complex domains. The algorithms are briefly described below:
- Random Forest Regressor: Random Forest is an ensemble learning method that constructs multiple decision trees during training and outputs the average prediction of the trees. It is robust to overfitting and can handle non-linear relationships and interactions between features.
- Gradient Boosting Regressor: Gradient Boosting is another ensemble method that builds trees sequentially, where each new tree corrects the errors of the previous ones. It is highly effective for structured/tabular data and can achieve high predictive performance by minimizing the loss function.
- K-Nearest Neighbors (KNN) Regressor: KNN is a non-parametric algorithm that predicts the output by averaging the outputs of the nearest data points in the feature space. It is simple to implement and useful for capturing local patterns in the data.
- Support Vector Regressor (SVR): SVR is based on Support Vector Machines (SVMs) and aims to find a hyperplane that best fits the data within a margin of tolerance. It works well for high-dimensional data and can model complex relationships using different kernel functions.
- Decision Tree Regressor: Decision Trees partition the feature space into regions and make predictions based on the average output within each region. They are interpretable and effective for datasets with non-linear patterns.
2.2.1. Evaluation Metrics
To assess the performance of the models, we employed several evaluation metrics. These metrics, namely the coefficient of determination (R2 score), mean squared error (MSE), mean absolute error (MAE), and root mean squared error (RMSE), provide a comprehensive understanding of how well the models predict both the training and testing data.
The R2 score measures the proportion of variance in the target variable that the model explains. It ranges from 0 to 1, and the higher the R2 score, the better the performance of the model. The MSE represents the average of the squared differences between predicted and actual values. A lower MSE indicates better performance.
The MAE represents the average of the absolute differences between predicted and actual values. The MAE is less sensitive to outliers compared to the MSE. Lastly, the RMSE is the square root of the MSE and provides a measure of error in the same units as the target variable. These metrics were calculated for both the training set and testing set to evaluate the models’ performance and identify potential overfitting (the case where a model memorizes the dataset instead of learning the patterns within it).
2.2.2. Cross-Validation
To obtain a reliable measure of the model’s performance, cross-validation was employed. Cross-validation is a statistical technique used to assess the generalization performance of machine learning models. It involves splitting the dataset into multiple subsets (folds) and iteratively training and evaluating the model on different subsets. The primary goal of cross-validation is to ensure that the model’s performance is consistent across different portions of the dataset and to reduce the risk of overfitting.
In our study, the dataset was divided into 5 folds. This means that our models are trained on four folds and evaluated on the remaining fold. This process is repeated 5 times, each time using a different fold for validation. The final performance is the average of the 5 individual evaluation scores. This reduces the bias associated with using a single train–test split. Moreover, it provides a more reliable estimate of model performance.
2.2.3. Grid Search
To optimize the hyperparameters of each model, we employed grid search, a systematic hyperparameter tuning approach. This is a technique for hyperparameter tuning that systematically searches through a specified set of hyperparameters to find the optimal combination for a machine learning model. It uses cross-validation to evaluate each combination of hyperparameters.
In our study, a grid of hyperparameters according to each model was defined. For each combination of hyperparameters in the grid, the models are trained and evaluated using cross-validation. The combination of hyperparameters that yields the best performance is selected as the optimal configuration.
The following section presents the results of our modeling efforts, detailing the performance of each algorithm and providing insights into their effectiveness in predicting the outcomes of the pyrometallurgical process.
3. Results and Discussion
3.1. Forward Prediction Results
The forward prediction task, which aimed to estimate the composition of the matte and slag from given ore characteristics, yielded strong overall performances across most models tested. As shown in Table 3, the Gradient Boosting Regressor emerged as a top performer, achieving an R2 of 0.9951 on the test set and substantially lower error metrics (Test MSE = 29.6716, Test MAE = 1.9327, Test RMSE = 5.4472) than the other models. This high R2 indicates that the Gradient Boosting model captured nearly all the variance in the outputs, suggesting that the complex ensemble structure effectively modeled the non-linearities and intricate relationships inherent in the pyrometallurgical system. The performances of the models in predicting matte and slag are shown in Figure 2 and Figure 3, respectively.

Table 3.
Summary of key evaluation metrics for each model in forward prediction.
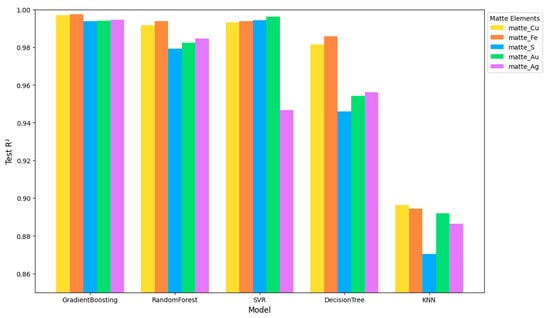
Figure 2.
Performance of models predicting matte.
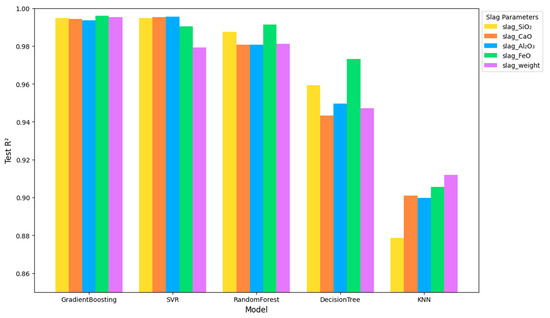
Figure 3.
Performance of models predicting slag.
Random Forest and SVR also performed admirably, with Random Forest reaching an R2 of 0.9853 and SVR achieving 0.9879. Both methods showed strong predictive capabilities, but were slightly less precise than Gradient Boosting. Notably, the KNN and Decision Tree Regressors lagged behind, particularly KNN with an R2 of 0.8936, suggesting that a simple non-parametric approach relying on proximity might not fully capture the complexity of high-dimensional elemental interactions. Decision Trees, while interpretable, appear limited in modeling the nuanced relationships without ensemble methods.
A closer look at the predictions for specific matte and slag components (Table 4 and Table 5) reinforces these findings. Gradient Boosting consistently outperformed other models across all matte outputs (Cu, Fe, S, Au, Ag), with R2 scores often exceeding 0.99 (Figure 2). Similarly, for slag composition (Figure 3), Gradient Boosting delivered near-perfect R2 values (e.g., FeO at 0.9961), indicating remarkable precision. The SVR and Random Forest performed nearly as well, achieving R2 values greater than 0.99 for most matte and slag components, underscoring that advanced, flexible models are particularly well suited for forward prediction tasks in pyrometallurgy.

Table 4.
Performance of each model predicting matte.

Table 5.
Performance of each model predicting slag.
Interestingly, even where simpler methods like Decision Trees and KNN underperformed relative to Gradient Boosting and SVR, they still maintained high R2 values, generally above 0.87. This suggests that the primary input–output relationships are quite robust and that even less complex models can capture a substantial portion of the variance. However, the ensemble and kernel-based methods truly excel at fine-tuning the predictions and reducing residual error.
3.2. Backward Prediction Results
The backward prediction task—predicting the original ore composition given the final matte and slag outputs—proved to be a more challenging endeavor. The overall results (Table 6) indicate a drop in performance compared to forward prediction, reflected in lower R2 values and higher error metrics for all models. This finding highlights the inherent complexity and potential many-to-one mapping of the backward problem, where multiple initial conditions may produce similar final outputs, making the inverse prediction more ambiguous and less stable.

Table 6.
Summary of key evaluation metrics for each model in backward prediction.
Among the tested algorithms, the SVR achieved the highest overall R2 of 0.8549, with a Test MSE of 546.1792 and MAE of 6.4437. This stronger performance by the SVR aligns with its ability to handle complex feature spaces and non-linear relationships. Gradient Boosting followed closely with an R2 of 0.8193, indicating that while ensemble methods remain potent, the inverse mapping is more elusive than the forward relationship. Random Forest also delivered respectable accuracy (R2 = 0.8037), though it showed more sensitivity to variations in the target space than in forward prediction.
KNN and Decision Trees struggled more notably in backward prediction, with R2 values falling to 0.6999 and 0.7277, respectively. This drop suggests that the backward relationship may lack the local smoothness or distinct partitions that these models can readily exploit. In other words, a simple proximity-based approach (KNN) or a single-tree partitioning strategy is less effective in reconstructing the original ore profile when only final outputs are known.
Examining the individual target variables (Table 7 and Table 8) offers further insights. Predicting the bulk ore weight (mixed ore) and precious metal concentrations (Au, Ag) proved challenging but still feasible. The SVR and Gradient Boosting models attained high R2 values (often exceeding 0.85 and even 0.95 in the case of SVR for Au), demonstrating that certain high-level relationships, particularly those associated with precious metals, are more directly inferable from the final outputs.

Table 7.
Performance of each model predicting the mixed ore gram, gold gram per ton, and silver gram per ton.

Table 8.
Performance in predicting element and compound masses.
For elemental and compound masses (SiO2, CaO, S, Fe, Cu, Al2O3, As), the backward prediction results were mixed. Iron (Fe) and sulfur (S) masses were predicted with greater accuracy (for instance, Fe with an R2 of 0.9635 under Random Forest and 0.9933 under SVR), possibly because these elements strongly influence the formation of matte and slag phases, leaving more distinguishable “fingerprints” in the outputs. In contrast, arsenic (As) proved notably difficult to predict in the backward mode. Across most models, As had low or even negative R2 values, highlighting that its contribution to the final product composition does not translate easily into a discernable pattern backward. This may reflect the volatile or more sensitive processes by which arsenic partitions between phases, as well as the complexity of its capture or release during smelting.
Taken together, the backward prediction results confirm that predicting initial ore composition from final products is not as straightforward as forward prediction. While advanced models like SVR and Gradient Boosting still perform relatively well, the inverse problem likely suffers from reduced identifiability: multiple ore compositions can lead to similar final smelting outputs. As a result, even the best models display less stability and higher uncertainty, particularly for elements that do not leave a clear signature in the final metallurgical products such as slag and matte.
The backward prediction findings offer critical insights: while forward modeling can be performed with near-perfect precision using ensemble and kernel-based methods, the backward inference remains more complex and less certain. This aligns with the intrinsic thermodynamic and kinetic complexities of the smelting process, underscoring the need for further feature engineering, domain-specific constraints, or additional data sources if backward prediction is to be refined further.
4. Conclusions
This research highlights a data-driven approach to improving the efficiency and sustainability of pyrometallurgical processes by leveraging advanced machine learning (ML) techniques. By employing forward and backward prediction models, we have demonstrated the potential to optimize ore compositions and predict output characteristics with significant accuracy in copper pyrometallurgy. These methods not only offer a way to minimize waste and environmental impact but also provide a pathway for more precise control over metallurgical processes.
The integration of ML models, particularly ensemble methods like Gradient Boosting and Support Vector Regressors, has proven effective in capturing complex, non-linear relationships within the data. Forward prediction exhibited near-perfect accuracy, underscoring the models’ ability to map ore characteristics to matte and slag compositions. However, backward prediction revealed the intrinsic challenges of inverse modeling due to the many-to-one nature of the relationship between input and output variables.
This work moves beyond traditional extraction methods by proposing a backward-driven strategy, where the desired product composition dictates the input requirements. This paradigm shift emphasizes efficiency, reducing energy consumption and the generation of harmful by-products. Additionally, synthetic data augmentation has shown to be a valuable tool in expanding the dataset and ensuring robust model training, further enhancing the applicability of ML in industrial contexts.
However, it is important to note that these results have not yet been validated against real-world industrial process data. They have only been validated against the test set, which was generated from synthetic data derived from real-world data. Two other limitations of this study remain. Firstly, the backward prediction approach is less accurate due to the many-to-one nature of inverse modeling, leading to greater uncertainty in predictions. Secondly, the model does not currently account for the analysis of formed gases, such as SO2, which are critical for ensuring mass balance and capturing environmental impact. Additionally, challenges such as limited availability of industrial process data, sensor interoperability, and real-time adaptability need to be addressed to ensure broader applicability in operational settings.
Future work aims to incorporate gas-phase dynamics to provide a more comprehensive understanding of the system. Future efforts should focus on refining backward prediction by incorporating domain-specific constraints and expanding data sources to address the identifiability challenges. With further development, this approach has the potential to transform copper smelting into a more sustainable and optimized process, balancing economic goals with environmental stewardship.
Author Contributions
Conceptualization, B.K. and T.I.; methodology, S.K. and N.T.; software, N.T., T.I. and A.M.; validation, B.K., S.K. and M.D.; formal analysis, B.K. and S.K.; investigation, B.K. and S.K.; resources, B.K. and S.K.; data curation, N.T. and T.I.; writing—original draft preparation, N.T. and A.M.; writing—review and editing, B.K. and M.D.; visualization, T.I. and A.M.; supervision, B.K. and S.K.; project administration, B.K.; funding acquisition, S.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Committee of Science of the Ministry of Science and Higher Education of the Republic of Kazakhstan (Grant No. BR21882140).
Data Availability Statement
The data are not publicly available due to confidentiality agreements with the Institute of Metallurgy and Ore Beneficiation.
Acknowledgments
We would like to thank the Institute of Metallurgy and Ore Beneficiation for providing access to critical data and their invaluable support in facilitating this research.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1

Table A1.
Dataset statistical description.
Table A1.
Dataset statistical description.
| Mean | Std | Min | 25% | 50% | 75% | Max | |
|---|---|---|---|---|---|---|---|
| Mixed ore (g) | 1220.631 | 205.3391 | 426.1399 | 1079.635 | 1219.474 | 1363.75 | 2023.22 |
| Au (g/t) | 3.534505 | 0.758277 | 0.824154 | 3.022564 | 3.534288 | 4.056264 | 6.147995 |
| Ag (g/t) | 289.172 | 65.11926 | 49.82177 | 244.9817 | 289.0545 | 334.1066 | 500.7158 |
| SiO2 (g) | 20.46104 | 4.827916 | 6.768644 | 16.92307 | 20.11709 | 23.60565 | 39.73211 |
| CaO (g) | 4.844294 | 1.016306 | 1.66832 | 4.127585 | 4.830972 | 5.542353 | 8.29717 |
| S (g) | 14.57366 | 3.939301 | 2.815215 | 11.75246 | 14.40475 | 17.20056 | 28.81434 |
| Fe (g) | 18.86163 | 4.357267 | 6.370343 | 15.75559 | 18.61931 | 21.75374 | 38.11985 |
| Cu (g) | 14.2972 | 4.093968 | 2.26742 | 11.36188 | 14.04228 | 16.95834 | 31.0578 |
| Al2O3 (g) | 10.44082 | 2.217306 | 3.717987 | 8.877292 | 10.36846 | 11.92614 | 19.10646 |
| As (g) | 0.274785 | 0.06251 | 0.069747 | 0.232001 | 0.275095 | 0.317347 | 0.477233 |
| Matte Weight | 514.7182 | 128.69 | 139.58 | 422.88 | 505.285 | 599.2525 | 1114.8 |
| Cu (matte) | 34.95127 | 11.61144 | 6.610017 | 26.44055 | 33.72201 | 41.9523 | 94.42937 |
| Fe (matte) | 29.42349 | 9.89551 | −20.863 | 23.40133 | 30.46504 | 36.58649 | 52.8748 |
| S (matte) | 25.55124 | 2.943878 | 11.28032 | 23.78448 | 25.88998 | 27.62974 | 32.55801 |
| Au (matte) | 8.511742 | 2.503133 | 2.35 | 6.75 | 8.26 | 9.94 | 24.03 |
| Ag (matte) | 639.5543 | 193.0984 | 126.3 | 503.3325 | 621.58 | 748.5725 | 2005.34 |
| SiO2 (slag) | 41.72918 | 10.15211 | 15.82126 | 34.50927 | 40.84745 | 47.84077 | 137.5558 |
| CaO (slag) | 10.02007 | 2.824932 | 3.05906 | 8.068481 | 9.67356 | 11.58465 | 29.36509 |
| Al2O3 (slag) | 21.54001 | 5.886338 | 6.874627 | 17.52283 | 20.82008 | 24.70677 | 57.58418 |
| FeO (slag) | 12.74237 | 19.95006 | −141.287 | 2.579179 | 15.60925 | 26.11928 | 68.31653 |
| Slag Weight | 608.5089 | 146.3633 | 181.63 | 505.7975 | 602.84 | 704.325 | 1234.63 |
References
- Izydorczyk, G.; Mikula, K.; Skrzypczak, D.; Moustakas, K.; Witek-Krowiak, A.; Chojnacka, K. Potential Environmental Pollution from Copper Metallurgy and Methods of Management. Environ. Res. 2021, 197, 111050. [Google Scholar] [CrossRef]
- Yan, B.; Xu, D.-M.; Chen, T.; Yan, Z.-A.; Li, L.-L.; Wang, M.-H. Leachability Characteristic of Heavy Metals and Associated Health Risk Study in Typical Copper Mining-Impacted Sediments. Chemosphere 2020, 239, 124748. [Google Scholar] [CrossRef] [PubMed]
- Alexander, C.; Johto, H.; Lindgren, M.; Pesonen, L.; Roine, A. Comparison of Environmental Performance of Modern Copper Smelting Technologies. Clean. Environ. Syst. 2021, 3, 100052. [Google Scholar] [CrossRef]
- Kuipers, K.J.J.; Van Oers, L.F.C.M.; Verboon, M.; Van Der Voet, E. Assessing Environmental Implications Associated with Global Copper Demand and Supply Scenarios from 2010 to 2050. Glob. Environ. Change 2018, 49, 106–115. [Google Scholar] [CrossRef]
- Nikolić, I.P.; Milošević, I.M.; Milijić, N.N.; Mihajlović, I.N. Cleaner Production and Technical Effectiveness: Multi-Criteria Analysis of Copper Smelting Facilities. J. Clean. Prod. 2019, 215, 423–432. [Google Scholar] [CrossRef]
- Kulczycka, J.; Lelek, Ł.; Lewandowska, A.; Wirth, H.; Bergesen, J.D. Environmental Impacts of Energy-Efficient Pyrometallurgical Copper Smelting Technologies: The Consequences of Technological Changes from 2010 to 2050. J. Ind. Ecol. 2016, 20, 304–316. [Google Scholar] [CrossRef]
- Parameswaran, K.; Wilhelm, J.; Camorlinga, R. Sustainable Development Considerations in Primary Copper Smelting. In Extraction 2018; Davis, B.R., Moats, M.S., Wang, S., Gregurek, D., Kapusta, J., Battle, T.P., Schlesinger, M.E., Alvear Flores, G.R., Jak, E., Goodall, G., et al., Eds.; The Minerals, Metals & Materials Series; Springer International Publishing: Cham, Switzerland, 2018; pp. 241–252. ISBN 978-3-319-95021-1. [Google Scholar]
- Reuter, M.A.; Van Schaik, A.; Gediga, J. Simulation-Based Design for Resource Efficiency of Metal Production and Recycling Systems: Cases—Copper Production and Recycling, e-Waste (LED Lamps) and Nickel Pig Iron. Int. J. Life Cycle Assess. 2015, 20, 671–693. [Google Scholar] [CrossRef]
- González, C.; Parra, R.; Klenovcanova, A.; Imris, I.; Sánchez, M. Reduction of Chilean Copper Slags: A Case of Waste Management Project. Scand. J. Metall. 2005, 34, 143–149. [Google Scholar] [CrossRef]
- Potysz, A.; Van Hullebusch, E.D.; Kierczak, J.; Grybos, M.; Lens, P.N.L.; Guibaud, G. Copper Metallurgical Slags—Current Knowledge and Fate: A Review. Crit. Rev. Environ. Sci. Technol. 2015, 45, 2424–2488. [Google Scholar] [CrossRef]
- Phiri, T.C.; Singh, P.; Nikoloski, A.N. The Potential for Copper Slag Waste as a Resource for a Circular Economy: A Review—Part II. Miner. Eng. 2021, 172, 107150. [Google Scholar] [CrossRef]
- Mikula, K.; Izydorczyk, G.; Skrzypczak, D.; Moustakas, K.; Witek-Krowiak, A.; Chojnacka, K. Value-Added Strategies for the Sustainable Handling, Disposal, or Value-Added Use of Copper Smelter and Refinery Wastes. J. Hazard. Mater. 2021, 403, 123602. [Google Scholar] [CrossRef] [PubMed]
- Gabasiane, T.S.; Danha, G.; Mamvura, T.A.; Mashifana, T.; Dzinomwa, G. Environmental and Socioeconomic Impact of Copper Slag—A Review. Crystals 2021, 11, 1504. [Google Scholar] [CrossRef]
- Wang, D.; Liang, Y.; Lin, Z.; Peng, C.; Peng, B. Comprehensive Recovery of Zinc, Iron and Copper from Copper Slag by Co-Roasting with SO2–O2. J. Mater. Res. Technol. 2022, 19, 2546–2555. [Google Scholar] [CrossRef]
- Wu, L.; Wang, H.; Dong, K. Effect of Sulfur Content on Copper Recovery in the Reduction Smelting Process. Metals 2022, 12, 857. [Google Scholar] [CrossRef]
- Guo, Z.; Zhu, D.; Pan, J.; Wu, T.; Zhang, F. Improving Beneficiation of Copper and Iron from Copper Slag by Modifying the Molten Copper Slag. Metals 2016, 6, 86. [Google Scholar] [CrossRef]
- Wang, H.-Y.; Zhang, G.-H.; Chou, K.-C. Recovery of High-Grade Copper Matte by Selective Sulfurization of CuO–Fe2O3–SiO2–CaO System. J. Mater. Res. Technol. 2021, 13, 1676–1683. [Google Scholar] [CrossRef]
- Busolic, D.; Parada, F.; Parra, R.; Sanchez, M.; Palacios, J.; Hino, M. Recovery of Iron from Copper Flash Smelting Slags. Miner. Process. Extr. Metall. 2011, 120, 32–36. [Google Scholar] [CrossRef]
- Li, K.; Ping, S.; Wang, H.; Ni, W. Recovery of Iron from Copper Slag by Deep Reduction and Magnetic Beneficiation. Int. J. Miner. Metall. Mater. 2013, 20, 1035–1041. [Google Scholar] [CrossRef]
- Sarfo, P.; Das, A.; Wyss, G.; Young, C. Recovery of Metal Values from Copper Slag and Reuse of Residual Secondary Slag. Waste Manag. 2017, 70, 272–281. [Google Scholar] [CrossRef] [PubMed]
- Erdenebold, U.; Choi, H.-M.; Wang, J.-P. Recovery of Pig Iron from Copper Smelting Slag by Reduction Smelting. Arch. Metall. Mater. 2018, 1793–1798. [Google Scholar] [CrossRef]
- Zhou, S.; Wei, Y.; Zhang, S.; Li, B.; Wang, H.; Yang, Y.; Barati, M. Reduction of Copper Smelting Slag Using Waste Cooking Oil. J. Clean. Prod. 2019, 236, 117668. [Google Scholar] [CrossRef]
- Savic, M.V.; Djordjevic, P.B.; Mihajlovic, I.N.; Zivkovic, Z.D. Statistical Modeling of Copper Losses in the Silicate Slag of the Sulfide Concentrate Smelting Process. Pol. J. Chem. Technol. 2015, 17, 62–69. [Google Scholar] [CrossRef]
- Tian, Q.; Li, Z.; Wang, Q.; Guo, X. Synergistic Recovery of Copper, Lead and Zinc via Sulfurization–Reduction Method from Copper Smelting Slag. Trans. Nonferrous Met. Soc. China 2023, 33, 3847–3859. [Google Scholar] [CrossRef]
- Palacios, J.; Sánchez, M. Wastes as Resources: Update on Recovery of Valuable Metals from Copper Slags. Miner. Process. Extr. Metall. 2011, 120, 218–223. [Google Scholar] [CrossRef]
- Banza, A.N.; Gock, E.; Kongolo, K. Base Metals Recovery from Copper Smelter Slag by Oxidising Leaching and Solvent Extraction. Hydrometallurgy 2002, 67, 63–69. [Google Scholar] [CrossRef]
- Zhang, C.; Hu, B.; Wang, H.; Wang, M.; Wang, X. Recovery of Valuable Metals from Copper Slag. Min. Metall. Explor. 2020, 37, 1241–1251. [Google Scholar] [CrossRef]
- Yang, Z.; Rui-lin, M.; Wang-dong, N.; Hui, W. Selective Leaching of Base Metals from Copper Smelter Slag. Hydrometallurgy 2010, 103, 25–29. [Google Scholar] [CrossRef]
- Das, B.; Mishra, B.K.; Angadi, S.; Pradhan, S.K.; Prakash, S.; Mohanty, J. Characterization and Recovery of Copper Values from Discarded Slag. Waste Manag. Res. 2010, 28, 561–567. [Google Scholar] [CrossRef]
- Sarrafi, A.; Rahmati, B.; Hassani, H.R.; Shirazi, H.H.A. Recovery of Copper from Reverberatory Furnace Slag by Flotation. Miner. Eng. 2004, 17, 457–459. [Google Scholar] [CrossRef]
- Karimi, N.; Vaghar, R.; Mohammadi, M.R.T.; Hashemi, S.A. Recovery of Copper from the Slag of Khatoonabad Flash Smelting Furnace by Flotation Method. J. Inst. Eng. India Ser. D 2013, 94, 43–50. [Google Scholar] [CrossRef]
- Bruckard, W.J.; Somerville, M.; Hao, F. The Recovery of Copper, by Flotation, from Calcium-Ferrite-Based Slags Made in Continuous Pilot Plant Smelting Trials. Miner. Eng. 2004, 17, 495–504. [Google Scholar] [CrossRef]
- Shibayama, A.; Takasaki, Y.; William, T.; Yamatodani, A.; Higuchi, Y.; Sunagawa, S.; Ono, E. Treatment of Smelting Residue for Arsenic Removal and Recovery of Copper Using Pyro–Hydrometallurgical Process. J. Hazard. Mater. 2010, 181, 1016–1023. [Google Scholar] [CrossRef]
- Gorai, B.; Jana, R.K.; Premchand. Characteristics and Utilisation of Copper Slag—A Review. Resour. Conserv. Recycl. 2003, 39, 299–313. [Google Scholar] [CrossRef]
- Flores, V.; Keith, B.; Leiva, C. Using Artificial Intelligence Techniques to Improve the Prediction of Copper Recovery by Leaching. J. Sens. 2020, 2020, 2454875. [Google Scholar] [CrossRef]
- Flores, V.; Leiva, C. A Comparative Study on Supervised Machine Learning Algorithms for Copper Recovery Quality Prediction in a Leaching Process. Sensors 2021, 21, 2119. [Google Scholar] [CrossRef]
- Herrera, N.; Sinche Gonzalez, M.; Okkonen, J.; Mollehuara, R. Soft Computing Application in Mining, Mineral Processing and Metallurgy with an Approach to Using It in Mineral Waste Disposal. Minerals 2023, 13, 1450. [Google Scholar] [CrossRef]
- Estay, H.; Lois-Morales, P.; Montes-Atenas, G.; Ruiz Del Solar, J. On the Challenges of Applying Machine Learning in Mineral Processing and Extractive Metallurgy. Minerals 2023, 13, 788. [Google Scholar] [CrossRef]
- Gholami, A.; Asgari, K.; Khoshdast, H.; Hassanzadeh, A. A Hybrid Geometallurgical Study Using Coupled Historical Data (HD) and Deep Learning (DL) Techniques on a Copper Ore Mine. Physicochem. Probl. Miner. Process. 2022, 58, 147841. [Google Scholar] [CrossRef]
- Zhang, H.; Fu, H.; Zhu, S.; Yong, W.; Xie, J. Machine Learning Assisted Composition Effective Design for Precipitation Strengthened Copper Alloys. Acta Mater. 2021, 215, 117118. [Google Scholar] [CrossRef]
- Veličkovska, I.; Mihajlović, I.; Njagulović, B. Prediction of the copper production in the framework of electrical energy consumption using artificial neural network. In An International Serial Publication for Theory and Practice of Management Science; University of Belgrade: Belgrade, Serbia, 2020; pp. 411–423. [Google Scholar]
- Anqi, A.E. Machine Learning Modeling for Optimization of Sulfur Compounds Separation from Fuels: Process Optimization for Reduction of Environmental Pollution. Case Stud. Therm. Eng. 2023, 45, 102989. [Google Scholar] [CrossRef]
- Zhao, L.; Zhu, D.; Liu, D.; Wang, H.; Xiong, Z.; Jiang, L. Prediction and Optimization of Matte Grade in ISA Furnace Based on GA-BP Neural Network. Appl. Sci. 2023, 13, 4246. [Google Scholar] [CrossRef]
- Kvyatkovskiy, S.; Kozhakhmetov, S.; Semenova, A.; Dyussebekova, M.; Shakhalov, A. Hydrothermal treatment of sinters containing thiosalts of non-ferrous metals. Kompleks. Ispolz. Miner. Syra = Complex Use Miner. Resour. 2024, 335, 42–49. [Google Scholar] [CrossRef]
- Zhalgas, A.; Toleubek, M. A comparative analysis of machine learning classifiers for stroke prediction. J. Probl. Comput. Sci. Inf. Technol. 2024, 2, 21–29. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).