Numerical Simulation of the Hot Isostatic Pressing Densification Behavior of Ti6Al4V Powder for a Thin-Walled Tubular Component with Non-Axisymmetric Inner Ribs
Abstract
1. Introduction
2. Numerical Modeling
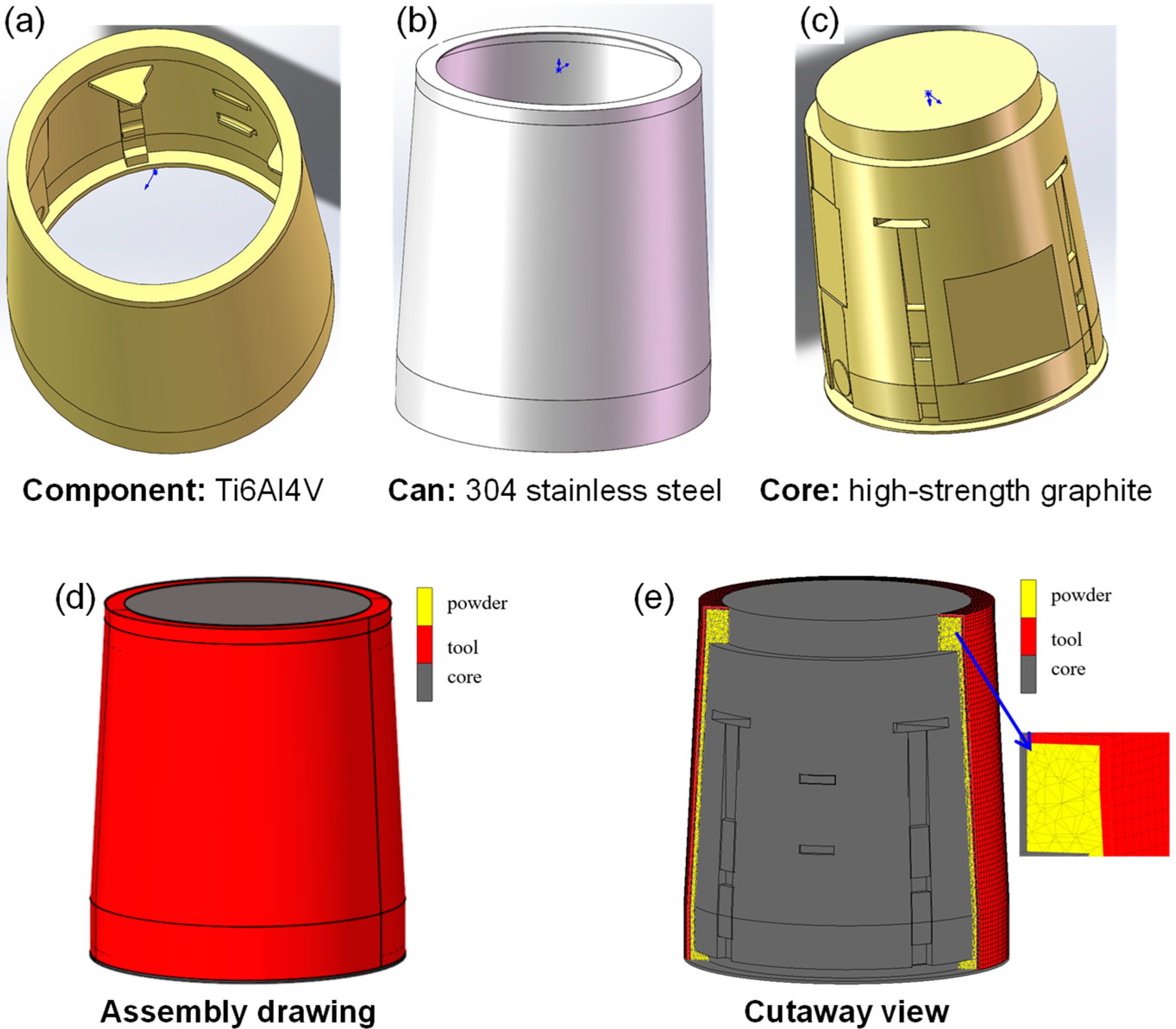
2.1. Geometric Modeling and Meshing
2.2. Plasticity Theory of Titanium Alloy Powder HIP
2.3. Boundary Conditions
2.4. Material Parameters
3. Results and Discussion
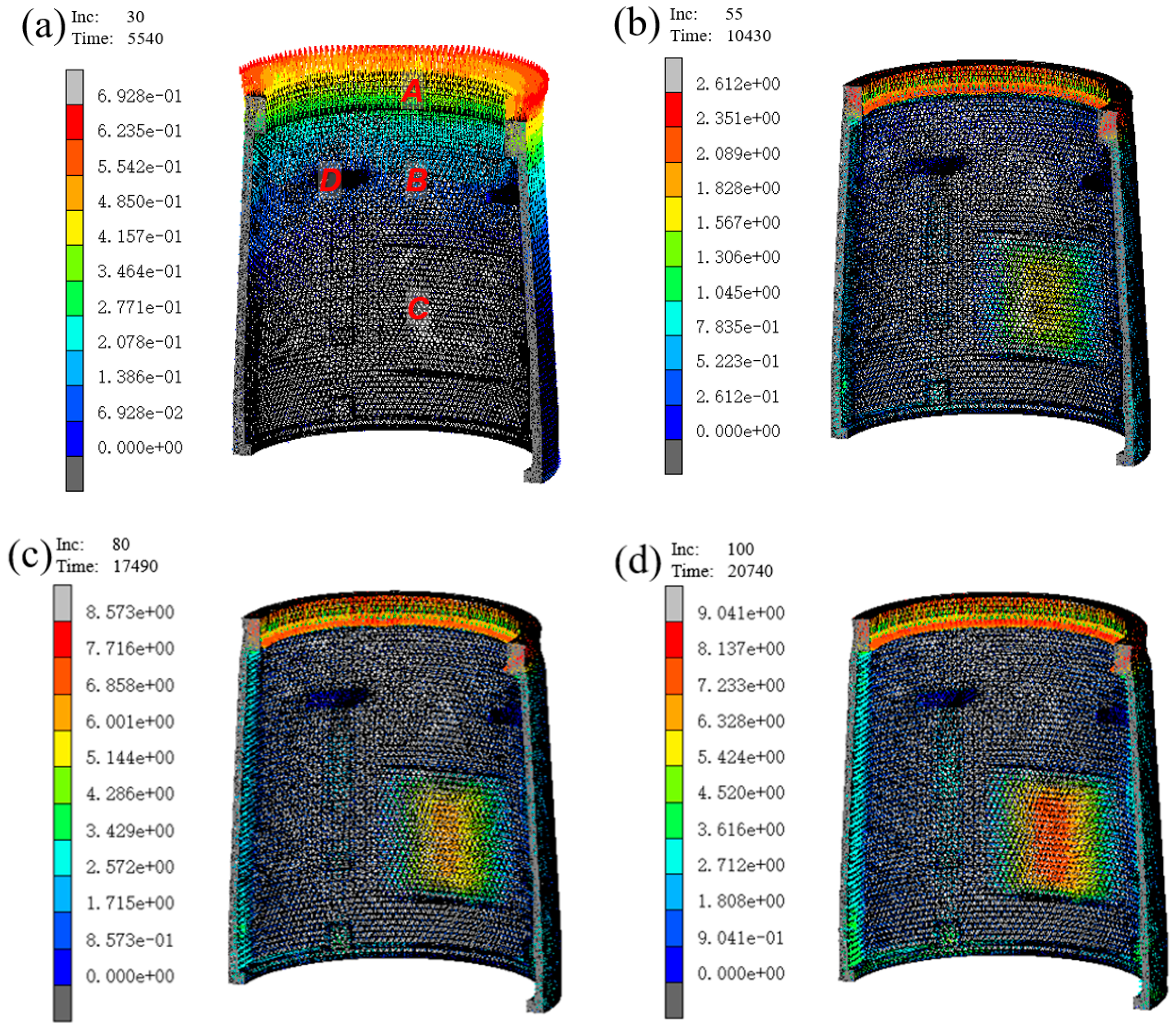
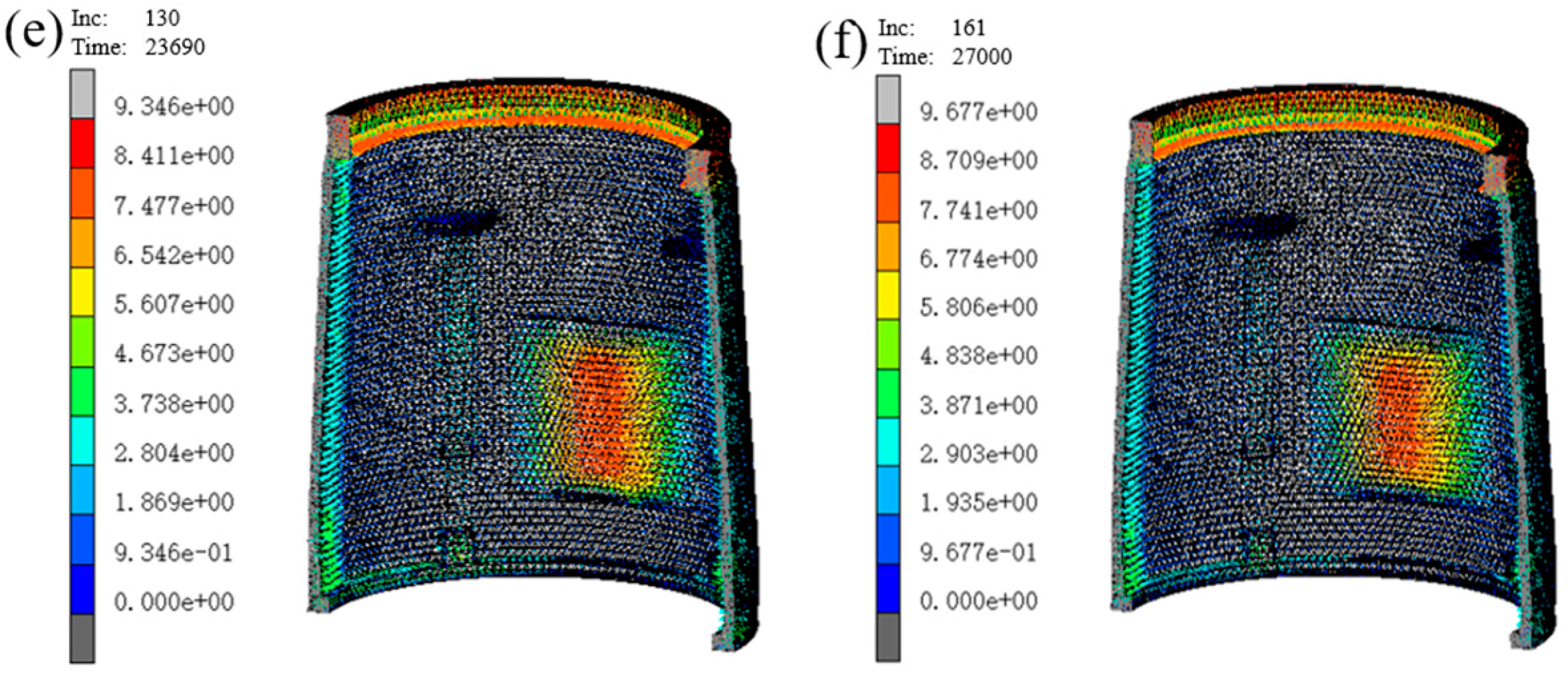
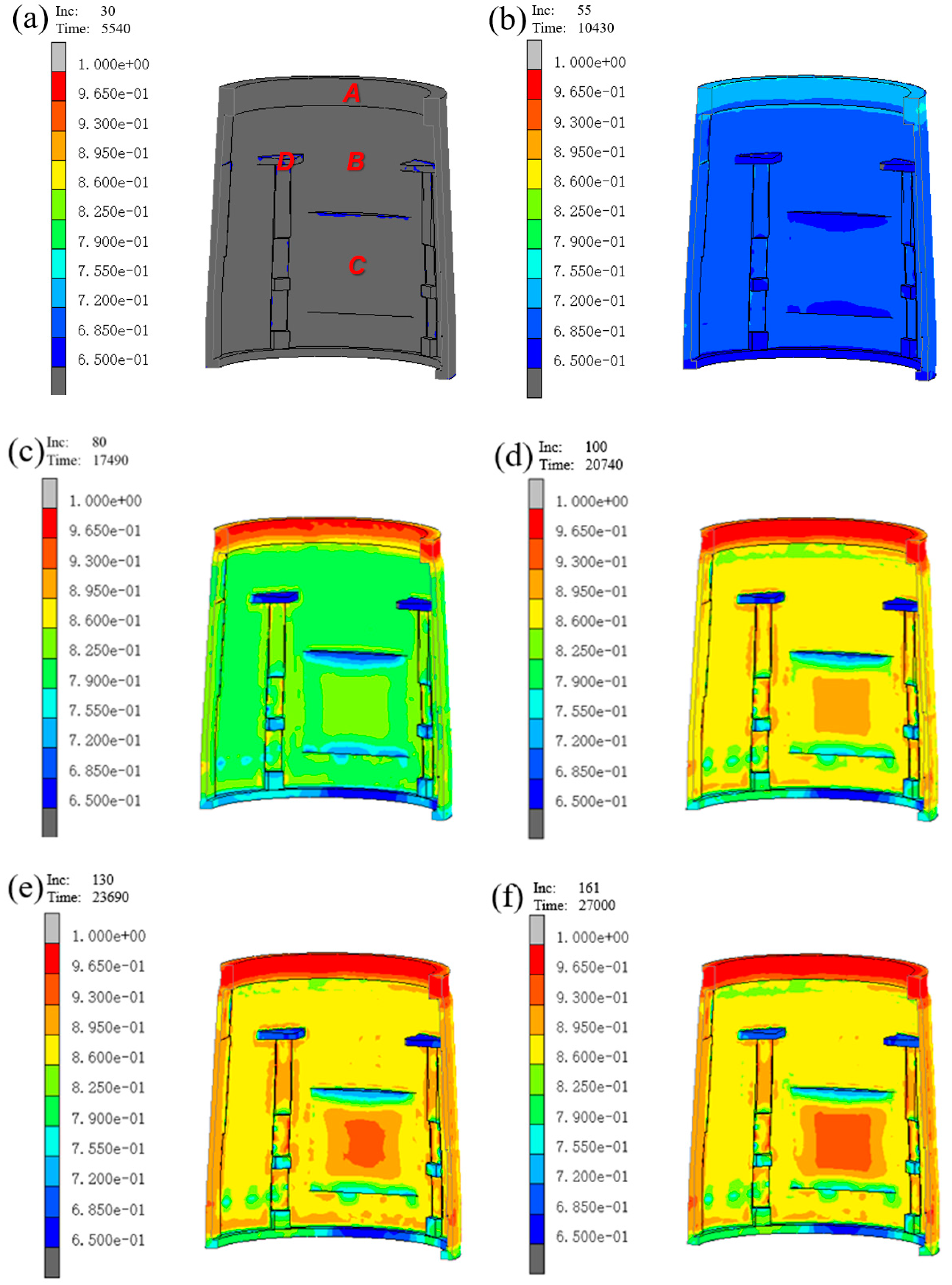
3.1. Analysis of the Powder Densification Process
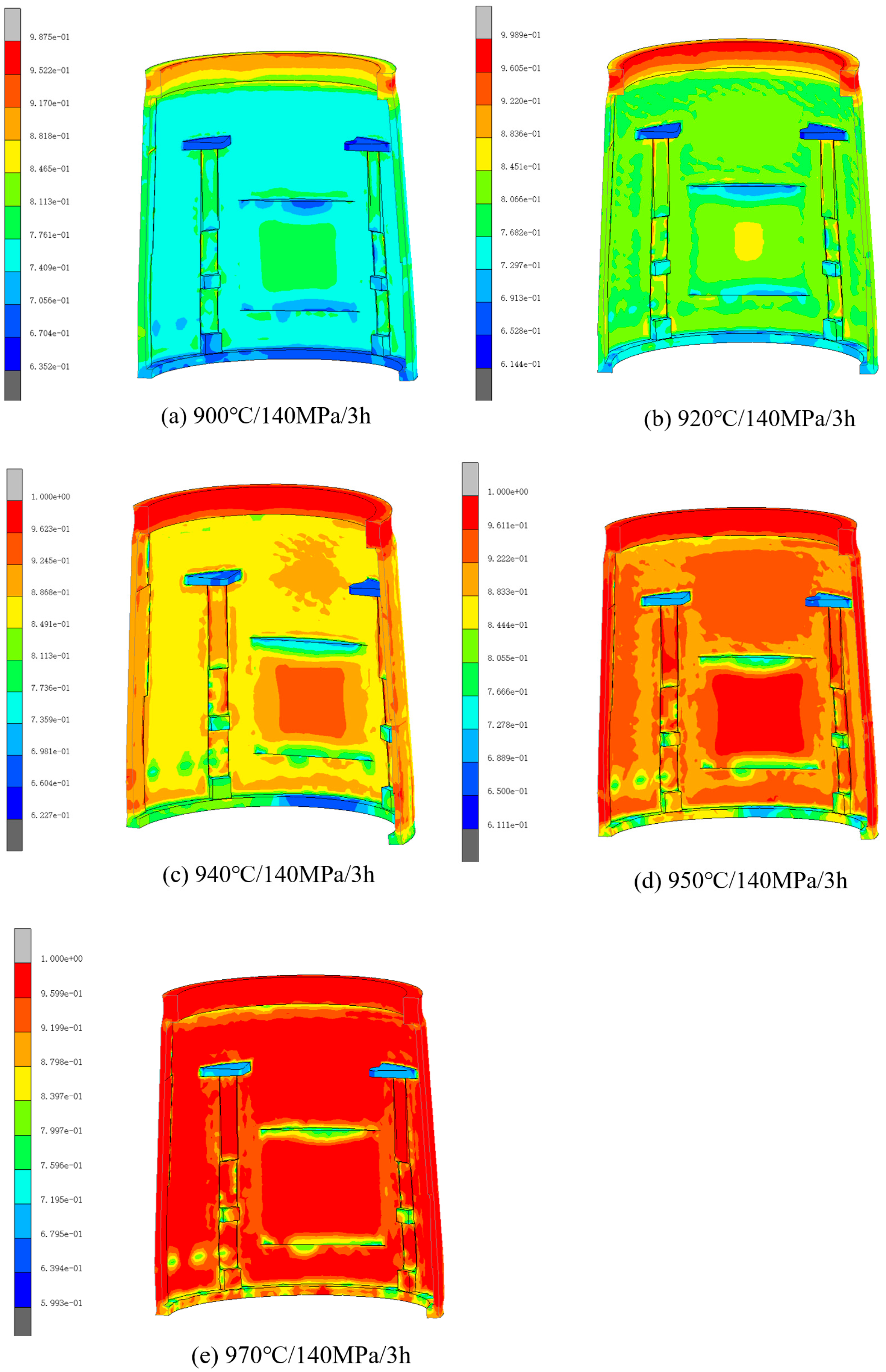
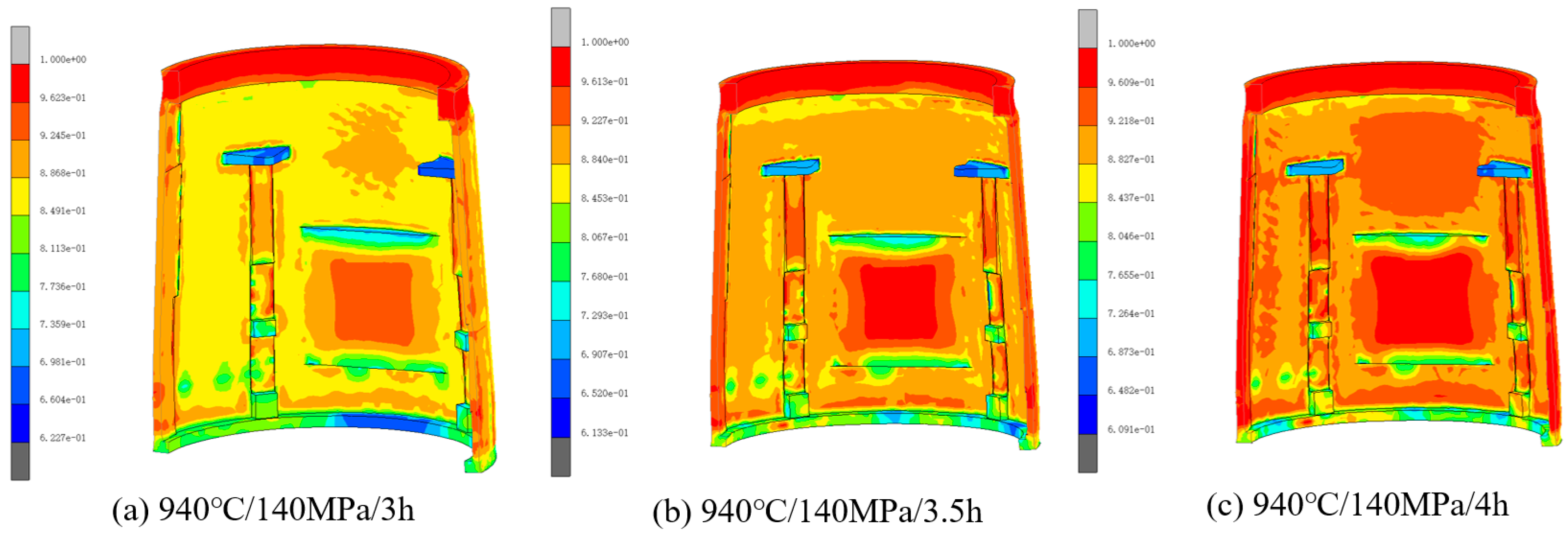
3.2. Effects of Processing Parameters on Densification
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bünck, M.; Stoyanov, T.; Schievenbusch, J.; Michels, H.; Gußfeld, A. Titanium aluminide casting technology development. JOM 2017, 69, 2565–2570. [Google Scholar] [CrossRef]
- Williams, J.C.; Boyer, R.R. Opportunities and issues in the application of titanium alloys for aerospace components. Metals 2020, 10, 705. [Google Scholar] [CrossRef]
- Zhao, Q.; Sun, Q.; Xin, S.; Chen, Y.; Wu, C.; Wang, H.; Xu, J.; Wan, M.; Zeng, W.; Zhao, Y. High-strength titanium alloys for aerospace engineering applications: A review on melting-forging process. Mater. Sci. Eng. A 2022, 845, 143260. [Google Scholar] [CrossRef]
- Luan, J.H.; Jiao, Z.B.; Liu, W.H.; Lu, Z.; Zhao, W.; Liu, C. Compositional and microstructural optimization and mechanical-property enhancement of cast Ti alloys based on Ti-6Al-4V alloy. Mater. Sci. Eng. A 2017, 704, 91–101. [Google Scholar] [CrossRef]
- Rielli, V.V.; Amigó-Borrás, V.; Contieri, R.J. Microstructural evolution and mechanical properties of in-situ as-cast beta titanium matrix composites. J. Alloys Compd. 2019, 778, 186–196. [Google Scholar] [CrossRef]
- Liu, J.; Chen, G.; Zhao, L.; Yu, Z.; Jia, X. Research status and development trend of cutting surface integrity of aerospace alloy materials. Int. J. Adv. Manuf. Technol. 2023, 127, 45–63. [Google Scholar] [CrossRef]
- Nabhani, F. Machining of aerospace titanium alloys. Robot. Comput.-Integr. Manuf. 2001, 17, 99–106. [Google Scholar] [CrossRef]
- Atkinson, H.V.; Davies, S. Fundamental aspects of hot isostatic pressing: An overview. Metall. Mater. Trans. A 2000, 31, 2981–3000. [Google Scholar] [CrossRef]
- Rao, G.; Sankaranarayana, M.; Balasubramaniam, S. Hot isostatic pressing technology for defence and space applications. Def. Sci. J. 2012, 62, 73–80. [Google Scholar] [CrossRef]
- You, D.; Wang, Y.; Yang, C.; Li, F. Comparative analysis of the hot-isostatic-pressing densification behavior of atomized and milled Ti6Al4V powders. J. Mater. Res. Technol. 2020, 9, 3091–3108. [Google Scholar] [CrossRef]
- Garibov, G. Hot isostatic pressing of Ni-base superalloy is a main development of new mate rials for production of critical gas turbine engine components. In Proceedings of the International Conference on Hot Isostatic, Pressing HIP’02, Moscow, Russia, 20–22 May 2002. [Google Scholar]
- Wang, Z.; Tan, Y.N.; Li, N. Powder metallurgy of titanium alloys: A brief review. J. Alloys Compd. 2023, 965, 171030. [Google Scholar] [CrossRef]
- Ying, Z.; Sun, Y.; Wang, L.; Zhang, X.H.; Xu, G. Near-net shaping of titanium alloy powders by HIP technology: A review. Mater. Rep. 2019, 33, 1099–1108. [Google Scholar]
- Xu, L.; Guo, R.; Bai, C.; Lei, J.; Yang, R. Effect of hot isostatic pressing conditions and cooling rate on microstructure and properties of Ti-6Al-4V alloy from atomized powder. J. Mater. Sci. Technol. 2014, 30, 1289–1295. [Google Scholar] [CrossRef]
- Kim, Y.; Song, Y.-B.; Lee, S.H. Microstructure and intermediate-temperature mechanical properties of powder metallurgy Ti-6Al-4V alloy prepared by the prealloyed approach. J. Alloys Compd. 2015, 637, 234–241. [Google Scholar] [CrossRef]
- Perevoshchikova, N.; Hutchinson, C.R.; Wu, X. The design of hot-isostatic pressing schemes for Ti-5Al-5Mo-5V-3Cr (Ti-5553). Mater. Sci. Eng. A 2016, 657, 371–382. [Google Scholar] [CrossRef]
- Redouani, L.; Boudrahem, S.; Alem, S. New hot isostatic pressing (HIP) simulation method with taking into account of the operating cycle ramp. Int. J. Adv. Manuf. Technol. 2019, 102, 3291–3299. [Google Scholar] [CrossRef]
- Kohar, C.P.; Martin, E.; Connolly, D.S.; Patil, S.; Krutz, N.; Wei, D.; Inal, K. A new and efficient thermo-elasto-viscoplastic numerical implementation for implicit finite element simulations of powder metals: An application to hot isostatic pressing. Int. J. Mech. Sci. 2019, 155, 222–234. [Google Scholar] [CrossRef]
- Kuhn, H.A. Deformation characteristics and plasticity theory of sintered powder materials. Int. J. Powder Metall. 1971, 7, 15–26. [Google Scholar]
- Shima, S.; Oyane, M. Plasticity theory for porous metals. Int. J. Mech. Sci. 1976, 18, 285–291. [Google Scholar] [CrossRef]
- Fleck, N.A.; Kuhn, L.T.; Mcmeeking, R. Yielding of metal powder bonded by isolated contacts. J. Mech. Phys. Solids 1992, 40, 1139–1162. [Google Scholar] [CrossRef]
- Mori, K.; Shiomi, M.; Osakada, K. Inclusion of microscopic rotation of powder particles during compaction in finite element method using Cosserat continuum theory. Int. J. Numer. Methods Eng. 1998, 42, 847–856. [Google Scholar] [CrossRef]
- Doraivelu, S.M.; Gegel, H.L.; Gunasekera, J.S. A new yield function for compressible, ja:math, materials. Int. J. Mech. Sci. 1984, 26, 527–535. [Google Scholar] [CrossRef]
- Park, J.J. Constitutive relations to predict plastic deformations of porous metals in compaction. Int. J. Mech. Sci. 1995, 37, 709–719. [Google Scholar] [CrossRef]
- Lee, D.N.; Kim, H.S. Plastic Yield Behaviour of Porous Metals. Powder Metall. 1993, 35, 275–280. [Google Scholar] [CrossRef]
- Liu, G.C.; Shi, Y.S.; Wei, Q.S.; Wang, J.W. Finite element analysis of pressure influence on densification of titanium alloy powder under hot isostatic pressing. Key Eng. Mater. 2011, 450, 206–209. [Google Scholar] [CrossRef]
- Meng, F.; Lang, L.; Xiao, Y. Comparative analysis of the hot isostatic pressing densification behavior of uniform and non-uniform distributed powder. Metals 2023, 13, 1319. [Google Scholar] [CrossRef]
- Lang, L.; Xu, W.; Huang, X.; Li, F. Numerical simulation of complex thin-walled aluminum alloy part manufactured by hot isostatic pressing. Forg. Stamp. Technol. 2019, 46, 65–72. [Google Scholar]
- Xu, B.; Dong, T.T.; Deng, T.Q.; Yi, Z.X.; Xu, Y.; Jia, J.B. Microstructure and mechanical properties of TC4 alloy cylinder with inner ribs prepared by hot isostatic pressing. Chin. J. Nonferrous Met. 2024, 34, 2257–2272. (In Chinese) [Google Scholar] [CrossRef]
- Ye, C.H.W.; Wang, L.; Zhang, X.H. Application of titanium alloy HIP near-net forming technology in aerospace. Mater. Guide 2012, 26, 112–114. [Google Scholar]
- Liu, D.H. Numerical Simulation and Densification Analysis of Ti6Al4V Powder by Hot Isostatic Pressing. Master’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2018. [Google Scholar]
- Kim, K.T.; Yang, H.C. Densification behaviour of titanium alloy powder under hot isostatic pressing. Powder Metall. 2013, 44, 41–47. [Google Scholar] [CrossRef]
- Noori Banu, P.S.; Devaki Rani, S. Beta transus prediction of titanium alloys through integration of artificial neural network and multifactor dimensionality reduction analyses. Mater. Discov. 2015, 2, 16–23. [Google Scholar] [CrossRef]
- Fellah, M.; Hezil, N.; Samad, M.A.; Djellabi, R.; Montagne, A.; Mejias, A.; Kossman, S.; Iost, A.; Purnama, A.; Obrosov, A. Effect of Molybdenum Content on Structural, Mechanical, and Tribological Properties of Hot Isostatically Pressed β-Type Titanium Alloys for Orthopedic Applications. J. Mater. Eng. Perform. 2019, 28, 5988–5999. [Google Scholar] [CrossRef]
- Ji, C.; Lang, L.; Huang, X.; Meng, F.; Xu, W. Study on the Powder Solid Interface and Coupled Deformation during high temperature and high pressure forming of Ti6Al4V Alloy Powder. J. Cent. South Univ. (Sci. Technol.) 2019, 50, 29–37. [Google Scholar]
- Gasik, M.; Zhang, B. A constitutive model and FE simulation for the sintering process of powder compacts. Comput. Mater. Sci. 2000, 18, 93–101. [Google Scholar] [CrossRef]

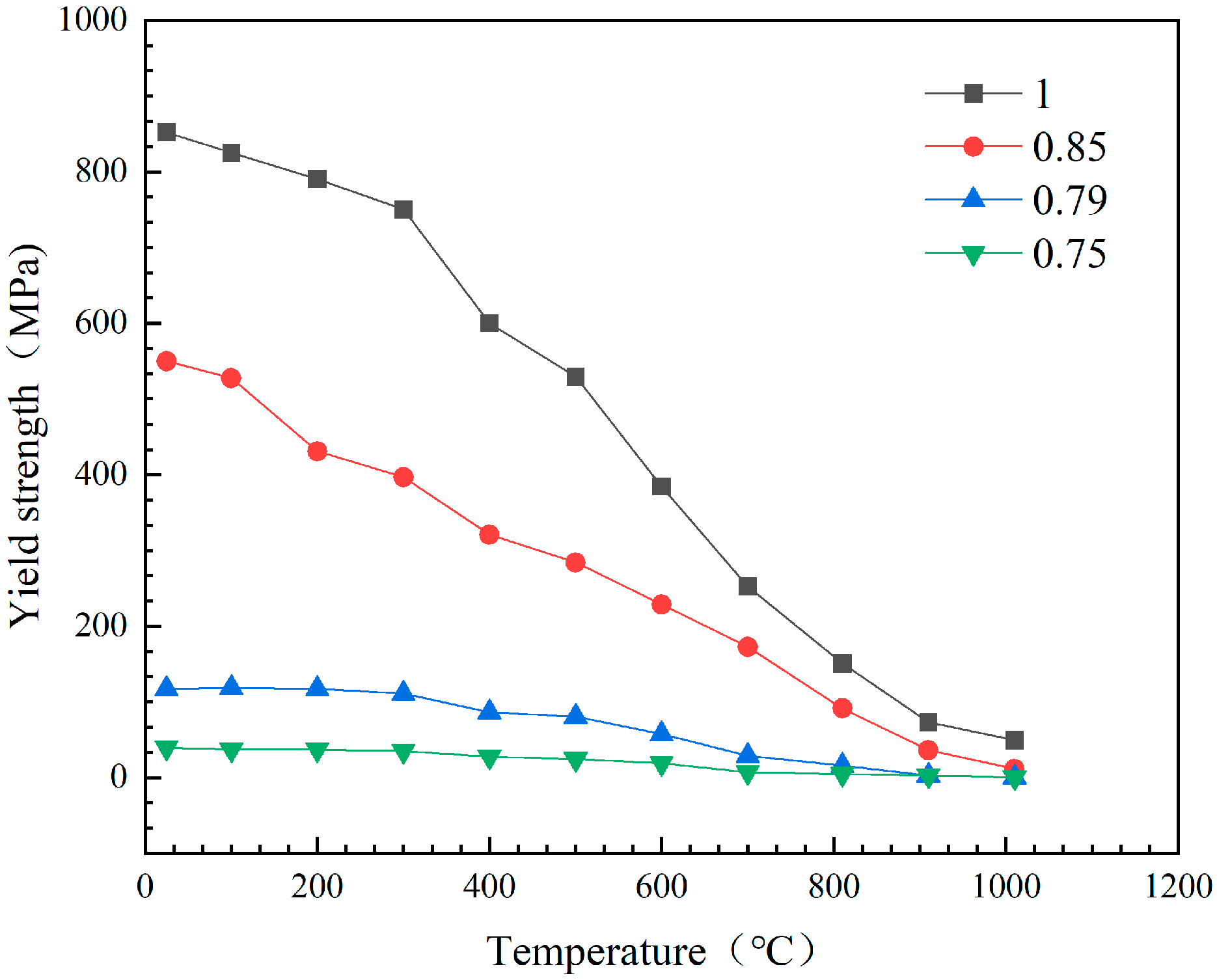
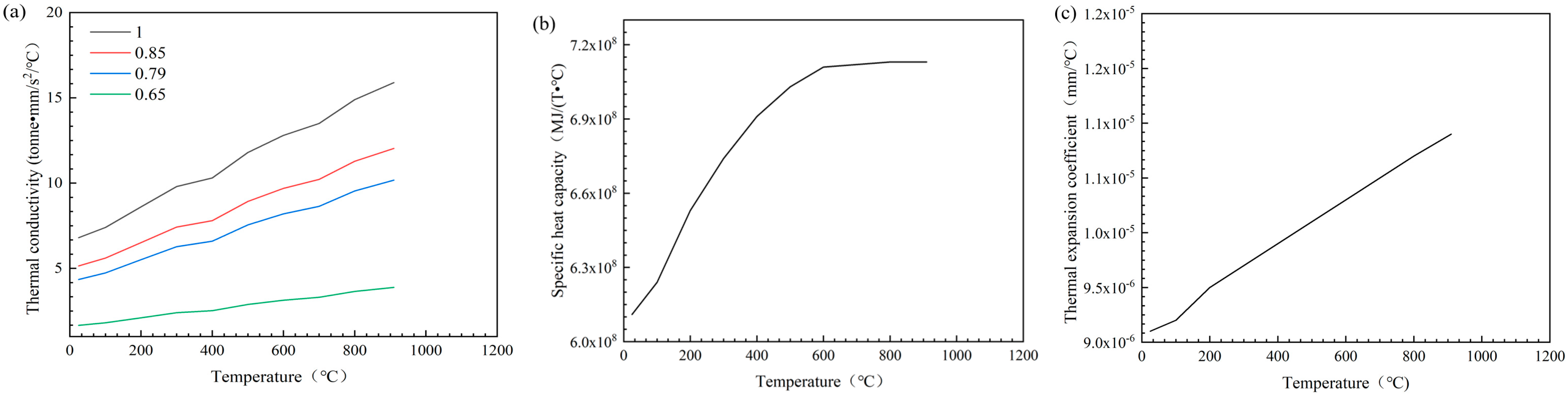

| Temperature (°C) | 25 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
|---|---|---|---|---|---|---|---|---|---|---|
| Elasticity (GPa) | 103 | 99 | 94 | 89 | 84 | 80 | 74 | 71 | 65 | 60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Geng, L.; Zhang, G. Numerical Simulation of the Hot Isostatic Pressing Densification Behavior of Ti6Al4V Powder for a Thin-Walled Tubular Component with Non-Axisymmetric Inner Ribs. Metals 2025, 15, 173. https://doi.org/10.3390/met15020173
Jiang Y, Geng L, Zhang G. Numerical Simulation of the Hot Isostatic Pressing Densification Behavior of Ti6Al4V Powder for a Thin-Walled Tubular Component with Non-Axisymmetric Inner Ribs. Metals. 2025; 15(2):173. https://doi.org/10.3390/met15020173
Chicago/Turabian StyleJiang, Yanqing, Lin Geng, and Guofeng Zhang. 2025. "Numerical Simulation of the Hot Isostatic Pressing Densification Behavior of Ti6Al4V Powder for a Thin-Walled Tubular Component with Non-Axisymmetric Inner Ribs" Metals 15, no. 2: 173. https://doi.org/10.3390/met15020173
APA StyleJiang, Y., Geng, L., & Zhang, G. (2025). Numerical Simulation of the Hot Isostatic Pressing Densification Behavior of Ti6Al4V Powder for a Thin-Walled Tubular Component with Non-Axisymmetric Inner Ribs. Metals, 15(2), 173. https://doi.org/10.3390/met15020173





