Integrating Temperature History into Inherent Strain Methodology for Improved Distortion Prediction in Laser Powder Bed Fusion
Abstract
1. Introduction
- Develop the EISM: incorporate thermal history effects to improve the physical accuracy of residual stress and distortion predictions.
- Validate predictive accuracy: compare EISM and ISM results with experimental data for parts with complex thermal gradients.
- Assess computational efficiency: evaluate and compare the computational cost and performance of ISM and EISM.
- Modelling Approach (Section 2) details the enhanced inherent strain modelling approach, including how macro-scale thermal histories are integrated into the original ISM framework.
- Experimental Campaign for Calibration and Validation (Section 3) describes the experimental campaign, including the tested geometries, materials, process parameters, and measurement techniques used for calibration and validation.
- Numerical Implementation (Section 4) presents the numerical implementation of the EISM in the selected testing geometries, including mesh generation, boundary conditions, and computational settings.
- Results and Discussion (Section 5) compares EISM and ISM predictions with experimental data, discussing the effects of mesh size, layer lumping, and computational efficiency.
- Conclusions (Section 6) summarizes the key findings and outlines future research directions.
2. Modelling Approach
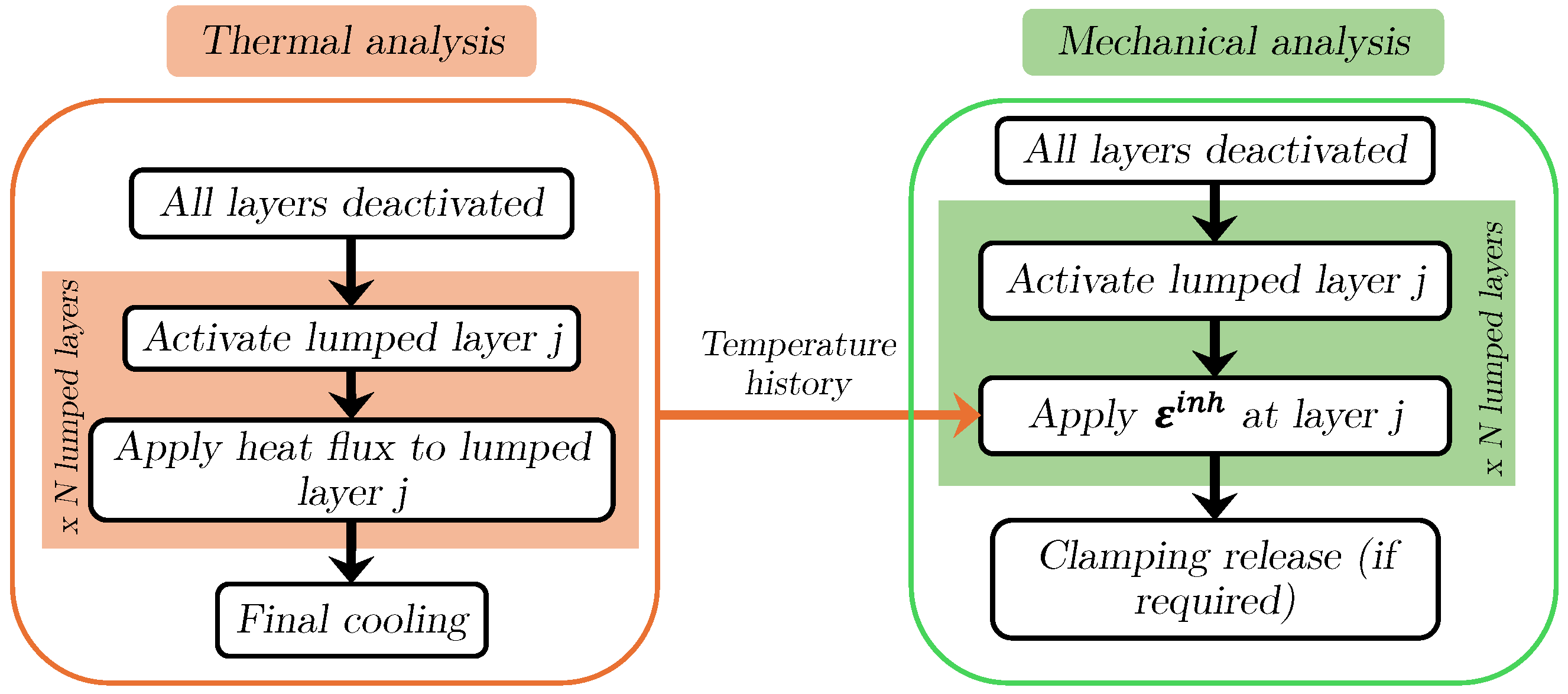
2.1. Thermal Analysis
- Convection: , where h is the heat transfer coefficient, and is the ambient temperature.
- Radiation: , where is the emissivity, and is the Stefan–Boltzmann constant.
2.2. Mechanical Analysis
2.3. EISM Considerations
2.4. Material Deposition Modelling
3. Experimental Campaign for Calibration and Validation
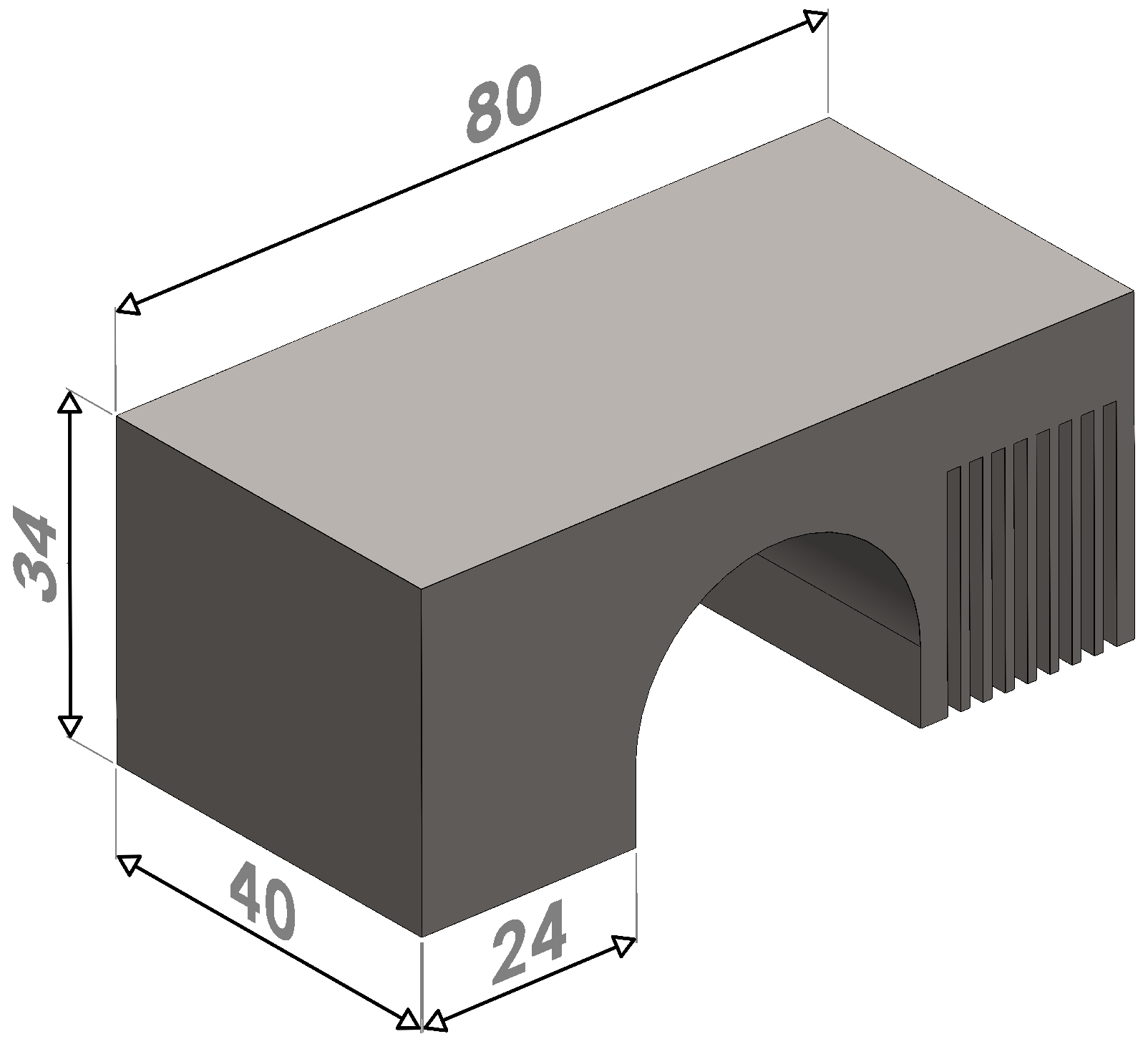
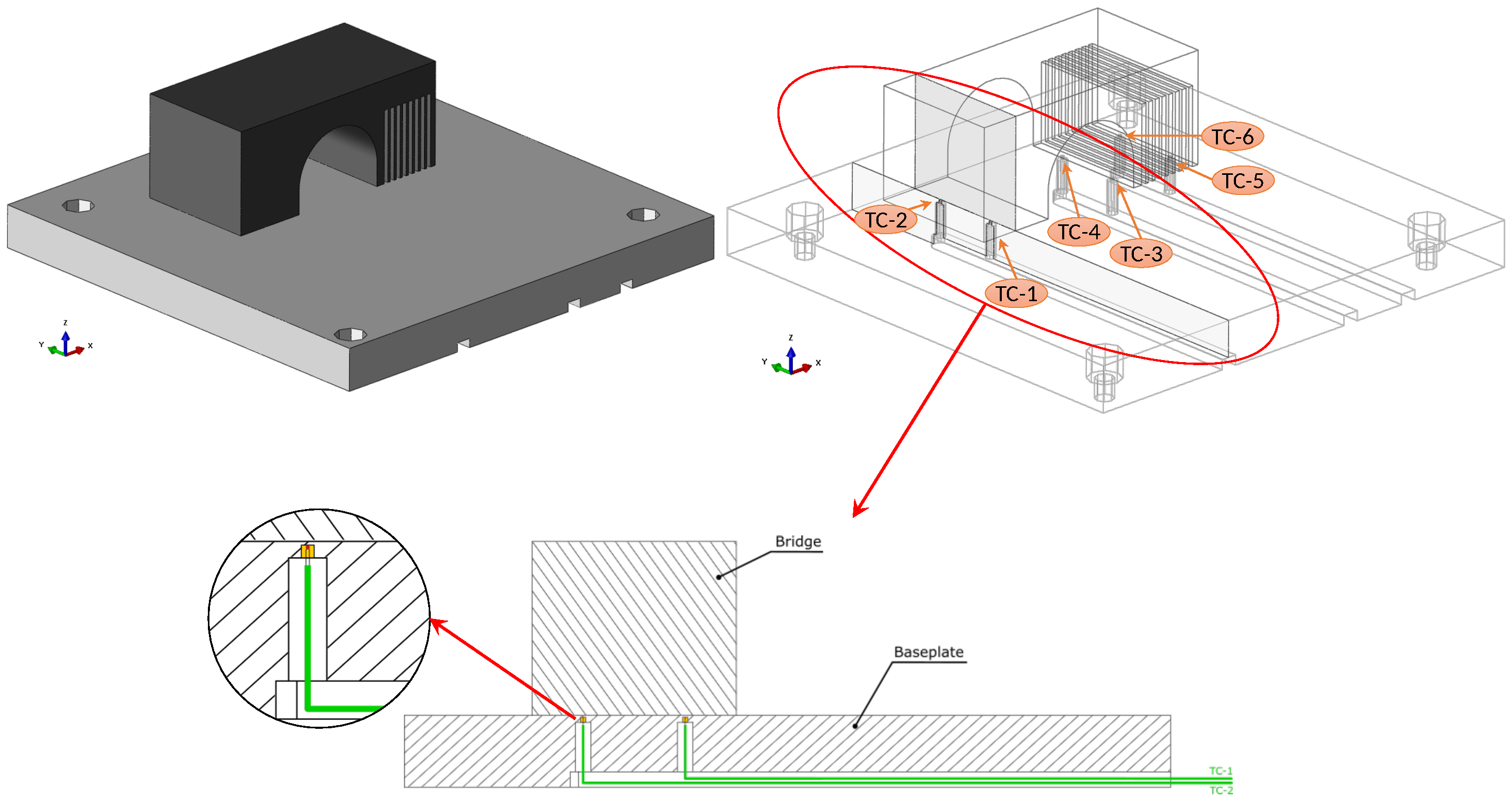
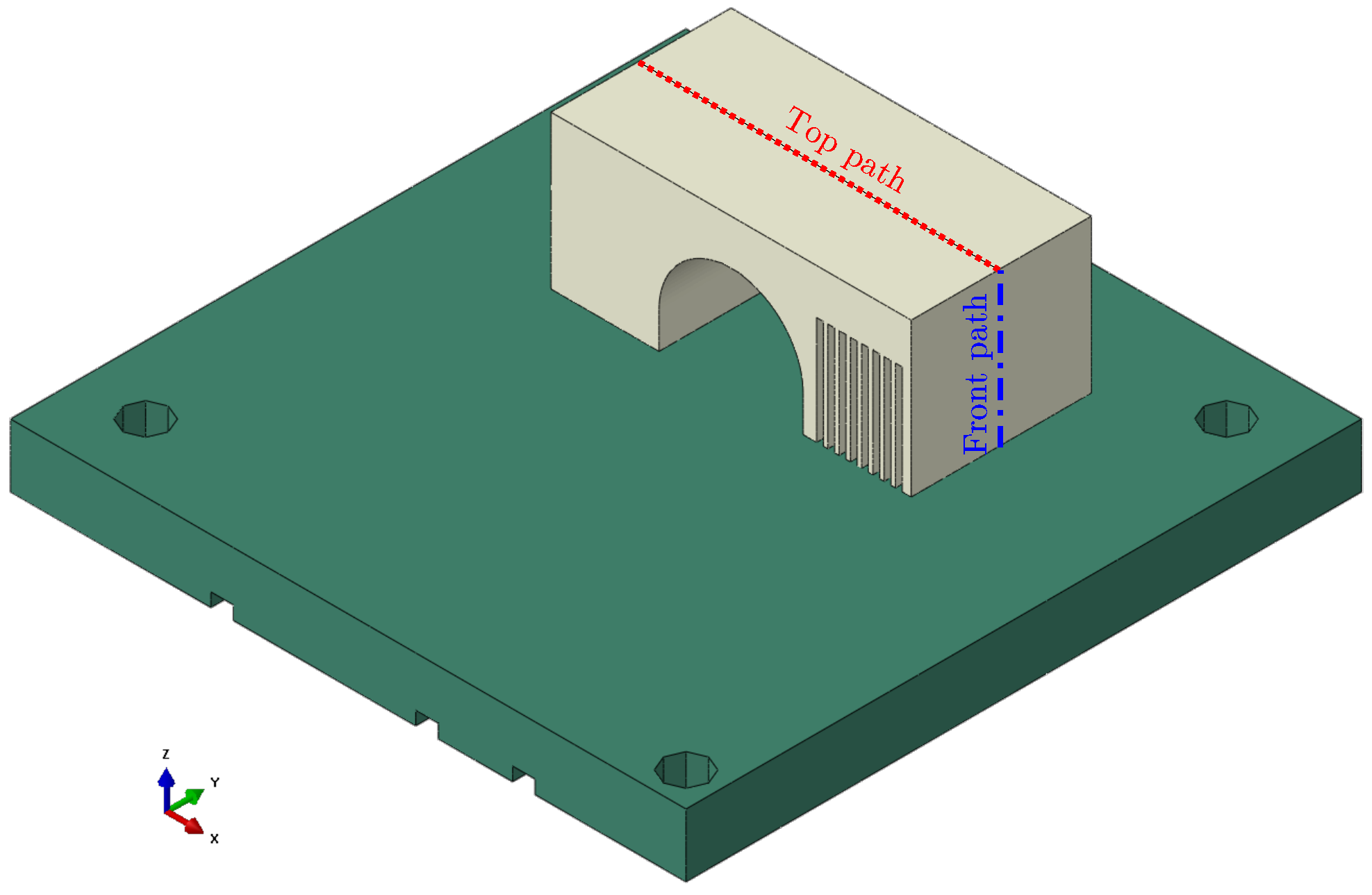
- The non-symmetric bridge geometry (Figure 2), chosen for its simplicity, allowed for an analysis of local temperature, distortion, and residual stress. It was manufactured on a baseplate with dimensions of .
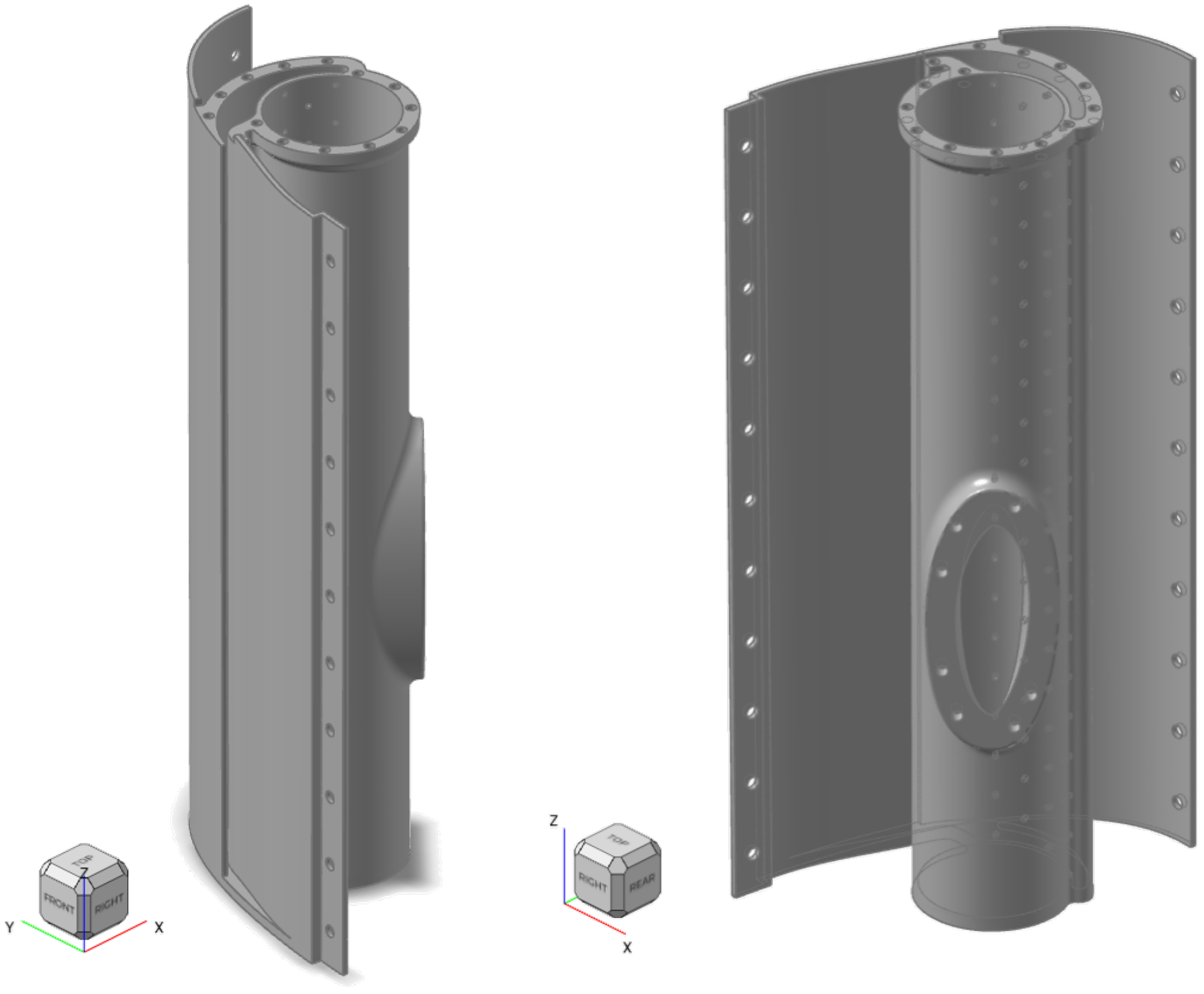
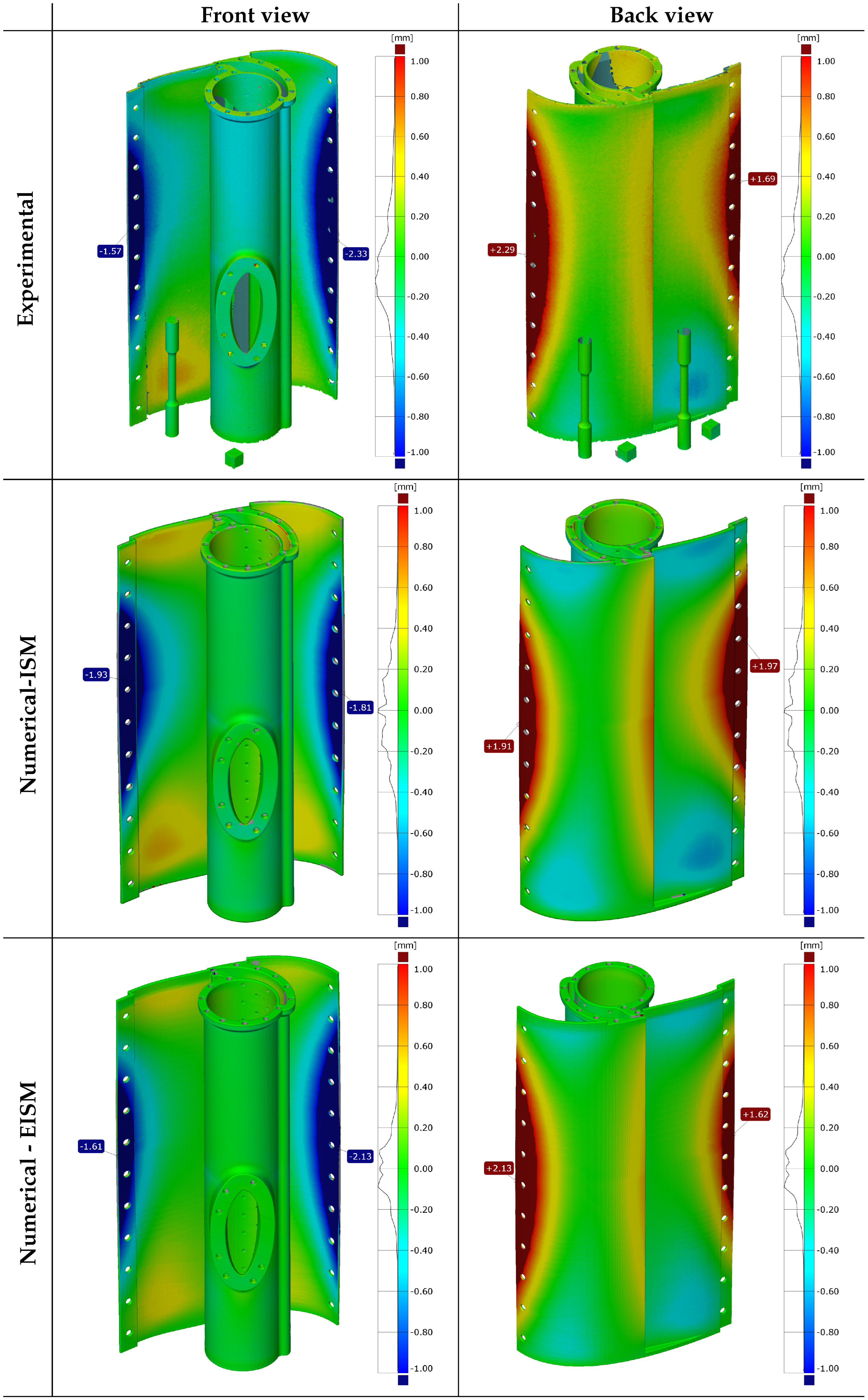
- The Steady Blowing Actuator (SBA) (Figure 3), representing a complex industrial application, was ideal for studying distortions in larger, more complex designs. It was manufactured on a baseplate with dimensions of .
4. Numerical Implementation
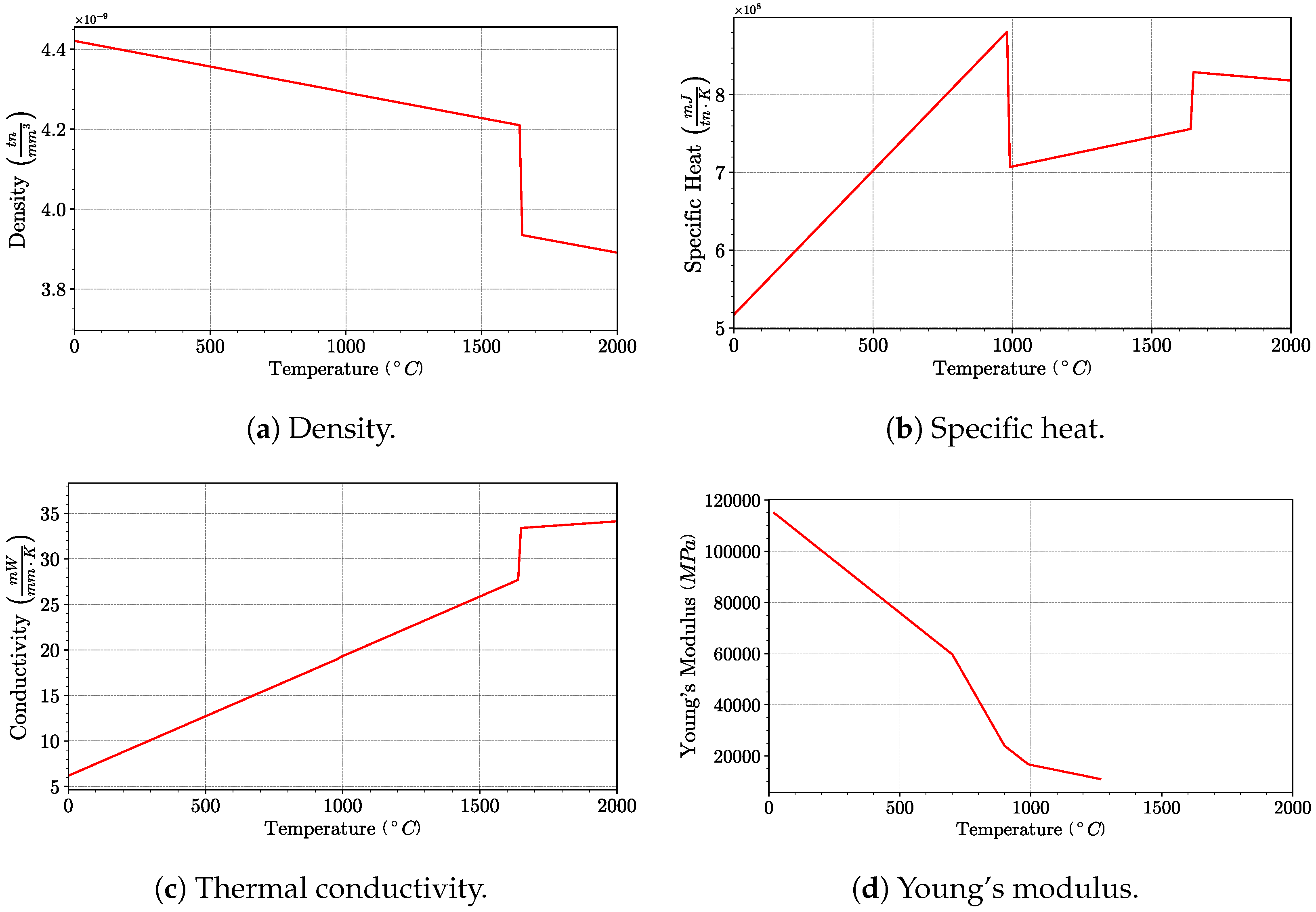
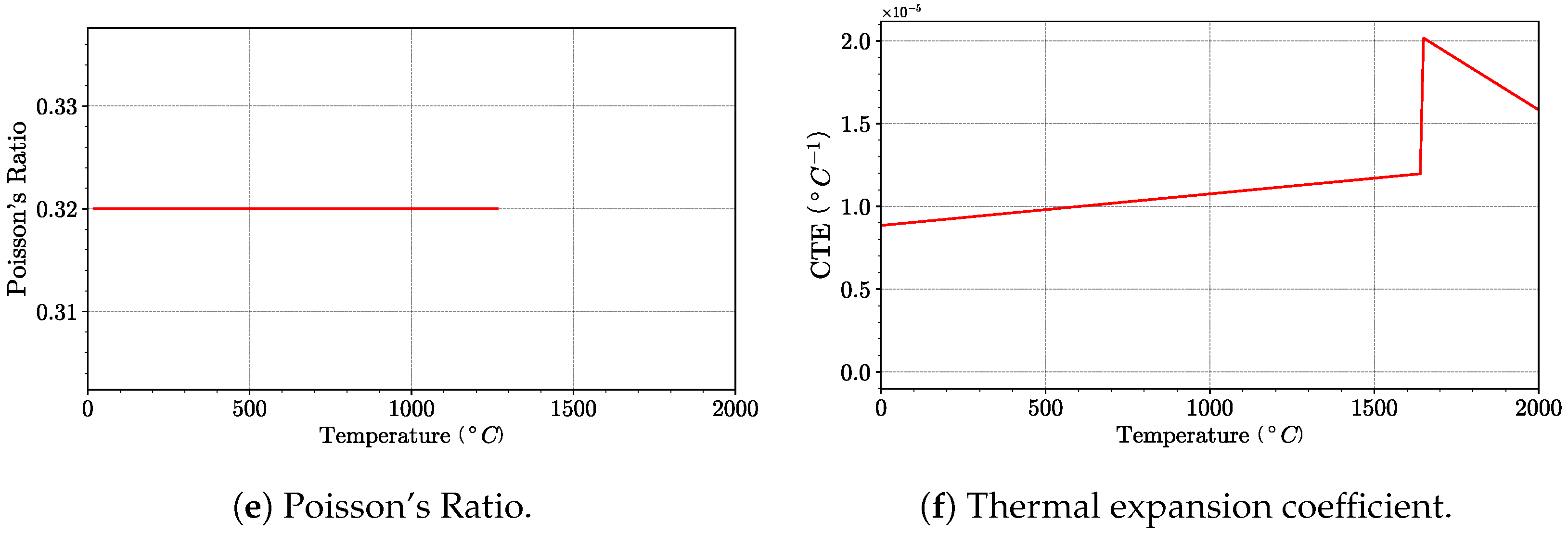
4.1. Material Properties
4.2. Geometrical Model and FE Mesh
4.3. Initial and Boundary Conditions
4.3.1. Thermal Analysis
4.3.2. Mechanical Analysis
4.4. EISM Analysis Characteristics
5. Results and Discussion
5.1. Non-Symmetric Bridge
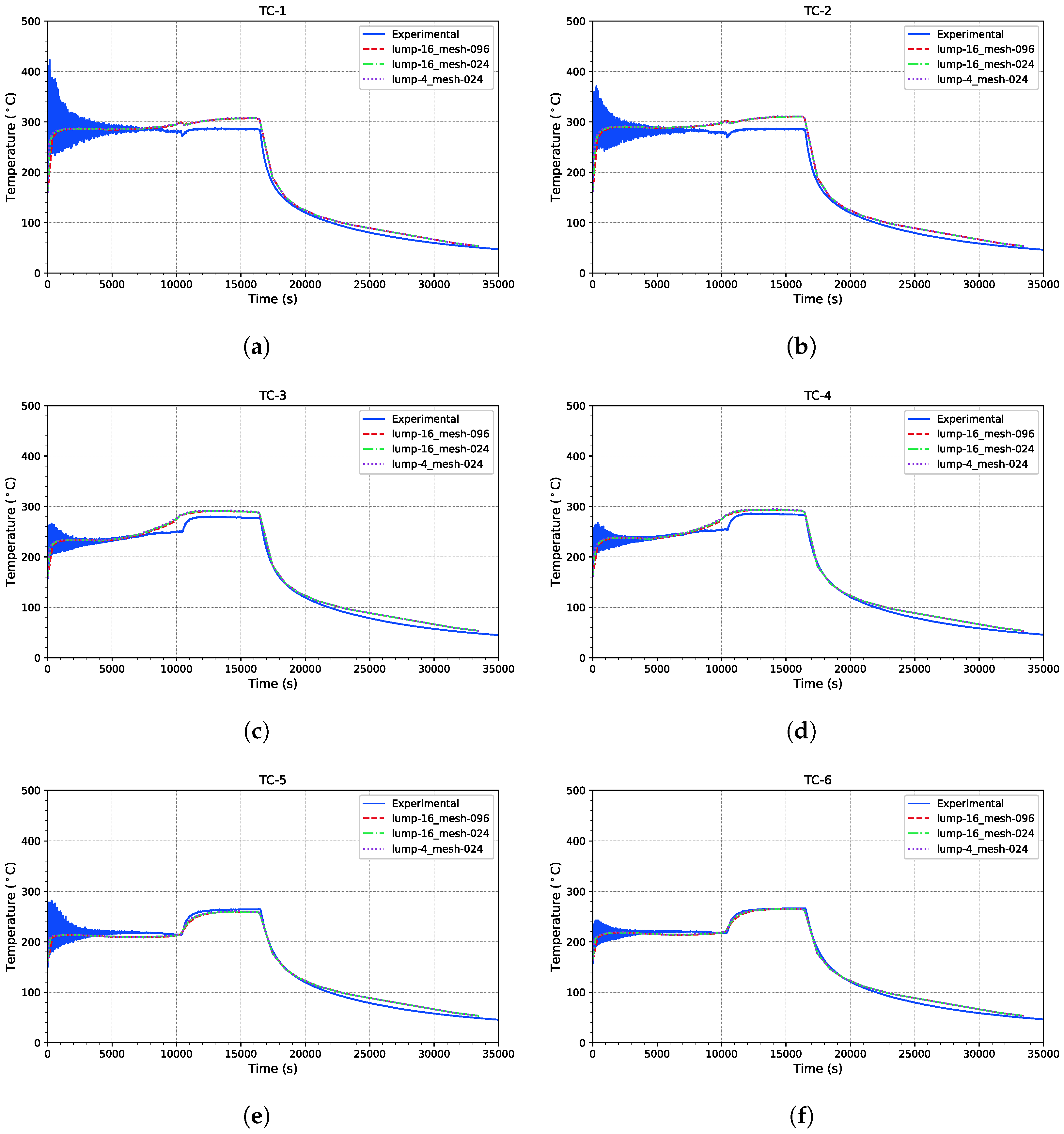
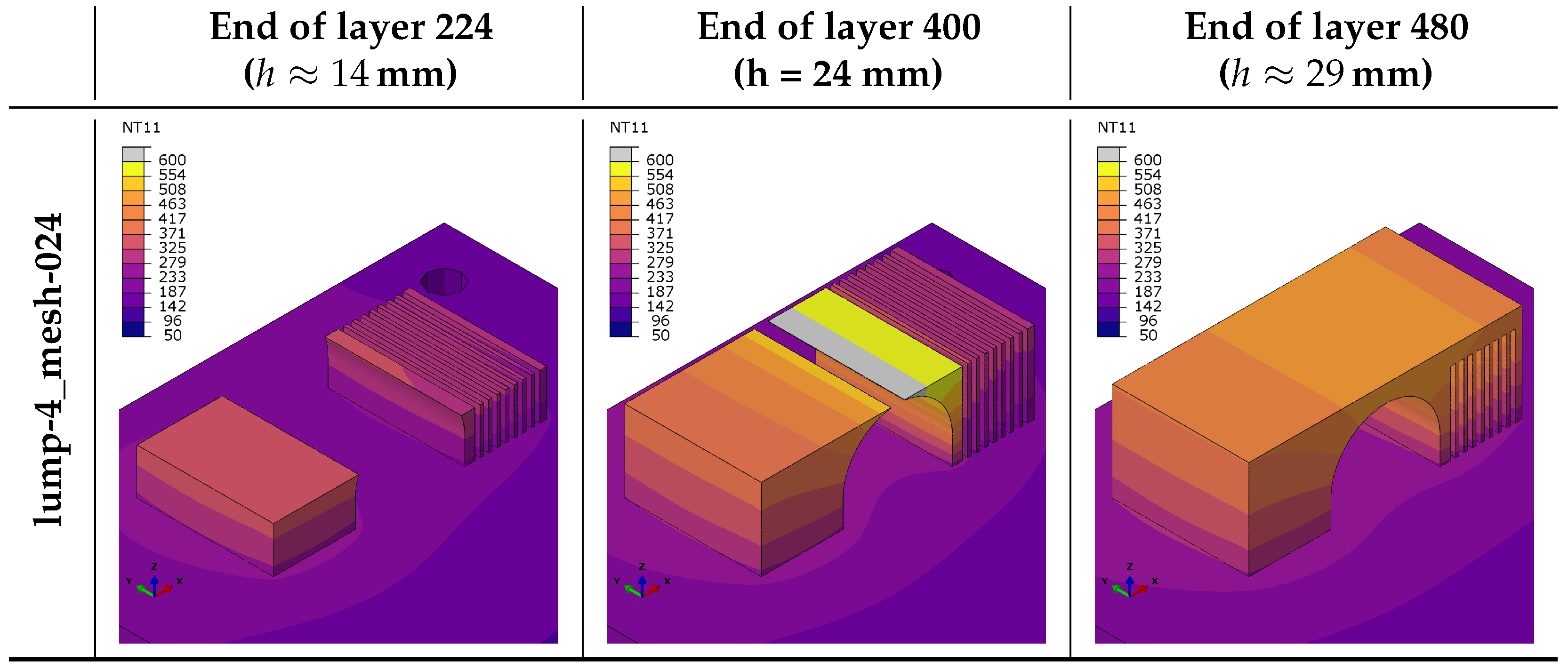
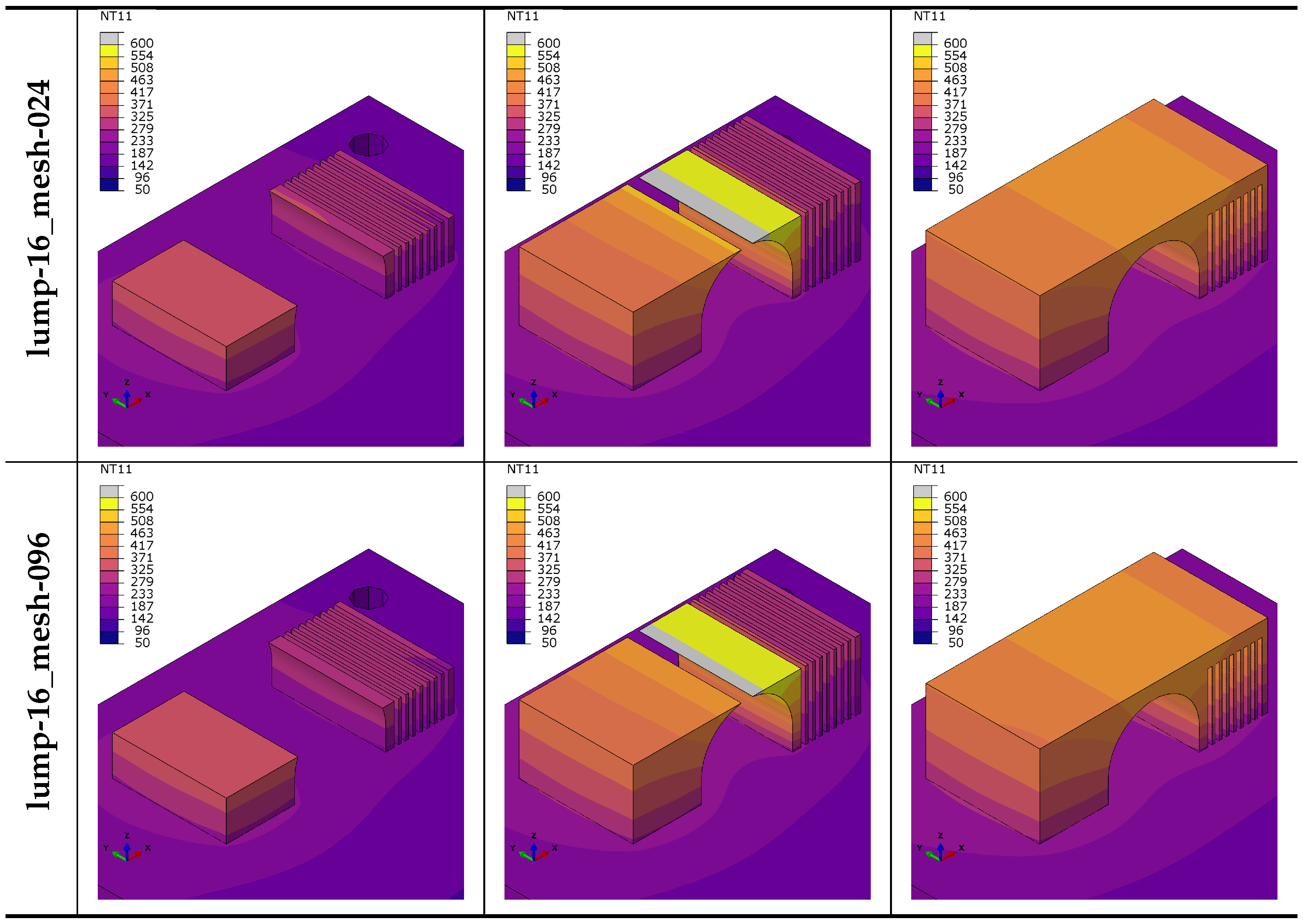
5.1.1. Temperature Evolution
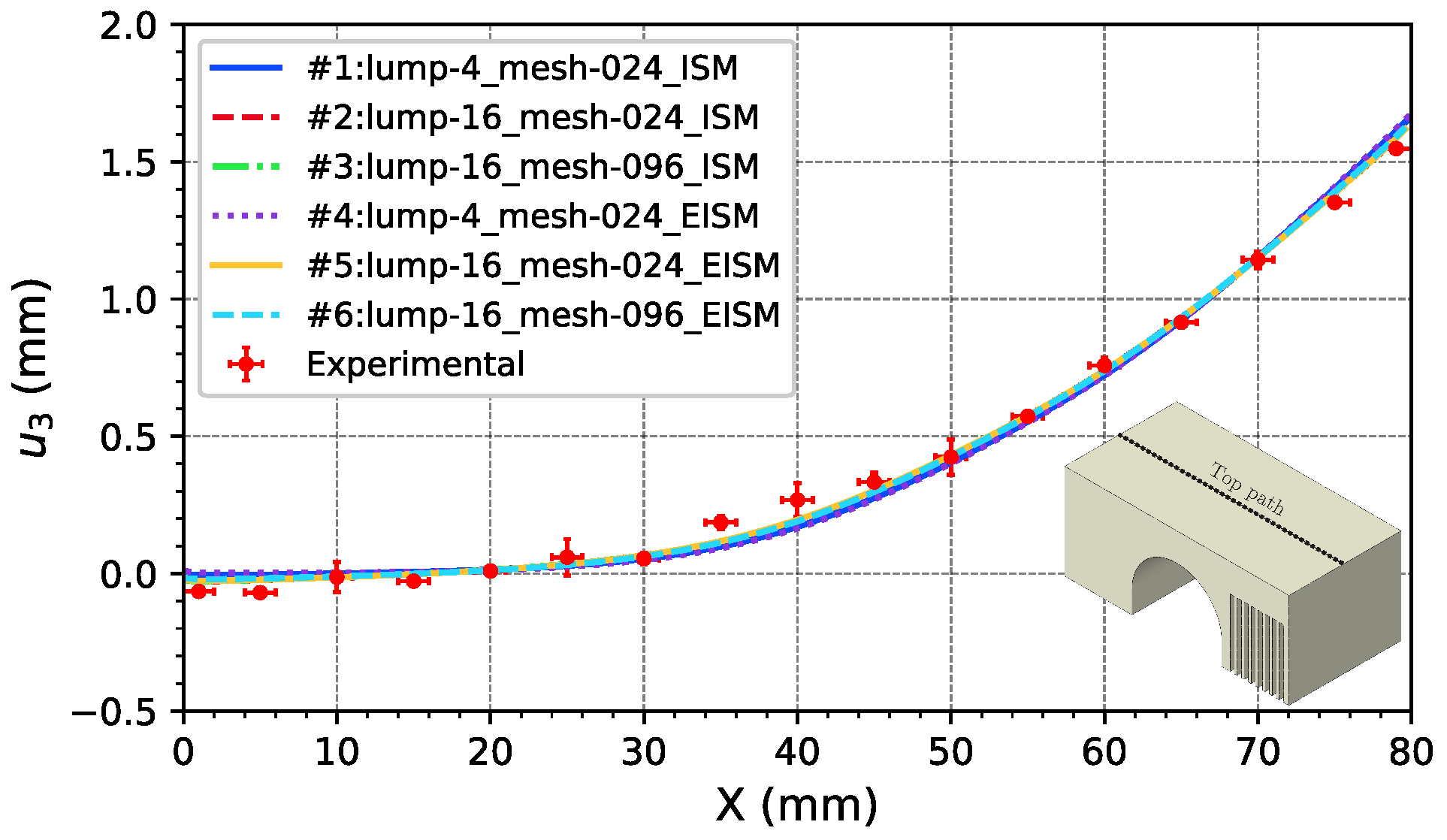
5.1.2. Distortion
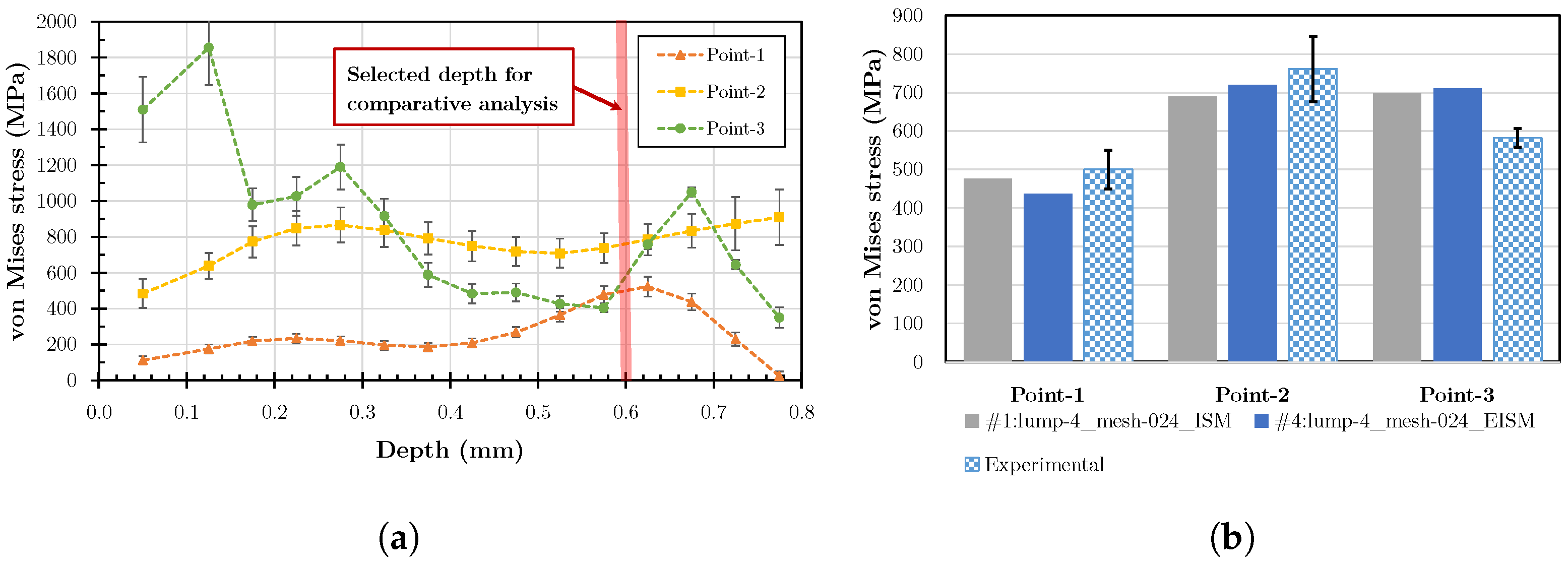
5.1.3. Residual Stress
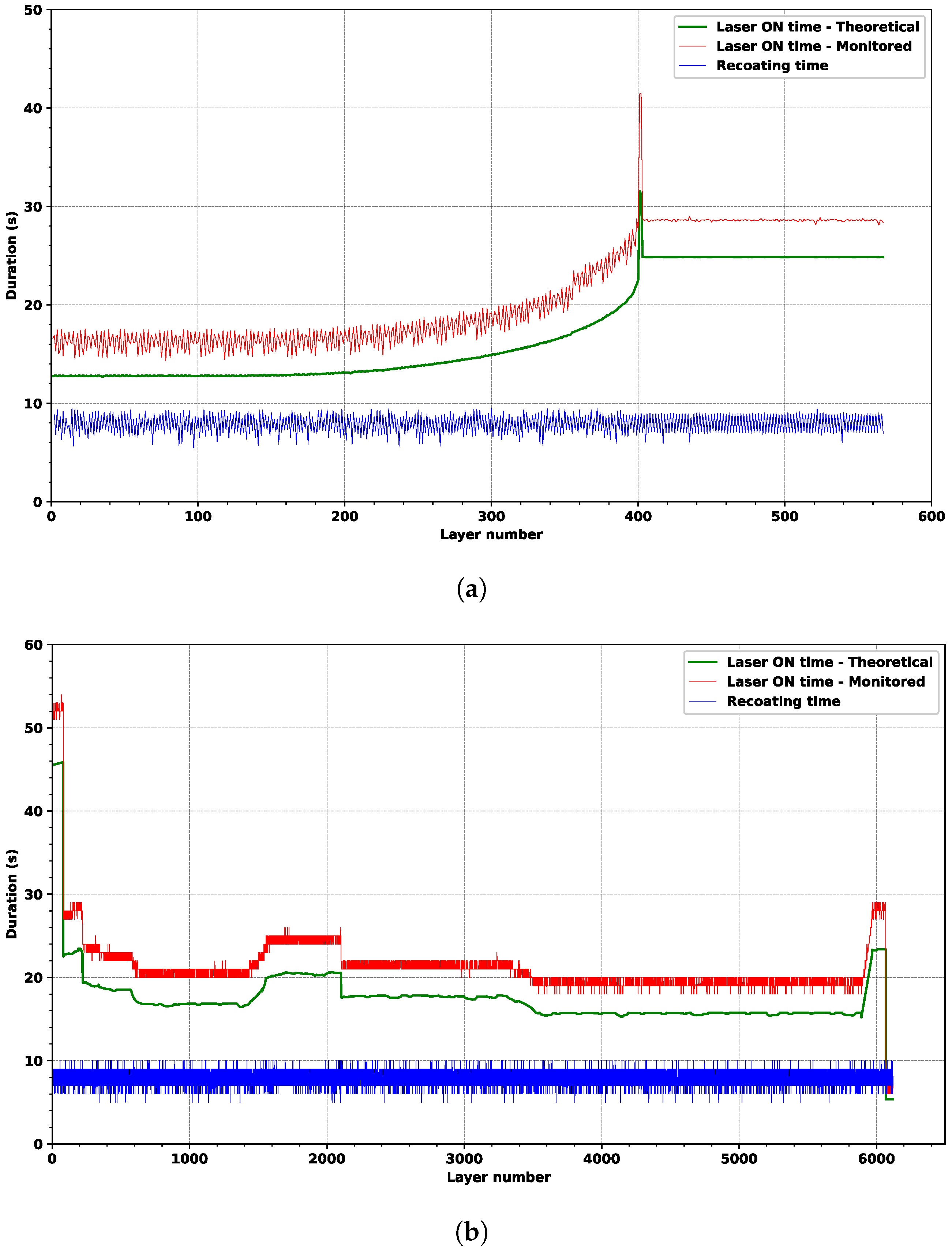
5.1.4. Computational Efficiency
5.2. SBA
5.2.1. Temperature Evolution
5.2.2. Inherent Strain Evolution
5.2.3. Distortion
5.2.4. Computational Efficiency
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Gibson, I.; Rosen, D.; Stucker, B. Additive Manufacturing Technologies; Springer: Berlin/Heidelberg, Germany, 2013; pp. 10–12. [Google Scholar]
- DebRoy, T.; Wei, H.; Zuback, J.; Mukherjee, T.; Elmer, J.; Milewski, J.; Beese, A.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Herzog, D.; Seyda, V.; Wycisk, E.; Emmelmann, C. Additive manufacturing of metals. Acta Mater. 2016, 117, 371–392. [Google Scholar] [CrossRef]
- Thompson, S.M.; Bian, L.; Shamsaei, N.; Yadollahi, A. An overview of Direct Laser Deposition for additive manufacturing; Part I: Transport phenomena, modeling and diagnostics. Addit. Manuf. 2015, 8, 36–62. [Google Scholar] [CrossRef]
- Ford, S.; Despeisse, M. Additive manufacturing and sustainability: An exploratory study of the advantages and challenges. J. Clean. Prod. 2016, 137, 1573–1587. [Google Scholar] [CrossRef]
- Kruth, J.; Froyen, L.; Vaerenbergh, J.V.; Mercelis, P.; Rombouts, M.; Lauwers, B. Selective laser melting of iron-based powder. J. Mater. Process. Technol. 2004, 149, 616–622. [Google Scholar] [CrossRef]
- Zaeh, M.F.; Branner, G. Investigations on residual stresses and deformations in selective laser melting. Prod. Eng. 2010, 4, 35–45. [Google Scholar] [CrossRef]
- Bayat, M.; Zinovieva, O.; Ferrari, F.; Ayas, C.; Langelaar, M.; Spangenberg, J.; Salajeghe, R.; Poulios, K.; Mohanty, S.; Sigmund, O.; et al. Holistic computational design within additive manufacturing through topology optimization combined with multiphysics multi-scale materials and process modelling. Prog. Mater. Sci. 2023, 138, 101129. [Google Scholar] [CrossRef]
- Ueda, Y.; Murakawa, H.; Nakacho, K.; Ma, N. Establishment of computational welding mechanics. Weld. Surf. Rev. 1997, 8, 265–299. [Google Scholar]
- Mohammadtaheri, H.; Sedaghati, R.; Molavi-Zarandi, M. Inherent strain approach to estimate residual stress and deformation in the laser powder bed fusion process for metal additive manufacturing—A state-of-the-art review. Int. J. Adv. Manuf. Technol. 2022, 122, 2187–2202. [Google Scholar] [CrossRef]
- Bayat, M.; Dong, W.; Thorborg, J.; To, A.C.; Hattel, J.H. A review of multi-scale and multi-physics simulations of metal additive manufacturing processes with focus on modeling strategies. Addit. Manuf. 2021, 47, 102278. [Google Scholar] [CrossRef]
- Wang, C.; Tan, X.P.; Tor, S.B.; Lim, C.S. Machine learning in additive manufacturing: State-of-the-art and perspectives. Addit. Manuf. 2020, 36, 101538. [Google Scholar] [CrossRef]
- Vulimiri, P.S.; Riley, S.; Dugast, F.X.; To, A.C. A mean–variance estimation bidirectional convolutional long short-term memory surrogate model predicting residual stress and model error for laser powder bed fusion. Addit. Manuf. 2025, 97, 104591. [Google Scholar] [CrossRef]
- Keller, N.; Ploshikhin, V. New Method for Fast Predictions of Residual Stress and Distortion of AM Parts; University of Texas at Austin: Austin, TX, USA, 2014; pp. 1229–1237. [Google Scholar]
- Setien, I.; Chiumenti, M.; van der Veen, S.; San Sebastian, M.; Garciandía, F.; Echeverría, A. Empirical methodology to determine inherent strains in additive manufacturing. Comput. Math. Appl. 2019, 78, 2282–2295. [Google Scholar] [CrossRef]
- Setien, I.; Chiumenti, M.; San Sebastian, M.; Moreira, C.A.; Caicedo, M.A. Defining and Optimizing High-Fidelity Models for Accurate Inherent Strain Calculation in Laser Powder Bed Fusion. Metals 2025, 15, 180. [Google Scholar]
- Chen, Q.; Liang, X.; Hayduke, D.; Liu, J.; Cheng, L.; Oskin, J.; Whitmore, R.; To, A.C. An inherent strain based multiscale modeling framework for simulating part-scale residual deformation for direct metal laser sintering. Addit. Manuf. 2019, 28, 406–418. [Google Scholar] [CrossRef]
- Dong, W.; Liang, X.; Chen, Q.; Hinnebusch, S.; Zhou, Z.; To, A.C. A new procedure for implementing the modified inherent strain method with improved accuracy in predicting both residual stress and deformation for laser powder bed fusion. Addit. Manuf. 2021, 47, 102345. [Google Scholar] [CrossRef]
- Dong, W.; Jimenez, X.A.; To, A.C. Temperature-dependent modified inherent strain method for predicting residual stress and distortion of Ti6Al4V walls manufactured by wire-arc directed energy deposition. Addit. Manuf. 2023, 62, 103386. [Google Scholar] [CrossRef]
- Bugatti, M.; Semeraro, Q. Limitations of the Inherent Strain Method in Simulating Powder Bed Fusion Processes. Addit. Manuf. 2018, 23, 329–346. [Google Scholar] [CrossRef]
- Du, T.; Yan, P.; Liu, Q.; Dong, L. A process-based inherent strain method for prediction of deformation and residual stress for wire-arc directed energy deposition. Comput. Mech. 2023, 73, 1053–1075. [Google Scholar] [CrossRef]
- Pourabdollah, P.; Farhang Mehr, F.; Cockcroft, S.; Maijer, D. A new variant of the inherent strain method for the prediction of distortion in powder bed fusion additive manufacturing processes. Int. J. Adv. Manuf. Technol. 2024, 131, 4575–4594. [Google Scholar] [CrossRef]
- Neiva, E.; Chiumenti, M.; Cervera, M.; Salsi, E.; Piscopo, G.; Badia, S.; Martín, A.F.; Chen, Z.; Lee, C.; Davies, C. Numerical modelling of heat transfer and experimental validation in powder-bed fusion with the virtual domain approximation. Finite Elem. Anal. Des. 2020, 168, 103343. [Google Scholar] [CrossRef]
- Systèmes, D. Abaqus Analysis User’s Manual. 2024. Available online: https://www.3ds.com/products-services/simulia/support/documentation/ (accessed on 20 December 2024).
- Moreira, C.A.; Caicedo, M.A.; Cervera, M.; Chiumenti, M.; Baiges, J. An accurate, adaptive and scalable parallel finite element framework for the part-scale thermo-mechanical analysis in metal additive manufacturing processes. Comput. Mech. 2024, 73, 983–1011. [Google Scholar] [CrossRef]
- Baiges, J.; Chiumenti, M.; Moreira, C.A.; Cervera, M.; Codina, R. An Adaptive Finite Element strategy for the numerical simulation of Additive Manufacturing processes. Addit. Manuf. 2021, 37, 101650. [Google Scholar] [CrossRef]
- Ganeriwala, R.; Strantza, M.; King, W.; Clausen, B.; Phan, T.; Levine, L.; Brown, D.; Hodge, N. Evaluation of a thermomechanical model for prediction of residualstress during laser powder bed fusion of Ti-6Al-4V. Addit. Manuf. 2019, 27, 489–502. [Google Scholar] [CrossRef]
- Gladbach, B.; Noe, A.; Rosenhövel, T. Warpage Reduction in Additively Manufactured Parts Based on Thermomechanical Modeling and a Novel Simulation Strategy for Laser Scanning. In New Achievements in Mechanics; Müller, W.H., Noe, A., Ferber, F., Eds.; Springer Nature Switzerland: Cham, Switzerland, 2024; pp. 301–339. [Google Scholar] [CrossRef]


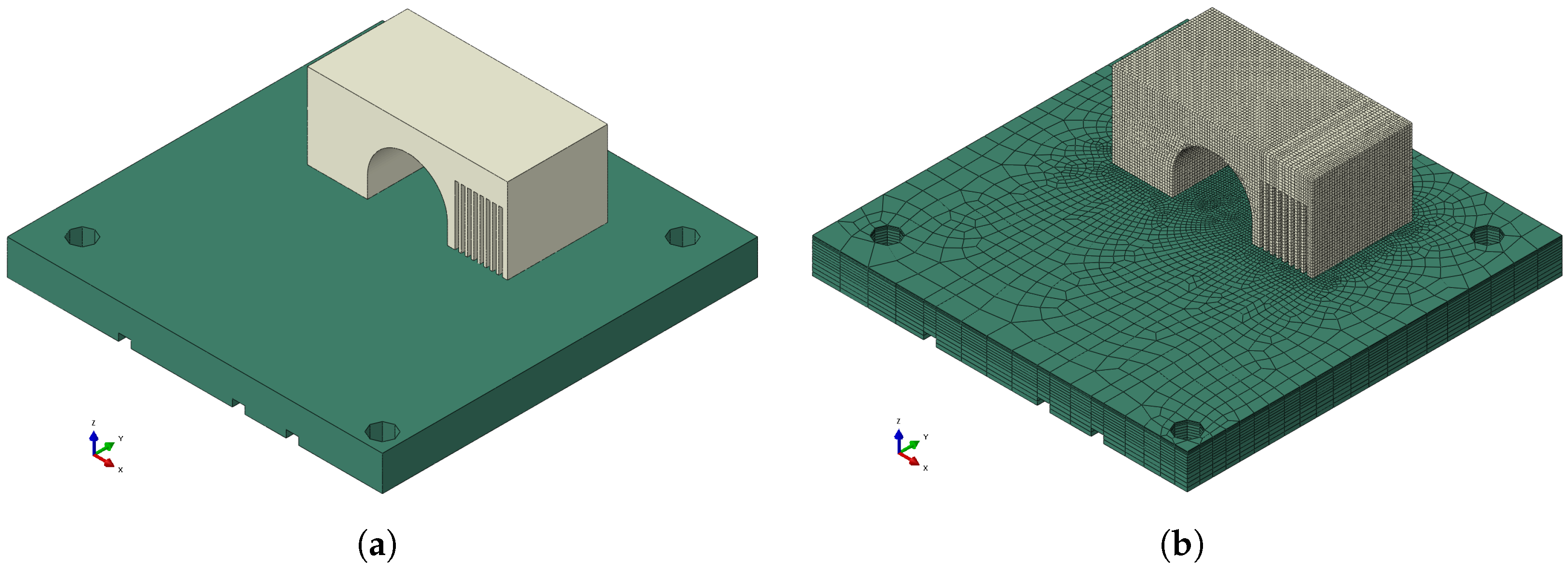
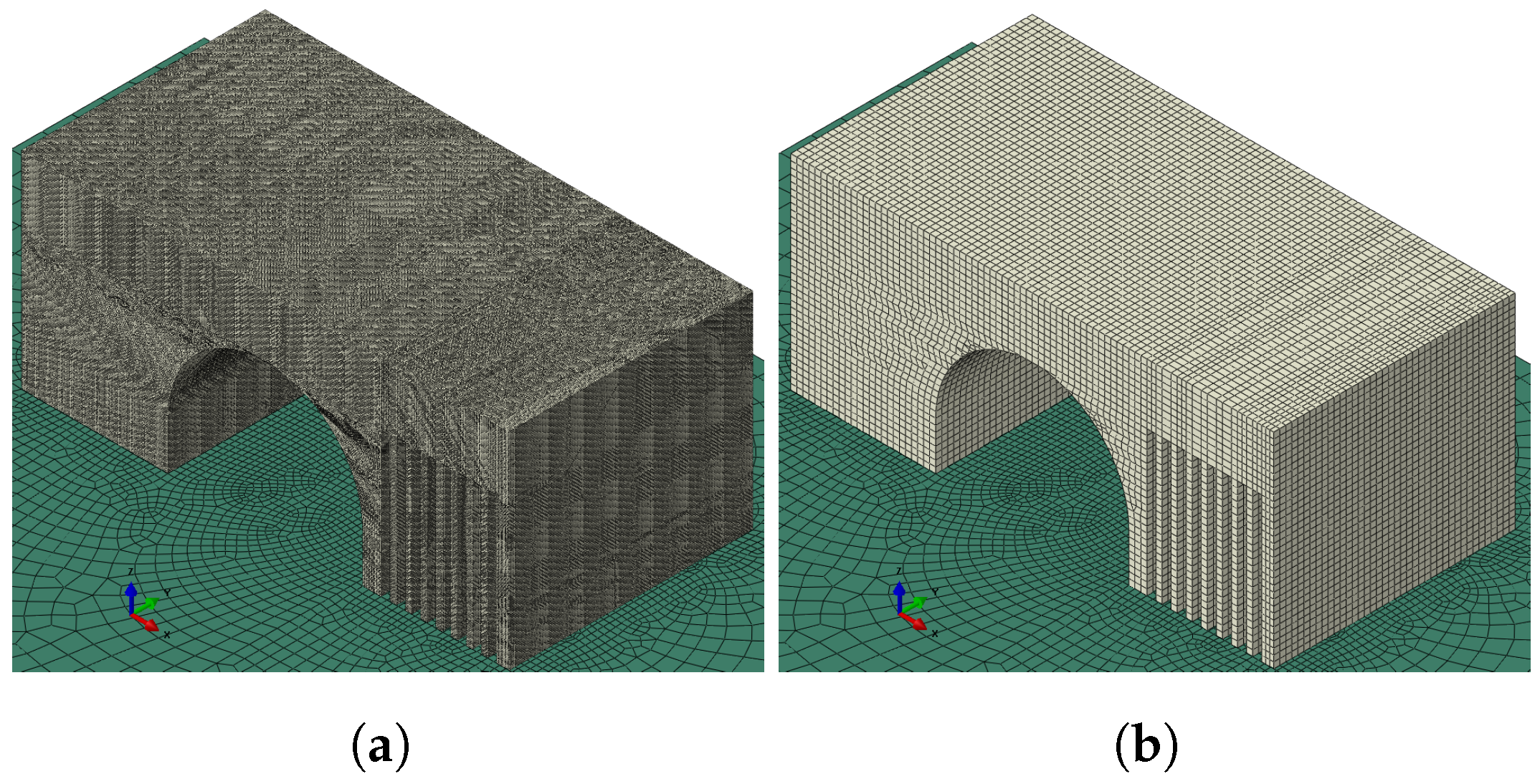




| Part Name | Number of Elements | Number of Nodes |
|---|---|---|
| Baseplate | 90,202 | 98,499 |
| Bridge 0.24 mm | 4,912,640 | 5,156,025 |
| Bridge 0.96 mm | 73,400 | 88,150 |
| Part Name | Number of Elements | Number of Nodes |
|---|---|---|
| Baseplate | 98,048 | 110,216 |
| SBA | 3,952,927 | 4,646,774 |
| Case | Name | Lumping | Element Characteristic Size (mm) | Methodology |
|---|---|---|---|---|
| #1 | lump-4_mesh-024_ISM | 4 | 0.24 | ISM |
| #2 | lump-16_mesh-024_ISM | 16 | 0.24 | ISM |
| #3 | lump-16_mesh-096_ISM | 16 | 0.96 | ISM |
| #4 | lump-4_mesh-024_EISM | 4 | 0.24 | EISM |
| #5 | lump-16_mesh-024_EISM | 16 | 0.24 | EISM |
| #6 | lump-16_mesh-096_EISM | 16 | 0.96 | EISM |
| Case | Name | MAPE (%) | PBIAS (%) |
|---|---|---|---|
| #1 | lump-4_mesh-024_ISM | 50.87 | −47.47 |
| #2 | lump-16_mesh-024_ISM | 56.63 | −56.64 |
| #3 | lump-16_mesh-096_ISM | 56.15 | −56.21 |
| #4 | lump-4_mesh-024_EISM | 10.85 | 0.01 |
| #5 | lump-16_mesh-024_EISM | 16.04 | −8.95 |
| #6 | lump-16_mesh-096_EISM | 15.96 | −9.09 |
| Case | Name | Total CPU Time (h) | ||
|---|---|---|---|---|
| Thermal | Mechanical | Total | ||
| #1 | Lump-4_Mesh-0.24_ISM | - | 5.64 | 5.64 |
| #3 | Lump-16_Mesh-0.96_ISM | - | 0.15 | 0.15 |
| #4 | Lump-4_Mesh-0.24_EISM | |||
| #6 | Lump-16_Mesh-0.96_EISM | |||
| Case Name | Lumping | Element Characteristic Size (mm) | Methodology |
|---|---|---|---|
| SBA_ISM | 16 | 0.96 | ISM |
| SBA_EISM | 16 | 0.96 | EISM |
| Case Name | Average Deviation (mm) | Sigma (mm) |
|---|---|---|
| SBA_ISM | −0.01 | 0.15 |
| SBA_EISM | 0.00 | 0.09 |
| Case Name | Total CPU Time (h) | ||
|---|---|---|---|
| Thermal | Mechanical | Total | |
| SBA_ISM | - | 12.35 | 12.35 |
| SBA_EISM | 8.69 | 14.19 | 22.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Setien, I.; Chiumenti, M.; San Sebastian, M.; Moreira, C.A.; Caicedo, M.A. Integrating Temperature History into Inherent Strain Methodology for Improved Distortion Prediction in Laser Powder Bed Fusion. Metals 2025, 15, 143. https://doi.org/10.3390/met15020143
Setien I, Chiumenti M, San Sebastian M, Moreira CA, Caicedo MA. Integrating Temperature History into Inherent Strain Methodology for Improved Distortion Prediction in Laser Powder Bed Fusion. Metals. 2025; 15(2):143. https://doi.org/10.3390/met15020143
Chicago/Turabian StyleSetien, Iñaki, Michele Chiumenti, Maria San Sebastian, Carlos A. Moreira, and Manuel A. Caicedo. 2025. "Integrating Temperature History into Inherent Strain Methodology for Improved Distortion Prediction in Laser Powder Bed Fusion" Metals 15, no. 2: 143. https://doi.org/10.3390/met15020143
APA StyleSetien, I., Chiumenti, M., San Sebastian, M., Moreira, C. A., & Caicedo, M. A. (2025). Integrating Temperature History into Inherent Strain Methodology for Improved Distortion Prediction in Laser Powder Bed Fusion. Metals, 15(2), 143. https://doi.org/10.3390/met15020143







