Theoretical Study on Error Compensation for Online Roll Profile Measurement Considering Roller System Deformation

Abstract

Online roll profile measurement technology can measure in real time without changing the rolls, which has advantages that traditional roll profile measurement methods cannot compare with. To improve the accuracy of online roll profile measurement during the rolling process, the influence function method was employed to calculate the deformation of the roller system, and an error compensation model for online roll profile measurement considering the deformation of the roller system was established. Numerical simulations of roller deformation and the error compensation of the roll profile measurement were conducted for different rolling processes. The results show that, during the rolling process, under the combined action of rolling force and bending force, the work rolls undergo deflection deformation and elastic flattening. The pressing process and bending force have a significant impact on the roller system deformation. Roll profile measurement errors are associated with both the deflection deformation and the elastic flattening of the rolls. The axial displacement of the rolls has a negligible effect on the rolls’ deflection and flattening. However, when the rolling mill adopts the axial displacement of the roll process, the roll profile measurement system requires displacement compensation. The magnitude and direction of the compensation should be consistent with the displacement and direction of the corresponding roll. This research is of great significance to improve the accuracy of online roll profile measurement, realize the fine management of mill roll in service, and improve the automation level of rolling mill systems.

1. Introduction

Strip steel is widely utilized across various sectors [1,2,3,4,5,6]. Automation is the inevitable path for the transformation and upgrading of the strip steel industry [7,8,9,10]. During the strip rolling process, the wear of the rolls is inevitable. The resulting changes in roll gap profile and deterioration of the roll surface quality significantly impact the strip’s shape and surface finish [11,12,13,14,15,16]. Particularly during hot rolling, roll wear in a rolling schedule may reach several hundred micrometers. To ensure product quality, frequent roll replacements are essential [17]. Frequent roll changes constrain the flexibility of rolling schedule planning and hinder further improvements in production efficiency [18].

For the reasons mentioned above, online roll grinding technology emerged. Online roll grinding technology involves installing grinding devices on the rolling mill to perform online grinding on the work rolls without removing them. This enhances roll profile quality, thereby reducing the frequency of roll replacements [19,20]. To achieve online roll grinding, it is first necessary to measure the wear condition of the rolls and the profile of the rolls after online grinding in real time, subsequently feeding this measurement data back to the online roll grinding system. Consequently, online roll profile measurement technology emerged accordingly. Most of the online roll grinding devices installed successively from the late 20th century to the early 21st century have now been dismantled and abandoned. One of the core issues that prevents the full realization of the technical advantages of online roll grinding is that the online roll profile measurement accuracy of the online roll grinding system cannot meet the requirements. Therefore, online roll profile measurement technology forms the foundation of online roll grinding technology. Only when measurement accuracy is assured can satisfactory roll profiles be achieved following online grinding. Moreover, even in hot tandem strip mills without an online roll grinding device, the application of online roll profile measurement technology provides valuable guidance for optimizing the roll changeover schedule.

Japan pioneered the online grinding technology and the online roll profile measurement technology, achieving industrial application and establishing a leading position in the international arena [21,22]. Numerous scholars have conducted a series of studies on online roll profile measurement technology. Hayashi et al. [23] employed ultrasonic displacement sensors to achieve online roll profile measurement, feeding the measurement data back to the online roll grinding device, to provide guidance for the formulation of grinding processes. Kinose et al. [24] elucidated the principle of online roll profile measurement by the contact force method and presented a computational model for roll profile curves. These studies laid the foundation for the development of online roll profile measurement technology but did not address the compensation of measurement errors. Based on the ultrasonic roll profile measurement scheme, Li [25] processed the raw data with a nonlinear filtering algorithm and adopted a three-point algorithm to eliminate the displacement error of the bench and the installation error of the probe. Shang [26] employs the principle of ultrasonic ranging, utilizing the single echo from two ultrasonic frequency waves for online roll profile measurement. This approach eliminates the impact on measurement accuracy caused by multiple echoes in the time domain due to absorption in the ultrasonic propagation medium, a limitation inherent in the pulse reflection method. Hua et al. [27,28] developed a radial motion device and positioning device for online roll profile measurement and built an experimental simulation system using the eddy current ranging method. They studied the influence of various factors on measurement accuracy such as material composition, surface roughness, surface temperature, rotational speed, iron oxide scale, and cooling water conditions. Guo [29] proposed a morphological filtering method employing multiple structural elements to characterize roll profiles based on CCD edge detection. Laboratory experiments were conducted to analyze the causes of detection errors, and a software-based error compensation method was subsequently proposed. Hu [30] investigated online roll profile measurement techniques using contact force measurement methods, presenting computational approaches for roll profiles under both constant-feed and constant-grinding-force conditions. He further conducted a dynamic characteristic analysis of the online roll profile measurement system. Zhou [31] conducted research on online roll profile measurement technology by the contact force method and proposed three methods to improve measurement accuracy, including comprehensive control of roll profile measurement and grinding, compensation for roll inclination errors, and control of target plate convexity. These works compensate for the errors in the online roll profile measurement from different perspectives, contributing to an improvement in measurement accuracy. However, none of them account for the impact of roll deflection and elastic flattening on measurement precision.

The aforementioned research has promoted the development of online roll profile measurement technology. However, these studies did not take into account the influence of roller system deformation during the rolling process on the measurement accuracy. Moreover, the relevant works were primarily concentrated in the late 20th century and early 21st century, with few new research findings emerging in this field over the past two decades. This paper employs the influence function method to calculate roller system deformation, establishing a unified model for calculation and measurement increments and an error compensation model for online roll profile measurement considering the roller system deformation. Numerical simulations of error compensation were conducted for various rolling processes. This research is of great significance for promoting the innovation of the theoretical system of online roll profile measurement technology and enhancing the automation level of rolling mills.

2. Materials and Methods

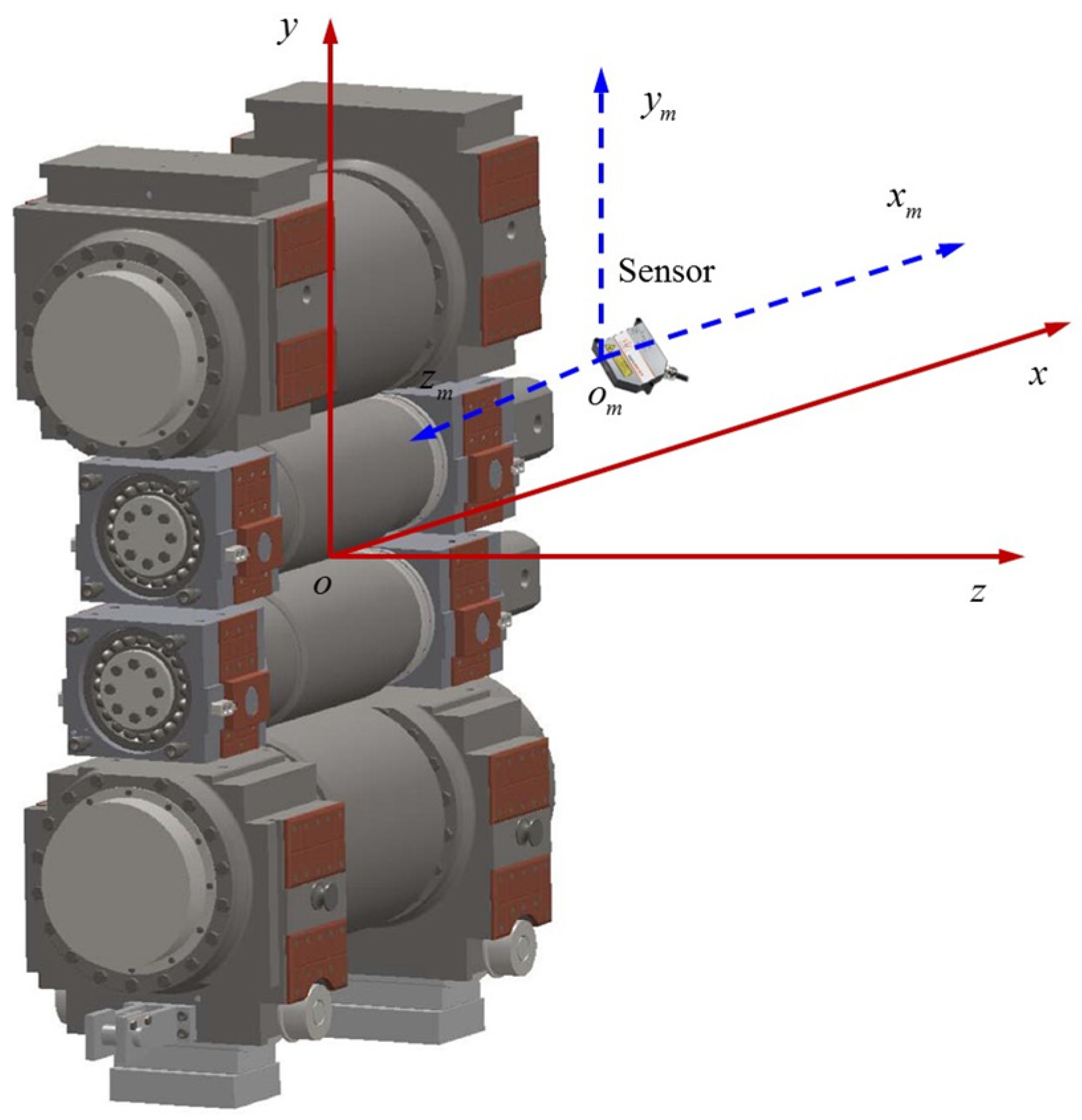
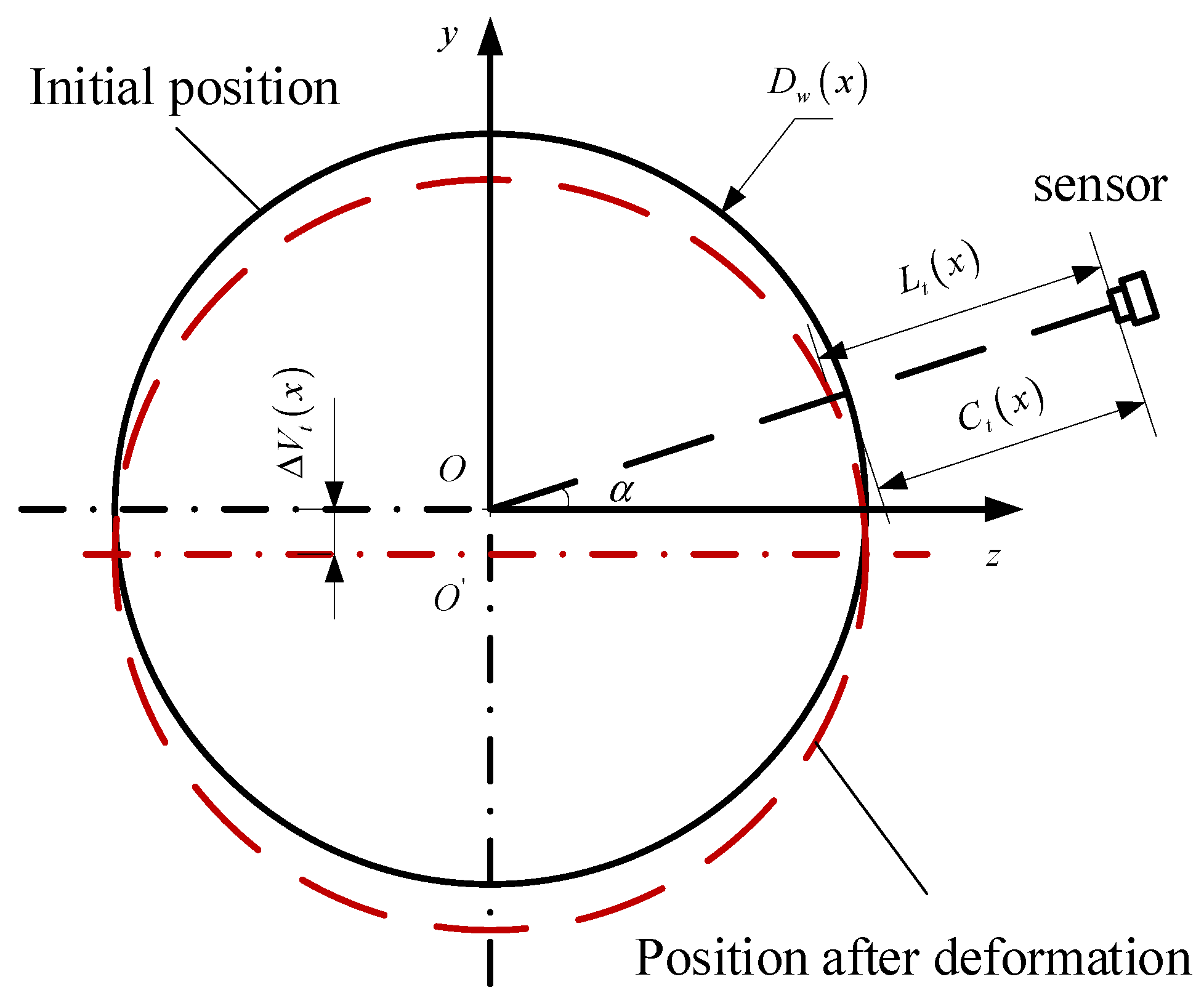
2.1. Rolling Mill Coordinate System and Measurement Coordinate System

The measurement system uses a laser displacement sensor for roller shape measurement. The sensor is based on the principle of laser triangulation, with a measurement range of 2 mm and an accuracy of 0.6 μm. The sensor is installed in a protective housing. The protective housing can blow the optical path of the sensor with compressed air, thereby ensuring its measurement accuracy remains unaffected by cooling water at the rolling site. The sensor is fixed on the guide rail of the measurement system via the protective housing and can move along the axis of the roll to perform roll profile measurements.

The three-dimensional Cartesian coordinate system of the rolling mill and the spatial oblique coordinate system of the measurement system were, respectively, established, as shown in Figure 1.

When establishing the rolling mill coordinate system, the point of intersection between the rolling mill centerline and the rolling plane shall serve as the origin ($o$) of the coordinate system. Define the $x$-axis as passing through point $o$ and parallel to the roll axis, with the $x$-axis pointing towards the drive side of the rolling mill. Define the $y$-axis passing through point $o$ and perpendicular to the horizontal plane, with the $y$-axis pointing directly upwards. According to the right-hand rule for Cartesian coordinate systems, the $z$-axis passes through point $o$, with the $z$-axis pointing towards the exit side of the rolling mill.

Taking a certain set of rolls as a reference, the initial position of the rolling mill is defined as the state in which there is no axial movement and the upper and lower work rolls are pressed against each other under small loads. In this state, adjust the position of the roll profile measurement system so that the sensor’s measurement direction is perpendicular and aligned with the axis of the roll being measured. The angle between the incident light of the sensor and the horizontal plane is $\alpha$.The detection signal of the sensor is at the center of its range, and the measurement point on the roll is positioned at the center of the roll’s length. At this point, the output signal is set to zero. The sensor’s current position shall be taken as its initial position. A spatial oblique coordinate system is established at the sensor’s initial position. The incident light intersects the outer surface of the lens on the sensor housing at a single point, which is defined as the origin ($o_m$) of the measurement coordinate system. Define the $x_m$-axis as passing through point $o_m$ and parallel to the axial direction of the measurement system, with the $x_m$-axis pointing towards the drive side of the rolling mill. Define the $y_m$-axis passing through point $o_m$, with the $y_m$-axis pointing directly upwards. Define the $z_m$-axis as passing through point $o_m$ and coinciding with the sensor’s incident light, with the $z_m$-axis directed towards the roll to be measured.

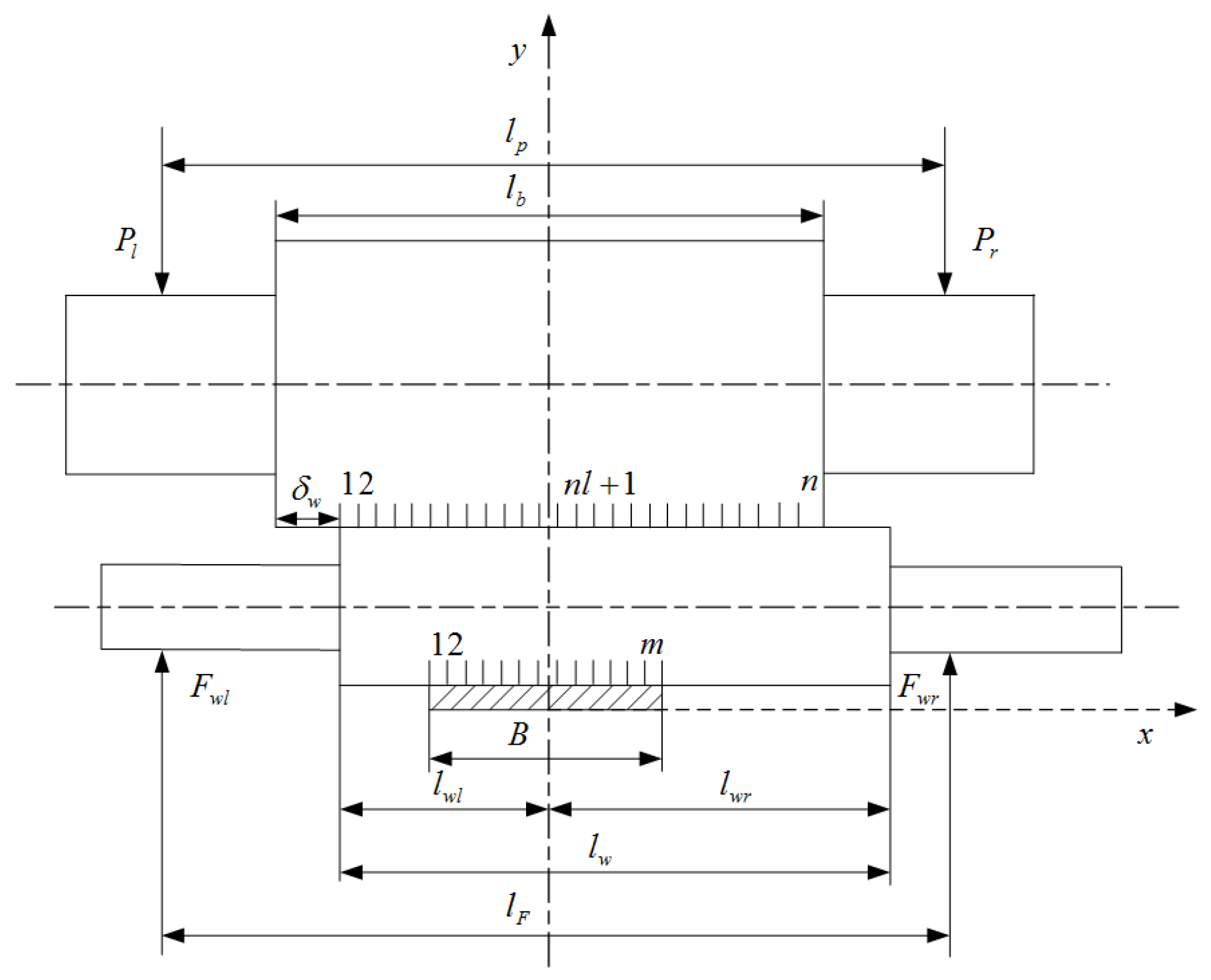
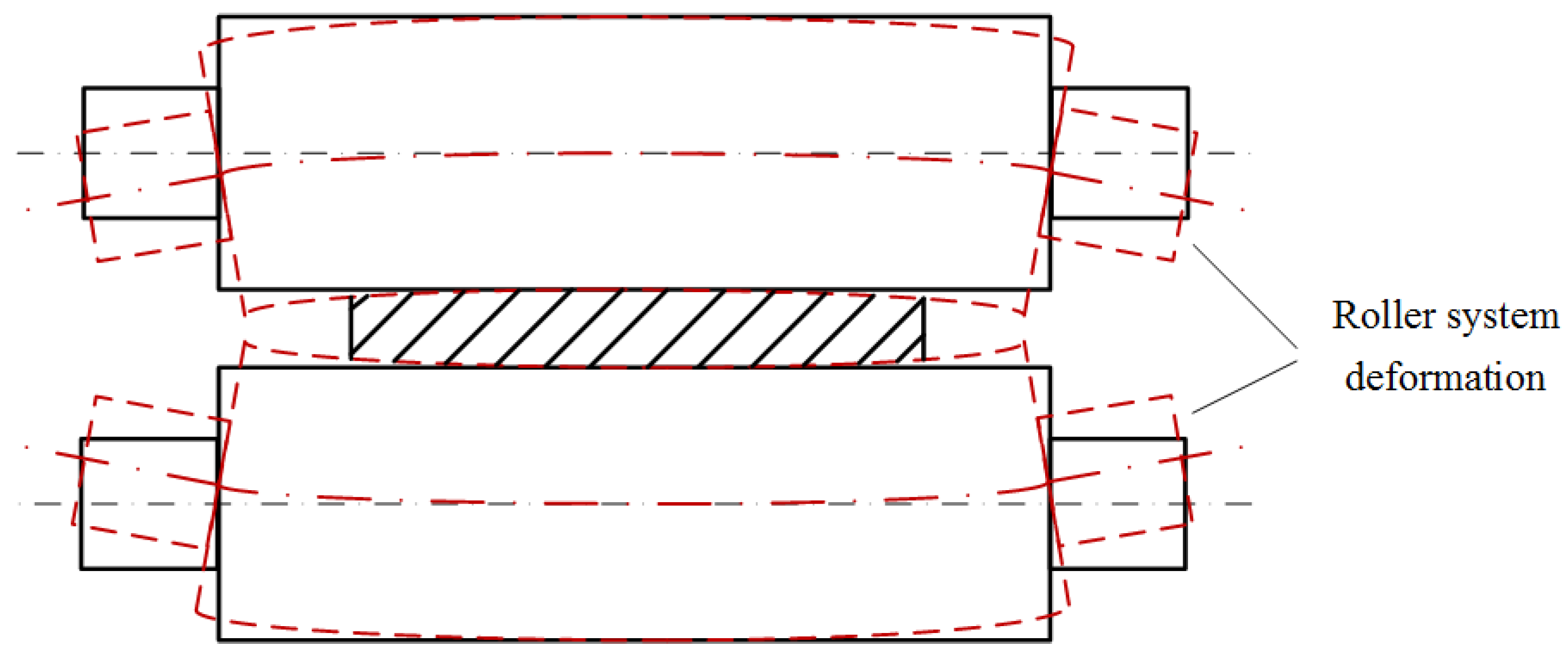
2.2. Roller System Deformation Model

The elastic deformation of the roll system is calculated by the influence function method [32,33]. The mechanical model of the four-high strip rolling mill is shown in Figure 2. Divide the width of the strip steel into $m$ segments. The pressure within each segment between the strip steel and the work roll is represented by the concentrated force $p\left(j\right)$. Divide the contact width between the work roll and the back-up roll into $n$ segments. The pressure within each segment between the work roll and the back-up roll is represented by the concentrated force $q\left(j\right)$.

When using the influence function method to calculate the deformation of the roller system, it is necessary to calculate the transverse distribution of the rolling pressure using the metal deformation model. The calculation of the metal deformation model requires the roller system deformation model to calculate the transverse distribution of the load roller gap (rolling mill exit strip thickness). The metal deformation mode includes the tension transverse distribution model and the average unit rolling pressure model. By employing the relevant equations from references [34,35], the transverse distribution of rolling pressure can be calculated. The roller system deformation model includes the roll bending deformation equation and the roll flattening equation. Among them, the work roll bending deformation equation can be expressed as

$$\left\{\begin{array}{l}{f}_w\left(i\right)={\displaystyle \sum _{j=1}^{nl+1}q\left(j\right)}{G}_{wl}\left(nl+1-i,nl+1-j\right)-{\displaystyle \sum _{j=1}^{m}p\left(j\right)}{G}_{wl}\left(nl+1-i,j\right)-\\ F_{wl}{G}_{F_{wl}}\left(nl+1-i\right)-{\theta }_{w}x\left(i\right)\left(1\le i\le nl\right)\\ f_w\left(i\right)={\displaystyle \sum _{j=nl+1}^{n}q\left(j\right)}{G}_{wr}\left(i-nl-1,j-nl-1\right)-{\displaystyle \sum _{j=1}^{m}p\left(j\right)}{G}_{wr}\left(i-nl-1,j\right)-\\ F_{wr}{G}_{F_{wr}}\left(i-nl-1\right)-{\theta }_{w}x\left(i\right)\left(nl+2\le i\le n\right)\end{array}\right.$$

(1)

where $G_{wl}$ and $G_{wr}$ are the bending influence coefficients for the operating side and drive side of the work roll, respectively; $G_{F_{wl}}$ and $G_{F_{wr}}$ are the bending influence coefficients of the bending force on the operating side and the drive side of the work roll, respectively; $q$ and $p$ are the inter-roll pressure and rolling pressure, respectively; ${\theta }_w$ is the rotational angle between the work roll and the back-up roll.

The back-up roll bending deformation equation can be expressed as

$$\left\{\begin{array}{l}{f}_b\left(i\right)=-{\displaystyle \sum _{j=1}^{nl+1}q\left(j\right)}{G}_{bl}\left(nl+1-i,nl+1-j\right)+P_l{G}_{P_l}\left(nl+1-i\right)\left(1\le i\le nl\right)\\ f_b\left(i\right)=-{\displaystyle \sum _{j=nl+1}^{n}q\left(j\right)}{G}_{br}\left(i-nl-1,j-nl-1\right)+P_r{G}_{P_r}\left(i-nl-1\right)\left(nl+2\le i\le n\right)\end{array}\right.$$

(2)

where $G_{bl}$ and $G_{br}$ are the bending influence coefficients for the operating side and drive side of the back-up roll, respectively; $G_{P_l}$ and $G_{P_r}$ are the bending influence coefficients of the rolling force on the operating side and the drive side of the back-up roll, respectively; $P$ and $P_r$ are the rolling forces on the operating side and drive side, respectively.

The force balance equation and torque balance equation of the roller system can be expressed as

$$\left\{\begin{array}{l}{P}_l+P_r=P_y+F_{wl}+F_{wr}\\ P_l{\displaystyle \frac{l_P}{2}}-P_r{\displaystyle \frac{l_P}{2}}=\left(F_{wl}-F_{wr}\right){\displaystyle \frac{l_F}{2}}=0\end{array}\right.$$

(3)

where $F_{wl}$ and $F_{wr}$ are the bending forces on the operating side and drive side, respectively; $P_y$ is the force exerted by the strip steel on the work roll in the vertical direction; $l_P$ is the distance between the centerlines of the operating side and drive side hydraulic cylinders; $l_F$ is the distance between the centerlines of the operating side and drive side bending roll hydraulic cylinders.

To determine the deformation of the roller system, the contact pressure between the work roll and the back-up roll must be a known parameter. To calculate the contact pressure between the rollers, the inter-roll indentation and the inter-roll contact pressure need to be iteratively calculated until convergence is achieved. The equations for flattening between rolls and flattening between the roll and workpiece can be expressed as

$$\left\{\begin{array}{l}{\mathrm{\Delta }}_{wb}\left(i\right)=Q\left(i\right)K_{wb}\\ {\mathrm{\Delta }}_{ws}\left(i\right)={\displaystyle \sum _{j=0}^m{G}_{ws}\left(i,j\right)p\left(j\right)}\end{array}\right.$$

(4)

where ${\mathrm{\Delta }}_{wb}$ is the inter-roll flattening amount; ${\mathrm{\Delta }}_{ws}$ is the flattening amount between the roll and the workpiece; $Q$ is the unit pressure between the rolls; $K_{wb}$ is the inter-roll flattening coefficient; $G_{ws}$ is the flattening coefficient between the roll and workpiece.

The deformation compatibility equation can be expressed as

$${\mathrm{\Delta }}_{wb}\left(i\right)=f_b\left(i\right)-f_w\left(i\right)-\left[{\displaystyle \frac{C_w\left(i\right)}{2}}-{\displaystyle \frac{C_w\left(nl+1\right)}{2}}\right]+{\mathrm{\Delta }}_{wb}\left(nl+1\right)$$

(5)

where $C_w$ is the profile of the work roll.

The transverse distribution of the rolling mill exit strip thickness may be expressed as

$$\begin{array}{l}h(i)=h-f_w(nl+1-i)-f_w(nl+1+i)+{\displaystyle \frac{C_w(nl+1+i)+C_w(nl+1-i)}{2}}-\\ C_w(nl+1)+{\mathrm{\Delta }}_{ws}(nl+1-i)+{\mathrm{\Delta }}_{ws}(nl+1+i)-2{\mathrm{\Delta }}_{ws}(nl+1)\end{array}$$

(6)

where $h$ is the thickness of the workpiece at the exit of the rolling mill.

By substituting the transverse distribution of the rolling pressure into the elastic deformation model of the roller system, the transverse distribution of the load roller gap can be calculated. By substituting the transverse distribution of the load roller gap into the metal plastic deformation model, the transverse distribution of the rolling pressure can be calculated. By iterative calculation until convergence, the bending deformation and elastic flattening of the work roll can be obtained. The calculation process is shown in Figure 3.

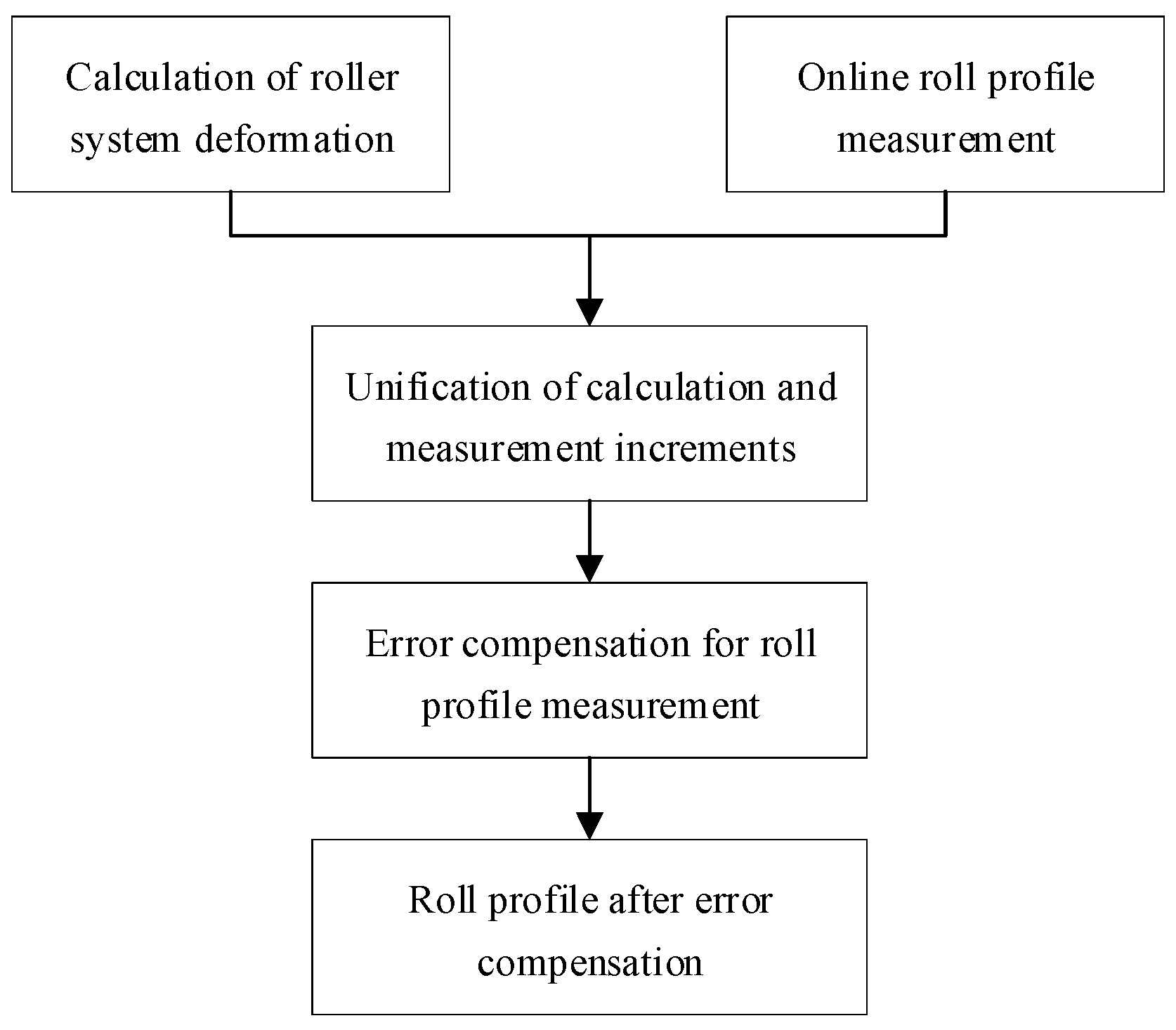
2.3. Unification of Calculation and Measurement Increments

In the roll deformation model, the discrete step size of the rolls should not be too small, as this would reduce computational efficiency. To ensure measurement accuracy, the measurement system should have a high sampling frequency. This results in a situation in which, in the $x$-axis direction of the roller system, the measured values of the sensor cannot be directly correlated with the calculated values of the roller deformation. To facilitate mathematical operations between calculated and measured values, it is necessary to standardize the calculation and measurement steps.

Assume that the sampling frequency of the sensor is $f_m$, and the feed speed of the measurement system in the $x_m$-axis direction is $v_m$. After time interval $t$, the displacement of the measurement system along the roller axis is $v_{m}t$, during which the amount of data collected by the sensor is $f_{m}t$. Then, the step length corresponding to the axial direction of the roll for the two adjacent measurement data of the sensor is A. Typically, the measurement step size of the sensor is smaller than the discrete step size used in calculations of roller system deformation. To facilitate calculations between the calculated values of roller system deformation and the sensor measurements, the calculated values require interpolation processing. By employing Lagrange linear interpolation to compute the intermediate values between two adjacent discrete elements of the roller system, a linear difference polynomial can be established:

$$L_1\left(x\right)=f\left(x_k\right)+{\displaystyle \frac{f\left(x_{k+1}\right)-f\left(x_k\right)}{x_{k+1}-x_k}}\left(x-x_k\right)$$

(7)

where $L_1\left(x\right)$ is the interpolation of the deformation between two adjacent discrete elements; $f\left(x\right)$ is the average deformation of discrete element calculated by the roller system deformation mode.

Based on the step length of the roll corresponding to two adjacent measurement data points of the sensor, the deformation interpolation between the centers of two adjacent discrete units can be calculated. The deformation of the roller system, after unification with the measurement increment, can be expressed as

$$L_1^{\prime }\left(x\right)=L_1\left(x_k+\eta {\displaystyle \frac{v}{f}}\right)\left(0\le \eta \le {\displaystyle \frac{f\cdot \left(x_{k+1}-x_k\right)}{v}}\right)$$

(8)

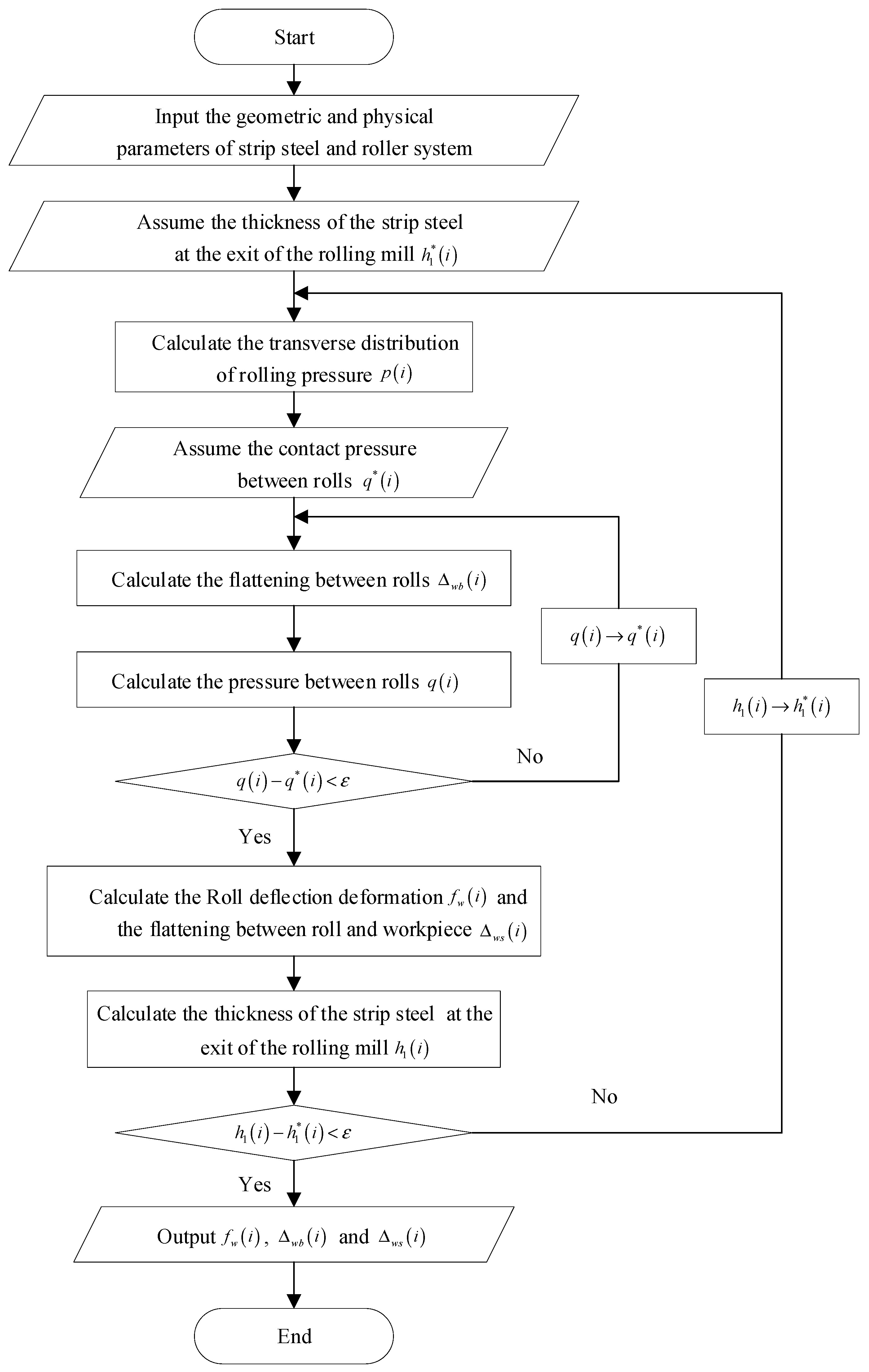
2.4. Roll Profile Measurement Error Compensation Model

Prior to measurement, the position of the roll profile measurement system must be adjusted according to the roll diameter and its position. The roll profile measurement system can adjust the position of the sensor in both the $x_m$ and $y_m$ directions. The position adjustment equation for the lower work roll measurement system can be expressed as

$$\left\{\begin{array}{l}\mathrm{\Delta }{x}_{ml}={\delta }_{wl}\\ \mathrm{\Delta }{y}_{ml}=\mathrm{\Delta }{D}_{bl}+\mathrm{\Delta }{D}_{wl}+\mathrm{\Delta }{h}_p\end{array}\right.$$

(9)

where $\mathrm{\Delta }{x}_{ml}$ and $\mathrm{\Delta }{y}_{ml}$ are the respective adjustment values of the lower work roll measurement system in the $x_m$ and $y_m$ directions; ${\delta }_{wl}$ is the axial displacement of the lower work roll; $\mathrm{\Delta }{D}_{bl}$ and $\mathrm{\Delta }{D}_{wl}$ are the respective changes in diameter of the lower back-up roll and lower work roll relative to the reference roll; D represents the adjustment value of the step pad thickness.

Correspondingly, the position adjustment equation for the upper work roll measurement system can be expressed as

$$\left\{\begin{array}{l}\mathrm{\Delta }{x}_{mu}={\delta }_{wu}\\ \mathrm{\Delta }{y}_{mu}=\mathrm{\Delta }{y}_{ml}+h+{\displaystyle \frac{\mathrm{\Delta }{D}_{wu}}{2}}\end{array}\right.$$

(10)

where $\mathrm{\Delta }{x}_{mu}$ and $\mathrm{\Delta }{y}_{mu}$ are the respective adjustment values of the upper work roll measurement system in the $x_m$ and $y_m$ directions; $\mathrm{\Delta }{D}_{wu}$ is the change in diameter of the upper work roll relative to the reference roll.

Under the influence of the rolling force, the roller system will undergo bending deformation and elastic flattening, as shown in Figure 4. Therefore, when conducting online measurement of the roll profile after adjusting the position of the measurement system, it is essential to correct the measurement signals from the sensor.

Assuming that, in the initial state, the incident light of the sensor passes through the axis of the work roll, due to the deformation of the roller system during the rolling process, according to the geometric relationship shown in Figure 5, the following equation can be derived:

$$\mathrm{\Delta }{z}_{m_t}\left(x\right)={\displaystyle \frac{D_w\left(x\right)}{2}}-\left\{\sqrt{{\left({\displaystyle \frac{D_w\left(x\right)}{2}}\right)}^2-{\left[-\mathrm{\Delta }{V}_t\left(x\right)\cos \alpha \right]}^2}+\mathrm{\Delta }{V}_t\left(x\right)\sin \alpha \right\}$$

(11)

where $\mathrm{\Delta }{z}_{m_t}$ is the measurement error caused by deformation of the roller system in the $z_m$-axis direction; $D_w$ is the diameter of the measured roll; $\mathrm{\Delta }{V}_t$ is the displacement of the measured roll in the $y$-axis caused by the deformation of the roller system at time B.

Then the roll profile error compensation model can be expressed as

$$C_t\left(x\right)=L_t\left(x\right)-\mathrm{\Delta }{z}_{m_t}\left(x\right)+E_{z_m}\left(x\right)$$

(12)

where $C_t$ is the profile information of the measured roll after error compensation at time $t$; $L_t$ is the direct sensor measurement value of the tested roll at time $t$; $E_{z_m}$ is the projection of the straightness error of the measurement system in the $z_m$-axis.

Based on Formula (12), the following formula can be derived:

$$C_t\left(x\right)=L_t\left(x\right)-{\displaystyle \frac{D_w\left(x\right)}{2}}+\left\{\sqrt{{\left[{\displaystyle \frac{D_w\left(x\right)}{2}}\right]}^2-{\left[-\mathrm{\Delta }{V}_t\left(x\right)\cos \alpha \right]}^2}+\mathrm{\Delta }{V}_t\left(x\right)\sin \alpha \right\}+E_{z_m}\left(x\right)$$

(13)

According to the deformation model of the roller system, the displacement $\mathrm{\Delta }{V}_t^l$ of the lower work roll in the $y$-axis at time $t$ caused by the roller system deformation can be expressed as

$$\mathrm{\Delta }{V}_t^l\left(x\right)=f_w^l\left(x\right)-{\mathrm{\Delta }}_{wb}\left(x_0\right)-\max \left(f_w\right)-\max \left(f_b\right)$$

(14)

where $f_w^l$ is the deflection of the lower work roll; ${\mathrm{\Delta }}_{wb}\left(x_0\right)$ is the flattening between the work roll and the back-up roll at the rolling centerline; $\max \left(f_w\right)$ is the maximum deflection of the work roll; $\max \left(f_b\right)$ is the maximum deflection of the back-up roll.

Similarly, the displacement $V_t^u$ of the upper work roll in the $y$-axis at time $t$ caused by the roller system deformation can be expressed as

$$\mathrm{\Delta }{V}_t^u\left(x\right)=V_t^l\left(x\right)-2{\mathrm{\Delta }}_{ws}\left(x_0\right)+f_w^u\left(x\right)$$

(15)

where ${\mathrm{\Delta }}_{ws}\left(x_0\right)$ is the flattening between the work roll and the strip steel at the rolling centerline; $f_w^u$ is the deflection of the upper work roll.

The methodological framework for error compensation for online roll profile measurement considering roller system deformation is shown in Figure 6.

3. Numerical Simulations

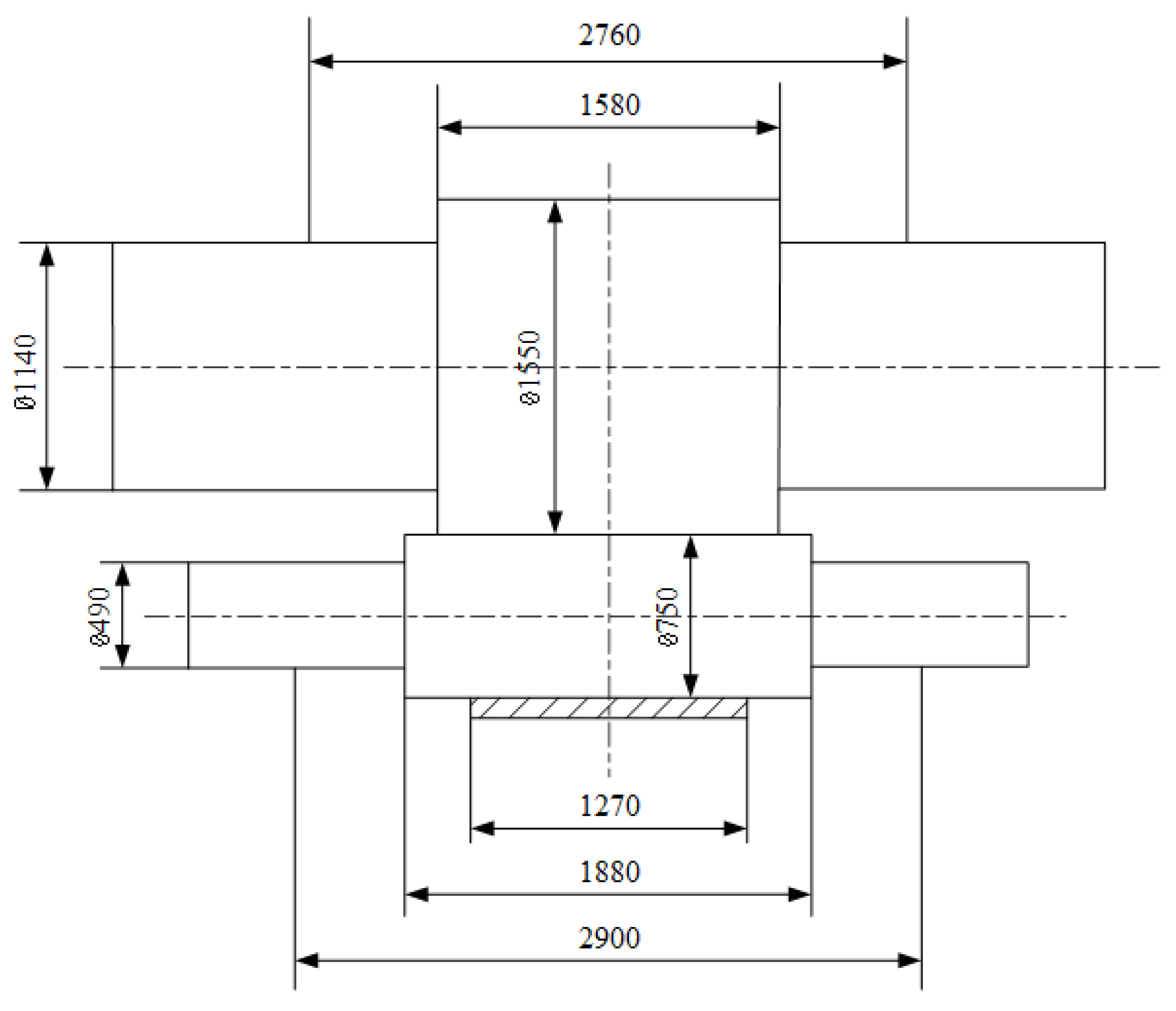
3.1. Parameters for Simulations

Based on industrial rolling mill equipment parameters and production process data, simulations of roller system deformation and roll profile measurement error compensation were carried out, respectively, by using MATLAB R2016a, and the impact of different rolling processes on roller system deformation and online roll profile measurement error was analyzed. The simulations adopt the parameters of the F3 stand of the 1580 mm hot tandem strip mill of the Qian’an Iron and Steel Company (Tangshan, China), as shown in Figure 7. The process parameters are detailed in

Table 1. Process parameters for calculating the deformation of roller system.

Number	Initial Thickness /mm	Thickness After Rolling /mm	Front Tension /MPa	Post-Tension /MPa	Roll Bending Force /KN	Axial Displacement of the Roll /mm
1	10.33	6.18	13.70	12.60	1000	0
2	8.75	5.50	14.80	13.90	1000	0
3	7.91	4.81	18.13	14.35	1000	0
4	8.75	5.50	14.80	13.90	0	0
5	8.75	5.50	14.80	13.90	800	0
6	8.75	5.50	14.80	13.90	1000	15
7	8.75	5.50	14.80	13.90	1000	30

.

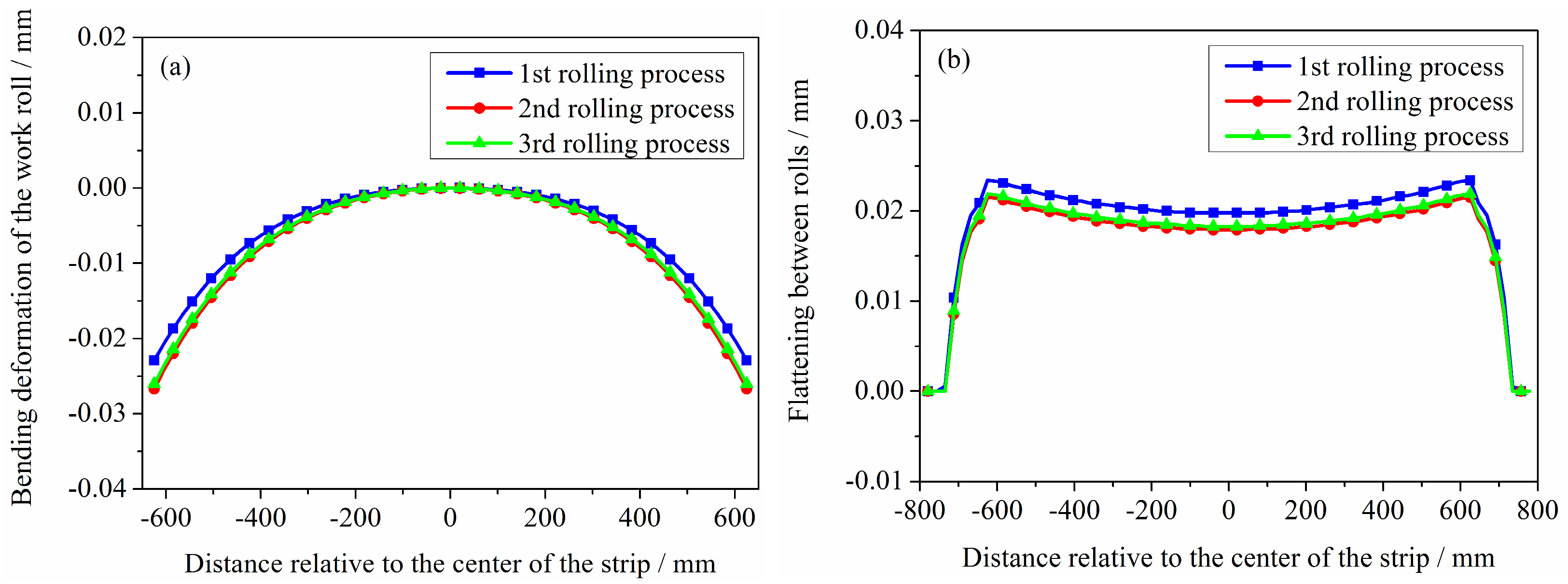
3.2. Results and Analysis

Assuming the rolls are unworn flat rolls, the corresponding roller system deformations were calculated under different rolling processes. The deflection deformation of the lower work roll, the flattening between rolls, and the flattening between roll and workpiece were obtained, and the influence of different process parameters on the roller system deformation were analyzed. During roller system deformation simulations, both the deflection of the work roll and the flattening between the roll and strip were calculated solely for the length of the roll in contact with the strip steel, and the flattening between rolls was calculated only for the length of the roll in contact with the back-up roll. Based on the simulation results of the roller system deformation, the roll profile measurement error compensation model was adopted to analyze the measurement errors of the lower work roll under each rolling process.

By simulating the first, second, and third rolling process parameters, computational results under different pressing processes can be obtained, as shown in Figure 8. As can be seen from Figure 8a, during the rolling process, the work roll undergoes flexural deformation due to the combined effects of the rolling force and the bending force. Due to the relatively high bending force applied in the numerical simulation, the work roll exhibited reverse bending. The pressing down amount of the first process parameter is relatively larger, corresponding to a greater rolling force, so the reverse bending amount of its work roll is smaller than that of the second and third ones. The pressing down amount in the second and third rolling processes is similar, so the deflection deformation of the work roll is also similar. The pressing down amount in the second rolling process exceeds that of the third, yet the work roll in the third rolling process exhibits lesser reverse bending under the influence of the bending force. This is because, with the same billet thickness, the strip steel produced by the third rolling process is thinner. At this stage, the strip steel exhibits greater deformation resistance, resulting in correspondingly higher rolling forces. It can be seen from Figure 8b,c that the greater the rolling force, the greater the flattening amount between rolls and the flattening between roll and strip steel. Moreover, under identical rolling processes, the flattening between roll and strip steel exceeds that between the rolls. As can be seen from Figure 8d, during online roll profile measurement in the rolling process, the pressing down amount significantly influences the measurement error when other parameters remain constant. Measurements without error compensation deviate significantly from the actual profile of the roll. Measurement errors are related to deflection deformation and elastic flattening of the rollers. The roll profile without error compensation is positively correlated with roll deflection.

Through the numerical simulations of the second, fourth, and fifth rolling process parameters, the simulation results under different bending forces can be obtained, as shown in Figure 9. As can be seen from Figure 9a, in the fourth rolling process, no bending force was applied, resulting in upward deflection deformation of the work roll. The second and fifth rolling processes exerted greater bending forces on the rollers, causing the work rolls to bend downward, and the greater the bending force, the more downward bending. It can be seen from Figure 9b,c that the bending force affects the transverse distribution of the roll flattening and has a particularly significant impact on the flattening between roll and strip steel. The greater the bending force, the lesser the flattening that occurs at both ends of the work roll, while the greater he flattening that occurs at its center. As shown in Figure 9d, during online roll profile measurement in the rolling process, the bending force significantly influences the measurement error when other parameters remain constant.

Through the numerical simulations of the second, sixth, and seventh rolling process parameters, the simulation results under different axial displacement of the roll can be obtained, as shown in Figure 10. As can be seen from Figure 10a, the deflection curve of the roll shifts in the opposite direction of the roll displacement, but the roll displacement has negligible influence upon the roll’s deflection. From Figure 10b,c, it can be seen that the impact of the axial displacement of the roll on flattening is negligible. As can be seen from Figure 10d, during online roll profile measurement in the rolling process, the axial displacement of the roll has a very small impact on the profile when other parameters remain constant. This is because, within the range of strip steel width, the axial displacement of the roll have a relatively minor impact on the bending and flattening. It should be noted that, when the rolling mill adopts the axial displacement of the roll process, the roll profile measurement system requires displacement compensation in the $x_m$-axis direction. The magnitude and direction of the compensation should be consistent with the displacement and direction of the corresponding roll.

Through the numerical simulations of the roller deformation and roll profile measurement error compensation of the 1580 mm hot tandem strip mill, it can be concluded that, during the rolling process, under the combined action of the rolling force and the bending roll force, the work rolls will undergo bending deformation and elastic flattening, with deformation amounts reaching tens of micrometers. In the case of deformation superposition, the displacement change at a certain point of the work roll caused by the deformation of the roller system may exceed one hundred micrometers. Therefore, during the online roll profile measurement during the rolling process, in order to ensure measurement accuracy, the roller system deformation must be taken into account, and the measurement errors caused by it must be compensated for.

As of now, all the relevant reports on the online roll profile measurement technology have been carried out under the no-load state of the rolling mills. This research overcomes the limitations of no-load measurement in rolling mills, laying the theoretical foundation for achieving full-time online roll profile measurement during both no-load and rolling processes.

4. Conclusions

This paper aims to improve online roll profile measurement accuracy. An error compensation model considering roller system deformation was established. Numerical simulations of roller deformation and the error compensation of the roll profile measurement were conducted for different rolling processes. Based on the analysis results, the following conclusions are drawn:

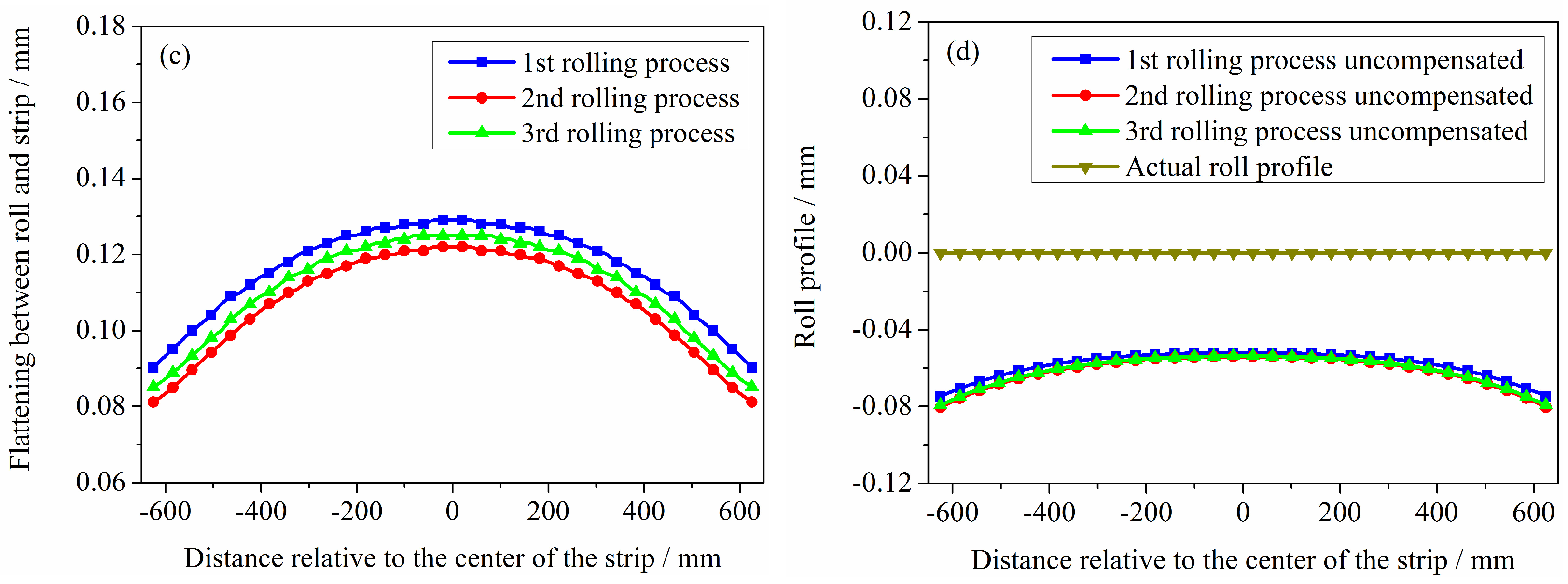
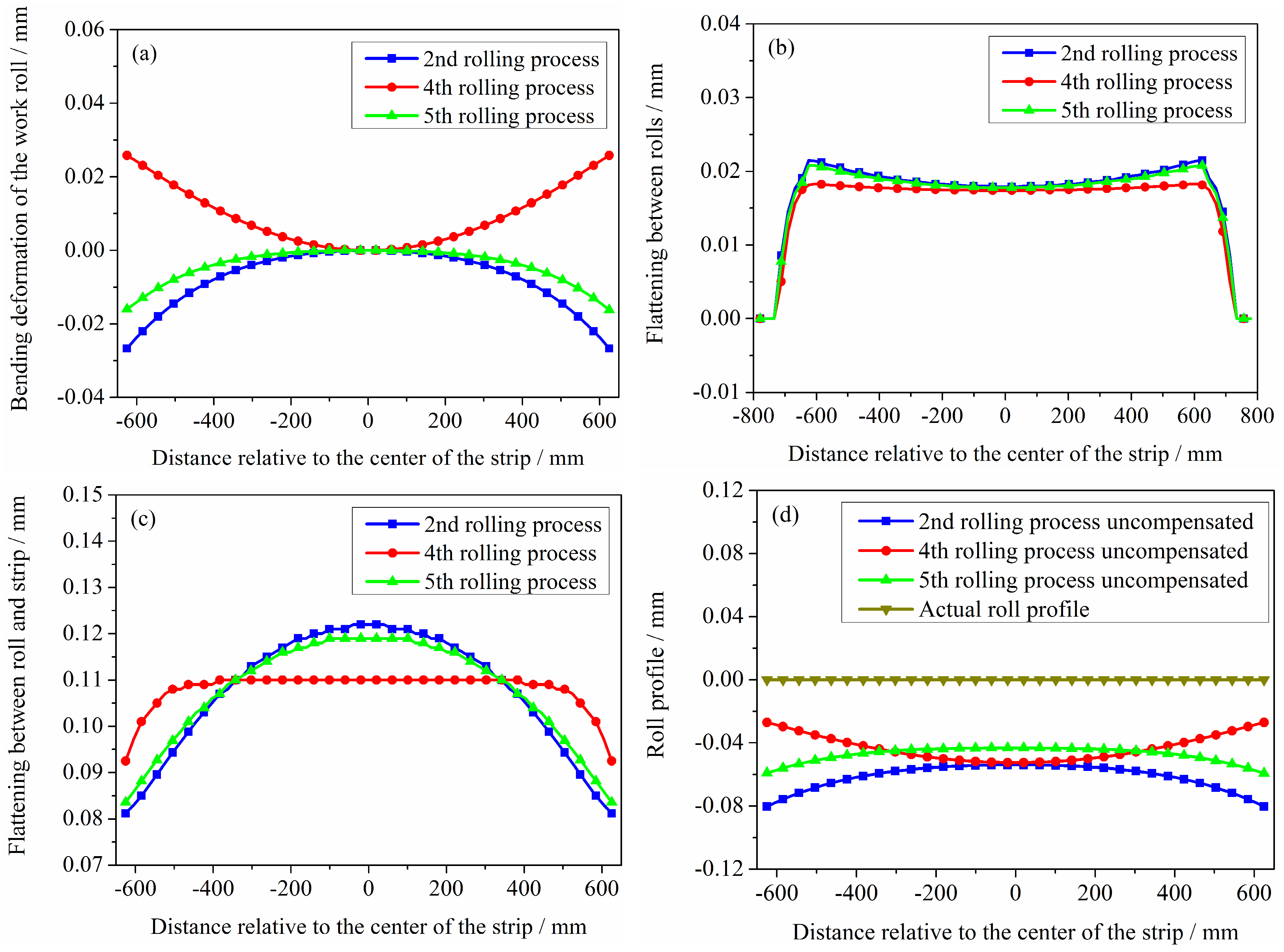
• During the rolling process, under the combined effects of rolling force and bending force, the work rolls undergo deflection deformation and elastic flattening. To ensure measurement accuracy during online roll profile measurement, it is necessary to compensate for the measurement errors caused by the roller system deformation.
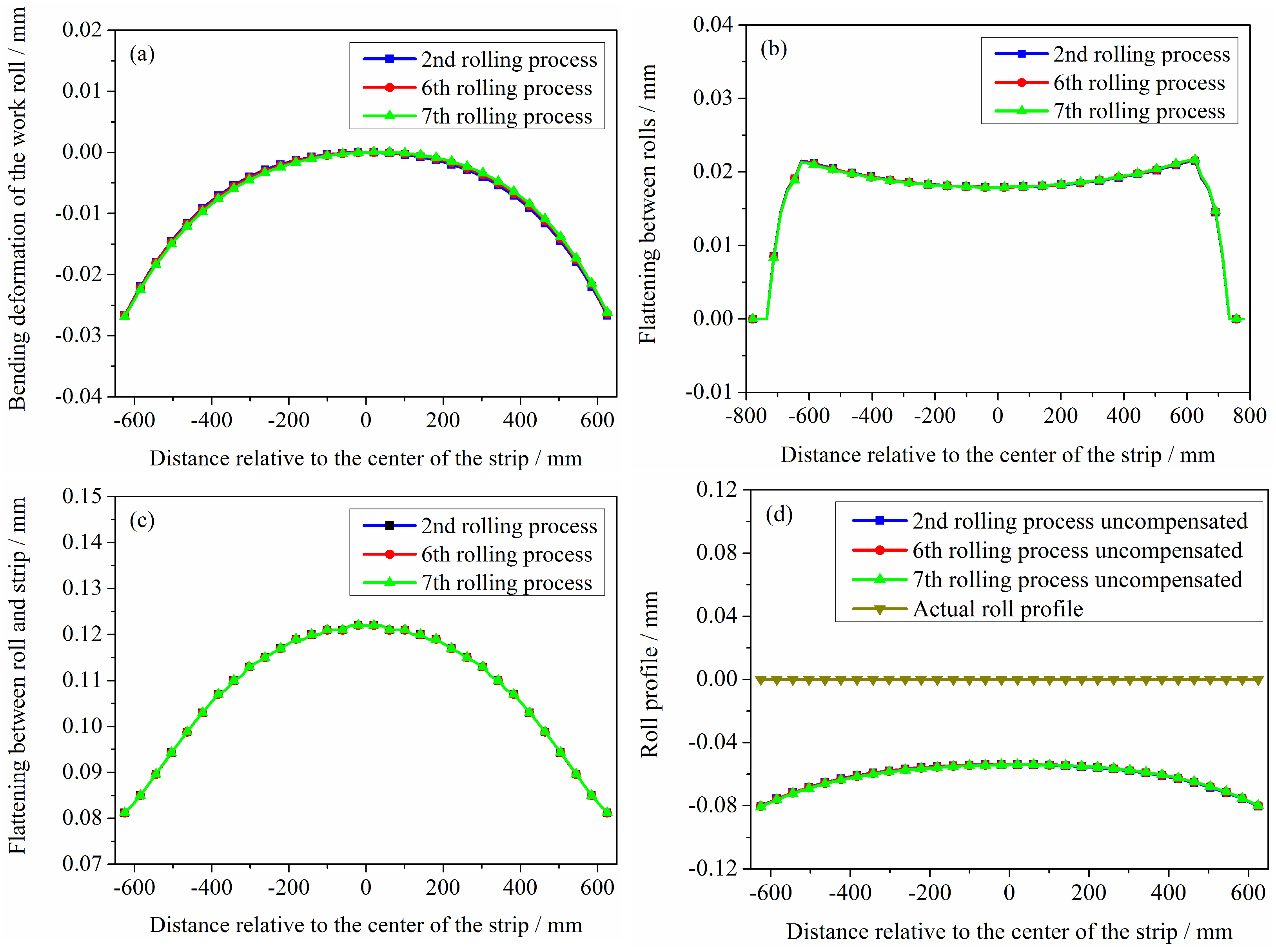
• The pressing process and bending force have a significant impact on the roller system deformation. Roll profile measurement errors are associated with both the deflection deformation and the elastic flattening of the rolls. The roll profile curves without error compensation have a high correlation with the bending deformation of the rolls. The axial displacement of the rolls has a negligible effect on the rolls’ deflection and flattening and consequently exerts minimal influence on roll profile measurement errors. However, when the rolling mill adopts the axial displacement of the roll process, the roll profile measurement system requires displacement compensation in the $x_m$-axis direction. The magnitude and direction of the compensation should be consistent with the displacement and direction of the corresponding roll.
• This paper primarily investigated the error compensation theory of online roll profile measurement considering the roller system deformation. This work was conducted on the premise that the sensor provides accurate measurements. Future research should focus on investigating the impact of factors such as sensor measurement accuracy, measurement system stability, and rolling mill vibration on measurement errors, thereby further enhancing the precision of roll profile measurement. Furthermore, research should be conducted into online roll grinding technology, integrating it with online roll profile measurement techniques to fully leverage the technical advantages of online roll grinding.