Numerical Investigation of Dual Vertical Water Jets Impinging on High-Temperature Steel
Abstract
1. Introduction
2. Materials and Methods
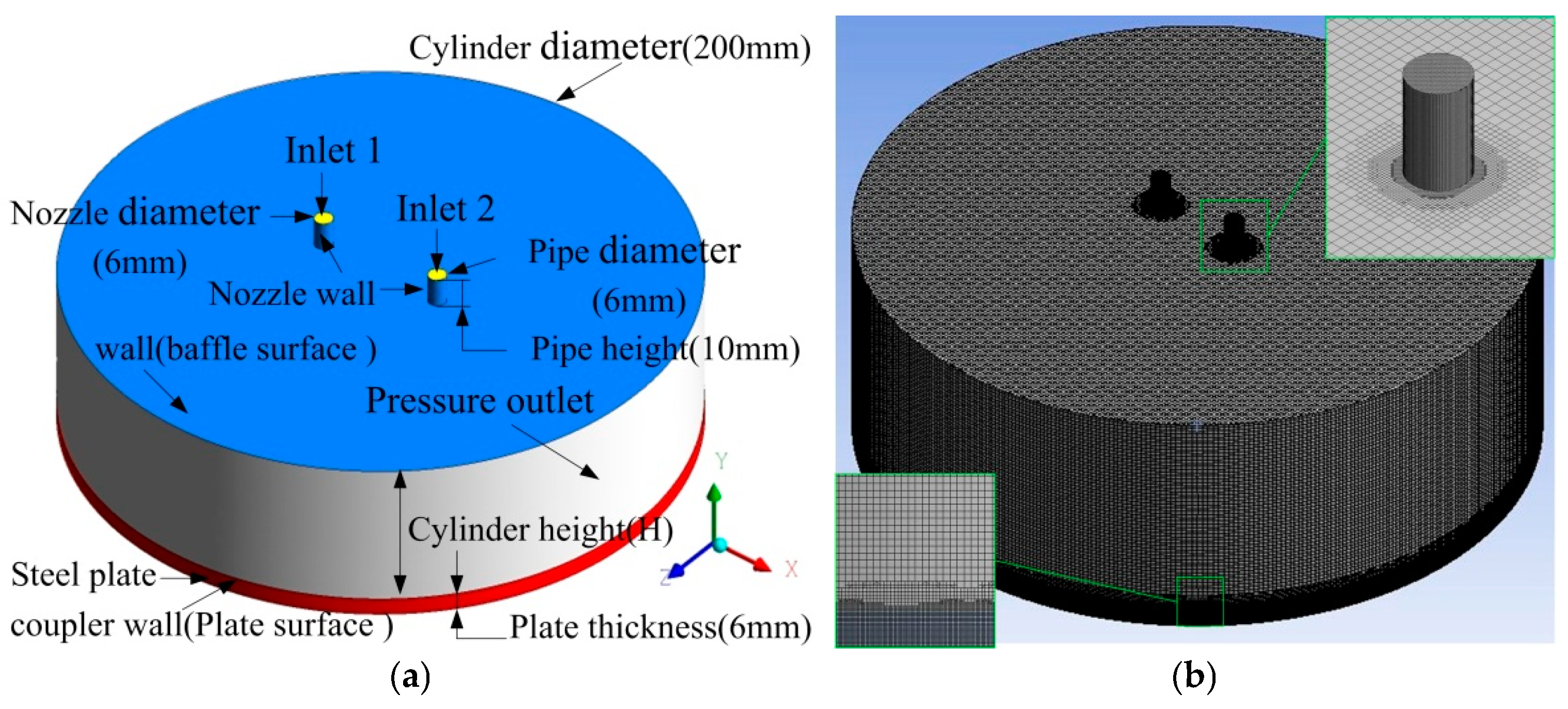
2.1. Computational Domain and Assumptions
2.2. Governing Equations
2.3. Boundary Conditions
2.4. Numerical Considerations
3. Results
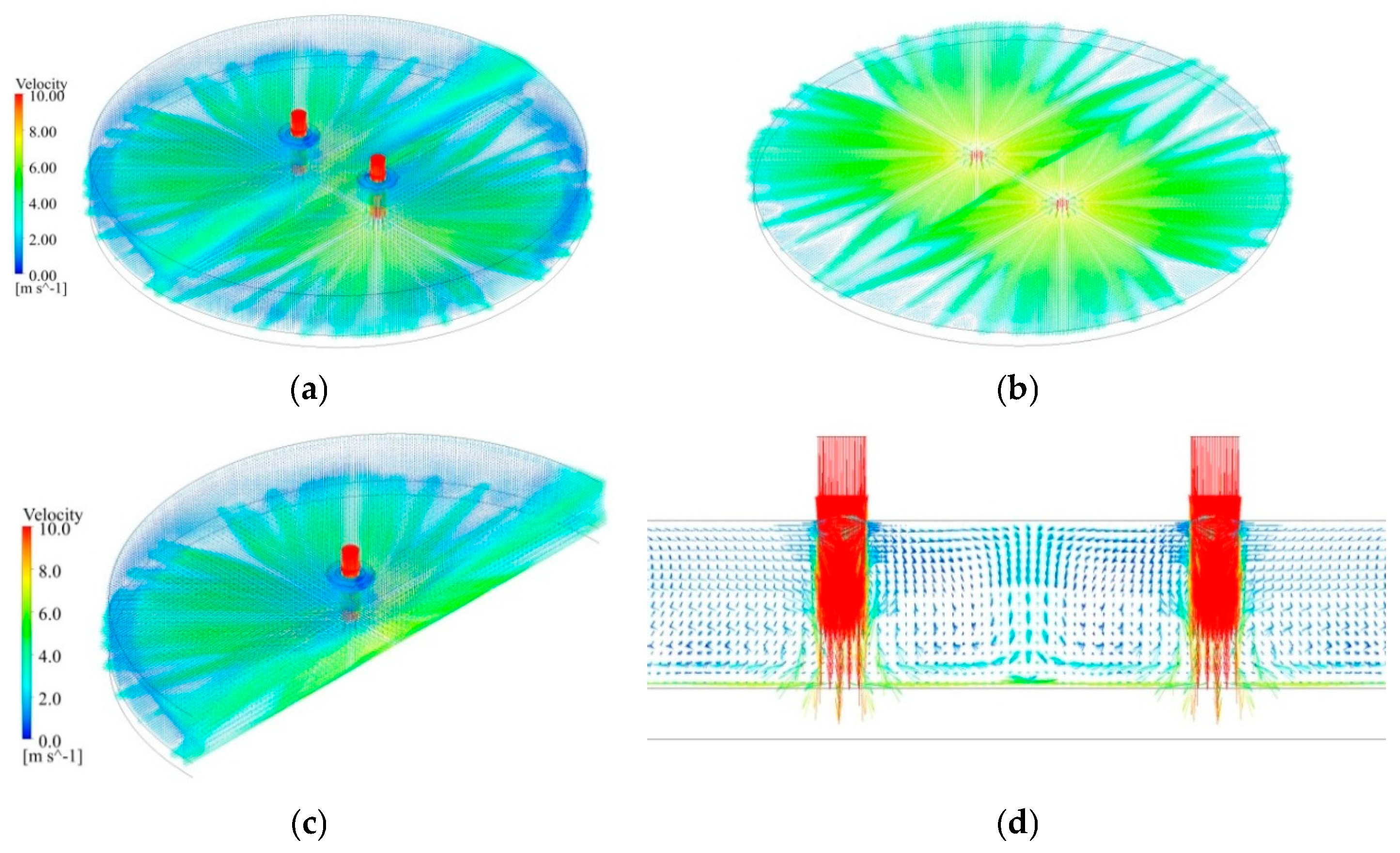
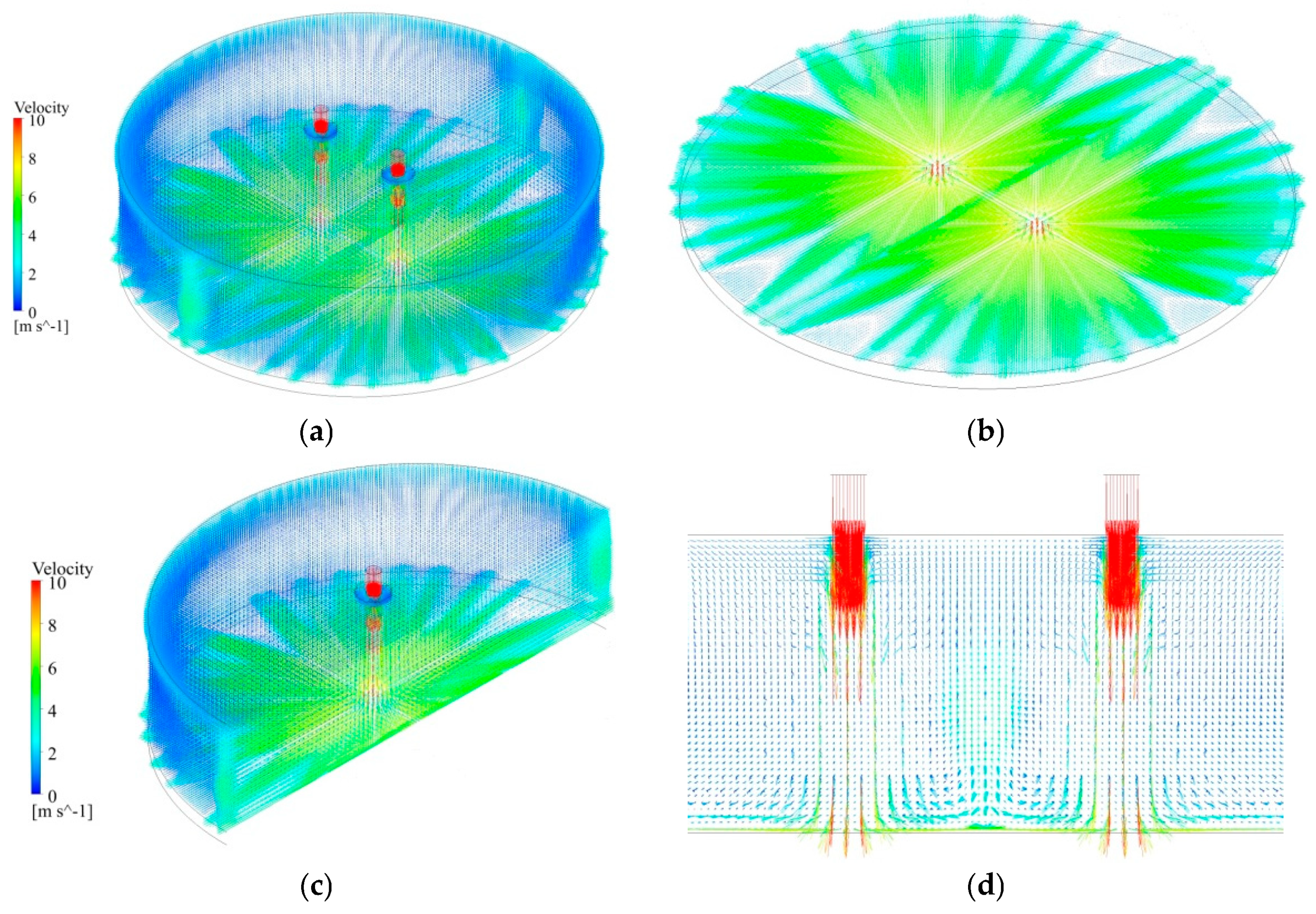
3.1. Velocity Distribution of the Flow Domains
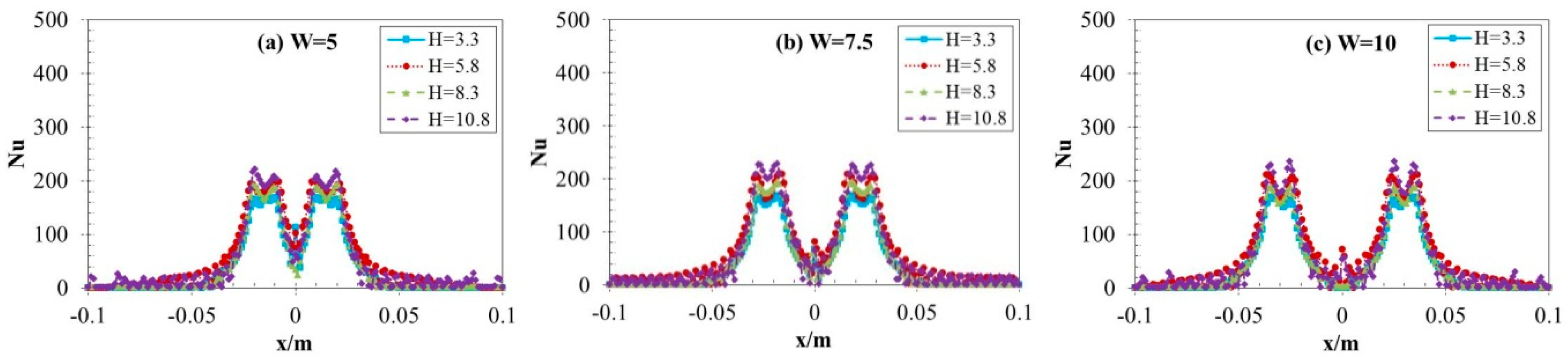
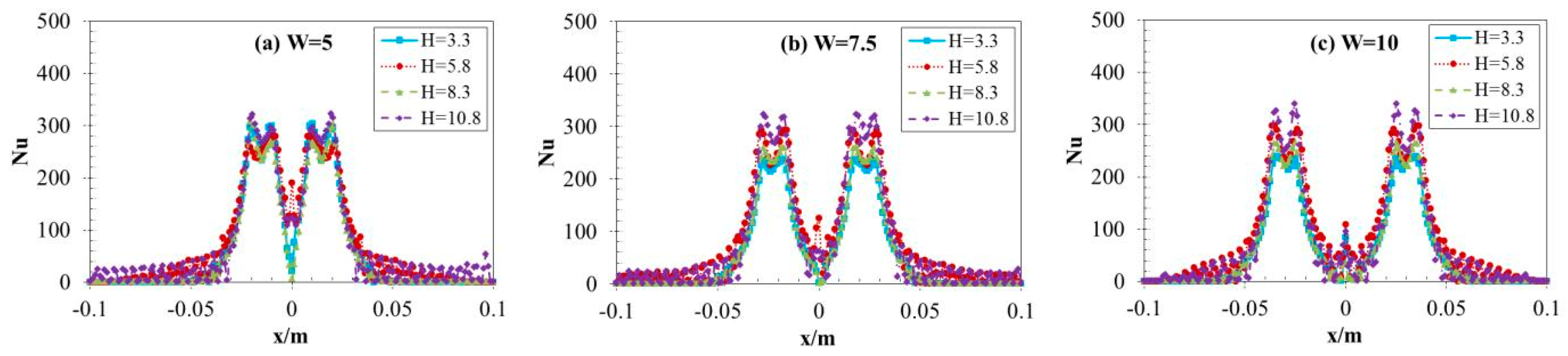
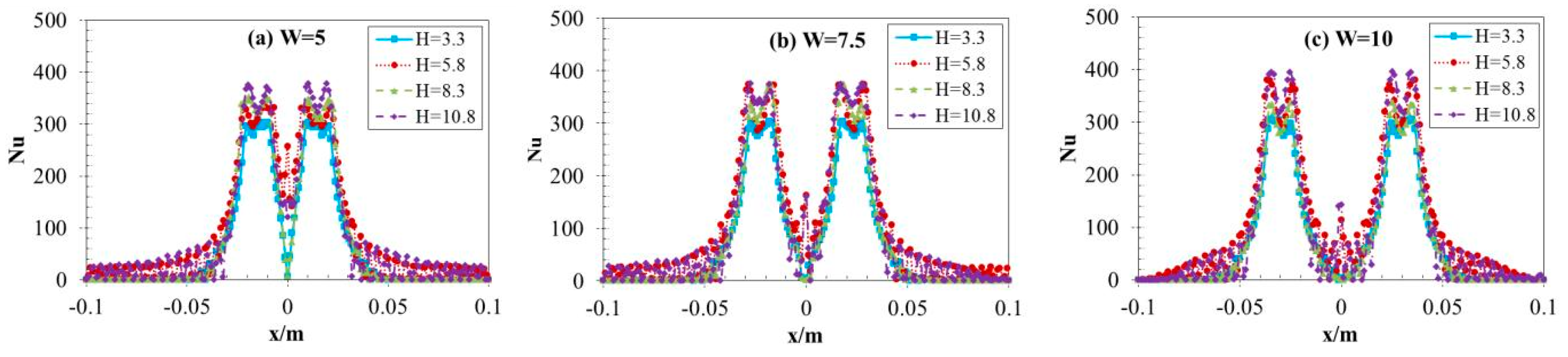
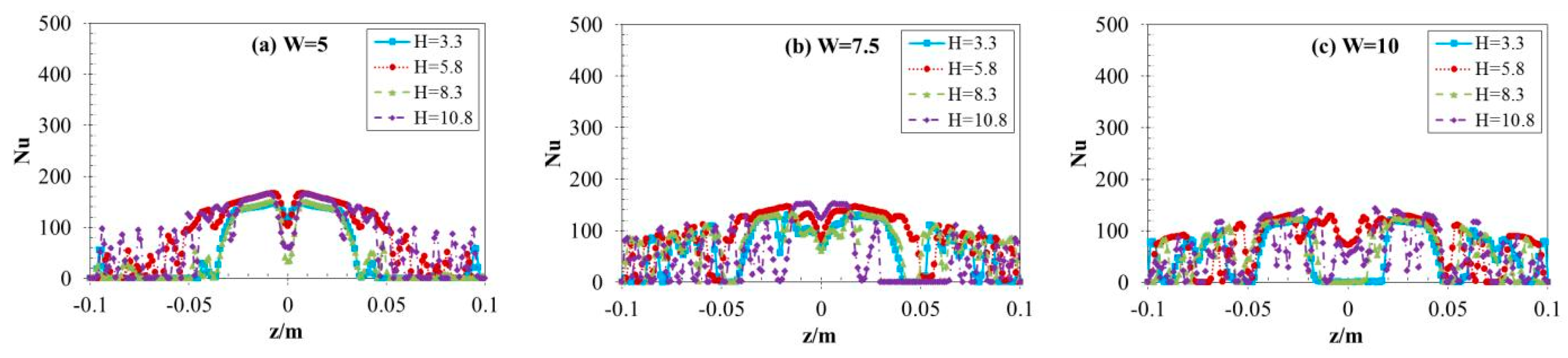
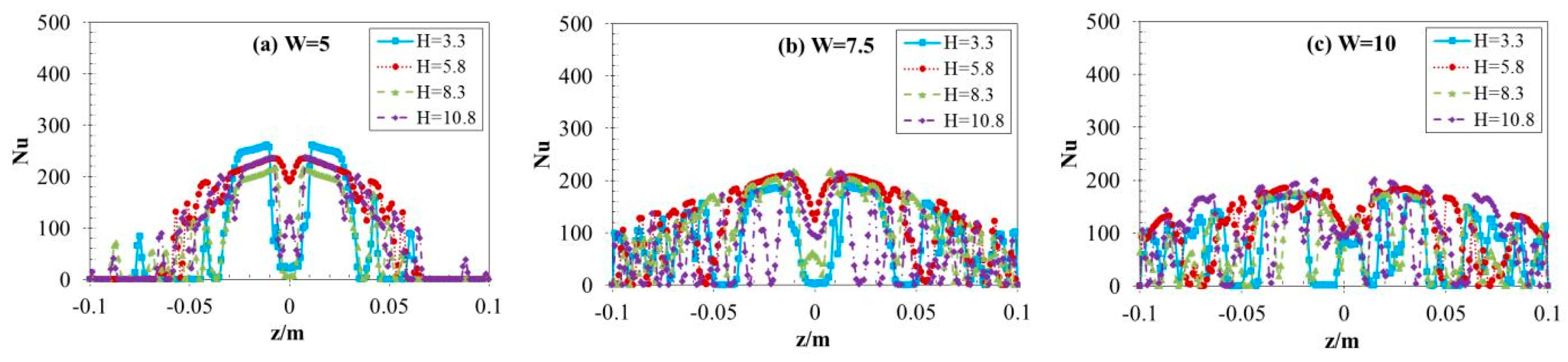
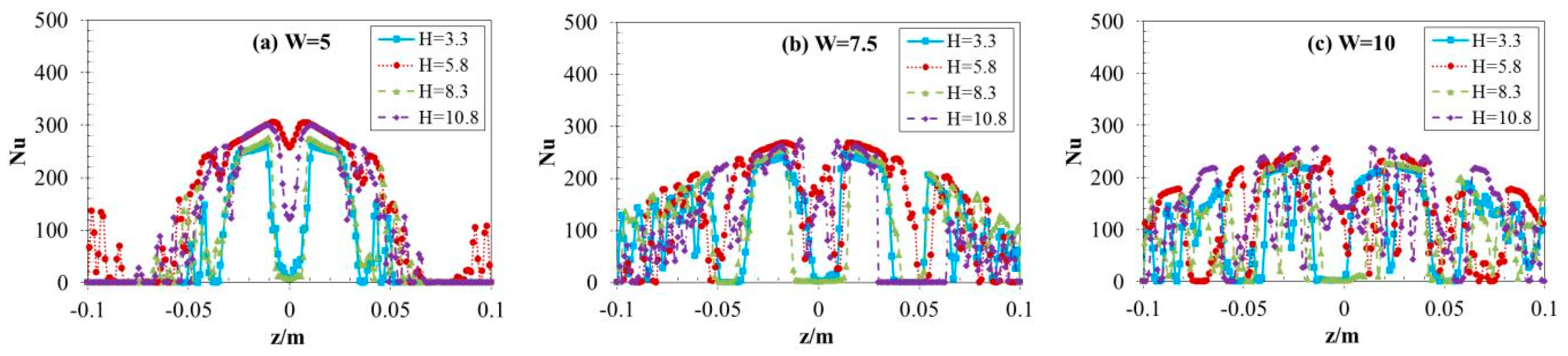
3.2. Local Nusselt Number Distribution
3.3. Average Nusselt Number Variation Along the Steel Surface
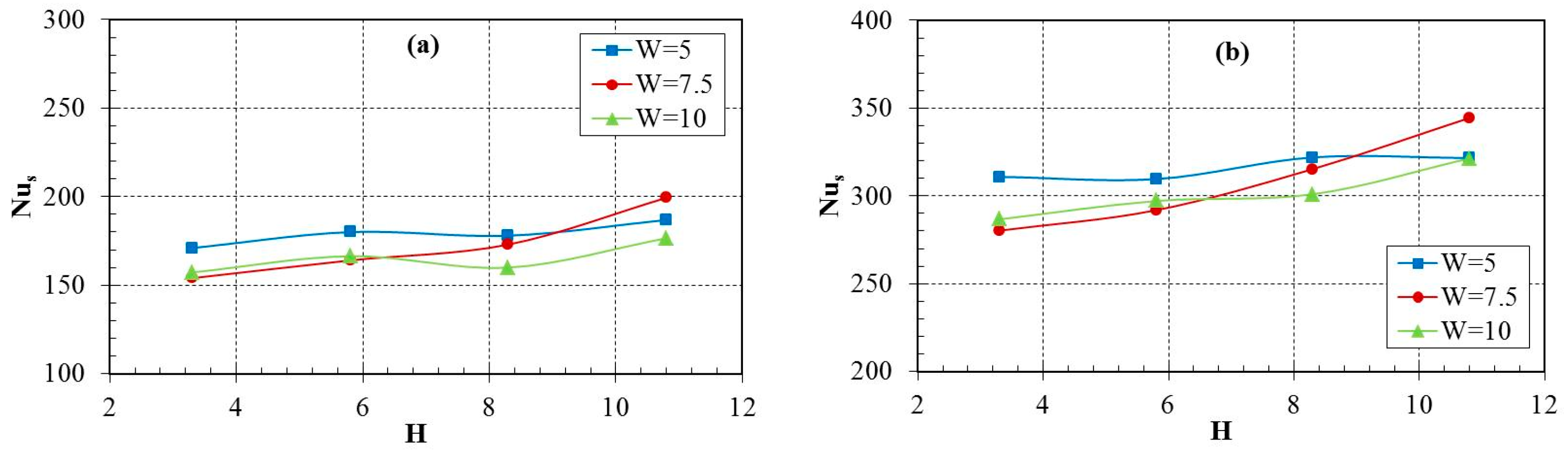
3.4. Nusselt Number at Stagnation Point
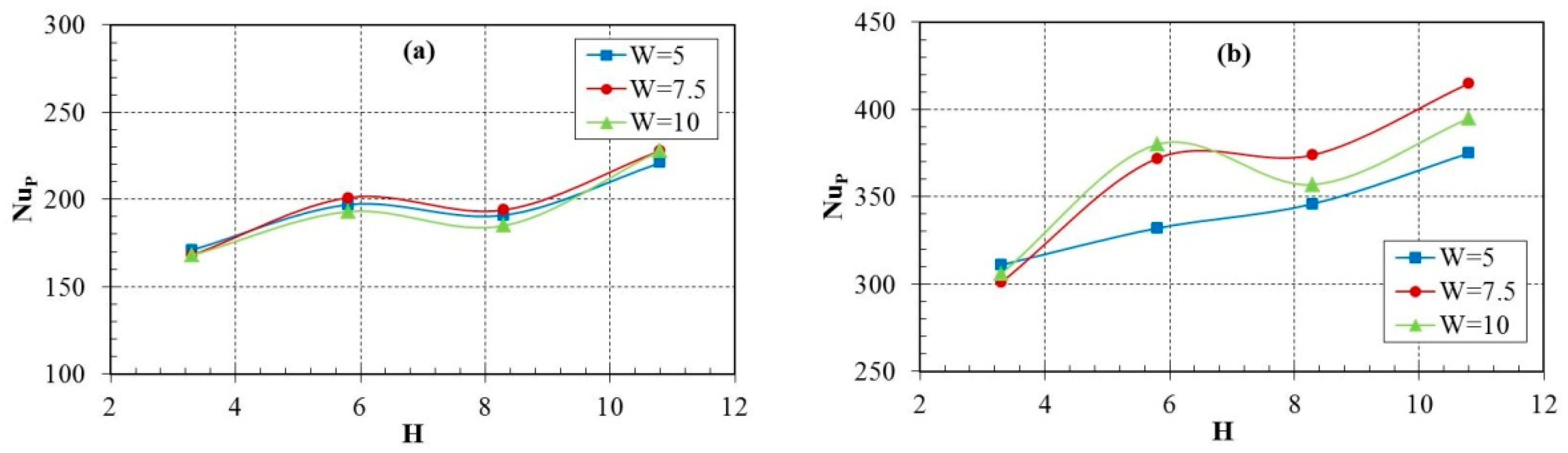
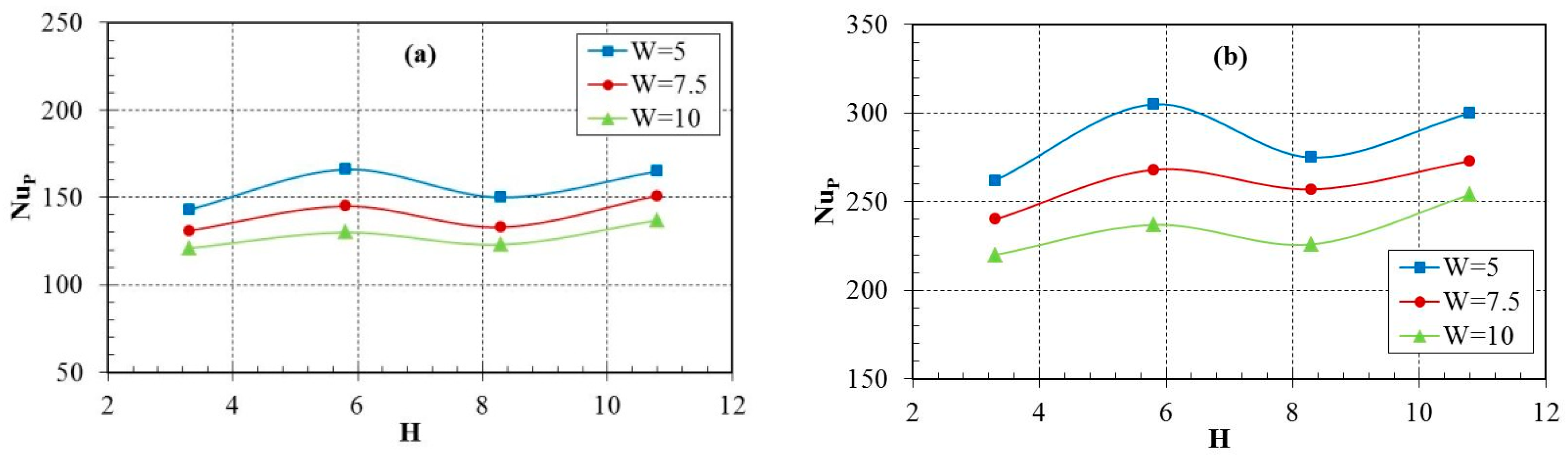
3.5. Peak Value of Nusselt Number
4. Discussion
5. Conclusions
- (1)
- When the jets strike the surface of the steel plate, several water flows are generated in the wall-jet area, and the distance between them grows as the radius of the plate surface increases. Between the two jets, there emerges an area of wall-jet interaction, and the fountain upwash flow presents as a straight line.
- (2)
- In the parallel direction of the two jets’ centerline, the local Nusselt number exhibits a characteristic profile, beginning with a minimum at the stagnation point, rapidly increasing to a peak value, and subsequently decaying sharply with radial distance from the impingement zone. Finally, it shows a slight decline as the distance increases. While in vertical direction, the Nusselt number of the interaction line of the two jets decreases with increasing non-dimensional spacing between twin nozzles (W), However, the thermal interaction length for W = 5 is shorter than the other two cases (W = 7.5 and 10).
- (3)
- The NuA of the plate surface fluctuates slightly with the distance from the nozzle to the plate surface, and the maximum value of NuA is obtained when the non-dimensional nozzle-to-plate distance (H) is 5.8. Meanwhile, due to the limitations within ±0.05 m, it shows a gradual decline as the non-dimensional distance between twin nozzles (W) increases from 5 to 10.
- (4)
- The heat transfer intensity of stagnation zone can be enhanced by appropriately increasing the distance of the nozzle-to-plate surface within a certain range, and the heat transfer intensity of the wall-jet interaction zone can be changed slightly by decreasing the nozzle-to-nozzle spacing.
6. Future Direction
- (1)
- The current work focused on a limited set of parameters. Future investigations should explore a wider parametric space, including a broader range of Reynolds numbers, nozzle-to-plate distances, and nozzle spacings. Furthermore, research should extend to more complex nozzle arrangements, such as jet arrays, and the use of inclined or swirling jets, which could offer superior control over cooling uniformity and heat transfer distribution on large-scale surfaces.
- (2)
- In this work, a constant isothermal wall condition and Realizable k-ε model were selected, the effect of phase change heat was disregarded, and the influence of the transient temperature drop of the high-temperature steel plate was not thoroughly investigated. Developing a completely transient-coupled model that includes a complete boiling curve is the key to future work. The application of more sophisticated numerical models is critical to unravel the underlying physics. Exploring the application of more advanced turbulence and multiphase models (e.g., RSM or LES) to capture finer flow dynamics is also critical.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| d | nozzle diameter (0.006 m) |
| h | distance between nozzle exit and target heated plate surface (mm) |
| H | non-dimensional nozzle-to-plate distance (-) |
| Nu | Nusselt number (-) |
| NuA | average Nusselt number (-) |
| NuS | Nusselt number at stagnation point (-) |
| NuP | peak value of Nusselt number (-) |
| Tw | initial temperature of water (298 K) |
| Ta | initial temperature of air (300 K) |
| T0 | initial temperature of steel plate (1123 K) |
| V | the jet velocity at the nozzle exit (m/s) |
| w | spacing between twin nozzles (mm) |
| W | the non-dimensional spacing between twin nozzles (-) |
References
- Gomez, C.F.; Geld, C.W.M.; Kuerten, J.G.M.; Bsibsi, M.; Esch, B.P.M. Quench cooling of fast moving steel plates by water jet impingement. Int. J. Heat Mass Transf. 2020, 163, 120545. [Google Scholar] [CrossRef]
- Li, X.Q.; Xia, W.H.; Yang, K.; Dai, L.F.; Wang, F.; Xie, Q.; Cai, J.J. Quench cooling of steel plates by reciprocating moving water jet impingement. Exp. Therm. Fluid Sci. 2024, 153, 111127. [Google Scholar] [CrossRef]
- Suresh, B.G.; Gaurav, A.K.; Stephan, R.; Eckehard, S. Heat transfer analysis during quenching of moving metal plates using water jets from a mold. Therm. Sci. Eng. Prog. 2025, 64, 103792. [Google Scholar] [CrossRef]
- Xu, R.; Zhang, R.Y.; Jiang, J.Y.; Wang, Z.B.; Zhang, Z.; Zheng, K.L.; Zhao, L. Investigation on the jet impingement cooling of steel discs using air-atomized water mist. Int. J. Heat Mass Transf. 2025, 245, 126989. [Google Scholar] [CrossRef]
- Wang, S.J.; Lin, Q.G.; Li, T.; Tan, M.Y.; Shi, Z.H.; Liu, H.F.; Li, W.F. Study on flow and heat transfer characteristics of cross-jet impingement cooling. Int. J. Heat Mass Transf. 2026, 255, 127772. [Google Scholar] [CrossRef]
- Dou, R.; Wen, Z.; Zhou, G.; Liu, X.; Feng, X. Experimental study on heat-transfer characteristics of circular water jet impinging on high-temperature stainless steel plate. Appl. Therm. Eng. 2014, 62, 738–746. [Google Scholar] [CrossRef]
- Guo, Q.; Wen, Z.; Dou, R. Experimental and numerical study on the transient heat-transfer characteristics of circular air-jet impingement on a flat plate. Int. J. Heat Mass Transf. 2017, 104, 1177–1188. [Google Scholar] [CrossRef]
- Avadhesh, K.S.; Santosh, K.S. An experimental study on heat transfer and rewetting behavior of hot horizontal downward facing hot surface by mist jet impingement. Appl. Therm. Eng. 2019, 151, 459–474. [Google Scholar] [CrossRef]
- Wang, C.; Wang, X.; Shi, W.; Lu, W.; Tan, S.K.; Zhou, L. Experimental investigation on impingement of a submerged circular water jet at varying impinging angles and Reynolds numbers. Exp. Therm. Fluid Sci. 2017, 89, 189–198. [Google Scholar] [CrossRef]
- Colucci, D.W.; Viskanta, R. Effect of nozzle geometry on local convective heat transfer to a confined impinging air jet. Exp. Therm. Fluid Sci. 1996, 13, 71–80. [Google Scholar] [CrossRef]
- Ibroheng, P.; Anil, K.; Natthaporn, K.; Chayut, N. Flow and heat transfer characteristics of submerged impinging air-water jets. Int. J. Therm. Sci. 2023, 193, 108503. [Google Scholar] [CrossRef]
- Wang, X.L.; Motala, D.; Lu, T.J.; Song, S.J.; Kimb, T. Heat transfer of a circular impinging jet on a circular cylinder in crossflow. Int. J. Therm. Sci. 2014, 78, 1–8. [Google Scholar] [CrossRef]
- Hadipour, A.; Zargarabadi, M.R. Heat transfer and flow characteristics of impinging jet on a concave surface at small nozzle to surface distances. Appl. Therm. Eng. 2018, 138, 534–541. [Google Scholar] [CrossRef]
- Joo, H.M.; Soyeong, L.; Jungho, L.; Seong, H.L. Numerical study on subcooled water jet impingement cooling on superheated surfaces. Case Stud. Therm. Eng. 2022, 32, 101883. [Google Scholar] [CrossRef]
- Chee, M.W.L.; Chauhan, P.; Georgiou, J.; Wilson, D.I. Flow distribution in the liquid film created by a coherent circular water jet impinging obliquely on a plane wall. Exp. Therm. Fluid Sci. 2023, 140, 110748. [Google Scholar] [CrossRef]
- Taghinia, J.; Rahman, M.M.; Siikonen, T. Numerical investigation of twin-jet impingement with hybrid-type turbulence modeling. Appl. Therm. Eng. 2014, 73, 650–659. [Google Scholar] [CrossRef]
- Sandoval, C.; Treviño, C.; Alvarez, A.; Matuz, D.; Lizardi, J.; Martínez-Suástegui, L. Flow field analysis of submerged oblique and normally impinging twin jets at varying impinging angles. Exp. Therm. Fluid Sci. 2025, 167, 111491. [Google Scholar] [CrossRef]
- Greco, C.S.; Castrillo, G.; Crispo, C.M.; Astarita, T.; Cardone, G. Investigation of impinging single and twin circular synthetic jets flow field. Exp. Therm. Fluid Sci. 2016, 74, 354–367. [Google Scholar] [CrossRef]
- Ozmen, Y. Confined impinging twin air jets at high Reynolds numbers. Exp. Therm. Fluid Sci. 2011, 35, 355–363. [Google Scholar] [CrossRef]
- Singh, D.; Premachandran, B.; Kohli, S. Double circular air jet impingement cooling of a heated circular cylinder. Int. J. Heat Mass Transf. 2017, 109, 619–646. [Google Scholar] [CrossRef]
- Yin, Z.; Zhang, H.; Lin, J. Experimental study on the flow field characteristics in the mixing region of twin jets. J. Hydrodyn. 2007, 19, 309–313. [Google Scholar] [CrossRef]
- Meslem, A.; Sobolik, V.; Bode, F.; Sodjavi, K.; Zaouali, Y.; Nastase, I.; Croitoru, C. Flow dynamics and mass transfer in impinging circular jet at low Reynolds number. Comparison of convergent and orifice nozzles. Int. J. Heat Mass Transf. 2013, 67, 25–45. [Google Scholar] [CrossRef]
- Nakabe, K.; Fornalik, E.; Eschenbacher, J.F.; Yamamoto, Y.; Ohta, T.; Suzuki, K. Interactions of longitudinal vortices generated by twin inclined jets and enhancement of impingement heat transfer. Int. J. Heat Fluid Flow 2001, 22, 287–292. [Google Scholar] [CrossRef]
- Kate, R.P.; Das, P.K.; Chakraborty, S. An experimental investigation on the interaction of hydraulic jumps formed by two normal impinging circular liquid jets. J. Fluid Mech. 2007, 590, 355–380. [Google Scholar] [CrossRef]
- Teamah, M.A.; Khairat, M.M. Heat transfer due to impinging double free circular jets. Alex. Eng. J. 2015, 54, 281–293. [Google Scholar] [CrossRef]
- Thibaut, J.; Ivana, V.; Serge, S. Flow dynamics, heat and mass transfer of laminar, round twin-jet impinging a uniformly heated flat plate. Int. J. Heat Mass Transf. 2025, 236, 126187. [Google Scholar]
- Abraham, S.; Vedula, R.P. Effectiveness distribution measurements for a row of heated circular jets impinging on a cylindrical convex surface at different inclinations. Int. J. Heat Fluid Flow 2018, 69, 210–223. [Google Scholar] [CrossRef]
- Dong, L.L.; Leung, C.W.; Cheung, C.S. Heat transfer of a row of three butane/air flame jets impinging on a flat plate. Int. J. Heat Mass Transf. 2003, 46, 113–125. [Google Scholar] [CrossRef]
- Chiu, H.; Jang, J.; Yan, W. Experimental study on the heat transfer under impinging elliptic jet array along a film hole surface using liquid crystal thermograph. Int. J. Heat Mass Transf. 2009, 52, 4435–4448. [Google Scholar] [CrossRef]
- Caliskan, S.; Baskaya, S.; Calisir, T. Experimental and numerical investigation of geometry effects on multiple impinging air jets. Int. J. Heat Mass Transf. 2014, 75, 685–703. [Google Scholar] [CrossRef]
- Geers, L.F.G.M.; Tummers, J.; Hanjalić, K. Experimental investigation of impinging jet arrays. Exp. Fluids 2004, 36, 946–958. [Google Scholar] [CrossRef]
- Mohammad, J.; Bahram, M. Quenching a rotary hollow cylinder by multiple configurations of water-impinging jets. Int. J. Heat Mass Transf. 2019, 137, 124–137. [Google Scholar] [CrossRef]
- Hosain, M.L.; Fdhila, R.B.; Daneryd, A. Heat transfer by liquid jets impinging on a hot flat surface. Appl. Energy 2016, 164, 934–943. [Google Scholar] [CrossRef]
- Liu, X.; Lienhard, V.J.H.; Lombara, J.S. Convective heat transfer by impingement of circular liquid jets. J. Heat Transf. 1991, 113, 571–582. [Google Scholar] [CrossRef]
- Lienhard, V.J.H. Heat transfer by impingement of circular free-surface liquid jets. In Proceedings of the 18th National & 7th ISHMT-ASME Heat and Mass Transfer Conference, Guwahati, India, 4–6 January 2006; pp. 1–16. [Google Scholar]
- Li, C.; Shi, Y.N.; Yang, H.; Zhang, Y.S.; Yuan, G.; Li, Z.L.; Zhang, F.B. Heat transfer characteristics of water jet impingement on high-temperature steel plate by angular nozzle. Int. Commun. Heat Transf. 2024, 151, 107243. [Google Scholar] [CrossRef]

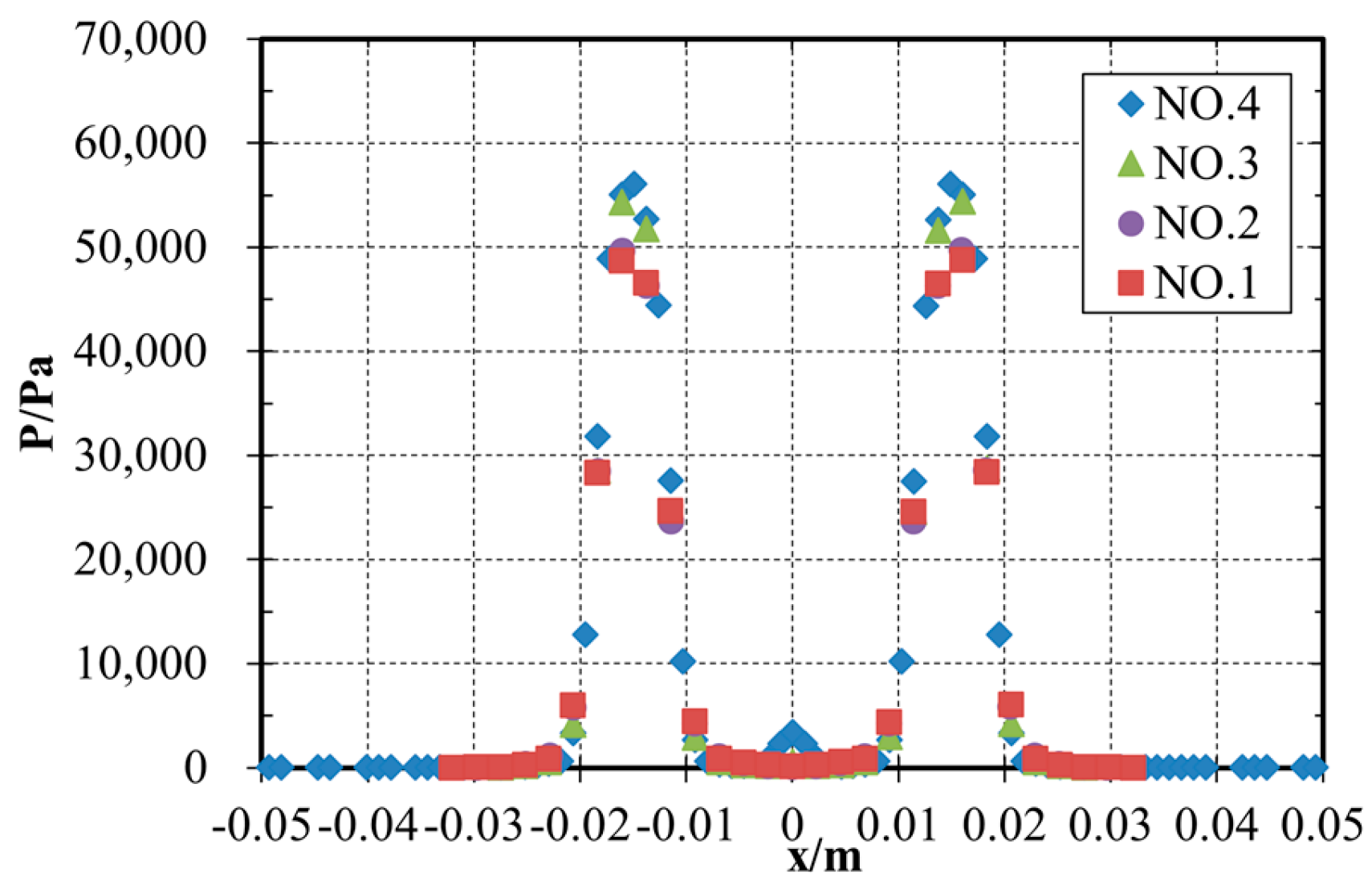



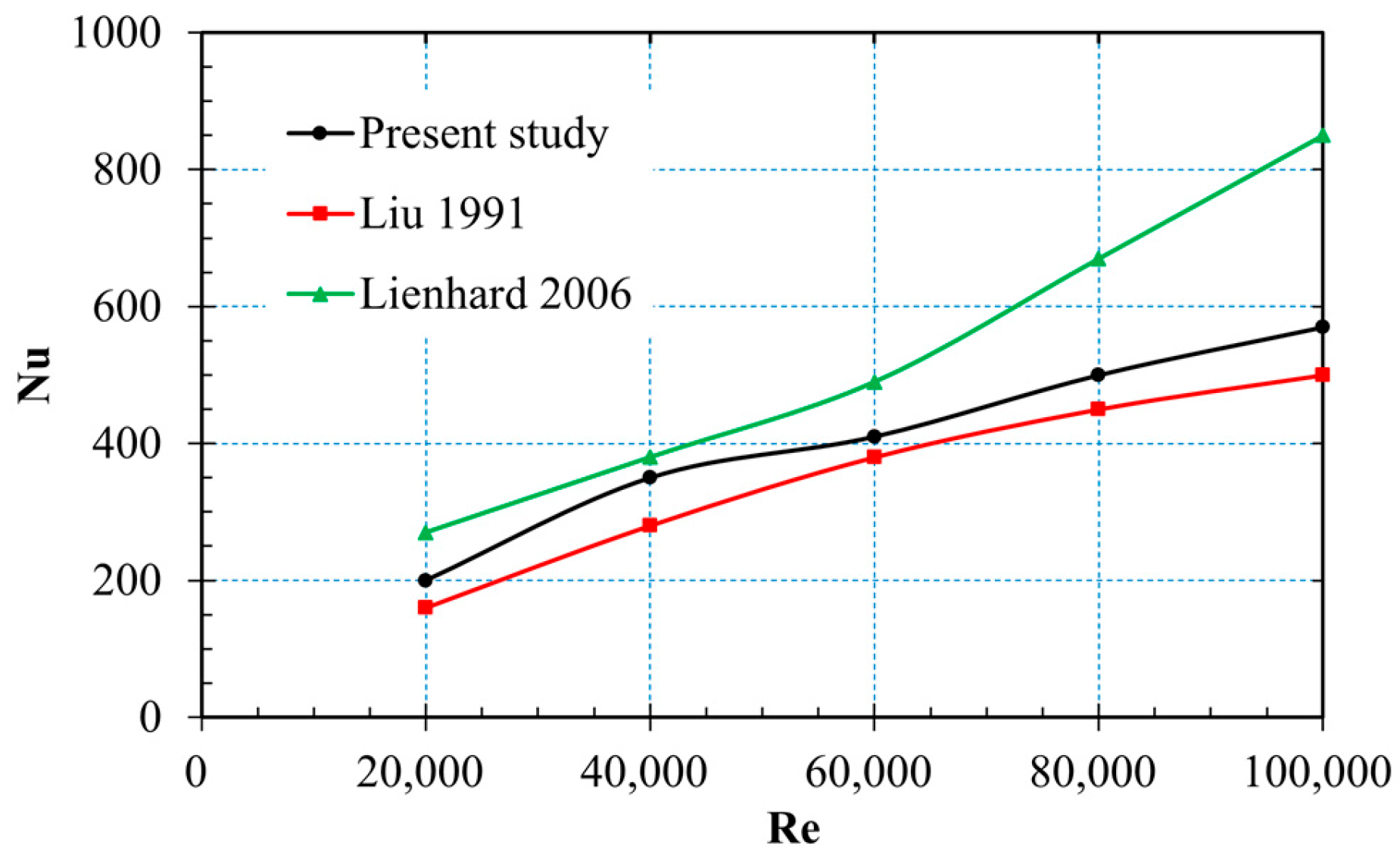
| Water Flow/(m3/s) | 0.01389 | 0.01667 | 0.01944 | 0.02222 | 0.03889 |
|---|---|---|---|---|---|
| V/(m/s), d = 0.045 m | 6.85 | 9.13 | 11.42 | 13.70 | 15.98 |
| V/(m/s), d = 0.006 m | 3.85 | 5.14 | 6.42 | 7.71 | 8.99 |
| Grid | Nodes | Elements |
|---|---|---|
| NO.1 | 295,215 | 259,788 |
| NO.2 | 675,922 | 588,724 |
| NO.3 | 800,104 | 714,306 |
| NO.4 | 1,247,153 | 1,103,653 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Zhang, Z.; Ji, X.; You, J.; Han, F. Numerical Investigation of Dual Vertical Water Jets Impinging on High-Temperature Steel. Metals 2025, 15, 1305. https://doi.org/10.3390/met15121305
Shi J, Zhang Z, Ji X, You J, Han F. Numerical Investigation of Dual Vertical Water Jets Impinging on High-Temperature Steel. Metals. 2025; 15(12):1305. https://doi.org/10.3390/met15121305
Chicago/Turabian StyleShi, Jianhui, Zhao Zhang, Xiangfei Ji, Jinwen You, and Feng Han. 2025. "Numerical Investigation of Dual Vertical Water Jets Impinging on High-Temperature Steel" Metals 15, no. 12: 1305. https://doi.org/10.3390/met15121305
APA StyleShi, J., Zhang, Z., Ji, X., You, J., & Han, F. (2025). Numerical Investigation of Dual Vertical Water Jets Impinging on High-Temperature Steel. Metals, 15(12), 1305. https://doi.org/10.3390/met15121305