A Deep Learning-Based CNN-LSTM Framework for Constitutive Parameter Inversion in Alloy Gradient-Grained Materials
Abstract
1. Introduction
2. Materials and Methods
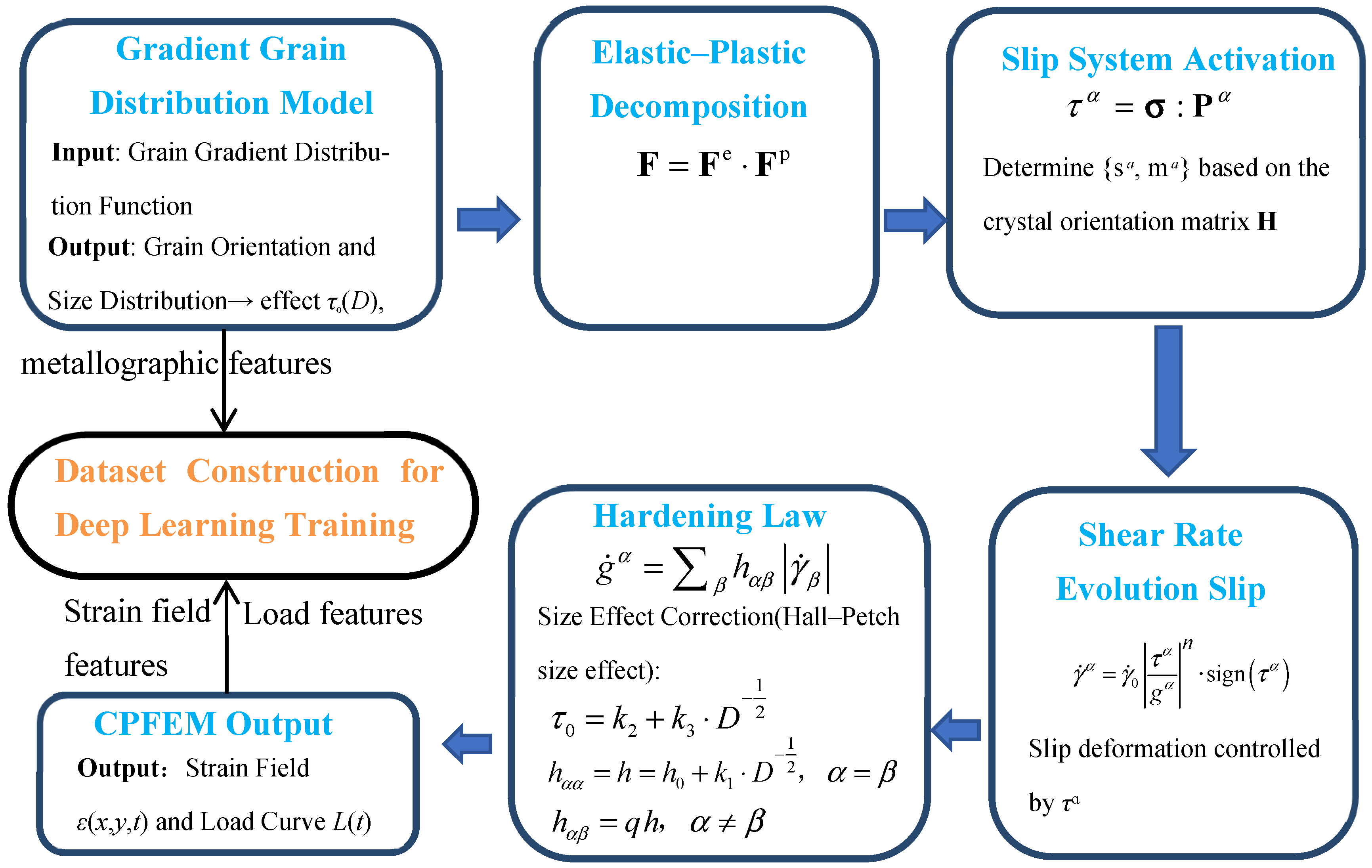
2.1. Classical Crystal Plasticity Theory
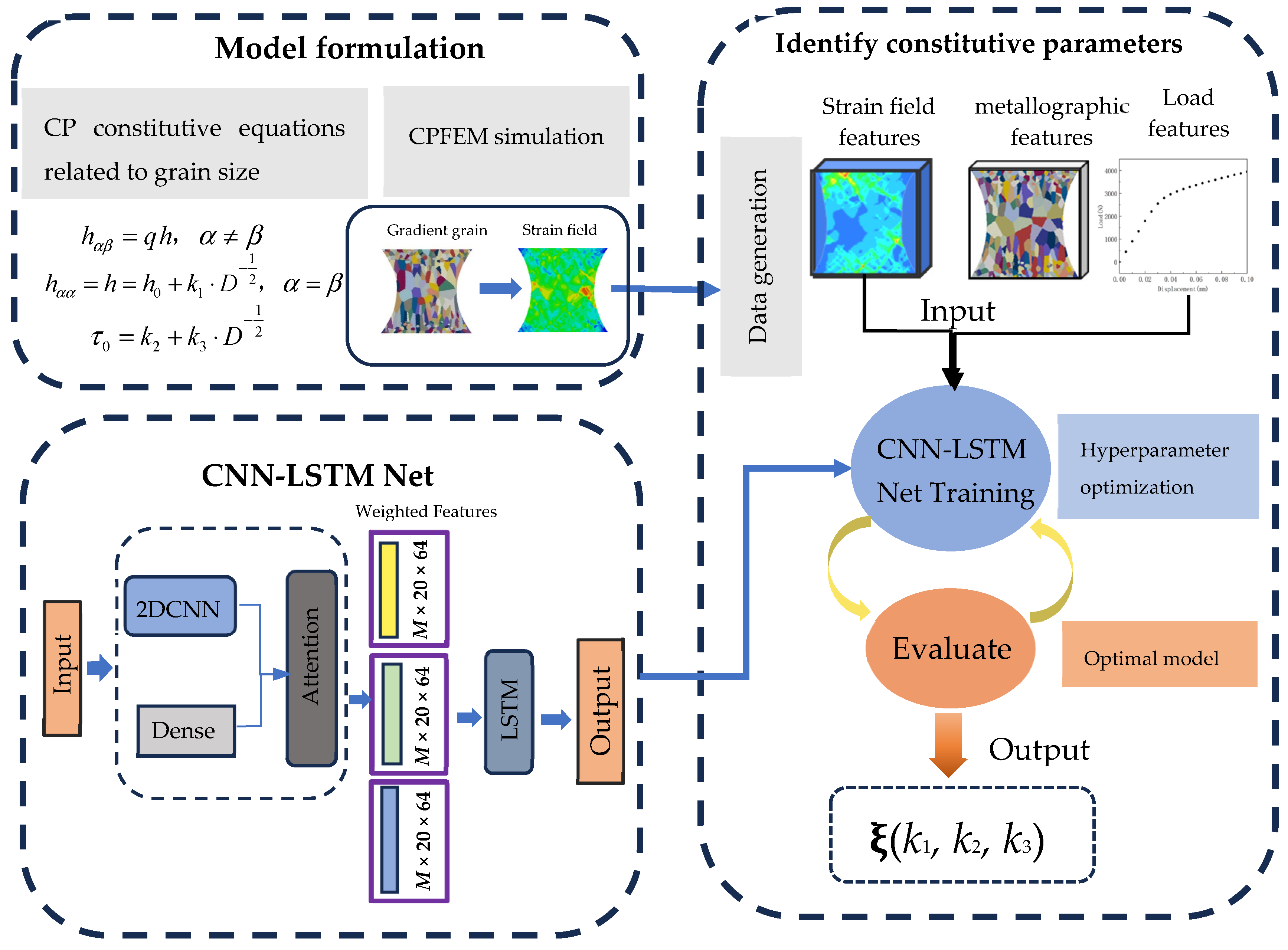
2.2. Plastic Constitutive Model Related to Grain Size and Orientation
- (1)
- The elastic constants C11, C12, C44, as well as the latent hardening matrix q, are considered constant and independent of the grain size D;
- (2)
- The initial critical resolved shear stress (τ0) is assumed to depend solely on the grain size D;
- (3)
- At the single-crystal level, the resistance-to-slip parameters—including the self-hardening modulus (hαα) and latent hardening modulus (hαβ)—are assumed to be invariant with the accumulated shear strain (γ) and depend only on the grain size D.
2.3. Finite Element Modeling of Gradient-Grained Structures
3. Deep Learning-Based Parameter Inversion Framework
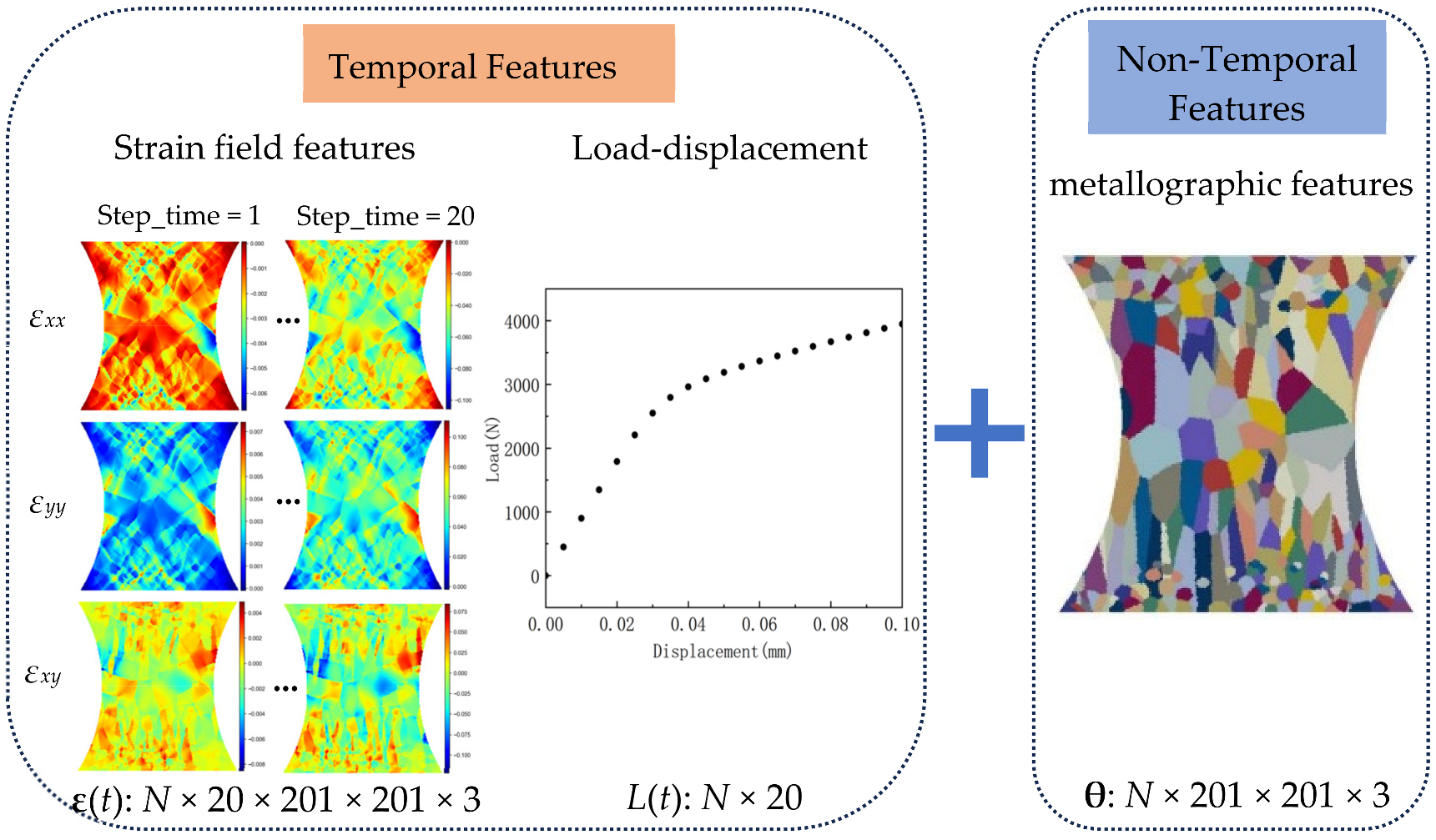
3.1. Data Generation and Preprocessing
- (1)
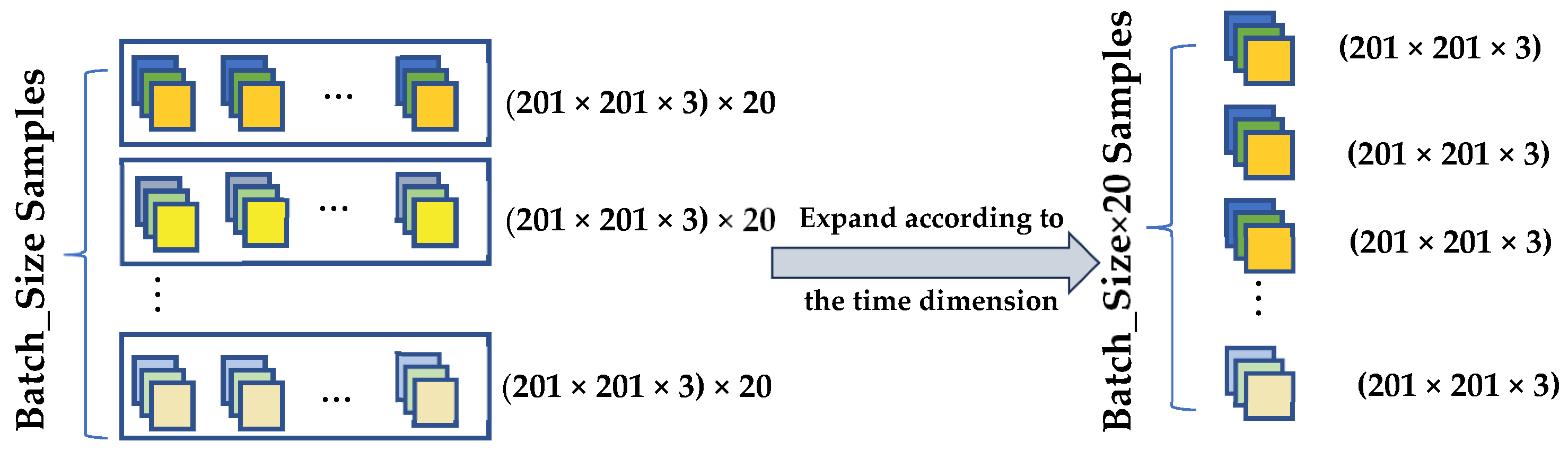
- Temporal strain field sequences: Since the strain field is a time series, a total of 20 time steps are extracted. For each time step, the data for εxx, εyy and εxy in three directions are collected as three separate channels. Each strain field in a given direction is stored as an image of size 201 × 201. The resulting temporal strain field sequence is represented as ε(t) ∈ R201×201×3×20.
- (2)
- Metallographic structural information: The grain distribution information is non-sequential data and does not include a temporal dimension. For each grain, the three orientation angles correspond to three separate channels, with each orientation angle map represented as an image of size 201 × 201. The resulting grain orientation distribution map (using orientation angles in place of morphological statistics) is given by θ ∈ R201×201×3.
- (3)
- Loading sequence: The loading information is time-series data. A total of 20 time steps are extracted, with each time step containing a single scalar load value. The resulting loading sequence is denoted as L(t) ∈ R20.
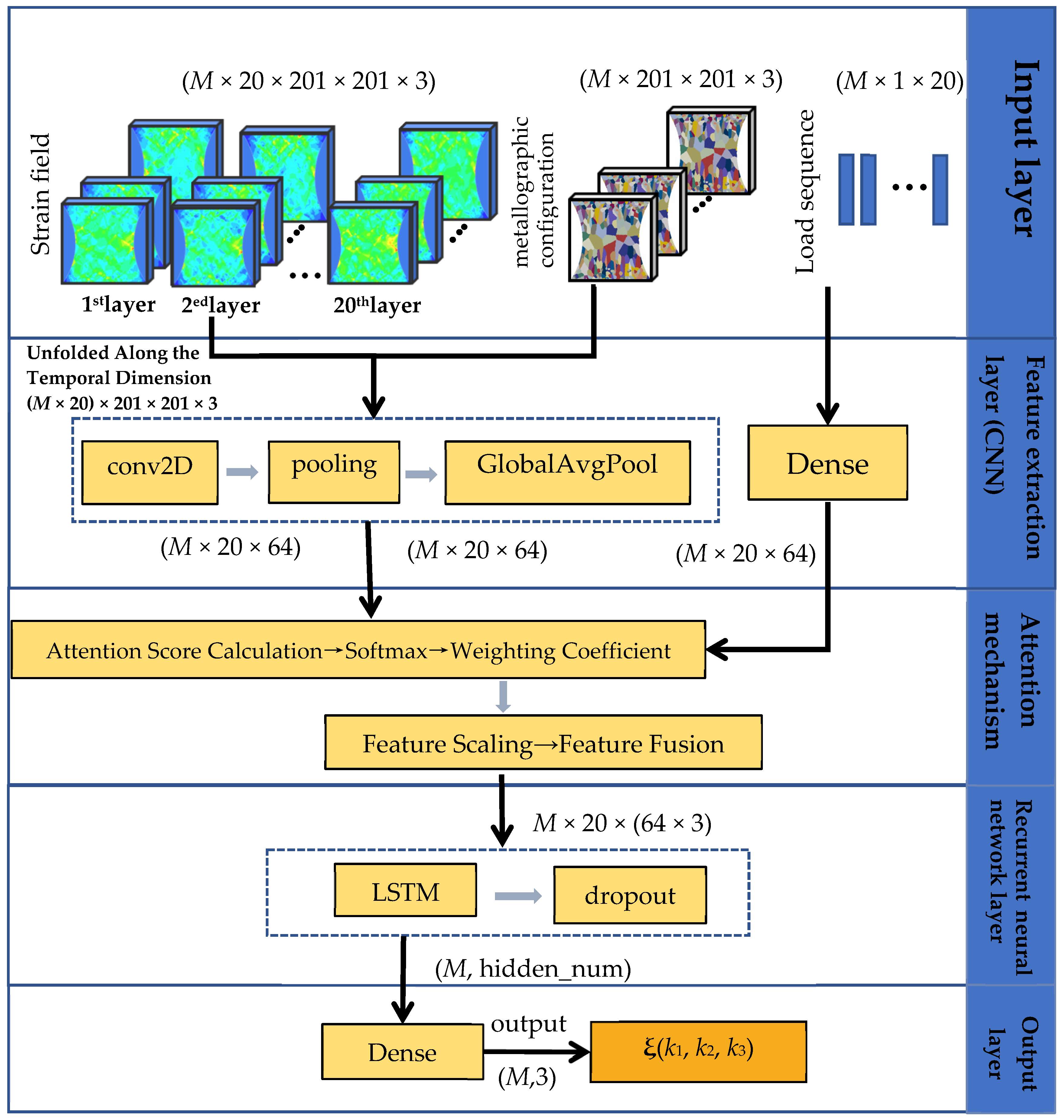
3.2. CNN-LSTM Network Architecture Design
3.2.1. CNN Module: Spatial Feature Extraction of Strain Fields and Metallographic Morphology
3.2.2. Attention Mechanism Module
3.2.3. LSTM Module: Temporal Modeling of Loading History and Evolution Path
3.3. Training Configuration and Optimization
3.3.1. Loss Function
3.3.2. Optimizer
3.3.3. Repeated 10-Fold Cross-Validation
4. Results and Discussion
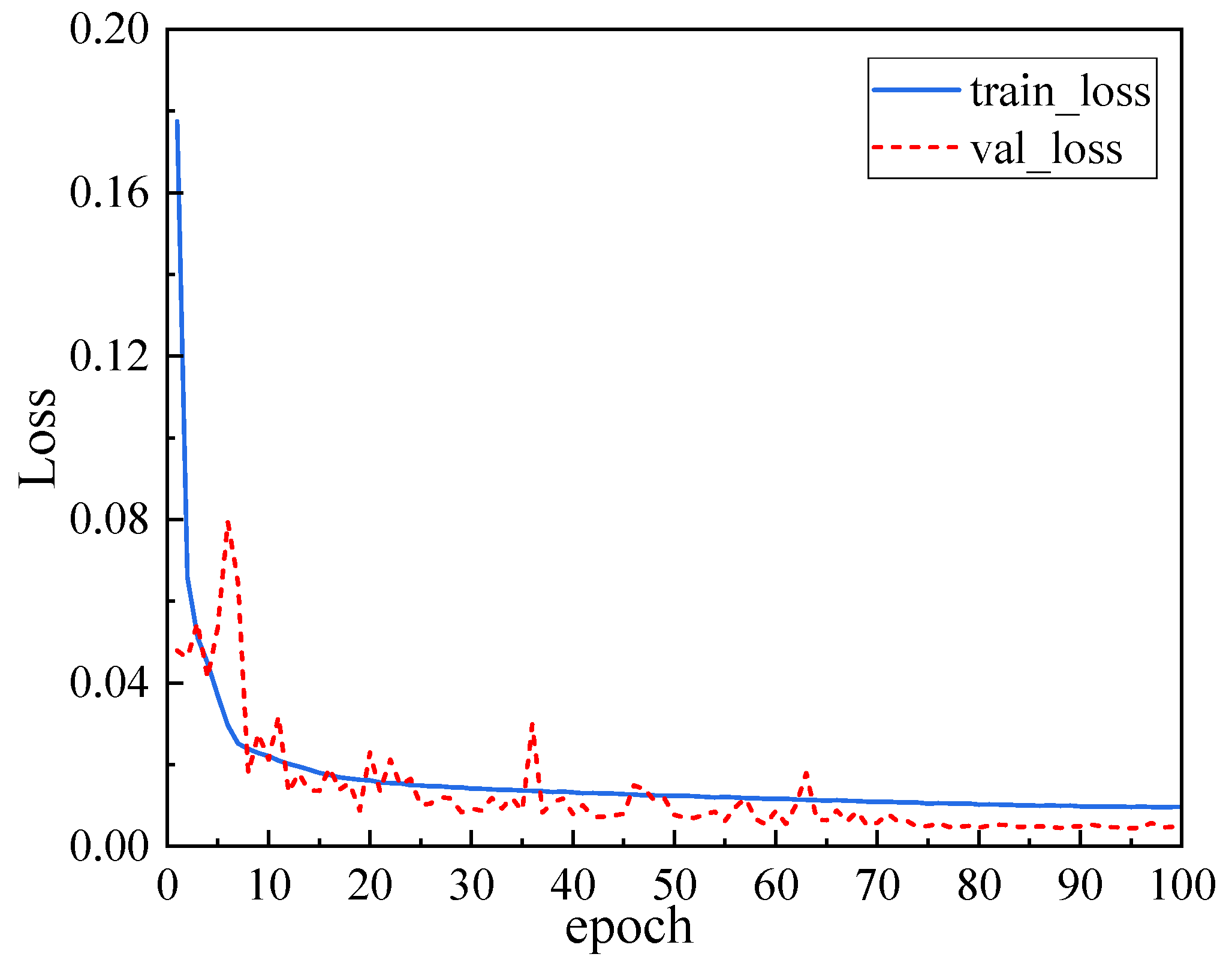
4.1. Training Results of the CNN-LSTM Model
4.2. Prediction Results of the CNN-LSTM Model
4.3. Model Validation and Stability Analysis
5. Conclusions and Outlook
- (1)
- This study extended the crystal plasticity constitutive model to quantify the influence of grain size and orientation on the plastic deformation behavior of gradient-grained FCC metals. The simulation results demonstrated that the model can effectively capture the deformation heterogeneity and strength variation induced by grain-size and orientation gradients, providing a reliable framework for analyzing gradient-grained structures in single-phase FCC alloys.
- (2)
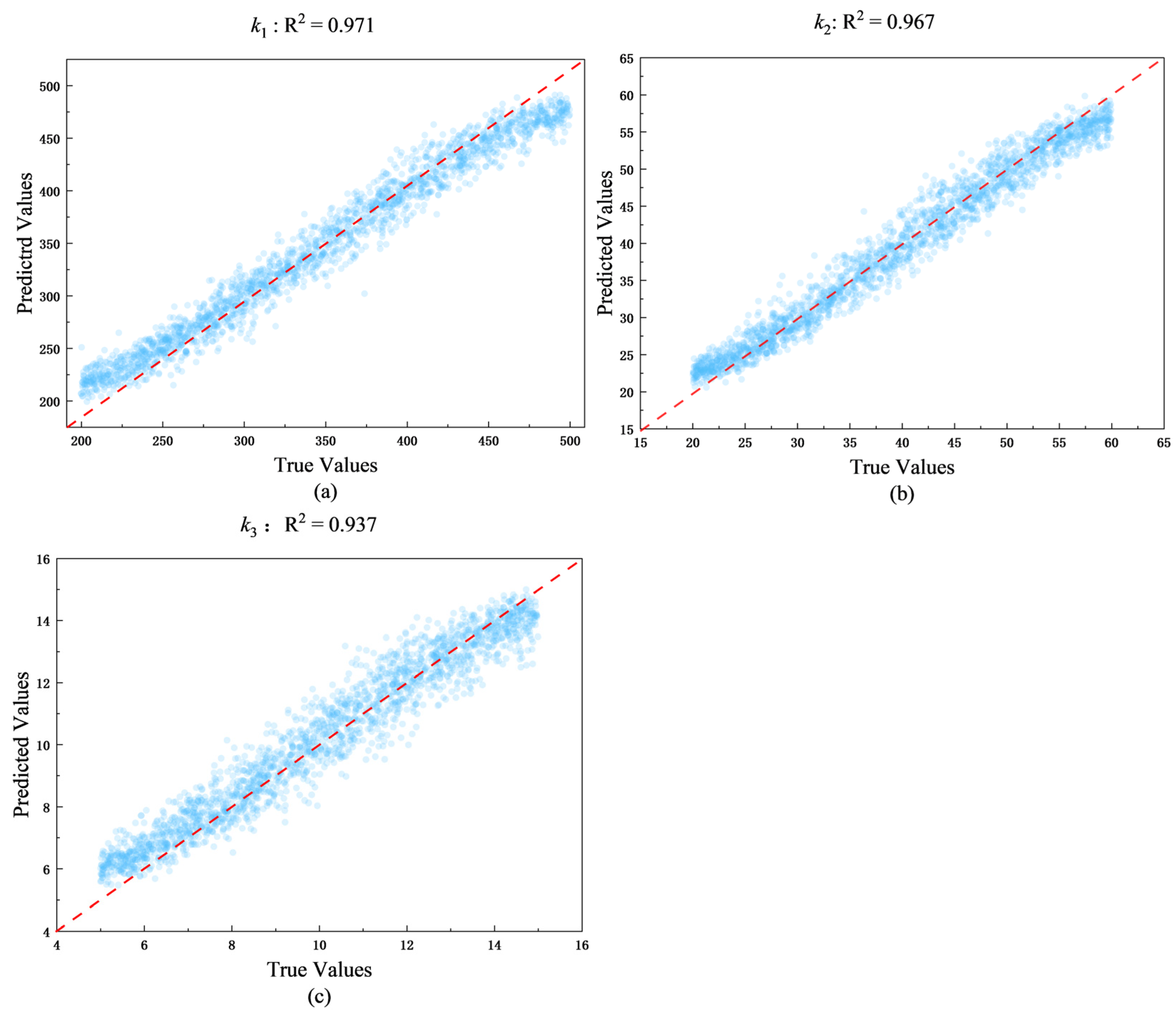
- The training data for the model were derived from CPFE simulations of gradient-grained distributions, encompassing a variety of grain structure configurations to ensure both representativeness and physical fidelity. Without the explicit incorporation of physical consistency constraints (e.g., residuals or conservation terms), the constructed end-to-end network—built upon high-fidelity CPFE data—was capable of autonomously learning and mapping physically reasonable constitutive parameters related to τ0 and h0. Experimental results demonstrated that the prediction accuracies for the three constitutive parameters inverted by the CNN-LSTM Net were 0.971, 0.967, and 0.937, respectively, with the overall prediction error for the three parameters being less than 5%.
- (3)
- The CNN-LSTM Net demonstrated excellent predictive accuracy and stability across multiple test scenarios. The proposed multimodal deep inversion method not only provides a high-precision, high-efficiency, and physically consistent solution for the identification of crystal plasticity constitutive parameters, but also exhibits broad generalizability, making it applicable to various gradient-grained constitutive models and specimen sizes. The introduction of this approach expands the application boundaries of data-driven methods in microstructure-sensitive materials modeling.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Zhao, J. Geometrically necessary dislocations and related kinematic hardening in gradient grained materials: A nonlocal crystal plasticity study. Int. J. Plast. 2023, 163, 103553. [Google Scholar] [CrossRef]
- Li, X.; Zhao, J. Revealing the inhibition mechanism of grain size gradient on crack growth in gradient nano-grained materials. Int. J. Solids Struct. 2019, 172–173, 1–9. [Google Scholar] [CrossRef]
- Shao, J.; Yu, G. Grain size evolution under different cooling rate in laser additive manufacturing of superalloy. Opt. Laser Technol. 2019, 119, 105662. [Google Scholar] [CrossRef]
- Kan, W.; Chen, B. Formation of columnar lamellar colony grain structure in a high Nb-TiAl alloy by electron beam melting. J. Alloys Compd. 2019, 809, 151673. [Google Scholar] [CrossRef]
- Wu, X.L.; Jiang, P. Synergetic strengthening by gradient structure. Mater. Res. Lett. 2014, 2, 185–191. [Google Scholar] [CrossRef]
- Yang, M.; Pan, Y.; Yuan, F.; Zhu, Y.; Wu, X. Back stress strengthening and strain hardening in gradient structure. Mater. Res. Lett. 2016, 4, 145–151. [Google Scholar] [CrossRef]
- Lin, Y.; Pan, J. Mechanical properties and optimal grain size distribution profile of gradient grained nickel. Acta Mater. 2018, 153, 279–289. [Google Scholar] [CrossRef]
- Zhao, J.; Lu, X. Constitutive modeling of the tension-compression behavior of gradient structured materials. arXiv 2020, arXiv:2002.03775. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Sedighiani, K.; Traka, K.; Roters, F.; Sietsma, J.; Raabe, D.; Diehl, M. Crystal plasticity simulation of in-grain microstructural evolution during large deformation of IF-steel. Acta Mater. 2022, 237, 118167. [Google Scholar] [CrossRef]
- Zheng, X.; Sun, T. Modeling of polycrystalline material microstructure with 3D grain boundary based on Laguerre-Voronoi tessellation. Materials 2022, 15, 1996. [Google Scholar] [CrossRef]
- Liu, L.-Y.; Yang, Q.-S. Crystal cracking of grain-gradient aluminum by a combined CPFEM-CZM method. Eng. Fract. Mech. 2021, 242, 107507. [Google Scholar] [CrossRef]
- Herath, C.; Wijesinghe, K. Hierarchical deformation and anisotropic behavior of (α+β) Ti alloys: A micro structure-informed multiscale constitutive model study. Int. J. Plast. 2024, 183, 104163. [Google Scholar] [CrossRef]
- Hu, Y.; Yu, H. Machine learned mechanical properties prediction of additively manufactured metallic alloys: Progress and challenges. Chin. J. Theor. Appl. Mech. 2024, 56, 1892–1915. [Google Scholar]
- Zeng, Q.; Zhao, Z. A deep learning approach for inverse design of gradient mechanical metamaterials. Int. J. Mech. Sci. 2023, 240, 107920. [Google Scholar] [CrossRef]
- Guo, Z.; Bai, R. CPINet: Parameter identification of path-dependent constitutive model with automatic denoising based on CNN-LSTM. Eur. J. Mech. A Solids 2021, 90, 104327. [Google Scholar] [CrossRef]
- Hu, Y.; Zhou, G. A temporal graph neural network for cross-scale modelling of polycrystals considering microstructure interaction. Int. J. Plast. 2024, 179, 104017. [Google Scholar] [CrossRef]
- Li, J.; Pokkalla, D.K.; Wang, Z.-P.; Wang, Y. Deep learning-enhanced design for functionally graded auxetic lattices. Eng. Struct. 2023, 292, 116477. [Google Scholar] [CrossRef]
- Jadoon, A.A.; Kalina, K.A.; Rausch, M.K.; Jones, R.; Fuhg, J.N. Inverse design of anisotropic microstructures using physics-augmented neural networks. J. Mech. Phys. Solids 2025, 203, 106161. [Google Scholar] [CrossRef]
- Bazyar, M.M.; Tabary, S.A.A.B.; Rahmatabdi, D.; Mohammadi, K.; Hashemi, R. A novel practical method for the production of Functionally Graded Materials by varying exposure time via photo-curing 3D printing. J. Manuf. Process. 2023, 103, 136–143. [Google Scholar] [CrossRef]
- Hu, Z.; Ma, Z.; Yu, L.; Liu, Y. Functionally graded materials with grain-size gradients and heterogeneous microstructures achieved by additive manufacturing. Scripta Mater. 2023, 226, 115197. [Google Scholar] [CrossRef]
- Dai, G.; Xue, M.; Guo, Y.; Sun, Z.; Chang, H.; Lu, J.; Li, W.; Panwisawas, C.; Alexandrov, I. Gradient microstructure and strength–ductility synergy improvement of 2319 aluminum alloys by hybrid additive manufacturing. J. Alloys Compd. 2023, 968, 171781. [Google Scholar] [CrossRef]
- Hill, R. On constitutive inequalities for simple materials-I. J. Mech. Phys. Solids 1968, 16, 229–242. [Google Scholar] [CrossRef]
- Rice, J.R. Inelastic constitutive relations for solids: An internal-variable theory and its application to metal plasticity. J. Mech. Phys. Solids 1971, 19, 433–455. [Google Scholar] [CrossRef]
- Lee, E.H. Elastic–plastic deformation at finite strains. J. Appl. Phys. 1969, 36, 1–6. [Google Scholar] [CrossRef]
- Peirce, D.; Asaro, R.J.; Needleman, A. An analysis of nonuniform and localized deformation in ductile single crystals. Acta Metall. 1982, 30, 1087–1119. [Google Scholar] [CrossRef]
- Kocks, U.F.; Mecking, H. Physics and phenomenology of strain hardening: The FCC case. Prog. Mater. Sci. 2003, 48, 171–273. [Google Scholar] [CrossRef]
- Tian, N.; Yuan, F. Prediction of the work-hardening exponent for 3104 aluminum sheets with different grain sizes. Materials 2019, 12, 2368. [Google Scholar] [CrossRef]
- Jiang, H.; Yang, Z. Interpretation of mechanical properties gradient in laser-welded joints: Experiments and grain morphology-dependent crystal plasticity modeling. J. Mater. Res. Technol. 2024, 33, 5934–5950. [Google Scholar] [CrossRef]
- Yang, M.; Wang, L.; Yan, W. Phase-field modeling of grain evolutions in additive manufacturing from nucleation, growth, to coarsening. Npj Comput. Mater. 2021, 7, 56. [Google Scholar] [CrossRef]
- Wu, Q.; Li, J.; Long, L.; Liu, L. Simulating the effect of temperature gradient on grain growth of 6061-T6 aluminum alloy via Monte Carlo Potts algorithm. Comput. Model. Eng. Sci. 2021, 129, 99–116. [Google Scholar] [CrossRef]
- Huang, Y. A User-Material Subroutine Incorporating Single Crystal Plasticity in the ABAQUS Finite Element Program; Harvard University: Cambridge, UK, 1991; pp. 1–21. [Google Scholar]
- Lu, S.; Zhang, X.; Hu, Y.; Chu, J.; Kan, Q.; Kang, G. Machine learning-based constitutive parameter identification for crystal plasticity models. Mech. Mater. 2025, 203, 105263. [Google Scholar] [CrossRef]
- Morris, M.D.; Mitchell, T.J. Exploratory designs for computational experiments. J. Stat. Plan. Inference 1995, 43, 381–402. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K. Neural machine translation by jointly learning to align and translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Vaswani, A.; Shazeer, N. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 1–11. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A method for stochastic optimization. Int. Conf. Learn. Represent. 2015. [Google Scholar] [CrossRef]
- Wu, X.L.; Jiang, P.; Chen, L.; Yuan, F.P.; Zhu, Y.T. Extraordinary strain hardening by gradient structure. Acta Mater. 2014, 80, 538–548. [Google Scholar] [CrossRef]

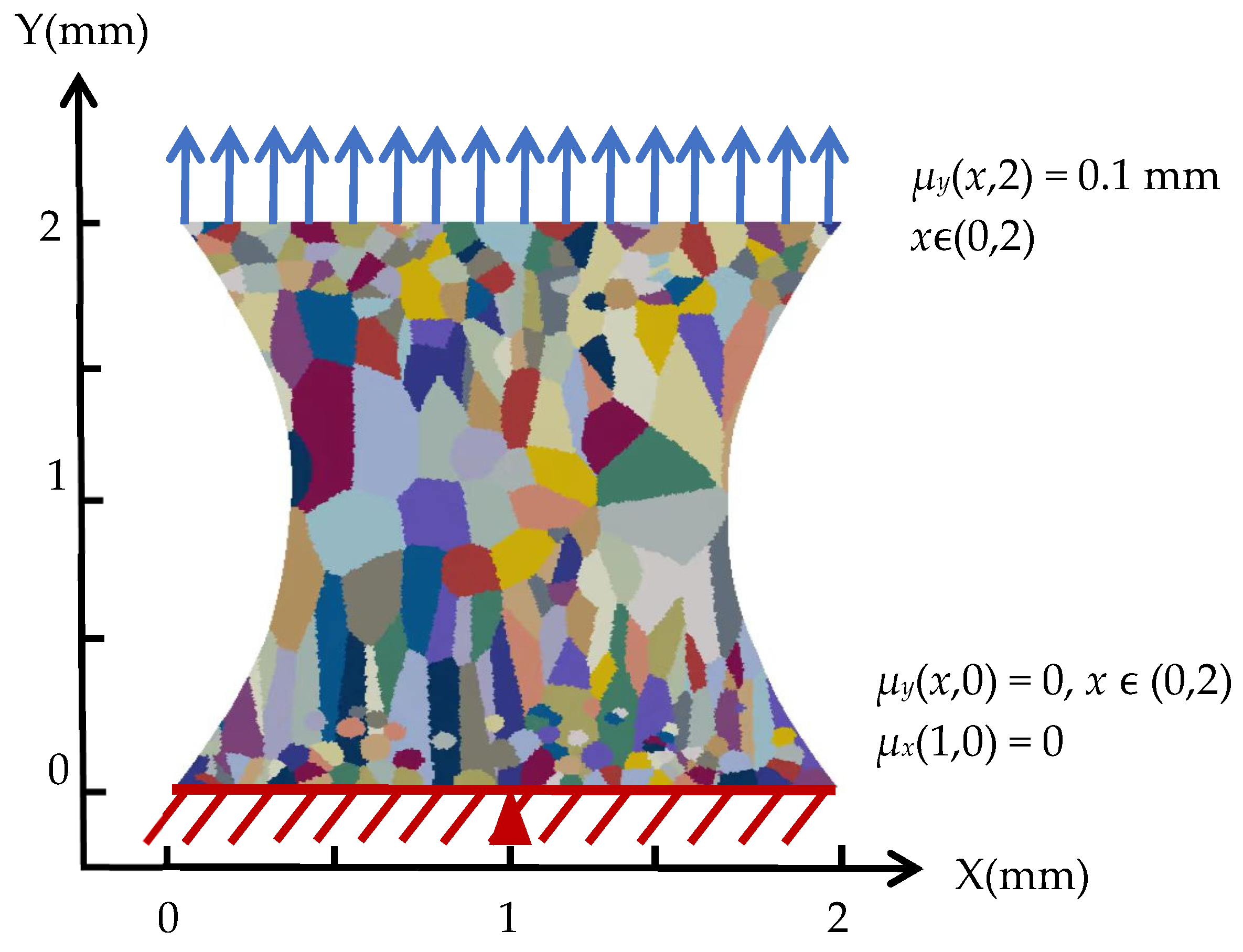
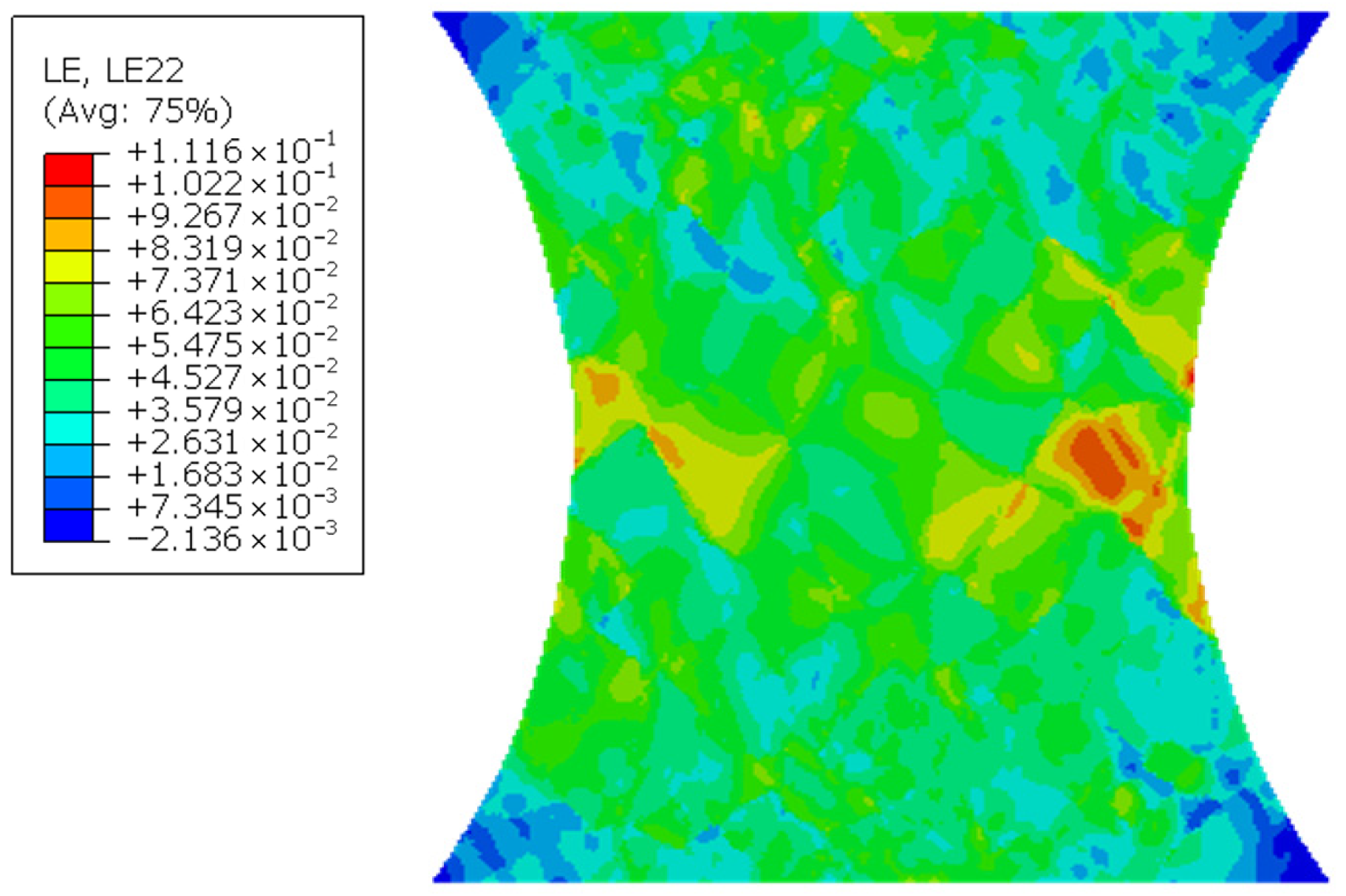

| Property | Value/Range | Unit |
|---|---|---|
| C11 | 168.4 | GPa |
| C12 | 121.4 | GPa |
| C44 | 75.4 | GPa |
| 0.001 | s−1 | |
| n | 10 | / |
| q | 1 | / |
| h0 | 800 | MPa |
| k1 | [200, 500] | MPa |
| k2 | [20, 60] | MPa |
| k3 | [5, 15] | MPa |
| Feature Category | Layer Name | Kernel Size | Stride | Operator | Number or Method | Padding | Activation Function | Dropout |
|---|---|---|---|---|---|---|---|---|
| Geometry/strain Features | Conv1 | 5 × 5 | (1, 1) | Conv2D | Filters 16 | Same | ReLU | - |
| Geometry/strain Features | Pool1 | 2 × 2 | (2, 2) | MaxPooling2D | - | Valid | - | - |
| Geometry/strain Features | Conv2 | 5 × 5 | (1, 1) | Conv2D | Filters 32 | Same | ReLU | - |
| Geometry/strain Features | Pool2 | 2 × 2 | (2, 2) | MaxPooling2D | - | Valid | - | - |
| Geometry/strain Features | Conv3 | 3 × 3 | (1, 1) | Conv2D | Filters 64 | Same | ReLU | - |
| Geometry/strain Features | Pool3 | 2 × 2 | (2, 2) | MaxPooling2D | - | Valid | - | - |
| Geometry/strain Features | Conv4 | 3 × 3 | (1, 1) | Conv2D | Filters 128 | Same | ReLU | - |
| Load Features | FC Layer1 | - | - | Dense | Number 64 | - | ReLU | - |
| Geometry/Strain/Load Features | Attention1 (Score) | - | - | Dense×2 | Number 32/1 | - | tanh/linear | - |
| Geometry/Strain/Load Features | Attention2 (Apply) | - | - | Softmax → Multiply | - | - | Softmax | - |
| Weighted Features | LSTM | - | - | LSTM | Hidden 128 | - | tanh | 0.3 |
| Output Features | FC Layer2 | - | - | Dense | Neurons 3 | - | - | - |
| Learning Rate | k1 | k2 | k3 | Overall |
|---|---|---|---|---|
| 0.01 | 0.955 | 0.928 | 0.909 | 0.930 |
| 0.001 | 0.974 | 0.960 | 0.925 | 0.953 |
| 0.0001 a | 0.971 | 0.963 | 0.937 | 0.958 |
| 0.00001 | 0.936 | 0.758 | 0.491 | 0.728 |
| Batch Size | k1 | k2 | k3 | Overall |
|---|---|---|---|---|
| 8 a | 0.971 | 0.963 | 0.937 | 0.958 |
| 16 | 0.958 | 0.942 | 0.902 | 0.933 |
| 32 | 0.972 | 0.965 | 0.931 | 0.955 |
| Number of Layers | k1 | k2 | k3 | Overall |
|---|---|---|---|---|
| 2 | 0.959 | 0.952 | 0.926 | 0.942 |
| 3 | 0.964 | 0.957 | 0.925 | 0.949 |
| 4 a | 0.971 | 0.963 | 0.937 | 0.958 |
| Metric | Constitutive Parameters | Mean | Standard Deviation (Std) | 95% Confidence Interval (95%CI) | Coefficients of Variation (CV) (%) |
|---|---|---|---|---|---|
| MAE | k1 | 11.425 | 0.576 | [11.344, 11.505] | 5.04 |
| k2 | 1.717 | 0.085 | [1.705, 1.729] | 4.95 | |
| k3 | 0.576 | 0.031 | [0.572, 0.580] | 5.42 | |
| RMSE | k1 | 14.539 | 0.748 | [14.435, 14.644] | 5.14 |
| k2 | 2.130 | 0.098 | [2.116, 2.143] | 4.58 | |
| k3 | 0.717 | 0.034 | [0.713, 0.722] | 4.74 | |
| R2 | k1 | 0.970 | 0.004 | [0.970, 0.971] | 0.37 |
| k2 | 0.969 | 0.004 | [0.966, 0.972] | 0.41 | |
| k3 | 0.937 | 0.006 | [0.936, 0.938] | 0.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Chen, M.; Hou, J.; Guo, Z.; Hu, Z.; Man, Z.; Wei, X.; Liu, D. A Deep Learning-Based CNN-LSTM Framework for Constitutive Parameter Inversion in Alloy Gradient-Grained Materials. Metals 2025, 15, 1286. https://doi.org/10.3390/met15121286
Jiang H, Chen M, Hou J, Guo Z, Hu Z, Man Z, Wei X, Liu D. A Deep Learning-Based CNN-LSTM Framework for Constitutive Parameter Inversion in Alloy Gradient-Grained Materials. Metals. 2025; 15(12):1286. https://doi.org/10.3390/met15121286
Chicago/Turabian StyleJiang, Hao, Mengyi Chen, Jianxin Hou, Zhenfei Guo, Zixuan Hu, Zongzhe Man, Xiao Wei, and Da Liu. 2025. "A Deep Learning-Based CNN-LSTM Framework for Constitutive Parameter Inversion in Alloy Gradient-Grained Materials" Metals 15, no. 12: 1286. https://doi.org/10.3390/met15121286
APA StyleJiang, H., Chen, M., Hou, J., Guo, Z., Hu, Z., Man, Z., Wei, X., & Liu, D. (2025). A Deep Learning-Based CNN-LSTM Framework for Constitutive Parameter Inversion in Alloy Gradient-Grained Materials. Metals, 15(12), 1286. https://doi.org/10.3390/met15121286






