Prediction Modeling and Parameter Optimization for Robotic Belt Grinding 42CrMo Steel Using Response Surface Methodology and Grey Relational Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Materials and Setup
2.2. Experimental Method
3. Results and Discussion
3.1. Regression Model Establishment
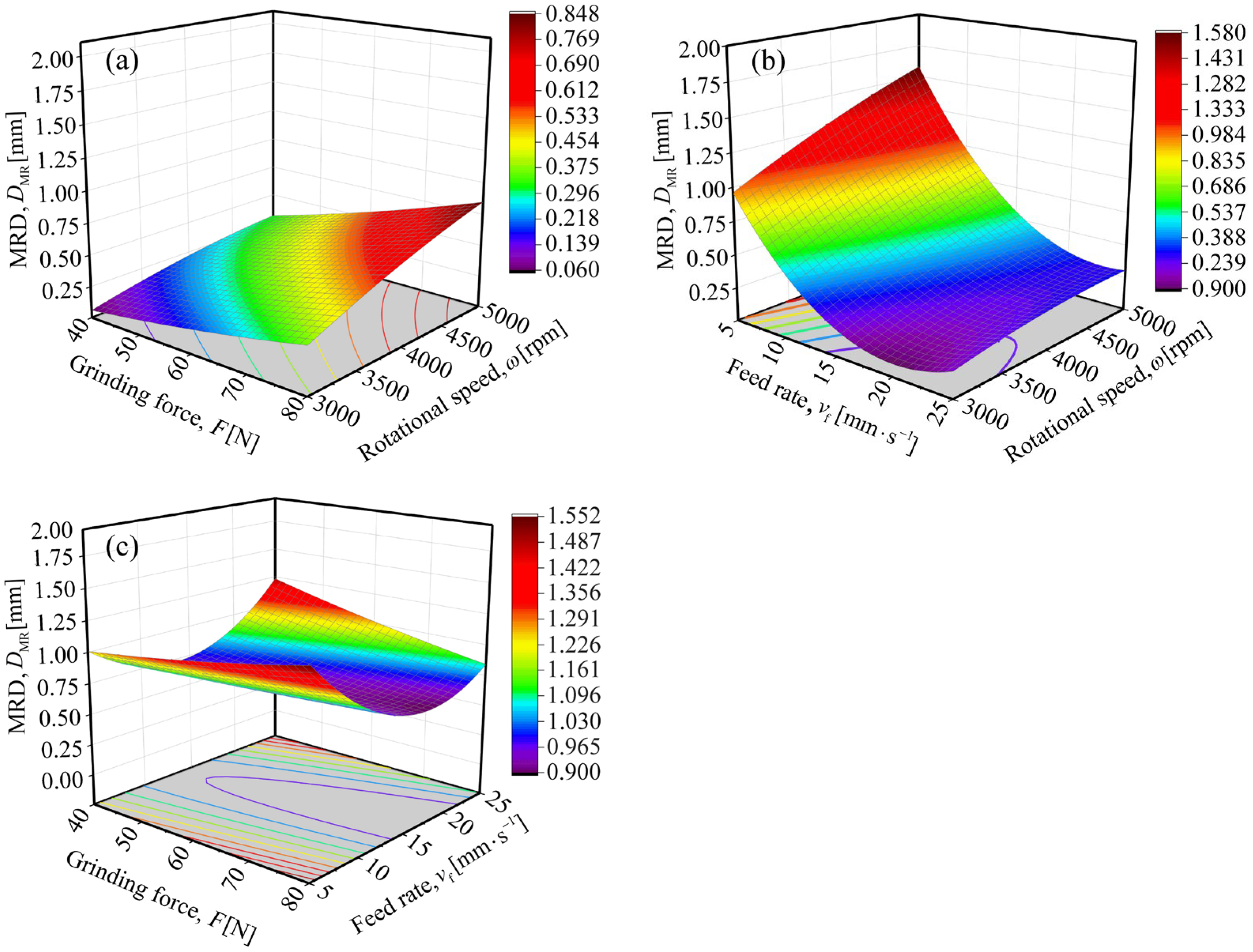
3.2. Response Surface Analysis for Material Removal Depth
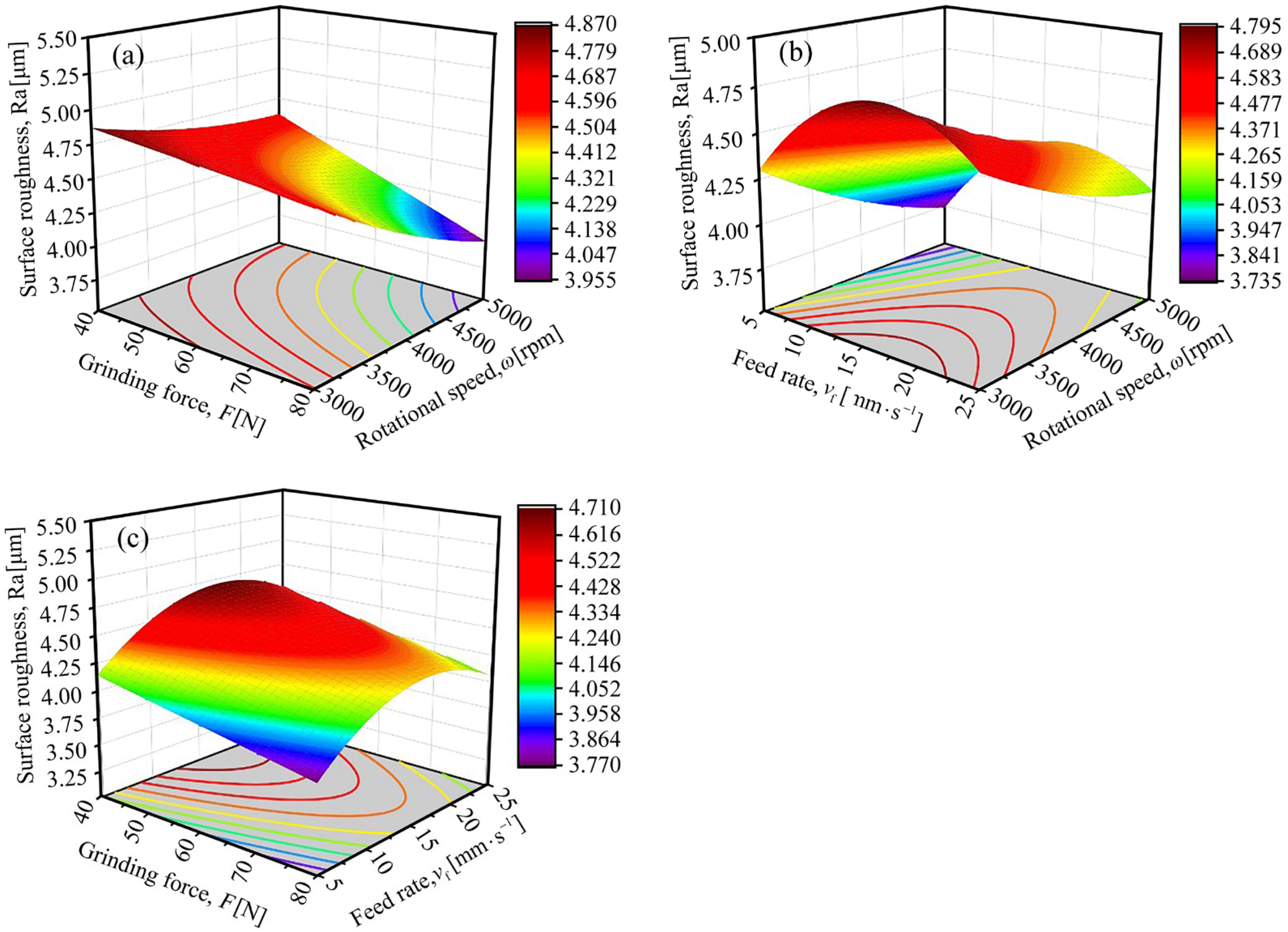
3.3. Response Surface Analysis for Surface Roughness
4. Optimization for Grinding Process Parameters
4.1. Grey Relational Analysis for Grinding Parameters
4.2. Uncertainty and Tolerance Analysis for the Optimal Grinding Parameter Solution
- V1: F = 70 N, vf = 20 mm·s−1, ω = 3000 rpm → DMR = 1.82 mm, Ra = 3.85 μm;
- V2: F = 80 N, vf = 24 mm·s−1, ω = 500 rpm → DMR = 1.95 mm, Ra = 3.98 μm;
- V3: F = 75 N, vf = 22.4 mm·s−1, ω = 3261 rpm (optimal value) → DMR = 1.975 mm, Ra = 3.506 μm (reference value).
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ANFIS | Adaptive neuro-fuzzy inference system |
| ATB | Adaptive Triangular abrasive Belt |
| ANOVA | Analysis of variance |
| DBN | Deep belief network |
| GRA | Grey relational analysis |
| MRD | Material removal depth |
| OCCD | Orthogonal central composite design |
| PRESS | Predicted Residual Sum of Squares |
| RSM | Response surface methodology |
| SEM | Scanning electron microscopy |
| UCT | Undeformed chip thickness |
| b | Cross-sectional width of the specimen |
| Confidence intervals | |
| df | Degrees of freedom |
| DMR | Material removal depth |
| F | Grinding force |
| Fn | Normal force |
| h | Abrasive grain protrusion height |
| Hv | Vickers hardness of the ground surface of the specimen |
| l | Cross-sectional length of the specimen |
| M | Removal weight of the specimen |
| m | Maximum penetration depth |
| N | The tested number |
| n | Sample size |
| Ra | Surface roughness |
| Initial surface roughness of the specimen | |
| vf | Feed rate |
| Tangential velocity of the abrasive belt | |
| Input variables | |
| Mean value of the measured data | |
| Confidence level | |
| Protrusion angle of the abrasive grains | |
| Grey relational grade | |
| ρ | Density of 42crmo steel |
| ω | Rotational speed |
| σ | Standard deviation |
| Maximum elastic deformation of the specimen | |
| Grey relational coefficient |
References
- Yu, Z.W.; Xu, X.L. Failure investigation of a truck diesel engine gear train consisting of crankshaft and camshaft gears. Eng. Fail. Anal. 2010, 17, 537–545. [Google Scholar] [CrossRef]
- Guo, H.F.; Yan, J.W.; Zhang, R.; He, Z.H.; Zhao, Z.Q.; Qu, T.; Wan, M.; Liu, J.S.; Li, C.D. Failure analysis on 42CrMo steel bolt fracture. Adv. Mater. Sci. Eng. 2019, 2019, 2382759. [Google Scholar] [CrossRef]
- Wang, Y.P.; Luo, Y.C.; Mo, Q.Y.; Huang, B.; Wang, S.Y.; Mao, X.F.; Zhou, L. Failure analysis and improvement of a 42CrMo crankshaft for a heavy-duty truck. Eng. Fail. Anal. 2023, 153, 107567. [Google Scholar] [CrossRef]
- Li, Y.T.; Ju, L.; Qi, H.P.; Zhang, F.; Chen, G.Z.; Wang, M.L. Technology and experiments of 42CrMo bearing ring forming based on casting ring blank. Chin. J. Mech. Eng. 2014, 27, 418–427. [Google Scholar] [CrossRef]
- Hoier, P.; Santhosh, D.K.; Hryha, E.; Krajnik, P. An investigation into the grindability of additively manufactured 42CrMo4 steel. CIRP Ann.-Manuf. Techn. 2024, 73, 257–260. [Google Scholar] [CrossRef]
- Li, N.; Chen, Y.; Kong, D.D. Wear mechanism analysis and its effects on the cutting performance of PCBN inserts during turning of hardened 42CrMo. Int. J. Precis. Eng. Man. 2018, 19, 1355–1368. [Google Scholar] [CrossRef]
- Kwak, J.S.; Sim, S.B.; Jeong, Y.D. An analysis of grinding power and surface roughness in external cylindrical grinding of hardened SCM440 steel using the response surface method. Int. J. Mach. Tool. Manu. 2006, 46, 304–312. [Google Scholar] [CrossRef]
- Hou, Z.; Zhang, X.; Yao, Z. Investigation of cutting mechanism and residual stress state with grooved grinding wheels. Int. J. Adv. Manuf. Tech. 2023, 128, 1455–1471. [Google Scholar] [CrossRef]
- Zaghal, J.; Molnar, V.; Benke, M. Improving surface integrity by optimizing slide diamond burnishing parameters after hard turning of 42CrMo4 steel. Int. J. Adv. Manuf. Tech. 2023, 128, 2087–2103. [Google Scholar] [CrossRef]
- Roy, R.; Ghosh, S.K.; Kaisar, T.; Ahmed, T.; Hossain, S.; Aslam, M.; Kaseem, M.; Rahman, M.M. Multi-response optimization of surface grinding process parameters of AISI 4140 alloy steel using response surface methodology and desirability function under dry and wet conditions. Coatings 2022, 12, 104. [Google Scholar] [CrossRef]
- Wang, C.Y.; Wang, G.C.; Shen, C.E. Analysis and prediction of grind-hardening surface roughness based on response surface methodology-BP neural network. Appl. Sci. 2022, 12, 12680. [Google Scholar] [CrossRef]
- Wang, Y.S.; Xiu, S.C.; Zhang, S.N. Controlling grain sizes of 42CrMo steel by pre-stress hardening grinding. Materials 2019, 12, 3124. [Google Scholar] [CrossRef]
- Zhang, W.; Gong, Y.D.; Sun, Y.; Zhao, J.B. Evaluation of abrasive belt grinding performance in nickel-based superalloy robot grinding. Mater. Manuf. Process. 2024, 39, 1260–1267. [Google Scholar] [CrossRef]
- Liu, Y.; Song, S.Y.; Xiao, G.J.; Huang, Y.; Zhou, K. A high-precision prediction model for surface topography of abrasive belt grinding considering elastic contact. Int. J. Adv. Manuf. Tech. 2023, 125, 777–792. [Google Scholar] [CrossRef]
- Li, F.P.; Xue, Y.; Zhang, Z.Y.; Song, W.L.; Xiang, J.W. Optimization of grinding parameters for the workpiece surface and material removal rate in the belt grinding process for polishing and deburring of 45 steel. Appl. Sci. 2020, 10, 6314. [Google Scholar] [CrossRef]
- Zhang, W.J.; Gong, Y.D.; Xu, Y.C.; Zhao, X.L.; Liang, C.Y.; Yin, G.Q.; Zhao, J.B. Modeling of material removal depth in robot abrasive belt grinding based on energy conversion. J. Manuf. Process. 2023, 97, 76–86. [Google Scholar] [CrossRef]
- Ren, L.J.; Wang, N.N.; Zhang, G.P.; Wang, X.H.; Li, X.T. Comprehensive analysis of the effects of different parameters on the grinding performance for surfaces. Int. J. Adv. Manuf. Tech. 2024, 130, 5147–5164. [Google Scholar] [CrossRef]
- Shang, Y.R.; Hu, S.B.; Qiao, H. Sensitivity study of surface roughness process parameters in belt grinding titanium alloys. Metals 2023, 13, 1825. [Google Scholar] [CrossRef]
- Pan, S.; Ma, L.J.; Yu, X.Q.; Shan, Q. Study on the influence of vibration characteristics on surface roughness in quick-point grinding and prediction model. Int. J. Adv. Manuf. Tech. 2023, 129, 2385–2398. [Google Scholar] [CrossRef]
- Tao, Z.; Li, S.; Zhang, L.; Zhang, D. Surface roughness prediction in robotic belt grinding based on the undeformed chip thickness model and GRNN method. Int. J. Adv. Manuf. Tech. 2022, 120, 6287–6299. [Google Scholar] [CrossRef]
- Jia, H.; Lu, X.; Cai, D.; Xiang, Y.; Chen, J.; Bao, C. Predictive modeling and analysis of material removal characteristics for robotic belt grinding of complex blade. Appl. Sci. 2023, 13, 4248. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, T.; Zou, Y.; Xiao, M. Model Predictive control of robotic grinding based on deep belief network. Complexity 2019, 2019, 1891365. [Google Scholar] [CrossRef]
- Surindra, M.D.; Alfarisy, G.A.F.; Caesarendra, W.; Petra, M.I.; Prasetyo, T.; Tjahjowidodo, T.; Królczyk, G.M.; Glowacz, A.; Gupta, M.K. Use of machine learning models in condition monitoring of abrasive belt in robotic arm grinding process. J. Intell. Manuf. 2025, 36, 3345–3358. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Xiao, G.J.; Gao, H.; Zhu, B.; Huang, Y.; Li, W. Roughness prediction and performance analysis of data-driven superalloy belt grinding. Front. Mater. 2022, 9, 765401. [Google Scholar] [CrossRef]
- Ren, L.J.; Wang, N.A.; Wang, X.H.; Li, X.T.; Li, Y.C.; Zhang, G.P.; Lei, X.Q. Modeling and analysis of material removal depth contour for curved-surfaces abrasive belt grinding. J. Mater. Process. Tech. 2023, 316, 117945. [Google Scholar] [CrossRef]
- Xiao, G.J.; Gao, H.; Zhang, Y.D.; Zhu, B.; Huang, Y. An intelligent parameters optimization method of titanium alloy belt grinding considering machining efficiency and surface quality. Int. J. Adv. Manuf. Tech. 2023, 125, 513–527. [Google Scholar] [CrossRef]
- Shi, D.Q.; Xu, Y.E.; Wang, X.H.; Zhang, H.J. Influence of grinding parameters on the removal depth of 42crmo steel and its prediction in robot electro-hydraulic-actuated abrasive belt grinding. J. Manuf. Mater. Proc. 2025, 9, 76. [Google Scholar] [CrossRef]
- Krajnik, P.; Kopac, J.; Sluga, A. Design of grinding factors based on response surface methodology. J. Mater. Process. Tech. 2005, 162, 629–636. [Google Scholar] [CrossRef]
- Chen, G.; Yang, J.Z.; Yao, K.W.; Xiang, H.; Liu, H. Robotic abrasive belt grinding with consistent quality under normal force variations. Int. J. Adv. Manuf. Tech. 2023, 125, 3539–3549. [Google Scholar] [CrossRef]
- Hokkirigawa, K.; Kato, K. An experimental and theoretical investigation of ploughing, cutting and wedge formation during abrasive wear. Tribol. Int. 1988, 21, 51–57. [Google Scholar] [CrossRef]
- Chen, X.; Opoz, T.T.; Oluwajobi, A. Analysis of grinding surface creation by single-grit approach. J. Manuf. Sci. Eng. 2017, 139, 121007. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, M.H.; Yan, Y.T. Hardness prediction of grind-hardening layer based on integrated approach of finite element and cellular automata. Materials 2021, 14, 5651. [Google Scholar] [CrossRef]
- Zhang, Y.; Ge, P.Q.; Be, W.B. The study for variable grinding depth to control plane grind-hardening layer depth distribution. Int. J. Adv. Manuf. Tech. 2016, 84, 1269–1276. [Google Scholar] [CrossRef]
- Ding, H.H.; Yang, J.Y.; Wang, W.J.; Liu, Q.Y.; Guo, J.; Zhou, Z.R. Wear mechanisms of abrasive wheel for rail facing grinding. Wear 2022, 504–505, 204421. [Google Scholar] [CrossRef]
- Shi, D.Q.; Zeng, X.Y.W.; Wang, X.H.; Zhang, H.J. Parameter optimization and surface roughness prediction for the robotic adaptive hydraulic polishing of NAK80 mold steel. Processes 2025, 13, 991. [Google Scholar] [CrossRef]
- Li, D.W.; Yang, J.X.; Ding, H. Process optimization of robotic grinding to guarantee material removal accuracy and surface quality simultaneously. J. Manuf. Sci. Eng. 2024, 146, 051005. [Google Scholar] [CrossRef]
- Manimaran, G.; Kumar, M.P. Multiresponse optimization of grinding AISI 316 stainless steel using grey relational analysis. Mater. Manuf. Process. 2013, 28, 418–423. [Google Scholar] [CrossRef]
- Zhang, L.Z. Optimization of grinding process parameters for slender tubes through orthogonal experiments and grey relational analysis. Adv. Mech. Eng. 2025, 17, 16878132251358317. [Google Scholar] [CrossRef]

| Factors | Levels | ||||
|---|---|---|---|---|---|
| −1.353 | −1 | 0 | 1 | 1.353 | |
| Grinding force, F [N] | 40 | 45 | 60 | 75 | 80 |
| Rotational speed, ω [rpm] | 3000 | 3261 | 4000 | 4739 | 5000 |
| Feed rate, vf [mm·s−1] | 5 | 7.6 | 15 | 22.4 | 25 |
| No. | Factors | DMR ± σ [mm] | Ra ± σ [μm] | ||
|---|---|---|---|---|---|
| F | ω | vf | |||
| 1 | −1 | −1 | −1 | 0.595 ± 0.031 | 4.429 ± 0.149 |
| 2 | 1 | −1 | −1 | 1.128 ± 0.052 | 4.361 ± 0.128 |
| 3 | −1 | 1 | −1 | 0.183 ± 0.028 | 4.194 ± 0.117 |
| 4 | 1 | 1 | −1 | 0.298 ± 0.036 | 3.682 ± 0.082 |
| 5 | −1 | −1 | 1 | 1.048 ± 0.04 | 3.883 ± 0.103 |
| 6 | 1 | −1 | 1 | 1.975 ± 0.042 | 3.506 ± 0.102 |
| 7 | −1 | 1 | 1 | 0.302 ± 0.035 | 4.753 ± 0.131 |
| 8 | 1 | 1 | 1 | 0.564 ± 0.045 | 4.022 ± 0.087 |
| 9 | −1.353 | 0 | 0 | 0.217 ± 0.033 | 4.975 ± 0.163 |
| 10 | 1.353 | 0 | 0 | 0.698 ± 0.056 | 4.164 ± 0.143 |
| 11 | 0 | −1.353 | 0 | 1.997 ± 0.048 | 3.706 ± 0.125 |
| 12 | 0 | 1.353 | 0 | 0.304 ± 0.057 | 4.108 ± 0.136 |
| 13 | 0 | 0 | −1.353 | 0.239 ± 0.026 | 4.496 ± 0.126 |
| 14 | 0 | 0 | 1.353 | 0.536 ± 0.037 | 4.102 ± 0.117 |
| 15 | 0 | 0 | 0 | 0.381 ± 0.041 | 4.427 ± 0.151 |
| 16 | 0 | 0 | 0 | 0.365 ± 0.034 | 4.519 ± 0.105 |
| 17 | 0 | 0 | 0 | 0.458 ± 0.037 | 4.325 ± 0.141 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Note |
|---|---|---|---|---|---|---|
| Model | 4.9600 | 9 | 0.5506 | 25.11 | 0.0002 | significant |
| F | 0.5315 | 1 | 0.5315 | 24.24 | 0.0017 | |
| vf | 2.8700 | 1 | 2.8700 | 126.57 | <0.0001 | |
| ω | 0.3734 | 1 | 0.3734 | 17.03 | 0.0044 | |
| F·vf | 0.1466 | 1 | 0.1466 | 6.69 | 0.0362 | |
| F·ω | 0.0366 | 1 | 0.0366 | 1.67 | 0.2375 | |
| vf·ω | 0.1047 | 1 | 0.1047 | 4.77 | 0.0652 | |
| 0.0001 | 1 | 0.0001 | 0.0025 | 0.9614 | ||
| 0.9789 | 1 | 0.9789 | 44.64 | 0.0003 | ||
| 0.0082 | 1 | 0.0082 | 0.3732 | 0.5606 | ||
| Residual | 0.1535 | 7 | 0.0219 | — | — | |
| Lack-of-fit | 0.1486 | 5 | 0.0297 | 12.02 | 0.0786 | not significant |
| Pure error | 0.0049 | 2 | 0.0025 | — | — | |
| Cor total | 5.11 | 16 | — | — | — |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | Note |
|---|---|---|---|---|---|---|
| Model | 2.3000 | 9 | 0.2557 | 21.77 | 0.0003 | significant |
| F | 0.6637 | 1 | 0.6637 | 56.52 | 0.0001 | |
| vf | 0.0885 | 1 | 0.0885 | 7.53 | 0.0287 | |
| ω | 0.0919 | 1 | 0.0919 | 7.82 | 0.0266 | |
| F·vf | 0.0796 | 1 | 0.0796 | 6.78 | 0.0352 | |
| F·ω | 0.0348 | 1 | 0.0348 | 2.97 | 0.1286 | |
| vf·ω | 0.6612 | 1 | 0.6612 | 56.31 | 0.0001 | |
| 0.0251 | 1 | 0.0251 | 2.14 | 0.1872 | ||
| 0.6088 | 1 | 0.6088 | 51.85 | 0.0002 | ||
| 0.0507 | 1 | 0.0507 | 4.31 | 0.0764 | ||
| Residual | 0.0882 | 7 | 0.0117 | — | — | |
| Lack-of-fit | 0.0634 | 5 | 0.0127 | 1.35 | 0.4783 | not significant |
| Pure error | 0.0188 | 2 | 0.0094 | — | — | |
| Cor total | 2.38 | 16 | — | — | — |
| Model | R2 | Adjusted R2 | Predicted R2 | PRESS | ||||
|---|---|---|---|---|---|---|---|---|
| Full | Simplified | Full | Simplified | Full | Simplified | Full | Simplified | |
| DMR | 0.9700 | 0.9407 | 0.9313 | 0.9137 | 0.9162 | 0.9065 | 1.2300 | 0.9373 |
| Ra | 0.9655 | 0.9294 | 0.9212 | 0.9071 | 0.8954 | 0.8824 | 0.5900 | 0.5353 |
| No. | F [N] | ω [rpm] | vf [mm·s−1] | DMR [mm] | Relative Error [%] | Ra [μm] | Relative Error [%] | ||
|---|---|---|---|---|---|---|---|---|---|
| Measured | Predicted | Measured | Predicted | ||||||
| 1 | 40 | 5000 | 25 | 0.606 | 0.640 | 5.6 | 4.597 | 4.946 | 7.6 |
| 2 | 45 | 5000 | 5 | 1.534 | 1.604 | 4.6 | 3.552 | 3.222 | −9.3 |
| 3 | 50 | 4000 | 5 | 1.458 | 1.495 | 2.5 | 4.101 | 3.831 | −6.6 |
| 4 | 55 | 5000 | 25 | 0.701 | 0.672 | −4.1 | 4.171 | 4.571 | 9.6 |
| 5 | 60 | 4500 | 15 | 0.498 | 0.522 | 4.8 | 4.213 | 4.388 | 4.2 |
| 6 | 65 | 3000 | 5 | 1.657 | 1.650 | −0.4 | 4.659 | 4.370 | −6.2 |
| 7 | 70 | 4000 | 10 | 1.068 | 1.109 | 3.8 | 3.985 | 4.126 | 8.6 |
| 8 | 75 | 3500 | 10 | 1.025 | 1.063 | 3.4 | 3.972 | 4.258 | 7.2 |
| 9 | 50 | 4500 | 10 | 0.801 | 0.822 | 2.6 | 4.503 | 4.166 | −7.5 |
| 10 | 65 | 4500 | 20 | 0.427 | 0.408 | −4.4 | 4.235 | 4.348 | 2.7 |
| 11 | 70 | 4500 | 20 | 0.435 | 0.449 | 3.2 | 3.987 | 4.246 | 6.5 |
| 12 | 70 | 3500 | 10 | 1.048 | 0.988 | −5.7 | 4.529 | 4.315 | −4.7 |
| 13 | 40 | 3000 | 5 | 0.935 | 0.978 | 4.6 | 4.472 | 4.545 | 1.6 |
| 14 | 40 | 3000 | 25 | 0.162 | 0.156 | −3.7 | 4.507 | 4.114 | −8.7 |
| 15 | 40 | 5000 | 5 | 1.397 | 1.472 | 5.4 | 3.398 | 3.257 | −4.1 |
| 16 | 40 | 5000 | 25 | 0.632 | 0.640 | 1.3 | 4.776 | 4.946 | 3.6 |
| 17 | 80 | 3000 | 25 | 0.253 | 0.240 | −5.1 | 3.440 | 3.115 | −9.4 |
| 18 | 80 | 5000 | 25 | 0.711 | 0.724 | 1.8 | 4.021 | 3.947 | −1.8 |
| Group | Comparison Sequence | Deviation Sequence | Grey Relational Coefficient | Grey Relational | |||
|---|---|---|---|---|---|---|---|
| 1 | 0.227 | 0.372 | 0.773 | 0.628 | 0.393 | 0.443 | 0.418 |
| 2 | 0.521 | 0.418 | 0.479 | 0.582 | 0.511 | 0.462 | 0.487 |
| 3 | 0 | 0.532 | 1.000 | 0.468 | 0.333 | 0.517 | 0.425 |
| 4 | 0.063 | 0.880 | 0.937 | 0.120 | 0.348 | 0.806 | 0.577 |
| 5 | 0.477 | 0.743 | 0.523 | 0.257 | 0.489 | 0.661 | 0.575 |
| 6 | 0.988 | 1.000 | 0.012 | 0 | 0.977 | 1.000 | 0.989 |
| 7 | 0.066 | 0.151 | 0.934 | 0.849 | 0.349 | 0.371 | 0.360 |
| 8 | 0.210 | 0.649 | 0.790 | 0.351 | 0.388 | 0.588 | 0.488 |
| 9 | 0.019 | 0 | 0.981 | 1.000 | 0.338 | 0.333 | 0.336 |
| 10 | 0.284 | 0.552 | 0.716 | 0.448 | 0.411 | 0.527 | 0.469 |
| 11 | 1.000 | 0.864 | 0 | 0.136 | 1.000 | 0.786 | 0.893 |
| 12 | 0.067 | 0.590 | 0.933 | 0.410 | 0.349 | 0.549 | 0.449 |
| 13 | 0.031 | 0.326 | 0.969 | 0.674 | 0.340 | 0.426 | 0.383 |
| 14 | 0.195 | 0.594 | 0.805 | 0.406 | 0.383 | 0.552 | 0.468 |
| 15 | 0.109 | 0.373 | 0.891 | 0.627 | 0.359 | 0.444 | 0.402 |
| 16 | 0.100 | 0.310 | 0.900 | 0.690 | 0.357 | 0.420 | 0.389 |
| 17 | 0.152 | 0.442 | 0.848 | 0.558 | 0.371 | 0.473 | 0.422 |
| Group | F [N] | ω [rpm] | vf [mm·s−1] | DMR ± σ [mm] | Ra ± σ [μm] | Ci | ||
|---|---|---|---|---|---|---|---|---|
| DMR [mm] | Ra [μm] | |||||||
| 6 | 0.989 | 75 | 3261 | 22.4 | 1.975 ± 0.042 | 3.506 ± 0.122 | 1.923–2.027 | 3.355–3.657 |
| 11 | 0.893 | 60 | 3000 | 15 | 1.997 ± 0.048 | 3.706 ± 0.125 | 1.937–2.057 | 3.551–3.861 |
| 4 | 0.577 | 75 | 4739 | 5 | 0.298 ± 0.036 | 3.682 ± 0.082 | 0.256–0.340 | 3.580–3.784 |
| 5 | 0.575 | 45 | 3261 | 22.4 | 1.048 ± 0.040 | 3.883 ± 0.103 | 0.998–1.098 | 3.755–4.011 |
| Optimized Parameter | Optimal Value | Tolerance Range | Basis (Response Surface Characteristics) |
|---|---|---|---|
| Grinding force, F [N] | 75 | 70–80 | When F < 70 N, DMR drops below 1.8 mm; when F > 80 N, Ra exceeds 4.0 μm (Figure 2c) |
| Feed rate, vf [mm·s−1] | 22.4 | 20–24 | When vf < 20 mm·s−1, DMR shows no significant improvement; when vf > 24 mm·s−1, Ra rises sharply to above 4.2 μm (Figure 2b) |
| Rotational speed, ω [rpm] | 3261 | 3000–3500 | When ω < 3000 rpm, Ra increases to 3.9 μm (close to the upper tolerance limit); when ω > 3500 rpm, DMR shows no significant improvement but energy consumption increases (Figure 2a) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, D.; Zhang, W.; Wang, J.; Gao, G.; Zhang, H. Prediction Modeling and Parameter Optimization for Robotic Belt Grinding 42CrMo Steel Using Response Surface Methodology and Grey Relational Analysis. Metals 2025, 15, 1265. https://doi.org/10.3390/met15111265
Shi D, Zhang W, Wang J, Gao G, Zhang H. Prediction Modeling and Parameter Optimization for Robotic Belt Grinding 42CrMo Steel Using Response Surface Methodology and Grey Relational Analysis. Metals. 2025; 15(11):1265. https://doi.org/10.3390/met15111265
Chicago/Turabian StyleShi, Dequan, Wuyang Zhang, Jiahao Wang, Guili Gao, and Huajun Zhang. 2025. "Prediction Modeling and Parameter Optimization for Robotic Belt Grinding 42CrMo Steel Using Response Surface Methodology and Grey Relational Analysis" Metals 15, no. 11: 1265. https://doi.org/10.3390/met15111265
APA StyleShi, D., Zhang, W., Wang, J., Gao, G., & Zhang, H. (2025). Prediction Modeling and Parameter Optimization for Robotic Belt Grinding 42CrMo Steel Using Response Surface Methodology and Grey Relational Analysis. Metals, 15(11), 1265. https://doi.org/10.3390/met15111265






