Application of Machine Learning and Data Augmentation Algorithms in the Discovery of Metal Hydrides for Hydrogen Storage
Abstract
1. Introduction
2. Methodology
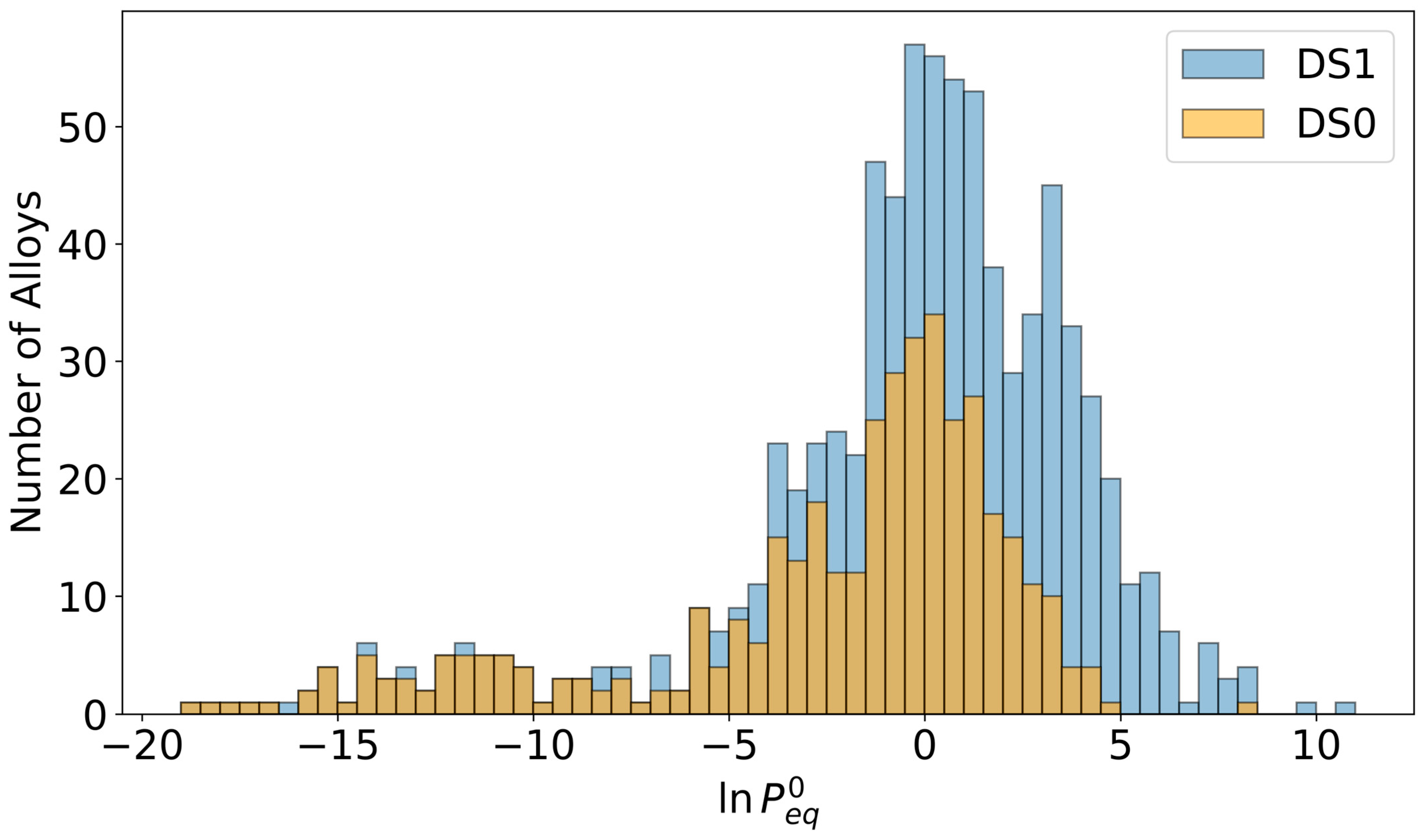
2.1. Datasets
2.2. Machine Learning
2.3. Data Augmentation (PADRE Algorithm)
3. Results and Discussion
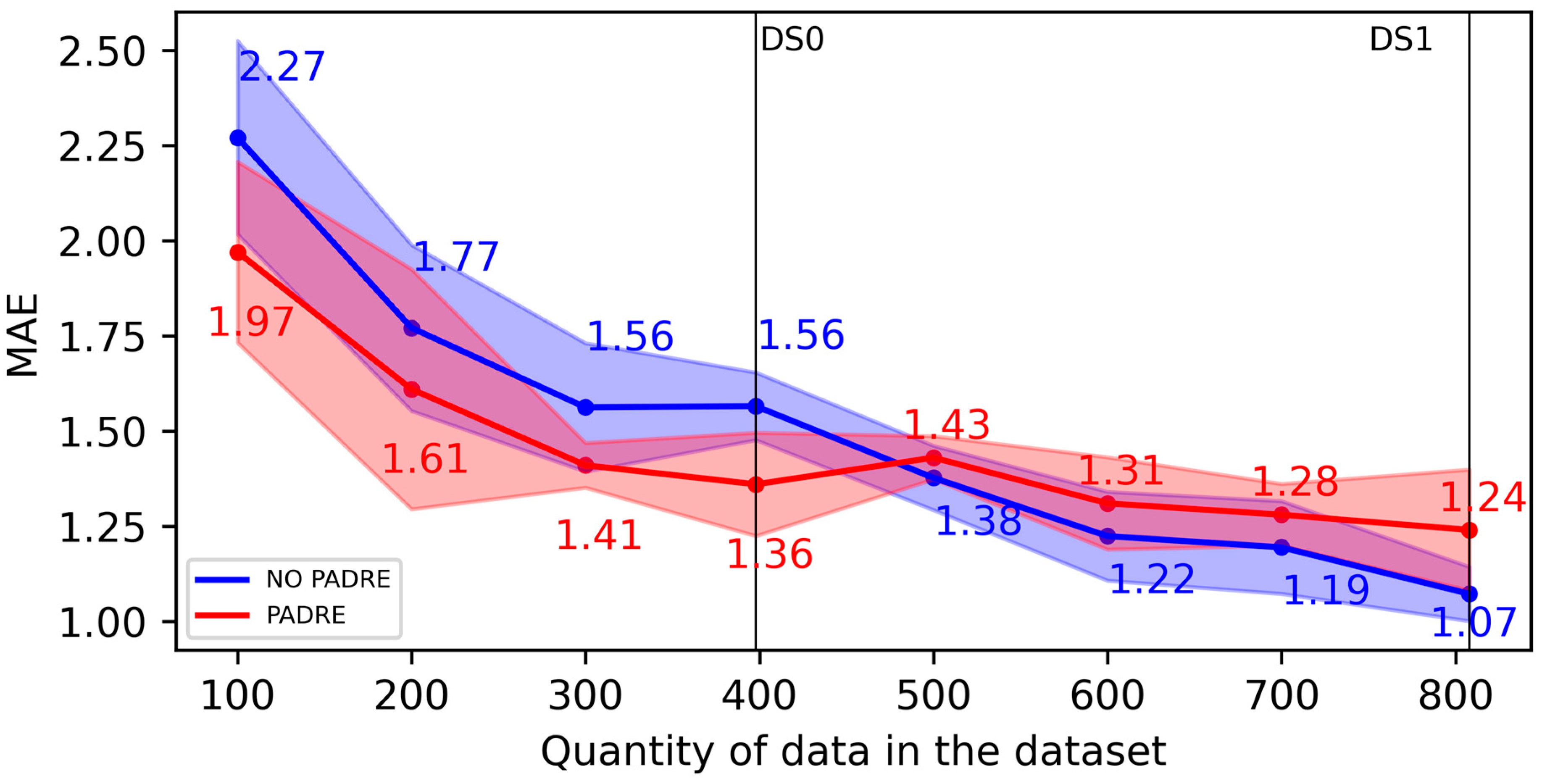
3.1. Effect of Increasing the Dataset Size with New Real Data
3.2. Effect of Increasing the Dataset Size with Data Augmentation
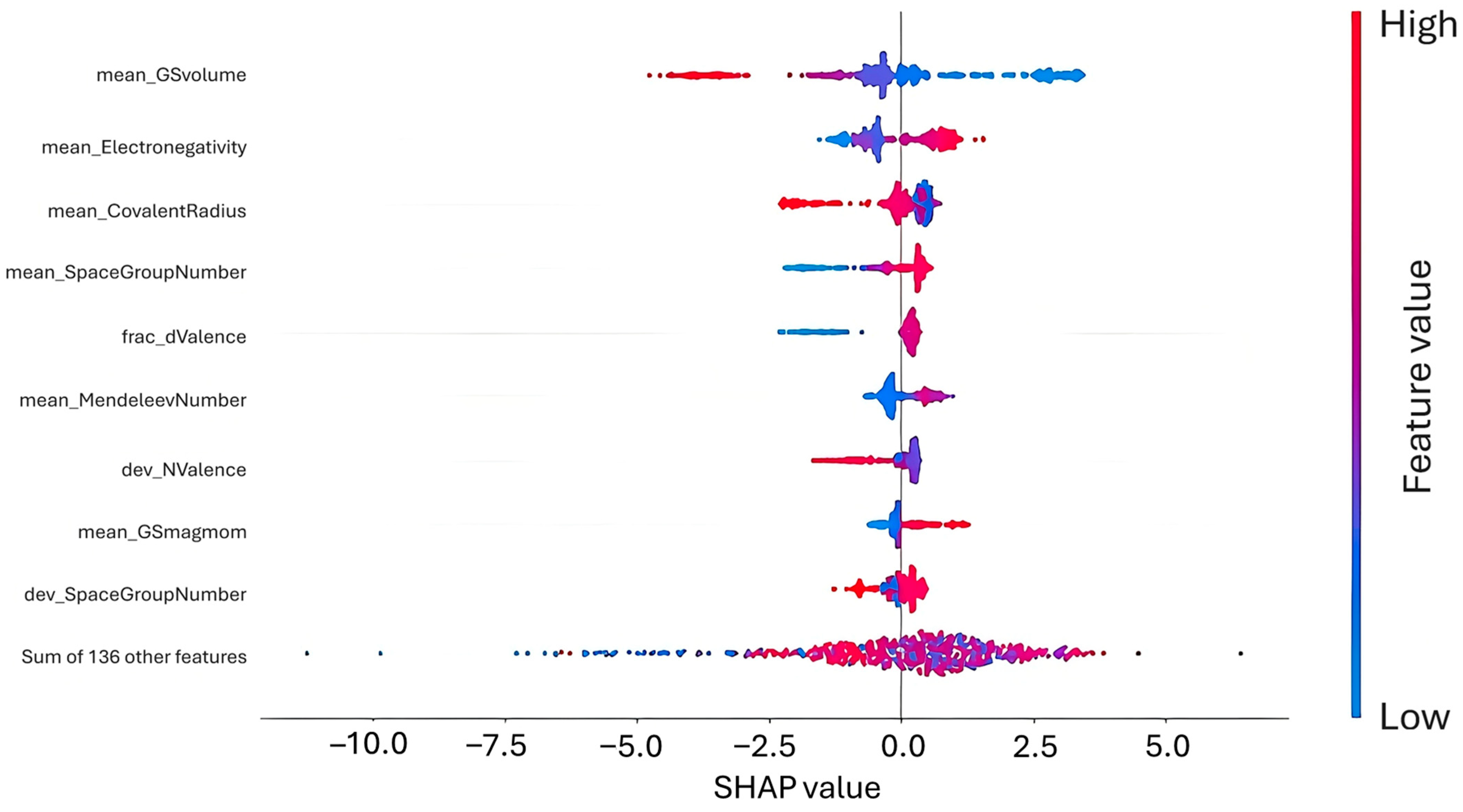
3.3. Clustering and Further Analysis
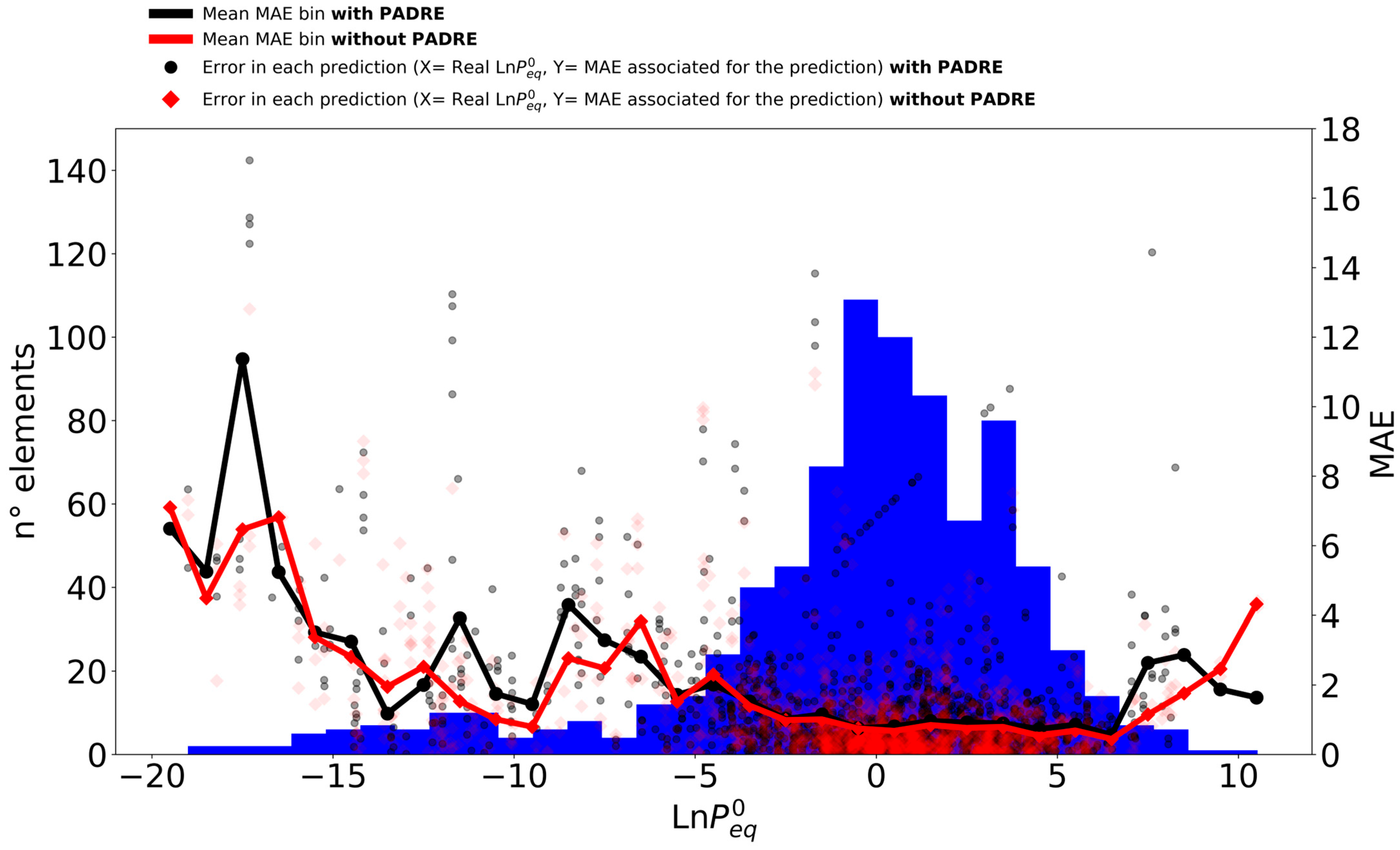
3.4. Validation of Model Predictions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ball, M.; Wietschel, M. The Future of Hydrogen—Opportunities and Challenges. Int. J. Hydrogen Energy 2009, 34, 615–627. [Google Scholar] [CrossRef]
- Züttel, A. Materials for Hydrogen Storage. Mater. Today 2003, 6, 24–33. [Google Scholar] [CrossRef]
- Allendorf, M.D.; Stavila, V.; Snider, J.L.; Witman, M.; Bowden, M.E.; Brooks, K.; Tran, B.L.; Autrey, T. Challenges to Developing Materials for the Transport and Storage of Hydrogen. Nat. Chem. 2022, 14, 1214–1223. [Google Scholar] [CrossRef]
- Hirscher, M.; Yartys, V.A.; Baricco, M.; Bellosta von Colbe, J.; Blanchard, D.; Bowman, R.C.; Broom, D.P.; Buckley, C.E.; Chang, F.; Chen, P.; et al. Materials for Hydrogen-Based Energy Storage—Past, Recent Progress and Future Outlook. J. Alloys Compd. 2020, 827, 153548. [Google Scholar] [CrossRef]
- Witman, M.; Ling, S.; Wadge, M.; Bouzidi, A.; Pineda-Romero, N.; Clulow, R.; Ek, G.; Chames, J.; Allendorf, E.; Agarwal, S.; et al. Towards Pareto Optimal High Entropy Hydrides via Data-Driven Materials Discovery. J. Mater. Chem. A 2023, 11, 15878–15888. [Google Scholar] [CrossRef]
- Witman, M.; Ek, G.; Ling, S.; Chames, J.; Agarwal, S.; Wong, J.; Allendorf, M.D.; Sahlberg, M.; Stavila, V. Data-Driven Discovery and Synthesis of High Entropy Alloy Hydrides with Targeted Thermodynamic Stability. Chem. Mater. 2021, 33, 4067–4076. [Google Scholar] [CrossRef]
- Marques, F.; Balcerzak, M.; Winkelmann, F.; Zepon, G.; Felderhoff, M. Review and Outlook on High-Entropy Alloys for Hydrogen Storage. Energy Environ. Sci. 2021, 14, 5191–5227. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, J.; Pei, Z. Machine Learning for High-Entropy Alloys: Progress, Challenges and Opportunities. Prog. Mater. Sci. 2023, 131, 101018. [Google Scholar] [CrossRef]
- Han, G.; Sun, Y.; Feng, Y.; Lin, G.; Lu, N. Artificial Intelligence Guided Thermoelectric Materials Design and Discovery. Adv. Electron. Mater. 2023, 9, 2300042. [Google Scholar] [CrossRef]
- Chen, C.; Zuo, Y.; Ye, W.; Li, X.; Deng, Z.; Ong, S.P. A Critical Review of Machine Learning of Energy Materials. Adv. Energy Mater. 2020, 10, 1903242. [Google Scholar] [CrossRef]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine Learning for Molecular and Materials Science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef]
- Rahnama, A.; Zepon, G.; Sridhar, S. Machine Learning Based Prediction of Metal Hydrides for Hydrogen Storage, Part I: Prediction of Hydrogen Weight Percent. Int. J. Hydrogen Energy 2019, 44, 7337–7344. [Google Scholar] [CrossRef]
- Rahnama, A.; Zepon, G.; Sridhar, S. Machine Learning Based Prediction of Metal Hydrides for Hydrogen Storage, Part II: Prediction of Material Class. Int. J. Hydrogen Energy 2019, 44, 7345–7353. [Google Scholar] [CrossRef]
- Suwarno, S.; Dicky, G.; Suyuthi, A.; Effendi, M.; Witantyo, W.; Noerochim, L.; Ismail, M. Machine Learning Analysis of Alloying Element Effects on Hydrogen Storage Properties of AB2 Metal Hydrides. Int. J. Hydrogen Energy 2022, 47, 11938–11947. [Google Scholar] [CrossRef]
- Kim, J.M.; Ha, T.; Lee, J.; Lee, Y.-S.; Shim, J.-H. Prediction of Pressure-Composition-Temperature Curves of AB2-Type Hydrogen Storage Alloys by Machine Learning. Met. Mater. Int. 2023, 29, 861–869. [Google Scholar] [CrossRef]
- Maghsoudy, S.; Zakerabbasi, P.; Baghban, A.; Esmaeili, A.; Habibzadeh, S. Connectionist Technique Estimates of Hydrogen Storage Capacity on Metal Hydrides Using Hybrid GAPSO-LSSVM Approach. Sci. Rep. 2024, 14, 1503. [Google Scholar] [CrossRef]
- Wen, C.; Zhang, Y.; Wang, C.; Xue, D.; Bai, Y.; Antonov, S.; Dai, L.; Lookman, T.; Su, Y. Machine Learning Assisted Design of High Entropy Alloys with Desired Property. Acta Mater. 2019, 170, 109–117. [Google Scholar] [CrossRef]
- Halpren, E.; Yao, X.; Chen, Z.W.; Singh, C.V. Machine Learning Assisted Design of BCC High Entropy Alloys for Room Temperature Hydrogen Storage. Acta Mater. 2024, 270, 119841. [Google Scholar] [CrossRef]
- Huang, W.; Martin, P.; Zhuang, H.L. Machine-Learning Phase Prediction of High-Entropy Alloys. Acta Mater. 2019, 169, 225–236. [Google Scholar] [CrossRef]
- Witman, M.; Ling, S.; Grant, D.M.; Walker, G.S.; Agarwal, S.; Stavila, V.; Allendorf, M.D. Extracting an Empirical Intermetallic Hydride Design Principle from Limited Data via Interpretable Machine Learning. J. Phys. Chem. Lett. 2020, 11, 40–47. [Google Scholar] [CrossRef]
- Tynes, M.; Gao, W.; Burrill, D.J.; Batista, E.R.; Perez, D.; Yang, P.; Lubbers, N. Pairwise Difference Regression: A Machine Learning Meta-Algorithm for Improved Prediction and Uncertainty Quantification in Chemical Search. J. Chem. Inf. Model. 2021, 61, 3846–3857. [Google Scholar] [CrossRef]
- Magpie Manual. Available online: https://wolverton.bitbucket.io/ (accessed on 15 July 2025).
- Ward, L.; Agrawal, A.; Choudhary, A.; Wolverton, C. A General-Purpose Machine Learning Framework for Predicting Properties of Inorganic Materials. NPJ Comput. Mater. 2016, 2, 16028. [Google Scholar] [CrossRef]
- Dematteis, E.M.; Berti, N.; Cuevas, F.; Latroche, M.; Baricco, M. Substitutional Effects in TiFe for Hydrogen Storage: A Comprehensive Review. Mater. Adv. 2021, 2, 2524–2560. [Google Scholar] [CrossRef]
- Zhou, P.; Xiao, X.; Zhu, X.; Chen, Y.; Lu, W.; Piao, M.; Cao, Z.; Lu, M.; Fang, F.; Li, Z.; et al. Machine Learning Enabled Customization of Performance-Oriented Hydrogen Storage Materials for Fuel Cell Systems. Energy Storage Mater. 2023, 63, 102964. [Google Scholar] [CrossRef]
- Scikit-Learn. Available online: https://scikit-learn.org/stable/ (accessed on 10 June 2025).
- Pandas. Available online: https://pandas.pydata.org/ (accessed on 15 July 2025).
- Lundberg, S.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar] [CrossRef]
- Meredig, B.; Antono, E.; Church, C.; Hutchinson, M.; Ling, J.; Paradiso, S.; Blaiszik, B.; Foster, I.; Gibbons, B.; Hattrick-Simpers, J.; et al. Can Machine Learning Identify the next High-Temperature Superconductor? Examining Extrapolation Performance for Materials Discovery. Mol. Syst. Des. Eng. 2018, 3, 819–825. [Google Scholar] [CrossRef]
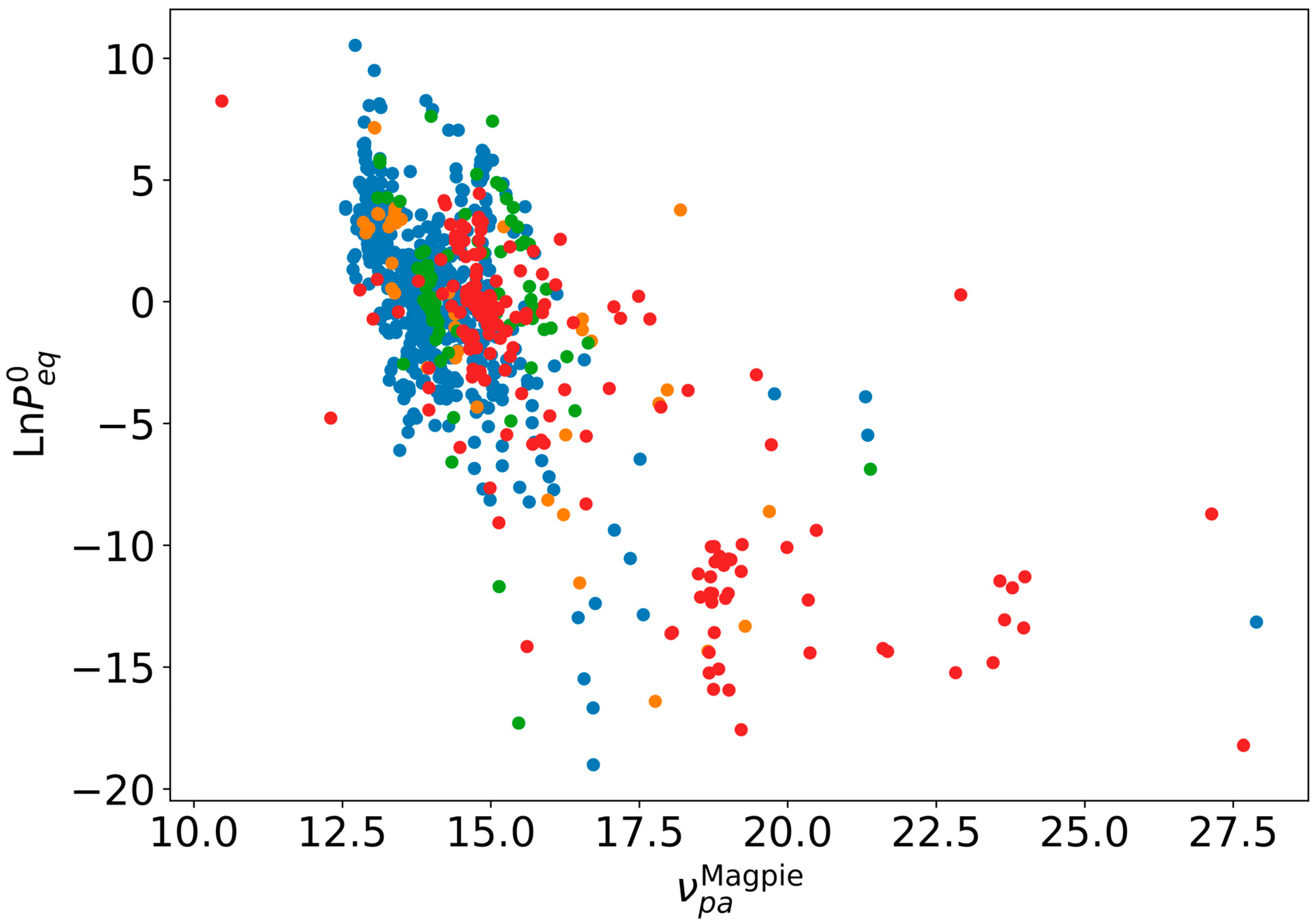
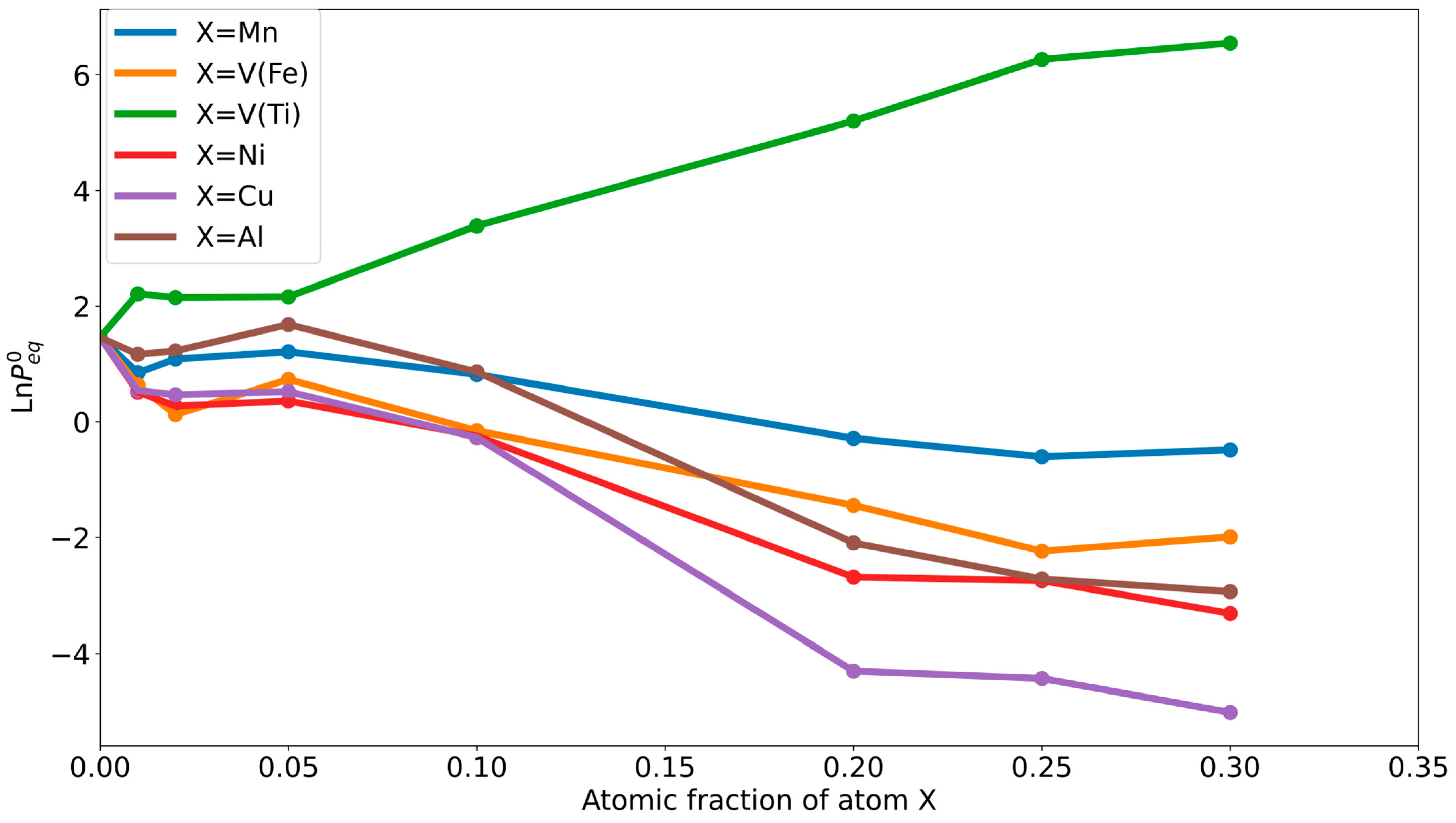
| Dataset | Before PADRE | After PADRE |
|---|---|---|
| DS0 | 398 items × 145 features | 158.404 items × 435 features |
| DS1 | 806 items × 145 features | 649.636 items × 435 features |
| Model | MAE | R2 |
|---|---|---|
| SVM | 1.13 | 0.82 |
| RFGB | 1.07 | 0.84 |
| RF | 1.47 | 0.74 |
| KNN | 1.82 | 0.64 |
| Kmean++ Cluster Used as Test Set | Number of Instances | MAE | R2 |
|---|---|---|---|
| 1 | 531 | 5.97 | −2.68 |
| 2 | 43 | 2.92 | 0.1 |
| 3 | 69 | 3.26 | 0.01 |
| 4 | 176 | 1.25 | 0.82 |
| Material Class | Quantity of Data | MAE | R2 |
|---|---|---|---|
| A2B | 10 | 1.65 | −4.06 |
| AB | 78 | 3.9 | 0.10 |
| AB2 | 454 | 2.10 | 0.37 |
| AB5 | 106 | 1.80 | −0.5 |
| Mg | 32 | 2.68 | −0.26 |
| MIC | 52 | 3.74 | −0.41 |
| SS | 85 | 2.25 | 0.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beltrame, G.; Dematteis, E.M.; Stavila, V.; Rizzi, P.; Baricco, M.; Palumbo, M. Application of Machine Learning and Data Augmentation Algorithms in the Discovery of Metal Hydrides for Hydrogen Storage. Metals 2025, 15, 1221. https://doi.org/10.3390/met15111221
Beltrame G, Dematteis EM, Stavila V, Rizzi P, Baricco M, Palumbo M. Application of Machine Learning and Data Augmentation Algorithms in the Discovery of Metal Hydrides for Hydrogen Storage. Metals. 2025; 15(11):1221. https://doi.org/10.3390/met15111221
Chicago/Turabian StyleBeltrame, Giancarlo, Erika Michela Dematteis, Vitalie Stavila, Paola Rizzi, Marcello Baricco, and Mauro Palumbo. 2025. "Application of Machine Learning and Data Augmentation Algorithms in the Discovery of Metal Hydrides for Hydrogen Storage" Metals 15, no. 11: 1221. https://doi.org/10.3390/met15111221
APA StyleBeltrame, G., Dematteis, E. M., Stavila, V., Rizzi, P., Baricco, M., & Palumbo, M. (2025). Application of Machine Learning and Data Augmentation Algorithms in the Discovery of Metal Hydrides for Hydrogen Storage. Metals, 15(11), 1221. https://doi.org/10.3390/met15111221







