Hot Deformation Behavior and Dynamic Recrystallization Mechanism of GH3230 Superalloy
Abstract
1. Introduction
2. Materials and Experimental Procedures
3. Results and Discussion
3.1. Stress–Strain Curve
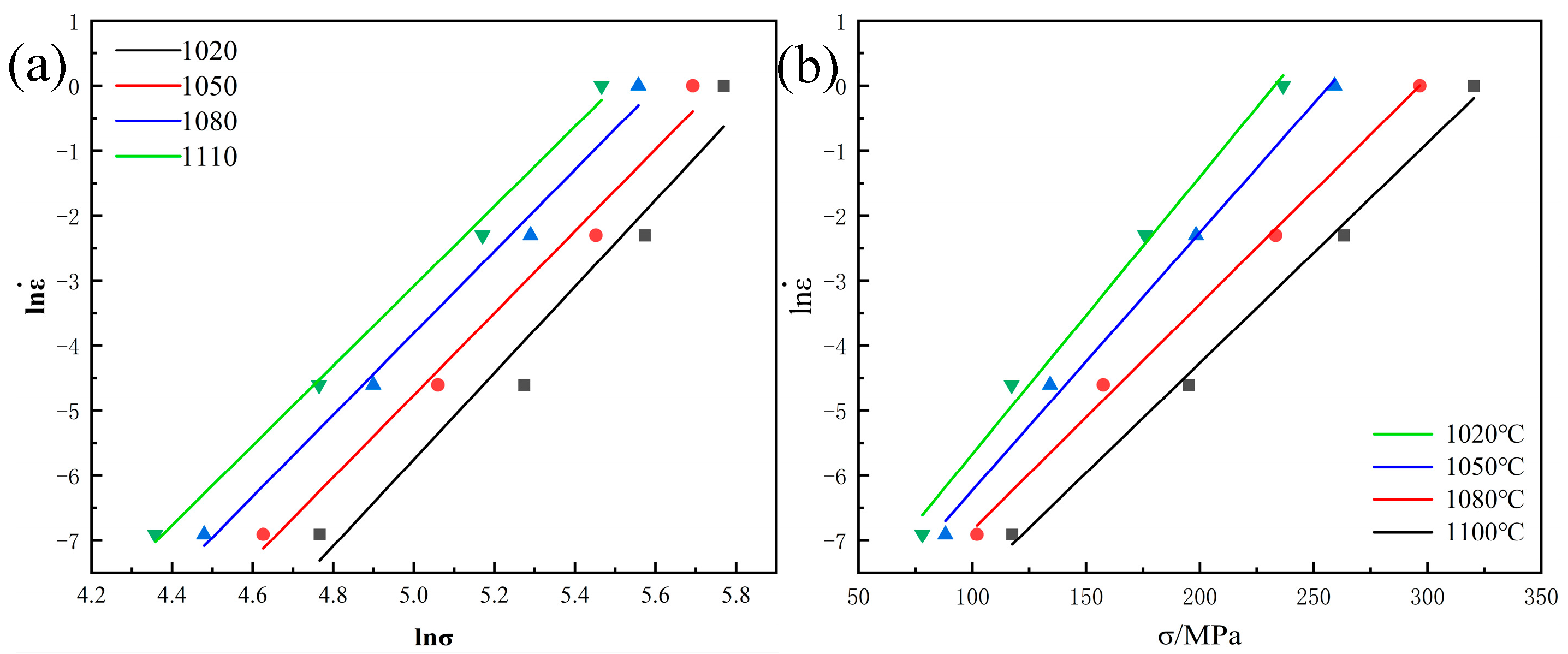
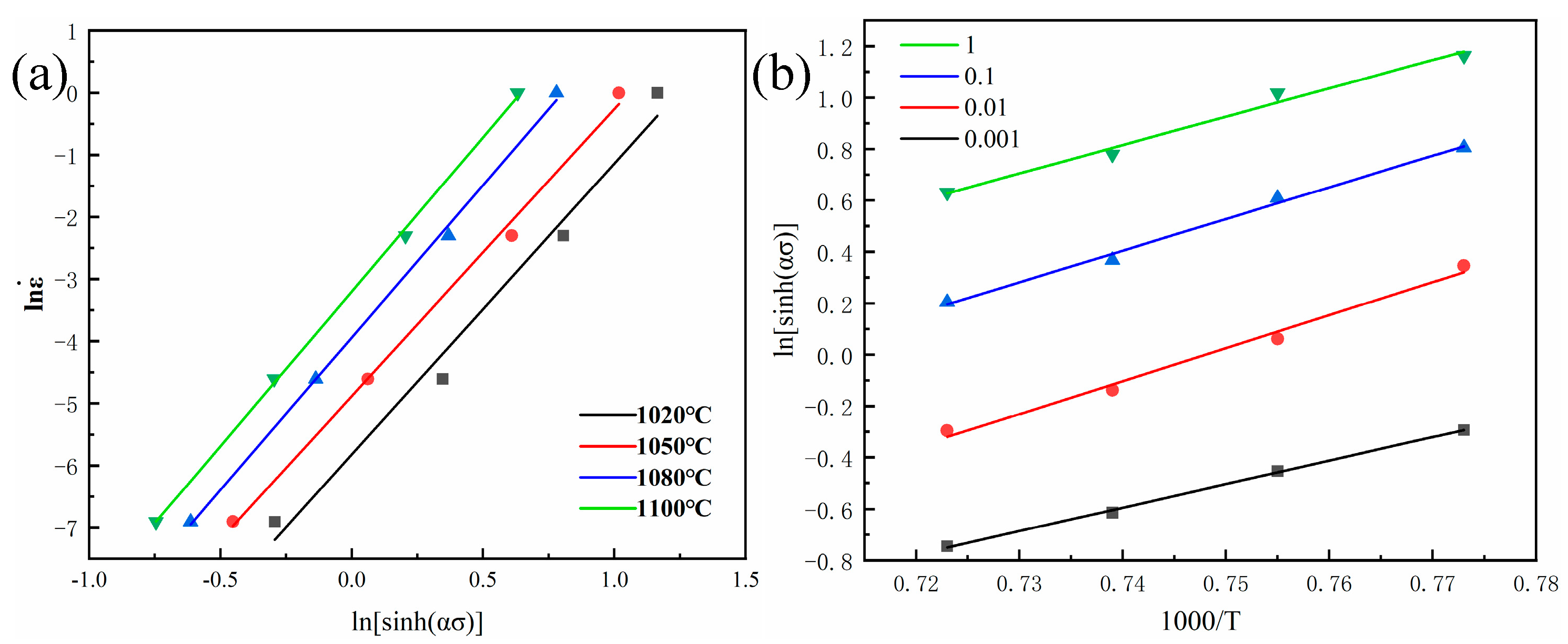
3.2. Constitutive Model
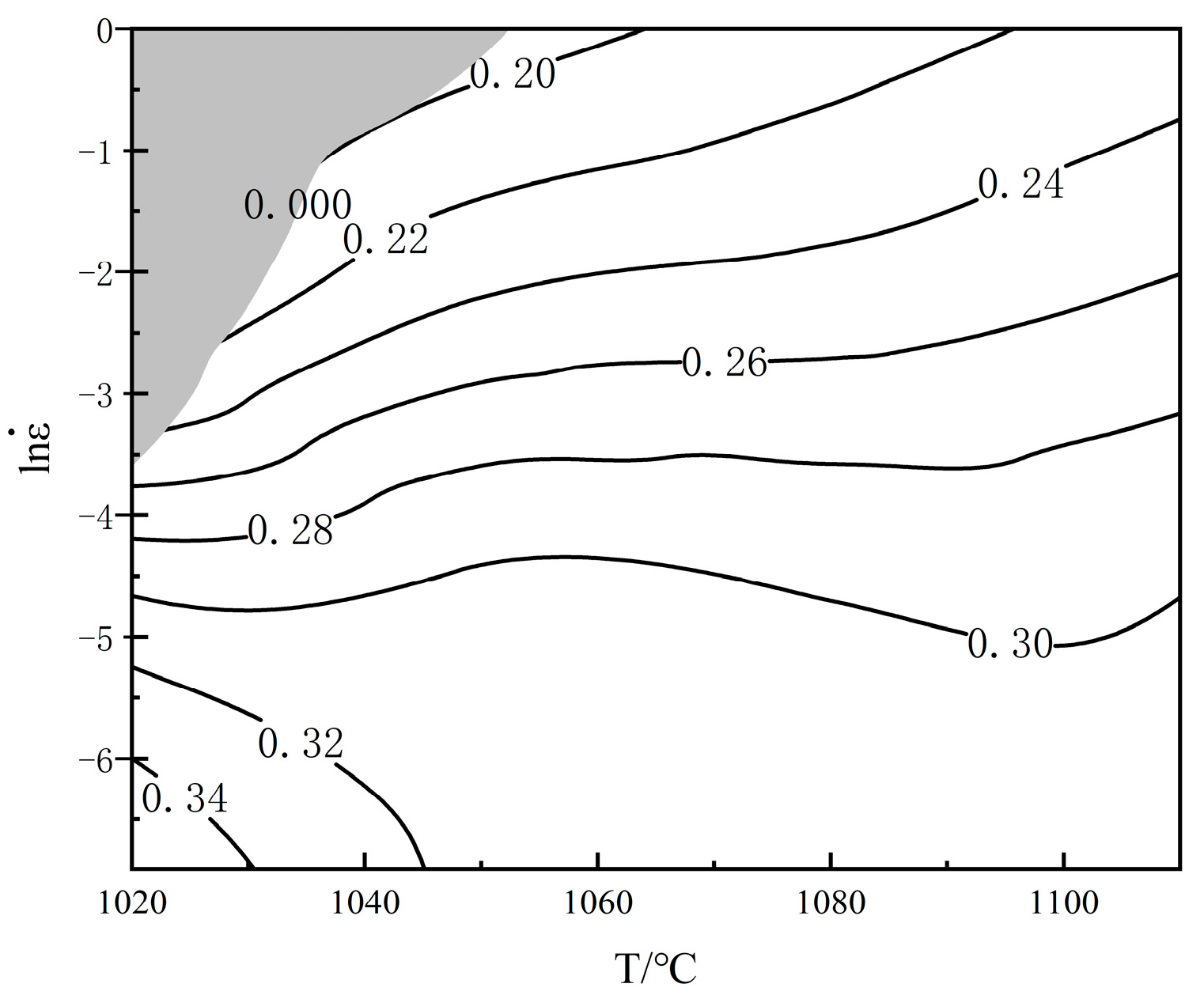
3.3. Processing Map
3.4. Structural Evolution
3.5. Twinning Evolution
3.6. Dynamic Recrystallization Behavior
3.7. Continuous Dynamic Recrystallization
3.8. Discontinuous Dynamic Recrystallization
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, S.I.; Yoo, Y.C. Continuous dynamic recrystallization of AISI 430 ferritic stainless steel. Met. Mater. Int. 2002, 8, 7–13. [Google Scholar] [CrossRef]
- Humphreys, F.J.; Prangnell, P.B.; Priestner, R. Fine-grained alloys by thermomechanical processing. Curr. Opin. Solid State Mater. Sci. 2001, 5, 15–21. [Google Scholar] [CrossRef]
- Wang, Y.; Shao, W.; Zhen, L.; Yang, L.; Zhang, X. Flow behavior and microstructures of superalloy 718 during high temperature deformation. Mater. Sci. Eng. A 2008, 497, 479–486. [Google Scholar] [CrossRef]
- Doherty, R.D.; Hughes, D.A.; Humphreys, F.J.; Jonas, J.J.; Jensen, D.J.; Kassner, M.E.; King, W.E.; McNelley, T.R.; McQueen, H.J.; Rollett, A.D. Current issues in recrystallization: A review. Mater. Today 1997, 238, 219–234. [Google Scholar] [CrossRef]
- Jiang, H.; Dong, J.X.; Zhang, M.C.; Zheng, L.; Yao, Z. Hot deformation characteristics of Alloy 617B nickel-based superalloy: A study using processing map. J. Alloys Compd. 2015, 647, 338–350. [Google Scholar] [CrossRef]
- Li, H.Z.; Yang, L.; Wang, Y.; Tan, G.; Qiao, S.; Huang, Z.; Liu, M. Thermal deformation and dynamic recrystallization of a novel HEXed P/M nickel-based superalloy. Mater. Charact. 2020, 163, 110285. [Google Scholar] [CrossRef]
- Wu, Y.S.; Zhang, M.C.; Xie, X.S.; Lin, F.; Zhao, S. Dynamic recrystallization of a new nickel-based alloy for 700 °C A-USC power plant applications with different initial states: As-homogenized and as-forged. J. Alloys Compd. 2016, 662, 283–295. [Google Scholar] [CrossRef]
- Montheillet, F.; Lurdos, O.; Damamme, G. A grain scale approach for modeling steady-state discontinuous dynamic recrystallization. Acta Mater. 2009, 57, 1602–1612. [Google Scholar] [CrossRef]
- Chen, L.L.; Ding, H.N.; Tian, L.; Luo, R.; Cao, Y.; Zhang, Y.; Liu, Y.; Yuan, F.; Qiu, Y.; Cui, S.; et al. Thermal deformation behavior and microstructure evolution of GH4169 superalloy under the shear-compression deformation conditions. Mater. Des. 2021, 212, 110195. [Google Scholar] [CrossRef]
- Azarbarmas, M.; Aghaie-Khafri, M.; Cabrera, J.M.; Calvo, J. Dynamic recrystallization mechanisms and twining evolution during hot deformation of Inconel 718. Mater. Sci. Eng. A 2016, 678, 137–152. [Google Scholar] [CrossRef]
- Song, Y.H.; Li, Y.G.; Li, H.Y.; Zhao, G.; Cai, Z.; Sun, M. Hot deformation and recrystallization behavior of a new nickel-base superalloy for ultra-supercritical applications. J. Mater. Res. Technol. 2022, 19, 4308–4324. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, D.; Yang, Y.; Liu, C.; Wang, J.; Zhang, Z.; Wang, H. Investigation on the influences of δ phase on the dynamic recrystallization of Inconel 718 through a modified cellular automaton model. J. Alloys Compd. 2020, 830, 154590. [Google Scholar] [CrossRef]
- Gao, J.; Han, Q.; Soe, S.; Wang, L.; Zhang, Z.; Zhang, H.; Song, J.; Liu, Y.; Setchi, R.; Yang, S. Laser additive manufacturing of TiB2-modified Cu15Ni8Sn/GH3230 heterogeneous materials: Processability, interfacial microstructure and mechanical performance. Mater. Sci. Eng. A 2024, 900, 146496. [Google Scholar] [CrossRef]
- Xi, X.; Lin, D.; Song, X.; Luo, X.; Ma, R.; Shi, Z.; Bian, H.; Fu, W.; Dong, Z.; Tan, C. Strength-plasticity transition mechanism after the solution treatment of GH3230 superalloy fabricated via laser powder bed fusion. Mater. Sci. Eng. A 2023, 876, 145124. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, X.; Liu, X.; Wang, N.; Yao, C.; Xu, Y. Effect of laser lower and remelting on the microstructure and tribological properties of GH3230 superalloy coating fabricated by laser melting deposition. J. Manuf. Process. 2024, 131, 2411–2419. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, J.; Xu, K.; Shi, K.; Ma, Z.-Y.; Liu, T.-Y.; Liu, S.-B.; Yan, J.-Q. Role of elemental reduction in microstructure, microcrack, and mechanical properties of GH3230 by laser powder bed fusion. China Foundry 2024, 21, 727–736. [Google Scholar] [CrossRef]
- Wang, Y.; Li, N.; Liu, W.; Jia, C.; Wu, Y.; Gao, C.; Xiong, H. Interfacial Microstructures and Mechanical Properties of TiC Reinforced GH 3230 Superalloy Manufactured by Laser Metal Deposition. Chin. J. Mech. Eng. 2024, 37, 144. [Google Scholar] [CrossRef]
- Zhang, D.; Wen, Z.; Yue, Z. Effects of strain rate and temperature on mechanical property of nickel-based superalloy GH3230. Rare Met. Mater. Eng. 2015, 44, 2601–2606. [Google Scholar] [CrossRef]
- Hao, R.; Zhang, S.; Lu, B.; Wang, H.; Gao, X. Anisotropy of Microstructure and Mechanical Property in GH3230 Superalloy Fabricated Laser Powder Bed Fusion. Mater. Today Commun. 2025, 44, 111797. [Google Scholar] [CrossRef]
- Yuan, Z.; Chen, A.; Xue, L.; Ma, R.; Bai, J.; Zheng, J.; Bai, X.; Zheng, J.; Mu, S.; Zhang, L. Effect of hot isostatic pressing and heat treatment on the evolution of precipitated phase and mechanical properties of GH3230 superalloy fabricated via selective laser melting. J. Mater. Res. Technol. 2024, 30, 507–519. [Google Scholar] [CrossRef]
- Pu, E.X.; Zheng, W.J.; Xiang, J.Z.; Song, Z.; Liu, J. Hot deformation characteristic and processing map of super- austenitic stainless steel S32654. Mater. Sci. Eng. A 2014, 598, 174–182. [Google Scholar] [CrossRef]
- Prasad, Y. Processing maps: A status report. J. Mater. Eng. Perform. 2003, 12, 638–645. [Google Scholar] [CrossRef]
- Sivakesavam, O.; Prasad, Y. Hot deformation behaviour of as-cast Mg–2Zn–1Mn alloy in compression: A study with processing map. J. Mater. Sci. Eng. A 2003, 362, 118–124. [Google Scholar] [CrossRef]
- Cavaliere, P.; Evangelista, E. Isothermal forging of metal matrix composites: Recrystallization behaviour by means of deformation efficiency. Compos. Sci. Technol. 2006, 66, 357–362. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, B.; Yang, Y.; Zhao, T.; Xu, Y.; Wang, Q.; Zan, B.; Cai, J.; Wang, K.; Chen, X. Evolution of hot processing map and microstructure of as-forged nickel-based superalloy during hot deformation. J. Mater. Res. Technol. 2023, 24, 7638–7653. [Google Scholar] [CrossRef]
- Zhang, B.; Ning, Y.; Wang, Z.; Liu, Q. PPB structure elimination, DRX nucleation mechanisms and grain growth behavior of the 3rd-generation PM superalloy for manufacturing aviation components. Chin. J. Aeronaut. 2024, 37, 325–344. [Google Scholar] [CrossRef]
- Yu, H.; Wang, Z.T.; Ning, Y.Q.; Huang, S.; Liu, Q. DRX mechanisms of a Ni-Co-W type superalloy with typical columnar grains during hot compression. J. Alloys Compd. 2023, 959, 170533. [Google Scholar] [CrossRef]
- Xie, B.C.; Zhang, B.Y.; Ning, Y.Q.; Fu, M.W. Mechanisms of DRX nucleation with grain boundary bulging and subgrain rotation during the hot working of nickel-based superalloys with columnar grains. J. Alloys Compd. 2019, 786, 636–647. [Google Scholar] [CrossRef]
- Zhang, P.; Lan, C.X.; Wang, L.; Liu, C.; Zhang, H.; Zhou, H. Influence of hot deformation parameters on the microstructure evolution of low-expansion GH2909 superalloy. Mater. Charact. 2025, 220, 114705. [Google Scholar] [CrossRef]
- Zhao, W.W.; Liu, N.; Li, Z.; Zhang, S.; Zhang, S.; Liu, Y.; Liu, Z.; Qu, X. The adjustability of hot workability of FGH96 superalloy toward the effect of oxygen on the microstructure. Mater. Sci. Eng. A 2025, 929, 148103. [Google Scholar] [CrossRef]
- Fan, X.Y.; Zhong, L.X.; Liu, Y.Z.; Cui, J.; Du, H.; Wei, Y.; Shi, Y.; Hou, X.; Wang, J.; Jin, P. The interaction between dynamic recrystallization and twinning during the hot compression in a novel nickel-based superalloy. J. Mater. Res. Technol. 2025, 35, 2144–2157. [Google Scholar] [CrossRef]
- Xie, B.C.; Luo, Y.W.; Wang, Z.T.; Meng, Q.Q.; Ning, Y.Q.; Fu, M.W. A novel strategy for ingot cogging without homogenization: Dynamical recrystallization and nucleation mechanisms associated with as-cast dendrites of nickel-based superalloys. J. Mater. Sci. Technol. 2025, 220, 78–91. [Google Scholar] [CrossRef]
- Zeng, X.; Huang, L.H.; Liu, W.C.; Luo, J.; Pei, L.; Song, W.; Mi, Z.; Xu, X. Hot deformation behavior and dynamic recrystallization mechanism of GH2132 superalloy. J. Alloys Compd. 2024, 1009, 176798. [Google Scholar] [CrossRef]
- Chen, X.M.; Ning, M.T.; Hu, H.W.; Lin, Y.; Zhou, X.; Zhang, J.; Lu, X.; Wu, Y. Investigation on microstructural and microhardness evolution of GH4698 superalloy under transiently varying strain rates. Mater. Sci. Eng. A 2024, 892, 146014. [Google Scholar] [CrossRef]
- Zhang, M.X.; Zhang, B.J.; Jiao, X.Y.; Ding, H. Hot deformation behaviors and microstructure evolution of a supersaturated nickel-based superalloy. Mater. Charact. 2024, 211, 113915. [Google Scholar] [CrossRef]
- He, W.Q.; Liu, F.; Tan, L.M.; Huang, L.; He, S.; Fan, C. Flow behaviors and microstructural evolutions of nickel-based ODS superalloys during hot deformation. J. Mater. Sci. Technol. 2024, 200, 13–26. [Google Scholar] [CrossRef]
- Han, Y.Z.; Zhu, H.C.; Qu, J.L.; Yang, C.; Wang, G.; Zhang, H.; Jiang, L.; Chen, S.; Meng, F. Flow stress and dynamic recrystallization behavior and modeling of GH4738 superalloy during hot compression. J. Mater. Res. Technol. 2023, 26, 4957–4974. [Google Scholar] [CrossRef]
- Eriksson, E.; Hanning, F.; Andersson, J.; Colliander, M.H. Dynamic recrystallization during hot compression of Ni-based superalloy Haynes 282. J. Alloys Compd. 2023, 960, 170837. [Google Scholar] [CrossRef]
- Wang, H.B.; Zhang, H.; Liu, C.H.; Ruan, J.; Huang, H.; Xin, Z.; Meng, F.; Zhu, L.; Zhang, S.; Jiang, L. Hot deformation behavior, superplasticity and microstructure evolution of a new hot isostatic pressed nickel-based superalloy. Mater. Sci. Eng. A 2024, 891, 145997. [Google Scholar] [CrossRef]










| Ni | Cr | W | Mo | Al | Ti | Fe |
|---|---|---|---|---|---|---|
| Bal | 24 | 15 | 3 | 0.5 | 0.1 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, S.; Liu, Y.; Zhang, H.; Li, H.; Li, Q.; Li, J. Hot Deformation Behavior and Dynamic Recrystallization Mechanism of GH3230 Superalloy. Metals 2025, 15, 1220. https://doi.org/10.3390/met15111220
Yuan S, Liu Y, Zhang H, Li H, Li Q, Li J. Hot Deformation Behavior and Dynamic Recrystallization Mechanism of GH3230 Superalloy. Metals. 2025; 15(11):1220. https://doi.org/10.3390/met15111220
Chicago/Turabian StyleYuan, Shichong, Yanhui Liu, Hua Zhang, Hao Li, Qing Li, and Jinshan Li. 2025. "Hot Deformation Behavior and Dynamic Recrystallization Mechanism of GH3230 Superalloy" Metals 15, no. 11: 1220. https://doi.org/10.3390/met15111220
APA StyleYuan, S., Liu, Y., Zhang, H., Li, H., Li, Q., & Li, J. (2025). Hot Deformation Behavior and Dynamic Recrystallization Mechanism of GH3230 Superalloy. Metals, 15(11), 1220. https://doi.org/10.3390/met15111220






