Particle Swarm Optimization–Model Predictive Control-Based Looper Angle Control in Hot Strip Rolling: A Speed Compensation Strategy
Abstract
1. Introduction
1.1. Background of Analysis
1.2. Contributions
- Existing research on looper angle control in hot strip rolling rarely addresses extreme scenarios such as strip tension and strip piling. This study proposes an active compensation control method based on speed compensation and investigates its performance under both strip tension and strip piling scenarios.
- By integrating the rolling mechanism of hot strip rolling, a nonlinear state-space model incorporating a speed compensation parameter is established, which describes the complex nonlinear relationship between the looper angle and the rolling speeds, thereby providing a mathematical foundation for the subsequent control algorithm design.
- A combined MPC–PSO strategy is adopted to formulate a nonlinear optimization problem for the hot strip rolling process, where the PSO algorithm is employed to obtain the optimal sequence of compensation parameters for dynamic adjustment during the control process.
2. Problem Formulation
3. Model Construction
- The looper length model: The primary relationship between the measurable looper angle and the unmeasurable looper length L is a fundamental geometric process. Starting from the exact geometric equation, a simplified third-order polynomial model is derived.
- An incremental model based on the speed compensation parameter: The core of speed compensation lies in governing the mass flow balance under abnormal conditions. Based on the principle of mass flow conservation and rolling deformation mechanics, an incremental speed–thickness model is developed. Crucially, a speed compensation parameter k is introduced, transforming the physical relationship into a tunable control input. The resulting incremental model is inherently discrete-time, aligning directly with digital control system requirements.
- Nonlinear state-space model construction: To provide a comprehensive foundation for advanced control algorithms, the aforementioned physical relationships are integrated into a nonlinear state-space model. This formulation is specifically constructed for algorithm design, enabling the prediction of system states and the calculation of optimal control actions.
3.1. Looper Length Model
3.2. Incremental Model Based on Speed Compensation Parameter
3.3. Nonlinear State-Space Model Construction
4. PSO-MPC-Based Speed Compensation Algorithm for Hot Strip Rolling
4.1. Control Model Formulation Based on MPC
4.2. Nonlinear Optimization Problem Solving Based on PSO
- The position vector represents the compensation factor sequence of particle j at generation g, i.e., the current solution;
- The velocity vector controls the search direction and amplitude of the particle;
- The personal best position is the position of the particle with the smallest cost function value in its history;
- The global best position is the best solution found among all particles so far.
4.3. Algorithm Implementation
| Algorithm 1 PSO-MPC-based speed compensation algorithm for hot rolling |
|
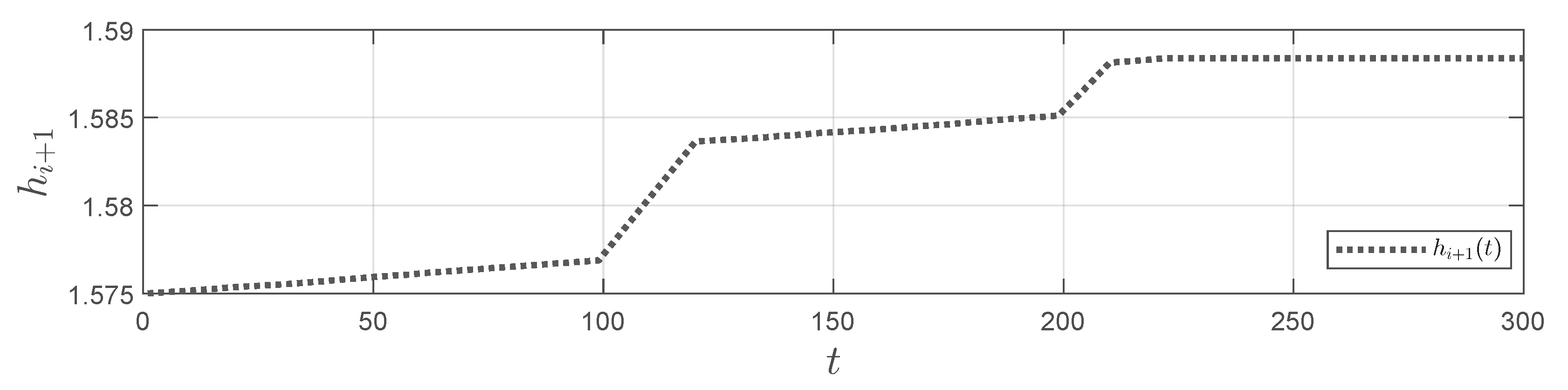
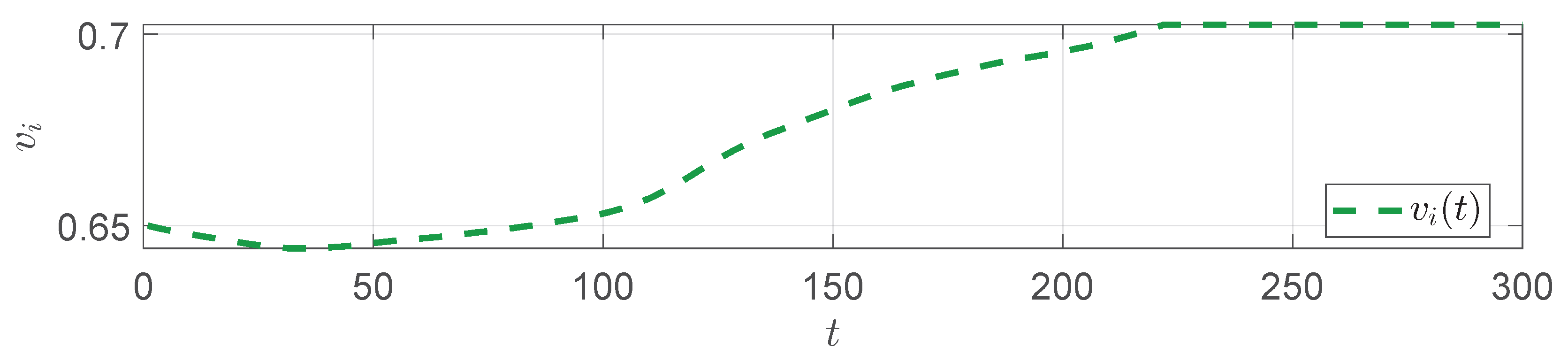
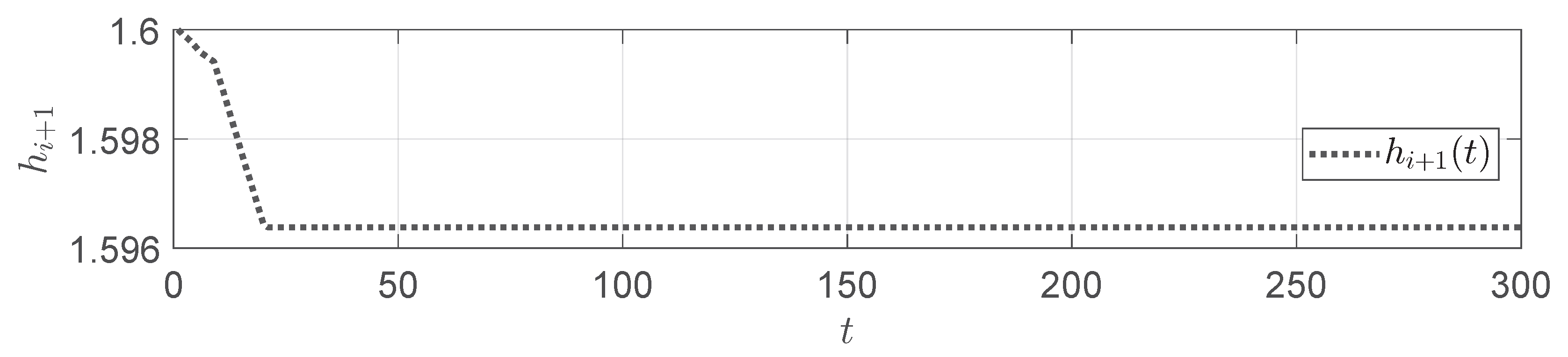
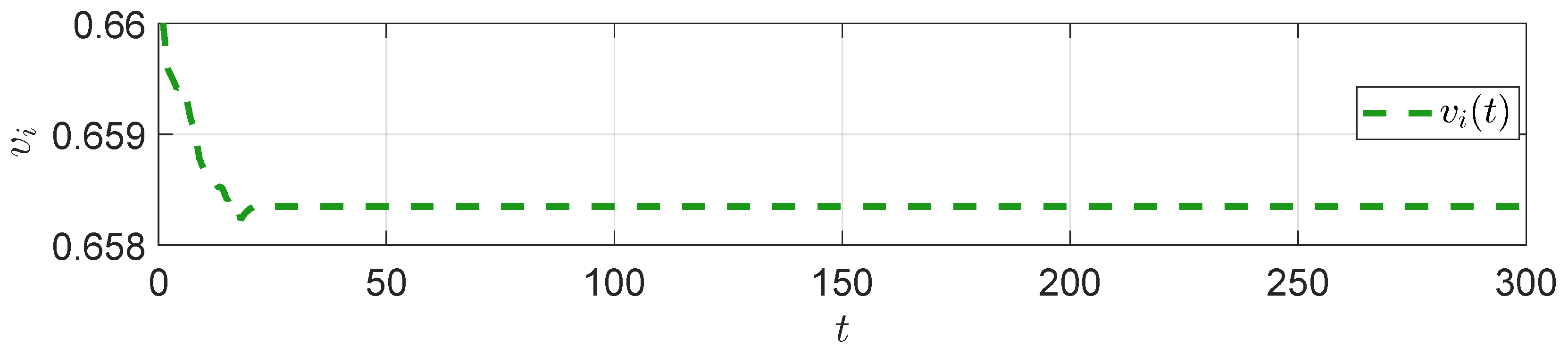
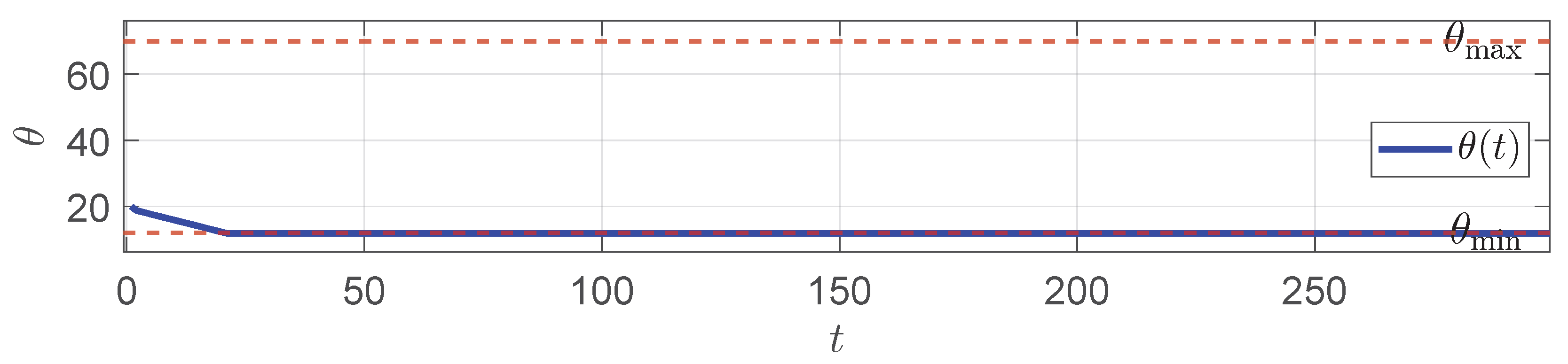
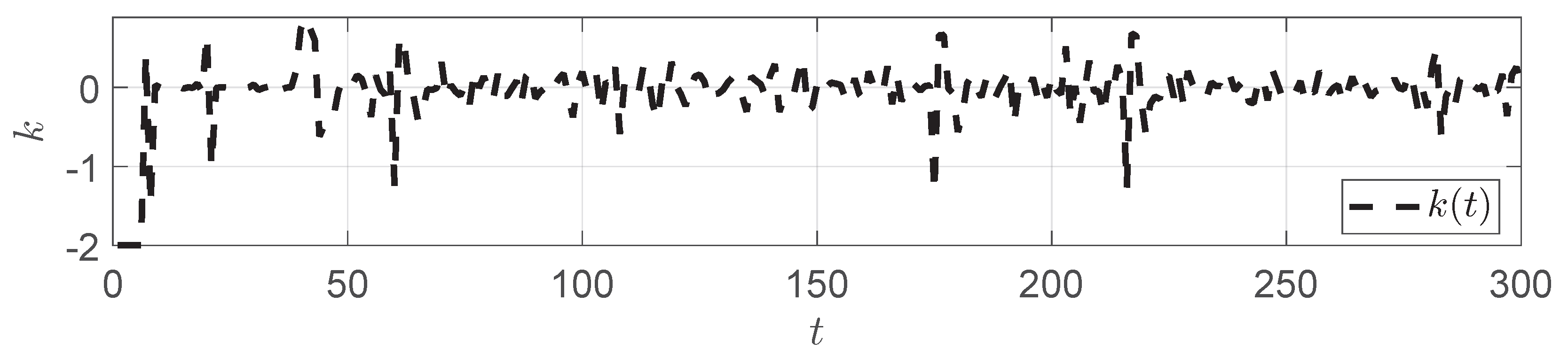
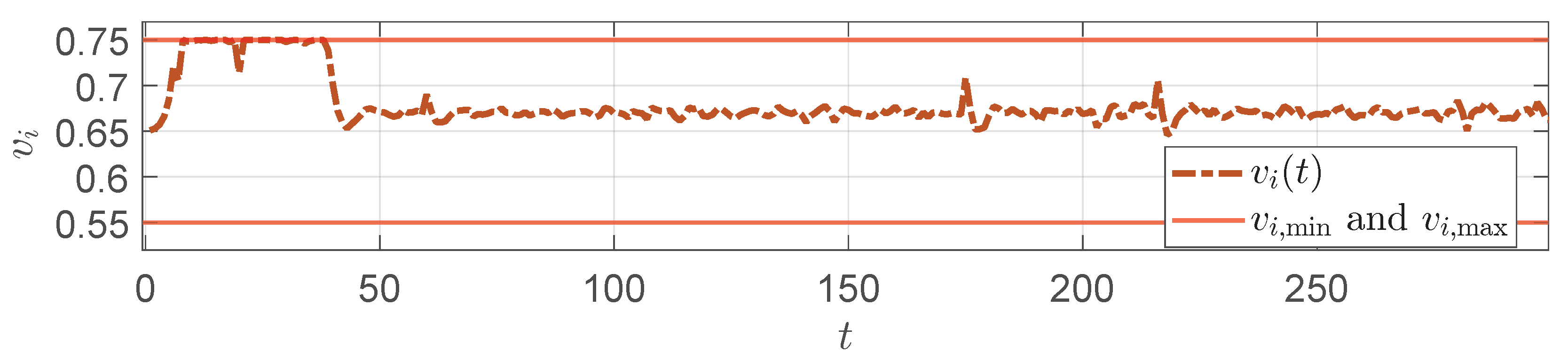
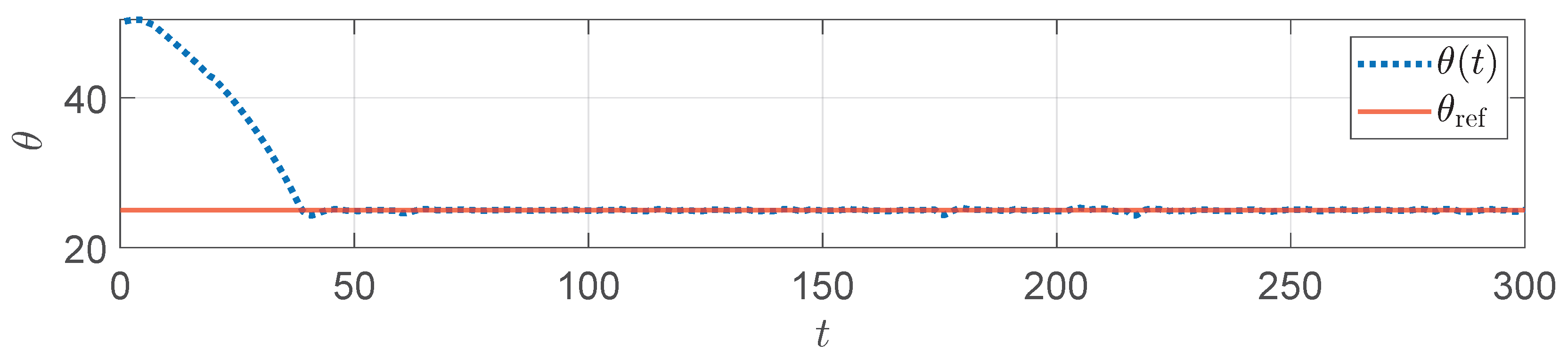
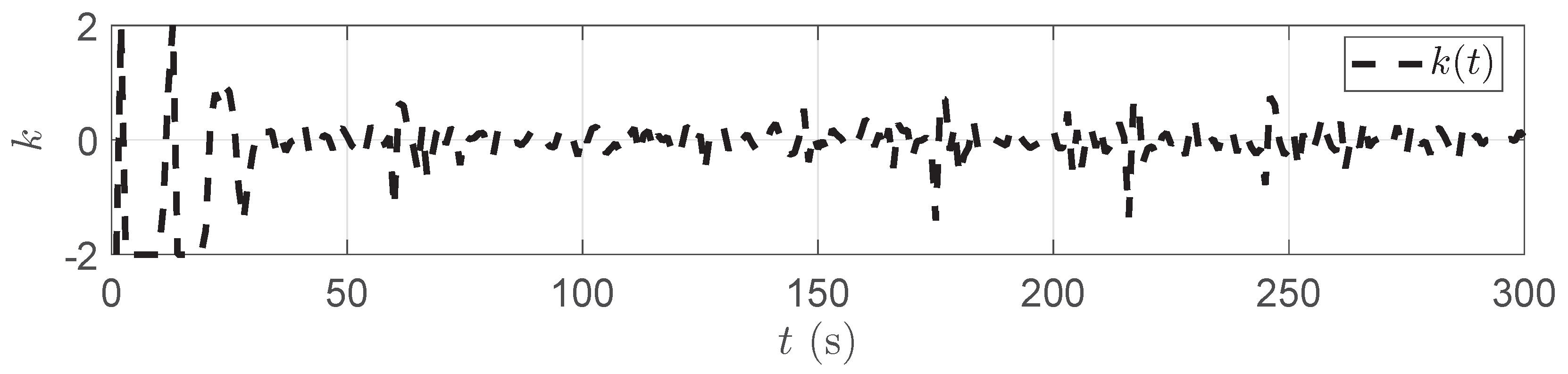
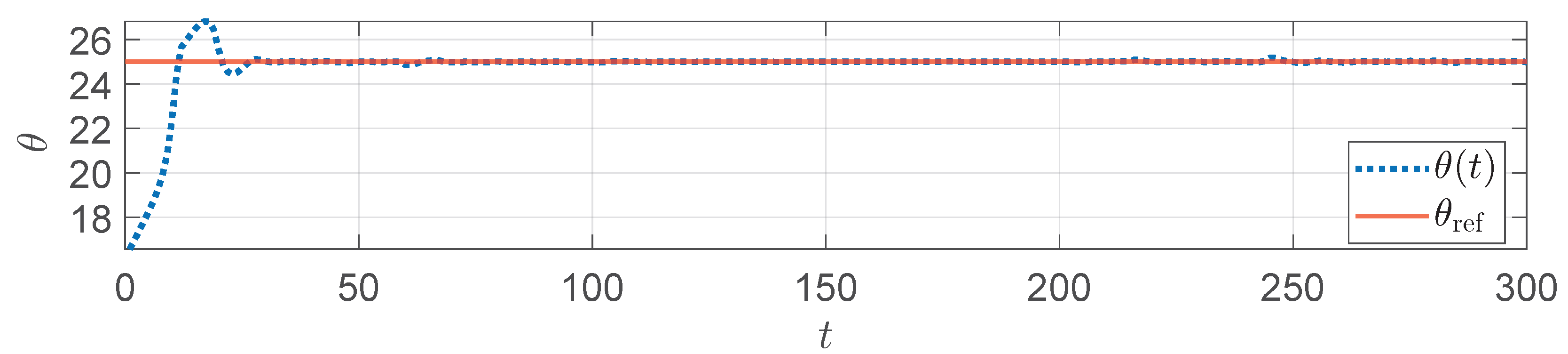
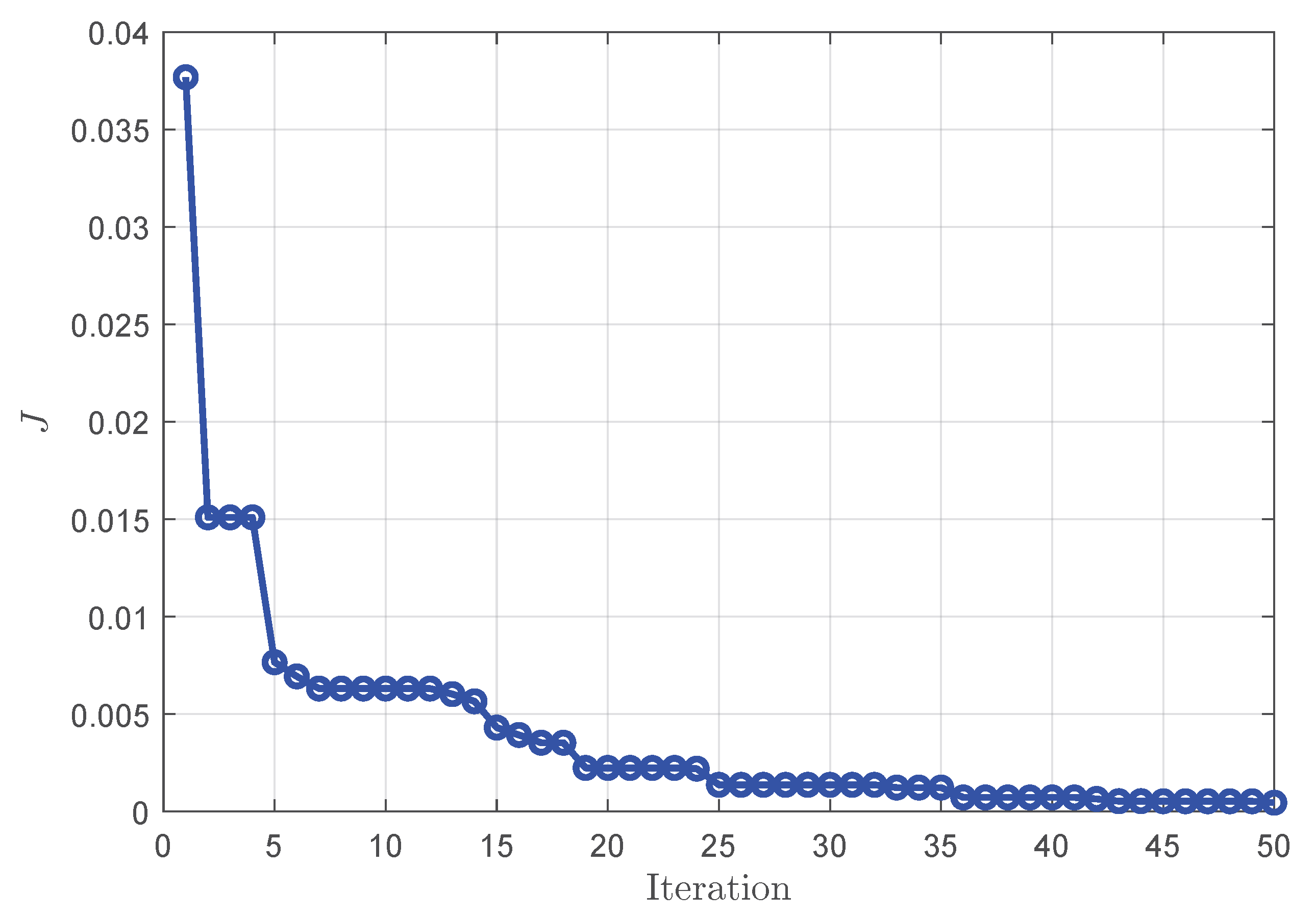
5. Numerical Simulation
6. Concluding Remarks
- Nonlinear state-space modeling: By introducing a speed compensation parameter, the incremental equations for the front and rear stand speeds, strip thickness, and looper angle are derived. Based on these relationships, a nonlinear state-space model is established, where the speed compensation parameter and roll gap variation serve as inputs, and the looper length and angle serve as outputs.
- PSO–MPC-based compensation strategy: In the control algorithm design, MPC is combined with PSO to formulate a rolling optimization problem. The looper angle is defined as the optimization objective, while the speed compensation factor acts as the control variable. Through iterative optimization, the PSO algorithm obtains the optimal compensation sequence, thereby achieving precise dynamic compensation under abnormal conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tan, Y.; Zhou, M.; Guo, X.; Qi, L. A hybrid MIP–CP approach to multistage scheduling problem in continuous casting and hot-rolling processes. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1860–1869. [Google Scholar] [CrossRef]
- Ding, H.; Wang, Y.; Shen, H. A reinforcement learning integral sliding mode control scheme against lumped disturbances in hot strip rolling. Appl. Math. Comput. 2024, 465, 128407. [Google Scholar] [CrossRef]
- Hu, K.; Ye, J.; Song, W. Vulnerability assessments of induction machine-based multistage rolling mill system under sensor integrity attacks. IEEE Trans. Ind. Inform. 2024, 20, 8616–8627. [Google Scholar] [CrossRef]
- Jing, F.; Li, F.; Song, Y.; Li, J.; Feng, Z.; Guo, J. Root cause tracing using equipment process accuracy evaluation for looper in hot rolling. Algorithms 2024, 17, 102. [Google Scholar] [CrossRef]
- Knight, C.W.; Hardy, S.J.; Lees, A.W.; Brown, K.J. Influence of roll speed mismatch on strip curvature during the roughing stages of a hot rolling mill. J. Mater. Process. Technol. 2005, 168, 184–188. [Google Scholar] [CrossRef]
- Dong, Q.; Cao, J.; Li, H.; Zhou, Y.; Yan, T.; Wang, W. Analysis of Spalling in Roughing Mill Backup Rolls of Wide and Thin Strip Hot Rolling Process. Steel Res. Int. 2015, 86, 129–136. [Google Scholar] [CrossRef]
- Park, C.; Hwang, I. New tension control at the head of strip in hot strip finishing mill. J. Mater. Process. Technol. 2008, 206, 69–77. [Google Scholar] [CrossRef]
- Andryushin, I.Y.; Shubin, A.G.; Gostev, A.N.; Radionov, A.A.; Karandaev, A.S.; Gasiyarov, V.R.; Khramshin, V.R. Automatic tension control in the continuous roughing train of a wide-strip hot-rolling mill. Metallurgist 2017, 61, 366–374. [Google Scholar] [CrossRef]
- Gao, H.; Li, X.; Jin, S.; Qin, Y.; Cao, J.; Luan, F.; Zhang, D. Strip deviation analysis and prediction based on time series methods in hot rolling process. J. Manuf. Process. 2024, 131, 1143–1157. [Google Scholar] [CrossRef]
- Hong, W.K.; Kim, P.H.; Moon, Y.H.; Yi, J.J. Hot strip width control method by using looper tension measuring system in finishing mill. J. Mater. Process. Technol. 2001, 111, 74–78. [Google Scholar] [CrossRef]
- Meng, L.; Ding, J.; Li, X.; Cao, G.; Li, Y.; Zhang, D.H. Novel shape control system of hot-rolled strip based on machine learning fused mechanism model. Expert Syst. Appl. 2024, 255, 124789. [Google Scholar] [CrossRef]
- Liu, H.; Li, X.J. Data-driven H_ /H∞ fault detection and control in finite-frequency domain with application to steel rolling process. IEEE Trans. Autom. Sci. Eng. 2025, 22, 252–263. [Google Scholar] [CrossRef]
- Wang, H.; Jing, Y.; Yu, C. Guaranteed cost sliding mode control for looper–tension multivariable uncertain systems. Nonlinear Dyn. 2015, 80, 39–50. [Google Scholar]
- Huang, Y.C.; Peng, C.C. Rolling mill looper-tension control for suppression of strip thickness deviation by adaptive PI controller with uncertain forward/backward slip. Machines 2025, 13, 238. [Google Scholar]
- Yin, F.; Sun, J.; Peng, W.; Wang, H.; Yang, J.; Zhang, D.H. Dynamic matrix predictive control for a hydraulic looper system in hot strip mills. J. Cent. South Univ. 2025, 2, 1369–1378. [Google Scholar] [CrossRef]
- Chen, J.; Yang, W.; Sun, Y. H∞ control of looper-tension control systems based on a discrete-time model. J. Iron Steel Res. Int. 2013, 20, 28–31. [Google Scholar] [CrossRef]
- Choi, I.S.; Rossiter, J.A.; Fleming, P.J. Looper and tension control in hot rolling mills: A survey. J. Process. Control 2006, 17, 509–521. [Google Scholar] [CrossRef]
- Yildiz, S.K.; Forbes, J.F.; Huang, B.; Zhang, Y.; Wang, F.; Vaculik, V.; Dudzic, M. Dynamic modelling and simulation of a hot strip finishing mill. Appl. Math. Model. 2009, 33, 3202–3225. [Google Scholar] [CrossRef]
- Gaber, A.; Elnaggar, M.; Fattah, H.A. Looper and tension control in hot strip finishing mills based on different control approaches. J. Eng. Appl. Sci. 2022, 69, 100. [Google Scholar] [CrossRef]
- Kugi, A.; Haas, W.; Schlacher, K.; Aistleitner, K.; Frank, H.M.; Rigler, G.W. Active compensation of roll eccentricity in rolling mills. IEEE Trans. Ind. Appl. 2002, 36, 625–632. [Google Scholar] [CrossRef]
- Yan, X.; Qi, J.; Wang, X. An active method suppressing rolling mill vibration: Disturbance estimation and compensation algorithm. J. Iron Steel Res. Int. 2019, 26, 697–703. [Google Scholar] [CrossRef]
- Abeyrathna, B.; Rolfe, B.; Hodgson, P.; Matthias, W. A first step towards a simple in-line shape compensation routine for the roll forming of high strength steel. Int. J. Mater. Form. 2016, 9, 423–434. [Google Scholar] [CrossRef]
- Peng, Y.; Hu, Y.; Wang, Y.; Jia, R.; Guo, J. Optimal Consensus Control Strategy for Multi-Agent Systems Under Cyber Attacks via a Stackelberg Game Approach. IEEE Trans. Autom. Sci. Eng. 2025, 22, 18875–18888. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, Q.; Zhao, Y. Identification of FIR Systems with binary-valued observations under replay attacks. Automatica 2025, 172, 112001. [Google Scholar] [CrossRef]
- Jia, R.; Wang, T.; Xue, W.; Guo, J.; Zhao, Y. Multi-Time Scale Consensus Algorithm of Multi-Agent Systems with Binary-valuedData under Tampering Attacks. IEEE Trans. Ind. Inform. 2025. [Google Scholar] [CrossRef]
- Guo, J.; Wang, X.; Xue, W.; Zhao, Y. System identification with binary-valued observations under data tampering attacks. IEEE Trans. Autom. Control 2021, 66, 3825–3832. [Google Scholar] [CrossRef]
- Xu, Q.; Dong, J.; Peng, K.; Yang, X. A novel method of neural network model predictive control integrated process monitoring and applications to hot rolling process. Expert Syst. Appl. 2024, 237, 121682. [Google Scholar] [CrossRef]
- Idzik, C.; Krämer, V.; Hirt, G.; Lohmar, J. Coupling of an analytical rolling model and reinforcement learning to design pass schedules: Towards properties controlled hot rolling. J. Intell. Manuf. 2024, 35, 1469–1490. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, M.; Du, S.; Chen, L. Plate shape recognition based on Gaussian function and particle swarm optimization for roller quenching process. J. Process Control 2022, 119, 115–127. [Google Scholar] [CrossRef]
- Huang, Y.; Lagare, R.B.; Bailey, P.; Sixon, D.; Gonzalez, M.; Nagy, Z.K.; Reklaitis, G.V. Hybrid model development and nonlinear model predictive control implementation for continuous dry granulation process. Comput. Chem. Eng. 2024, 183, 108586. [Google Scholar] [CrossRef]
- Liu, Y.; Peng, P.; Wang, L.; Wu, J.; Lei, M.; Zhang, C.; Lei, R. PSO-NMPC control strategy based path tracking control of mining LHD (scraper). Sci. Rep. 2024, 14, 28516. [Google Scholar] [CrossRef] [PubMed]


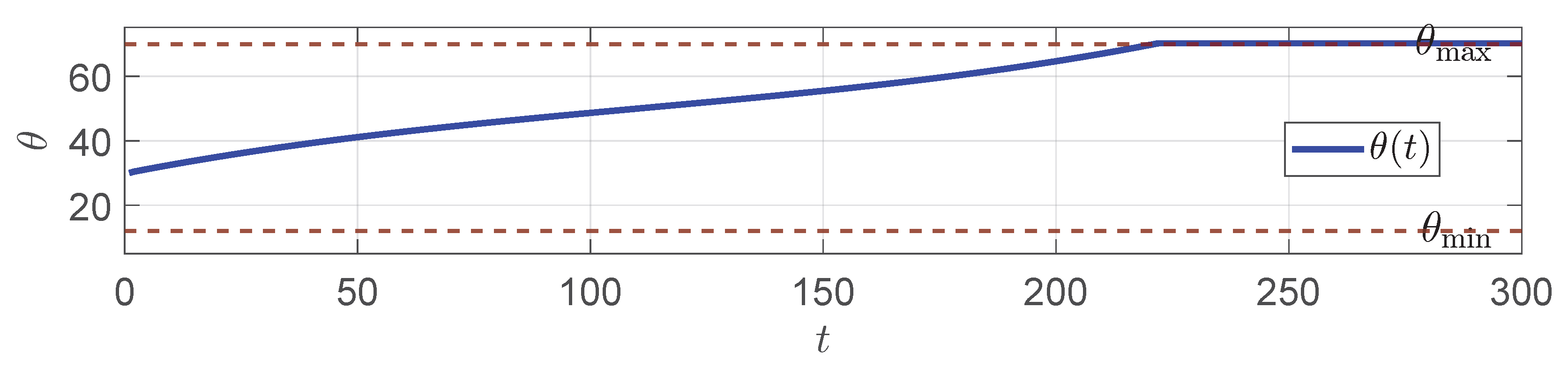

| Others | ||
| Symbol | Meaning | Unit |
|---|---|---|
| T | Control sampling period | ms |
| Entry thickness of the i-th stand | mm | |
| Entry thickness of the -th stand | mm | |
| Thickness change at the -th stand within the given sampling period | mm | |
| Rolling speed of the i-th stand | m/s | |
| Rolling speed of the -th stand | m/s | |
| Speed change in the i-th stand without compensation within the given sampling period | m/s | |
| Speed change in the i-th stand with compensation within the given sampling period | m/s | |
| Roll gap change at the -th stand | mm | |
| k | Speed compensation parameter | Dimensionless |
| L | Loop length between the i-th and -th stands | mm |
| Looper angle | rad | |
| Target looper angle | rad | |
| C | Mill stiffness coefficient | N/mm2 |
| Q | Metal plasticity coefficient | N/mm2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zong, S.; Gao, J. Particle Swarm Optimization–Model Predictive Control-Based Looper Angle Control in Hot Strip Rolling: A Speed Compensation Strategy. Metals 2025, 15, 1202. https://doi.org/10.3390/met15111202
Zong S, Gao J. Particle Swarm Optimization–Model Predictive Control-Based Looper Angle Control in Hot Strip Rolling: A Speed Compensation Strategy. Metals. 2025; 15(11):1202. https://doi.org/10.3390/met15111202
Chicago/Turabian StyleZong, Shengyue, and Jingjie Gao. 2025. "Particle Swarm Optimization–Model Predictive Control-Based Looper Angle Control in Hot Strip Rolling: A Speed Compensation Strategy" Metals 15, no. 11: 1202. https://doi.org/10.3390/met15111202
APA StyleZong, S., & Gao, J. (2025). Particle Swarm Optimization–Model Predictive Control-Based Looper Angle Control in Hot Strip Rolling: A Speed Compensation Strategy. Metals, 15(11), 1202. https://doi.org/10.3390/met15111202





