Abstract
Gradient structure provides an effective approach to improve the combination of high strength and toughness compared to a uniform one. The gradient interfaces or boundaries in gradient-structured metallic glass composites play a crucial role in influencing mechanical properties. Our findings indicate the gradient microstructure significantly induces temporal and spatial stress localization, which can modulate the generation and propagation of shear bands. The synergistic gradient effects generated by heterogeneous grain sizes and interface characteristics can enhance both the strength (yield stress and peak stress) and the toughness of gradient network-structured metallic glass composites as the grain size gradient and the boundary width increase. Our work demonstrates the appropriate gradient of grain size, and the boundary structure should potentially lead to enhanced work hardening.
1. Introduction
Metallic glasses (MGs), characterized by their disordered atomic structure and the absence of crystalline defects, exhibit extraordinary mechanical properties, including high strength and near-theoretical elasticity. However, their widespread structural application is significantly impeded by a critical drawback: plastic deformation in MGs is highly localized into narrow shear bands (SBs), leading to catastrophic failure with minimal macroscopic ductility [1,2,3,4,5,6]. This inherent brittleness stems from the rapid autocatalytic propagation of SBs, which limits energy dissipation and structural reliability under load. To overcome this challenge, recent advancements in microstructural engineering, particularly boundary engineering, have focused on heterogenous structures that facilitate the proliferation and delocalization of SBs. Strategies such as dual-phase amorphous structures [7,8,9,10,11,12,13,14,15,16], chemically modulated glasses [17,18,19,20,21,22,23,24,25,26,27,28,29], and nano-glass composites [30,31,32,33,34,35], have demonstrated improved plasticity by introducing controlled heterogeneity.
In analogy to polycrystals, network-structured metallic glass composites (NMGCs) with either nano-sized or micro-sized glassy grains exhibit network-structured boundaries or interfaces, which can be produced by inert gas condensation, magnetron sputtering, and electro-deposition [31,32,33,34,35,36]. These glassy boundaries or interfaces in NMGCs, including nano-glass (NG), contain excess free volumes (FVs), which act as potential sites for the nucleation of SBs and serve as preferred channels for plastic flow to influence mechanical properties of NMGCs. Nevertheless, the ductility of the NGs is attained at the cost of their strength [31]. Recent studies have demonstrated that mechanical properties of the NG can be tailored by controlling the size of the glassy grains, as well as by adjusting the characteristics and width of the network-structured boundaries/interfaces [31,32].
When the submicron grain size of polycrystals decreases to a critical dimension (less than 10 nm), the Hall-Petch relationship between yield strength and grain size transitions into the inverse Hall-Petch effect [36]. For the NMGCs with the softer properties of glassy boundary compared to the glassy grain, the strength increases as the glassy grain size increases [37,38,39,40]. It was reported that the gradient nanostructure should provide an effective approach to improve the combination of high strength and toughness compared to uniform nano-grained or coarse-grained structures [40,41,42,43,44,45,46,47]. Inspired by gradient nanostructured crystalline metals [41]—where spatial variations in grain size facilitate unprecedented strength-ductility synergies—researchers have begun exploring analogous gradient architectures in micro/nano-glass systems. Gradient network-structured metallic glass composites (GNMGCs) represent a paradigm shift in the design of amorphous materials, featuring spatially tuned variations in both the size and size gradient of the glassy grain, as well as the width of the boundary or interface.
This innovation should create progressive mechanical properties and provide the unique advantages for mitigating shear band formation. Numerous molecular dynamics (MD) simulations [47,48] demonstrate that the heterogeneous gradient nano-microstructure can delay the generation of a dominant shear band, thereby further delocalizing plastic deformation. In MD models of GNMGCs, glassy grain size is usually less than 20 nm at a small scale, with glassy boundaries exhibiting greater free volume and serving as weaker zones compared to the grain regions. Gradient structures exist ubiquitously in nature and are increasingly being introduced in engineering, such as gradient nanotwinned metals, gradient dislocation structures, gradient grain sizes, and so on [41,42,43,44,45,46,47]. The combined experiments and modellings show that an increasing structural gradient produces an increasing plastic strain and raises the extra back stress [45]. The experimental results have shown that the ductility of the NGs (no-grain size gradient) is attained at the cost of their strength for the soft and loose boundary. In the experiments and MD models, GNMGCs, or nano-glass with a grain size gradient, also contain the loose and soft boundary. It is challenging to improve the strength of the interface through elemental composition modifications during experimental procedures. Therefore, theoretical simulations should precede the experiments. However, the interaction between the gradient microstructure at a large scale (submicron dimensions) and hard boundaries, as well as its influence on the mechanical properties of GNMGCs, remains largely unexplored. In particular, the fundamental relationships between size–gradient parameters and deformation mechanisms remain poorly understood, significantly hindering the rational design of GNMGCs with various properties and characteristics of boundaries. Therefore, this study aims to investigate how the gradient hard and soft interfaces influence the overall mechanical properties of GNMGCs on a large scale.
2. Methods and Sample Preparation
In this work, we systematically explore how gradient architectures modulate shear band dynamics and mechanical performance through finite element analysis. The NMGCs, including NGs, by far have a polycrystal-like microstructure, i.e., the pattern of so-called Voronoi structure. By patterning the boundary in Voronoi geometries, we establish the initial boundary for uniform grain size (Figure 1a) and varying gradient structures (Figure 1b,c). To gain the size gradient effect on the mechanical performance, all systems are designed to maintain an identical mean boundary fraction as they have the same boundary width. Through the finite element models (FEMs), which emphasize the free volume parameter as a characteristic quantity to gauge the variation and evolution of the structure, we will reveal the following four key parameters underpinning the strength and plasticity: the gradient of grain size, as well as the width, the orientation, and the density of the boundary or interface.
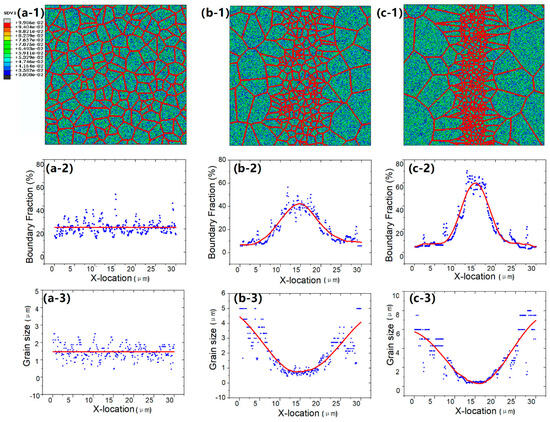
Figure 1.
The initial FV state (-1) of GNMGCs with grain size gradients of 0 (a), 0.29 (b), and 0.42 (c). The distribution of the boundary fraction (-2) and grain size (-3) along the gradient direction for the corresponding GNMGCs.
To establish the relationship between the gradient architecture and the mechanical properties of the GNMGCs with various properties of boundaries on relatively large scales, we use a continuum approach to model the mechanical behaviors of the GNMGCs that contain the micro-sized grains and boundaries. The constitutive models that incorporate explicitly the FV variations [49,50,51,52,53] are used in the FEMs. We assign the FV values at the mesh element according to certain spatial distributions, such as those following size gradient structures of Voronoi grains. In the FEMs, all elements are square, and the side length is designated as d = 0.1 μm. By distributing different FV densities and in the grains or matrix, and grain boundaries, we can make a GNMGC heterogeneous structure in the spatial patterns. The FV density in grains can be drawn from the statistical uniform distribution, which is obtained via the transformation of the beta distribution, 0.04*Beta(1,1) + 0.03, and the mean FV density for the grains is 0.05 in the monolithic MG [52,53]. The range of the FV within grain is limited from 0.03 to 0.07. The FV values at the boundary are from 0.01 to 0.10, so we can see how the boundaries affect the overall mechanical properties with the FV change from small (=0.01), or “hard” boundaries, to larger (=0.10), or “soft” boundaries. The width W of grain boundary can be measured by the number of elements across the boundary, so W is expressed as a multiple of d. The narrowest boundary has the width with only one element, i.e., W = 1. W is taken as 1, 2, or 3. For the equivalent grain size D, the wider the grain boundary is, the larger the fraction of grain boundary is, and vice versa.
As equivalent grain size D is changed along the cross section, we can quantify and measure the mean gradient of GNMGCs. Figure 1 shows the GNMGC samples with the mean gradient of 0 (Figure 1(a-1)), 0.29 (Figure 1(b-1)), and 0.42 (Figure 1(c-1)). These gradients are labeled as Gradient-0, Gradient-A, and Gradient-B, respectively. For the samples labeled Gradient-0 with boundary width W = 1, 2 and 3, the boundary fractions are 7.20%, 14.11%, and 20.87%, respectively; For the samples labeled Gradient-A with boundary width W = 1, 2, and 3, the boundary fractions are 7.40%, 14.34%, and 21.08%, respectively; for the samples labeled Gradient-B with boundary width W = 1, 2, and 3, the boundary fractions are 7.69%, 14.56%, and 21.21%, respectively. In Figure 1, the larger the size gradient is, the larger the size distribution range is. The Gradient-B samples have the largest grain size and the smallest grain size. Figure 1(a-2,b-2,c-2) and Figure 1(a-3,b-3,c-3) present the distributions of the boundary fraction and the average sizes along the cross section. Since the volume fraction f of the boundary phases is related to the boundary width W and grain size D by f~W/D. For a given interface width, the boundary fraction increases as the equivalent grain size decreases. For the Gradient-0 sample with boundary width W = 3, the average boundary fraction is about 21.5%, and the average grain size D is about 15; for the Gradient-A sample with boundary width W = 3, the average boundary fractions range from 7.0% to 42.5%, and the grain size ranges from 8 to 44; for the Gradient-B sample with boundary width W = 3, the average boundary fractions range from 4.8.0% to 60.0%, and the grain size varies from 3 to 60. In our previous work [37,38,39], we have demonstrated the size effect of the grain and the boundary effect: the overall strength in the NMGCs can either increase or decrease with the grain size change, which depends sensitively on the boundary parameters, namely, W and . If the boundaries are harder or have lower FV density , the decreasing grain size induces hardening (increase in yield stress, peak stress, and flow stress). In addition, this trend becomes more dramatic when the boundary width W becomes wider. For the softer boundary one, the strengths increase as the grain sizes increase. In this work, we further explore the size gradient effect in the GNMGC.
As shown before, the choice of these parameters allows us to carry out a systematic and quantitative investigation of the size gradient effect on the mechanical property of the GNMGCs. To obtain the mechanical properties of the samples, we use an elastoplastic constitutive model that incorporates FV as an internal state variable. The deformation strain in this model includes an elastic and a plastic part, , where is the elastic strain. We obtain the plastic strain from the plastic flow equation , where g is the plastic potential function, , is the plastic deformation parameter related to FV change, is the Cauchy stress, and is the first invariant of the stress tensor , and is the second invariant of the deviatoric stress. The effective stress and increment of equivalent plastic strain are obtained through the relations and , where , and are constant and for the associated flow rule. The plastic strain is a function of the FV production via the relation and , where is the mean FV, a geometrical factor close to 1, the hard-sphere volume of the atom, the Boltzmann constant, the atomic volume, the equivalent shear stress, the activation energy, the frequency of atomic vibration, temperature, and the number of atomic jumps needed to annihilating a free volume equal to , which ranges between 3 and 10, and , where is the Young’s modulus and Poisson ratio, and a free volume gradient coefficient. By solving the equations of FV evolution and the strain and stress under a given external load, we can obtain the mechanical properties of GNMGCs containing various FVs in boundaries and different size gradients. The material-related parameters pertaining to the constitutive models, i.e., , are implemented in ABAQUS 6.13 finite element software through a UMAT subroutine [51,52,53]. The material properties of bulk Zr41.25Ti13.75Ni10Cu12.5Be22.5 MG are used [52]. The systems have a total number of 90,000 regular elements and the periodic boundary conditions. Plane strain tensile loadings are applied with an effective strain rate of 0.1/s.
3. Results and Discussion
The tensile stress–strain relations of all systems with different size gradients and various characteristics of the boundary are shown in Figure 2. Results corroborate our early finding that boundary networks with FV density of 0.01 (or harder boundary) enhance the strength of the composite (as illustrated by the blue lines, violet lines, and olive lines in Figure 2). Conversely, softer boundaries with FV density of 0.10 lead to a reduction in composite strength (as illustrated by the red lines, orange lines, and magenta lines in Figure 2) as compared to that in the monolithic sample (as represented by the black lines in Figure 2). This is evidenced by changes observed in stress parameters such as yield stress, first peak stress, and flow stress. The yield stress is determined by the 0.2% strain offset method. The peak stress is taken at the first occurrence of extreme stress. The flow stress is the asymptotic stress value at the large deformation strain. It is important to note that this definition excludes scenarios in which work hardening occurs, as under such conditions, flow stress cannot be accurately defined. Here the flow stress is defined as the stress that corresponds to the strain 0.1. In Figure 2, the flow stresses of GNMGCs with the harder boundary increase with the increase in the size gradient, and this trend becomes more pronounced as boundary width W expands wider. Notably, when employing a harder boundary width of W = 3, an observable saddle-shaped curve emerges, along with a noticeable strengthening trend following the peak stress point.
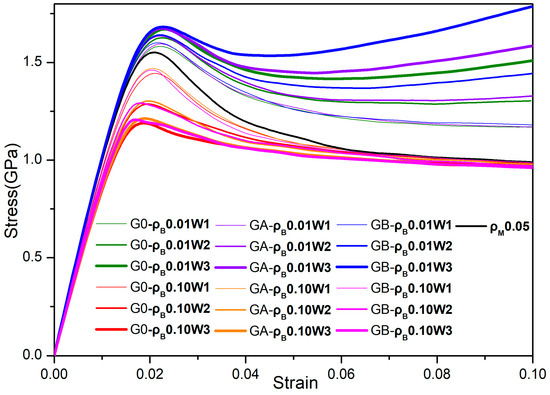
Figure 2.
The stress–strain curves for GNMGCs with the soft boundary ( = 0.10) and the hard boundary ( = 0.01), grain density ( = 0.05), and boundary width W = 1, 2, and 3, with different equivalent grain sizes gradient of 0 (G0), 0.125 (GA), and 0.180 (GB). The black line with the legend of “0.05” is for the monolithic MG.
On the other hand, GNMGC samples with the softer boundary exhibit minimal variation in flow stresses despite changes in the size gradient. As illustrated in Figure 2, following the yield points, the modulus exhibits an increase corresponding to a rise in the size gradient. This phenomenon suggests that size gradients play a crucial role in regulating the temporal evolution of stress and consequently delaying the onset of shear banding.
The general trend of the change in strengths and their corresponding strains versus the grain size gradient can be extracted in Figure 3. Compared with the monolithic MG, the hard boundary enhances the strength (yield and peak stress), while the soft boundary results in a reduction in strength. This trend becomes increasingly pronounced as the width or fraction of the boundary increases. As shown in Figure 3a,b, one can see the strengths (yield and peak stress) of all GNMGC samples quantitatively increase with an increasing grain size gradient. Figure 3c indicates that the yield strains of all samples also show an increase as the size gradient rises; however, the strain corresponding to the first peak stress decreases with an increase in the size gradient, as depicted in Figure 3d. For the GNMGC samples with harder boundaries, the strains corresponding to the strength (yield and first peak stress) are larger than the ones of the monolithic MG. The larger the fraction or width of the grain boundary, the larger the strains corresponding to the strength. In Figure 3e, GNMGC samples with the softer boundary exhibit minimal variation in flow stresses despite changes in the size gradient and boundary width, while the samples with the harder boundary show the flow stress is proportional to the size gradient, and an increase in boundary width will enhance and amplify the trend.
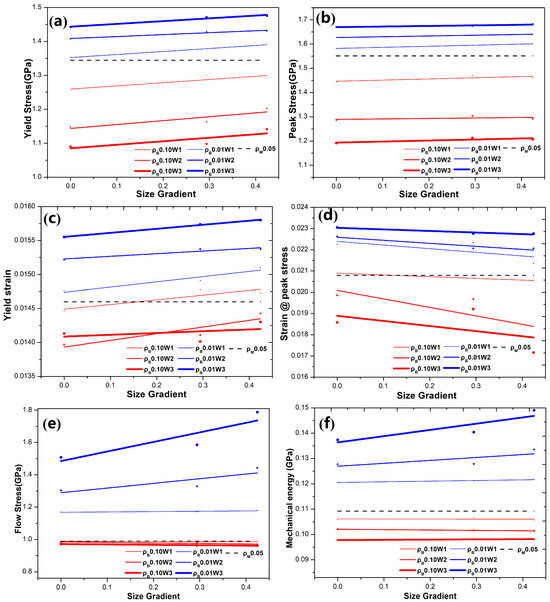
Figure 3.
The mechanical strengths (yield stress (a) and peak stress (b)) and their corresponding yield strains (c), their corresponding strains at first peak stress (d), flow stress (e), and mechanical energy per unit volume (f) versus the size gradient. The red lines are for GNMGCs samples with soft boundary with = 0.10 and the blue lines are for GNMGCs samples with hard boundary with = 0.01. The black line with the legend of “0.05” is for the monolithic MG.
For GNMGC samples with harder and wider boundaries, after reaching the first peak point, the stress shows a saddle-shaped curve, as illustrated in Figure 2. The finding implies that the saddle point will completely vanish when the specific grain size gradient, the grain size, and the width of the hard boundary are optimized. The variation in toughness with increasing size gradient can be quantitatively assessed by calculating the area (mechanical energy per unit volume) under the stress–strain curve up to the final strain, as illustrated in Figure 3f. For the GNMGC samples with a hard boundary, the mechanical energies increase as the size gradient increases and are larger than the one of the comparing MG. In contrast, for the GNMGC samples with a specific width of soft boundary, the mechanical energies remain relatively constant despite variations in the size gradient.
The enhancement in strength and toughness indicates new deformation mechanisms in the GNMGCs originating not only from the size gradient effect but also from the size effect of grain and interface effect (width, FV density, and orientation of boundary). To investigate the new deformation mechanism of GNMGCs, the spatial FV distributions (-1), strain (-2), and stress (-3) of all systems under applied strain states are examined to analyze the behaviors of local shear in Figure 4. In the following, we present a detailed examination of GNMGCs with the boundary width W = 3 under 10% tensile strain. Figure 4a,c,e show the final state of systems (Gradient-0, Gradient-A, and Gradient-B) with the soft boundary. We observe that the shear banding occurs predominantly in the softer boundary regions, with shear bands initiating and growing only in a few boundaries that have orientations closely aligned with the direction of maximum shear stress during the deformation. In the small size region, the orientation of the boundary is randomly distributed. In contrast, in the large-grained zones, there exist several individual orientations. For the systems with large size gradients (Figure 4c,e), the primary mature shear bands are predominantly located within the large-grained zones. As the shear bands propagate toward the conjunction point along the soft boundary, they will be impeded by the grain interiors and subsequently traverse through the grain as the stress concentrations reach a sufficiently high level. The obstacle of SBs leads to the enhancement of the strength. As we mentioned the size effect of samples with soft boundaries or interfaces, the strengths increase as the grain sizes increase. The large-grained zones contribute to an increase in strength, whereas small-grained zones may result in a reduction in strength. The synthetic effect results from the temporal and spatial stress localization. We will discuss and elucidate the synthetic effect induced by the stress localization later.
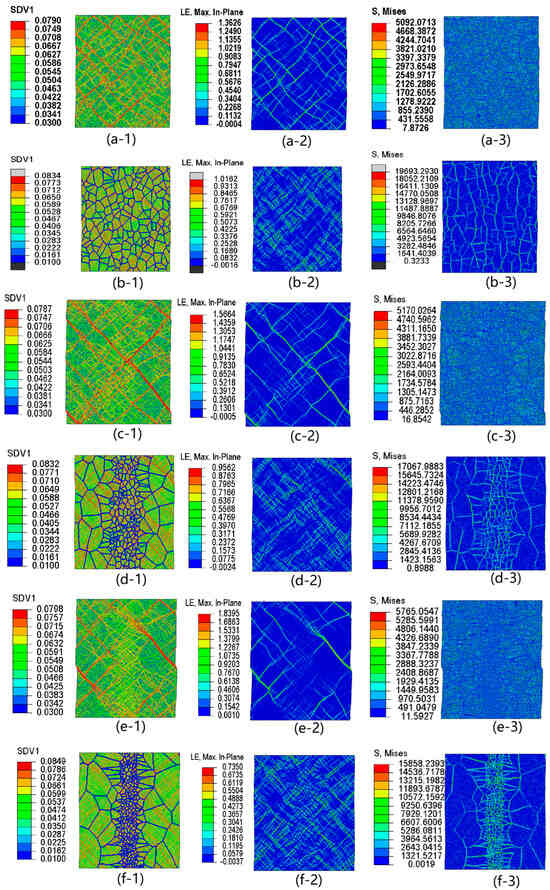
Figure 4.
Contour plots for free volume (-1), shear strain (-2) and shear stress (-3) for system Gradient-0 (a,b), Gradient-A (c,d), and Gradient-B (e,f) with the soft boundary with = 0.10 (a,c,e) and the hard boundary with = 0.01 (b,d,f) and with boundary width W = 3 under 10% tensile strain. The color scheme is shown on the left of each figure.
Figure 4b,d,f show the final states of systems with the hard boundary. In the strain contour plot (-2), the shear banding is indeed initiated and contained inside the grains, and the internal stresses are carried out by the hard boundaries during deformation. The hard boundary confines SBs within the grains during the deformation. The non-propagating local strain in the grains contributes to both hardening and toughness. The hard boundaries can effectively bear the primary load and absorb deformation energy. As we mentioned the size effect of samples with hard boundaries, the strength increases as the grain sizes decrease. Figure 4(b-3) demonstrates a uniform stress distribution along the boundaries, whereas the gradient structures result in a localized distribution of the primary stress in Figure 4d,f.
The synthetic effect on the size gradient arises from the temporal and spatial stress localization. Figure 5 shows the distribution of stress along the cross section under various applied strain states for the systems Gradient-0 (a), Gradient-A (b), and Gradient-B (c) with the soft boundary ( = 0.10) and the hard boundary ( = 0.01), alongside a boundary width W = 3. Figure 5(a-1,a-2) show that the profiles of the average stress along the cross section remain flat. Figure 5(b-2,c-2) show that the profiles of the average stress are similar to the distribution profile of the boundary fraction, whereas Figure 5(b-1,c-1) exhibit the trends that are opposite to those observed in the boundary fraction profile. For the samples with the soft boundary, the stress reaches the maximum value at the first peak point and subsequently decreases as the deformation continues. For the sample with the hard boundary, the fluctuating variation in stress increases as the larger deformation increases. The larger the size gradient, the larger the stress on the small-grained region for the sample with a hard boundary during severe deformation, while the stress on the large-grained region remains relatively constant.
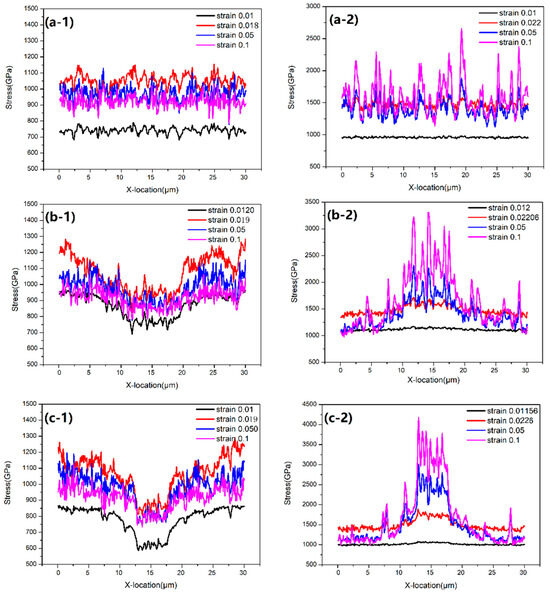
Figure 5.
The distribution of stress along the cross section at different applied strain states for system Gradient-0 (a), Gradient-A (b), and Gradient-B (c) with the soft boundary of = 0.10 (-1) and the hard boundary of = 0.01 (-2), alongside a boundary width W = 3.
For the samples with a hard boundary, the gradient structure of GNMGC exhibits elastically homogeneous but plastically heterogeneous characteristics. This phenomenon results in a macroscopic stress gradient. The gradient structures convert the simple uniaxial stress to complicated stresses owing to the incompatible deformation. Consequently, the spatial gradient of the stress may delay the nucleation and obstacle propagation of SBs, thereby inducing the increase in strengths (yield stress and peak stress). The deformation mechanism of GNMGC with a hard boundary will be revealed as follows. In the first stage, the systems of GNMGC deform elastically. In the second stage, the small-grained boundary begins to bear larger stress than that of the large-grained boundary. The wider boundary leads to more boundary fraction and thereby enhances the phenomenon. Therefore, the SBs will nucleate in the large grains prior to their nucleation in the small grains. In the last stage, both large- and small-grained zones undergo plastic deformation, which induces more contained SBs. The propagation of mature SBs within grain interiors will result in the abrupt stress drop; simultaneously, the SB contained by the hard boundary will store the energy and increase the local concentrated stress at the interface region until the mature SBs break through the interfaces and propagate into the adjacent new grains. The large-grained zone will have more contained SBs than the small-grained zone. Additionally, as illustrated in Figure 5(b-2,c-2), boundaries of smaller grains exhibit higher concentrations of localized stress.
For the samples with soft boundaries, the systems also deform elastically during the first stage. However, as the size gradient increases, the duration of this first stage becomes shorter and diminishes. In the second stage, the small-grained boundary begins to deform plastically prior to the deformation in the boundaries of large grains. The abrupt stress drop by the propagation of mature SBs in the boundary will lead to a spatial stress–gradient as shown in Figure 5(b-1,c-1). The propagation of SBs will be influenced by the orientation of the soft boundary and then be stopped by the grain zones, which contain low FV. The large-grained zone will induce more localized strain than the small-grained zone because more orientations are close to the direction of maximum shear stress during the deformation and rotation. In the third stage, the SBs will propagate toward the conjunction point along the soft boundaries. This propagation will continue if the orientation of the neighboring boundary is close to the preceding one; otherwise, they will be obstructed by the adjacent grain and subsequently traverse through the neighboring grain when the stress concentrations reach sufficiently high levels at the boundary or junction point. The propagation of mature SBs within the large-grained zone will lead to a more abrupt stress drop than the one in the small-grained zone.
We here reveal four key parameters that underpin the mechanical property of GNMGCs: the gradient of grain size, as well as the width, the orientation, and the density of boundaries. The synergistic gradient effects arising from heterogeneous grain sizes and interface characteristics can enhance both strength and toughness, especially in the GNMGCs with hard boundary. The gradient microstructure induces significant temporal and spatial stress localization, which can modulate the generation and propagation of shear bands and the evolution of FV or microstructure. The orientation of a soft boundary affects the propagation of mature SBs, while the orientation of a hard boundary effectively alters the distribution of principal stresses. Additionally, the wider boundary enhances the synergistic gradient effects generated by grain size gradient and interface characteristics.
4. Conclusions
Using finite element modeling, we can obtain the mechanical properties of GNMGCs with different size gradients and interface properties to quantitatively investigate the influences of the gradient structural factors on their mechanical properties and the mechanisms of shear banding. The gradient microstructure can tune the generation and propagation of SBs through the temporal and spatial stress localization. A larger gradient at the hard boundary results in a greater stress gradient and higher stress on the boundary during severe deformation. Conversely, a larger gradient at the soft boundary leads to an increased stress gradient but lower stress on the boundary under similar conditions of severe deformation. To understand the microscopic mechanisms of GNMGCs, it is important to note that the creation or annihilation of FV on the boundary or shear band is generally happening at the plastic deformation. Our findings indicate that size gradient architecture of GNMGCs can combine with the width and orientation of the boundary and then indeed achieve simultaneous strengthening and toughening. By elucidating the micro-scale mechanics of GNMGC systems, we provide foundational insights for designing GNMGC with tunable deformation modes and fundamental understanding of shear banding. The quantitative framework correlating structure parameters and mechanical properties demonstrates that optimally designed GNMGCs achieve increases in strength and toughness even lead to work hardening. We anticipate that experimental results will validate our simulated or theoretical findings, as improved techniques will produce GNMGCs with robust glassy interfaces in the future.
Author Contributions
Y.W.: Writing—review and editing, writing—original draft, investigation, formal analysis, data curation, and funding acquisition. G.Z.: Writing—review and editing, writing—original draft, investigation, formal analysis, and data curation. M.L.: Writing—review and editing, validation, supervision, resources, project administration, methodology, investigation, Formal analysis, and conceptualization. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Fundamental Research Funds for the Central Universities (FRF-TP-20-028A1, FRF-BD-25-002 and No. FRF-BD-23-02) and the Fundamental Research Funds for the Central Universities and The Youth Teacher International Exchange & Growth Program (QNXM20210044), and the Research Grants Council of Hong Kong Special Administrative Region, China (grant number 15233823).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
Y.W. Wang thanks his daughter JIALV for the mental support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Klement, W.I.; Willens, R.H.; Duwez, P. Non-crystalline structure in solidified gold-silicon alloys. Nature 1960, 187, 869–870. [Google Scholar] [CrossRef]
- Greer, A.L. metallic glasses on the threshold. Mater. Today 2009, 12, 14–22. [Google Scholar] [CrossRef]
- Kumar, G.; Rector, D.; Conner, R.D.; Schroers, J. Embrittlement of Zr-based bulk metallic glasses. Acta Mater. 2009, 57, 3572. [Google Scholar] [CrossRef]
- Scudino, S.; Jerliu, B.; Pauly, S. Ductile bulk metallic glasses produced through designed heterogeneities. Scr. Mater. 2011, 65, 815–818. [Google Scholar] [CrossRef]
- Demetriou, M.D.; Launey, M.E.; Garrett, G.; Schramm, G.P.; Hofmann, D.C.; Johnson, W.L.; Ritchie, R.O. A damage-tolerant glass. Nat. Mater. 2011, 10, 123–128. [Google Scholar] [CrossRef]
- He, Q.; Shang, J.K.; Ma, E.; Xu, J. Crack-resistance curve of a Zr-Ti-Cu-Al bulk metallic glass with extraordinary fracture toughness. Acta Mater. 2012, 60, 4940–4949. [Google Scholar] [CrossRef]
- Choi-Yima, H.; Johnson, W.L. Bulk metallic glass matrix composites. Appl. Phys. Lett. 1997, 71, 3808–3810. [Google Scholar] [CrossRef]
- Conner, R.D.; Dandliker, R.B.; Johnson, W.L. Mechanical properties of tungsten and steel fiber reinforced Zr41.25Ti13.75Cu12.5Ni10Be22.5 metallic glass matrix composites. Acta Mater. 1998, 46, 6089–6102. [Google Scholar] [CrossRef]
- Kim, C.P.; Busch, R.; Masuhr, A.; Choi-Yim, H.; Johnson, W.L. Processing of carbon-fiber-reinforced Zr41.2Ti13.8Cu12.5Ni10.0Be22.5 bulk metallic glass composites. Appl. Phys. Lett. 2001, 79, 1456–1458. [Google Scholar] [CrossRef]
- Hofmann, D.C.; Suh, J.Y.; Wiest, A.; Duan, G.; Lind, M.L.; Demetriou, M.D.; Johnson, W.L. Designing metallic glass matrix composites with high toughness and tensile ductility. Nature 2008, 451, 1085–1089. [Google Scholar] [CrossRef] [PubMed]
- Hays, C.C.; Kim, C.P.; Johnson, W.L. Microstructure Controlled Shear Band Pattern Formation and Enhanced Plasticity of Bulk Metallic Glasses Containing in situ Formed Ductile Phase Dendrite Dispersions. Phys. Rev. Lett. 2000, 84, 2901–2904. [Google Scholar] [CrossRef]
- Das, J.; Tang, M.B.; Kim, K.B.; Theissmann, R.; Baier, F.; Wang, W.H.; Eckert, J. “Work-hardenable” ductile bulk metallic glass. Phys. Rev. Lett. 2005, 94, 205501. [Google Scholar] [CrossRef]
- Fan, J.; Yan, Z.; Eckert, J.; Rao, W.; Qiao, J.; Zhou, D. Effect of cold rolling on the microstructure and plastic deformation behavior of Ti41Zr32Ni6Ta7Be14 metallic glass matrix composites. J. Alloys Compd. 2025, 1032, 81248. [Google Scholar] [CrossRef]
- Hofmann, D.C. Bulk Metallic Glasses and Their Composites: A Brief History of Diverging Fields. J. Mater. 2013, 2013, 517904. [Google Scholar] [CrossRef]
- Sun, Y.F.; Wei, B.C.; Wang, Y.R.; Li, W.H.; Cheung, T.L.; Shek, C.H. Plasticity-improved Zr-Cu-Al bulk metallic glass matrix composites containing martensite phase. Appl. Phys. Lett. 2005, 87, 051905. [Google Scholar] [CrossRef]
- Pauly, S.; Das, J.; Bednarcik, J.; Mattern, N.; Kim, K.B.; Kimd, D.H.; Eckert, J. Deformation-induced martensitic transformation in Cu-Zr-(Al,Ti) bulk metallic glass composites. Scr. Mater. 2009, 60, 431–434. [Google Scholar] [CrossRef]
- Fan, L.; Yang, Y.; Geng, J.; Zhang, S.; Cao, Y.; Shi, B. Mechanical properties of gradient metallic glass induced by spatially non-uniform dynamics. J. Non-Cryst. Solids 2025, 654, 1237449. [Google Scholar] [CrossRef]
- Lu, Y.; Su, S.; Zhang, S.; Huang, Y.; Qin, Z.; Lu, X.; Chen, W. Controllable additive manufacturing of gradient bulk metallic glass composite with high strength and tensile ductility. Acta Mater. 2021, 206, 116632. [Google Scholar] [CrossRef]
- Wan, R.; Long, Z.; Cui, Y.; You, L. Achieving controllable strength-plasticity balance in metallic glass: Potential energy gradient. Intermetallics 2025, 181, 108757. [Google Scholar] [CrossRef]
- Fan, J.; Chen, A.; Fu, M.; Lu, J. A novel structural gradient metallic glass composite with enhanced mechanical properties. Scr. Mater. 2009, 6, 608–611. [Google Scholar] [CrossRef]
- Wang, Y.W.; Li, M.; Xu, J.W. Free volume gradient effect on mechanical properties of metallic glasses. Scr. Mater. 2017, 130, 12–16. [Google Scholar] [CrossRef]
- Hutchingson, J.W. Shear band formation in plane strain. Int. J. Solids Struct. 1981, 17, 451. [Google Scholar] [CrossRef]
- Li, X.; Li, G.; Ma, J.; Cao, Y.; Xu, Y.; Ming, W. Progress in the preparation, forming and machining of metallic glasses. J. Manuf. Process. 2024, 117, 244–277. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, D.Q.; Song, W.L.; Wang, H.; Zhang, Z.Y.; Ma, D.; Wang, X.L.; Lu, Z.P. Ductilizing Bulk Metallic Glass Composite by Tailoring Stacking Fault Energy. Phys. Rev. Lett. 2012, 109, 245506. [Google Scholar] [CrossRef]
- Hofmann, D.C. Shape memory bulk metallic glass composites. Science 2010, 329, 1294–1295. [Google Scholar] [CrossRef]
- Liu, B.; Zhang, P.; Liu, Z.; Wu, D.; Jiang, Q.; Sun, T.; Liu, C.; Yan, H.; Shi, H.; Ma, S.; et al. Preparation of Zr-based metallic glasses gradient composites with designable amorphous fraction by laser powder bed fusion. J. Manuf. Process. 2024, 120, 506–516. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, Z.; Tang, Y.; Zhou, H. Unravelling the relation between free volume gradient and shear band deflection induced extra plasticity in metallic glasses. J. Mech. Phys. Solids 2024, 192, 105806. [Google Scholar] [CrossRef]
- Messick, C.; Li, L.; Homer, E. Examining the mechanics responsible for strain delocalization in metallic glass matrix composites. Comp. Mater. Sci. 2024, 244, 113253. [Google Scholar] [CrossRef]
- Zhou, F.; Du, C.; Cheng, C.; Xu, L.; Du, Z.; Gao, G.; Liu, A.; Fu, H. Penetration performance and fragmentation mechanism behind target of tungsten fibre/zirconium-based bulk metallic glass matrix composite rod. Int. J. Refract. Met. H. 2023, 112, 106160. [Google Scholar] [CrossRef]
- Sohrabi, S.; Fu, J.; Li, L.; Zhang, Y.; Li, X.; Sun, F.; Ma, J.; Wang, W.H. Manufacturing of metallic glass components: Processes, structures and properties. Prog. Mater. Sci. 2024, 144, 101283. [Google Scholar] [CrossRef]
- Wang, X.L.; Jiang, F.; Hahn, H.; Li, J.; Gleiter, H.; Sun, J.; Fang, J.X. Plasticity of a scandium-based nanoglass. Scr. Mater. 2015, 98, 40–43. [Google Scholar] [CrossRef]
- Wu, G.; Zhang, J.; Liu, C.; Wang, Q.; Lu, J. Ductility of an ultrastrong glass-crystal nano-dual-phase alloy in sub-micron. Scr. Mater. 2020, 183, 17–21. [Google Scholar] [CrossRef]
- Nandam, S.H.; Ivanisenko, Y.; Schwaiger, R.; Sniadecki, Z.; Mua, X.; Wang, D.; Chellali, R.; Boll, T.; Kilmametov, A.; Gleiter, H.; et al. Cu-Zr nanoglasses: Atomic structure, thermal stability and indentation properties. Acta Mater. 2017, 136, 181–189. [Google Scholar] [CrossRef]
- Guo, C.; Fang, Y.; Wu, B.; Lan, S.; Peng, G.; Wang, X.; Hahn, H.; Gleiter, H.; Feng, T. Ni-P nanoglass prepared by multi-phase pulsed electrodeposition. Mater. Res. Lett. 2016, 5, 293–299. [Google Scholar] [CrossRef]
- Cui, Z.; Pei, C.; Wu, S.; Fu, S.; Guo, C.; Fang, Y.; Yan, M.; Lan, S. Ultrastable Ni-P amorphous alloy formed via high temperature electrodeposition. J. Non-Cryst. Solids 2021, 551, 12039. [Google Scholar] [CrossRef]
- Sun, L.G.; Wu, G.; Wang, Q.; Lu, J. Nanostructural metallic materials: Structures and mechanical properties. Mater. Today 2020, 38, 114–135. [Google Scholar] [CrossRef]
- Wang, Y.W.; Gleiter, H.; Li, M. From patterning heterogeneity to nanoglass: A new approach to harden and toughen metallic glasses. MRS Bull. 2023, 48, 56–67. [Google Scholar] [CrossRef]
- Wang, Y.W.; Zheng, G.P.; Li, M. Manage local deformation by patterning structural heterogeneity: Controlling toughness in honeycomb patterned metallic glass composites. Mater. Des. 2025, 253, 113846. [Google Scholar] [CrossRef]
- Wang, Y.W.; Zheng, G.P.; Li, M. Orientation effects on strengthening mechanism of network-structured metallic glass composites and nanoglasses. J. Non-Cryst. Solids 2025, 666, 123702. [Google Scholar] [CrossRef]
- Li, X.; Lu, L.; Li, J.; Zhang, X.; Gao, H. Mechanical properties and deformation mechanisms of gradient nanostructured metals and alloys. Nat. Rev. Mater. 2020, 5, 706–723. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhou, H.; Lu, Q.; Gao, H.; Lu, L. Extra strengthening and work hardening in gradient nanotwinned metals. Science 2018, 362, 559. [Google Scholar] [CrossRef]
- Pan, Q.; Zhang, L.; Feng, R.; Lu, Q.; An, K.; Chuang, A.; Poplawsky, J.; Liaw, P.K.; Lu, L. Gradient cell-structured high-entropy alloy with exceptional strength and ductility. Science 2021, 374, 984–989. [Google Scholar] [CrossRef]
- Cheng, Z.; Bu, L.; Zhang, Y.; Wu, H.; Zhu, T.; Gao, H.; Lu, L. Unraveling the origin of extra strengthening in gradient nanotwinned metals. Proc. Natl. Acad. Sci. USA 2022, 119, 2116808119. [Google Scholar] [CrossRef]
- Pan, Q.; Yang, M.; Feng, R.; Chuang, A.; An, K.; Liaw, P.K.; Wu, X.; Tao, N.; Lu, L. Atomic faulting induced exceptional cryogenic strain hardening in gradient-cell-structured alloy. Science 2023, 382, 185–190. [Google Scholar] [CrossRef]
- Pan, Q.; Ding, K.; Guo, S.; Lu, N.; Tao, N.; Zhu, T.; Lu, L. Superior resistance to cyclic creep in a gradient structured steel. Science 2025, 388, 82–88. [Google Scholar] [CrossRef]
- Zeng, Z.; Li, X.; Xu, D.; Lu, L.; Gao, H.; Zhu, T. Gradient plasticity in gradient nano-grained metals. Extrem. Mech. Lett. 2016, 8, 213–219. [Google Scholar] [CrossRef]
- Yuan, S.; Branicio, P.S. Gradient microstructure induced shear band constraint, delocalization, and delayed failure in CuZr nanoglasses. Int. J. Plast. 2020, 134, 102845. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, M.; Wang, X.; Li, M. Gradient network architecture design induced strain delocalization and delayed failure in metallic glass matrix composites. Scr. Mater. 2023, 237, 115721. [Google Scholar] [CrossRef]
- Spaepen, F. A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Metall. 1977, 25, 407–415. [Google Scholar] [CrossRef]
- Argon, A. Plastic deformation in metallic glasses. Acta Metall. 1979, 27, 47–58. [Google Scholar] [CrossRef]
- Gao, Y.F. An implicit finite element method for simulating inhomogeneous deformation and shear bands of amorphous alloys based on the free-volume model. Modell. Simul. Mater. Sci. Eng. 2006, 14, 1329–1345. [Google Scholar] [CrossRef]
- Zhao, M.; Li, M. Interpreting the change in shear band inclination angle in metallic glasses. Appl. Phys. Lett. 2008, 93, 241906. [Google Scholar] [CrossRef]
- Wang, Y.W.; Li, M.; Xu, J.W. Toughen and harden metallic glass through designing statistical heterogeneity. Scr. Mater. 2016, 113, 10–13. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).