Numerical Analysis of the Three-Roll Bending Process of 6061-T6 Aluminum Profiles with Multiple Bending Radii Using the Finite Element Method
Abstract
1. Introduction
2. Materials and Methods
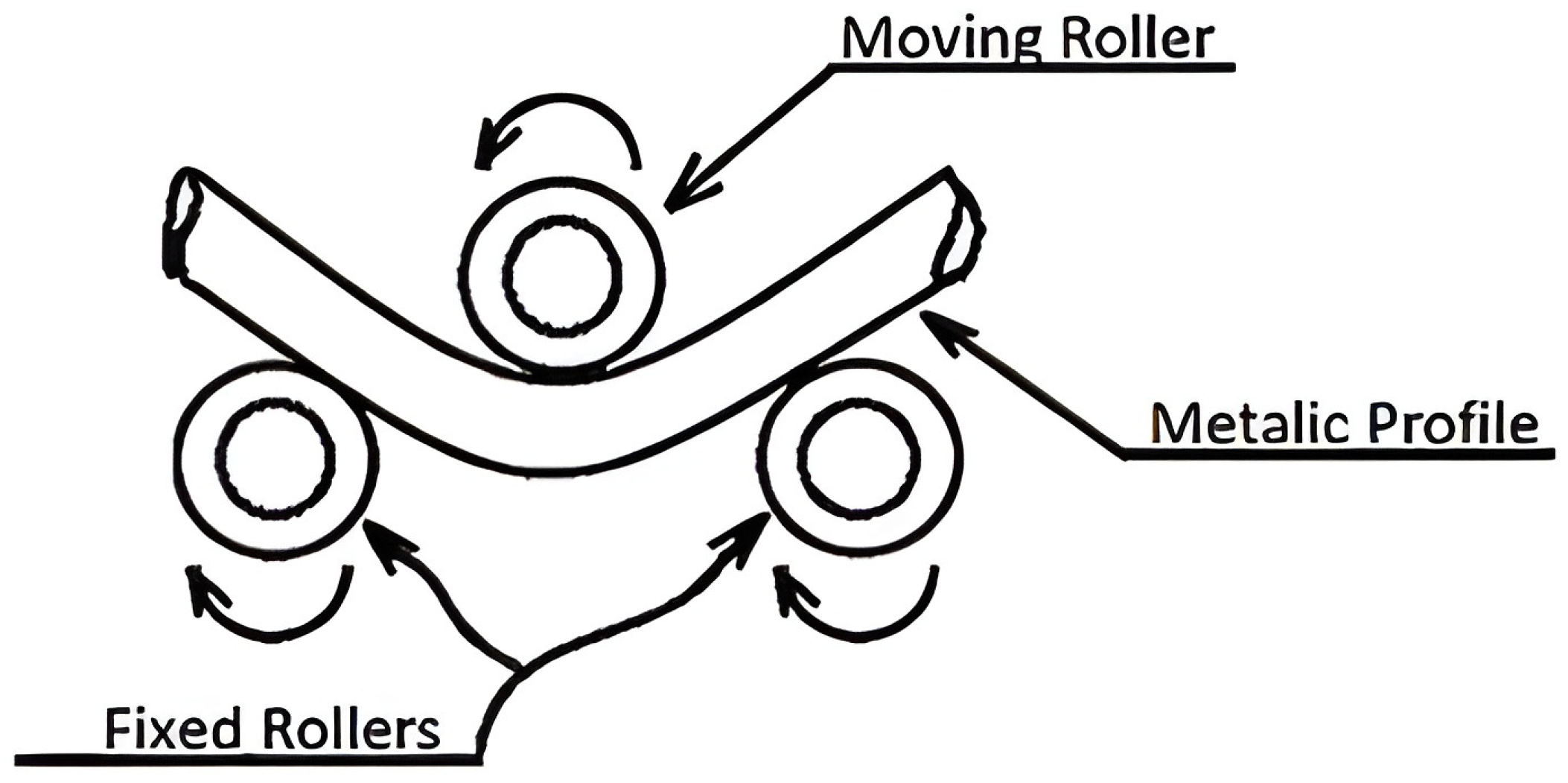
2.1. Roll Bending Process Fundamentals for a Pyramid Arrangement
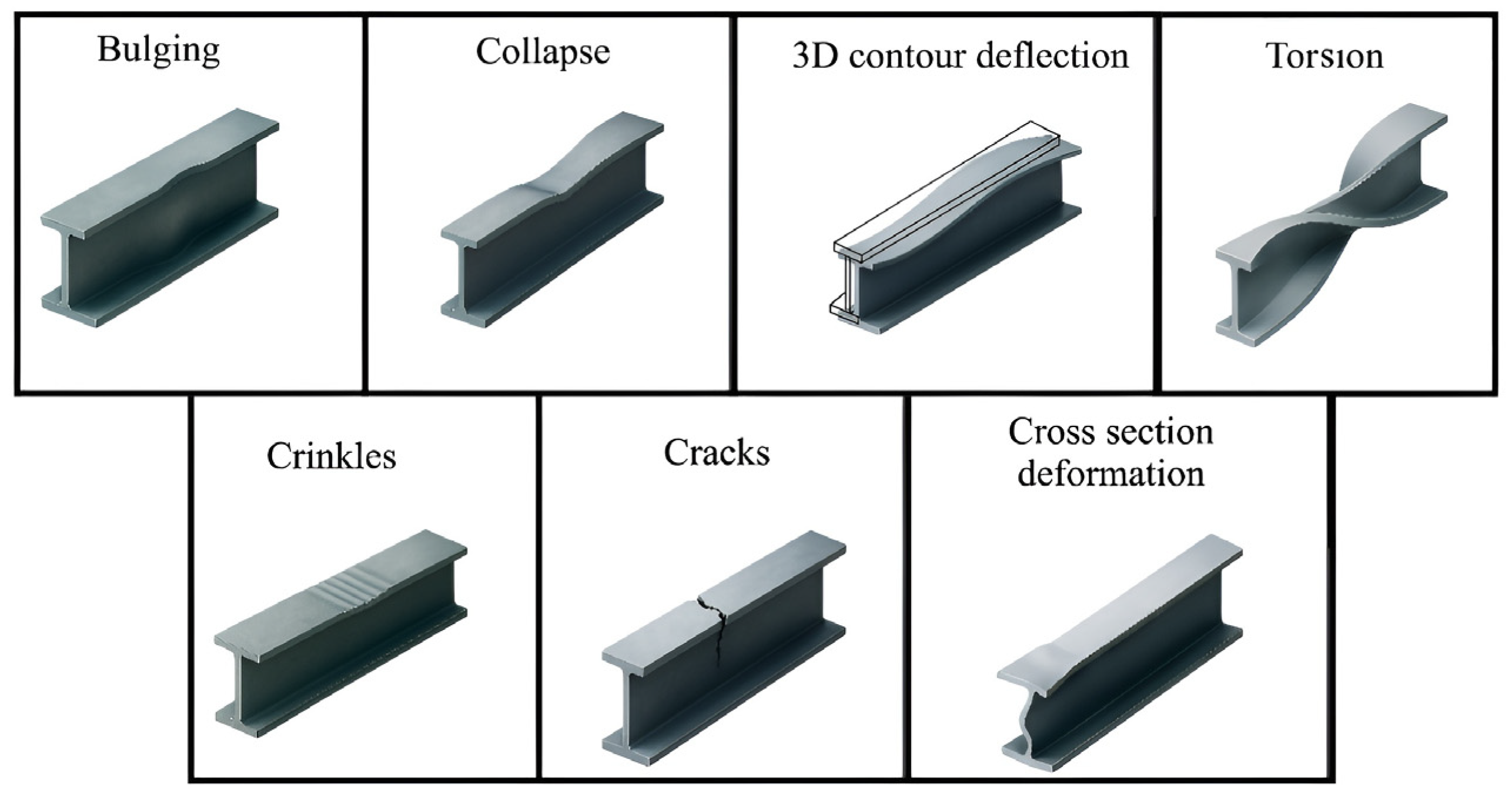
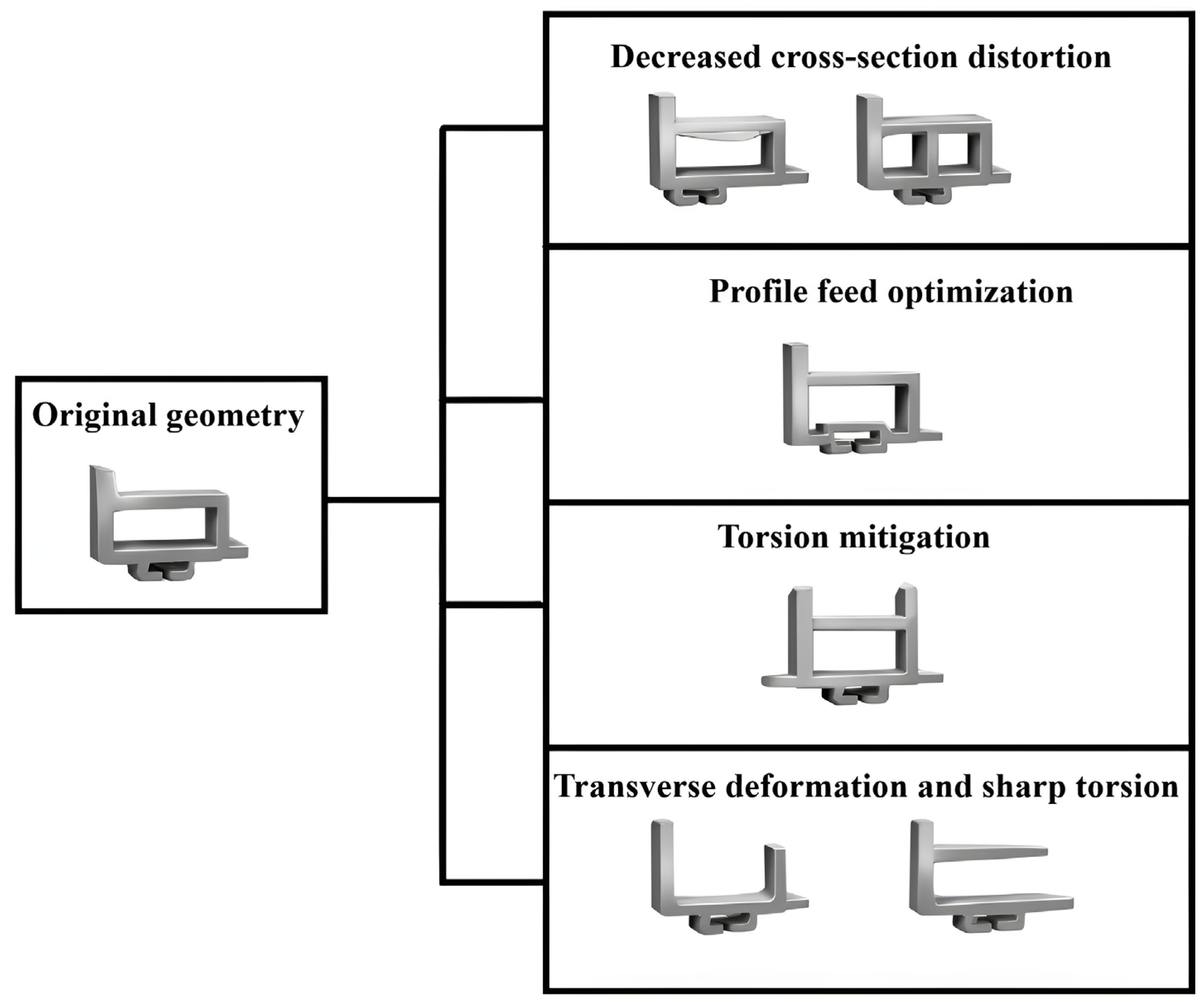
2.2. Origin, Typology, and Impact of Defects in Metal Profile Bending
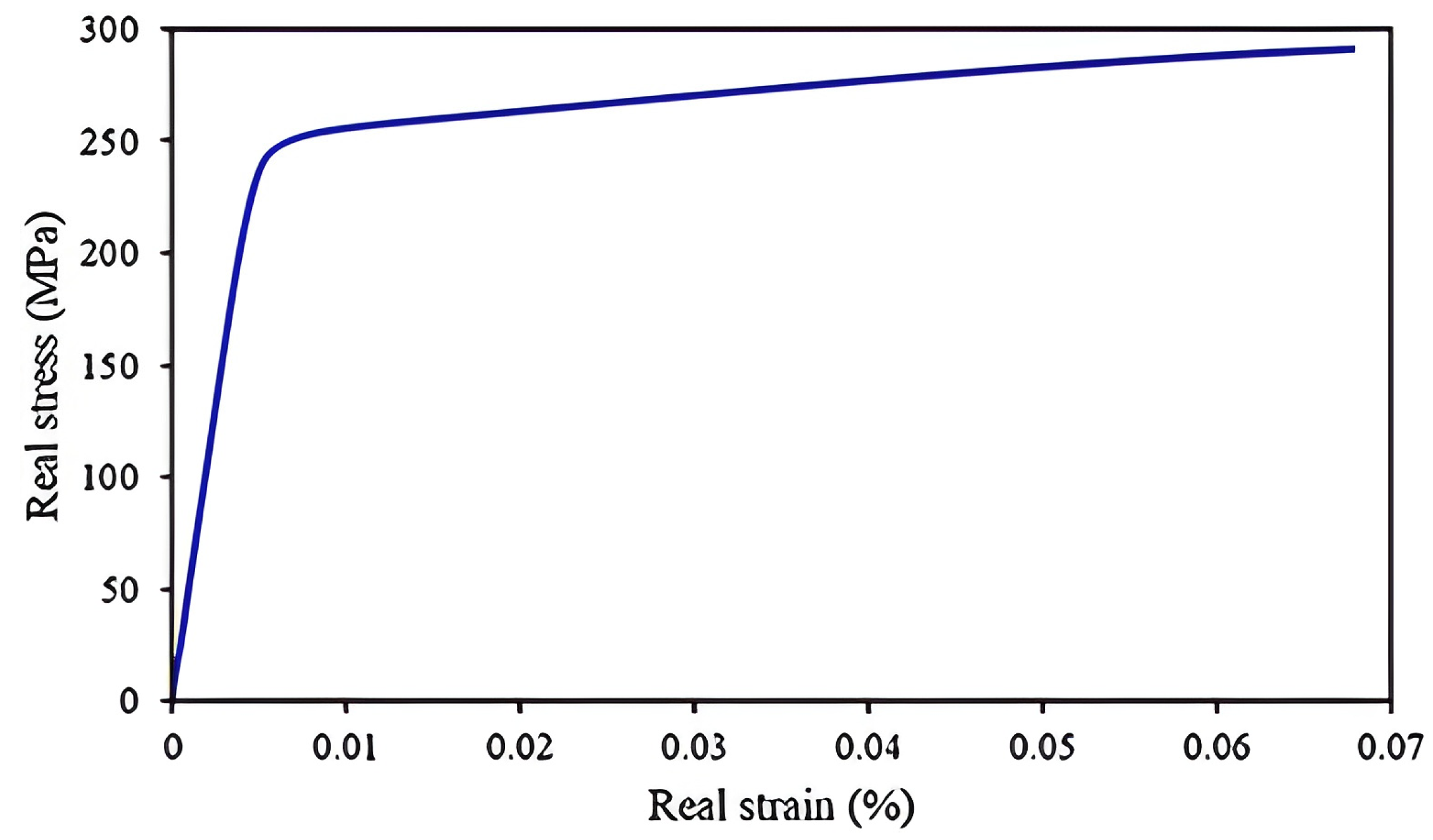
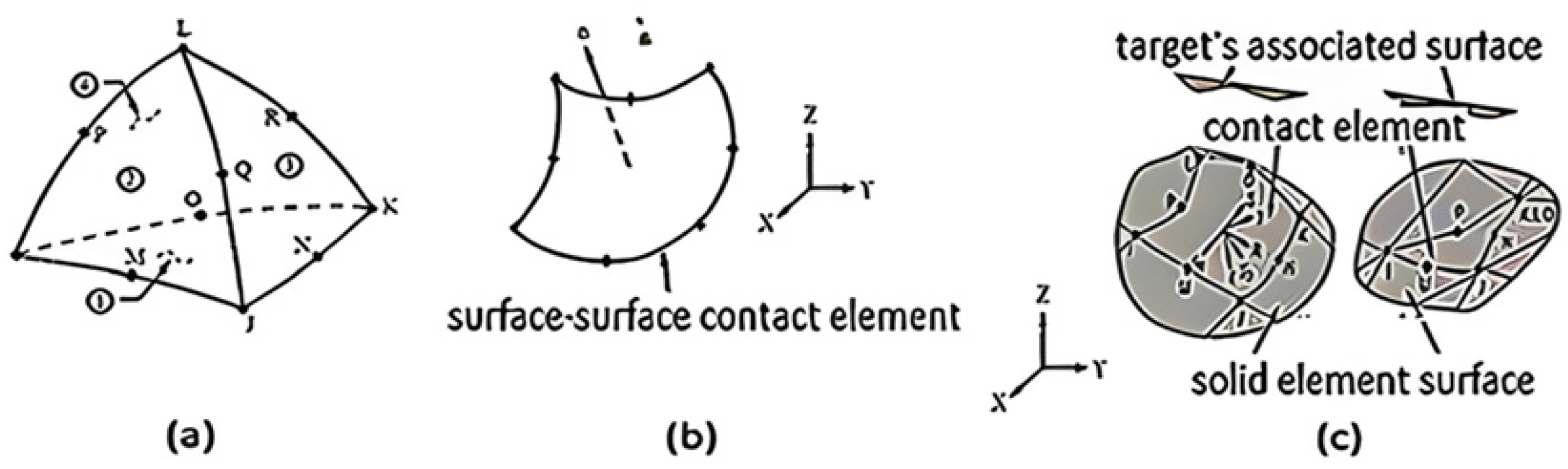
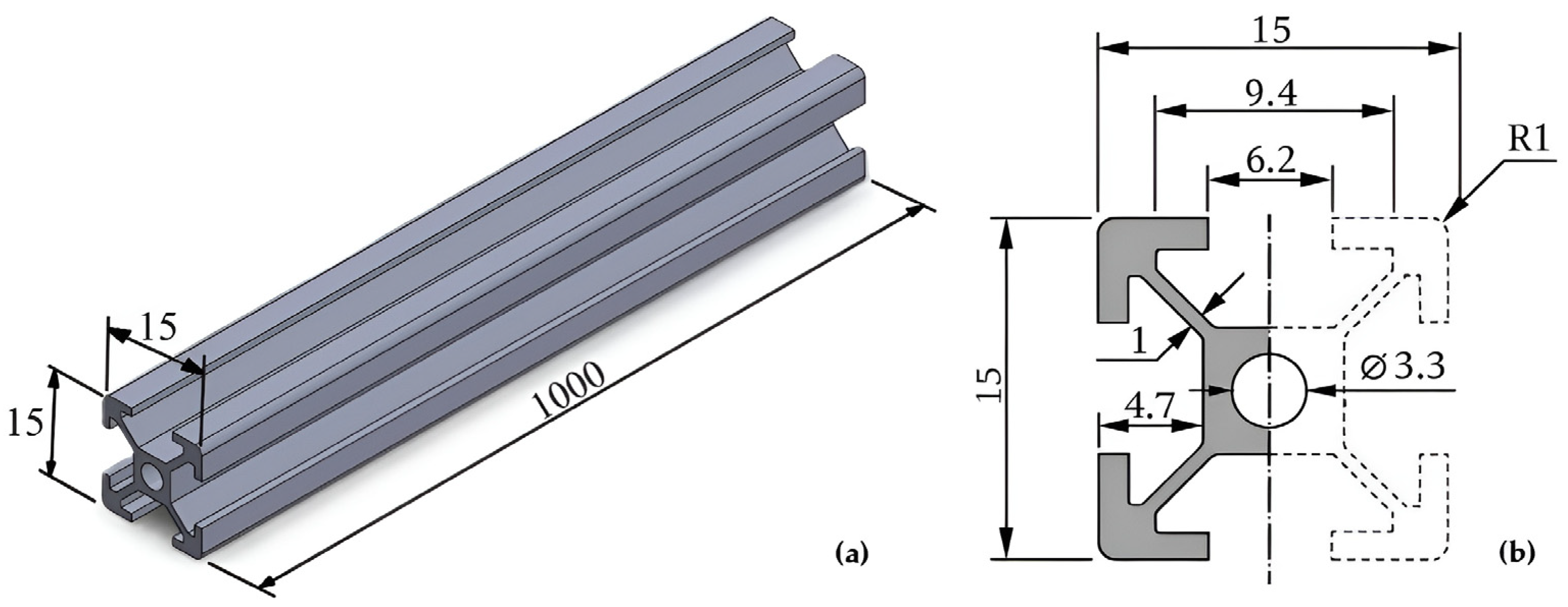
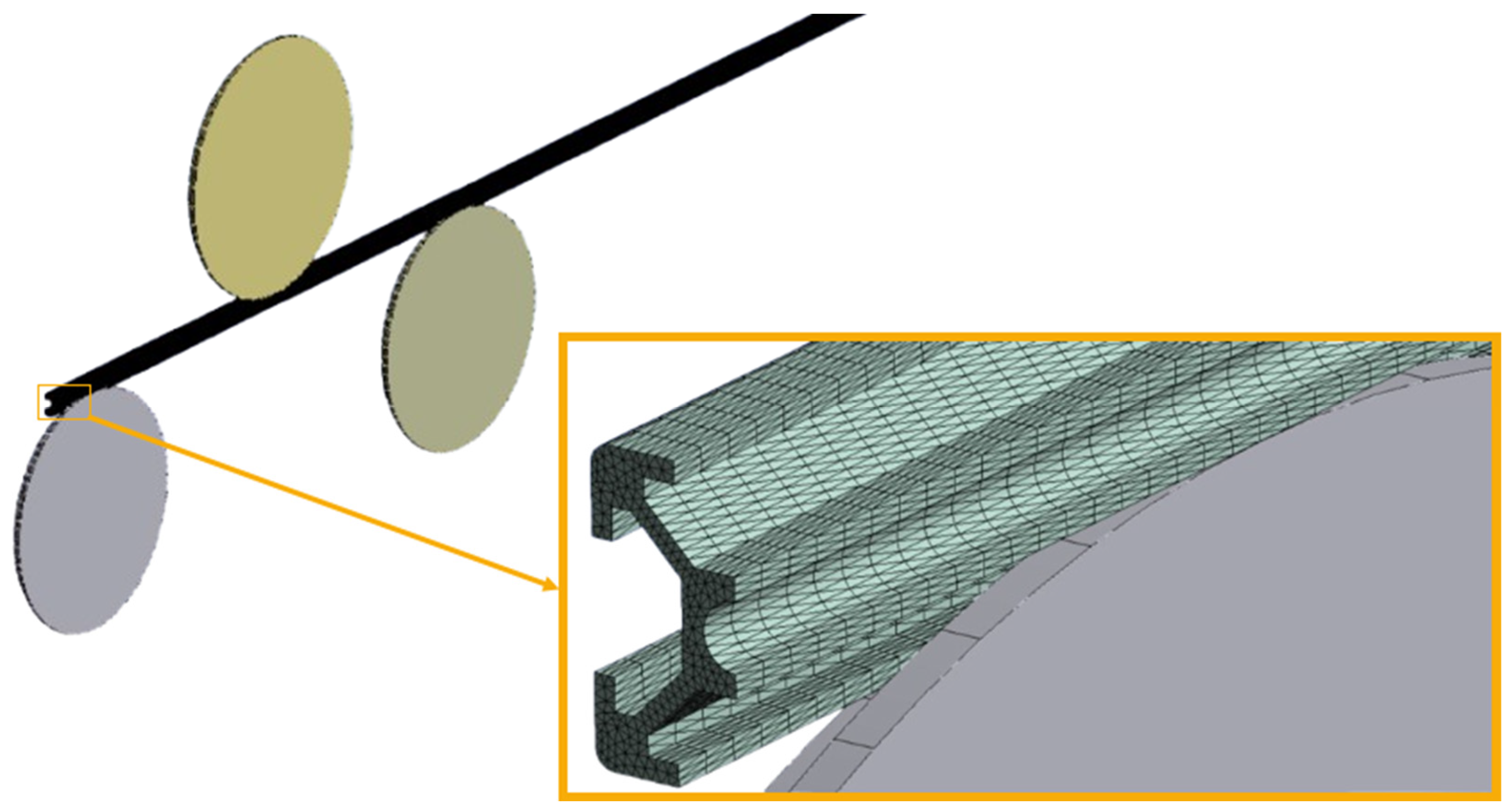
2.3. Computational Modeling
3. Results and Discussions
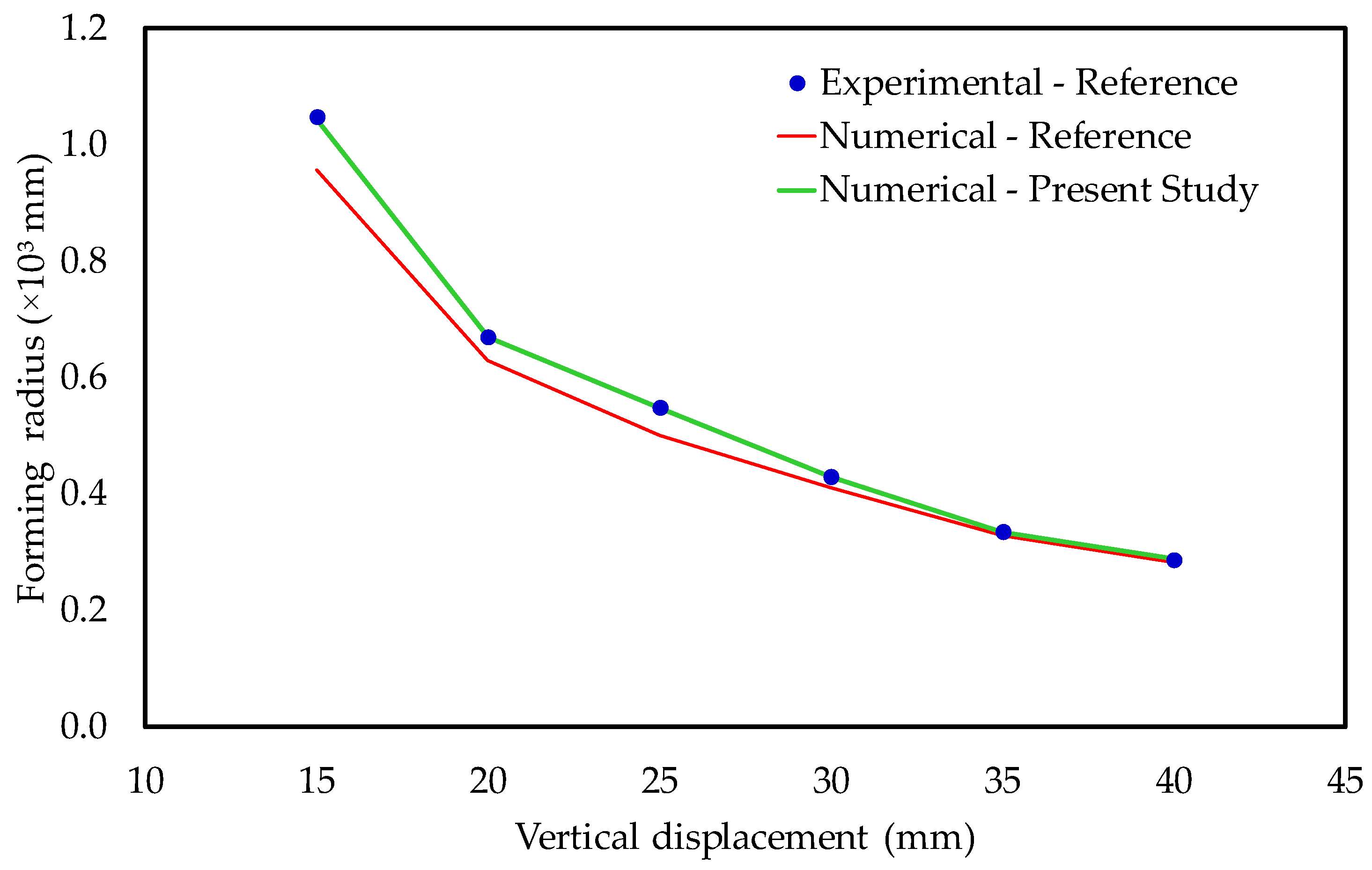
3.1. Validation and Verification Results
3.2. Case Study Results
3.2.1. Numerical Analysis of the Mechanical Behavior of Profile 1 in Direction 1 (Vertical) and Direction 2 (Horizontal)
3.2.2. Numerical Analysis of the Mechanical Behavior of Profile 2
3.2.3. Numerical Analysis of the Mechanical Behavior of Profile 3
3.2.4. Numerical Analysis of the Mechanical Behavior of Profile 4
3.2.5. Numerical Analysis of the Mechanical Behavior of Profile 5
3.2.6. Numerical Analysis of the Mechanical Behavior of Profile 6 in Direction 1 (Vertical) and Direction 2 (Horizontal)
3.2.7. Synthesis of Minimum Safe Bending Radii
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FEM | Finite Element Method |
| RD | Relative Difference between maximum stresses of two successive meshes |
| UTS | Ultimate Tensile Strength |
| Number of elements in mesh j and mesh j + 1 in the mesh-convergence test | |
| r | Bending radius applied in the forming process |
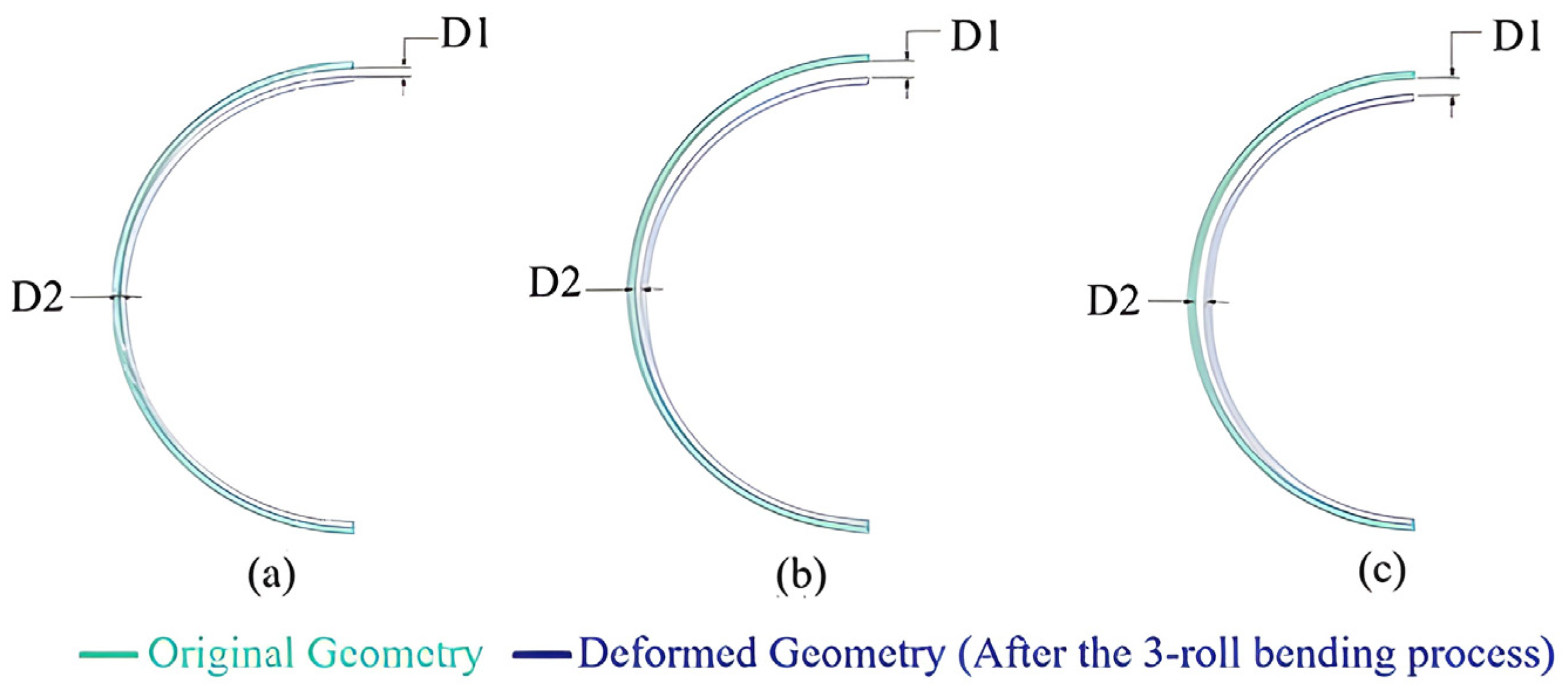
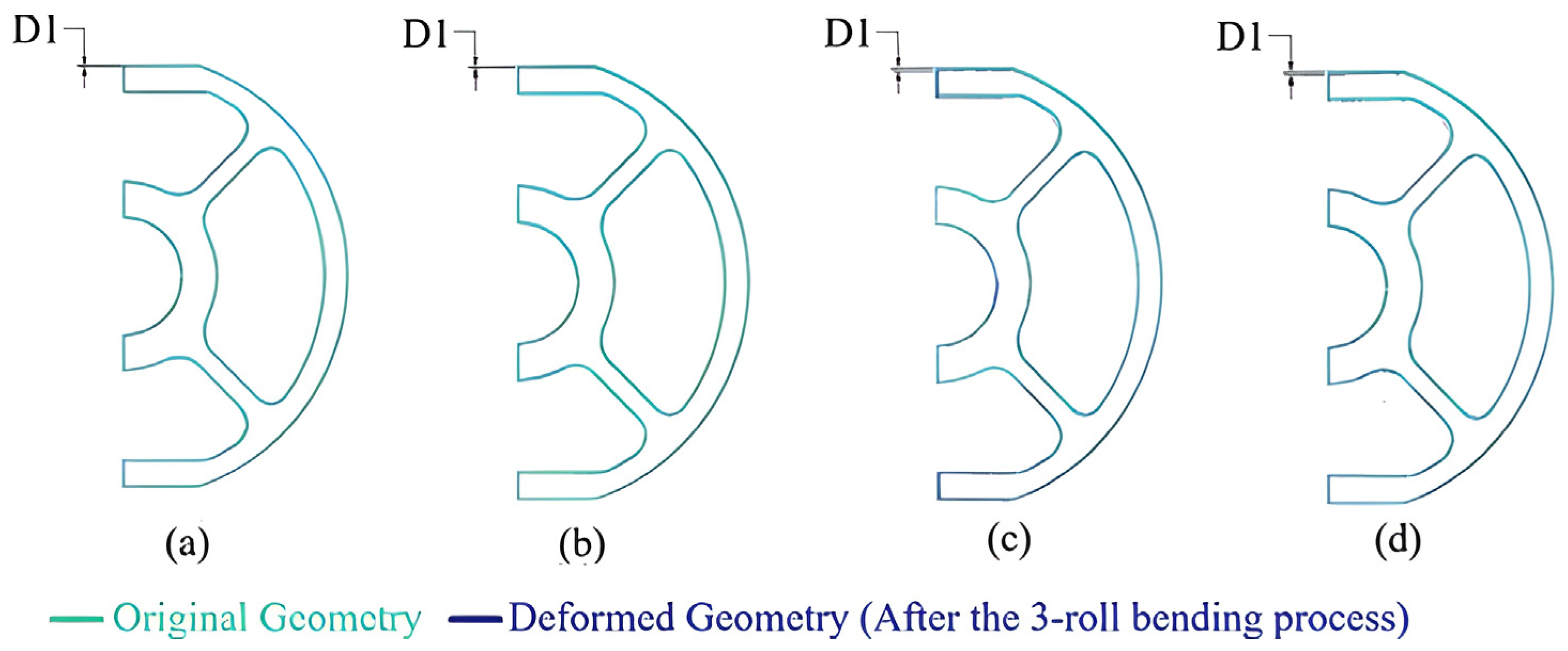
| D1, D2, D3… | Displacement measurement points on specific regions of the profile |
| LR | Lateral curvature radius |
| h | Hour |
| min | Minute |
| ABNT | Brazilian Association of Technical Standards |
| CNPq | National Council for Scientific and Technological Development |
References
- KUMAR, Ritesh. 6061-T6 Aluminum Properties and Its Uses. Available online: https://www.zetwerk.com/resources/knowledge-base/aluminum-extrusions/6061-t6-aluminum-properties-and-its-uses/ (accessed on 7 April 2025).
- HUAWEI ALUMINUM. Introduction to 6061 t6 Aluminum Properties. Available online: https://aludepot.com/blog/introduction-to-6061-t6-aluminum-properties/ (accessed on 7 April 2025).
- THE WORLD MATERIAL. Aluminum 6061, Al 6061-T6 Alloy Properties, Density, Tensile & Yield Strength, Thermal Conductivity, Modulus of Elasticity, Welding. Available online: https://www.theworldmaterial.com/al-6061-t6-aluminum-alloy/ (accessed on 7 April 2025).
- Wang, H.; Lee, H.-W.; Kang, S.-H.; Kim, D.-K. Crystal Plasticity Finite Element Analyses on the Formability of AA6061 Aluminum Alloy with Different Ageing Treatments. Metals 2024, 14, 503. [Google Scholar] [CrossRef]
- Huang, X.; Yu, G.; Zhao, J.; Mu, Z.; Zhang, Z.; Ma, R. Numerical simulation and experimental investigations on a three-roller setting round process for thin-walled pipes. Int. J. Adv. Manuf. Technol. 2020, 107, 355–369. [Google Scholar] [CrossRef]
- Yu, G.; Zhao, J.; Zhai, R.; Ma, R.; Wang, C. Theoretical analysis and experimental investigations on the symmetrical three-roller setting round process. Int. J. Adv. Manuf. Technol. 2018, 94, 45–56. [Google Scholar] [CrossRef]
- Ancellotti, S.; Fontanari, V.; Slaghenaufi, S.; Cortelletti, E.; Benedetti, M. Forming rectangular tubes into complicated 3D shapes by combining three-roll push bending, twisting and rotary draw bending: The role of the fabrication loading history on the mechanical response. Int. J. Mater. Form. 2019, 12, 907–926. [Google Scholar] [CrossRef]
- Merklein, M.; Hagenah, H.; Cojutti, M. Investigations on Three-Roll Bending of Plain Tubular Components. Key Eng. Mater. 2009, 410, 325–334. [Google Scholar] [CrossRef]
- Kamaş, T.; Sarıkaya, M. Explicit dynamics finite element analyses of asymmetrical roll bending process. Int. Adv. Res. Eng. J. 2021, 5, 435–443. [Google Scholar] [CrossRef]
- Cheng, X.; Zhao, Y.; Abd El-Aty, A.; Guo, X.; You, S. Deformation behavior of convolute thin-walled AA6061-T6 rectangular tubes manufactured by the free bending forming technology. Int. J. Adv. Manuf. Technol. 2022, 118, 2933–2948. [Google Scholar] [CrossRef]
- Li, T.; Wang, H.; El-Aty, A.A.; Li, J.; Zhang, Y.; Wei, W.B.; Chen, H.; Cheng, X.; Tao, J.; Guo, X.Z. Theoretical modelling and finite element simulation of AA6061 involute components based on 3D free bending process. Int. J. Mech. Sci. 2020, 178, 105607. [Google Scholar] [CrossRef]
- Dev, G.P.; Livingston, P.S.; Shunmuganathan, M.; Surendar, R.; Subramanian, A.S.; Simon Christopher, A.; Ganesh, K.C. Analysis of 6061 aluminium alloy sheet metal bending process for various thickness using finite element modelling. Int. J. Theor. Appl. Math. 2016, 2, 93–99. [Google Scholar]
- Khan, Z.; Khan, M.; Yook, S.-J.; Khan, A.; Younas, M.; Zahir, M.Z.; Asad, M. Dynamic Analysis of Closed Die Electromagnetic Sheet Metal Forming to Predict Deformation and Failure of AA6061-T6 Alloy Using a Fully Coupled Finite Element Model. Materials 2022, 15, 7997. [Google Scholar] [CrossRef]
- Gavrilescu, I.; Boazu, D.; Stan, F. Estimating of Bending Force and Curvature of the Bending Plate in a Three-Roller Bending System Using Finite Element Simulation and Analytical Modeling. Materials 2021, 14, 1204. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, L.; Cui, X.; Zhu, X. Research on numerical simulation and process parameters of three-roll bending based on thickness characteristics of extra-thick plate. Adv. Mech. Eng. 2019, 11, 168781401984786. [Google Scholar] [CrossRef]
- Kong, Q.S.; Yu, Z.Q.; Zhao, Y.X.; Li, S.H. The Finite Element Analysis for Dimensional Accuracy in Roll Bending of Aluminum-Polymer Laminated Sheet. Appl. Mech. Mater. 2013, 390, 574–578. [Google Scholar] [CrossRef]
- Chung, C.-C.; Lee, K.-L.; Pan, W.-F. Finite element analysis on the response of 6061-T6 aluminum alloy tubes with a local sharp cut under cyclic bending. J. Vibro Eng. 2016, 18, 5691–5703. [Google Scholar] [CrossRef]
- Saai, A.; Westermann, I.; Dumoulin, S.; Hopperstad, O.S. Crystal plasticity finite element simulations of pure bending of aluminium alloy AA7108. Int. J. Mater. Form. 2016, 9, 457–469. [Google Scholar] [CrossRef]
- Tomaszewski, T.; Stopek, M.; Skibicki, A.; Seyda, J.; Piątkowski, T. Effect of plastic strain under roller bending on fatigue properties of extruded 6063 T66 aluminium alloy profile. Trans. Nonferrous Met. Soc. China 2023, 33, 3282–3294. [Google Scholar] [CrossRef]
- Feng, Z.; Champliaud, H. Modeling and simulation of asymmetrical three-roll bending process. Simul. Model. Pract. Theory 2011, 19, 1913–1917. [Google Scholar] [CrossRef]
- Shi, L.; Zhu, C.; Ma, R. Numerical simulation and optimization on three-roll bending based on thick plate. Forg. Stamp. Technol. 2022, 47, 1–7. [Google Scholar]
- Liu, H.; Sun, Q.; Zhao, Y.; Song, Z.; Wang, J. Design of three-roll bending machine tool and research on compensation algorithm. Adv. Mech. Eng. 2023, 15, 1–12. [Google Scholar] [CrossRef]
- Moreira, M.S.; Souza, J.H.C.; Guilherme, C.E.M.; Isoldi, L.A. Computational model validation of the rolled shapes calendaring process. Ciência E Nat. 2023, 45, e74455. [Google Scholar] [CrossRef]
- Zheng, Z.; Shao, J.; Zhang, Z.; Li, C. Roller Position Design in the Roll Bending Process of a Non-Uniform Curvature Profile. Axioms 2024, 13, 613. [Google Scholar] [CrossRef]
- da Silva Moreira, M.; Guilherme, C.E.M.; Corrêa de Souza, J.H.; dos Santos, E.D.; Pavlovic, A.; Isoldi, L.A. Influence of Curvature Radius on Mechanical Behavior of Extruded 6061-T6 Aluminum in Roll Bending. J. Appl. Comput. Mech. 2025, 11, 120–133. [Google Scholar]
- Gao, E.; Xue, D.; Li, Y. Springback angle prediction for high-strength aluminum alloy bending via multi-stage regression. Metals 2025, 15, 358. [Google Scholar] [CrossRef]
- Wang, T.; Fang, W.; Jiang, Y.; Weng, H.; Qian, Y.; Zhang, D. Research on springback compensation method of roll forming based on improved fuzzy PID control. Appl. Sci. 2025, 15, 3748. [Google Scholar] [CrossRef]
- Zhi, Y.; Feng, Y.; Wang, D.; Hu, X.; Sun, T.; Liu, X. Forming characteristics of tailor rolled blank of aluminum alloy during three-point bending. Materials 2024, 17, 591. [Google Scholar] [CrossRef]
- Boazu, D.; Gavrilescu, I.; Stan, F. Analytical and finite element analysis of the rolling force for the three-roller cylindrical bending process. Materials 2024, 17, 5230. [Google Scholar] [CrossRef]
- Li, X.M.; Liu, Y.; Wu, H.; Ding, C.Y.; Dong, J.; Peng, W.; Zhang, D.H.; Sun, J. A comprehensive analytical model for tensile-bending straightening in strip processing by coupling residual stress and buckling deformation. J. Mater. Process. Technol. 2025, 339, 118802. [Google Scholar] [CrossRef]
- Iandiorio, C.; Salvini, P. A geometrically nonlinear shell theory for thin-walled tubes and beams subjected to large displacements and cross-section deformation. Thin-Walled Struct. 2025, 216 Pt A, 113583. [Google Scholar]
- Erisov, Y.; Kuzin, A.; Sedelnikov, A. An Analytical Model for the Plastic Bending of Anisotropic Sheet Materials, Incorporating the Strain-Hardening Effect. Technologies 2024, 12, 236. [Google Scholar] [CrossRef]
- Spoorenberg, R.C.; Snijder, H.H.; Hoenderkamp, J.C.D. Finite element simulations of residual stresses in roller bent wide flange sections. J. Constr. Steel Res. 2010, 67, 737–747. [Google Scholar]
- Mercury, A.; Fanelli, P.; Giorgetti, F.; Rubino, G.; Stefanini, C. Experimental and numerical analysis of roll bending process of thick metal sheets. IOP Conf. Ser. Ciência E Eng. Mater. 2021, 1038, 012067. [Google Scholar] [CrossRef]
- Selvaggio, A.; Dirksen, U.; Tekkaya, A.E.; Schikorra, M.; Kleiner, M. Increasing the Production Accuracy of Profile Bending withMethods of Computational Intelligence. Evol. Comput. 2009, 17, 561–576. [Google Scholar] [CrossRef]
- Kissell, J.T.; Ferry, R.J. Aluminum Structures: A Guide to Their Specifications and Design, 2nd ed.; John Wiley Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Vollertsen, F.; Sprenger, A.; Kraus, J.; Arnet, H. Extrusion, channel, and profile bending: A review. J. Mater. Process. Technol. 1999, 87, 1–27. [Google Scholar] [CrossRef]
- Zhou, W.; Shao, Z.; Yu, J.; Lin, J. Advances and Trends in Forming Curved Extrusion Profiles. Materials 2021, 14, 1603. [Google Scholar] [CrossRef]
- Hashemi, R.; Niknam, S.A. Flexible bending of rectangular profiles: Numerical and experimental investigations. J. Manuf. Process. 2020, 56, 390–399. [Google Scholar] [CrossRef]
- Wang, A.; Xue, H.; Bayraktar, E.; Yang, Y.; Saud, S.; Chen, P. Analysis and Control of Twist Defects of Aluminum Profiles with Large Z-Section in Roll Bending Process. Metals 2020, 10, 31. [Google Scholar] [CrossRef]
- Hosford, W.F.; Caddell, R.M. Metal Forming: Mechanics and Metallurgy, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Suresh, S. Fatigue of Materials, 2nd ed.; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- EN 1999; Eurocode 9—Design of Aluminium Structures. European Committee for Standardization: Brussels, Belgium, 2020.
- NBR 8800; NBR 8800: Projeto de Estruturas de Aço em Edificações. Associação Brasileira de Normas Técnicas: Rio de Janeiro, Brazil, 2008.
- The Aluminum Association. Aluminum Design Manual; The Aluminum Association: Arlington, VA, USA, 2021. [Google Scholar]
- Chapra, S.C.; Canale, R.P. Numerical Methods for Engineers (Métodos Numéricos para Engenheiros), 7th ed.; McGraw Hill: New York, NY, USA, 2014. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method: Its Basis and Fundamentals, 7th ed.; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Bathe, K.J. Finite Element Procedures, 2nd ed.; Klaus-Jürgen Bathe: Cambridge, MA, USA, 2021. [Google Scholar]
- Cook, R.D.; Malkus, D.S.; Plesha, M.E.; Witt, R.J. Concepts and Applications of Finite Element Analysis, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Hughes, T.J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Dover Publications: Garden City, NY, USA, 2000. [Google Scholar]
- Ansys Inc. ANSYS User’s Manual; Ansys, Inc.: Canonsburg, PA, USA, 2022. [Google Scholar]
- Oñate, E. Structural Analysis with the Finite Element Method—Linear Statics, 2nd ed.; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Song, Z.; Xu, L.; Zhao, Y.; Sun, Q. Research on three-roller bending of aluminum profiles considering roller center distance and radius. Res. Sq. 2024; preprint. [Google Scholar] [CrossRef]
- Souza, J.H.C. Curso de Fundamentos de Estamparia. TechnNOVA. 2022. Available online: https://www.technnova.com.br/Engsuperficies.html#portfolio (accessed on 15 May 2023).
- Belytschko, T.; Liu, W.K.; Moran, B. Nonlinear Finite Elements for Continua and Structures, 2nd ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Hibbeler, R.C. Mechanics of Materials, 11th ed.; Pearson: London, UK, 2022. [Google Scholar]
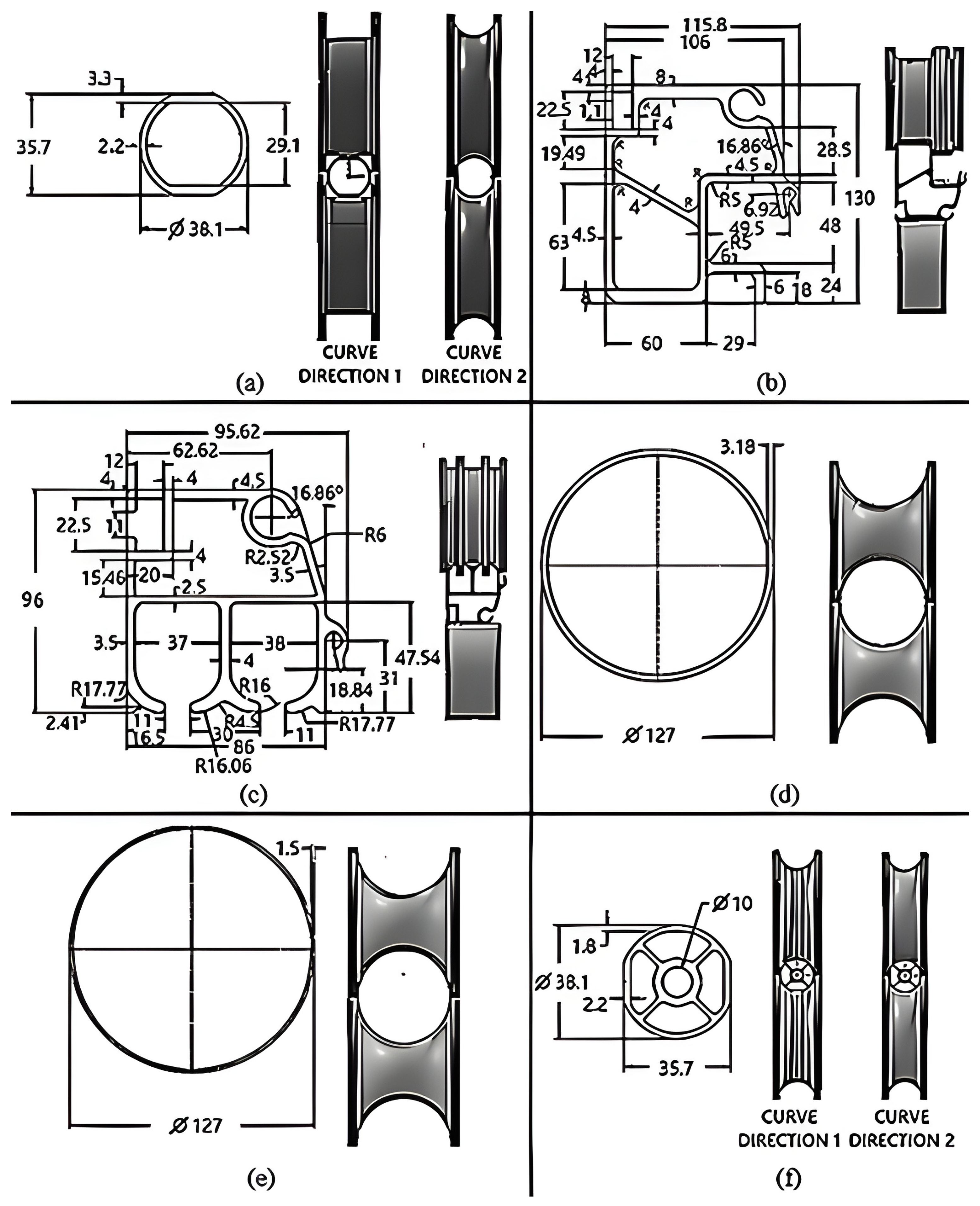
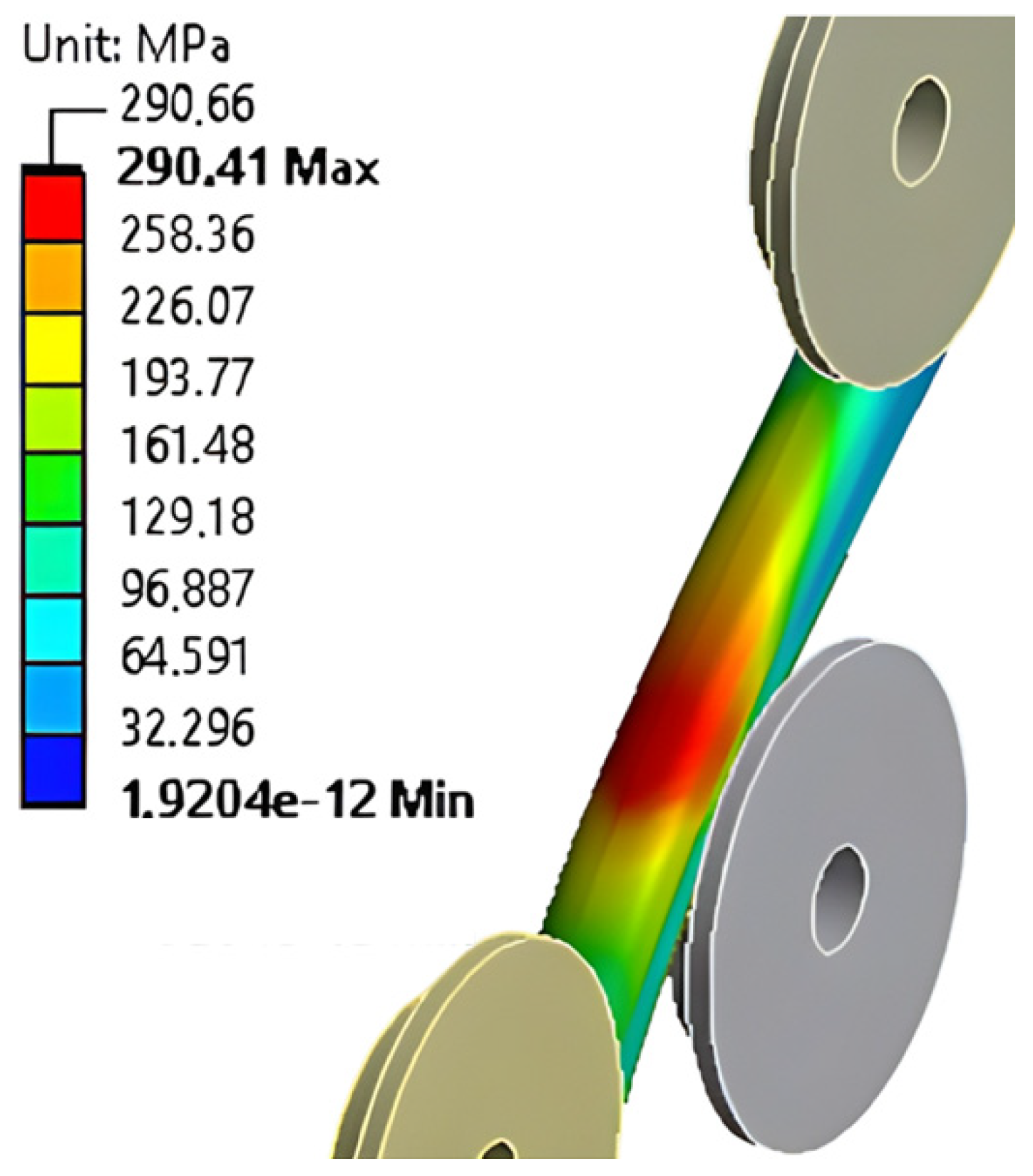
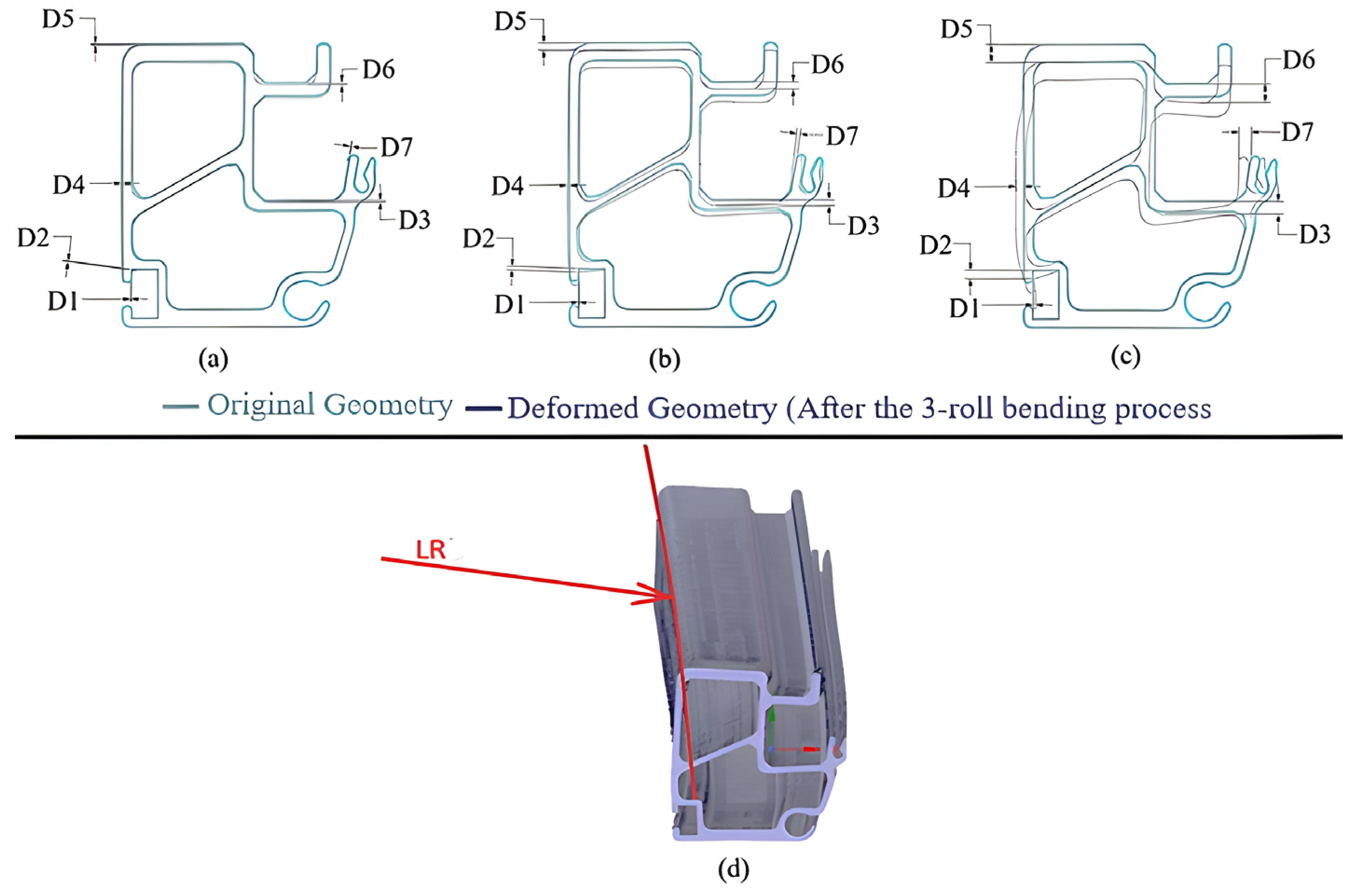
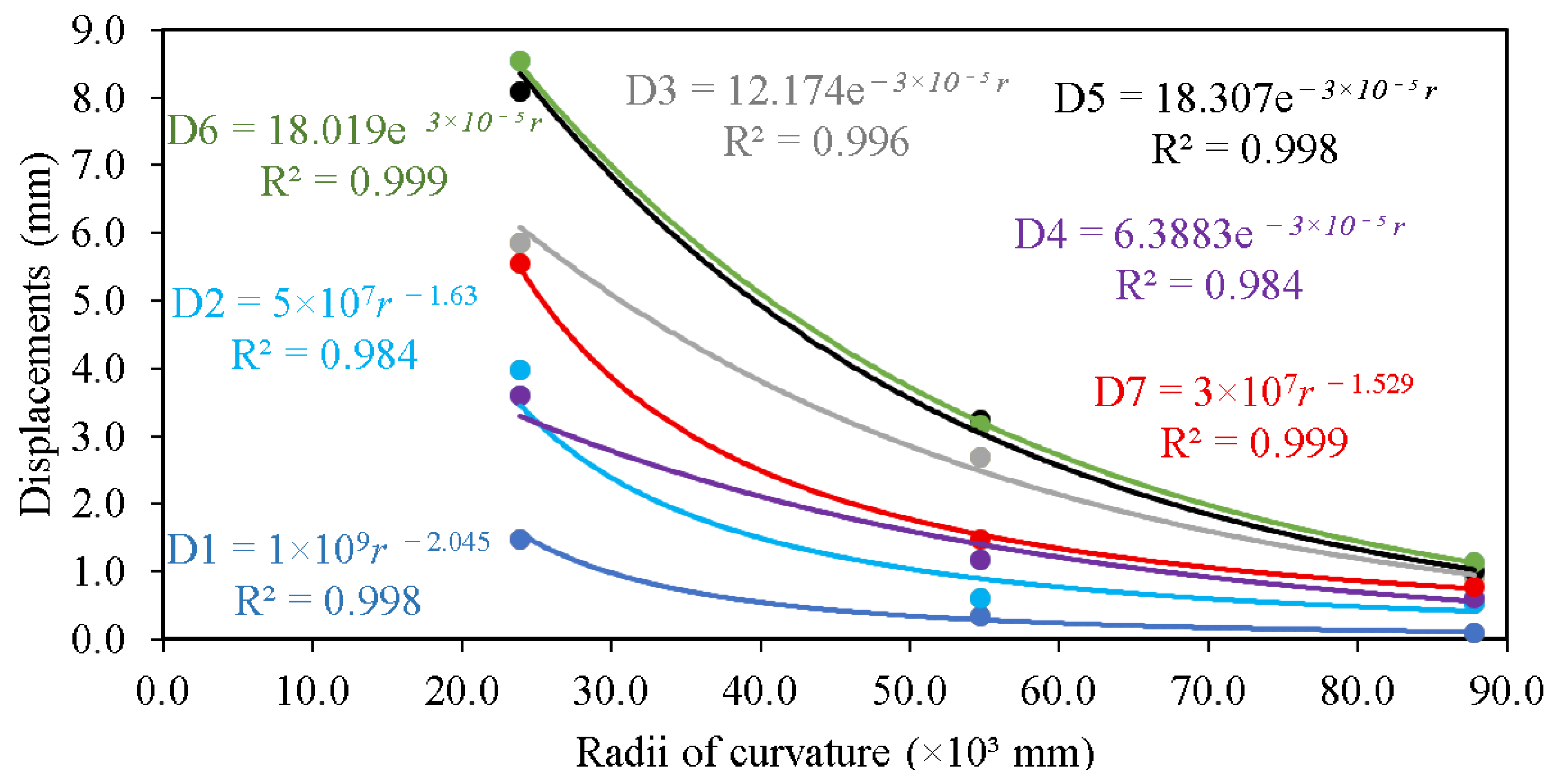
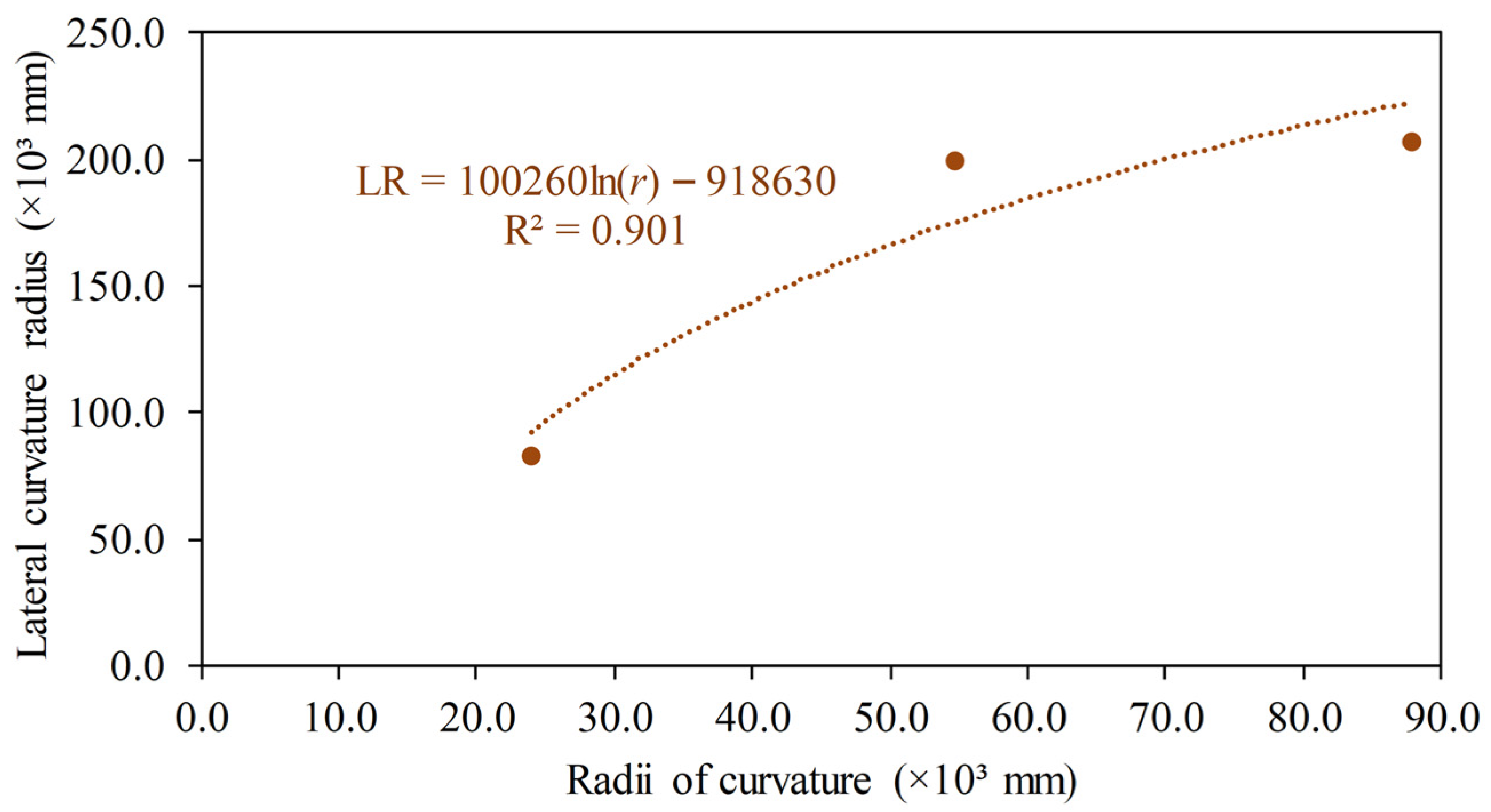
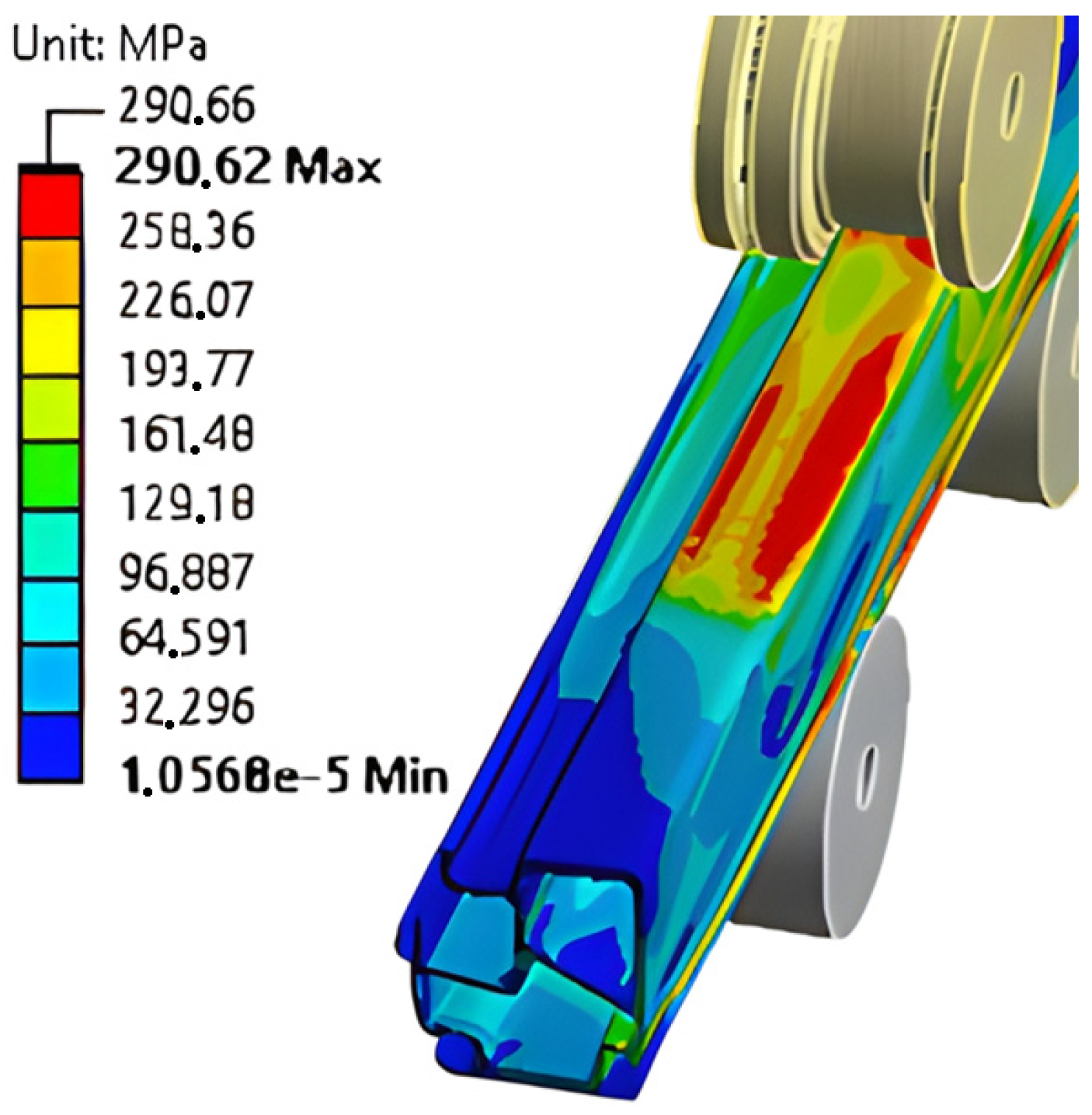
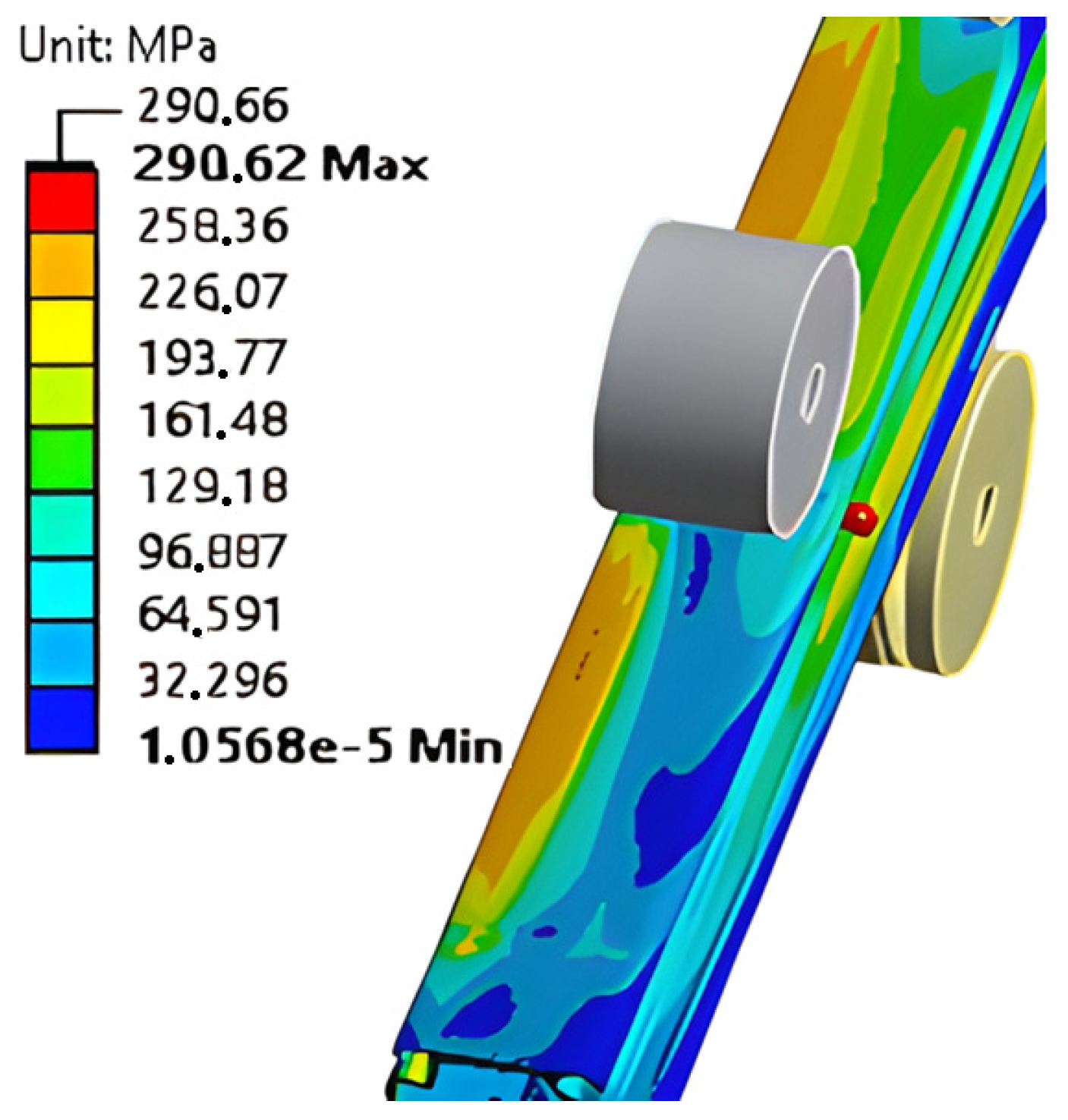
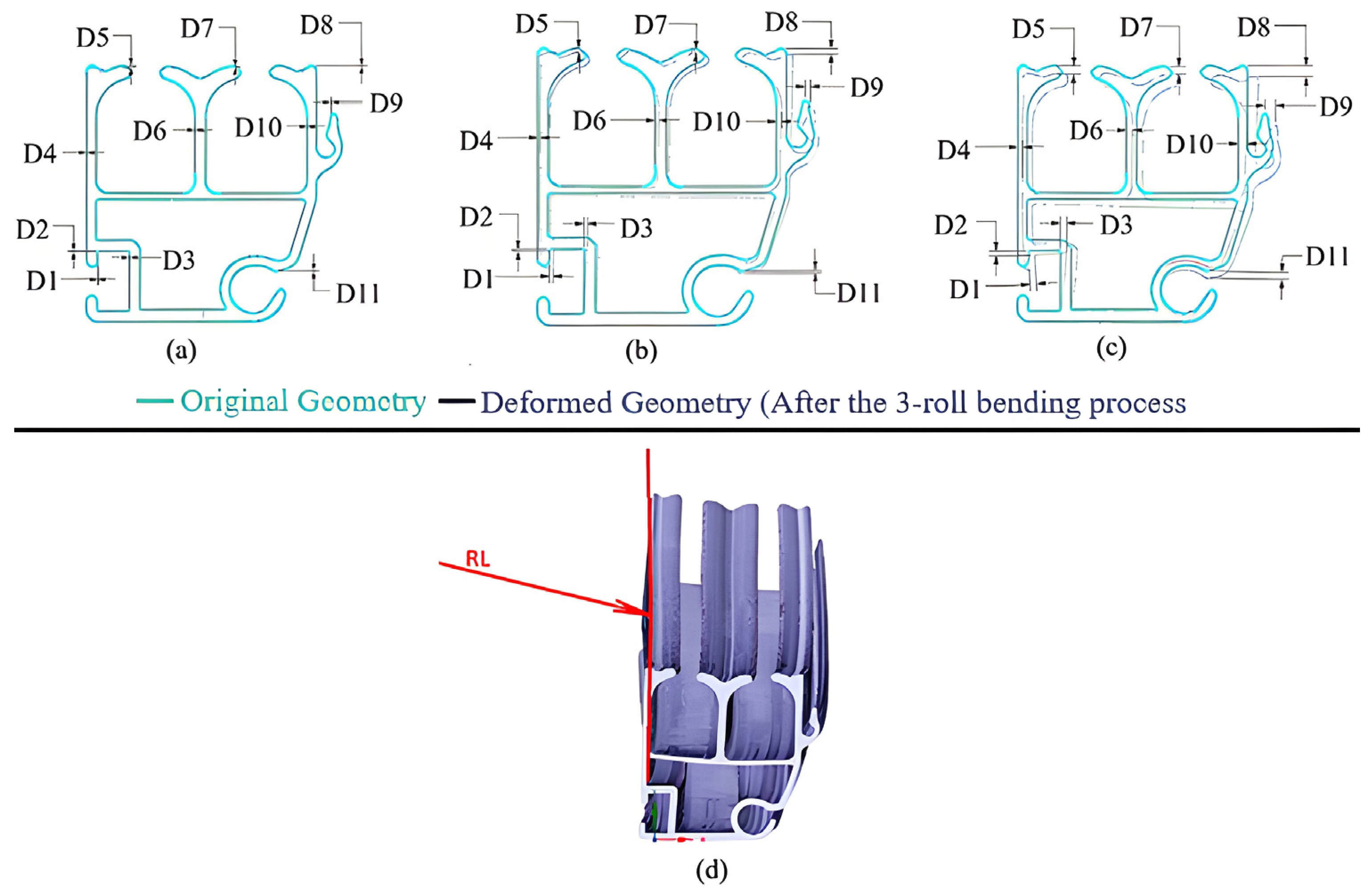
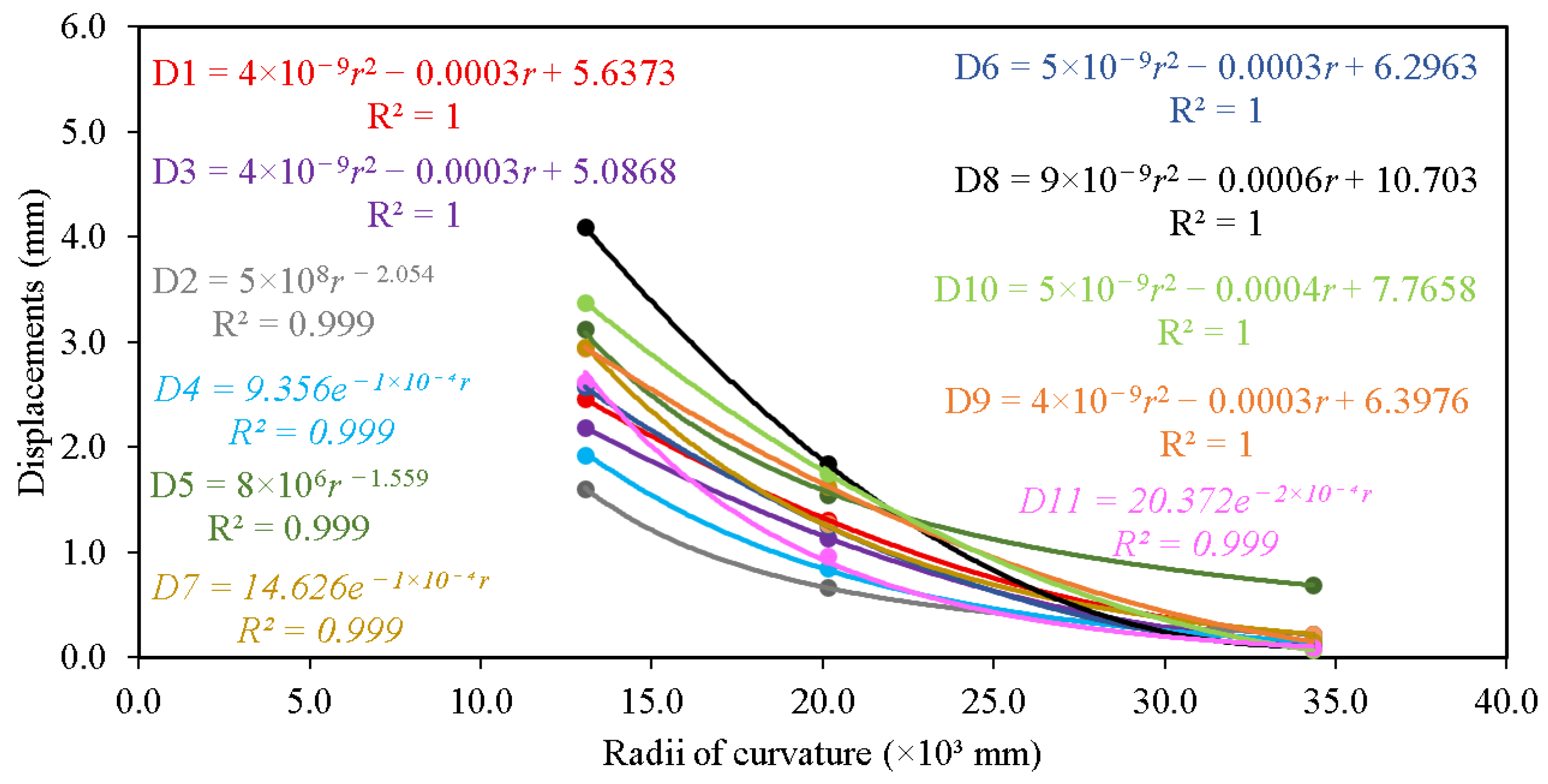
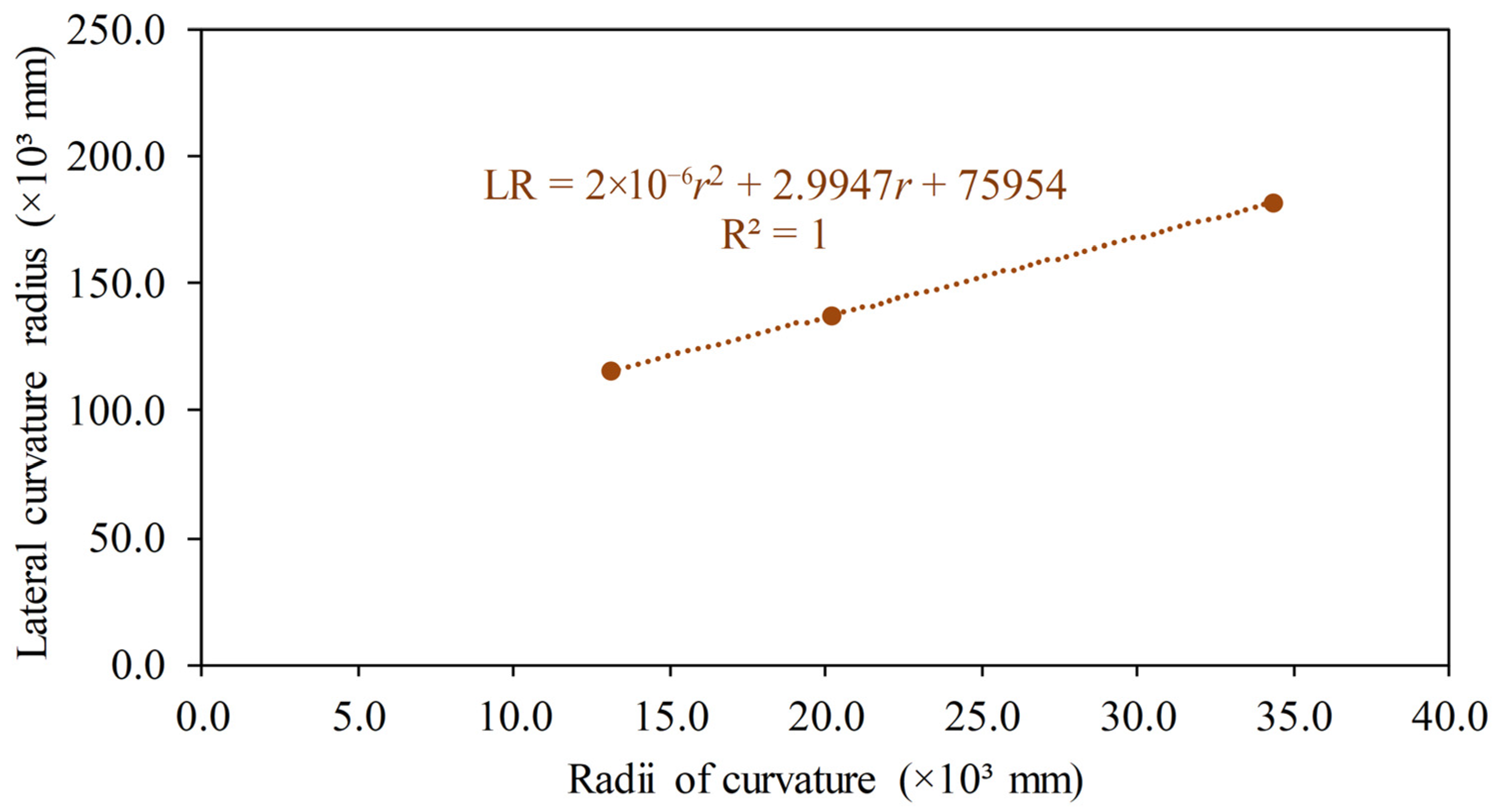
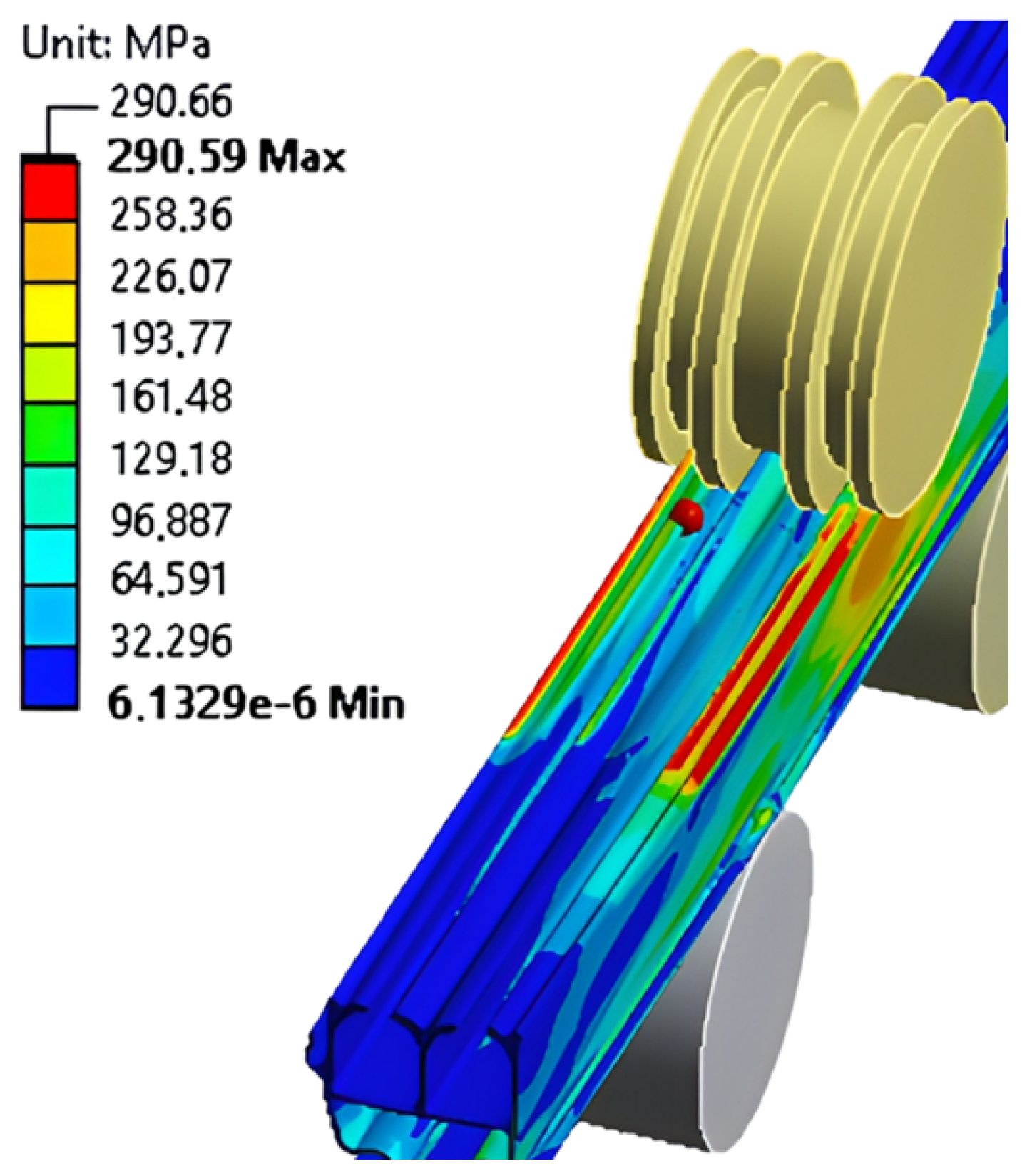
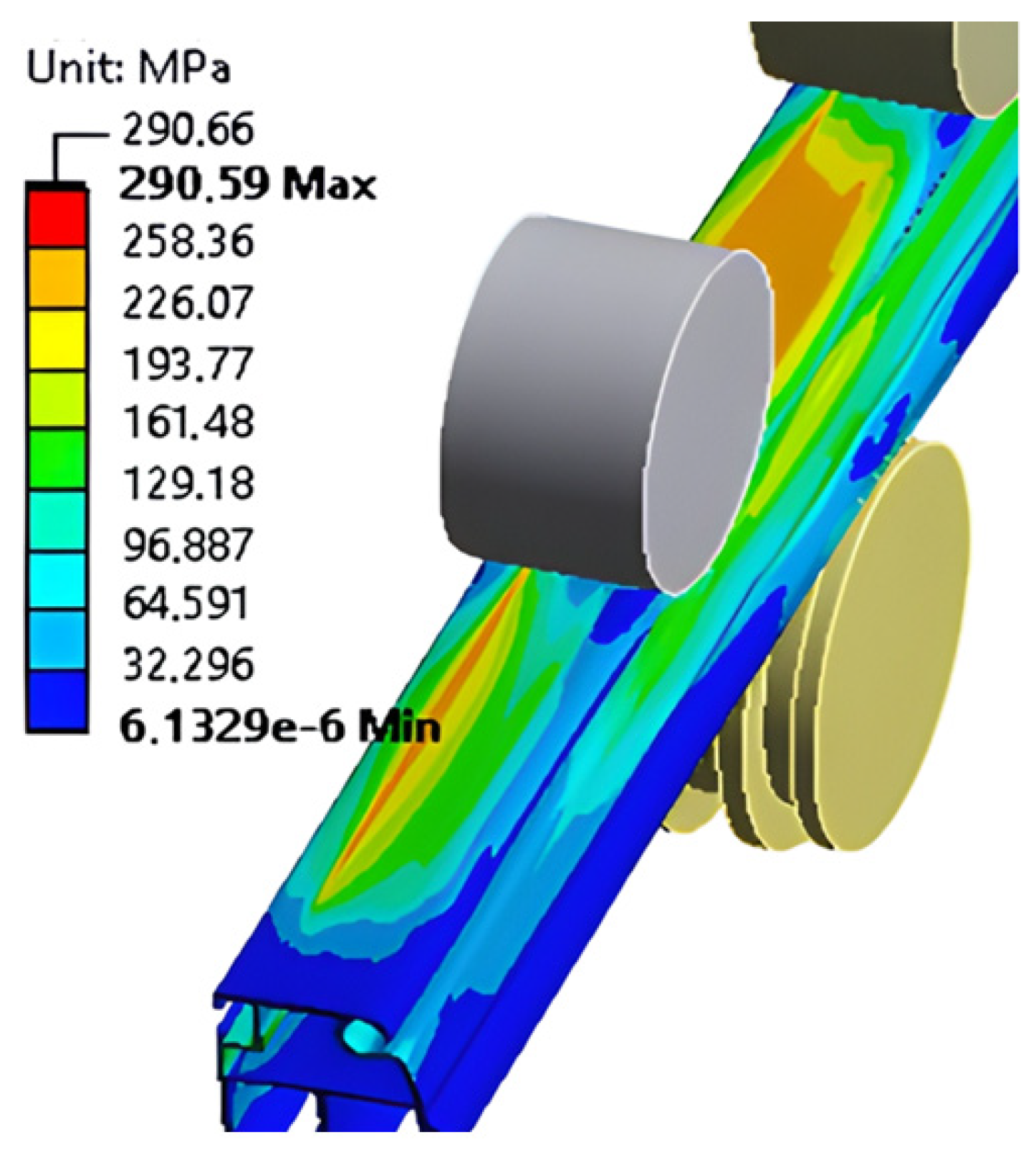
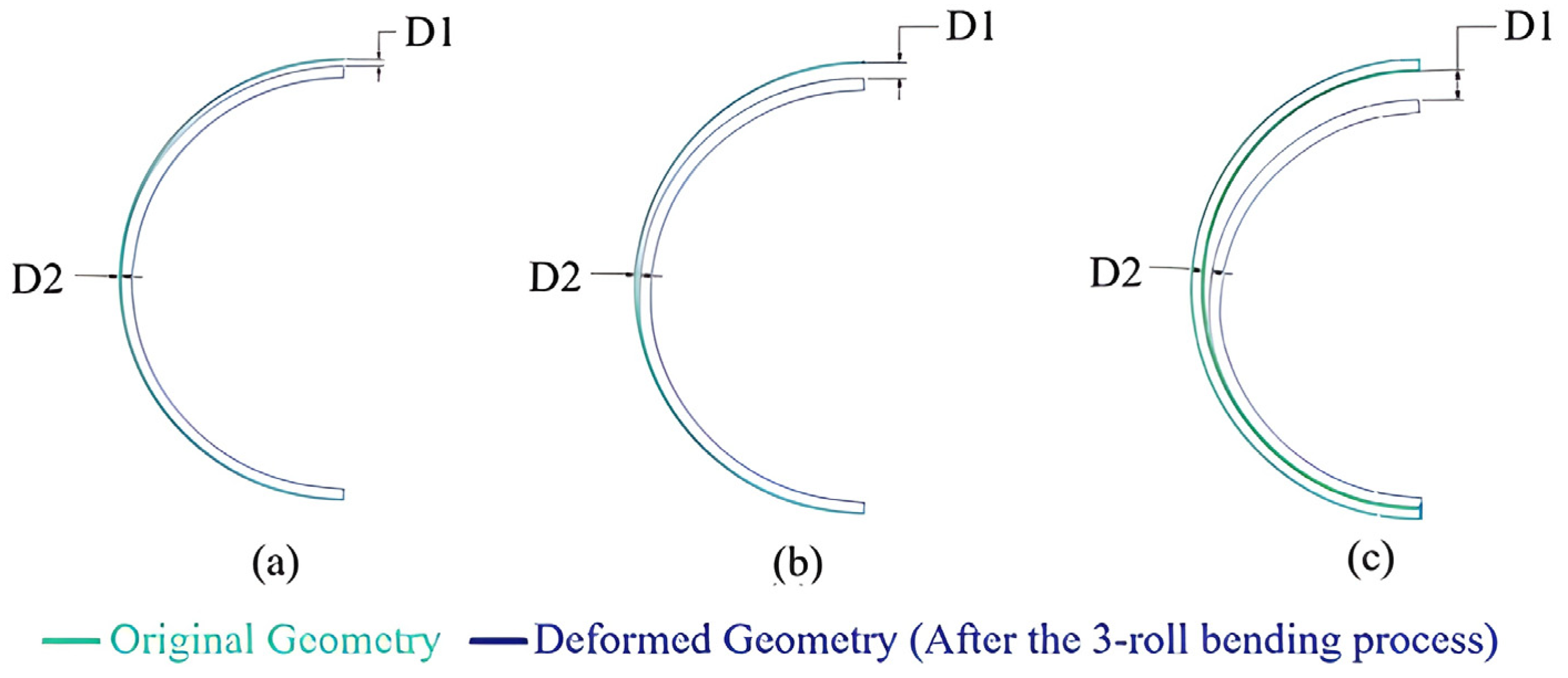
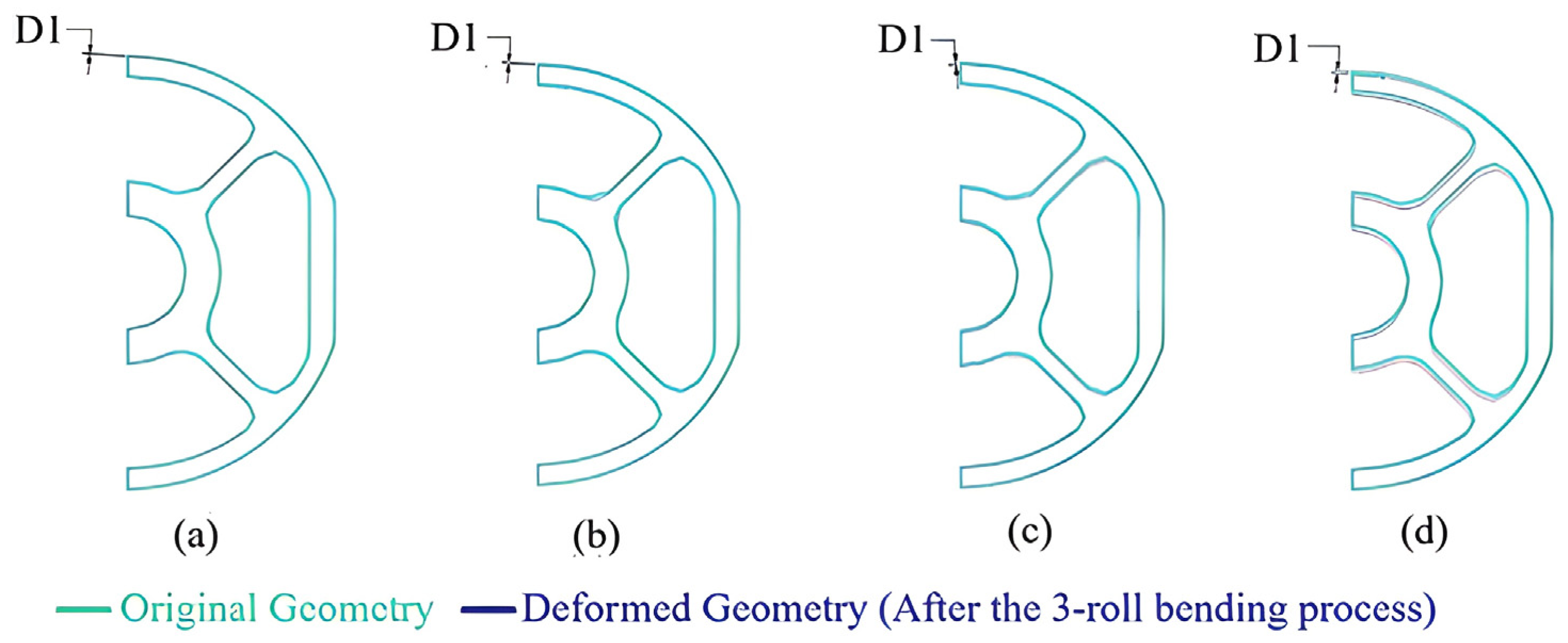
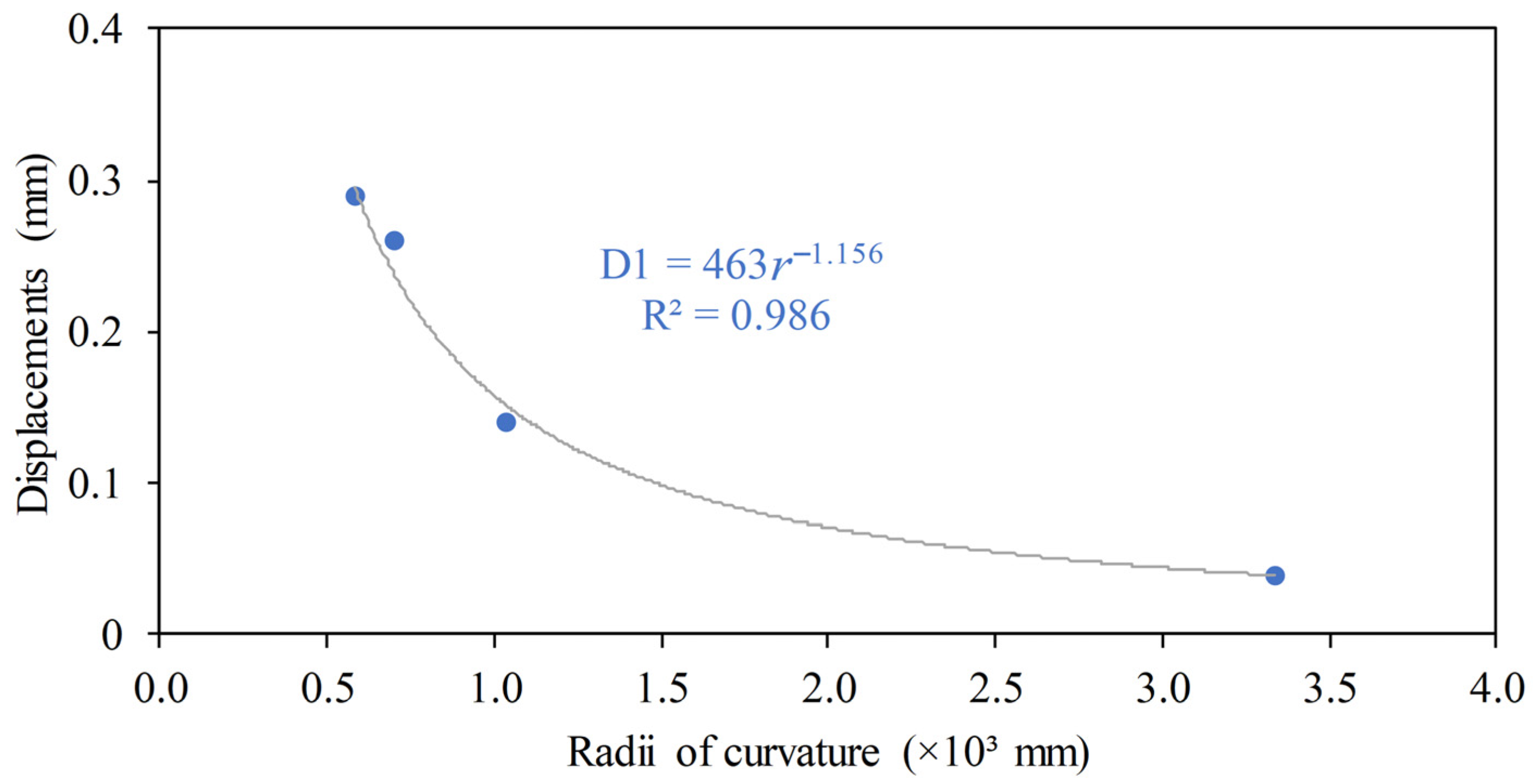
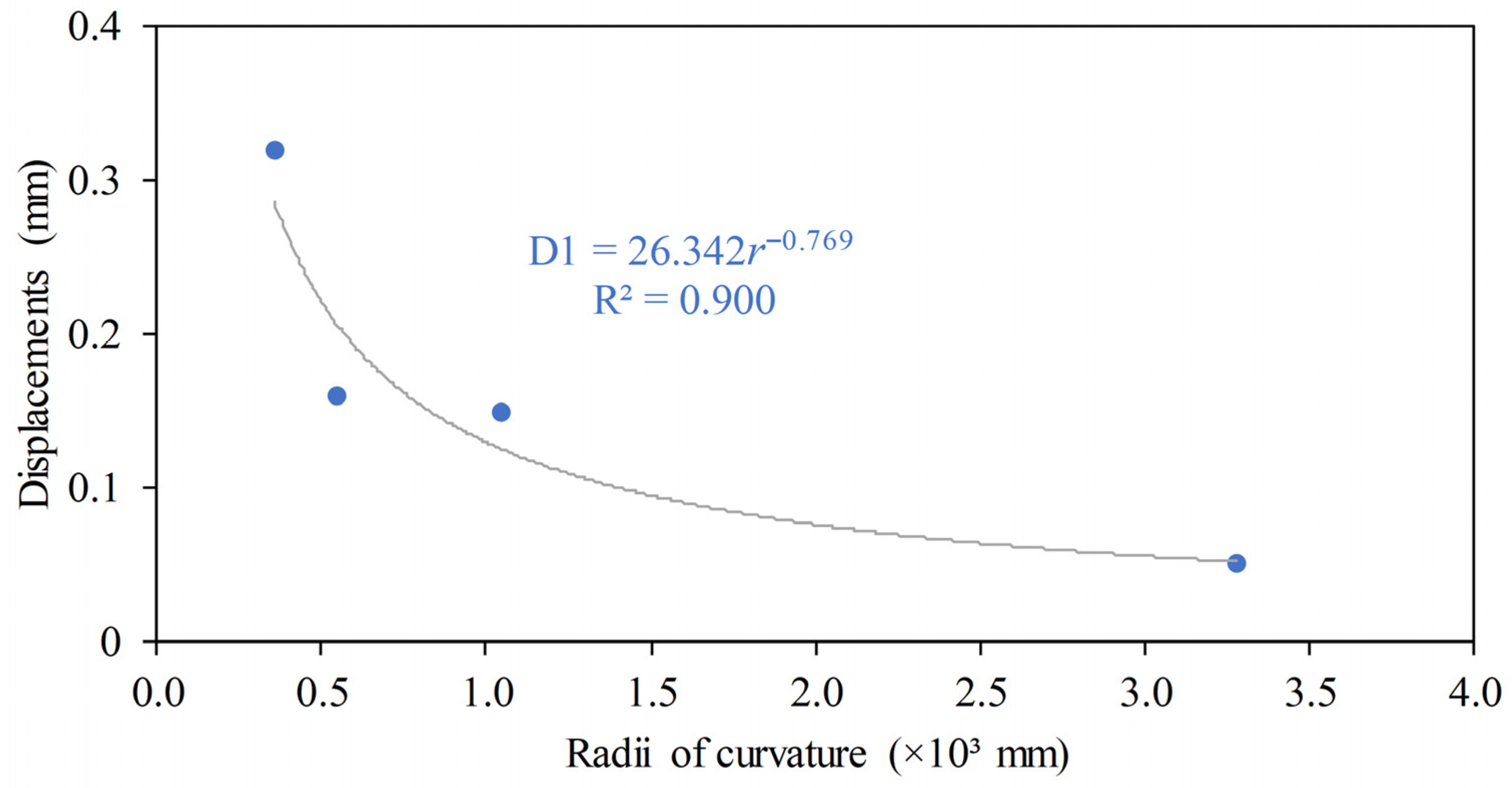
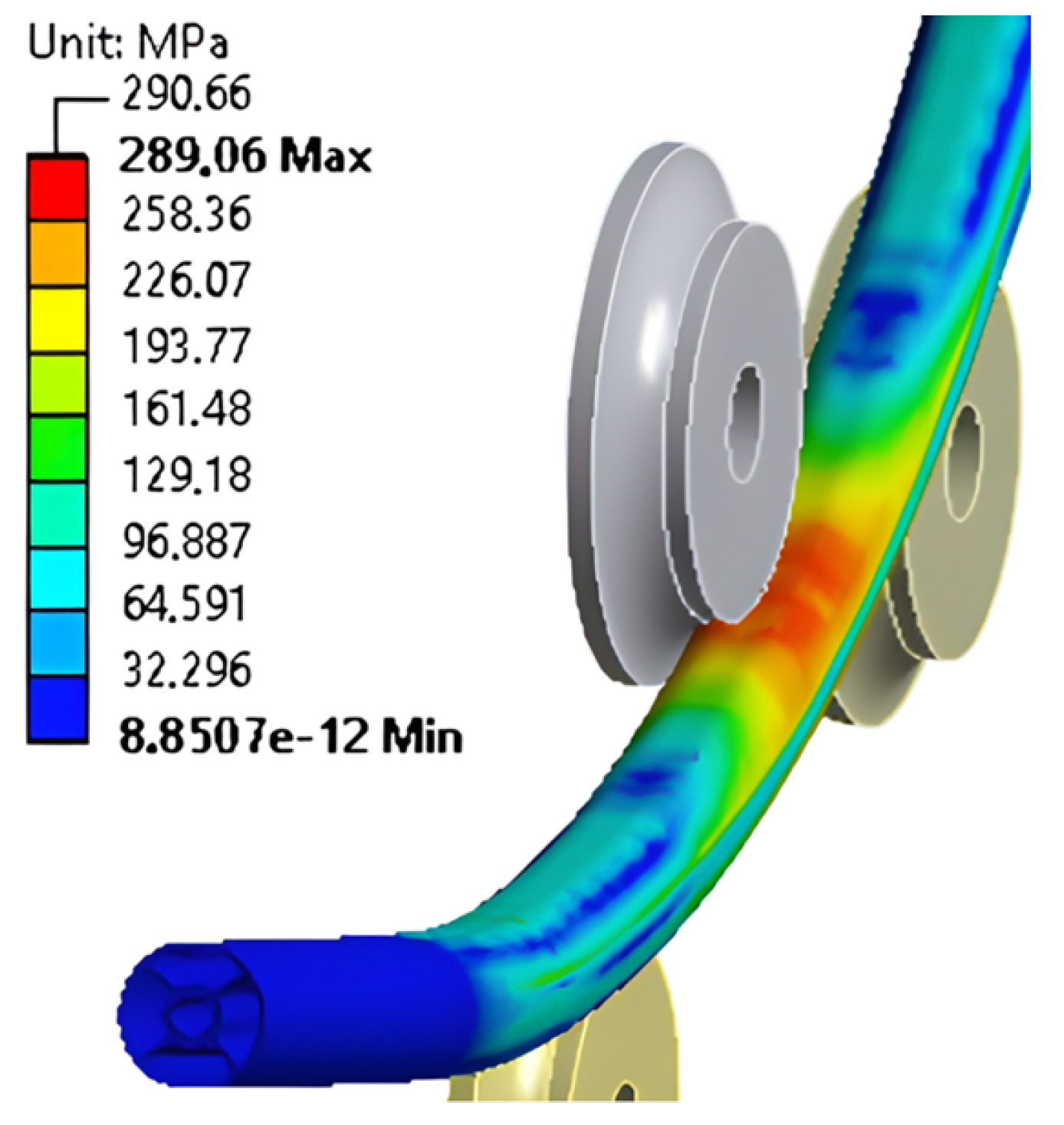
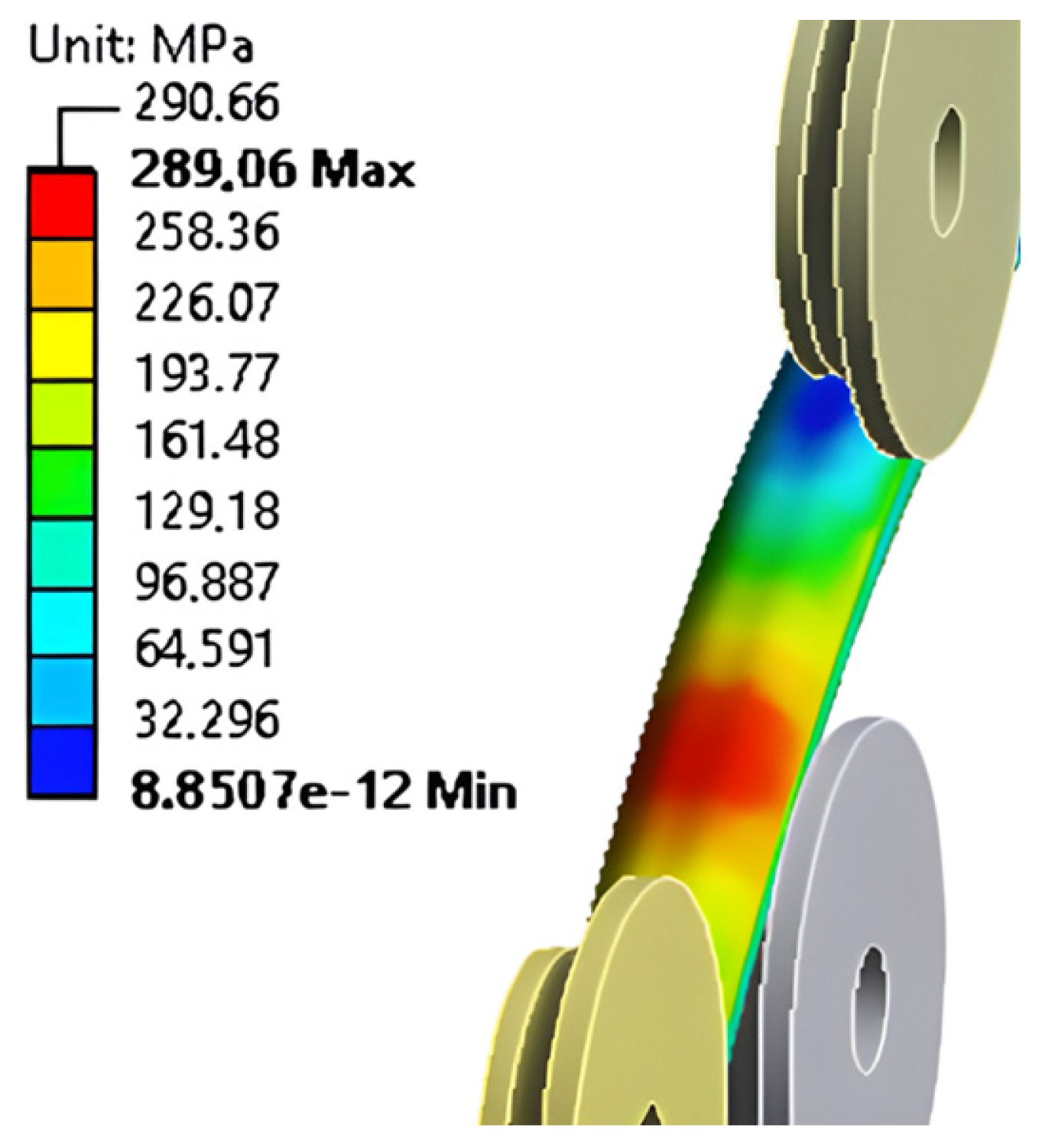
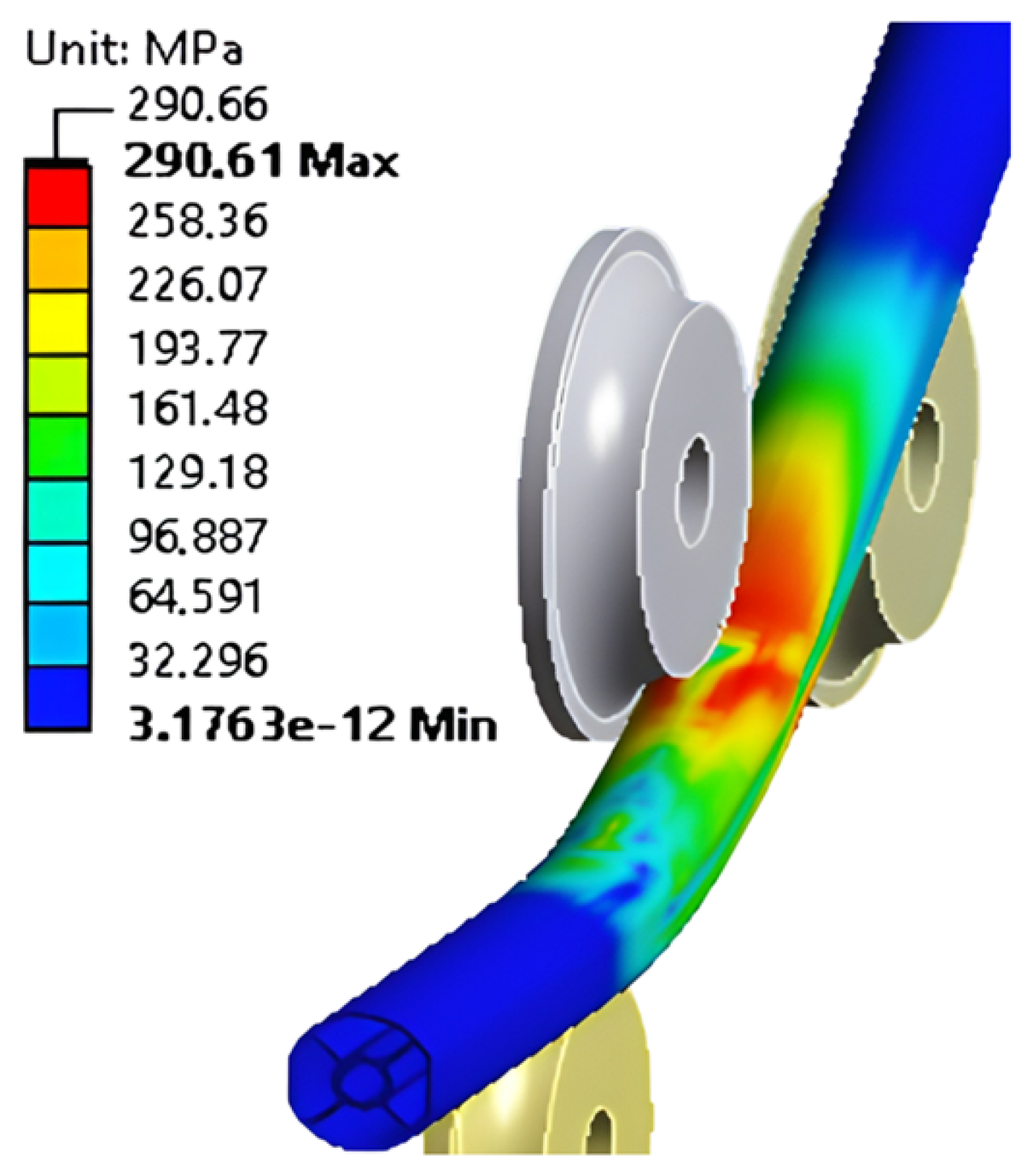
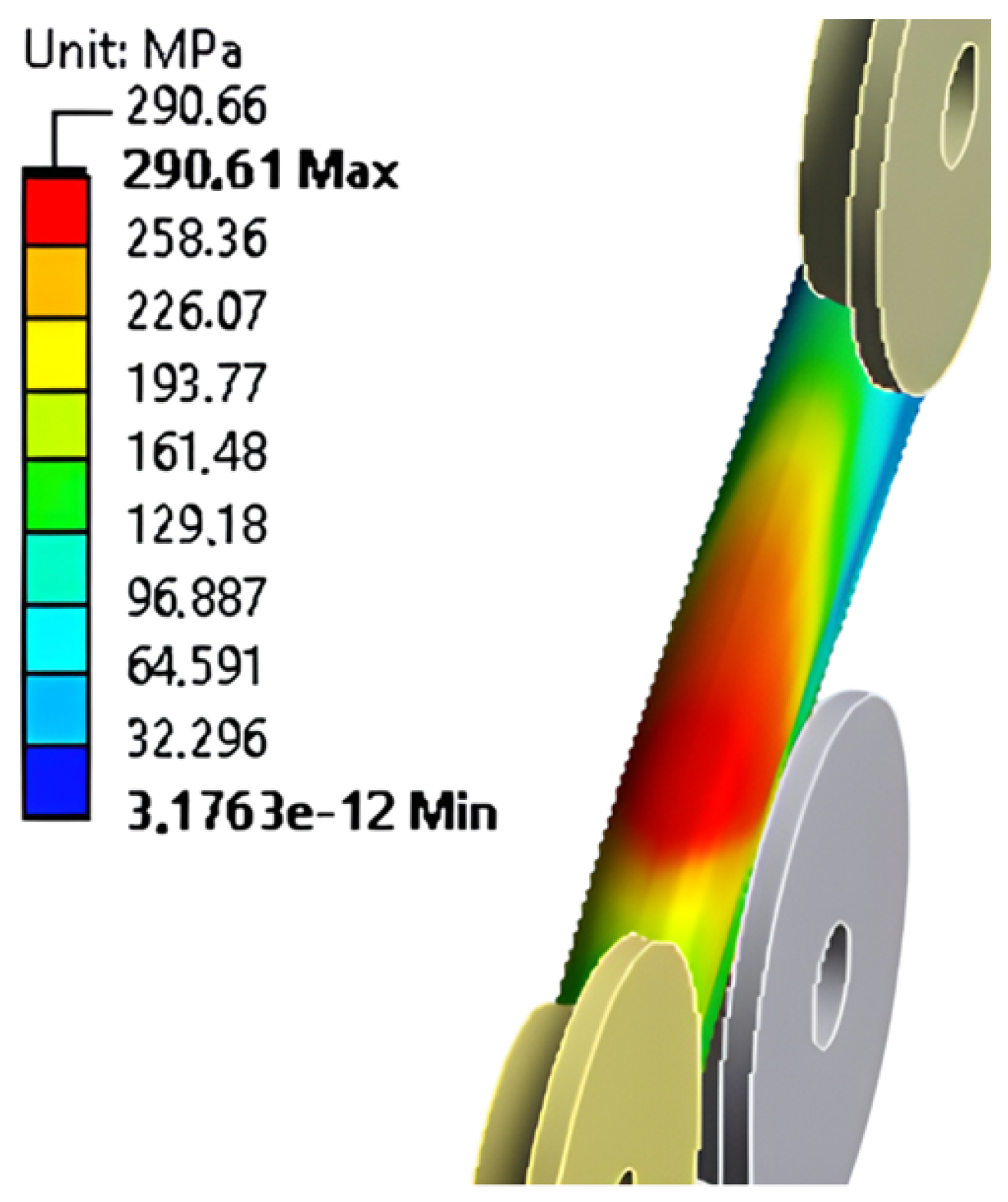
| Discretization (Cross-Section Size/Length Size/R1 Divisions) | Number of Finite Elements | Forming Radius (mm) | Absolute Successive Difference (%) |
|---|---|---|---|
| 2 mm/8 mm/3 div | 23,890 | 485.11 | 6.69 |
| 1 mm/5 mm/3 div | 65,372 | 452.67 | 3.55 |
| 0.6 mm/4 mm/4 div | 109,320 | 436.61 | 1.94 |
| 0.5 mm/2 mm/5 div | 261,271 | 428.15 | 0.17 |
| 0.3 mm/1.5 mm/7 div | 614,195 | 428.88 | --- |
| Vertical Displacement (mm) | Experimental Reference (mm) | Numerical Reference (mm) | Numerical Present Study (mm) | RDev (%) Validation | RDev (%) Verification |
|---|---|---|---|---|---|
| 15 | 1047.61 | 955.55 | 1044.34 | −0.31 | 9.29 |
| 20 | 669.84 | 628.57 | 668.78 | −0.16 | 6.40 |
| 25 | 549.21 | 500.00 | 546.79 | −0.44 | 9.36 |
| 30 | 430.16 | 411.11 | 428.15 | −0.47 | 4.14 |
| 35 | 334.92 | 326.92 | 334.27 | −0.19 | 2.25 |
| N° of Finite Elements | (MPa) | RD (%) | Processing Time |
|---|---|---|---|
| 4265 | 207.97 | 10.43 | 00 h 07 min |
| 5817 | 229.67 | 9.28 | 00 h 10 min |
| 8258 | 250.99 | 1.87 | 00 h 19 min |
| 13,255 | 255.68 | 0.03 | 00 h 34 min |
| 17,153 | 255.59 | 0.24 | 01 h 01 min |
| 24,571 | 254.97 | - | 01 h 51 min |
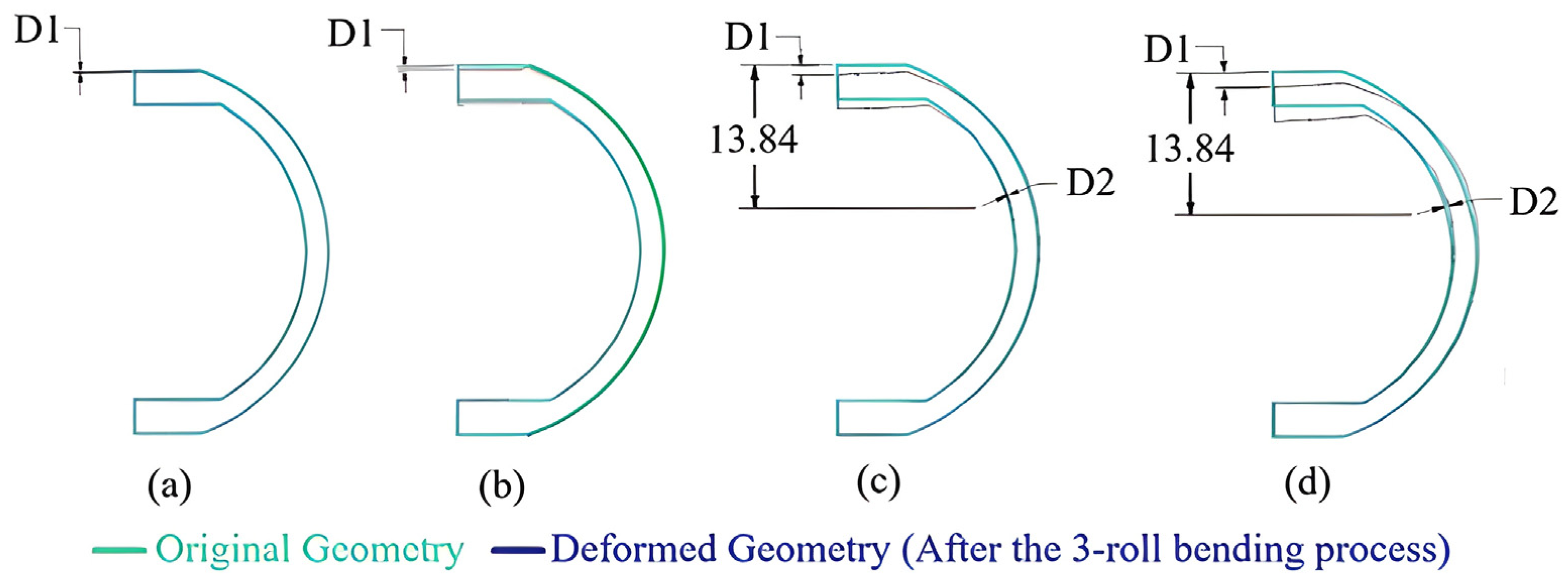
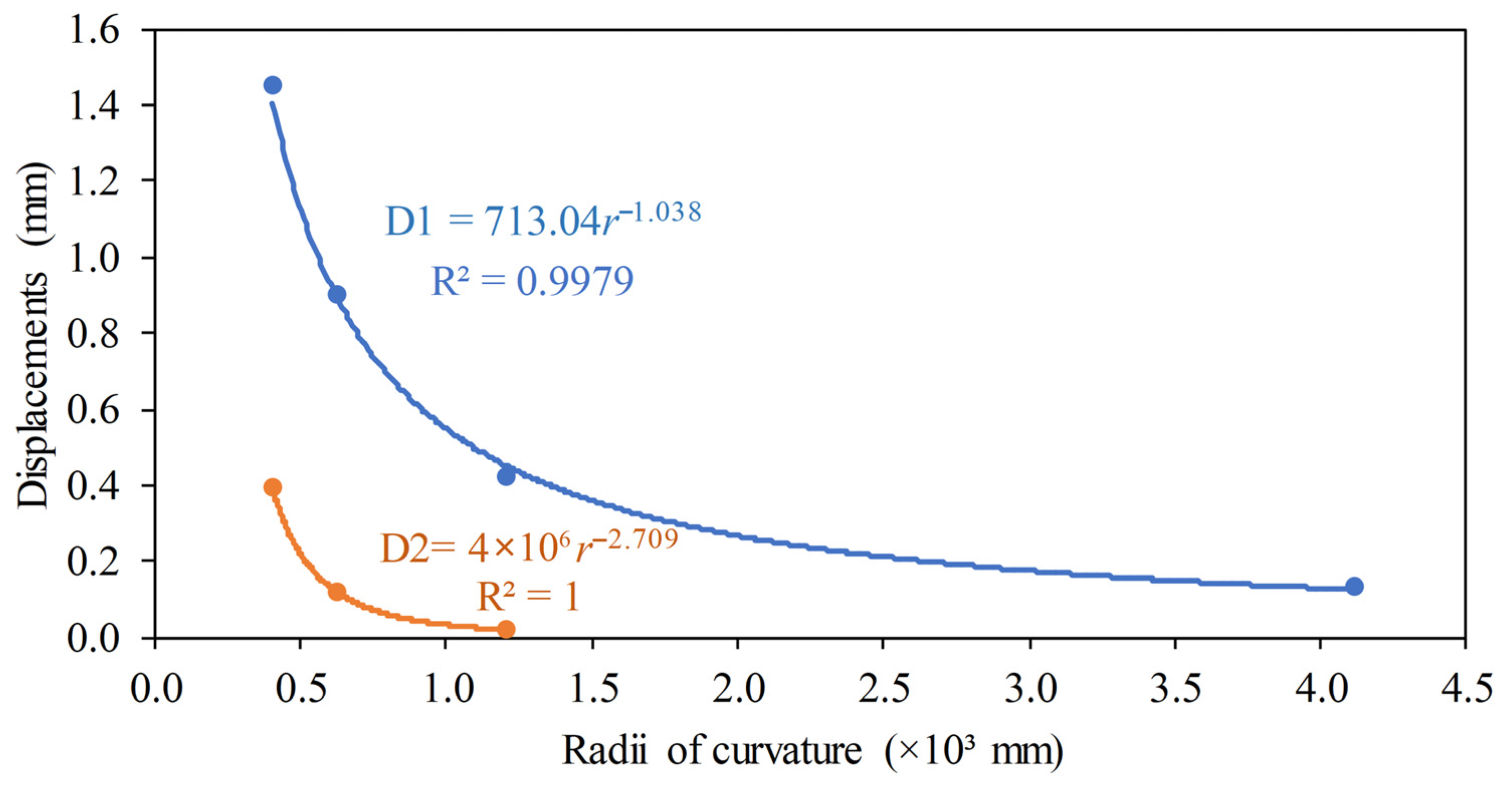
| r (mm) | (MPa) | Safety Factor | Displacement (mm) | |
|---|---|---|---|---|
| D1 | D2 | |||
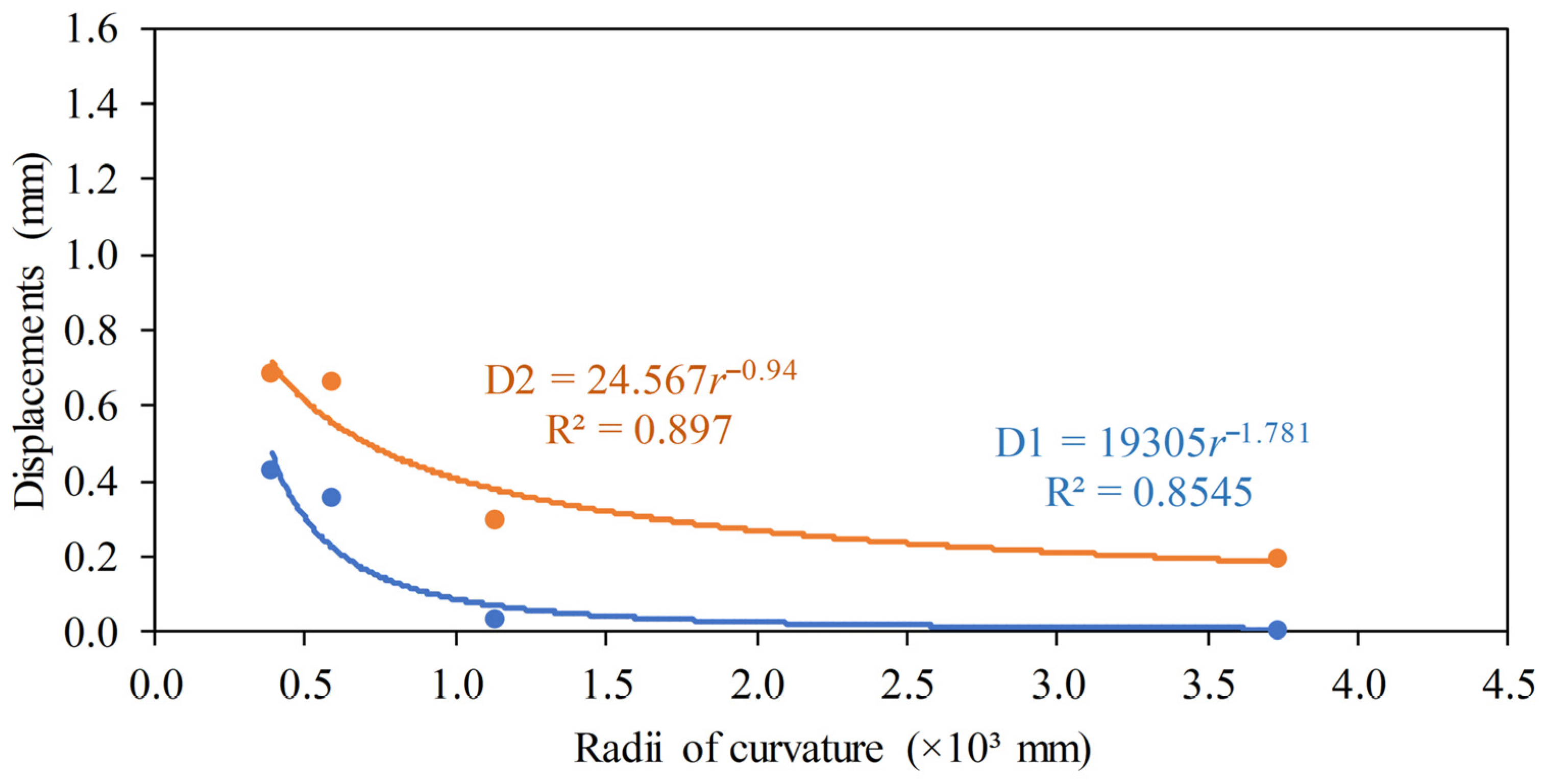
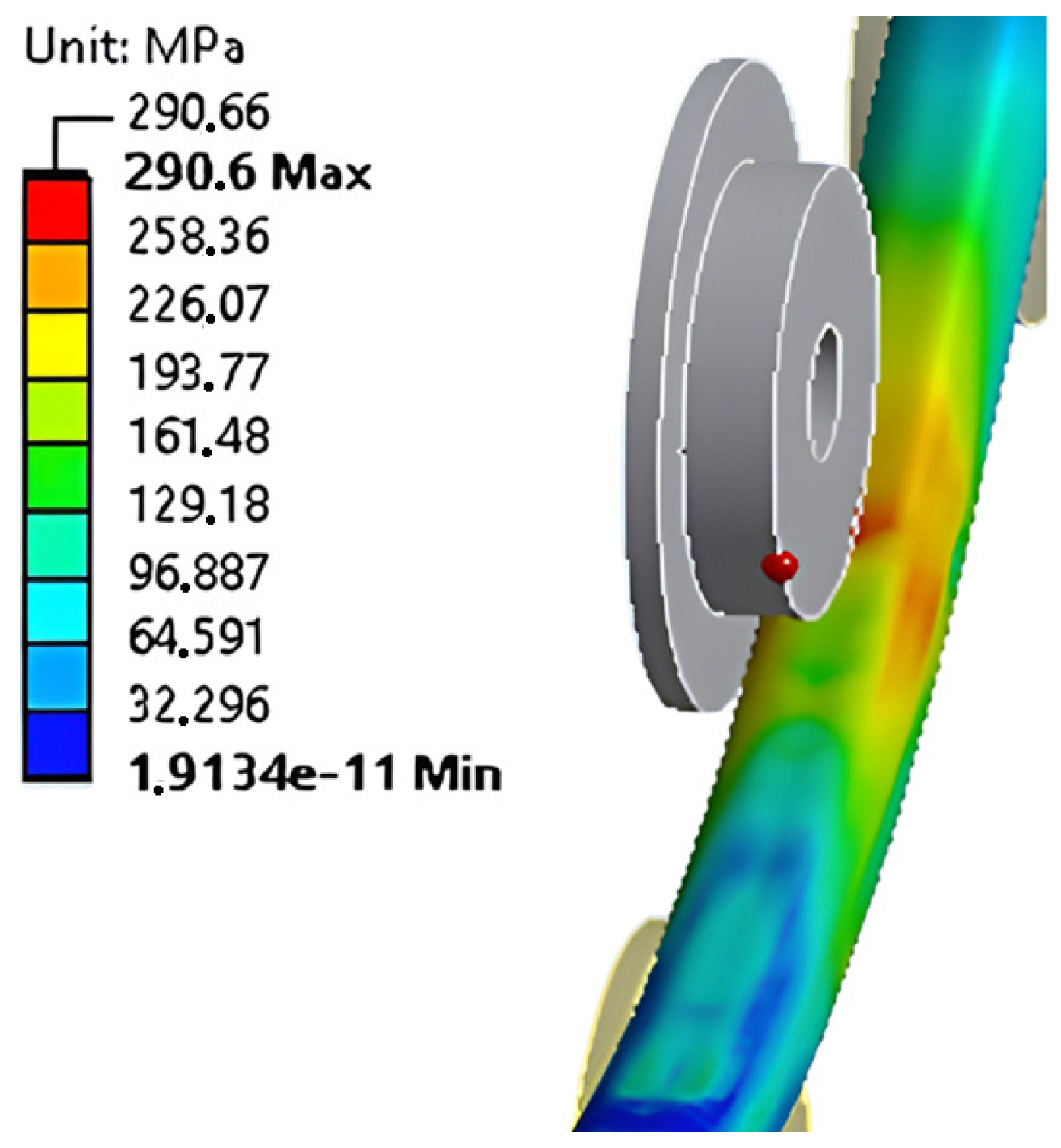
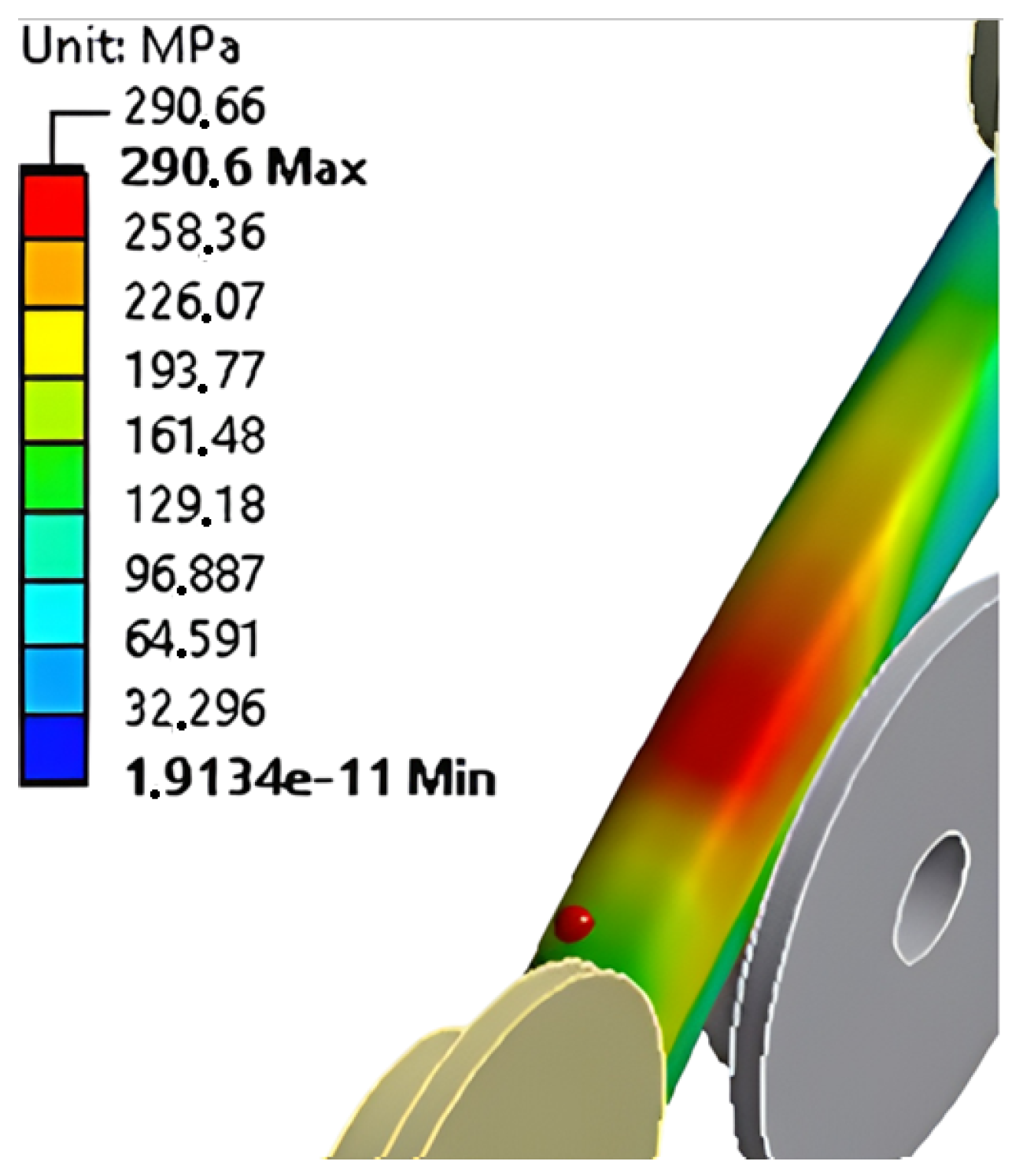
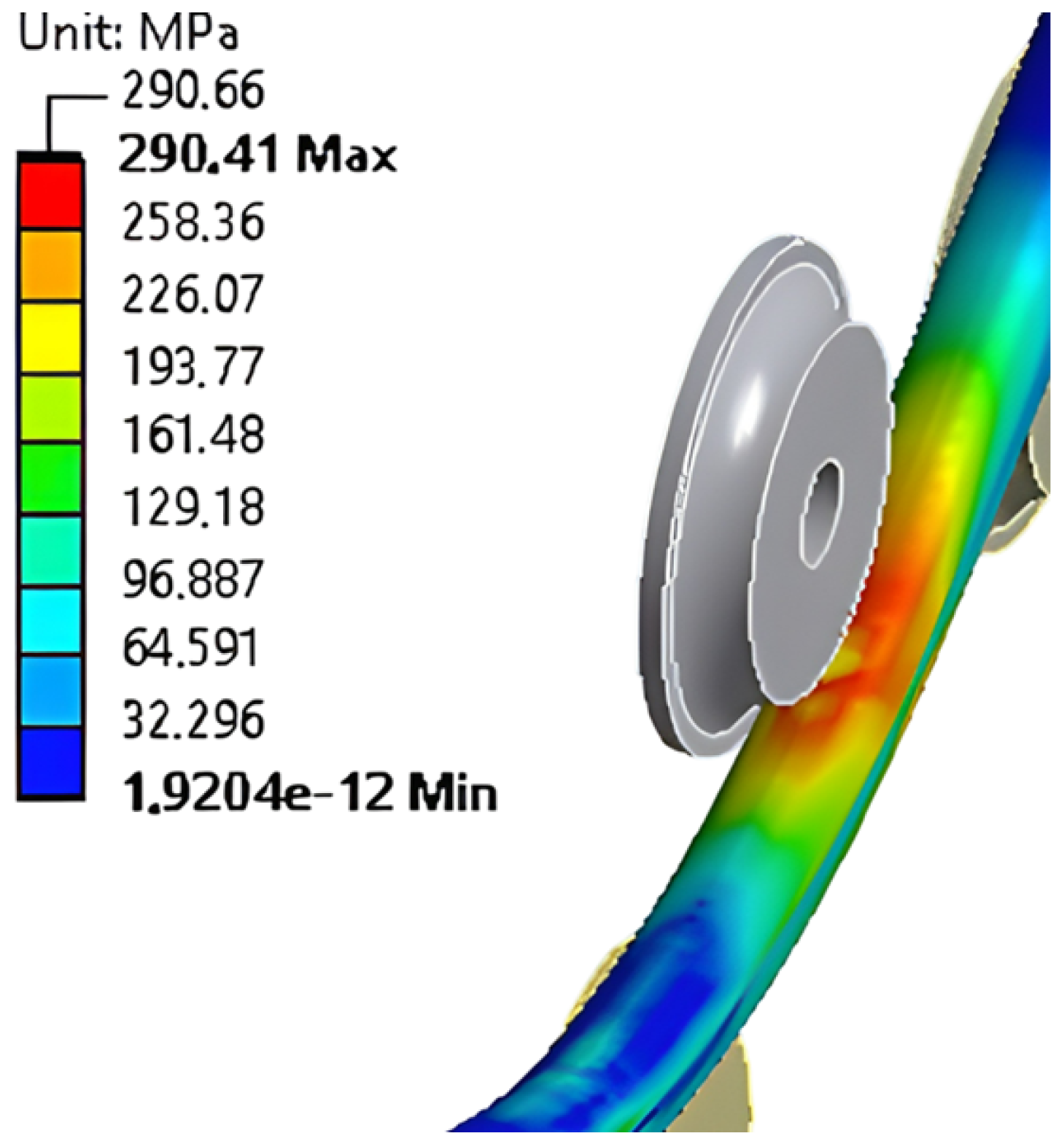
| 4120.40 | 253.43 | 1.15 | 0.13 | - |
| 1208.00 | 278.31 | 1.04 | 0.42 | - |
| 624.35 | 286.54 | 1.01 | 0.90 | 0.12 |
| 403.38 | 290.60 | 1.00 | 1.45 | 0.39 |
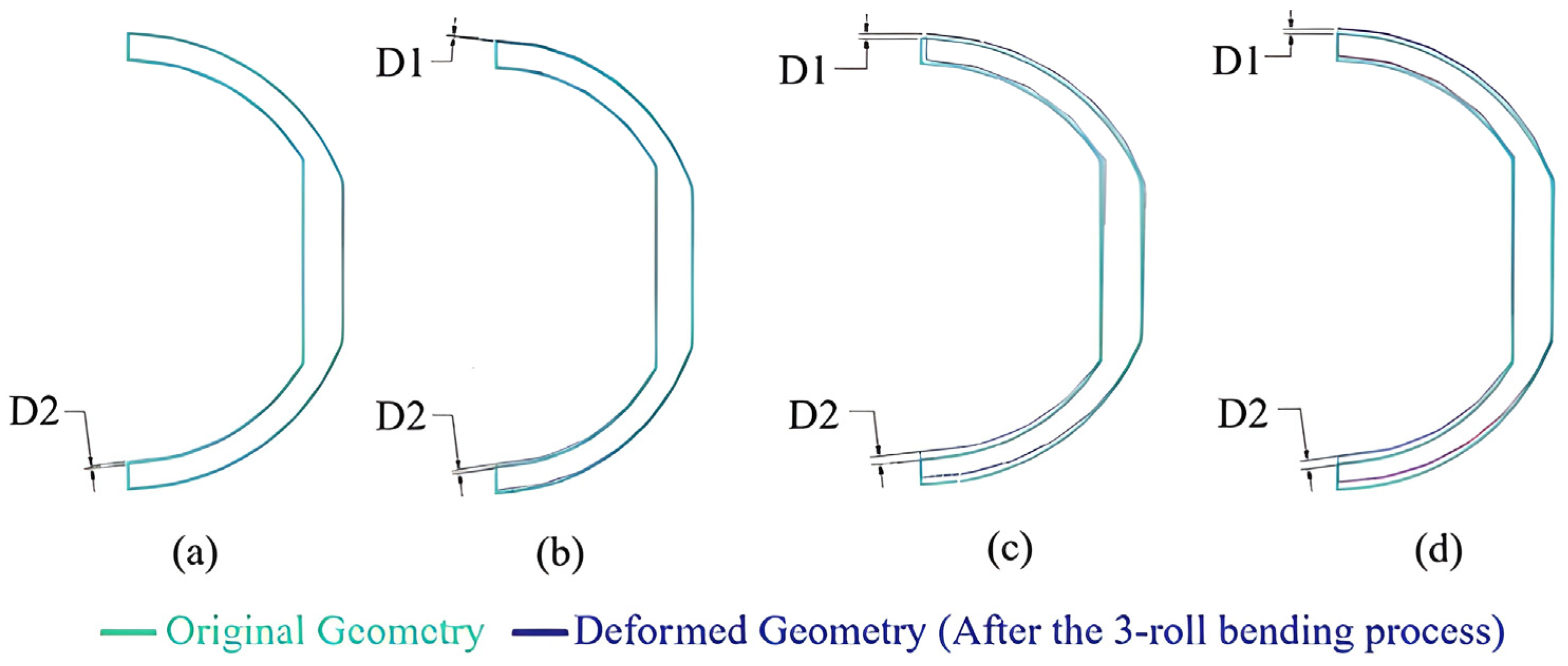
| r (mm) | (MPa) | Safety Factor | Displacement (mm) | |
|---|---|---|---|---|
| D1 | D2 | |||
| 3730.00 | 251.50 | 1.16 | - | 0.20 |
| 1127.50 | 274.15 | 1.06 | 0.04 | 0.30 |
| 591.92 | 288.56 | 1.00 | 0.36 | 0.67 |
| 388.21 | 290.41 | 1.00 | 0.43 | 0.69 |
| N° of Finite Elements | (MPa) | RD (%) | Processing Time |
|---|---|---|---|
| 41,444 | 203.29 | 23.36 | 16 h 41 min |
| 71,949 | 250.77 | 7.99 | 23 h 10 min |
| 81,082 | 270.82 | 5.47 | 29 h 03 min |
| 102,073 | 285.63 | 1.04 | 38 h 11 min |
| 158,954 | 288.61 | 0.53 | 60 h 22 min |
| 209,941 | 290.15 | 0.05 | 80 h 49 min |
| 293,825 | 289.99 | - | 121 h 12 min |
| r (mm) | (MPa) | Safety Factor | Displacement and Lateral Curvature Radius (mm) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| D1 | D2 | D3 | D4 | D5 | D6 | D7 | LR | |||
| 87,762.94 | 271.58 | 1.07 | 0.10 | 0.53 | 0.92 | 0.61 | 1.00 | 1.14 | 0.77 | 206,761.20 |
| 54,688.19 | 290.37 | 1.00 | 0.33 | 0.61 | 2.68 | 1.18 | 3.24 | 3.16 | 1.48 | 200,010.10 |
| 2335.39 | 290.62 | 1.00 | 1.48 | 3.97 | 5.85 | 3.60 | 8.09 | 8.54 | 5.55 | 83,255.08 |
| N° of Finite Elements | (MPa) | RD (%) | Processing Time |
|---|---|---|---|
| 49,532 | 211.87 | 13.38 | 45 h 44 min |
| 66,571 | 240.22 | 10.60 | 32 h 21 min |
| 78,522 | 265.69 | 3.46 | 55 h 27 min |
| 90,054 | 274.88 | 1.19 | 79 h 33 min |
| 109,857 | 278.15 | 0.34 | 107 h 22 min |
| 125,054 | 279.09 | - | 159 h 56 min |
| r (mm) | (MPa) | Safety Factor | Displacement (mm) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | D10 | D11 | LR | |||
| 34,321.23 | 288.17 | 1.01 | 0.22 | 0.22 | 0.14 | 0.15 | 0.69 | 0.09 | 0.22 | 0.11 | 0.15 | 0.07 | 0.10 | 181,603.26 |
| 20,133.95 | 289.93 | 1.00 | 1.31 | 0.67 | 1.14 | 0.85 | 1.55 | 1.25 | 1.27 | 1.84 | 1.63 | 1.75 | 0.96 | 137,235.65 |
| 13,052.88 | 290.59 | 1.00 | 2.46 | 1.60 | 2.19 | 1.92 | 3.12 | 2.57 | 2.94 | 4.10 | 2.95 | 3.38 | 2.62 | 115,457.82 |
| N° of Finite Elements | (MPa) | RD (%) | Processing Time |
|---|---|---|---|
| 7900 | 158.15 | 16.77 | 01 h 01 min |
| 12,723 | 184.68 | 17.90 | 01 h 22 min |
| 17,214 | 217.74 | 12.18 | 02 h 04 min |
| 20,255 | 244.26 | 7.39 | 02 h 51 min |
| 29,736 | 262.30 | 7.08 | 04 h 21 min |
| 36,012 | 243.72 | 0.71 | 05 h 32 min |
| 47,667 | 245.45 | 0.52 | 08 h 28 min |
| 54,142 | 246.73 | 0.25 | 09 h 37 min |
| 84,611 | 246.12 | - | 14 h 55 min |
| r (mm) | (MPa) | Safety Factor | Displacement (mm) | |
|---|---|---|---|---|
| D1 | D2 | |||
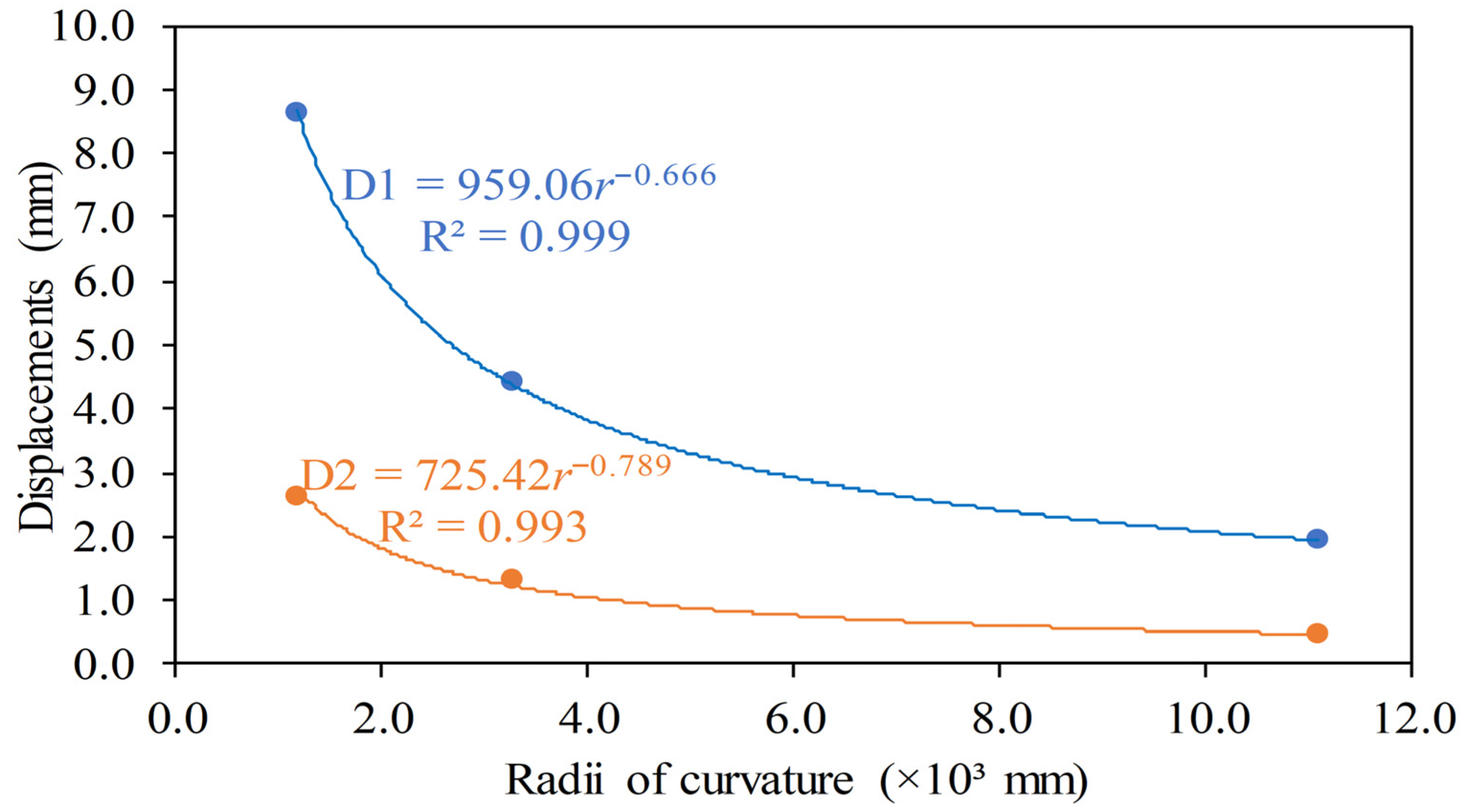
| 11,084.39 | 286.72 | 1.01 | 1.93 | 0.45 |
| 3267.92 | 290.26 | 1.00 | 4.42 | 1.33 |
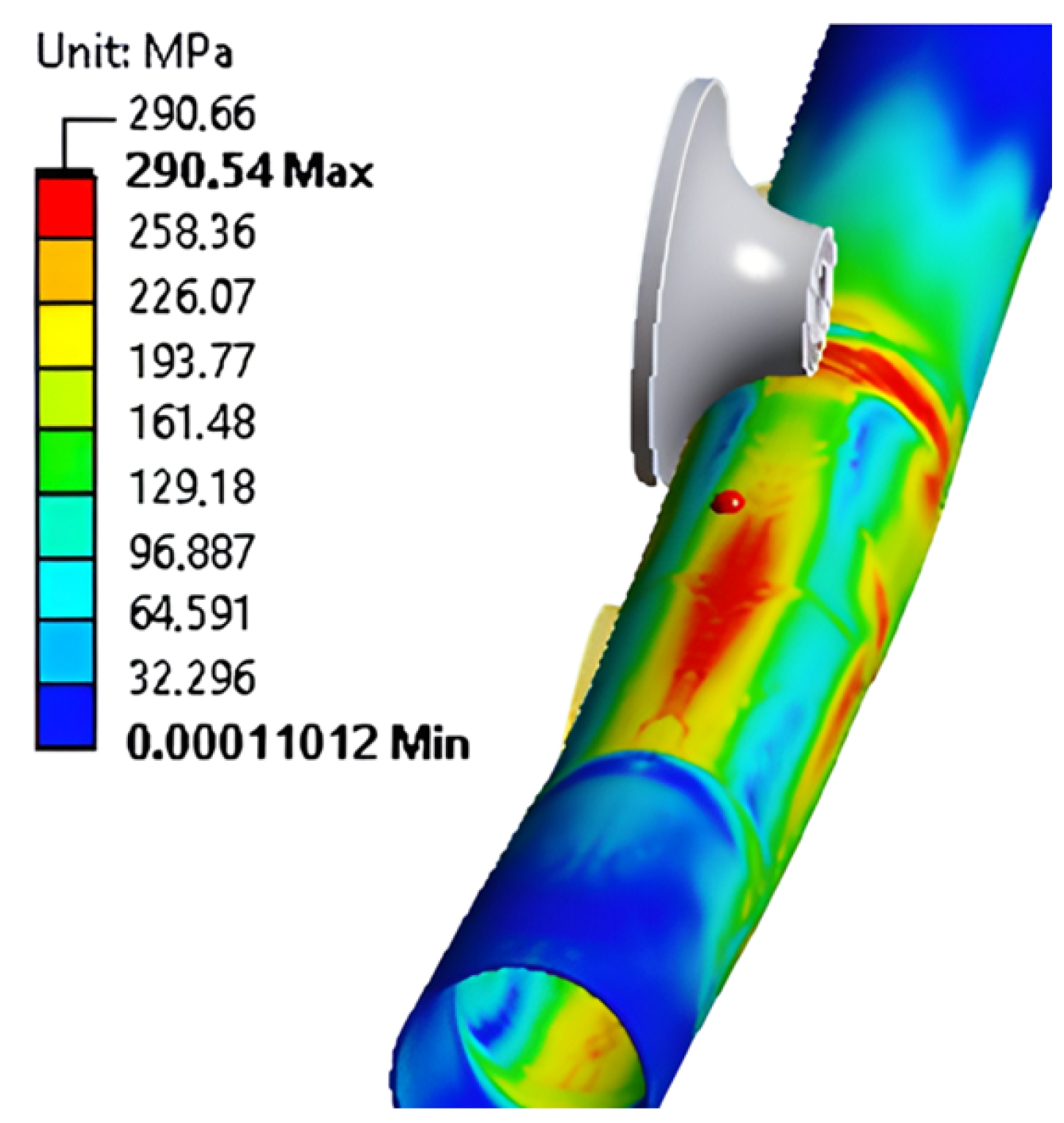
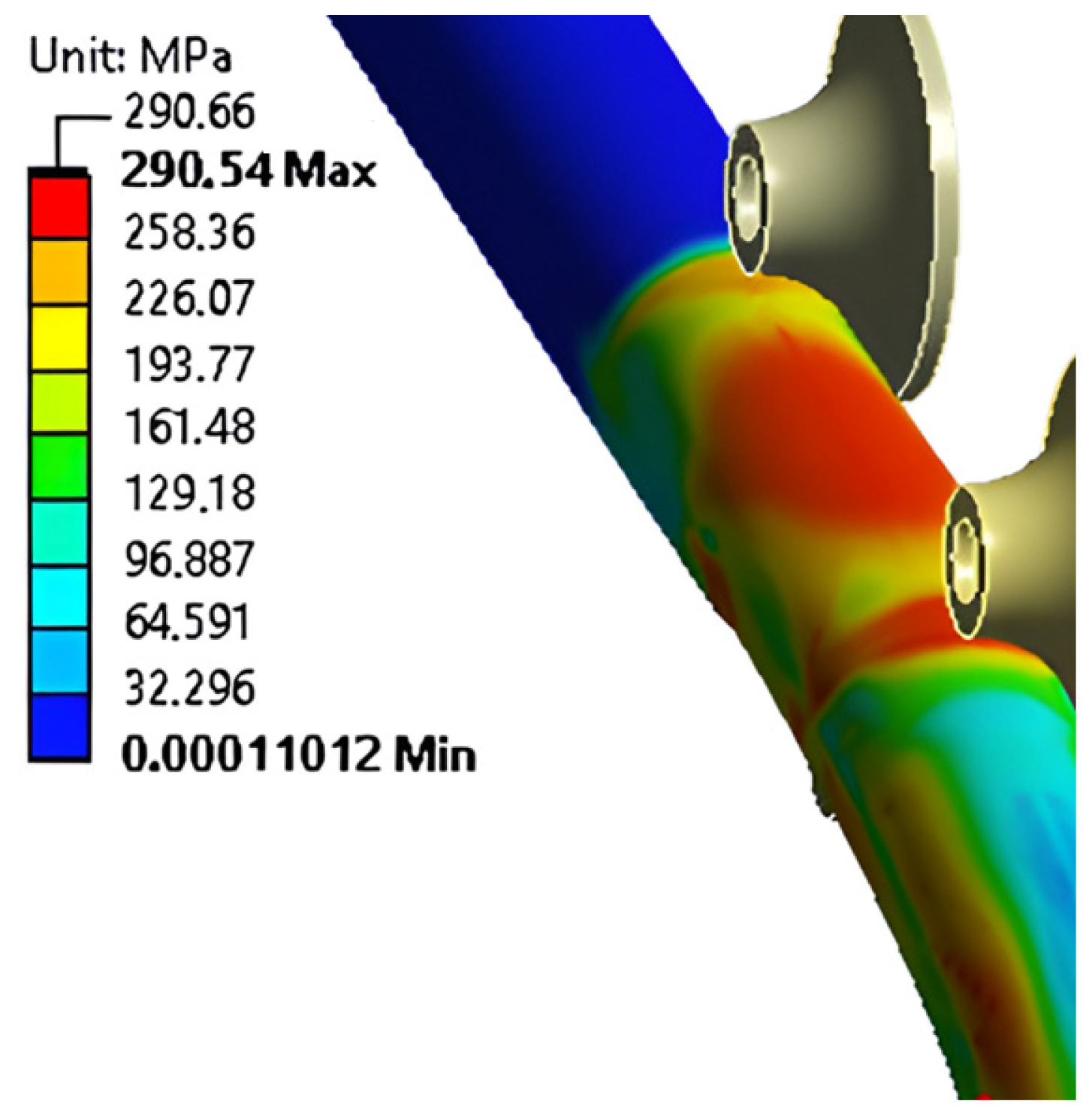
| 1166.53 | 290.54 | 1.00 | 8.64 | 2.64 |
| N° of Finite Elements | (MPa) | RD (%) | Processing Time |
|---|---|---|---|
| 9029 | 178.25 | 11.88 | 01 h 01 min |
| 17,875 | 199.42 | 6.59 | 02 h 20 min |
| 20,488 | 212.57 | 2.27 | 03 h 13 min |
| 28,843 | 207.74 | 1.32 | 04 h 29 min |
| 34,147 | 209.44 | 0.50 | 05 h 27 min |
| 43,436 | 210.49 | - | 08 h 21 min |
| r (mm) | (MPa) | Safety Factor | Displacement (mm) | |
|---|---|---|---|---|
| D1 | D2 | |||
| 38,517.83 | 285.61 | 1.02 | 2.3 | 0.46 |
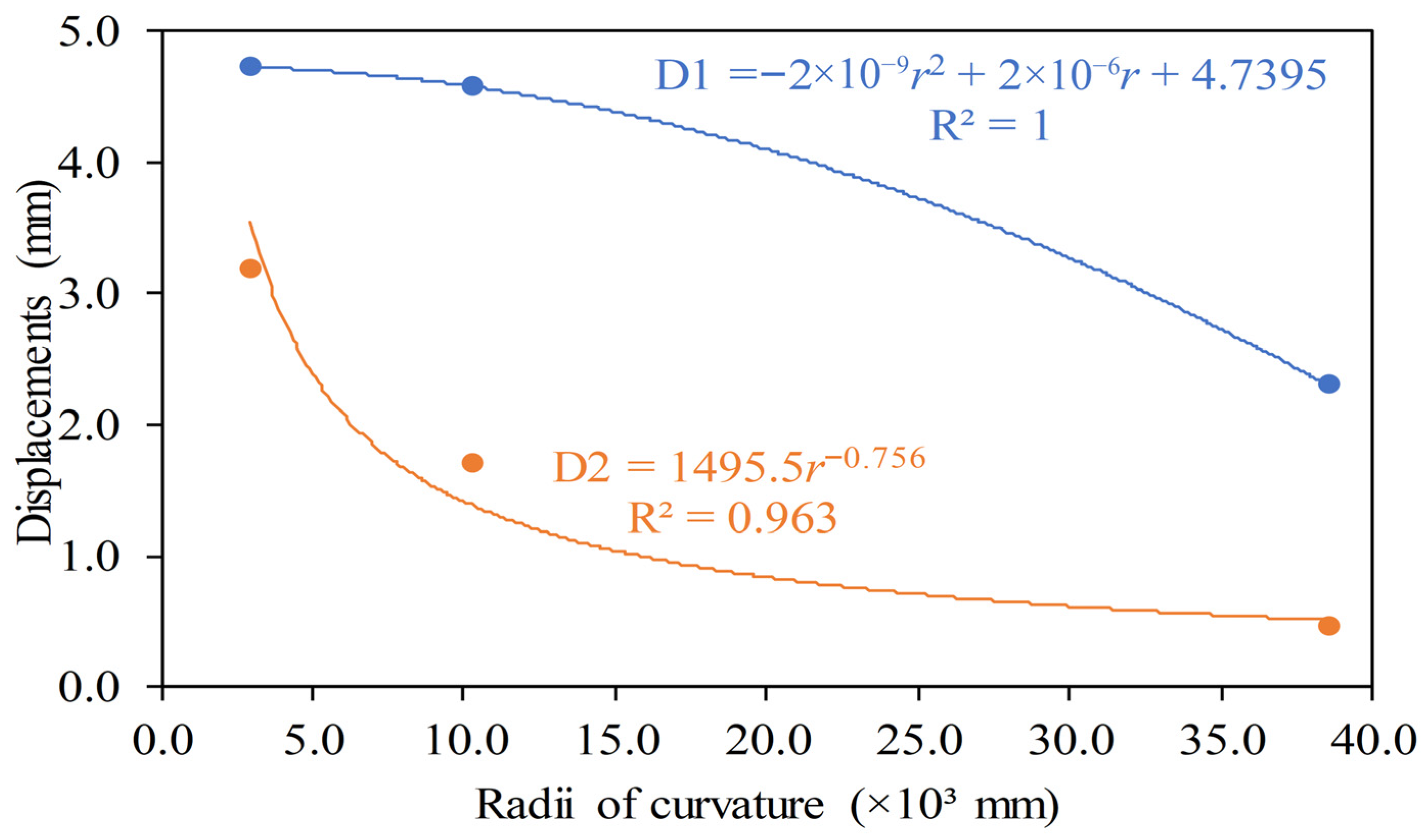
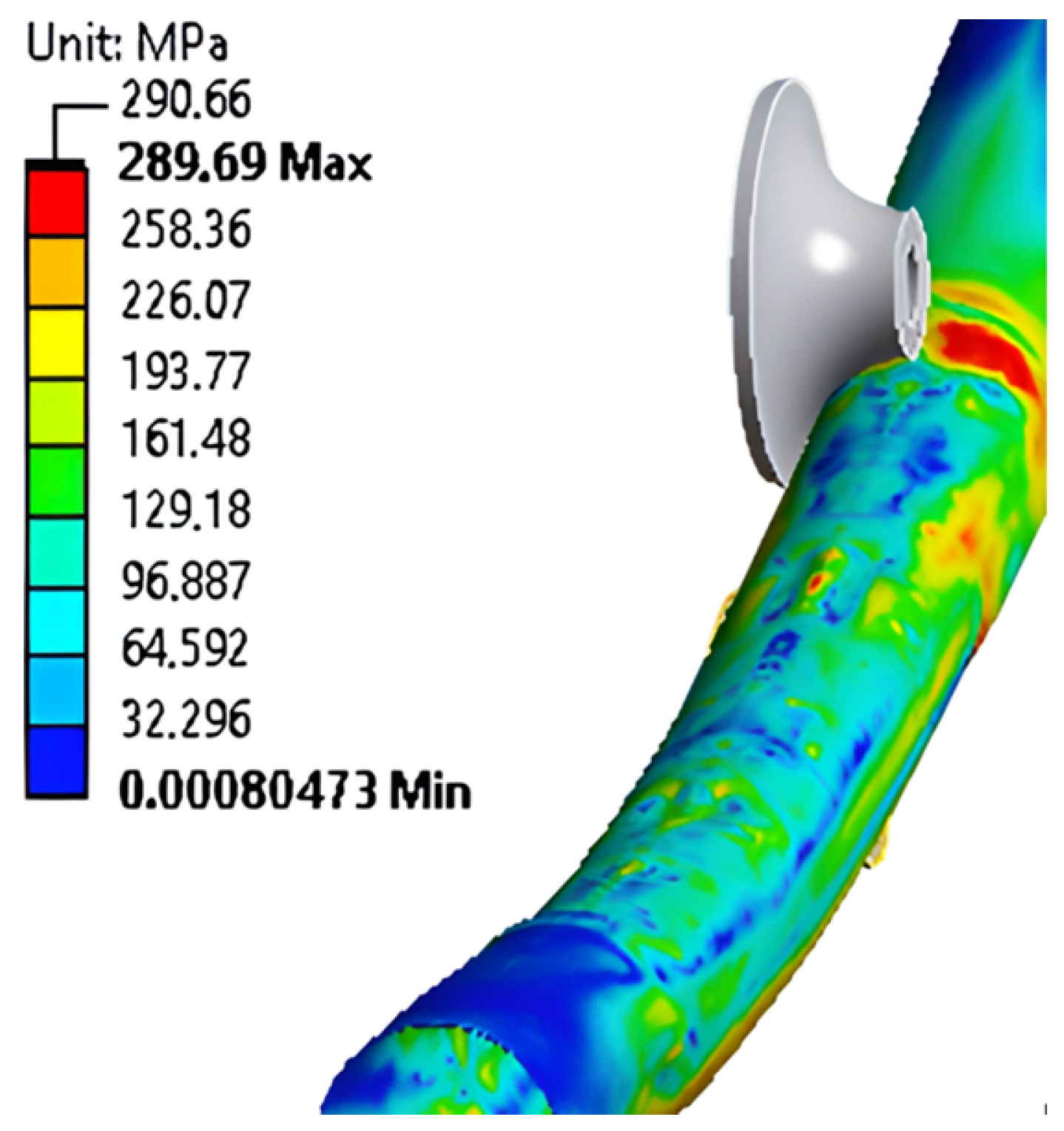
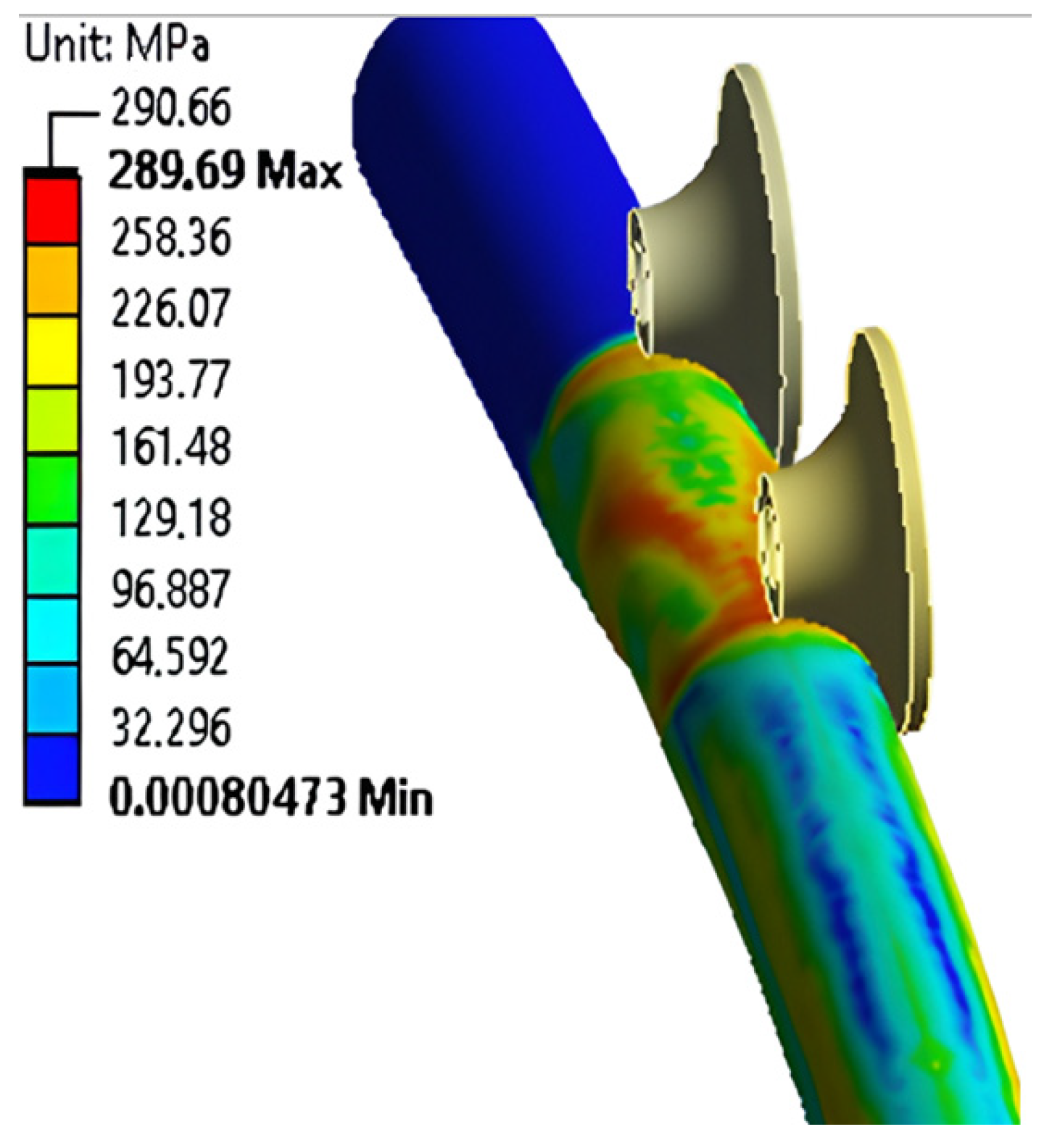
| 10,257.22 | 289.67 | 1.00 | 4.58 | 1.71 |
| 2961.42 | 289.69 | 1.00 | 4.73 | 3.18 |
| N° of Finite Elements | (MPa) | RD (%) | Processing Time |
|---|---|---|---|
| 17,471 | 147.47 | 96.45 | 02 h 31 min |
| 25,110 | 289.78 | 16.88 | 03 h 22 min |
| 33,423 | 240.86 | 10.36 | 04 h 46 min |
| 42,260 | 215.89 | 1.78 | 06 h 21 min |
| 54,629 | 212.05 | 0.49 | 08 h 45 min |
| 87,469 | 213.09 | - | 13 h 33 min |
| r (mm) | (MPa) | Safety Factor | Displacement (mm) |
|---|---|---|---|
| D1 | |||
| 3332.62 | 249.49 | 1.16 | 0.04 |
| 1035.73 | 274.25 | 1.06 | 0.14 |
| 696.30 | 286.44 | 1.01 | 0.26 |
| 581.53 | 289.06 | 1.00 | 0.29 |
| r (mm) | (MPa) | Safety Factor | Displacement (mm) |
|---|---|---|---|
| D1 | |||
| 3280.12 | 256.17 | 1.13 | 0.05 |
| 1045.88 | 280.55 | 1.04 | 0.15 |
| 548.58 | 290.15 | 1.00 | 0.16 |
| 356.16 | 290.61 | 1.00 | 0.32 |
| Profile | Smallest Radius Analyzed (mm) | Maximum Stress at Smallest r (MPa) | Safe Minimum Bending Radius (mm) | Limiting Factor |
|---|---|---|---|---|
| 1 | 4120.40 | 253.43 | ≈4000 | Orientation effects (D1 vs. D2) |
| 2 | 2335.39 | 290.62 | >54,688 | Stresses at UTS and strong LR |
| 3 | 13,052.88 | 290.59 | >20,000 | Thin branches, ovalization, local buckling and strong LR |
| 4 | 1166.53 | 290.54 | >3200 | Thin-walled tube, ovalization |
| 5 | 2961.42 | 289.69 | >10,000 | Very thin wall (1.50 mm), global ovalization |
| 6 | 356.16 | 290.61 | ≈500 | Risk of failure despite small displacements |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreira, M.d.S.; Guilherme, C.E.M.; de Souza, J.H.C.; dos Santos, E.D.; Isoldi, L.A. Numerical Analysis of the Three-Roll Bending Process of 6061-T6 Aluminum Profiles with Multiple Bending Radii Using the Finite Element Method. Metals 2025, 15, 1097. https://doi.org/10.3390/met15101097
Moreira MdS, Guilherme CEM, de Souza JHC, dos Santos ED, Isoldi LA. Numerical Analysis of the Three-Roll Bending Process of 6061-T6 Aluminum Profiles with Multiple Bending Radii Using the Finite Element Method. Metals. 2025; 15(10):1097. https://doi.org/10.3390/met15101097
Chicago/Turabian StyleMoreira, Mauricio da Silva, Carlos Eduardo Marcos Guilherme, João Henrique Corrêa de Souza, Elizaldo Domingues dos Santos, and Liércio André Isoldi. 2025. "Numerical Analysis of the Three-Roll Bending Process of 6061-T6 Aluminum Profiles with Multiple Bending Radii Using the Finite Element Method" Metals 15, no. 10: 1097. https://doi.org/10.3390/met15101097
APA StyleMoreira, M. d. S., Guilherme, C. E. M., de Souza, J. H. C., dos Santos, E. D., & Isoldi, L. A. (2025). Numerical Analysis of the Three-Roll Bending Process of 6061-T6 Aluminum Profiles with Multiple Bending Radii Using the Finite Element Method. Metals, 15(10), 1097. https://doi.org/10.3390/met15101097









