Microstructural Analysis and Constitutive Modeling of Superplastic Deformation Behavior of Al-Mg-Zn-Cu-Zr-xNi Alloys with Different Ni Contents
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Microstructure Analysis
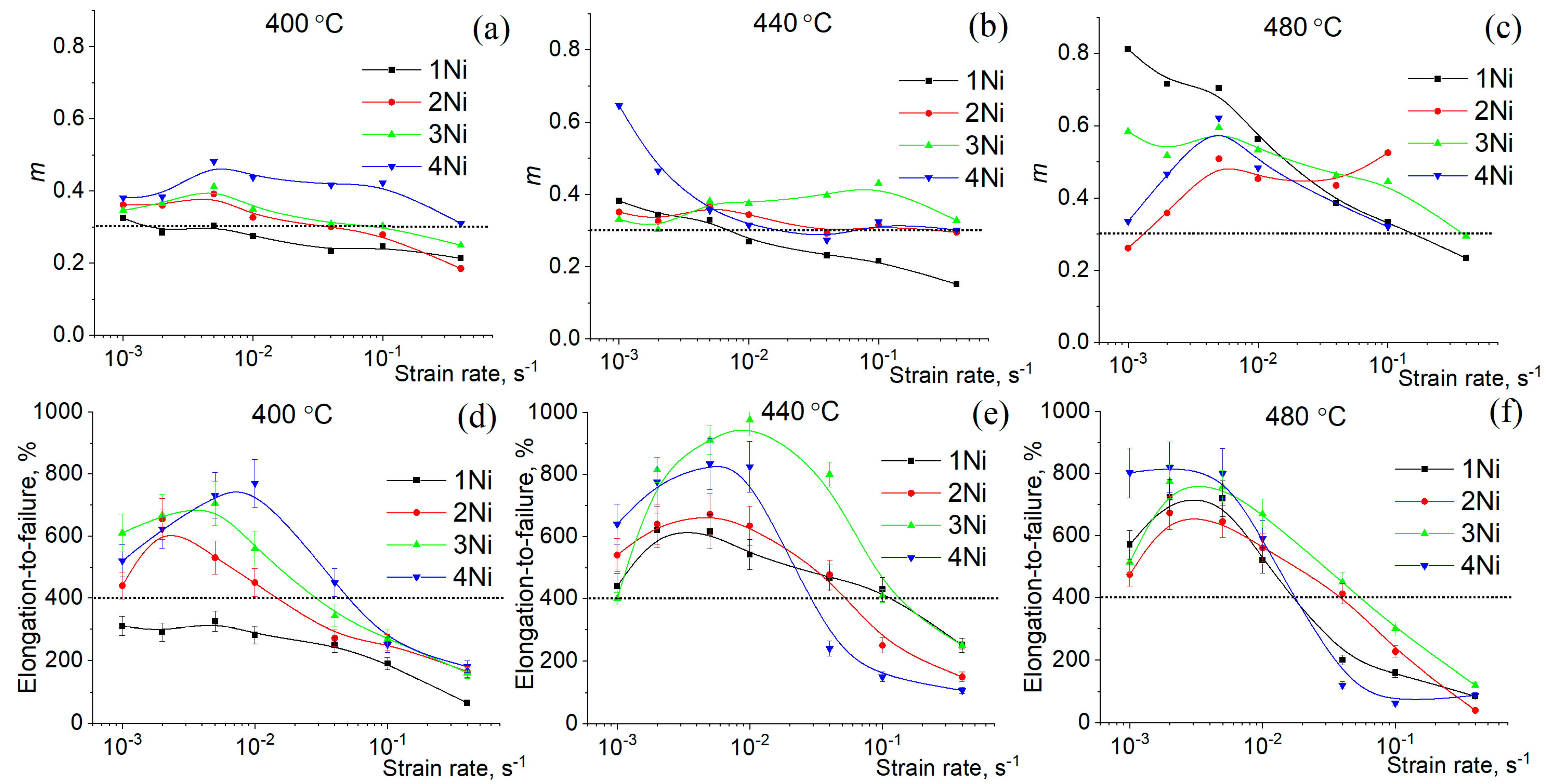
3.2. Superplastic Deformation Behavior
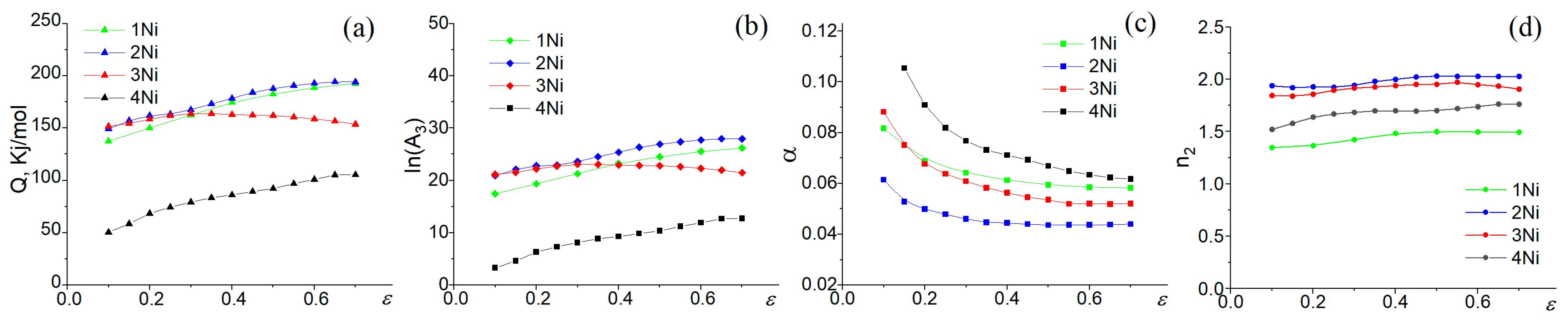
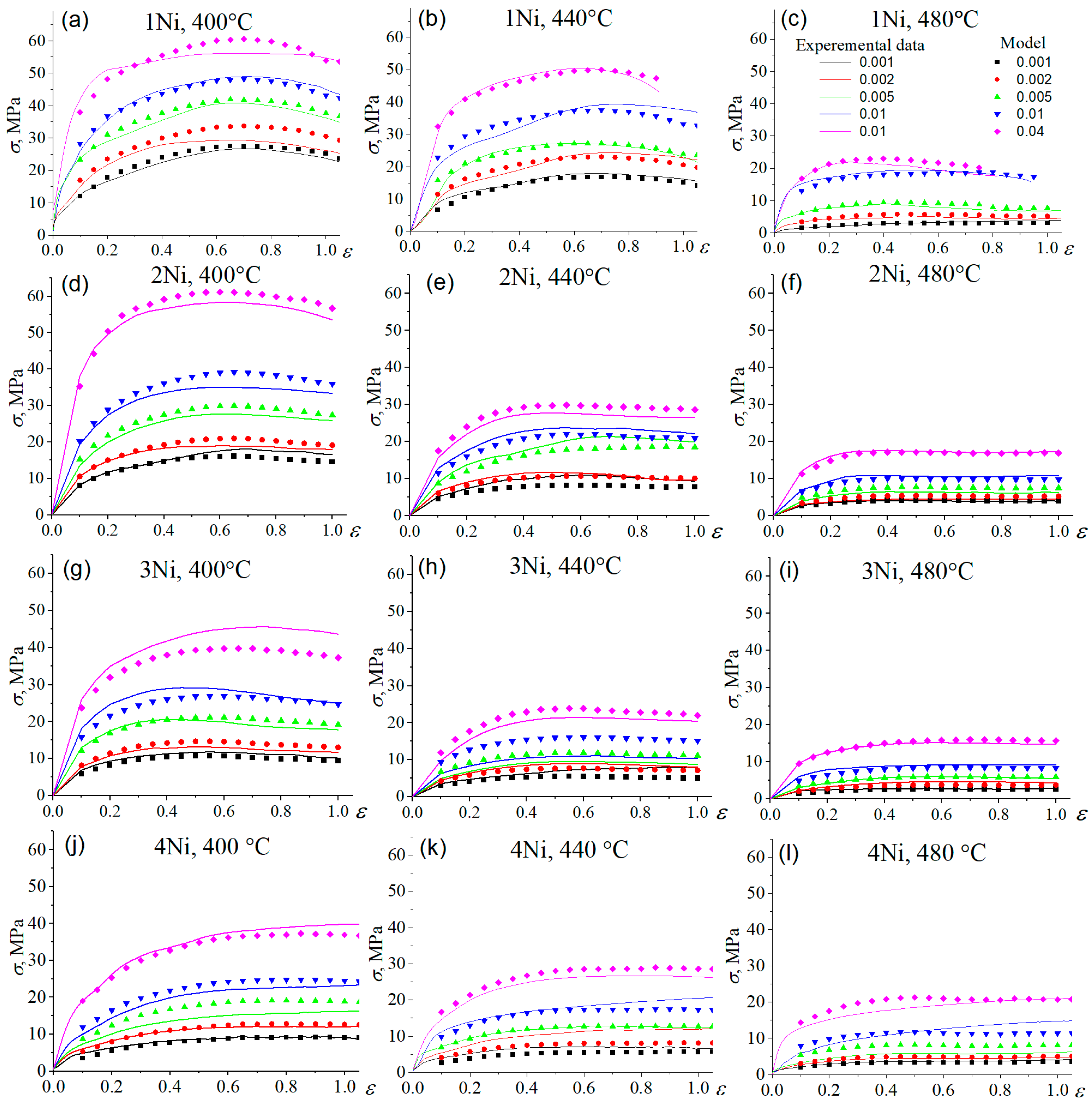
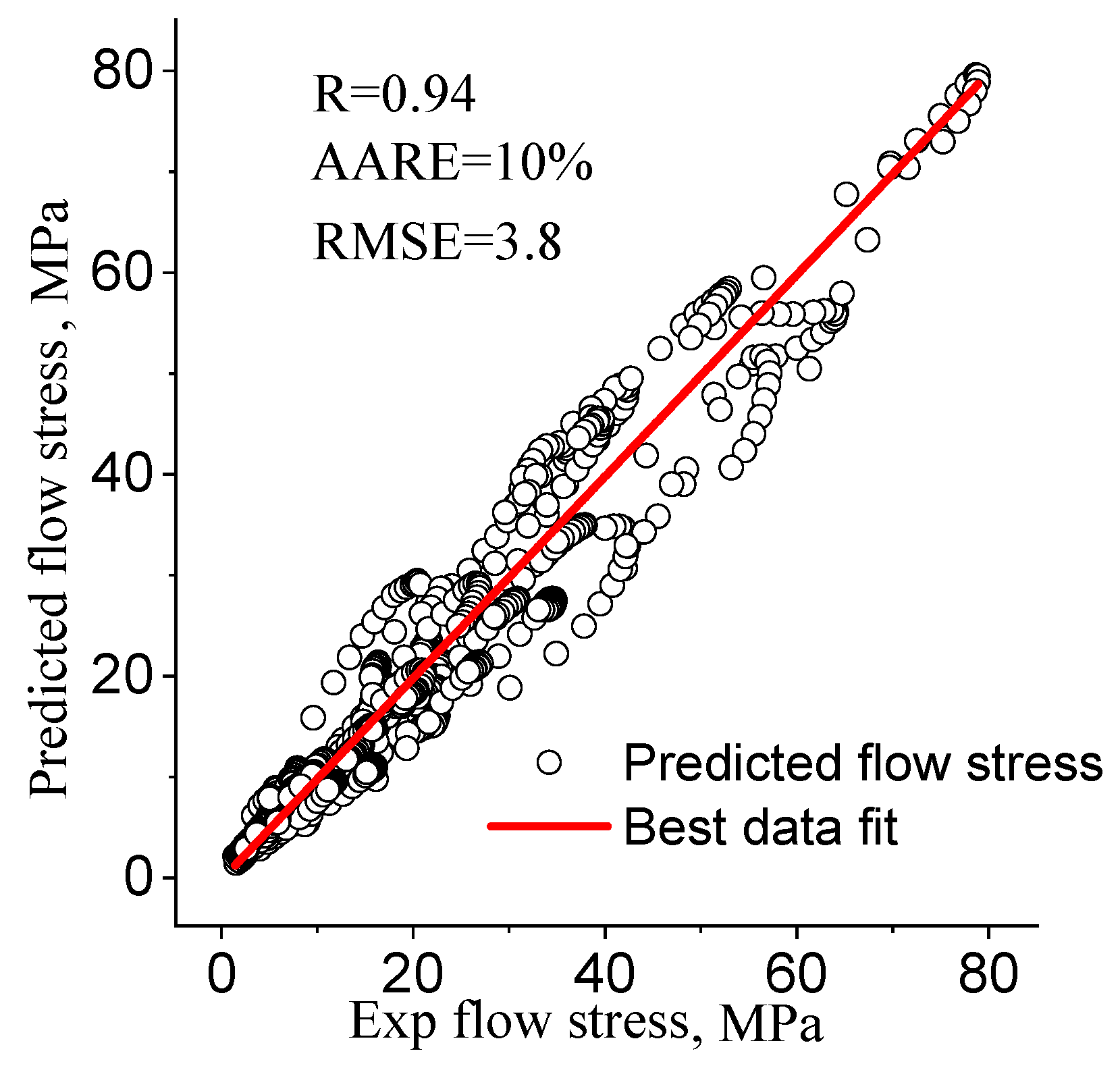
3.3. The Constitutive Model
4. Conclusions
- According to the microstructural and XRD data, the alloys contained coarse particles of the Al3Ni and T(Mg32(Al,Zn)49 phase in which Cu was dissolved. The T-phase fraction was ~3% for the low temperature of 400 °C and >1% at 440 °C, and it was completely dissolved at 480 °C. The particle size varied in the range of 0.6–1.3 µm, and the total fraction increased from 2 to 16% with an increasing Ni content and decreasing temperature.
- Prior to the onset of superplastic flow, the grain structure of the alloys was non-recrystallized at 400 °C and partially recrystallized at 440–480 °C. Increasing the fraction of micrometer-sized particles increased the proportions of high-angle grain boundaries and recrystallized grains and decreased the mean grain size. Significant changes were defined when the total fraction of particles increased from ~2.5 to ~6%.
- The alloys showed excellent superplasticity in a temperature range of 400–480 °C and a wide strain rate range of 10−3 to 10−2 s−1 with elongation above 400% and a strain rate sensitivity coefficient m above 0.3. The alloys with 1.9–3.2% Ni and 6–9% coarse particles were superplastic up to 10−1 s−1 at 440–480 °C with elongation up to 950%. A high fraction of second T-phase and Al3Ni-phase particles of ~12% with a mean size of 0.6 µm provided good superplasticity, with an elongation of ~700–800% at a low temperature of 400 °C and a high strain rate of (0.5–1) × 10−2 s−1.
- The effect of strain on the flow stress was integrated into the material constants, specifically A, n, α, and Q. A fifth-order polynomial was identified as the optimal representation of the influence of strain on the material constants, exhibiting excellent correlation and generalization. The strain-compensated constitutive model demonstrated accurate prediction of the flow behavior of the investigated alloys. The effective activation energy (Q) of superplastic deformation decreased from ~150–160 kJ/mol to ~90–100 kJ/mol with an increase in the fraction of Al3Ni particles, which facilitated dynamic recrystallization, high-angle grain boundary formation, and the grain boundary sliding deformation mechanism.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Langdon, T.G. Seventy-Five Years of Superplasticity: Historic Developments and New Opportunities. J. Mater. Sci. 2009, 44, 5998–6010. [Google Scholar] [CrossRef]
- Bhatta, L.; Pesin, A.; Zhilyaev, A.P.; Tandon, P.; Kong, C.; Yu, H. Recent Development of Superplasticity in Aluminum Alloys: A Review. Metals 2020, 10, 77. [Google Scholar] [CrossRef]
- Mohamed, F.A. Creep and Superplasticity: Evolution and Rationalization. Adv. Eng. Mater. 2020, 22, 1900532. [Google Scholar] [CrossRef]
- Padmanabhan, K.A.; Divinski, S.V. A Mean Field Description of Steady State Isotropic Structural Superplastic Deformation. Mater. Sci. Eng. A 2024, 908, 146713. [Google Scholar] [CrossRef]
- Savaedi, Z.; Motallebi, R.; Mirzadeh, H.; Mehdinavaz Aghdam, R.; Mahmudi, R. Superplasticity of Fine-Grained Magnesium Alloys for Biomedical Applications: A Comprehensive Review. Curr. Opin. Solid State Mater. Sci. 2023, 27, 101058. [Google Scholar] [CrossRef]
- Blandin, J.J. Superplasticity of Metallic Alloys: Some Current Findings and Open Questions. Mater. Sci. Forum 2016, 838–839, 13–22. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, Z.; Jiang, S.; Wang, Y.; Chen, Y.; Li, X.; Wang, Q. Effect of Temperature on Superplastic Deformation Behavior of 2198 Al–Cu–Li Alloy. Mater. Sci. Eng. A 2024, 891, 145988. [Google Scholar] [CrossRef]
- Kweitsu, E.K.; Sarkar, D.K.; Chen, X.-G. A Short Review on Superplasticity of Aluminum Alloys. In Proceedings of the 15th International Aluminium Conference, Québec, QC, Canada, 11–13 October 2023; MDPI: Basel, Switzerland, 27 September 2023; p. 43. [Google Scholar]
- Barnes, A.J. Superplastic Forming 40 Years and Still Growing. J. Mater. Eng. Perform. 2007, 16, 440–454. [Google Scholar] [CrossRef]
- Shveykin, A.I.; Vshivkova, A.A.; Trusov, P.V. Methods of Accounting for Temperature and Strain Rate Variation in Multilevel Constitutive Models of Metal Deformation (Analytical Review). Phys. Mesomech. 2024, 27, 133–151. [Google Scholar] [CrossRef]
- Higashi, K. High Strain Rate Superplasticity in Japan. Mater. Sci. Technol. 2000, 16, 1320–1329. [Google Scholar] [CrossRef]
- Singh, N.; Agrawal, M.K. Effect of Equal Channel Angular Pressing on Strain Deformation Behavior of Ultrafine Grained during Low Temperature Superplasticity of AA5083. Results Eng. 2024, 22, 102221. [Google Scholar] [CrossRef]
- Figueiredo, R.B. Strain-Rate Sensitivity Maps and the Estimation of Ductility for Low Temperature Superplasticity. J. Mater. Sci. 2024, 59, 5854–5871. [Google Scholar] [CrossRef]
- Kawasaki, M.; Langdon, T.G. Developing Superplasticity in Ultrafine-Grained Metals. Acta Phys. Pol. A 2015, 128, 470–478. [Google Scholar] [CrossRef]
- Song, Z.; Niu, R.; Cui, X.; Bobruk, E.V.; Murashkin, M.Y.; Enikeev, N.A.; Gu, J.; Song, M.; Bhatia, V.; Ringer, S.P.; et al. Mechanism of Room-Temperature Superplasticity in Ultrafine-Grained Al–Zn Alloys. Acta Mater. 2023, 246, 118671. [Google Scholar] [CrossRef]
- Kotov, A.D.; Mikhaylovskaya, A.V.; Kishchik, M.S.; Tsarkov, A.A.; Aksenov, S.A.; Portnoy, V.K. Superplasticity of High-Strength Al-Based Alloys Produced by Thermomechanical Treatment. J. Alloys Compd. 2016, 688, 336–344. [Google Scholar] [CrossRef]
- Jia, Z.; Hu, G.; Forbord, B.; Solberg, J.K. Effect of Homogenization and Alloying Elements on Recrystallization Resistance of Al-Zr-Mn Alloys. Mater. Sci. Eng. A 2007, 444, 284–290. [Google Scholar] [CrossRef]
- Bennett, T.A.; Petrov, R.H.; Kestens, L.A.I.; Zhuang, L.Z.; de Smet, P. The Effect of Particle-Stimulated Nucleation on Texture Banding in an Aluminium Alloy. Scr. Mater. 2010, 63, 461–464. [Google Scholar] [CrossRef]
- Troeger, L.P.; Starke, E.A. Particle-Stimulated Nucleation of Recrystallization for Grain-Size Control and Superplasticity in an Al-Mg-Si-Cu Alloy. Mater. Sci. Eng. A 2000, 293, 19–29. [Google Scholar] [CrossRef]
- Li, J.; Ye, Z.; Fu, J.; Qi, W.; Tian, Y.; Liu, L.; Wang, X. Microstructure Evolution, Texture and Laser Surface HEACs of Al-Mg-Si Alloy for Light Automobile Parts. Mater. Charact. 2020, 160, 110093. [Google Scholar] [CrossRef]
- Goetz, R.L. Particle Stimulated Nucleation during Dynamic Recrystallization Using a Cellular Automata Model. Scr. Mater. 2005, 52, 851–856. [Google Scholar] [CrossRef]
- Hyde, K.B.; Bate, P.S. Dynamic Grain Growth in Al-6Ni: Modelling and Experiments. Acta Mater. 2005, 53, 4313–4321. [Google Scholar] [CrossRef]
- Mikhaylovskaya, A.V.; Esmaeili Ghayoumabadi, M.; Mochugovskiy, A.G. Superplasticity and Mechanical Properties of Al–Mg–Si Alloy Doped with Eutectic-Forming Ni and Fe, and Dispersoid-Forming Sc and Zr Elements. Mater. Sci. Eng. A 2021, 817, 141319. [Google Scholar] [CrossRef]
- Jin, H.; Amirkhiz, B.S.; Lloyd, D.J. Improvement of Superplasticity in High-Mg Aluminum Alloys by Sacrifice of Some Room Temperature Formability. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2018, 49, 1962–1979. [Google Scholar] [CrossRef]
- Komelkov, A.V.; Nokhrin, A.V.; Bobrov, A.A.; Sysoev, A.N. Thermal Stability of Microstructure and Properties of Ingots and Fine Wires from Al–Zr Alloys. Phys. Met. Metallogr. 2024, 125, 673–682. [Google Scholar] [CrossRef]
- Nokhrin, A.; Gryaznov, M.; Shotin, S.; Nagicheva, G.; Chegurov, M.; Bobrov, A.; Kopylov, V.; Chuvil’deev, V. Effect of Sc, Hf, and Yb Additions on Superplasticity of a Fine-Grained Al-0.4%Zr Alloy. Metals 2023, 13, 133. [Google Scholar] [CrossRef]
- Myshlyaev, M.; Korznikova, G.; Konkova, T.; Korznikova, E.; Aletdinov, A.; Khalikova, G.; Raab, G.; Mironov, S. Microstructural Evolution during Superplastic Deformation of Al-Mg-Li Alloy: Dynamic Recrystallization or Grain-Boundary Sliding? J. Alloys Compd. 2023, 936, 168302. [Google Scholar] [CrossRef]
- Gomes, C.F.S.; Antunes, A.d.S. Effects of Mn Concentration on Grain Boundary Pinning of 5083 Aluminum Alloy. Mater. Res. 2023, 26, e20220585. [Google Scholar] [CrossRef]
- Kishchik, A.A.A.; Mikhaylovskaya, A.V.V.; Kotov, A.D.D.; Rofman, O.V.V.; Portnoy, V.K.K. Al-Mg-Fe-Ni Based Alloy for High Strain Rate Superplastic Forming. Mater. Sci. Eng. A 2018, 718, 190–197. [Google Scholar] [CrossRef]
- Chuvil’deev, V.N.; Gryaznov, M.Y.; Shotin, S.V.; Nokhrin, A.V.; Likhnitskii, C.V.; Nagicheva, G.S.; Chegurov, M.K.; Kopylov, V.I.; Bobrov, A.A.; Shadrina, I.S. Effect of Sc/Zr Ratio on Superplastic Behavior of Ultrafine-Grained Al–6%Mg Alloys. Mater. Sci. Eng. A 2024, 898, 146409. [Google Scholar] [CrossRef]
- Zha, M.; Tian, T.; Jia, H.-L.; Zhang, H.-M.; Wang, H.-Y. Sc/Zr Ratio-Dependent Mechanisms of Strength Evolution and Microstructural Thermal Stability of Multi-Scale Hetero-Structured Al–Mg–Sc–Zr Alloys. J. Mater. Sci. Technol. 2023, 140, 67–78. [Google Scholar] [CrossRef]
- Kumar, V.S.S.; Viswanathan, D.; Natarajan, S. Theoretical Prediction and FEM Analysis of Superplastic Forming of AA7475 Aluminum Alloy in a Hemispherical Die. J. Mater. Process. Technol. 2006, 173, 247–251. [Google Scholar] [CrossRef]
- Mukhopadhyay, P.; Biswas, S.; Chokshi, A.H. Deformation Characterization of Superplastic AA7475 Alloy. Trans. Indian Inst. Met. 2009, 62, 149–152. [Google Scholar] [CrossRef]
- Chen, C.; Tan, M. Cavity Growth and Filament Formation of Superplastically Deformed Al 7475 Alloy. Mater. Sci. Eng. A 2001, 298, 235–244. [Google Scholar] [CrossRef]
- Mikhaylovskaya, A.V.; Yakovtseva, O.A.; Sitkina, M.N.; Kotov, A.D.; Irzhak, A.V.; Krymskiy, S.V.; Portnoy, V.K. Comparison between Superplastic Deformation Mechanisms at Primary and Steady Stages of the Fine Grain AA7475 Aluminium Alloy. Mater. Sci. Eng. A 2018, 718, 277–286. [Google Scholar] [CrossRef]
- Nguyena, M.T.; Nguyena, T.A. Evaluation of Superplastic Properties of AA7075 Aluminum Alloy Sheet Fabricated by Thermomechanical Processing. Int. J. Mod. Manuf. Technol. 2024, 16, 64–70. [Google Scholar] [CrossRef]
- Yakovtseva, O.A.; Sitkina, M.N.; Kotov, A.D.; Rofman, O.V.; Mikhaylovskaya, A.V. Experimental Study of the Superplastic Deformation Mechanisms of High-Strength Aluminum-Based Alloy. Mater. Sci. Eng. A 2020, 788, 139639. [Google Scholar] [CrossRef]
- Taylor, S.; Janik, V.; Grimes, R.; Dashwood, R. Study on the Influence of Nickel Additions on AA7020 Formability Under Superplastic Forming Like Conditions. Met. Mater. Int. 2023, 29, 2597–2604. [Google Scholar] [CrossRef]
- Sun, J.-H.; Gu, H.; Zhang, J.; Jiang, J.; Wu, G.-Q.; Sun, Z.-G. Ti6Al4V-0.72H on the Establishment of Flow Behavior and the Analysis of Hot Processing Maps. Crystals 2024, 14, 345. [Google Scholar] [CrossRef]
- Tan, S.; He, D.; Lin, Y.; Zheng, B.; Wu, H. Dislocation Substructures Evolution and an Informer Constitutive Model for a Ti-55511 Alloy in Two-Stages High-Temperature Forming with Variant Strain Rates in β Region. Materials 2023, 16, 3430. [Google Scholar] [CrossRef] [PubMed]
- Kondratev, N.S.; Trusov, P.V.; Podsedertsev, A.N. Multilevel Model of Polycrystals: Application to Assessing the Effect of Texture and Grains Misorientation on the Critical Deformation of the Dynamic Recrystallization Initiation. PNRPU Mech. Bull. 2021, 4, 83–97. [Google Scholar] [CrossRef] [PubMed]
- Khokhlov, A.V. Hybridization of a Linear Viscoelastic Constitutive Equation and a Nonlinear Maxwell-Type Viscoelastoplastic Model, and Analysis of Poisson’s Ratio Evolution Scenarios under Creep. Phys. Mesomech. 2024, 27, 229–255. [Google Scholar] [CrossRef]
- Khokhlov, A.V.; Gulin, V.V. Analysis of the Properties of a Nonlinear Model for Shear Flow of Thixotropic Media Taking into Account the Mutual Influence of Structural Evolution and Deformation. Phys. Mesomech. 2023, 26, 621–642. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Z.; Ma, X.; Peng, Q.; Zhang, G.; Wang, Y.; Li, Z. Microstructural-Mechanical Property Evolution of AA7075 Welds with Different Filler during Heat Treatment. Mater. Sci. Technol. 2024, 40, 1193–1201. [Google Scholar] [CrossRef]
- Azpeitia, M.R.; Elizabeth Martínez Flores, E.; Castillo, A.A.T.; Rivera, J.L.H.; Villaseñor, G.T. Phenomenological Model for the Dynamic Superplastic Deformation Mechanism in a Zn-Al Eutectoid Alloy Modified with 2 Wt% Cu. Met. Mater. Int. 2024, 30, 3014–3029. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Q.; Wang, K.; Wu, J.; Hu, P. A Multi-Scale Constitutive Model Based Gas Pressure Determination Method for the Grain Size Evolution of Superplastic Forming. Int. J. Lightweight Mater. Manuf. 2024, 7, 825–837. [Google Scholar] [CrossRef]
- Lv, J.; Zheng, J.H.; Yardley, V.A.; Shi, Z.; Lin, J. A Review of Microstructural Evolution and Modelling of Aluminium Alloys under Hot Forming Conditions. Metals 2020, 10, 1516. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, G.; Deng, G.; Zhang, Y.; Zhou, J. The Quadratic Constitutive Model Based on Partial Derivative and Taylor Series of Ti6242s Alloy and Predictability Analysis. Materials 2023, 16, 2928. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Lian, T.; Zhang, B.; Du, Y.; Du, K.; Liu, B.; Li, Z.; Tian, X.; Jung, D.-W. The Parameters Identification of High-Temperature Constitutive Model Based on Inverse Optimization Method and 3D Processing Map of Cr8 Alloy Steel. Materials 2021, 14, 2216. [Google Scholar] [CrossRef]
- Wang, H.; Wang, C.; Li, M.; Ma, R.; Zhao, J. Constitutive Equations for Describing the Hot Compressed Behavior of TC4–DT Titanium Alloy. Materials 2020, 13, 3424. [Google Scholar] [CrossRef] [PubMed]
- He, D.; Xie, H.; Lin, Y.; Xu, Z.; Tan, X.; Xiao, G. High-Temperature Compression Behaviors and Constitutive Models of a 7046-Aluminum Alloy. Materials 2023, 16, 6412. [Google Scholar] [CrossRef] [PubMed]
- Aksenov, S.; Mikolaenko, V. Accurate Determination of Uniaxial Flow Behaviour of Superplastic Materials. Eur. J. Mech. A/Solids 2025, 109, 105469. [Google Scholar] [CrossRef]
- He, D.; Xie, H.; Lin, Y.C.; Yan, X.-T.; Xu, Z.; Xiao, G. Microstructure Evolution Mechanisms and a Physically-Based Constitutive Model for an Al–Zn–Mg–Cu–Zr Aluminum Alloy during Hot Deformation. J. Mater. Res. Technol. 2023, 26, 4739–4754. [Google Scholar] [CrossRef]
- Xue, D.; Wei, W.; Shi, W.; Zhou, X.; Rong, L.; Wen, S.; Wu, X.; Qi, P.; Gao, K.; Huang, H.; et al. Microstructural Evolution and Constitutive Analysis of Al-Mg-Zn-Er-Zr Based on Arrhenius-Type and Machine-Learning Algorithm. Mater. Today Commun. 2022, 32, 104076. [Google Scholar] [CrossRef]
- Feng, R.; Bao, Y.; Ding, Y.; Chen, M.; Ge, Y.; Xie, L. Three Different Mathematical Models to Predict the Hot Deformation Behavior of TA32 Titanium Alloy. J. Mater. Res. 2022, 37, 1309–1322. [Google Scholar] [CrossRef]
- O’Brien, M.J.; von Bremen, H.F.; Furukawa, M.; Horita, Z.; Langdon, T.G. A Finite Element Analysis of the Superplastic Forming of an Aluminum Alloy Processed by ECAP. Mater. Sci. Eng. A 2007, 456, 236–242. [Google Scholar] [CrossRef]
- Tan, H.; Gao, P.; Lian, J. Microstructural Modeling And Numerical Analysis For The Superplastic Forming Process. Mater. Manuf. Process. 2001, 16, 331–340. [Google Scholar] [CrossRef]
- Chandra, N. Constitutive Behavior of Superplastic Materials. Int. J. Non-Linear Mech. 2002, 37, 461–484. [Google Scholar] [CrossRef]
- ASTM E2448-11; Standard Test Method for Determining the Superplastic Properties of Metallic Sheet Materials. ASTM International: West Conshohocken, PA, USA, 2011.
- Samberger, S.; Weißensteiner, I.; Stemper, L.; Kainz, C.; Uggowitzer, P.J.; Pogatscher, S. Fine-Grained Aluminium Crossover Alloy for High-Temperature Sheet Forming. Acta Mater. 2023, 253, 118952. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, S.; Zhang, Y.; Bai, Y.; Fang, Z.; Cui, T.; Liang, J.; Sun, X. Effects of Post Heat Treatment on Key T-Phase Evolution and the Matching Mechanism of Enhanced Strength-Toughness, Wear Resistance and Corrosion Resistance in Al-Mg-Zn-(Cu-Er-Zr) Alloy by Laser Powder Bed Fusion. J. Alloys Compd. 2024, 1005, 175976. [Google Scholar] [CrossRef]
- Glazoff, M.V.; Khvan, A.; Zolotorevsky, V.S.; Belov, N.A.; Dinsdale, A.; Glazoff, M.V. Casting Aluminum Alloys; Elsevier: Amsterdam, The Netherlands, 2019; ISBN 9780128118054. [Google Scholar]
- Flower, H.M.; Boyle, G.J.; Dashwood, R.J.; Grimes, R. The Influence of Al3Zr Precipitation on the Superplastic Behaviour of Aluminium Alloys. Mater. Sci. Forum 2004, 447–448, 389–394. [Google Scholar] [CrossRef]
- Zhang, H.-M.; Jiang, P.; Pan, H.-J.; Peng, J.; Wang, Z.-Z.; Yan, K.-T.; Zha, M. Dynamic Recrystallization-Dependent High-Temperature Tensile Properties and Deformation Mechanisms in Al-Mg-Sc-Zr Alloys. Mater. Sci. Eng. A 2023, 880, 145304. [Google Scholar] [CrossRef]
- Knipling, K.E.; Dunand, D.C.; Seidman, D.N. Precipitation Evolution in Al-Zr and Al-Zr-Ti Alloys during Aging at 450–600 °C. Acta Mater. 2008, 56, 1182–1195. [Google Scholar] [CrossRef]
- Mochugovskiy, A.G.; Tabachkova, N.Y.; Ghayoumabadi, M.E.; Cheverikin, V.V.; Mikhaylovskaya, A.V. Joint Effect of Quasicrystalline Icosahedral and L12-Strucutred Phases Precipitation on the Grain Structure and Mechanical Properties of Aluminum-Based Alloys. J. Mater. Sci. Technol. 2021, 87, 196–206. [Google Scholar] [CrossRef]
- Duan, Y.; Xu, G.; Zhou, L.; Xiao, D.; Deng, Y.; Yin, Z.; Peng, B.; Pan, Q.; Wang, Y.; Lu, L. Achieving High Superplasticity of a Traditional Thermal–Mechanical Processed Non-Superplastic Al–Zn–Mg Alloy Sheet by Low Sc Additions. J. Alloys Compd. 2015, 638, 364–373. [Google Scholar] [CrossRef]
- Lv, S.; Jia, C.; He, X.; Wan, Z.; Li, X.; Qu, X. Superplastic Deformation and Dynamic Recrystallization of a Novel Disc Superalloy GH4151. Materials 2019, 12, 3667. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Xia, W.; Yan, H.; Chen, J.; Su, B. Effects of Zn Addition on Dynamic Recrystallization of High Strain Rate Rolled Al–Mg Sheets. Met. Mater. Int. 2022, 28, 1264–1276. [Google Scholar] [CrossRef]
- Novikov, I.I.; Portnoy, V.K.; Titov, A.O.; Belov, D.Y. Dynamic Recrystallization at Superplastic Deformation of Duralumin with Initial Recrystallized Structure. Scr. Mater. 2000, 42, 899–904. [Google Scholar] [CrossRef]
- Sakai, T.; Belyakov, A.; Kaibyshev, R.; Miura, H.; Jonas, J.J. Dynamic and Post-Dynamic Recrystallization under Hot, Cold and Severe Plastic Deformation Conditions. Prog. Mater. Sci. 2014, 60, 130–207. [Google Scholar] [CrossRef]
- Dougherty, L.M.; Robertson, I.M.; Vetrano, J.S. A TEM Study of Dynamic Continuous Recrystallization in a Superplastic Al-4Mg-0.3Sc Alloy. Mater. Res. Soc. Symp. Proc. 2000, 601, 25–30. [Google Scholar] [CrossRef]
- Kanazawa, T.; Masuda, H.; Tobe, H.; Kakehi, K.; Sato, E. Initial Process of Continuous Dynamic Recrystallization in a Superplastic Al–Mg–Mn Alloy. J. Jpn. Inst. Light Met. 2017, 67, 95–100. [Google Scholar] [CrossRef][Green Version]
- Zenner, C.; Hollomon, J.H. Effect of Strain Rate Upon Plastic Flow of Steel Contributed Original Research. J. Appl. Phys. 2004, 22, 12. [Google Scholar]
- Majidi, O.; Jahazi, M.; Bombardier, N. Characterization of Mechanical Properties and Formability of a Superplastic Al-Mg Alloy. J. Phys. Conf. Ser. 2018, 1063, 012165. [Google Scholar] [CrossRef]
- Mosleh, A.O.; Mikhaylovskaya, A.V.; Kotov, A.D.; Kwame, J.S.; Aksenov, S.A. Superplasticity of Ti-6Al-4V Titanium Alloy: Microstructure Evolution and Constitutive Modelling. Materials 2019, 12, 1756. [Google Scholar] [CrossRef] [PubMed]
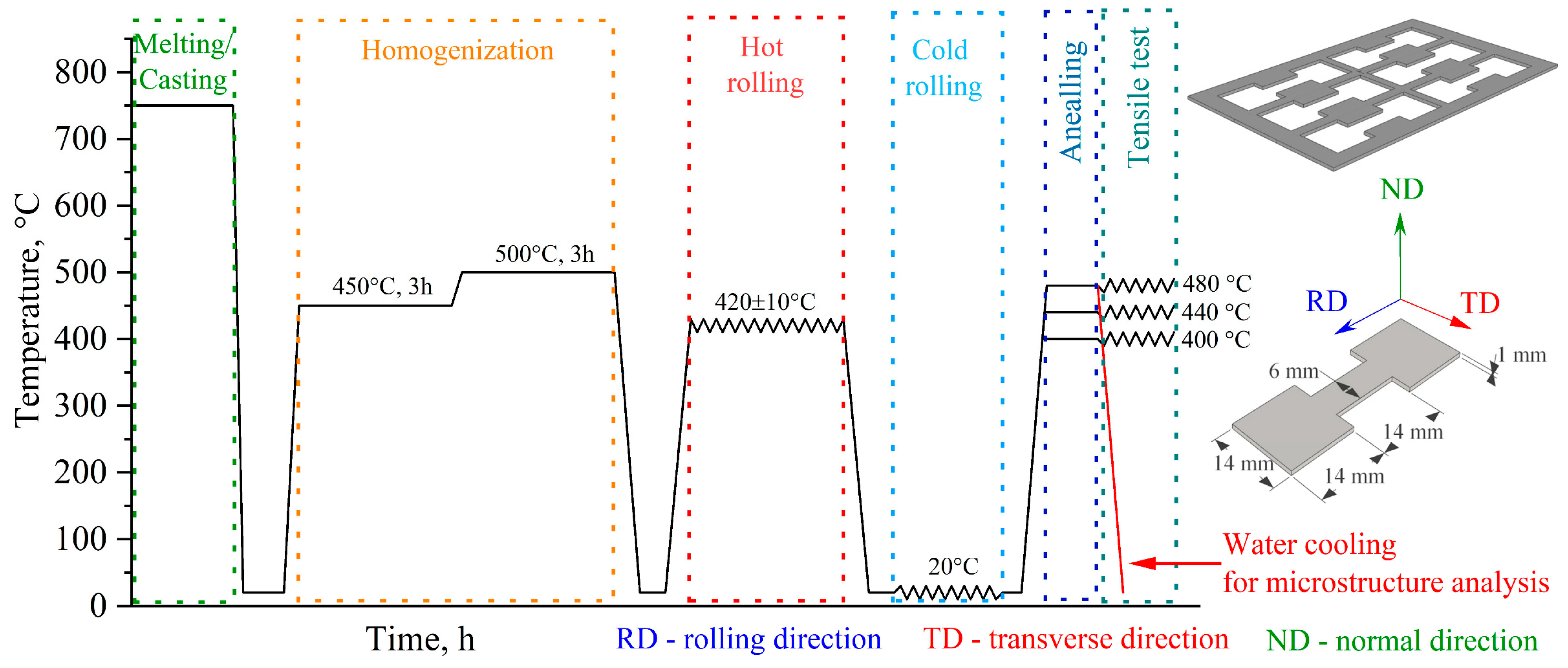
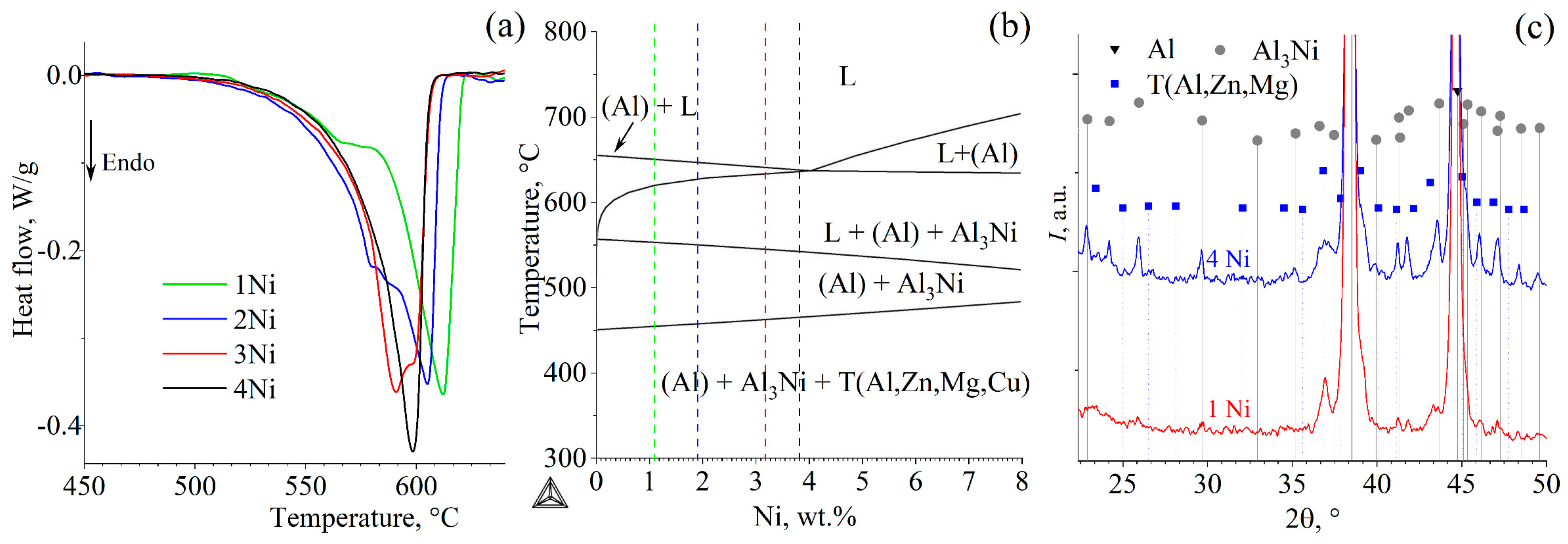



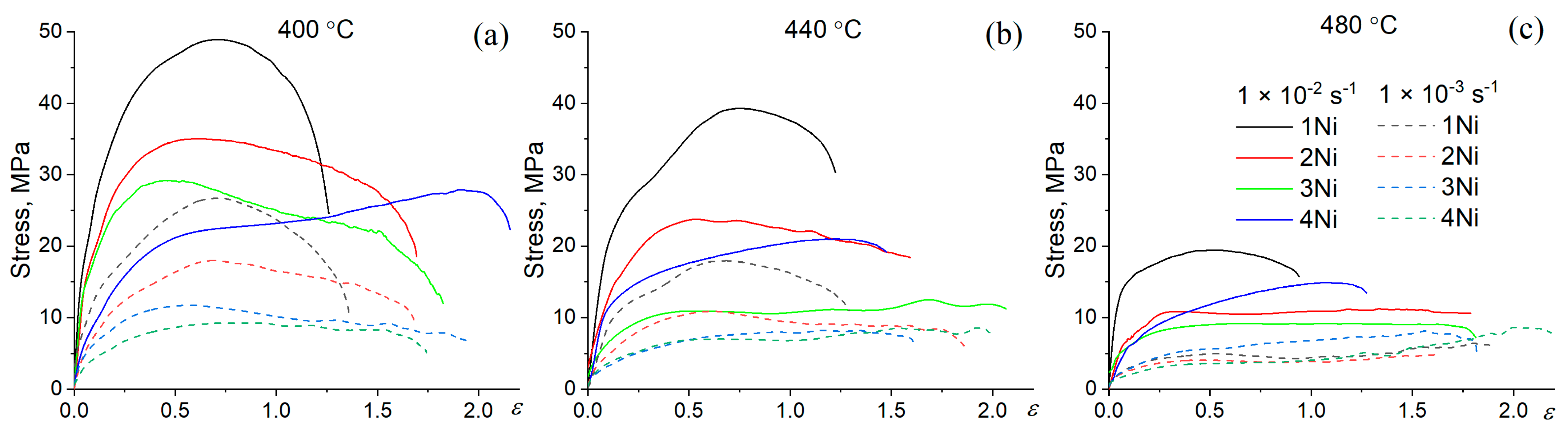
| Alloy | Mg | Zn | Ni | Zr | Cu | Al |
|---|---|---|---|---|---|---|
| 1Ni | 4/4.1 | 4/3.9 | 1/1.1 | 0.25/0.25 | 0.7/0.72 | Bal. |
| 2Ni | 4/4.1 | 4/4.1 | 2/1.9 | 0.25/0.26 | 0.7/0.69 | Bal. |
| 3Ni | 4/4.0 | 4/4.0 | 3/3.2 | 0.25/0.26 | 0.7/0.71 | Bal. |
| 4Ni | 4/4.0 | 4/3.8 | 4/3.8 | 0.25/0.25 | 0.7/0.72 | Bal. |
| State/Alloy | Volume Fraction (%)/Particle Size, d (μm) | |||
|---|---|---|---|---|
| 1Ni | 2Ni | 3Ni | 4Ni | |
| Cold rolling (CW) | 9 ± 1/0.6 ± 0.1 | 13 ± 1/0.7 ± 0.1 | 15 ± 2/0.9 ± 0.1 | 16 ± 2/1.2 ± 0.1 |
| Annealing at 400 °C | 5 ± 1/0.6 ± 0.1 | 8 ± 1/0.6 ± 0.1 | 10 ± 1/0.9 ± 0.1 | 12 ± 2/1.2 ± 0.1 |
| Annealing at 440 °C | 2.3 ± 0.5/1.0 ± 0.1 | 6 ± 1/0.9 ± 0.1 | 7 ± 1/1.0 ± 0.1 | 9 ± 1/1.3 ± 0.1 |
| Annealing at 480 °C | 2.1 ± 0.2/0.9 ± 0.1 | 6 ± 1/0.9 ± 0.1 | 7 ± 1/1.0 ± 0.1 | 9 ± 1/1.3 ± 0.1 |
| Alloy | 1Ni | 2Ni | 3Ni | 4Ni |
|---|---|---|---|---|
| 14.9 | 21.4 | 16.9 | 7.4 | |
| 1.8 | 2.6 | 2.5 | 2.3 | |
| 148 ± 6 | 200 ± 11 | 167 ± 6 | 111 ± 8 | |
| 19.7 | 17.3 | 12.9 | 5.5 | |
| m | 0.71 | 0.49 | 0.51 | 0.57 |
| β [MPa−1] | 0.08 | 0.11 | 0.12 | 0.14 |
| 157 ± 6 | 144 ± 9 | 119 ± 6 | 90 ± 8 | |
| α | 0.04 | 0.04 | 0.05 | 0.06 |
| 22.5 | 27.7 | 22.3 | 12 | |
| 1.4 | 2.0 | 1.9 | 1.7 | |
| 162 ± 7 | 193 ± 15 | 159 ± 7 | 107 ± 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turaeva, Z.S.; Mosleh, A.O.; Yakovtseva, O.A.; Kotov, A.D.; Mikhaylovskaya, A.V. Microstructural Analysis and Constitutive Modeling of Superplastic Deformation Behavior of Al-Mg-Zn-Cu-Zr-xNi Alloys with Different Ni Contents. Metals 2025, 15, 45. https://doi.org/10.3390/met15010045
Turaeva ZS, Mosleh AO, Yakovtseva OA, Kotov AD, Mikhaylovskaya AV. Microstructural Analysis and Constitutive Modeling of Superplastic Deformation Behavior of Al-Mg-Zn-Cu-Zr-xNi Alloys with Different Ni Contents. Metals. 2025; 15(1):45. https://doi.org/10.3390/met15010045
Chicago/Turabian StyleTuraeva, Zarnigor S., Ahmed O. Mosleh, Olga A. Yakovtseva, Anton D. Kotov, and Anastasia V. Mikhaylovskaya. 2025. "Microstructural Analysis and Constitutive Modeling of Superplastic Deformation Behavior of Al-Mg-Zn-Cu-Zr-xNi Alloys with Different Ni Contents" Metals 15, no. 1: 45. https://doi.org/10.3390/met15010045
APA StyleTuraeva, Z. S., Mosleh, A. O., Yakovtseva, O. A., Kotov, A. D., & Mikhaylovskaya, A. V. (2025). Microstructural Analysis and Constitutive Modeling of Superplastic Deformation Behavior of Al-Mg-Zn-Cu-Zr-xNi Alloys with Different Ni Contents. Metals, 15(1), 45. https://doi.org/10.3390/met15010045








