Fracture Load Prediction of Non-Linear Structural Steels through Calibration of the ASED Criterion
Abstract
1. Introduction
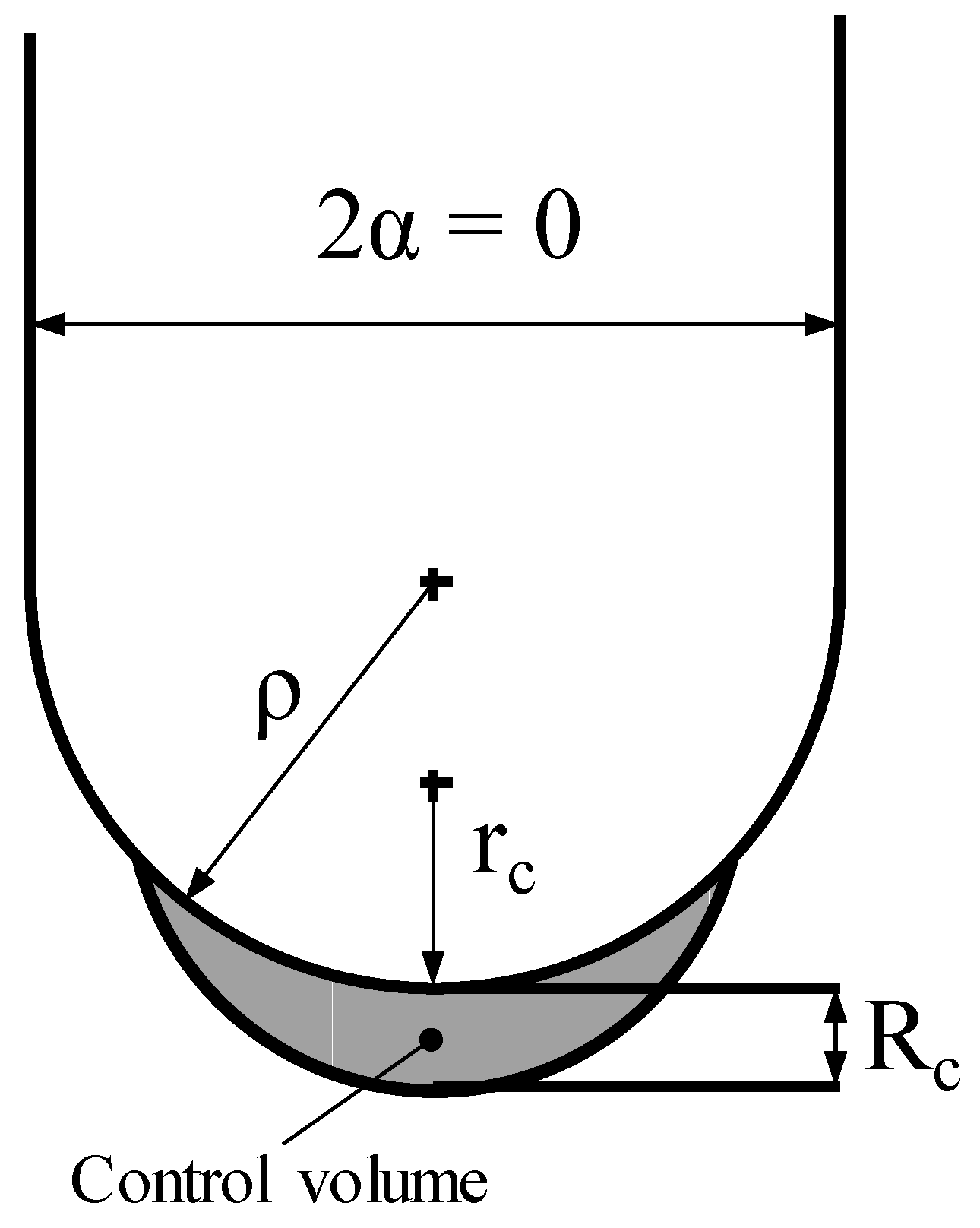
2. The Average Strain Energy Density Criterion
3. Materials and Methods
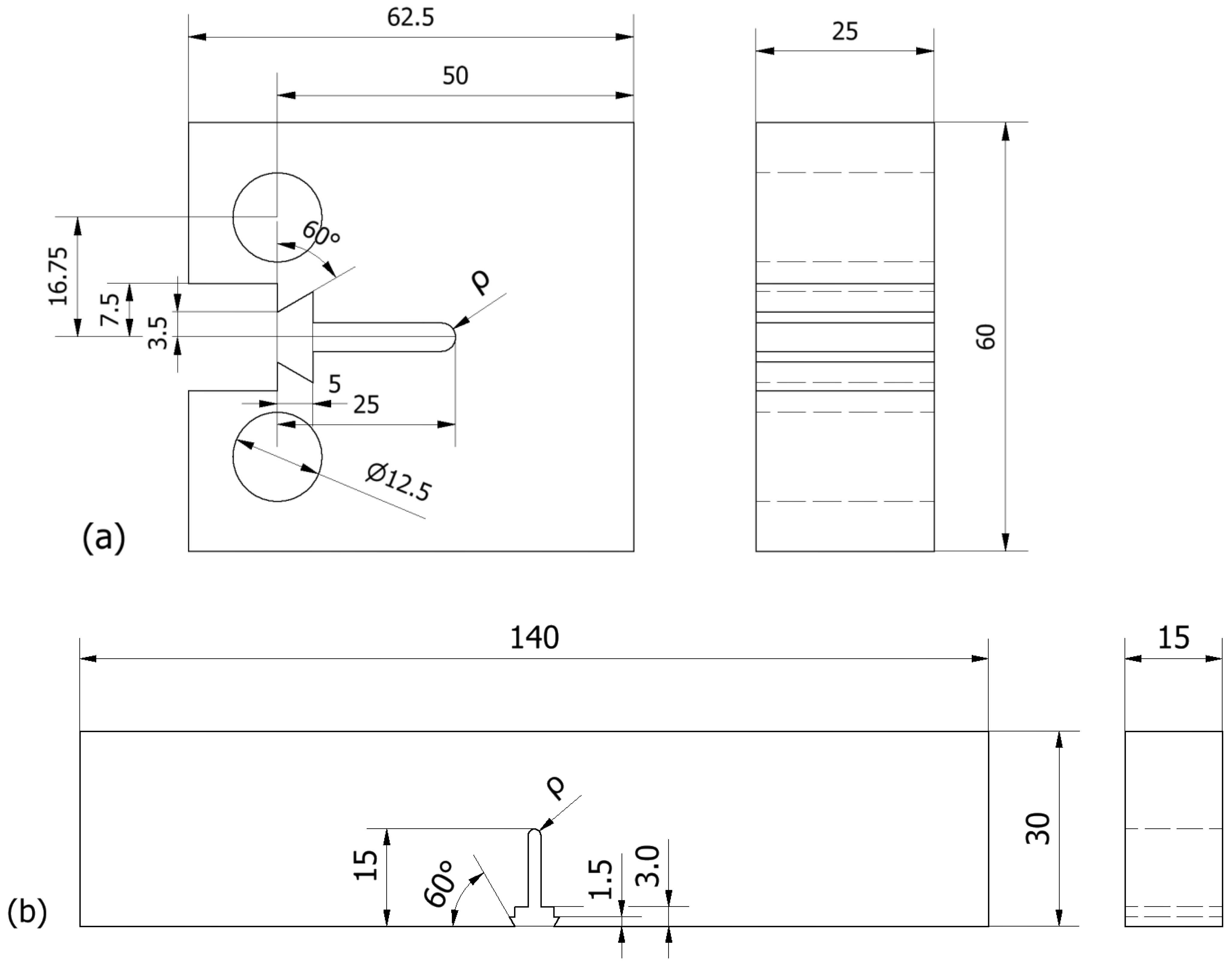
- Steel S275JR: 84 compact tension (CT) specimens with a thickness of 25 mm were tested, as shown in Figure 2a, covering six different notch radii (0 mm, 0.15 mm, 0.25 mm, 0.50 mm, 1.0 mm, and 2.0 mm) and five different temperatures within the ductile-to-brittle transition range (DBTR) of −10 °C, −30 °C, and −50 °C and two temperatures in the lower shelf (LS) of −90 °C and −120 °C. A complete description of the experimental procedure can be found in [26];
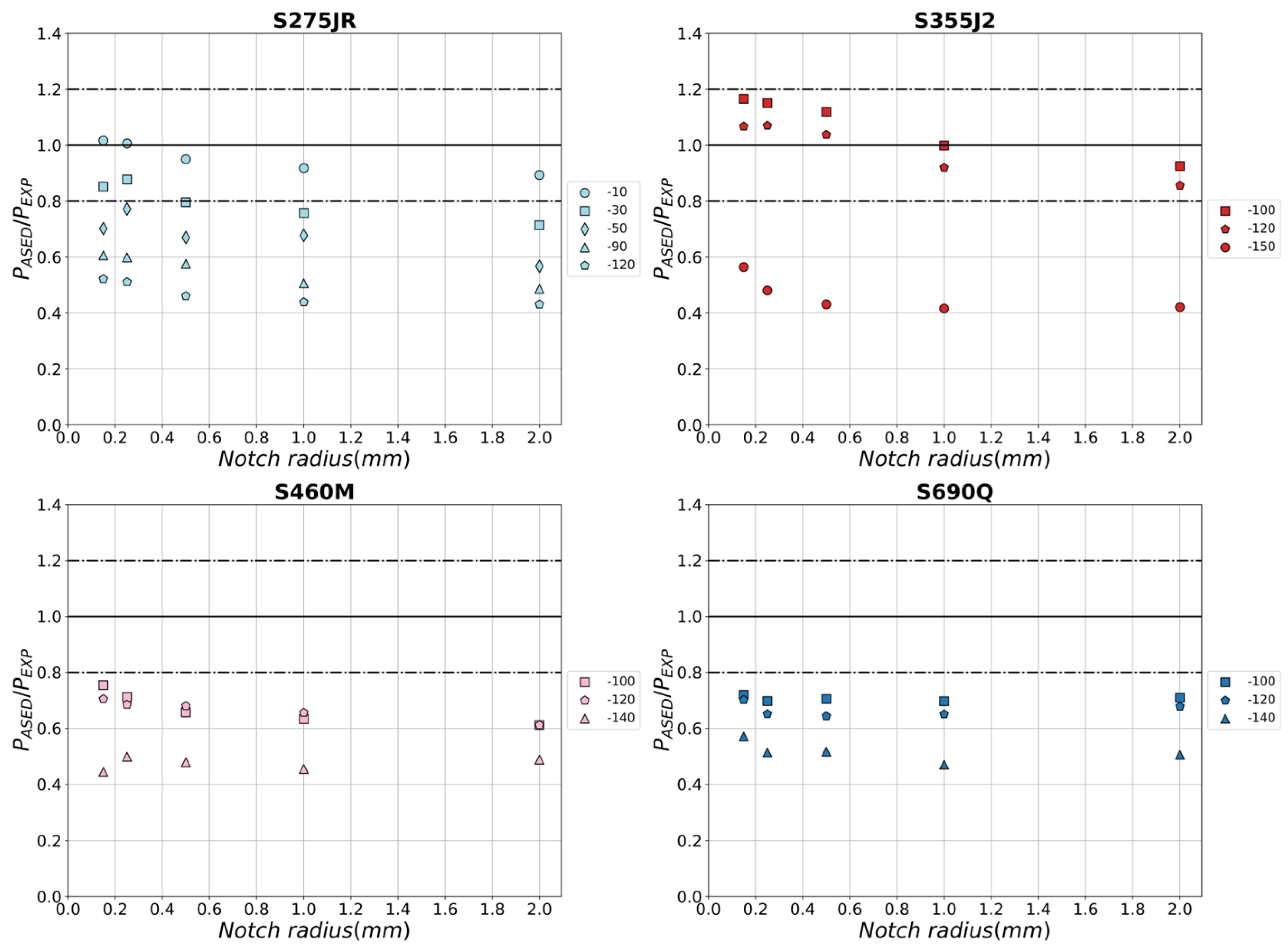
3.1. Direct Application of the ASED Criterion
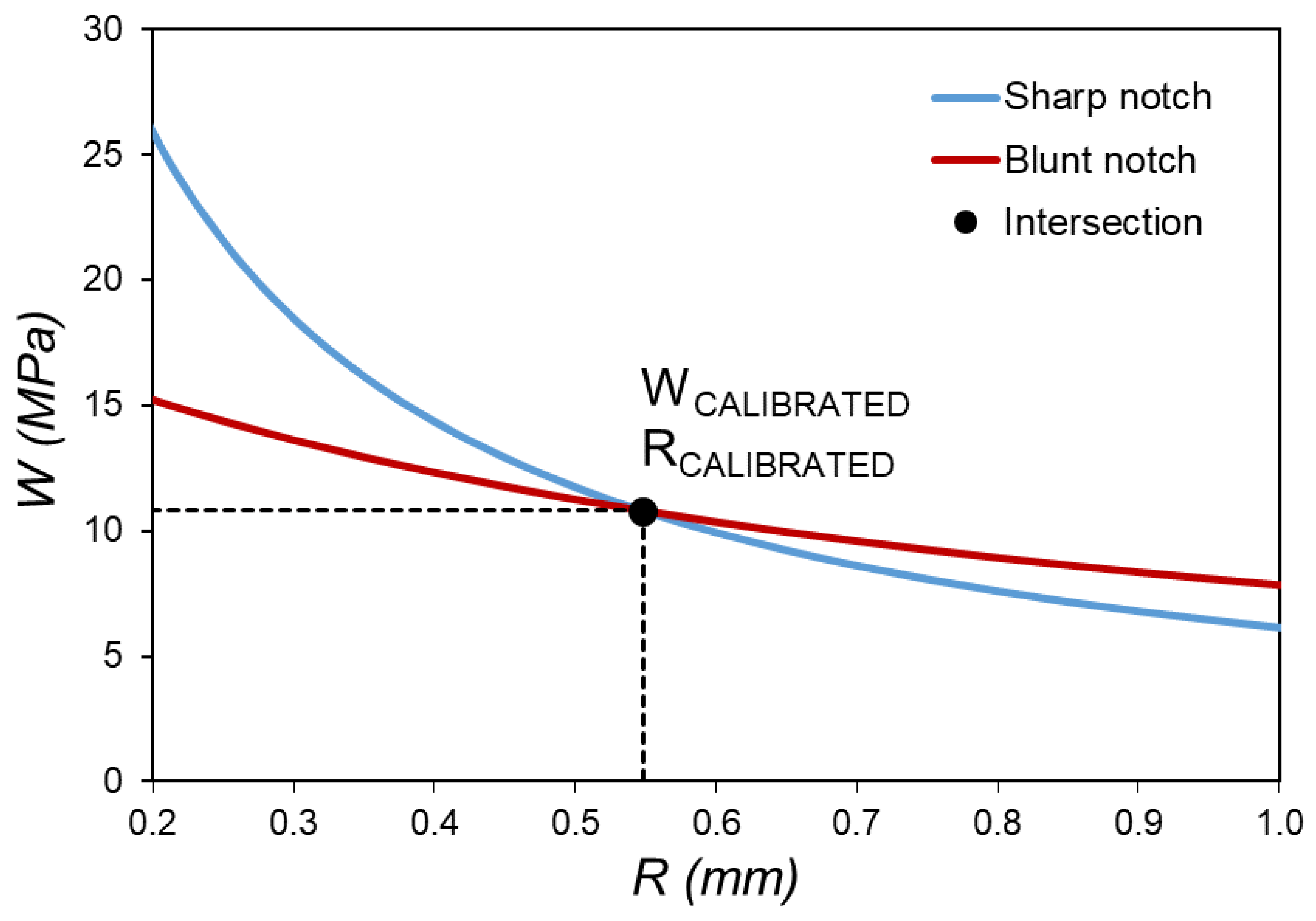
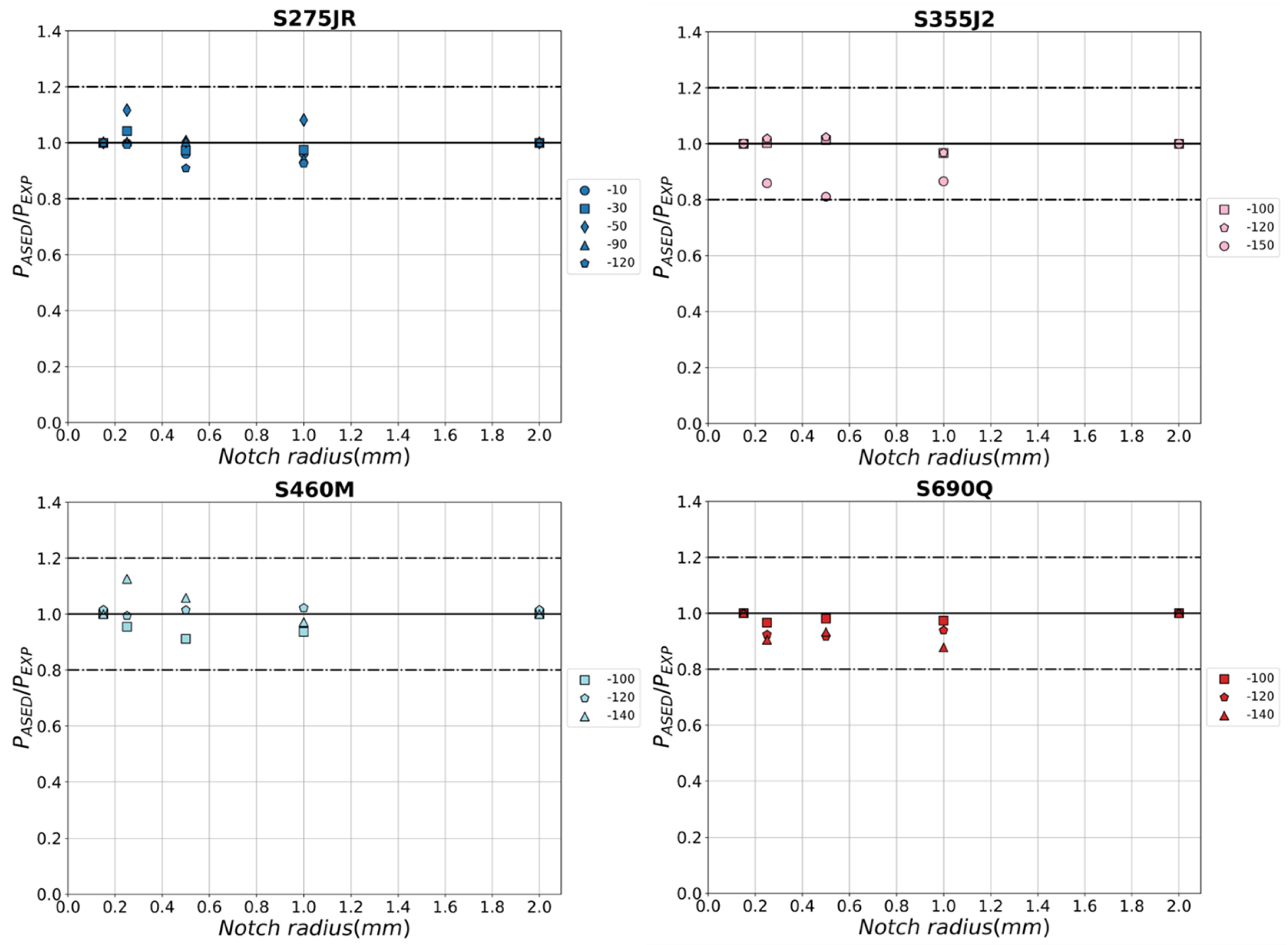
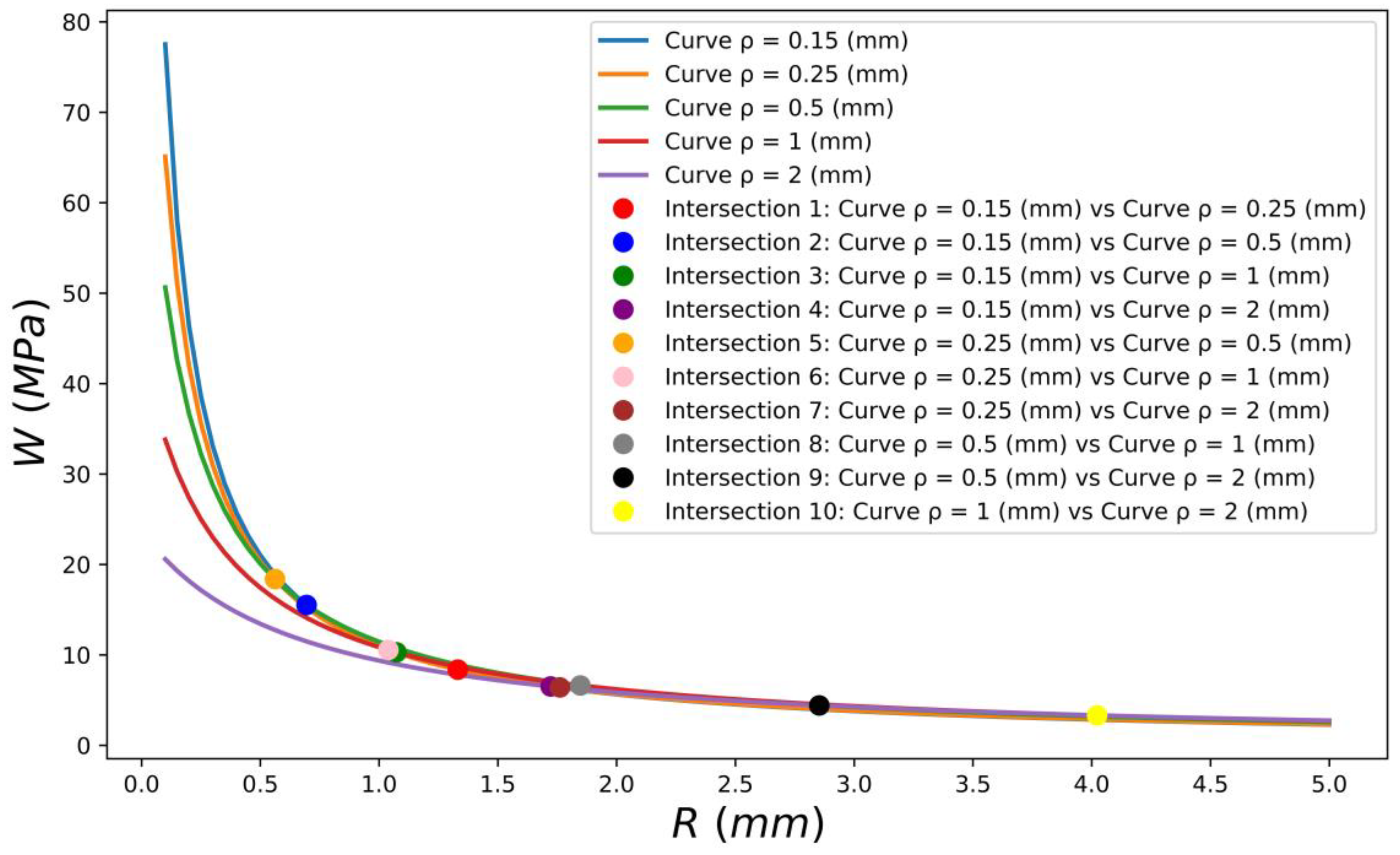
3.2. Proposed Calibration of the ASED Criterion
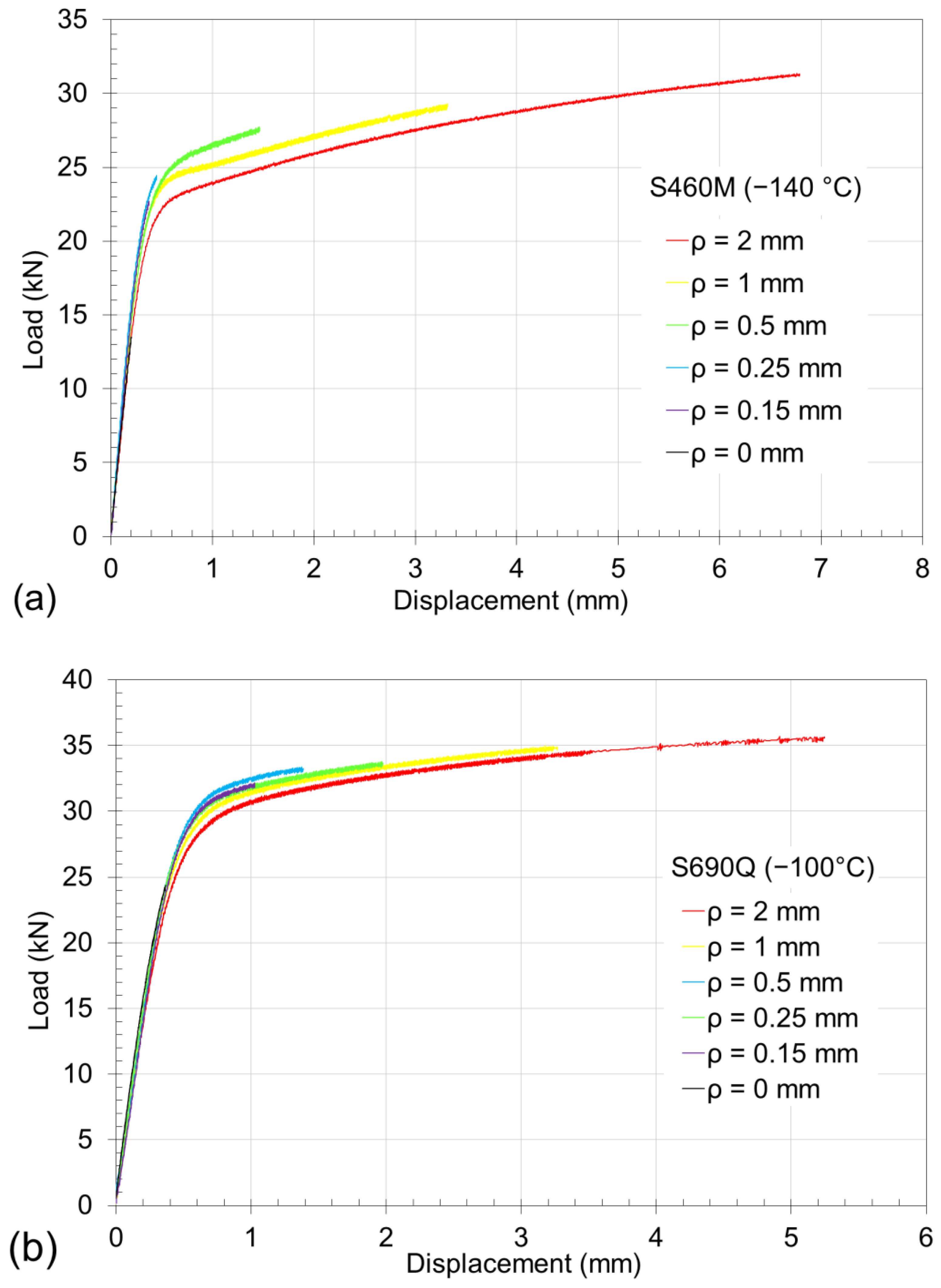
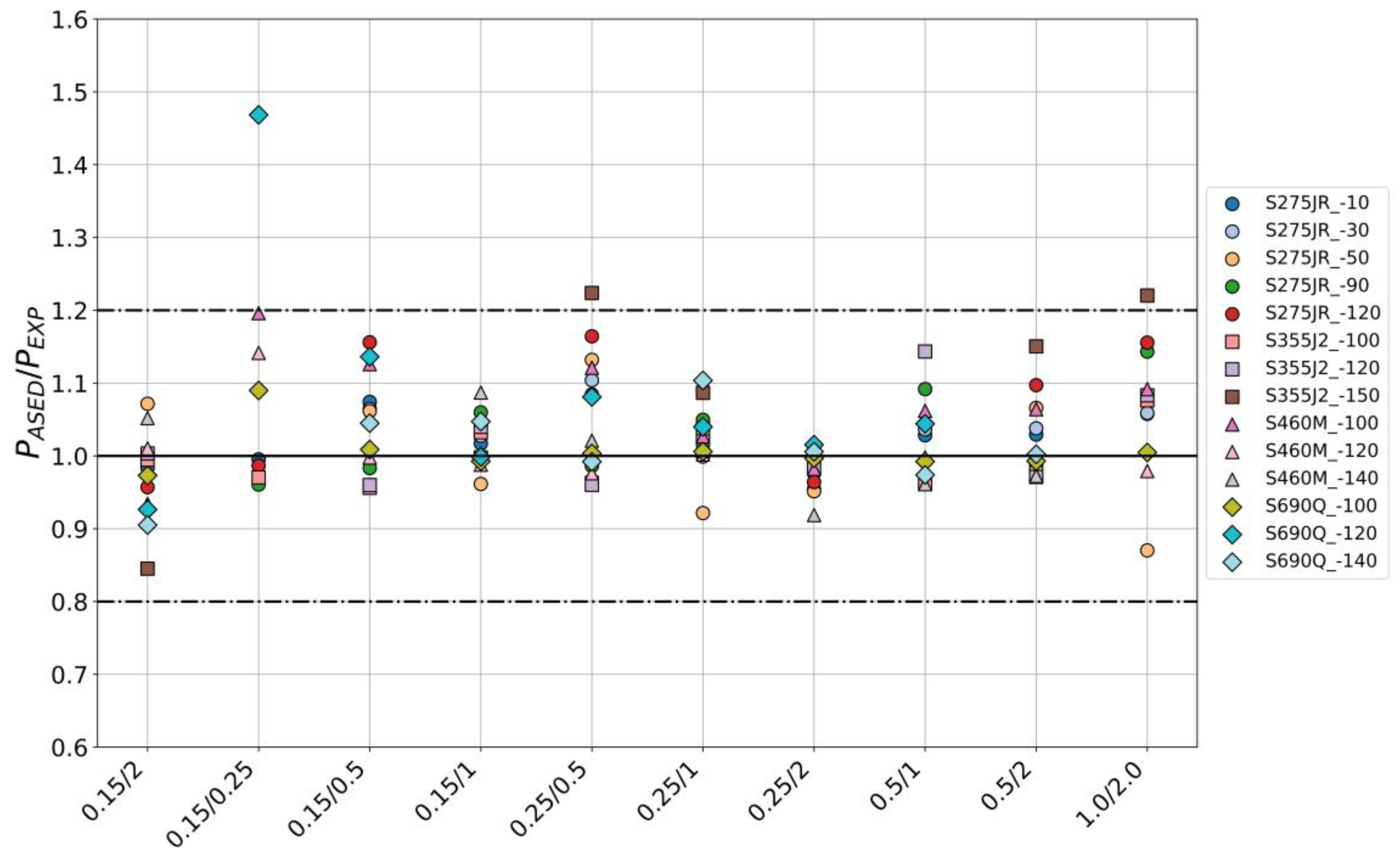
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shah, V.N.; MacDonald, P.E. Aging and Life Extension of Major Light Water Reactor Components, 1st ed.; Shah, V.N., MacDonald, P.E., Eds.; Elsevier Science Pub. Co., Inc.: New York, NY, USA, 1993; ISBN 9780444894489. [Google Scholar]
- Taylor, D. The Theory of Critical Distances; Elsevier: London, UK, 2007; Volume 75, ISBN 9780080444789. [Google Scholar]
- Cicero, S.; Madrazo, V.; García, T. Analysis of Notch Effect in the Apparent Fracture Toughness and the Fracture Micromechanisms of Ferritic–Pearlitic Steels Operating within Their Lower Shelf. Eng. Fail. Anal. 2014, 36, 322–342. [Google Scholar] [CrossRef]
- Cicero, S.; Madrazo, V.; García, T.; Cuervo, J.; Ruiz, E. On the Notch Effect in Load Bearing Capacity, Apparent Fracture Toughness and Fracture Mechanisms of Polymer PMMA, Aluminium Alloy Al7075-T651 and Structural Steels S275JR and S355J2. Eng. Fail. Anal. 2013, 29, 108–121. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications, 4th ed.; CRC Press: Boca Raton, FL, USA, 2005; ISBN 1498728146. [Google Scholar]
- Berto, F.; Lazzarin, P.; Ayatollahi, M.R. Recent Developments in Brittle and Quasi-Brittle Failure Assessment of Graphite by Means of SED Approach. Key Eng. Mater. 2013, 2, 854–861. [Google Scholar]
- Seibert, P.; Susmel, L.; Berto, F.; Kästner, M.; Razavi, S.M.J. Applicability of Strain Energy Density Criterion for Fracture Prediction of Notched PLA Specimens Produced via Fused Deposition Modeling. Eng. Fail. Mech. 2021, 258, 108103. [Google Scholar] [CrossRef]
- Sánchez, M.; Cicero, S.; Arrieta, S.; Martínez, V. Fracture Load Predictions in Additively Manufactured ABS U-Notched Specimens Using Average Strain Energy Density Criteria. Materials 2022, 15, 2372. [Google Scholar] [CrossRef] [PubMed]
- Shahbaz, S.; Ayatollahi, M.R.; Petru, M.; Torabi, A.R. U-Notch Fracture in Additively Manufactured ABS Specimens under Symmetric Three-Point Bending. Theor. Appl. Fract. Mech. 2022, 119, 103318. [Google Scholar] [CrossRef]
- Seibert, P.; Taylor, D.; Berto, F.; Mohammad Javad Razavi, S. Energy TCD–Robust and Simple Failure Prediction Unifying the TCD and ASED Criterion. Eng. Fail. Mech. 2022, 271, 108652. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Rezaeian, P.; Nabavi-Kivi, A.; Khosravani, M.R. Heat Treatment Effects on Fracture Resistance of Additively Manufactured PLA Specimens under Mode I Loading. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 1045–1059. [Google Scholar] [CrossRef]
- Albinmousa, J.; AlSadah, J.; Hawwa, M.A.; Al-Qahtani, H.M. Estimation of Mode I Fracture of U-Notched Polycarbonate Specimens Using the Equivalent Material Concept and Strain Energy Density. Appl. Sci. 2021, 11, 3370. [Google Scholar] [CrossRef]
- Cicero, S.; Torabi, A.R.; Majidi, H.R.; Gómez, F.J. On the Use of the Combined FMC-ASED Criterion for Fracture Prediction of Notched Specimens with Nonlinear Behavior. Procedia Struct. Integr. 2020, 28, 84–92. [Google Scholar] [CrossRef]
- Sánchez, M.; Cicero, S.; Torabi, A.R.; Ayatollahi, M.R. Critical Load Prediction in Notched e/Glass–Epoxy-Laminated Composites Using the Virtual Isotropic Material Concept Combined with the Average Strain Energy Density Criterion. Polymers 2021, 13, 1057. [Google Scholar] [CrossRef]
- Beaumont, P.W.R. The Failure of Fibre Composites: An Overview. J. Strain Anal. Eng. Des. 1989, 24, 189–205. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of Steel Sheets Containing Slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Beremin, F.M.; Pineau, A.; Mudry, F.; Devaux, J.-C.; D’Escatha, Y.; Ledermann, P. A Local Criterion for Cleavage Fracture of a Nuclear Pressure Vessel Steel. Metall. Trans. A 1983, 14, 2277–2287. [Google Scholar] [CrossRef]
- Ritchie, R.O.; Knott, J.F.; Rice, J.R. On the Relationship between Critical Tensile Stress and Fracture Toughness in Mild Steel. J. Mech. Phys. Solids 1973, 21, 395–410. [Google Scholar] [CrossRef]
- Churyumov, A.Y.; Medvedeva, S.V.; Mamzurina, O.I.; Kazakova, A.A.; Churyumova, T.A. United Approach to Modelling of the Hot Deformation Behavior, Fracture, and Microstructure Evolution of Austenitic Stainless AISI 316Ti Steel. Appl. Sci. 2021, 11, 3204. [Google Scholar] [CrossRef]
- Kim, M.-S.; Kim, H.-T.; Choi, Y.-H.; Kim, J.-H.; Kim, S.-K.; Lee, J.-M. A New Computational Method for Predicting Ductile Failure of 304L Stainless Steel. Metals 2022, 12, 1309. [Google Scholar] [CrossRef]
- Sih, G.C. Strain-Energy-Density Factor Applied to Mixed Mode Crack Problems. Int. J. Fract. 1974, 10, 305–321. [Google Scholar] [CrossRef]
- Lazzarin, P.; Berto, F. Some Expressions for the Strain Energy in a Finite Volume Surrounding the Root of Blunt V-Notches. Int. J. Fract. 2005, 135, 161–185. [Google Scholar] [CrossRef]
- Lazzarin, P.; Zambardi, R. A Finite-Volume-Energy Based Approach to Predict the Static and Fatigue Behavior of Components with Sharp V-Shaped Notches. Int. J. Fract. 2001, 112, 275–298. [Google Scholar] [CrossRef]
- Berto, F.; Lazzarin, P. A Review of the Volume-Based Strain Energy Density Approach Applied to V-Notches and Welded Structures. Theor. Appl. Fract. Mech. 2009, 52, 183–194. [Google Scholar] [CrossRef]
- Yosibash, Z. Failure Criteria for Brittle Elastic Materials. Interdiscip. Appl. Math. 2012, 37, 185–220. [Google Scholar] [CrossRef]
- Cicero, S.; Madrazo, V.; García, T. The Notch Master Curve: A Proposal of Master Curve for Ferritic–Pearlitic Steels in Notched Conditions. Eng. Fail. Anal. 2014, 42, 178–196. [Google Scholar] [CrossRef]
- Cicero, S.; García, T.; Madrazo, V. Application and Validation of the Notch Master Curve in Medium and High Strength Structural Steels. J. Mech. Sci. Technol. 2015, 29, 4129–4142. [Google Scholar] [CrossRef]
- Justo, J.; Castro, J.; Cicero, S. Energy-Based Approach for Fracture Assessment of Several Rocks Containing U-Shaped Notches through the Application of the SED Criterion. Int. J. Rock Mech. Min. Sci. 2018, 110, 306–315. [Google Scholar] [CrossRef]
- Creager, M.; Paris, P.C. Elastic Field Equations for Blunt Cracks with Reference to Stress Corrosion Cracking. Int. J. Fract. Mech. 1967, 3, 247–252. [Google Scholar] [CrossRef]
- Cicero, S.; Fuentes, J.D.; Torabi, A.R. Using the Equivalent Material Concept and the Average Strain Energy Density to Analyse the Fracture Behaviour of Structural Materials. Appl. Sci. 2020, 10, 1601. [Google Scholar] [CrossRef]
- Torabi, A.R.; Majidi, H.R.; Cicero, S.; Ibáñez-Gutiérrez, F.T.; Fuentes, J.D. Experimental Verification of the Fictitious Material Concept for Tensile Fracture in Short Glass Fibre Reinforced Polyamide 6 Notched Specimens with Variable Moisture. Eng. Fract. Mech. 2019, 212, 95–105. [Google Scholar] [CrossRef]

| Rc/ρ | υ = 0.25 | υ = 0.30 | υ = 0.35 | υ = 0.40 |
|---|---|---|---|---|
| 0.01 | 0.5813 | 0.5638 | 0.5432 | 0.5194 |
| 0.05 | 0.5258 | 0.5086 | 0.4884 | 0.4652 |
| 0.1 | 0.4687 | 0.4518 | 0.4322 | 0.4099 |
| 0.3 | 0.3216 | 0.3069 | 0.2902 | 0.2713 |
| 0.5 | 0.2401 | 0.2276 | 0.2135 | 0.1976 |
| 1 | 0.1399 | 0.1314 | 0.1217 | 0.1110 |
| Material | Temperature (°C) | E (GPa) | σy (MPa) | σu (MPa) | Kmat (MPa∙√m) |
|---|---|---|---|---|---|
| S275JR [26] | −10 | 207 | 338 | 536 | 123 |
| −30 | 208 | 345 | 549 | 101 | |
| −50 | 209 | 349 | 558 | 81 | |
| −90 | 211 | 381 | 597 | 63 | |
| −120 | 213 | 398 | 614 | 49 | |
| S355J2 [26] | −100 | 212 | 426 | 647 | 158 |
| −120 | 212 | 460 | 672 | 147 | |
| −150 | 215 | 527 | 758 | 61 | |
| S460M [27] | −100 | 212 | 605 | 727 | 77 |
| −120 | 213 | 647 | 758 | 77 | |
| −140 | 214 | 702 | 795 | 52 | |
| S690Q [27] | −100 | 212 | 907 | 1015 | 104 |
| −120 | 213 | 949 | 1060 | 98 | |
| −140 | 214 | 1004 | 1111 | 69 |
| Material | C | Si | P | S | Cr | Mn | Ni | Cu | Mo | V | Nb | Al | Ti |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S275JR | 0.180 | 0.260 | 0.012 | 0.009 | 0.018 | 1.180 | 0.085 | 0.060 | 0.120 | 0.020 | - | 0.034 | 0.022 |
| S355J2 | 0.200 | 0.320 | 0.012 | 0.008 | 0.050 | 1.390 | 0.090 | 0.060 | 0.120 | 0.020 | - | 0.014 | 0.022 |
| S460M | 0.120 | 0.450 | 0.012 | 0.001 | 0.062 | 1.490 | 0.016 | 0.011 | - | 0.066 | 0.036 | 0.048 | 0.003 |
| S690Q | 0.150 | 0.400 | 0.006 | 0.001 | 0.020 | 1.420 | 0.160 | 0.010 | - | 0.058 | 0.029 | 0.056 | 0.003 |
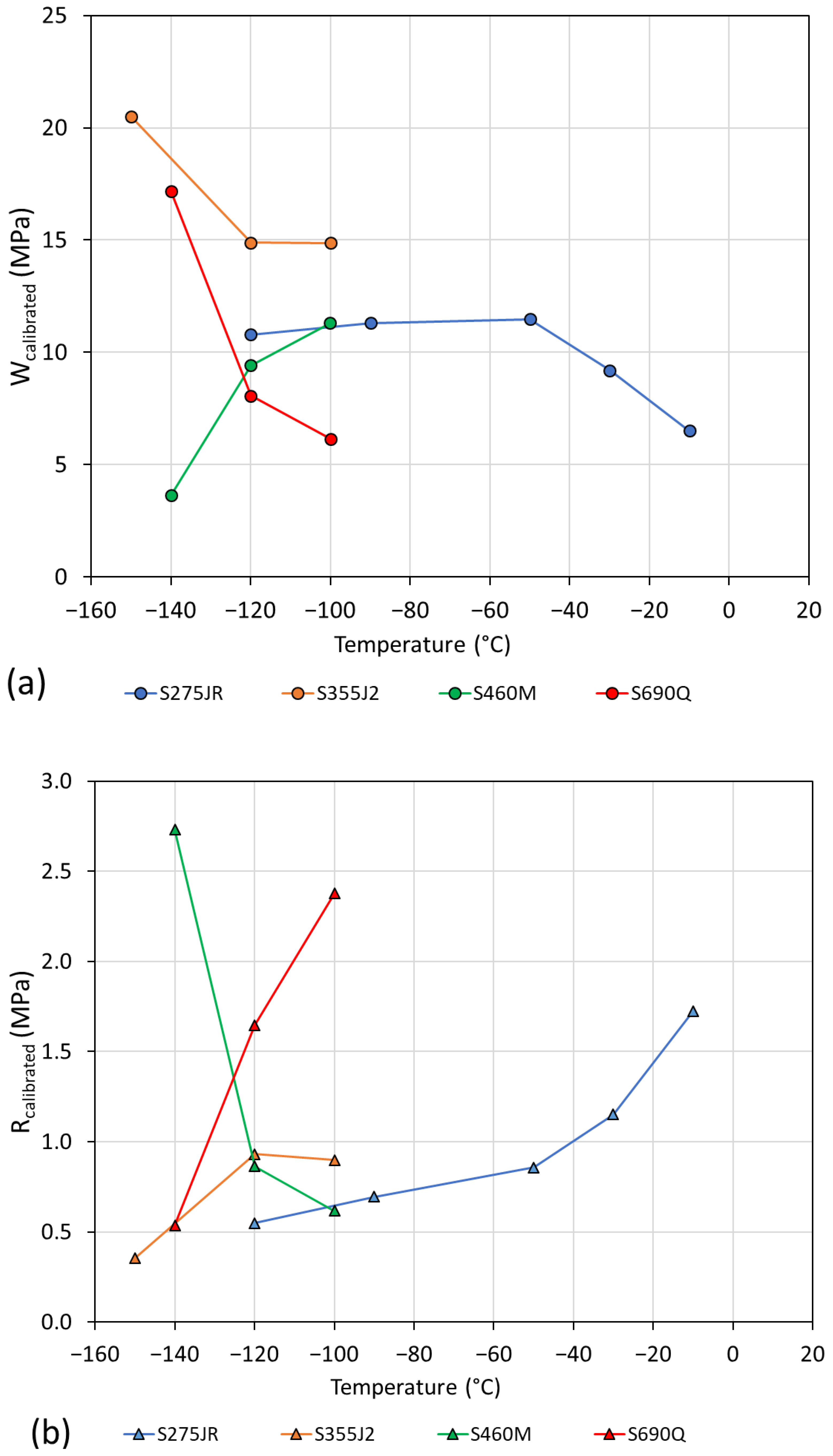
| Material | Temperature (°C) | Wc (MPa) | WCALIBRATED (MPa) | RCALIBRATED (mm) |
|---|---|---|---|---|
| S275JR | −10 | 0.69 | 6.52 | 1.722 |
| −30 | 0.72 | 9.19 | 1.151 | |
| −50 | 0.74 | 11.47 | 0.857 | |
| −90 | 0.85 | 11.31 | 0.695 | |
| −120 | 0.88 | 10.80 | 0.548 | |
| S355J2 | −100 | 0.99 | 14.88 | 0.899 |
| −120 | 1.06 | 14.89 | 0.931 | |
| −150 | 1.34 | 20.50 | 0.356 | |
| S460M | −100 | 1.25 | 11.31 | 0.617 |
| −120 | 1.35 | 9.42 | 0.863 | |
| −140 | 1.47 | 3.64 | 2.73 | |
| S690Q | −100 | 2.43 | 6.15 | 2.376 |
| −120 | 2.64 | 8.07 | 1.646 | |
| −140 | 2.88 | 17.18 | 0.537 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez, M.; Cicero, S.; Arrieta, S.; Torabi, A.R. Fracture Load Prediction of Non-Linear Structural Steels through Calibration of the ASED Criterion. Metals 2023, 13, 1211. https://doi.org/10.3390/met13071211
Sánchez M, Cicero S, Arrieta S, Torabi AR. Fracture Load Prediction of Non-Linear Structural Steels through Calibration of the ASED Criterion. Metals. 2023; 13(7):1211. https://doi.org/10.3390/met13071211
Chicago/Turabian StyleSánchez, Marcos, Sergio Cicero, Sergio Arrieta, and Ali Reza Torabi. 2023. "Fracture Load Prediction of Non-Linear Structural Steels through Calibration of the ASED Criterion" Metals 13, no. 7: 1211. https://doi.org/10.3390/met13071211
APA StyleSánchez, M., Cicero, S., Arrieta, S., & Torabi, A. R. (2023). Fracture Load Prediction of Non-Linear Structural Steels through Calibration of the ASED Criterion. Metals, 13(7), 1211. https://doi.org/10.3390/met13071211








