Physically-Based Methodology for the Characterization of Wrinkling Limit Curve Validated by Yoshida Tests
Abstract
1. Introduction
- Typical sheet forming parts;
- Simple geometries indirectly generate a stress state that induces wrinkling.
2. Experimentation
2.1. Mechanical Characterization
2.2. Experimental Plan
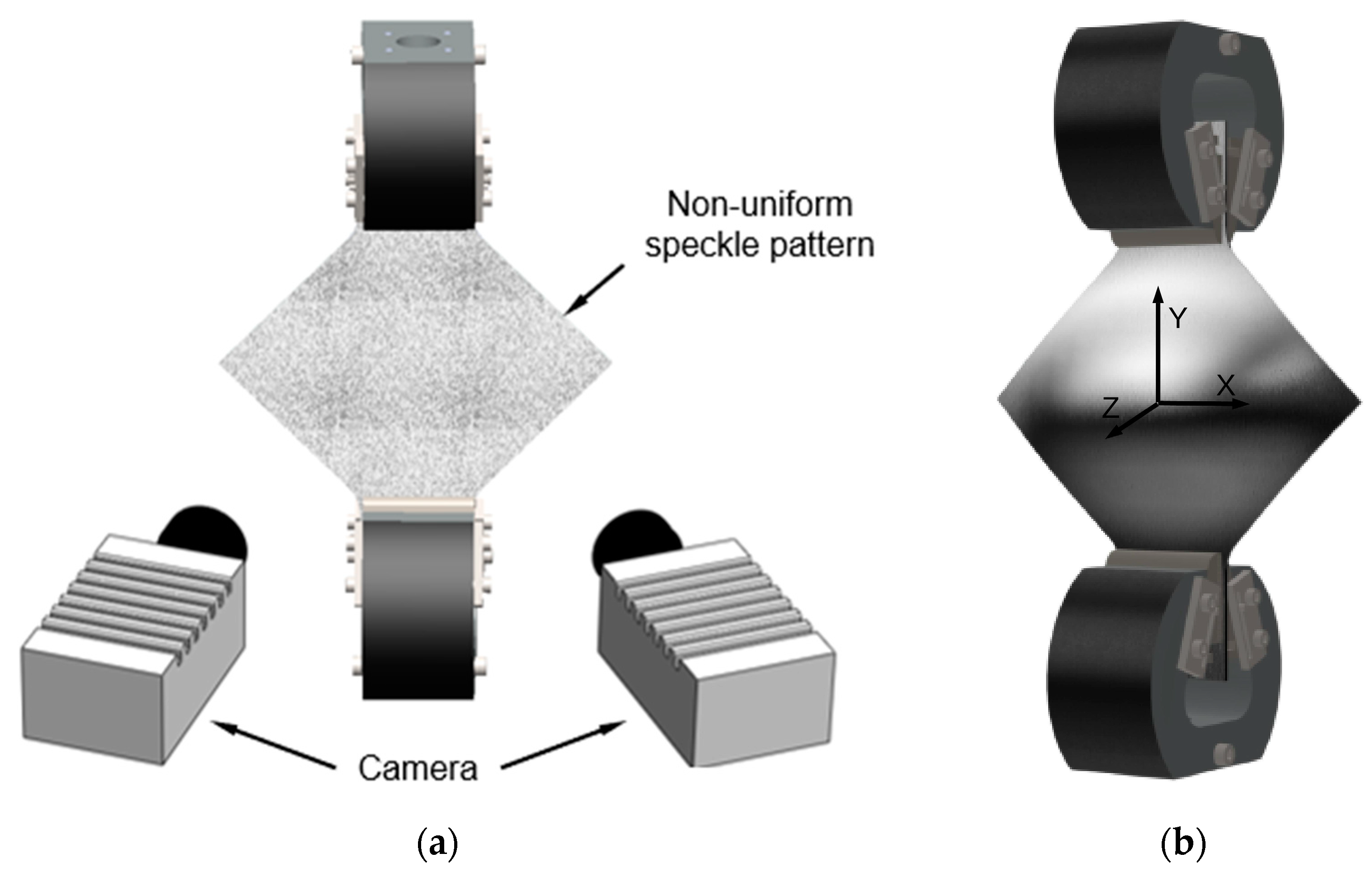
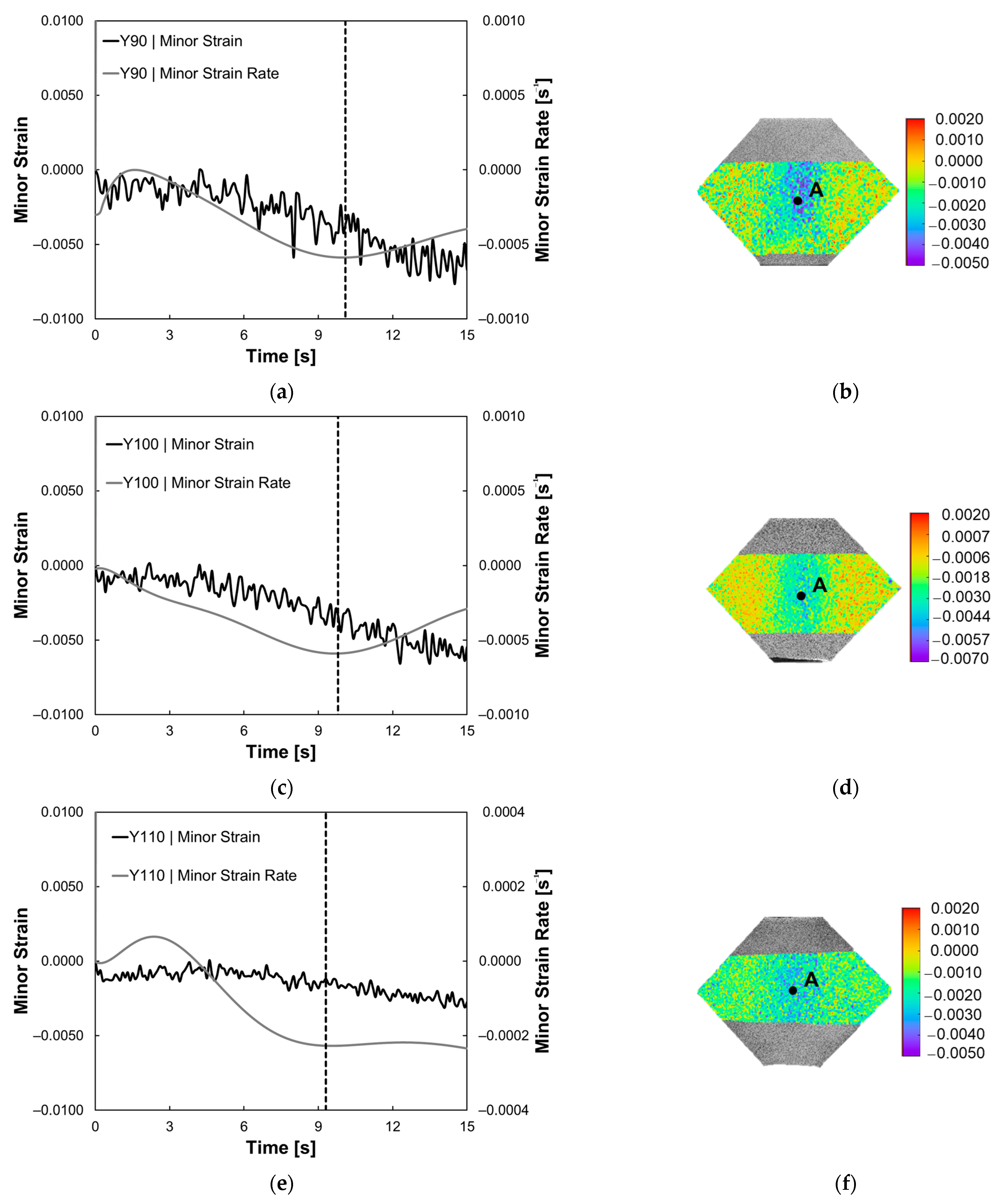
2.3. Displacement and Strain Measurements
3. Methodology
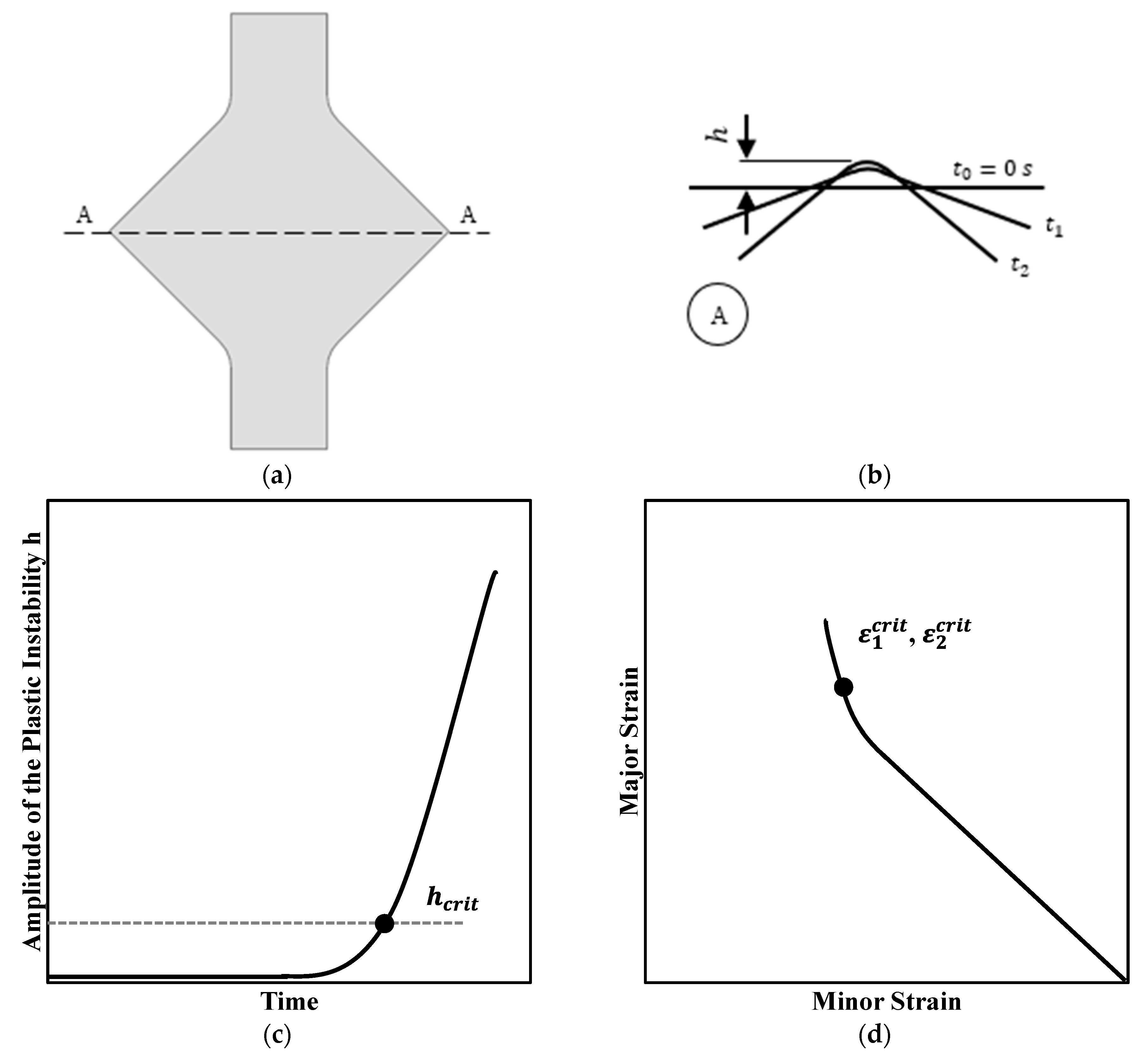
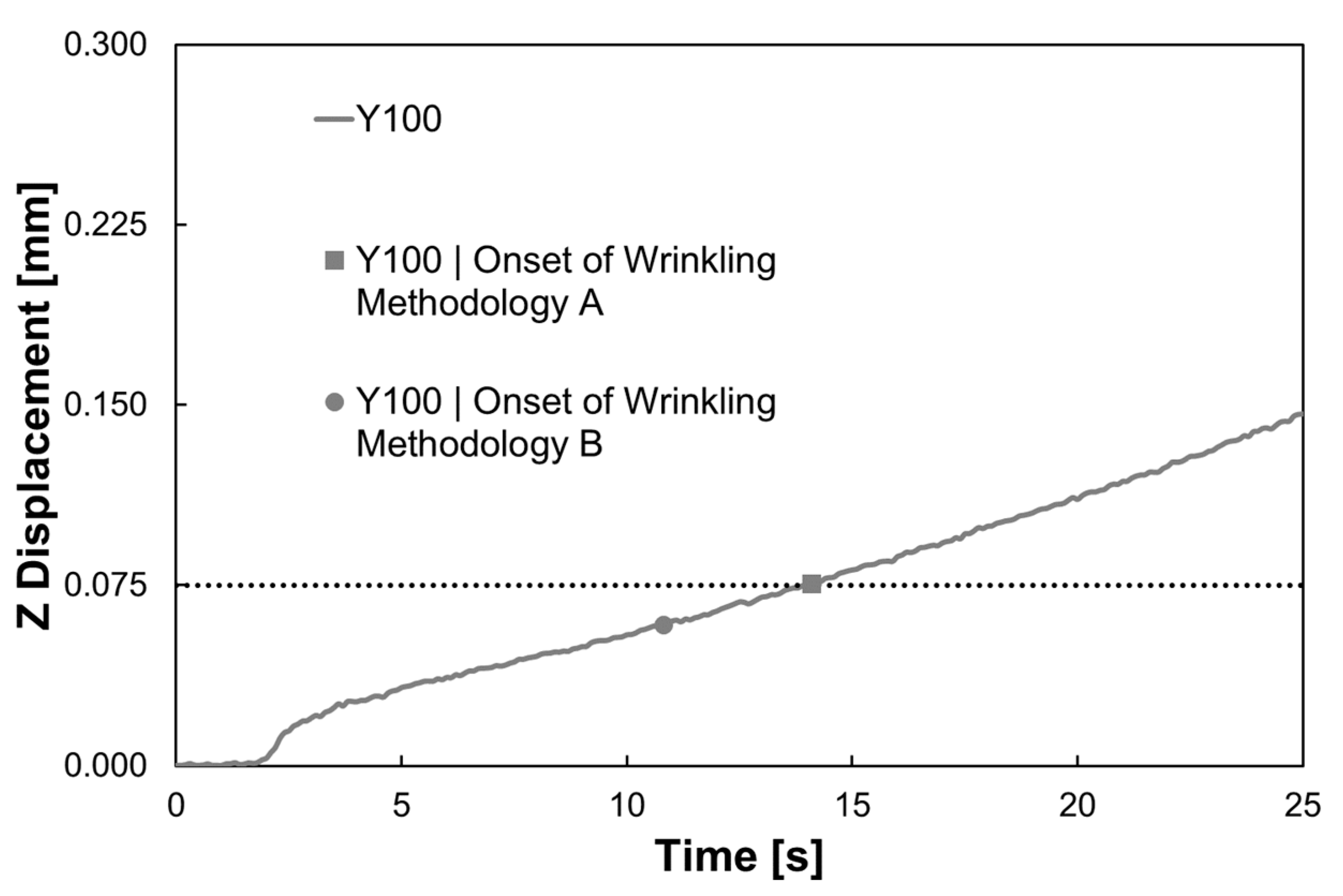
3.1. Methodology A
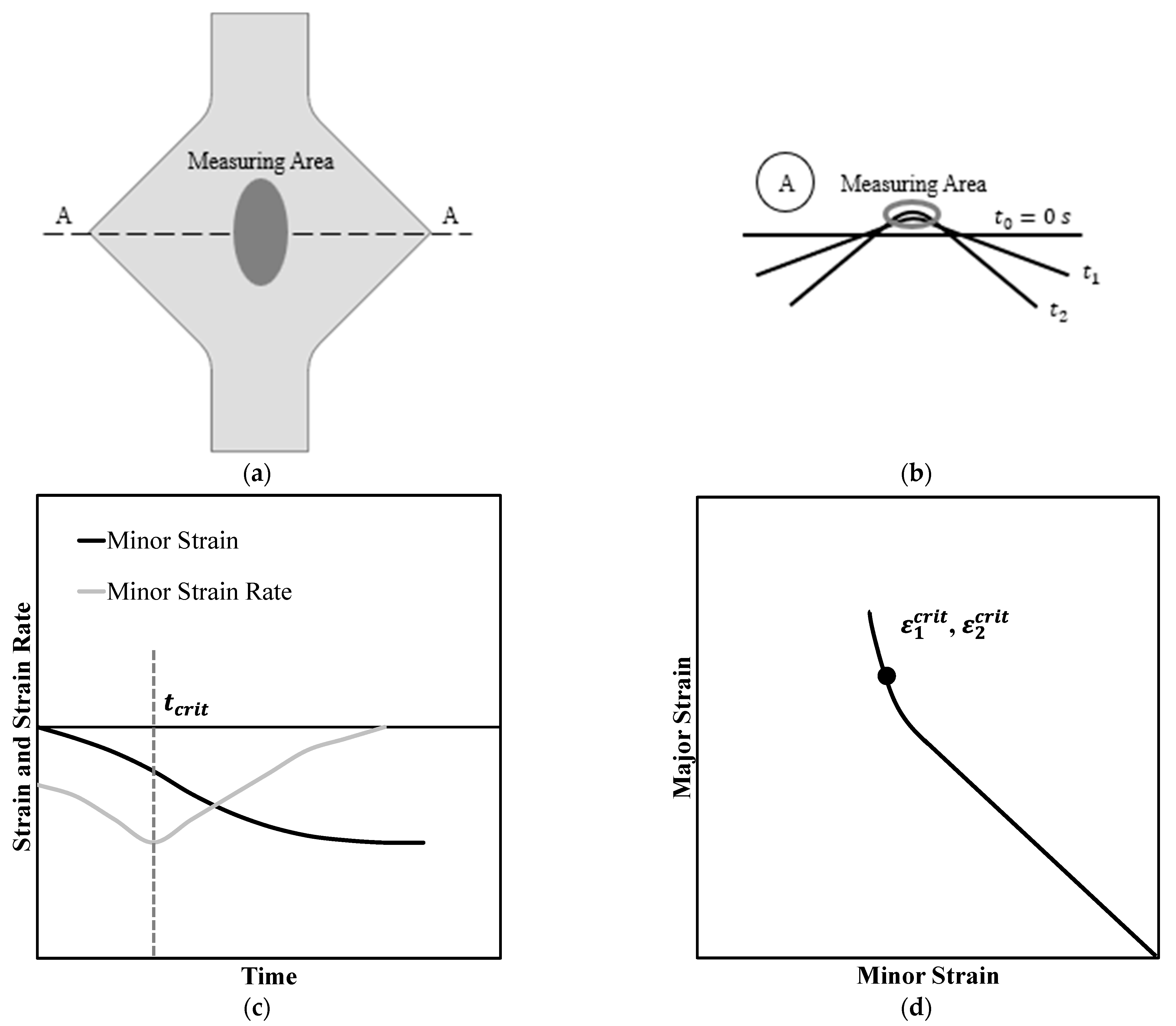
3.2. Methodology B
4. Results and Discussion
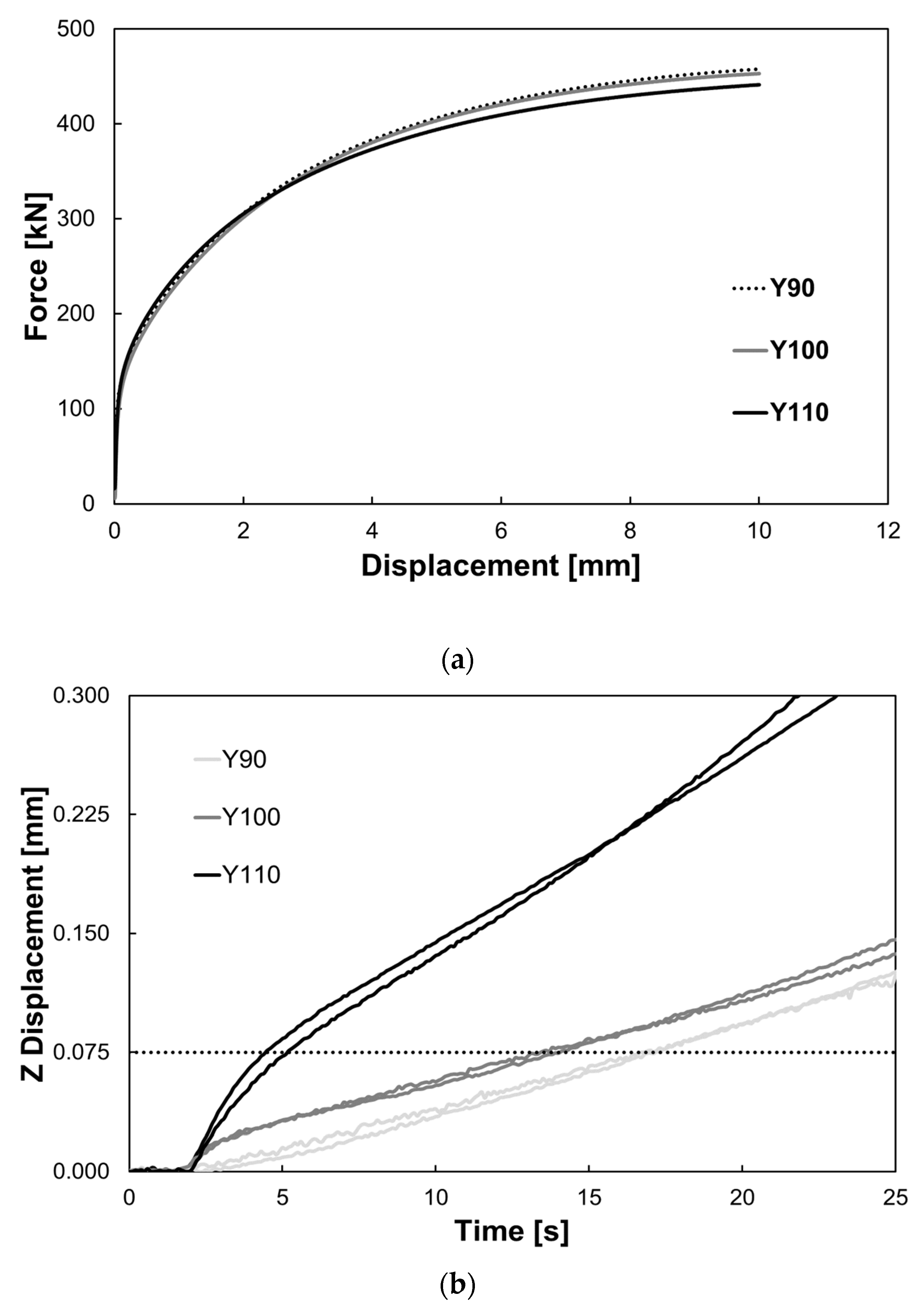
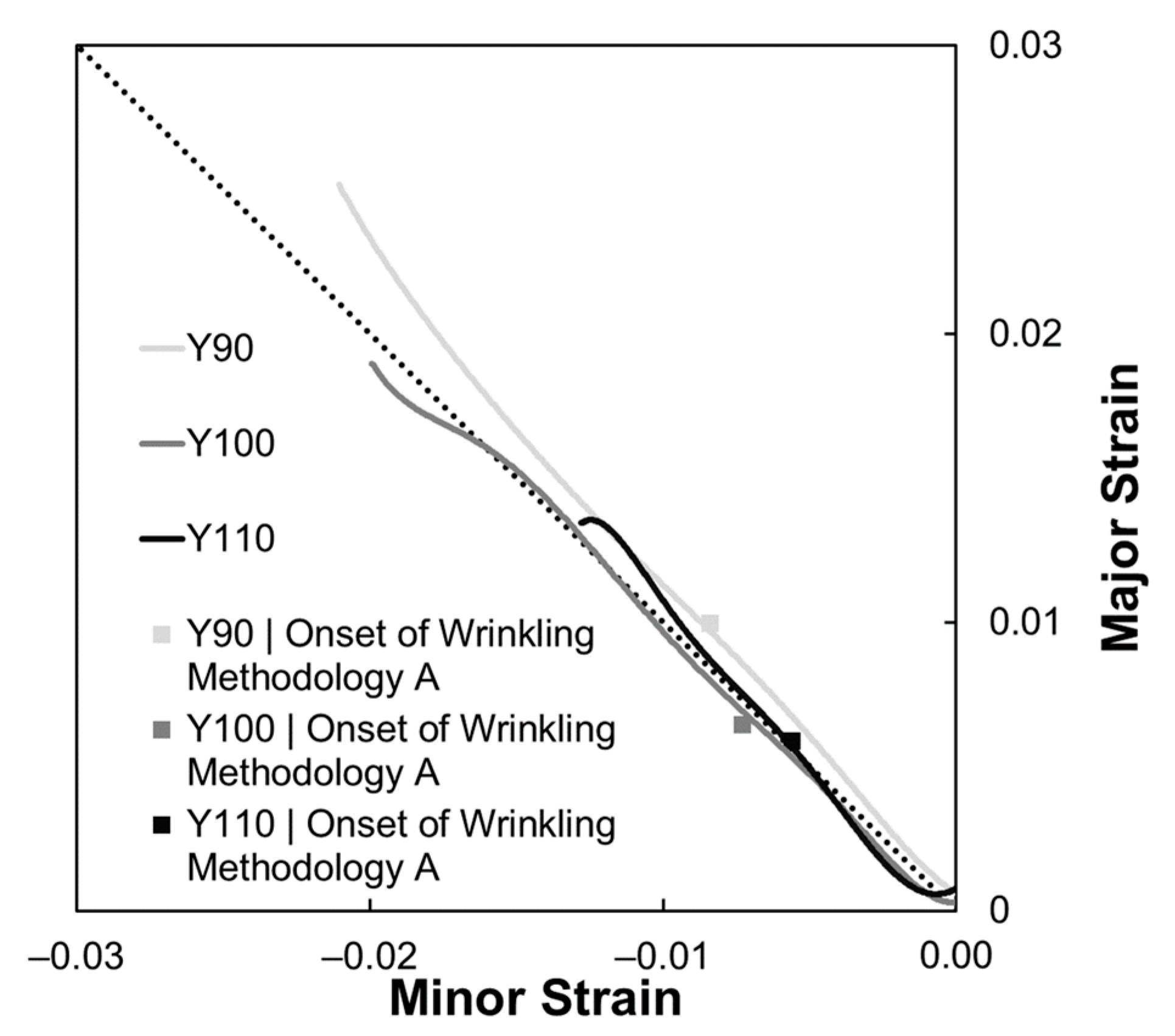
4.1. Methodology A
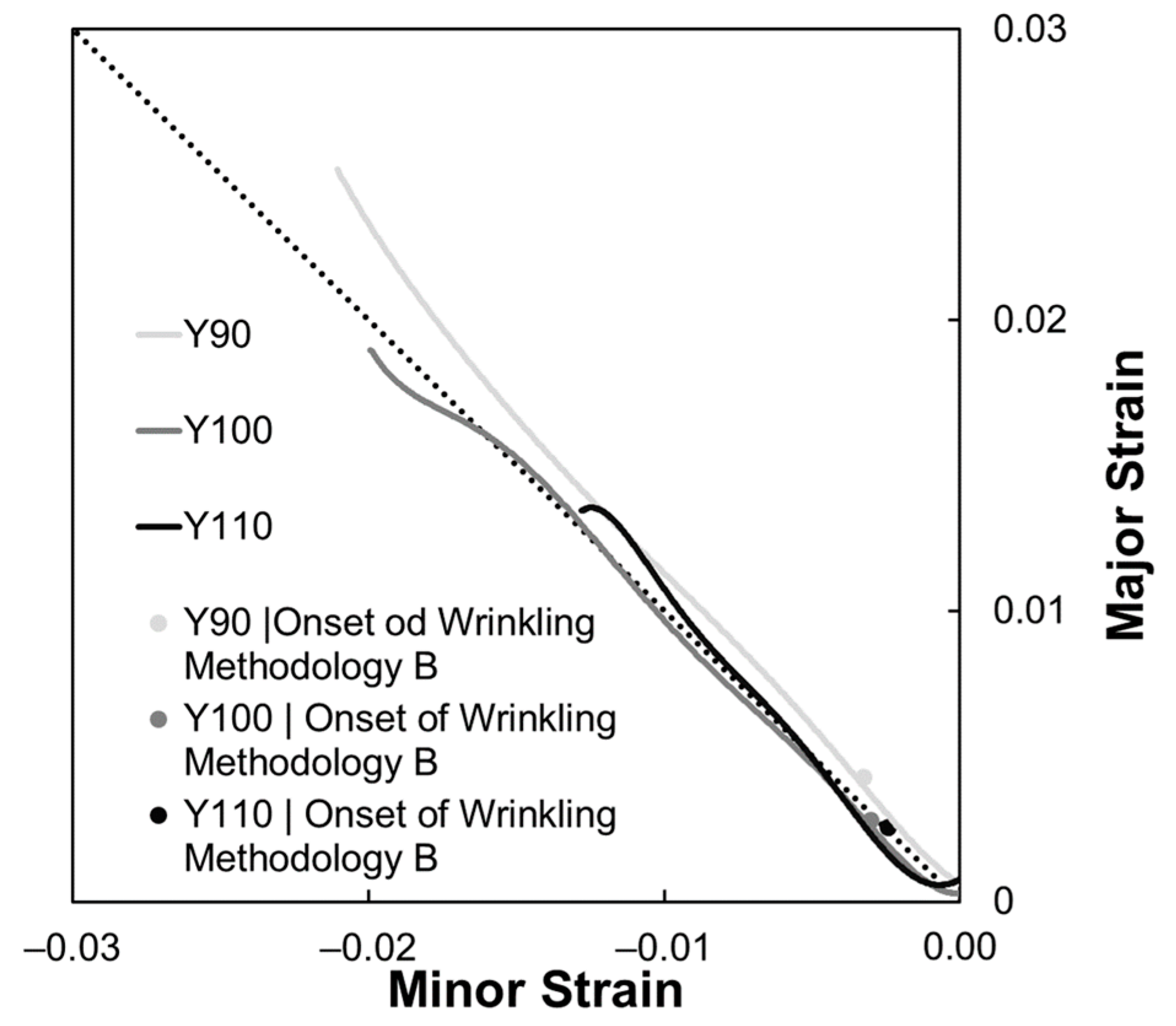
4.2. Methodology B
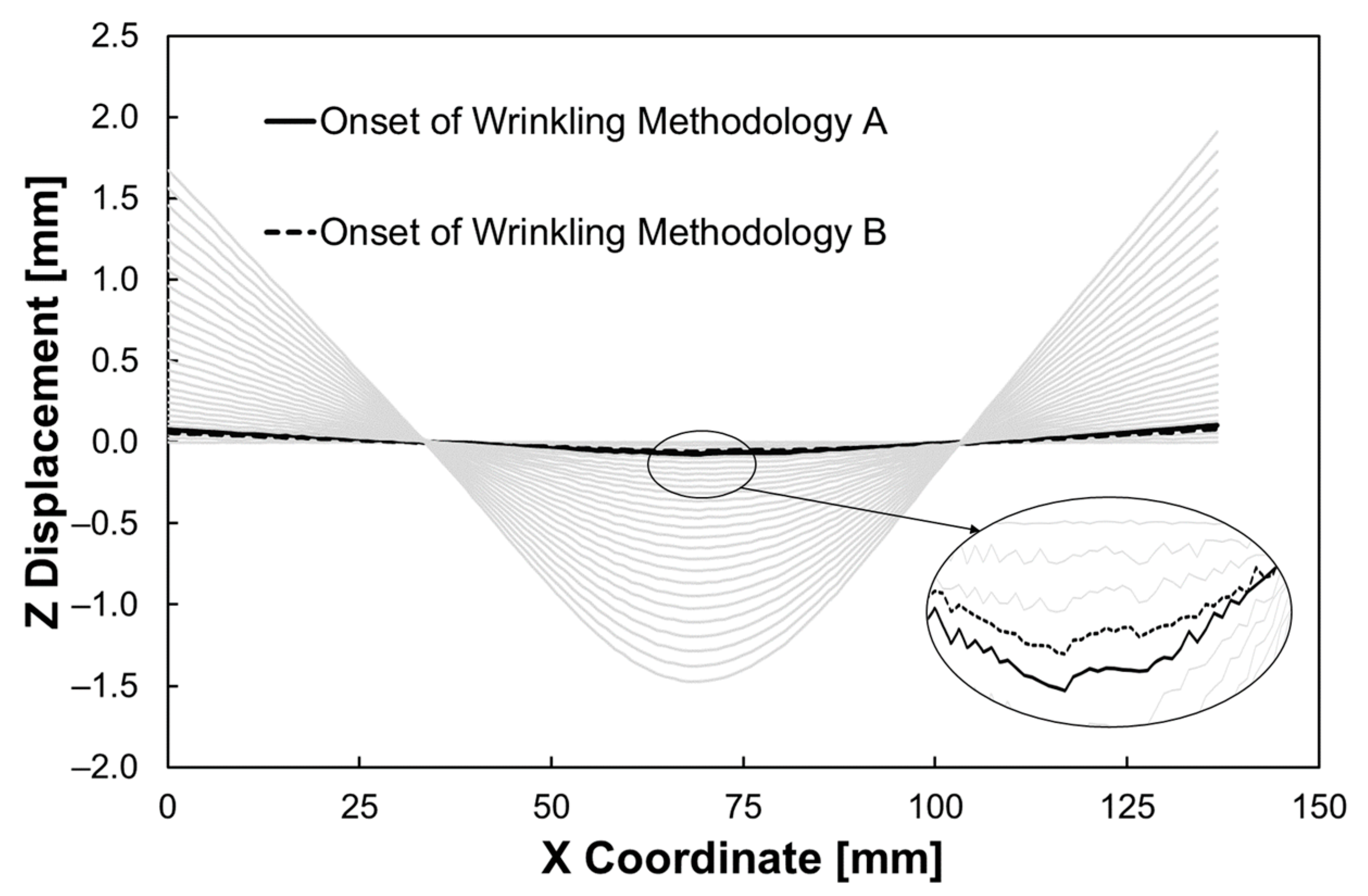
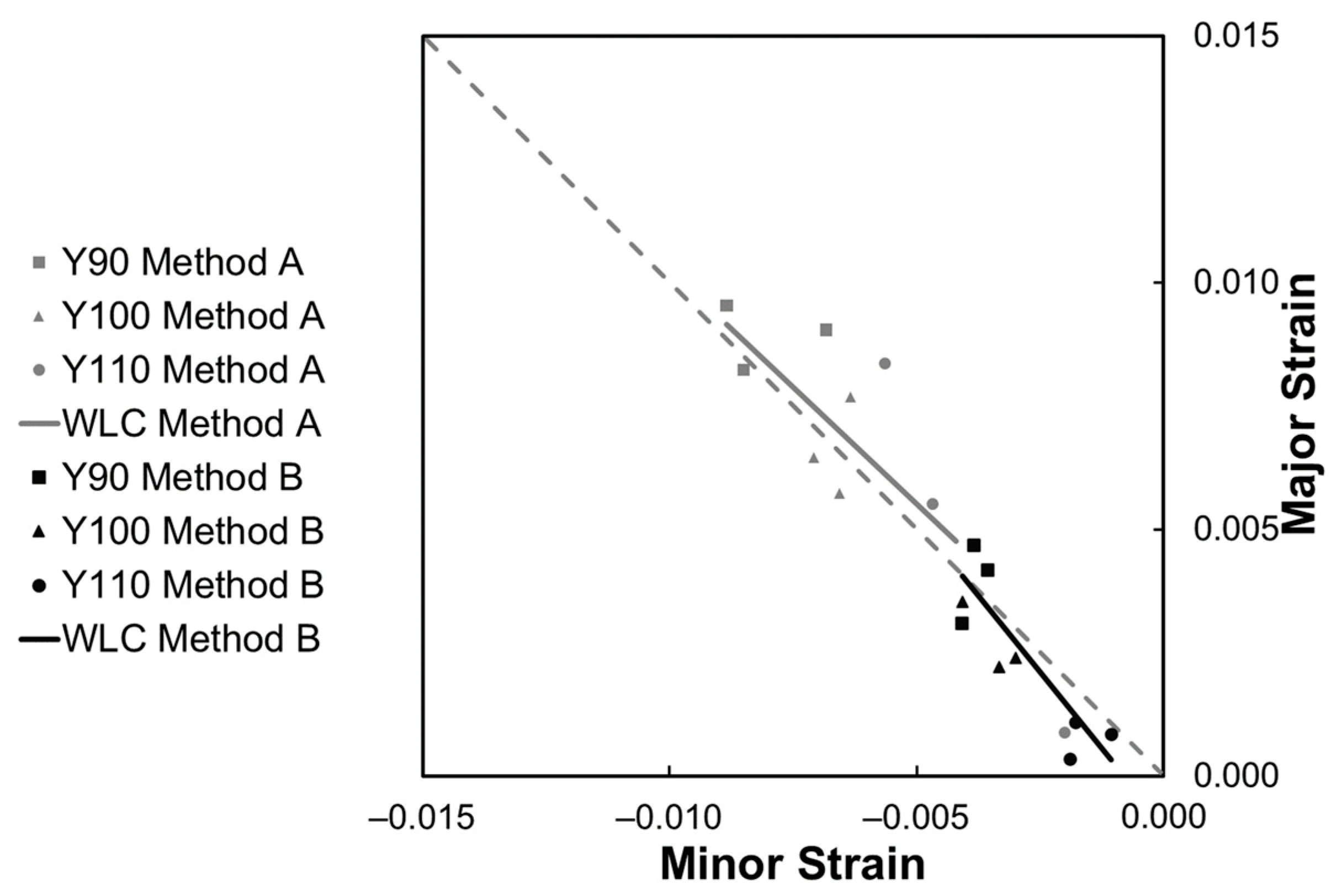
4.3. Methodologies Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kleiner, M.; Geiger, M.; Klaus, A. Manufacturing of Lightweight Components by Metal Forming. CIRP Ann. 2003, 52, 521–542. [Google Scholar] [CrossRef]
- Martins, P.A.F.; Bay, N.; Tekkaya, A.E. Atkins AG. Characterization of fracture loci in metal forming. Int. J. Mech. Sci. 2014, 83, 112–123. [Google Scholar] [CrossRef]
- Magrinho, J.P.; Silva, M.B.; Reis, L.; Martins, P.A.F. Formability Limits, Fractography, and Fracture Toughness in Sheet Metal Forming. Materials 2019, 12, 1493. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.B.; Yoon, J.W.; Yang, D.Y. Wrinkling initiation and growth in modified Yoshida buckling test: Finite element analysis and experimental comparison. Int. J. Mech. Sci. 2000, 42, 1683–1714. [Google Scholar] [CrossRef]
- Cao, J. Prediction of Plastic Wrinkling Using the Energy Method. J. Appl. Mech. 1999, 66, 646–652. [Google Scholar] [CrossRef]
- Chen, K.; Carter, A.J.; Korkolis, Y.P. Flange Wrinkling in Deep-Drawing: Experiments, Simulations and a Reduced-order Model. J. Manuf. Mater. Process. 2022, 6, 76. [Google Scholar] [CrossRef]
- Abe, H.; Nakagawa, K.; Sato, S. Proposal of conical cup buckling test. In Proceedings of the Congress of the International Deep Drawing Research Group, Kyoto, Japan, 14–15 May 1981; pp. 1–19. [Google Scholar]
- Narayanasamy, R.; Sowerby, R. Wrinkling of sheet metals when drawing through a conical die. J. Mater. Process. Technol. 1994, 41, 275–290. [Google Scholar] [CrossRef]
- Triantafyllidis, N.; Needleman, A. An Analysis of Wrinkling in the Swift Cup Test. J. Eng. Mater. Technol. 1980, 102, 241–248. [Google Scholar] [CrossRef]
- Huang, J.; Jin, J.; Deng, L.; Wang, X.; Gong, P.; Zhang, M.; Gao, C. Theoretical prediction of flange wrinkling in the first-pass conventional spinning of dual-metal sheets. J. Manuf. Process. 2021, 62, 368–377. [Google Scholar] [CrossRef]
- Liu, N.; Yang, H.; Li, H.; Li, Z.J. A hybrid method for accurate prediction of multiple instability modes in in-plane roll-bending of strip. J. Mater. Process. Technol. 2014, 214, 1173–1189. [Google Scholar] [CrossRef]
- Hutchinson, J.W.; Neale, K.W. Wrinkling of curved thin sheet metal. In Proceedings of the Considere Memorial Symposium—Plastic instability, Paris, France, 9–13 September 1985; pp. 71–78. [Google Scholar]
- Kasaei, M.M.; Moslemi Naeini, H.; Liaghat, G.H.; Silva, C.M.A.; Silva, M.B.; Martins, P.A.F. Revisiting the wrinkling limits in flexible roll forming. J. Strain Anal. 2015, 50, 528–541. [Google Scholar] [CrossRef]
- Magrinho, J.P.G.; Silva, C.M.A.; Silva, M.B.; Martins, P.A.F. Formability limits by wrinkling in sheet metal forming. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2016, 232, 681–692. [Google Scholar] [CrossRef]
- Yoshida, K.; Hayashi, H.; Miauchi, K.; Hirata, M.; Hira, T.; Ujihara, S. Yoshida buckling test. In Proceedings of the International Symposium on New Aspects of Sheet Metal Forming, Tokyo, Japan, 14–15 May 1981; pp. 125–148. [Google Scholar]
- Tang, H.; Wen, T.; Zhou, Y.; You, J.; Ma, D. Study of the wrinkling behavior of perforated metallic plates using uniaxial tensile tests. Thin-Walled Struct. 2021, 167, 108132. [Google Scholar] [CrossRef]
- Du, B.; Xie, J.; Li, H.; Zhao, C.; Zhang, X.; Yuan, X. Determining factors affecting sheet metal plastic wrinkling in response to nonuniform tension using wrinkling limit diagrams. Thin-Walled Struct. 2020, 147, 106535. [Google Scholar] [CrossRef]
- ASTM Standard E8/E8M; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2016. [CrossRef]
- Sharma, S.; Singh, R.; Kumar, S. Mechanical Anisotropy of Aluminium AA1050 and Aluminium Alloy AA6016 produced by Accumulative Roll Bonding. Int. J. Innov. Eng. Technol. 2016, 7, 350–356. [Google Scholar] [CrossRef]
- Han, F.; Liewald, M. A new method to enhance the accuracy of the buckling test using modified Yoshida sample. Adv. Mater. Res. 2018, 1018, 199–206. [Google Scholar] [CrossRef]
- Du, B.; Wang, X.; Wang, J.; Yang, H.; Cehn, X.; Yang, Z. The establishment of critical wrinkling judgment line for shear wrinkling instability of thin plate and its influencing factors. Thin-Walled Struct. 2022, 175, 109226. [Google Scholar] [CrossRef]

| Specimen Direction | Modulus of Elasticity [GPa] | Yield Strength [MPa] | Ultimate Tensile Strength [MPa] | Elongation at Break, A [%] | Anisotropy Coefficient | K [MPa] | n |
|---|---|---|---|---|---|---|---|
| 0° | 78.63 | 24.78 | 72.74 | 45.98 | 1.08 | 136.94 | 0.27 |
| 45° | 79.40 | 25.64 | 82.12 | 52.86 | 3.20 | 159.07 | 0.30 |
| 90° | 78.36 | 24.11 | 71.48 | 47.26 | 0.81 | 134.44 | 0.27 |
| Average | 78.95 | 25.04 | 77.11 | 49.74 | 2.08 | 147.38 | 0.29 |
| Geometry | Thickness [mm] | L [mm] |
|---|---|---|
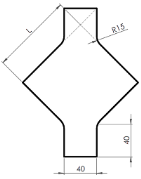 | 90 | |
| 1.5 | 100 | |
| 110 |
| Test Geometry | Instability Time Instant (s) | Strain 1 | Strain2 |
|---|---|---|---|
| Y90 | 208 | 0.00998 | −0.00843 |
| Y100 | 177 | 0.00645 | −0.00730 |
| Y110 | 153 | 0.00581 | −0.00556 |
| Test Geometry | Instability Time Instant (s) | Strain 1 | Strain2 |
|---|---|---|---|
| Y90 | 100 | 0.00430 | −0.00326 |
| Y100 | 99 | 0.00354 | −0.00363 |
| Y110 | 84 | 0.00256 | −0.00244 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, J.A.O.; Magrinho, J.P.G.; Silva, M.B. Physically-Based Methodology for the Characterization of Wrinkling Limit Curve Validated by Yoshida Tests. Metals 2023, 13, 746. https://doi.org/10.3390/met13040746
Santos JAO, Magrinho JPG, Silva MB. Physically-Based Methodology for the Characterization of Wrinkling Limit Curve Validated by Yoshida Tests. Metals. 2023; 13(4):746. https://doi.org/10.3390/met13040746
Chicago/Turabian StyleSantos, João A.O., João P.G. Magrinho, and Maria Beatriz Silva. 2023. "Physically-Based Methodology for the Characterization of Wrinkling Limit Curve Validated by Yoshida Tests" Metals 13, no. 4: 746. https://doi.org/10.3390/met13040746
APA StyleSantos, J. A. O., Magrinho, J. P. G., & Silva, M. B. (2023). Physically-Based Methodology for the Characterization of Wrinkling Limit Curve Validated by Yoshida Tests. Metals, 13(4), 746. https://doi.org/10.3390/met13040746







