Abstract
Fatigue fracture simulation based on phase field methods is a promising numerical approach. As a typical continuum approach, phase field methods can naturally simulate complex fatigue fracture behavior. Moreover, the cracking is a natural result of the simulation without additional fracture criterion. This study first introduced the phase field fracture principle, then reviewed some recent advances in phase field methods for fatigue fracture modeling, and gave representative examples in macroscale, microscale, and multiscale structural simulations. In addition, some strategies to improve the performance of phase field models were summarized from different perspectives. The applications of phase field methods to fatigue failure demonstrate the ability to handle complex fracture behaviors under multiple loading forms and their interactions, and the methods have great potential for development. Finally, an outlook was made in four aspects: loading form, fatigue degradation criterion, coupled crystal plasticity, and performance improvement.
1. Introduction
Material failure prediction is of great importance in engineering and materials science, and fatigue fracture as a typical form of failure has been of concern to scholars [1]. The process of generating cracks in components under fatigue loading can be decomposed into stages such as crack nucleation, steady-state propagation, and transient fracture. The fundamental challenge in simulating fatigue fracture is accurately tracing the crack surface under complex load conditions and material constitutive models [2,3]. Therefore, to handle the problem, numerous numerical techniques have been created, which can be classified into discontinuous and continuous methods [4,5]. However, discontinuous approaches frequently call for a way to represent the fracture topology and the related crack-tracking algorithm, which makes numerical integration and convergence challenging [6,7]. As a typical continuous method, the phase field method has recently received a wide range of attention [8,9]. The method can naturally model complex fracture processes including crack nucleation, propagation, coalescence, and branching [10,11]. Furthermore, the crack is a natural result of the simulation, obtained by solving differential equations related to the phase field, without additional fracture criteria. The crack evolution can be modeled on the fixed mesh, which avoids the tedious task of constructing the crack surface [12,13].
In the past few years, researchers have made many efforts to develop phase field methods for fatigue crack growth, and considerable progress has been made [14,15,16,17]. Phase field methods are widely applied to reproduce fatigue fracture behaviors, such as brittle [18], ductile [19], hyperelastic [20], and corrosion [21] fracture. Complex loading conditions, such as mechanical [22], thermal [23], and chemical [24] loads, as well as their interactions, are commonly the root cause of these fatigue failure issues. Related phase field modeling has been applied in macroscale [25], microscale [26], and multiscale [27] models, as shown in Figure 1. Most of the phase field models proposed in these studies accurately built the crack morphology and reasonably predicted the fatigue life. Meanwhile, some strategies for improving the performance of phase field models are proposed from various perspectives to further improve efficiency, accuracy, and convergence. The performance of phase field models has been satisfactorily improved due to the application of these techniques. This paper aims to review the advances in these directions.
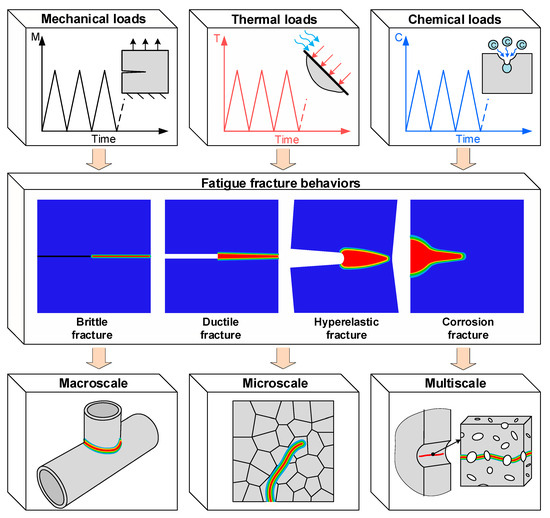
Figure 1.
Fatigue fracture behaviors simulated with phase field methods.
The paper is organized as follows: the phase field fracture principle is introduced in Section 2. Brittle, ductile, hyperelastic, and corrosion fracture behaviors in phase field fatigue modeling are given in Section 3, including the macroscale, microscale, and multiscale models. Strategies for improving the performance of phase field models are given in Section 4, including accelerated solution technologies, element processing technologies, and discretization methods. Finally, the concluding remarks and future directions are given in Section 5.
2. Phase Field Fracture Principle
In this section, a linear elastic phase field model based on Griffith’s fracture theory is introduced to illustrate the phase field fracture principle.
For a one-dimensional case, the topology of a sharp crack (Figure 2a) can be described by an auxiliary field variable ∈ [0, 1] with:
which is called the crack phase field order parameter, with ϕ = 0 and ϕ = 1 denoting the intact and fully broken states of the solid, respectively. The non-smooth crack phase field can be approximated by the exponential function, given by [13]:
ϕ is phase field variable, representing a diffusive or regularized crack topology (Figure 2b). The regularization parameter l specifies the width of the smearing function, approaching the discrete crack topology as l → 0.
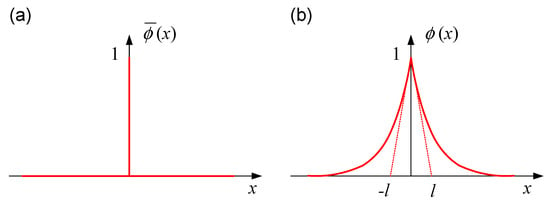
Figure 2.
Sharp (a) and diffusive (b) crack topologies.
Consider a discrete internal discontinuity Γ in a solid body Ω (Figure 3a), a regularized crack function Γl can be defined (Figure 3b):
where ϒ is the crack surface density function.
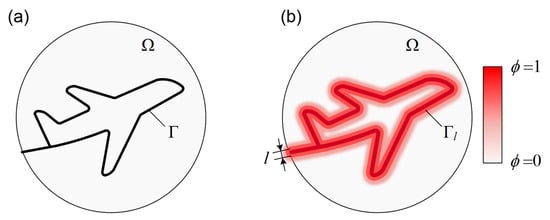
Figure 3.
Schematic representation of a solid body. (a) Internal discontinuity boundaries, and (b) a phase field approximation of the discrete discontinuities.
Phase field variable ϕ is smooth and continuous, and discrete cracks are represented in a diffuse form. Thus, the robust modeling of crack interactions and branches with arbitrary topological complexity is possible. The objective of the diffuse representation is to introduce the following fracture energy approximation over a discrete internal discontinuity Γ:
where and are the fracture energy and its density, respectively. Gc is fracture toughness. The rate-independent fracture description is extended to include time and history dependent concerns [25]:
where is the cumulative history variable, which fulfils , and is a fatigue degradation function. This form achieves fatigue degradation of materials by degrading fracture toughness.
The total potential energy of the solid is defined as the sum of the strain energy and fracture energy, which is expressed as:
where and are total potential energy and its density, respectively. is the undamaged elastic strain energy density. is a phase field degradation function, and one of its general expressions is described as:
In order to explain the inconsistency in the contribution of tensile and compressive behavior to material degradation, the elastic strain energy density must be additively divided into active and inactive components [13,28]:
Damage is an irreversible process: . To enforce irreversibility, a history field variable is introduced, which must satisfy the Karush-Kuhn-Tucker conditions:
For a current time , over a total time , the history field is understood as:
The fracture energy density is further defined as:
where is the geometric crack function, and is a scaling constant. The dissipation function rules the energy dissipation due to the formation of a new crack. There are two widely used models [18]:
The AT2 model has a vanishing threshold for the onset of damage, resulting in a material behavior without an initial linear elastic branch, while the AT1 model has the ability to reproduce the initial linear elastic constitutive behavior.
The total potential energy and its density of the solid are reformulated as:
Based on the above equation, the weak form of the equilibrium equations for the displacement and phase fields can be derived using the variational principle and applied to the subsequent solutions.
To sum up, phase field models at the mechanical level can be considered an extension of the Griffith fracture theory. The potential energy used for variational analysis includes the fracture energy, which is regularized with the aim to build up a diffuse form of the crack. As a result, phase field methods offer the enormous possibility for handling challenging fracture problems.
3. Typical Fracture Behavior in Phase Field Fatigue Modeling
In this section, four typical fracture behaviors in phase field fatigue modeling will be reviewed, including brittle, ductile, hyperelastic, and corrosion fracture. The scales of the model involve macroscale, microscale, and multiscale. Note that the characteristic length to differentiate between macroscale and microscale is 0.1 mm in this paper.
3.1. Brittle Fracture
3.1.1. Macroscale Brittle Fracture
In the field of research on macroscale brittle fracture, Alessi [29] proposed a new variational fatigue phase field model using a phenomenological approach for the study of the one-dimensional case. The model is capable to describe a typical Wöhler curve and to recover the known trends in the description of the mean-stress effects. Mesgarnejad et al. [30] developed a class of phase field models to describe fatigue fracture phenomenologically through local fracture toughness degradation. The model is the ability to detail the growth of a collection of interacting cracks in complex geometries. A similar approach is also reflected in the work of Grossman-Ponemon et al. [31] and Hasan et al. [14]. Carrara et al. [18] modified the standard regularized free energy function by introducing a sui fatigue history variable and a fatigue degradation function, which effectively reduces the fracture toughness. Numerical results demonstrate that the crack propagation rate curve and the Paris law are naturally recovered, and subsequently demonstrate that the framework is available to handle complex geometries and loading conditions in 2D (Figure 4a) and 3D (Figure 4b).
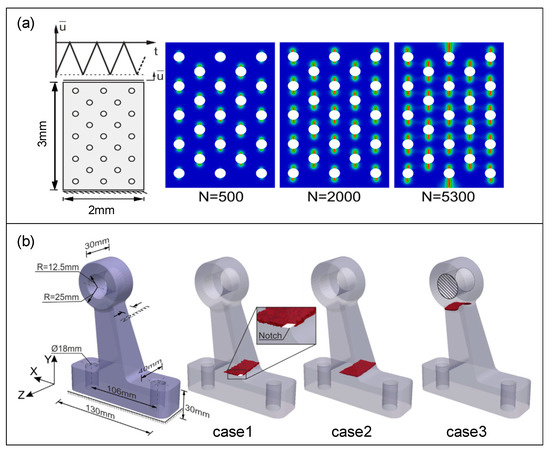
Figure 4.
Macroscale brittle fracture. (a) A 2D plate with holes model and (b) a 3D steering arm model [18].
Lo et al. [32] introduced a crack expansion viscosity parameter into the standard phase field model for the brittle fracture to account for the rate- or period-dependent crack propagation phenomenon. An elastic energy decomposition method is employed to ensure that the compressive stresses do not contribute to the phase field evolution, and a modified J-integral is proposed to reproduce the Paris law using the phase field approach. Finally, the ability of the model to reproduce a 3D crack is illustrated. To effectively simulate fatigue crack growth in thin-walled structures, Liu et al. [33] presented a global-local phase field method for large deformation shells to provide an efficient modeling framework. The global model can be coarsely meshed, while the local model can be meshed more finely to handle the displacement-phase field problem. The capability of the global-local model is proved by simulating crack propagation in a cylindrical thin-walled structure under fatigue cyclic loading.
3.1.2. Microscale Brittle Fracture
The failure mechanism of materials generally depends on their microstructures, such as grain size and orientation, grain boundary characteristics, impurities, and voids. Emdadi and Zaeem [34] proposed a modified phase field model based on Griffith’s theory for the study of intergranular and transgranular crack growth in polycrystalline brittle materials. The simulation results demonstrate that the specific combination of grain boundary strength and crack surface energy can promote along-crystal crack growth in, thus affecting the fracture performance of polycrystalline materials.
The micro crack in some components has a significant impact on their performance, such as heat transfer, mass transfer, and energy storage. Relevant failure problems can be handled using the phase field method. For the failure of thermal barrier coatings (TBCs), Xiao et al. [35] presented a growth chemical model for the Thermal growth oxide (TGO) and thermal mechanical interaction phase field model and discussed the delamination mechanism of TBCs under thermal cycling from a microscopic perspective. The result proves that the phase field model is a good reproduction of the complex failure behavior in TBCs. The electrode particles in Lithium-ion batteries are small in size and their cracking drive battery capacity degradation. Ai et al. [36] developed a multi-physics phase field fatigue model to investigate the crack growth in battery electrode particles undergoing hundreds of cycles. In addition, the electro-chemo-mechanical formulation is combined with CT imaging to simulate the fatigue fracture of real particle microstructure. Using the method, the nonlinear crack growth behavior can be accurately predicted, and the crack length is observed to increase exponentially with the number of cycles.
3.2. Ductile Fracture
3.2.1. Macroscale Ductile Fracture
Ulloa et al. [37] offered a coupled gradient-enhanced plastic damage model that uniformly captures the features of both low and high circumferential fatigue. The suggested variational model can explain cyclic failure under both force and displacement loading by combining cyclic plasticity and the phase field description of the fatigue fracture. The simulation result of an asymmetric notched plate model is shown in Figure 5. To ensure that the compressive plastic energy does not contribute to crack formation in elastoplastic materials, Shi et al. [19] established a plastic history field and presented an alternate elastic energy decomposition technique. The model can eliminate the fictitious propagation of compression cracks and predict the results closer to the experimental observations. Haveroth et al. [38] proposed a general thermodynamically consistent non-isothermal phase field model for fatigue evolutions in elastoplastic materials under the hypothesis of small strains. The ductile fracture and fatigue processes can be qualitatively and statistically reproduced using the model. Song et al. [39] developed a phase field viscoplasticity coupling method to model the crack growth in a nickel-based superalloy under fatigue. The result shows that the method is very effective in predicting the fatigue crack growth under varied dwell times at peak load, and it is further used to simulate the growth path of the 3D corner crack model. Cyclic plasticity in fatigue behavior often leads to large computational costs. Therefore, Khalil et al. [25] proposed a generalized phase field model for fatigue crack growth in elastoplastic solids with an efficient solver. Both non-linear kinematic and isotropic hardening are investigated, as well as the combination of the two models. By testing typical numerical examples, the framework is found to be efficient in predicting fatigue crack propagation in arbitrary geometries as well as cyclic hardening in elastoplastic materials. Some advanced materials tend to have anisotropic elastoplastic fracture behavior, and phase field methods have been applied to related fields. Li et al. [40] presented a phase field model for anisotropic elastoplastic fracture behavior. The model contains three innovations: an extension to a phase field model of anisotropic elastoplasticity, a transformation from quasi-brittle to elastoplastic fracture behavior, and a novel method to identify the macroscale strain density as a function of microscale interface damage variables. The application of the model for 3D printed polymer materials has been approved through an experimental comparison.
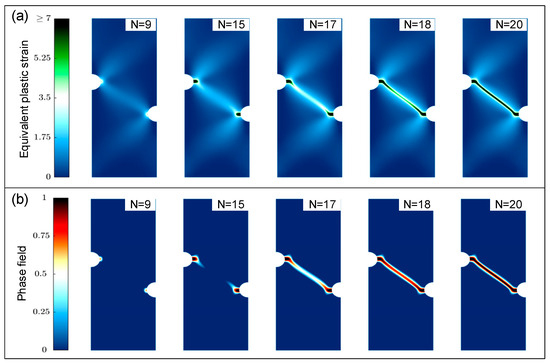
Figure 5.
Macroscale ductile fracture. (a) Equivalent plastic strain field and (b) phase field [37].
3.2.2. Microscale Ductile Fracture
It is challenging to simulate ductile fracture in microscale models. Seleš et al. [41] simulated complex fracture and fatigue failure processes in the microstructure of nodular cast irons to investigate the transition between brittle and ductile fracture material behavior. It is concluded that under cyclic loading conditions, the transition between low and high cycle fatigue regimes is captured by analyzing the fracture patterns and Wöhler curve of the specimens. As the load amplitude decreases, the model shows less plasticity and thus transitions to high cyclic regimes. The phase field modeling of microcracks in polycrystalline materials is equally of concern. Tu et al. [42] developed a coupled crystal plasticity-phase field (CP-PF) model for simulating image-based crack growth in polyphase-polycrystalline microstructures of aluminum alloy. The problem is characterized by elastoplasticity anisotropy and cracking features such as nucleation, propagation, coalescence, and branching. Simulations of structural deformation, crack nucleation, and propagation in polycrystalline microstructures were carried out under monotonic and cyclic loading conditions, and the robustness and effectiveness of the model in modeling microcracks was demonstrated.
3.2.3. Multiscale Ductile Fracture
In terms of multiscale methodological studies, Sadeghirad et al. [27] proposed a method for predicting crack initiation in the microstructure, which uses a phase field model combined with an extended finite element method (XFEM) to achieve an accurate modeling of macroscale crack growth. The macroscopic model assumes linear elastic material behavior while coupling the phase field model and the crystal plasticity model at the microscopic scale to capture the plastic behavior of non-uniform polycrystals. Compared with experimental results, it is found that the proposed multiscale approach utilizes the advantages of each method to provide an accurate prediction with minimal computational cost.
3.3. Hyperelastic Fracture
To describe rubber damage caused by cyclic loading, Loew et al. [43,44,45] extended the previous method to establish a phase field model for rate-dependent rubber fracture in a finite strain condition. A rate-dependent fatigue model is developed based on a load-history dependent fatigue damage source. The Wöhler curve and the rate of the crack growth curve are given by the simulation, and the failure behavior of the single notch under cyclic tensile load is also predicted, which is in good agreement with the experimental findings. The simulation results of two kinds of fatigue tests are shown in Figure 6a,b. Although this model accurately describes fatigue failure, its calculation speed is slow. Therefore, Loew et al. [44] provided an acceleration scheme for the cyclic loading of the phase field damage model, and the simulation speed is improved by using the cyclic skipping technique.
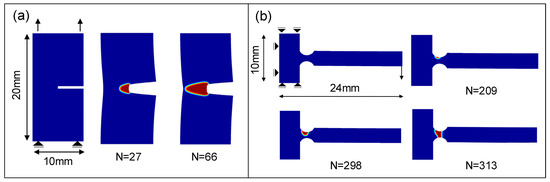
Figure 6.
Hyperelastic fracture. (a) A single edge notched plate model and (b) a bending beam model [44].
Fatigue failure simulation of Shape Memory Alloys (SMAs) has been a difficult problem owing to nonlinear constitutive behavior. Simoes et al. [46,47] developed the first phase field fracture formulation for SMAs. The hyperelasticity and shape memory effects are caught by the constitutive behavior, which includes phase transitions induced by stress and temperature. An implicit time integration scheme with both monolithic and staggered solution strategies is applied for the numerical implementation of the theoretical formulation. Based on this framework, fatigue failure studies are carried out for complex SMAs structures. The result shows that the phase field approach can simulate several typical 2D and 3D problems involving subcritical crack propagation, unstable cracking, crack coalescence, and fatigue crack growth, which demonstrates the potential and robustness of the model. The design of SMAs components can also be optimized using the framework.
3.4. Corrosion Fracture
Predicting the failure of engineering parts in aggressive environments is a long-standing scientific challenge. The interaction of mechanical loading and the corrosive environment promotes the nucleation and propagation of cracks, a process known as stress corrosion cracking (SCC). It occurs in a wide variety of metallic materials and settings and is frequently facilitated by pre-existing flaws [24]. Martínez-Pañeda et al. [48] presented a phase field formulation for the long-term problem of hydrogen assisted cracking. A coupled mechanical-diffusion-phase field finite element framework is used to analyze hydrogen transport to the fracture area and subsequent cracking, and the plate with preexisting defects is considered. The model has the ability to capture complex crack growth caused by inherent defects in the corrosive environment. The strategy has quickly gained in popularity as an approach for combining different hydrogen embrittlement models [49,50,51], however, the majority of analyses are restricted to 2D boundary value problems. The deformation-diffusion-damage coupling framework developed by Kristensen et al. [52] considers the AT1 and AT2 models, inertial effects, and 3D model implementation for the first time, which can predict the defect evolution under operating conditions until the ultimate failure. Cui et al. [21,24] presented a new framework for modeling mechanically-assisted corrosion in elastoplastic solids and proposed a formulation based on the film fracture-dissolution-repassivation mechanism. The model takes into account the electrochemical driving force of mechanical straining, which speeds up the kinetics of corrosion. The simulated crack of the C-ring reveals a good agreement with the experimental observation, as shown in Figure 7. Golahmar et al. [53] proposed a multi-physics phase field model for hydrogen-assisted fatigue by combining hydrogen assisted failures and mechanical fatigue. To capture how newly formed fracture surfaces are quickly exposed to the environment, a penalty technique was used to implicitly enforce moving chemical boundary requirements. The study shows that the model sufficiently captures the sensitivity of fatigue crack growth rates to hydrogen content, and recovers the Paris law naturally, which can quantify the influence of hydrogen on the Paris law parameters.
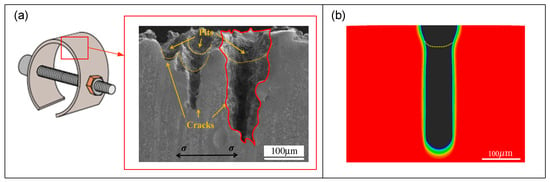
Figure 7.
Corrosion fracture. (a) Experimental observation and (b) simulated crack of the C-ring [21].
Corrosion fracture in the microstructures is equally of attention. To achieve the simulation of the SCC initiated from surface pits, Mai et al. [54,55] implemented the film rupture-dissolution-repassivation model, which relates the interface kinetics parameter to the stress distribution near the crack tip. The evolution of the cracking interface is approximated by coupling the governing equations of electrochemical corrosion with the elastoplastic deformation of metals. It is demonstrated that the model can reliably replicate experimental results after proper calibration and show applications for the material microstructure on SCC.
4. Performance Improvement Strategies for Phase Field Models
The phase field method has advantages for addressing complicated fracture problems, but it has a high computational cost and modeling difficulty. It is necessary to develop studies on the performance improvement of phase field models. In this section, some typical performance improvement strategies for phase field models are reviewed from three aspects, including accelerated solution technologies, element processing technologies, and discretization methods.
4.1. Accelerated Solution Technology
4.1.1. Cycle Skipping Technique
Improving the computational efficiency of phase field models is also a concern for researchers. The computational cost of cyclic loading is quite large, especially for high cycle fatigue. To keep the solution time within acceptable limits, Schreiber et al. [56] collected a similar number of cycles into blocks, and additional fatigue damage processed within one simulation step referred to these blocks. The block size was adaptively selected to control the damage rate. Yan et al. [57] developed an adaptive cyclic incremental adjustment algorithm, which can reduce the computational cost of the simulation without sacrificing accuracy. The whole simulation is divided into three stages: elastic stages, transition phase, and fatigue stages. The damage increment is controlled to obtain a moderate fatigue energy growth, where the number of cycle increments is chosen adaptively according to the damage increment.
When nonlinear material constitutive is involved, Seleš et al. [58] presented a full range phenomenological fatigue fracture model able to reproduce the main features of low and high cycle fatigue which consider cyclic plasticity. A two-part cycle skipping technique is implemented in this work. The technique precisely solves the highly nonlinear time-evolutionary behavior by automatically calculating the lower number of cycles to be skipped or by not skipping cycles at all. Loew et al. [44] presented explicit and implicit cycle skipping schemes to simulate the fatigue crack growth of rubber. It is found that both schemes reduce the calculation time significantly, while the accuracy remains substantially unaffected. The adaptive cycle skipping method for the implicit acceleration framework is dependent on the number of iterations since the size of the cycle step controls how quickly simulations accelerate, but may give rise to incorrect results. The method proposed by Loew can reduce the calculated costs by 99.5%.
4.1.2. Quasi-Newton Monolithic Scheme
One of the main reasons for the high computational cost of phase field models is that the robust but inefficient alternating minimization (AM) or staggered scheme is widely used. Aiming to tackle the difficulty, Wu et al. [59,60] proposed, for the first time, to use the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm to solve the coupled governing equations in a monolithic manner rather than the standard Newton iterative scheme in a staggered manner. Representative example shows that the quasi-Newton monolithic scheme is about 3–7 times faster than the staggered solver, and the larger the model scale is, the more costs can be saved. On this basis, Kristensen and Khalil et al. [25,61] proposed a generalized phase field model for fatigue crack growth in elastic and elastoplastic solids by combining the phase field framework with the quasi-Newton monolithic scheme. In addition, a new adaptive time increment scheme is introduced to further reduce the cost while allowing sudden changes in fracture behavior to be accurately resolved. Liu et al. [33] presented a phase field model for large deformation shells based on the quasi-Newton monolithic scheme, and the excellent convergence performance of the form was proved. To further save computational costs, a specific global-local method using solid shell elements was proposed, and its capability is verified by simulating crack growth in cylindrical structures.
4.2. Element Processing Technology
4.2.1. Adaptive Mesh Refinement Technology
The adaptive mesh refinement technology is an effective means to solving the contradiction between the computational efficiency and accuracy of the phase field model. Freddi et al. [62] investigated the global and global/local refinement strategies. Compared with the global technique, the global/local strategy can reduce the calculation cost by about 20–30%, but it is more sensitive to parameter selection. Xu et al. [63] proposed a multi-level adaptive mesh refinement technique suitable for the phase field model. In addition, an improved backtracking algorithm enables the adaptive mesh to handle complex crack propagation. The calculation efficiency of this method can be increased by around 30 times over global mesh refinement. Aiming at the problem that the existing adaptive mesh refinement technology cannot accurately simulate crack initiation without a prior local refinement, Gupta et al. [64] developed an adaptive mesh refinement algorithm for phase field models using a multi-level mark–unmark strategy. The algorithm utilizes a threshold to mark elements based on effective crack driving energy and reduces the calculation time by 5–50 times as compared to simulations that adopt a priori non-adaptively strategy. Eldahshan et al. [65] combined the framework of ductile fracture phase field modeling with adaptive refinement technology to effectively simulate ductile fracture without the need to predefine the crack initiation site.
4.2.2. Combined Extended Finite Element Method (XFEM)
XFEM is one of the most popular methods to simulate crack propagation. As a discontinuous method, it has the following advantages: (a) Explicit representation is helpful to the modeling of crack morphology; (b) Any wrong interaction between crack surfaces can be avoided; and (c) The rear area of the crack tip may be roughly discretized. Therefore, if the phase field model can be combined with XFEM, the efficiency and performance of the model can be effectively improved. Existing studies have confirmed this conjecture. Giovanardi et al. [66] established a hybrid XFEM-Phase field (Xfield) method. A global solution for the displacement field is calculated with XFEM. Then, using a finer mesh and Dirichlet boundary conditions that are derived from the overall solution, a phase field model in overlapping subdomains including the crack points is solved to determine the growth. Patil et al. [67] proposed a similar strategy called the local moving extended phase field method (LMXPFM). The crack is described by XFEM, and the phase field model is employed in small circular subdomains around the crack tips. These works are limited to 2D problems. Muixí et al. [68] developed a combined XFEM phase field model (PF-XFEM) without remeshing. The same background mesh is used throughout the simulation. The discretization is automatically updated as the crack grows, avoiding remeshing to improve efficiency. The robustness of the model is proved in 2D and 3D instances.
4.3. Discretization Method
4.3.1. Fast Fourier Transform (FFT) Method
The application of phase field methods to simulate fractures in heterogeneous materials usually requires fine meshing and hence a large number of elements in the model, weakening the efficiency of standard finite element solvers. Motivated by this limitation, Chen et al. [69] proposed an FFT solver of a variational phase-field model for brittle fracture. Relying on the staggered scheme, the phase field and elastic problem are resolved by the FFT technique. As an alternative, FFT methods use matrix-free iterative algorithms to solve partial differential equations with periodic boundary conditions. Moreover, segmented digital images can be used as input for the simulation without the meshing step. To further improve the performance of a fixed-point algorithm, an improved convergence acceleration approach is presented. Sadeghirad and Ma et al. [27,70] simulated the crack growth inside the polycrystalline microstructure with the help of the FFT-solver, and the accuracy and efficiency of this method are proved.
4.3.2. Machine Learning: Physics Informed Neural Network (PINN) Algorithm
Goswami et al. [71] proposed a new physics informed neural network (PINN) algorithm for predicting the crack propagation based on the phase field method. The suggested approach offers two key advantages over the conventional residual-based PINN. Firstly, the imposition of the boundary conditions is simpler and more robust. Moreover, training the network is quicker because the derivatives in the functional form of the variational energy are of a lower order than those in the residual form employed in standard PINN. The proposed machine learning method has less code and is easy to implement. After the network is trained, compared with the finite element method, the method can have good calculation savings, but the discrete elements required are significantly smaller. The potential application of this approach is to be a low-fidelity surrogate for the high-fidelity numerical solvers, which is very useful in reliability analysis and design optimization.
4.3.3. Meshfree Method
Amiri et al. [72] developed a fourth order phase field model based on the meshless local maximum entropy (LME) approximants. This meshless method allows the model to directly solve the fourth order phase field equation without splitting the fourth order differential equation into two second order differential equations. Representative examples, such as the mode-I tension specimen and the single edge notched beam, show that both second-order and fourth-order phase field models are capturing complex crack behavior, and the fourth-order model can capture crack surfaces more accurately. In addition, the fourth order model requires fewer nodes. The simulation results are in good agreement with the analytical solutions and experimental data.
4.4. Summary
The seven performance enhancement strategies reviewed above all have achieved effective performance enhancement for phase field models, providing a basis for subsequent related studies. However, these strategies still have certain disadvantages, which are summarized in Table 1.

Table 1.
Summary of the main performance improvement strategies.
5. Conclusions
Phase field methods is a promising tool for numerical simulation. This work first introduces the principle of phase field approximation of cracks and then reviews some recent advances in phase field methods for simulating fatigue fracture. Representative examples from macroscale, microscale, and multiscale structural simulations are given, and some strategies for improving the performance are summarized. The application of phase field methods to fatigue failure fully demonstrates its ability to reproduce complex fracture behaviors under multiple loading forms and their interactions, and the methods have great potential for development. For future work, four aspects are proposed:
- Phase field models need to be further applied to fatigue failure simulation of advanced materials under complex loading forms, such as thermal fatigue, thermo-mechanical fatigue, and high temperature vibration fatigue.
- Most of the fatigue degradation criteria in existing phase field models are phenomenological. The establishment of fatigue degradation criteria that correspond to the real physical mechanism can contribute to the improvement of the prediction accuracy of phase field models.
- The combination of phase field methods and crystal plasticity finite element has great potential to simulate fatigue crack growth in microscale, which can clearly understand the damage mechanism of metal microstructure. More advanced algorithms need to be built to accomplish this coupling process.
- Some effective strategies for improving the performance of phase field models are proposed. However, these methods have certain disadvantages and continue to have their own limitations when faced with some complex simulations. It is still essential to further improve the performance of phase field models.
Author Contributions
Conceptualization, H.C.; methodology, H.Z.; investigation, C.D.; writing—original draft preparation, H.C. and C.D.; writing—review and editing, H.C., C.D. and H.Z.; supervision, H.C. and H.Z.; project administration, H.C.; funding acquisition, H.C. and H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China, grant number 91860111.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Correction Statement
This article has been republished with a minor correction to resolve equation errors. This change does not affect the scientific content of the article.
References
- Qiu, S.; Cui, H.; Zhang, H.; Wen, W.; Guo, J. A dual-threshold modelling approach for fatigue life prediction under combined high and low cycle fatigue. Int. J. Fatigue 2022, 164, 107110. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Y.; Yu, J.; Wang, J.; Du, F.; Zhang, Y. Fatigue Life Evaluation Considering Fatigue Reliability and Fatigue Crack for FV520B-I in VHCF Regime Based on Fracture Mechanics. Metals 2020, 10, 371. [Google Scholar] [CrossRef]
- Sadananda, K.; Nani Babu, M.; Vasudevan, A.K. A review of fatigue crack growth resistance in the short crack growth regime. Mater. Sci. Eng. A 2019, 754, 674–701. [Google Scholar] [CrossRef]
- Egger, A.; Pillai, U.; Agathos, K.; Kakouris, E.; Chatzi, E.; Aschroft, I.A.; Triantafyllou, S.P. Discrete and Phase Field Methods for Linear Elastic Fracture Mechanics: A Comparative Study and State-of-the-Art Review. Appl. Sci. 2019, 9, 2436. [Google Scholar] [CrossRef]
- Fang, J.; Wu, C.; Rabczuk, T.; Wu, C.; Ma, C.; Sun, G.; Li, Q. Phase field fracture in elasto-plastic solids: Abaqus implementation and case studies. Theor. Appl. Fract. Mec. 2019, 103, 102252. [Google Scholar] [CrossRef]
- Brockman, R.A.; Hoffman, R.M.; Golden, P.J.; Musinski, W.D.; Jha, S.K.; John, R. A computational framework for microstructural crack propagation. Int. J. Fatigue 2021, 152, 106397. [Google Scholar] [CrossRef]
- Gairola, S.; Jayaganthan, R. XFEM Simulation of Tensile and Fracture Behavior of Ultrafine-Grained Al 6061 Alloy. Metals 2021, 11, 1761. [Google Scholar] [CrossRef]
- Ambati, M.; Gerasimov, T.; De Lorenzis, L. A review on phase-field models of brittle fracture and a new fast hybrid formulation. Comput. Mech. 2015, 55, 383–405. [Google Scholar] [CrossRef]
- Zhuang, X.; Zhou, S.; Huynh, G.D.; Areias, P.; Rabczuk, T. Phase field modeling and computer implementation: A review. Eng. Fract. Mech. 2022, 262, 108234. [Google Scholar] [CrossRef]
- Wu, J. A geometrically regularized gradient-damage model with energetic equivalence. Comput. Method. Appl. Mech. 2018, 328, 612–637. [Google Scholar] [CrossRef]
- Molnár, G.; Gravouil, A. 2D and 3D Abaqus implementation of a robust staggered phase-field solution for modeling brittle fracture. Finite Elem. Anal. Des. 2017, 130, 27–38. [Google Scholar] [CrossRef]
- Badnava, H.; Etemadi, E.; Msekh, M. A Phase Field Model for Rate-Dependent Ductile Fracture. Metals 2017, 7, 180. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Method. Appl. Mech. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Hasan, M.M.; Baxevanis, T. A phase-field model for low-cycle fatigue of brittle materials. Int. J. Fatigue 2021, 150, 106297. [Google Scholar] [CrossRef]
- Živković, J.; Dunić, V.; Milovanović, V.; Pavlović, A.; Živković, M. A Modified Phase-Field Damage Model for Metal Plasticity at Finite Strains: Numerical Development and Experimental Validation. Metals 2021, 11, 47. [Google Scholar] [CrossRef]
- Fang, J.; Wu, C.; Li, J.; Liu, Q.; Wu, C.; Sun, G.; Li, Q. Phase field fracture in elasto-plastic solids: Variational formulation for multi-surface plasticity and effects of plastic yield surfaces and hardening. Int. J. Mech. Sci. 2019, 156, 382–396. [Google Scholar] [CrossRef]
- Molnár, G.; Gravouil, A.; Seghir, R.; Réthoré, J. An open-source Abaqus implementation of the phase-field method to study the effect of plasticity on the instantaneous fracture toughness in dynamic crack propagation. Comput. Method. Appl. Mech. 2020, 365, 113004. [Google Scholar] [CrossRef]
- Carrara, P.; Ambati, M.; Alessi, R.; De Lorenzis, L. A framework to model the fatigue behavior of brittle materials based on a variational phase-field approach. Comput. Method. Appl. Mech. 2020, 361, 112731. [Google Scholar] [CrossRef]
- Shi, Q.; Yu, H.; Guo, L.; Hao, L.; Huang, K. A phase field model with plastic history field for fracture of elasto-plastic materials. Eng. Fract. Mech. 2022, 268, 108447. [Google Scholar] [CrossRef]
- Russ, J.; Slesarenko, V.; Rudykh, S.; Waisman, H. Rupture of 3D-printed hyperelastic composites: Experiments and phase field fracture modeling. J. Mech. Phys. Solids 2020, 140, 103941. [Google Scholar] [CrossRef]
- Cui, C.; Ma, R.; Martínez-Pañeda, E. A phase field formulation for dissolution-driven stress corrosion cracking. J. Mech. Phys. Solids 2021, 147, 104254. [Google Scholar] [CrossRef]
- Schreiber, C.; Kuhn, C.; Müller, R.; Zohdi, T. A phase field modeling approach of cyclic fatigue crack growth. Int. J. Fract. 2020, 225, 89–100. [Google Scholar] [CrossRef]
- Wang, T.; Ye, X.; Liu, Z.; Liu, X.; Chu, D.; Zhuang, Z. A phase-field model of thermo-elastic coupled brittle fracture with explicit time integration. Comput. Mech. 2020, 65, 1305–1321. [Google Scholar] [CrossRef]
- Cui, C.; Ma, R.; Martínez-Pañeda, E. A generalised, multi-phase-field theory for dissolution-driven stress corrosion cracking and hydrogen embrittlement. J. Mech. Phys. Solids 2022, 166, 104951. [Google Scholar] [CrossRef]
- Khalil, Z.; Elghazouli, A.Y.; Martínez-Pañeda, E. A generalised phase field model for fatigue crack growth in elastic–plastic solids with an efficient monolithic solver. Comput. Method. Appl. Mech. 2022, 388, 114286. [Google Scholar] [CrossRef]
- Shanthraj, P.; Sharma, L.; Svendsen, B.; Roters, F.; Raabe, D. A phase field model for damage in elasto-viscoplastic materials. Comput. Method. Appl. Mech. 2016, 312, 167–185. [Google Scholar] [CrossRef]
- Sadeghirad, A.; Momeni, K.; Ji, Y.; Ren, X.; Chen, L.; Lua, J. Multiscale crystal-plasticity phase field and extended finite element methods for fatigue crack initiation and propagation modeling. Int. J. Fract. 2019, 216, 41–57. [Google Scholar] [CrossRef]
- Amor, H.; Marigo, J.; Maurini, C. Regularized formulation of the variational brittle fracture with unilateral contact: Numerical experiments. J. Mech. Phys. Solids 2009, 57, 1209–1229. [Google Scholar] [CrossRef]
- Alessi, R.; Vidoli, S.; De Lorenzis, L. A phenomenological approach to fatigue with a variational phase-field model: The one-dimensional case. Eng. Fract. Mech. 2018, 190, 53–73. [Google Scholar] [CrossRef]
- Mesgarnejad, A.; Imanian, A.; Karma, A. Phase-field models for fatigue crack growth. Theor. Appl. Fract. Mec. 2019, 103, 102282. [Google Scholar] [CrossRef]
- Grossman-Ponemon, B.E.; Mesgarnejad, A.; Karma, A. Phase-field modeling of continuous fatigue via toughness degradation. Eng. Fract. Mech. 2022, 264, 108255. [Google Scholar] [CrossRef]
- Lo, Y.; Borden, M.J.; Ravi-Chandar, K.; Landis, C.M. A phase-field model for fatigue crack growth. J. Mech. Phys. Solids 2019, 132, 103684. [Google Scholar] [CrossRef]
- Liu, Z.; Reinoso, J.; Paggi, M. Phase field modeling of brittle fracture in large-deformation solid shells with the efficient quasi-Newton solution and global–local approach. Comput. Method. Appl. Mech. 2022, 399, 115410. [Google Scholar] [CrossRef]
- Emdadi, A.; Asle Zaeem, M. Phase-field modeling of crack propagation in polycrystalline materials. Comp. Mater. Sci. 2021, 186, 110057. [Google Scholar] [CrossRef]
- Xiao, Y.Q.; Yang, L.; Zhu, W.; Zhou, Y.C.; Pi, Z.P.; Wei, Y.G. Delamination mechanism of thermal barrier coatings induced by thermal cycling and growth stresses. Eng. Fail. Anal. 2021, 121, 105202. [Google Scholar] [CrossRef]
- Ai, W.; Wu, B.; Martínez-Pañeda, E. A coupled phase field formulation for modelling fatigue cracking in lithium-ion battery electrode particles. J. Power Sources 2022, 544, 231805. [Google Scholar] [CrossRef]
- Ulloa, J.; Wambacq, J.; Alessi, R.; Degrande, G.; François, S. Phase-field modeling of fatigue coupled to cyclic plasticity in an energetic formulation. Comput. Method. Appl. Mech. 2021, 373, 113473. [Google Scholar] [CrossRef]
- Haveroth, G.A.; Vale, M.G.; Bittencourt, M.L.; Boldrini, J.L. A non-isothermal thermodynamically consistent phase field model for damage, fracture and fatigue evolutions in elasto-plastic materials. Comput. Method. Appl. Mech. 2020, 364, 112962. [Google Scholar] [CrossRef]
- Song, J.; Zhao, L.G.; Qi, H.; Li, S.; Shi, D.; Huang, J.; Su, Y.; Zhang, K. Coupling of phase field and viscoplasticity for modelling cyclic softening and crack growth under fatigue. Eur. J. Mech. A/Solids 2022, 92, 104472. [Google Scholar] [CrossRef]
- Li, P.; Yvonnet, J.; Combescure, C.; Makich, H.; Nouari, M. Anisotropic elastoplastic phase field fracture modeling of 3D printed materials. Comput. Method. Appl. Mech. 2021, 386, 114086. [Google Scholar] [CrossRef]
- Seleš, K.; Tomić, Z.; Tonković, Z. Microcrack propagation under monotonic and cyclic loading conditions using generalised phase-field formulation. Eng. Fract. Mech. 2021, 255, 107973. [Google Scholar] [CrossRef]
- Tu, X.; Ray, A.; Ghosh, S. A coupled crystal plasticity FEM and phase-field model for crack evolution in microstructures of 7000 series aluminum alloys. Eng. Fract. Mech. 2020, 230, 106970. [Google Scholar] [CrossRef]
- Loew, P.J.; Peters, B.; Beex, L.A.A. Rate-dependent phase-field damage modeling of rubber and its experimental parameter identification. J. Mech. Phys. Solids 2019, 127, 266–294. [Google Scholar] [CrossRef]
- Loew, P.J.; Poh, L.H.; Peters, B.; Beex, L.A.A. Accelerating fatigue simulations of a phase-field damage model for rubber. Comput. Method. Appl. Mech. 2020, 370, 113247. [Google Scholar] [CrossRef]
- Loew, P.J.; Peters, B.; Beex, L.A.A. Fatigue phase-field damage modeling of rubber using viscous dissipation: Crack nucleation and propagation. Mech. Mater. 2020, 142, 103282. [Google Scholar] [CrossRef]
- Simoes, M.; Braithwaite, C.; Makaya, A.; Martínez Pañeda, E. Modelling fatigue crack growth in shape memory alloys. Fatigue Fract. Eng. M. 2022, 45, 1243–1257. [Google Scholar] [CrossRef]
- Simoes, M.; Martínez-Pañeda, E. Phase field modelling of fracture and fatigue in Shape Memory Alloys. Comput. Method. Appl. Mech. 2021, 373, 113504. [Google Scholar] [CrossRef]
- Martínez-Pañeda, E.; Golahmar, A.; Niordson, C.F. A phase field formulation for hydrogen assisted cracking. Comput. Method. Appl. Mech. 2018, 342, 742–761. [Google Scholar] [CrossRef]
- Huang, C.; Gao, X. Phase field modeling of hydrogen embrittlement. Int. J. Hydrogen Energ. 2020, 45, 20053–20068. [Google Scholar] [CrossRef]
- Wu, J.; Mandal, T.K.; Nguyen, V.P. A phase-field regularized cohesive zone model for hydrogen assisted cracking. Comput. Method. Appl. Mech. 2020, 358, 112614. [Google Scholar] [CrossRef]
- Duda, F.P.; Ciarbonetti, A.; Toro, S.; Huespe, A.E. A phase-field model for solute-assisted brittle fracture in elastic-plastic solids. Int. J. Plast. 2018, 102, 16–40. [Google Scholar] [CrossRef]
- Kristensen, P.K.; Niordson, C.F.; Martínez-Pañeda, E. Applications of phase field fracture in modelling hydrogen assisted failures. Theor. Appl. Fract. Mec. 2020, 110, 102837. [Google Scholar] [CrossRef]
- Golahmar, A.; Kristensen, P.K.; Niordson, C.F.; Martínez-Pañeda, E. A phase field model for hydrogen-assisted fatigue. Int. J. Fatigue 2022, 154, 106521. [Google Scholar] [CrossRef]
- Mai, W.; Soghrati, S. A phase field model for simulating the stress corrosion cracking initiated from pits. Corros. Sci. 2017, 125, 87–98. [Google Scholar] [CrossRef]
- Mai, W.; Soghrati, S.; Buchheit, R.G. A phase field model for simulating the pitting corrosion. Corros. Sci. 2016, 110, 157–166. [Google Scholar] [CrossRef]
- Schreiber, C.; Müller, R.; Kuhn, C. Phase field simulation of fatigue crack propagation under complex load situations. Arch. Appl. Mech. 2021, 91, 563–577. [Google Scholar] [CrossRef]
- Yan, S.; Schreiber, C.; Müller, R. An efficient implementation of a phase field model for fatigue crack growth. Int. J. Fract. 2022, 237, 47–60. [Google Scholar] [CrossRef]
- Seleš, K.; Aldakheel, F.; Tonković, Z.; Sorić, J.; Wriggers, P. A general phase-field model for fatigue failure in brittle and ductile solids. Comput. Mech. 2021, 67, 1431–1452. [Google Scholar] [CrossRef]
- Wu, J.; Huang, Y.; Nguyen, V.P. On the BFGS monolithic algorithm for the unified phase field damage theory. Comput. Method. Appl. Mech. 2020, 360, 112704. [Google Scholar] [CrossRef]
- Wu, J.; Huang, Y. Comprehensive implementations of phase-field damage models in Abaqus. Theor. Appl. Fract. Mec. 2020, 106, 102440. [Google Scholar] [CrossRef]
- Kristensen, P.K.; Martínez-Pañeda, E. Phase field fracture modelling using quasi-Newton methods and a new adaptive step scheme. Theor. Appl. Fract. Mec. 2020, 107, 102446. [Google Scholar] [CrossRef]
- Freddi, F.; Mingazzi, L. Mesh refinement procedures for the phase field approach to brittle fracture. Comput. Method. Appl. Mech. 2022, 388, 114214. [Google Scholar] [CrossRef]
- Xu, W.; Li, Y.; Li, H.; Qiang, S.; Zhang, C.; Zhang, C. Multi-level adaptive mesh refinement technique for phase-field method. Eng. Fract. Mech. 2022, 276, 108891. [Google Scholar] [CrossRef]
- Gupta, A.; Krishnan, U.M.; Mandal, T.K.; Chowdhury, R.; Nguyen, V.P. An adaptive mesh refinement algorithm for phase-field fracture models: Application to brittle, cohesive, and dynamic fracture. Comput. Method. Appl. Mech. 2022, 399, 115347. [Google Scholar] [CrossRef]
- Eldahshan, H.; Alves, J.; Bouchard, P.; Perchat, E.; Munoz, D.P. CIPFAR: A 3D unified numerical framework for the modeling of ductile fracture based on the phase field model and adaptive remeshing. Comput. Method. Appl. Mech. 2021, 387, 114171. [Google Scholar] [CrossRef]
- Giovanardi, B.; Scotti, A.; Formaggia, L. A hybrid XFEM –Phase field (Xfield) method for crack propagation in brittle elastic materials. Comput. Method. Appl. Mech. 2017, 320, 396–420. [Google Scholar] [CrossRef]
- Patil, R.U.; Mishra, B.K.; Singh, I.V. A local moving extended phase field method (LMXPFM) for failure analysis of brittle materials. Comput. Method. Appl. Mech. 2018, 342, 674–709. [Google Scholar] [CrossRef]
- Muixí, A.; Marco, O.; Rodríguez-Ferran, A.; Fernández-Méndez, S. A combined XFEM phase-field computational model for crack growth without remeshing. Comput. Mech. 2021, 67, 231–249. [Google Scholar] [CrossRef]
- Chen, Y.; Vasiukov, D.; Gélébart, L.; Park, C.H. A FFT solver for variational phase-field modeling of brittle fracture. Comput. Method. Appl. Mech. 2019, 349, 167–190. [Google Scholar] [CrossRef]
- Ma, R.; Sun, W. FFT-based solver for higher-order and multi-phase-field fracture models applied to strongly anisotropic brittle materials. Comput. Method. Appl. Mech. 2020, 362, 112781. [Google Scholar] [CrossRef]
- Goswami, S.; Anitescu, C.; Chakraborty, S.; Rabczuk, T. Transfer learning enhanced physics informed neural network for phase-field modeling of fracture. Theor. Appl. Fract. Mec. 2020, 106, 102447. [Google Scholar] [CrossRef]
- Amiri, F.; Millán, D.; Arroyo, M.; Silani, M.; Rabczuk, T. Fourth order phase-field model for local max-ent approximants applied to crack propagation. Comput. Method. Appl. Mech. 2016, 312, 254–275. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).