Investigation on the Alloy Mixing and Inclusion Removement through Using a New Slot-Porous Matched Tuyeres
Abstract
1. Introduction
2. Mathematical Model and Boundary Conditions
2.1. Bubble Transportation Model
2.2. Bubble Transport Model
2.3. Boundary Condition and Numerical Details
3. Results
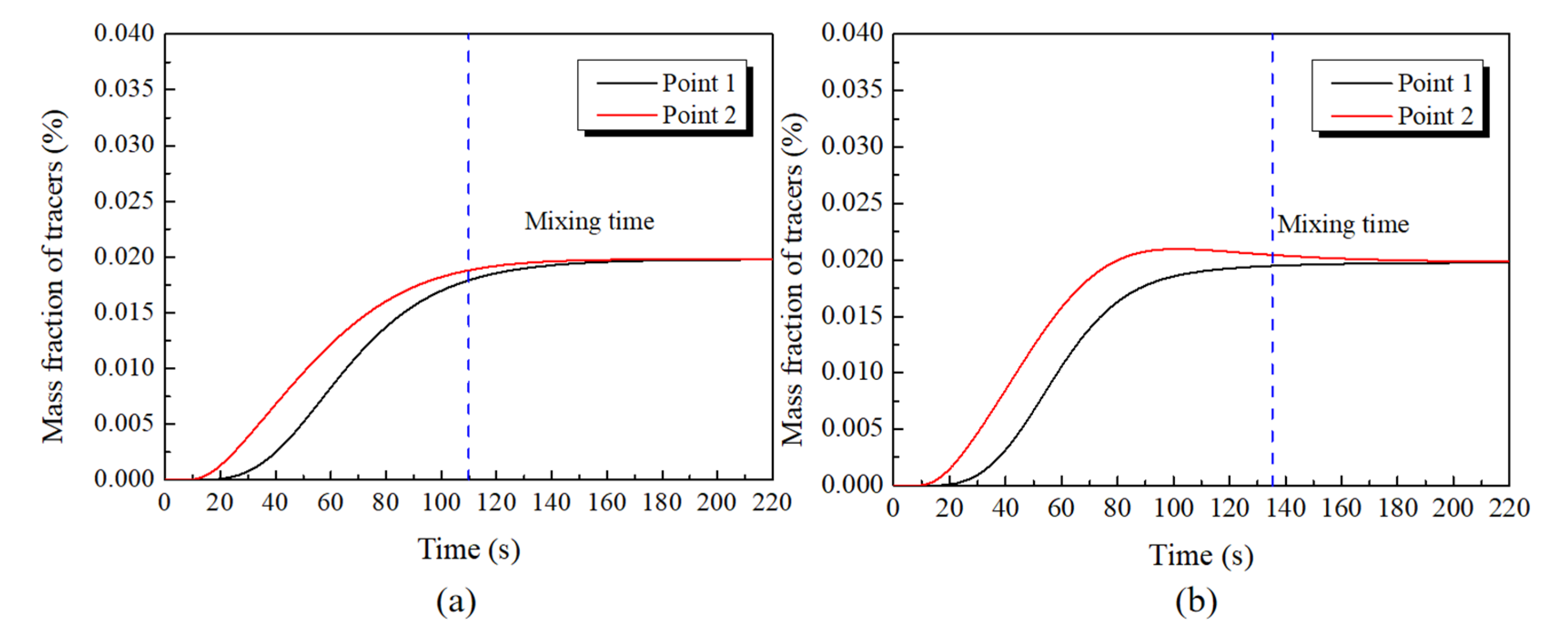
3.1. Validation for Mathematical Model
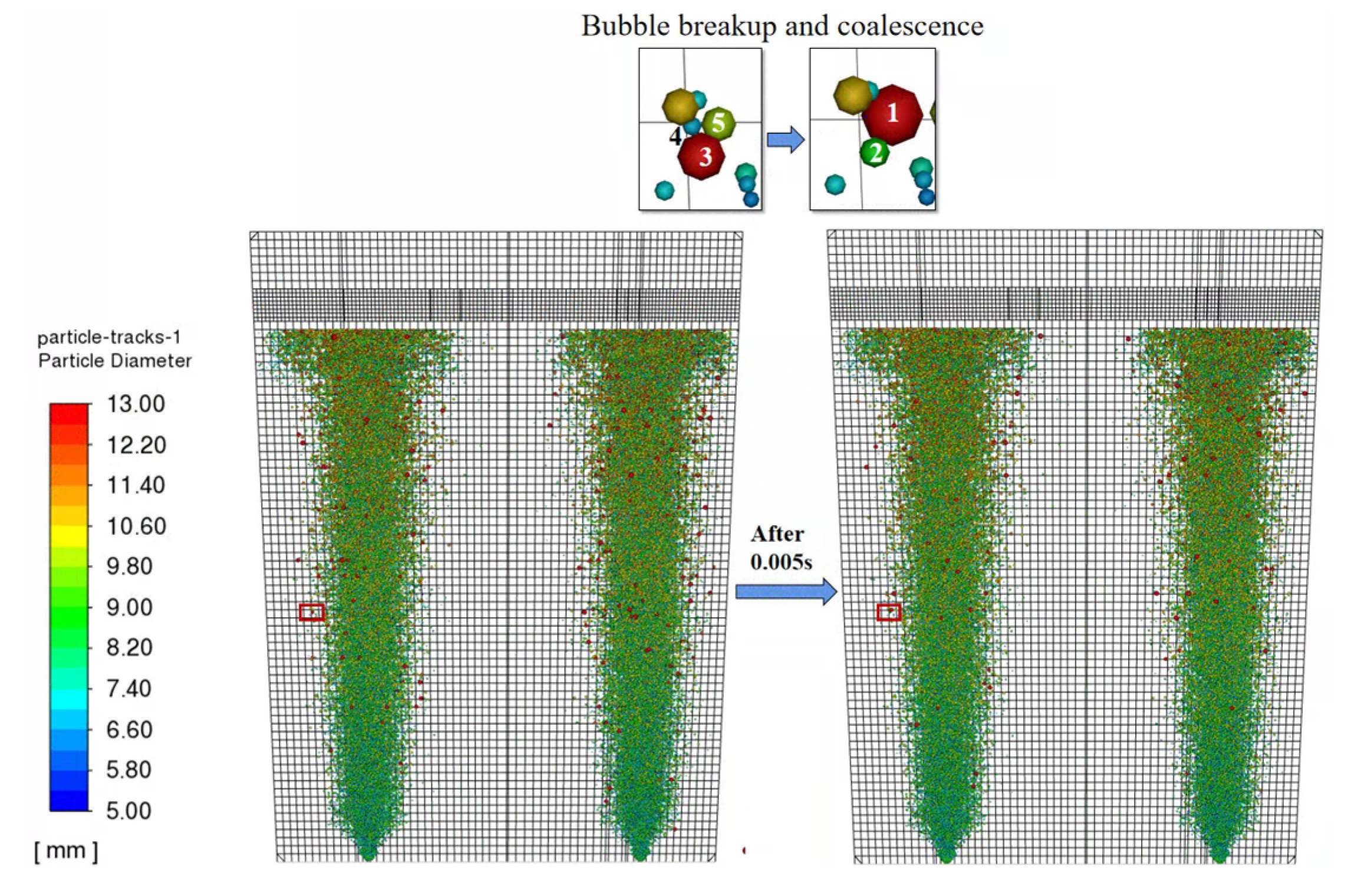
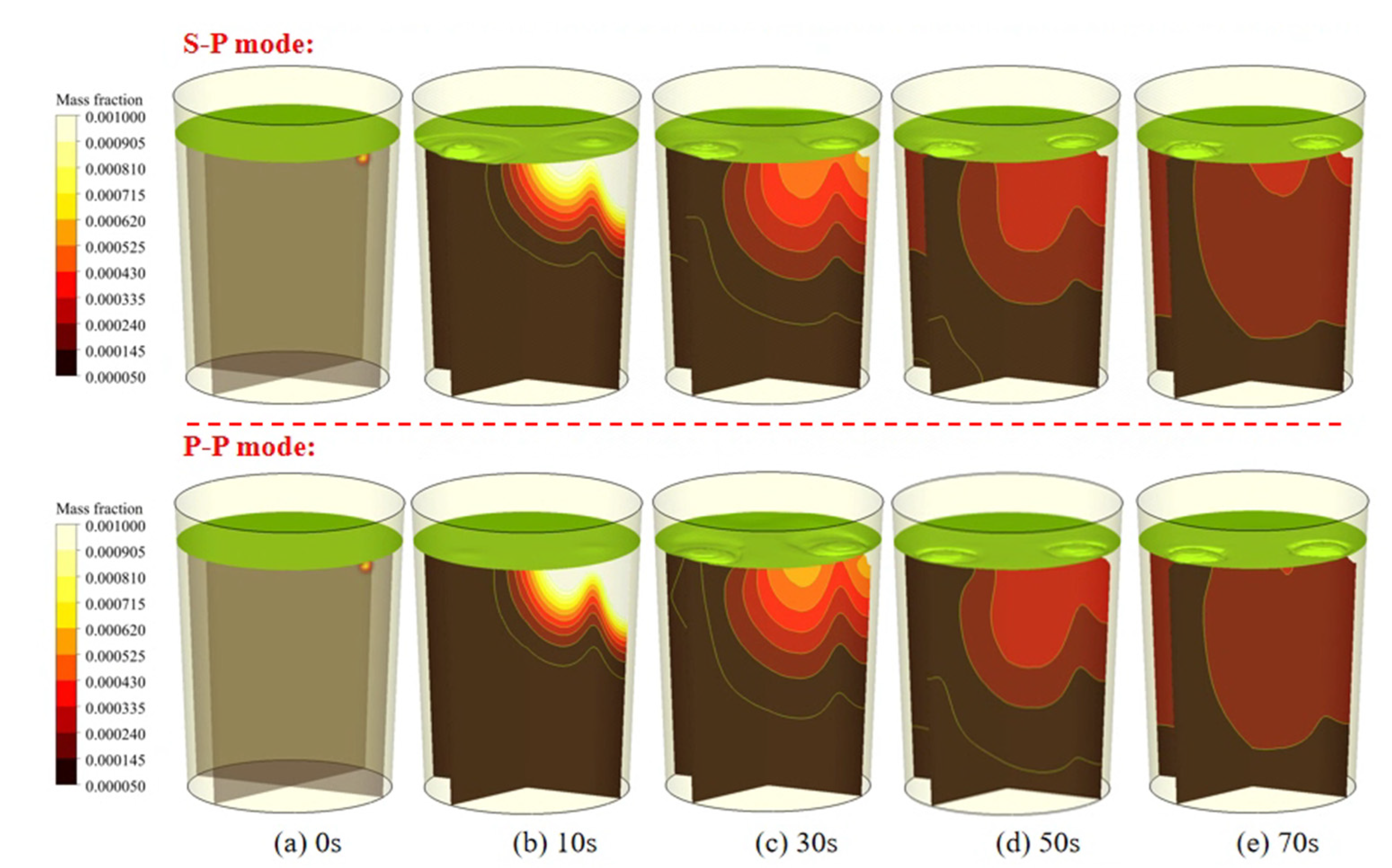
3.2. Coalescence and Breakup of Bubbles and Attachment of Inclusions
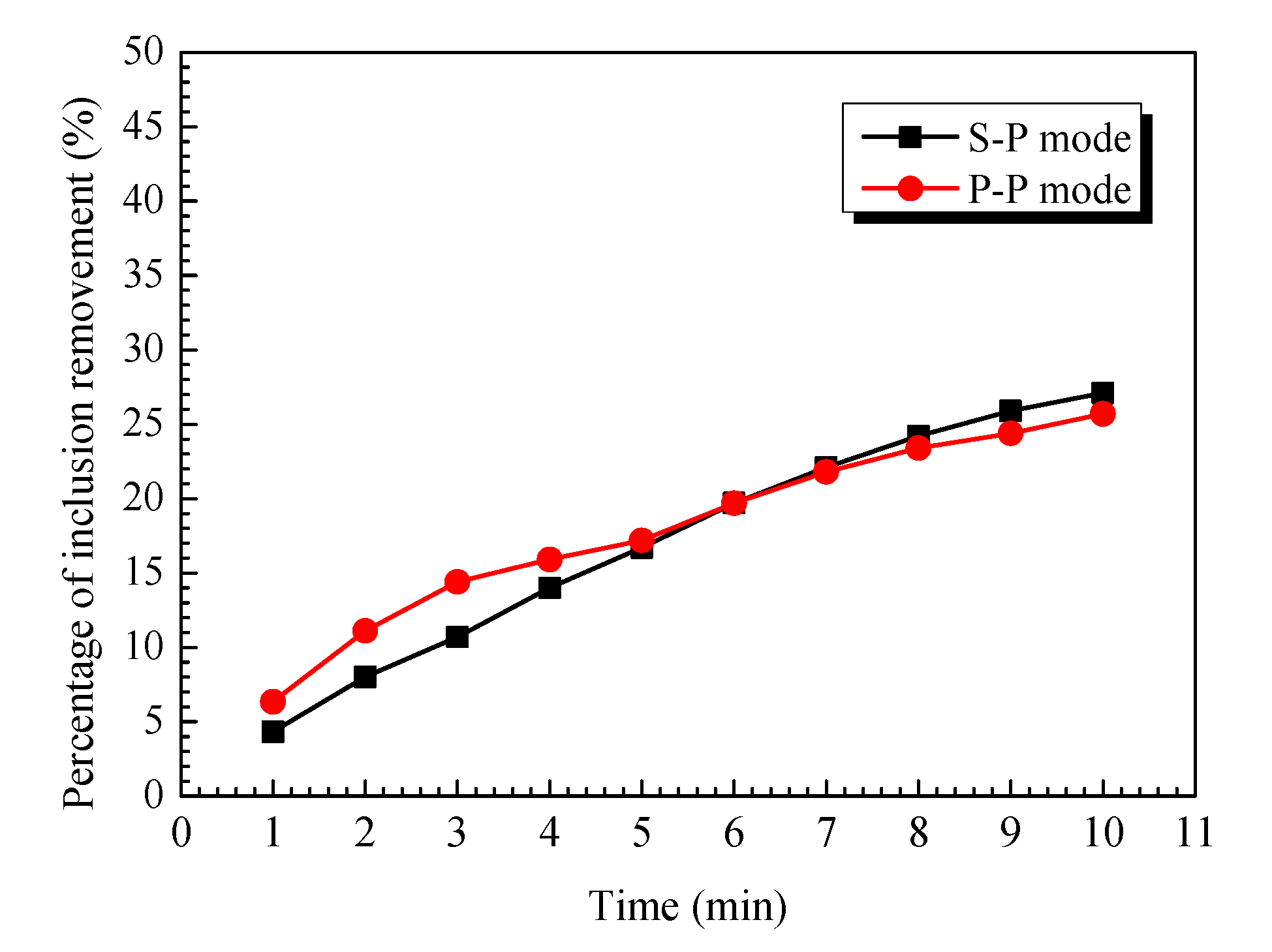
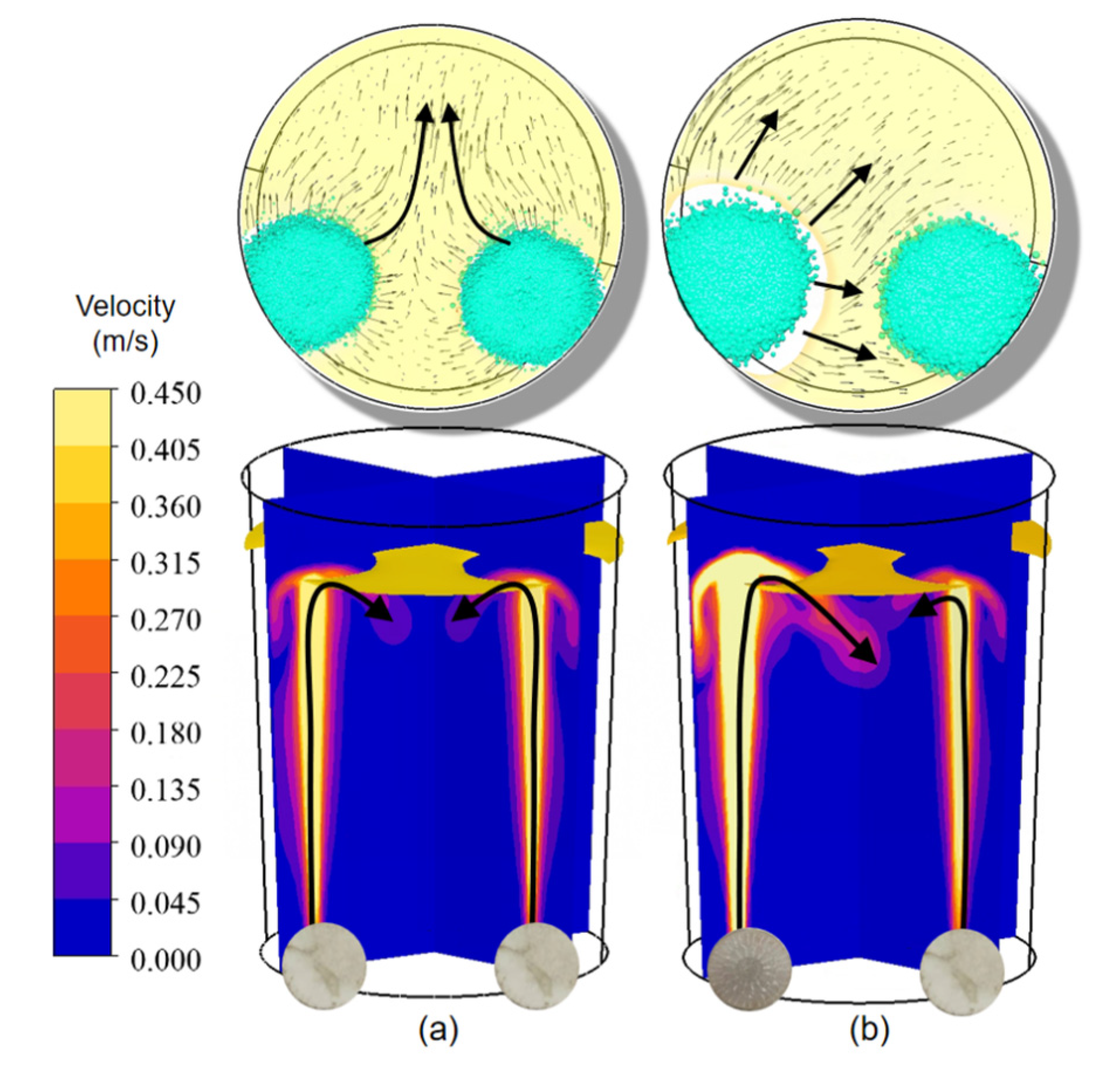
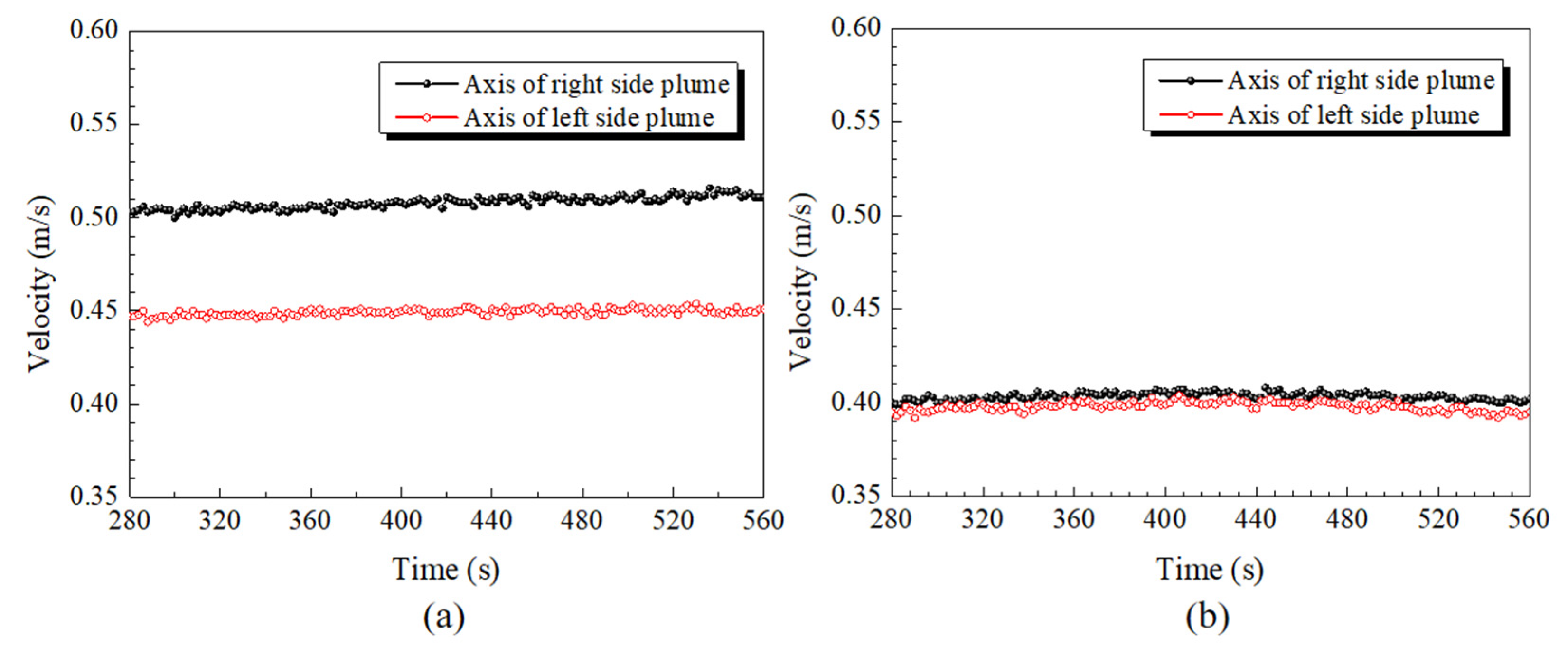
3.3. Effect of Tuyere Matches on the Flow Field and Inclusion Transport
3.4. Diameter and Density Distribution of Bubbles
4. Conclusions
- (1)
- The flow field under S–P mode is quite asymmetrical due to the differences of bubbles in size, which is beneficial for shortening mixing time during ladle refining;
- (2)
- Due to the decrease of hydraulic pressure, bubbles would expand when rising to the top. This is why the velocity near the top is higher;
- (3)
- The slot–porous matched dual tuyeres can significantly increase the inclusion removal ratio and shorten the mixing time at the same time. Therefore, this type of injection argon is recommended for use in future refining.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lobanov, S.P.; Ovsyannikov, V.G.; Voronov, G.A.; Sarychev, A.V. Bottom blowing tuyeres for 175-ton steel ladles in service at an open-hearth furnace shop (MISW JSC). Refract. Ind. Ceram. 2005, 46, 85–86. [Google Scholar] [CrossRef]
- Krishna, R.; Baten, J.M. CFD Simulations of Wall Mass Transfer for Taylor Flow in Circular Capillaries. Chem. Eng. Res. Des. 2001, 79, 283–309. [Google Scholar] [CrossRef]
- Geng, D.Q.; Lei, H.; He, J.C. Effect of Electromagnetic Swirling Flow in Slide-gate SEN on Flow Field in Square Billet Continuous Casting Mold. ISIJ Int. 2010, 50, 1597–1605. [Google Scholar] [CrossRef]
- Hibiki, T.; Ishii, M. Development of One-group Interfacial Area Transport Equation in Bubbly Flow Systems. Int. J. Heat Mass Transf. 2002, 45, 2351–2372. [Google Scholar] [CrossRef]
- Kitagawa, A.; Sugiyama, K.; Murai, Y. Experimental Detection of Bubble-bubble Interactions in a Wall-sliding Bubble Swarm. Int. J. Multiph. Flow 2004, 30, 1213–1234. [Google Scholar] [CrossRef]
- Xiao, Z.Y.; Tan, R.B.H. A Model for Bubble-Bubble and Bubble-Wall Interaction in Bubble Formation. AIChE J. 2006, 52, 86–98. [Google Scholar] [CrossRef]
- Sanyal, J.; Marchisio, D.L.; Fox, O.; Dhanasekharan, K. On the Comparison between Population Balance Models for CFD Simulation of Bubble Columns. Ind. Eng. Chem. Res. 2005, 44, 5063–5072. [Google Scholar] [CrossRef]
- Lou, W.T.; Zhu, M.Y. Numerical Simulations of Inclusion Behavior and Mixing Phenomena in Gas-stirred Ladles with Different Arrangement of Tuyeres. ISIJ Int. 2014, 54, 9–18. [Google Scholar] [CrossRef]
- Wang, L.T.; Peng, S.H.; Zhang, Q.Y.; Li, Z.B. Mathematical Model for Growth and Removal of Inclusion in a Multi-tuyere Ladle during Gas-stirring. Steel Res. Int. 2006, 77, 25–31. [Google Scholar] [CrossRef]
- Sha, Z.; Laari, A.; Turunen, I. Multi-Phase-Multi-Size Group Model for the Inclusion of Population Balances into the CFD Simulation of Gas-Liquid Bubbly Flows. Chem. Eng. Technol. 2006, 29, 550–559. [Google Scholar] [CrossRef]
- Thomas, B.G.; Yuan, Q.; Mahmood, S.; Liu, R.; Chaudhary, R. Transport and Entrapment of Particles in Steel Continuous Casting. Metall. Mater. Trans. B 2014, 45, 22–35. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Li, L.M.; Li, B.K.; Jiang, M.F. Large Eddy Simulation of Transient Flow, Solidification, and Particle Transport Processes in Continuous-Casting Mold. JOM 2014, 66, 1184–1196. [Google Scholar] [CrossRef]
- Yin, Y.B.; Zhang, J.M.; Dong, Q.P.; Li, Y.Y. Modelling on Inclusion Motion and Entrapment during the Full Solidification in Curved Billet Caster. Metals 2018, 8, 320. [Google Scholar] [CrossRef]
- Lei, H.; Geng, D.Q.; He, J.C. A Continuum Model of Solidification and Inclusion Collision-growth in the Slab Continuous Casting Caster. ISIJ Int. 2009, 49, 1575–1582. [Google Scholar] [CrossRef]
- Colella, D.; Vinci, D.; Bagatin, R.; Masi, M.; Bakr, E.A. A Study on Coalescence and Breakage Mechanisms in Three Different Bubble Columns. Chem. Eng. Sci. 1999, 54, 4767–4777. [Google Scholar] [CrossRef]
- Olmos, E.; Gentric, C.; Vial, C.; Wild, G.; Midoux, N. Numerical Simulation of Multiphase Flow in Bubble Column Reactors: Influence of Bubble Coalescence and Break-up. Chem. Eng. Sci. 2001, 56, 6359–6365. [Google Scholar] [CrossRef]
- Liu, W.J.; Lee, J.; Guo, X.P.; Silaen, A.K.; Zhou, C.Q. Argon Bubble Coalescence and Breakup in a Steel Ladle with Bottom Plugs. ISIJ Int. 2018, 90, 1800396. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Li, B.K.; Xiao, L.J.; Gan, Y. Physical and Numerical Simulation of Mixed Columnar-equiaxed Solidification during Cold Strip Feeding in Continuous Casting. Acta Metall. Sin. 2022, 58, 1236–1252. [Google Scholar] [CrossRef]
- Wu, Y.D.; Liu, Z.Q.; Fang, W.; Li, B.K.; Gan, Y. Experimental investigation of trajectories, velocities and size distributions of bubbles in a continuous-casting mold. Powder Technol. 2021, 387, 325–335. [Google Scholar] [CrossRef]
- Li, X.L.; Li, B.K.; Liu, Z.Q.; Wang, D.Y.; Qu, T.P.; Hu, S.Y.; Wang, C.J.; Gao, R.Z. Evaluation of Slag Entrapment in Continuous Casting Mold Based on the LES-VOF-DPM Coupled Model. Metall. Mater. Trans. B 2021, 52, 3246–3264. [Google Scholar] [CrossRef]
- Li, X.L.; Li, B.K.; Liu, Z.Q.; Niu, R.; Liu, Q.; Huang, X.C. Detection and Numerical Simulation of Non-Metallic Inclusions in Continuous Casting Slab. Steel Res. Int. 2019, 90, 1800423. [Google Scholar] [CrossRef]
- Li, L.M.; Liu, Z.Q.; Li, B.K. Modelling of Bubble Aggregation, Breakage and Transport in Slab Continuous Casting Mold. J. Iron Steel Res. Int. 2015, 22, 30–35. [Google Scholar] [CrossRef]
- Li, Q.; Cheng, J.C.; Yang, C.; Mao, Z.S. Simulation of a Bubble Column by Computational Fluid Dynamics and Population Balance Equation using the Cell Average Method. Chem. Eng. Technol. 2017, 40, 1792–1801. [Google Scholar] [CrossRef]
- Chen, S.F.; Lei, H.; Hou, H.C.; Ding, C.Y.; Zhang, H.; Zhao, Y. Collision-coalescence among Inclusions with Bubble Attachment and Transport in Molten Steel of RH. J. Mater. Res. Technol. 2021, 15, 5141–5150. [Google Scholar] [CrossRef]
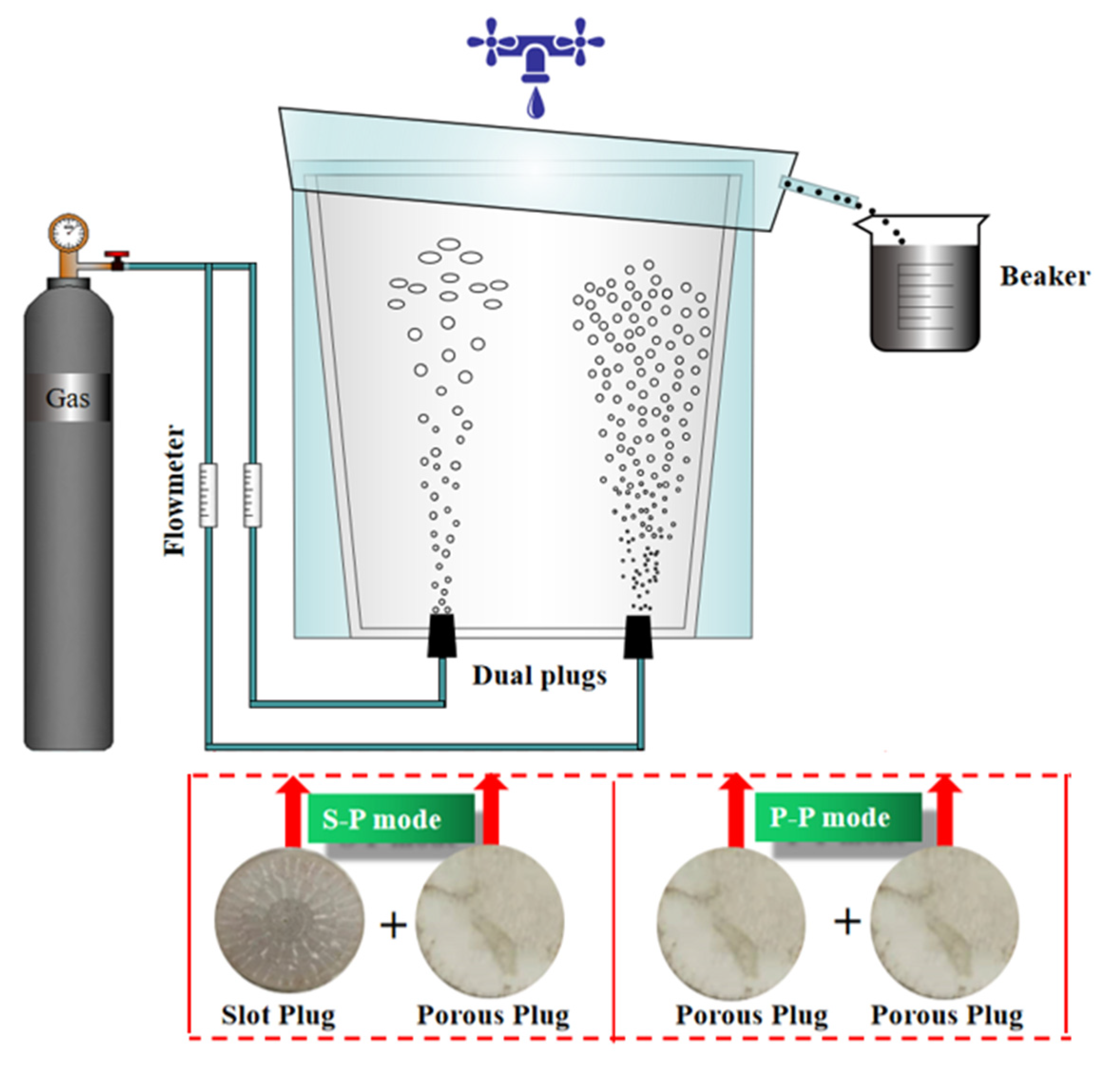
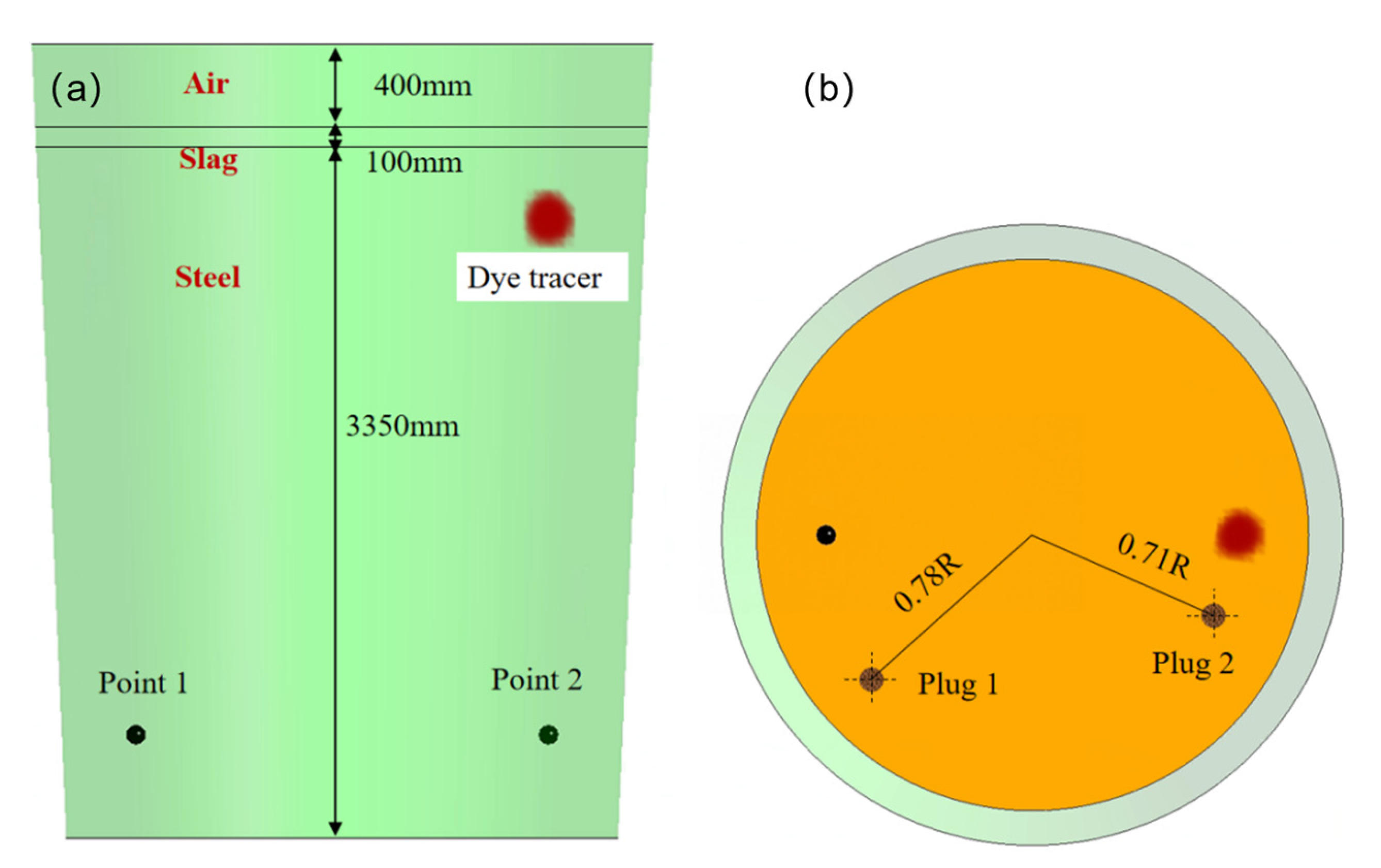



| Parameters | Real Ladle | Water Model (Scale 1:7) |
|---|---|---|
| Gas flow rate, NL/min | 150 + 150 | 0.765 + 0.765 |
| tuyere angle ° | 114° | 114° |
| Dynamic viscosity of steel, kg/(m·s) | 0.0051 | 0.001 |
| Dynamic viscosity of air, kg/(m·s) | 1.79 × 10−5 | 1.79 × 10−5 |
| Density of dioctyl phthalate, kg/(m3) | 2800 | 900 |
| Radius of ladle bottom, mm | 2717 | 388 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wang, H.; Tian, J.; Wang, D.; Qu, T.; Hou, D.; Hu, S.; Wu, G. Investigation on the Alloy Mixing and Inclusion Removement through Using a New Slot-Porous Matched Tuyeres. Metals 2023, 13, 667. https://doi.org/10.3390/met13040667
Li X, Wang H, Tian J, Wang D, Qu T, Hou D, Hu S, Wu G. Investigation on the Alloy Mixing and Inclusion Removement through Using a New Slot-Porous Matched Tuyeres. Metals. 2023; 13(4):667. https://doi.org/10.3390/met13040667
Chicago/Turabian StyleLi, Xianglong, Huihua Wang, Jun Tian, Deyong Wang, Tianpeng Qu, Dong Hou, Shaoyan Hu, and Guangjun Wu. 2023. "Investigation on the Alloy Mixing and Inclusion Removement through Using a New Slot-Porous Matched Tuyeres" Metals 13, no. 4: 667. https://doi.org/10.3390/met13040667
APA StyleLi, X., Wang, H., Tian, J., Wang, D., Qu, T., Hou, D., Hu, S., & Wu, G. (2023). Investigation on the Alloy Mixing and Inclusion Removement through Using a New Slot-Porous Matched Tuyeres. Metals, 13(4), 667. https://doi.org/10.3390/met13040667










