Abstract
In this paper, the fundamental principles of plastic flow localization are briefly outlined. During the development of plastic flow, there is a changeover in the localization patterns conforming to the corresponding stage of work hardening based on the autowave nature of plastic flow localization. In particular, the evolution of plastic flow from yield point to fracture involves the following four stages of autowave generation: switching autowave → phase autowave → stationary dissipative structure → collapse of autowave. The most intriguing localization pattern is attributed to a phase autowave, which forms at the stage of linear work hardening. The characteristics of the phase autowave (propagation velocity, dispersion, and grain size dependence of the wavelength) have been determined experimentally. Moreover, an elastic-plastic strain invariant is introduced to describe the elastic and plastic properties of the deforming medium, as well as to establish the above characteristics of autowaves. A hypothetic quasi-particle, corresponding to the autowave of localized plasticity, is considered and its potential properties are estimated to interpret the localization process characteristics.
Keywords:
elasticity; plasticity; localization; pattern; crystal lattice; self-organization; autowave; quasi-particle 1. Introduction
The plasticity nature problem can be regarded as a significant challenge for the modern physics of solids. Moreover, although plasticity has been studied from antiquity to the present day, some of its aspects are still poorly understood. During recent decades, the salient features of plastic flow in solids have been investigated intensively, and new experimental data have provided insight into the understanding of plasticity nature. Meanwhile, all the published papers concerning this topic of research cannot be listed herein, except for a few experimental and theoretical studies related to dislocation theory [1,2] and solids mechanics [3,4]. At the same time, the general physical model explaining the problem of plasticity is lacking today, making it urgent to proceed with the development of new approaches to the comprehension of the nature of plasticity.
Seeger and Frank [5] were first to point out the new way to solve the plasticity problem. They have hypothesized that “the development of a dislocation pattern during glide deformation constitute structurization processes”. In parallel, Nicolis and Prigogine [6] have declared that, apart from their nature, processes in the deforming media must be studied “as part of the general problem of nonlinear dynamical systems operating away from equilibrium”, i.e., in the framework of synergetics [7]. The experiments have shown [8,9,10] that the plastic flow in solids exhibits complicated space-time behavior. This point should be taken properly into account to markedly advance our understanding of the deforming medium stratification into alternating deformation and non-deformation. Taken together, the observable flow layers form the widely varying pattern of localized plastic flow [11], which evolves naturally in space and time during deformation. Given this fact and the conclusions drawn in work [5], it was assumed that “macroscopic localization of deformation is the integral property of plastic flow. The localization develops throughout the flow process and takes on this way some typical shapes [12]. Since the pattern allows one to distinguish between the localized plastic flow distributions across the specimen surface, this study is aimed at solving the problem of the nature of plastic deformation.
2. Materials and Methods
The extensive information of this study was provided by combining mechanical tests with the optical observations of localized plasticity patterns [9]. The flat specimens with the dimensions of 50 mm × 6 mm × 2 mm were exposed to tension at a rate of 3.5∙10−5 s−1 using Instron-1185(Instron, Buckinghamshire, UK) and LMF-125 testing machines (Walter + Bai AG, Löhningen, Switzerland) y at 300 K. The specimens prepared from non-metallic materials were subjected to compression tests.
The processing of σ(ε) diagrams consisted in the identification of work hardening stages [13] through the approximation by the Lüdwick equation [4]:
where σ0 and K are the empirical constants, depending on the kind of material. The work hardening stages of the σ(ε) diagrams were identified by calculating the exponent value conforming with a rule that n = 0 is attributed to the yield plateau, n = 1 is ascribed to the linear work hardening stage, n = 1/2 is for the parabolic stage and, finally, 0 < n < 1/2 stands for the pre-failure stage. The applicability of this rule has been verified experimentally for plastic flow in numerous materials.
The mechanical tests consisting in recording the σ(ε) diagram were completed by double-exposure speckle photography and digital image correlation data (Figure 1), so as to reconstruct the displacement vector field, . The devices used have a field of vision of ~100 mm, the real-time mode of operation and a spatial resolution of ~1 μm, which is comparable to that of optical microscopy.
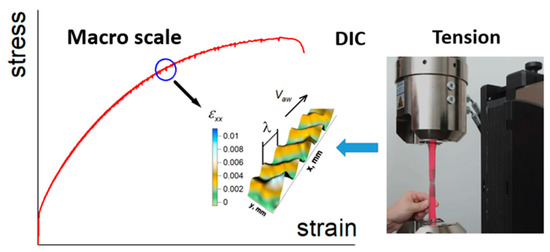
Figure 1.
A schematic illustrating the length scale of the current study. Tensile test data are analyzed via digital image correlation (DIC) method at the macro scale level. Here, εxx is the local elongation; x and y are the specimen length and width, respectively; λ is the nucleus spacing (the autowave length); Vaw is the autowave propagation rate.
The plastic distortion tensor for the plane stressed state is defined as [14]:
in which the longitudinal (εxx), transverse (εyy), shear (εxy = εyx), and rotation (ωz) components can be calculated in the xyz coordinate system for all the points of the test sample surface for different time instants. The experimental data for the inhomogeneous deformation distribution can be presented in different forms (Figure 1). The localized plasticity pattern was matched against the respective work hardening stage of the material. The quantitative characteristics of the pattern can be obtained using the X-t diagrams, where X is the x-coordinate of the deformation nucleus and t is the time (Figure 2). It illustrates the procedure for measuring the spatial (λ) and temporal (T) periods of the deformation process. The motion rate of the localization nucleus is Vaw = λ/T.
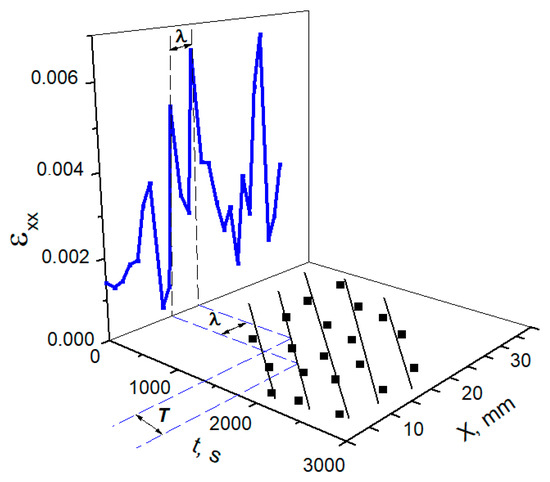
Figure 2.
The distribution of local elongations εxx, observed for the sample midline, and the diagrams for measuring λ and T values.
Considerable efforts have been made to study single-crystal and polycrystalline metals and alloys, which differ in chemical and phase composition, crystal lattice type, grain size and deformation mechanisms (i.e., dislocation slide [1], twinning [2] or phase transformation induced plasticity [15]). In addition, particular attention has been paid to ceramics, single alkali halide crystals, and several rocks (see Table 1). A comparative analysis of the above materials was performed to experimentally identify plastic flow features common to all systems.

Table 1.
The test materials and the main data on deformation localization autowaves obtained for the same materials.
Numerous observations showed that the localization behavior of plastic deformation is its most salient feature. During the constant-rate tensile loading, the space-time periodic structures (the so-called deformation patterns) emerge in the deforming sample from the yield point to its failure. Localization structures will occur spontaneously in the sample upon constant-rate loading without any specific action from the outside. Moreover, due to work hardening, the deforming medium’s defect structure undergoes irreversible changes, which are reflected in the emerging pattern.
The direct independent evidence in favor of our data has been presented in reports [16,17,18,19,20,21] through the observation of a localization nucleus traveling along the extension axis during plastic flow. However, no convincing explanation has been suggested.
3. Results
3.1. The Deformation Localization Pattern and Some Important Features
The plastic flow possesses two characteristics which are common to all deforming solids. First, the deformation is found to exhibit a localization behavior on the macro-scale level from the yield point to the ultimate stress. Second, the dependence of the work hardening coefficient on the deformation would occur by stages in which each hardening stage involves a certain dislocation mechanism [1,2]. To gain an insight into the nature of plastic deformation, the existence of an explicit connection between the two characteristics must be disclosed. Thus, the distinctive features of localization patterns remain the same, with only quantitative differences. It is noteworthy that there should be a correlation between plastic deformation non-homogeneities for the entire material volume. The localized plasticity nuclei are distributed periodically in space at a distance of λ ≈ 10−2 m between them. In this way, phenomena appear spontaneously at the macroscopic scale during the deformation process.
An analysis of experimental data reveals that these regularities serve to provide a unified explanation of plastic flow behavior. Four types of localized plasticity patterns have been observed experimentally for all studied materials. At each flow stage, there is a certain type of localization pattern. In particular, there is the yield plateau identified by a single mobile plastic flow nucleus, the linear work hardening stage with a set of synchronously moving nuclei, the parabolic work hardening stage with a set of equidistant stationary nuclei, and the pre-failure stage with a set of mobile nuclei that are forerunners of failure. These results together furnish a reliable proof for the one-to-one correspondence between the localization pattern and the plastic flow stages. This regularity, named the ‘correspondence rule’, is fulfilled for all the materials investigated up until now.
A key aspect of this many-faceted problem to be dealt with is the nature of localized plasticity. Hähner [22] has proposed a very attractive idea about the wave character of plastic flow, which was close to the well-known concept on stress waves formulated by Kolsky [23]. However, our basic viewpoint is that there are striking parallels between the localized plasticity patterns and the synergetics of the relevant dissipative structures [24]. These structures are also known as switching autowaves, phase autowaves, and stationary dissipative structures. They have been described in detail for various chemical and biological systems [25], and were assumed to be useful for solving the plasticity problem.
The observed pattern of localized plasticity is a projection of the autowave modes on the surface of the deforming specimen. The relationship between the localization pattern and autowaves takes its origin from a formal resemblance between these kinds of phenomena. This fact can be taken as an unequivocal physical evidence of the autowave nature of processes under consideration.
Thus, the well-known Lüders front, being observable on the yield plateau, separates the elastically and plastically deforming material volumes. As this front propagates along the sample, it leaves behind an increasing volume of the deformed material [13]. Because of the structural changes, the deforming material volume acquires a new state, which is characterized by increased density of defects, so that deformation occurs via the dislocation mechanism. As the total deformation increases, the plastic flow exhibits an intermittent behavior on the macro-scale level. Therefore, the Lüders band motion might be regarded as “a switching autowave”.
A different scenario is realized at the linear work hardening stage where a set of mobile nuclei is observed. In this case, the nuclei move at a constant rate Vaw = const along the test sample conforming to the phase constancy condition (). This pattern corresponds to a phase autowave. The parabolic stage of work hardening is characterized by the values n = 1/2 and Vaw = 0. The localization picture emerging at the latter stage fits the definition of a stationary dissipative structure [24]. Finally, at the pre-failure stage (0 < n < 1/2), the deformation pattern evolution is nearing completion. The autowave process collapse [26], observed at this stage, is coupled with the transition to a viscous failure.
Thus, the plastic flow process occurring in the deforming medium can be regarded as the regular continuous evolution of localized autowaves. Thus, it can be claimed that the transition from one to another flow stage involves a changeover in the modes of autowaves generated by the deformation. In a word, the plastic flow stages are closely related to the respective modes of autowave processes. This enables one to infer that the localized plastic flow is the evolution of the autowave pattern. Because of a changeover in the flow stages, the autowave modes will emerge from a random strain distribution in an orderly sequence: switching autowave → phase autowave → stationary dissipative structure → autowave collapse. However, some stages of the processes may be absent.
It is well known that experimental investigations of autowaves in chemistry or biology require the use of a special-purpose reaction cell. Such cells differ widely in type and size, depending on the kind of a studied system and its chemical composition as well as the kinetics of chemical reactions involved, temperatures employed, etc. However, autowaves in deforming media are another matter. Under constant-rate loading, localized plasticity autowaves will be generated spontaneously in the stretched sample at any temperature. Hence, the deforming solids can be regarded as a universal reaction cell, which can be conveniently used for studying the generation and evolution of all kinds of autowaves. As it is established experimentally, the plastic flow exhibits a regular localization behavior, which is markedly pronounced at the linear work hardening stage. Here the localization nuclei will move in a concerted manner at a constant rate along the stretched sample, forming a phase autowave according to the mechanisms below.
First, the propagation rates of localized plasticity autowaves in the studied materials are in the range 10−5 ≤ Vaw ≤ 10−4 m/s. They depend solely on the non-dimensional work hardening coefficient as follows:
Here, V0 and Ξ are the empirical constants with the dimensionality LT−1.
Second, the dispersion relation ω(k) for localized plasticity autowaves, where is the frequency and is the wave number, is defined as
in which ω0, k0 and α are the constants. Using the substitutions and , where and are the dimensionless frequency and wave number, correspondingly, one can reduce Equation (4) to a canonical dimensionless form (Figure 3).
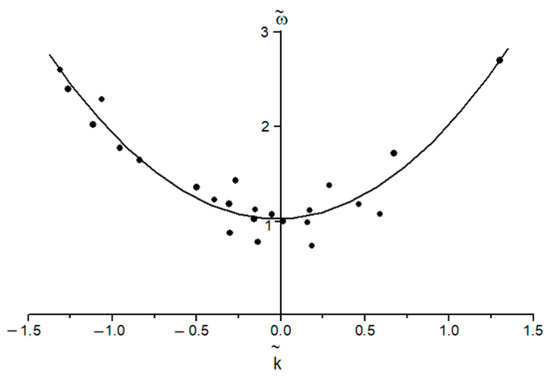
Figure 3.
The distribution of local elongations εxx, observed for the sample midline, and the diagrams for measuring λ and T values.
Third, the experiments were carried out for the polycrystalline aluminum specimens with the grain sizes in the range of 5·10−3 ≤ δ ≤ 5 mm. The grain size dependence of the autowave length λ(δ) has the general form of a logistic curve [27]
where a1 and a2 are the empirical coefficients, λ0 ≈ 5 mm, and C = 2.25. The inflection point for the plot described by Equation (5) and found from the condition is δ = δ0 ≈ 0.2 mm. There are two limit cases for Equation (5), which are at δ < δ0 and at δ > δ0.
Based on the studies, one can conclude that the plastic flow of solids is related to macroscopic features of localized phenomena.
3.2. The Physical Basic of the Autowave Model
Now it is clear that the problem at hand is the development of the new model of plastic flow evolution during plastic deformation. This is also evident from works [8,9,10,12], revealing that the nature of the macroscopic length of localized plastic flow autowaves remains poorly understood. As mentioned above [7], the plastic flow localization can be regarded as a spontaneous process of self-organization (‘structure formation’) in an open system. This suggestion is supported by the features in the localized plastic flow pattern, which are identified at different work hardening stages and demonstrate the spatial distribution of deforming and undeforming layers in media. This concept has been developed for self-organization of open non-equilibrium systems [6,24]. A similar system can attain spatial, temporal or functional inhomogeneity without any specific action from the outside (here specific action implies any external action which causes the system to acquire a certain kind of structure). It is worth noting that the definition implies no certain underlying mechanism responsible for the self-organization process. The formation of the localization pattern can be regarded as an ordering phenomenon in the deforming medium.
The concept of self-organization is frequently and successfully used to explain the structural formation in all kinds of active media studied in physics, chemistry, materials science or biology. The deforming medium can be likened to an active medium far from thermodynamic equilibrium in which the sources of energy are distributed over the material volume.
It is also evident that plastic flow also involves self-organization phenomena. According to [8], the generation of localized plastic flow autowaves causes a decrease in the entropy of the deforming system, which is the fundamental condition of self-organization processes. When studying the plastic flow localization in solids, one should take into account the significant changes in the acoustic characteristics during the material deformation, such as the velocity of transverse elastic waves (Vt) [28,29]. Up to now, the acoustic characteristics of the deforming medium have been considered in terms of energy dissipation, especially in internal friction studies and related problems.
Another characteristic of the medium is the phonon gas viscosity [30]. At first glance, this quantity seems to be out of place in the analysis of slow processes of the localized plasticity autowave propagation. However, it can be assumed that dislocations move inside the localized plasticity nuclei between and over the local obstacles under the control of the phonon gas viscosity B conforming with the law . The electron gas viscosity in metals also makes a significant contribution to the coefficient B.
It is found that mechanical and acoustic characteristics of the deforming medium are closely related to each other. This finding is supported by the experimental evidence suggesting that the acoustic processes play an important role in the development of localized plastic flow. The available acoustic emission data imply that structural nonhomogeneities emerge in the deforming medium due to a traveling deformation front. Thus, the acoustic emission sources distributed over the material bulk are associated with the localized plastic flow nuclei occurring in the same material. To elucidate the nature of localized plasticity, a two-component model was formulated. In this case, a key role is assigned to the acoustic properties of the deforming solid so that acoustic emission pulses play the role of the information system which controls the structural transformation dynamics.
In the framework of the concept used to describe the autowave formation, the basic problem is the nature of self-organization, which manifests itself in the deforming medium as a spontaneous emergence of the pattern. To solve the problem, a self-organizing system must be separated spontaneously into dynamic and information interacting subsystems [25].
The principles of the proposed model are as follows. In the course of plastic deformation, local stress concentrators would form and disintegrate, which are considered the dislocation pile-ups [1]. The elementary stress relaxation is due to the breaking from a local obstacle, which involves acoustic emission [30]. These acoustic signals can activate other stress concentrators so that the same process is repeated. Thus, acoustic emission signals propagating in the deforming medium play the role of information subsystems, whereas dislocation shears are involved in the plastic deformation proper and operate as a dynamic subsystem. The developed model is hence made up of two components, acoustic emission and dislocation mechanisms of plasticity, which have been extensively studied, though in different contexts. The generation of acoustic signals was considered in connection with the initiation of dislocation shears, while the reverse process, i.e., the initiation of shears due to acoustic pulses, has not been touched on so far.
The next step consists in assessing the validity of the proposed model. Let an acoustic signal propagate in a non-uniform dislocation substructure, which is formed by deformation, e.g., a dislocation cell with a size 0.01 mm, which is observable via transmission electron microscopy. Such a cell can be regarded through an acoustic lens with a focal length fl defined as:
where is the ratio of rates for the non-deformed and deformed volumes, playing the role of the acoustic refractive index. The initiation of plastic flow is due to the localization of ultrasound waves at the distance 10−2 m from the active localized plasticity nuclei.
The delay times of thermally activated spontaneous relaxation acts [31,32] in the absence of acoustic pulses can be expressed as follows:
and the same under the action of inducting pulses:
Here, ωD is the Debye frequency, U0 is the potential barrier to be overcome during the relaxation event, is the activation volume of this event, b is the Burgers vector of dislocations, l is the size of the shear zone, kB is the Boltzmann constant, and T is the temperature. Based on Equations (7) and (8), the activation enthalpy of the process is set as 0.5 eV, and the acoustic pulse with the elastic strain amplitude decreases this parameter by 0.1 eV. The calculation at T = 300 K yields 5·10−5 s and 9·10−7 s These estimations provide evidence for the principal possibility of plastic flow acceleration under the action of acoustic pulses, and confirm the correctness of the model.
Therefore, Equations (7) and (8) demonstrate also the possibility of induced decay of stress concentrators. It seems that the rate of localized plasticity autowave dynamics is determined by the time of plasticity center growth from a nucleus that can be identified with the intergrowth of the Lüders band through the sample as . Moreover, it is well known that the perfect crystal lattice is a source of crystal defects responsible for the change in plastic form, which must be taken into consideration when describing self-organization processes as well. Hence, the basic premise of the paper is that the regular features of plastic flow macrolocalization are directly related to the lattice characteristics.
3.3. Fundamental Equations of the Autowave Model for Plasticity
The difference between the waves and autowaves can be shown as follows. In the simplest case, waves are described by the function , where ω is the frequency, and k is the wave number. These functions are the solutions of partial hyperbolic differential equations [25]. The wave rate c is determined by the material constants, e.g., for the transverse elastic waves, (here G is the shear modulus, ρ is the material density). The second derivative with respect to time is the sign of reversibility of processes, in particular elastic waves.
Autowaves have long been recognized as solutions of partial parabolic differential equations [25]. A similar equation can be obtained formally by adding a nonlinear function to the right-hand side of the equation , describing the transport phenomena by analogy with diffusion or heat conductivity. The coefficient κ has the dimensionality of L2T-1 and does not refer to the material’s properties. The first derivative with respect to time, , means that the above equation is suitable for determining the irreversible processes similar to those involved in the plastic deformation.
To offer adequate tools for describing the autowave processes, a set of two equations must be produced: one considering the rate of change for the catalytic factor and another for the damping factor. The choice of these factors is far from trivial. In case of plasticity, it is reasonable to guess that plastic deformation ε is a catalytic factor and stress σ is damping the same.
Hence, the equations for rates and can be derived from the general principles. The equation for obeys the following condition of deformation flow continuity [4]:
where , and the value is the transport coefficient for the autocatalytic factor; the term is the deformation flow in the deformation gradient field. For the uniaxial elongation along the x-axis, the autowave equation can be derived from Equation (9) as follows:
Here, is a non-linear stress-strain function, which is used to satisfy the condition .
The equation for the damping factor change rate can be derived from the Euler equation for a liquid flow as follows [33]:
Here, the momentum flux density tensor is , is the unit tensor, and and are the flow rate components. The stress tensor includes viscous and elastic stresses, i.e., ; hence, or The viscous stress is due to the plastic deformation inhomogeneity; the value is related to the variation in the elastic wave velocity in the deforming medium, i.e., . In turn, is the dynamic viscosity and is the propagation velocity of transverse elastic waves. The equation yields . The value behaves as a linear function of stress, i.e., [28]. Hence, the equation for stress change rate is . Then, the autowave equation for stresses takes the form
where and . It is of great importance that solving a set of Equations (10) and (12) enables one to predict adequately the regularities of different plastic flow modes [8].
The uniformity of localized plasticity phenomena for various materials implies the existence of a general law for the localized plastic flow autowaves. This section focuses on searching for a similar relationship. One can assume that there is the relationship between plastic flow macro-parameters and crystal lattice characteristics. To verify this, one can match products and for plastic flow and elastic deformation, respectively (Figure 4). The quantities and are the interplanar spacings of the crystal lattice and the transverse ultrasound wave velocity, respectively. Both the experimentally found values (λ and ) and textbook values (χ and ) were used in the analysis. It was found that
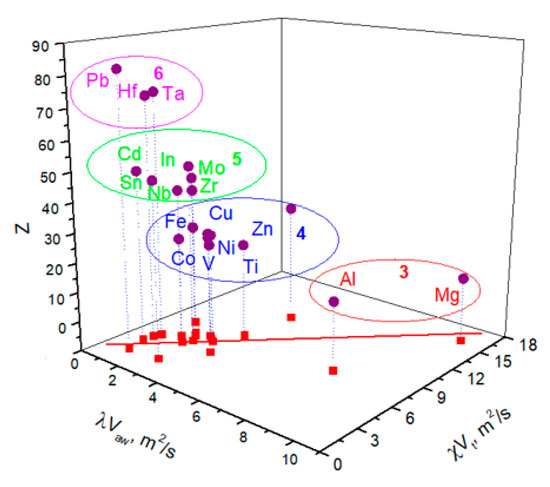
Figure 4.
The elastic-plastic strain invariant (here Z is the atomic number of any element from the 3rd–6th periods of the periodic table).
The obtained relationship is valid for all the studied materials. The values of are distributed according to the normal law [33] relative to the average quantity This result indicates that elastic and plastic deformation processes are closely related to each other by the plastic flow. It is noteworthy that the products and in Equation (13) are related to the transport coefficients and in Equations (10) and (12), as follows: and Thus, Equation (13) was called the “elastic-plastic strain invariant”.
Further, it is of interest to discuss some remarkable properties of the invariant. For example, the product , included in Equation (13), characterizes the stable development of the linear work hardening stage. If , then
where is the small displacement, W is the interparticle potential, and is the shear modulus [34]. The value is the specific acoustic resistance of the medium.
The potential W can be expanded into a power series [35] as follows:
where f is the quasi-elastic coupling coefficient and g is the anharmonicity coefficient [34]. With the proviso that , Equation (14) takes the form:
The invariant (13) is also suitable for describing deformation initiated by chaotically distributed dislocations. If the density of a mobile dislocation is , then the average distance between dislocations is . It can be assumed [2] that , i.e., . The speed of a quasi-viscous motion of dislocations is , where B is the coefficient of dislocation drag by the phonon and electron gases [30]. Thus,
The values G ≈ 40 GPa and B ≈ 10−4 Pa·s are conventionally employed to describe the dislocation motion. Using these values, it can be found from Equation (17) that 10−6 m2/s. The latter value is close to the calculated product for materials under consideration. The above suggests that a reliable quantitative criterion has been established for analyzing the interaction between elastic and plastic deformation, which occurs on the macro- and micro-scale levels. This criterion, in its universal form, is applicable to autowaves as well as to elastic and plastic deformation during the dislocation motion. Therefore, this criterion can be considered as a useful generalization parameter of the elastic-plastic strain invariant:
In view of the above, the invariant (13) is promising for gaining an insight into the nature of localized plastic flow. All the basic regularities of localized autowaves can be deduced from Equation (12); therefore, the invariant is expected to play an important role in the development of new models of plasticity.
A very important dependence of the product on the interplanar spacing was recorded for studied materials. This dependence () falls into three sections, which correspond to the 3rd, 4th or 5th period of the periodic table. This implies a close relation between the deformation processes and the electronic structure of metals according to their position in the periodic table.
Since the invariant (13) is referred to the characteristics of simultaneously proceeding elastic and plastic processes in a deforming medium, it plays an important role of ‘master equation’ in the autowave theory of localized plastic flow under consideration. This is confirmed by the fact that the invariant (13) has a number of consequences that can be used not only to understand the nature of some important features of dynamics of localized plasticity, but also to describe them quantitatively. Certain consequences will be discussed below.
For example, one can show that the velocity of phase autowaves follows from the invariant. Indeed, the derivative of the invariant (13) with respect to the deformation ε has the form
Thus
The value χ is independent of the plastic strain, so that , and
Therefore, Equation (21) can be rewritten as follows:
This result coincides with the experimentally established Equation (3), if the work hardening coefficient is expressed as the ratio of the structural parameters [2].
The dispersion relation for the localized plasticity autowaves can be also obtained from Equation (13) as follows:
where . If , then Evidently,
and the dispersion law of autowaves acquires the quadratic form:
where is the parameter used in Equation (5). In this case, the coefficients in Equation (25) can also be calculated by rewriting Equation (23) as
where is the Debye temperature [34]. Then, . Using the reference values χ(Fe), χ(Al), and , one can find that 3.7·10−7 m2/s and 4.45·10−7 m2/s. These are consistent with the values 10−7 m2/s and 12.9·10−7 m2/s, experimentally found from the dependence (Figure 5).
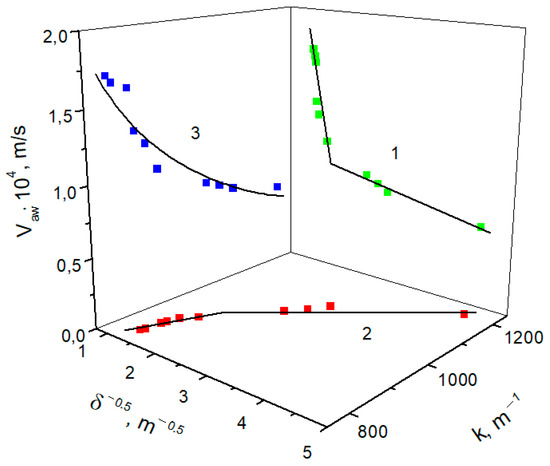
Figure 5.
The dependences of the propagation velocity of localized plasticity autowaves (1) and wave number (2) on the grain size; the dependence of the propagation velocity of localized plasticity autowaves on the wave number (3) for Al.
There is a very interesting problem concerning the influence of the structure (e.g., grain size) on the length of the autowave. Supposing that it follows from the invariant (13), one obtains
If the velocities and depend on the grain size δ (Figure 5), then the differentiation of Equation (27) with respect to δ yields:
from which it follows that
where and since A solution of Equation (29) is the logistic function [27]
Apparently, Equation (30) is equal to Equation (5) obtained experimentally for Al.
The Hall–Petch relationship [13] is close to the dependence determined by Equation (30). It is well known that the mechanical characteristics of polycrystalline materials (yield limit and flow stress) depend on the grain size. The corresponding dependences are usually linear in the coordinates ‘property–’. Being plotted in the coordinates ‘’, this dependence is separated into two parts at the point mm. Therefore, it makes sense to check the validity of Equation (13) for two ranges of grain sizes, namely and . The results of estimations indicate that for both ranges.
The dimension effect of the plastic flow can also be explained in terms of Equation (13). If the autowave length is measured in samples of different length L, then
and
For and , it obtains and , that is, , as established previously in the experiments [8].
It is worth mentioning that the autowave equation of deformation can be derived from the invariant Equation (13) as follows:
where is the plastic deformation. It is possible to introduce the differential operator and to act on both sides of Equation (33). Thus,
The ultrasound velocity depends weakly on the strain, so that in Equation (34). Since , then
This relationship is equivalent to Equation (10) for the strain rate, if .
A key question is the relationship between the autowave approach and the dislocation theory, which is used usually [1,2] to explain the nature of plastic deformation and work hardening in real crystals. The dislocation models are mostly based on the Taylor–Orovan equation [2]
bringing the plastic strain rate into correspondence with the mobile dislocation density and their rate . A comparison of Equations (34) and (36) shows that the term in Equation (34) is analogous to in Equation (36). Indeed, it can be assumed that and . If then for the dislocation chaos , where l is the free path of dislocations. In this case
By setting , one can write , so that:
Evidently, Equation (38) differs from the Taylor–Orovan Equation (36) by the term which is responsible for the macroscopic strain redistribution over the volume at a certain distance from the existing fronts. This means that the Taylor–Orovan equation is a special case of Equation (38), which includes the diffusion-like component of the strain flow along with the hydrodynamic component .
Hence, it follows that the autowave plastic flow model is reduced to the dislocation model the same in the limit case. It is obvious that the application of the Taylor–Orovan Equation (36) at small dislocation densities (small strain) allows one to obtain reliably correct results. However, for large strains corresponding to the high defect densities and the nonlinear dislocation properties, it is more expedient to use the universal autowave Equation (38).
It is noteworthy that the invariant enables one to explain the origin of localized plasticity autowaves. Indeed, according to the Taylor–Orovan Equation (36), the condition set to a testing machine is fulfilled by . This condition can be violated under strain hardening, as well as at the decrease in the density of mobile dislocations with increasing strain or the decrease of dislocation velocity when the effective stress decreases from σ to [2] (here is the total dislocation density). In this case, the condition is satisfied only if the diffusion-like strain mechanism described by the term in Equation (7) is incorporated and the relaxation act of the localized plastic flow nucleus at the distance from the initial nucleus is induced by one of the above-considered mechanisms. This assumption can be used to explain the generation of the macroscopically localized plastic flow autowave.
Finally, Equation (13) enables one to calculate the work hardening coefficient. For this aim, using the autowave velocity from Equation (22) and the dispersion component from Equation (25), the following expression can be written:
According to Equation (39), , which is close to the experimental values at this stage in single and polycrystalline metals and alloys [2].
Thus, the consequences from Equation (13) explain many regularities of plastic flow. For this reason, the invariant can be thought as the master equation for the autowave theory of plasticity.
4. Discussion
The Macroscopic Quantum Phenomena of Plastic Flow
The quasi-particle conception is very fruitful for condensed-state physics [35]. The conception allows one to simplify the description of the corresponding problem. The first step consists in writing the product , where ρ is the metal density and is the ion radius of metal. The calculations carried out for nineteen different metals (see Table 2) show that

Table 2.
Data for verification of strain invariant (13).
It was found that the values are distributed conforming to the normal law and = (6.9 ± 0.45)·10-34 J·s. This value is close to the Planck constant h = 6.63⋅10−34 J·s, and there is the ratio 1.04 ± 0.06 ≈ 1. The result obtained looks surprising, and it is conceivable to match the quantities and h using the standard statistical procedure [34]. It is known that the statistical significance of the coincidence of the quantities and h is determined by the level of the Student -test parameter as follows:
where the value is the square root of the overall estimate of dispersion. The value is defined as the average of nineteen measurements (n1 = 19). It also appears that the value h can be determined in a single measurement (n2 = 1) in the absence of dispersion. The estimation reveals that the values and h are statistically identical, i.e., . It is pertinent to note that h is the fundamental constant; hence, its appearance in Equation (41) is not accidental. This suggests that plastic deformation physics is related to quantum mechanics.
The relationship between the Planck constant and the autowave characteristics λ and Vaw implies the existence of a quasi-particle, which corresponds to the localized plastic flow autowave. The mass of such quasi-particle is of principal importance. Clearly, its characteristics are related to those of the autowave, which is evident from the definition [35]:
where the values and p denote, respectively, the energy and quasi-momentum of the quasi-particle. On the basis of data obtained for dispersion autowaves in Al and γ-Fe, Equation (42) can be used for calculations. The second variant uses directly the de Broglie formula
Finally, according to Equation (40), it is found that
The effective mass of a quasi-particle with a volume was defined from Equations (42) and (44) as 0.3 4.2 amu (the atomic mass unit, 1 amu, is 1.66 × 10−27 kg). The averaged quantity 1.8 ± 0.3 ≈ 2.0 amu is a rough estimate of . The quasi-particle under consideration is named “autolocalizon”. Below, we discuss some possibilities offered by this approach.
The phonon and electron gas viscosity affects the mobility of the autolocalizon. Thus, the effective mass of the autolocalizon is regarded as a virtual mass, which is defined by the resistance of both gases to the autolocalizon’s motion. A strong evidence was recently obtained in support of this conjecture. The effective mass was calculated from Equation (44) for a range of metals.
Using Equation (40), the equation for elastic-plastic strain invariant (13) can be rewritten as
where and are the masses of the phonon and the autolocalizon, respectively. Then, Equation (45) is equipotent to the equality and hence accounts for the mechanism which is responsible for the generation of dislocations in the lattice due to the phonon condensation [34].
It has been shown that the activation volume of an elementary act of the interatomic bond rupture is close to that of an atom. The underlying theoretical premises for this fact are based on the discreteness of the crystal lattice in which the generation and evolution of elementary acts of plasticity and fracture take place. The autowave and quasi-particle concepts are therefore distinct regardless of the complementary and interrelated approaches.
In the frame of the above concept, the length of the localized plastic flow autowave can be estimated if considering the motion of autolocalizon in the phonon gas as the Brownian motion. In accordance with the Einstein theory, the free path of the Brownian particle is
In this equation, is the dynamic viscosity of the medium (phonon gas) and , ω is the frequency of the localized plastic flow autowave.
Hence, the free path of the quasi-particle can be presented as a correlation length of localized plasticity zones (the autowave length λ) as follows. Assume that the autolocalizon is of size 10−10 m; the autowave period is 103 s; T = 300 K; and 10−4 Pa·s [30]; hence the resultant value is 10−2 m, which is evidently close to the autowave length λ. Thus, the application of Equations (35) and (36) yields the equivalent numerical estimates. This suggests that both the autowave and the quasi-particle concepts correspond to the principle of duality. The proposed conceptual representation appears to be productive for theoretical purposes, especially in plasticity physics. A close relation between the plastic and acoustic characteristics of the deforming medium implies that the deformation processes can be described by a hybridized spectrum of excitations [9]. Such a spectrum is obtained by imposing the linear dispersion relation for phonons and the quadratic dispersion relation for autowaves.
To validate the hybridized dependence , the coordinates and were estimated for the point of intersection of the plots in a high-frequency range of the spectrum. The frequency and the wave number correspond to the minimum length of the elastic wave, which is of the order of distance between closely packed planes, i.e., . This directly indicates that the generalized dispersion relation is valid for both phonons and autolocalizons.
The dispersion curve in Figure 3 is assumed to be analogous to the dispersion curve for superfluid 4He [35]. The latter dispersion relation has a minimum corresponding to the nucleation of ‘rotons’, i.e., quasi-particles with an effective mass 0.64 amu and the quadratic dispersion law. The above similarity is indicative of that between the localized plasticity and superfluidity. Meanwhile, the question of whether this is a formal similarity or it has a physical meaning remains open.
The additional argument in favor of this attractive conjecture is as follows. The superfluidity of 4He is attributed to the occurrence of normal and superfluid components in liquid 4He at 2.17 K. The dynamic viscosities corresponding to these components are and . The plastic flow occurring in the deforming medium would involve both the slow motion of individual material volumes undergoing form changing and the high-rate dislocation motion. The slow process corresponds to the high material viscosity 1010 Pa·s (here 103 s is a characteristic time of the process). The velocity of the fast motion of dislocations is controlled by the phonon gas viscosity 10−4 Pa·s, i.e., 1014.
It is well known that there are only three quantum effects at macroscopic level. They are superconductivity, superfluidity, and the quantum Hall effect [35]. However, one can assume that the localized plasticity phenomena might be included in the same list. Indeed, it is possible to use a quasi-particle approach for the analysis of serrated plasticity (the Portevin–Le Chatelier effect) [36]. Using Equation (35) on the assumption that the number of autowaves arranged over the sample length is , where n = 1, 2, 3…, one obtains . In this case, it follows from Equation (47) that
The autolocalizon mass appears in Equation (47), which states that a jump-wise elongation of the stretched sample is . Because for the linear work hardening stage, it is found that . Given the sufficient instrumentation sensitivity, the flow σ(ε) curves will invariably exhibit a serrated behavior. Depending on the kind of material, the deformation occurs via different mechanisms. The estimates were made to suggest that ρ ≈ 5∙103 kg/m3 and χ ≈ 3∙10−10 m for n = 1; hence, the elongation jump is 10−4 m. For the sample length L ≈ 10−1 m, the elongation jump corresponds to the deformation 10−3, which closely matches the experimentally obtained value.
It follows from Equation (47) that an increase in the loading rate would cause a decrease in the deformation jumps, i.e., . This dependence was established experimentally in [37] for Al samples tested at 1.4 K at different loading rates. Thus, the autowave velocity was found to be proportional to the motion speed of the testing machine crossheads, i.e., Vaw ~Vmach. According to [37], the velocity Vaw will increase with Vmach, while the deformation jumps will grow in a slower manner.
5. Conclusions
- A new idea concerning the nature of plasticity was discussed. In the frame of the proposed concept, the plastic flow localization is due to not only the formation and redistribution of dislocations in the deforming medium but also to the lattice and material characteristics related to quantum mechanics. It is found that the parameters of plastic flow localization are related to the quantities h, χ, and Vt.
- It is shown that the plastic flow in solids exhibits a macro-localization behavior over the entire plastic flow. The types of localization patterns are limited in number and correspond to certain stages of work hardening.
- The elastic-plastic invariant of strain was introduced to explain the features of plastic flow. It is shown that they are the consequences of this invariant.
- The localized plasticity was assumed to belong to the category of macroscopic quantum effects, which was proven by introducing a quasi-particle of localized plastic deformation (autolocalizon).
Author Contributions
Conceptualization, S.B.; validation, S.B.; writing—original draft preparation, S.B.; writing—review and editing, L.Z.; investigation, S.B.; visualization, S.B.; funding acquisition, L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the Russian Science Foundation (grant No. 21-19-00075).
Data Availability Statement
Not applicable.
Acknowledgments
We thank Vladimir Danilov for helpful discussion of this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Argon, A. Strengthening Mechanisms in Crystal Plasticity; University Press: Oxford, UK, 2008; p. 404. [Google Scholar]
- Messerschmidt, U. Dislocation Dynamics during Plastic Deformation; Springer: Berlin, Germany, 2010; p. 503. [Google Scholar]
- Han-Chin, W. Continuum Mechanics and Plasticity; CRS Press: London, UK, 2005; p. 670. [Google Scholar]
- Lubarda, V.A. Elastoplasticity Theory; CRS Press: London, UK, 2001; p. 648. [Google Scholar]
- Seeger, A.; Frank, W. Structure formation by dissipative processes in crystals with high defect densities. In Non-linear Phenomena in Material Science; Trans Tech Publications: New York, NY, USA, 1987; pp. 125–138. [Google Scholar]
- Nicolis, G.; Prigogine, I. Self-Organization in Nonequilibrium Systems; A. Wiley Publications: New York, NY, USA, 1997; p. 510. [Google Scholar]
- Haken, H. Information and Self-Organization; Springer: Berlin, Germany, 2006; p. 300. [Google Scholar]
- Zuev, L.B. Autowave mechanics of plastic flow. In Multiscale Biomechanics and Tribology of Inorganic and Organic Systems; Springer: Berlin, Germany, 2021; pp. 245–274. [Google Scholar]
- Zuev, L.B. Plasticity autowave characteristics of metals and the Periodic table of elements. Metals 2021, 11, 1270. [Google Scholar] [CrossRef]
- Zuev, L.B.; Barannikova, S.A. Hall–Petch Relation and the Localized Plasticity Parameters. Russ. Metal. 2020, 4, 265–270. [Google Scholar] [CrossRef]
- Zuev, L.B. On the waves of plastic flow localization in pure metals and alloys. Ann. Phys. 2007, 16, 287–310. [Google Scholar] [CrossRef]
- Zuev, L.B.; Barannikova, S.A. Autowave physics of material plasticity. Crystals 2018, 9, 458. [Google Scholar] [CrossRef]
- Pelleg, J. Mechanical Properties of Materials; Springer: Dordrecht, Germany, 2013; p. 634. [Google Scholar]
- Kadić, A.; Edelen, D. A Gauge Theory of Dislocations and Disclination; Springer: Berlin, Germany, 1983; p. 168. [Google Scholar]
- Otsuka, K.; Shimizu, K. Pseudoelasticity and shape memory effects in alloys. Int. Met. Rev. 1986, 31, 93–114. [Google Scholar] [CrossRef]
- Asharia, A.; Beaudoin, A.; Miller, R. New perspectives in plasticity theory: Dislocation nucleation, waves, and partial continuity of plastic strain rate. Math. Mech. Solids 2008, 13, 292–315. [Google Scholar]
- Fressengeas, C.; Beaudoin, A.; Entemeyer, D.; Lebedkina, T.; Lebyodkin, M.; Taupin, V. Dislocation transport and intermittency in the plasticity of crystalline solids. Phys. Rev. B 2009, 79, 014108. [Google Scholar] [CrossRef]
- Kobayashi, M. Analysis of deformation localization based on proposed theory of ultrasonic velocity propagation in plastically deformed solids. Int. J. Plast. 2010, 26, 107–125. [Google Scholar] [CrossRef]
- Lebyodkin, M.; Bougherira, Y.; Lebedkina, T.; Entemeyer, D. Scaling in the local strain-rate field during jerky flow in an Al-3% Mg alloy. Metals 2020, 10, 134. [Google Scholar] [CrossRef]
- McDonald, R.J.; Efstathiou, C.; Kurath, P. The wave-like plastic deformation of single crystal copper. J. Eng. Mater. Technol. 2009, 131, 692–703. [Google Scholar] [CrossRef]
- Mudrock, R.N.; Lebyodkin, M.A.; Kurath, P.; Beaudoin, A.; Lebedkina, T.A. Strain-rate fluctuations during macroscopically uniform deformation of a solid strengthened alloy. Scr. Mater. 2011, 65, 1093–1095. [Google Scholar] [CrossRef]
- Rizzi, E.; Hähner, P. On the Portevin—Le Chtelier effect: Theoretical modeling and numerical results. Int. J. Plast. 2004, 29, 121–165. [Google Scholar] [CrossRef]
- Kolsky, H. Stress Waves in Solids; Dover Publications: New York, NY, USA, 2003; p. 224. [Google Scholar]
- Othmer, H.G. Nonlinear Wave Processes in Excitable Media; Plenum Press: New York, NY, USA, 1991; p. 213. [Google Scholar]
- Krinsky, V.I. Autowaves: Results, problems, outlooks. In Self-Organization; Autowaves and Structures far from Equilibrium; Springer: Berlin, Germany, 1984; pp. 9–19. [Google Scholar]
- Kadomtsev, B.B. Dynamics and information. Russ. Phys.–Uspekhi 1994, 164, 449–530. [Google Scholar]
- Hudson, D.J. Statistics; CERN: Geneva, Switzerland, 1964; p. 242. [Google Scholar]
- Lüthi, B. Physical Acoustics in the Solids; Springer: Berlin, Germany, 2007; p. 418. [Google Scholar]
- Williams, R.V. Acoustic Emission; Adam Hilger: Bristol, UK, 1980; p. 118. [Google Scholar]
- Alshits, V.I.; Indenbom, V.L. Mechanisms of dislocation drag. In Dislocations in Crystals; Nabarro, F.R.N., Ed.; North-Holland: Amsterdam, the Netherlands, 1986; Volume 7, pp. 43–111. [Google Scholar]
- Bell, J.F. The generation of transverse radial shear waves at a boundary between the domains of plasticity and elasticity. Int. J. Plast. 1997, 3, 91–114. [Google Scholar] [CrossRef]
- Caillard, D.; Martin, J.L. Thermally Activated Mechanisms in Crystal Plasticity; Elsevier: Oxford, UK, 2003; p. 433. [Google Scholar]
- Landau, L.D.; Lifshits, E.M. Course of Theoretical Physics. Fluid Mechanics; Pergamon Press: Oxford, UK, 1987; Volume 6, p. 539. [Google Scholar]
- Jeffreys, H.; Swirles, B. Methods of Mathematical Physics; University Press: Cambridge, MA, USA, 1966; p. 718. [Google Scholar]
- Newnham, R.E. Properties of Materials; University Press: Oxford, UK, 2005; p. 378. [Google Scholar]
- Shibkov, A.A.; Gasanov, M.F.; Zheltov, M.A.; Zolotov, A.E.; Ivolgin, V.I. Intermittent plasticity associated with the spatio-temporal dynamics of deformation bands during creep tests in an AlMg polycrystal. Int. J. Plast. 2016, 86, 37–55. [Google Scholar] [CrossRef]
- Pustovalov, V.V. Serrated deformation of metals and alloys at low temperatures. Phys. Low Temp. 2008, 34, 871–913. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).