Constitutive Equation and Characterization of the Nickel-Based Alloy 825
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Initial Microstructures
3.2. Thermal Deformation Behavior
3.3. Kinetic Analysis
3.4. Kinetic Analysis
3.4.1. Part I. Constitutive Models Considering Work Hardening-Dynamic Recovery
3.4.2. Part II. Constitutive Model Based on Dynamic Recrystallization
3.4.3. Verification of the Developed Constitutive Model
4. Discussion
4.1. Applicability and Physical Meanings of Developed Constitutive Models
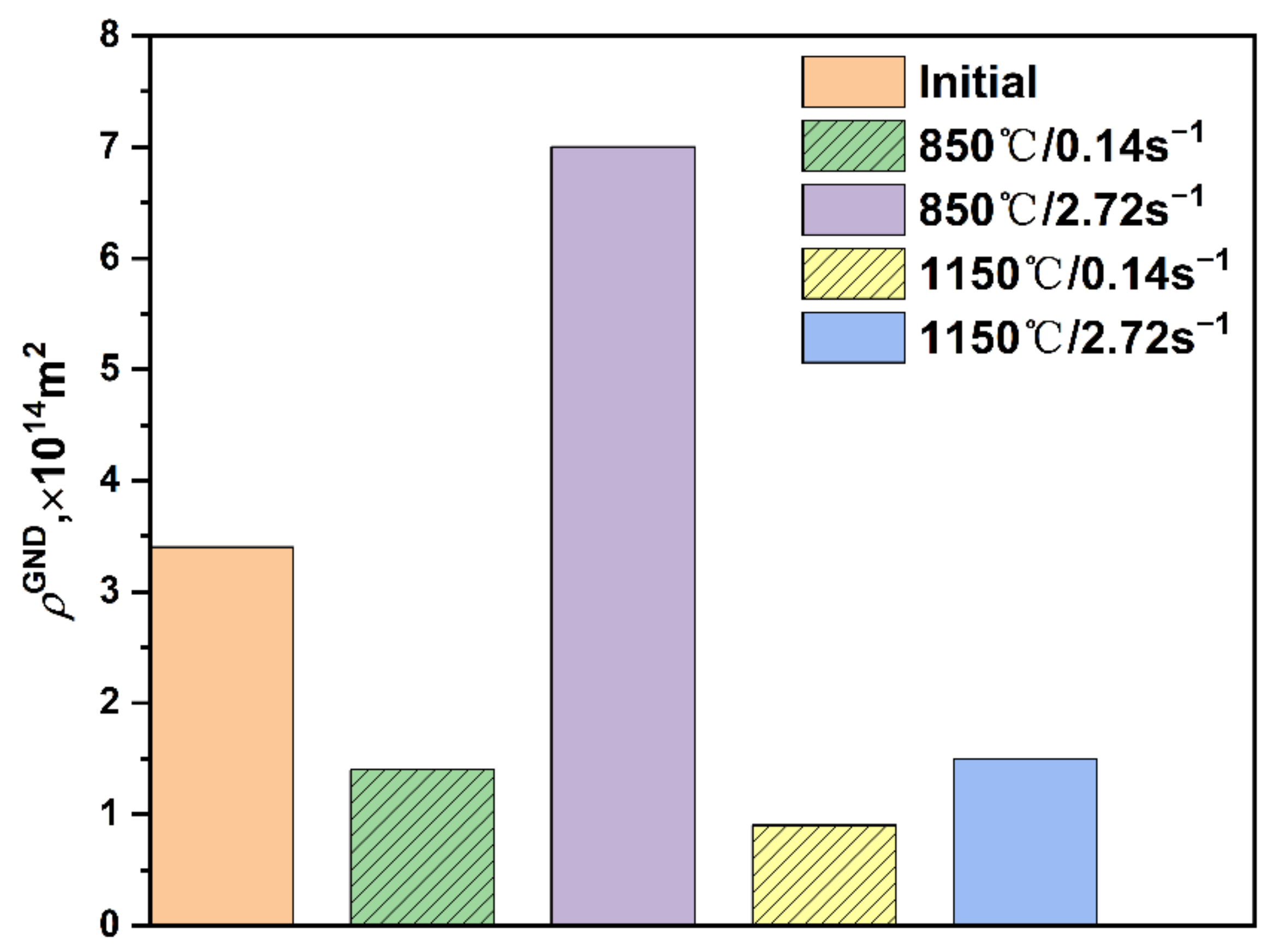
4.2. Microstructure Evolution
4.3. Mechanisms of Dynamic Recrystallization
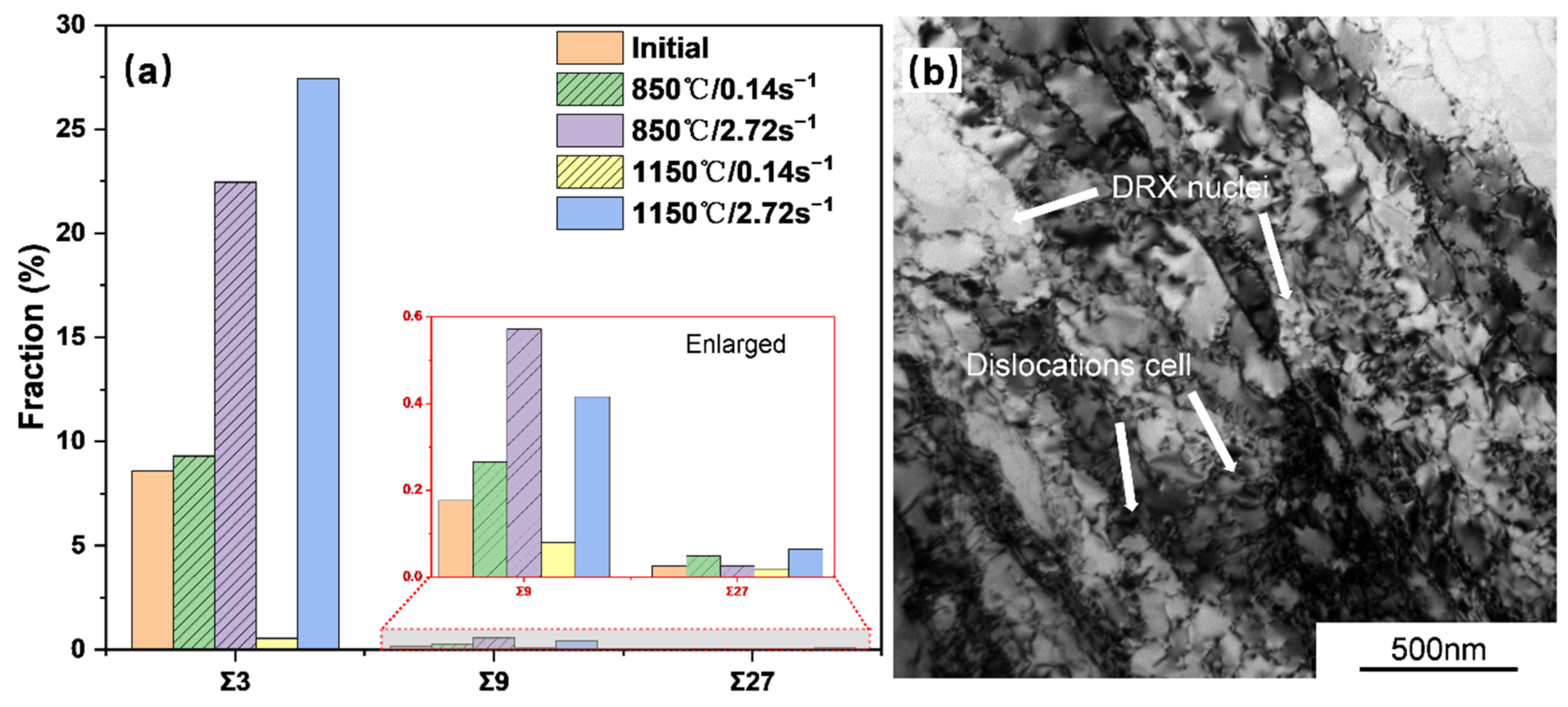
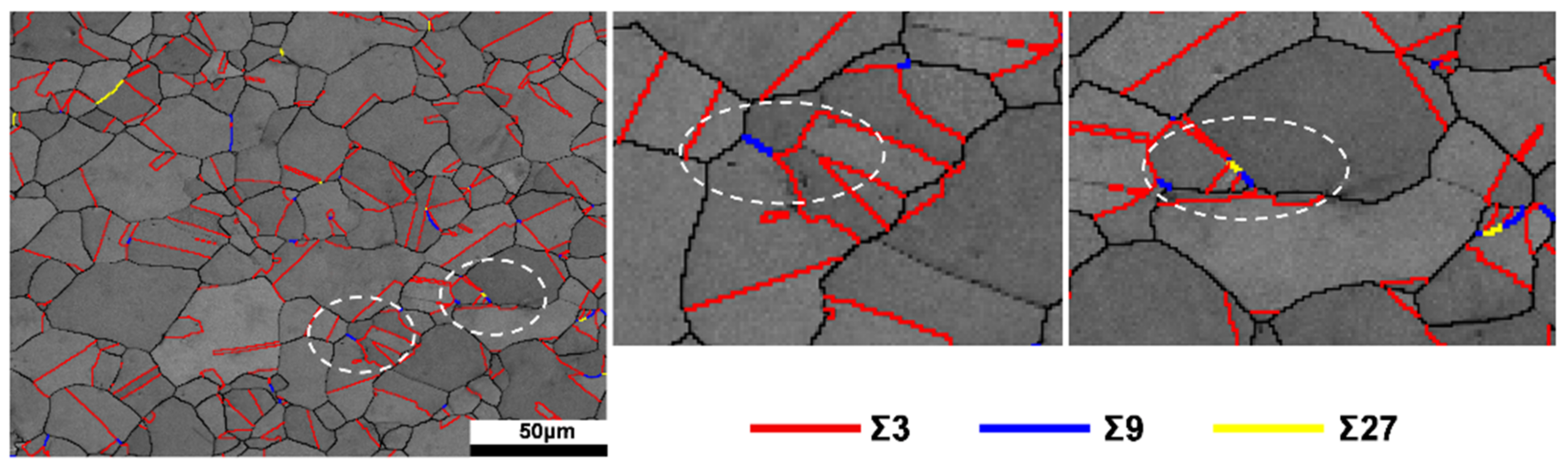
4.4. Evolution of Twin Boundaries
5. Conclusions
- (1)
- Hot deformation of nickel-based alloy 825 was investigated at deformation temperature ranges of 850–1150 °C and strain rate ranges of 0.14–2.27 s−1. The peak stress combined with Zener–Hollomon parameter was developed. The minimum activation energy needed for an energy barrier to stimulate the dislocation motion by diffusion is 616.725 KJ/Mol.
- (2)
- Constitutive equations were developed based on Bergstrom’s model and Kolmogorov–Johnson–Mehl–Avrami’s model. Comparison between predicted and experimental data indicates that the established constitutive model is in good agreement with experimental results. The correlation parameters (R) and average absolute relative error (AARE) are 0.997 and 3.53%, respectively.
- (3)
- A relationship between interaction and production exists between Σ3, Σ9, and Σ27 during DRX. The major contribution which results in the growth of new twins in DRX grains is the new boundary of Σ3 twins.
- (4)
- Dynamic recrystallisation mechanisms are DDRX and CDRX, which occur simultaneously in all deformation conditions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, C.; Qian, N.; Su, H.; Zhang, Z.; Ding, W.; Xu, J. Effect of energy distribution on the machining efficiency and surface morphology of Inconel 718 nickel-based superalloy using plasma electrolytic polishing. Surf. Coat. Technol. 2022, 441, 128506. [Google Scholar] [CrossRef]
- Li, G.; Liu, Z.; Wang, B.; Liu, Y.; Zhao, J. Effect of element Te on alterations of microstructure and mechanical property of nickel-based superalloy Inconel 718 through alloy infiltration. Appl. Surf. Sci. 2021, 544, 148730. [Google Scholar] [CrossRef]
- Sanchez, S.; Smith, P.; Xu, Z.; Gaspard, G.; Hyde, C.J.; Wits, W.W.; Ashcroft, I.A.; Chen, H.; Clare, A.T. Powder Bed Fusion of nickel-based superalloys: A review. Int. J. Mach. Tools Manuf. 2021, 165, 103729. [Google Scholar] [CrossRef]
- Kumar, A.; Pandey, C. Development and Evaluation of Dissimilar Gas Tungsten Arc-Welded Joint of P92 Steel/Inconel 617 Alloy for Advanced Ultra-Supercritical Boiler Applications. Metall. Mater. Trans. A 2022, 53, 3245–3273. [Google Scholar] [CrossRef]
- Dak, G.; Pandey, C. A critical review on dissimilar welds joint between martensitic and austenitic steel for power plant application. J. Manuf. Processes 2020, 58, 377–406. [Google Scholar] [CrossRef]
- Akbari, Z.; Mirzadeh, H.; Cabrera, J.-M. A simple constitutive model for predicting flow stress of medium carbon microalloyed steel during hot deformation. Mater. Des. 2015, 77, 126–131. [Google Scholar] [CrossRef]
- Jia, D.; Sun, W.; Xu, D.; Yu, L.; Xin, X.; Zhang, W.; Qi, F. Abnormal dynamic recrystallization behavior of a nickel based superalloy during hot deformation. J. Alloys Compd. 2019, 787, 196–205. [Google Scholar] [CrossRef]
- Pollock, T.M.; Tin, S. Nickel-Based Superalloys for Advanced Turbine Engines: Chemistry, Microstructure and Properties. J. Propuls. Power 2006, 22, 361–374. [Google Scholar] [CrossRef]
- Mingjie, Z.; Fuguo, L.; Shuyun, W.; Chenyi, L. Characterization of hot deformation behavior of a P/M nickel-base superalloy using processing map and activation energy. Mater. Sci. Eng. A 2010, 527, 6771–6779. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.-S. Study of microstructural evolution during static recrystallization in a low alloy steel. J. Mater. Sci. 2009, 44, 835–842. [Google Scholar] [CrossRef]
- Zhu, H.; Ou, H. Constitutive modelling of hot deformation behaviour of metallic materials. Mater. Sci. Eng. A 2022, 832, 142473. [Google Scholar] [CrossRef]
- Lin, Y.C.; Xiao-Min, C. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater. Des. 2011, 32, 1733–1759. [Google Scholar] [CrossRef]
- Kotkunde, N.; Nitin Krishnamurthy, H.; Kumar Gupta, A.; Kumar Singh, S. Study of Hot Deformation Behavior Using Phenomenological Based Constitutive Model for Austenitic Stainless Steel 316. Mater. Today Proc. 2018, 5, 4870–4877. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, M.-S.; Zhong, J. Prediction of 42CrMo steel flow stress at high temperature and strain rate. Mech. Res. Commun. 2008, 35, 142–150. [Google Scholar] [CrossRef]
- Wang, L.; Liu, F.; Zuo, Q.; Chen, C.F. Prediction of flow stress for N08028 alloy under hot working conditions. Mater. Des. 2013, 47, 737–745. [Google Scholar] [CrossRef]
- Singh, K.; Rajput, S.K.; Mehta, Y. Modeling of the hot deformation behavior of a high phosphorus steel using artificial neural networks. Mater. Discov. 2016, 6, 1–8. [Google Scholar] [CrossRef]
- Pandey, C.; Mahapatra, M.M.; Kumar, P.; Saini, N. Effect of strain rate and notch geometry on tensile properties and fracture mechanism of creep strength enhanced ferritic P91 steel. J. Nucl. Mater. 2018, 498, 176–186. [Google Scholar] [CrossRef]
- Mandal, S.; Bhaduri, A.K.; Subramanya Sarma, V. Role of Twinning on Dynamic Recrystallization and Microstructure during Moderate to High Strain Rate Hot Deformation of a Ti-Modified Austenitic Stainless Steel. Metall. Mater. Trans. A 2012, 43, 2056–2068. [Google Scholar] [CrossRef]
- Mandal, S.; Jayalakshmi, M.; Bhaduri, A.K.; Subramanya Sarma, V. Effect of Strain Rate on the Dynamic Recrystallization Behavior in a Nitrogen-Enhanced 316L(N). Metall. Mater. Trans. A 2014, 45, 5645–5656. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, Z.; Qin, X.; Wang, C.; Zhou, L. Effect of initial state on hot deformation and dynamic recrystallization of Ni-Fe based alloy GH984G for steam boiler applications. J. Alloys Compd. 2019, 795, 370–384. [Google Scholar] [CrossRef]
- Chen, X.-M.; Lin, Y.C.; Wen, D.-X.; Zhang, J.-L.; He, M. Dynamic recrystallization behavior of a typical nickel-based superalloy during hot deformation. Mater. Des. 2014, 57, 568–577. [Google Scholar] [CrossRef]
- Tan, G.; Li, H.-Z.; Wang, Y.; Qiao, S.-C.; Yang, L.; Huang, Z.-Q.; Cheng, T.-W.; Zhao, Z.-X. Effect of Zener-Hollomon parameter on microstructure evolution of a HEXed PM nickel-based superalloy. J. Alloys Compd. 2021, 874, 159889. [Google Scholar] [CrossRef]
- Tang, K.; Zhang, Z.; Tian, J.; Wu, Y.; Jiang, F. Hot deformation behavior and microstructural evolution of supersaturated Inconel 783 superalloy. J. Alloys Compd. 2021, 860, 158541. [Google Scholar] [CrossRef]
- Wang, S.; Luo, J.R.; Hou, L.G.; Zhang, J.S.; Zhuang, L.Z. Physically based constitutive analysis and microstructural evolution of AA7050 aluminum alloy during hot compression. Mater. Des. 2016, 107, 277–289. [Google Scholar] [CrossRef]
- Tahreen, N.; Zhang, D.F.; Pan, F.S.; Jiang, X.Q.; Li, C.; Li, D.Y.; Chen, D.L. Characterization of hot deformation behavior of an extruded Mg–Zn–Mn–Y alloy containing LPSO phase. J. Alloys Compd. 2015, 644, 814–823. [Google Scholar] [CrossRef]
- Gong, B.; Duan, X.W.; Liu, J.S.; Liu, J.J. A physically based constitutive model of As-forged 34CrNiMo6 steel and processing maps for hot working. Vacuum 2018, 155, 345–357. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.-M.; Wen, D.-X.; Chen, M.-S. A physically-based constitutive model for a typical nickel-based superalloy. Comput. Mater. Sci. 2014, 83, 282–289. [Google Scholar] [CrossRef]
- Mecking, H.; Kocks, U.F. Kinetics of flow and strain-hardening. Acta Metall. 1981, 29, 1865–1875. [Google Scholar] [CrossRef]
- Hansen, N.; Kuhlmann-Wilsdorf, D. Low energy dislocation structures due to unidirectional deformation at low temperatures. Mater. Sci. Eng. 1986, 81, 141–161. [Google Scholar] [CrossRef]
- McQueen, H.J.; Yue, S.; Ryan, N.D.; Fry, E. Hot working characteristics of steels in austenitic state. J. Mater. Process. Technol. 1995, 53, 293–310. [Google Scholar] [CrossRef]
- Yanagida, A.; Yanagimoto, J. A novel approach to determine the kinetics for dynamic recrystallization by using the flow curve. J. Mater. Process. Technol. 2004, 151, 33–38. [Google Scholar] [CrossRef]
- Mirzadeh, H.; Najafizadeh, A. Prediction of the critical conditions for initiation of dynamic recrystallization. Mater. Des. 2010, 31, 1174–1179. [Google Scholar] [CrossRef]
- Liu, J.; Cui, Z.; Ruan, L. A new kinetics model of dynamic recrystallization for magnesium alloy AZ31B. Mater. Sci. Eng. A 2011, 529, 300–310. [Google Scholar] [CrossRef]
- Mofarrehi, M.; Javidani, M.; Chen, X.G. Effect of Mn content on the hot deformation behavior and microstructure evolution of Al–Mg–Mn 5xxx alloys. Mater. Sci. Eng. A 2022, 845, 143217. [Google Scholar] [CrossRef]
- Song, Y.; Li, Y.; Li, H.; Zhao, G.; Cai, Z.; Sun, M. Hot deformation and recrystallization behavior of a new nickel-base superalloy for ultra-supercritical applications. J. Mater. Res. Technol. 2022, 19, 4308–4324. [Google Scholar] [CrossRef]
- Oh, J.-H.; Yoo, B.-G.; Choi, I.-C.; Santella, M.L.; Jang, J. Influence of thermo-mechanical treatment on the precipitation strengthening behavior of Inconel 740, a Ni-based superalloy. J. Mater. Res. 2011, 26, 1253–1259. [Google Scholar] [CrossRef]
- Zhang, J.-S.; Xia, Y.-F.; Quan, G.-Z.; Wang, X.; Zhou, J. Thermal and microstructural softening behaviors during dynamic recrystallization in 3Cr20Ni10W2 alloy. J. Alloys Compd. 2018, 743, 464–478. [Google Scholar] [CrossRef]
- Chen, W.; Jia, C.; Hu, B.; Zheng, C.; Li, D. Evolution of twins and sub-boundaries at the early stage of dynamic recrystallization in a Ni-30%Fe austenitic model alloy. Mater. Sci. Eng. A 2018, 733, 419–428. [Google Scholar] [CrossRef]
- Xie, B.; Zhang, B.; Yu, H.; Yang, H.; Liu, Q.; Ning, Y. Microstructure evolution and underlying mechanisms during the hot deformation of 718Plus superalloy. Mater. Sci. Eng. A 2020, 784, 139334. [Google Scholar] [CrossRef]
- Sugui, T.; Zhenrong, L.; Zhonggang, Z.; Liqing, C.; Wenru, S.; Xianghua, L. Influence of deformation level on microstructure and creep behavior of GH4169 alloy. Mater. Sci. Eng. A 2012, 550, 235–242. [Google Scholar] [CrossRef]
- Qian, M.; Lippold, J.C. The effect of annealing twin-generated special grain boundaries on HAZ liquation cracking of nickel-base superalloys. Acta Mater. 2003, 51, 3351–3361. [Google Scholar] [CrossRef]

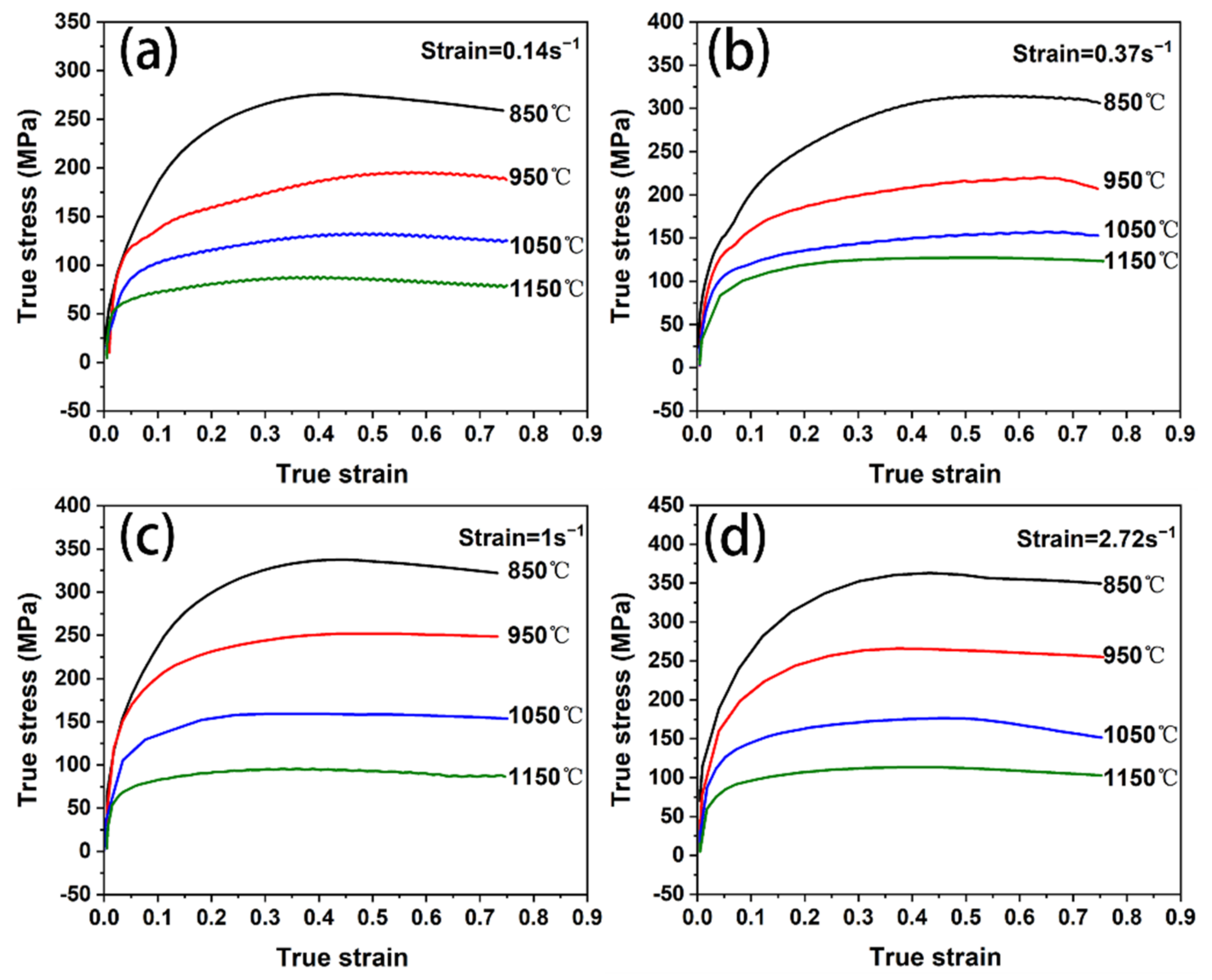
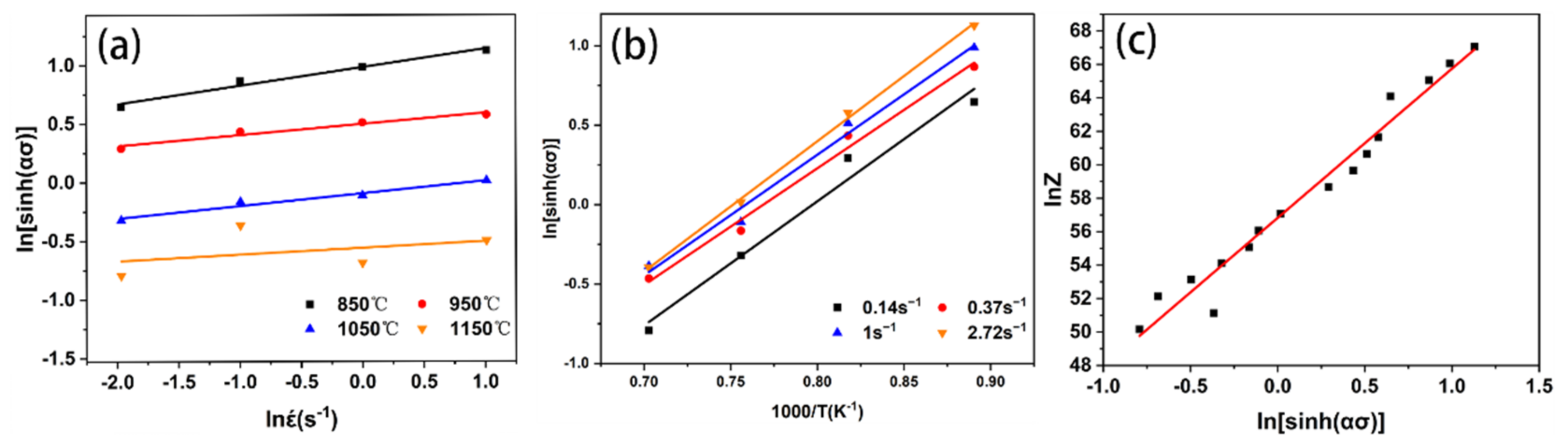
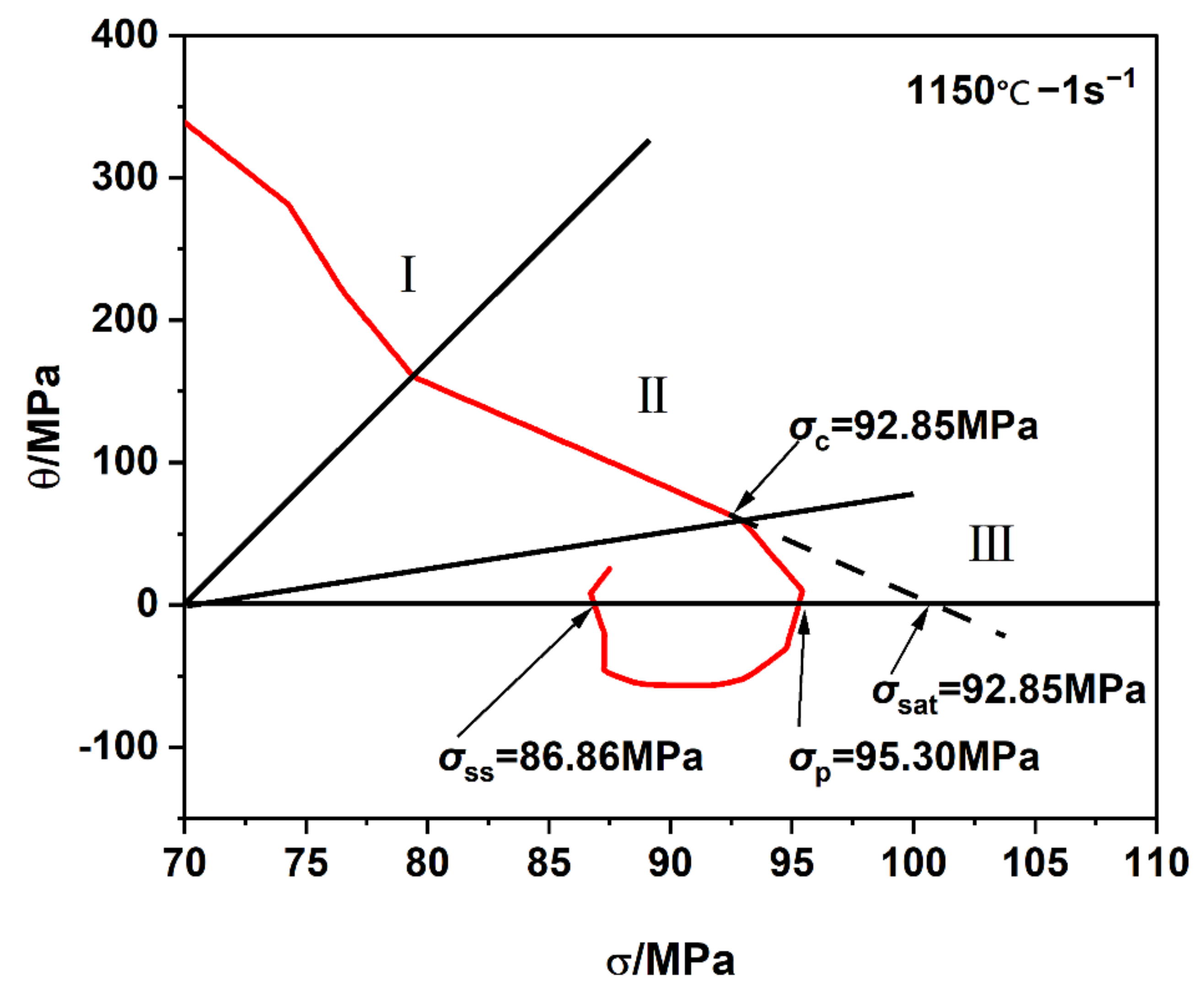




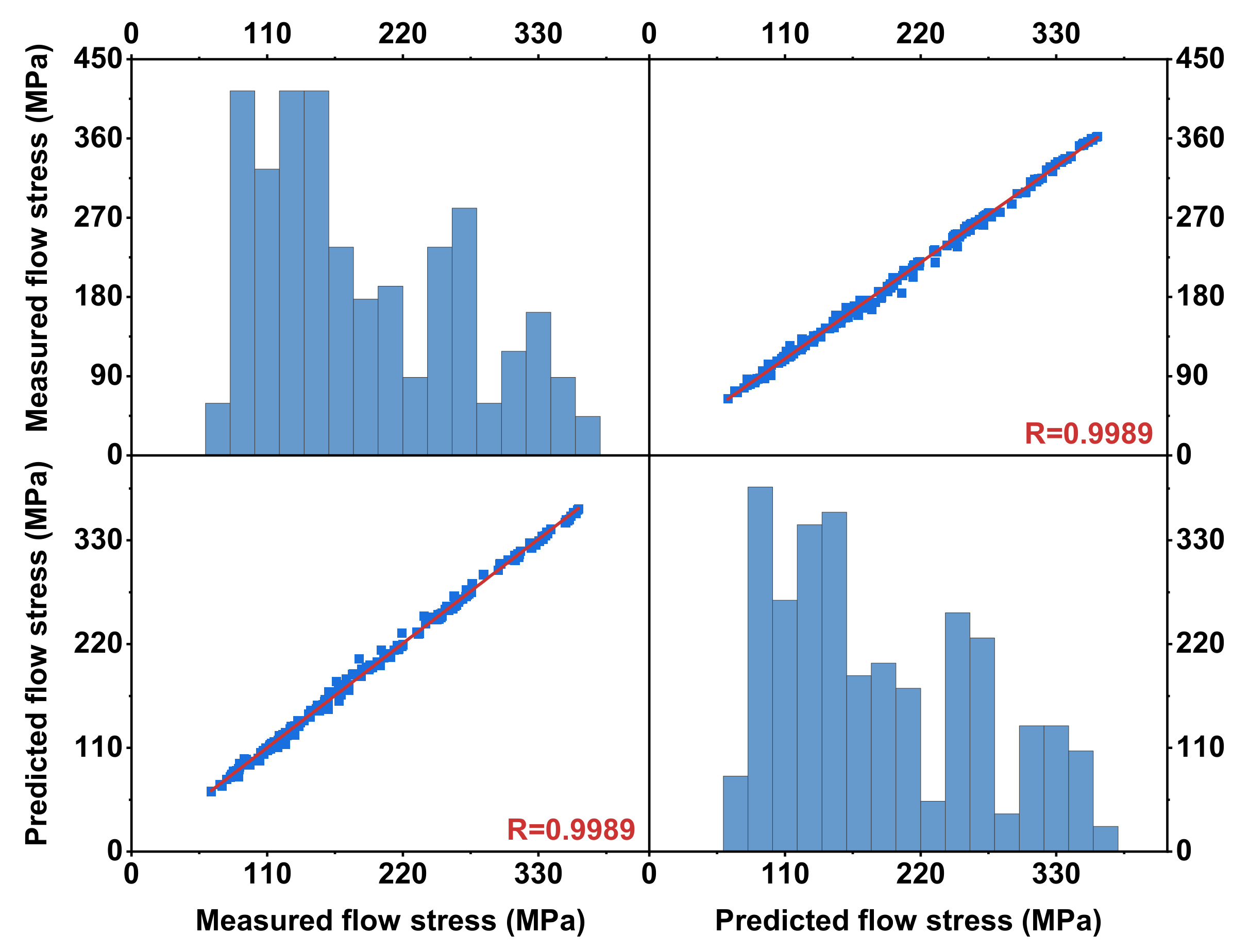



| Strain Rate (s−1) | Temperature (°C) | |||
|---|---|---|---|---|
| 850 | 950 | 1050 | 1150 | |
| 0.14 | 275 | 195 | 132 | 87 |
| 0.37 | 314 | 219 | 157 | 95 |
| 1 | 337 | 252 | 159 | 113 |
| 2.72 | 362 | 266 | 176 | 127 |
| Constant | α | A | n |
|---|---|---|---|
| Value | 0.0051 | 2.09 × 1024 | 9.633 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Li, Y.; Li, H.; Wang, J.; Liu, G.; Song, Y. Constitutive Equation and Characterization of the Nickel-Based Alloy 825. Metals 2022, 12, 1496. https://doi.org/10.3390/met12091496
Xu H, Li Y, Li H, Wang J, Liu G, Song Y. Constitutive Equation and Characterization of the Nickel-Based Alloy 825. Metals. 2022; 12(9):1496. https://doi.org/10.3390/met12091496
Chicago/Turabian StyleXu, Hui, Yugui Li, Huaying Li, Jinbin Wang, Guangming Liu, and Yaohui Song. 2022. "Constitutive Equation and Characterization of the Nickel-Based Alloy 825" Metals 12, no. 9: 1496. https://doi.org/10.3390/met12091496
APA StyleXu, H., Li, Y., Li, H., Wang, J., Liu, G., & Song, Y. (2022). Constitutive Equation and Characterization of the Nickel-Based Alloy 825. Metals, 12(9), 1496. https://doi.org/10.3390/met12091496






