On the Influence of the Initial Shear Damage to the Cyclic Deformation and Damage Mechanism
Abstract
1. Introduction
2. Testing
2.1. Metallography
2.2. Transmission Electron Microscopy (TEM)
2.3. Tensile Test
2.4. Hardness Test
2.5. Fatigue Test Program
3. Test Results and Discussion
3.1. Dynamic Characteristics of Materials
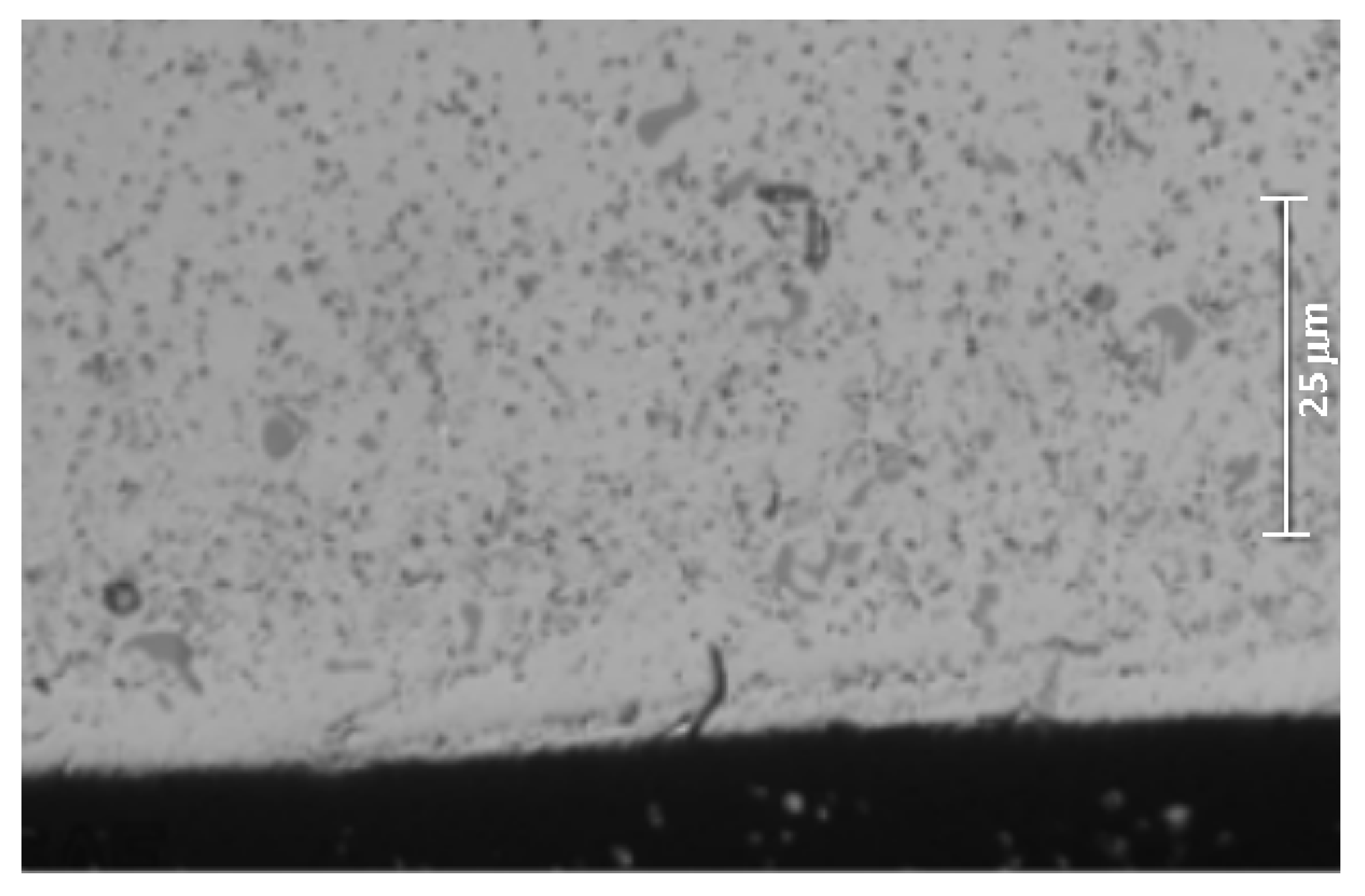
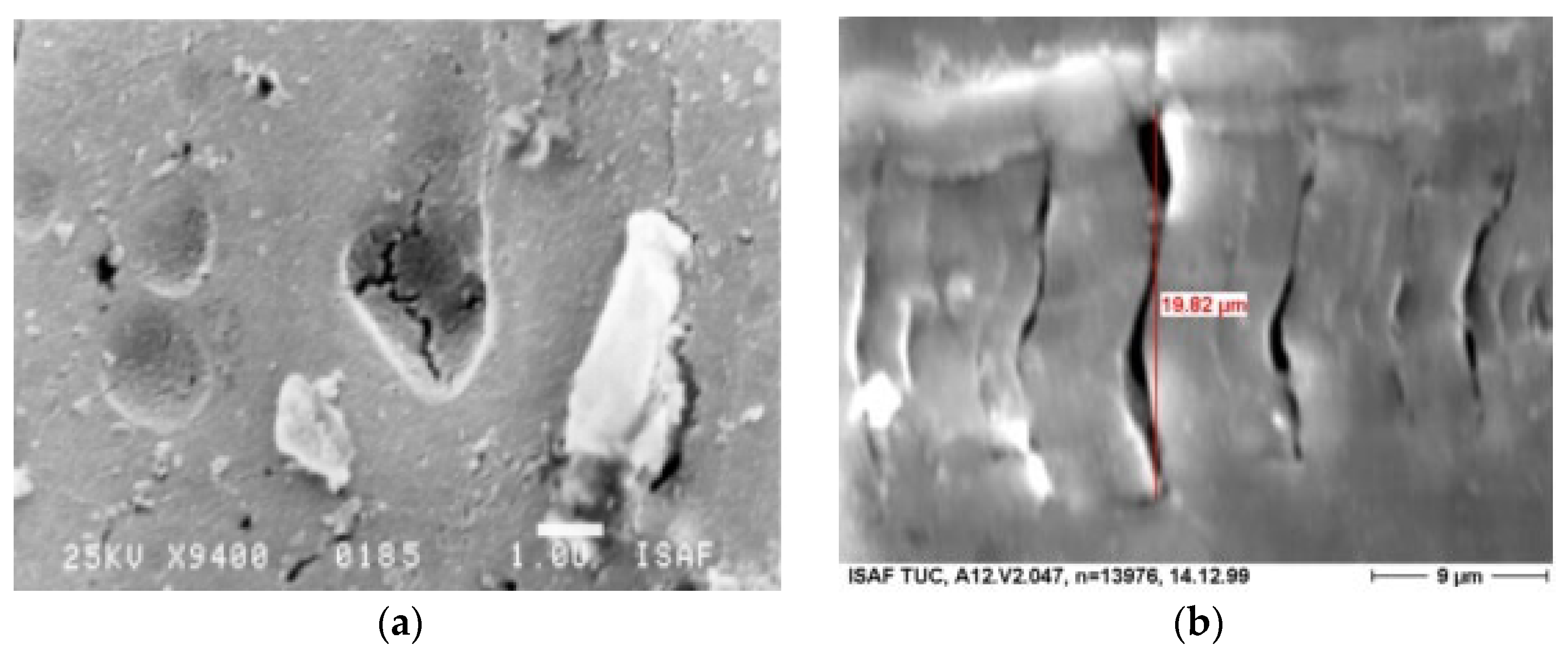
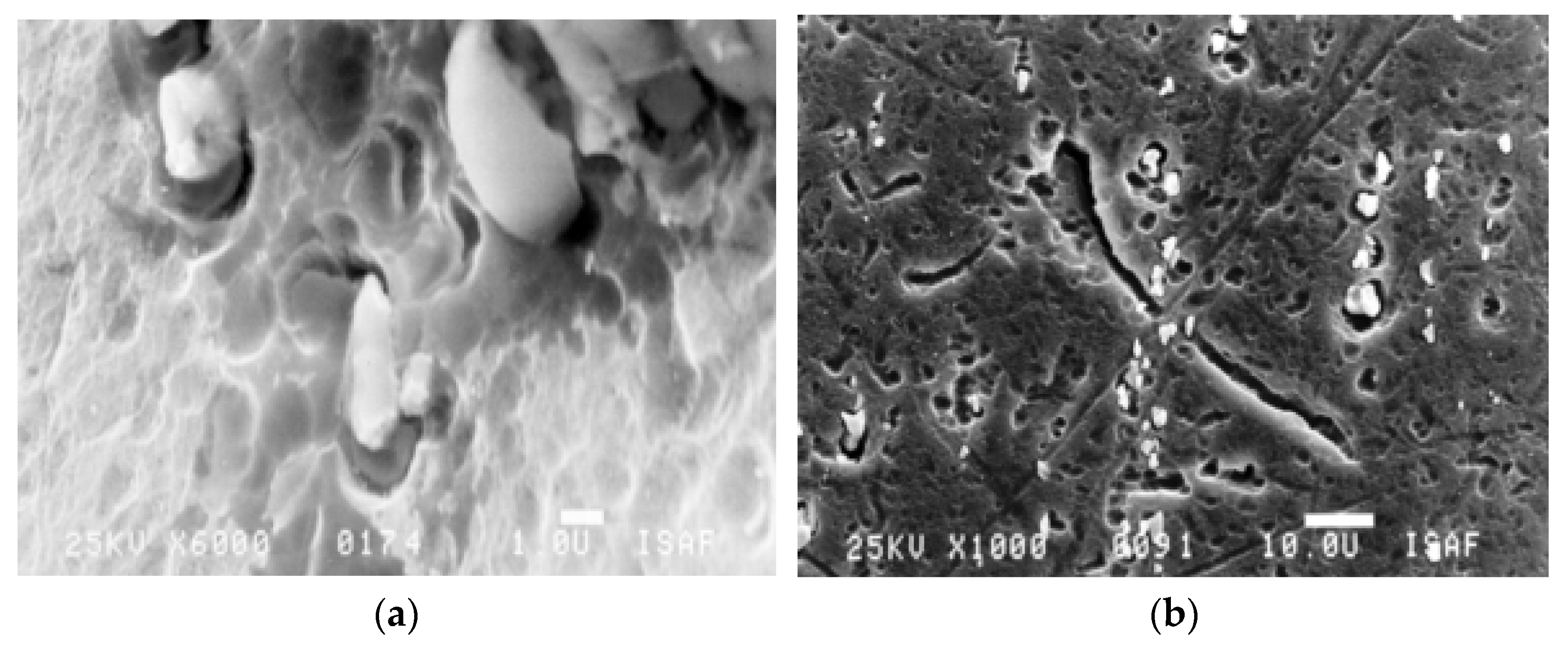
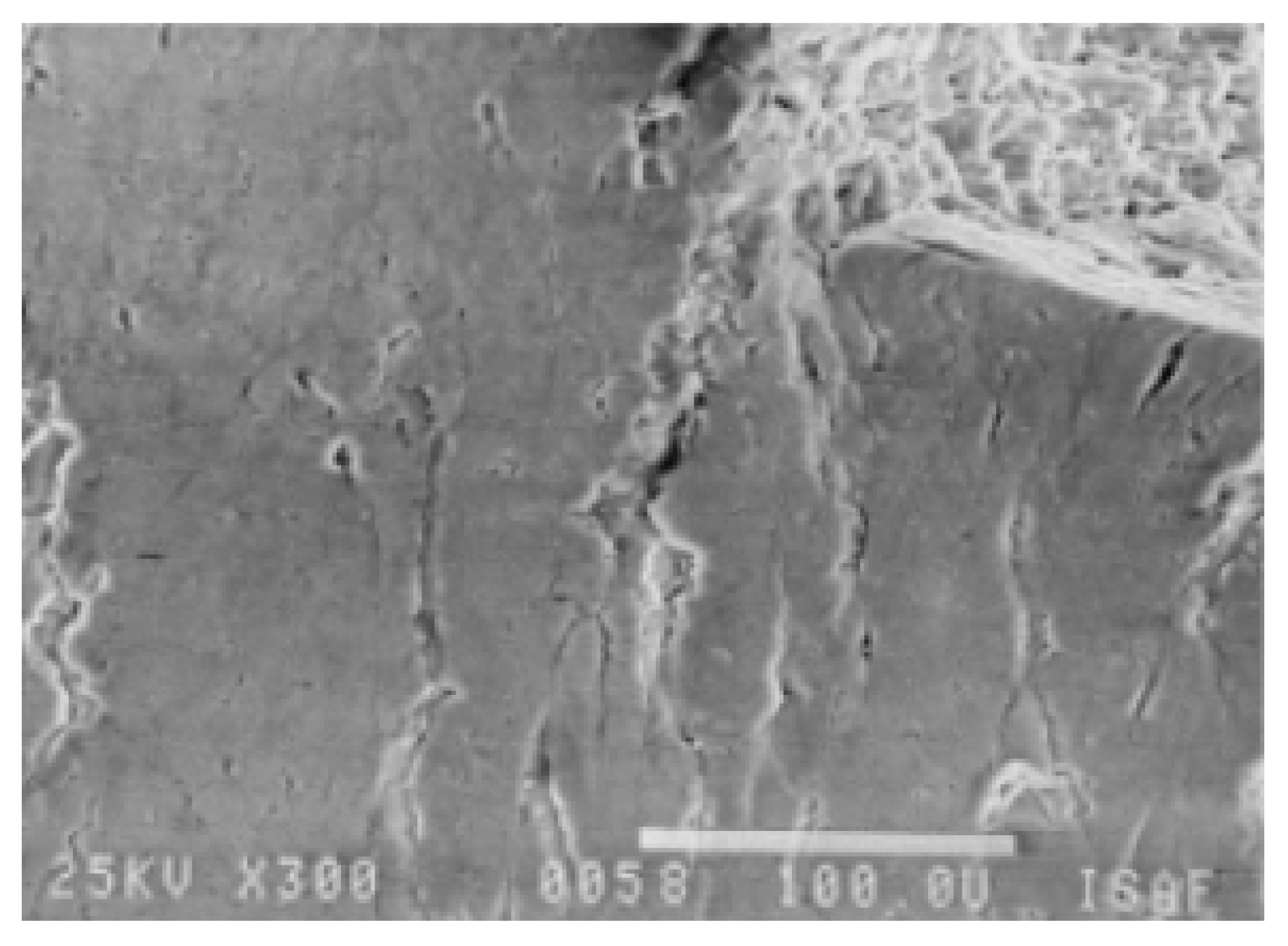
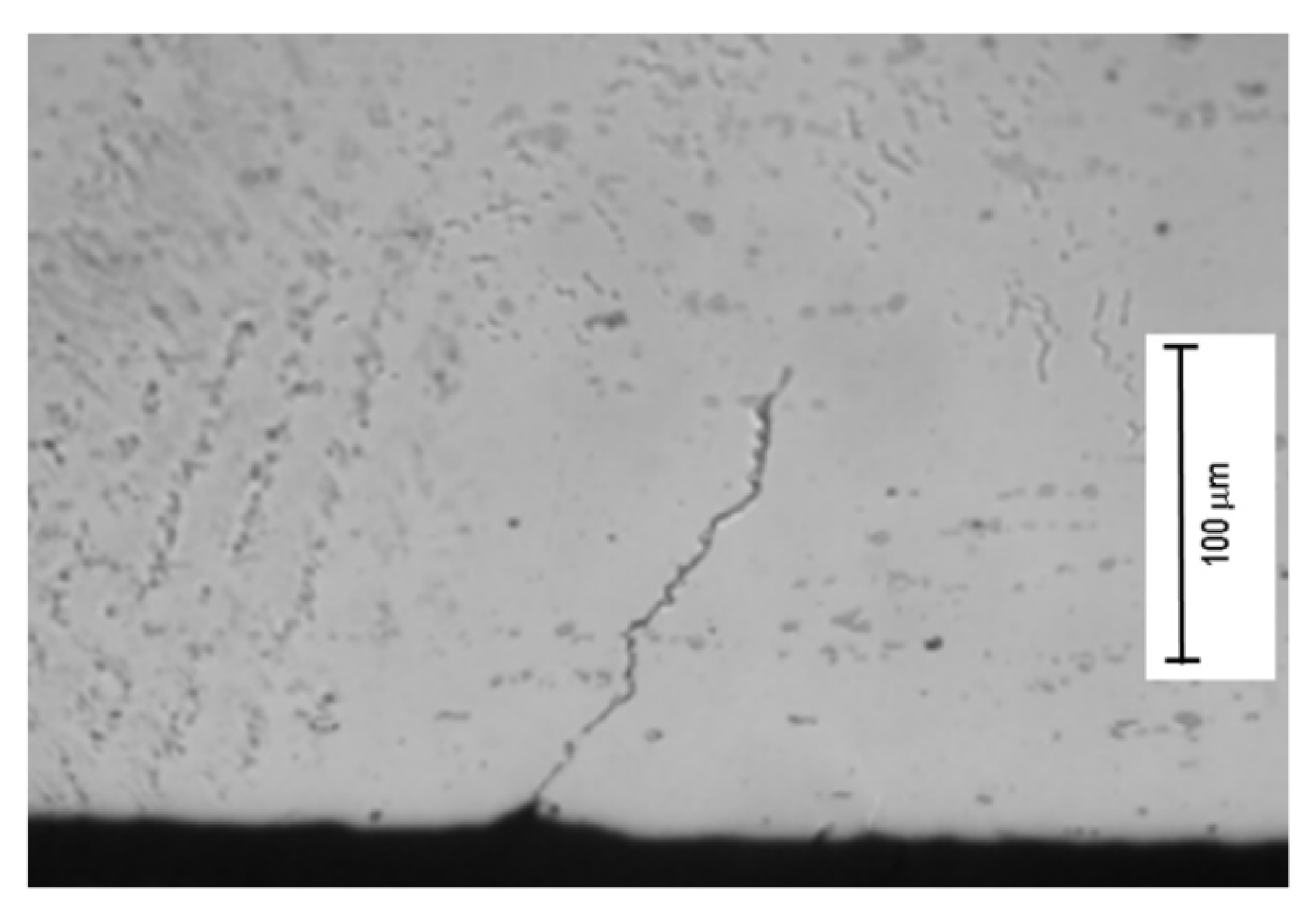
3.2. Crack Research
SEM Observations
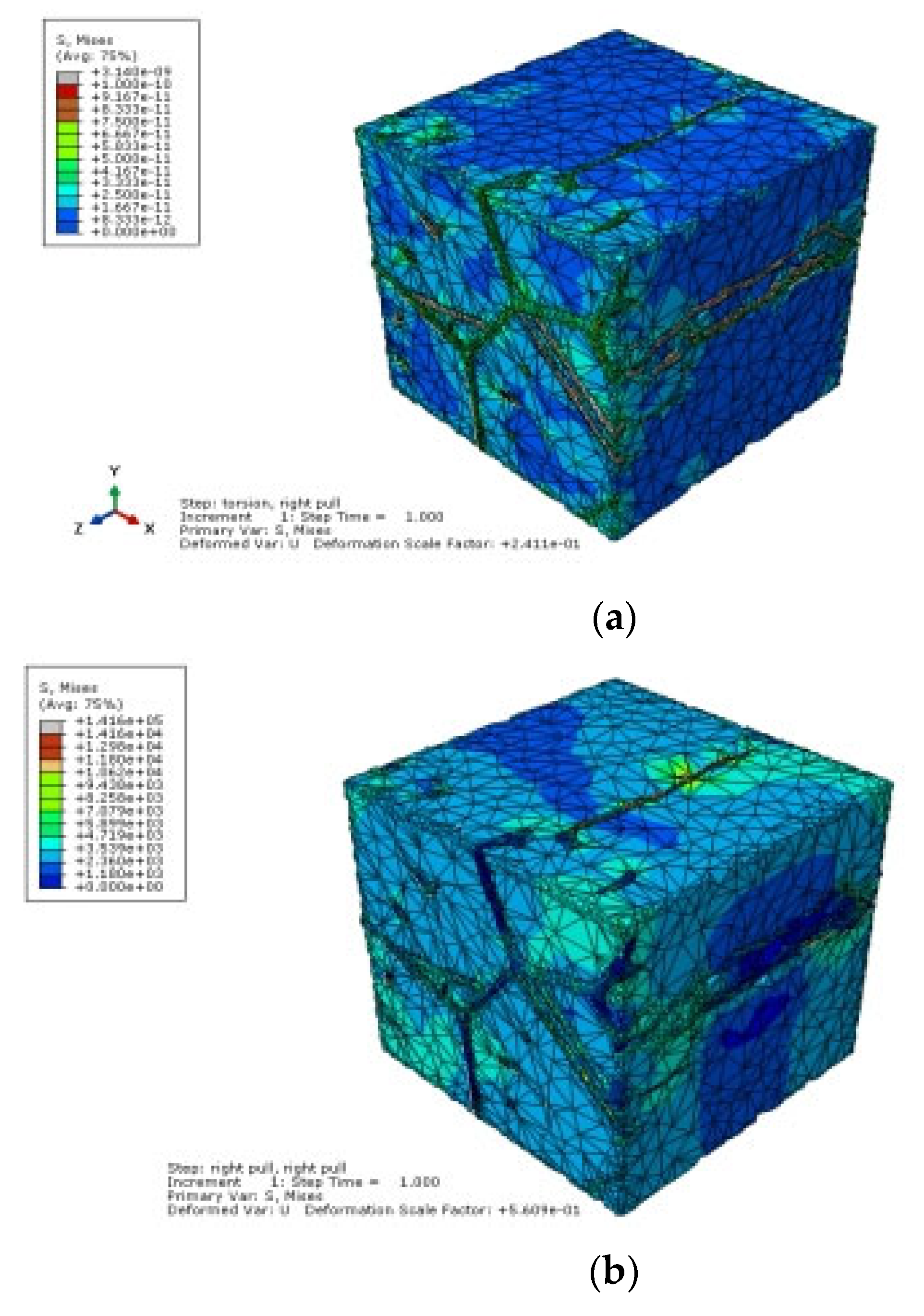
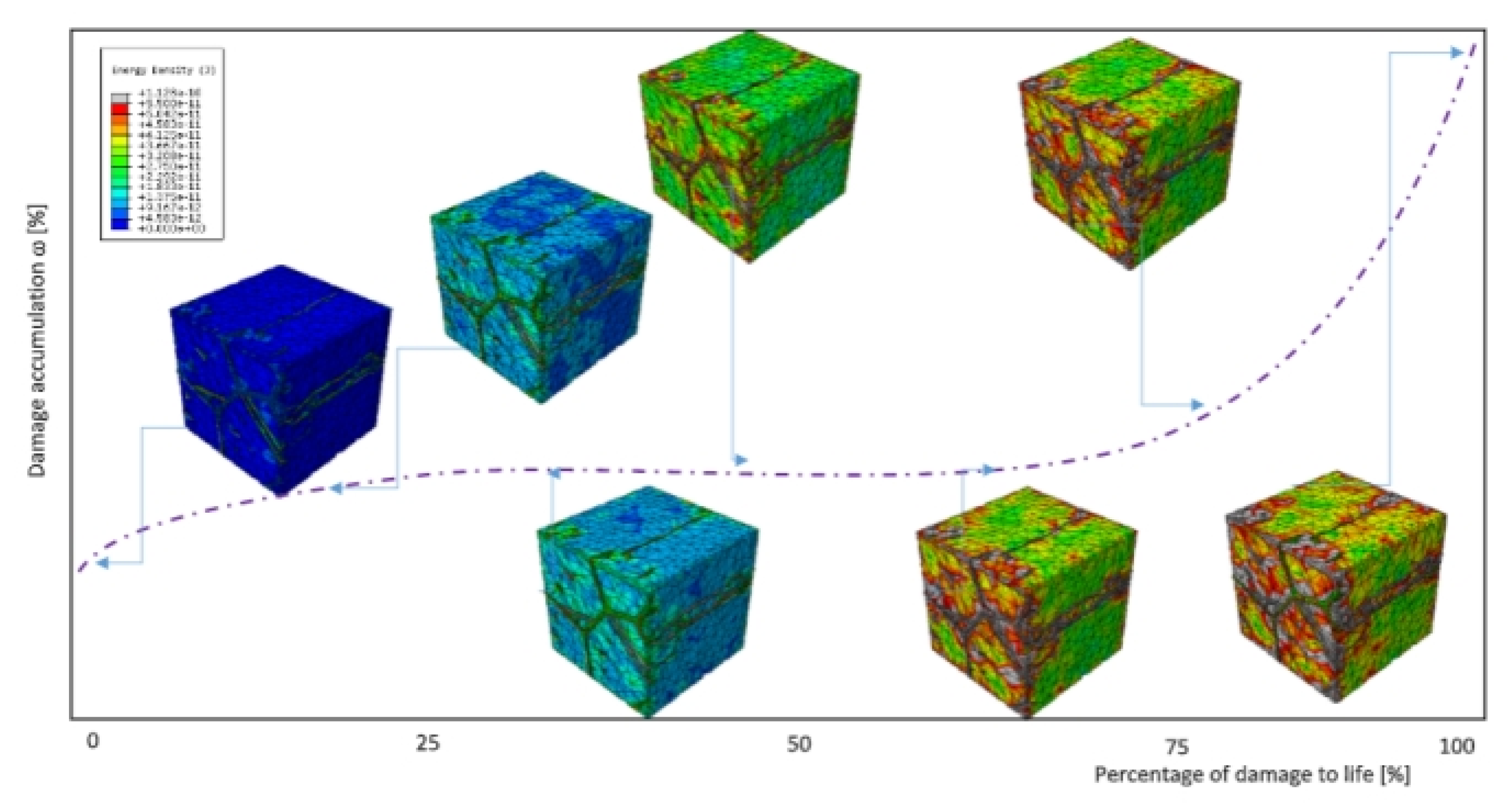
4. Modeling and Simulation
4.1. Computational Modeling
4.1.1. Aluminum Matrix
4.1.2. Mg2Si Precipitates
4.1.3. Grain Boundary
4.1.4. Subgrain Boundaries
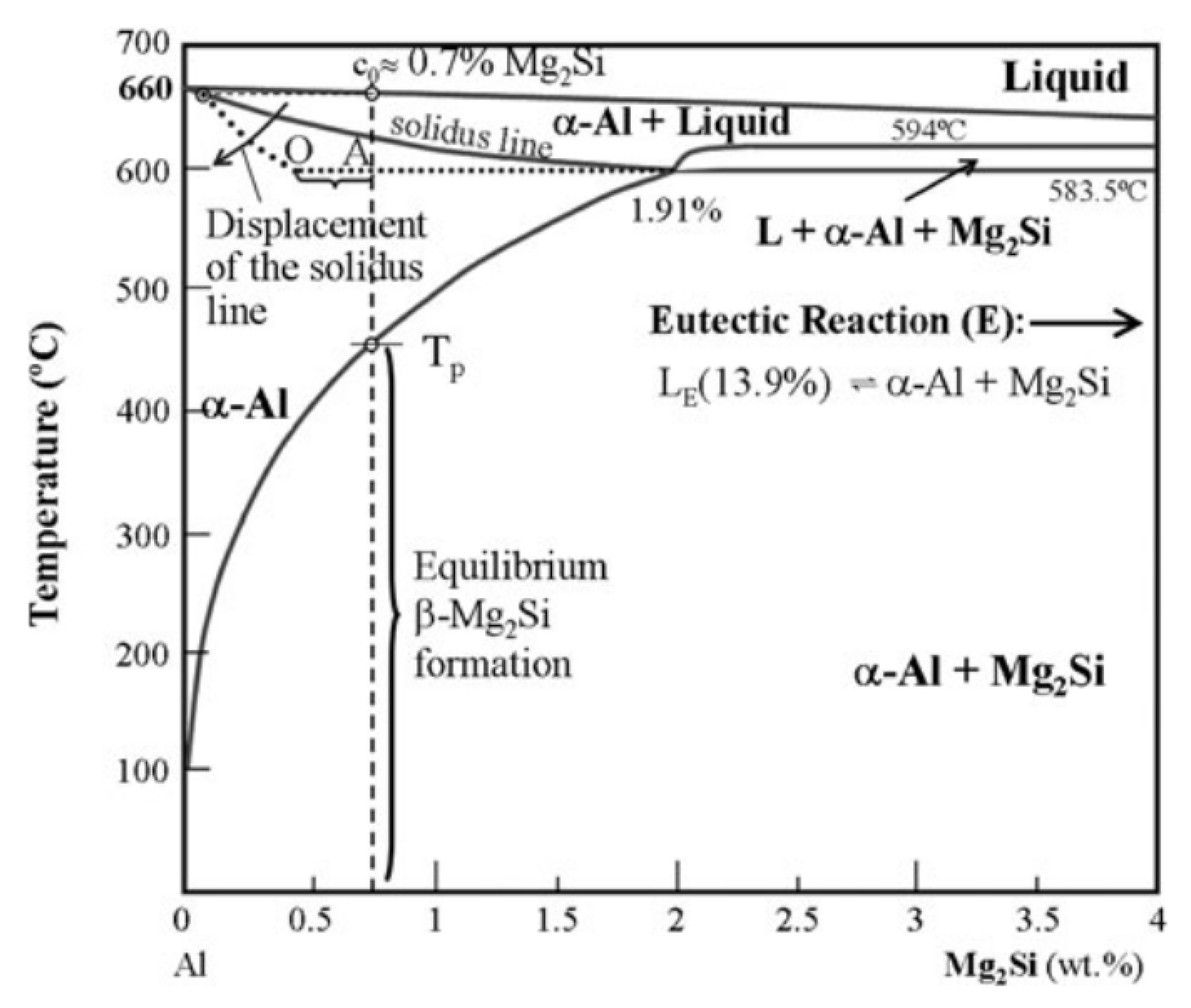
4.1.5. Mg2Si Eutectic (Coarse Mg2Si)
4.1.6. β-Al5FeSi
4.1.7. π-(FeMg3Si6Al8)
4.1.8. AlCr
4.1.9. Si Particles
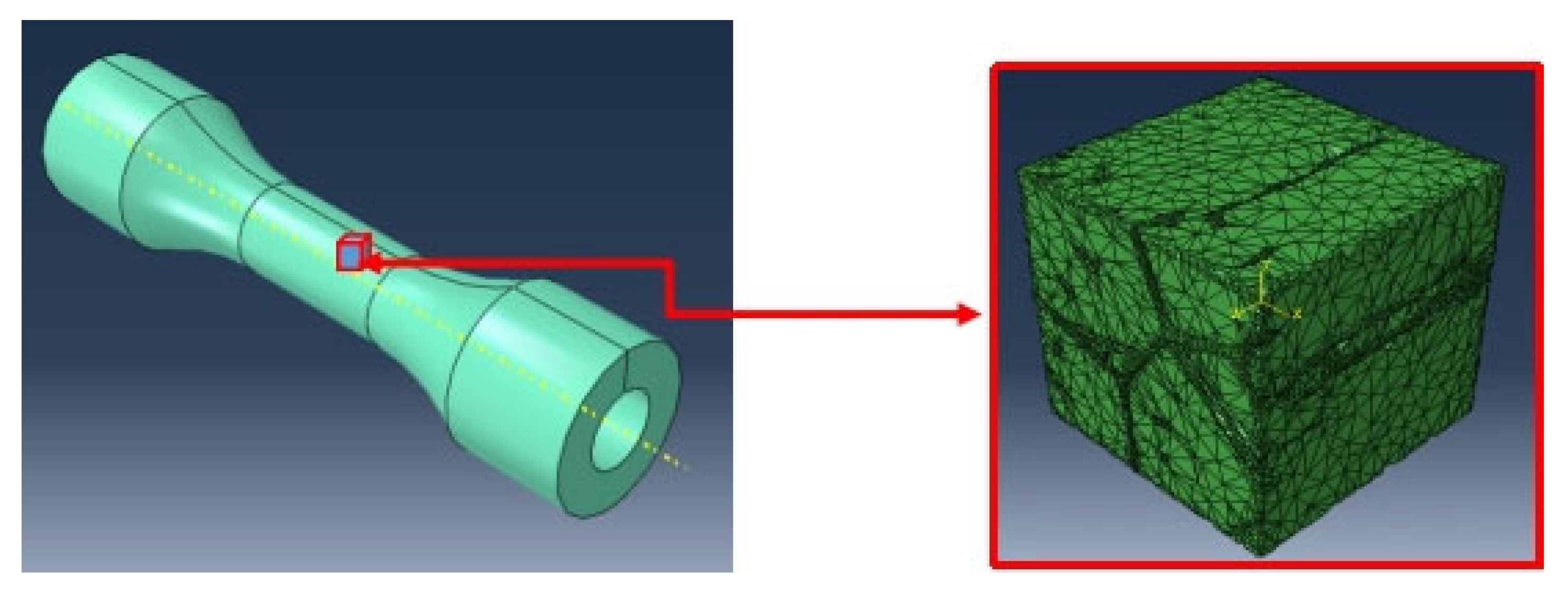
4.1.10. Computational Approach
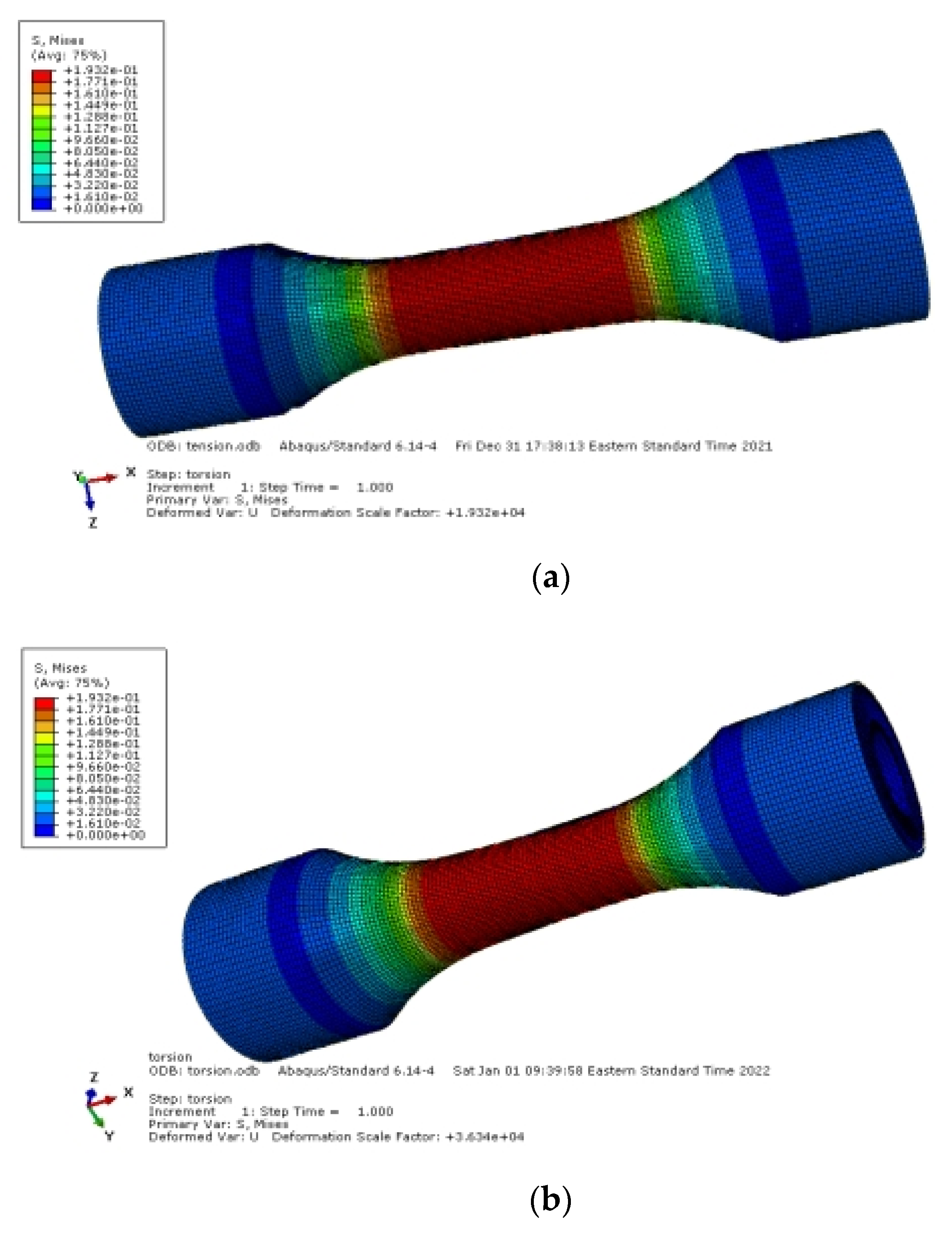
4.2. From the Standpoint of Mechanics
4.3. From a Metallurgical Standpoint
4.4. Experimentation-Based Verification
5. Conclusions
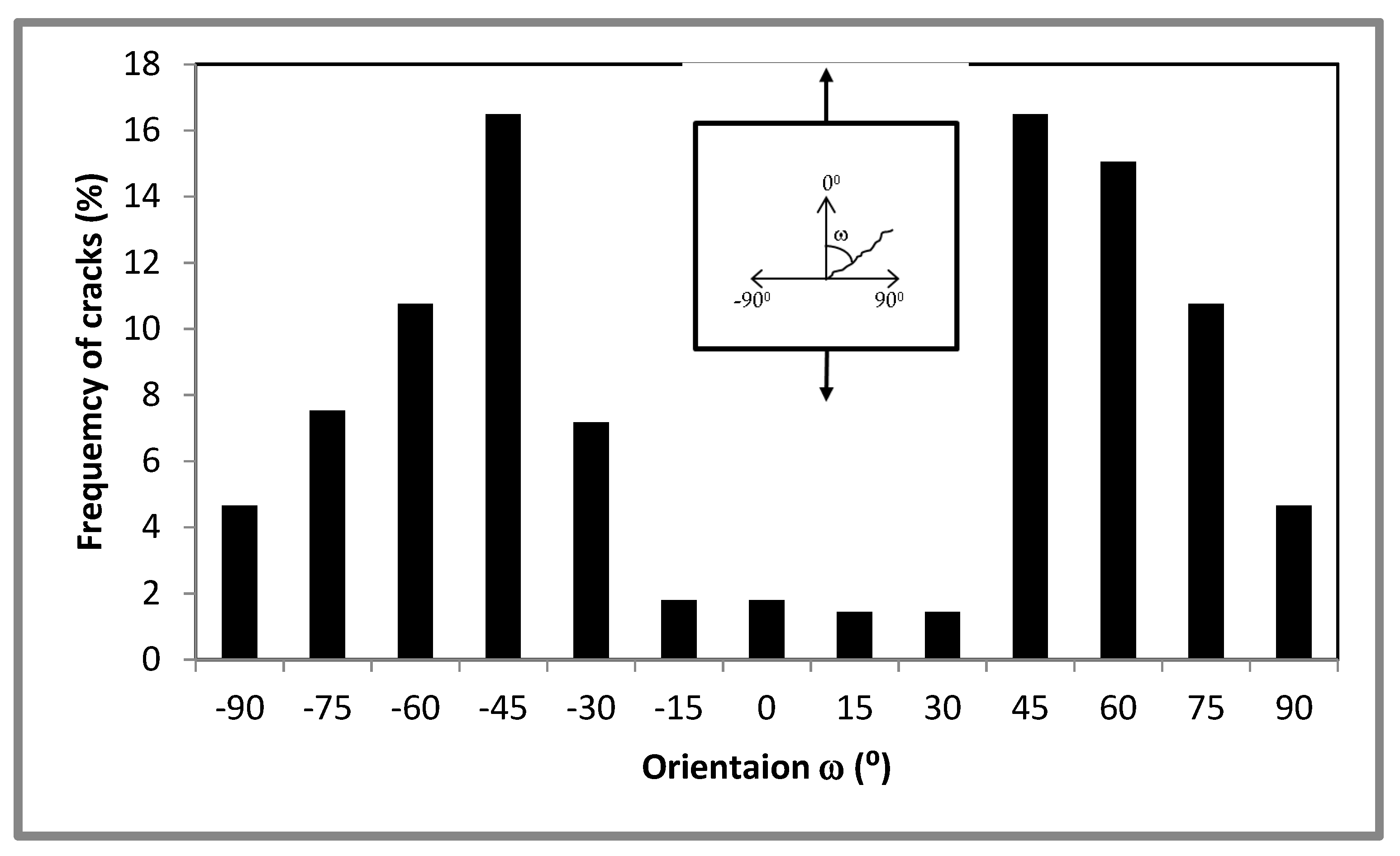
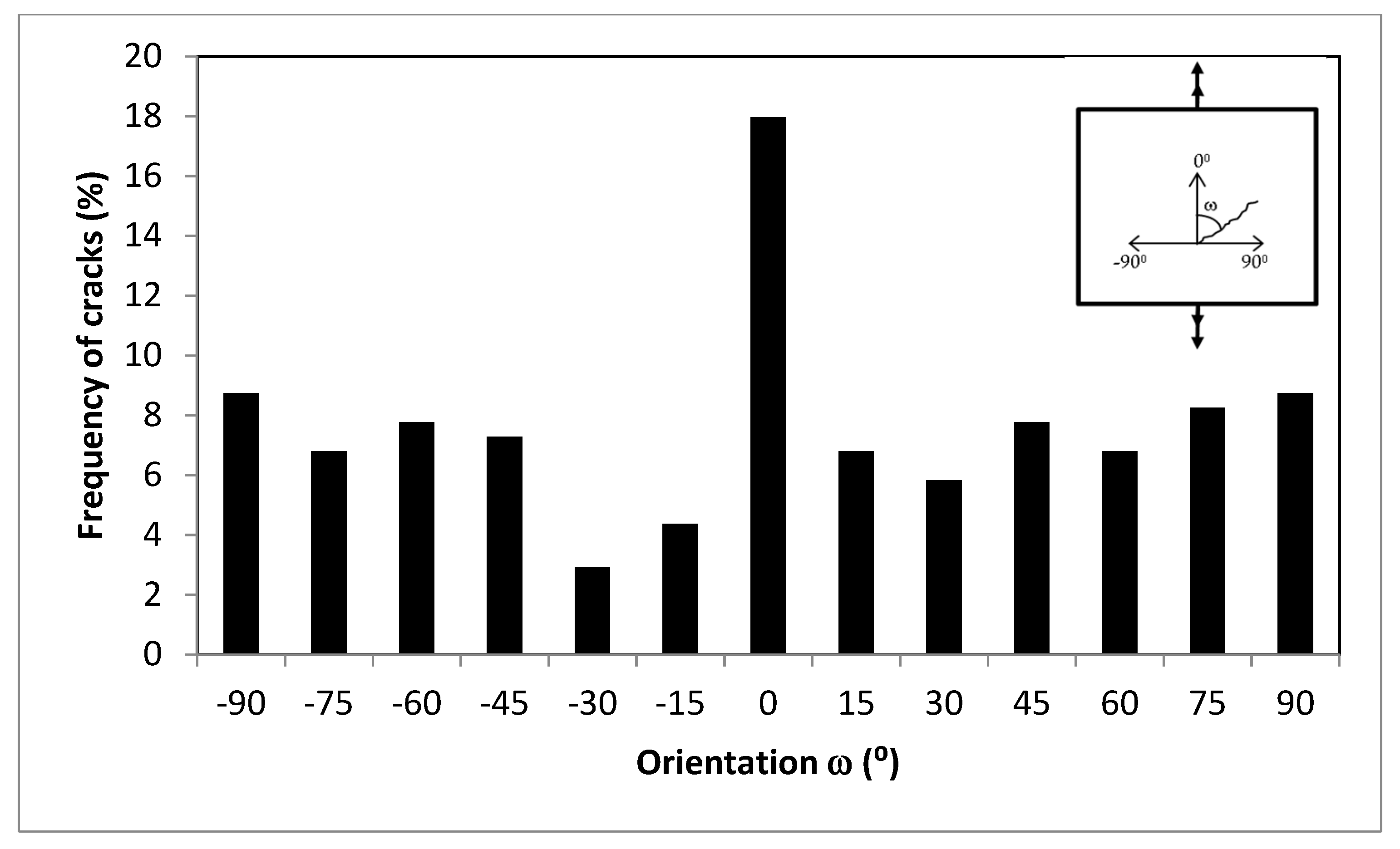
- Most of the initial fatigue cracks are found in planes parallel to the maximum shear stress. Based on the experimental results, a crack propagation model can be proposed by following the laws of crack mechanics, starting with the cracks in the plane with the maximum shear stress;
- The initial cracks are mostly found in planes parallel to the maximum shear stress. Statistically, the microcracks under tension modes are highest at 45° (approximately 30%), while under torsion are highest at 0° (approximately 20%) with respect to the sample orientation. The influence of the microstructure is explained by finite element analysis;
- The initial cracks not only propagate on the surface but also propagate towards the inside of the material;
- With the application of SEM, it is possible to find crack propagation that is hampered by the microstructural barriers;
- The stress distribution and cracking in the AlMgSi were both modeled. The model took into account the load-carrying function’s constituent phases. The calculation results from the specimen were used as inputs for the boundary conditions. The local models were positioned on the surface. Hard and soft materials are treated differently in the models, with various failure rules. The findings suggest that the constituents and the microstructure have a crucial role in increasing the material strength at low stress levels, analogous to the hard fibers of a composite material. The hard and especially sharp elements, on the other hand, become damaging to the system as the stress increases to the point where cracking can occur. They serve as a starting point for cracking. This discovery corresponds to what is known in the field of metallurgy. Three mechanical parameters influence the cracking conditions, namely the particle form (microstructure), strain rate, and matrix failure law.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eulitz, K.-G.; Döcke, H.; Esderts, A.; Kotte, K.L.; Zenner, H. Lebensdauervorhersage II, Verbesserung der Lebensdauerabschätzung durch systematische Aufarbeitung und Auswertung vorliegender Versuchsdaten, Forschungskuratorium Maschinenbau, 227; FKM: Frankfurt, Germany, 1997. [Google Scholar]
- Zenner, H. Lebensdauerkonzepte, Beschreibung-Kritik-Entwicklungen, in Fatigue Life Concepts, Description—Review—Developments; DVM: Berlin, Germany, 1997. [Google Scholar]
- Wang, Q.; Berard, J.Y.; Rathery, S.; Bathias, C. High-cycle fatigue crack initiation and propagation behaviour of high-strength spring steel wires. Fatigue Fract. Eng. Mater. Struct. 2003, 22, 673–677. [Google Scholar] [CrossRef]
- Murakami, Y. What is fatigue damage? A viewpoint from the observation of a low-cycle fatigue process. In Metal Fatigue; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Murakami, J.; Miller, K.J. What is Fatigue Damage? A View Point from the Observation of Low Cycle Fatigue Process. Int. J. Fatigue 2005, 27, 991–1005. [Google Scholar] [CrossRef]
- Mbuyaa, T.O.; Gub, Y.; Thomson, R.C.; Reed, P.A.S. Effect of intermetallic particles and grain boundaries on short fatigue crack growth in a cast Al–4Cu–3Ni–0.7Si piston alloy. Fatigue Fract. Eng. Materals Struct. 2017, 40, 1428–1442. [Google Scholar] [CrossRef]
- Liu, G.; Winwood, S.; Rhodes, K.; Birosca, S. The Effects of Grain Size, Dendritic Structure and Crystallographic Orientation on Fatigue Crack Propagation in IN713C Nickel-Based Superalloy. Int. J. Plast. 2020, 125, 150–168. [Google Scholar] [CrossRef]
- Fleishel, R.; Cauthen, C.; Daniewicz, S.; Baker, A.; Jordon, B.; TerMaath, S. Characterization of Surface Fatigue Crack Nucleation and Microstructurally Small Crack Growth in High Strength Aluminum Alloys. Front. Mater. 2021, 7, 590747. [Google Scholar] [CrossRef]
- Carpinteri, A. Handbook of Crack Propagation in Metallic Structures; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Gottstein, G. Physical Foundations of Materials Science; Springer: Berlin, Germany, 2014. [Google Scholar]
- Husein, S. Crystal Structure of Metals. In Metalurgy; University of Baghdad: Baghdad, Iraq, 2019; pp. 1–25. [Google Scholar]
- Soboyejo, W. Mechanical Properties-of-Engineered-Materials, Crystal Stucture and Dislocation Motion; Marcel Dekker Inc.: New York, NY, USA, 2002. [Google Scholar]
- Zhang, Y.H.; Edward, L. On the blocking effect of grain boundaries on small crystallographic fatigue crack growth. In Materials Science and Engineering; Elsevier: Amsterdam, The Netherlands, 1994; Volume A188, pp. 121–123. [Google Scholar]
- Asensiio-Lozano, J.; Pena, J.S.; Vander Voort, G.F. Effect of Processing Steps on the Mechanical Properties and Surface Appearance of 6063 Aluminium Extruded Products. Materials 2014, 7, 4224–4242. [Google Scholar] [CrossRef]
- Vander Voort, G.; Suarez-Pena, B.; Asensio-Lozano, J. Microstructure Investigations of Streak Formation in 6063 Alumunium Extrusions by Optical Metallographic Techniques, Microscopy and Microanalysi; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Dedov, S.; Lehmann, G.; Kawalla, R. Application of Combined Casting-Forging Process for Production of Durable Lightweight Aluminum Parts, Key Engineering Materials; Scientific Nets: Kapellweg, Switzerland, 2013; Volume 554–557. [Google Scholar]
- Polák, J.; Mazanova, V.; Heczko, M.; Petráš, R. The Role of Extrusions and Intrusions in Fatigue Crack Initiation, Engineering Fracture Mechanics; Elsevier: Amsterdam, The Netherlands, 2017; Volume 185, pp. 46–60. [Google Scholar]
- Hopson, P.D.; Brown, M.W.; De Los Rios, E.R. Two Phases of Short Crack Growth in Medium Carbon Steel; EGF Pub: London, UK, 1986; Volume 1, pp. 441–459. [Google Scholar]
- Miller, K.J. Multiaxial Fatigue: A Review, Schaedigungsfrueherkenung und Schadensablauf bei metalischen Bauteilen; DVM: Darmstadt, Germany, 1993. [Google Scholar]
- Plumbridge, W.J. Review: Fatigue Crack propagation in metallic and polymeric materials. J. Mater. Sci. 1972, 7, 939–962. [Google Scholar] [CrossRef]
- Issler, L.; Ruos, H.; Haefele, P. Fesfigkeitslehre Grundlagen; Springer: Berlin, Germany, 2013. [Google Scholar]
- Gancarz, T.; Jourdan, J.; Gasior, W.; Henein, H. Physicochemical properties of Al, Al-Mg and Al-Mg-Zn Aloys. J. Mol. Liq. 2018, 249, 470–476. [Google Scholar] [CrossRef]
- Li, H.; Cao, F.; Guo, S.; Jia, Y.; Zhang, D.; Liu, Z.; Wang, P.; Scudino, S.; Sun, J. Effects of Mg and Cu on microstructures and properties of sprays-deposited Al-Zn-Mg-Cu alloys. J. Alloy. Compd. 2017, 719, 89–96. [Google Scholar] [CrossRef]
- Rodríguez, S.V.; Martínez, L.; Pech-Canul, M. Solidification Physics and Microstructure: A Study of AlMg and AlMgSi Alloys by Vortex Method. [pengar. buku] Alicia Esther Ares. In Solidification; Intechopen: London, UK, 2018. [Google Scholar] [CrossRef][Green Version]
- Davis, J.R. ASM Specialty Handbook: Alumunum and Alumimum Alloys; ASM International: Materials Park, OH, USA, 2001; pp. 352–416. [Google Scholar]
- Monteiro, W.A.; Espósito, I.M.; Ferrari, R.B.; Buso, S.J. Microstructural and Mechanical Characterization after Thermomechanical Treatments in 6063 Aluminum Alloy. Mater. Sci. Appl. 2011, 2, 1529–1541. [Google Scholar] [CrossRef][Green Version]
- ASM Handbook Committee. Properties and Selection: Non-ferrous Alloys and Special Purpose Materials; ASM International: Materials Park, OH, USA, 1990. [Google Scholar]
- Tan, L.; Sridharan, K.; Allen, T.; Nanstad, R. Microstructure tailoring for property improvements by grain boundary engineering. J. Nucl. Mater. 2008, 374, 270–280. [Google Scholar] [CrossRef]
- Shimada, M.; Kokawa, H.; Wang, Z.J.; Sato, Y.S.; Karibe, I. Optimization of grain boundary character distribution for intergranular corrosion resistant 304 stainless steel by twin-induced grain boundary engineering. Acta Mater. 2002, 50, 2331–2341. [Google Scholar] [CrossRef]
- Sharmaa, P.; Ganti, S. On the grain-size-dependent elastic modulus of nanocrystalline materials with and without grain-boundary sliding. J. Mater. Res. 2003, 18, 1267–1279. [Google Scholar] [CrossRef]
- Asensio-Lozano, J.; Van der Voort, G. The Al-Si Phase Diagram; Technical Note; Buehler, a Division of Illinois Tool Works: Waukegan Road Lake Bluff, IL, USA, 2015; Volume 5, p. 1. [Google Scholar]
- Castillo-Hernande, G.; Yasseri, M.; Klobes, B.; Ayachia, S.; Müller, E.; de Boor, J. Room and high temperature mechanical properties of Mg2Si, Mg2Sn and their solid solutions. J. Alloy. Compd. 2020, 845, 156205. [Google Scholar] [CrossRef]
- Gruzlesky, J.E. Segregation phenomena: In Microstructure Development during Metalcasting; American Foundy Society Inc.: Schaumburg, IL, USA, 2000; pp. 117–131. [Google Scholar]
- Kliauga, A.M.; Vieira, E.A.; Ferrante, M. The influence of impurity level and tin addition on the ageing heat treatment of the 356 class alloy. Mater. Sci. Eng. 2008, 480, 5–16. [Google Scholar] [CrossRef]
- Zajac, S.; Hutchinson, B.; Johansson, A.; Gullman, L.O. Microstructure control and extrudability of Al-Mg-Si alloys microalloyed with manganese. Mater. Sci. Technol. 1994, 10, 323–333. [Google Scholar] [CrossRef]
- AlMgSi Alloys. Total Materia, The World’s Most Comprehensive Materials Database. Available online: https://www.totalmateria.com/page.aspx?ID=Home&LN=EN (accessed on 16 April 2022).
- Kenyon, M.; Robson, J.; Fellowes, J.; Liang, Z. Effect of Dispersoids on the Microstructure Evolution in Al-Mg-Si Alloys; Advance Engineering Materia; lWILEY-VCH Verlag GmbH & Co.: Weinheim, Germany, 2019; Volume 1800494, pp. 1–7. [Google Scholar]
- Ostermann, F. Andungstechnologie Aluminium; Springer: Berlin, Germany, 2014. [Google Scholar]
- Zainon, F.; Ahmad, K.R.; Daud, R. Effect of intermetallic phase on microstructure and mechanical properties of AA332/Mg2Si(p) composite. AIP Conf. Proc. 2017, 1835, 020043. [Google Scholar] [CrossRef]
- Prawoto, Y.; Martin-Fanone, M.; Shahedi, S.; Ismail, M.S.; Nik, W.S.W. Computational approach using Johnson–Cook model on dual phase steel. Comput. Mater. Sci. 2012, 54, 48–55. [Google Scholar] [CrossRef]
- Johnson, G.; Cook, W. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Johnson, G.; Cook, W. Fracture Characteristics of Three Metals Subjected to Various Strains, Strain Rates, Temperatures and Pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Prawoto, Y. Designing steel microstructure based on fracture mechanics approach. Mater. Sci. Eng. A 2009, 507, 74–86. [Google Scholar] [CrossRef]
- Prawoto, Y.; Idris, R.; Kamsah, N.; Tamin, N. Two-dimensional modeling to compute plastic zone in front of compact tension sample of a multiphase material. Comput. Mater. Sci. 2009, 47, 482–490. [Google Scholar] [CrossRef]
- Chen, A.; Ruan, H.H.; Wang, J.; Chan, H.L.; Li, Q.; Lu, J. The influence of strain rate on the microstructure transition of 304 stainless steel. Acta Mater. 2011, 59, 3697–3709. [Google Scholar] [CrossRef]
- Lee, W.-S.; Lin, C.-F. Impact properties and microstructure evolution of 304L stainless steel. Mater. Sci. Eng. 2001, 308, 124–135. [Google Scholar] [CrossRef]
- Sen, I.; Amankwah, E.; Kumar, N.S.; Fleury, E.; Oh-ishi, K.; Hono, K.; Ramamurty, U. Microstructure and mechanical properties of annealed SUS 304H austenitic stainless steel with copper. Mater. Sci. Eng. 2011, 528, 4491–4499. [Google Scholar] [CrossRef]
- Salahinejad, E.; Amini, R.; Hadianfard, M. Structural evolution during mechanical alloying of stainless steels under nitrogen. Powder Technol. 2012, 215, 247–253. [Google Scholar] [CrossRef]
- Martin, M.; Weber, S.; Theisen, W.; Michler, T.; Naumann, J. Development of a stable high-aluminum austenitic stainless steel for hydrogen applications. Int. J. Hydrog. Energy 2011, 36, 15888–15898. [Google Scholar] [CrossRef]
- Fatahalla, A.; Abu Elezz, N.A.; Semeida, M. Experimental characterization of a Si–Mo–Cr ductile cast iron. Mater. Sci. Eng. 2009, 504, 81–89. [Google Scholar] [CrossRef]
- Wang, Y.D.; Tang, H.B.; Fang, Y.L.; Wang, H.M. Effect of heat treatment on microstructure and mechanical properties of laser melting deposited 1Cr12Ni2WMoVNb steel, Mater. Sci. Eng. A 2010, 528, 474–479. [Google Scholar] [CrossRef]
- Isfahany, A.N.; Saghafian, H.; Borhan, G. The effect of heat treatment on mechanical properties and corrosion behavior of AISI420 martensitic stainless steel. J. Alloy. Compd. 2011, 509, 3931–3936. [Google Scholar] [CrossRef]
- Szabo, P.J. Effect of partial recrystallization on the grain size and grain boundary structure of austenitic steel. Mater. Charact. 2012, 66, 99–103. [Google Scholar] [CrossRef]
- Gavriljuk, V.; Berns, H.; Escher, C.; Glavatskaya, N.I.; Sozinov, A.; Petrov, Y.N. Grain boundary strengthening in austenitic nitrogen steels. Mater. Sci. Eng. A 1999, 271, 14–21. [Google Scholar] [CrossRef]
- Mishin, O.; Gertsman, V.Y.; Alexandrov, I.V.; Valiev, R.Z. Grain boundary character distributions and mechanical properties of 304 stainless steel1, Mater. Sci. Eng. A 1996, 212, 281–283. [Google Scholar] [CrossRef]
- Sauzay, M. Modelling of the evolution of micro-grain misorientations during creep of tempered martensite ferritic steels. Mater. Sci. Eng. A 2009, 74–80, 510–511. [Google Scholar]
- Woo, N.S. Assessment of damage and life prediction of austenitic stainless steel under high temperature creep–fatigue interaction condition. Mater. Sci. Eng. A 2002, 322, 64–72. [Google Scholar]
- Chen, B.; Flewitt, P.E.J.; Smith, D.J.; Jones, C.P. An improved method to identify grain boundary creep cavitation in 316H austenitic stainless steel. Ultramicroscopy 2011, 111, 309–313. [Google Scholar] [CrossRef]
- Spigarelli, S.; Cabibbo, M.; Evangelista, E. Analysis of the creep strength of a low-carbon AISI 304 steel with low-Σ grain boundaries, Mater. Sci. Eng. A 2003, 352, 93–99. [Google Scholar] [CrossRef]
- Lo, K.; Shek, C.; Lai, J. Stainless steels: An introduction and their recent developments. Mater. Sci. Eng. R Rep. 2009, 65, 39–104. [Google Scholar] [CrossRef]
- Bugat, S.; Besson, J.; Pineau, A. Micromechanical modeling of the behavior of duplex stainless steel. Comput. Mater. Sci. 1999, 16, 158–166. [Google Scholar] [CrossRef]
- Alvarez-Armas, I.; Marinelli, M.C.; Malarrı, J.A.; Degallaix, S.; Armas, A.F. Microstructure associated with crack initiation during low-cycle fatigue in a low nitrogen duplex stainless steel. Int. J. Fatigue 2007, 29, 758–764. [Google Scholar] [CrossRef]
- Iacoviello, F. Microstructure influence on fatigue crack propagation in sintered stainless steels. Int. J. Fatigue 2005, 27, 155–163. [Google Scholar] [CrossRef]
- Das, A.; Tarafder, S. Experimental investigation on martensitic transformation and fracture morphologies of austenitic stainless steel, Int. J. Plasticity 2009, 25, 2222–2247. [Google Scholar] [CrossRef]
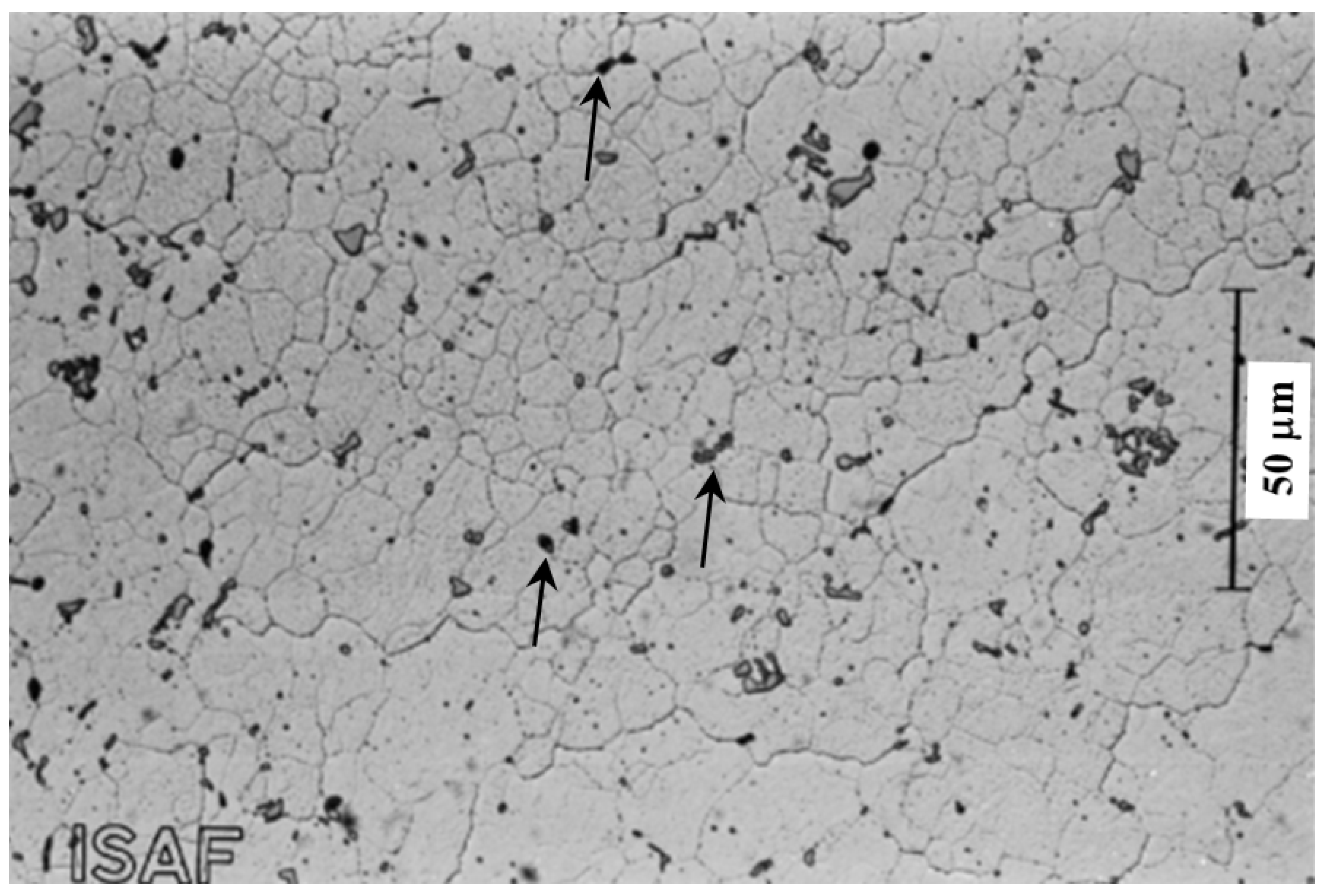


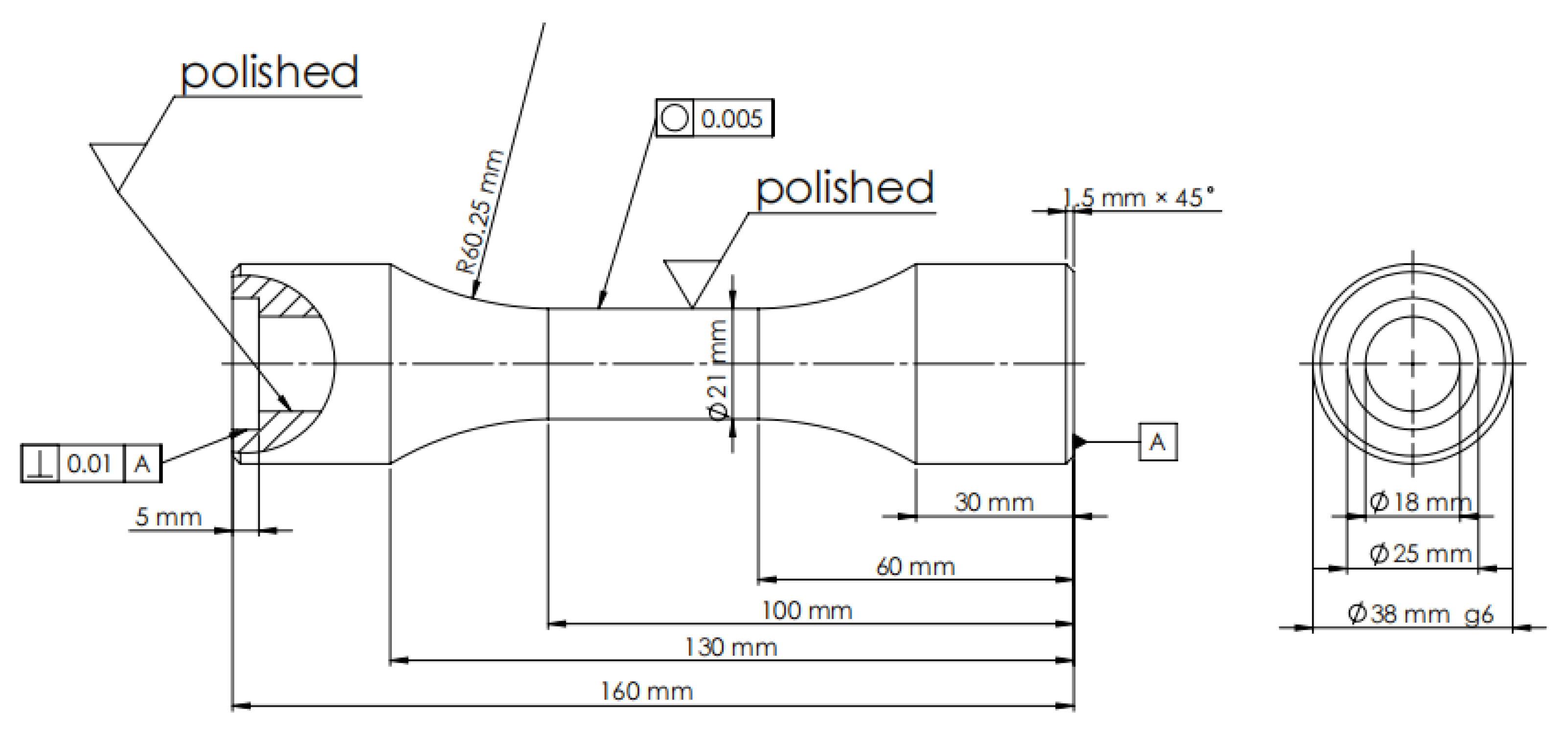

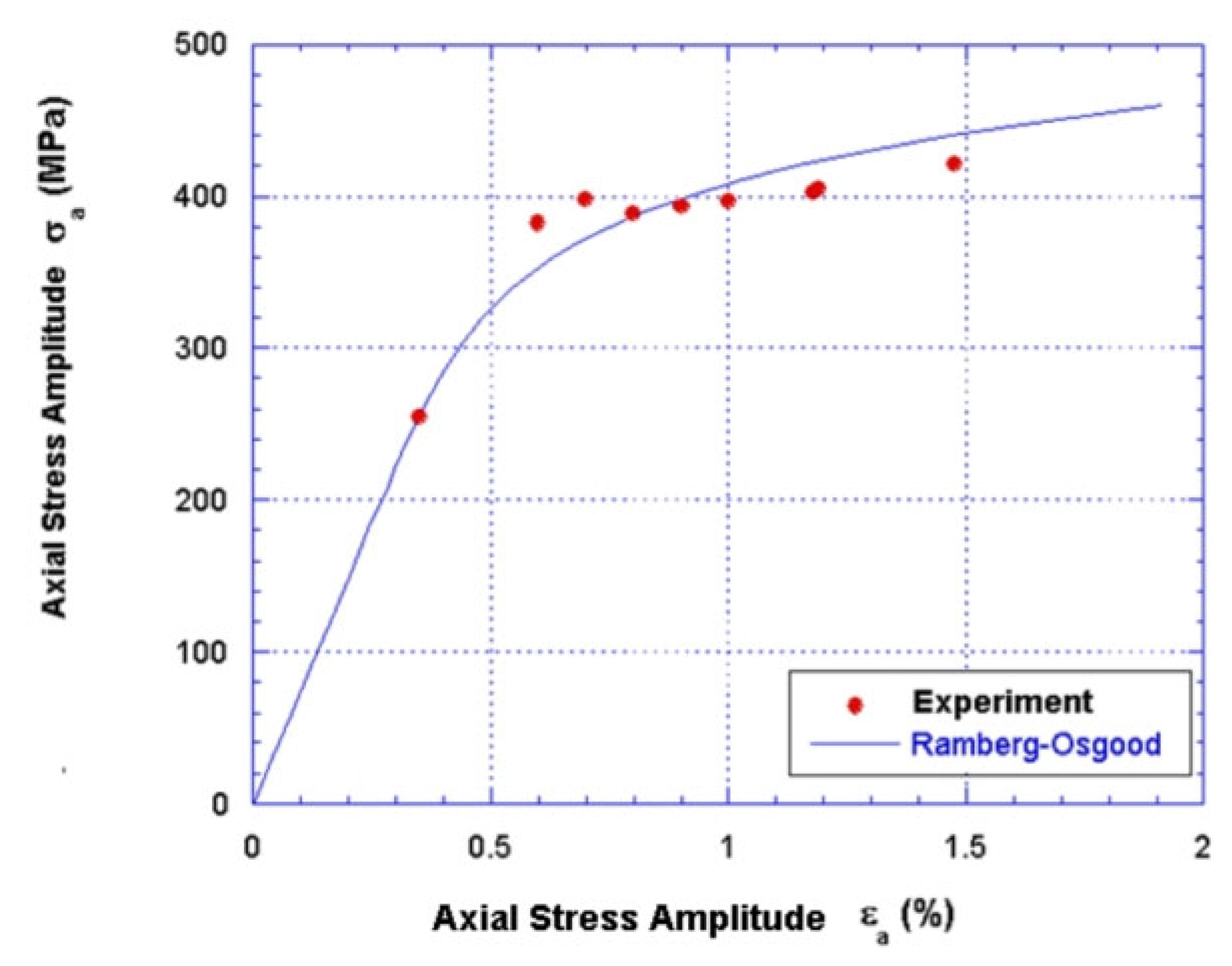
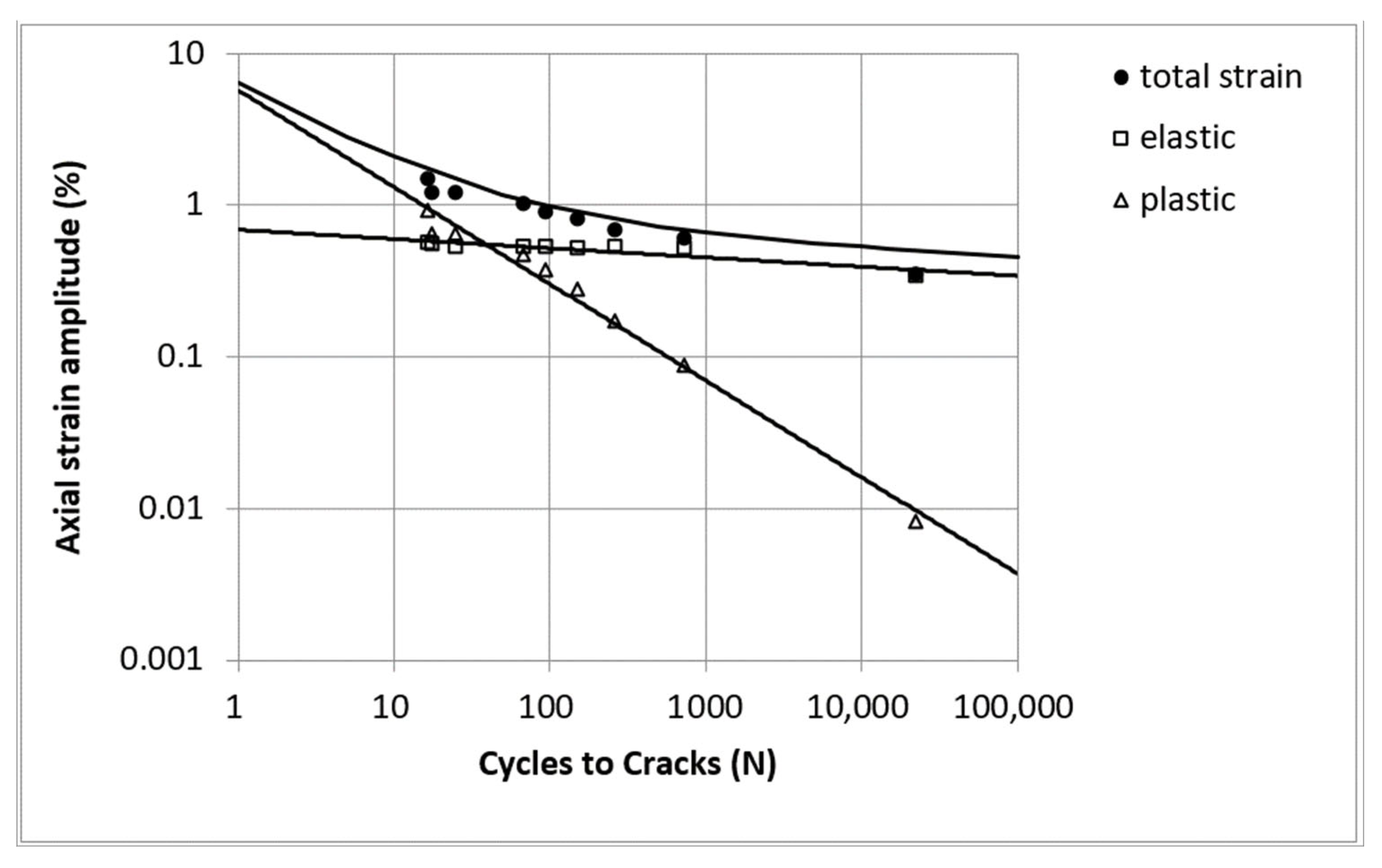



| Element | % Weight | Element | % Weight |
|---|---|---|---|
| Si | 0.47 | Cr | 0.88 |
| Fe | 1.11 | Zn | 0.01 |
| Cu | 0.36 | Ti | 0.10 |
| Mn | 0.07 | Pb | 0.01 |
| Mg | 0.74 | Al | 92.72 |
| σu (MPa) | σ0.2% (MPa) | A5 (%) | Z (%) | E (MPa) |
|---|---|---|---|---|
| 437 | 420 | 12.2 | 37.3 | 86,000 |
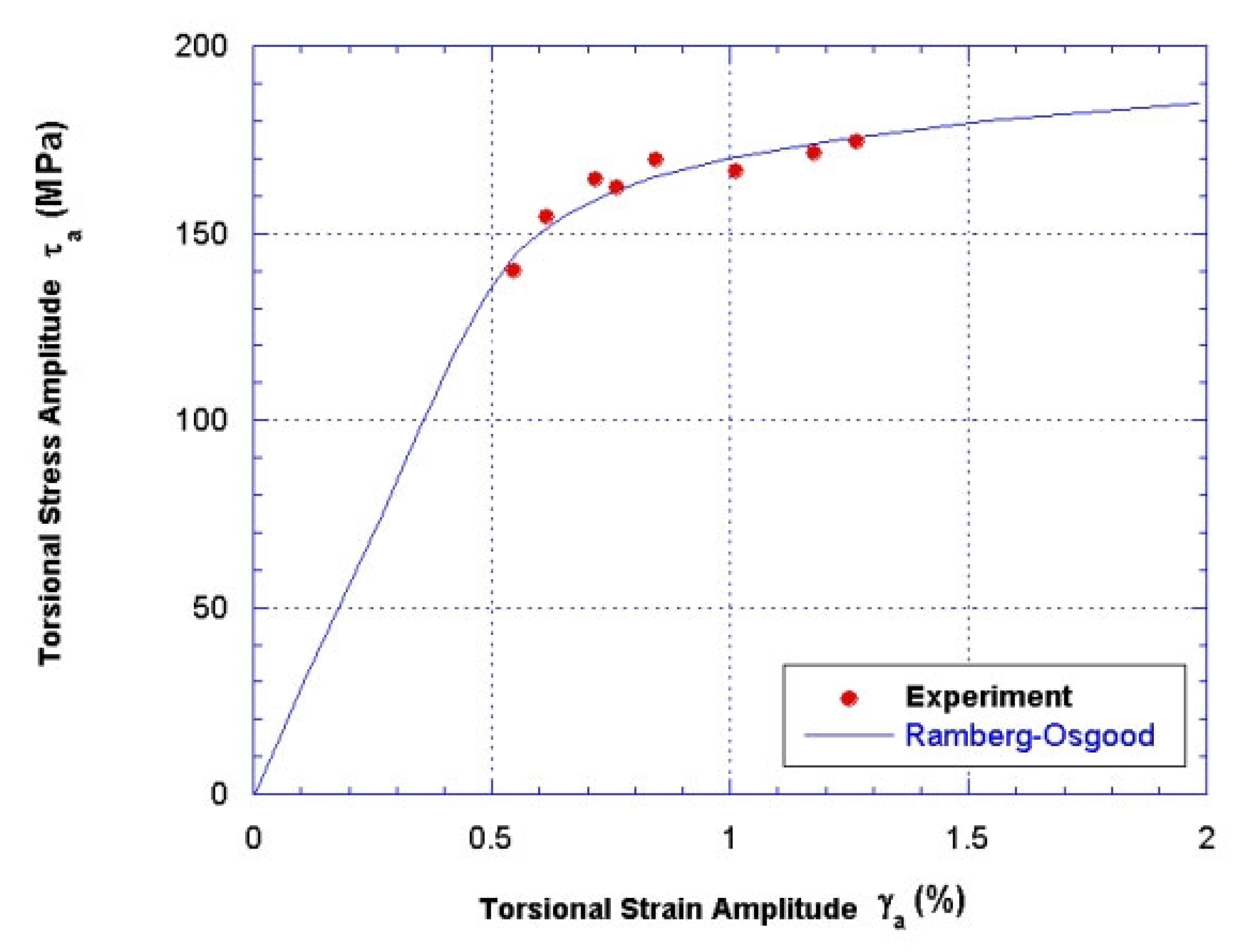
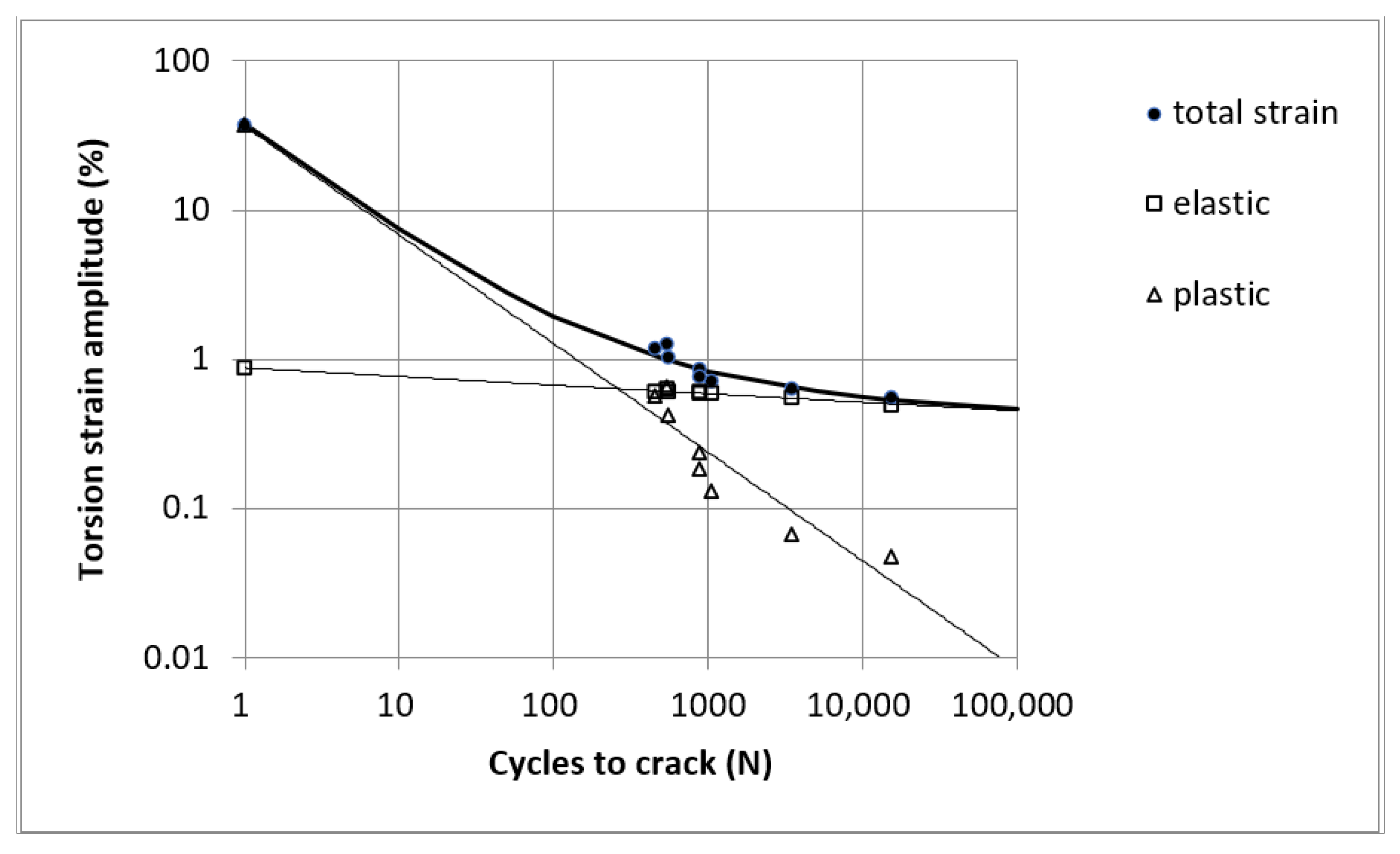
| Parameter | Tension Fatigue Testing | Torsion Fatigue Testing |
|---|---|---|
| Modulus E | 74,499 MPa | - |
| Modulus G | - | 28,822 MPa |
| ε′f | 0.0967 | - |
| γ′f | - | 2.204 |
| σ′f | 577.560 | - |
| τ′f | - | 263.040 |
| bσ or bγ | −0.074 | −0.062 |
| bσ or bγ | −0.655 | −0.894 |
| 0.113 | 0.069 | |
| 752.130 | 249.130 |
| Name of Constituent | Modulus GPa | Poisson’s Ratio | Failure Condition | Main Characteristics Related to Modeling | Ref. |
|---|---|---|---|---|---|
| Al matrix | 68.0 | 0.30 | Johnson–Cook | This can usually be model with elastoplastic | [25] |
| β-Mg2Si | 105.0 | 0.29 | Mises | Disrupt the homogeneity, brittle cracking failure | [26,27] |
| Sub GB | 66.5 | 0.30 | Johnson–Cook | Atomic mismatch stronger than the matrix | [10] |
| GB | 67.0 | 0.29 | Johnson–Cook | Similar with low angle with even higher UTS | [28,29,30] |
| Eutectic Mg2Si | 105.0 | 0.29 | Mises | segregation around the grain boundary also called coarse Mg2Si | [31] |
| β-Al5FeSi | 150.0 | 0.28 | Max strain | Disrupt the homogeneity, brittle cracking failure | [15,32] |
| π-FeMg3Si6Al8 | 43.0 | 0.27 | Mises | - | [20] |
| AlCr | 111.161 | 0.27 | Strain energy | - | [18] |
| Si | 112.0 | 0.28 | Strain energy | - | [24] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suhartono, H.A.; Kirman, K.; Prawoto, Y. On the Influence of the Initial Shear Damage to the Cyclic Deformation and Damage Mechanism. Metals 2022, 12, 1072. https://doi.org/10.3390/met12071072
Suhartono HA, Kirman K, Prawoto Y. On the Influence of the Initial Shear Damage to the Cyclic Deformation and Damage Mechanism. Metals. 2022; 12(7):1072. https://doi.org/10.3390/met12071072
Chicago/Turabian StyleSuhartono, Hermawan Agus, Kirman Kirman, and Yunan Prawoto. 2022. "On the Influence of the Initial Shear Damage to the Cyclic Deformation and Damage Mechanism" Metals 12, no. 7: 1072. https://doi.org/10.3390/met12071072
APA StyleSuhartono, H. A., Kirman, K., & Prawoto, Y. (2022). On the Influence of the Initial Shear Damage to the Cyclic Deformation and Damage Mechanism. Metals, 12(7), 1072. https://doi.org/10.3390/met12071072







