Abstract
The columnar-to-equiaxed transition (CET) is commonly observed in laser welds. It is able to prevent the growth of large columnar grains and consequently improve the mechanical properties of welded joints. In this paper, the CET behaviors at different locations in the laser weld of an Al–Mg alloy are observed experimentally and studied systematically. In order to describe the dynamic CET behaviors, an integrated phase-field (PF) model coupled with transient thermal conditions and a Gaussian heterogeneous nucleation model is developed. Investigations on columnar growth under steady conditions are performed first. In particular, the effects of thermal conditions, i.e., solidification rate and temperature gradient, on the constitutionally undercooled degree and region ahead of the solidification front are quantitatively studied. In a laser weld, it is found that the CET behaviors vary significantly along the thickness direction. Our PF simulation results indicate that the CET depends strongly on the locally transient thermal conditions in the fusion zone. The transient thermal conditions affect CET behaviors by dynamically adjusting the constitutionally undercooled degree and region during the solidification process. The predicted CET behaviors under transient conditions exhibit reasonably good agreements with corresponding experimental results.
1. Introduction
Laser welding has been employed extensively in many fields of the manufacturing industry due to the advantages of high power intensity, high penetration, narrow heat-effected zone, and high productivity. The quality of weldments is primarily dependent on the solidification behavior and resulting microstructures [1]. A significant phenomenon that can be observed in an extensive range of solidification processes, especially laser welding, is the columnar-to-equiaxed transition (CET) [2]. The CET could be characterized by a morphological transition of the solidifying phase microstructure from columnar domains to equiaxed dendritic grains [3]. Generally, large columnar grains cause anisotropic mechanical properties of the weld and lead to the propagation of solidification cracks [4]. Meanwhile, the plastic deformation of the columnar grains is extremely difficult due to this structure anisotropy [5]. Consequently, it is of significance to understand CET behaviors in order to prevent columnar grain growth in laser welding.
The CET has been studied for many years, and several theoretical models [6,7,8,9,10] have been developed. The first theoretical model for predicting the CET was proposed by Hunt in 1984 [6]. It is assumed that CET occurs when the advance of the columnar front is blocked by equiaxed grains nucleated in the constitutionally undercooled region ahead of columnar dendrites. Hunt’s model indicates that the CET is primarily determined by the growth velocity of the solidification front, applied temperature gradient in the melt, the nucleation undercooling, and the number density of equiaxed grains. Several further efforts have been made to extend and improve this model by many researchers [7,8,9,10]. Particularly, Gäumann, Trivedi, and Kurz (GTK) modified Hunt’s model by including the non-equilibrium effects, thus extending its application to rapid solidification [7]. Both Hunt’s model and the GTK model have obtained almost the same qualitative behavior, but significant quantitative differences [7]. The thermal gradient is constant during the progressive CET as proved by some numerical simulations performed and it can be concluded that the stationary state is ensured during the CET occurrence [11]. A simple conclusion is that the transition occurs more easily when an alloy has a high solute concentration, high nucleation density, low thermal gradient G, and high solidification rate R. Furthermore, based on Hunt’s model, Schempp et al. [4] developed an analytical approach to model the transition from columnar-to-equiaxed grain growth for gas tungsten arc welding of the aluminum alloys. This model allows the qualitative prediction of critical G and R values at which the CET happens.
With significant advances in computational power and numerical simulation techniques, direct simulation of the CET is attainable. The phase-field (PF) model has recently emerged as a powerful computational tool to describe the microstructural pattern formation during solidification. Unique to the PF model is the diffusion interface concept. The interface in the PF model is merely an inhomogeneous localization of the state variable called “phase field”, instead of a specific entity to be described separately [12]. This avoids explicit tracking of phase boundaries. Therefore, the PF model is readily able to handle complex topological changes of dendritic growth. So far, the PF model has been successfully applied to the solidification process for pure material [13], binary [14,15], multi-component [16,17], and multiphase [18,19] alloy systems. In particular, Beckermann et al. [20] performed a parametric study to investigate the applied temperature gradient, solidification rate, the preset seed spacing, nucleation undercooling, and the anisotropy strength on the CET using the PF model. This work offered us better insight into the CET during directional solidification. However, only a few studies have been reported in the literature where the phase-field model is used to simulate the dendritic growth and the CET in the welding pool. Farzadi et al. [21] investigated the solidification microstructure at different locations along the fusion line during gas tungsten arc welding of Al-3 wt.% Cu alloy using the PF model. A macroscopic heat transfer and fluid flow model was developed to assess the solidification parameters, i.e., G and R. Zheng et al. [22] investigated the microstructure evolution near the fusion line during solidification of gas tungsten arc welding (GTAW) pool for aluminum alloy 2A14. The time-dependent equations for temperature gradient G(t) and solidification rate R(t) are employed considering the transient thermal conditions in the welding pool. Wang et al. [23] extended the above model to simulate columnar dendrite growth in the laser welding pool of aluminum alloy 2024 under transient thermal conditions. By incorporating the misorientation angle into the PF equations, Yu et al. [24] studied the effect of misorientation angle between the preferred crystalline orientation and the temperature gradient direction on solidification morphologies during GTAW of Al-4 wt.% Cu. These studies demonstrated the outstanding capacity of the PF model for simulating microstructure evolution in the welding pool. However, most of the previous studies are limited to the simulation of the columnar growing stage near the fusion boundary, not involving the CET. Since the CET has significant influences on the mechanical performance of laser welds, it is of importance to understand CET behaviors in the fusion zone during the laser welding process.
The objective of this study is to investigate the effects of transient thermal conditions on CET behaviors in laser welding using the PF model. Particularly, we focus on CET behaviors at different locations in the fusion zone of the laser weld. The rest of the paper is summarized as follows: The laser welding experiments are conducted in Section 2. The numerical models, including heat transfer model, determination of transient thermal conditions, PF model, and nucleation model, are demonstrated in Section 3. Results and discussions consisting of experimental results and PF simulations are described in Section 4 and finally, conclusions are given in Section 5.
2. Experimental Method
Deep penetration laser welding experiments of 4 mm thick Al–Mg alloy (see Table 1) were performed using a continuous wave fiber laser (IPG YLR-4000, IPG Photonics, Auburn, MA, USA) with a maximum power of 4000 W. The wavelength was 1.07 μm and the beam parameter product (BPP) was 6.3 mm•mrad. The spot diameter was focused into approximately 0.3 mm by laser optics with a focal distance of 250 mm. The welding head, equipped with coaxial air blowing protection device, was attached to a welding robot (ABB IRC5 M2004, Asea Brown Boveri, Zurich, Switzerland). Before welding, the base metal plates were machined to 200 mm × 100 mm × 4 mm and cleaned carefully by acetone to remove possible oil stains and oxide films. During laser welding, a high-speed CMOS camera (Phantom v611, Vision Research, Wayne, NJ, USA) was used to monitor the evolution of the welding pool with a photographing speed of 2000 frames per second (fps). After welding, the welds were cut, ground, polished, and etched by Keller’s reagent (2.5 mL HNO3 + 1.5 mL HCl + 1.0 mL HF + 95 mL H2O, Sinopharm, Shanghai, China). Then the weld dimensions were measured by a stereoscopic microscope and microstructure was observed using a metallographic microscope. In this study, a laser welding experiment with laser power 3500 W, welding speed 20 mm/s, and defocusing distance −2 mm was carried out to investigate the microstructure evolution.

Table 1.
Composition of Al–Mg alloy used in this study (wt. %).
3. Numerical Modeling
The relationship between the macroscale heat transfer model and the micro-scale phase-field model is shown in Figure 1. The macro-scale model is used to obtain the temperature and dimensions (such as length a and width b) of the molten pool. Then, the transient temperature gradient and solidification rate are calculated, which are input into the micro-scale phase-field model for simulating the microstructure evolution.
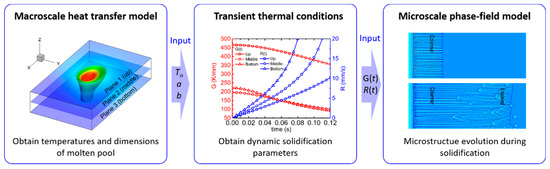
Figure 1.
Flowchart illustrating the relationship between macroscale model and micro-scale model.
3.1. Transient Thermal Conditions
In order to obtain the transient thermal conditions during laser welding, a three-dimensional transient heat transfer model is used to predict the thermal field. The governing equations and boundary conditions are available in References [25,26,27]. A moving hybrid heat source consisting of a double ellipsoid heat source and a linear attenuation peak Gaussian heat source was employed in this study, and its formulas can be found in our previous papers [26,28].
During the laser welding process, the temperature gradient and solidification rate at the solidification front vary as the welding pool moves forward with time proceeding, which is called the transient conditions by Wei et al. [22,29,30]. It is assumed that the shape of the welding pool remains unchanged under steady-state welding conditions. It is significantly supported by the appearance of the same state during the progressive CET occurrence in the static steel ingot as it was proved by the numerical simulation of heat transfer [11]. In reality, the heat flow is three-dimensional. However, we neglect the heat flux in the z-direction for simplicity. It should be noted that this will affect the model’s prediction accuracy, but the solidification mode variation can be revealed to a certain extent. This assumption is widely used when discussing the solidification mode variation in fusion welding [3,23]. The shape of all the cross-sections of the welding pool perpendicular to the z-axis, i.e., thickness direction, can be assumed as a connection of two ellipsoids as shown in Figure 2. The red solid line represents the shape of the welding pool in cross Section 1 at time t, and the red dotted line represents the shape at time t + dt. The average temperature gradient of each point at the fusion boundary on a given cross-section is given as [21]:
where is the temperature at the center of the welding pool (center of the back half of the ellipsoid), is the liquidus temperature. r is the distance between the location of the center and the corresponding point at the fusion boundary. The steady-state solidification rate at all locations along the fusion boundary is related to welding speed, which is defined as [3]:
where is welding speed, and is the angle between the welding direction and the normal of the fusion boundary. The back half ellipsoid is considered to investigate the solidification process. At the given cross-section of the the length and width of the behind half ellipsoid are given by a and b. According to the ellipsoid equation and the point’s coordinate, the transient temperature gradient (Equation (1)) and solidification rate (Equation (2)) can be rewritten as:
where is the local temperature at the origin of coordinates O. In this study, parameters such as the temperature , length a, and width b are determined by the three-dimensional heat transfer computation, which is validated by the experiments. It should be noted that , a, and b are variable for different cross-sections, indicating different solidification conditions at these cross-sections.
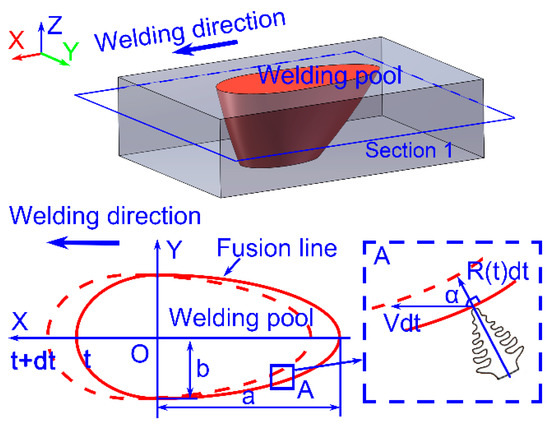
Figure 2.
Schematic of the macroscopic welding pool (upper), and determination of the temperature gradient and solidification rate along the fusion boundary of welding pool on cross Section 1 (below).
3.2. Phase-Field Model
In this study, we employed a quantitative field-phase model developed originally by Ohno and Matsuura [12] for the isothermal solidification of a dilute binary alloy and further modified it for directional solidification [31]. In this model, the phase-field variable, , is defined as +1 for solids and −1 for liquids. According to the mixture rule, the local concentration, , is defined as , where and are the solute concentrations in solid and liquid phases, respectively. In a dilute alloy, and satisfy the relation , where is the partition coefficient, according to the condition of equal chemical potential proposed by Kim, Kim, and Suzuki (the KKS model). Further, the dimensionless supersaturation, , is defined as:
where and are the equilibrium concentrations of the liquid and solid at , respectively. During directional solidification, the temperature, , is assumed to follow the frozen temperature approximation after neglecting the effect of latent heat and convection [31,32]:
where is the temperature gradient along the y-axis, is the solidification rate, and is the reference temperature. In particular, considering transient conditions of welding pool, the temperature can be expressed as:
By taking the interface anisotropy into account, the time evolution of is given by:
where is the relaxation time. is the interface thickness parameter. is a dimensionless parameter associated with the thermodynamic driving force. The numerical constants and are given by and , respectively. is the chemical capillary length defined as with the Gibbs–Thomson coefficient , liquid slope , and initial alloy concentration . and are interpolating functions associated with the double-well potential and the free energy of the bulk, respectively. represents the crystalline anisotropy and is a function of growth orientation. is expressed as:
where is the anisotropy parameter and the coordinates are the material coordinates aligned to . The following relation is used for the coordinate transformation between and :
Here, is the angle between and the x-coordinate for the ith grain. is the nondimensional undercooling corresponding to the frozen temperature approximation and is given by:
where is the thermal length and is given by . The time evolution of is described by:
where and are the solutal diffusivity in liquid and solid, respectively. Note that the anomalously large solute trapping effect caused by the interface thickness is canceled by introducing a phenomenological “antitrapping current”. is a fluctuating current of the Gaussian random number with the variance of for generating higher-order branching of dendrites, where is the constant noise magnitude depending on interface thickness, is the time increment, is the lattice size, and is the dimension.
When it comes to polycrystalline solidification, two main approaches, i.e., the multiphase-field method [33,34] and the Kobayashi, Warren, and Carter-type [35,36] model, have been proposed. However, the computational efficiency is lower than that for single-phase-field simulations [31]. Our study is focused on CET behavior. This is unaffected by the dynamics of the physical triple junction between the two grains and the liquid, which is deep inside the mushy zone. Therefore, we employed a simple method that is able to simulate the growth of multiple dendrites growing in various directions using the single-phase-field method [31]. In this method, an additional parameter for describing crystal orientation, , is introduced. The parameter takes a finite value only when , and the value changes in keeping with the evolution of .
3.3. Nucleation Model
For the CET, several different mechanisms, such as dendrite fragmentation, grain detachment, and heterogeneous nucleation have been proposed to explain the formation of equiaxed grains ahead of the columnar front [3,37,38,39,40]. However, the predominant mechanism is still unclear due to the lack of conclusive evidence. Since several studies [3,41,42] have shown that the addition of foreign inoculants can promote CET, it is believed that heterogeneous nucleation is an important contributing factor for the formation of equiaxed grain. Therefore, we consider heterogeneous nucleation as the sole mechanism of equiaxed grain formation. In particular, the Gaussian nucleation distribution model proposed by Thevoz et al. [43] is employed in this study. Because of the solute built-up ahead of the solid–liquid interface, a solutally undercooled region forms ahead of the growth front. In the present model, the constitutional undercooling is defined as , where is the equilibrium liquidus temperature corresponding to local solute concentration in the melt, and is the local temperature. The nucleation of equiaxed grains is determined by the constitutional undercooling stochastically. As for the Gaussian nucleation distribution model, it is supposed that, at each undercooling , a certain density of nucleation sites become active regardless of the time. Therefore, the nucleation density increase, , can relate to the increased effective undercooling, , through a continuous Gaussian distribution. The density of nuclei for a given is thus given by:
with
where is the maximum density of nuclei given by the integral of the distribution, is the mean nucleation undercooling corresponding to the maximum of the distribution, and is the standard deviation of the distribution. The above nucleation parameters control the CET during solidification. However, it is difficult to determine the exact value of these parameters. A detailed investigation on how these parameters affect the CET has been performed in references [20,44]. In the present study, we set nmax = 1012 m−3, = 6.0 K, and = 0.5 K, which are typically used for aluminum alloys during welding [4,40,45]. The detailed nucleation procedure is as follows. Firstly, at every time step, for every mesh in the undercooled liquid region, the nucleation probability P is calculated with P = n(ΔT)* Δx3, where n(ΔT) is the density of nuclei for a given ΔT (i.e., local constitutional undercooling) and dx is the mesh size. Then the calculated value of P for each mesh in the undercooled region is compared with a random number r between 0 and 1. A nucleation event is then triggered whenever r < P. When this happens, a circular grain with a diameter equal to 5Δx and random orientation ranging from 0 to 2π is seeded with its center located on the corresponding mesh.
3.4. Implementation
As for the macroscopic heat transfer calculation, the computational domain was set as 20 mm in length, 12 mm in width, and 4 mm in height. In total, 960,000 uniform cells were used with cell dimensions of 0.1 mm × 0.1 mm × 0.1 mm. The governing and boundary equations are solved using the successive over-relaxation (SOR) iterative scheme. The composition of the base metal, which can be assumed as Al-1.3 wt.% Mg binary alloy, is presented in Table 1, and the data used for the calculation are listed in Table 2. It should be noted that the equilibrium partition coefficient was adopted in this work since the growth rate is only ~10 mm/s, much lower than the speed of diffusion at the solid–liquid interface (several m/s) [46,47].

Table 2.
Physical parameters of the Al–Mg alloy prepared for the heat transfer calculation and PF simulations [23,48,49].
The PF simulations were performed on a 1600 × 4200 foursquare grid. The normal finite-differential method was used to solve the governing equations. The time differentiations were discretized by the first-order forward difference method. The bottom boundary was initialized as solid-phase with and . The top boundary kept unchangeable with and . The left and right boundary conditions were set to the cyclic conditions for all variables. In order to reduce the simulation cost, the moving-frame algorithm was used [32]. At the beginning of the simulation, the temperature was calculated through Equation (7). After a few steps, we switched to the moving-framework scheme and guaranteed the distance from the tip location to the top boundary to be 600Δx. The grid size is taken as 0.8 W, which has been tested to meet the convergence requirement. The coupling parameter λ is set as 11.9, leading to . In order to consider the epitaxial solidification in the fusion zone, it is assumed that the initial state of grain is planar and its orientation is perpendicular to the fusion boundary. The effect of crystallographic orientation of the columnar dendrites upon CET has been investigated by Dong et al. [44]. Their simulation results indicated that this effect was not significant. Besides, we assume that the normal of the solidification front is always parallel to the temperature gradient.
The macroscopic heat transfer calculation was implemented on a workstation with an Intel Xeon (R) CPU E5-2697 v3 @ 2.60 GHz (Intel, Clara, CA, USA). In total, six CPU cores were used to accelerate the computation. As for PF simulations, parallel computations using graphic process units (GPU) with the computer unified device architecture (CUDA) programing language were employed. The advanced GPU shared memory was used to deal with the cache memory. We ran each simulation on one individual NVIDIA Tesla K80 GPU. The calculations were executed on the GPU nodes of the Tianhe-2 supercomputer (Tianhe-2, Guangzhou, China) at the National Supercomputer Center in Guangzhou (NSCC-GZ).
4. Results and Discussion
4.1. Microstructural Observations
In order to investigate the CET phenomenon in laser weld, a laser welding experiment with laser power 3500 W, welding speed 20 mm/s, and defocusing distance −2 mm was performed on 4 mm thick Al–Mg plates. Microstructures at three different locations (upper, middle, and bottom) in the weld, each corresponding to a different set of transient thermal conditions, were observed as shown in Figure 3a–d, displaying the corresponding optical microstructure of Regions I, II, and III in Figure 3a, respectively. It is well known that the solidification microstructure for a given alloy is primarily dominated by the temperature gradient G and the solidification rate R. Particularly, the ratio G/R determines the mode of solidification while the product GR governs the grain size [3]. During the welding process, G/R decreases from the fusion line to the centerline, indicating that the solidification mode may change accordingly. Figure 3a shows the optical microstructure of Region I. It can be seen that the solidification mode changes typically from planar to cellular, columnar, and equiaxed grains across the fusion zone from the left to right. The grains are shown to grow epitaxially from the fusion line and grow along the preferential-growth direction of base metal grains. Afterward, the solidification turns into the cellular mode with a very short distance away from the fusion line. Farther away from the fusion line, solidification transforms into the columnar mode, with only a part of grains surviving after the competitive growth. No obvious secondary dendrites are observed in this region. This is attributed to the small primary dendritic arm spacing due to the high solidification rate and temperature gradient. As solidification goes on, the CET occurs, and the equiaxed grains nucleate and grow, blocking off the columnar grains. Figure 3b,c show a similar microstructural variation trend as in Figure 3a. However, it is interesting that the size of columnar regions is significantly varied at different locations in the laser weld. This is mainly attributed to the distinguishing local thermal conditions, which will be discussed in detail in the following sections.

Figure 3.
(a) Three different locations, i.e., upper (Region I), middle (Region II), and bottom (Region III), in the laser weld; (b–d) optical micrograph corresponding to Regions I, II, and III, respectively.
4.2. Columnar Growth under Steady Conditions
4.2.1. Validation of Phase-Field Model
The PF model and its numerical implementation were validated by comparing with PF simulated results from Echebarria et al. [50]. In this validation, the steady-state cell shapes with narrow cell spacing were compared. The impure succinonitrile (SCN) alloy system was chosen and the parameters used in PF simulations are shown in Reference [50]. The initial conditions and boundary conditions are also given in detail in Reference [50]. Figure 4 compares our simulated results with results from Echebarria et al. [50] for the steady-state cell shape. The length is renormalized by the wavelength (λwave). As shown, our simulated results are in good agreement with previous ones. Moreover, several quantities associated with steady-state cell shapes, such as the tip radius ρ/d0, the tip undercooling Ω = 1 − ztip/lT (where z = 0 corresponds to the position of the steady-state interface), and the solute concentration in the solid in the center of the cell are compared in detail as shown in Figure 5. It should be mentioned that the formation of the tip radius is connected with the validity/satisfaction of the marginal stability criterion when the columnar cells or dendrites are formed under a steady state [38]. As for the latter, both the values directly obtained from the simulations (the value of the field u in the center of the cell) and those expected from the Gibbs–Thomson condition (, where the values of Ω and ρ are obtained from numerical PF simulations) are compared. Again, we can see our simulated results agree well with results from Echebarria et al. [50]. On the other hand, it can be seen that well convergence can be obtained for W0/d0 lower than about 50. Therefore, the coupling parameter λ = 11.9 (corresponding to W0/d0 = 13.46) used in the following simulations is small enough to provide results that are reasonably independent of the interface width.
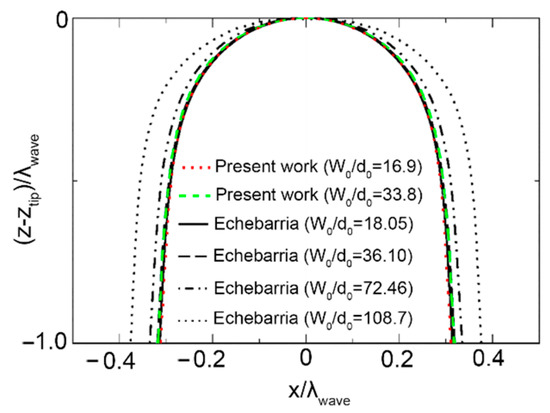
Figure 4.
Comparison of simulated results with results from Echebarria et al. [50].
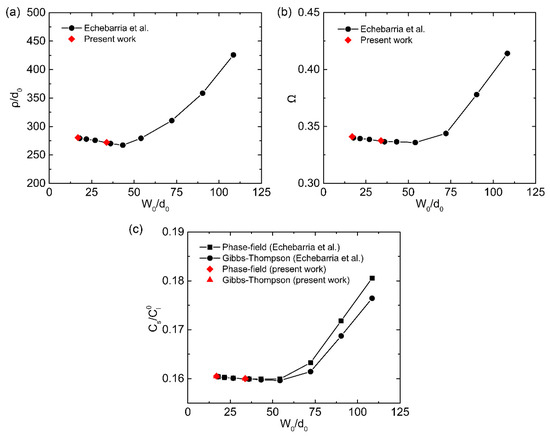
Figure 5.
Comparison of various quantities associated with steady-state cell shapes: (a) tip radius ρ, (b) dimensionless tip undercooling Ω, and (c) solid concentration in the center of the cell.
4.2.2. Columnar Growth under Steady State
Before discussing the transient thermal conditions and the CET, it is of value to examine the predictions for steady columnar growth, which can provide preliminary knowledge for investigating the CET under transient thermal conditions. In this section, we focus on the columnar growth with temperature gradient ranging from 100 K/mm to 500 K/mm and solidification rate ranging from 2 mm/s to 6 mm/s. The reason why these solidification conditions were considered is attributed to the analysis of thermal conditions during laser welding which will be discussed later. During the solidification process, the change in solute concentration can influence the undercooling distribution ahead of the solidification front, and thus affects the nucleation and growth of equiaxed grains. The solute distribution and constitutional undercooling distribution corresponding to the solidification conditions G = 300 K/mm and Vp = 3 mm/s are plotted in Figure 6a,b, respectively. Far ahead of the dendrite, the undercooling decreases linearly because of the imposed temperature field and the uniform solute concentration . At the top domain boundary, the undercooling has nearly vanished. The undercooling also approaches zero at the solid–liquid interface because it is in equilibrium (the curvature undercooling is not taken into consideration when calculating the undercooling). The largest undercoolings are present just in front of the diffusion boundary layer along the dendrite growth direction. In these regions of large undercooling, the nucleation will first occur according to the nucleation model.
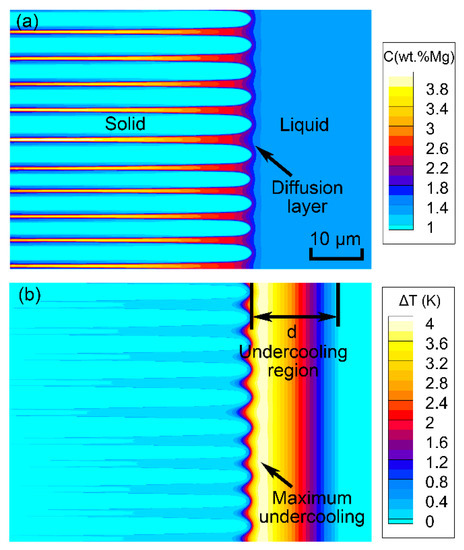
Figure 6.
Contour plot of (a) solute distribution and (b) constitutional undercooling distribution for solidification conditions G = 300 K/mm and Vp = 3 mm/s.
As for CET in a given alloy system, the nucleation events depend directly on two aspects, i.e., the constitutionally undercooled degree, and the constitutionally undercooled region [3,4,6]. In general, the constitutionally undercooled degree determines the occurrence probability of a nucleation event for a specified location in the liquid. The nucleation event would occur with a great probability only when the constitutional undercooling reaches a threshold value which is controlled by the mean nucleation undercooling and the standard deviation of the distribution . On the other hand, the constitutionally undercooled region reflects the activated sites for nucleation ahead of the solidification front. A larger undercooled region would provide more occasion for nucleation. In this study, the maximum constitutional undercooling in the liquid ahead of the solidification front was recorded to evaluate the undercooling degree during the solidification process. Figure 7a illustrates the variation of maximum undercooling at fixed solidification rate R = 3 mm/s as the temperature gradient ranges from 100 K/mm to 500 K/mm. It can be seen that the steady value of maximum undercooling decreases from approximately 4.4 K to 3.8 K as the temperature gradient changes from 100 K/mm to 500 K/mm. The difference is slight (about 0.6 K), which means that the temperature gradient has slight influences on the maximum undercooling in the liquid. Figure 7b compares the maximum undercooling in the liquid as the solidification rate varies from 2 mm/s to 6 mm/s. The steady-state maximum undercooling increases significantly from approximately 3.5 K to 7.0 K as the solidification rate changes. By comparing Figure 7a,b, it is clear that the maximum undercooling in the liquid is primarily dependent on the solidification rate rather than the temperature gradient within the parameter scope of the present study. Moreover, the constitutionally undercooled region for different solidification conditions is investigated as shown in Figure 7. The size of the undercooled region is characterized by the distance d measured from the solidification front to the isoline where the undercooling vanishes (see Figure 6b). Figure 8a shows that the undercooling region decreases obviously from about 55 μm to 10 μm with the temperature gradient increasing from 100 K/mm to 500 K/mm (Vp = 3 mm/s). By contrast, the undercooling region ascends from approximately 14 μm to 22 μm as the solidification rate increases from 2 mm/s to 6 mm/s (G = 300 K/mm) (Figure 8b). From Figure 8, it can be concluded that the temperature gradient has a greater influence on the size of the undercooled region compared with the solidification rate within the parameter range involved in this study.
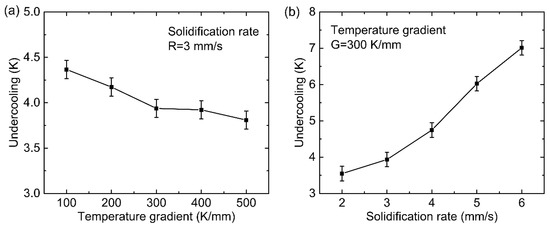
Figure 7.
Maximum undercooling in the liquid ahead of solidification front with varying (a) temperature gradients and (b) solidification rates.
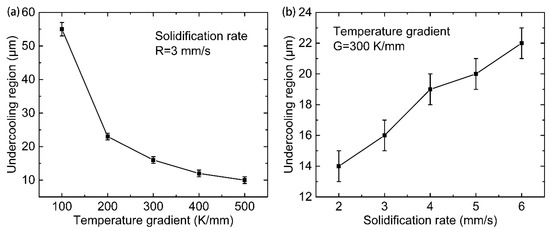
Figure 8.
Size of the constitutionally undercooled region ahead of solidification front with different (a) temperature gradients and (b) solidification rates.
4.3. CET under Transient Thermal Conditions in Laser Welding
4.3.1. Determination of Transient Thermal Conditions
In order to determine the transient thermal conditions, we conducted a simple transient heat transfer simulation, by which the stable-status laser welding pool was obtained. The simulation results were validated by comparing them with corresponding experiments. In the laser welding experiment, the laser power was 3500 W, the welding speed was 20 mm/s, and the defocused distance was −2 mm. Figure 9a shows the steady temperature contour from our numerical simulation. Figure 9b compares the fusion profiles between the experimental and simulated results. Note that the fusion profile from the simulation is extracted from the isotherm at the liquidus temperature, i.e., 926.7 K. The marked dimensions indicate a good agreement between the experimental and simulated results. The maximum error is around 4.8% at the middle of the weld, which may result from the neglect of fluid flow during laser welding. In fact, it is difficult to make the simulated and experimental results match well in the numerical simulation due to the complex physical phenomena involved in the laser welding process. Figure 9c displays the high-speed camera images of the laser welding pool with time proceeding. The red dashed line illustrates the profiles of the welding pool, which indicates that a stable-status welding pool is obtained. Furthermore, we compared the profile of the laser welding pool (at time t0) from experiments with the calculated results, as shown in Figure 9d. It can be seen that the simulated profile (isotherm 926.7 K) also agrees reasonably well with the experimental results.
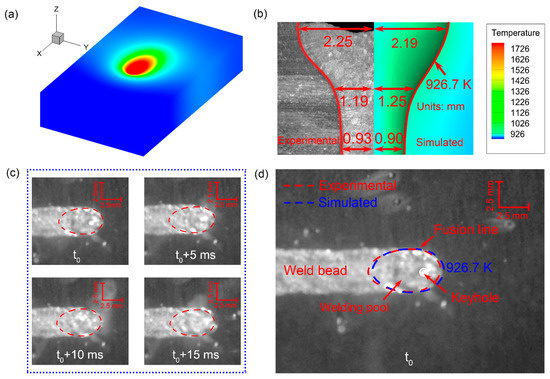
Figure 9.
(a) Temperature contour from heat transfer calculation; (b) comparison of fusion profiles between the experimental and simulated results; (c) evolution of laser welding pool with time proceeding captured by the high-speed camera; (d) comparison between the experimental results with the simulated results (here the simulated fusion profile (isotherm 926.7 K) was converted into the same scale as the high-speed camera image).
Figure 10a displays the three-dimensional shape of the simulated laser welding pool. As can be seen, both the length and width of the welding pool decrease along the thickness direction from the top to the bottom surface. Particularly, three cross-sections, i.e., planes 1, 2, and 3, are extracted from the top, middle, and bottom of the welding pool, respectively. Figure 10b–d show the temperature contour of planes 1, 2, and 3, respectively. The black solid line indicates the fusion profile of the steady welding pool, from which the length a, width b, and central temperature TO can be determined in Equations (3) and (4). Figure 11 illustrates the variation of temperature gradient G and solidification rate R as time proceeds. We can see that the temperature gradient decreases with time proceeding for all planes. The temperature gradient ranges from about 475 K/mm to 100 K/mm, and the temperature gradient of the top plane is the largest. As for the solidification rate, it can be seen that they increase rapidly from zero to more than 10 mm/s over time for all planes. Particularly, the solidification rate of the bottom plane rises most rapidly compared to that of the middle and upper planes. The difference in temperature gradient and solidification rate will lead to distinguishing transient solidification conditions and varying microstructures as we can expect.
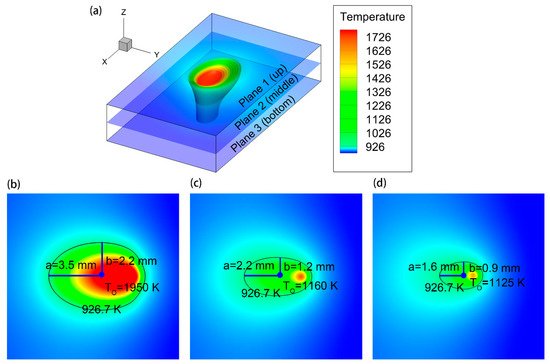
Figure 10.
(a) Three-dimensional shape of the laser welding pool from heat transfer calculation; (b) temperature contour of plane 1; (c) temperature contour of plane 2; (d) temperature contour of plane 3. From (b–d), the parameters for calculating transient thermal conditions (Equations (3) and (4)) are obtained.
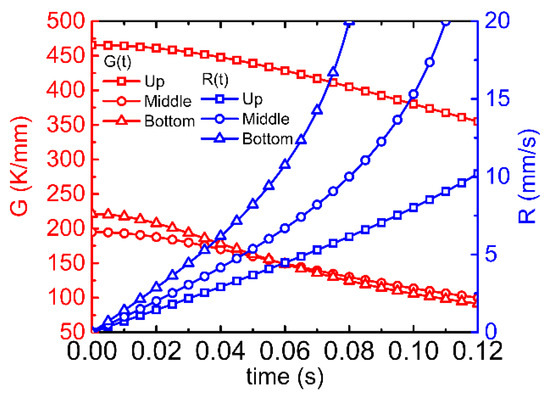
Figure 11.
Transient thermal conditions, i.e., transient temperature gradient G and transient solidification rate R, during solidification of laser welding pool calculated by Equations (3) and (4) using the parameters obtained from heat transfer simulation results.
4.3.2. Effect of Transient Thermal Conditions on CET
Generally, the solidification process in the laser welding pool is much more complicated than under steady conditions, because both the temperature gradient G and the solidification rate R are time-varying instead of constant. Therefore, a detailed investigation of the dynamic solidification process under transient thermal conditions is essential to better understand microstructure formation in laser weld. As an example, we focus on the dynamic solidification process in the middle region of laser weld, i.e., Region II in Figure 3a. The time evolution of the concentration field and relevant constitutional undercooling distribution under transient thermal conditions are displayed in Figure 12. At first, the solid–liquid interface maintains in a planar structure, with the solute rejected by solid enriched in front of the solid–liquid interface (Figure 12a). At this moment, only a small constitutionally undercooled degree and region exist ahead of the solidification front (Figure 12d). As solidification progresses, the planar interface becomes unstable and generates the columnar array after competitive growth (Figure 12b). Note that side branches are not observed due to the small primary arm spacing, which is consistent with our experimental results. Besides, the constitutionally undercooled degree and region increase simultaneously compared with those of prior time (Figure 12e). This can be explained by the increase in solidification rate and decrease in temperature gradient as discussed in the columnar growth under steady conditions in Section 4.2.2. When the constitutionally undercooled degree increases over the threshold undercooling (close to the mean nucleation undercooling ), the nucleation events would occur ahead of the columnar front and block the growth of columnar grains as shown in Figure 12c,f. Overall, we can see that the constitutionally undercooled degree and region are dynamically adjusted along with the varying thermal conditions, and consequently lead to the continuous change in solidification mode.
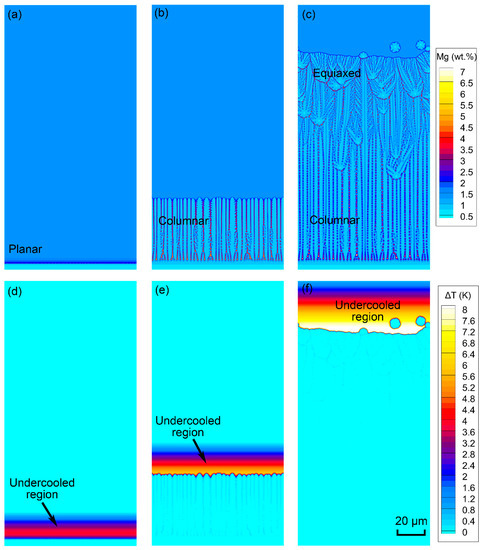
Figure 12.
Predicted concentration field and constitutional undercooling distribution under transient conditions of the middle of weld as time progresses: (a,d) 24 ms; (b,e) 45 ms; (c,f) 73 ms.
Furthermore, the CET behaviors at different locations in laser weld are investigated under transient thermal conditions using the PF model. Figure 13 illustrates the predicted microstructure at different locations of the laser weld. Particularly, the length of the columnar region was characterized and compared quantitatively with that of experimental results as shown in Figure 14. Clearly, the simulated result is in reasonably good accordance with experimental results. It is difficult to make the simulated results fully compatible with the experimental results for the following three reasons: (1) the PF simulations are in two-dimensional systems, while the experiments are actually in the full three-dimensional system; (2) the flow field may have significant influences on the microstructure evolution, but it is not considered in the present PF simulations; (3) some of the critical parameters, such as nmax and , are uncertain, leading to the imprecision of simulations. On the other hand, it must be noted that the reported length of the columnar region carries a fair amount of uncertainty in both the PF simulations and the experiments. This is mainly because the length of columnar length was measured visually and the CET appeared as a gradual transition, making it hard to define the limits of each region. Even so, it is noticeable that the length of the columnar region presents a significant downward trend from the upper region (Figure 13a) to the bottom region (Figure 13c) in the laser weld, which can be explained by the change in transient thermal conditions. In Section 4.2.2, we have demonstrated that the solidification rate R and temperature gradient G play a dominating role in the constitutionally undercooled degree and region ahead of the solidification front. Therefore, a consideration of the solidification rate and temperature gradient variation at different locations is critical here. As for the bottom region, because the solidification rate increases faster than other regions, the constitutionally undercooled degree and the size of the undercooled region increase faster than other regions. This leads to the earlier occurrence of CET and hence the shorter length of the columnar region. By contrast, the upper region has a longer columnar region due to the slower increasing solidification rate and larger temperature gradient. To better understand this phenomenon, the maximum constitutional undercooling ahead of the solidification front was recorded during the solidification process under transient thermal conditions, which is shown in Figure 15. It can be seen that the maximum undercooling increases relatively quicker at the bottom region, which agrees well with the above analysis.
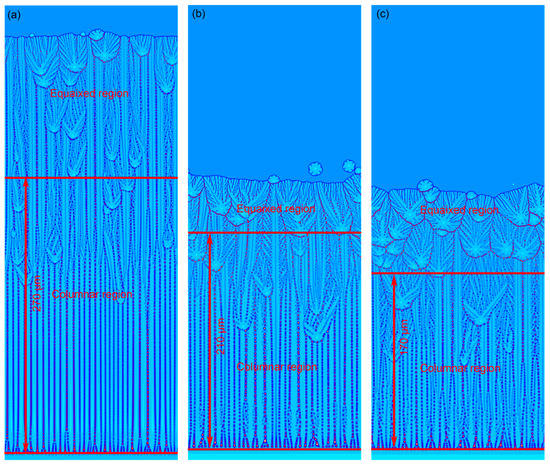
Figure 13.
Predicted microstructure under transient thermal conditions at different locations in the fusion zone of laser weld: (a) upper (Region I), (b) middle (Region II), and (c) bottom (Region III).
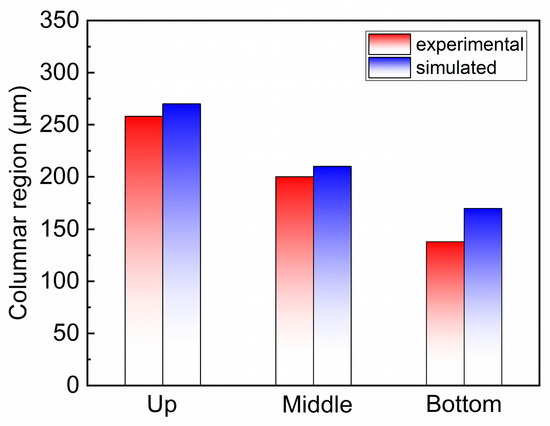
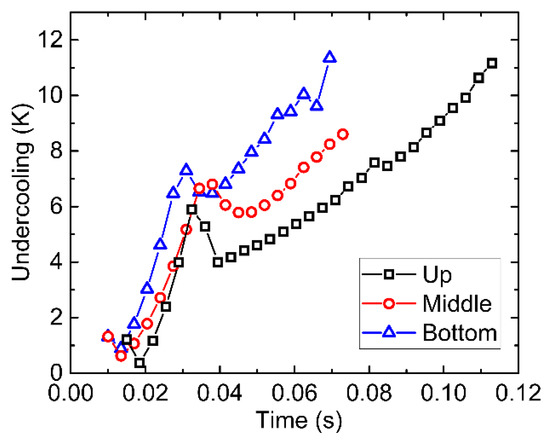
Figure 15.
Time evolution of maximum undercooling in the liquid ahead of solidification front under transient conditions during laser welding.
Although the CET behaviors at different locations of laser weld are preliminarily investigated, there are several advances that need to be made before the predicted microstructure can be fully compatible with the experiments. Firstly, the simulations need to be extended to three dimensions. In a realistic 3D system, the tip operating state is significantly different from that in the reduced 2D system according to References [51,52]. This will further affect the solute diffusion field and thus the constitutional undercooling distribution ahead of the solidification front. Due to the recent development of computer technology, large-scale 3D PF simulations are now available using multi-GPU acceleration [53,54,55]. We are preparing a future 3D work on a more complex CET during laser welding using multi-GPU accelerated large-scale PF simulations. Secondly, the transient thermal conditions employed in this study are in 2D and several assumptions have been made in order to obtain the simplified formulas, i.e., Equations (3) and (4). Therefore, more realistic 3D temperature profiles are required in future work.
5. Conclusions
The CET behaviors at different locations of fusion zone in laser weld of Al–Mg alloy were observed experimentally and investigated systematically using the quantitative PF model. In order to describe the dynamic CET behaviors, the transient thermal conditions, and Gaussian heterogeneous nucleation model were integrated into the PF model. It is shown that CET depends strongly on the locally transient thermal conditions during the laser welding process. The following key points should be emphasized:
- (1)
- Different CET behaviors are observed experimentally at different locations in laser weld. The size of the columnar region decreases significantly from the upper region to the bottom region.
- (2)
- Investigation on columnar growth under steady conditions indicates that the constitutionally undercooled degree and region are quantitatively determined by the applied thermal conditions. It is found that the undercooled degree ahead of the solidification front is primarily dependent on the solidification rate, while the size of the undercooled region is mainly affected by the applied temperature gradient within the parameter range involved in this study.
- (3)
- The heat transfer during the laser welding process is calculated and validated by corresponding experiments. It is shown that the transient thermal conditions vary greatly at different locations in the fusion zone. In particular, the solidification rate increases more rapidly from the upper to the bottom region.
- (4)
- The predicted length of the columnar region is in reasonably good accordance with experimental results. According to PF simulations, the transient thermal conditions influence CET behaviors through dynamically adjusting the constitutionally undercooled degree and region ahead of the solidification front. Particularly, the smaller columnar region at the bottom of laser weld can be explained by the lower temperature gradient and the more rapidly increasing solidification rate, which leads to a larger constitutionally undercooled degree and region, and thus higher CET tendency.
Author Contributions
Conceptualization, L.G.; methodology, L.G.; software, L.G.; validation, L.G., C.H., L.R., W.Y. and A.Y.; formal analysis, L.G.; investigation, L.G., C.H., L.R., W.Y. and A.Y.; resources, L.G.; data curation, L.G.; writing—original draft preparation, L.G.; writing—review and editing, L.G., C.H. and L.R.; visualization, L.G. and C.H.; supervision, L.G.; project administration, L.G.; funding acquisition, L.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded bythe National Natural Science Foundation of China grant number No.52075201 and No.52188102 and the Postdoctoral Science Foundation of China under Grant No.2020M682407.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- David, S.A.; Vitek, J.M. Correlation between solidification parameters and weld microstructures. Int. Mater. Rev. 1989, 34, 213. [Google Scholar] [CrossRef]
- Wei, H.L.; Elmer, J.W.; DebRoy, T. Origin of grain orientation during solidification of an aluminum alloy. Acta Mater. 2016, 115, 123. [Google Scholar] [CrossRef]
- Kou, S. Welding Metallurgy; John Wiley and Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Schempp, P.; Cross, C.E.; Pittner, A.; Rethmeier, M. Solidification of GTA Aluminum Weld Meal: Part 2- Thermal Conditions and Model for Columnar-to-Equiaxed Transition. Weld. J. 2014, 93, 69. [Google Scholar]
- Wołczyński, W.; Ivanowa, A.A.; Kwapisiński, P. Mathematical predictions of brass/steel ingot structures. Sci. J. Marit. Univ. Szczec. 2018, 56, 47. [Google Scholar]
- Hunt, J.D. Steady state columnar and equiaxed growth of dendrites and eutectic. Mater. Sci. Eng. 1984, 65, 75. [Google Scholar] [CrossRef]
- Gäumann, M.; Trivedi, R.; Kurz, W. Nucleation ahead of the advancing interface in directional solidification. Mater. Sci. Eng. A 1997, 226–228, 763–769. [Google Scholar] [CrossRef]
- Flood, S.C.; Hunt, J.D. Columnar and equiaxed growth: I. A model of a columnar front with a temperature dependent velocity. J. Cryst. Growth 1987, 82, 543. [Google Scholar] [CrossRef]
- Flood, S.C.; Hunt, J.D. Columnar and equiaxed growth: II. Equiaxed growth ahead of a columnar front. J. Cryst. Growth 1987, 82, 552. [Google Scholar] [CrossRef]
- Gäumann, M.; Bezençon, C.; Canalis, P.; Kurz, W. Single-crystal laser deposition of superalloys: Processing–microstructure maps. Acta Mater. 2001, 49, 1051. [Google Scholar] [CrossRef]
- Wołczyński, W.; Ivanova, A.A.; Kwapisiński, P. On Consonance between a Mathematical Method for the CET Prediction and Constrained / Unconstrained Solidification. Procedia Manuf. 2019, 30, 459. [Google Scholar] [CrossRef]
- Ohno, M.; Matsuura, K. Quantitative phase-field modeling for dilute alloy solidification involving diffusion in the solid. Phys. Rev. E 2009, 79, 31603. [Google Scholar] [CrossRef]
- Nestler, B.; Danilov, D.; Galenko, P. Crystal growth of pure substances: Phase-field simulations in comparison with analytical and experimental results. J. Comput. Phys. 2005, 207, 221. [Google Scholar] [CrossRef]
- Wheeler, A.A.; Boettinger, W.J.; Mcfadden, G.B. Phase-field model for isothermal phase transitions in binary alloys. Phys. Rev. A 1992, 45, 7424. [Google Scholar] [CrossRef]
- Ramirez, J.C.; Beckermann, C.; Karma, A.; Diepers, H.J. Phase-field modeling of binary alloy solidification with coupled heat and solute diffusion. Phys. Rev. E 2004, 69, 51607. [Google Scholar] [CrossRef]
- Cha, P.R.; Yeon, D.H.; Yoon, J.K. A phase field model for isothermal solidification of multicomponent alloys. Acta Mater. 2001, 49, 3295. [Google Scholar] [CrossRef]
- Ohno, M. Quantitative phase-field modeling of nonisothermal solidification in dilute multicomponent alloys with arbitrary diffusivities. Phys. Rev. E 2012, 86, 51603. [Google Scholar] [CrossRef]
- Nestler, B.; Garcke, H.; Stinner, B. Multicomponent alloy solidification: Phase-field modeling and simulations. Phys. Rev. E 2005, 71, 41609. [Google Scholar] [CrossRef]
- Singerloginova, I.; Singer, H.M. The phase field technique for modeling multiphase materials. Rep. Prog. Phys. 2008, 71, 106501. [Google Scholar] [CrossRef]
- Badillo, A.; Beckermann, C. Phase-field simulation of the columnar-to-equiaxed transition in alloy solidification. Acta Mater. 2006, 54, 2015. [Google Scholar] [CrossRef]
- Farzadi, A.; Doquang, M.; Serajzadeh, S.; Kokabi, A.H.; Amberg, G. Phase-field simulation of weld solidification microstructure in an Al Cu alloy. Model. Simul. Mater. Sci. Eng. 2008, 16, 65005. [Google Scholar] [CrossRef]
- Zheng, W.J.; Dong, Z.B.; Wei, Y.H.; Song, K.J.; Guo, J.L.; Wang, Y. Phase field investigation of dendrite growth in the welding pool of aluminum alloy 2A14 under transient conditions. Comput. Mater. Sci. 2014, 82, 525. [Google Scholar] [CrossRef]
- Wang, L.; Wei, Y.H.; Zhan, X.H.; Yu, F.Y.; Cao, X.Y.; Gu, C.; Ou, W.M. Simulation of dendrite growth in the laser welding pool of aluminum alloy 2024 under transient conditions. J. Mater. Process. Technol. 2017, 246, 22. [Google Scholar] [CrossRef]
- Yu, F.Y.; Wei, Y.H.; Ji, Y.Z.; Chen, L.Q. Phase field modeling of solidification microstructure evolution during welding. J. Mater. Process. Technol. 2018, 255, 285. [Google Scholar] [CrossRef]
- Pang, S.Y.; Chen, W.D.; Zhou, J.X.; Liao, D.M. Self-consistent modeling of keyhole and weld pool dynamics in tandem dual beam laser welding of aluminum alloy. J. Mater. Process. Technol. 2015, 217, 131. [Google Scholar] [CrossRef]
- Ai, Y.W.; Jiang, P.; Shao, X.Y.; Li, P.G.; Wang, C.M. A three-dimensional numerical simulation model for weld characteristics analysis in fiber laser keyhole welding. Int. J. Heat Mass Transf. 2017, 108, 614. [Google Scholar] [CrossRef]
- Gao, X.S.; Wu, C.S.; Goecke, S.F.; Kügler, H. Numerical simulation of temperature field, fluid flow and weld bead formation in oscillating single mode laser-GMA hybrid welding. J. Mater. Process. Technol. 2017, 242, 147. [Google Scholar] [CrossRef]
- Gao, Z.M.; Jiang, P.; Mi, G.Y.; Cao, L.C.; Liu, W. Investigation on the weld bead profile transformation with the keyhole and molten pool dynamic behavior simulation in high power laser welding. Int. J. Heat Mass Transf. 2018, 116, 1304. [Google Scholar] [CrossRef]
- Zheng, W.J.; Dong, Z.B.; Wei, Y.H.; Song, K.J. Onset of the initial instability during the solidification of welding pool of aluminum alloy under transient conditions. J. Cryst. Growth 2014, 402, 203. [Google Scholar] [CrossRef]
- Wang, L.; Wei, Y.H.; Zhan, X.H.; Yu, F.Y. A phase field investigation of dendrite morphology and solute distributions under transient conditions in an Al–Cu welding molten pool. Sci. Technol. Weld. Join. 2016, 21, 1. [Google Scholar] [CrossRef]
- Takaki, T.; Ohno, M.; Shimokawabe, T.; Aoki, T. Two-dimensional phase-field simulations of dendrite competitive growth during the directional solidification of a binary alloy bicrystal. Acta Mater. 2014, 81, 272. [Google Scholar] [CrossRef]
- Diepers, H.J.; Ma, D.; Steinbach, I. History effects during the selection of primary dendrite spacing. Comparison of phase-field simulations with experimental observations. J. Cryst. Growth 2002, 237–239, 149–153. [Google Scholar] [CrossRef]
- Steinbach, I.; Pezzolla, F. A generalized field method for multiphase transformations using interface fields. Phys. D Nonlinear Phenom. 1999, 134, 385. [Google Scholar] [CrossRef]
- Böttger, B.; Eiken, J.; Steinbach, I. Phase field simulation of equiaxed solidification in technical alloys. Acta Mater. 2006, 54, 2697. [Google Scholar] [CrossRef]
- Kobayashi, R.; Warren, J.A.; Carter, W.C. Vector-valued phase field model for crystallization and grain boundary formation. Phys. D Nonlinear Phenom. 1998, 119, 415. [Google Scholar] [CrossRef]
- Gránásy, L.; Pusztai, T.; Warren, J.A.; Douglas, J.F.; Börzsönyi, T.; Ferreiro, V. Growth of ’dizzy dendrites’ in a random field of foreign particles. Nat. Mater. 2003, 2, 92. [Google Scholar] [CrossRef]
- Villafuerte, J.C.; Pardo, E.; Kerr, H.W. The effect of alloy composition and welding conditions on columnar-equiaxed transitions in ferritic stainless steel gas-tungsten arc welds. Metall. Trans. A 1990, 21, 2009. [Google Scholar] [CrossRef]
- Kwapisiński, P.; Lipnicki, Z.; Ivanova, A.A.; Wołczyński, W. Role of the Structural and Thermal Peclet Numbers in the Brass Continuous Casting. Arch. Foundry Eng. 2017, 17, 49. [Google Scholar] [CrossRef][Green Version]
- Qiu, D.; Zhang, M.X.; Taylor, J.A.; Fu, H.M.; Kelly, P.M. A novel approach to the mechanism for the grain refining effect of melt superheating of Mg–Al alloys. Acta Mater. 2007, 55, 1863. [Google Scholar] [CrossRef]
- Han, R.H.; Li, Y.Y.; Lu, S.P. Macro-micro modeling and simulation for the morphological evolution of the solidification structures in the entire weld. Int. J. Heat Mass Transf. 2017, 106, 1345. [Google Scholar] [CrossRef]
- Xiao, L.; Liu, L.; Zhou, Y.; Esmaeili, S. Resistance-Spot-Welded AZ31 Magnesium Alloys: Part, I. Dependence of Fusion Zone Microstructures on Second-Phase Particles. Metall. Mater. Trans. A 2010, 41, 1511. [Google Scholar] [CrossRef]
- Kou, S.; Le, Y. Welding parameters and the grain structure of weld meta - A thermodynamic consideration. Metall. Trans. A 1988, 19, 1075. [Google Scholar] [CrossRef]
- Thévoz, P.; Desbiolles, J.L.; Rappaz, M. Modeling of equiaxed microstructure formation in casting. Metall. Trans. A 1989, 20, 311. [Google Scholar] [CrossRef]
- Dong, H.B.; Lee, P.D. Simulation of the columnar-to-equiaxed transition in directionally solidified Al–Cu alloys. Acta Mater. 2005, 53, 659. [Google Scholar] [CrossRef]
- Han, R.H.; Lu, S.P.; Dong, W.C.; Li, D.Z.; Li, Y.Y. Multi-scale Simulation for the Columnar to Equiaxed Transition in the Weld Pool. ISIJ Int. 2016, 56, 1003. [Google Scholar] [CrossRef]
- Smith, P.M.; Aziz, M.J. Solute trapping in aluminum alloys. Acta Metall. Et Mater. 1994, 42, 3515. [Google Scholar] [CrossRef]
- Wolczynski, W. Pattern Selection in the Eutectic Growth—Thermodynamic Interpretation. Arch. Metall. Mater. 2020, 65, 653. [Google Scholar]
- Gündüz, M.; Hunt, J.D. Solid-liquid surface energy in the Al-Mg system. Acta Metall. 1989, 37, 1839. [Google Scholar] [CrossRef]
- Xie, F.Y.; Kraft, T.; Zuo, Y.; Moon, C.H.; Chang, Y.A. Microstructure and microsegregation in Al-rich Al-Cu-Mg alloys. Acta Mater. 1999, 47, 489. [Google Scholar] [CrossRef]
- Echebarria, B.; Folch, R.; Karma, A.; Plapp, M. Quantitative phase-field model of alloy solidification. Phys. Rev. E 2004, 70, 61604. [Google Scholar] [CrossRef]
- Bollada, P.C.; Goodyer, C.E.; Jimack, P.K.; Mullis, A.M. Simulations of three-dimensional dendritic growth using a coupled thermo-solutal phase-field model. Appl. Phys. Lett. 2015, 107, 589. [Google Scholar] [CrossRef]
- Tsai, Y.L.; Chen, C.C.; Lan, C.W. Three-dimensional adaptive phase field modeling of directional solidification of a binary alloy: 2D–3D transitions. Int. J. Heat Mass Transf. 2010, 53, 2272. [Google Scholar] [CrossRef]
- Sakane, S.; Takaki, T.; Rojas, R.; Ohno, M.; Shibuta, Y.; Shimokawabe, T.; Aoki, T. Multi-GPUs parallel computation of dendrite growth in forced convection using the phase-field-lattice Boltzmann model. J. Cryst. Growth 2017, 474, 154. [Google Scholar] [CrossRef]
- Takaki, T.; Sakane, S.; Ohno, M.; Shibuta, Y.; Shimokawabe, T.; Aoki, T. Large-scale Phase-field Studies of Three-dimensional Dendrite Competitive Growth at the Converging Grain Boundary during Directional Solidification of a Bicrystal Binary Alloy. ISIJ Int. 2016, 56, 1427. [Google Scholar] [CrossRef]
- Takaki, T.; Sakane, S.; Ohno, M.; Shibuta, Y.; Shimokawabe, T.; Aoki, T. Primary arm array during directional solidification of a single-crystal binary alloy: Large-scale phase-field study. Acta Mater. 2016, 118, 230. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).