Multipoint Forming Using Hole-Type Rubber Punch
Abstract
:1. Introduction
2. Experimental and Methods
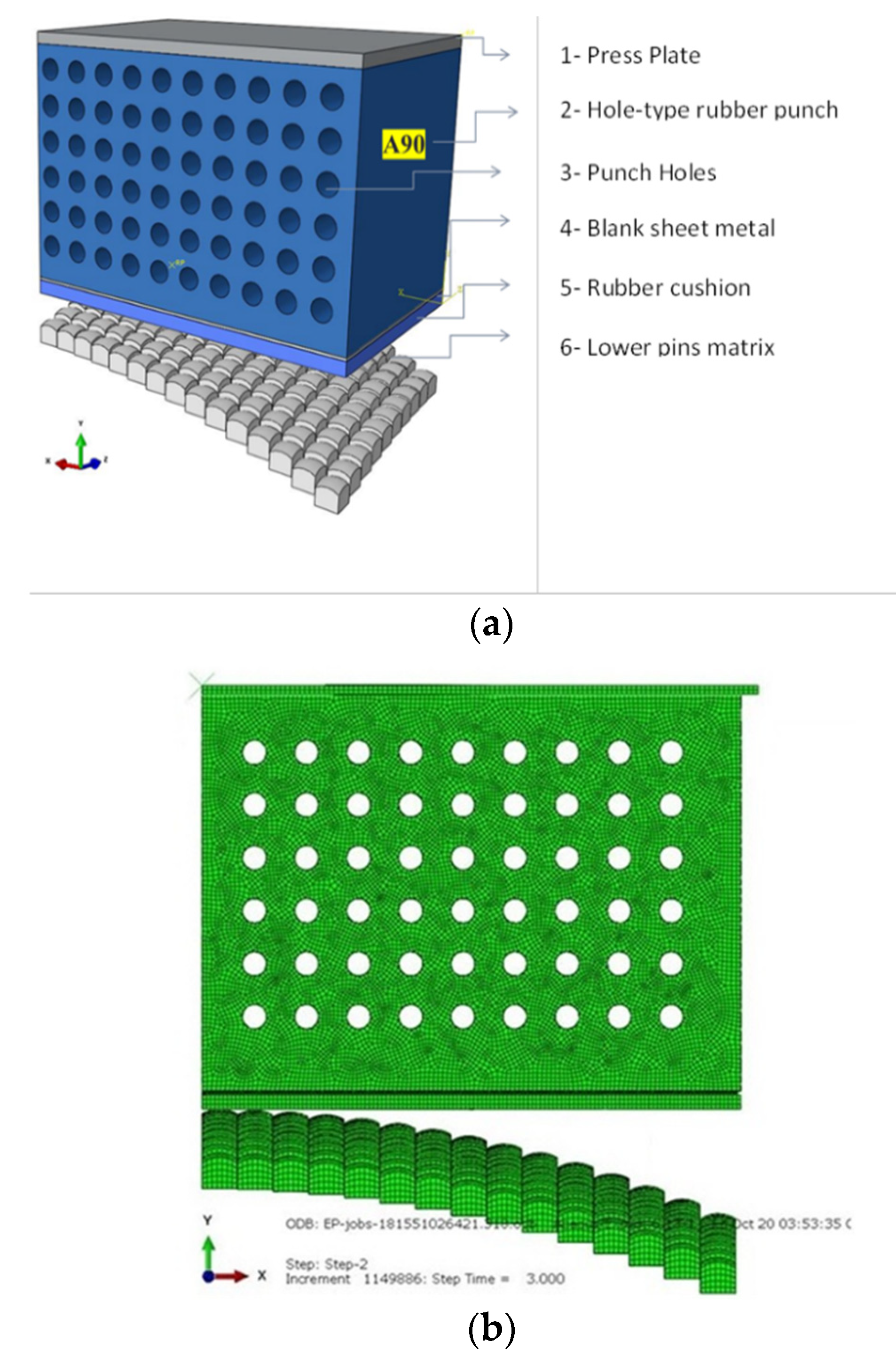
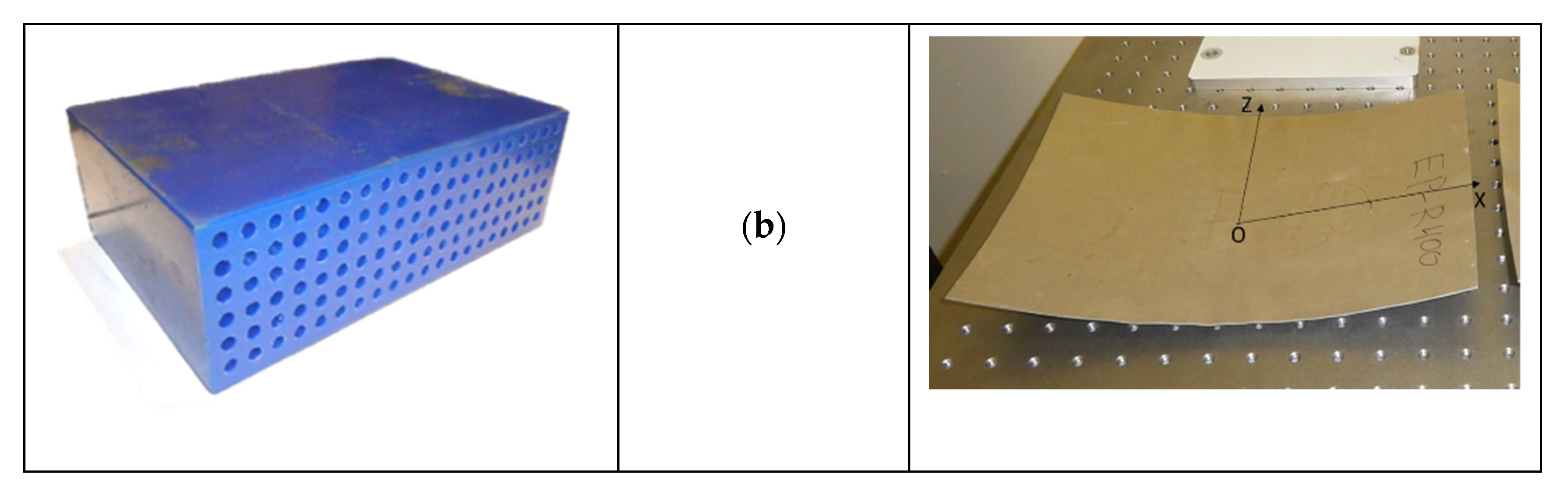
2.1. Experimental Setup
2.2. Finite Element Modelling
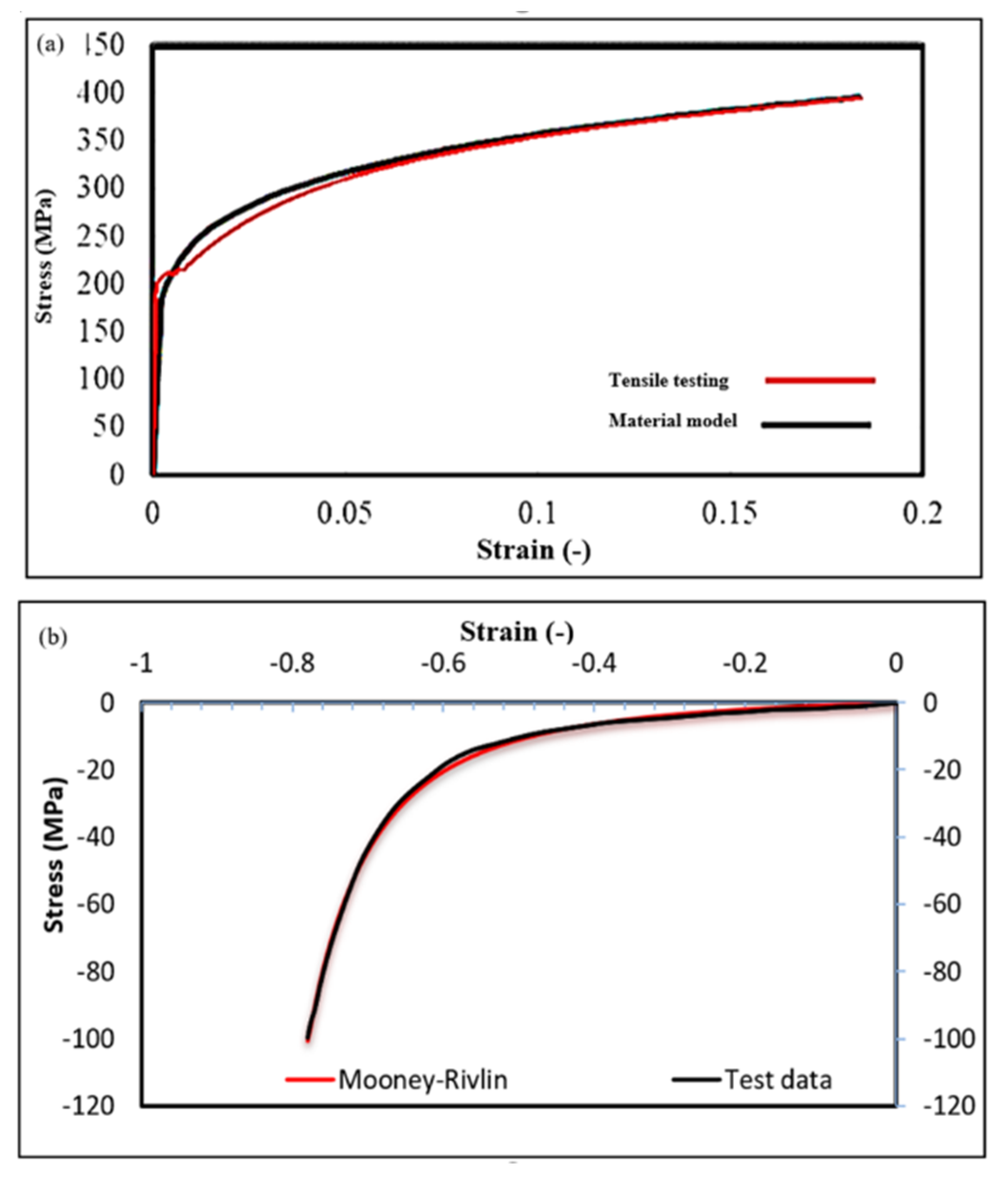
2.3. Materials Properties
2.4. Statistical Optimisation
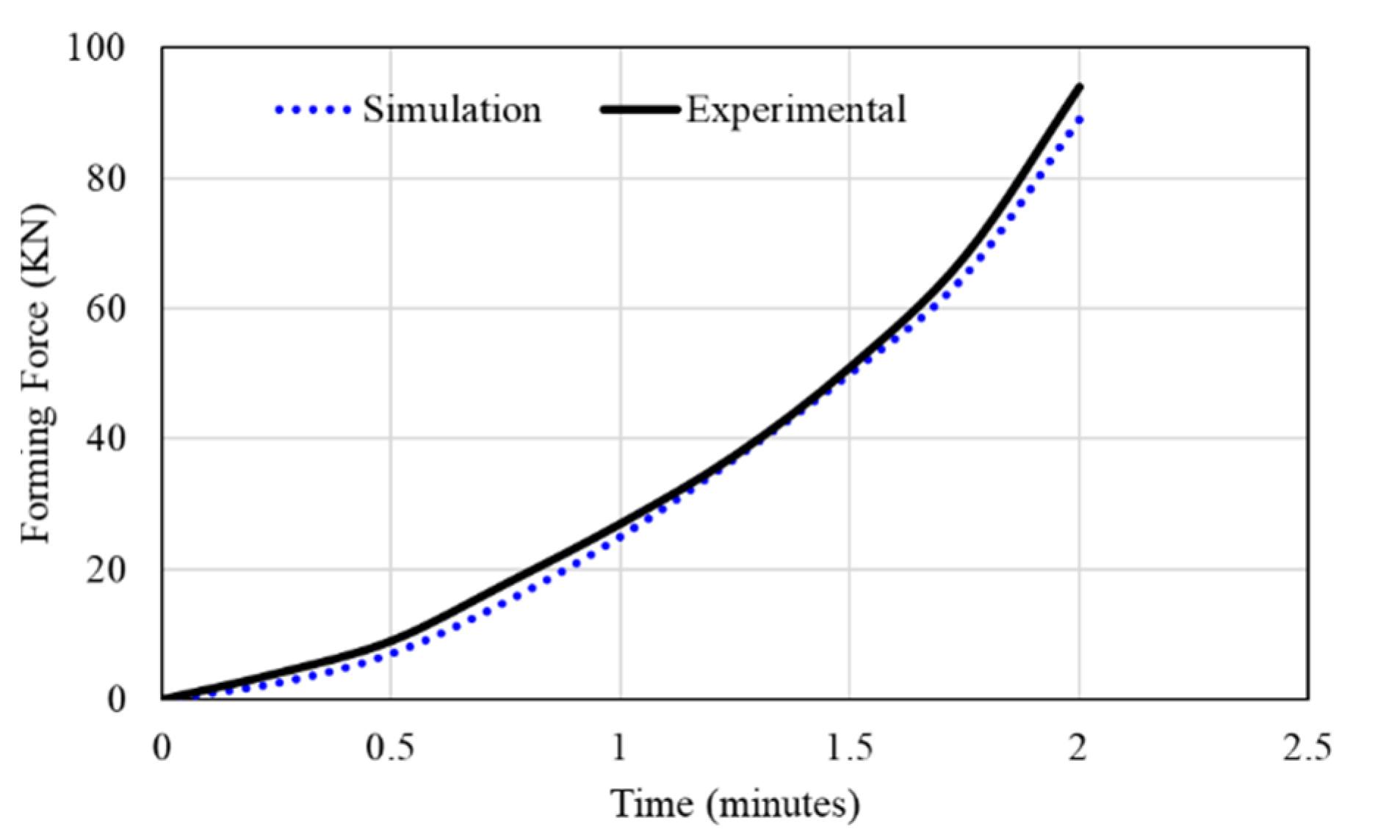
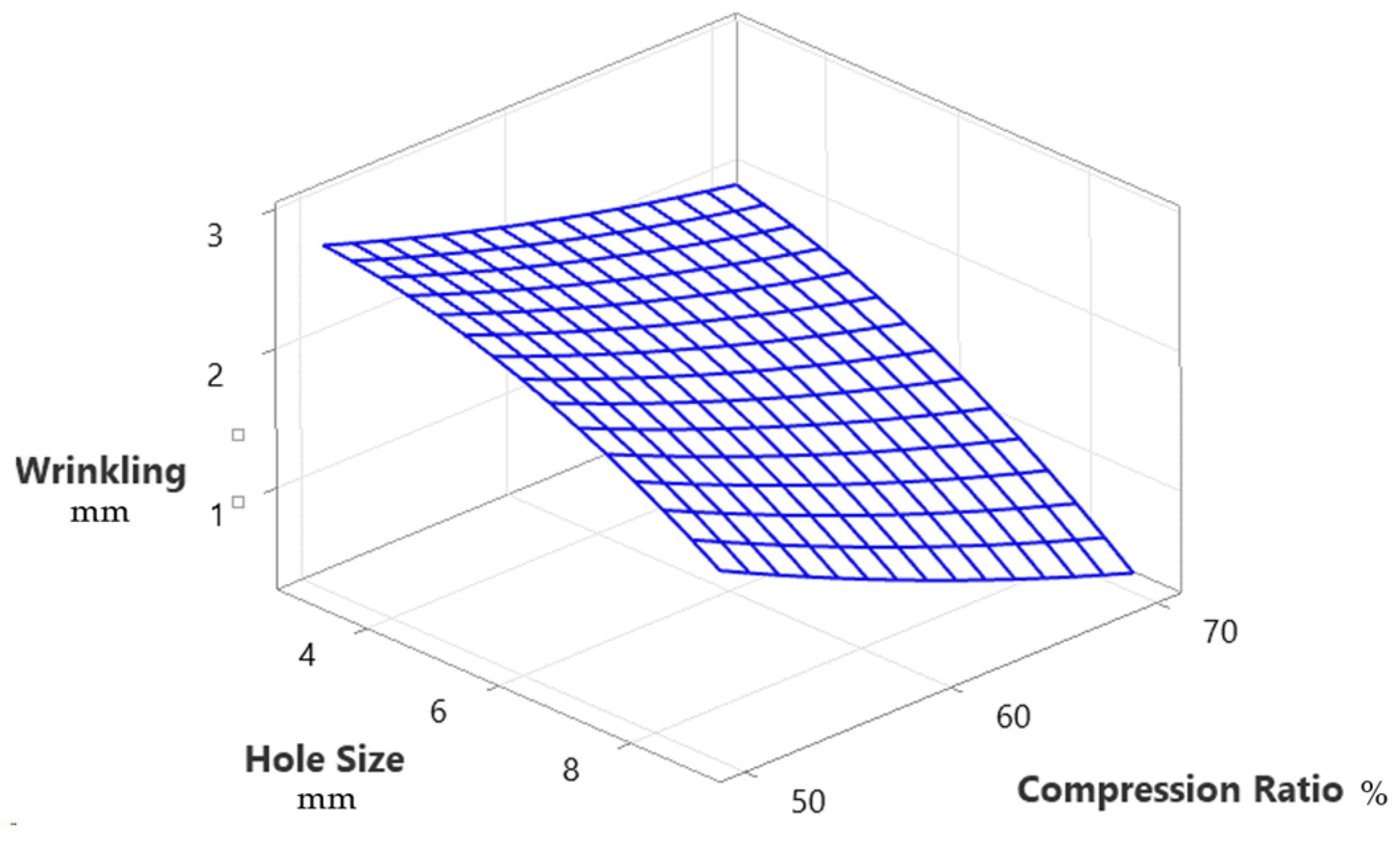
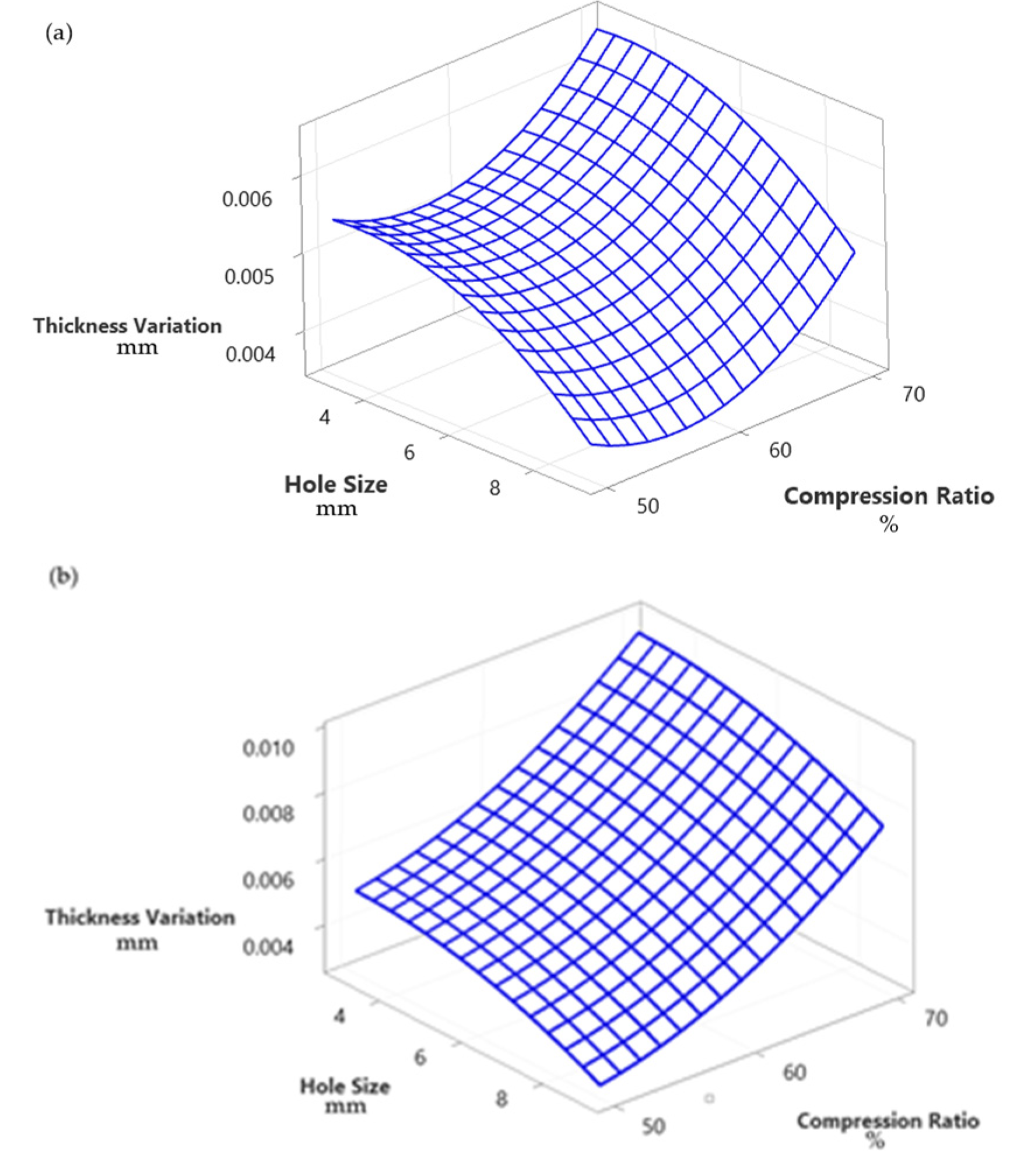
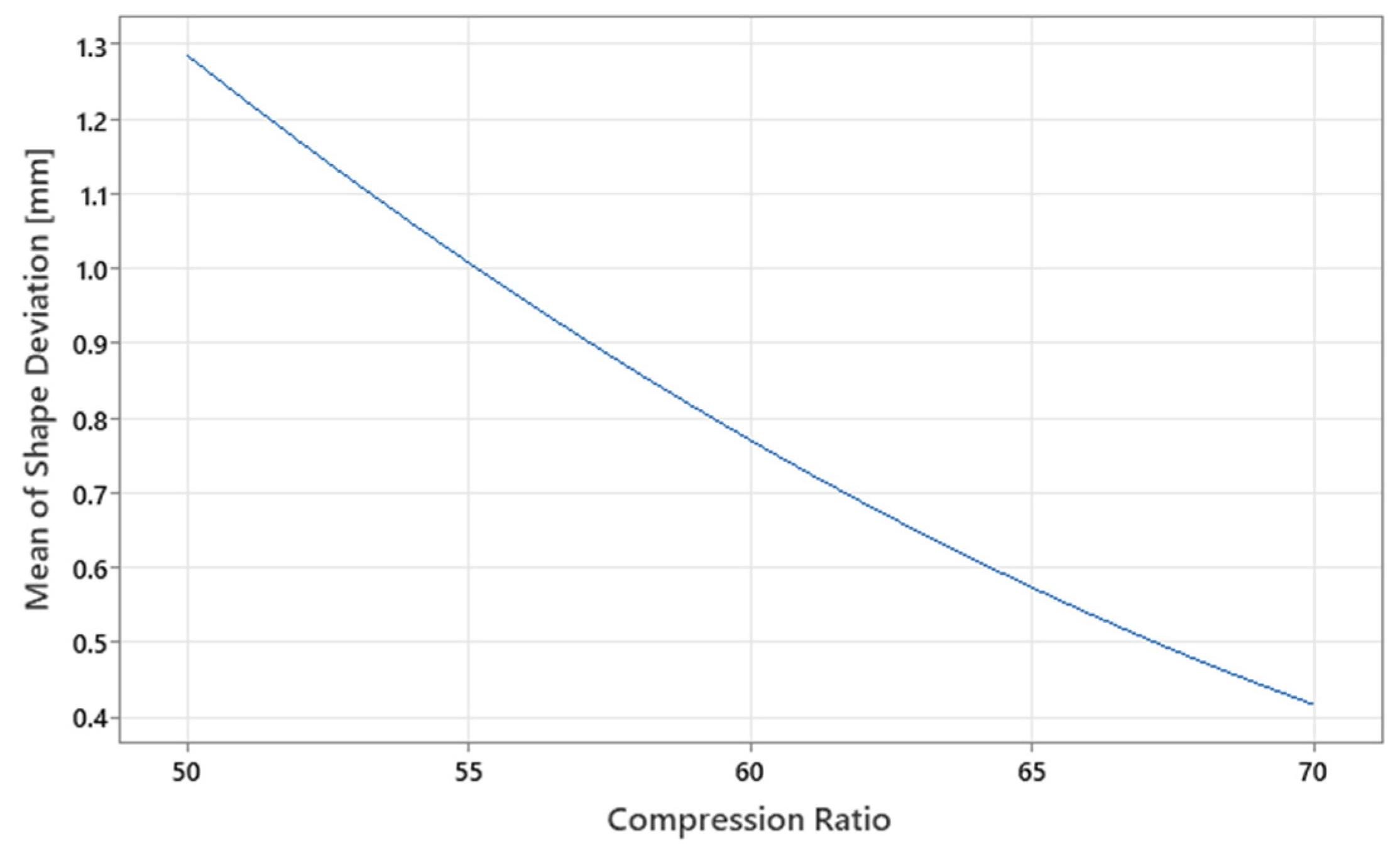
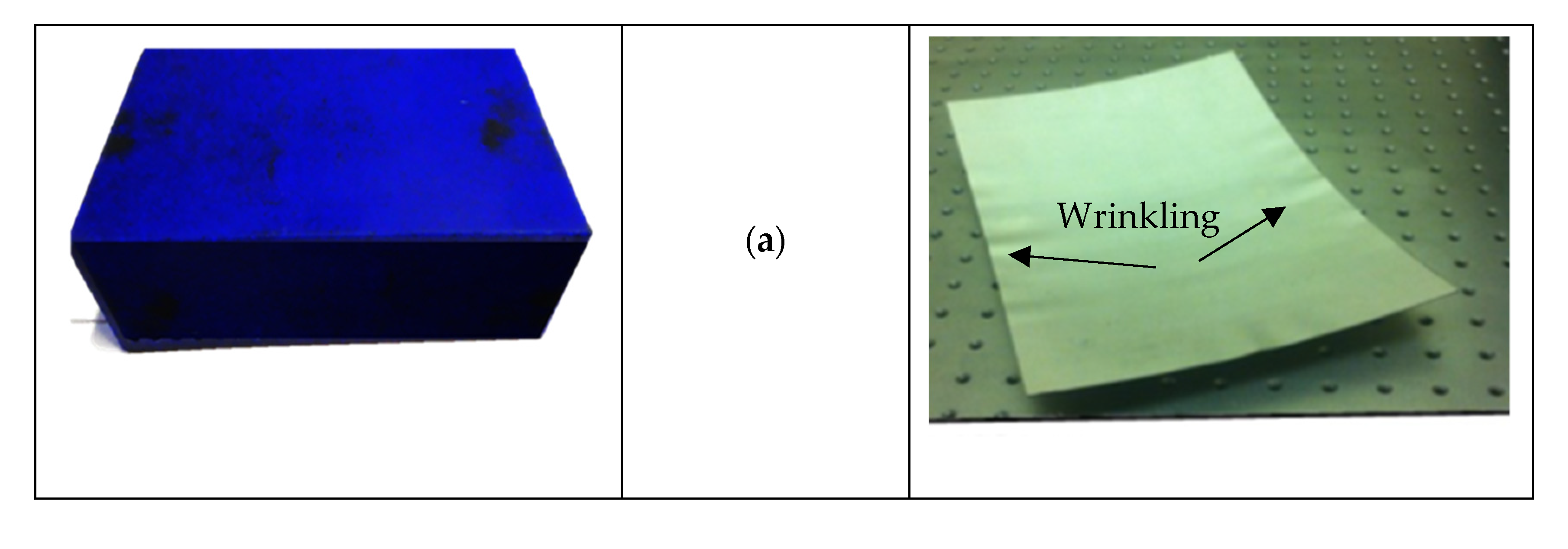
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Atul, S.T.; Babu, M.C.L. A review on effect of thinning, wrinkling and spring-back on deep drawing process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2019, 233, 1011–1036. [Google Scholar] [CrossRef]
- Wifi, A.S.; Abdelmaguid, T.F.; El-Ghandour, A.I. A review of the optimization techniques applied to the Deep Drawing process. In Proceedings of the 37th International Conference on Computers and Industrial Engineering 2007, Alexandria, Egypt, 20–23 October 2007; Computers and Industrial Engineering. pp. 97–107. [Google Scholar]
- Hagan, E.; Jeswiet, J. A review of conventional and modern single-point sheet metal forming methods. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2003, 217, 213–225. [Google Scholar] [CrossRef]
- Wankhede, P.; Suresh, K. A review on the evaluation of formability in sheet metal forming. Adv. Mater. Processing Technol. 2020, 6, 402–429. [Google Scholar] [CrossRef]
- Essa, K. Finite Element Prediction of Deformation Mechanics in Incremental Forming Processes; The University of Birmingham: Birmingham, UK, 2011; p. 217. [Google Scholar]
- Petunin, A.A.; Stylios, C. Optimization models of tool path problem for CNC sheet metal cutting machines. IFAC Pap. Online 2016, 49, 23–28. [Google Scholar] [CrossRef]
- Schuh, G.; Bergweiler, G.; Fiedler, F.; Bickendorf, P.; Colag, C. A Review on Flexible Forming of Sheet Metal Parts. In Proceedings of the 2019 IEEE International Conference on Industrial Engineering and Engineering Management, IEEM 2019, Macao, China, 15–18 December 2019; IEEE Computer Society: Washington, DC, USA, 2019; pp. 1221–1225. [Google Scholar]
- Yadav, A.; Jayswal, S.C. Modelling of flexible manufacturing system: A review. Int. J. Prod. Res. 2018, 56, 2464–2487. [Google Scholar] [CrossRef]
- Zhu, H.; Ou, H.; Popov, A. Incremental sheet forming of thermoplastics: A review. Int. J. Adv. Manuf. Technol. 2020, 111, 565–587. [Google Scholar] [CrossRef]
- Soltani-Tehrani, A.; Lee, S.; Sereshk, M.R.V.; Shamsaei, N. Effects of unit cell size on the mechanical performance of additive manufactured lattice structures. In Proceedings of the 30th Annual International Solid Freeform Fabrication Symposium—An Additive Manufacturing Conference, SFF 2019, Austin, TX, USA, 12–14 August 2019; pp. 2254–2262. [Google Scholar]
- Tolipov, A.; Elghawail, A.; Abosaf, M.; Pham, D.; Hassanin, H.; Essa, K. Multipoint forming using mesh-type elastic cushion: Modelling and experimentation. Int. J. Adv. Manuf. Technol. 2019, 103, 2079–2090. [Google Scholar] [CrossRef] [Green Version]
- Abosaf, M.; Essa, K.; Alghawail, A.; Tolipov, A.; Su, S.; Pham, D. Optimisation of multi-point forming process parameters. Int. J. Adv. Manuf. Technol. 2017, 92, 1849–1859. [Google Scholar] [CrossRef] [Green Version]
- Tolipov, A.A.; Elghawail, A.; Shushing, S.; Pham, D.; Essa, K. Experimental research and numerical optimisation of multi-point sheet metal forming implementation using a solid elastic cushion system. J. Phys. Conf. Ser. 2017, 896, 012120. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Li, M.; Yue, T. Springback prediction method for double-curved workpiece considering plate anisotropy in multi-point forming. J. Mech. Sci. Technol. 2021, 35, 2623–2636. [Google Scholar] [CrossRef]
- Yang, J.; Fu, W.; Li, M.; Yang, Y. Optimization of multi-point forming for aluminum alloy profile. In Materials Science Forum; Trans Tech Publications Ltd.: Freienbach, Switzerland, 2021; pp. 13–17. [Google Scholar]
- Liu, C.; Li, M.; Qu, E. Springback prediction and compensation method for anisotropy sheet in multi-point forming. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 511–524. [Google Scholar] [CrossRef]
- Liang, J.; Han, C.; Li, Y.; Liang, C.; Jin, W. The influence of multi-point roller-dies on the shape deviation differences of profile in flexible stretch-bending forming. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2021, 09544054211041067. [Google Scholar] [CrossRef]
- Moheen, M.; Abdel-Wahab, A.; Hassanin, H.; Essa, K. Reconfigurable Multipoint Forming Using Waffle-Type Elastic Cushion and Variable Loading Profile. Materials 2020, 13, 4506. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.W.; Kwon, H.C.; Rhee, M.H.; Im, Y.T. Determination of forming limit of a structural aluminum tube in rubber pad bending. J. Mater. Processing Technol. 2003, 140, 487–493. [Google Scholar] [CrossRef]
- Quadrini, F.; Santo, L.; Squeo, E. Flexible forming of thin aluminum alloy sheets. Int. J. Mod. Manuf. Technol. 2010, 2, 79–84. [Google Scholar]
- Chen, L.; Chen, H.; Guo, W.; Chen, G.; Wang, Q. Experimental and simulation studies of springback in rubber forming using aluminium sheet straight flanging process. Mater. Des. 2014, 54, 354–360. [Google Scholar] [CrossRef]
- Păunoiu, V.; Maier, C.; Teodor, V.; Găvan, E. Numerical analysis of multipoint forming process. Int. J. Mod. Manuf. Technol. 2011, 3, 85–90. [Google Scholar]
- Quan, G.-Z.; Ku, T.-W.; Kang, B.-S. Improvement of formability for multi-point bending process of AZ31B sheet material using elastic cushion. Int. J. Precis. Eng. Manuf. 2011, 12, 1023–1030. [Google Scholar] [CrossRef]
- Zareh-Desari, B.; Habibi-Yengejeh, S.; Davoodi, B.; Vafaeesefat, A. Experimental Investigation and Finite Element Simulation of Effect of Mechanical Properties of Elastic Cushion on Spring-Back in Multi-Point Forming Process. Aerosp. Mech. J. 2014, 11, 63–73. [Google Scholar]
- Younis, K.M.; Aljarjary, A.I.; Shukur, J.J. Numerical and experimental investigation of parameters affect the forming load during rubber pad sheet metal forming. In Proceedings of the 2nd International Conference on Sustainable Engineering Techniques (ICSET 2019), Baghdad, Iraq, 6–7 March 2019; IOP Publishing: Bristol, UK, 2019; pp. 032012–032049. [Google Scholar]
- Spoelstra, P.; Djakow, E.; Homberg, W. Rubber pad forming—Efficient approach for the manufacturing of complex structured sheet metal blanks for food industry. In Proceedings of the 20th International ESAFORM Conference on Material Forming (ESAFORM 2017), Dublin, Ireland, 26–28 April 2017; AIP—American Institute of Physics: College Park, MD, USA, 2017; pp. 080004–080006. [Google Scholar]
- Hongyu, W.; Zhen, W.; Fei, T.; Pengchao, Z.; Juncai, S.; Shijun, J. Numerical simulation and experiment research on forming of two-step channel based on rubber pad pressing. Int. J. Adv. Manuf. Technol. 2019, 101, 2175–2189. [Google Scholar] [CrossRef]
- Fei, T.; Hongyu, W.; Juncai, S.; Xiangwei, K.; Jie, S.; Shunhu, Z. Thickness analysis of complex two-step micro-groove on plate during rubber pad forming process. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 122–135. [Google Scholar]
- Elghawail, A.; Essa, K.; Abosaf, M.; Tolipov, A.; Su, S.; Pham, D. Low-cost metal-forming process using an elastic punch and a reconfigurable multi-pin die. Int. J. Mater. Form. 2019, 12, 391–401. [Google Scholar] [CrossRef] [Green Version]
- Cai, Z.-Y.; Wang, S.-H.; Li, M.-Z. Numerical investigation of multi-point forming process for sheet metal: Wrinkling, dimpling and springback. Int. J. Adv. Manuf. Technol. 2008, 37, 927–936. [Google Scholar] [CrossRef]
- Abebe, M.; Lee, K.; Kang, B.-S. Surrogate-based multi-point forming process optimization for dimpling and wrinkling reduction. Int. J. Adv. Manuf. Technol. 2016, 85, 391–403. [Google Scholar] [CrossRef]
- Shaohui, W.; Zhongyi, C.; Mingzhe, L.; Yingwu, L. Numerical simulation on the local stress and local deformation in multi-point stretch forming process. Int. J. Adv. Manuf. Technol. 2012, 60, 901–911. [Google Scholar]
- Zhou, B.-J.; Xu, Y.-C. The effect of upper sheet on wrinkling and thickness distribution of formed sheet part using double-layer sheet hydroforming. Int. J. Adv. Manuf. Technol. 2018, 99, 1175–1182. [Google Scholar] [CrossRef]
- Elghawail, A.; Essa, K.; Abosaf, M.; Tolipov, A.; Su, S.; Pham, D. Prediction of springback in multi-point forming. Cogent Eng. 2017, 4, 1400507. [Google Scholar] [CrossRef]
- Peng, L.; Hu, P.; Lai, X.; Ni, J. Fabrication of metallic bipolar plates for proton exchange membrane fuel cell by flexible forming process-numerical simulations and experiments. J. Fuel Cell Sci. Technol. 2010, 7, 031009. [Google Scholar] [CrossRef]

| Parameter | Unit | Level | ||
|---|---|---|---|---|
| −1 | 0 | 1 | ||
| Hole size (A) | mm | 3 × 3 | 6 × 6 | 9 × 9 |
| Compression ratio % (B) | % | 50 | 60 | 70 |
| Hole geometry (C) | Square | Circular | ||
| Run | Factor 1 Hole Size (mm) | Factor 2 Compression Ratio (%) | Factor 3 Hole Shape | Response 1 Wrinkling [mm] | Response 2 Thickness Variation [mm] | Response 3 Shape Deviation [mm] |
|---|---|---|---|---|---|---|
| 1 | 6 | 50 | Circular | 2.0600 | 0.00504 | 1.323 |
| 2 | 9 | 70 | Circular | 0.3066 | 0.00318 | 0.399 |
| 3 | 9 | 50 | Square | 1.8010 | 0.00313 | 1.801 |
| 4 | 6 | 60 | Circular | 2.0040 | 0.00613 | 0.54 |
| 5 | 3 | 50 | Circular | 3.1280 | 0.00545 | 1.078 |
| 6 | 9 | 60 | Circular | 1.0110 | 0.00545 | 0.97 |
| 7 | 3 | 60 | Square | 2.8790 | 0.00662 | 0.67 |
| 8 | 3 | 70 | Circular | 1.6940 | 0.00700 | 0.3 |
| 9 | 3 | 50 | Square | 2.2770 | 0.00545 | 1.58 |
| 10 | 6 | 60 | Square | 2.0070 | 0.00545 | 0.79 |
| 11 | 9 | 50 | Circular | 1.6010 | 0.00313 | 1.011 |
| 12 | 6 | 70 | Circular | 1.7720 | 0.00654 | 0.44 |
| 13 | 9 | 60 | Square | 1.0440 | 0.00345 | 0.47 |
| 14 | 6 | 50 | Square | 3.0700 | 0.00481 | 1.067 |
| 15 | 3 | 70 | Square | 2.6994 | 0.00998 | 0.4 |
| 16 | 3 | 60 | Circular | 2.0710 | 0.00388 | 1.33 |
| 17 | 6 | 70 | Square | 1.1710 | 0.00788 | 0.79 |
| 18 | 9 | 70 | Square | 1.1820 | 0.00921 | 0.32 |
| Process Parameter | Response Factors | |||
|---|---|---|---|---|
| Wrinkling | Thickness Variation | Shape Deviation | ||
| Hole size (A) | mm | 0.001 | 0.010 | 0.757 |
| Compression Ratio (B) | % | 0.012 | 0.047 | 0.002 |
| Hole shape (C) | 0.246 | 0.006 | 0.746 | |
| Significant Interactions | - | AB = 0.46 AC = 0.06 BC = 0.32 | AB = 0.992 AC = 0.727 BC = 0.051 | AB = 0.895 AC = 0.829 BC = 0.597 |
| Polynomial Coefficient | Response Variable | ||
|---|---|---|---|
| Wrinkling [mm] | Thickness Variation [mm] | Shape Deviation [mm] | |
| 14.33 | 6.488 | −261. 9 | |
| −0.011 | 0.029 | 0.179 | |
| −0.052 | −0.089 | −0.019 | |
| −0.255 | −0.199 | 4.690 | |
| −0.00001 | −0.00004 | 0 | |
| 0.00006 | −0.00017 | 0 | |
| 0.00027 | 0.00910 | 0 | |
| 0.00001 | −0.00107 | 0 | |
| 0.00016 | 0.00252 | 0 | |
| 0.00160 | 0.01410 | 0 | |
| Parameter | Hole Size [mm] | Compression Ratio % | Hole-Type | - | Wrinkling (mm) | Thickness Variation (mm) | Shape Deviation (mm) |
|---|---|---|---|---|---|---|---|
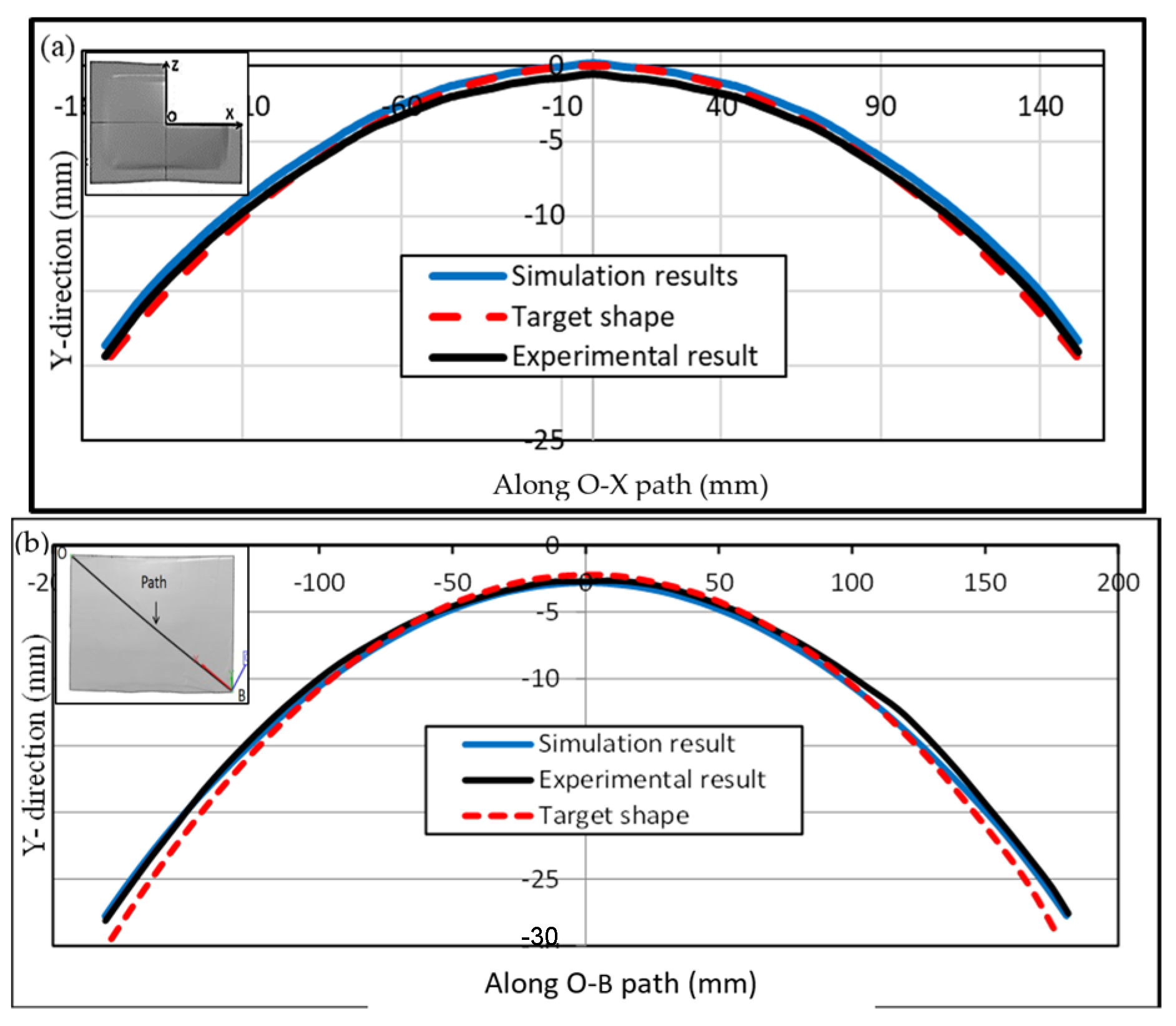
| Optimal conditions | 9 | 75 | Circular | FEM | 0.1066 | 0.00318 | 0.399 |
| Exp. | 0.1082 | 0.00322 | 0.393 | ||||
| Elghawail et al. [24]. | Solid Punch | Exp. | 0.534 | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tolipov, A.; Hassanin, H.; El-Sayed, M.A.; Eldessouky, H.M.; Alsaleh, N.A.; Alfozan, A.K.; Essa, K.; Ahmadein, M. Multipoint Forming Using Hole-Type Rubber Punch. Metals 2022, 12, 491. https://doi.org/10.3390/met12030491
Tolipov A, Hassanin H, El-Sayed MA, Eldessouky HM, Alsaleh NA, Alfozan AK, Essa K, Ahmadein M. Multipoint Forming Using Hole-Type Rubber Punch. Metals. 2022; 12(3):491. https://doi.org/10.3390/met12030491
Chicago/Turabian StyleTolipov, Abror, Hany Hassanin, Mahmoud Ahmed El-Sayed, Hossam Mohamed Eldessouky, Naser A. Alsaleh, Adel Khalid Alfozan, Khamis Essa, and Mahmoud Ahmadein. 2022. "Multipoint Forming Using Hole-Type Rubber Punch" Metals 12, no. 3: 491. https://doi.org/10.3390/met12030491
APA StyleTolipov, A., Hassanin, H., El-Sayed, M. A., Eldessouky, H. M., Alsaleh, N. A., Alfozan, A. K., Essa, K., & Ahmadein, M. (2022). Multipoint Forming Using Hole-Type Rubber Punch. Metals, 12(3), 491. https://doi.org/10.3390/met12030491









