First Principles Investigation of the Effects of Chemical Short-Range Ordering Clusters on the Ideal Tensile Strength and Ductility of Aluminum Alloys

Abstract

As important structural features of the metal materials, chemical short-range ordering clusters play a critical role in the mechanical properties of the materials. They have been discovered in dilute Al-alloy systems and are usually generated by annealing processes at high temperatures or by severe plastic deformation at room temperature. In the present work, systematic first-principle calculations were conducted to evaluate the influences of the chemical short-range ordering clusters L1₂-Al₃Zr on the mechanical properties of the pure Al supercell. Results showed that the mechanical properties including both ideal tensile strength and ductility were improved simultaneously when the chemical short-range ordering clusters L1₂-Al₃Zr were introduced to the pure Al. The larger the volume fraction of chemical short-range ordering clusters L1₂-Al₃Zr, the larger the ideal tensile strength. The deformation charge density, the electron localization function and the density of state were computed to reveal the nature of the strengthening of the chemical short-range ordering clusters L1₂-Al₃Zr on the pure Al supercell. It was found that excellent ideal tensile strength for the Al supercell with the chemical short-range ordering clusters L1₂-Al₃Zr was due to strong charge accumulations and strong electronic interactions between the solute atoms Zr and the host Al atoms. In addition, the Pugh ratio (B/G) and ratio (W_sep/G_disl) of the work of the separation W_sep to the work of dislocation emission G_disl were computed to reveal the effect of the chemical short-range ordering clusters L1₂-Al₃Zr on the ductility of the Al supercell. Results showed that the addition of L1₂-Al₃Zr chemical short-range ordering clusters addition to pure Al supercell brought about an increase in ductility as compared to pure Al supercell, which is ascribed to large the Pugh ratio B/G and ratio (W_sep/G_disl) of the work of the separation W_sep to the work of dislocation emission G_disl. This work is important for simultaneously improving the tensile strength and ductility of Al alloys.

1. Introduction

Al alloys are crucial engineering materials, which are used in a wide range of structural applications [1,2,3,4,5,6,7,8]. This is because they usually show excellent mechanical properties (such as good machinability and excellent high-temperature resistance and creep resistance) as compared to pure Al [1,2,3,4,5,6,7,8]. However, similar to other dilute alloys, the mechanical properties including both tensile strength and ductility of the dilute Al alloys are two contradictory properties, which cannot be improved simultaneously. It has been found that the chemical short-range ordering structures play an important role in mechanical properties including both tensile strength and ductility. The experimental results showed that the complex concentrated alloys possess exceptional mechanical properties including both tensile strength and ductility. This may be attributed to the emergence of chemical short-range ordering (SRO) structures, which have a strong interaction with dislocation [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27]. For instance, in the Cr-Co-Ni medium-entropy alloy, the effects of the chemical SRO structures on the tensile strength and ductility were investigated by Ruopeng Zhang et al. Bulk tensile tests indicated that the chemical SRO structures had a strengthening effect (an approximately 25% increase of the yield strength as well as a marked change of the work hardening behavior) on the Cr-Co-Ni medium-entropy alloy, which was due to that the formation of SRO has a strong impact on dislocation [10].

In addition, in dilute alloys such as Al alloys and Cu alloys, the chemical short-range ordering structures (L1₂-Al₃Zr, L1₀-AlZn, FCC-Fe and B2-Fe) were also observed by using HAADF-STEM experimental technology [11,13,14,15,20,24,25,26,27]. For instance, in the Al-Zn alloys, the authors reported chemical short-range ordering structure L1₀-AlZn in an ultrafine-grained supersaturated Al-Zn alloy introduced by severe plastic deformation (strain (%) > 1) at room temperature [11]. It is believed that vacancies introduced by severe plastic deformation play an important role in the formation of the chemical short-range ordering at room temperature. The chemical SRO was also found in Guinier-Preston (GP) zones in Al-Cu alloys, which promotes dispersion strengthening [20,21]. Moreover, in the Al-Mg-Si alloys, co-clusters ≥20 solute atoms were observed by using atom probe tomography technology and DFT calculations [16]. It is indicated that the stability of the single-species Si clusters is improved as the vacancies exist. In turn, the single-species Si-vacancy clusters can attract further solute atoms to serve as a pathway to the formation of the larger Mg-Si co-cluster. The larger Mg-Si co-cluster can more effectively improve the mechanical properties of the AA6016 Al-Mg-Si alloy. The tensile mechanical properties of the 6016 alloy of the PA + PB exhibited excellent ultimate tensile strength (UTS) (291 MPa) and good ductility with a uniform elongation of 18% and a total elongation of 23% [16]. For the Cu-Fe alloys, it has been demonstrated that the chemical short-range ordering structures (FCC-Fe and B₂-Fe) were obtained by annealing processes at high temperatures [13]. The chemical short-range ordering cluster structures L1₂-Al₃Zr has been found in Al-Zn-Mg-Cu-Zr, and can promotes dispersion strengthening [20]. In these dilute alloys and complex concentrated alloys, the formation of the chemical short-range ordering structures leads to the improvement of the mechanical properties including tensile strength and ductility.

Therefore, in order to trade off the tensile strength and ductility in Al-alloy systems, it is necessary to develop new Al alloys with chemical short-range ordering cluster structures. Traditionally, the investigation of a new generation of Al alloys with excellent mechanical properties adopts the ‘trial and error’ approach, which requires a systematical production of alloys with varied compositions and aging conditions. Therefore, the theory method such as the first-principle calculations based on density function theory (DFT) was used because the “trial and error” approach is usually costly and time-consuming. To the best of our knowledge, the mechanical properties including tensile strength and ductility for the Al alloys with the chemical short-range ordering structures have rarely been investigated by using theory methods such as the first-principle calculations based on density function theory (DFT).

In the present work, the mechanical properties of the Al alloys with the chemical short-range ordering structures L1₂-Al₃Zr were studied using the first-principle calculations based on density function theory (DFT). Firstly, for comparative purposes, the supercells of the solid solution with varied compositions of the solute atoms Zr were constructed by using the special quasirandom structures (SQSs). Next, the Al supercells with the chemical short-range ordering cluster structures L1₂-Al₃Zr were obtained by substituting the Al atoms with the Zr atoms. Then, the bulk modulus B, shear modulus G, Young’s modulus E, Poisson’s ratio ν, hardness H and Pugh ratio B/G of the polycrystal were calculated to investigate the elastic property below a specific stress. Finally, the ideal tensile strength was calculated for the FCC-Al solid solution and Al supercells with the chemical short-range ordering structures L1₂-Al₃Zr. In addition, the projected density of state (PDOS), electron localization function (ELF) and deformation charge density were computed to reveal the nature of the strengthening effects of the chemical short-range ordering structures L1₂-Al₃Zr on the pure Al supercell. In particular, the work of dislocation emission G_disl and the work of separation W_sep for the pure Al supercells and the Al supercells with the chemical short-range ordering cluster structures L1₂-Al₃Zr were computed. We evaluated the ductility of the Al solid solution supercells with varied compositions of the solute atoms Zr and the Al supercells with the chemical short-range ordering cluster structure L1₂-Al₃Zr adopting the Pugh ratio B/G and the ratio (W_sep/G_disl) of the work of separation W_sep to the work of separation G_disl. The main findings of this work were twofold: (1) compared with the pure Al, the solid solutions with varied compositions of the solute atoms Zr and the chemical short-range ordering cluster structures L1₂-Al₃Zr had a strengthening effect on the pure Al supercell, which is attributed to more significant charge accumulations and electronic interactions between the host Al atoms and the Zr atoms and (2) addition of the L1₂-Al₃Zr chemical short-range ordering clusters to the pure Al brought an increase in ductility as compared to pure Al, which is ascribed to large the Pugh ratio B/G and the ratio (W_sep/G_disl) of the work of the separation W_sep to the work of dislocation emission G_disl. The paper is organized as follows: in Section 2, we describe, in detail, and using the computational approach, the supercells of the solid solution with varied compositions of the solute atoms Zr and Al supercell with the chemical short-range ordering cluster structure L1₂-Al₃Zr and in Section 3, the results and discussion about the ideal tensile strength, the elastic property, the work of the dislocation emission G_disl, the deformation charge density, the electron localization function (ELF) and the density of state (DOS) are presented. All main findings are summarized in Section 4.

2. Computational Methods and Details

2.1. The First-Principle Calculations and Supercell Model

In the present work, the first-principle calculations based on density functional theory (DFT) [28,29] were conducted by using the Vienna Ab initio Simulation Package (VASP) [28,29]. The interactions between ions and electronics were described by using the projector augmented wave potential (PAW) [30] method. The exchange-correlation functions were treated by utilizing the Perdew, Burke and Ernzerhof (PBE) form of generalized gradient approximation (GGA) [31]. In all calculations, a plane wave cutoff energy of 450 eV was adopted to guarantee converged total energies. The convergence criteria of 10⁻⁶ eV/atom for the total energy and 0.01 eV/Å for the atomic force were adopted. The k-space integrations were conducted adopting the Monkhorst–Pack sampling scheme with an equivalent of the k-point mesh of 26 × 26 × 26 for the bulk Al [32]. The equilibrium crystal structure data of bulk Al were calculated to be a_Al = 4.040 Å, which is consistent with the result of previous studies [8].

The chemical short-range ordering cluster structures (L1₂-Al₃Zr) are shown in Figure 1. The supercells of the Al solid solution with varied compositions (3.12%Zr, 6.25%Zr, 9.37%Zr, 12.50%Zr and 15.62%Zr) of the solute atoms Zr were constructed to assess the mechanical properties of the Al solid solution, as shown in Figure 2 and Figure 3. Figure 2 shows the supercells before relaxing atomic positions and volumes, while Figure 3 denotes the supercells after relaxing atomic positions and volumes. The special quasirandom structures (SQSs) were adopted to qualitatively consider the solubility of individual solute atoms in the Al lattices [33,34,35]. Special quasirandom structures (SQSs) have been successfully used in many alloy systems, and they can serve as structural templates to derive the mixing energies within the context of DFT total energy computations [33,34,35]. In the present work, 32-atom SQSs were generated, which could successfully satisfy correlation functions of pair clusters up to 3rd-nearest neighbors and perfect triplet matches on SQSs. The atomic positions and the volumes of the supercells of the solid solution were relaxed. A k-point mesh of 7 × 7 × 7 was adopted during the optimization of the supercells of the solid solution. In addition, when the first-principles tensile test of the supercells of the solid solution was conducted, a k-point mesh of 7 × 7 × 7 was sufficiently employed to guarantee converged total energies to balance the accuracy and efficiency of calculation. The Al supercells with the chemical short-range ordering (SRO) cluster structures L1₂-Al₃Zr were obtained by substituting the Al atoms with the Zr atoms, as shown in Figure 2 and Figure 3. The Al supercell with the chemical short-range ordering (SRO) cluster structures L1₂-Al₃Zr possesses 108 atoms. Therefore, to balance the accuracy and efficiency of calculation, 5 × 5 × 5 Monkhorst–Pack k-point meshes were employed to perform optimization and first-principles tensile tests of the Al supercells with the chemical short-range ordering (SRO) cluster structures L1₂-Al₃Zr. Firstly, the atomic positions and volumes were relaxed to obtain the most stable structures, as shown in Figure 3. It can be seen that after relaxing the atoms and volumes of the supercells of the Al solid solution with varied compositions of the solute atoms Zr, the volumes were greatly changed, as shown in Figure 3a–e. This is due to the fact that the size mismatch between the solute atoms Zr and host Al atoms is high (28.00%), as shown in

Table 1. The size mismatch and the electronegativity differences between the solute atoms Zr and host Al atoms, data from [36,37,38].

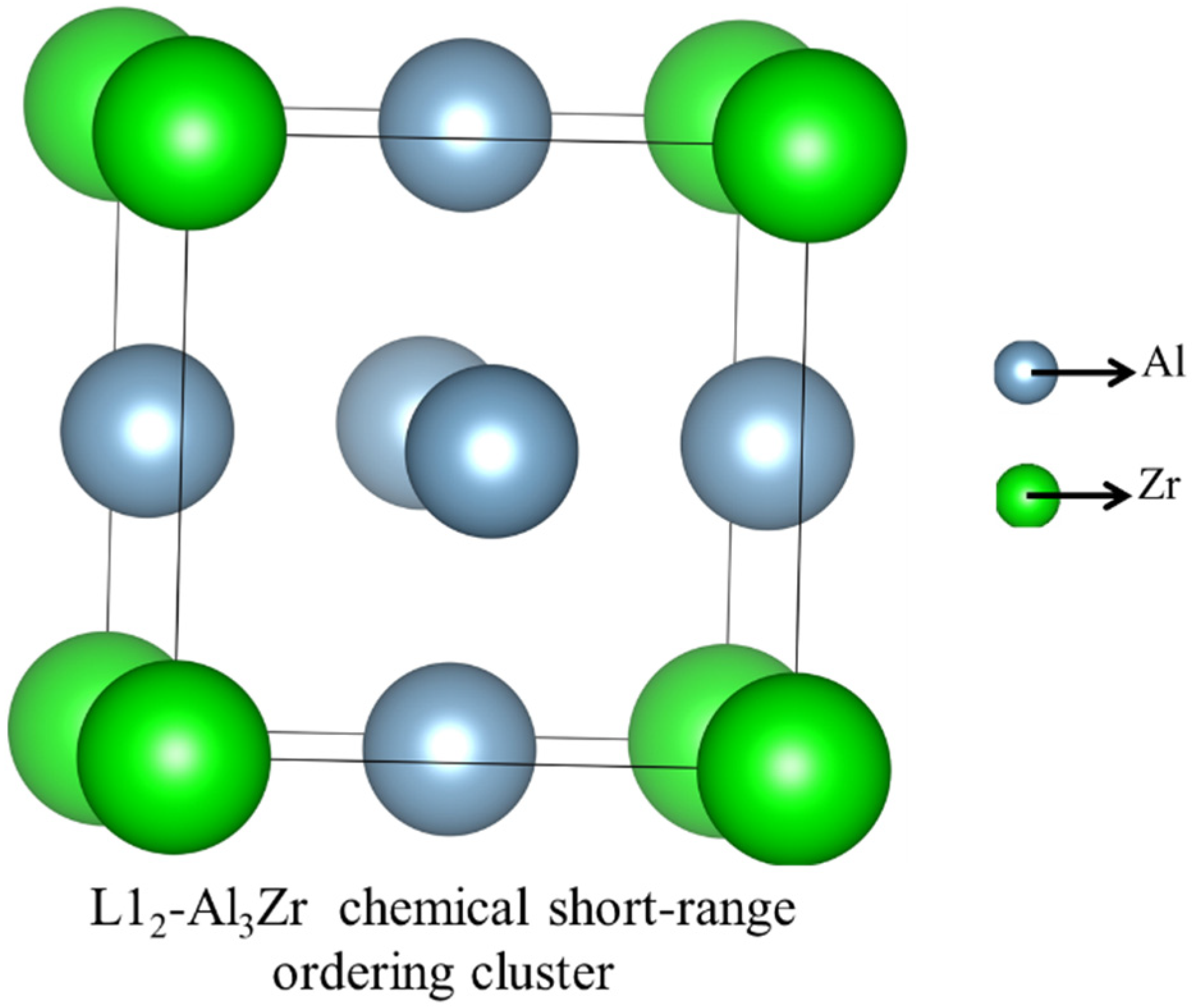
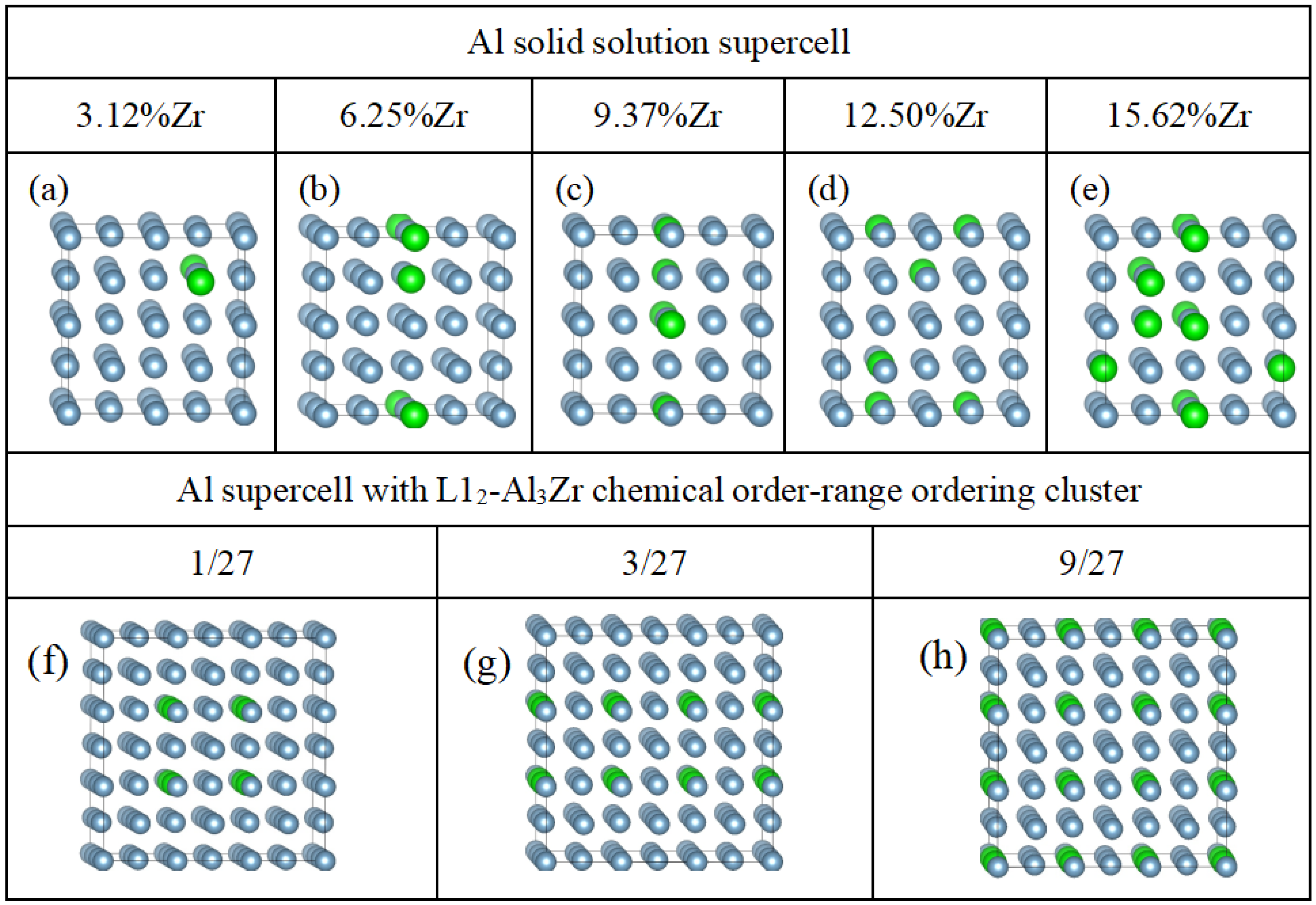
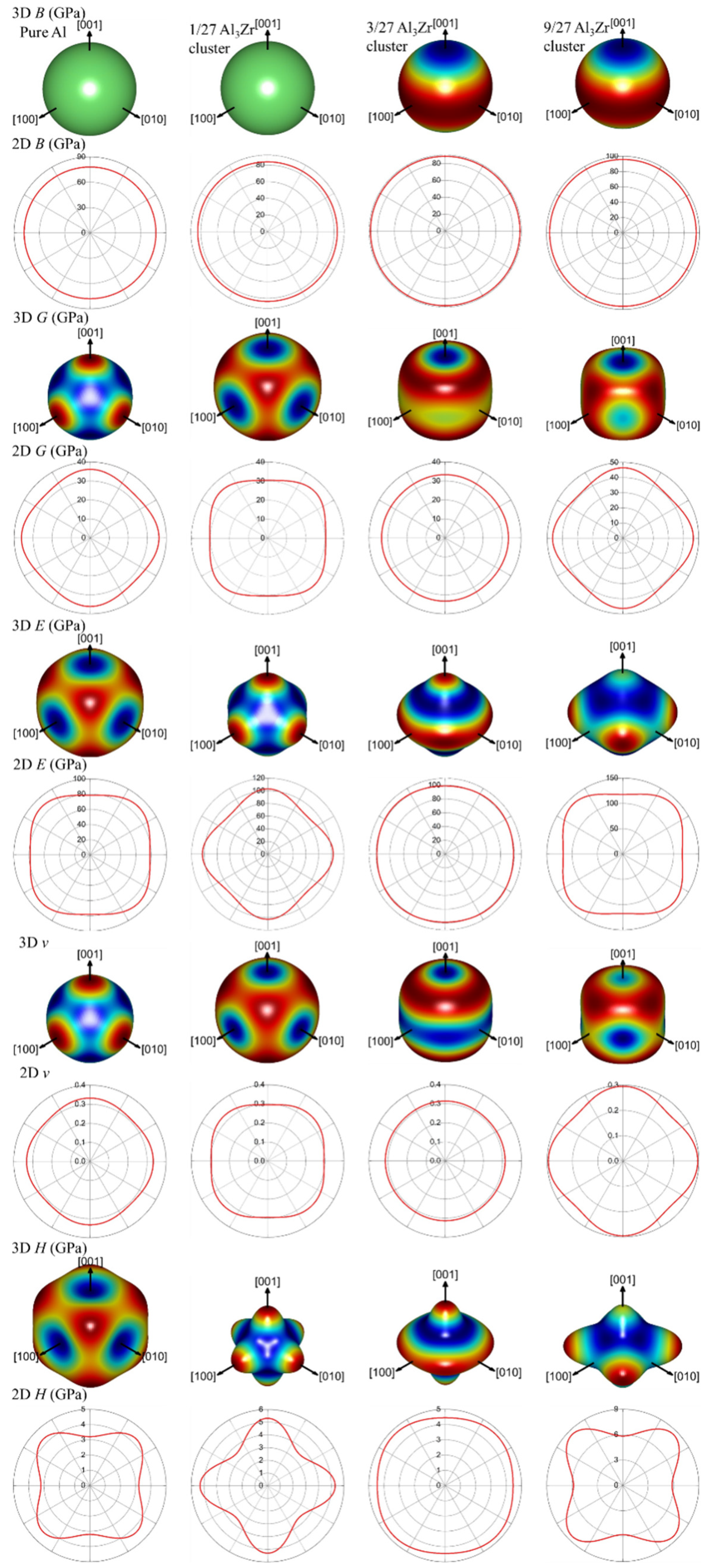
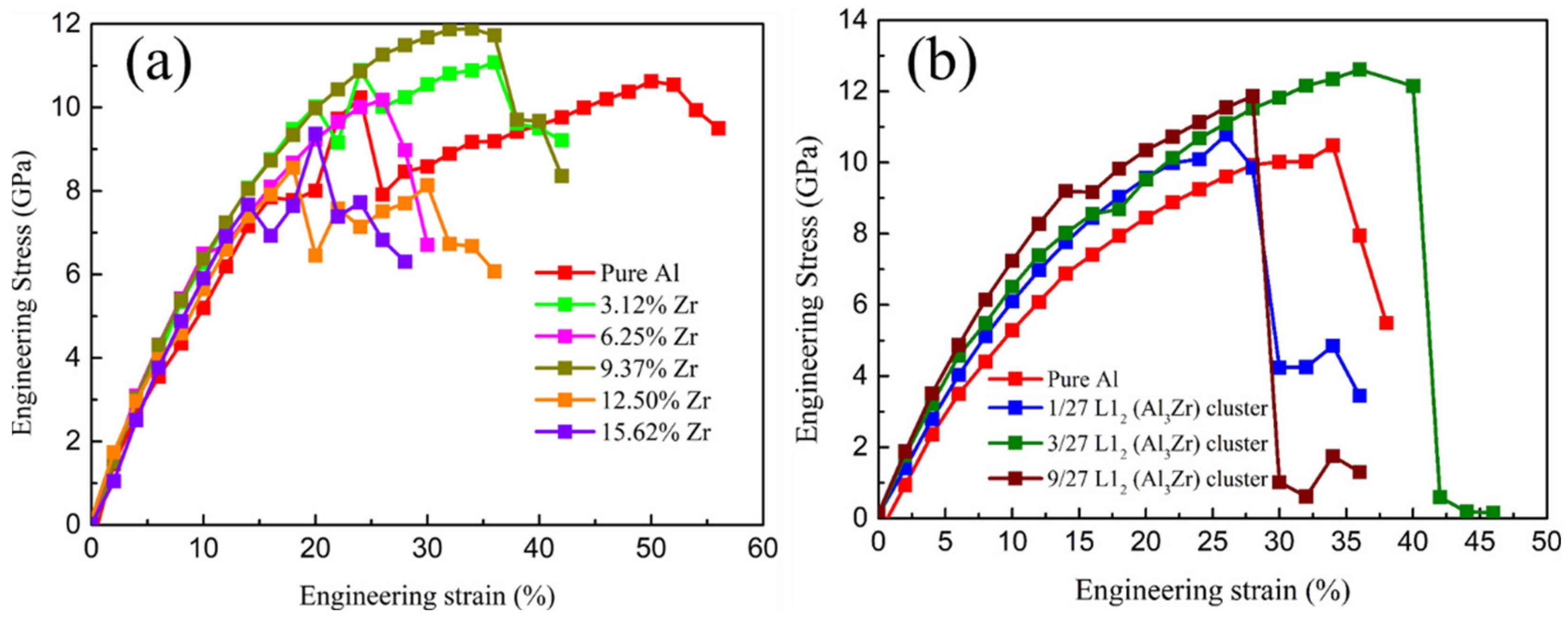
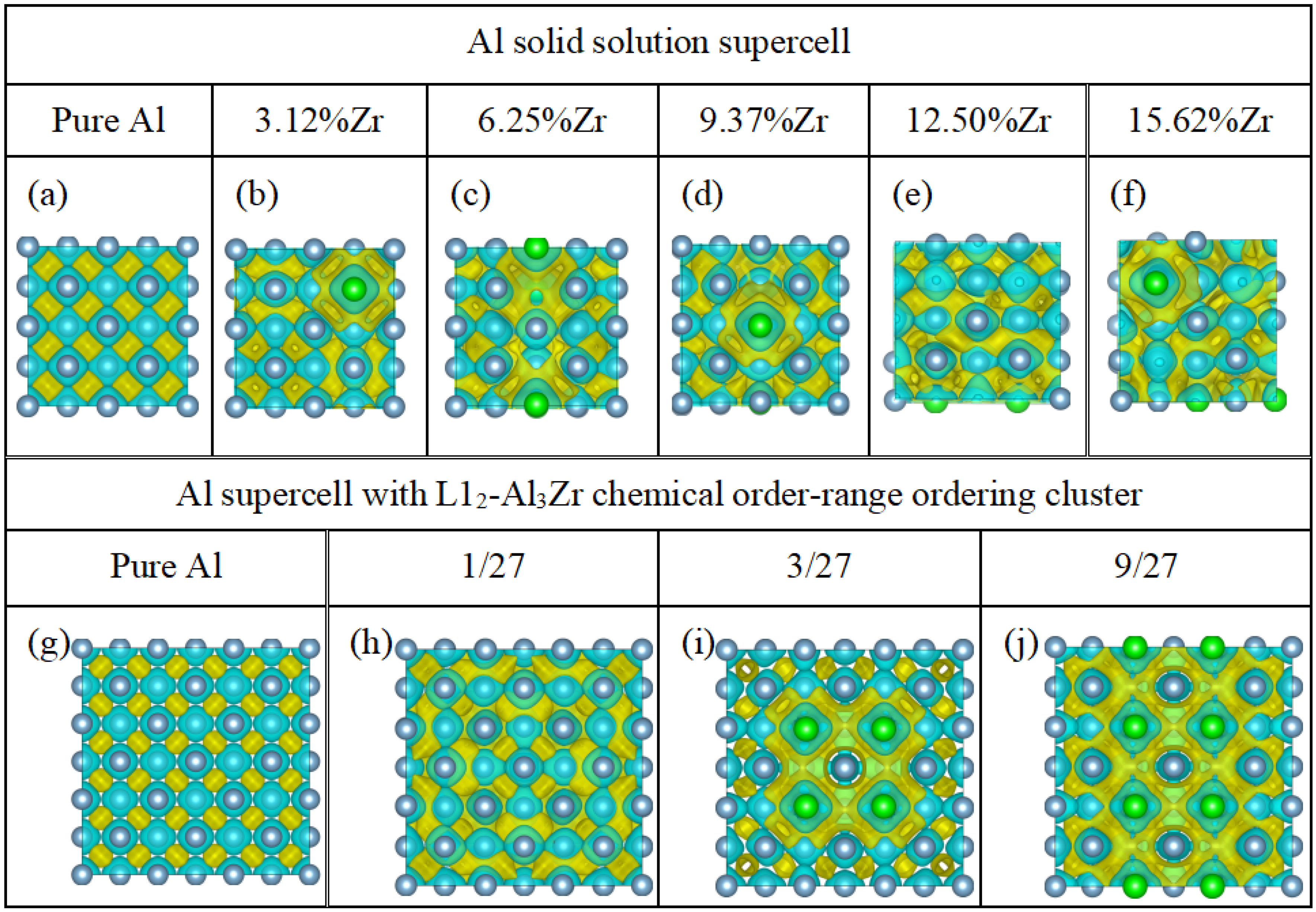
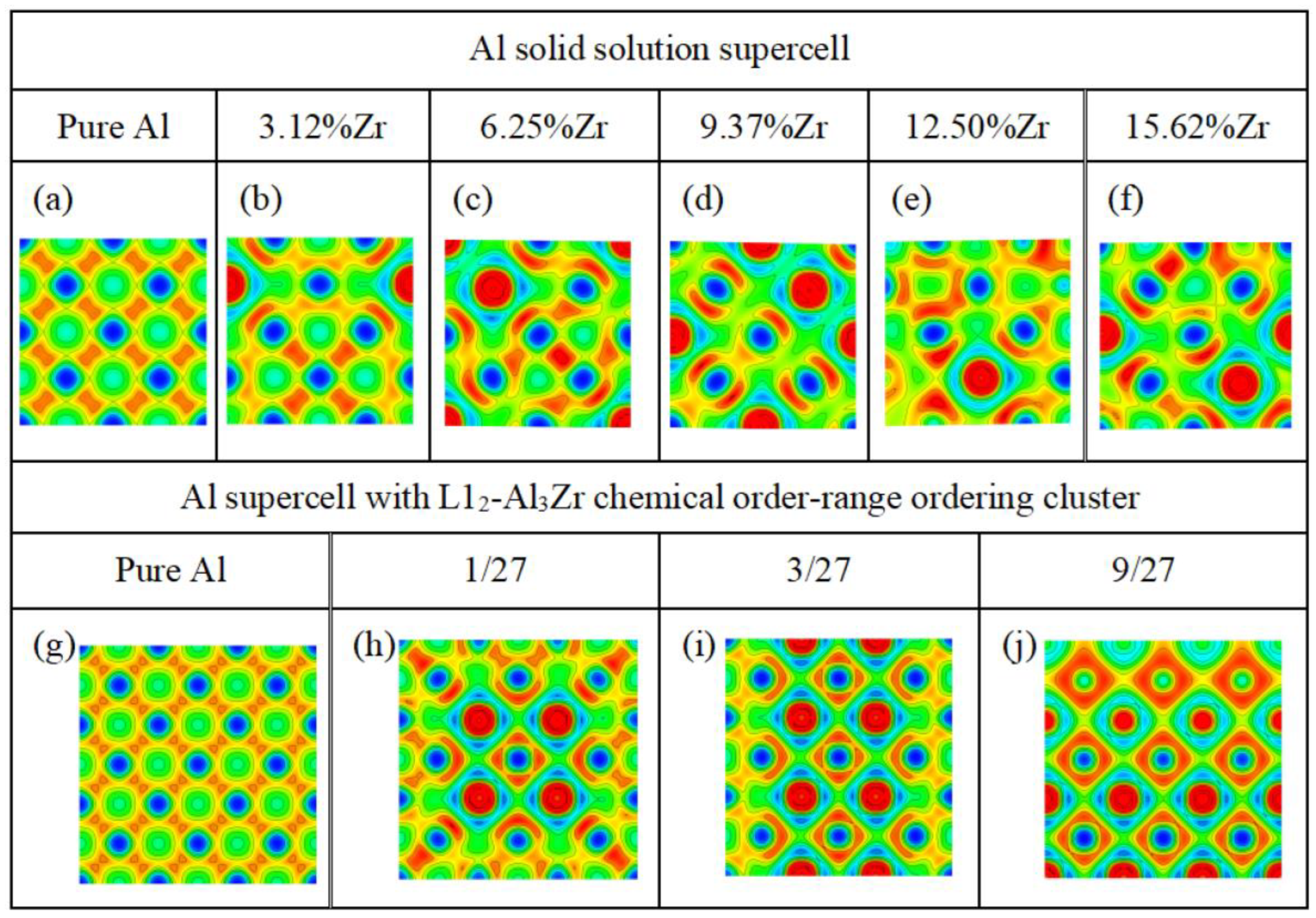
	Zr	Al
Size (Å)	1.60	1.25
Size mismatch	28.00%	–
Electronegativity	1.33	1.61
Electronegativity differences	17.39%	–

. This results in the tendency for the formation of the Al solid solution to be weak. In contrast, the volumes of the Al supercells with the chemical short-range ordering (SRO) cluster structures hardly changed after relaxing the atoms and volumes, as shown in Figure 3f–h. Because the electronegativity difference between the solute atoms Zr and host Al atoms is big (17.39%), as shown in Table 1. This leads to the formation of chemical short-range ordering (SRO) cluster structures L1₂-Al₃Zr being energetically favorable.

2.2. Elastic Property

To investigate the elastic property below a specific stress, the bulk modulus B, shear modulus G, Young’s modulus E, Poisson’s ratio ν and hardness H of the polycrystal were calculated. The pure Al supercell and the Al supercell with the chemical short-range ordering cluster Al₃Zr of volume fraction of 1/27 possess a cubic characteristic after optimizing the structure. However, the crystal structures of the Al supercell with the chemical short-range ordering cluster Al₃Zr of volume fraction of 3/27 and 9/27 change from the cubic structure before optimizing to a tetragonal structure after optimizing. For the cubic structure material, the equations of the bulk modulus B of the Voigt [39], Reuss [40] and Hill [41] approximations are expressed as follows:

$$B_H=B_V=B_R=(C_{11}+C_{12})/3$$

(1)

The shear modulus G_V and G_R are expressed as follows based on Voigt and Reuss approximations, respectively:

$$G_V=(C_{11}-C_{12}+3C_{44})/5$$

(2)

$$G_R=\frac{5(C_{11}-C_{12})C_{44}}{4C_{44}+3(C_{11}-C_{12})}$$

(3)

The shear modulus G_H is expressed as follows based on Hill approximations:

$$G_H=\frac{G_V+G_R}{2}$$

(4)

Young’s modulus E and Poisson’s ratio ν are expressed as follows:

$$E=\frac{9GB}{3B+G}$$

(5)

$$\nu =\frac{3B-2G}{2(3B+G)}$$

(6)

The hardness H is expressed as follows:

$$H=\frac{(1-2\nu )E}{6(1+\nu )}$$

(7)

The universal anisotropy index is expressed as follows:

$$A^u=5\frac{G_V}{G_R}+\frac{B_V}{B_R}-6$$

(8)

The Hill values of Young’s modulus E_H are obtained by taking the average of the values by Voigt and Reuss approximations:

$$E_H=\frac{E_R+E_V}{2}.$$

(9)

For the tetragonal structure material, the bulk modulus B_V and B_R of the Voigt and Reuss approximations are expressed as follows:

$$B_V=(2C_{11}+4C_{12}+2C_{13}+C_{33})/9$$

(10)

$$B_R=\frac{2}{9C_{11}}+\frac{1}{9C_{33}}+\frac{4}{C_{12}}+\frac{2}{C_{13}}$$

(11)

The shear modulus G_V and G_R of the Voigt and Reuss approximations are expressed as follows:

$$G_V=(2C_{11}-2C_{12}-C_{13}+C_{33}+8C_{44}+4C_{66})/15$$

(12)

$$G_R=(2C_{11}-8C_{12}-4C_{13}+C_{33}+6C_{44}+3C_{66})/15.$$

(13)

In addition, to reveal the mechanical behavior of the pure Al supercell and the Al supercell with the chemical short-range ordering cluster Al₃Zr, the Pugh ratio B/G is adopted to characterize the ductile or brittle of these materials. The bulk modulus B is considered to be resistant to fracture, while the shear modulus G is considered to be resistant to plastic deformation. If the Pugh ratio B/G > 1.75, the material is more ductile, otherwise, it shows a brittle characteristic [42].

The bulk modulus B, shear modulus G, Young’s modulus E, Poisson’s ratio ν and hardness H of the pure Al supercell and the Al supercell with the chemical short-range ordering cluster Al₃Zr of volume fraction of 1/27, 3/27 and 9/27 are displayed in

Table 2. The calculated bulk modulus B, shear modulus G, Young’s modulus E, Poisson’s ratio ν, hardness H and Pugh ratio B/G.

Supercell	B (GPa)	G (GPa)	E (GPa)	ν	H (GPa)	B/G
Al	77.964	33.283	87.411	0.313	4.180	2.340
1/27Al3Zr	83.763	33.830	89.448	0.322	3.970	2.476
3/27Al3Zr	87.610	34.053	90.442	0.328	3.819	2.573
9/27Al3Zr	93.568	44.370	114.942	0.295	5.774	2.109

. When the chemical short-range ordering cluster Al₃Zr is introduced to the Al supercell, it is seen that the increase of the volume fraction of the chemical short-range ordering cluster Al₃Zr leads to an increase in the bulk modulus B, shear modulus G and Young’s modulus E. The Poisson’s ratio ν first increases when the volume fraction of the chemical short-range ordering cluster Al₃Zr increases from 1/27 to 3/27. Then it decreases with the increase of the volume fraction of the chemical short-range ordering cluster Al₃Zr. The smaller values (<0.5) of the Poisson’s ratio ν indicate the good compressibility of the Al supercell without or with the chemical short-range ordering cluster Al₃Zr. The hardness H decreases first with the volume fraction of the chemical short-range ordering cluster Al₃Zr and then increases. In particular, the value of the Pugh ratio B/G increases with an increase of the volume fraction of the chemical short-range ordering cluster Al₃Zr from 1/27 to 3/27. Then, when the volume fraction of the chemical short-range ordering cluster Al₃Zr increases from 3/27 to 9/27, the value of the Pugh ratio B/G is decreased from 2.572 to 2.109. Furthermore, it is seen that the value of the Pugh ratio B/G > 1.75, implying that the Al supercell without or with the chemical short-range ordering cluster Al₃Zr is ductile. The ductility of the Al supercell with the chemical short-range ordering cluster Al₃Zr of the volume fraction of 3/27 is the largest, which is consistent with the result of the first-principles tensile test. The calculated anisotropy of the bulk modulus B, shear modulus G, Young’s modulus E and Poisson’s ratio ν are displayed in

Table 3. The calculated anisotropy of bulk modulus B, shear modulus G, Young’s modulus E and Poisson’s ratio ν.

Supercell	B (GPa)	G (GPa)	E (GPa)	ν
Al	1.000	1.228	1.197	1.592
1/27Al3Zr	1.000	1.310	1.268	1.680
3/27Al3Zr	1.027	1.345	1.235	1.723
9/27Al3Zr	1.073	1.548	1.355	2.226

and Figure 4. From Table 3 and Figure 4, it is seen that the chemical short-range ordering cluster Al₃Zr altered the anisotropy of the Al supercell. The larger the volume fraction of the chemical short-range ordering cluster Al₃Zr the more significant the calculated anisotropy.

2.3. Ideal Tensile Strength

In this study, the first-principles tensile test loaded in the [001] direction was conducted for the supercells of the Al solid solution with varied compositions (3.12%Zr, 6.25%Zr, 9.37%Zr, 12.50%Zr and 15.62%Zr) of the solute atoms Zr and Al supercells with the chemical short-range ordering clusters L12-Al3Zr (the volume fraction of 1/27, 3/27 and 9/27). It is well known that the theoretical tensile strengths are much larger along [001] directions as compared to the [110] and [111] directions. As a result, in this work, the [001] direction was set as the tensile direction for the solid solution supercell and the Al supercell without or with the chemical short-range ordering clusters L1₂-Al₃Zr. In the absence of strain, the atomic positions and the volumes were relaxed. It should be noted that the lattice parameters of pure Al supercells in the zero-strain state coincide with the previous calculation [8]. Under distortion, a uniaxial tensile strain was applied along the [001] direction, and at each application, the lattice vector c along the [001] direction was fixed. In contrast, the other two lattice vectors (a ([100] direction) and b ([010] direction)) perpendicular to the [001] direction were relaxed. From this quasistatic procedure, the engineering stress σ versus engineering strain ε data were obtained. The engineering stress σ can be expressed as the first order derivative of total energy E(ε) concerning strain ε as

$$\sigma =\frac{1+\epsilon }{V(\epsilon )}\frac{\partial E(\epsilon )}{\partial \epsilon }$$

(14)

where V(ε) is the volume of the supercell under uniaxial strain ε and E(ε) is the total energy of the supercell under uniaxial strain ε. The engineering stain ε of the supercell in the [001] direction is expressed as

$$\epsilon =\frac{a_{\mathrm{strain}}-a_{\mathrm{initial}}}{a_{\mathrm{initial}}}$$

(15)

in the equation, the a_strain and a_initial denote the lengths of the supercells parallel to the applied strain in the strained and initial states, respectively.

2.4. The Deformation Charge Density

The deformation charge density $\Delta \rho (r)$ is expressed as

$$\Delta \rho =\rho {(r)}_{\mathrm{self}-\mathrm{consistent}}-\rho {(r)}_{\mathrm{atomic}}$$

(16)

where $\rho {(r)}_{\mathrm{self}-\mathrm{consistent}}$ is the total valence charge density of the supercell and $\rho {(r)}_{\mathrm{atomic}}$ represents the superposition of the valence charge densities of neutral atoms of the supercell. The stronger the charge accumulation, the larger the bonding between the atoms.

2.5. The Competing Fracture Mechanisms

If Griffith cleavage decohesion occurs before conditions for crack tip blunting by dislocation nucleation, the deformation of the Al supercell is in the form of brittle. Conversely, if crack tip blunting by dislocation nucleation occurs before conditions for Griffith cleavage decohesion, the deformation of the Al supercell is in the form of ductile [43,44]. The Griffith cleavage decohesion (work of the separation W_sep) for the Al supercell with the chemical short-range ordering clusters L1₂-Al₃Zr is expressed as

$$W_{\mathrm{sep}}=\left(E_{\mathrm{tot}}^1+E_{\mathrm{tot}}^2-E_{\mathrm{tot}}^{\mathrm{Al}-\mathrm{supercell}}\right)/A$$

(17)

where $E_{\mathrm{tot}}^1$ and $E_{\mathrm{tot}}^2$ represent the total energies of the supercell slabs 1 and 2 after separating the Al supercell, respectively; A denotes the cross-sectional area perpendicular to the [001] direction; $E_{\mathrm{tot}}^{\mathrm{Al}-\mathrm{supercell}}$ is the total energy of the Al supercell before separating. For comparison, the work of the separation W_sep of the pure Al supercell was also calculated using Equation (4). When the dislocation nucleation at the crack of the Al supercell with the chemical short-range ordering clusters L1₂-Al₃Zr under tensile loading is normal to the crack plane, the threshold for dislocation nucleation G_disl is closely related to the unstable stacking fault energy γ_usf as [43]

$$G_{\mathrm{disl}}=8\frac{1+(1-\nu {)\tan }^2\varphi }{(1+\cos \theta ){\sin }^2\theta }{\gamma }_{\mathrm{usf}}$$

(18)

where θ denotes the inclination angle of the crack plane with respect to the slip plane, φdenotes the angle between the Burgers vector along the slip plane and the normal to the crack tip front, and ν is the Poisson’s ratio. In the present work, a uniaxial tensile strain was applied along the [001] direction for the Al supercell. A crack is assumed on a (001) plane and tip along a <110> direction. In addition, the stressed slip system is (111) <211> for fcc Al supercell. Therefore, the angle θ between the slip plane and the crack plane is 54.73° [43]. In the fcc crystal, the dislocation nucleation involves slip along the <$10\overline{1}$> direction under the loading, meaning that the angle $\varphi$ between the Burgers vector along the slip plane and the normal to the crack tip front is 0° [43]. In order to calculate the G_disl, the unstable stacking fault energies of the Al supercells with and without the chemical short-range ordering clusters L1₂-Al₃Zr at the faulted region were obtained from the generalized stacking fault energy (GSFE) curve. To assess the unstable stacking fault energy of the Al matrix, a supercell slab of a vacuum layer 20 Å thick that possessed 11 layers of atoms was built. An unstable stacking fault was generated between layers 6 and 7 by translating atomic layers 7 to 11. The chemical short-range ordering cluster L1₂-Al₃Zr was introduced to the unstable stacking fault region of the Al matrix to assess further the influence of the chemical short-range ordering cluster L1₂-Al₃Zr on the unstable stacking fault energy (USF) γ_usf of the Al matrix. For calculating the generalized stacking fault energy (GSFE), a selective dynamics mode was adopted. That is, during the relaxing atom, the atom along the shearing vectors direction was fixed, while it was relaxed along another two directions. The generalized stacking fault energy is expressed as

$${\gamma }_{\mathrm{GSFE}}=\frac{E_{faulted}-E_{perfect}}{A}$$

(19)

where A is the cross-sectional area over the faulted region and E_perfect and E_faulted represent the total energies of perfect and faulted supercells, respectively.

3. Results and Discussion

3.1. Ideal Tensile Strength

The calculated engineering stress–strain curves in the [001] direction for the supercells of the Al solid solution with varied compositions of the solute atoms Zr and the Al supercells with the chemical short-range ordering clusters L1₂-Al₃Zr are plotted in Figure 5a and Figure 5b, respectively. As shown in Figure 5a,b, the increase of the engineering strain resulted in an increase in the engineering stress, yielding the ideal tensile strength (the maximum of the tensile stress), which is listed in

Table 4. The calculated ideal tensile strength in the [001] direction for the models of the Al solid solution with varied compositions of the solute atom Zr and Al supercell models with the chemical short-range ordering clusters L1₂-Al₃Zr.

	Solid Solution						Chemical Short-Range Ordering Cluster
	Pure Al	3.12%Zr	6.25%Zr	9.37%Zr	12.50%Zr	15.62%Zr	Pure Al	1/27 Al3Zr	3/27 Al3Zr	9/27 Al3Zr
Stress (GPa)	10.63	11.08	10.18	11.88	8.56	9.37	10.48	10.78	12.15	11.87
Strain (%)	50.00	36.00	26.00	34.00	18.00	20.00	34.00	26.00	40.00	28.00

. It can be seen from Figure 5 and Table 4 that the ideal tensile strength for the supercells of the Al solid solution with the solute atoms Zr of 3.125% and 9.375% and the Al supercells with the chemical short-range ordering clusters L1₂-Al₃Zr was much larger as compared to the pure Al supercell, meaning that Al solid solution and the chemical short-range ordering clusters L1₂-Al₃Zr bring a strengthening effect to the pure Al. Moreover, it can be seen from Figure 5b and Table 4 that when the volume fraction of the chemical short-range ordering clusters L1₂-Al₃Zr increased from 1/27 to 9/27, the ideal tensile strength first increased from 10.78 GPa to 12.15 GPa, and then decreased from 12.15 GPa to 11.87 GPa That is to say, the chemical short-range ordering clusters L1₂-Al₃Zr of the volume fraction of 3/27 resulted in the largest ideal tensile strength. In addition, it was found that the ideal tensile strength for the supercells of the Al solid solution was smaller than that for the Al supercells with the chemical short-range ordering clusters L1₂-Al₃Zr. This means that the strengthening effects of the chemical short-range ordering clusters L1₂-Al₃Zr on the Al supercells were more significant than that of the Al solid solution. In particular, it can be seen that the ductility of the Al supercell with the chemical short-range ordering clusters L1₂-Al₃Zr of the volume fraction of 3/27 was the largest. These results indicate that the introduction of the chemical short-range ordering clusters L1₂-Al₃Zr of the volume fraction of 3/27 not only results in an increase in the strength of the Al supercell but also brings an increase in the ductility of the Al supercell. The result is consistent with the calculated elastic property.

3.2. The Competing Fracture Mechanisms

The generalized stacking fault energy (GSFE) curves for the Al matrix with and without the chemical short-range ordering clusters L1₂-Al₃Zr were obtained from Equation (19), as plotted in Figure 6. The unstable stacking fault energy was obtained from Figure 6, as listed in

Table 5. The work of dislocation emission G_disl, the work of separation W_sep, the unstable stacking fault energy γ_usf and the ratio (W_sep/G_disl).

	Al3Zr (1/27)	Al3Zr (3/27)	Pure Al Matrix
Wsep (J/m2)	2.76	2.82	2.50
Gdis (J/m2)	0.97	0.95	1.46
Wsep/Gdisl	2.85	2.97	1.71

. It is obvious that the unstable stacking fault energy decreases when the chemical short-range ordering clusters L1₂-Al₃Zr are located in the faulted region. After obtaining the unstable stacking fault energy, the work of the dislocation emission G_disl for the Al supercell with and without the chemical short-range ordering clusters L1₂-Al₃Zr at the faulted region was obtained from Equation (18), as listed in Table 5. The work of the separation W_sep of the Al supercell with and without the chemical short-range ordering clusters L1₂-Al₃Zr was calculated from Equation (17), as displayed in Table 5. When the chemical short-range ordering clusters L1₂-Al₃Zr were located in the faulted region of the Al supercells, the ratio (W_sep/G_disl) of the work of the separation W_sep to the work of dislocation emission G_disl was larger as compared to the pure Al supercells. This indicates that the chemical short-range ordering clusters L1₂-Al₃Zr addition to the Al supercells brings an increase in the ductile. In addition, the ratio (W_sep/G_disl) of the work of the separation W_sep to the work dislocation emission G_disl for the Al supercell with the chemical short-range ordering clusters L1₂-Al₃Zr of volume fraction of 3/27 was much larger than that for the Al supercell with the chemical short-range ordering clusters L1₂-Al₃Zr of volume fraction of 1/27, indicating that the ductility of the Al supercell with the chemical short-range ordering clusters L1₂-Al₃Zr of volume fraction of 3/27 was much larger than that of 1/27. This result is consistent with the calculated engineering stress and strain curve, as shown in Figure 5b.

3.3. The Deformation Charge Density

To further understand the nature of the stress enhancement (or weakening), the three-dimensional deformation charge density was obtained from Equation (16). Figure 7a–f show the three-dimensional deformation charge density of pure Al and Al solid solution with varied compositions of the solute atoms Zr after relaxing atoms and volumes. The three-dimensional deformation charge density of pure Al and Al supercell with the chemical short-range ordering clusters L1₂-Al₃Zr after relaxing atoms and volumes are shown in Figure 7g–j. It can be seen that the charge redistribution was significant in these supercells. An accumulation of the charge is represented by a yellow color, while depletion of the charge is shown by a cyan color. An accumulation of the charge indicates bond strengthening, while depletion of the charge means bond weakening. In Figure 7a–f, the charge accumulations were significant between Al atoms. In particular, the charge accumulations between Al atoms and the solute atoms Zr for the Al solid solution of 3.12% Zr and 9.37% Zr were more significant than that between Al atoms for the pure Al. This explains why the ideal tensile strength of Al solid solution of 3.12% Zr and 9.37% Zr was bigger than that of the pure Al (See Figure 5a). The charge accumulations between Al atoms and the solute atoms Zr for the Al supercells with the chemical short-range ordering clusters L1₂-Al₃Zr were stronger than that between Al atoms for the pure Al supercells, which leads to larger ideal tensile strength for the Al supercell with chemical short-range ordering clusters L1₂-Al₃Zr as compared to the pure Al (See Figure 5b). These results are in agreement with the calculated engineering stress–strain curves.

3.4. The Electron Localization Function (ELF)

As shown in Figure 8, the electron localization function (ELF) of Al solid solution with varied compositions of the solute atoms Zr and the Al supercells with the chemical short-range ordering clusters L1₂-Al₃Zr was calculated to further reveal the nature of the strengthening effects of the Al solid solution and the chemical short-range ordering clusters L1₂-Al₃Zr on the pure Al supercell. The ELF can clearly characterize the formation of bonds and electron occupation of the atomic orbitals. The type of bonding is indicated by the distribution and overall intensity of the ELF. For instance, the regions of space between the atomic cores are occupied homogeneously by the free electrons of the metal. In addition, in metals, the relative intensities of the ELF remain low. However, in ionic and covalent materials, the electronic distribution in the region between neighboring atoms is more localized. Moreover, ionic and covalent materials show a larger overall intensity of the ELF. It can be seen from Figure 8a,c) that the pure Al displays a low overall ELF intensity (~0.5 e/Bohr³), indicating that there is a metallic bonding characterization in the pure Al. When the solute atom Zr and chemical short-range ordering clusters L1₂-Al₃Zr are introduced to the pure Al supercell, the regions around the Zr show a lower overall ELF intensity (~0.0 e/Bohr³), suggesting that the delocalization of the electronics is more significant in the region around the Zr. However, the regions around the Al show a larger overall ELF intensity (~0.7 e/Bohr³), indicating that the localization of the electronics is more significant in the region around the Al. This means that the metallic bonding between Al atoms for the pure Al will shift towards partially covalent or ionic bonding between the Al atom and Zr atom for the Al solid solution supercell and the Al supercells with the chemical short-range ordering clusters L1₂-Al₃Zr, which increases the bonding interaction between the Al and the nearest neighbor Zr atoms. These results are consistent with the charge density differences (See Figure 7) and the calculated engineering stress–strain curves (See Figure 5).

3.5. The Projected Density of State (PDOS)

Apart from the charge density difference and electron localization function (ELF), the electronic interactions of solute atoms Zr and surrounding host Al atoms in the Al supercells with the chemical short-range ordering cluster L1₂-Al₃Zr were also analyzed further by computing the projected density of state (PDOS) to uncover the nature of the strengthening effects of the chemical short-range ordering clusters L1₂-Al₃Zr on the pure Al supercell. The projected density of state (PDOS) of the host Al atoms for the pure Al supercell was also calculated for comparison, as shown in Figure 9a. Figure 9b–d represent the projected density of state (PDOS) of the solute atoms Zr and surrounding host atom Al for the Al supercells with the chemical short-range ordering clusters L1₂-Al₃Zr of the volume fraction of 1/27, 3/27 and 9/27, respectively. In Figure 9b, there are no significant hybrid peaks of the p electronic state of the host Al atoms and the d electronic state of the solute atoms Zr. In addition, it can be seen from Figure 9c that the hybrid peaks of the p electronic state of the host Al atoms and the d electronic state of the solute atoms Zr are significant, as indicated by the arrows. Figure 9d shows that the p electronic state of the host Al atoms and the d electronic state of the solute atoms Zr only exist as a hybrid peak below the Fermi level, as denoted in the arrow. These results indicate that the interactions between the solute atoms Zr and nearest the host Al atoms in the Al supercells with the chemical short-range ordering clusters L1₂-Al₃Zr of the volume fraction of 3/27 are the strongest. This explains why the strengthening effect of the chemical short-range ordering clusters L1₂-Al₃Zr of the volume fraction of 3/27 is the most significant. These results are in agreement with the calculated engineering stress–strain curves (See Figure 5).

4. Conclusions

In conclusion, in the present work, the mechanical properties of the Al solid solution with varied compositions of the solute atoms Zr and the Al supercells with the chemical short-range ordering structures L1₂-Al₃Zr were evaluated using first-principle calculations. Firstly, the supercells of the solid solution with varied compositions of the solute atoms Zr were constructed by using special quasirandom structures (SQSs). Next, the Al supercells with the chemical short-range ordering structures L1₂-Al₃Zr were obtained by substituting the Al atoms with the Zr atoms. Then, the bulk modulus B, shear modulus G, Young’s modulus E, Poisson’s ratio ν, hardness H and Pugh ratio B/G of the polycrystal were calculated to investigate the elastic property below a specific stress. Finally, the ideal tensile strength was investigated by conducting the first-principles tensile test. In addition, the deformation charge density, electron localization function (ELF) and the projected density of state (PDOS) were computed to reveal the nature of the strengthening effects of the solid solutions and the chemical short-range ordering structures L1₂-Al₃Zr on the pure Al. The work of the separation W_sep and the work of dislocation emission G_disl were also calculated to reveal the competing fracture mechanisms. Here, the main findings of this work are as follows:

(1)

The solid solutions with varied compositions of the solute atoms Zr and the chemical short-range ordering clusters L1₂-Al₃Zr can improve the strength of the pure Al. In particular, the chemical short-range ordering clusters L1₂-Al₃Zr of the volume fraction of 3/27 can simultaneously improve the strength and ductility of the Al supercell. which is confirmed by the calculated elastic property such as Pugh ratio B/G and computed the ratio (W_sep/G_disl) of the work of the separation W_sep to the work of dislocation emission G_disl.

(2)

The significant charge accumulations and the electronic interactions between the Al atoms and the nearest Zr atoms bring an excellent ideal tensile strength for the Al supercells with the chemical short-range ordering clusters L1₂-Al₃Zr. In addition, the ratio (W_sep/G_disl) of the work of the separation W_sep to the work of dislocation emission G_disl for Al supercells with the chemical short-range ordering clusters L1₂-Al₃Zr of the volume fraction of 3/27 is larger than that of the pure Al supercell. This explains that the ductility of the Al supercell with the chemical short-range ordering clusters L1₂-Al₃Zr is much larger than that of the pure Al supercell.