Abstract
Plastic deformation and fracture of Zr–1% Nb alloys exposed to quasi-static tensile testing have been studied via a joint analysis of stress-strain curves, ultrasound velocity and double-exposure speckle photographs. The possibilities of ductility evaluation through the εxx strain distribution in thin-walled parts of zirconium alloys are shown in this paper. The stress-strain state of zirconium alloys in a cold rolling site is investigated considering the development of localized deformation bands and changes in ultrasound velocity. It is established that the transition from the upsetting to the reduction region is accompanied by the significant exhaustion of the plasticity margin of the material; therefore, the latter is more prone to fracture in this zone exactly. It is shown that traditional methods estimating the plasticity margin from the mechanical properties cannot reveal this region, requiring a comprehensive study of macroscopically localized plastic strain in combination with acoustic measurements. In particular, the multi-pass cold rolling of Zr alloys includes various localized deformation processes that can result in the formation of localized plasticity autowaves. Recommendations for strain distribution division over the deformation zone length in the alloy in the pilger roll grooves are provided as well.
1. Introduction
It is known that the macroscopic localization of plastic flow has an autowave behavior, and the type of autowave is determined by the strain hardening law [1,2]. Thus, at the stage of linear work hardening, a system of equidistant localization foci moves at a constant speed, that is, a phase autowave. At the stage of parabolic work hardening, the distribution of deformation foci remains spatially periodic, but their motion stops and, in terms of synergetics [3], a stationary dissipative structure appears. With the beginning of the pre-failure stage, a stationary zone with the high amplitude and local strain accumulation rate (the future fracture point) is formed at the site of one of the foci. The remaining foci come into a self-consistent movement in the direction of the specified fixed zone so as to simultaneously reach the failure point. This phenomenon is interpreted as the collapse of the localized plasticity autowave [4]. Earlier, it was proposed to use quantitative characteristics of the entire evolution process of autowaves as a criterion of viscous failure [1,2,4]. Numerous experimental data reveal [1,2,5,6] that plastic strain localization observed in many materials has identical form. However, searching for the ways for observing such autowave processes in hexagonal close-packed (HCP) structures and solving problems associated with the plasticity control of workpieces pre-deformed at earlier stages of the technological processing has become an urgent task.
The use of zirconium-based alloys as fundamental structural materials for nuclear reactors [7,8] requires knowledge of their structure and properties during plastic deformation [9]. This is of great importance, especially when assessing the technological plasticity of alloys in the manufacturing of finished products. Despite the continuing interest in Zr-based alloys [10,11,12,13,14,15], the nature of their plastic deformation has not been fully studied. As for doped Zr alloys, their deformation and plastic characteristics are mainly determined by the complex phase composition and microstructure [16,17,18,19,20,21,22]. To gain insight into the plastic flow features of zirconium alloys, the evolution of their micro- and macroscopic defective structures with the development of strain requires thorough study.
Further improvement of the operational parameters of zirconium also necessitates the application of reliable laboratory tools for performance assessment of related products, associated with fracture resistance and plasticity. Traditional techniques consist in the direct testing of the material in thin-walled products, which often makes it impossible to use standard mechanical and corrosion evaluation approaches. Therefore, methods based on nonlinear fracture mechanics are applied to determine the crack resistance of such products and to establish a relationship between the fracture resistance and the ability of alloys to deformation hardening and stable plastic flow. The condition for the irregular growth of a viscous crack is the local deformation instability at its apex. In this case, strain and fracture are determined by the degree of deformation accommodation of the structural components of the alloy with different deformation capacity. This makes it possible to identify the structural element that determines the plastic flow localization and the crack development. Acoustic emission (AE) measurements during the testing of samples and upon the manufacture and operation of products are one of the effective tools of monitoring the quality of materials and technologies. In addition to high sensitivity, the main advantage of the AE method is the possibility of the operational study of deformation and fracture processes. The AE experiments combined with electron microscopy, X-ray diffraction and fractography, as well as mechanical, corrosion and other tests, allow one to highlight the phenomena occurring in composites. This is essential for the quality control of materials and processes during their design, production and operation [23].
A powerful technique for the study of heat formation processes caused by energy dissipation during deformation is infrared (IR) thermography [24], which consists of non-contact measurements of the temperature of products under various conditions, as well as in gathering information about the power distribution of heat sources on their surface. IR thermography is widely used for the non-destructive control of the phenomena associated with initiation and development of cracks, pores and other inhomogeneities of the material, which may affect the durability of welded joints [25]. The mechanical behavior of coarse-grained and ultrafine-grained Zr–1.0%Nb alloys during quasi-static tensile tests, as well as local strain distributions and temperature regime evolution were investigated in a study [26] using digital image correlation methods [27,28] and infrared thermography.
The corrosion resistance of products made from the zirconium alloy (Zr–Nb–Sn), among other factors, is determined by the size of second-phase particles (SPPs). The presence of large SPPs in the alloy structure reduces its corrosion resistance. Conducting the quenching operation immediately before cold-rolling stages is the main way to reduce the SPP size, but this is not applicable in industrial conditions due to the low workability of the alloy in the quenched state. In correspondence with the Zr–Nb–Fe ternary phase diagram, the Zr–1% Nb–1.2% Sn–0.35% Fe–0.1% O alloy structure in regular composition is an α–Zr matrix with precipitates of intermetallic particles of the Laves phase type (Zr(Nb, Fe)2) with an average size of 100 nm. In the structure of industrial products from the Zr–Sn–Nb–Fe–Cu–O alloy (claddings, sheets, and rods), in addition to the Laves phase, there can be observed larger precipitates of T-phase particles ((Zr,Nb)2Fe) with a size of up to 1 μm, which is connected with the thermal-deformation conditions of their production. The influence of size, distribution and type of second-phase particles on the corrosion resistance of the Zr–Sn–Nb–Fe–Cu–O alloy were studied in several works [29,30,31] using scanning electron microscope, transmission electron microscope, electron back scattering diffraction, tensile tests and autoclave corrosion tests. The results of structural and corrosion researches of model specimens from the Zr–Sn–Nb–Fe–Cu–O alloy produced by different modes and with different structural-phase state were presented in [13]. It has been shown that the presence of the T phase within the structure of the alloy lowers the corrosion resistance of products from the Zr–Sn–Nb–Fe–Cu–O alloy to a larger extent than an increase in the size of the Laves phase.
Currently, multicomponent Zr–Nb–Sn–Fe alloys with outstanding strength and a complex of excellent operational properties are used for manufacturing the parts of the power frame of the fuel assembly of nuclear reactors [10,12,13]. As a rule, ready-made pipes of zirconium alloys are obtained by cold rolling from a special semi-finished thick-walled pipe with high mechanical characteristics and precise geometric dimensions [32]. The TREX (Tube Rolling Extrusion) technology consists in hot pressing of the front pipes and subsequent cold rolling [32]. Meanwhile, carrying out the first stage of cold rolling of a thick-walled workpiece after annealing at a temperature of 380 °C to 650 °C to obtain, for example, a TREX Zr–Nb–Sn–Fe alloy product with dimensions of 63.5 × 10.9 mm and a deformation of 50–60% leads to a violation of the continuity of the metal, which is due to the low ductility of the alloy before cold rolling [33,34]. A lack of special heat treatment of workpieces after hot deformation may cause accumulations of large intermetallides in the alloy structure, which significantly reduce the viscosity of the material and hinder cold rolling of alloys with severe deformations [35]. To improve the quality of products made of zirconium alloys by creating deformation conditions without breaking the continuity of the relevant material, the melted ingot is subjected to hot processing into a workpiece on a screw rolling mill at the equilibrium temperature of beta-zirconium [32]. After machining, the workpiece is exposed to hot pressing into the sleeve in the temperature range of 600–650 °C. Then, the sleeve undergoes quenching at a temperature of 920–960 °C, machining and subsequent tempering at 560–600 °C. Finally, cold deformation on a cold rolling mill is applied to the released workpiece in two stages before receiving a pipe semi-finished product with specific dimensions. Intermediate and final heat treatment of semi-finished products is then carried out at temperatures of 540–600 °C [32].
Such a complex fabrication of products via pressure-assisted metal processing causes a problem of accurate estimation and prediction of plasticity, thereby affecting the semi-finished or finished product. This is especially important in cold rolling. In that regard, this work is devoted to the study of mechanical properties and plasticity of a multicomponent Zr–1.0% Nb alloy that finds application in the manufacture of thin-walled pipes in rolls with variable caliber rotating towards the supplied workpiece (sleeve). The samples were exposed to multi-pass cold rolling. The pipe rolling was accompanied by large and inhomogeneous deformations of the material in the rolling center. It should be noted that the traditional methods of determining the plasticity in different zones of the rolling center based on the mechanical properties do not provide a reliable assessment due to the macroscopic localization of plastic deformation during any shaping process.
2. Materials and Methods
The material under consideration was a metal pipe billet made of a multicomponent Zr–1% Nb–1.2% Sn–0.35% Fe–0.1% O–0.01% Si alloy, forged to a diameter of 300 mm at 750–800 °C, annealed after forging at 900–1000 °C for 2 h and naturally cooled [32]. The axes of the samples cut out for testing were oriented along the radius of the cylinder.
In the recrystallized state, the alloy consisted of a-Zr grains with a size of 3–4 μm, which were composed of dispersed incoherent particles of Zr(Nb, Fe)2, (Zr,Nb)2Fe and (Zr,Nb)Fe2 intermetallides with an average size of 0.08 μm.
The focus of deformation during rolling is traditionally divided into three zones: upsetting A, reduction B and calibration C (Figure 1) [32], where the degrees of reduction vary significantly, thus endowing the material to different stress-strain states. To assess the level of residual internal stresses in these zones, local measurements of the ultrasound velocity were carried out via an autocirculatory method, as described in detail in reference [36]. The development of this approach led to the equation below:
where is the change in the speed of ultrasound, is the difference between the principal stresses, and ρ is the density of the material. This relationship was verified and confirmed in numerous works [36,37]. The value of at any structural changes does not exceed 1…10 m/s, being 0.1…1% of ≈ 103 m/s.
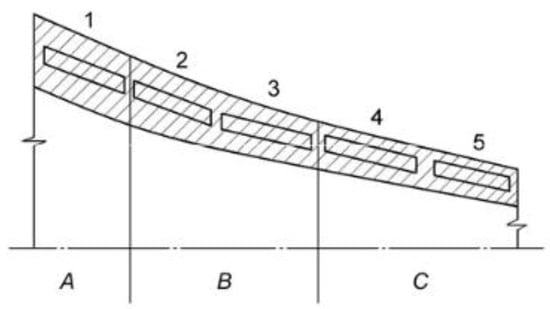
Figure 1.
A schematic of the cutoff of specimens from the pipe billet: 1–5, sample number; A, upsetting zone, B, reduction zone, C, calibration zone.
To check the correlation between the level of macro-stresses and the speed of ultrasound according to Equation (1), internal macro-stresses were determined radiographically by means of the approximation approach on the DRONE 01-04 (Burevestnik, Saint Petersburg, Russia) X-ray diffractometer using CoKα radiation monochromatized with pyrolytic graphite. The sample (a pilgerhead of Zr alloy) was scanned with an X-ray beam along several generatrices. In this case, the stress magnitude significantly depended on only the coordinate along the axis of the pipe and changed little during the transition from one generatrix to another. Residual stresses are determined from the diffraction data by calculating the strain from the diffraction peak positions.
The residual internal stress , determined via XRD, was calculated as follows:
where E is the Young’s modulus; ν is the Poisson’s coefficient; and and are the Bragg angles for strained and initial (reference) states, respectively. The reference sample was the pre-annealed specimen of the same alloy.
According to the calculated degrees of reduction and their gradients, the largest gradient corresponded to the beginning of the reduction zone (Figure 1, Table 1). Therefore, this place was critical from the point of view of providing the necessary margin of plasticity.

Table 1.
Degrees and gradients of reduction at the rolling center.
To evaluate the plasticity via autowave structural analysis, double-exposure speckle photography was used [1,2,32] for in situ recording of the displacement fields of the points r(x, y) upon uniaxial tension, starting from up to , with a step of 0.2% of the total strain (after each 60 s). The differentiation of this array over x and y coordinates yielded the longitudinal , shear and rotational components of a plastic distortion tensor = ∇r at different moments in time. The spatial and temporal correlation functions of the components, such as were also used in the analysis.
Loading was carried out on an Instron-1185 testing machine (Instron, High Wycombe, UK) at room temperature at a strain rate of 1.67 × 10−5 s−1. Flat samples with heads had a working part with dimensions of 40 × 6 mm and a thickness of 2 mm. The samples were cut from different zones of the rolling center and were referred to as: No. 1 (from the upsetting zone), No. 2 and 3 (from the reduction zone) and No. 4 and 5 (from the calibration zone).
For each sample, a stress-strain curve was recorded in the “true stress (s) - true strain (e)” coordinates for the subsequent identification of the stages of strain and their duration. The stages were distinguished based on the value of the strain hardening index n assuming that the strain-stress curve could be described by the function s = s0 + K·en with variables K and n. In this representation, the linear work hardening stage corresponded to n = 1, the parabolic work hardening stage was attributed to n = 1/2, and the pre-failure stage was assigned to n < 1/2 [38]. The displacement fields were thereby transformed into strain fields by numerical differentiation; the localization foci were identified and the spatiotemporal evolution of a system of the foci was thereby considered.
3. Results
All the results that were obtained during the testing of samples from different zones of the rolling center are summarized in Figure 2. According to the data, the conditional yield strength and the strength stress of the samples increased with an increase in the degree of reduction (Figure 2a). The greatest increase in these parameters occurred in sample No. 2 in relation to sample No. 1, that is, during the transition from the upsetting to the reduction zone.
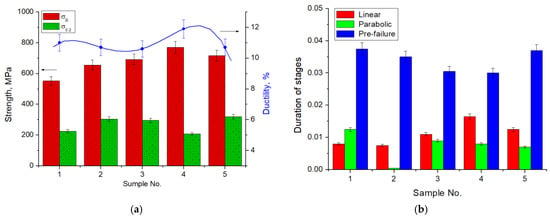
Figure 2.
Mechanical characteristics (a) and duration of plastic flow stages (b) from various zones of the rolling center. The numbers of samples correspond to those from Figure 1.
An increase in the degree of reduction led to an increase in the duration of the linear hardening stage, and the beginning of this stage shifted towards a large integral strain range (Figure 2b).
The duration of the parabolic hardening stage in the samples from the reduction and calibration zones was almost two times less than from the upsetting zone.
In sample No. 2, no parabolic stage was observed during the transition from the upsetting to the reduction zone, and the pre-failure stage occurred immediately after the linear hardening. Even though the duration of the pre-failure stage was the same in all specimens, in sample No. 2, it emerged and ended much earlier than in the others (Figure 2b).
The evolution of localized plasticity autowaves in the samples was found to obey the rule of correspondence of localization patterns to the stages of the stress-strain curve [1,2]. Thus, at the stages of linear work hardening, a phase autowave of localized strain was observed in all specimens. However, the autowave speeds (Vaw, Table 2) nonmonotonically increased with an increasing degree of reduction, and the most intense growth corresponded to the transition from sample No. 1 to sample No. 2. The autowave lengths λl in samples Nos. 1, 3 and 4 were statistically the same, but significantly higher than that in sample No. 2. In all samples with the detected parabolic work hardening stage, stationary spatially periodic distributions of localized plastic strain foci were similar to those in Figure 3a, with the same local elongation amplitudes in the foci. The spatial periods of the distributions λT in samples Nos. 1, 3 and 4 did not differ significantly and coincided with the lengths of the phase autowaves λl (Table 2).

Table 2.
Degrees and gradients of reduction at the rolling center.
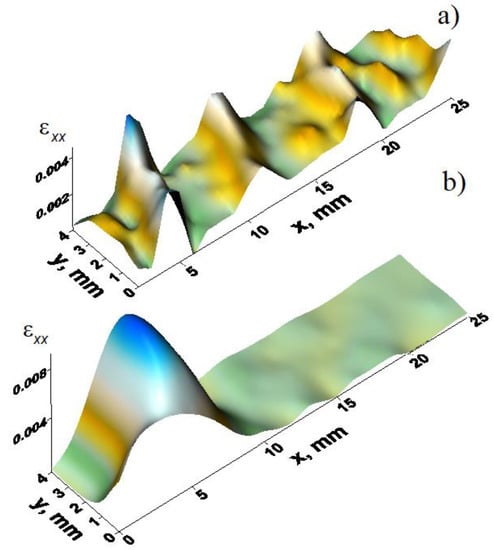
Figure 3.
Zones of localized plastic strain distributed across the samples (a) No. 1 and (b) No. 2.
In sample No. 2, where the stage of parabolic work hardening was absent, heterogeneous amplitude distributions of localized plastic strain foci were formed at the stage of linear work hardening (Figure 3b).
The rate of strain accumulation in a high-amplitude focus remained higher throughout the deformation. The failure of sample No. 2 occurred precisely in the area of the specified focus. According to works [1,2,4], the existence of foci with abnormally high strain accumulation is characterized by the stage of pre-failure, when the reserve of plasticity of the material is largely exhausted.
The heterogeneity of the plastic properties of zirconium alloys may be owing to residual internal stresses arising from plastic strain at previous stages of production. Another cause of stress may be the recrystallization of alloys during intermediate thermal treatments. Residual stresses are distributed inhomogeneously in the billet or in the finished pipe, and their high amplitude can lead to the deformation or failure. Under laboratory conditions, residual stress control is usually implemented via radiographic techniques that, however, often fail to examine large-sized objects.
In this situation, indirect methods seem to be more suitable for assessing the stress state through some informative quantities whose correlation with macroscopic residual stresses has a clear physical nature. In that regard, measuring the velocity of ultrasound is especially convenient [36,37], since it depends on the internal stresses in the material. The method is based on the experimentally established dependence of the ultrasound propagation velocity on macro-stresses.
The unfavorable state of the material in sample No. 2 was confirmed by the speed of ultrasound measured along the length of the rolling center (see Curve 1 in Figure 4). It was evident that, upon the transition from the upsetting zone A to the reduction zone B, the ultrasound velocity had a minimum. This meant there was the greatest amount of residual tensile stresses. It has been previously established that there is a linear correlation between the stress and the frequency of autocirculation f of ultrasonic signals proportional to the velocity of ultrasound propagation (), and the regression line equation has the following form [32]:
where σ0 = 420 MPa, α = 0.42 MPa⋅s, and the coefficient of correlation between σi and f parameters is ~0.72, being statistically significant. The data were acquired during a series of experiments conducted on pilgerheads of Zr–1.0% Nb alloys.
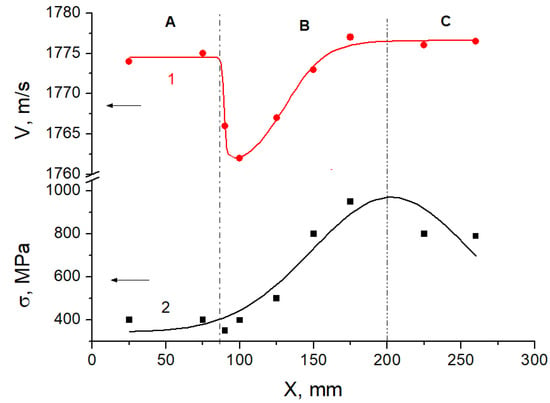
Figure 4.
(1) Speed of ultrasound and (2) residual stress at different zones of the cold rolling center. The zone designations are the same as in Figure 1.
Figure 4 (Curve 2) shows the dependence of the stresses recalculated from the ultrasound velocity values using formula (1) on the coordinates along the axis of the pipe billet. In the cross section with a coordinate of 75...100 mm, there was an internal stress surge. Its position exactly corresponded to a sharp boundary between the maximum reduction and compression of the pipe in the strain focus, as it was established above by the speckle photography method (see Figure 3). It was exactly this section that might have undergone failure of the pipe billet during further rolling.
Thus, ultrasonic measurements confirmed the drastic changes in the properties of the Zr–1.0% Nb alloy pilgerheads and demonstrated the ability to reliably control these states in blanks at different stages of the manufacture of zirconium alloy pipes.
4. Discussion
The abrupt variation of internal stresses in the pilgerheads under consideration is owing to the heterogeneity of the forged billet structure revealed by metallographic analysis. Thus, a predominately martensite layer with a thickness of 0.5...2 μm was observed near the surface (Figure 5a). Thin (up to 0.2 μm) layers of a residual β-Zr phase were highlighted along the boundaries of martensitic crystals. The zone in the range of ~1/2R...3/4R (R is the radius of the billet) was distinguished by an inhomogeneous structure (Figure 5b). Colonies of α′-Zr plates with a thickness of 1...2 μm, bordered by β-Zr layers, and areas of a fine-needle (up to 1 micron) martensitic phase were also present here [29]. In addition, there were regions with strain traces after forging, composed of coarse (up to 5 μm) strongly curved plates of the primary α-Zr phase. The boundaries of the α-Zr plates exhibited β-Zr layers with a thickness of 0.5...1 μm, as well as particles of Zr(Fe, Nb)2 and Zr(Fe, Nb)3 intermetallides of up to 0.1 μm in size, which were released in the grain bodies and along the grain boundaries of the α-Zr phase. The volume fraction of such areas was about 30%.

Figure 5.
Microstructure of a forged workpiece of Zr–1.0% Nb alloy: (a) surface, (b) middle part, (c) center of the pipe billet.
The structure of the alloy at the center of the workpiece was more uniform (Figure 5c). Small sections of the residual strongly deformed α-phase were observed between the groups of 1…3 μm plates of the α′-phase. It was obvious that the loosest zone of various structures near ~2/3R was also the most “dangerous” in terms of possible failure, which was concluded from the speckle patterns of plastic flow localization (Figure 3).
Microscopic examination of the crack edge formed in this zone revealed that it could originate and propagate in predominately the areas of a residual coarse-grained α-structure with phase separation along the boundaries. A comprehensive study of the plasticity of the billet made of Zr–1.0% Nb alloy made it possible to clearly identify a forged rod zone considered dangerous from the point of view of feasible failure during deformation.
The hardening of forged billets made of Zr alloys does not allow the desired alignment of the material structure along the section of the billet. Obviously, this is primarily due to a natural decrease in the cooling rate of the solid workpiece. Meanwhile, inhomogeneous deformation of the billet during forging may be also decisive. In any case, the most unfavorable part of the structure is located closer to the surface rather than along the axis, creating a wide belt. The structural heterogeneity, in turn, determines the existence of elevated residual stresses in this zone. All this reduces the resistance to fracture of the material in the specified layer and may cause a decrease in the quality of finished products or the failure of semi-finished products during hot and cold working.
Based on the findings of the current study, some recommendations concerning the effective development of cold rolling technology can be made. One of the main issues to be solved is associated with the maximum possible reduction in the course of one or more passes that would cause neither continuity violations nor failure of the material. Such reduction is usually established empirically on the basis of laborious and expensive production tests. However, if the limits of macroscopically uniform deformation are known, then the degree of reduction must suit them. According to the above results, these are the sections of the stress-strain curves, corresponding to chaotically localized plastic flow patterns or moving deformation foci. In the latter case, even though the plastic flow is localized at each specific moment of time, it exhibits a quasi-uniform process during the loading.
Thus, preference should be given to reduction within the linear work hardening and the parabolic work hardening stage with a low parabolicity index (0.2 < n < 0.5). Plastic flow localization at the parabolic work hardening stage is a stationary process, but there are still many localization zones without internal continuity disturbances (microcracks). Therefore, reduction at the beginning of the parabolic work hardening stage is also acceptable. The only exception is the modes with stationary single zones of plastic flow localization, which are technologically unacceptable and even dangerous. Thus, the analysis of the plasticity during pressure-assisted treatment cannot be limited to only the assessment of traditional indicators (, , δ and ψ), but should include a thorough study of the patterns of macroscopically localized plastic flow [1,2]. These recommendations can be useful, for example, when optimizing the manufacture technology of industrial products made of Zr alloys.
5. Conclusions
Based on the findings of the present work, the plastic flow was localized throughout the entire length of the Zr–1.0% Nb alloy pipe billets. It was established that macroscopic patterns of localized plastic flow furnished information about the nature of plastic deformation taking into account the microstructural changes of alloys in the technological process. This enabled one to also gain insight into the technological deformability of Zr alloys.
A thorough analysis of the results revealed that the sample referred to as No. 2 was in an extremely inhomogeneous stress-strain state and had the highest level of residual stresses after rolling. Therefore, the high-amplitude localization foci were formed in this sample immediately after the beginning of the loading. Moreover, further accumulation of strain therein ultimately led to failure.
Consequently, as a result of cold rolling at the upsetting-to-reduction transition zone, there was a significant depletion of the plasticity of the Zr–1.0% Nb alloy. Therefore, failure was most likely to occur at exactly this zone. To avoid adverse consequences, the degree of reduction should be redistributed across the rolling center, being slightly reduced in the upsetting zone and increased in the reduction zone by simply changing the shapes of the gauges and the mandrel.
It is noteworthy that this conclusion is due to a comprehensive analysis of the acoustic parameters and the macroscopic patterns of plastic flow localization, which is hard to achieve via traditional methods of assessing the plasticity of alloys.
Author Contributions
Conceptualization, L.B.Z.; methodology, D.V.O.; software, D.V.O.; formal analysis, S.A.B.; investigation, D.V.O.; writing—original draft preparation, S.A.B.; writing—review and editing, S.A.B.; visualization, D.V.O.; supervision, L.B.Z.; project administration, L.B.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Russian Science Foundation (grant no. 21-19-00075).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We thank Vladimir Danilov for helpful discussion of this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zuev, L.B.; Barannikova, S.A. Autowave physics of material plasticity. Crystals 2019, 9, 458. [Google Scholar] [CrossRef] [Green Version]
- Zuev, L.B.; Barannikova, S.A. Quasi-particle approach to the autowave physics of metal plasticity. Metals 2020, 10, 1446. [Google Scholar] [CrossRef]
- Olemskoi, A.I.; Katsnelson, A.A. A Synergetic of Condensed Medium; URSS: Moscow, Russia, 2003; 335p. [Google Scholar]
- Orlova, D.V.; Barannikova, S.A.; Zuev, L.B. On the kinetics of localized plasticity domains emergent at the pre-failure stage of deformation process. AIP Conf. Proc. 2016, 1783, 020168. [Google Scholar]
- Zuev, L.B.; Danilov, V.I.; Poletika, T.M.; Barannikova, S.A. Plastic deformation localization in commercial Zr-base alloys. Int. J. Plast. 2004, 20, 1227–1249. [Google Scholar] [CrossRef]
- Zuev, L.B.; Barannikova, S.A.; Zavodchikov, S.Y. Localization of tensile deformation in a polycrystalline Zr-based alloy. Phys. Met. Metal. 1999, 87, 244–246. [Google Scholar]
- Douglass, D.L. Metallurgy of Zirconium; International Atomic Energy Agency: Vienna, Austria, 1971; 466p. [Google Scholar]
- Zaimovskii, A.S.; Nikulina, A.V.; Reshetnikov, N.G. Zirconium Alloys in Nuclear Power; Energoatomizdat: Moscow, Russia, 1981; 256p. [Google Scholar]
- Tenckhoff, E. Review of deformation mechanisms, texture and mechanical anisotropy in zirconium and zirconium base alloys. ASTM Int. 2005, 2, 25–50. [Google Scholar]
- Nikulina, A.V.; Markelov, V.A.; Peregud, M.M.; Voevodin, V.N.; Panchenko, V.L.; Kobylyansky, G.P. Irradiation-induced microstructural changes in Zr-1% Sn-1% Nb-0.4% Fe. J. Nucl. Mater. 1996, 238, 205–210. [Google Scholar] [CrossRef]
- Nikulina, A.V. Zirconium-niobium alloys for core elements of pressurized water reactors. Met. Sci. Heat Treat. 2003, 45, 287–292. [Google Scholar] [CrossRef]
- Kim, H.G.; Baek, J.H.; Kim, S.D.; Jeong, Y.H. Microstructure and corrosion characteristics of Zr-1.5Nb-0.4Sn-0.2Fe-0.1Cr alloy with a β-annealing. J. Nucl. Mater. 2008, 372, 304–311. [Google Scholar] [CrossRef]
- Markelov, V.A. On correlation of composition, structural-phase state, and properties of E635 zirconium alloy. Inorg. Mater. Appl. Resear. 2010, 1, 245–253. [Google Scholar]
- Zinkle, S.J.; Was, G.S. Materials challenges in nuclear energy. Acta Mater. 2013, 61, 735–758. [Google Scholar] [CrossRef]
- Valizadeh, S.; Ledergerber, G.; Abolhassan, S.; Jädernäs, D.; Dahlbäck, M.; Mader, E.V.; Zhou, G.; Wright, J.; Hallstadius, L. Effects of secondary phase particle dissolution on the in-reactor performance of BWR cladding. J. ASTM Int. 2014, 8, 729–753. [Google Scholar]
- Harte, A.; Griffiths, M.; Preuss, M. The characterisation of second phases in the Zr-Nb and Zr-Nb-Sn-Fe alloys: A critical review. J. Nucl. Mater. 2018, 505, 227–239. [Google Scholar] [CrossRef] [Green Version]
- Tao, B.; Qiu, R.; Zhao, Y.; Liu, Y.; Tan, X.; Luan, B.; Liu, Q. Effects of alloying elements (Sn, Cr and Cu) on second phase particles in Zr-Sn-Nb-Fe-(Cr, Cu) alloys. J. Alloys Comp. 2018, 748, 745–757. [Google Scholar] [CrossRef]
- Yagnik, S.; Garde, A. Zirconium Alloys for LWR Fuel Cladding and Core Internals. In Structural Alloys for Nuclear Energy Applications; Odette, R., Zinkle, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 247–291. [Google Scholar]
- Wei, T.; Dai, X.; Long, C.; Sun, C.; Long, S.; Zheng, J.; Wang, P.; Jia, Y.; Zhang, J. Comparison on the microstructure, aqueous corrosion behavior and hydrogen uptake of a new Zr-Sn-Nb alloy prepared by different hot rolling temperature. Corros. Sci. 2021, 192, 109808. [Google Scholar] [CrossRef]
- Feng, Z.H.; Li, D.; Dong, H.C.; Li, J.H.; Su, R.; Wu, D.Y.; Chen, Y.Q.; Zhang, X.Y.; Liu, R.P. Evolution of β phase and mechanical mechanisms in an α-type Zr alloy processed by rolling at different temperatures. Mater. Charac. 2021, 172, 110873. [Google Scholar] [CrossRef]
- Daniel, C.S.; Garner, A.; Honniball, P.D.; Bradley, L.; Preuss, M.; Prangnell, P.B.; da Fonseca, J.Q. Co-deformation and dynamic annealing effects on the texture development during alpha–beta processing of a model Zr-Nb alloy. Acta Mater. 2021, 205, 116538. [Google Scholar] [CrossRef]
- Ozhmegov, K.; Kawalek, A.; Garbiec, D.; Dyja, H.; Arbuz, A. Development of alternative method for manufacturing structural zirconium elements for nuclear engineering. Materials 2021, 14, 5006. [Google Scholar] [CrossRef]
- Nikulin, S.A.; Khanzhin, V.G.; Rozhnov, A.B.; Babukin, A.V.; Belov, V.A. Methods for Analyzing Deformation and Fracture Processes of Thin-Walled Parts from Low-Strength Alloys. Met. Sci. Heat. Treat. 2005, 47, 202–209. [Google Scholar] [CrossRef]
- Meola, C.; Carlomagno, G.M. Recent advances in the use of infrared thermography—A review. Meas. Sci. Technol. 2004, 15, R27–R58. [Google Scholar] [CrossRef]
- Plekhov, O.A.; Saintier, N.; Naimark, O. Experimental study of energy accumulation and dissipation in iron in an elastic-plastic transition. Tech. Phys. 2007, 52, 1236–1238. [Google Scholar] [CrossRef]
- Sharkeev, Y.P.; Vavilov, V.P.; Skrypnyak, V.A.; Legostaeva, E.V.; Eroshenko, A.Y.; Belyavskaya, O.A.; Ustinov, A.M.; Klopotov, A.A.; Chulkov, A.O.; Kozulin, A.A.; et al. Research on the processes of deformation and failure in coarse- and ultrafine-grain states of Zr1–Nb alloys by digital image correlation and infrared thermography. Mater. Sci. Eng. A 2020, 784, 139203. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.M.; Xie, H.M.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Tretiakova, T.V.; Vildeman, V.E. Relay-Race Deformation Mechanism during Uniaxial Tension of Cylindrical Specimens of Carbon Steel: Using Digital Image Correlation Technique. Fract. Struct. Integ. 2013, 24, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Li, J.; Zhang, Y.; Lu, W.; Zhang, L.; Wang, L.; Zhang, D. Effect of low-temperature pre-deformation on precipitation behavior and microstructure of a Zr-Sn-Nb-Fe-Cu-O alloy during fabrication. J. Nucl. Sci. Tech. 2016, 53, 496–507. [Google Scholar] [CrossRef]
- Doriot, S.; Onimus, F.; Gilbon, D.; Mardon, J.-P.; Bourlier, F. Transmission electron microscopy study of second phase particles irradiated by 2 MeV protons at 350 °C in Zr alloys. J. Nucl. Mater. 2017, 494, 398–410. [Google Scholar] [CrossRef]
- Chen, L.; Zeng, Q.; Li, J.; Lu, J.; Zhang, Y.; Zhang, L.-C.; Qin, X.; Lu, W.; Zhang, L.; Wang, L.; et al. Effect of microstructure on corrosion behavior of a Zr–Sn–Nb–Fe–Cu–O alloy. Mater. Des. 2016, 92, 888–896. [Google Scholar] [CrossRef]
- Zavodchikov, S.Y.; Zuev, L.B.; Kotrekhov, V.A. Physical Metallurgy Aspects of the Production of Zirconium Alloy. Components; Glezer, A.M., Ed.; Nauka: Novosibirsk, Russia, 2012; 257p. [Google Scholar]
- Fan, Q.; Yuan, B.; Xie, M.; Shi, M.; Zhou, J.; Yang, Z.; Zhao, W. Effects of hot rolling temperature and aging on the second phase particles of Zr-Sn-Nb-Fe zirconium alloy. Nucl. Mater. Eng. 2019, 20, 100700. [Google Scholar] [CrossRef]
- Dyja, H.; Kawałek, A.; Ozhmegov, K. Experimental studies on Zr–1%Nb alloy properties in technological conditions of cold pilger tube rolling process. Arch. Civil. Mech. Eng. 2019, 19, 268–273. [Google Scholar] [CrossRef]
- Abe, H.; Furugen, M. Method of evaluting workability in cold pilgering of zirconium alloy tube. Mater. Trans. 2010, 51, 1200–1205. [Google Scholar] [CrossRef] [Green Version]
- Lunev, A.G.; Orlova, D.V.; Danilova, L.V.; Zuev, L.B. Ultrasonic and Optical Evaluation of Deformation Stages from the Beginning to Fracture: A Case Study of Low-Carbon Steels. J. Nondestruct. Eval. 2021, 40, 31. [Google Scholar] [CrossRef]
- Lunev, A.G.; Nadezhkin, M.V.; Barannikova, S.A.; Zuev, L.B. Acoustic parameters as criteria of localized deformation in aluminum alloys. Acta Phys. Pol. A 2018, 134, 342–345. [Google Scholar] [CrossRef]
- Pelleg, J. Mechanical Properties of Materials; Springer: Dordrecht, Germany, 2013. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).