Recent Developments and Future Challenges in Incremental Sheet Forming of Aluminium and Aluminium Alloy Sheets
Abstract
:1. Introduction
2. Methods of Review
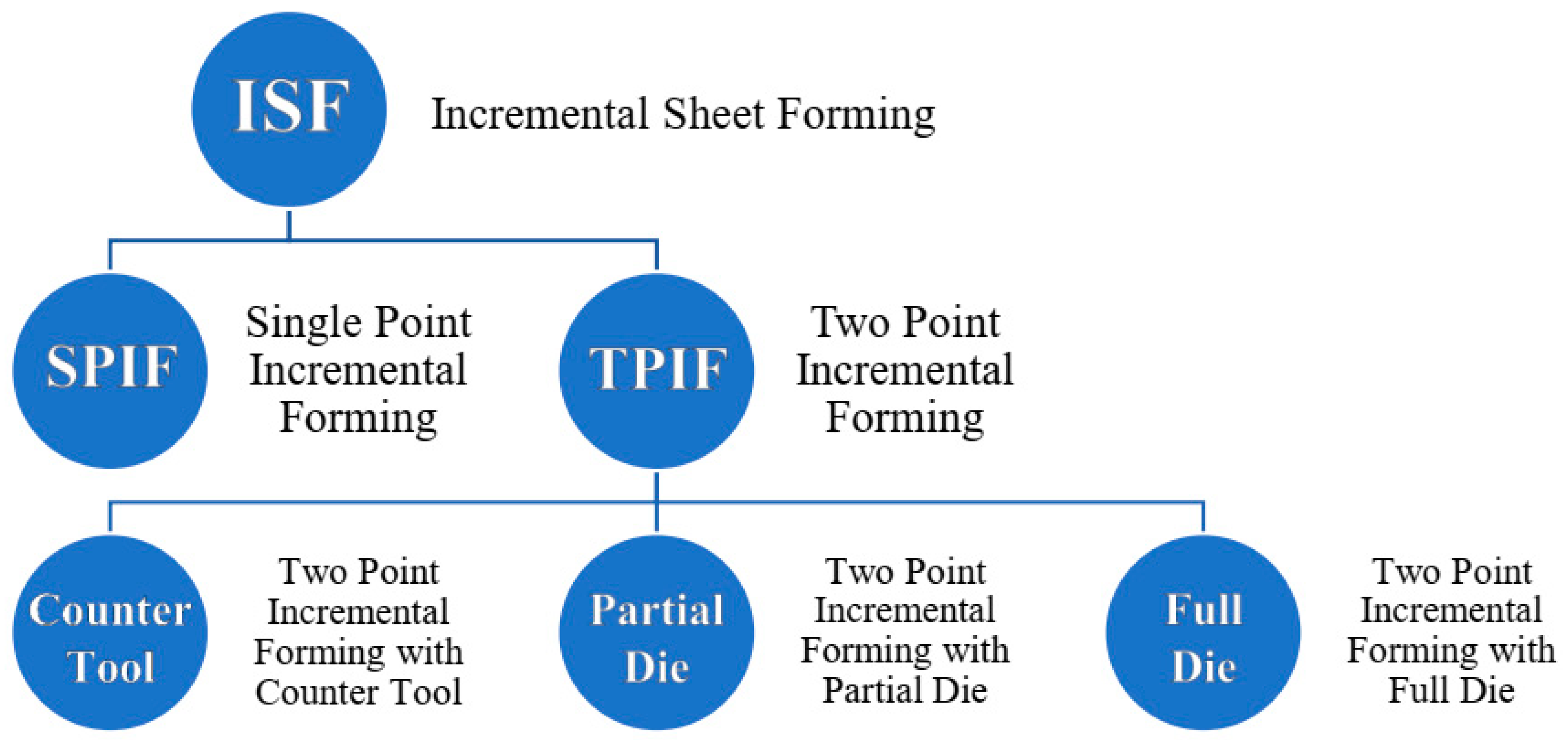
3. Methods of Incremental Forming
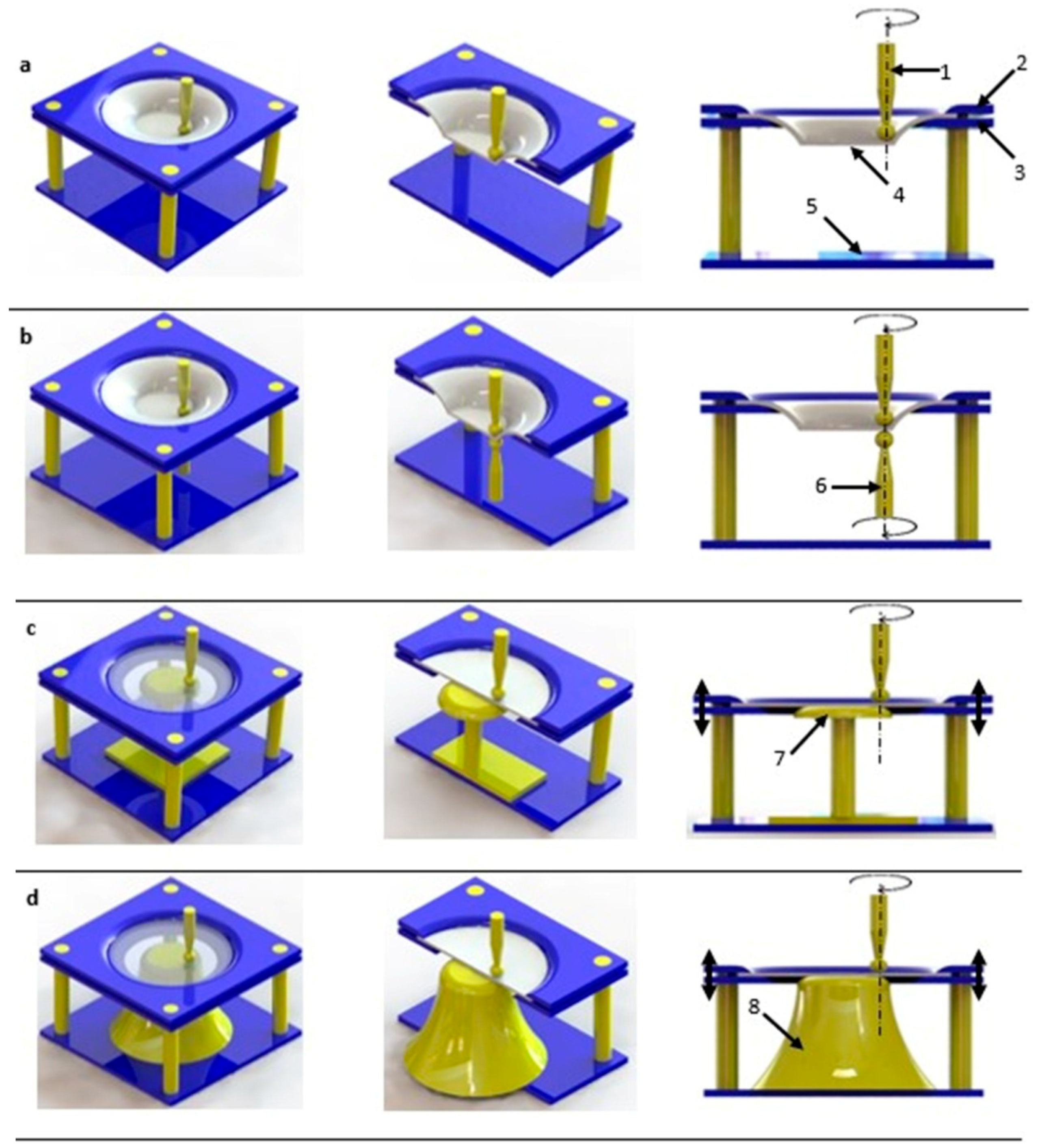
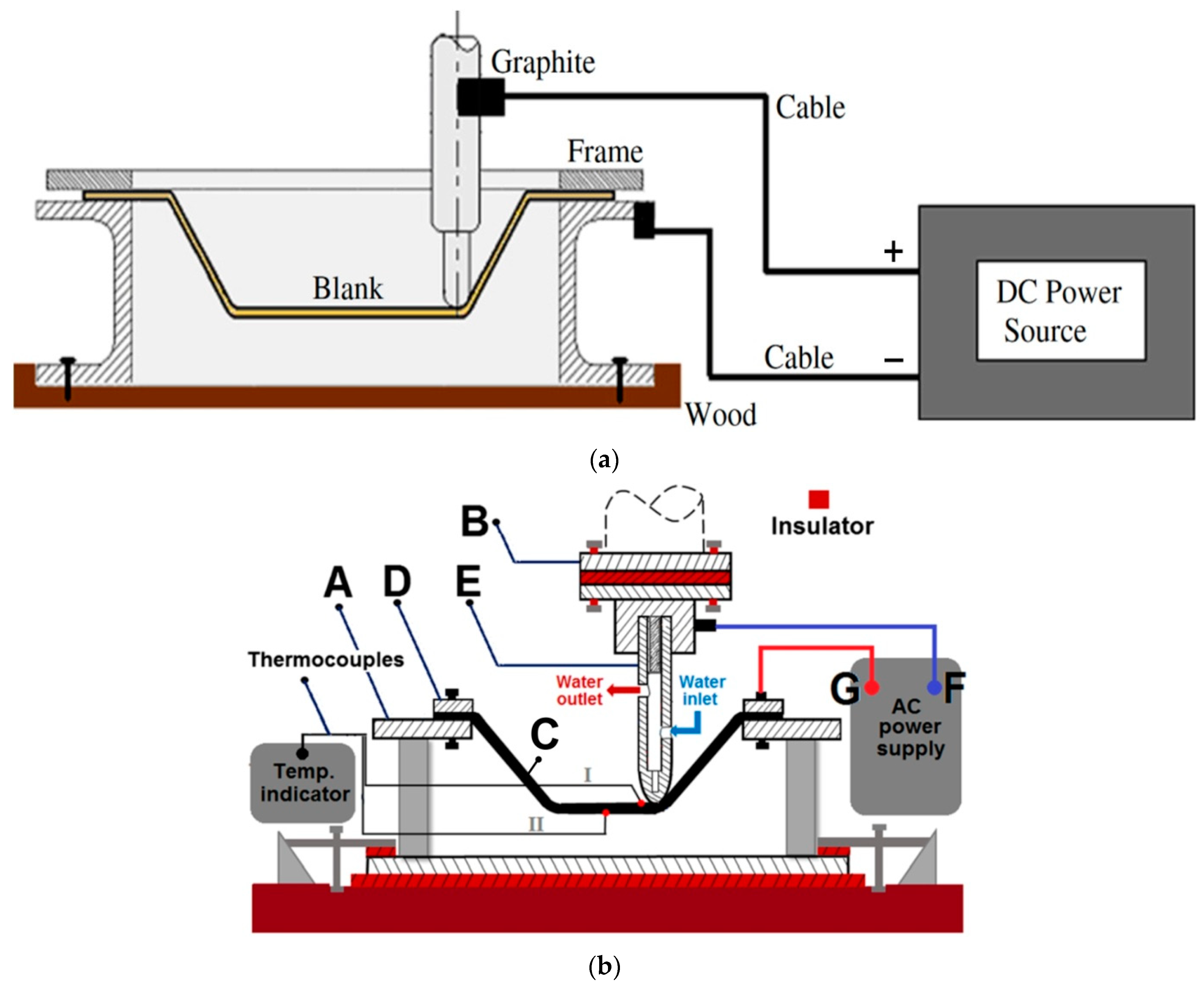
3.1. Single- and Two-Point Incremental Forming
- Single Point ISF—only one contact point, in which one tool is used on one side of the sheet.
- Two Point ISF—two contact points from two tools, one on each side of the sheet.
3.2. Water Jet Incremental Forming
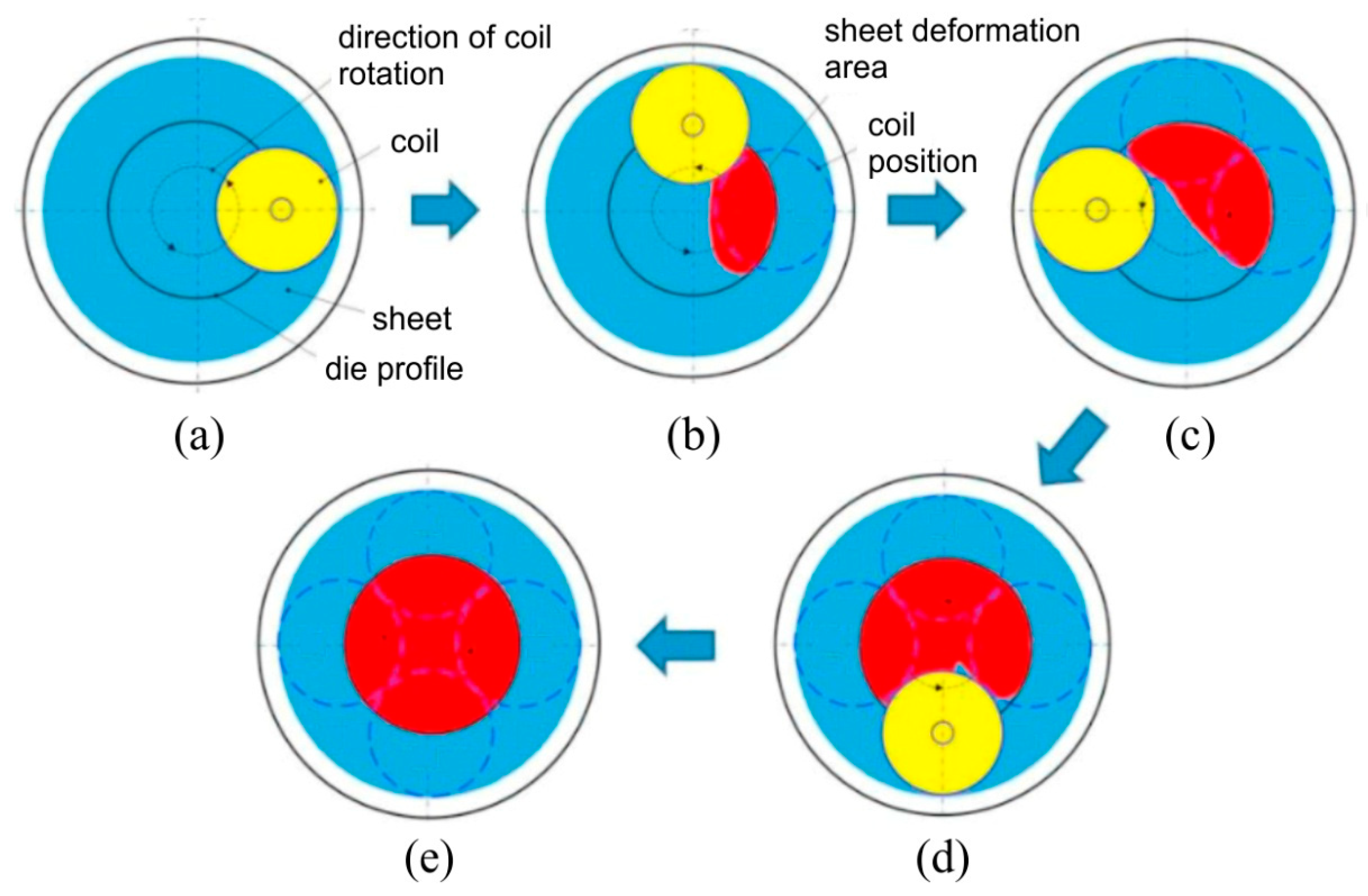
3.3. Electromagnetic Incremental Forming
- there is no mechanical contact with the work piece,
- no lubricants are needed,
- the process can be fully controlled,
- high technological flexibility,
- parts formed by EMF exhibit good surface quality and high dimensional accuracy,
- there is significant increase in workpiece ductility over conventional sheet metal forming methods,
- the formability limit is increased during electromagnetic forming due to high deformation velocity,
4. Process Formability of Aluminium and Aluminium Alloys
4.1. Forming Limit Diagram
4.2. Effect of Process Parameters on Formability
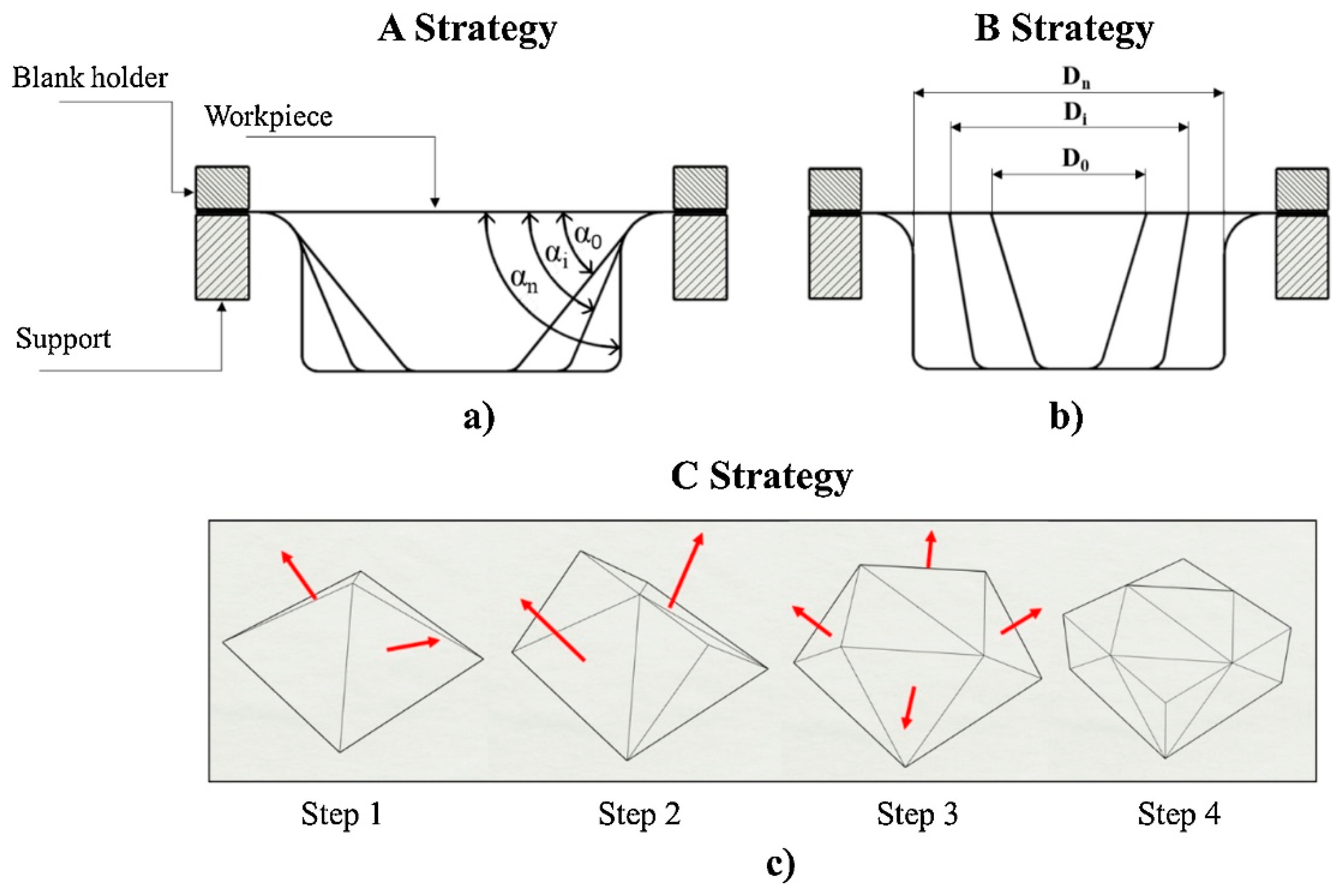
5. Accuracy in SPIF and TPIF
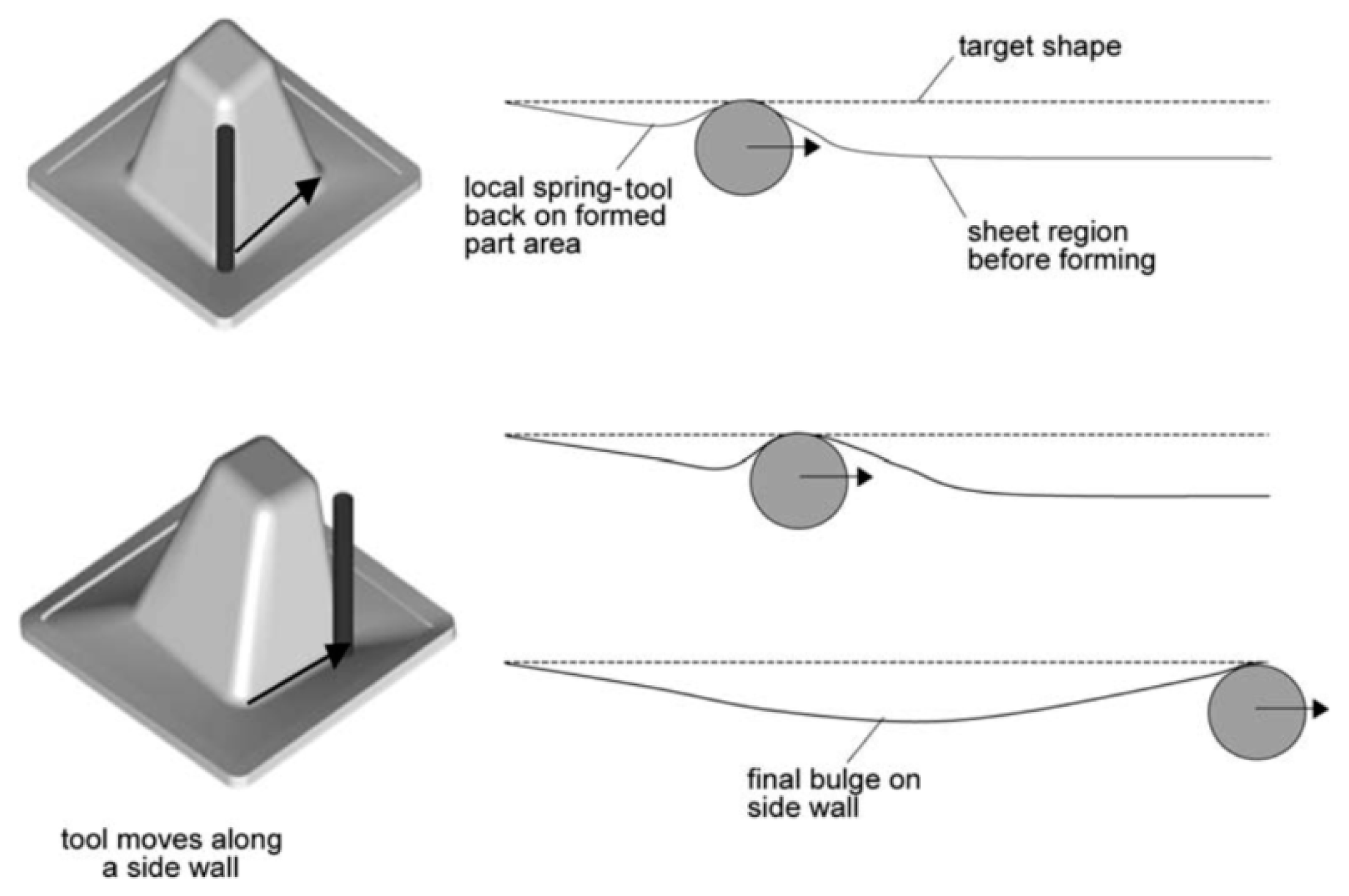
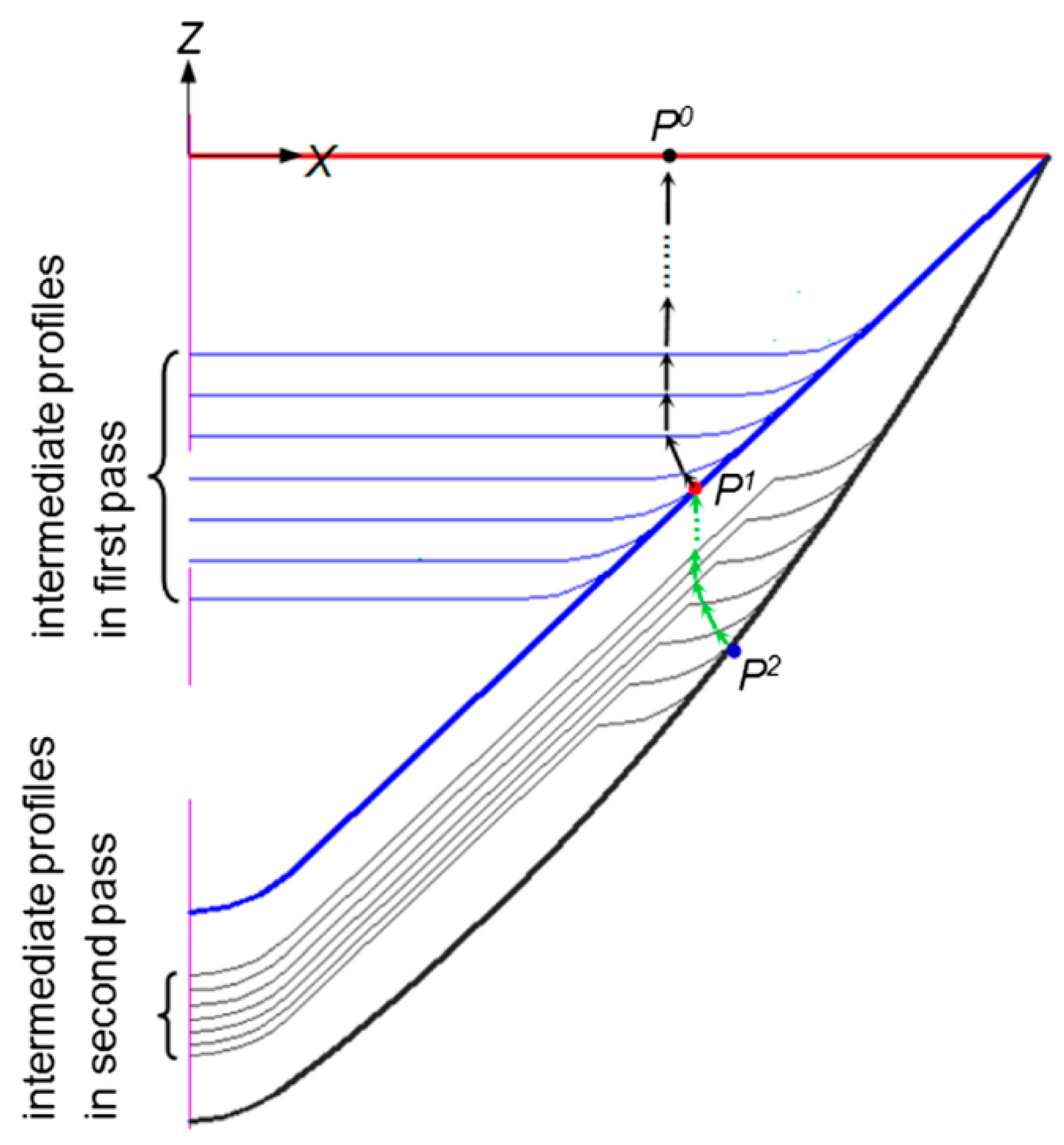
5.1. Springback Reduction
5.2. Toolpath Compensation
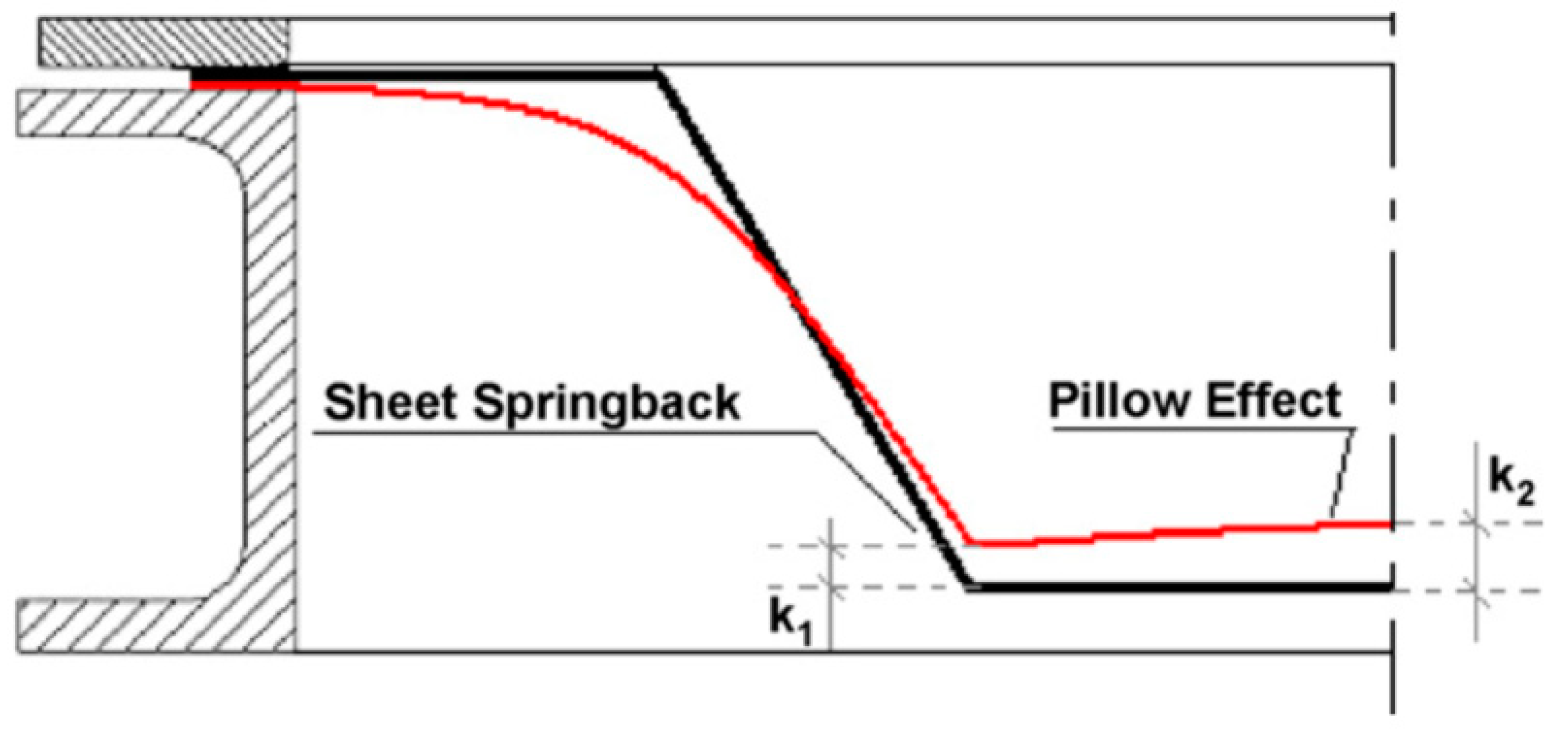
5.3. Pillow Effect
5.4. Thickness Distribution
6. Surface Finish
6.1. Process Parameters
6.2. Friction Conditions
7. Heat-Assisted Incremental Forming
7.1. Electrically Assisted ISF
7.2. Friction-Assisted ISF
7.3. Laser-Assisted ISF
8. Conclusions
- The dieless nature of SPIF and TPIF greatly reduces the cost associated with making the dies required in conventional SMF processes. Changes can be made to the product design very quickly and easily, with minimal cost.
- A limitation of the industrial application of SPIF technique is that the forming time is much higher than in the conventional methods of sheet metal forming. After implementing a multi-point tool technique, it is possible to reduce the forming time drastically.
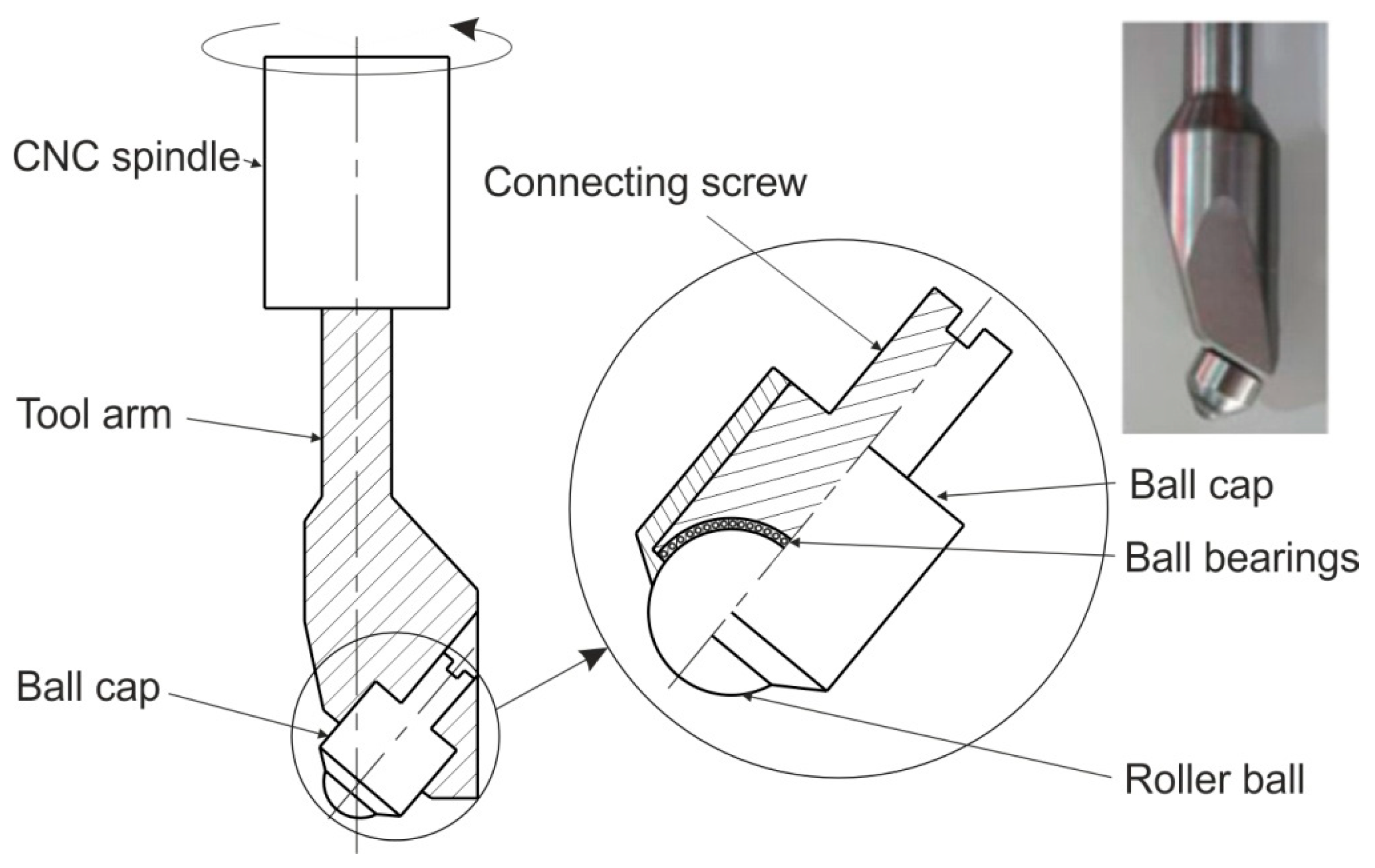
- The inner surfaces of the drawpieces are of low quality, which can be improved by the optimisation of the process parameters, especially step size and tool path strategy. New types of tool designs, i.e., an oblique roller ball tool, were developed to improve the surface finish of parts.
- By increasing the rotational speed of the tool, it is possible to increase the formability of the sheet material by friction-stir-assisted heating of the material.
- The presence of lubricant is important in the ISF of aluminium and Al-based alloys to avoid wear in the abrasive form when the tool is relatively hard in comparison with the workpiece material.
- The dimensional accuracy of an ISFed component may be improved by using different algorithms to optimise the tool path trajectory.
- Some Al-based alloys are included in the group of difficult-to-form materials. The formability of these alloys may be improved with methods of hot ISF. These methods include electrically assisted ISF, induction-heating-assisted ISF, laser-assisted ISF and combined electric- and friction-stir-assisted ISF.
- The use of modern variants of SPIF (i.e., ultrasonic-assisted ISF) permits a significant reduction in the manufacturing costs when forming “difficult-to-form” materials.
- Robotic ISF is more flexible than the CNC machine method, more cost-effective for large parts and easy to achieve when the right tools are used.
- The effect of step size in SPIF and TPIF is not unequivocal; some researchers have concluded that step size has a negative effect on formability; however, others have shown that step size does not affect formability.
- It is still hard to form parts with right angles or it cannot be achieved with one step. Parts with a 90° wall angle can be obtained by adopting non-linear strain paths by multi-stages, but to this end, the initial thickness of the sheet must be increased.
- The geometric accuracy attributed to and residual stresses and springback effects is one of the dominant limits for the further development of the ISF methods. There are the following two ways to reduce springback: (i) the use of an algorithm to compensate the elastic strains of the material after unloading and modifying the tool path strategy, and (ii) increasing the tool diameter and spindle speed and reducing the vertical step size.
- The surface roughness of the inner surface of an ISFed component may be improved by (i) reducing the tool size and vertical step size, and (ii) using a rotating tool as compared to a non-rotating one.
- There are no universal surface roughness parameters to describe the surface finish of SPIFed components. A more comprehensive parametric study can be beneficial to investigate the interdependence and interaction between forming parameters and surface roughness parameters of inner and outer surfaces of drawpieces.
- The parts produced by ISF have high surface roughness due to the waviness caused by the forming tool. When ISF is performed with a dummy sheet at the top of the main or target sheet, the surface roughness is minimized to some extent. In the SPIF process using a dummy sheet, two sheets are deformed simultaneously.
- Compared to traditional rigid tool incremental forming, water jet ISF has the following several advantages: no metallic contact between the tool and workpiece, environmental friendliness resulting from the absence of friction-reducing lubricants and a closed circuit for the working fluid and no tool wear during the forming process.
- It is suggested that future research should be focused on optimising process parameters for the use of SPIF methods to form various lightweight alloys used in the aerospace industry, in which products are manufactured in relatively small series.
- Finite element-based simulations can be used to predict forming defects, clarify the forming characteristics and improve the forming process. Accurate and efficient approaches for predicting the forming accuracy of drawpieces are awaited by the industrial designers of SPIF.
- There is little research on phenomenological or physical constitutive and damage models to describe the material behaviour of aluminium and aluminium alloy sheets. The effects of strain hardening and material anisotropy on the formability of hard-to-deform materials require further research.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheng, L.M.; Poole, W.J.; Embury, J.D.; Lloyd, D.J. The influence of precipitation on the work-hardening behavior of the aluminum alloys AA6111 and AA7030. Metall. Mater. Trans. 2003, 34, 2473–2481. [Google Scholar] [CrossRef]
- Ubertalli, G.; Matteis, P.; Ferraris, S.; Marcianò, C.; D’Aiuto, F.; Tedesco, M.M.; De Caro, D. High Strain Rate Behavior of Aluminum Alloy for Sheet Metal Forming Processes. Metals 2020, 10, 242. [Google Scholar] [CrossRef] [Green Version]
- Schneider, R.; Heine, B.; Grant, R.J.; Zouaoui, Z. Aluminium Sheet Metal Forming at Low Temperatures. IOP Conf. Ser. Mater. Sci. Eng. 2015, 74, 012014. [Google Scholar] [CrossRef]
- Huber, G.; Djurdjevic, M.B.; Manasijevic, S. Determination some thermo-physical and metallurgical properties of aluminum alloys using their known chemical composition. Int. J. Heat Mass Trans. 2019, 139, 548–553. [Google Scholar] [CrossRef]
- Taher, M.; Mao, F.; Berastegui, P.; Andersson, A.M.; Jansson, U. The influence of chemical and phase composition on mechanical, tribological and electrical properties of Silver-Aluminum alloys. Tribol. Int. 2018, 119, 680–687. [Google Scholar] [CrossRef]
- Dudareva, N.; Gallyamova, R. The Cnfluence of Chemical Composition of Aluminum Alloys on the Quality of Oxide Layers Formed by Microarc Oxidation. Mater. Today Proc. 2019, 11, 89–94. [Google Scholar] [CrossRef]
- Vijayakumar, M.D.; Dhinakaran, V.; Sathish, T.; Muthu, G.; Bupathiram, P.M. Experimental study of chemical composition of aluminium alloys. Mater. Today Proc. 2021, 37, 1790–1793. [Google Scholar] [CrossRef]
- Ravikumar, R.N.; Rajesh, G.H. The mechanical properties and microstructure behavior of aluminium alloys subjected to shock waves. Mater. Today Proc. 2021, 46, 9132–9138. [Google Scholar] [CrossRef]
- Hattori, C.S.; Almeida, G.F.C.; Gonçalves, R.L.C.; Santos, R.G.; Souza, R.C.; da Silva, W.C.; Cunali, J.R.C.; Couto, A.A. Microstructure and fatigue properties of extruded aluminum alloys 7046 and 7108 for automotive applications. J. Mater. Res. Technol. 2021, 14, 2970–2981. [Google Scholar] [CrossRef]
- Garric, V.; Colas, K.; Donnadieu, P.; Loyer-Prost, M.; Leprêtre, F.; Cloute-Cazalaa, V.; Kapusta, B. Impact of the microstructure on the swelling of aluminum alloys: Characterization and modelling bases. J. Nuclear Mater. 2021, 557, 153273. [Google Scholar] [CrossRef]
- Puga, H. Casting and Forming of Advanced Aluminum Alloys. Metals 2020, 10, 494. [Google Scholar] [CrossRef] [Green Version]
- Dou, S.; Wang, X.; Xia, J.; Wilson, L. Analysis of Sheet Metal Forming (Warm Stamping Process): A Study of the Variable Friction Coefficient on 6111 Aluminum Alloy. Metals 2020, 10, 1189. [Google Scholar] [CrossRef]
- Xiang, P.; Jia, L.J.; Shi, M.; Wu, M. Ultra-low cycle fatigue life of aluminum alloy and its prediction using monotonic tension test results. Eng. Fract. Mech. 2017, 186, 449–465. [Google Scholar] [CrossRef]
- Zhao, X.; Li, H.; Chen, T.; Cao, B.; Li, X. Mechanical Properties of Aluminum Alloys under Low-Cycle Fatigue Loading. Materials 2019, 12, 2064. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shaha, S.K.; Czerwinski, F.; Kasprzak, W.; Friedman, J.; Chen, D.L. Improving High-Temperature Tensile and Low-Cycle Fatigue Behavior of Al-Si-Cu-Mg Alloys Through Micro-additions of Ti, V, and Zr. Metall. Mater. Trans. A 2015, 46, 3063–3078. [Google Scholar] [CrossRef]
- EN 573-3:2019-12. Aluminum and Aluminum Alloys-Chemical Composition and Types of Wrought Products-Part 3: Chemical Composition and Types of Articles; European Committee For Standardization: Brussels, Belgium, 2019. [Google Scholar]
- EN 1706:2020-10. Aluminium and Aluminium Alloys. Castings. Chemical Composition and Mechanical Properties; European Committee For Standardization: Brussels, Belgium, 2020. [Google Scholar]
- Zheng, K.; Politis, D.J.; Wang, L.; Lin, J. A review on forming techniques for manufacturing lightweight complex—Shaped aluminium panel components. Int. J. Light. Mater. Manuf. 2018, 1, 55–80. [Google Scholar] [CrossRef]
- Ismail, A.; Mohamed, M.S. Review on sheet metal forming process of aluminium alloys. In Proceedings of the 17th International Conference on Applied Mechanics and Mechanical Engineering, Cairo, Egypt, 19–21 April 2016; pp. 1–13. [Google Scholar]
- Chen, J.; Lan, F.; Wang, J.; Wang, Y. Material Selection and Sheet Metal Forming Simulation of Aluminium Alloy Engine Hood Panel. In Global Design to Gain a Competitive Edge; Yan, X.T., Ion, W.J., Eynard, B., Eds.; Springer: London, UK, 2008; pp. 529–538. [Google Scholar]
- Yahaya, S.N.M.; Ng, C.H.; Lai, C.F.; Sharrifuddin, S.; Grote, K.H. Reviews on the Forming Process of Heat Treatable Aluminium Alloys. Int. J. Integr. Eng. 2018, 10, 74–79. [Google Scholar] [CrossRef]
- Jeswiet, J.; Geiger, M.; Engel, U.; Kleiner, M.; Schikorra, M.; Duflou, J.; Neugebauer, R.; Bariani, P.; Brushi, S. Metal forming progress since 2000. CIRP J. Manuf. Sci. Technol. 2008, 1, 2–17. [Google Scholar] [CrossRef]
- Scholz, P.; Börner, R.; Kühn, R.; Müller, R. Dry Forming of Aluminium Sheet Metal: Influence of Different Types of Forming Tool Microstructures on the Coefficient of Friction. Key Eng. Mater. 2015, 651–653, 516–521. [Google Scholar] [CrossRef]
- Jeswiet, J.; Hagan, E.; Szekeres, A. Forming parameters for incremental forming of aluminium alloy sheet metal. Proc. Inst. Mech. Eng., Part B J. Eng. Manuf. 2002, 216, 1367–1371. [Google Scholar] [CrossRef]
- Meier, M.; Pfestorf, M.; Geiger, M.; Merklein, M. The use of dry film lubricants in aluminum sheet metal forming. Wear 2003, 255, 1455–1462. [Google Scholar]
- Gronostajski, Z.; Pater, Z.; Madej, L.; Gontarz, A.; Lisiecki, L.; Łukaszek-Sołek, A.; Ziółkiewicz, S. Recent development trends in metal forming. Arch. Civ. Mech. Eng. 2019, 19, 898–941. [Google Scholar] [CrossRef]
- Quadrini, F.; Santo, L.; Squeo, E.A. Flexible forming of thin aluminum alloy sheets. Int. J. Modern. Manuf. Technol. 2010, 2, 79–84. [Google Scholar]
- Jaremenko, C.; Ravikumar, N.; Affronti, E.; Merklein, M.; Maier, A. Determination of Forming Limits in Sheet Metal Forming Using Deep Learning. Materials 2019, 12, 1051. [Google Scholar] [CrossRef] [Green Version]
- Riaz, A.A.; Ullah, N.; Hussain, G.; Alkahtani, M.; Khan, M.N.; Khan, S. Experimental Investigations on the Effects of Rotational Speed on Temperature and Microstructure Variations in Incremental Forming of T6– Tempered and Annealed AA2219 Aerospace Alloy. Metals 2020, 10, 809. [Google Scholar] [CrossRef]
- Behera, A.K.; Gu, J.; Lauwers, B.; Duflou, J.R. Influence of material properties on accuracy response surfaces in single point incremental forming. Key Eng. Mater. 2012, 504, 919–924. [Google Scholar] [CrossRef]
- Bautista-Monsalve, F.; García-Sevilla, F.; Miguel, V.; Naranjo, J.; Manjabacas, M.C. A Novel Machine-Learning-Based Procedure to Determine the Surface Finish Quality of Titanium Alloy Parts Obtained by Heat Assisted Single Point Incremental Forming. Metals 2021, 11, 1287. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Kubit, A.; Dzierwa, A.; Krasowski, B.; Jurczak, W. Surface Finish Analysis in Single Point Incremental Sheet Forming of Rib-Stiffened 2024-T3 and 7075-T6 Alclad Aluminium Alloy Panels. Materials 2021, 14, 1640. [Google Scholar] [CrossRef]
- Durante, M.; Formisano, A.; Langella, A. Observations on the influence of tool-sheet contact conditions on an incremental forming process. J. Mater. Eng. Perform. 2011, 20, 941–946. [Google Scholar] [CrossRef] [Green Version]
- Ambrogio, G.; Filice, L.; Manco, G.L. Warm incremental forming of magnesium alloy AZ31. CIRP Ann-Manuf Technol. 2008, 57, 257–260. [Google Scholar] [CrossRef]
- Ramulu, P.J. Aluminum Alloys Behavior during Forming. In Aluminium Alloys and Composites; Cooke, K., Ed.; IntechOpen Ltd.: London, UK, 2020; pp. 695–728. [Google Scholar]
- Trzepieciński, T.; Oleksik, V.; Pepelnjak, T.; Najm, S.M.; Paniti, I.; Maji, K. Emerging Trends in Single Point Incremental Sheet Forming of Lightweight Metals. Metals 2021, 11, 1188. [Google Scholar] [CrossRef]
- Sieniawski, J. Stopy aluminium stosowane w technice lotniczej. Mechanik 2009, 7, 649–654. [Google Scholar]
- Djukanovic, G. Aluminium Alloys in the Automotive Industry: A Handy Guide. Available online: https://aluminiuminsider.com/aluminium-alloys-automotive-industry-handy-guide/ (accessed on 21 October 2021).
- Kwiatkowski, L. Podatność na korozję i skuteczność aktualnych metod ochrony przed korozją stopów aluminium stosowanych w budownictwie. Inżynieria Powierzchni 2009, 4, 24–33. [Google Scholar]
- Ambrogio, G.; Filice, L.; Gagliardi, F. Formability of lightweight alloys by hot incremental sheet forming. Mater. Des. 2012, 34, 501–508. [Google Scholar] [CrossRef]
- Bao, W.; Chu, X.; Lin, S.; Gao, J. Experimental investigation on formability and microstructure of AZ31B alloy in electropulse-assisted incremental forming. Mater. Des. 2015, 87, 632–639. [Google Scholar] [CrossRef]
- Dou, S.; Xia, J. Analysis of Sheet Metal Forming (Stamping Process): A Study of the Variable Friction Coefficient on 5052 Aluminum Alloy. Metals 2019, 9, 853. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Cai, Z.; He, D.; Li, L. Aluminum Alloy Sheet-Forming Limit Curve Prediction Based on Original Measured Stress-Strain Data and Its Application in Stretch-Forming Process. Metals 2019, 9, 1129. [Google Scholar] [CrossRef] [Green Version]
- Xu, D.; Lu, B.; Cao, T.; Chen, J.; Long, H.; Cao, J. A comparative study on process potentials for frictional stir-and electric hot-assisted incremental sheet forming. Procedia Eng. 2014, 81, 2324–2329. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Jiang, S.; Zhang, K. Pulse current-assisted hot-forming of light metal alloy. Int. J. Adv. Manuf. Technol. 2012, 63, 931–938. [Google Scholar] [CrossRef]
- Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA). Available online: http://prisma-statement.org/ (accessed on 10 October 2021).
- Kumar, Y.; Kumar, S. Incremental Sheet Forming (ISF). In Advances in Material Forming and Joining; Narayanan, R.G., Dixit, U.S., Eds.; Springer: New Delhi, India, 2015; pp. 29–46. [Google Scholar]
- Jackson, K.; Allwood, J. The mechanics of incremental sheet forming. J. Mater. Process. Technol. 2009, 209, 1158–1174. [Google Scholar] [CrossRef] [Green Version]
- Azaouzi, M.; Lebaal, N. Tool path optimization for single point incremental sheet forming using response surface method. Simul. Model. Pract. Theory 2012, 24, 49–58. [Google Scholar] [CrossRef]
- Selvam, A.J.M.; Velu, R.; Dheerankumar, T. Study of the Influence of the Process Variables on Formability and Strain Distribution in Incremental Sheet Metal Working of AA 1050 Sheets. In Innovative Design and Development Practices in Aerospace and Automotive Engineering; Bajpai, R., Chandrasekhar, U., Eds.; Springer: Singapore, 2014; pp. 493–505. [Google Scholar]
- Leszak, E. Apparatus and Process for Incremental Dieless Forming. Patent No. US3342051A, 19 September 1967. [Google Scholar]
- Berghan, W.G.; Murray, J.G.F. Method of Dielessly Forming Surfaces of Revolution. Patent No. US3316745A, 8 February 1965. [Google Scholar]
- Berghan, W.G.; Murray, J.G.F. Process for the Production of Surfaces of Revolution. Patent No. DE1527973A1, 8 February 1965. [Google Scholar]
- Emmens, W.C.; Sebastiani, G.; van den Boogaard, A.H. The technology of Incremental Sheet Forming—A brief review of the history. J Mater. Process. Technol. 2010, 210, 981–997. [Google Scholar] [CrossRef] [Green Version]
- Mason, B. Sheet Metal Forming for Small Batches. Bachelor’s Thesis, University of Nottingham, Nottingham, UK, 1978. [Google Scholar]
- Appleton, E.; Mason, B. Sheet metal forming for small batches using sacrificial tooling. Prod. Eng. 1984, 63, 58. [Google Scholar] [CrossRef]
- Matsubara, S. Incremental Backward Bulge Forming of a Sheet Metal with a Hemispherical Head Tool—A Study of a Numerical Control Forming System II. J. Jpn. Soc. Technol. Plast. 1994, 35, 1311–1316. [Google Scholar]
- Oleksik, V.; Trzepieciński, T.; Szpunar, M.; Chodoła, Ł.; Ficek, D.; Szczęsny, I. Single-Point Incremental Forming of Titanium and Titanium Alloy Sheets. Materials 2021, 14, 6372. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Najm, S.M.; Sbayti, M.; Belhadjsalah, H.; Szpunar, M.; Lemu, H.G. New Advances and Future Possibilities in Forming Technology of Hybrid Metal–Polymer Composites Used in Aerospace Applications. J. Compos. Sci. 2021, 5, 217. [Google Scholar] [CrossRef]
- Silva, M.B.; Martins, P.A.F. Two-Point Incremental Forming with Partial Die: Theory and Experimentation. J. Mater. Eng. Perform. 2013, 22, 1018–1027. [Google Scholar] [CrossRef]
- Li, X.; Han, K.; Li, D. Multi-Stage Two Point Incremental Sheet Forming. J. Phys Conf. Ser. 2018, 1063, 012064. [Google Scholar] [CrossRef]
- Iseki, H. A simple deformation analysis for incremental bulging of sheet metal using high speed water jet. In Proceedings of the 6th International Conference on Technology of Plasticity, Nuremberg, Germany, 19–24 September 1999; pp. 1483–1490. [Google Scholar]
- Iseki, H. Flexible and incremental bulging of sheet metal using high–speed water jet. JSME Int. J. Ser. C 2001, 44, 468–493. [Google Scholar] [CrossRef] [Green Version]
- Jurisevic, B.; Kuzman, K.; Junkar, M. Water jetting technology: An alternative in incremental sheet metal forming. Int. J. Adv. Manuf. Technol. 2006, 31, 18–23. [Google Scholar] [CrossRef]
- Lu, B.; Bazeer, M.W.M.; Cao, J.F.; Ai, S.; Chen, J.; Ou, H.; Long, H. A study of incremental sheet forming by using water jet. Int. J. Adv. Manuf. Technol. 2017, 91, 2291–2301. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Zhang, T.T.; Lei, L.; Dai, M.Q. The high-pressure liquid jet incremental forming for the aluminum sheet. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2014, 229, 682–690. [Google Scholar] [CrossRef]
- Emmens, W.C. Water jet forming of steel beverage cans. Int. J. Mach. Tool. Manuf. 2006, 46, 1243–1247. [Google Scholar] [CrossRef]
- Jurisevic, B.; Sajn, V.; Kosel, F.; Junkar, M. Introduction of laminated supporting tools in water jet incremental sheet metal forming. Int. J. Adv. Manuf. Technol. 2008, 37, 496–503. [Google Scholar] [CrossRef]
- Sajn, V.; Jurisevic, B.; Kosel, F. Water jet incremental sheet metal forming: Pressure distribution analysis. Int. J. Interact. Des. Manuf. 2011, 5, 95–102. [Google Scholar] [CrossRef]
- Teymoori, F.; LohMousavi, M.; Etesam, A. Numerical analysis of fluid structure interaction in water jet incremental sheet forming process using coupled Eulerian–Lagrangian approach. Int. J. Interact. Des. Manuf. 2016, 10, 203–210. [Google Scholar] [CrossRef]
- Kai, H.; Li, J.H.; Luo, Q.; Mao, H.; Du, R.X. A study on dieless incremental sheet metal forming using water jet technology. Adv. Mater. Res. 2011, 189–193, 795–800. [Google Scholar] [CrossRef]
- Lu, B.; Cao, J.; Jun, C.; Bin, L.; Bin, L.; Jian, C.; Jun, C. High-Pressure Water Jet Plate Incremental Forming and Cutting Device. Patent No. CN102218706A, 24 March 2011. [Google Scholar]
- He, K.; Li, J.; Mao, H.; Luo, Q.; Li, Q.; Kai, H.; Jiuhua, L.; He, M.; Qun, L.; Quanchang, L. High-Pressure Water Jet Flexible Incremental Forming Process and Device for Plates. Patent No. CN 201110347675, 4 November 2011. [Google Scholar]
- Psyk, V.; Kurka, P.; Kimme, S.; Werner, M.; Landgrebe, D.; Ebert, A.; Schwarzendahl, M. Structuring by electromagnetic forming and by forming with an elastomer punch as a tool for component optimisation regarding mechanical stiffness and acoustic performance. Manuf. Rev. 2015, 2, 23. [Google Scholar] [CrossRef] [Green Version]
- Thibaudeau, E.; Kinsey, B.L. Analytical design and experimental validation of uniform pressure actuator for electromagnetic forming and welding. J. Mater. Process. Technol. 2015, 215, 251–263. [Google Scholar] [CrossRef]
- Zhang, S.H.; Chen, S.F.; Ma, Y.; Song, H.W.; Cheng, M. Developments of new sheet metal forming technology and theory in China. Acta Metall. Sin. 2015, 28, 1452–1470. [Google Scholar] [CrossRef]
- Long, A.; Wan, M.; Wang, W.; Wu, X.; Cui, X.; Ma, B. Forming methodology and mechanism of a novel sheet metal forming technology-electromagnetic superposed forming(EMSF). Int. J. Solids Struct. 2018, 151, 165–180. [Google Scholar] [CrossRef]
- Psyk, V.; Risch, D.; Kinsey, B.L.; Tekkaya, A.E.; Kleiner, M. Electromagnetic forming—A review. J. Mater. Process. Technol. 2011, 211, 787–829. [Google Scholar] [CrossRef]
- Kamal, M.; Shang, J.; Cheng, V.; Hatkevich, S.; Daehn, G.S. Agile manufacturing of a micro-embossed case by a two-step electromagnetic forming process. J. Mater. Process. Technol. 2007, 190, 41–80. [Google Scholar] [CrossRef]
- Li, J.; Qiu, W.; Huang, L.; Su, H.; Tao, H.; Li, P. Gradient electromagnetic forming (GEMF): A new forming approach for variable-diameter tubes by use of sectional coil. Int. J. Mach. Tools Manuf. 2018, 135, 65–77. [Google Scholar] [CrossRef]
- Yu, H.; Chen, J.; Liu, W.; Yin, H.; Li, C. Electromagnetic forming of aluminum circular tubes into square tubes: Experiment and numerical simulation. J. Manuf. Process. 2018, 31, 613–623. [Google Scholar] [CrossRef]
- Centeno, G.; Martínez-Donaire, A.J.; Bagudanch, I.; Morales-Palma, D.; Garcia-Romeu, M.L.; Vallellano, C. Revisiting Formability and Failure of AISI304 Sheets in SPIF: Experimental Approach and Numerical Validation. Metals 2017, 7, 531. [Google Scholar] [CrossRef] [Green Version]
- Cui, X.; Zhang, Z.; Yu, H.; Xiao, X.; Cheng, Y. Springback Calibration of a U-Shaped Electromagnetic Impulse Forming Process. Metals 2019, 9, 603. [Google Scholar] [CrossRef] [Green Version]
- Feng, F.; Li, J.; Huang, L.; Liu, X.; Ma, H.; Li, G. The research of electromagnetic incremental forming process of Aluminum alloy sheet and the interaction between the die and the sheet. Procedia Eng. 2017, 207, 329–334. [Google Scholar] [CrossRef]
- Cui, X.H.; Mo, J.H.; Li, J.J.; Zhao, J.; Zhu, Y.; Huang, L.; Li, Z.W.; Zhong, K. Electromagnetic incremental forming (EMIF): A novel aluminum alloy sheet and tube forming technology. J. Mater. Process. Technol. 2014, 214, 409–427. [Google Scholar] [CrossRef]
- Imbert, J.M.; Winkler, S.L.; Worswick, M.J.; Oliveira, D.A.; Golovashchenko, S. The effect of tool–sheet interaction on damage evolution in electromagnetic forming of aluminum alloy sheet. J. Eng. Mater. Technol. 2005, 127, 145–153. [Google Scholar] [CrossRef]
- Liu, X.; Huang, L.; Li, J.; Su, H. An electromagnetic incremental forming (EMIF) strategy for large-scale parts of aluminum alloy based on dual coil. Int. J. Adv. Manuf. Technol. 2019, 104, 411–431. [Google Scholar] [CrossRef]
- Su, H.; Huang, L.; Li, J.; Ma, F.; Ma, H.; Huang, P.; Zhu, H.; Feng, F. Inhomogeneous deformation behaviors of oblique hole-flanging parts during electromagnetic forming. J. Manuf. Process. 2020, 52, 1–11. [Google Scholar] [CrossRef]
- Guo, K.; Lei, X.; Zhan, M.; Tan, J. Electromagnetic incremental forming of integral panel under different discharge conditions. J. Manuf. Process. 2017, 28, 373–382. [Google Scholar] [CrossRef]
- Trzepieciński, T. Recent Developments and Trends in Sheet Metal Forming. Metals 2000, 10, 779. [Google Scholar] [CrossRef]
- Balanethiram, V.S.; Hu, X.; Altynova, M.; Daehn, G.S. Hyperplasticity: Enhanced formability at high rates. J. Mater. Process. Technol. 1994, 45, 595–600. [Google Scholar] [CrossRef]
- Golovashchenko, S.F. Material formability and coil design in electromagnetic forming. J. Mater. Eng. Perform. 2007, 16, 314–320. [Google Scholar] [CrossRef]
- Neto, D.M.; Martins, J.M.P.; Oliveira, M.C.; Menezes, L.F.; Alves, J.L. Evaluation of strain and stress states in the single point incremental forming process. Int. J. Adv. Manuf. Technol. 2016, 85, 521–534. [Google Scholar] [CrossRef] [Green Version]
- Shrivastava, P.; Tandon, P. Microstructure and texture based analysis of forming behavior and deformation mechanism of AA1050 sheet during Single Point Incremental Forming. J. Mater. Process. Technol. 2019, 266, 292–310. [Google Scholar] [CrossRef]
- Barnwal, V.K.; Chakrabarty, S.; Tewari, A.; Narasimhan, K.; Mishra, S.K. Forming behavior and microstructural evolution during single point incremental forming process of AA-6061 aluminum alloy sheet. Int. J. Adv. Manuf. Technol. 2018, 95, 921–935. [Google Scholar] [CrossRef]
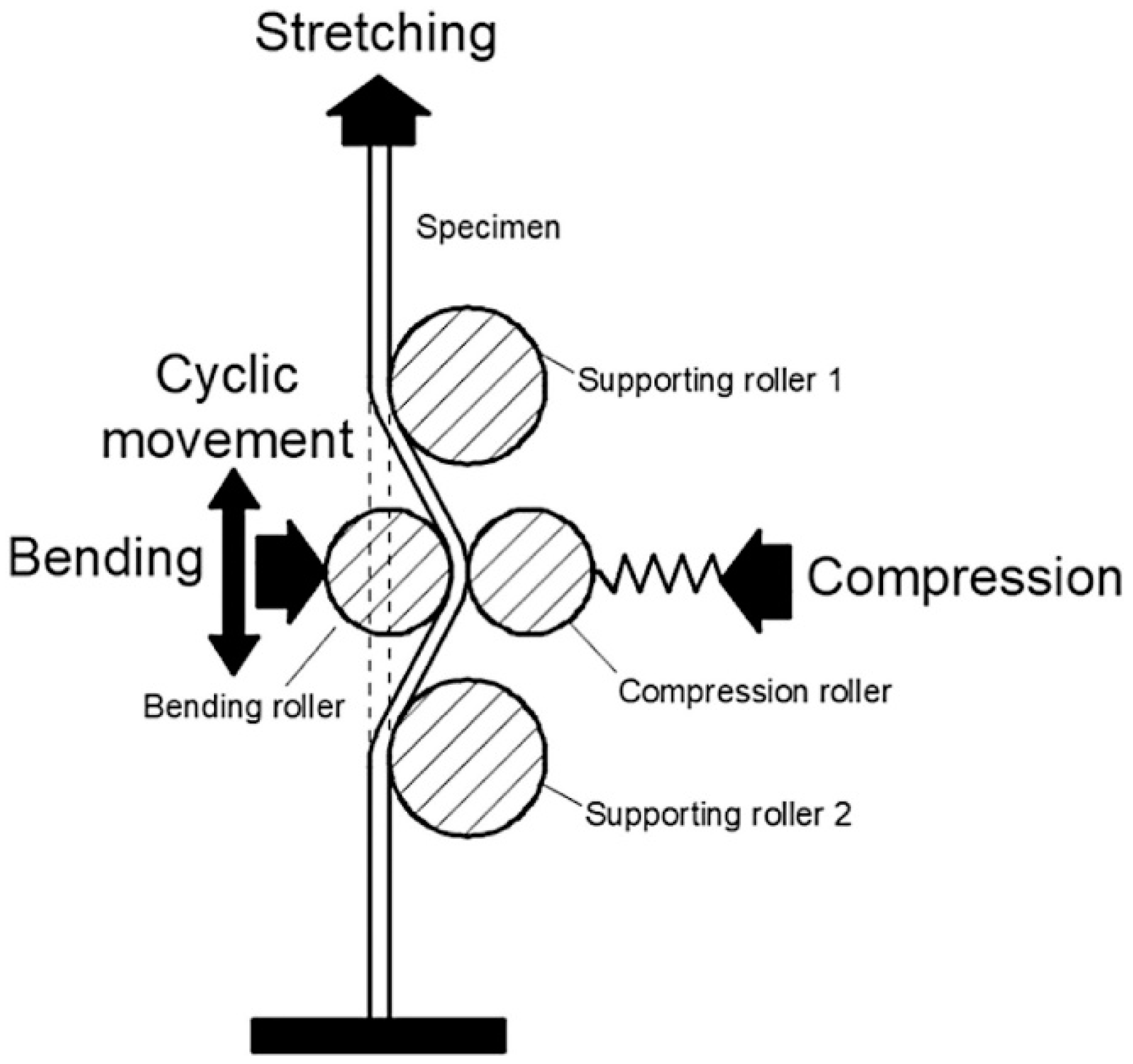
- Ai, S.; Dai, R.; Long, H. Investigating formability enhancement in double side incremental forming by developing a new test method of tension under cyclic bending and compression. J. Mater. Process. Technol. 2020, 27, 116349. [Google Scholar] [CrossRef]
- Ingarao, G.; Zaheer, O.; Campanella, D.; Fratini, L. Re-forming end-of-life components through single point incremental forming. Manuf. Lett. 2020, 24, 132–135. [Google Scholar] [CrossRef]
- Do, V.C.; Nguyen, D.T.; Cho, J.H.; Kim, Y.S. Incremental forming of 3D structured aluminum sheet. Int. J. Precis. Eng. Manuf. 2016, 17, 217–223. [Google Scholar] [CrossRef]
- Abd Ali, R.; Chen, W.; Jin, K.; Bao, Y.; Hussein, A.W. Formability and failure analyses of Al/SUS bilayer sheet in single point incremental forming. Int. J. Adv. Manuf. Technol. 2019, 105, 2785–2798. [Google Scholar] [CrossRef]
- Jeswiet, J.; Young, D. Forming limit diagrams for single-point incremental forming of aluminium sheet. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2005, 219, 359–364. [Google Scholar] [CrossRef]
- Mugendiran, V.; Gnanavelbabu, A. Comparison of FLD and thickness distribution on AA5052 aluminium alloy formed parts by incremental forming process. Procedia Eng. 2014, 97, 1983–1990. [Google Scholar] [CrossRef] [Green Version]
- Madeira, T.; Silva, C.M.A.; Silva, M.B.; Martins, P.A.F. Failure in single point incremental forming. Int. J. Adv. Manuf. Technol. 2015, 80, 1471–1479. [Google Scholar] [CrossRef]
- Kumar, G.; Maji, K. Investigations into Enhanced Formability of AA5083 Aluminum Alloy Sheet in Single-Point Incremental Forming. J. Mater. Eng. Perform. 2021, 30, 1289–1305. [Google Scholar] [CrossRef]
- Alinaghian, I.; Ranjbar, H.; Beheshtizad, M.A. Forming Limit Investigation of AA6061 Friction Stir Welded Blank in a Single Point Incremental Forming Process: RSM Approach. Trans. Indian Inst. Met. 2017, 70, 2303–2318. [Google Scholar] [CrossRef]
- Carlone, P.; Thuillier, S.; Andrade-Campos, A.; de Sousa, R.J.A.; Valente, R. Incremental forming of friction-stir welded aluminium blanks: An integrated approach. Int. J. Mater. Form. 2021, 14, 1121–1137. [Google Scholar] [CrossRef]
- Buffa, G.; Gucciardi, M.; Fratini, L.; Micari, F. Multi-directional vs. mono-directional multi-step strategies for single point incremental forming of non-axisymmetric components. J. Manuf. Processes 2020, 55, 22–30. [Google Scholar] [CrossRef]
- Kumar, A.; Gulati, V.; Kumar, P.; Singh, V.; Kumar, B.; Singh, H. Parametric Effects on Formability of AA2024-O Aluminum Alloy Sheets in Single Point Incremental Forming. J. Mater. Res. Technol. 2019, 8, 1461–1469. [Google Scholar] [CrossRef]
- Baruah, A.; Pandivelan, C.; Jeevanantham, A.K. Optimization of AA5052 in incremental sheet forming using grey relational analysis. Measurement 2017, 106, 95–100. [Google Scholar] [CrossRef]
- Ebrahimzadeh, P.; Baseri, H.; Mirnia, M.J. Formability of aluminum 5083 friction stir welded blank in two-point incremental forming process. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2018, 232, 267–280. [Google Scholar] [CrossRef]
- Vanhove, H.; Mohammadi, A.; Duflou, J.R. Incremental forming of aluminium alloys in cryogenic environment. AIP Conf. Proc. 2016, 1769, 070020. [Google Scholar] [CrossRef]
- Yang, M.; Bai, L.; Li, Y.; Yuan, Q. Influences of Vibration Parameters on Formability of 1060 Aluminum Sheet Processed by Ultrasonic Vibration-Assisted Single Point Incremental Forming. Adv. Mater. Sci. Eng. 2019, 2019. [Google Scholar] [CrossRef] [Green Version]
- Callebaut, B.; Duflou, J.; Verbert, J. Asymmetric Incremental Sheet Forming System. Patent No. US7984635B2, 26 July 2011. [Google Scholar]
- Ren, F.; Xia, Z.C. Method to Improve Geometrical Accuracy of an Incrementally Formed Workpiece. Patent No. US8783078B2, 22 July 2014. [Google Scholar]
- Ren, F.; Xia, Z. The Method of Gradually Forming the Workpiece. Patent No. CN102343386A, 8 February 2012. [Google Scholar]
- Ren, F.; Xia, Z.C. Verfahren Zum Verbessern Der Geometrischen Genauigkeit Eines Inkrementell Ausgebildeten Werkstücks. Patent No. DE102011079734A1, 10 May 2012. [Google Scholar]
- Ren, F.; Xia, Z.C. Method of Geometric Accuracy Increasing of Part Produced by Incremental Formation. Patent No. RU2576792C2, 10 March 2016. [Google Scholar]
- Johnson, C.F.; Kiridena, V.S.; Ren, F.; Cedric, Z. System and Method for Incrementally Forming a Workpiece. Patent No. US8322176B2, 4 December 2012. [Google Scholar]
- Johnson, C.F.; Vigeda, S.K.; Ren, F.; Xia, Z. System for Progressively Forming Workpieces. Patent No. CN201744547U, 16 February 2011. [Google Scholar]
- Janos, S.; Paniti, I. Device for Two Sided Incremental Sheet Forming. Patent No. EP2505279A1, 3 October 2012. [Google Scholar]
- Roth, J.T.; Grimm, T.J.; Craig, G. Incremental Forming Tools and Method. Patent No. US11072015B2, 27 July 2021. [Google Scholar]
- Roth, J.T.; Grimm, T.J.; Craig, G. New Incremental Forming Tools and Method. Patent No. US62311689, 22 March 2017. [Google Scholar]
- Cao, J.; Malhotra, R. System and Method for Accumulative Double Sided Incremental Forming. Patent No. US9168580B2, 27 October 2015. [Google Scholar]
- Cao, J.; Malhotra, R. System and Method for Accumulative Double Sided Incremental Forming. Patent No. WO2013062827A1, 2 May 2013. [Google Scholar]
- Konka, P.; Nallagundla, V.R.; Prakash, O.; Sahu, M. Tool for Enhanced Accuracy in Double-Sided Incremental Forming. Patent No. US20210237140A1, 5 August 2021. [Google Scholar]
- Konka, P.; Nallagundla, V.R.; Prakash, O.; Sahu, M. A Tool for Improved Accuracy in Double-Sided Incremental Forming. Patent No. EP3858511A1, 5 January 2021. [Google Scholar]
- Konka, P.; Nallagundla, V.R.; Prakash, O.; Sahu, M. A Tool for Improved Accuracy in Double-Sided Incremental Forming. Patent No. CN113198919A, 15 November 2020. [Google Scholar]
- Kiridena, V.S.; Xia, Z.C.; Ren, F. High Stiffness and High Access Forming Tool for Incremental Sheet Forming. Patent No. US8021501B2, 19 May 2016. [Google Scholar]
- Edwards, W.L.; Grimm, T.J.; Ragai, I.; Roth, J.T. Optimum Process Parameters for Springback Reduction of Single Point Incrementally Formed Polycarbonate. Procedia Manuf. 2017, 10, 329–338. [Google Scholar] [CrossRef]
- Gatea, S.; Ou, H.; McCartney, G. Review on the influence of process parameters in incremental sheet forming. Int. J. Adv. Manuf. Technol. 2016, 87, 479–499. [Google Scholar] [CrossRef] [Green Version]
- Bambach, M.; Taleb Araghi, B.; Hirt, G. Strategies to improve the geometric accuracy in asymmetric single point incremental forming. Prod. Eng. 2009, 3, 145–156. [Google Scholar] [CrossRef]
- Liu, Y.C. Method of Reducing Springback in Mechanically Pressed Sheet Materials. Patent No. EP0055435A2A, 18 December 1981. [Google Scholar]
- Liu, Y.C. Method of Reducing Springback in Mechanically Pressed Sheet Materials. Patent No. US4373371A, 15 February 1983. [Google Scholar]
- Roth, J.; Cao, J. Electrical-Assisted Double Side Incremental Forming and Processes Thereof. Patent No. US8741079B2, 3 June 2014. [Google Scholar]
- Roth, J.; Cao, J. Electrical-Assisted Double Side Incremental Forming and Processes Thereof. Patent No. WO2012030835A2, 8 March 2012. [Google Scholar]
- Roth, J.T. Single Point Incremental Forming of Metallic Materials using Applied Direct Current. Patent No. US8021501B2, 20 September 2011. [Google Scholar]
- Roth, J.T. Method for Reducing Springback Using Electrically-Assisted Manufacturing. Patent No. US10500629B2, 10 December 2019. [Google Scholar]
- Roth, J.T. Method for Reducing Springback Using Electrically-Assisted Manufacturing. Patent No. WO2016057688Al, 14 April 2016. [Google Scholar]
- Roth, J.; Cao, J. Apparatus for Electrically Assisted Incremental Forming and Process Thereof. Patent No. US9951397B2, 25 June 2018. [Google Scholar]
- Okada, N.; Ro, G.; Suzuki, Y. Method and Apparatus for Incremental Forming. Patent No. US6971256B2, 6 December 2005. [Google Scholar]
- Okada, N.; Ro, G.; Suzuki, Y. Method and Apparatus for Incremental Forming. Patent No. EP1462189B1, 29 September 2004. [Google Scholar]
- Okada, N.; Ro, G.; Suzuki, Y. Method and Apparatus for Incremental Forming. Patent No. JP2004291067A, 21 October 2004. [Google Scholar]
- Najm, S.M.; Paniti, I. Study on Effecting Parameters of Flat and Hemispherical end Tools in SPIF of Aluminium Foils. Teh. Vjesn.-Tech. Gaz. 2020, 27, 1844–1849. [Google Scholar]
- Najm, S.M.; Paniti, I. Experimental Investigation on the Single Point Incremental Forming of AlMn1Mg1 Foils using Flat End Tools. IOP Conf. Ser. Mater. Sci. Eng. 2018, 448, 012032. [Google Scholar] [CrossRef]
- Wei, H.; Zhou, L.; Heidarshenas, B.; Ashraf, I.K.; Han, C. Investigation on the influence of springback on precision of symmetric-cone-like parts in sheet metal incremental forming process. Int. J. Light. Mater. Manuf. 2019, 2, 140–145. [Google Scholar] [CrossRef]
- Sun, Y.; Lu, Z.; Li, C.; Wang, R.; Zhai, W. Study on the Springback Effect and Surface Property for Ultrasonic-Assisted Incremental Sheet Forming of Aluminum Alloy. Symmetry 2021, 13, 1217. [Google Scholar] [CrossRef]
- Rusu, G.P.; Bârsan, A.; Popp, M.O.; Maroșan, A. Comparison between aluminum alloys behavior in incremental sheet metal forming process of frustum pyramid shaped parts. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1009, 012054. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, C.; Sedaghat, H. Ultrasonic vibration–assisted incremental sheet metal forming. Int. J. Adv. Manuf. Technol. 2021, 114, 3311–3323. [Google Scholar] [CrossRef]
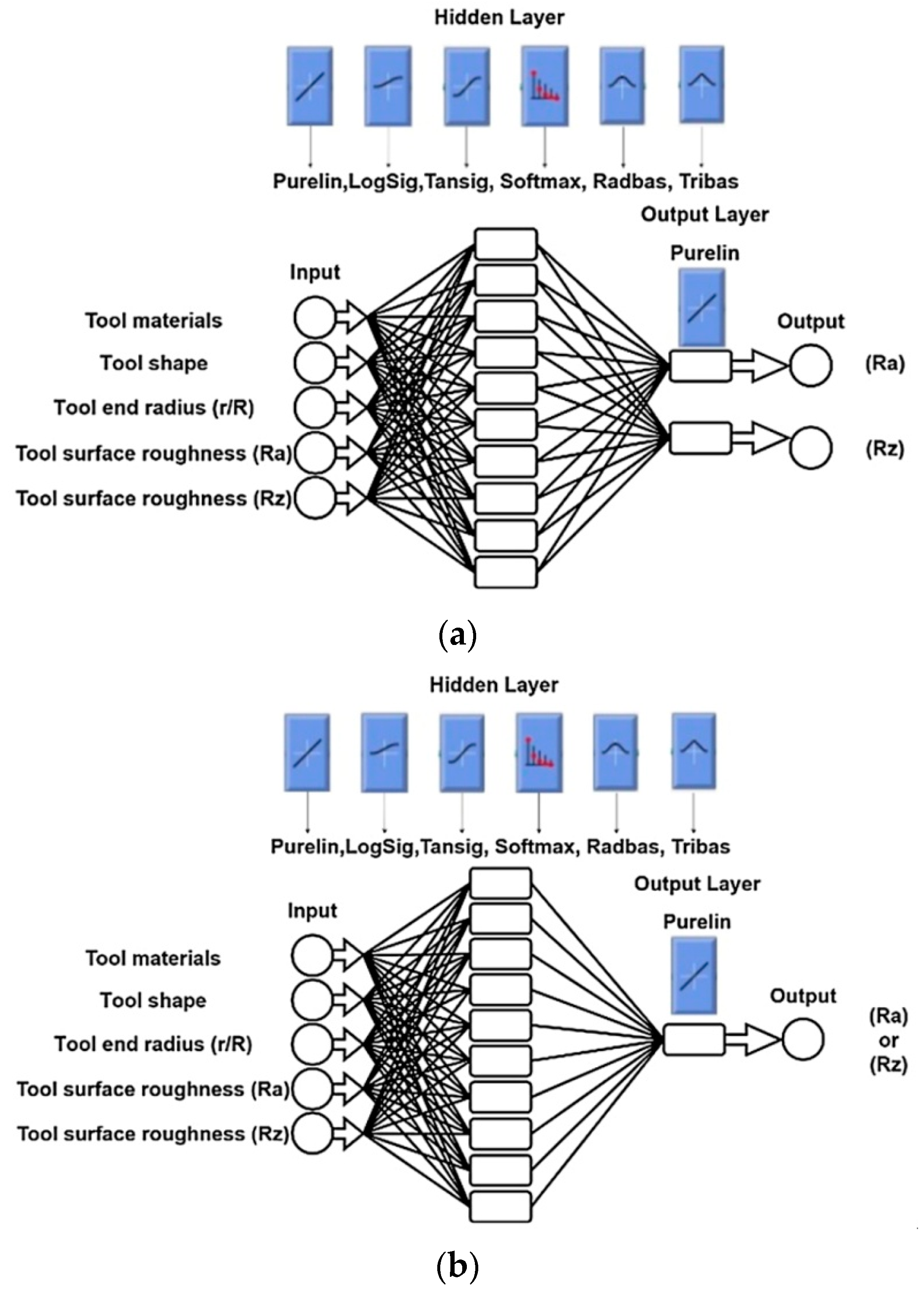
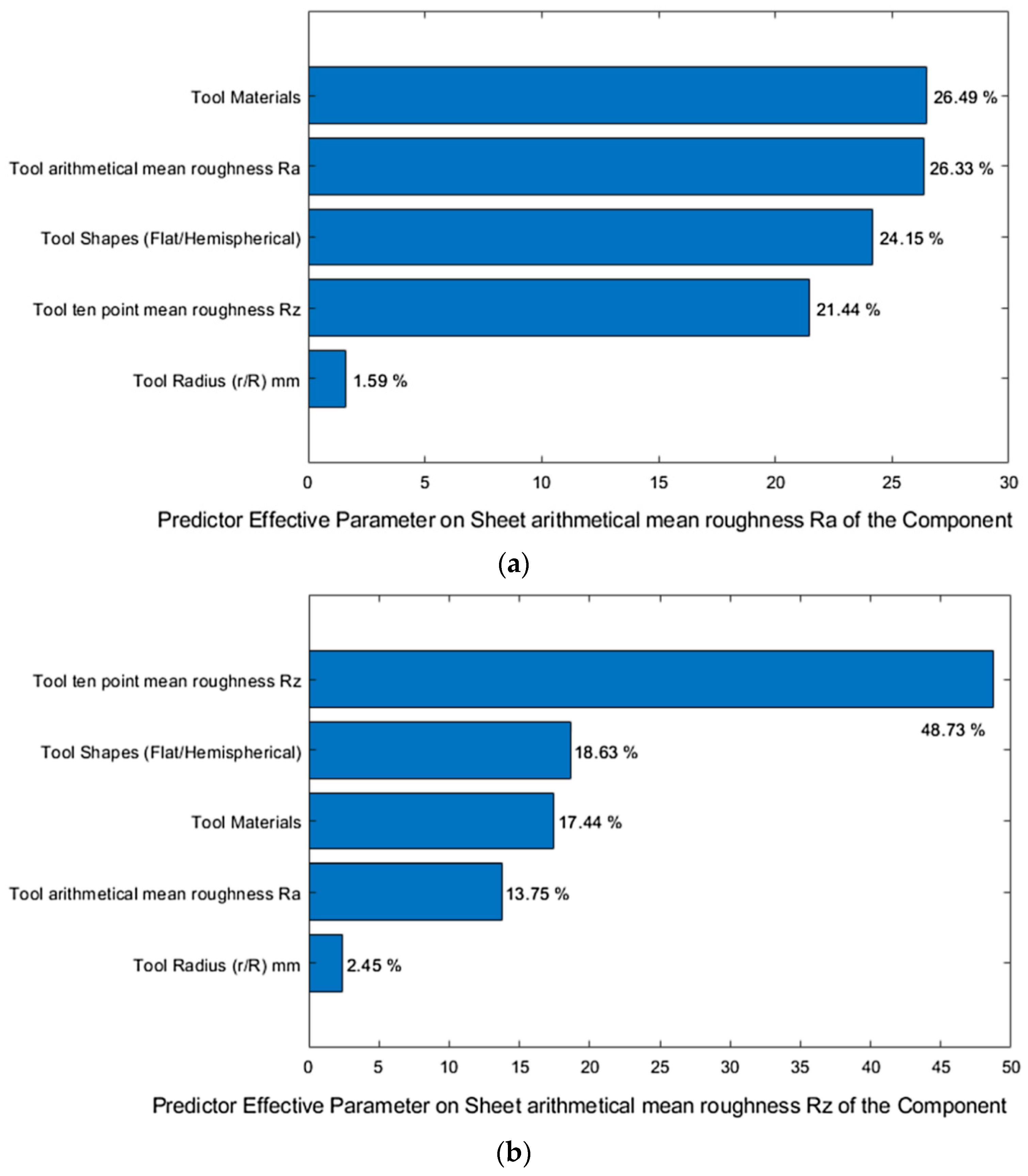
- Najm, S.M.; Paniti, I. Predict the Effects of Forming Tool Characteristics on Surface Roughness of Aluminum Foil Components Formed by SPIF Using ANN and SVR. Int. J. Precis. Eng. Manuf. 2021, 22, 13–26. [Google Scholar] [CrossRef]
- Najm, S.M.; Paniti, I. Artificial neural network for modeling and investigating the effects of forming tool characteristics on the accuracy and formability of thin aluminum alloy blanks when using SPIF. Int. J. Adv. Manuf. Technol. 2021, 114, 2591–2615. [Google Scholar] [CrossRef]
- Han, F.; Mo, J.; Qi, H.; Long, R.; Cui, X.; Li, Z. Springback prediction for incremental sheet forming based on FEM-PSONN technology. Trans. Nonferrous Met. Soc. China 2013, 23, 1061–1071. [Google Scholar] [CrossRef]
- Jeswiet, J.; Micari, F.; Hirt, G.; Bramley, A.; Duflou, J.; Allwood, J. Asymmetric single point incremental forming of sheet metal. CIRP Ann.–Manuf. Technol. 2005, 54, 88–114. [Google Scholar] [CrossRef]
- Hirt, G.; Kordtomeikel, R.; Bremen, T.; Laugwitz, M.; Bailly, D. On the Geometrical Accuracy in Incremental Sheet Forming. In Forming the Future. The Minerals, Metals & Materials Series; Daehn, G., Cao, J., Kinsey, B., Tekkaya, E., Vivek, A., Yoshida, Y., Eds.; Springer: Cham, Switzerland; pp. 507–521.
- Ambrogio, G.; Costantino, I.; de Napoli, L.; Filice, L.; Fratini, L.; Muzzupappa, M. Influence of some relevant process parameters on the dimensional accuracy in incremental forming: A numerical and experimental investigation. J. Mater. Process. Technol. 2004, 153, 501–507. [Google Scholar] [CrossRef]
- Hirt, G.; Ames, J.; Bambach, M.; Kopp, R.; Kopp, R. Forming strategies and Process Modelling for CNC Incremental Sheet Forming. CIRP Ann. 2004, 53, 203–206. [Google Scholar] [CrossRef]
- Lu, B.; Chen, J.; Ou, H.; Cao, J. Feature-based tool path generation approach for incremental sheet forming process. J. Mater. Process. Technol. 2013, 213, 1221–1233. [Google Scholar] [CrossRef]
- Jung, K.S.; Yu, J.H.; Chung, W.J.; Lee, C.W. Tool Path Design of the Counter Single Point Incremental Forming Process to Decrease Shape Error. Materials 2020, 13, 4719. [Google Scholar] [CrossRef]
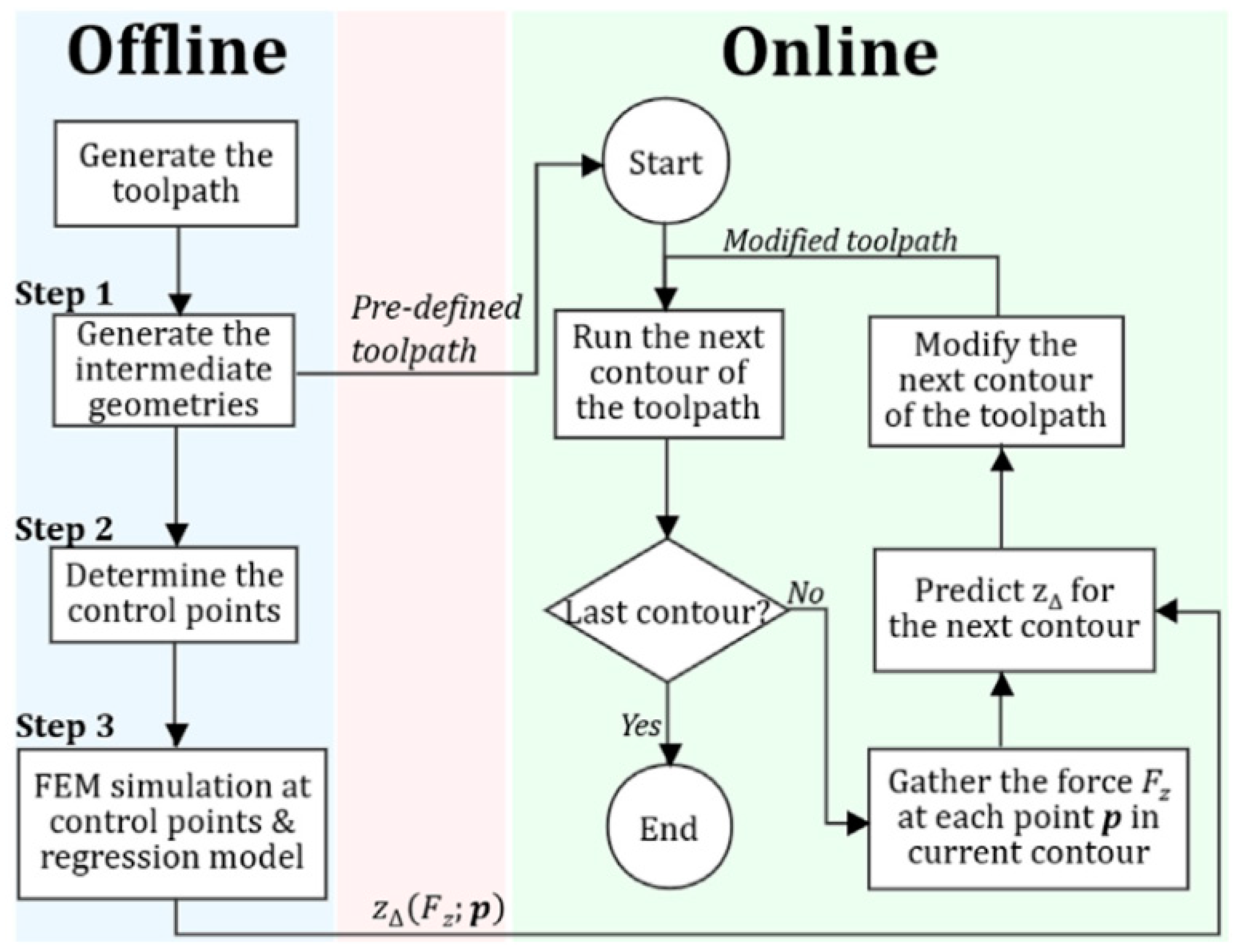
- Ren, H.; Xie, J.; Liao, S.; Leem, D.; Ehmann, K.; Cao, J. In-situ springback compensation in incremental sheet forming. CIRP Ann. 2019, 68, 317–320. [Google Scholar] [CrossRef]
- Fiorentino, A.; Feriti, G.C.; Ceretti, E.; Giardini, C.; Bort, C.M.G.; Bosetti, P. Development of Tool Path Correction Algorithm in Incremental Sheet Forming. Key Eng. Mater. 2014, 622, 382–389. [Google Scholar] [CrossRef]
- Rauch, M.; Hascoet, J.Y.; Hamann, J.C.; Plenel, Y. Tool path programming optimization for incremental sheet forming applications. Comput. Aided Des. 2009, 41, 877–885. [Google Scholar] [CrossRef]
- Behera, A.K.; Verbert, J.; Lauwers, B.; Duflou, J.R. Tool path compensation strategies for single point incremental sheet forming using multivariate adaptive regression splines. Comput. Des. 2013, 45, 575–590. [Google Scholar] [CrossRef]
- Fu, Z.; Mo, J.; Han, F.; Gong, P. Tool path correction algorithm for single-point incremental forming of sheet metal. Int. J. Adv. Manuf. Technol. 2013, 64, 1239–1248. [Google Scholar] [CrossRef]
- Nasulea, D.; Oancea, G. Achieving Accuracy Improvements for Single-Point Incremental Forming Process Using a Circumferential Hammering Tool. Metals 2021, 11, 482. [Google Scholar] [CrossRef]
- Ambrogio, G.; Cozza, V.; Filice, L.; Micari, F. An analytical model for improving precision in single point incremental forming. J. Mater. Process. Technol. 2007, 191, 92–95. [Google Scholar] [CrossRef]
- Micari, F.; Ambrogio, G.; Filice, L. Shape and dimensional accuracy in Single Point Incremental Forming: State of the art and future trends. J. Mater. Process. Technol. 2007, 191, 390–395. [Google Scholar] [CrossRef]
- Isidore, B.B.L.; Hussain, G.; Shamchi, S.P.; Khan, W.A. Prediction and control of pillow defect in single point incremental forming using numerical simulations. J. Mech. Sci. Technol. 2016, 30, 2151–2161. [Google Scholar] [CrossRef]
- Isidore, B.B.L. Controlling Pillow Defect in Single Point Incremental Forming Through Varying Tool Geometry. Master’s Thesis, Eastern Mediterranean Universit, Gazimağusa, North Cyprus, June 2014. [Google Scholar]
- Zhang, H.; Lu, B.; Chen, J.; Feng, S.; Li, Z.; Long, H. Thickness control in a new flexible hybrid incremental sheet forming process. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2017, 231, 779–791. [Google Scholar] [CrossRef]
- Wei, H.; Hussain, G.; Shi, X.; Isidore, B.B.L.; Alkahtani, M.; Abidi, M.H. Formability of Materials with Small Tools in Incremental Forming. Chinese J. Mech. Eng. 2020, 33, 55. [Google Scholar] [CrossRef]
- Al-Ghamdi, K.; Hussain, G. The pillowing tendency of materials in single-point incremental forming: Experimental and finite element analyses. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 744–753. [Google Scholar] [CrossRef]
- Afzal, M.J. Study on the Single Point Incremental Sheet Forming of AISI 321 Variable Wall Angle Geometry. Available online: https://doi.org/10.21203/rs.3.rs-836822/v1 (accessed on 31 October 2021).
- Essa, K.; Hartley, P. An assessment of various process strategies for improving precision in single point incremental forming. Int. J. Mater. Form. 2011, 4, 401–412. [Google Scholar] [CrossRef]
- Li, J.; Yang, F.; Zhou, Z. Thickness distribution of multistage incremental forming with different forming stages and angle intervals. J. Cent. South Univ. 2015, 22, 842–848. [Google Scholar] [CrossRef]
- Gonzalez, M.M.; Lutes, N.A.; Fischer, J.D.; Woodside, M.R.; Bristow, D.A.; Landers, R.G. Analysis of geometric accuracy and thickness reduction in multistage incremental sheet forming using digital image correlation. Procedia Manuf. 2019, 34, 950–960. [Google Scholar] [CrossRef]
- Li, J.; Hu, J.; Pan, J.; Geng, P. Thickness distribution and design of a multistage process for sheet metal incremental forming. Int. J. Adv. Manuf. Technol. 2012, 62, 981–988. [Google Scholar] [CrossRef]
- Ambrogio, G.; Gagliardi, F.; Serratore, G.; Ramundo, E.; Filice, L. SPIF of tailored sheets to optimize thickness distribution along the shaped wall. Procedia Manuf. 2019, 29, 80–87. [Google Scholar] [CrossRef]
- Salem, E.; Shin, J.; Nath, M.; Banu, M.; Taub, A.I. Investigation of Thickness Variation in Single Point Incremental Forming. Procedia Manuf. 2016, 5, 828–837. [Google Scholar] [CrossRef] [Green Version]
- Awankar, G.B.; Rathi, M.G.; Brahmagiri, A.S. Experimental Investigation of Thickness Distribution in Incremental Sheet Forming for Aluminium. J. Mater. Sci. Mech. Eng. 2015, 2, 31–34. [Google Scholar]
- Zhu, H.; Cheng, G.; Jung, D. Toolpath Planning and Generation for Multi-Stage Incremental Forming Based on Stretching Angle. Materials 2021, 14, 4818. [Google Scholar] [CrossRef]
- Li, J.; Li, C.; Zhou, T.T. Thickness distribution and mechanical property of sheet metal incremental forming based on numerical simulation. Trans. Nonferr. Met. Soc. China 2012, 22, s54–s60. [Google Scholar] [CrossRef]
- Hrairi, M.; Echrif, S.B.M. Process Simulation and Quality Evaluation in Incremental Sheet Forming. IIUM Eng. J. 2011, 12, 185–196. [Google Scholar] [CrossRef]
- Hussain, G.; Gao, L. A novel method to test the thinning limits of sheet metals in negative incremental forming. Int. J. Mach. Tools Manuf. 2007, 47, 419–435. [Google Scholar] [CrossRef]
- Li, X.; Han, K.; Xu, P.; Wang, H.; Li, D.; Li, Y.; Li, Q. Experimental and theoretical analysis of the thickness distribution in multistage two point incremental sheet forming. Int. J. Adv. Manuf. Technol. 2020, 107, 191–203. [Google Scholar] [CrossRef]
- Avitzur, B.; Yang, C.T. Analysis of Power Spinning of Cones. J. Eng. Ind. 1960, 82, 231–244. [Google Scholar] [CrossRef]
- Young, D.; Jeswiet, J. Wall thickness variations in single-point incremental forming. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2004, 218, 1453–1459. [Google Scholar] [CrossRef]
- Ambrogio, G.; Filice, L.; Gagliardi, F.; Micari, F. Sheet Thinning Prediction in Single Point Incremental Forming. Adv. Mater. Res. 2005, 6, 479–486. [Google Scholar] [CrossRef]
- Bambach, M. A geometrical model of the kinematics of incremental sheet forming for the prediction of membrane strains and sheet thickness. J. Mater. Process. Technol. 2010, 210, 1562–1573. [Google Scholar] [CrossRef]
- Yang, M.; Yao, Z.; Li, Y.; Li, P.; Cui, F.; Bai, L. Study on Thickness Thinning Ratio of the Forming Parts in Single Point Incremental Forming Process. Adv. Mater. Sci. Eng. 2018, 2018, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Cao, T.; Liu, B.; Xu, D.; Zhang, H.; Chen, J.; Long, H.; Cao, J. An efficient method for thickness prediction in multi-pass incremental sheet forming. Int. J. Adv. Manuf. Technol. 2015, 77, 469–483. [Google Scholar] [CrossRef] [Green Version]
- Dohda, K.; Yamamoto, M.; Hu, C.; Dubar, L.; Ehmann, K.F. Galling phenomena in metal forming. Friction 2021, 9, 665–685. [Google Scholar] [CrossRef]
- Pujante, J.; Pelcastre, L.; Vilaseca, M.; Casellas, D.; Prakash, B. Investigations into wear and galling mechanism of aluminium alloy-tool steel tribopair at different temperatures. Wear 2013, 308, 193–198. [Google Scholar] [CrossRef] [Green Version]
- Dabwan, A.; Ragab, A.E.; Saleh, M.A.; Anwar, S.; Ghalab, A.M.; Rehman, A.U. Study of the Effect of Process Parameters on Surface Profile Accuracy in Single-Point Incremental Sheet Forming of AA1050-H14 Aluminum Alloy. Adv. Mater. Sci. Eng. 2020, 2020, 7265941. [Google Scholar] [CrossRef] [Green Version]
- Shamchi, S.P. Microstructures and Mechanical properties of AA-5754 and AA-6061 Aluminum alloys formed by Single Point Incremental Forming Process. Master’s Thesis, Eastern Mediterranean University, Gazimağusa, Cyprus, 2014. [Google Scholar]
- Viet, M.V.; Thinh, N.T.; Sy, L.V.; Antonov, S. Study on the formability by TPIF technology for aluminium sheet at room temperature. E3S Web Conf. 2020, 207, 05005. [Google Scholar] [CrossRef]
- Azpen, Q.; Beharudin, H.; Sulaiman, S.; Mustapha, F. Effect of process parameters on the surface roughness of aluminum alloy AA 6061-T6 sheets in frictional stir incremental forming. Adv. Prod. Eng. Manag. 2018, 13, 405–416. [Google Scholar] [CrossRef]
- Durante, M.; Formisano, A.; Langella, A.; Minutolo, F.M.C. The influence of tool rotation on an incremental forming process. J. Mater. Process. Technol. 2009, 209, 4621–4626. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Maneesh, K.; Venkata Reddy, N.; Cao, J. Formability and surface finish studies in single point incremental forming. J. Manuf. Sci. Eng. 2011, 133, 061020. [Google Scholar] [CrossRef]
- Hamilton, K.; Jeswiet, J. Single point incremental forming at high feed rates and rotational speeds: Surface and structural consequences. CIRP Annals 2010, 59, 311–314. [Google Scholar] [CrossRef]
- Ambrogio, G.; Filice, L.; Gagliardi, F. Improving industrial suitability of incremental sheet forming process. Int. J. Adv. Manuf. Technol. 2012, 58, 941–947. [Google Scholar] [CrossRef]
- Lasunon, O.U. Surface roughness in incremental sheet metal forming of AA5052. Adv. Mater. Res. 2013, 753–755, 203–206. [Google Scholar] [CrossRef]
- Filice, L.; Fratini, L.; Micari, F. Analysis of material formability in incremental forming. CIRP Annals 2002, 51, 199–202. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, S.; Li, Y.; Meehan, P.A. Modeling and optimization of surface roughness in incremental sheet forming using a multi-objective function. Mater. Manuf. Process. 2014, 29, 808–818. [Google Scholar] [CrossRef]
- Mugendiran, V.; Gnanavelbabu, A.; Ramadoss, R. Parameter optimization for surface roughness and wall thickness on AA5052 aluminium alloy by incremental forming using response surface methodology. Procedia Eng. 2014, 97, 1991–2000. [Google Scholar] [CrossRef] [Green Version]
- Lu, B.; Fang, Y.; Xu, D.K.; Chen, J.; Ou, H.; Moser, N.H.; Cao, J. Mechanism investigation of friction-related effects in single point incremental forming using a developed oblique roller-ball tool. Int. J. Mach. Tools Manuf. 2014, 85, 14–29. [Google Scholar] [CrossRef]
- Powers, B.M.; Ham, M.; Wilkinson, M.G. Small data set analysis in surface metrology: An investigation using a single point incremental forming case study. Scanning 2010, 32, 199–211. [Google Scholar] [CrossRef] [PubMed]
- Singh, S. A review on computer aided manufacturing factors affecting reduction of surface roughness and thickness. Int. Res. J. Eng. Technol. 2017, 4, 1474–1478. [Google Scholar]
- Mulay, A.; Ben, B.S.; Ismail, S.; Kocańda, A.; Jasiński, C. Performance evaluation of high-speed incremental sheet forming technology for AA5754 H22 aluminum and DC04 steel sheets. Arch. Civ. Mech. Eng. 2018, 18, 1275–1287. [Google Scholar] [CrossRef]
- Nama, S.A.; Namer, N.S.M.; Najm, S.M. The effect of using grease on the surface roughness of aluminum 1100 sheet during the Single Point Incremental Forming Process. Trends Mach. Des. 2014, 1, 53–56. [Google Scholar]
- Hagan, E.; Jeswiet, J. Analysis of surface roughness for parts formed by computer numerical controlled incremental forming. Proc. Inst. MEch. Eng, Part B J. Eng. Manuf. 2004, 218, 1307–1312. [Google Scholar] [CrossRef]
- Hussain, G.; Gao, L.; Hayat, N.; Cui, Z.; Pang, Y.; Dar, N. Tool and lubrication for negative incremental forming of a commercially pure titanium sheet. J. Mater. Process. Technol. 2008, 203, 193–201. [Google Scholar] [CrossRef]
- Bambach, M.; Hirt, G.; Junk, S. Modelling and Experimental Evaluation of the Incremental CNC Sheet Metal Forming Process. In Proceedings of the COMPLAS 7: 7th International Conference on Computational Plasticity, Barcelona, Spain, 7–10 April 2003; pp. 1–16. [Google Scholar]
- Eyckens, P.; Duflou, J.; Bael, A.; Houtte, P. The significance of friction in the single point incremental forming process. Int. J. Mater. Form. 2010, 3, 947–950. [Google Scholar] [CrossRef]
- Lee, B.H.; Keum, Y.K.; Wagoner, R.H. Modeling of the Friction Caused by Lubrication and Surface Roughness in Sheet Metal Forming. J. Mater. Process. Technol. 2002, 130, 60–63. [Google Scholar] [CrossRef]
- Trzepieciński, T. Tribological Performance of Environmentally Friendly Bio-Degradable Lubricants Based on a Combination of Boric Acid and Bio-Based Oils. Materials 2020, 13, 3892. [Google Scholar] [CrossRef]
- Azevedo, N.G.; Farias, J.S.; Bastos, R.P.; Teixeira, P.; Davim, J.P.; de Sousa, R.J.A. Lubrication aspects during single point incremental forming for steel and aluminum materials. Int. J. Precis. Eng. Manuf. 2015, 16, 589–595. [Google Scholar] [CrossRef]
- Suriyaprakan, P. Single Point Incremental Forming and MultiStage Incremental Forming on Aluminium Alloy 1050. Master’s Thesis, University of Porto, Porto, Portugal, February 2013. [Google Scholar]
- Gulati, V.; Aryal, A.; Katyal, P.; Goswami, A. Process parameters optimization in single point incremental forming. J. Inst. Eng. (India) Ser. A 2016, 97, 185–193. [Google Scholar] [CrossRef]
- Oraon, M.; Sharma, V. Prediction of surface roughness in single point incremental forming of AA3003-O alloy using artificial neural network. Int. J. Mater. Eng. Innov. 2018, 9, 1–19. [Google Scholar] [CrossRef]
- Patel, J.R.; Samvatsar, K.S.; Prajapati, H.P.; Rangrej, S.S. Optimization of process parameters for reducing surface roughness produced during single point incremental forming process. Int. J. Recent Technol. Mech. Electrical Eng. 2015, 2, 19–23. [Google Scholar]
- Duflou, J.; Tunckol, Y.; Szekeres, A.; Vanherck, P. Experimental study on force measurements for single point incremental forming. J. Mater. Process. Technol. 2007, 189, 65–72. [Google Scholar] [CrossRef]
- Kim, Y.H.; Park, J.J. Effect of process parameters on formability in incremental forming of sheet metal. J. Mater. Process. Technol. 2002, 130–131, 42–46. [Google Scholar] [CrossRef]
- Buffa, G.; Campanella, D.; Fratini, L. On the Improvement of Material Formability in SPIF Operation through Tool Stirring Action. Int. J. Adv. Manuf. Technol. 2013, 66, 1343–1351. [Google Scholar] [CrossRef]
- Xu, D.; Wu, W.; Malhotra, R.; Chen, J.; Lu, B.; Cao, J. Mechanism Investigation for the Influence of Tool Rotation and Laser Surface Texturing (LST) on Formability in Single Point Incremental Forming. Int. J. Mach. Tools Manuf. 2013, 73, 37–46. [Google Scholar] [CrossRef]
- Liu, Z. Friction Stir Incremental Forming of AA7075-O Sheets: Investigation on Process Feasibility. Procedia Eng. 2017, 207, 783–788. [Google Scholar] [CrossRef]
- Duflou, J.R.; Callebaut, B.; Verbert, J.; De Baerdemaeker, H. Improved SPIF Performance through Dynamic Local Heating. Int. J. Mach. Tools Manuf. 2008, 48, 543–549. [Google Scholar] [CrossRef]
- Hino, R.; Yoshida, F.; Nagaishi, N.; Naka, T. Incremental Sheet Forming with Local Heating for Lightweight Hard-to-Form Material. Int. J. Mod. Phys. B 2008, 22, 6082–6087. [Google Scholar] [CrossRef]
- Sy, L.V.; Thanh Nam, N. Hot Incremental Forming of Magnesium and Aluminum Alloy Sheets by Using Direct Heating System. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2013, 227, 1099–1110. [Google Scholar]
- Singh, S.A.; Priyadarshi, S.; Tandon, P. Investigations on the Influence of Heat on AA1050 Sheet during Incremental Forming. Lett. Mater. 2019, 9, 523–527. [Google Scholar] [CrossRef] [Green Version]
- Vahdani, M.; Mirnia, M.J.; Bakhshi-Jooybari, M.; Gorji, H. Electric Hot Incremental Sheet Forming of Ti-6Al-4V Titanium, AA6061 Aluminum, and DC01 Steel Sheets. Int. J. Adv. Manuf. Technol. 2019, 103, 1199–1209. [Google Scholar] [CrossRef]
- Najm, S.M.; Paniti, I.; Trzepieciński, T.; Nama, S.A.; Viharos, Z.J.; Jacso, A. Parametric Effects of Single Point Incremental Forming on Hardness of AA1100 Aluminium Alloy Sheets. Materials 2021, 14, 7263. [Google Scholar] [CrossRef]
- Gupta, P.; Jeswiet, J. Observations on Heat Generated in Single Point Incremental Forming. Procedia Eng. 2017, 183, 161–167. [Google Scholar] [CrossRef]
- Xiao, X.; Kim, C.-I.; Lv, X.-D.; Hwang, T.-S.; Kim, Y.-S. Formability and Forming Force in Incremental Sheet Forming of AA7075-T6 at Different Temperatures. J. Mech. Sci. Technol. 2019, 33, 3795–3802. [Google Scholar] [CrossRef]
- Li, Z.; Lu, S.; Zhang, T.; Zhang, C.; Mao, Z. 1060 Al Electric Hot Incremental Sheet Forming Process: Analysis of Dimensional Accuracy and Temperature. Trans. Indian. Inst. Met. 2018, 71, 961–970. [Google Scholar] [CrossRef]
- Pacheco, P.A.P.; Silveira, M.E. Numerical Simulation of Electric Hot Incremental Sheet Forming of 1050 Aluminum with and without Preheating. Int. J. Adv. Manuf. Technol. 2018, 94, 3097–3108. [Google Scholar] [CrossRef]
- Pacheco, P.A.P.; Silveira, M.E.; Silva, J.A. Heat Distribution in Electric Hot Incremental Sheet Forming. Int. J. Adv. Manuf. Technol. 2019, 102, 991–998. [Google Scholar] [CrossRef]
- Bejan, A.; Kraus, A.D. Heat Transfer Handbook; John Wiley & Sons, Inc.: New York, NY, USA, 2003. [Google Scholar]
- Darzi, S.; Mirnia, M.J.; Elyasi, M. Single-Point Incremental Forming of AA6061 Aluminum Alloy at Elevated Temperatures. Int. J. Adv. Manuf. Technol. 2021, 116, 1023–1039. [Google Scholar] [CrossRef]
- Zhang, P.; Li, J.; Chen, M. Effect of Different Temperatures on the Metallographic Structure and Tensile Property of 2024-T4 Alloy in Integral Heating Single Point Incremental Forming. Microsc. Res. Techn. 2020, 83, 920–927. [Google Scholar] [CrossRef]
- Rahmani, F.; Seyedkashi, S.M.H.; Hashemi, S.J. Experimental Study on Warm Incremental Tube Forming of AA6063 Aluminum Tubes. Int. J. Eng. 2020, 33, 1773–1779. [Google Scholar]
- Otsu, M.; Katayama, Y.; Muranaka, T. Effect of Difference of Tool Rotation Direction on Forming Limit in Friction Stir Incremental Forming. Key Eng. Mater. 2014, 622–623, 390–397. [Google Scholar] [CrossRef]
- Gupta, P.; Jeswiet, J. Effect of Temperatures during Forming in Single Point Incremental Forming. Int. J. Adv. Manuf. Technol. 2018, 95, 3693–3706. [Google Scholar] [CrossRef]
- Wang, Z.; Cai, S.; Chen, J. Experimental Investigations on Friction Stir Assisted Single Point Incremental Forming of Low-Ductility Aluminum Alloy Sheet for Higher Formability with Reasonable Surface Quality. J. Mater. Process. Technol. 2020, 277, 116488. [Google Scholar] [CrossRef]
- Zhan, X.; Huang, W.; Li, D.; Chen, J. An Optimum Process Window to Preferable Microstructure Distribution and Improved Macroscopic Property for Friction Stir–Assisted Incremental Aluminum Alloy Sheet Forming. Int. J. Adv. Manuf. Technol. 2021, 115, 1589–1603. [Google Scholar] [CrossRef]
- Zhan, X.; Liu, X.; Yang, M.; Li, M.; Li, X.; Chen, J. Dynamic Recrystallization and Solute Precipitation during Friction Stir Assisted Incremental Forming of AA2024 Sheet. Mater. Charact. 2021, 174, 111046. [Google Scholar] [CrossRef]
- Li, M.; Wu, R.; Cai, S.; Chang, Z.; Wang, Z.; Chen, J. Experimental Investigation on Friction-Stir-Assisted Incremental Forming with Synchronous Bonding of Aluminum Alloy and Steel Sheets. J. Mater. Eng. Perform. 2020, 29, 750–759. [Google Scholar] [CrossRef]
- Wu, R.; Li, M.; Liu, X.; Cai, S.; Chen, J. Characterization of Material Flow in Friction Stir-Assisted Incremental Forming with Synchronous Bonding of Dissimilar Sheet Metals. Int. J. Adv. Manuf. Technol. 2020, 109, 2523–2534. [Google Scholar] [CrossRef]
- Wu, R.; Li, M.; Liu, X.; Yang, Z.; Chen, J. Interfacial Quality Prediction Model for Al/Steel Sheets during Friction Stir Assisted Double-Sided Incremental Forming with Synchronous Bonding. Available online: https://www.researchsquare.com/article/rs-531361/v1 (accessed on 1 November 2021).
- Wu, R.; Liu, X.; Li, M.; Chen, J. Investigations on Deformation Mechanism of Double-Sided Incremental Sheet Forming with Synchronous Thermomechanical Steel-Aluminum Alloy Bonding. J. Mater. Process. Technol. 2021, 294, 117147. [Google Scholar] [CrossRef]
- Mohammadi, A.; Vanhove, H.; Bael, A.; Seefeldt, M.; Duflou, J. The Effect of Laser Radiation on the Residual Stress Levels of Single Point Incrementally Formed (SPIF) Parts. Available online: https://core.ac.uk/download/pdf/34624438.pdf (accessed on 1 November 2021).
- Lehtinen, P.; Väisänen, T.; Salmi, M. The Effect of Local Heating by Laser Irradiation for Aluminum, Deep Drawing Steel and Copper Sheets in Incremental Sheet Forming. Phys. Procedia 2015, 78, 312–319. [Google Scholar] [CrossRef]
- Mohammadi, A.; Vanhove, H.; van Bael, A.; Weise, D.; Duflou, J.R. Formability Enhancement in Incremental Forming for an Automotive Aluminium Alloy Using Laser Assisted Incremental Forming. Key Eng. Mater. 2015, 639, 195–202. [Google Scholar] [CrossRef]
- Mohammadi, A.; Qin, L.; Vanhove, H.; Seefeldt, M.; Van Bael, A.; Duflou, J.R. Single Point Incremental Forming of an Aged AL-Cu-Mg Alloy: Influence of Pre-Heat Treatment and Warm Forming. J. Mater. Eng. Perform. 2016, 25, 2478–2488. [Google Scholar] [CrossRef]






| Series of Al-Based Alloy | Main Alloying Elements | Properties |
|---|---|---|
| 1xxx | lack (content of contaminations <1%) | good formability in cold forming and at elevated temperature, low strength, good resistance to corrosion, high electrical and heat conductivity |
| 2xxx | Cu | low resistance to corrosion |
| 3xxx | Mn | good formability but low strength, good weldability and corrosion resistance |
| 4xxx | Si | high strength and corrosion resistance |
| 5xxx | Mg | good corrosion resistance in salt water, good weldability and ability to anodising |
| 6xxx | Mg + Si | high corrosion resistance, good formability |
| 7xxx | Zn + Mg | the highest strength from all Al-based alloys, low and medium resistance to corrosion |
| 8xxx | various alloying elements, the rest of aluminium alloys | - |
| Lubricant | Workpiece Material | Conditions | Reference |
|---|---|---|---|
| MoS2 | AA2024-T3 | hot forming | [40] |
| SAE 75W-85 gear oil | 2024-T3 Alclad 7075-T6 | cold forming | [32] |
| mineral oil | 2219-O and 2219-T6 | cold forming | [29] |
| without lubrication | 3003 | cold forming | [24] |
| without lubrication | 1050 | cold forming | [220] |
| oil | 7075-T0 | cold forming | [195] |
| 10w30 servo oil | 5754 H22 | cold forming | [206] |
| machine oil | AlMgSi0.5 | cold forming | [148] |
| Weicon AL-M paste | 1050 | cold forming | [214] |
| Moly Slip AS40 paste | 1050 | cold forming | [214] |
| oil | 1050-O, 1050-H24, 6082 | hot forming | [221] |
| mechanical oil | 5052-H32 | hot forming | [222] |
| Mineral oil (Total Finarol B 5746) | 1050 | cold forming | [214] |
| Moly Slip HSB paste | 1050 | cold forming | [214] |
| SAE 30 oil | 1050 | cold forming | [214] |
| Graphite powder + mineral oil (1:4) | 7075-O | hot forming | [223] |
| SAE 0W-4 | 6061-T6 | hot forming | [194] |
| water–oil emulsion cutting fluid | 3003-H14 | cold forming | [197] |
| graphite 33 | 5182 | hot forming | [224] |
| solid lubricant (stick wax lubricant) | 5052-H32 | cold forming | [199] |
| MoS2 | 5083 | hot forming | [225] |
| MoS2 | 5055 | hot forming | [226] |
| without lubrication | 1050 | hot forming | [227] |
| graphite | 6061 | hot forming | [228] |
| solid graphite powder and lithium grease with scale 1:1 | 1050 H14 | cold forming | [193] |
| 20W-50 | 1050 H14 | cold forming | [193] |
| machine oil | AlMn1Mg1 foil | cold forming | [142,143] |
| mineral oil | 1050-O | cold forming | [185] |
| coolant oil, Gp Grease Calcium, Supergrees EP2, Zinol grease | AA1100 | cold forming | [229] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trzepieciński, T.; Najm, S.M.; Oleksik, V.; Vasilca, D.; Paniti, I.; Szpunar, M. Recent Developments and Future Challenges in Incremental Sheet Forming of Aluminium and Aluminium Alloy Sheets. Metals 2022, 12, 124. https://doi.org/10.3390/met12010124
Trzepieciński T, Najm SM, Oleksik V, Vasilca D, Paniti I, Szpunar M. Recent Developments and Future Challenges in Incremental Sheet Forming of Aluminium and Aluminium Alloy Sheets. Metals. 2022; 12(1):124. https://doi.org/10.3390/met12010124
Chicago/Turabian StyleTrzepieciński, Tomasz, Sherwan Mohammed Najm, Valentin Oleksik, Delia Vasilca, Imre Paniti, and Marcin Szpunar. 2022. "Recent Developments and Future Challenges in Incremental Sheet Forming of Aluminium and Aluminium Alloy Sheets" Metals 12, no. 1: 124. https://doi.org/10.3390/met12010124
APA StyleTrzepieciński, T., Najm, S. M., Oleksik, V., Vasilca, D., Paniti, I., & Szpunar, M. (2022). Recent Developments and Future Challenges in Incremental Sheet Forming of Aluminium and Aluminium Alloy Sheets. Metals, 12(1), 124. https://doi.org/10.3390/met12010124









