Low-Cycle Fatigue Behavior of Hot-Bent Basal Textured AZ31B Wrought Magnesium Alloy
Abstract
:1. Introduction
2. Material and Methods
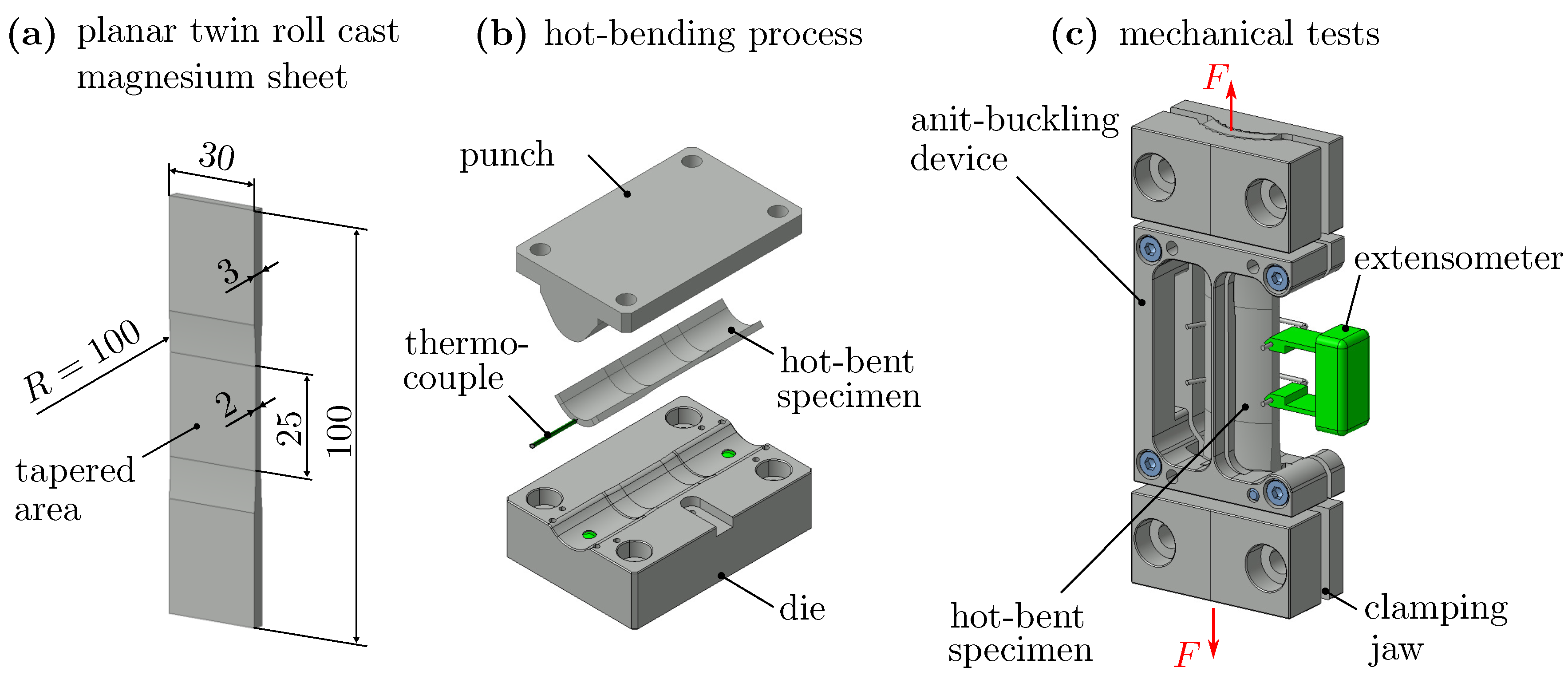
2.1. Hot-Bending Process
2.2. Microstructural Investigations
2.3. Uniaxial Quasi-Static and Cyclic Tests at Room Temperature
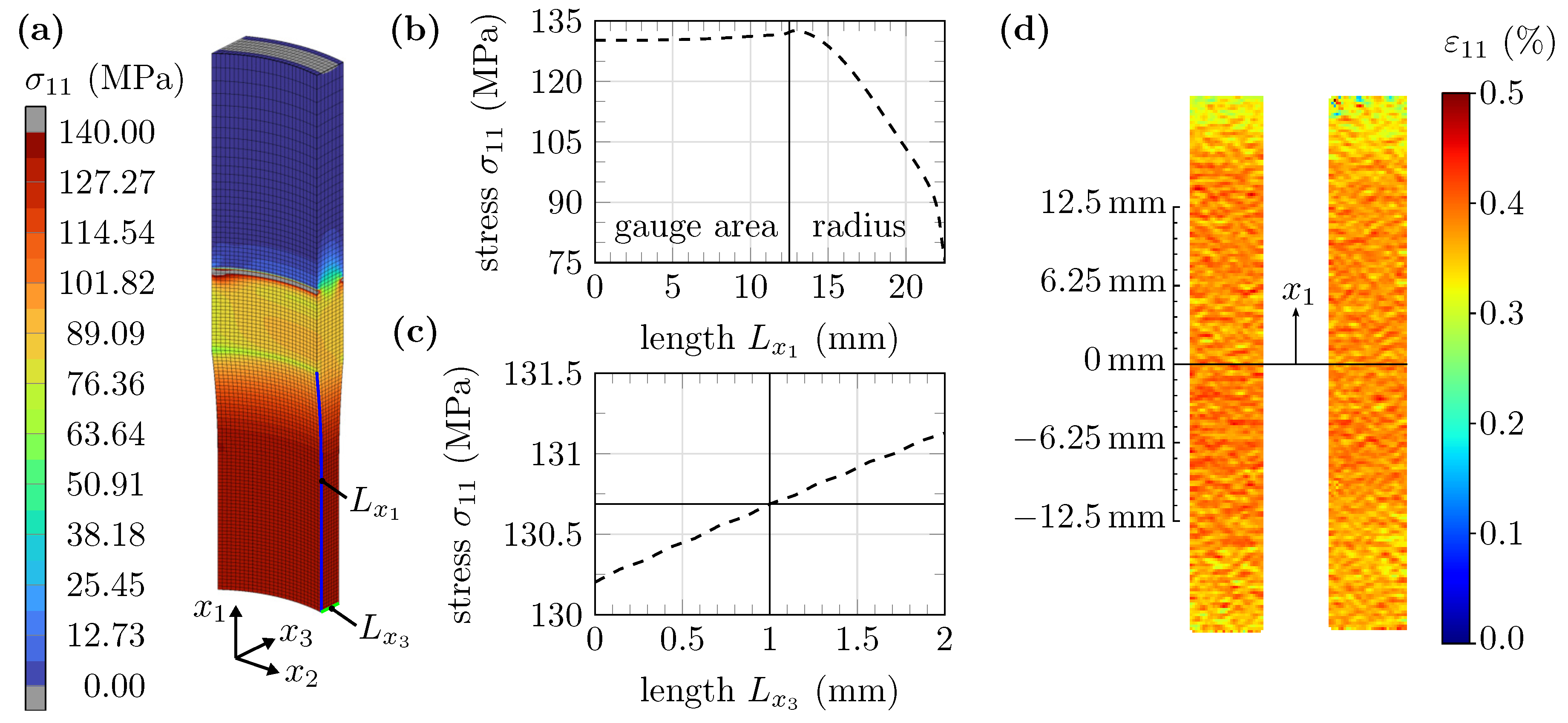
3. Numerical and Experimental Verification of the Novel, Hot-Bent Uniaxial Specimen
4. Results and Discussion
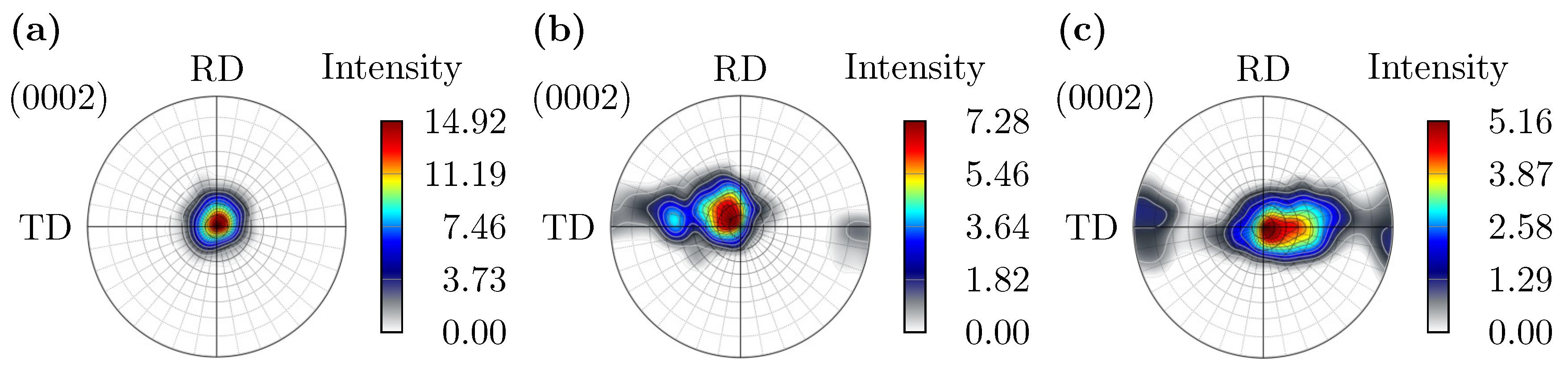
4.1. Microstructural Analyses
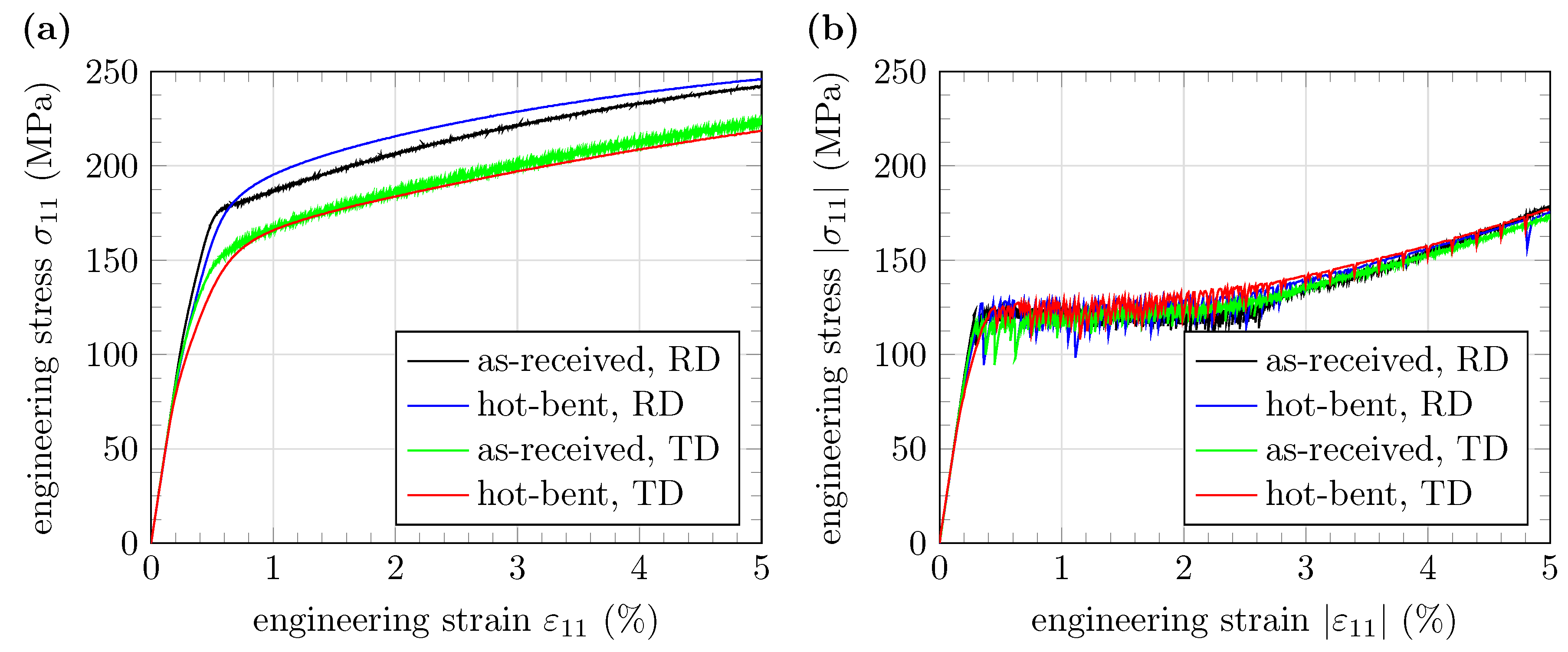
4.2. Quasi-Static Tests
4.3. Low-Cycle Fatigue Tests
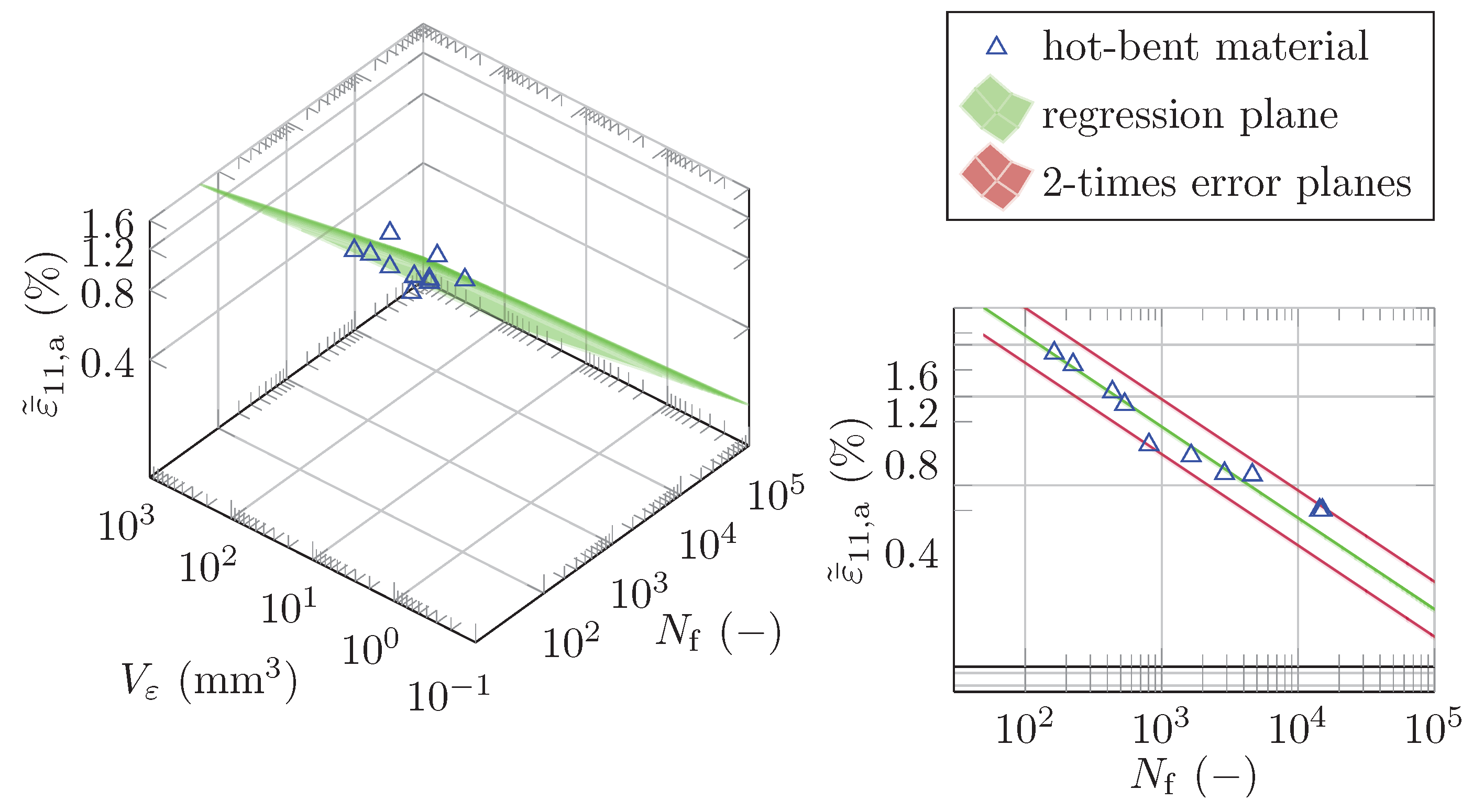
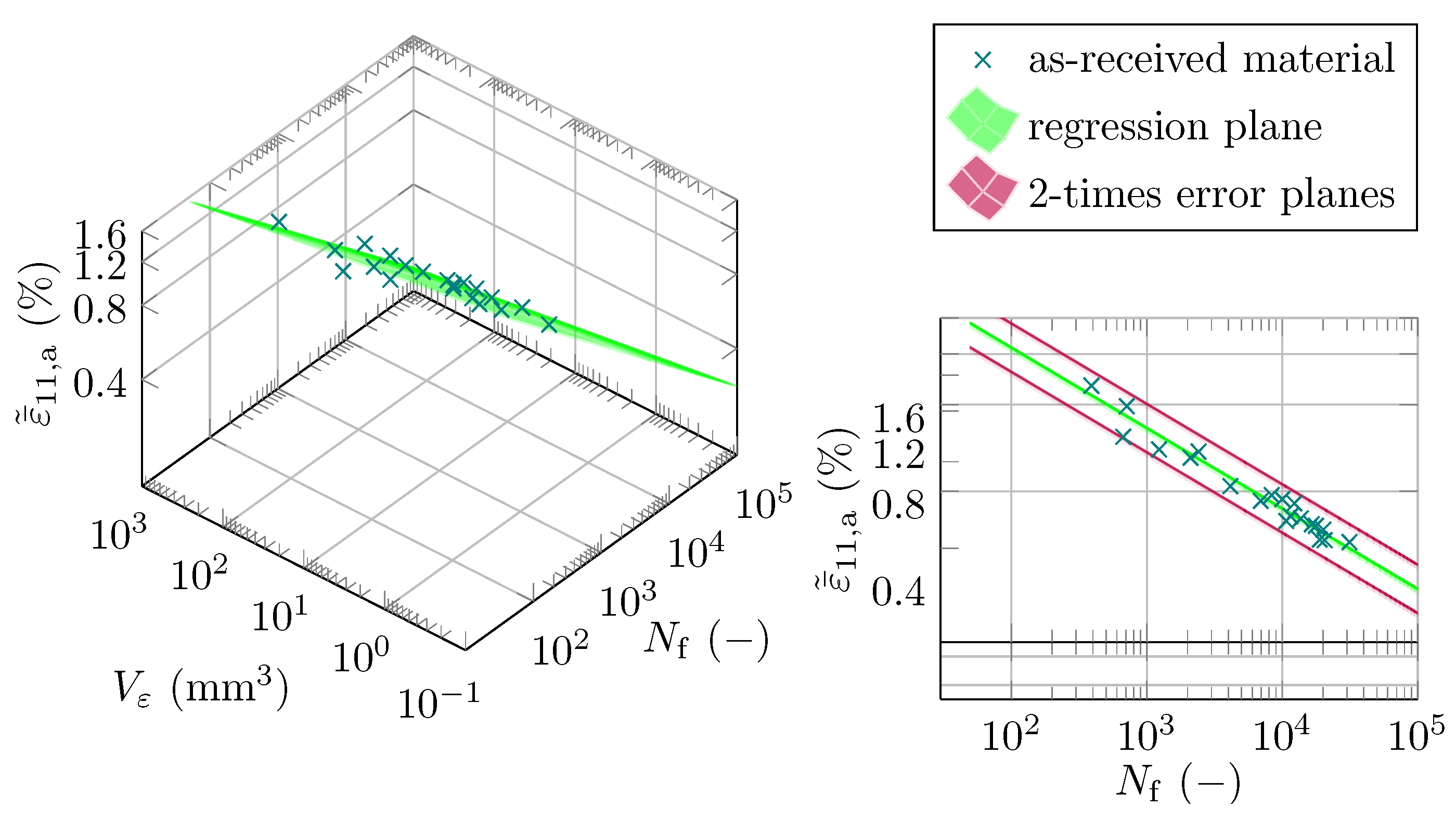
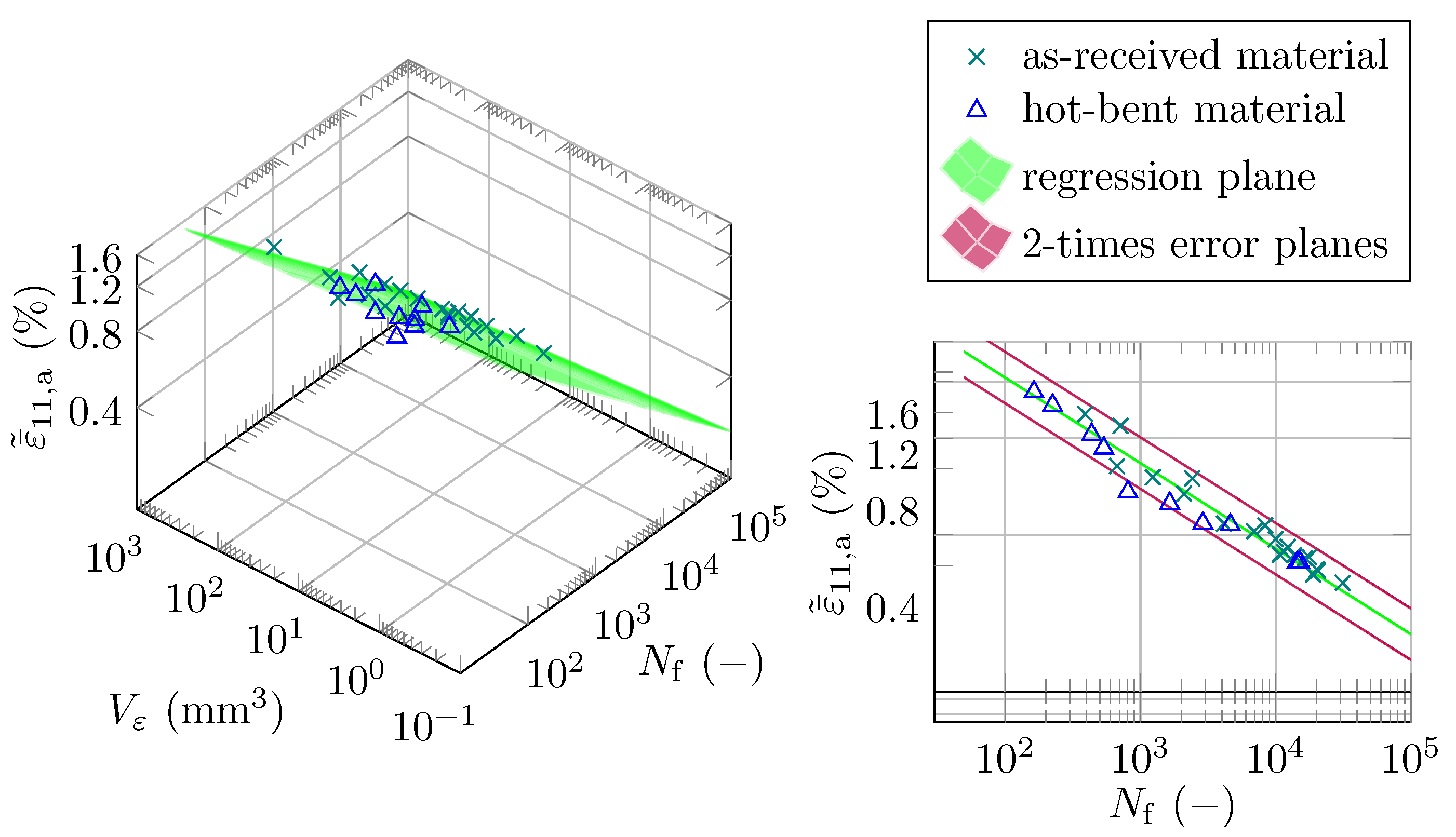
4.3.1. The Concept of Highly Strained Volume
4.3.2. Fatigue Modeling
5. Conclusions
- Numerical and experimental results of the hot-bent specimen show that a homogeneous and uniaxial stress state with a tolerable low superimposed bending stress of 5% in the gauge area can be realized.
- The hot-bending process leads to changes in the microstructure with a smaller average grain size and deformed grain boundaries. Furthermore, it is observed that the c-axes become inclined from the normal direction (ND) towards the transverse direction (TD), which is more pronounced on the compression layer compared with the tension layer due to the formation of tension twins. Hence, the Schmid factor for basal slip in RD and TD increases.
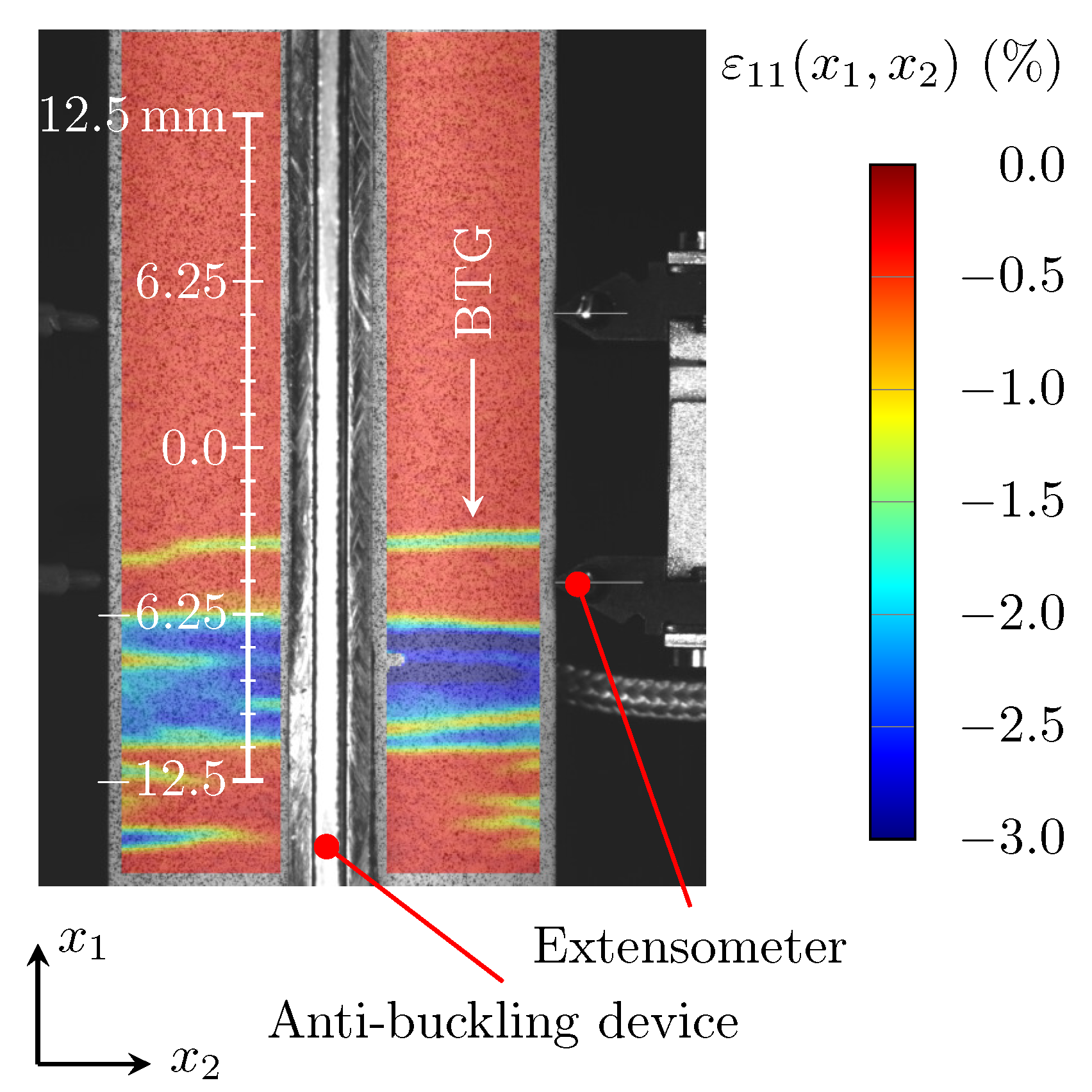
- The uniaxial tension and compression tests reveal that the anisotropic and asymmetric elasto-plastic material behavior persists after the hot-bending process. In addition, lower Young’s moduli are observed for the hot-bent material compared with the as-received material. Compression tests show that even in the hot-bent specimens, the massive formation of tension twins causes macroscopic bands of twinned grains (BTGs). Within the BTGs, the compressive strain is considerably higher compared with the areas outside the BTGs.
- Finally, the study proves that the recently proposed concept of highly strained volume (CHV) can accurately estimate the lifetime of as-received and hot-bent AZ31B magnesium alloy, even by combining the two materials in one model. This allows the CHV to be applied to geometrically complex hot-bent components in order to estimate their lifetime.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BTG | Band of twinned grains |
| CHV | Concept of highly strained volume |
| DIC | Digital image correlation |
| EBSD | Electron backscatter diffraction |
| FEM | Finite Element Method |
| HSR | Highly strained region |
| HSRA | Highly strained region with high strain amplitudes |
| LLL | Lower load level |
| Mg | Magnesium |
| ND | Normal direction |
| PTFE | Polytetrafluoroethylene |
| RD | Rolling direction |
| SEM | Scanning electron microscope |
| TD | Transverse direction |
| ULL | Upper load level |
| Highly strained volume |
References
- Kulekci, M.K. Magnesium and its alloys applications in automotive industry. Int. J. Adv. Manuf. Technol. 2008, 39, 851–865. [Google Scholar] [CrossRef]
- Mordike, B.L.; Ebert, T. Magnesium Properties—Applications—Potential. Mater. Sci. Eng. A 2001, 302, 37–45. [Google Scholar] [CrossRef]
- Ucuncuoglu, S.; Ekerim, A.; Secgin, G.O.; Duygulu, O. Effect of asymmetric rolling process on the microstructure, mechanical properties and texture of AZ31 magnesium alloys sheets produced by twin roll casting technique. J. Magnes. Alloy. 2014, 2, 92–98. [Google Scholar] [CrossRef] [Green Version]
- Masoumi, M.; Zarandi, F.; Pekguleryuz, M. Microstructure and texture studies on twin-roll cast AZ31 (Mg-3wt.%Al-1wt.%Zn) alloy and the effect of thermomechanical processing. Mater. Sci. Eng. A 2011, 528, 1268–1279. [Google Scholar] [CrossRef]
- Ball, E.A.; Prangnell, P.B. Tensile-compressive yield asymmetries in high strength wrought magnesium alloys. Scr. Metall. Mater. 1994, 31, 111–116. [Google Scholar] [CrossRef]
- Agnew, S.R.; Duygulu, O. Plastic anisotropy and the role of non-basal slip in magnesium alloy AZ31B. Int. J. Fatigue 2005, 21, 1161–1193. [Google Scholar] [CrossRef]
- Koike, J.; Ohyama, R. Geometrical criterion for the activation of prismatic slip in AZ61 Mg alloy sheets deformed at room temperature. Acta Mater. 2005, 53, 1963–1972. [Google Scholar] [CrossRef]
- Lou, X.Y.; Li, M.; Boger, R.K.; Agnew, S.R.; Wagoner, R.H. Hardening evolution of AZ31B Mg sheet. Int. J. Plast. 2007, 23, 44–86. [Google Scholar] [CrossRef]
- Albinmousa, J.; Jahed, H.; Lambert, S. Cyclic behaviour of wrought magnesium alloy under multiaxial load. Int. J. Fatigue 2011, 33, 1127–1139. [Google Scholar] [CrossRef]
- Wu, L.; Agnew, S.R.; Ren, Y.; Brown, D.W.; Clausen, B.; Stoica, G.M.; Wenk, H.R.; Liaw, P.K. The effects of texture and extension twinning on the low-cycle fatigue behavior of a rolled magnesium alloy, AZ31B. Mater. Sci. Eng. A 2010, 527, 7057–7067. [Google Scholar] [CrossRef]
- Roostaei, A.A.; Ling, Y.; Jahed, H.; Glinka, G. Applications of Neuber’s and Glinka’s notch plasticity correction rules to asymmetric magnesium alloys under cyclic load. Theor. Appl. Fract. Mech. 2020, 105, 102431. [Google Scholar] [CrossRef]
- Dallmeier, J.; Huber, O.; Saage, H.; Eigenfeld, K. Uniaxial cyclic deformation and fatigue behavior of AM50 magnesium alloy sheet metals under symmetric and asymmetric loadings. Mater. Des. 2015, 70, 10–30. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.M.; Liu, Z.H.; Chen, J. Investigation of uniaxial low-cycle fatigue failure behavior of hot-rolled AZ91 magnesium alloy. Int. J. Fatigue 2013, 48, 122–132. [Google Scholar] [CrossRef]
- Roostaei, A.A.; Jahed, H. Multiaxial cyclic behaviour and fatigue modelling of AM30 Mg alloy extrusion. Int. J. Fatigue 2017, 97, 150–161. [Google Scholar] [CrossRef]
- Shih, T.S.; Liu, W.S.; Chen, Y.J. Fatigue of as-extruded AZ61A magnesium alloy. Mater. Sci. Eng. A 2002, 325, 152–162. [Google Scholar] [CrossRef]
- Nischler, A.; Denk, J.; Huber, O. Fatigue modeling for wrought magnesium structures with various fatigue parameters and the concept of highly strained volume. Continuum. Mech. Therm. 2020. [Google Scholar] [CrossRef] [Green Version]
- Denk, J.; Nischler, A.; Whitmore, L.; Huber, O.; Saage, H. Discontinuous and inhomogeneous strain distributions under monotonic and cyclic loading in textured wrought magnesium alloys. Mater. Sci. Eng. A 2019, 764, 138182. [Google Scholar] [CrossRef]
- Anten, K.; Scholtes, B. Formation of macroscopic twin bands and inhomogeneous deformation during cyclic tension-compression loading of the Mg-wrought alloy AZ31. Mater. Sci. Eng. A 2019, 746, 217–228. [Google Scholar] [CrossRef]
- Denk, J.; Dallmeier, J.; Huber, O.; Saage, H. The fatigue life of notched magnesium sheet metals with emphasis on the effect of bands of twinned grains. Int. J. Fatigue 2017, 98, 212–222. [Google Scholar] [CrossRef]
- Kuguel, R. The Highly Stressed Volume of Material as a Fundamental Parameter in the Fatigue Strength of Metal Members; Theoretical and Applied Mechanics Report No. 169; Department of Theoretical and Applied Mechanics, University of Illinois, Urbana: Champaign, IL, USA, 1960. [Google Scholar]
- Cho, J.H.; Lee, G.Y.; Lee, Y.S. Dynamic evolution of texture and microstructure of AZ31 magnesium sheets during tensile-drawing bending. J. Alloys Compd. 2020, 813, 152120. [Google Scholar] [CrossRef]
- Yang, Q.; Jiang, B.; Wang, L.; Dai, J.; Zhang, J.; Pan, F. Enhanced formability of a magnesium alloy sheet via in-plane pre-strain paths. J. Alloys Compd. 2020, 814, 152278. [Google Scholar] [CrossRef]
- Huang, G.; Wang, L.; Zhang, H.; Wang, Y.; Shi, Z.; Pan, F. Evolution of neutral layer and microstructure of AZ31B magnesium alloy sheet during bending. Mater. Lett. 2013, 98, 47–50. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, G.; Zhang, H.; Song, B. Cold stamping formability of AZ31B magnesium alloy sheet undergoing repeated unidirectional bending process. J. Mater. Process. Technol. 2011, 211, 644–649. [Google Scholar] [CrossRef]
- Song, B.; Huang, G.; Li, H.; Zhang, L.; Huang, G.; Pan, F. Texture evolution and mechanical properties of AZ31B magnesium alloy sheets processed by repeated unidirectional bending. J. Alloys Compd. 2010, 489, 475–481. [Google Scholar] [CrossRef]
- Denk, J.; Whitmore, L.; Huber, O.; Diwald, O.; Saage, H. Concept of the highly strained volume for fatigue modeling of wrought magnesium alloys. Int. J. Fatigue 2018, 117, 283–291. [Google Scholar] [CrossRef]
- Beausir, B.; Fundenberger, J.J. Analysis Tools for Electron and X-Ray Diffraction, ATEX-Software. 2017. Available online: http://www.atex-software.eu/help.html (accessed on 23 June 2021).
- Al-Samman, T.; Gottstein, G. Dynamic recrystallization during high temperature deformation of magnesium. Mater. Sci. Eng. A 2008, 490, 411–420. [Google Scholar] [CrossRef]




| Mg | Al | Zn | Mn | Cu | Si | Fe | Ni | Ca | Other Impurities |
|---|---|---|---|---|---|---|---|---|---|
| balance | 2.75 | 1.08 | 0.368 | 0.00262 | 0.0187 | 0.00282 | 0.00038 | 0.00041 | <0.004 |
| (%) | (MPa) | (%) | (%) | (MPa) |
|---|---|---|---|---|
| 0.100 | 41.1 | 0.100 | 0.0900 | 2.05 |
| 0.200 | 82.1 | 0.210 | 0.180 | 6.16 |
| 0.300 | 123 | 0.320 | 0.290 | 6.16 |
| Uniaxial Tension Tests | Uniaxial Compression Tests | |||
|---|---|---|---|---|
| ID | (MPa) | (MPa) | (MPa) | (MPa) |
| hot-bent, RD | 177.1 | 41,067 | 128.3 | 40,862 |
| as-received, RD | 178.1 | 42,673 | 122.8 | 43,880 |
| hot-bent, TD | 142.5 | 38,945 | 124.9 | 38,422 |
| as-received, TD | 150.6 | 42,034 | 116.4 | 42,879 |
| Specimen ID | (%) | (−) | f (Hz) | (mm3) | (%) | (−) |
|---|---|---|---|---|---|---|
| UG12-060 | 0.35 | −1 | 1 | 132 | 0.344 | 14,377 |
| UG12-061 | 0.35 | −1 | 1 | 523 | 0.334 | 15,075 |
| UG12-062 | 0.45 | −1 | 0.5 | 43.0 | 0.469 | 2890 |
| UG12-063 | 0.45 | −1 | 0.5 | 23.3 | 0.470 | 4619 |
| UG12-065 | 0.55 | −1 | 0.2 | 24.4 | 0.595 | 807 |
| UG12-071 | 0.55 | −1 | 0.2 | 81.7 | 0.532 | 1645 |
| UG12-067 | 0.8 | −1 | 0.1 | 46.5 | 0.885 | 435 |
| UG12-072 | 0.8 | −1 | 0.1 | 16.0 | 0.822 | 535 |
| UG12-068 | 1.2 | −1 | 0.1 | 32.2 | 1.21 | 163 |
| UG12-070 | 1.2 | −1 | 0.1 | 4.99 | 1.15 | 224 |
| Specimens | (%) | (−) | (−) | (−) |
|---|---|---|---|---|
| hot-bent | 6.13 | −0.310 | −0.0189 | 0.968 |
| as-received | 6.30 | −0.279 | −0.0460 | 0.942 |
| hot-bent & as-received | 4.94 | −0.266 | −0.0231 | 0.944 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nischler, A.; Denk, J.; Saage, H.; Klaus, H.; Huber, O. Low-Cycle Fatigue Behavior of Hot-Bent Basal Textured AZ31B Wrought Magnesium Alloy. Metals 2021, 11, 1004. https://doi.org/10.3390/met11071004
Nischler A, Denk J, Saage H, Klaus H, Huber O. Low-Cycle Fatigue Behavior of Hot-Bent Basal Textured AZ31B Wrought Magnesium Alloy. Metals. 2021; 11(7):1004. https://doi.org/10.3390/met11071004
Chicago/Turabian StyleNischler, Anton, Josef Denk, Holger Saage, Hubert Klaus, and Otto Huber. 2021. "Low-Cycle Fatigue Behavior of Hot-Bent Basal Textured AZ31B Wrought Magnesium Alloy" Metals 11, no. 7: 1004. https://doi.org/10.3390/met11071004
APA StyleNischler, A., Denk, J., Saage, H., Klaus, H., & Huber, O. (2021). Low-Cycle Fatigue Behavior of Hot-Bent Basal Textured AZ31B Wrought Magnesium Alloy. Metals, 11(7), 1004. https://doi.org/10.3390/met11071004






