Numerical Simulation of Some Steel Structural Elements with Uncertain Initial Porosity
Abstract
1. Introduction
2. Theoretical Background
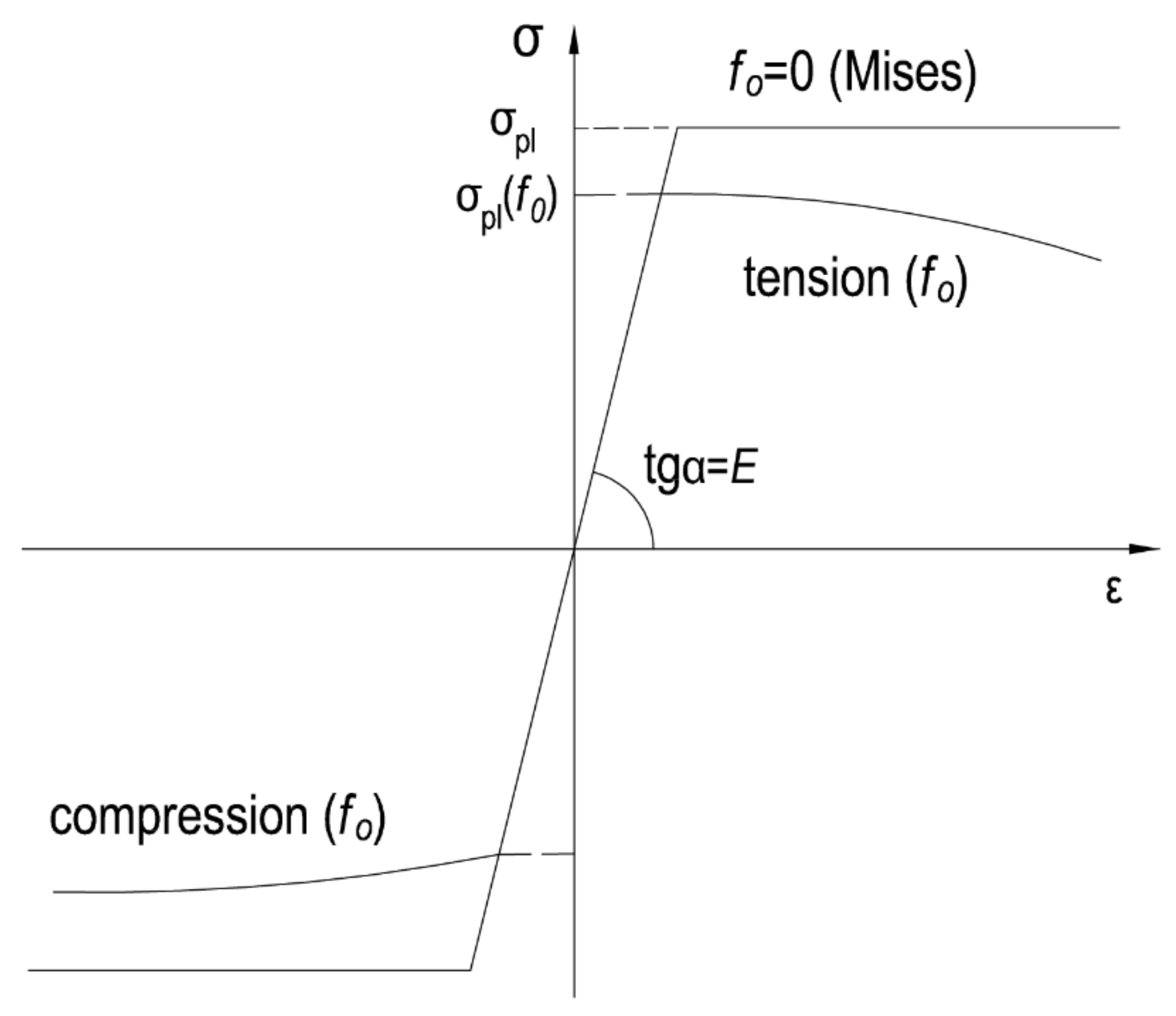
2.1. Governing Equations
2.2. The Generalized Stochastic Perturbation Technique
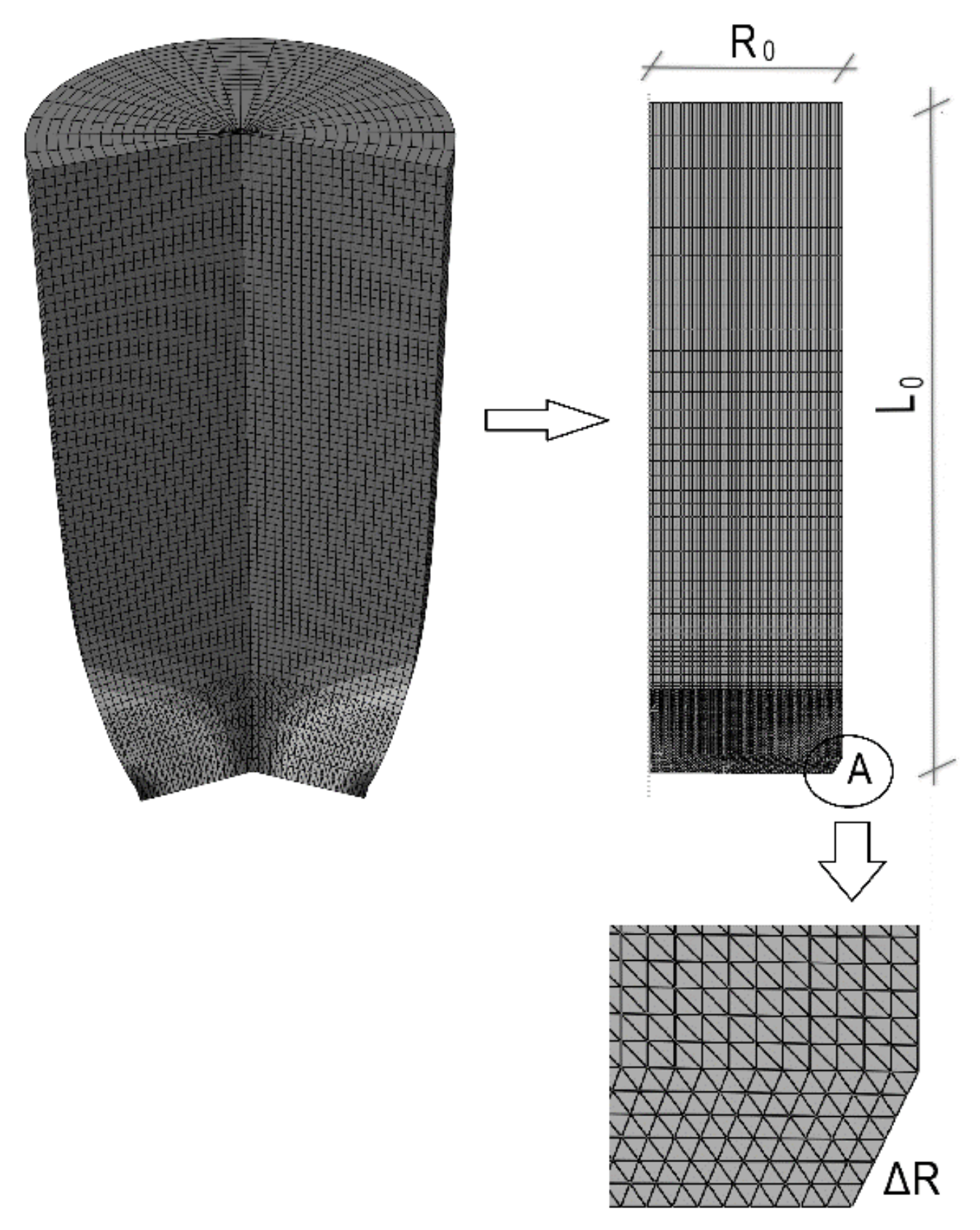
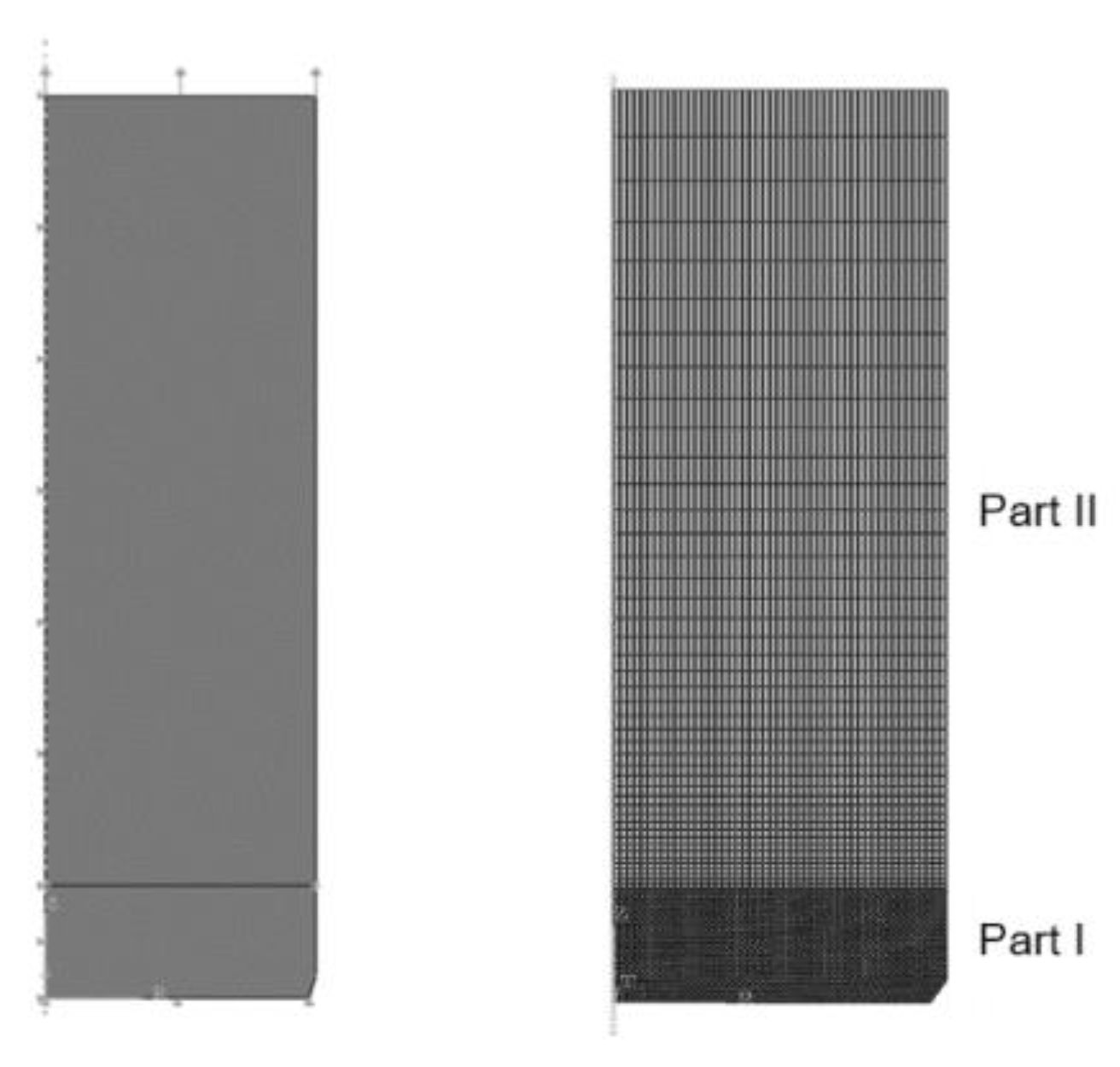
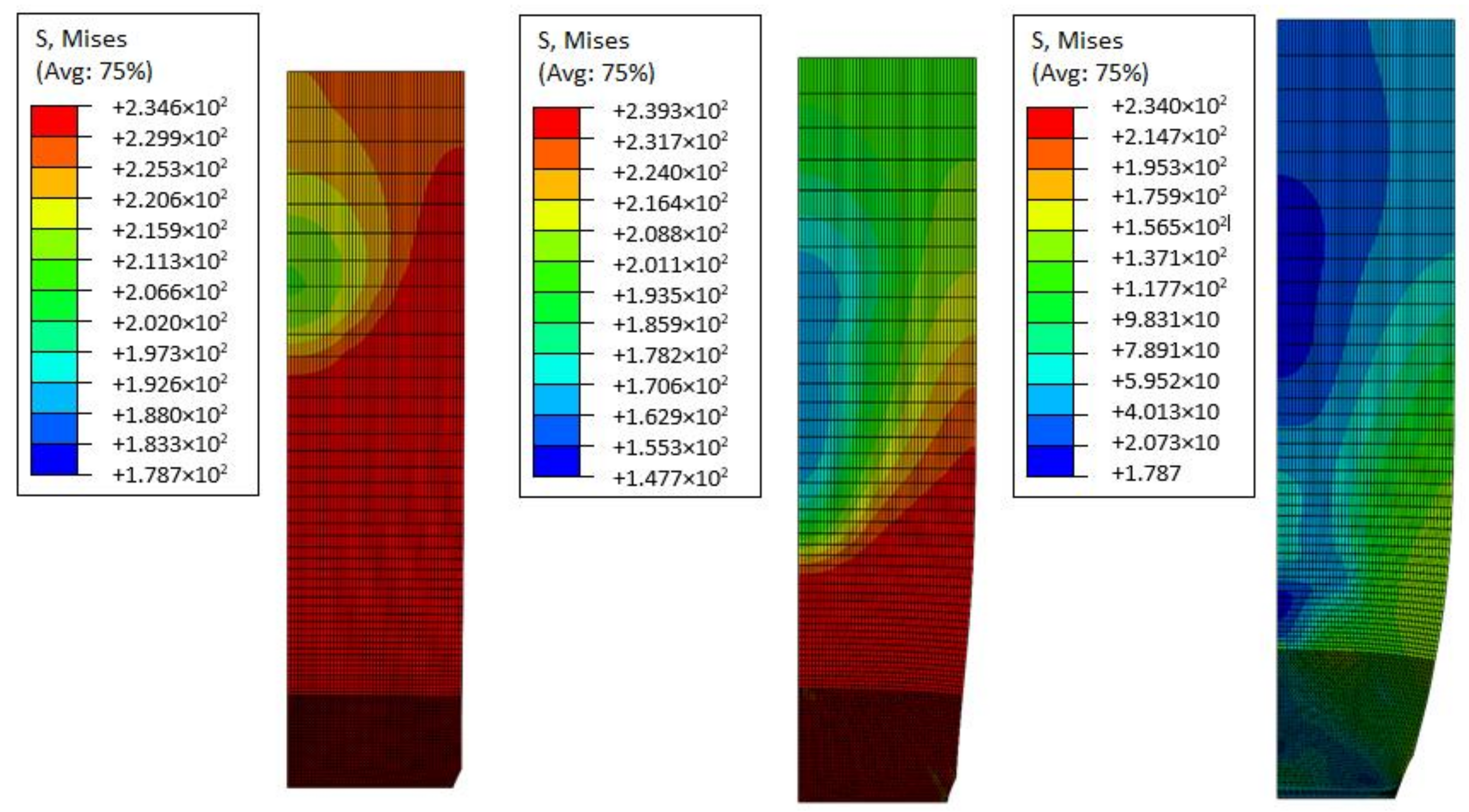
3. Numerical Simulation of the Uniform Tension of the Steel Cylinder
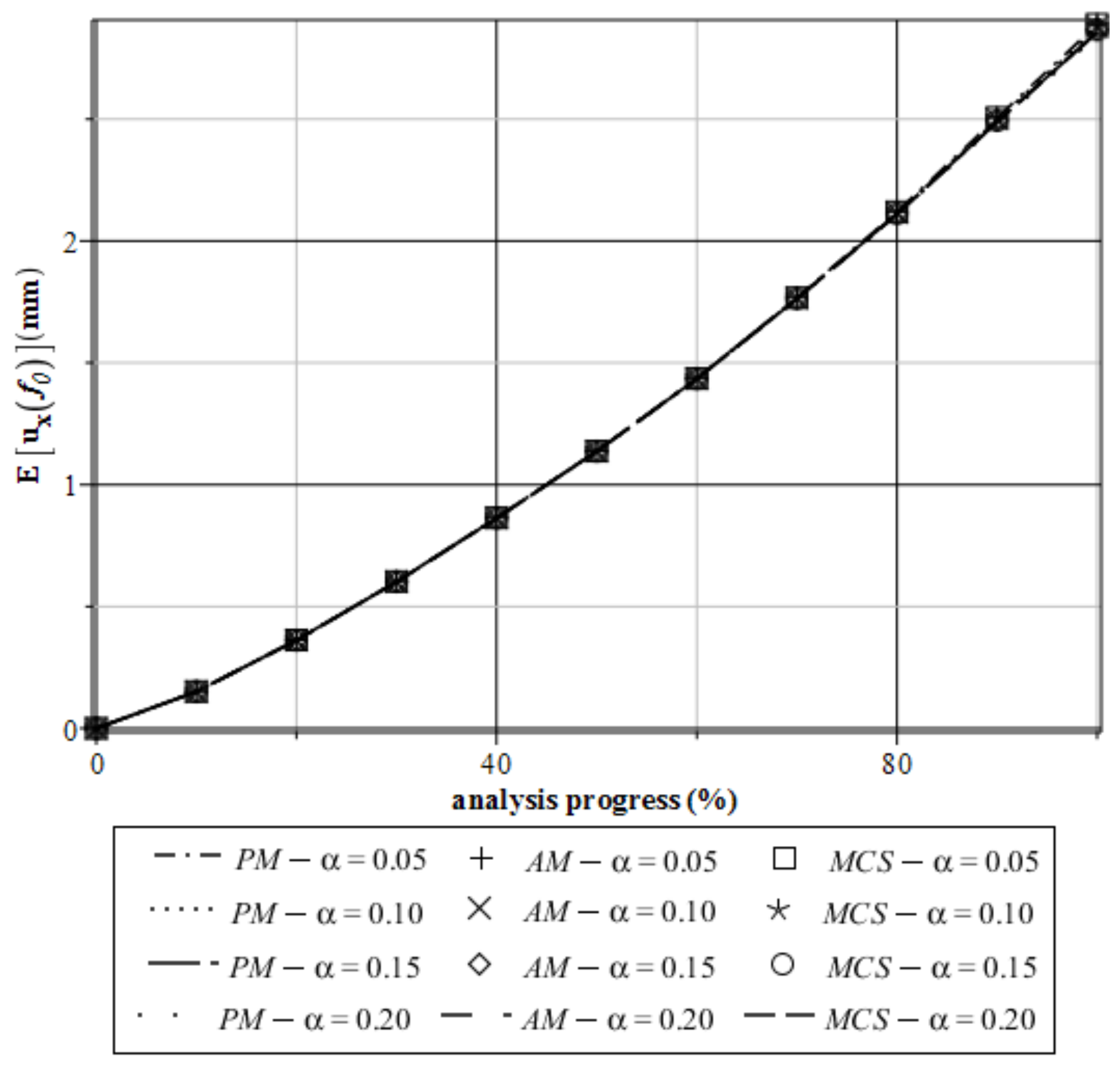
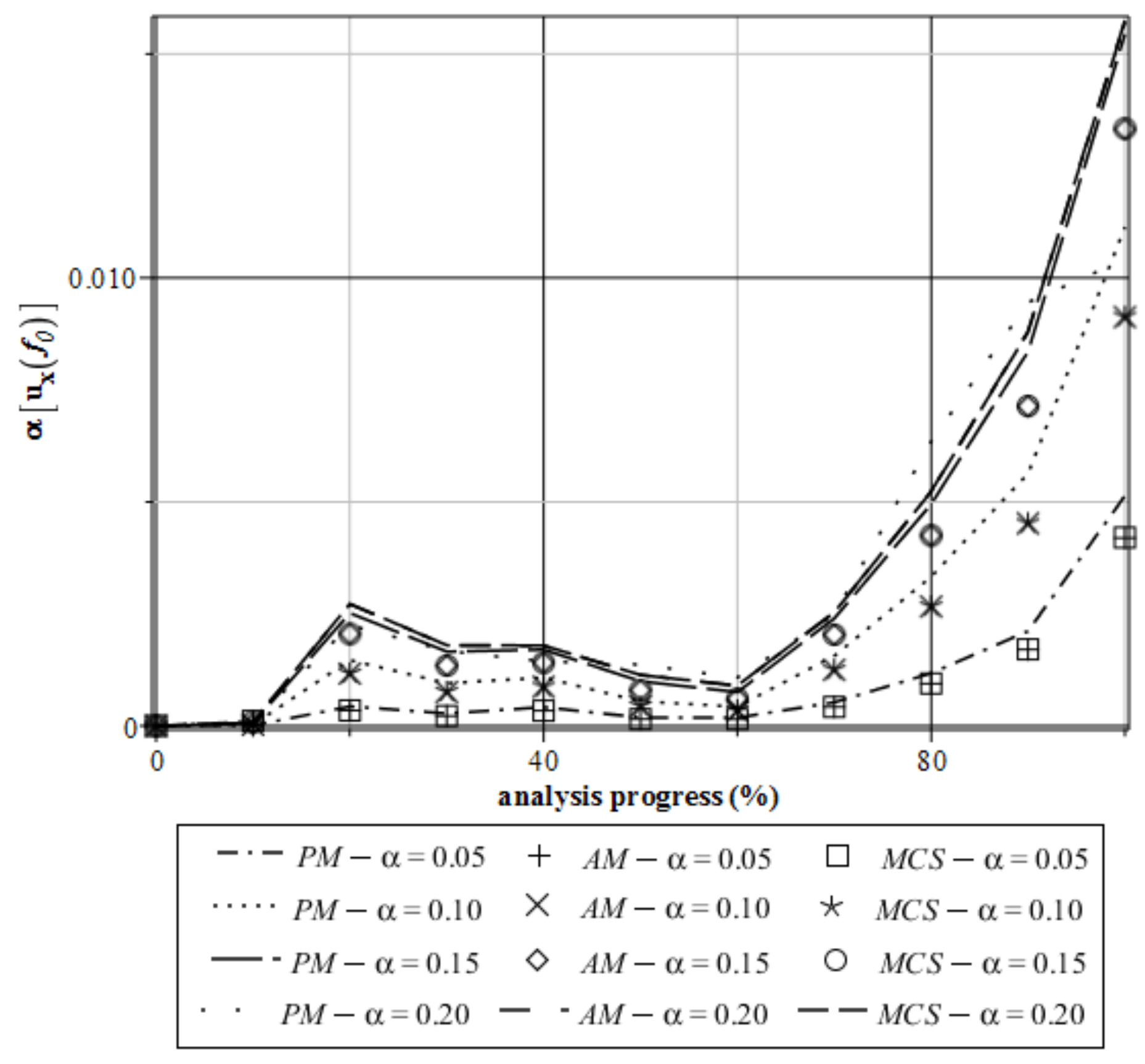
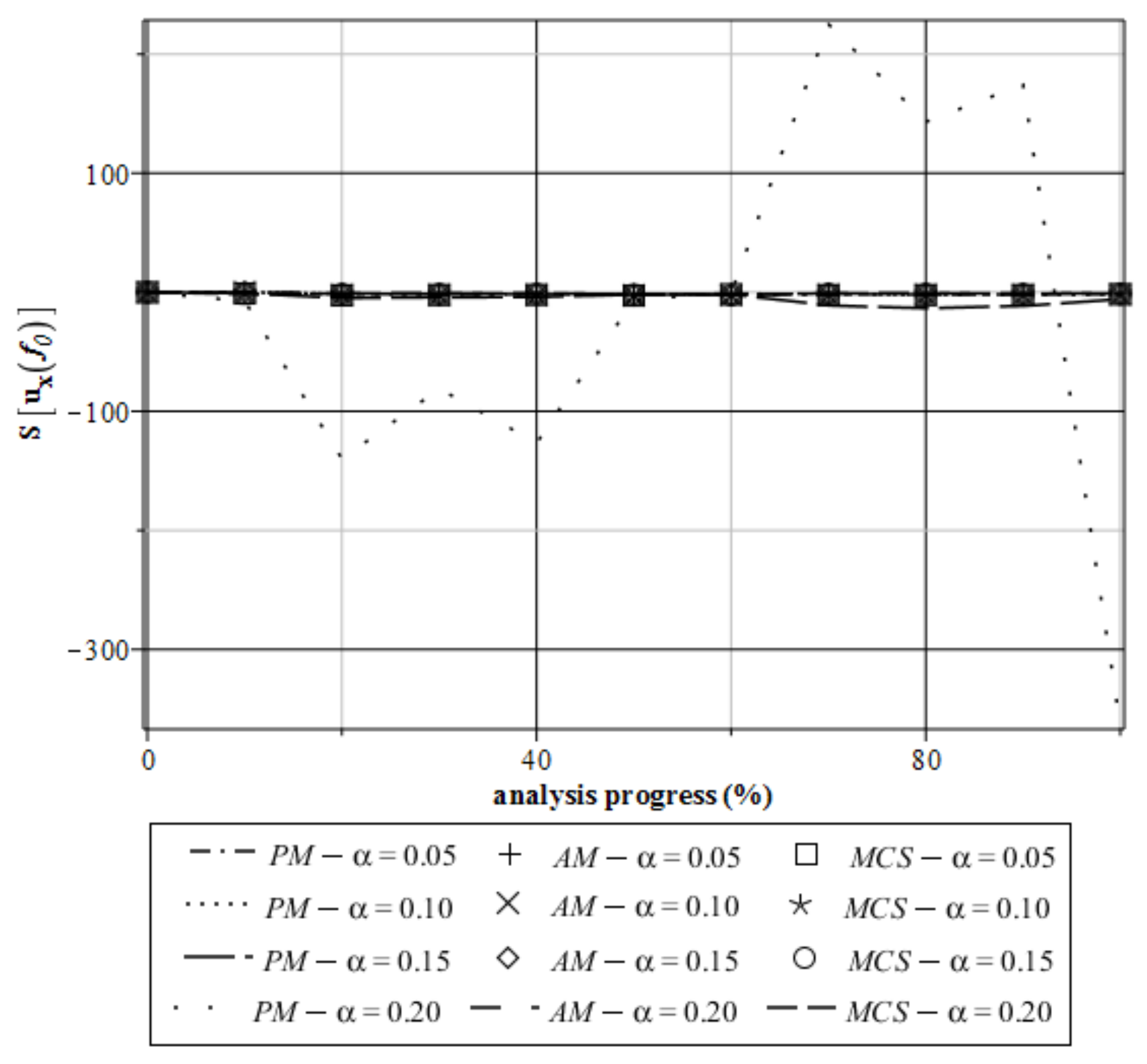
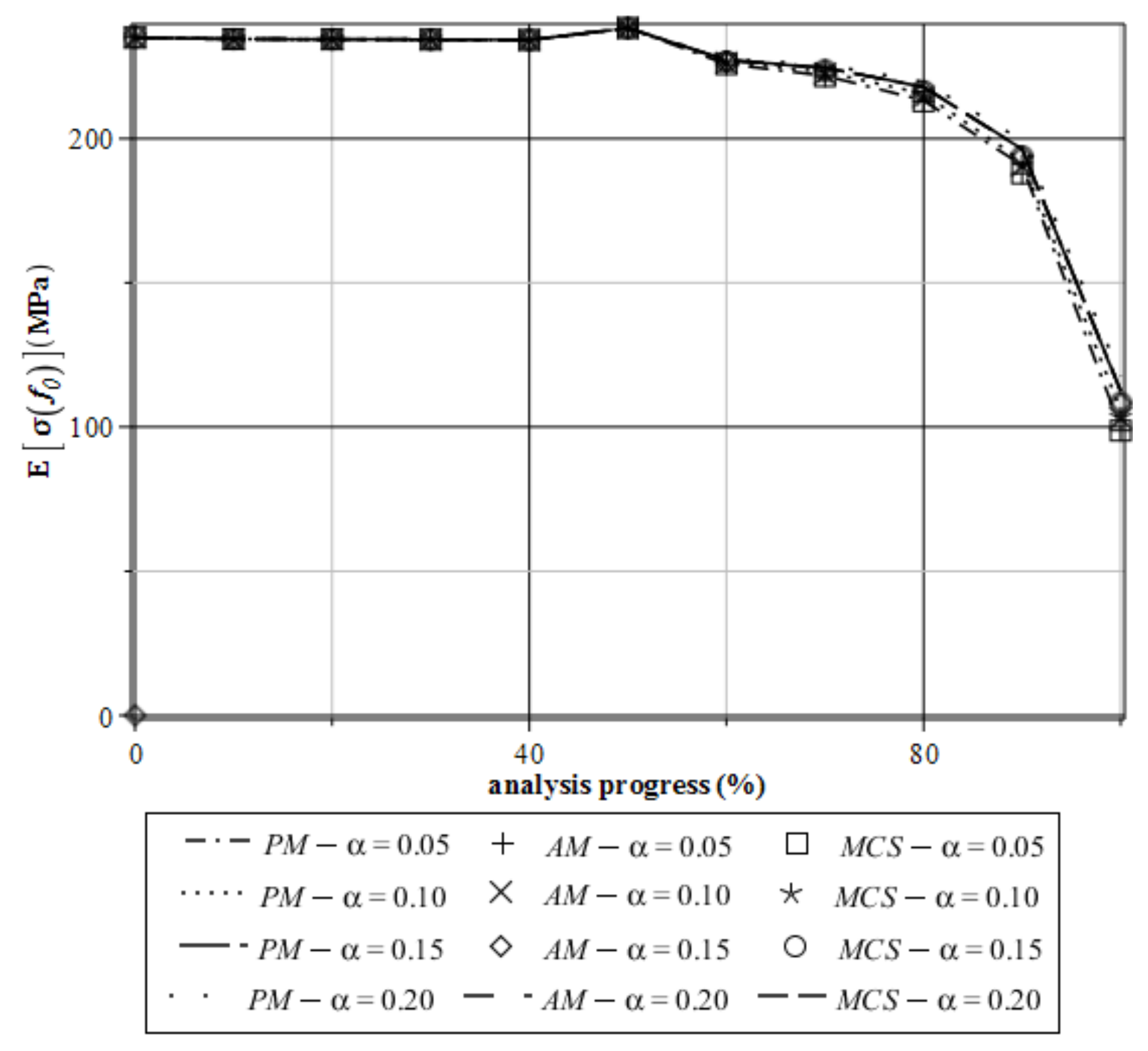
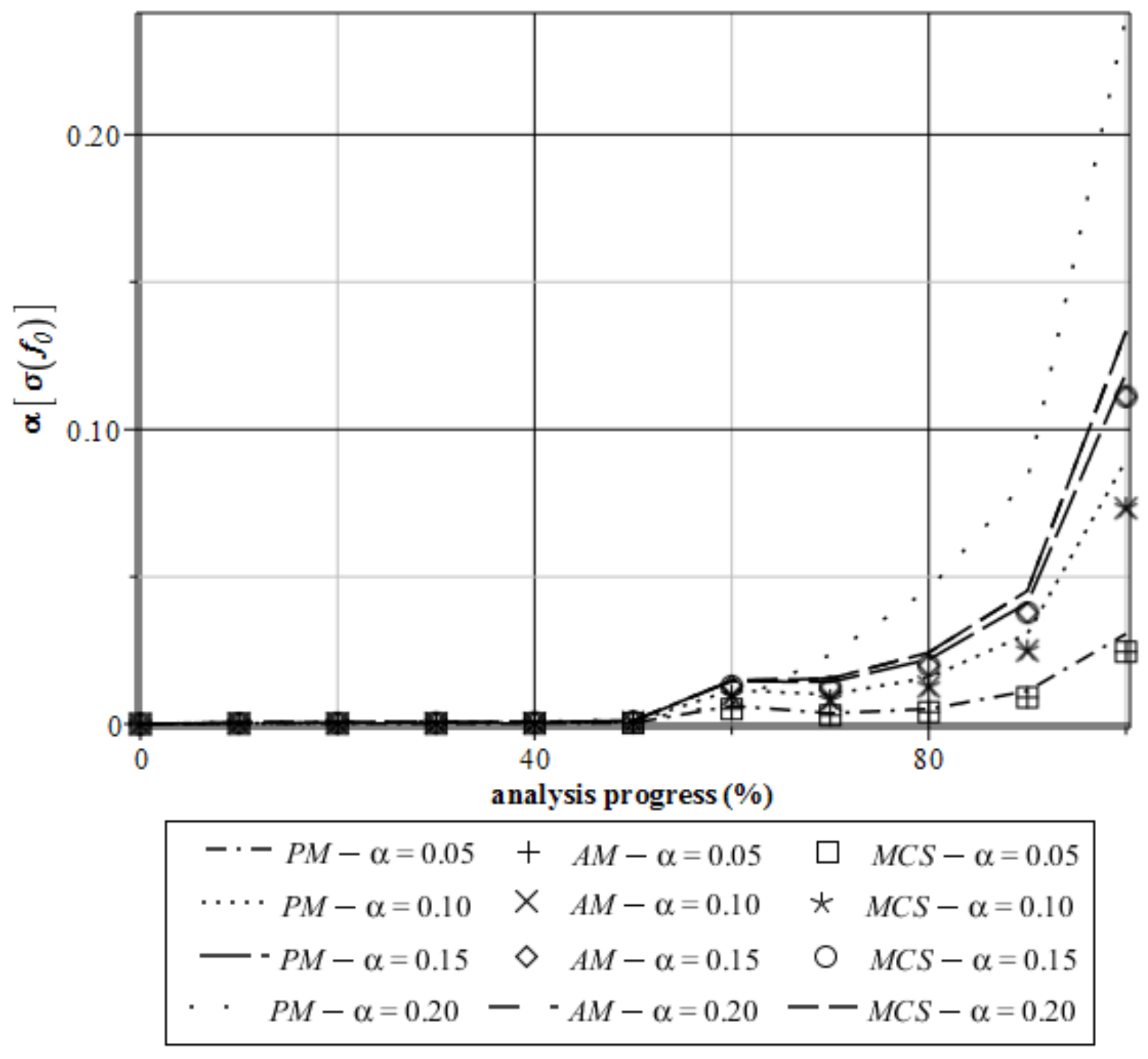
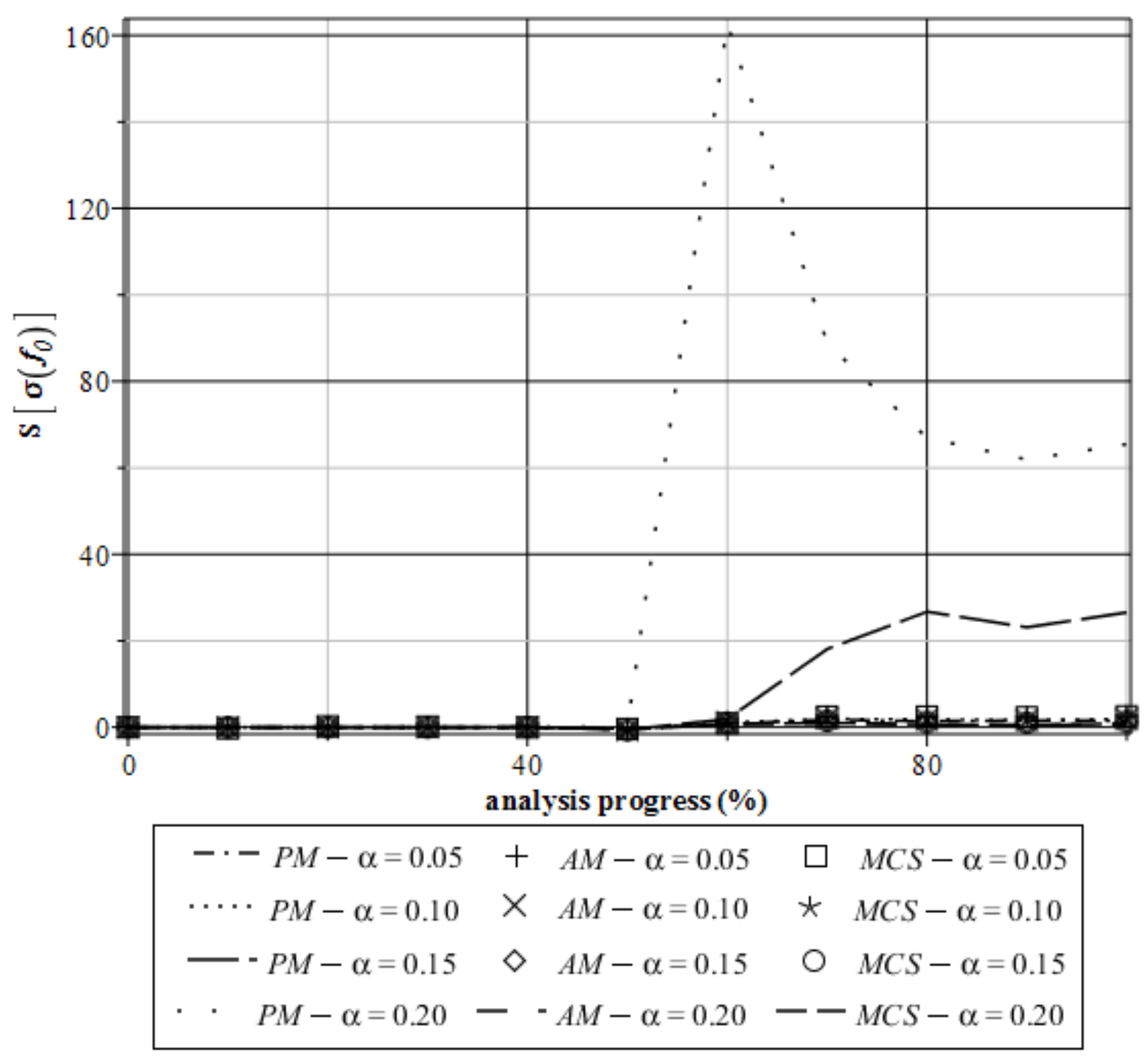
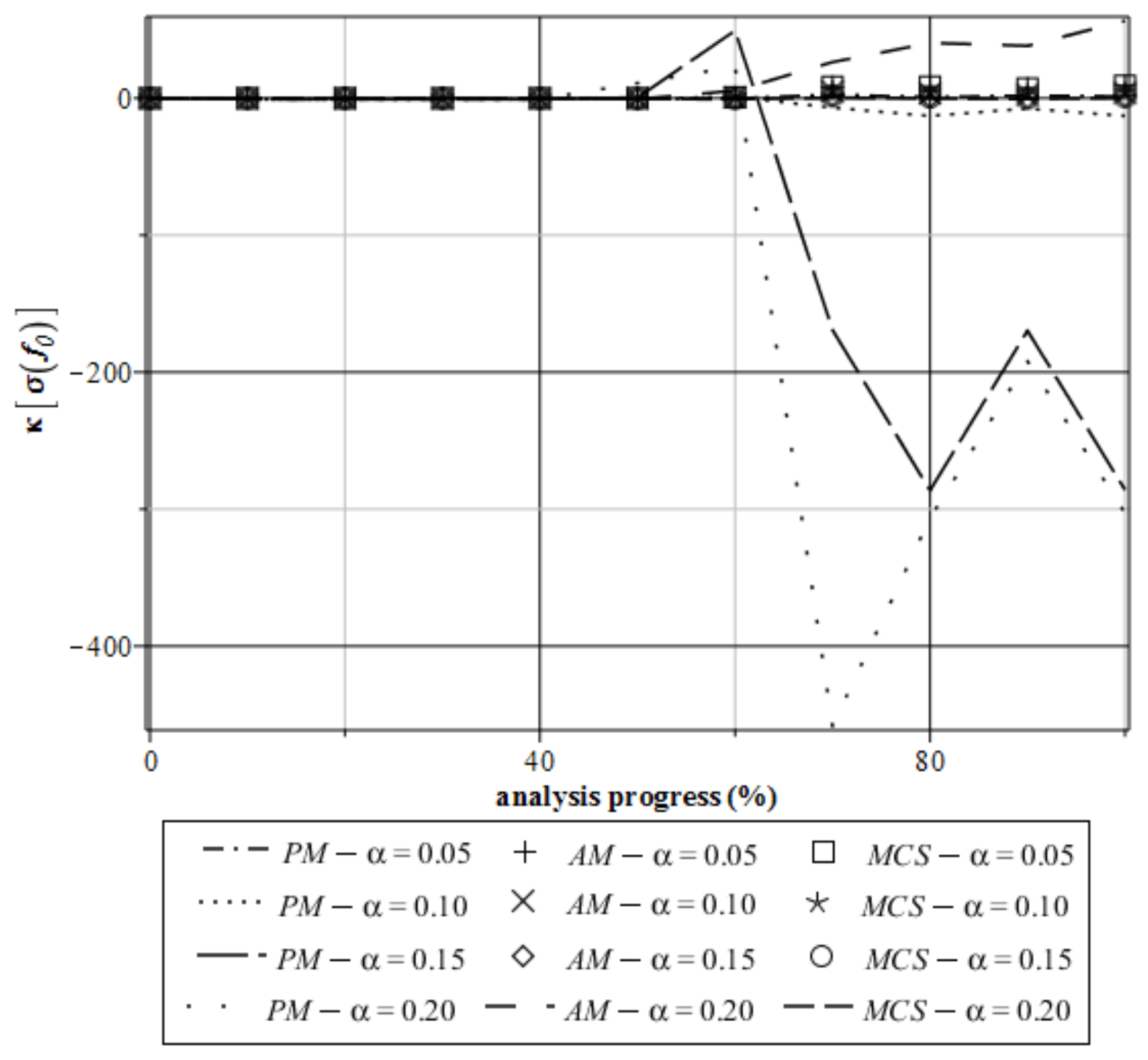
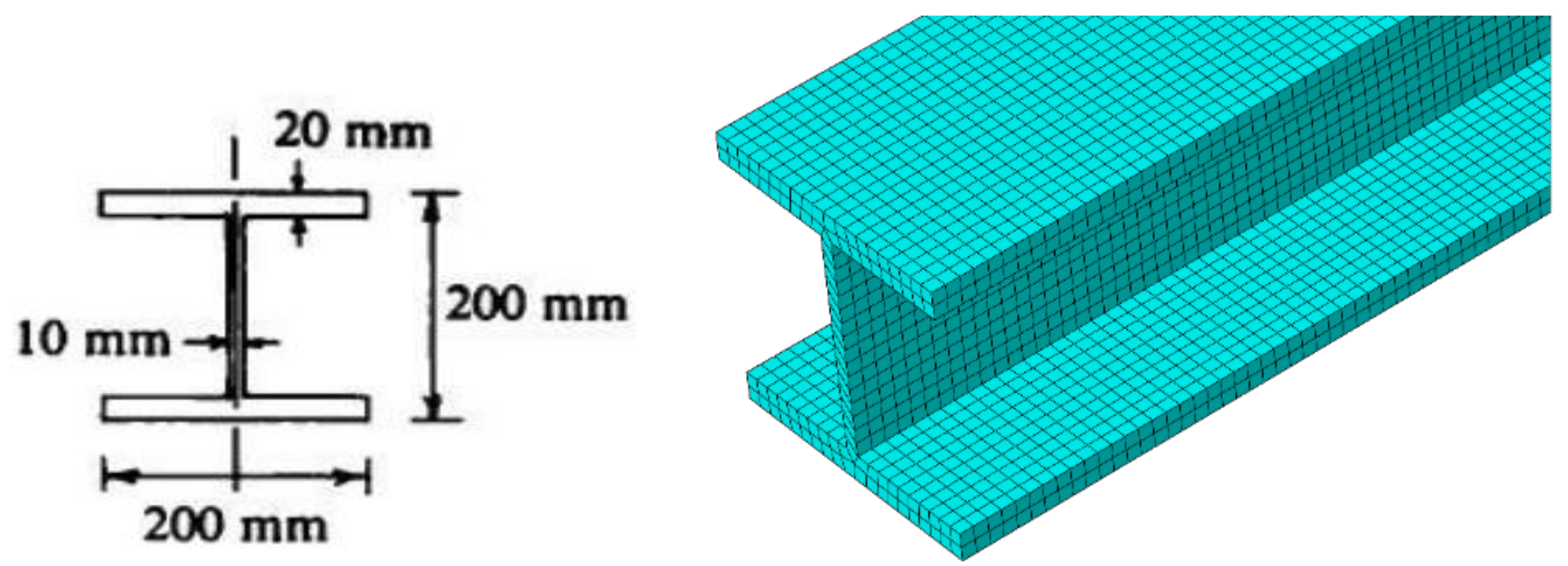
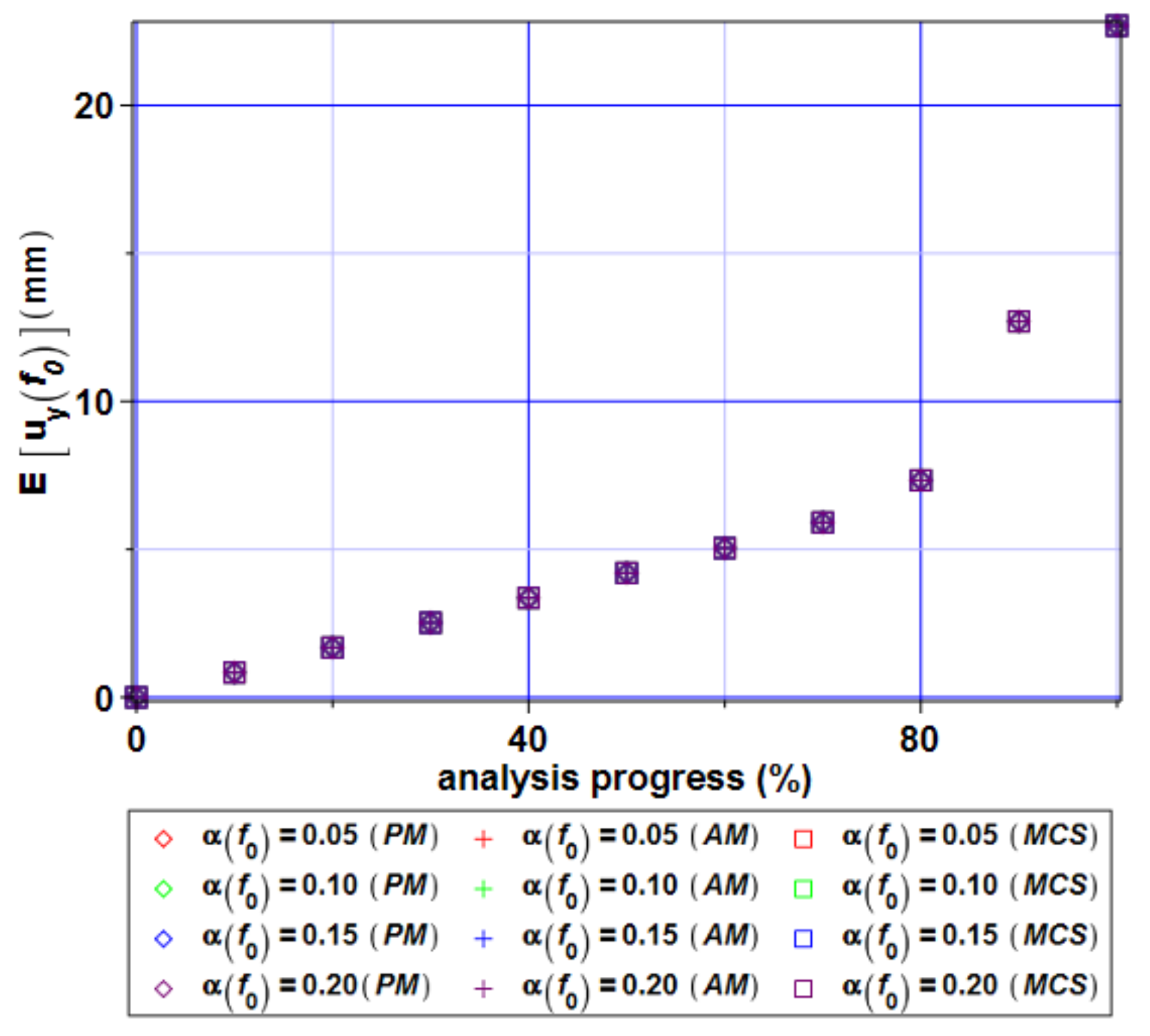
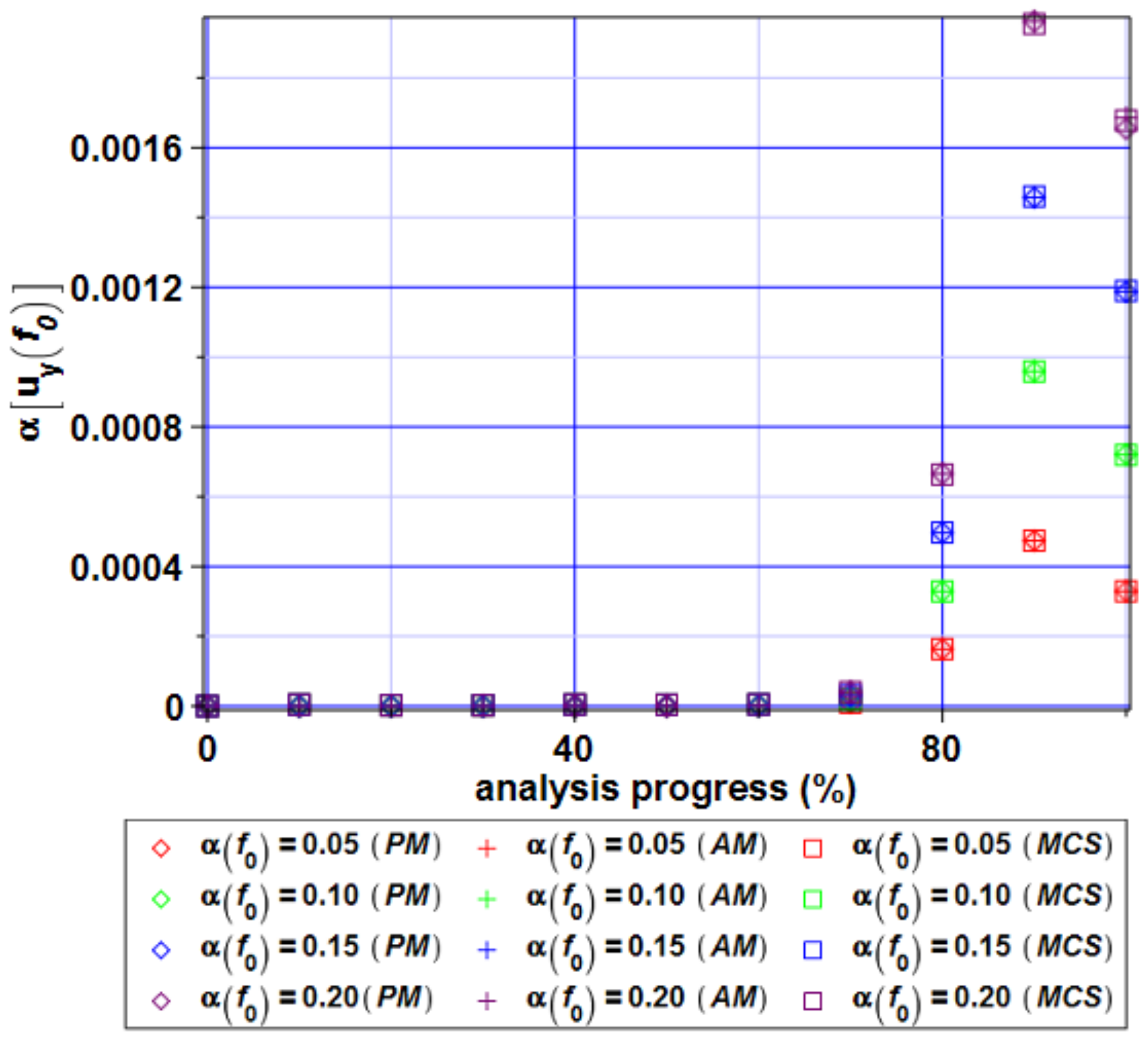
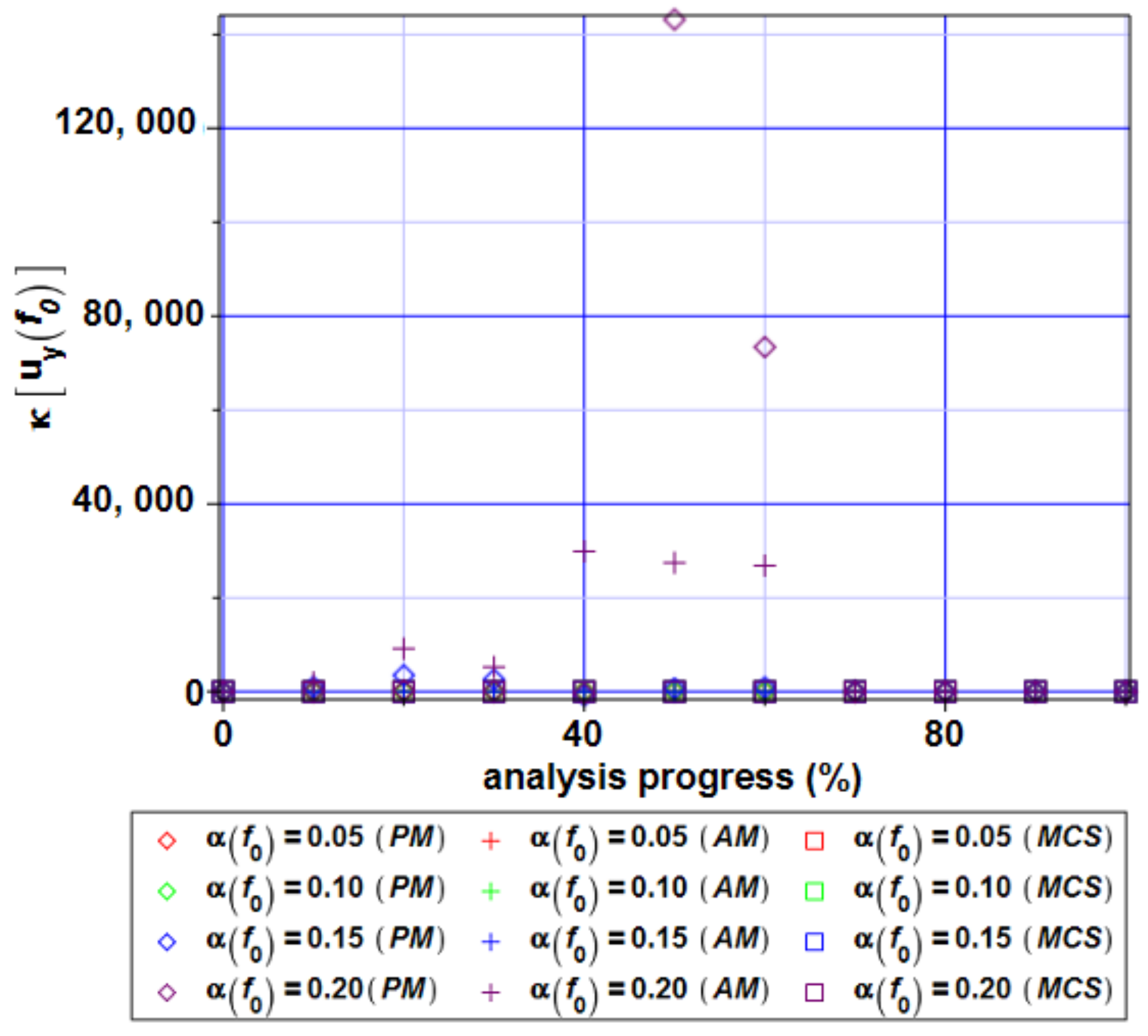
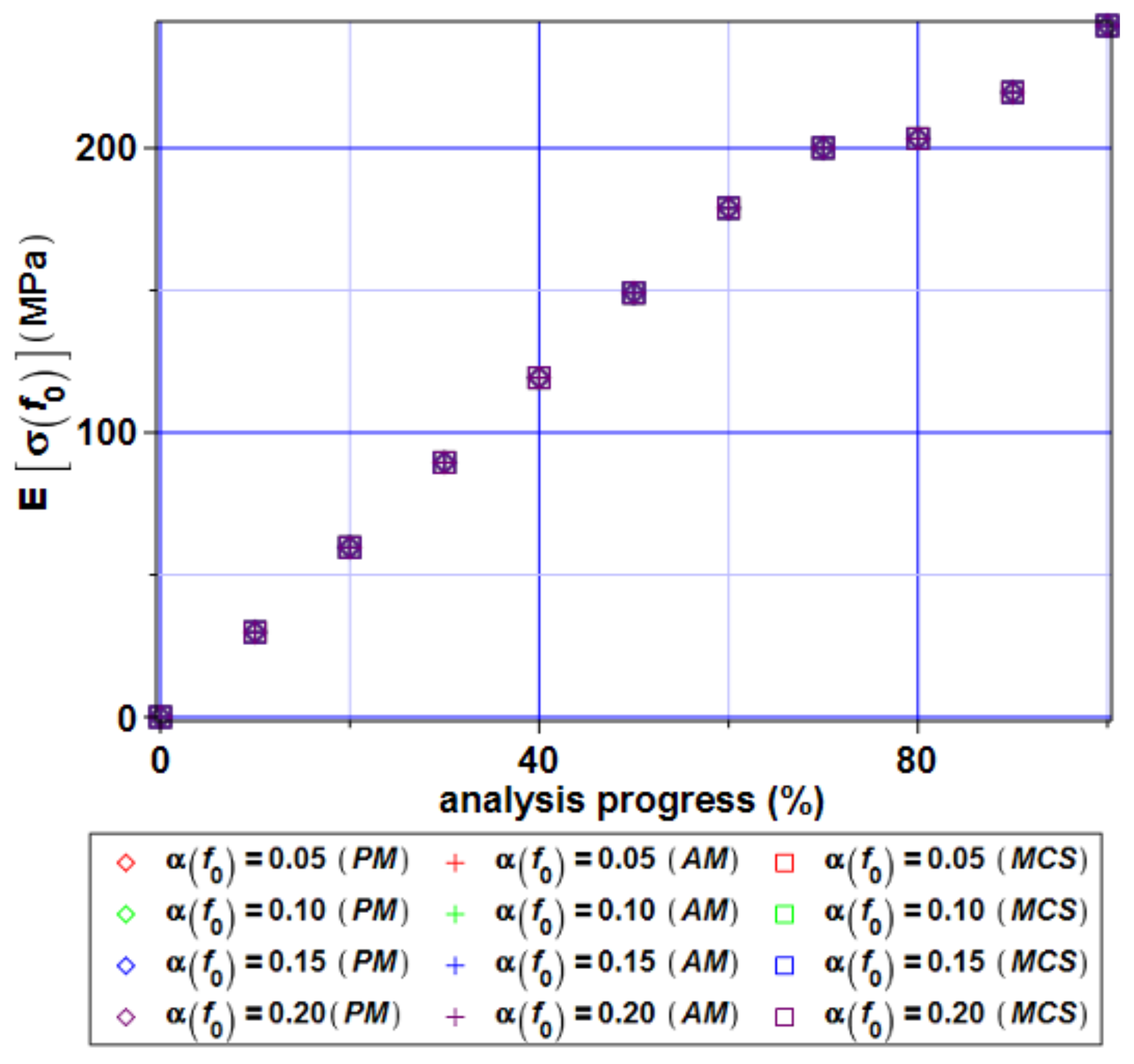
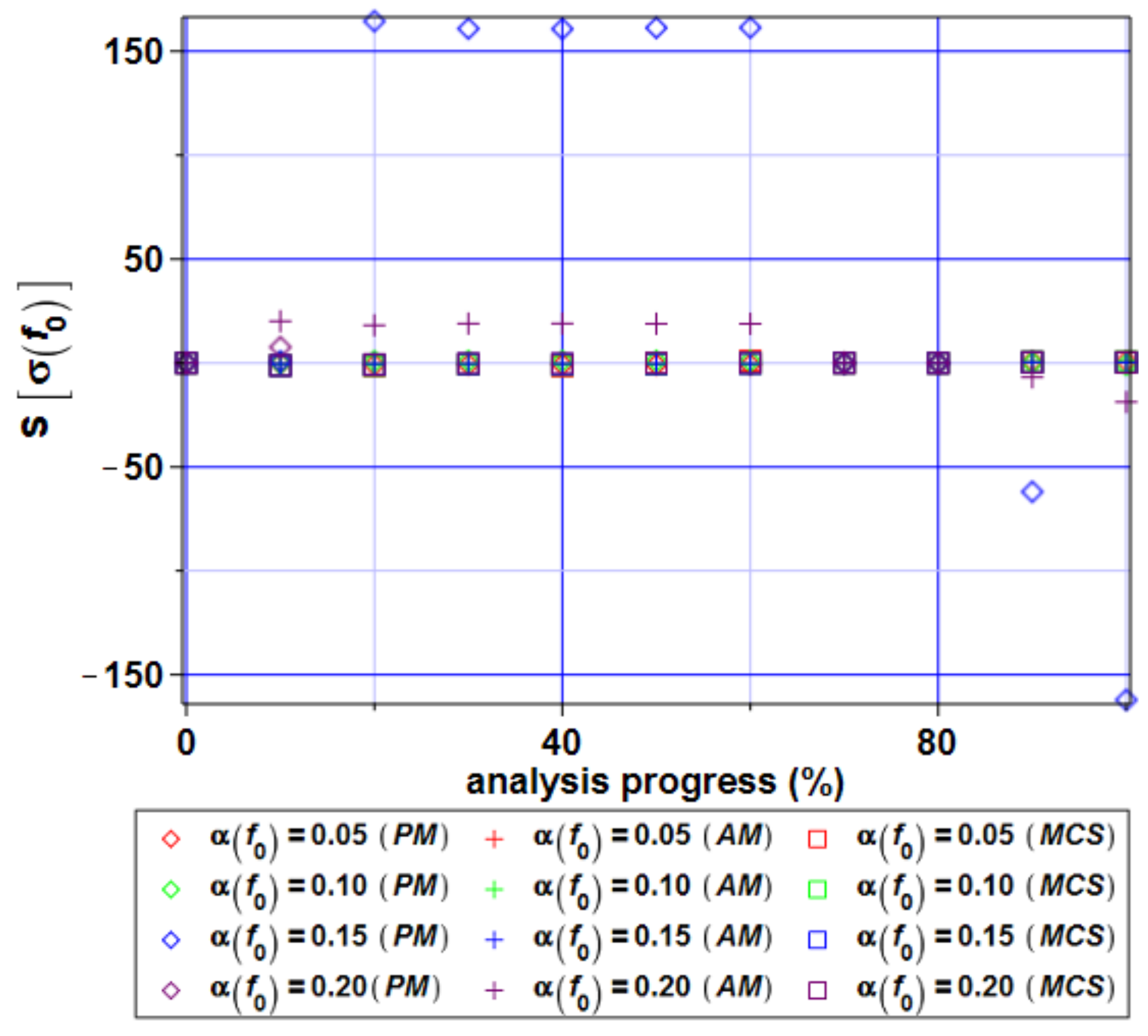
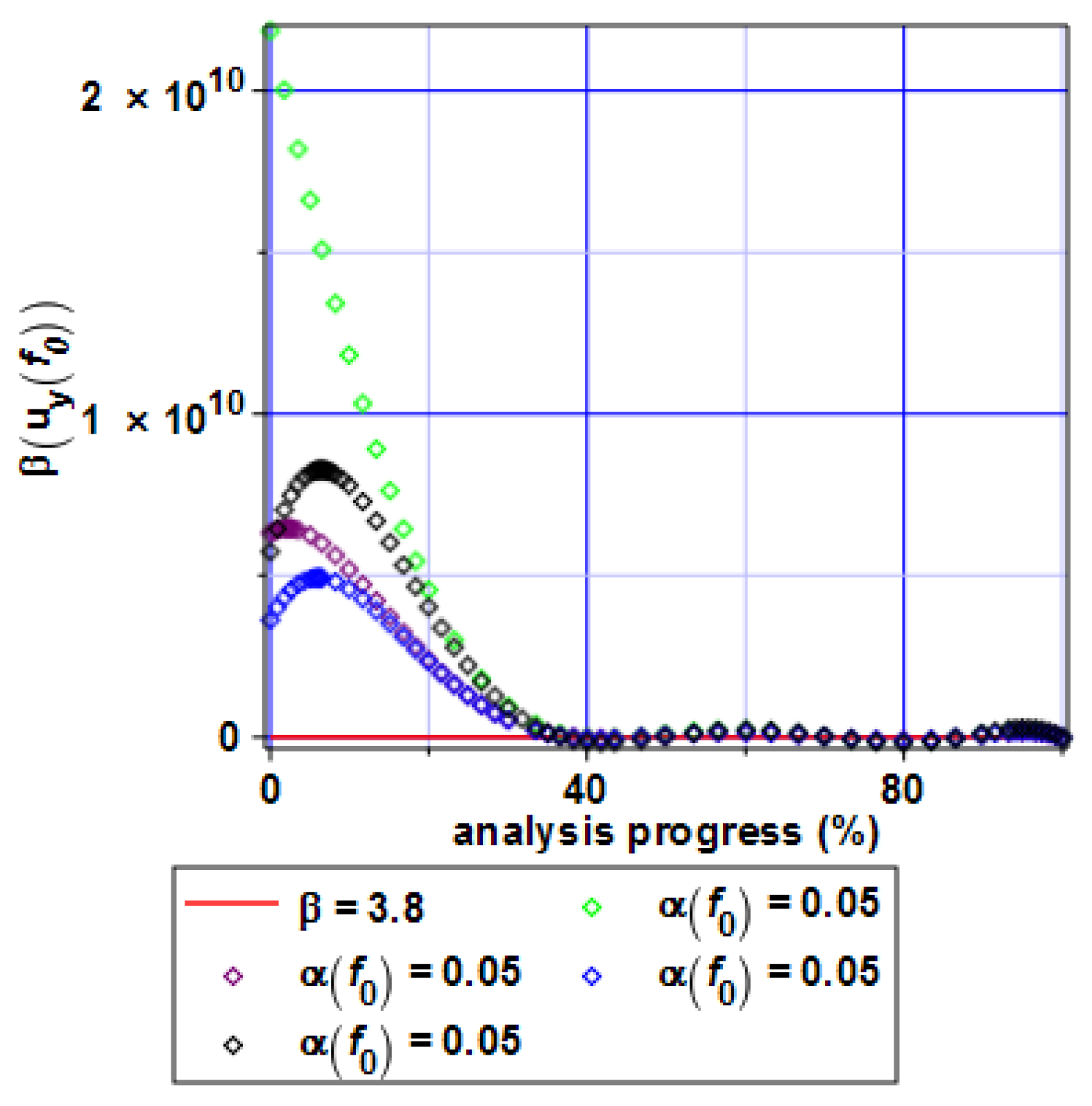
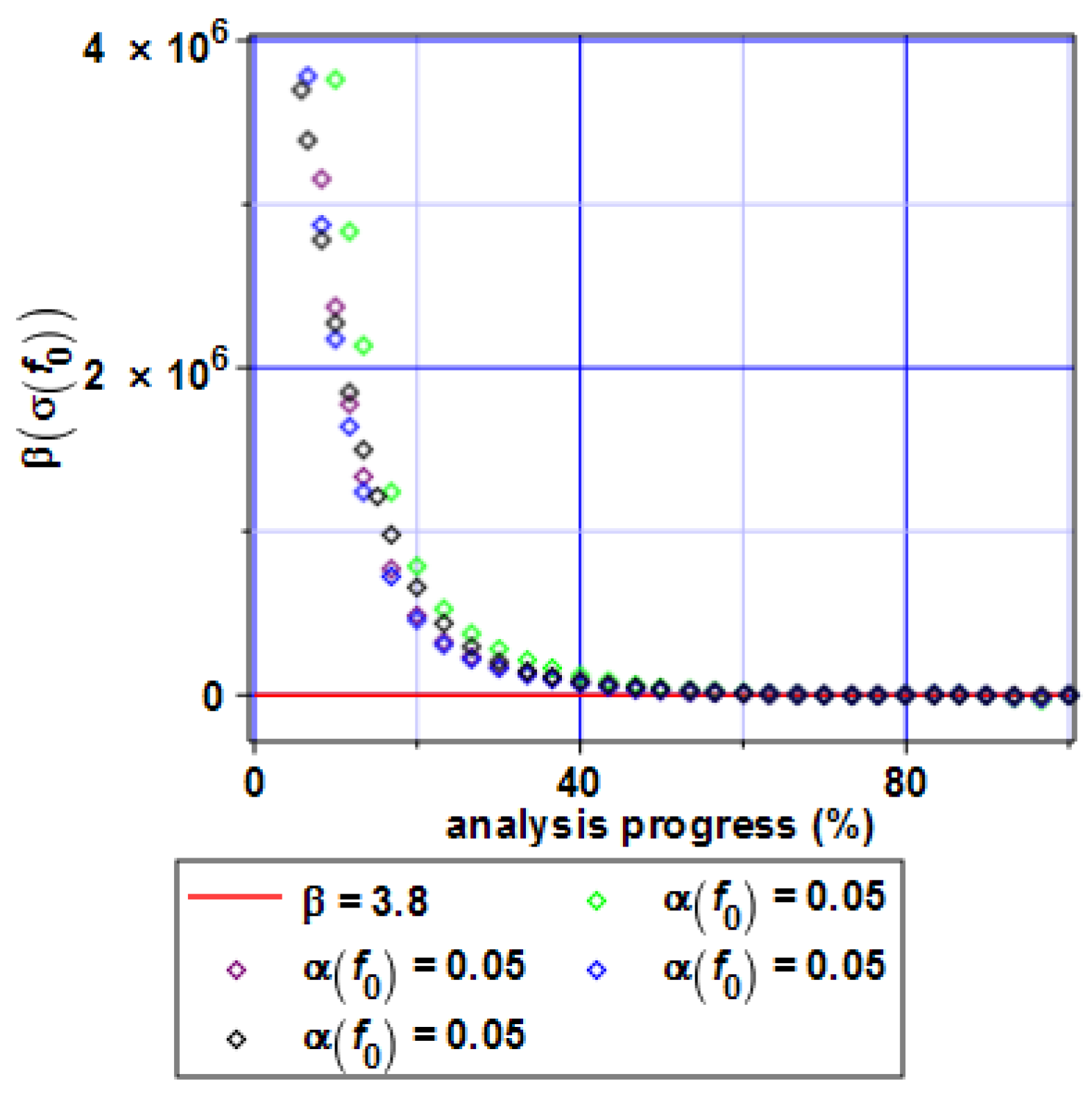
4. Computer Analysis of Bending Process for the Restrained Steel I-Beam
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rahimidehgolan, F.; Majzoobi, G.; Alinejad, F.; Sola, J.F. Determination of the Constants of GTN Damage Model Using Experiment, Polynomial regression and Kriging Methods. Appl. Sci. 2017, 7, 11. [Google Scholar] [CrossRef]
- Strąkowski, M.; Kamiński, M. Stochastic Finite Element Method elasto-plastic analysis of the necking bar with material microdefects. ASCE ASME J. Risk Uncert. Eng. Sys. Part B Mech. Eng. 2019, 5, 030908. [Google Scholar] [CrossRef]
- Franklin, A.G. Comparison between a Quantitative Microscope and Chemical Methods for Assessment of Non-Metallic Inclusions. J. Iron Steel Inst. 1969, 207, 181–186. [Google Scholar]
- Dormieux, L.; Kondo, D. An extension of Gurson model incorporating interface stresses effects. Int. J. Eng. Sc. 2010, 48, 575–581. [Google Scholar] [CrossRef]
- Tvergaard, V.; Needleman, A. Analysis of the cup-cone fracture in a round tensile bar. Act. Metall. 1984, 32, 157–169. [Google Scholar] [CrossRef]
- Malcher, L.; Reis, F.J.P.; Andrade Pires, F.M.; César de Sá, J.M.A. Evaluation of shear mechanisms and influence of the calibration point on the numerical results of the GTN model. Int. J. Mech. Sci. 2013, 75, 407–422. [Google Scholar] [CrossRef]
- Buryachenko, V. Elastic-plastic behavior of elastically homogeneous materials with a random field of inclusions. Int. J. Plast. 1999, 15, 687–720. [Google Scholar] [CrossRef]
- Kleiber, M.; Hien, T.D. The Stochastic Finite Element Method: Basic Perturbation Technique and Computational Implementation; Wiley: Chichester, UK, 1992. [Google Scholar]
- Kamiński, M. Probabilistic characterization of porous plasticity in solids. Mech. Res. Comm. 1999, 26, 99–106. [Google Scholar] [CrossRef]
- Kamiński, M. On the dual Iterative Stochastic perturbation-based Finite Element Method in solid mechanics with Gaussian uncertainties. Int. J. Num. Meth. Eng. 2015, 104, 1038–1060. [Google Scholar] [CrossRef]
- Oh, C.K.; Kim, Y.J.; Baek, J.H.; Kim, Y.P.; Kim, W. A phenomenological model of ductile fracture for API X65 steel. Int. J. Mech. Sci. 2007, 49, 1399–1412. [Google Scholar] [CrossRef]
- Kossakowski, P. Analysis of the void volume fraction for S235JR steel at failure for low initial stress triaxiality. Arch. Civ. Eng. 2018, 64, 101–115. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech. 1985, 21, 31–48. [Google Scholar] [CrossRef]
- Boyer, J.C.; Vidal-Salle, E.; Staub, C. A shear stress dependent ductile damage models. Int. J. Mater. Process. Technol. 2003, 121, 87–93. [Google Scholar] [CrossRef]
- Weck, A.; Seguarado, J.; Lorca, J.L.; Wilkinson, D. Numerical simulations of void linkage in model materials using a nonlocal ductile damage approximation. Int. J. Fract. 2007, 148, 205–219. [Google Scholar] [CrossRef][Green Version]
- Aravas, N. On the numerical integration of a class of pressure-dependent plasticity models. Int. J. Num. Meth. Eng. 1987, 24, 1395–1416. [Google Scholar] [CrossRef]
- Morin, L.; Kondo, D.; Leblond, J.-B. Numerical assessment, implementation and application of an extended Gurson model accounting for void size effects. Euro. J. Mech. Sol. 2015, 51, 183–192. [Google Scholar] [CrossRef]
- Kleiber, M.; Woźniak, C. Nonlinear Mechanics of Structures; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1991. [Google Scholar]
- Oden, J.T. Finite Elements of Nonlinear Continua; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Kossakowski, P. The numerical modeling of failure of 235JR steel using Gurson-Tvergaard-Needleman material model. Roads Bridges 2012, 11, 295–310. [Google Scholar]
- Ockewitz, A.; Sun, D.-Z. Damage modeling of automobile components of aluminum materials under crash loading. In Proceedings of the LS-DYNA Anwenderforum, Ulm, Germany, 12–13 October 2006. [Google Scholar]
- Tvergaard, V. Influence of voids on shear band instabilities under plane strain conditions. Int. J. Frac. 1981, 17, 389–407. [Google Scholar] [CrossRef]
- Zhou, J.; Gao, X.; Sobotka, J.C.; Webler, B.A.; Cockerman, B.V. On the extension of the Gurson-type porous plasticity models for prediction of ductile fracture under shear-dominated conditions. Int. J. Sol. Struct. 2014, 51, 3273–3291. [Google Scholar] [CrossRef]
- Kamiński, M.; Świta, P. Generalized stochastic finite element method in elastic stability problems. Comp. Struc. 2011, 89, 1241–1252. [Google Scholar] [CrossRef]
- Kamiński, M. The Stochastic Perturbation Method for Computational Mechanics; Wiley: Chichester, UK, 2013. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.C. The Finite Element Method, 4th ed.; McGraw Hill: New York, NY, USA, 1989. [Google Scholar]
- EN 1993-1-1:2005. Eurocode 3: Design of Steel Structures-Part 1-1: General Rules and Rules for Buildings; CEN/European Committee for Standardization: Brussels, Belgium, 2005.
- Oh, Y.R.; Kim, J.S.; Kim, Y.-J. Determination Damage Parameters for Application to Pipe Ductile Fracture Simulation. Proc. Eng. 2015, 130, 845–852. [Google Scholar] [CrossRef][Green Version]
- Wciślik, W. Experimental determination of critical void volume fraction fF for the Gurson Tvergaard Needleman (GTN) model. Proc. Struct. Integ. 2016, 2, 1676–1683. [Google Scholar] [CrossRef]
- Bjorck, A. Numerical Methods for Least Squares Problems; SIAM: Philadelphia, PA, USA, 1996. [Google Scholar]
- Melchers, R.E. Structural Reliability Analysis and Prediction; Wiley: Chichester, UK, 2002. [Google Scholar]
- Leblond, J.-B.; Morin, L.; Cazacu, O. An improved description of spherical void growth in plastic porous materials with finite porosities. Proc. Mat. Sc. 2014, 3, 1232–1237. [Google Scholar] [CrossRef]









| Polynomial Order | Correlation Index | RMS Error |
|---|---|---|
| 2 | 0.9954721794 | 0.825882 |
| 3 | 0.9986646659 | 0.448865 |
| 4 | 0.998884485 | 0.410281 |
| 5 | 0.9992027318 | 0.346882 |
| 6 | 0.9997217842 | 0.204971 |
| 7 | 0.9997218748 | 0.204915 |
| 8* | 0.9998935197 | 0.129167 |
| 9 | 0.5496160627 | 328.245 |
| 10 | 0.9998334416 | 0.158824 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamiński, M.; Strąkowski, M. Numerical Simulation of Some Steel Structural Elements with Uncertain Initial Porosity. Metals 2021, 11, 689. https://doi.org/10.3390/met11050689
Kamiński M, Strąkowski M. Numerical Simulation of Some Steel Structural Elements with Uncertain Initial Porosity. Metals. 2021; 11(5):689. https://doi.org/10.3390/met11050689
Chicago/Turabian StyleKamiński, Marcin, and Michał Strąkowski. 2021. "Numerical Simulation of Some Steel Structural Elements with Uncertain Initial Porosity" Metals 11, no. 5: 689. https://doi.org/10.3390/met11050689
APA StyleKamiński, M., & Strąkowski, M. (2021). Numerical Simulation of Some Steel Structural Elements with Uncertain Initial Porosity. Metals, 11(5), 689. https://doi.org/10.3390/met11050689







