Ballistic Impact Resistance of Bulletproof Vest Inserts Containing Printed Titanium Structures
Abstract
1. Introduction
2. Materials and Methods
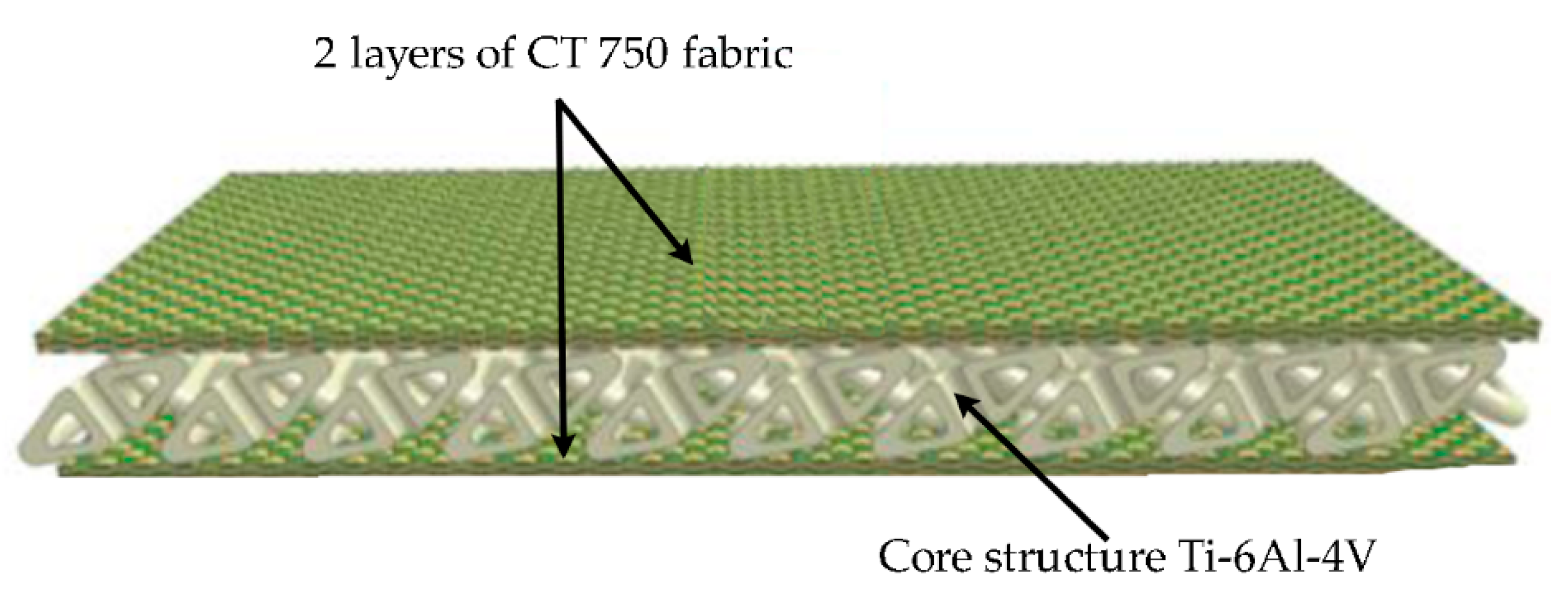
2.1. Materials Insert Configurations
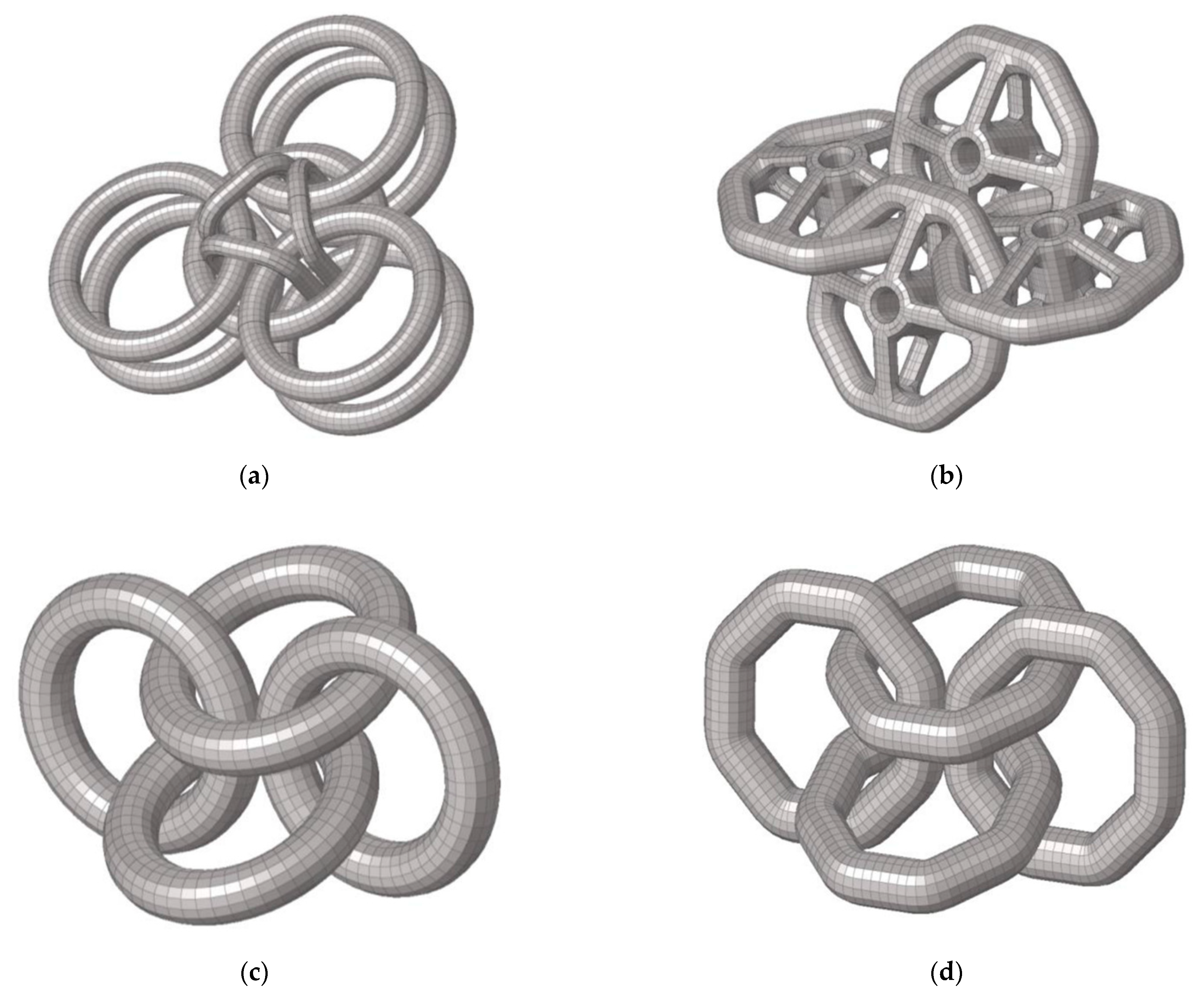
2.2. Construction of the 3D Printed Structures
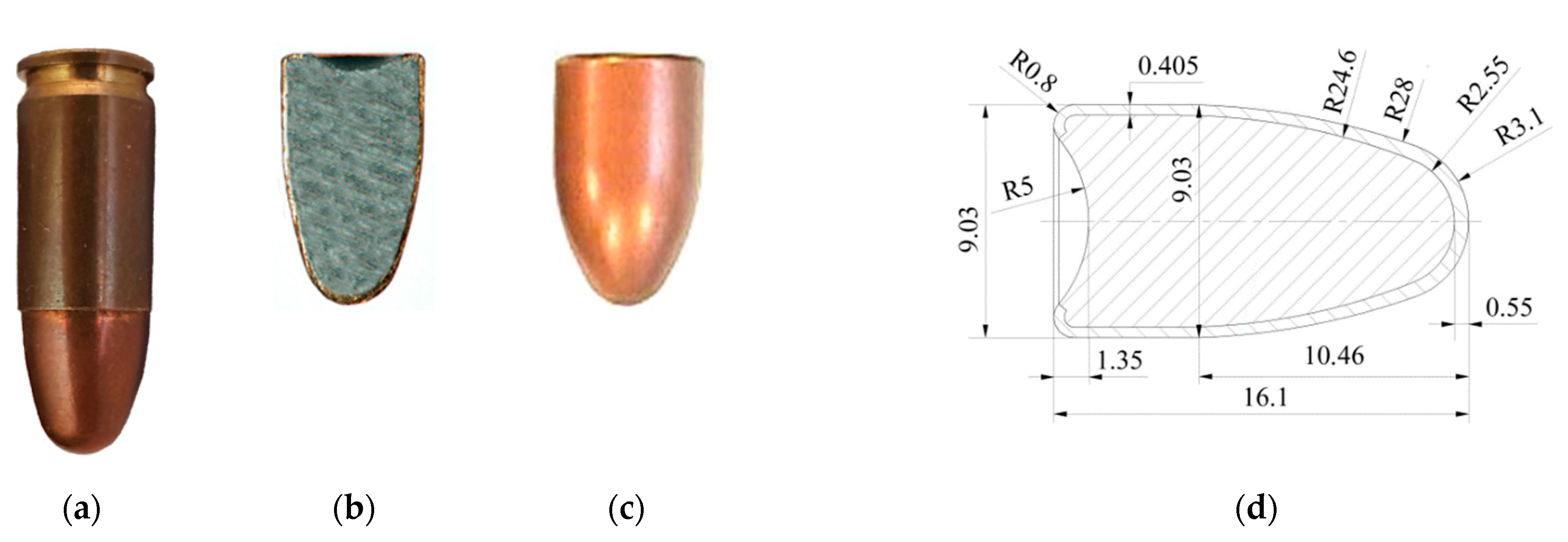
2.3. 9 mm FMJ Parabellum Projectile
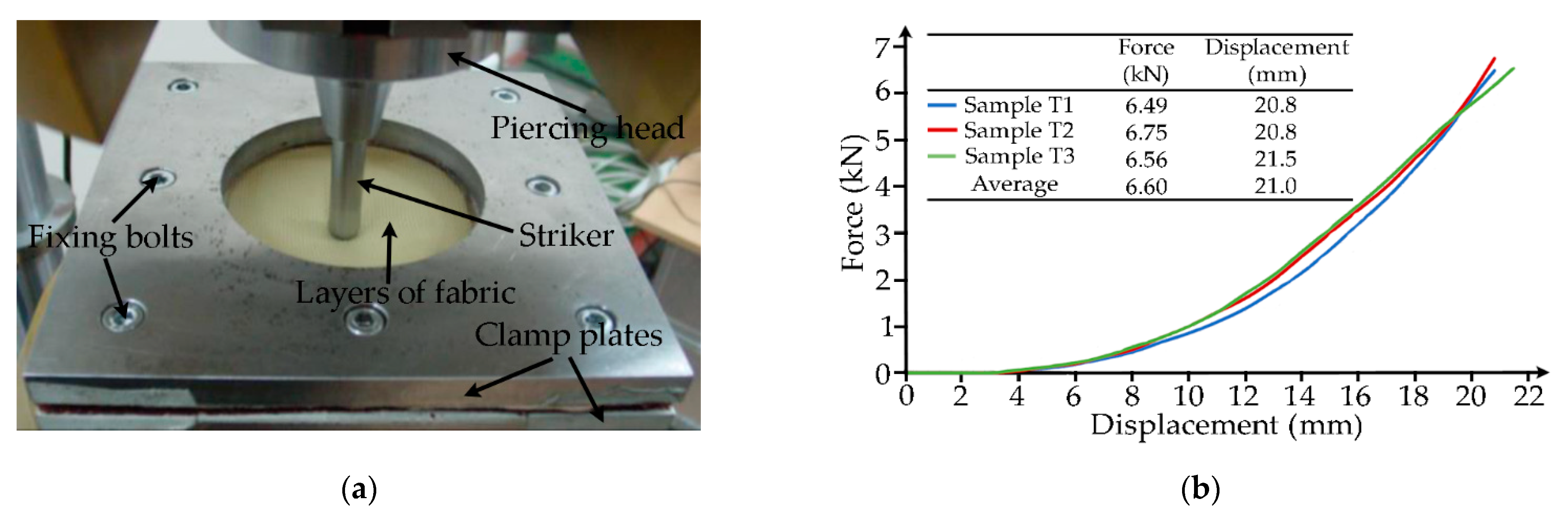
2.4. Determination of Material Characteristics for Numerical Modeling
3. Numerical Investigations
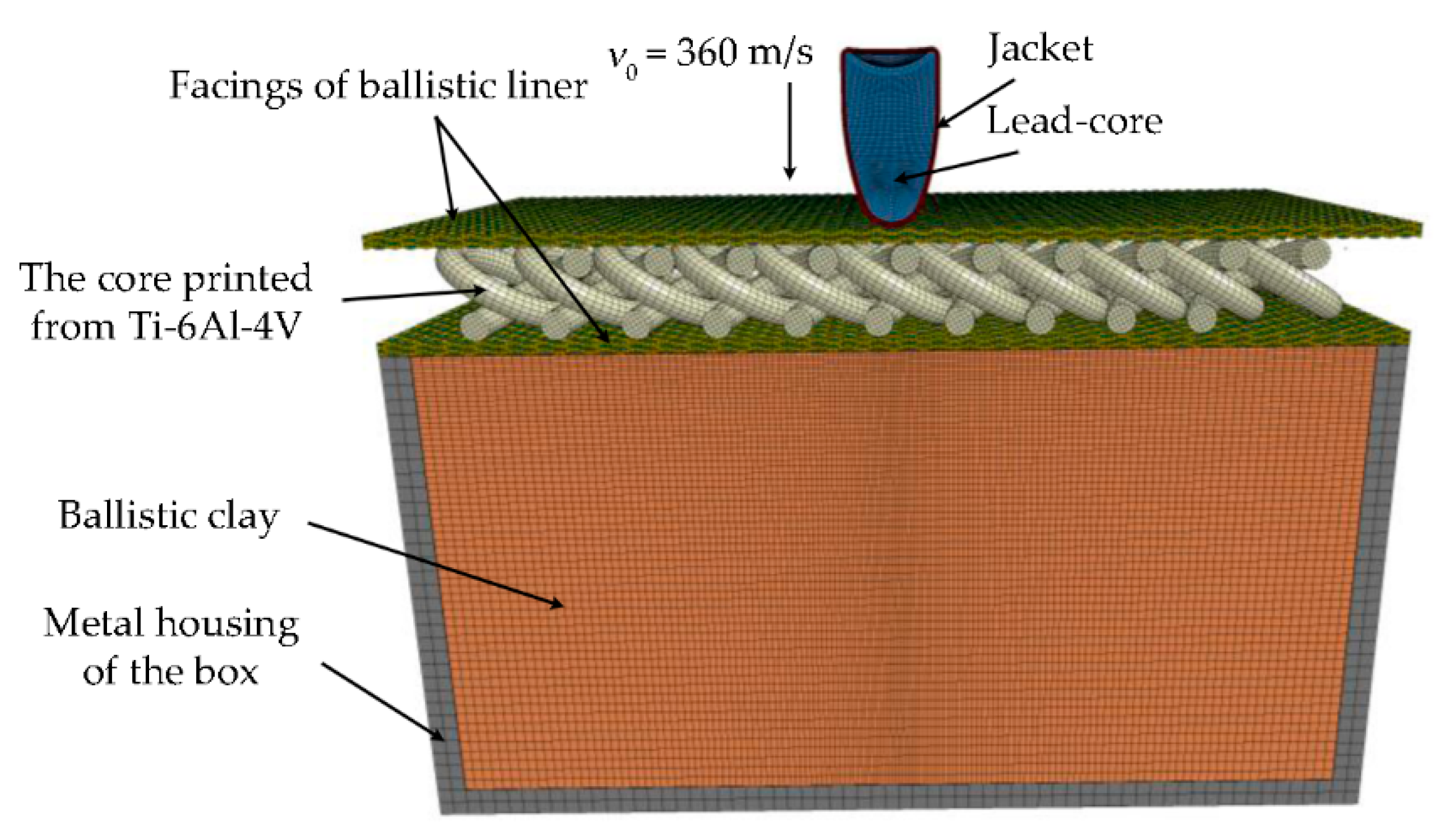
3.1. Assumptions Adopted for Modeling
3.2. Numerical Models
3.2.1. General Assumptions
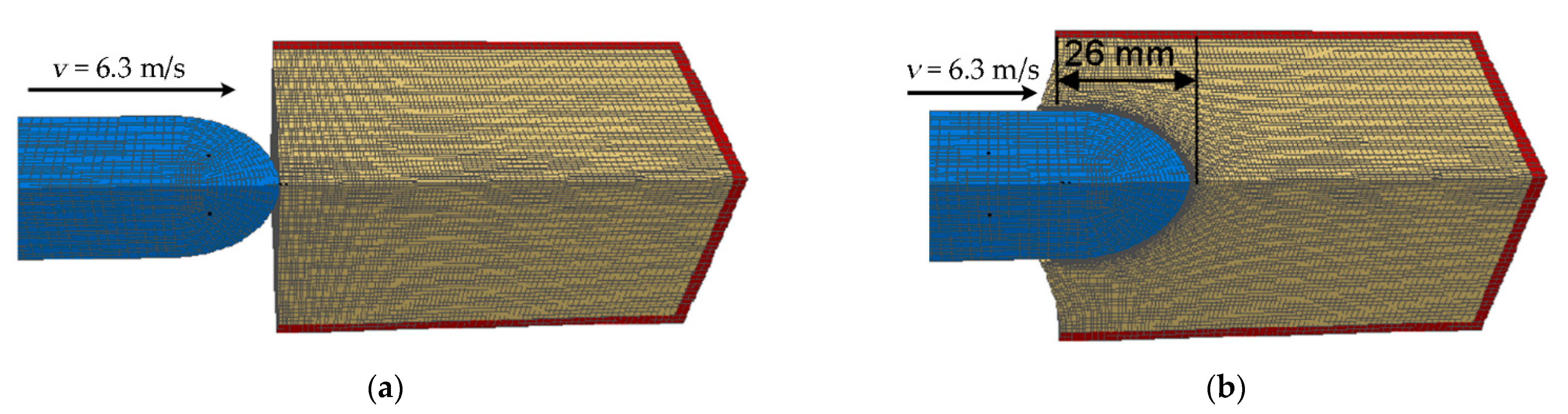
3.2.2. Projectile Model
3.2.3. Ballistic Clay Model
3.2.4. Fabric Model
3.2.5. Titanium Structures Model
- 316,080 elements for S1 structure;
- 113,152 elements for S2 structure;
- 199,680 elements for S3 structure;
- 352,560 elements for S4 structure.
- LCK1: effective stress–effective plastic strain curves for different strain rates (1.0 × 10−4–5.0 × 104 (s−1);
- LCKT: effective stress–effective strain curves for different temperature values (223–2500 K);
- LCF: curves that define plastic failure strain as a function of the triaxiality parameter;
- LCG: curves that define plastic failure strain as a function of plastic strain rate;
- LCH: curves that define plastic failure strain as a function of temperature;
- LCI: curves that define plastic failure strain as a function of element size.
4. Results and Discussion
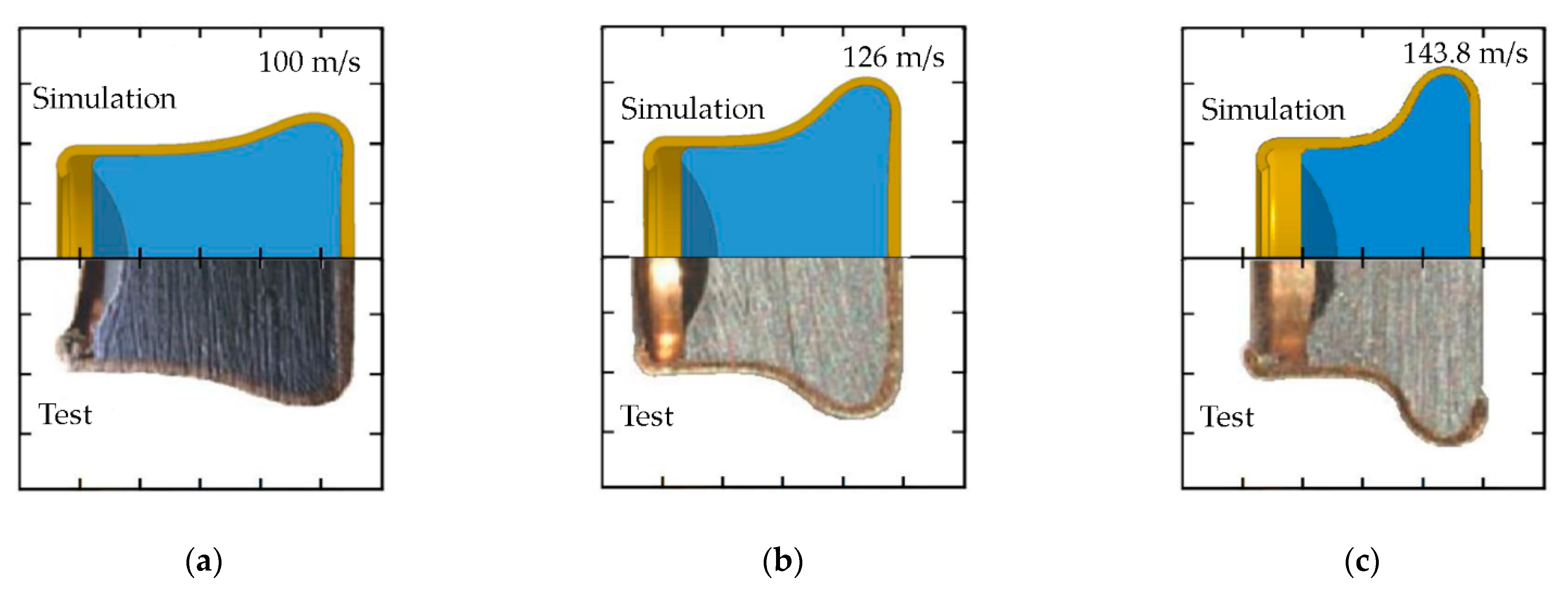
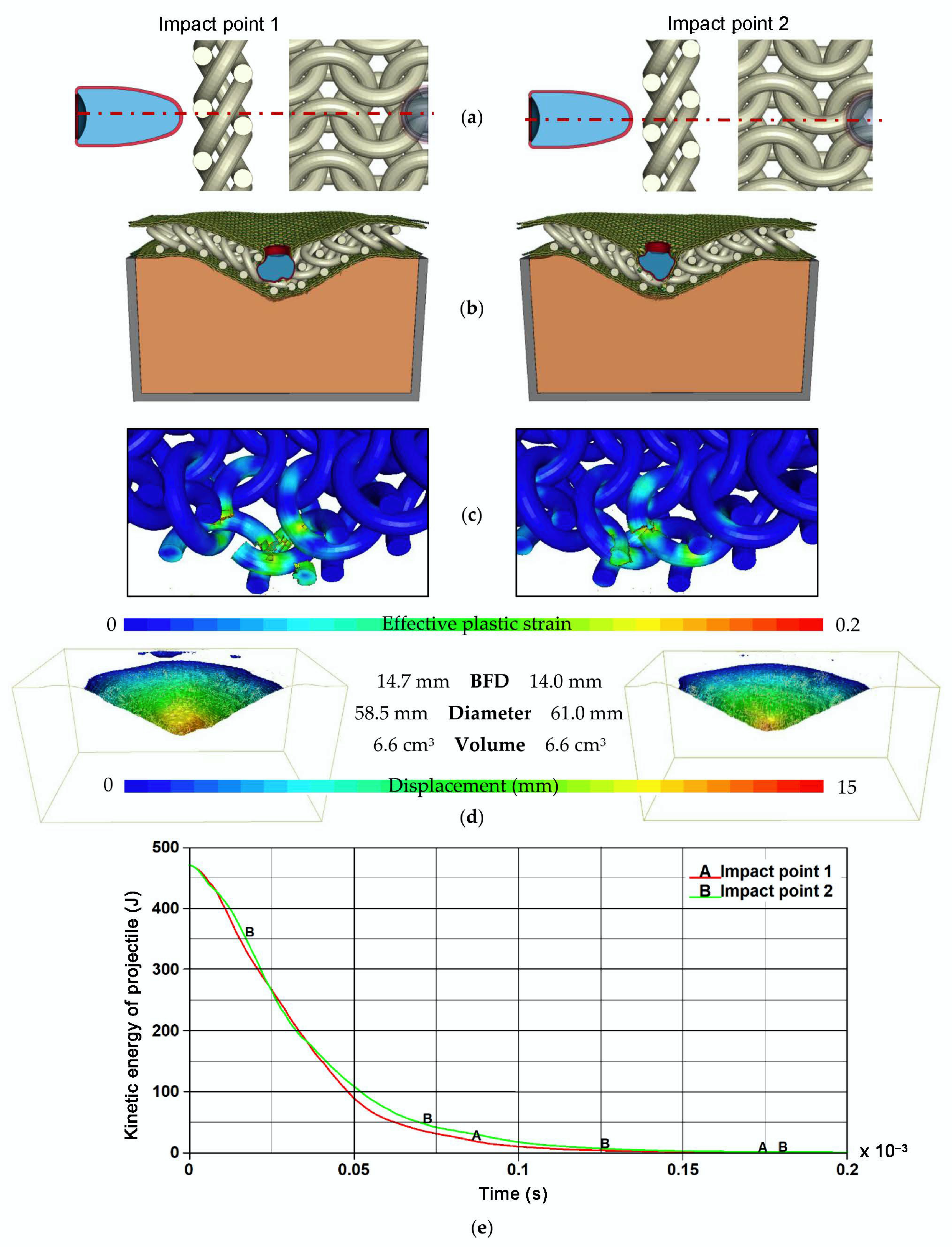
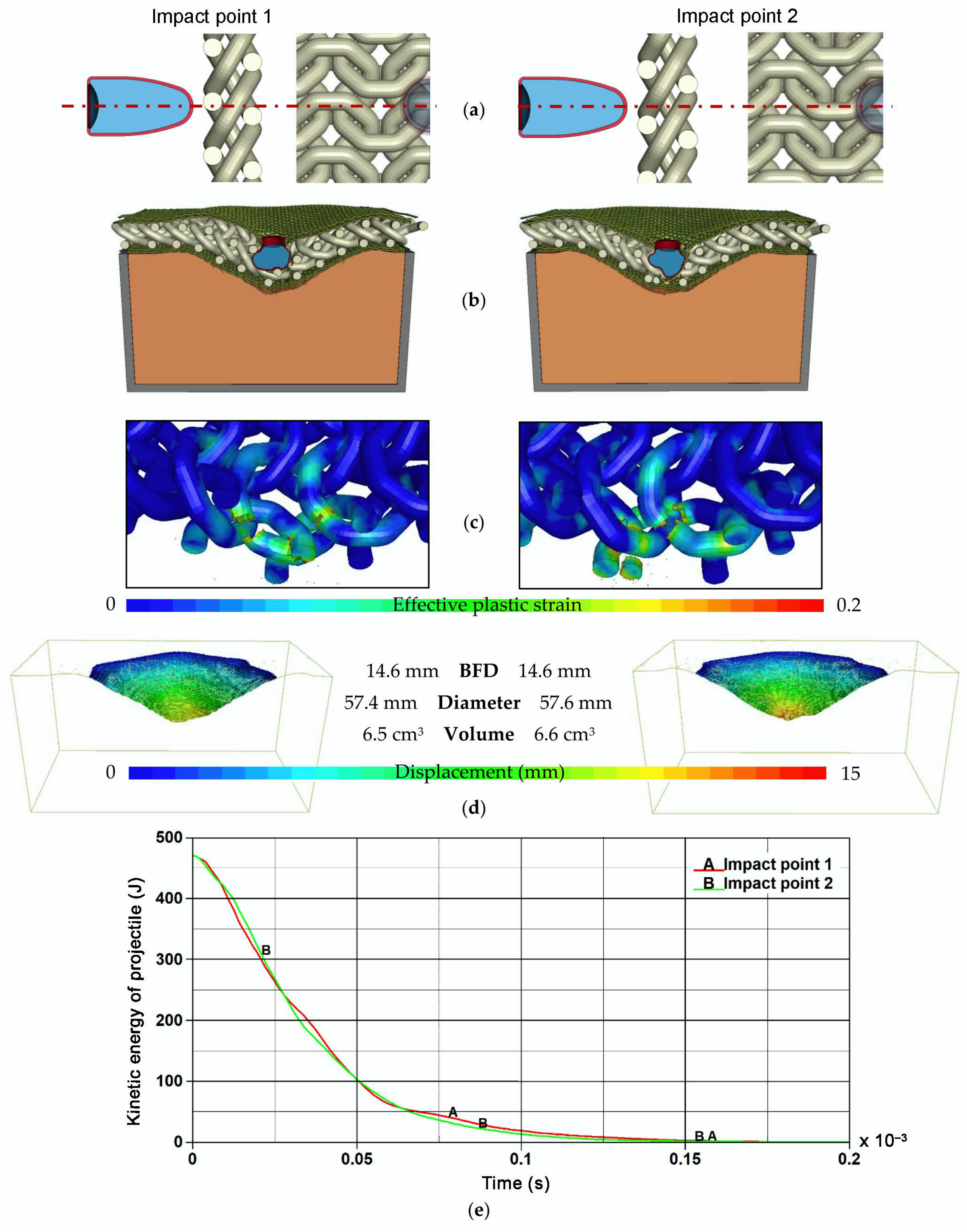
4.1. Results of Ballistic Impact Simulations
- Final deformations of the phenomenon components;
- Distribution of plastic strain in the 3D printed titanium structures;
- Volumes, shapes and dimensions of characteristic deformation parameters of the ballistic clay;
- Plots of kinetic energy of the projectile versus time.
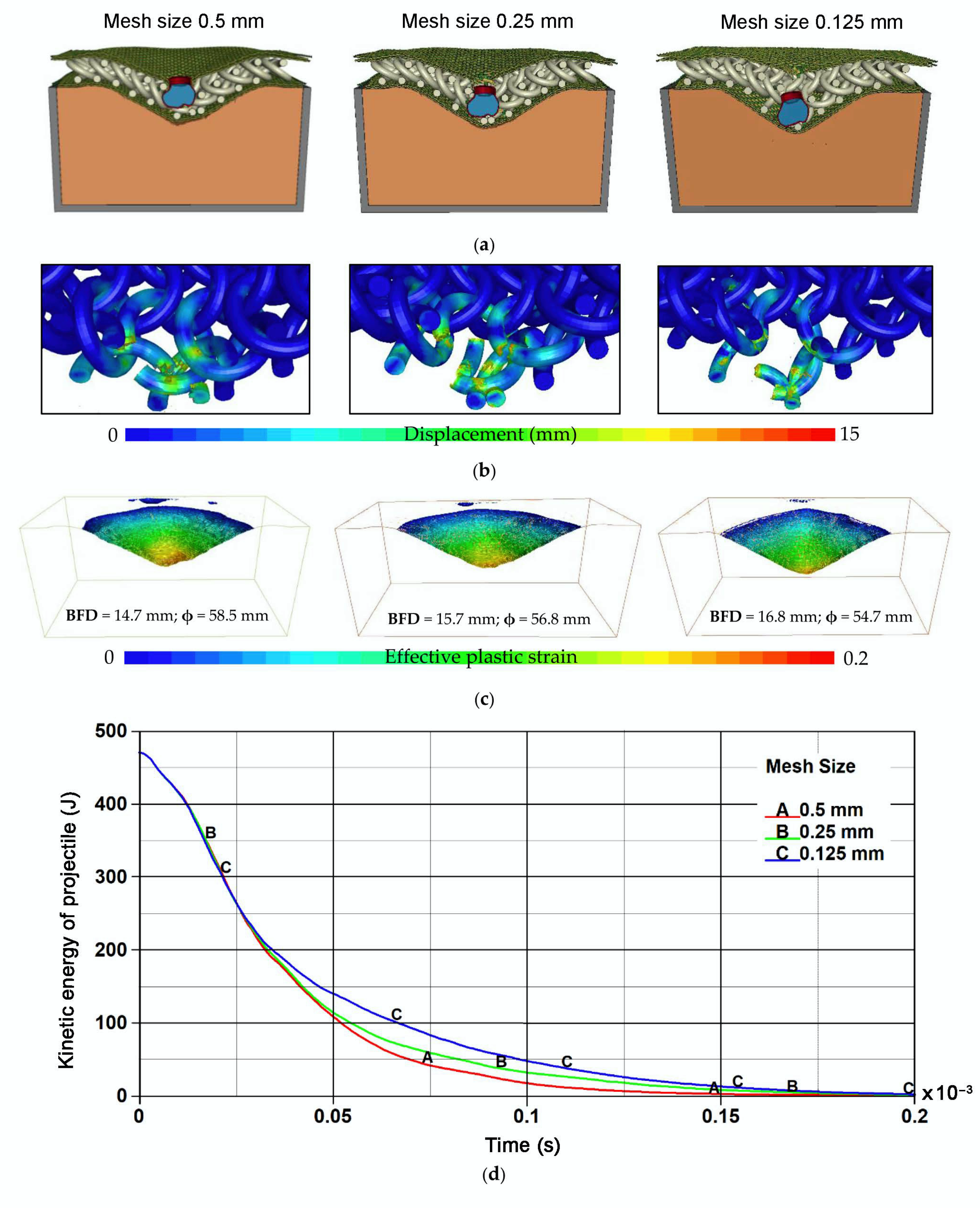
4.2. Mesh Sensitivity Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pach, J.; Mayer, P.; Jamroziak, K.; Polak, S.; Pyka, D. Experimental Analysis of Puncture Resistance of Aramid Laminates on Styrene-Butadiene-Styrene and Epoxy Resin Matrix for Ballistic Applications. Arch. Civ. Mech. Eng. 2019, 19, 1327–1337. [Google Scholar] [CrossRef]
- Clifton, S.; Thimmappa, B.H.S.; Selvam, R.; Shivamurthy, B. Polymer Nanocomposites for High-Velocity Impact Applications-A Review. Compos. Commun. 2020, 17, 72–86. [Google Scholar] [CrossRef]
- Benzait, Z.; Trabzon, L. A Review of Recent Research on Materials Used in Polymer–Matrix Composites for Body Armor Application. J. Compos. Mater. 2018, 52, 3241–3263. [Google Scholar] [CrossRef]
- Fejdyś, M.; Kośla, K.; Kucharska-Jastrząbek, A.; Łandwijt, M. Hybride Composite Armour Systems with Advanced Ceramics and Ultra-High Molecular Weight Polyethylene (UHMWPE) Fibres. Fibres Text. East. Eur. 2016, 24, 79–89. [Google Scholar] [CrossRef]
- Crouch, I.G. Critical Interfaces in Body Armour Systems. Def. Technol. 2020. [Google Scholar] [CrossRef]
- Da Luz, F.S.; Filho, F.d.C.G.; Oliveira, M.S.; Nascimento, L.F.C.; Monteiro, S.N. Composites with Natural Fibers and Conventional Materials Applied in a Hard Armor: A Comparison. Polymers 2020, 12, 1920. [Google Scholar] [CrossRef]
- Fejdyś, M.; Kośla, K.; Kucharska-Jastrząbek, A.; Łandwijt, M. Influence of Ceramic Properties on the Ballistic Performance of the Hybrid Ceramic–Multi-Layered UHMWPE Composite Armour. J. Aust. Ceram. Soc. 2020. [Google Scholar] [CrossRef]
- Kurzawa, A.; Pyka, D.; Jamroziak, K.; Bajkowski, M.; Bocian, M.; Magier, M.; Koch, J. Assessment of the Impact Resistance of a Composite Material with EN AW-7075 Matrix Reinforced with α-Al2O3 Particles Using a 7.62 × 39 mm Projectile. Materials 2020, 13, 769. [Google Scholar] [CrossRef]
- Kurzawa, A.; Pyka, D.; Jamroziak, K.; Bocian, M.; Kotowski, P.; Widomski, P. Analysis of Ballistic Resistance of Composites Based on EN AC-44200 Aluminum Alloy Reinforced with Al2O3 Particles. Compos. Struct. 2018, 201, 834–844. [Google Scholar] [CrossRef]
- Chusov, S.Y.; Yankov, V.P. Investigation of Properties of Titanium Alloys with Mechanically Stable Beta-Structure for Body Armor Application. Tech. Wyrob.Włók. 2009, 17, 54–57. [Google Scholar]
- Cimpoeru, S.J.; Alkemade, S.J.; Szymczak, M.; Rupert, N.L.; Green, W.H.; Wells, J.M. Ballistic Assessment of a Low-Cost Ti-6Al-4V Titanium Alloy. Aust. J. Mech. Eng. 2003, 1, 5–9. [Google Scholar] [CrossRef]
- Karahan, M.; Jabbar, A.; Karahan, N. Ballistic Impact Behavior of the Aramid and Ultra-High Molecular Weight Polyethylene Composites. J. Reinf. Plast. Compos. 2015, 34, 37–48. [Google Scholar] [CrossRef]
- Shtertser, A.A.; Zlobin, B.S.; Kiselev, V.V.; Shemelin, S.D.; Bukatnikov, P.A. Characteristics of Reinforced Ultra-High Molecular Weight Polyethylene During Its Ballistic Penetration. J. Appl. Mech. Tech. Phys. 2020, 61, 471–478. [Google Scholar] [CrossRef]
- Jamroziak, K. Evaluation of Gunshot Wounds in Aspect of Injury Criterion. Aktual. Probl. Biomech. 2016, 11, 33–46. [Google Scholar]
- Wang, L.; Kanesalingam, S.; Nayak, R.; Padhye, R. Recent Trends in Ballistic Protection. Text. Light Ind. Sci. Technol. 2014, 3, 37–47. [Google Scholar] [CrossRef]
- Baranowski, P.; Płatek, P.; Antolak-Dudka, A.; Sarzyński, M.; Kucewicz, M.; Durejko, T.; Małachowski, J.; Janiszewski, J.; Czujko, T. Deformation of Honeycomb Cellular Structures Manufactured with Laser Engineered Net Shaping (LENS) Technology under Quasi-Static Loading: Experimental Testing and Simulation. Addit. Manuf. 2019, 25, 307–316. [Google Scholar] [CrossRef]
- Szymczyk, P.; Hoppe, V.; Ziółkowski, G.; Smolnicki, M.; Madeja, M. The Effect of Geometry on Mechanical Properties of Ti6Al4V ELI Scaffolds Manufactured Using Additive Manufacturing Technology. Arch. Civ. Mech. Eng. 2020, 20, 1–13. [Google Scholar] [CrossRef]
- Horn, K.; Biever, K.; Burkman, K.; Sheikh, P.D.; Jamison, L.; Kolb, M. Lightening Body Armor: Arroyo Support to the Army Response to Section 125 of the National Defense Authorization Act for Fiscal Year 2011; Report No. W74V8H-06-C-0001; United States Army: Santa Monica, SM, USA, 2011.
- Kristoffersen, M.; Costas, M.; Koenis, T.; Brøtan, V.; Paulsen, C.O.; Børvik, T. On the Ballistic Perforation Resistance of Additive Manufactured AlSi10Mg Aluminium Plates. Int. J. Impact Eng. 2020, 137. [Google Scholar] [CrossRef]
- Ngo, T.D.; Kashani, A.; Imbalzano, G.; Nguyen, K.T.Q.; Hui, D. Additive Manufacturing (3D Printing): A Review of Materials, Methods, Applications and Challenges. Compos. Part B Eng. 2018, 143, 172–196. [Google Scholar] [CrossRef]
- Dunaj, P.; Berczyński, S.; Miądlicki, K.; Iskra, I.; Niesterowicz, B. Increasing Damping of Thin-Walled Structures Using Additively Manufactured Vibration Eliminators. Materials 2020, 13, 2125. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, D.; Rusinek, A.; Jankowiak, T.; Arias, A. Mechanical Impact Behavior of Polyether-Ether-Ketone (PEEK). Compos. Struct. 2015, 124, 88–99. [Google Scholar] [CrossRef]
- Szymczyk, P.; Ziółkowski, G.; Junka, A.; Chlebus, E. Application of Ti6Al7Nb Alloy for the Manufacture of Biomechanical Functional Structures (BFS) for Custom-Made Bone Implants. Materials 2018, 11, 971. [Google Scholar] [CrossRef] [PubMed]
- Yuan, M.Q.; Liu, Y.; Gong, Z.; Qian, X.M. The Application of PA/CF in Stab Resistance Body Armor. IOP Conf. Ser. Mater. Sci. Eng. 2017, 012027. [Google Scholar] [CrossRef]
- Connors, M.; Yang, T.; Hosny, A.; Deng, Z.; Yazdandoost, F.; Massaadi, H.; Eernisse, D.; Mirzaeifar, R.; Dean, M.N.; Weaver, J.C.; et al. Bioinspired Design of Flexible Armor Based on Chiton Scales. Nat. Commun. 2019, 10, 1–13. [Google Scholar] [CrossRef]
- Costas, M.; Morin, D.; de Lucio, M.; Langseth, M. Testing and Simulation of Additively Manufactured AlSi10Mg Components under Quasi-Static Loading. Eur. J. Mech. A/Solids 2020, 81, 103966. [Google Scholar] [CrossRef]
- Masood, S.H.; Ruan, D.; Rajapatruni, P. Mechanical Performance of Plymetal Structures Subjected to Impact Loading. Int. J. Prot. Struct. 2018, 9, 65–76. [Google Scholar] [CrossRef]
- Zhao, L.; Qian, X.; Sun, Y.; Yuan, M.; Tang, F.; Zhao, Y.; Zhang, Q.; Chen, Y. Ballistic Behaviors of Injection-Molded Honeycomb Composite. J. Mater. Sci. 2018, 53, 14287–14298. [Google Scholar] [CrossRef]
- Płatek, P.; Rajkowski, K.; Cieplak, K.; Sarzyński, M.; Małachowski, J.; Woźniak, R.; Janiszewski, J. Deformation Process of 3D Printed Structures Made from Flexible Material with Different Values of Relative Density. Polymers 2020, 12, 2120. [Google Scholar] [CrossRef]
- Platek, P.; Sienkiewicz, J.; Janiszewski, J.; Jiang, F. Investigations on Mechanical Properties of Lattice Structures with Different Values of Relative Density Made from 316L by Selective Laser Melting (SLM). Materials 2020, 13, 2204. [Google Scholar] [CrossRef]
- Kluczyński, J.; Sniezek, L.; Grzelak, K.; Janiszewski, J.; Płatek, P.; Torzewski, J.; Szachogłuchowicz, I.; Gocman, K. Influence of Selective Laser Melting Technological Parameters on the Mechanical Properties of Additively Manufactured Elements Using 316L Austenitic Steel. Materials 2020, 13, 1449. [Google Scholar] [CrossRef]
- Płatek, P.; Baranowski, P.; Janiszewski, J.; Kucewicz, M. Problems of Deformation and Damage Studies of Additively Manufactured Regular Cellular Structures. In Handbook of Damage Mechanics: Nano to Macro Scale for Materials and Structures; Voyiadjis, G.Z., Ed.; Springer: New York, NY, USA, 2020; pp. 1–33. [Google Scholar] [CrossRef]
- Bajkowski, M.; Grygoruk, R.; Nita, Z.; Floriańczyk, A. Method for Producing Additional Ballistic Insert and the Additional Ballistic Insert for Bulletproof. Jackets. Patent PL224964, 28 February 2017. [Google Scholar]
- Gmbh, T.A. Teijin Aramid @ Techtextile Middle East Symposium. Available online: https://www.intersecexpo.com/uploads/editor_images/file/ReneLohmann-DubaiTTS2014_SHOW-locked.pdf (accessed on 20 November 2020).
- Pawlak, A.; Szymczyk, P.; Ziolkowski, G.; Chlebus, E.; Dybala, B. Fabrication of Microscaffolds from Ti-6Al-7Nb Alloy by SLM. Rapid Prototyp. J. 2015, 21, 393–401. [Google Scholar] [CrossRef]
- Del Guercio, G.; Galati, M.; Saboori, A.; Fino, P.; Luliano, L. Microstructure and Mechanical Performance of Ti–6Al–4V Lattice Structures Manufactured via Electron Beam Melting (EBM): A Review. Acta Metall. Sin. (Engl. Lett.) 2020, 33, 183–203. [Google Scholar] [CrossRef]
- Cotton, R.; Palanisamy, S.; Avdeev, M.; Jarvis, T.; Henry, C.; Cuiuri, D.; Balogh, L.; Rashid, R.A.R. Diffraction Line Profile Analysis of 3D Wedge Samples of Ti-6Al-4V Fabricated Using Four Different Additive Manufacturing Processes. Metals 2019, 9, 60. [Google Scholar] [CrossRef]
- STANAG 4090. Technical Performance Specification Providing for the Interchangeability of 9 mm × 19 Ammunition; North Atlantic Treaty Organization (NATO): Brussels, Belgium, 2020. [Google Scholar]
- Panowicz, R.; Janiszewski, J.; Kochanowski, K. Effects of Sample Geometry Imperfections on the Results of Split Hopkinson Pressure Bar Experiments. Exp. Tech. 2019, 43, 397–403. [Google Scholar] [CrossRef]
- Chapman, D.J.; Radford, D.; Walley, S.M. A History of the Taylor Test and Its Present Use in the Study of Lightweight Materials. In 3rd Light-Weight Armour Group Workshop. Design and Use of Light-Weight Materials; Teixeria-Dias, F., Dodd, B., Lach, E., Schulz, P., Eds.; Universidade de Aveiro: Aveiro, Portugal, 2005; pp. 12–24. [Google Scholar]
- Kruszka, L.; Magier, M.; Zielenkiewicz, M. Experimental Analysis of Visco-Plastic Properties of the Aluminium and Tungsten Alloys by Means of Hopkinson Bars Technique. Appl. Mech. Mater. 2014, 566, 110–115. [Google Scholar] [CrossRef]
- Mukasey, M.B.; Sedgwick, J.L.; Hagy, D.W. Ballistic Resistance of Body Armor; U.S. Department of Justice Office of Justice Programs: Washington, DC, USA, 2008; pp. 1–89.
- LS-DYNA® Keyword User’s Manual; LS-DYNA R12, (r:13109); Livermore Software Technology (LST): Pittsburgh, PA, USA, 2020; Volume I.
- Materials Modeles. In LS-DYNA® Keyword User’s Manual; LS-DYNA R12, (r:13191); Livermore Software Technology (LST): Pittsburgh, PA, USA, 2020; Volume II.
- Bocian, M.; Jamroziak, K.; Kosobudzki, M. Analysis of Material Punching Including a Rotational Speed of the Projectile. Solid State Phenom. 2015, 220–221, 571–576. [Google Scholar] [CrossRef]
- Mazurkiewicz, Ł.; Małachowski, J.; Baranowski, P. Optimization of Protective Panel for Critical Supporting Elements. Compos. Struct. 2015, 134, 493–505. [Google Scholar] [CrossRef]
- Mackiewicz, A.; Pyka, D.; Pach, J.; Jamroziak, K.; Bocian, M. Comparison of Numerical Modelling Methods of Innovative Materials for Ballistic Shields. In Advanced Materials for Defense; Fangueiro, R., Rana, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; pp. 119–127. [Google Scholar]
- Hernandez, C.; Maranon, A.; Ashcroft, I.A.; Casas-Rodriguez, J.P. Inverse Methods for the Mechanical Characterization of Materials at High Strain Rates. EPJ Web Conf. 2012, 26, 04022. [Google Scholar] [CrossRef]
- Coefficient of Friction. Available online: https://www.teachengineering.org/content/nyu_/activities/nyu_heavy/nyu_heavy_activity1_coftable.pdf (accessed on 8 January 2021).
- Nilakantan, G.; Keefe, M.; Gillespie, J.W.; Bogetti, T.A. Novel Multi-Scale Modeling of Woven Fabric. In 10th International LS-DYNA® Users Conference; Mindle, W.L., Ed.; Livermore Software Technology Corporation: Dearbon, MI, USA, 2008; pp. 19–38. [Google Scholar]
- Nilakantan, G.; Nutt, S. Effects of Ply Orientation and Material on the Ballistic Impact Behavior of Multilayer Plain-Weave Aramid Fabric Targets. Def. Technol. 2018, 14, 165–178. [Google Scholar] [CrossRef]
- Nilakantan, G.; Keefe, M.; Bogetti, T.A.; Gillespie, J.W. Multiscale Modeling of the Impact of Textile Fabrics Based on Hybrid Element Analysis. Int. J. Impact Eng. 2010, 37, 1056–1071. [Google Scholar] [CrossRef]
- Haight, S.; Wang, L.; Du Bois, P.; Carney, K.; Kan, C. Development of a Titanium Alloy Ti-6Al-4V Material Model Used in LS-DYNA; Report DOT/FAA/TC-15/23; U.S. Department of Transportation: Washington, DC, USA, 2016; 1, p. 353.
- Burian, W.; Żochowski, P.; Gmitrzuk, M.; Marcisz, J.; Starczewski, L.; Juszczyk, B.; Magier, M. Protection Effectiveness of Perforated Plates Made of High Strength Steel. Int. J. Impact Eng. 2019, 126, 27–39. [Google Scholar] [CrossRef]
- Meyer, H.W.; Kleponis, D.S. Modeling the High Strain Rate Behavior of Titanium Undergoing Ballistic Impact and Penetration. Int. J. Impact Eng. 2001, 26, 509–521. [Google Scholar] [CrossRef]








| Style | Type Warp/Weft | Weave | Set (per 10 cm) Warp/Weft | Areal Density (g/m2) | Thickness (mm) | Minimum Break Strength (N/5 cm × 1000) Warp/Weft |
|---|---|---|---|---|---|---|
| CT 750 | 2000 | plain | 69/69 | 460 | 0.70 | 16.5/18.0 |
| Specification | RO, (Tonnes) | E, (MPa) | PR, (-) | A, (MPa) | B, (MPa) | n, (-) | C, (-) | m, (-) | D1, (-) | D2, (-) | D3, (-) | D4, (-) | D5, (-) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Lead-Core | 1.01 × 10−8 | 18.4 × 103 | 0.42 | 24 | 40 | 1.00 | 0.01 | 1.00 | 3 | 0 | 0 | 0 | 0 |
| Brass-Jacket | 8.52× 10−9 | 11.5× 104 | 0.31 | 206 | 899 | 0.42 | 0.01 | 1.68 | - | WC | 1414 | - | - |
| Specification | RO, (Tonnes) | E, (MPa) | PR, (-) | K, (MPa) | N, (-) | SRC, (s–1) | SRP, (-) | SIGY, (MPa) | EPSF, (-) | VP, (-) | Source |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ballistic clay | 1878 | 14.2 | 0.49 | 0.24 | 0.014 | 0 | 0 | 0 | 2.5 | 1 | [48] |
| Specification | RO, (Tonnes) | EA, (MPa) | EB, (MPa) | EC, (MPa) | PRBA, (-) | PRCA, (-) | PRCB, (-) | GAB, (MPa) | GBC, (MPa) | GCA, (MPa) | Source |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Twaron CT 750 | 1.158 × 10−9 | 62,800 | 628 | 628 | 0 | 0 | 0 | 31,000 | 158 | 31,000 | [50,51,52] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zochowski, P.; Bajkowski, M.; Grygoruk, R.; Magier, M.; Burian, W.; Pyka, D.; Bocian, M.; Jamroziak, K. Ballistic Impact Resistance of Bulletproof Vest Inserts Containing Printed Titanium Structures. Metals 2021, 11, 225. https://doi.org/10.3390/met11020225
Zochowski P, Bajkowski M, Grygoruk R, Magier M, Burian W, Pyka D, Bocian M, Jamroziak K. Ballistic Impact Resistance of Bulletproof Vest Inserts Containing Printed Titanium Structures. Metals. 2021; 11(2):225. https://doi.org/10.3390/met11020225
Chicago/Turabian StyleZochowski, Pawel, Marcin Bajkowski, Roman Grygoruk, Mariusz Magier, Wojciech Burian, Dariusz Pyka, Miroslaw Bocian, and Krzysztof Jamroziak. 2021. "Ballistic Impact Resistance of Bulletproof Vest Inserts Containing Printed Titanium Structures" Metals 11, no. 2: 225. https://doi.org/10.3390/met11020225
APA StyleZochowski, P., Bajkowski, M., Grygoruk, R., Magier, M., Burian, W., Pyka, D., Bocian, M., & Jamroziak, K. (2021). Ballistic Impact Resistance of Bulletproof Vest Inserts Containing Printed Titanium Structures. Metals, 11(2), 225. https://doi.org/10.3390/met11020225










