Free Energy of Metals from Quasi-Harmonic Models of Thermal Disorder

Abstract

A simple modeling method to extend first-principles electronic structure calculations to finite temperatures is presented. The method is applicable to crystalline solids exhibiting complex thermal disorder and employs quasi-harmonic models to represent the vibrational and magnetic free energy contributions. The main outcome is the Helmholtz free energy, calculated as a function of volume and temperature, from which the other related thermophysical properties (such as temperature-dependent lattice and elastic constants) can be derived. Our test calculations for Fe, Ni, Ti, and W metals in the paramagnetic state at temperatures of up to 1600 K show that the predictive capability of the quasi-harmonic modeling approach is mainly limited by the electron density functional approximation used and, in the second place, by the neglect of higher-order anharmonic effects. The developed methodology is equally applicable to disordered alloys and ordered compounds and can therefore be useful in modeling realistically complex materials.

1. Introduction

The first successful applications of Debye–Grüneisen theory to derive thermal properties of metals [1] from the total energies calculated on the basis of density functional theory (DFT) [2,3] were later overshadowed by the great success of quasi-harmonic evaluation of the phonon free energy from DFT-computed phonon spectra [4,5,6,7,8,9]. Furthermore, free energy evaluation by means of thermodynamic integration of ab initio (or classical ab-initio based) molecular dynamical simulation is now often used for describing systems with strong anharmonic effects at high temperatures [10,11,12]. All these recent developments are truly impressive and yield extremely valuable data about the behaviors of anharmonic systems, but at an extremely high computational cost.

A number of approaches for reducing the computational cost have been proposed, to enable modeling realistically complex systems [11,13,14,15,16,17]. In multi-scale modeling, the data obtained from very detailed atomic-scale models [18] must be represented in the form of effective parameters of coarser-grained models, for example as thermophysical properties of alloy phases considered in continual models [19,20,21,22,23,24,25]. In the context of coarse-graining, as a part multiscale modeling, most useful are simple models that can capture the essential physics of complex behavior of a real system.

Due to its nice analytic properties, the Debye model is a very attractive choice for representing vibrational free energy of close-packed crystalline systems (such as elemental metals, substitutional metallic alloys, or intermetallic compounds) at temperatures much below the melting point [19,20]. One clear advantage of Debye model is that it yields the vibrational energy and entropy contributions to the Helmholtz free energy as closed expressions, from which all related thermodynamic properties can be derived.

In this work, we follow the idea of Ehteshami and Korzhavyi [26] to connect the Debye model to finite-temperature electronic structure calculations via Debye temperature ${\mathsf{\Theta }}_D$ parameter evaluated from the elastic constants. In contrast to previous formulations of the Debye model [1], we do not introduce an “isotropic” Grüneisen constant to represent the volume dependence of compressibility, but describe the volume dependence of ${\mathsf{\Theta }}_D$ through directionally-averaged longitudinal and transverse stiffness constants [27,28,29,30] that are computed as functions of volume and temperature.

Performance of the so-formulated quasi-harmonic Debye model is tested here for selected elemental metals with the face-centered cubic (fcc) and body-centered cubic (bcc) crystal structures. Equilibrium lattice parameters, elastic constants, and their temperature dependencies are derived from the modeled Helmholtz free energy containing the electronic and vibrational contributions. By comparing the calculated results with available experimental data, we demonstrate the advantages and limitations of the present formulation of quasi-harmonic Debye model (QDM) and discuss its possible generalizations.

2. Materials and Methods

First-principles calculations, interfaced to a quasi-harmonic formulation of the Debye model, are employed in this work for modeling the Helmholtz free energy of fcc Cu, Ni, and γ-Fe metals (the latter two are considered in the high-temperature paramagnetic state), as well as for bcc β-Ti, Cr, Mo, and W metals. Anharmonic effects are known to play a crucial role in the stabilization of β-Ti at high temperature, so that a quasi-harmonic treatment is clearly insufficient in this case, which is included in the present study mainly for pedagogic reasons.

Self-consistent electronic structure calculations were performed in the generalized gradient approximation (GGA) using the PBE (parameterized by Perdew, Burke, and Ernzerhof) exchange-correlation functional [31] and the exact muffin-tin orbital (EMTO) method [32], implemented within Green’s function formalism augmented by the coherent potential approximation (CPA) [33,34]. The electronic free energy was calculated from the self-consistent electron density using the full charge density technique [35,36]. The method allows for evaluating the electronic and magnetic free energy contributions associated, respectively, with partial occupancy of electron states [37] and with paramagnetism of disordered local moments (DLM) [38] at a non-zero electronic temperature, see Reference [26] for further details of the theoretical treatment.

Technical details of the calculations were as follows. Monkhorst–Pack meshes of special points [39] were used for Brillouin zone integration, 33 × 33 × 33 for bcc and 29 × 29 × 29 for fcc metals. For each metal, the electronic free energy and its derivatives with respect to two volume-conserving shear distortions (related to cubic elastic constants $C_{44}$ and $C^{\prime }$) were evaluated on a grid of temperature and Wigner–Seitz radius ($R_{\mathrm{WS}}$, related to atomic volume as $V=4\pi R_{\mathrm{WS}}^3/3$) values. The results of such calculations for fcc Cu metal are presented in Figure 1a,b.

For the two types of shear, the partial (electronic) free energy of Cu shown in Figure 1a is a quadratic function of the distortion, with the proportionality coefficients that are almost temperature-independent, especially $C_{44}$. The volume dependence of partial free energy shown in Figure 1b is a function that changes very little with temperature, indicating a small value of the electronic heat capacity typical of a metal with a closed d-electron shell. As a result, the Debye temperature, Figure 1c, evaluated from the elastic constants, is practically independent of electronic temperature in the range from 800 to 1200 K. Its volume dependence is rather strong and slightly non-linear. By plugging the calculated Debye temperature into the Debye model and adding the modeled vibrational free energy to the partial free energy, one gets the Helmholtz free energy plotted in Figure 1d. Its minimum at each temperature corresponds to the equilibrium Wigner–Seitz radius; by following the evolution of the minimum point with temperature (down triangles connected with a dashed line) one can derive thermal properties such as heat capacity and thermal expansion coefficient (TEC).

Figure 2 illustrates the application of a similar computational procedure to the case of fcc Ni, the element preceding Cu in the Periodic table. The 3d-electron shell of Ni is incompletely filled, giving rise to its local magnetic moment. The high-temperature paramagnetic state of Ni is considered here.

Several schemes based on the DLM approach have been proposed for the treatment of paramagnetic disorder [26,40,41,42,43]. Here we use the self-consistent mean-field approach of Reference [26], where an average magnetic-moment magnitude $m$ (in Bohr magneton units) is ascribed to every atom. The orientation of each atomic moment is completely arbitrary in the paramagnetic state, generating a magnetic entropy $S_{\mathrm{mag}}=k_{\mathrm{B}}\ln \left(m+1\right)$ per magnetic atom. Here $k_{\mathrm{B}}$ is the Boltzmann constant. For an integer magnetic moment, $m+1$ gives the number of its possible projections on a quantization axis. It can be shown that, in the harmonic approximation where the energy is assumed to be a parabolic function of $m$, longitudinal fluctuations of magnetic moment around its average value do not additionally contribute to $S_{\mathrm{mag}}$.

By self-consistently including the magnetic entropy contribution into the electronic free energy, one gets a splitting of the one-electron potential by $\Delta U_{\uparrow ,\downarrow }=\mp k_{\mathrm{B}}T/\left(m+1\right)$, where the up- and down-arrows denote, respectively, the majority and minority spin channels in the spin coordinate framework associated with an atom. It is noteworthy that this mean-field potential shift does not depend on the curvature of the parabolic function, but is temperature-dependent, favoring larger values of $m$ at a higher temperature.

This makes the values of m and $S_{\mathrm{mag}}$ depend not only on volume, but also on temperature. This magnetic contribution, in addition to the electronic contribution proportional to the density of states at the Fermi level (which is higher in the case of Ni with an open d-shell), causes a stronger temperature dependence of the partial (electronic) free energy in the case of Ni as compared to Cu, see Figure 2a,b. The onset of magnetic moment and electronic excitations contribute to the Debye temperature shown in Figure 2c, whose volume dependence exhibits a kink at $R_{\mathrm{WS}}\cong 2.65$ bohr and whose temperature dependence becomes more pronounced at larger volumes.

By comparing the rates at which the free energy curves accelerate down with temperature (Figure 1b and Figure 2b), one can deduce that electronic contributions to the thermal properties are much stronger in the case of Ni (paramagnetic transition metal) than in the case of Cu (normal metal with no atomic moments). Still, the magnetic moment on Ni is relatively small, so the magnetic contributions to thermal expansion and heat capacity of Ni, which can be deduced from Figure 2b,d, are also small compared to the respective vibrational contributions, see Reference [44] for further details.

Iron, as an element from the middle of the 3d transition series, exhibits high values of magnetic moment, exceeding 2 Bohr magnetons at large volumes. The strong volume dependence of magnetic moment enhances the volume dependencies of elastic constants, Figure 3a,b, to make the Debye temperature non-linear at large volumes, showing increasingly strong positive deviations from linearity at higher temperatures, see Figure 3c. The origin of this “upturn” of Debye temperature at large volumes is due to a competition of magnetic entropy and energy contributions: The entropy gain is overwhelmed by the high energy cost of increasing an already large paramagnetic moment.

This interplay of magnetic contributions has important consequences for the equilibrium volume and other thermal propertied of fcc Fe. As Figure 3b shows, the minimum of partial free energy occurs at a much lower $R_{\mathrm{WS}}$ value of about 2.62 bohr, to be compared to about 2.70 corresponding to the Helmholtz free energy minimum in Figure 3d at 1250 K. As the Figure also shows, the initially very rapid thermal expansion slows down at high temperature (anti-invar effect).

Another well-known example of strong temperature effect is the case of β-Ti, which is mechanically unstable in the bcc structure at low temperature but is stabilized at elevated temperatures due to a complex interplay of electronic and vibrational (both harmonic and anharmonic) contributions [12,45,46,47]. Although it is clear that the present quasi-harmonic treatment of lattice vibrations is insufficient in such a complex case, it is instructive to analyze it to see the capabilities and the limits of our methodology.

The instability of facilitates itself in the negative values of tetragonal shear constant $C^{\prime }$, that makes both Debye temperature and vibrational free energy ill-defined (imaginary) at large volumes and low temperatures. However, electronic temperature tends to remove this instability by changing the slope of the partial free energy as a function of tetragonal distortion, Figure 4a so that at 1500 K the $C^{\prime }$ attains a positive value, making the Debye temperature and Helmholtz free energy of β-Ti real-valued. They are shown as full lines in Figure 4c,d. It is noteworthy that, in the present model, this stabilization (i.e., removal of an electronic instability) is caused solely by the Fermi smearing of electron state occupancy. In reality, there is another strong contribution to the stabilization, coming from anharmonicity (namely, changes in the electron structure caused by large amplitudes of random atomic displacements from the ideal bcc lattice sites) [10,11,12,13,14,45,46,47]. An extension of the CPA methodology can take this effect into account [48], but has yet to be implemented on the basis of EMTO method.

Despite the limitations of quasi-harmonic Debye model in the present formulation, it is able to describe the thermal stabilization of the bcc crystal structure of β-Ti and even to closely reproduce the large value of its lattice parameter measured at high temperature [49]: the free energy minimum in Figure 4d occurs at $R_{\mathrm{WS}}\cong 3.08$ bohr, which corresponds to a lattice parameter of 3.31 Å. This observation shows that the present modeling methodology, in the present or extended [48] form, may be very useful in studies of the alloy phases that exhibit a lattice instability in a certain domain of temperature and composition. However, we leave this interesting subject for future studies.

In the rest of this paper, let us consider elemental metals that are stable in a cubic crystal structure, fcc (Cu, Ni, and γ-Fe) and bcc (Cr, Mo, W). These elements are relevant to many technological applications and exhibit a variety of thermal properties, such as thermal expansion and temperature-dependent elastic moduli, for which experimental data are available.

3. Results

In this section we benchmark the present modeling approach by comparing its results for the selected fcc and bcc metals with experimental data on their respective equilibrium lattice parameter, thermal expansion coefficient, and elastic constants. When comparing the theory and experiment, one should keep in mind that more approximations underlie the theoretical results than those involved in the present formulation of quasi-harmonic Debye model. Such approximations as the GGA may be the main cause for the discrepancy with experiment in some cases [50]. Additionally, in some cases the scatter of experimental data is too large to make a quantitative comparison, so it is important to analyze qualitative trends, as well.

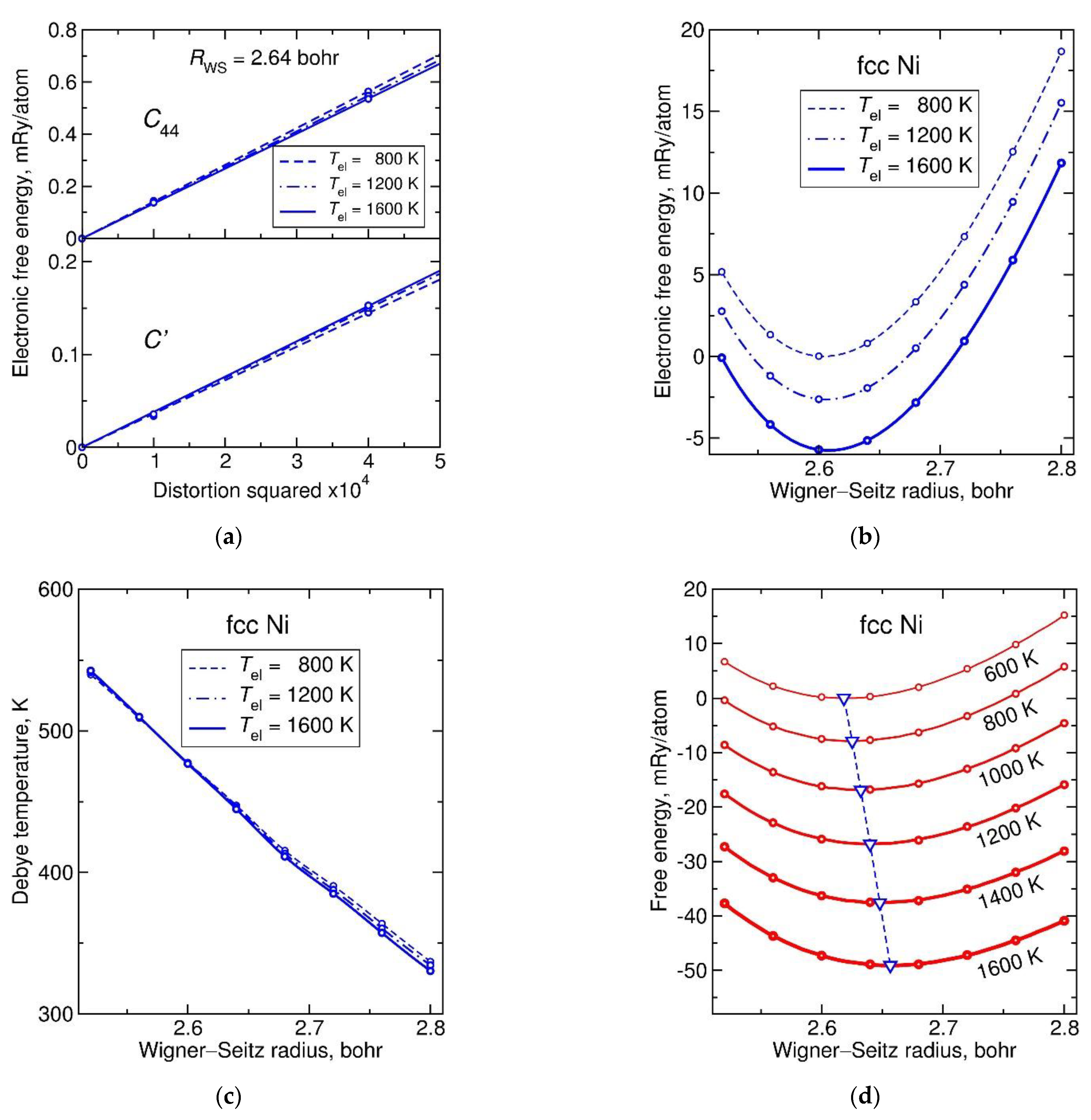
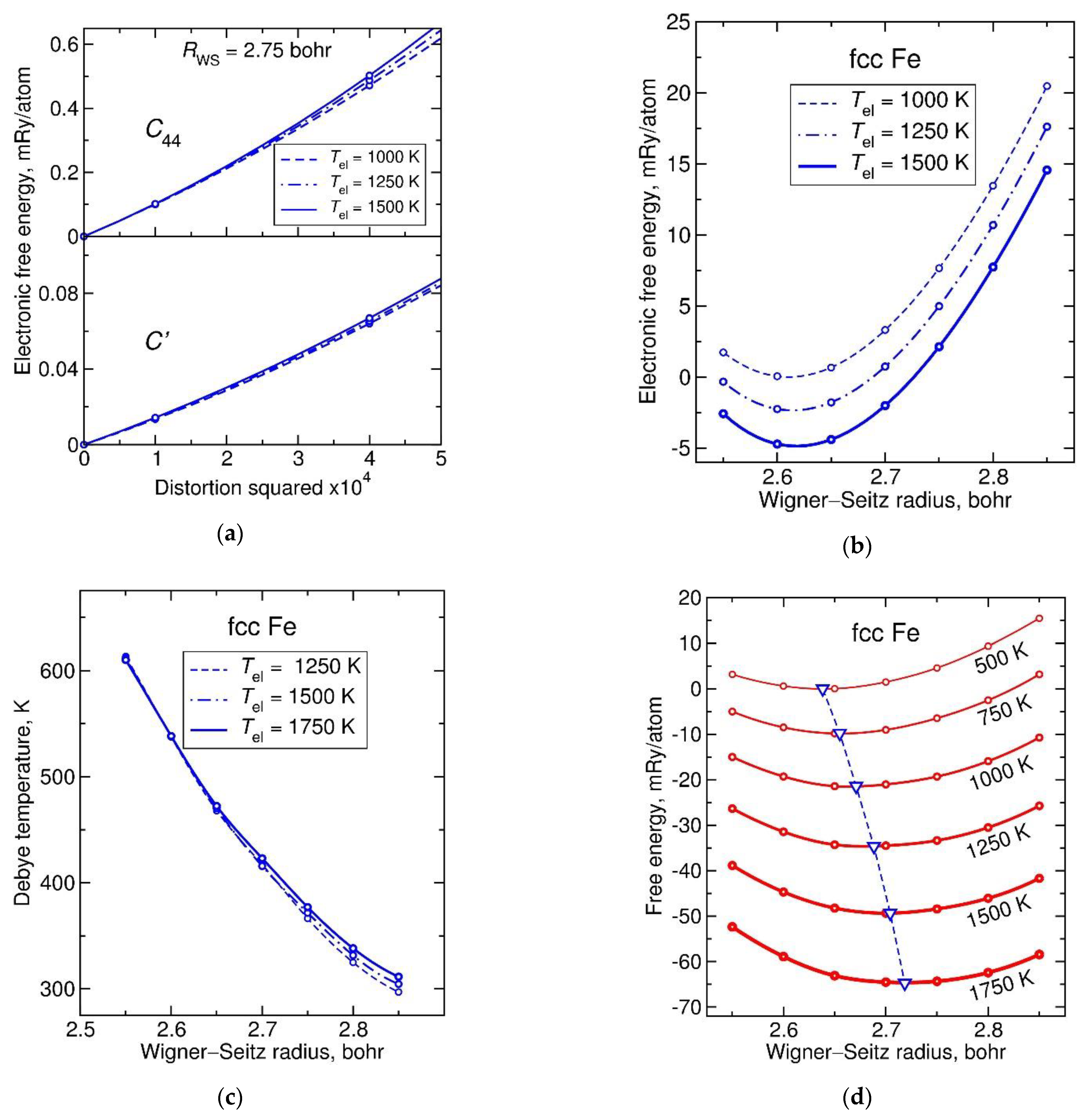
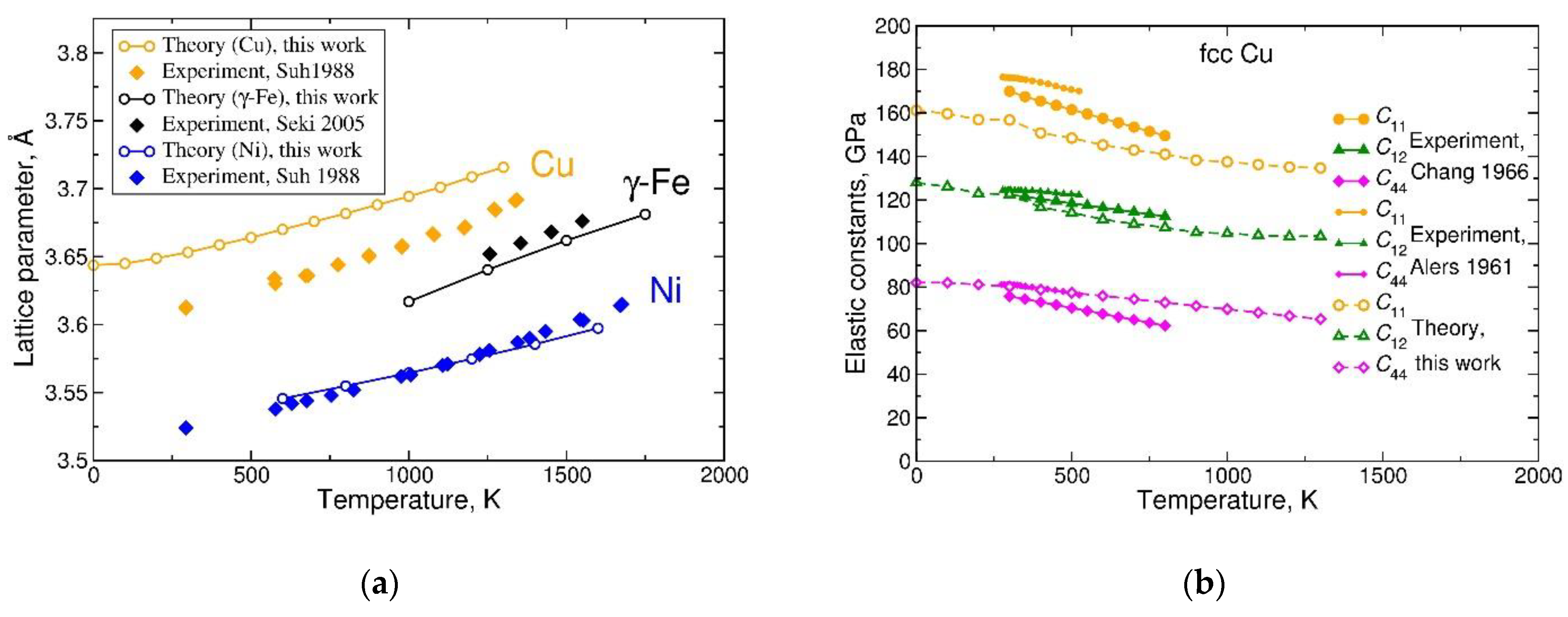
3.1. Face-Centered Cubic Metals

We begin our analysis with the three fcc metals of the 3d series, of which Cu and Ni exist as fcc in the whole temperature range below the melting temperature, while γ-Fe is a medium-temperature crystalline phase sandwiched between two bcc phases, α- and δ-Fe. As Figure 2a,b and Figure 3a,b show, the fcc crystal structure of Ni and Fe is mechanically stable when these metals are treated as disordered-local-moment paramagnets. To describe Pauli-paramagnetic state of fcc Cu, standard non-spin-polarized calculations are sufficient. In the GGA approximation, they reproduce the mechanical stability of the fcc crystal structure, Figure 1a,b, but slightly overestimate its equilibrium lattice parameter [50], see Figure 5a. The calculated lattice parameters of Ni and γ-Fe presented in Figure 5a are much closer to the experimental data points, as compared to the case of Cu. The slopes of temperature dependence for the lattice parameters of Cu, Ni, and γ-Fe are qualitatively reproduced by the model; a more quantitative comparison will be made below.

The GGA-calculated elastic constants of Cu metal are compared with two sets of experimental data in Figure 5b. The tendency of elastic constants to decrease with increasing temperature is reproduced well by the calculations, but the $C_{11}$ and $C_{12}$ values, as well as the value of bulk modulus $B_T=\left(C_{11}+2C_{12}\right)/3$, are underestimated compared to experiment, which is a consequence of the overestimated lattice parameter $a_T$ of Cu by the GGA [50], see Figure 5a.

Our calculations for other metals, summarized in

Table 1. Calculated lattice parameters and bulk moduli of selected cubic metals at elevated temperatures, in comparison with experimental data. “Electronic” $a_{\mathrm{el}}$ and $B_{\mathrm{el}}$ are determined, respectively, from the minimum and the curvature of the partial free energy curve as in Figure 1b. Equilibrium $a_T$ and $B_T$ are calculated from the minimum and the curvature of the Helmholtz free energy curve corresponding to temperature T, see Figure 1d for example.

Metal	T, K	Lattice Parameter, Å			Bulk Modulus, GPa
		${\mathit{a}}_{\mathbf{e}\mathbf{l}}$	${\mathit{a}}_{\mathit{T}}$	${\mathit{a}}_{\mathbf{e}\mathbf{x}\mathbf{p}}{ }^1$	${\mathit{B}}_{\mathbf{e}\mathbf{l}}$	${\mathit{B}}_{\mathit{T}}$	${\mathit{B}}_{\mathbf{e}\mathbf{x}\mathbf{p}}{ }^1$
Cu	800	3.638	3.682	3.646	140.0	118.0	124.8
% error, Reference		−0.2	+1.0	[51]	+12.2	−5.4	[53]
Ni	800	3.526	3.555	3.550	194.1	174.4	171.0
% error, Reference		−0.7	+0.1	[51]	+13.5	+2.0	[55]
γ-Fe	1250	3.540	3.640	3.652	136.7	103.1	102.7
% error, Reference		−3.0	−0.3	[52]	+33.1	+0.4	[56]
β-Ti	1250	3.27	3.32	3.31	106.2	90.9	87.7
% error, Reference		−1.3	+0.3	[49]	+21.0	+3.6	[57]
Cr	1000	2.851	2.871	2.901	249.7	229.6	190
% error, Reference		−1.7	−1.0	[58]	+31.4	+20.8	[59]
Mo	1000	3.164	3.181	3.159	249.1	231.5	247.5
% error, Reference		+0.2	+0.7	[60]	+0.6	−6.5	[61]
W	1000	3.192	3.206	3.175	294.2	275.9	298.3
% error, Reference		+0.5	+1.0	[62]	+12.2	−5.4	[63]

¹ Experimental data have been interpolated or extrapolated to the given temperature.

, show a clear anti-correlation tendency between the errors in theoretical estimates of the lattice parameter and bulk modulus: if the lattice parameter $a_T$ is overestimated by the GGA, then the bulk modulus $B_T$ is underestimated (as in the cases of Cu, Mo, and W) and vice versa (as in the case of Cr). It is remarkable that for the two other fcc metals studied, Ni and γ-Fe, our calculations yield very close estimates of their lattice parameters and bulk moduli.

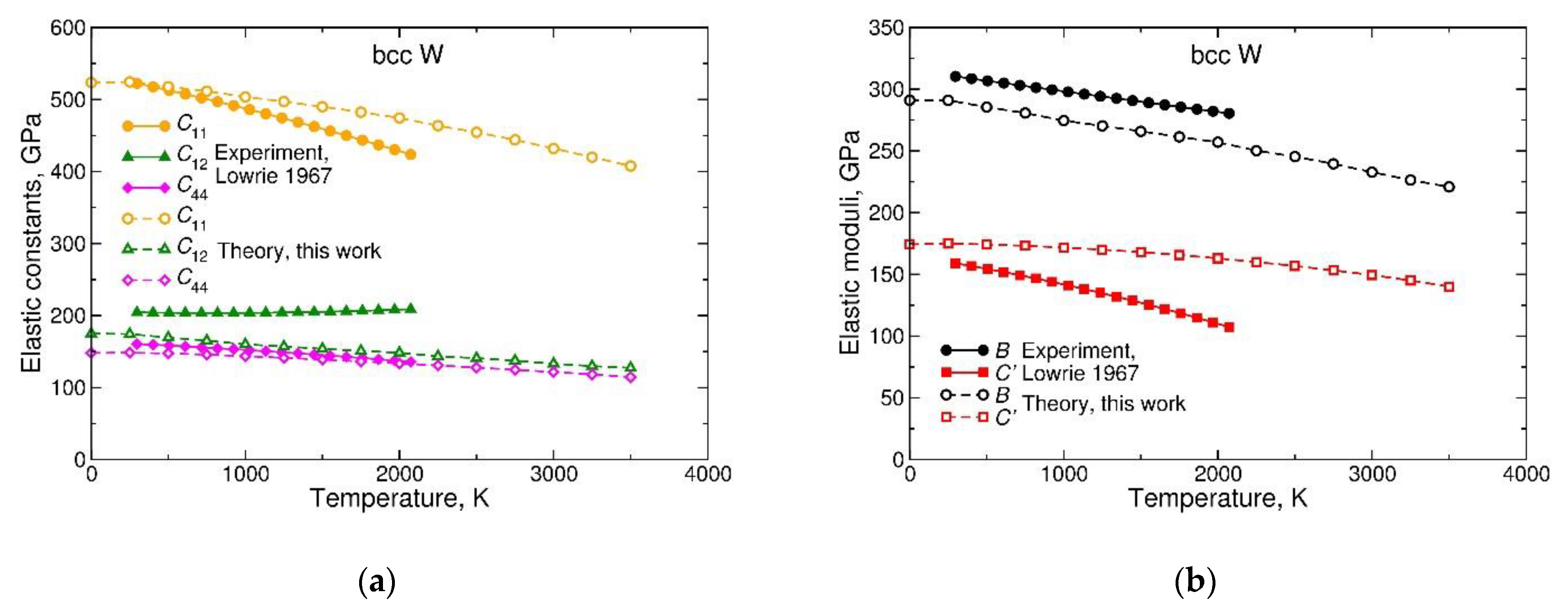
3.2. Body-Centered Cubic Metals

Of the studied bcc metals, β-Ti represents a special case as its cubic crystal structure is temperature-stabilized due to electronic and vibrational effects. Since the anharmonic vibrational effects are not fully incorporated into the present model, it predicts the bcc structure to become fully stable at too high temperature of about 1500 K, see Figure 4d.

However, Table 1 shows that the quasi-harmonic Debye model predicts the lattice parameter and the bulk modulus of β-Ti quite accurately. It also shows that the vibrational contributions to these properties are essential because the estimates based on partial “electronic” free energies, $a_{\mathrm{el}}$ and $B_{\mathrm{el}}$, are too far from the experimental data, deviating by −1.3% and +21.0%, respectively. The lattice parameters of Mo and W metals are overestimated in the GGA, which is expectable [31,50]. An overestimation of $a_T$ by 1% corresponds to a 3% error in the unit cell volume and in a bulk modulus that is smaller by about 6% in comparison with experiment.

However, in the case of Cr, the theory fails in a very different way. First of all, the lattice parameter is quite strongly underestimated, see Table 1. Although the inclusion of vibrational effects brings the calculated values of lattice parameter and bulk modulus at 1000 K closer to the experimental values, still the errors are quite large.

Secondly, one can try to cancel out some of the systematic errors by calculating the linear thermal expansion coefficient, defined relative to the calculated room-temperature lattice parameter $a_0$ as $\alpha =a_0^{-1}\Delta (d{a}_T/dT$). As Figure 6 shows [51,52,58,62,64,65,66], for most of the studied metals, one finds the calculated TEC values (open circles) are in reasonable agreement with experimental data (lines representing the original or new fits through the data points). The calculated values are systematically below the measured values; the difference between them increases with temperature. This is consistent with the fact that some anharmonic contributions are missing in the present model, they become more important at temperatures approaching the melting point. Exceptions are paramagnetic metals γ-Fe and bcc Cr. The present model predicts the high value of TEC of γ-Fe correctly, but fails to accurately describe its temperature (in)dependence [67]. For Cr, the model seems to work well below about 1000 K, but at higher temperatures, where an accelerated thermal expansion of Cr begins, the theory fails to predict the strongly increased TEC values.

The case of β-Ti is not considered here because it is clearly beyond the capability of the present model. However, the model is capable of describing the differences in TEC between the other considered elements, at temperatures that are not too high, predicting their values to decrease along the sequence Fe, Cu, Ni, Cr, Mo, W. The case of Cr at T > 1000 K deserves a special consideration.

4. Discussion

The ability to model thermodynamic properties of materials, as a function of temperature and composition, is in the core of materials design [21]. Approaches starting from first-principles calculations of material’s electronic structure make the modeling truly predictive, but they become computationally very expensive when taking into account various kinds of temperature-induced disorder. Therefore, simple and capable models such as the Debye model are of practical interest, especially for extending the modeling to complex multicomponent alloys [17,68,69,70].

The Debye model is fully set up by specifying the Debye temperature, treated as a volume-dependent parameter in the quasi-harmonic approximation is. Some previous formulations of quasi-harmonic Debye model describe the volume dependence in terms of another parameter called Grüneisen constant [1,71]. Both parameters are determined from the DFT-calculated equation of state for the solid considered under hydrostatic pressure conditions (corresponding to a uniform volume distortion in the case of a cubic crystal). This “isotropic” parameterization is known to overestimate the Grüneisen constant and predict a too strong temperature dependence of the properties [8].

In the present formulation of QDM, the volume dependence of Debye temperature is not parameterized, but is evaluated [27] from the whole set of anisotropic elastic constants calculated as a function of volume and temperature. Its results for selected fcc and bcc metals, summarized in Table 1 and Figure 5 and Figure 6, demonstrates that QDM can adequately describe the temperature-dependent properties of these industrial-relevant metals. The accuracy, in the present formulation, is limited mainly by the other approximations involved, such as the GGA or CPA, as well as by the neglect of higher-order anharmonic effects in the electronic structure caused by the large amplitude of atomic displacements at high temperatures.

For 3d transition metals with the fcc structure, Cu, Ni, and γ-Fe, the quasi-harmonic Debye model gives reasonably accurate descriptions of the effect of temperature on the equilibrium lattice parameter and elastic properties, see also References [26,44]. Also, the fact that the present modeling is based on the EMTO-CPA electronic structure method makes it easily extendable to random alloys in the high-temperature paramagnetic state, such as austenitic steels [70].

This work and some previous applications of the present model have established certain limits of its applicability. Thus, in the important case of Fe, the model fails to describe the α → γ and γ → δ phase transitions, yielding the Helmholtz free energy of paramagnetic bcc Fe always lower than that of fcc Fe [44]. In view of the small energy free difference between these two structures in the temperature range of thermodynamic stability of γ-Fe, this failure is not surprising. The case of Cr is more alarming, because nearly all properties that one derives from the modeled free energy deviate quite strongly from the experimental values, especially at high temperatures. These discrepancies obtained for bcc Fe and Cr may be traced back to the (quasi)harmonic approximations used in the description of their vibrational and magnetic degrees of freedom.

One of these harmonic approximations deals with paramagnetism of γ-Fe and Cr at high temperatures. The dependence of energy on the absolute magnitude of the paramagnetic moment is approximated (locally) by a parabola, to simplify the theoretical treatment of longitudinal fluctuations of the disordered local moments. It seems that this approximation becomes too crude at high temperatures, especially in the case of Cr. Moreover, a strong coupling of magnetic and vibrational degrees of freedom may be responsible for the anomalous thermal expansion of Cr at high temperatures [72], but this complex anharmonic effect is not captured by the present quasi-harmonic model.

In this connection, the limited success of QDM in describing the high-temperature properties of β-Ti looks quite unexpected, but may be related to the fact that here, in contrast to Fe and Cr, one does not have the complications due to magnetism. However, the neglect of higher-order anharmonic effects does not permit for a quantitative description of temperature-induced stabilization of β-Ti.

To illustrate and additionally emphasize the importance of the neglected anharmonic effects, in Figure 7 we plot, as functions of temperature, the calculated and experimental elastic properties of bcc W. Figure 7a shows a good agreement between the calculated and measured elastic constants at room temperature. With increasing temperature, softening of $C_{44}$ takes place, and this effect is well reproduced by the quasi-harmonic theory. However, $C_{11}$ softens much faster in experiment than in theory, while the experimentally derived $C_{12}$ grows with temperature, in striking contrast with calculations. The anomalous softening of $C_{11}$ and “hardening” of $C_{12}$ are related to each other. Figure 7b shows that, when these two elastic constants are combined as $(C_{11}+2C_{12})/3$ into the bulk modulus, the anomaly disappears: the temperature dependence of $B_T$ is accurately reproduced by the QDM. On the contrary, when the two constants are combined to form $C^{\prime }=(C_{11}-C_{12})/2$, the anomaly is enhanced. In fact, the very rapid softening of the tetragonal shear modulus $C$’ with temperature is the origin of the anomalous temperature dependencies of both $C_{11}$ and $C_{12}$.

The shear distortion corresponding to $C$’ is also related to Bain’s path connecting the bcc and fcc structures. Therefore, the softening of $C$’ may be indicative of changes in the relative stability of the two structures. These changes, in turn, are due to anharmonic effects of the same kind as those involved in the stabilization of β-Ti. This chain of reasoning allows us to link the discrepancies between the calculated and experimental temperature dependencies of elastic properties of W (and, possibly, of other bcc metals) with anharmonic vibrational effects in the electronic structure and in the lattice stability.

In view of the discussed advantages and shortcomings of the present QDM implementation, the following extensions of the model seem to be necessary. In its present form, the QDM in conjunction with EMTO-CPA calculations can be applied to model the free energy and derived properties of substitutional alloys such as Ni-based alloys or austenitic steels based on γ-Fe at temperatures not too close to the melting point. To achieve quantitatively accurate descriptions of Cu-based alloys, one has to use an exchange-correlation functional that performs for this metal better than the PBE [50]. For all the considered metals, the quality of finite-temperature modeling will greatly improve by extending the model beyond the quasi-harmonic approximations for magnetic and vibrational degrees of freedom. CPA-based approaches using alloy analogy [48] provide a possible way of including longitudinal spin fluctuations and random atomic displacement directly into the electronic structure calculations.

5. Conclusions

We have tested the performance of a new implementation of the quasi-harmonic Debye model on selected cubic metals of technological importance. The Debye model is parameterized using the full set of elastic constants calculated from first principles as functions of volume and temperature. The first-principles calculations self-consistently take into account the thermal disorder associated with “fast” (electronic and magnetic) degrees of freedom in the solid, while considering ions as static (the vibrational free energy contributions in the Debye model are added to the electronic free energy in a post-processing).

In this formulation, the model has the following advantages:

(1)

The present modeling approach is faster than existing quasi-harmonic approaches that rely on full phonon spectrum calculations, molecular dynamics, or spin-lattice dynamics simulations.

(2)

It is more accurate than the previous Debye model implementations, as it does not involve a Grüneisen parameter. Instead, the full volume dependence (and also the temperature dependence) of the Debye temperature is evaluated.

(3)

The temperature dependence of the model parameter (Debye temperature) allows one to treat high-temperature phases such as γ-Fe and β-Ti.

(4)

It yields the Helmholtz free energy in a numerical or semi-analytic form that is easy use for the evaluation of thermodynamic properties that are high-order derivatives of the free energy.

(5)

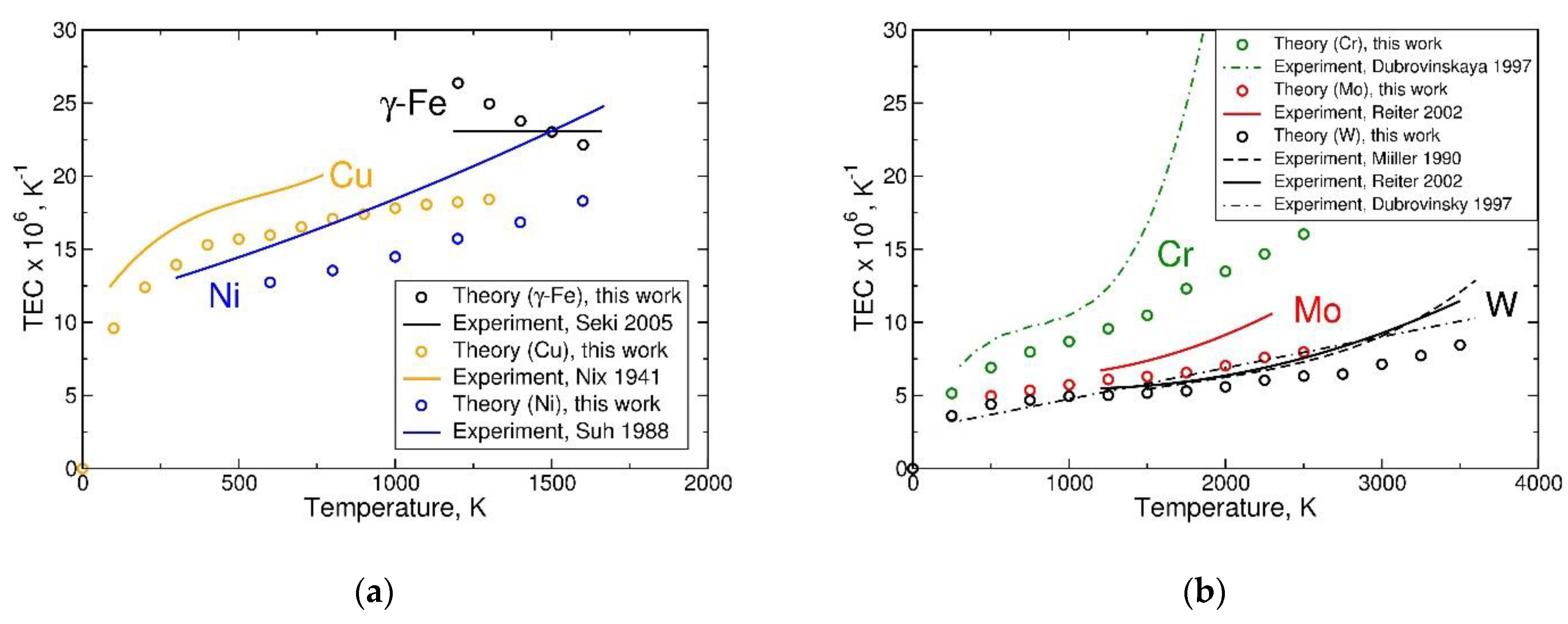
At temperatures far below the melting point, the model yields lattice parameters, elastic moduli, and thermal expansion coefficients of the studied metals in good agreement with experiment (the agreement is limited mainly by the approximate exchange-correlation functional used in the electronic structure calculations).

(6)

Thanks to the coherent potential approximation used in the electronic structure calculations, the model is naturally applicable to random alloys or disordered alloy phases (including cases of magnetic disorder).

As a result of our analysis, the following limitations of the present modeling approach have been identified:

(1)

The present modeling, already at the stage of electronic structure calculations, inaccurately reproduces the low-temperature equilibrium lattice parameter of non-magnetic Cu, Cr, Mo, and W metals. Although the errors are of the order of 1%, they cause further errors in the elastic constant and Debye temperature calculations, thereby limiting the accuracy of free-energy modeling.

(2)

The model falls short in describing the explosive thermal expansion of Cr metal at high-temperatures (above 1000 K), which identifies the need to extend the presently used model of paramagnetic state beyond the quasi-harmonic approximation.

(3)

For the considered bcc metals, the quasi-harmonic treatment of vibrational free energy is clearly insufficient for describing the temperature dependence of their thermodynamic properties such as elastic constants and thermal expansion coefficients at high temperatures.

However, the present model may be systematically improved by including random atomic displacements and magnetic moment fluctuations directly into the electronic structure calculations, to go beyond the quasi-harmonic approximations. This task is to be undertaken in our future studies.