1. Introduction
Selective Laser Melting (SLM) 3D-printing as a technology of rapid fabrication of net shape or near-net shape metal parts for various applications has matured in last 20 years and reached the stage of readiness for mass-production. In this context, issues of quality stability and service life management have become the principal focus of further development. This is especially important for 3D-printable Ti, Ni, and Al alloys that have recently began to see increasing use in the aerospace domain [
1,
2,
3]. Fatigue fracture tolerance is known to be sensitive to microstructure variability and tensile residual stress (RS) that persist after various fabrication operations [
4]. Gas turbine engine components made of Ti and Ni are susceptible to fatigue linked to flight-related thermal and mechanical cyclic loading, and to the higher frequency loading related to turbine rotation and blade vibration [
5]. To pave the way for widespread adoption, 3D-printed parts made from these alloys must be carefully assessed in terms of fatigue durability with the same rigor as traditional materials [
6].
SLM 3D-printable Al-Si-Mg alloy has been recently utilized for the fabrication of thermoregulation casing of a gamma-ray detectors used in satellite applications [
7]. Heating-cooling cycles are typical for many outer-space structures and devices forming parts of satellite equipment that alternatively pass lit and shadowed zones. These thermal excursions cause cycles of expansion and contraction that may promote fatigue cracking in 3D-printed parts, especially when tensile residual stress (RS) is inherited after fabrication. Relaxation annealing or surface modification (shot peening or laser shock peening) are traditional approaches to controlling the residual stresses. Both techniques have some drawbacks: annealing may cause intolerable distortions that require subsequent machining that brings additional costs and new residual stresses in the surface layers, while surface modification may increase roughness and give rise to significant residual stresses in the non-treated core regions.
Repeated localized laser melting that leads to the fusion of metal powder particles followed by cooling are the fundamental physical mechanisms involved in SLM 3D-printing. The complexity of the thermal history of a certain material volume becomes apparent if many important phenomena are considered, e.g., the completeness of homogenization in the liquid phase, phase separation for alloys with a solid solution phase and the associated liquation and localized oversaturation of solid solutions, grain nucleation and growth from overcooled liquids. shrinkage at solidification, aging of solid solutions, and many others. High-temperature gradients and steep cooling rates during building provoke diverse structure formation and variation processes that ultimately give rise to non-uniform plastic deformation and the associated permanent inelastic strains (eigenstrains) that act as the origins of residual stresses [
8].
The amount of literature and accompanying technical information devoted to additive manufacturing at large and laser printing with metals is vast and difficult to cover within a specific research paper (not a review article). Rational studies devoted to this topic seek to distil the key underlying relationships between processing conditions and sample shapes, with different degrees of success, e.g., [
9,
10,
11,
12,
13] The present authors have made a number of contributions to this effort [
9,
10,
11,
12,
13] that address different aspects of AM productivity, dependence on printing sequence and orientation, analysis of the microstructure, etc. The present study represents another step towards improving the reliability of analysis and interpretation.
The quantitative evaluation of residual stresses in SLM 3D-printed metallic materials has come into the focus of research interest since the first decade of the 21st century [
14], which paved the way for new techniques based on X-ray scattering and various sectioning-based methods at the macro- to micro- to nano-scales. Currently, dozens of publications on this subject are published annually, including highly cited comprehensive overviews [
15]. Steels of the stainless and maraging varieties, Ti-6Al-4V, and Ni alloys (Inconels and Invars) are leading in terms of the number of publications devoted to residual stresses in SLM 3D-printed metals. Nevertheless, a significant number of reports [
16,
17,
18,
19,
20,
21,
22,
23,
24,
25] have been published recently aiming to elucidate different aspects of residual stresses in SLM-printable Al-Si-Mg alloys.
To the best of the authors’ knowledge, the first article on residual stresses in a SLM 3D-printed aluminum alloy (AlSi10Mg) [
16] was published in 2018, reporting the use of the X-ray diffraction method for experimental measurements. Tensile and compressive stresses as high as 100 MPa were found in 3D-printed thin (
= 1.2 mm) sheet parts of complex curveted shape. Generally speaking, laboratory X-ray diffraction remains the dominant method for experimental evaluation of residual stresses due to its non-destructive nature, in spite of the numerous known disadvantages such as the shallow region of interaction and large lateral averaging area. Other non-destructive (e.g., precise external shape measurements by means of contact and contactless scanning) and destructive techniques (such as hole drilling) have been applied and reported. The interpreting and modeling of residual stresses commonly require various computational data processing approaches and computer simulations.
The FIB-DIC micro-ring-core drilling method is the extension of the hole drilling method towards the microscopic dimensional scale. The method has been a developing project since the middle of 2000s [
26]. At present, this method gives unprecedented opportunities to correlate structural peculiarities and residual stresses and is clearly relevant for 3D-printed materials. The FIB-DIC micro-ring-core drilling method requires the use of relatively complex dual FIB-SEM microscopes and skilled operators, but the robustness of the measurements has already reached the pre-standardization stage [
27]. There are very few reports of using the FIB ring-core drilling method to measure residual stresses in SLM 3D-printed materials [
22] and no reports on SLM 3D-printed Al-alloys were found in the literature to date. One of the reasons is believed to be the scale factor; the correspondence of the drilled ring diameter and average grain size is very important for the FIB ring-core drilling method. In order to probe Type I stresses (equivalent to engineering scale residual stresses), the diameter of a ring must be set to several grain sizes, a condition that is hard to satisfy with the most popular Ga FIB-SEM microscopes for large and medium-size grains (20 μm and bigger) in materials such as Al-Si-Mg printable alloys.
Most recent published reports devoted to residual stresses in SLM 3D-printed Al-Si-Mg alloy components consider geometries that are either over-simplified (rectangular blocks) or overly complex, i.e., containing multiple features that are difficult to parameterize and draw firm conclusions from. In the present study, a simple “double tower” sample geometry was chosen that consists of a larger and a smaller block, representing a change in the horizontal cross-section causing a modification of the heat flow and introducing the possibility of local (residual) stress concentration.
Furthermore, previous studies have typically employed conventional experimental characterization techniques based on X-ray diffraction, the contour method, and mechanical blind hole drilling. These approaches have limitations in terms of achievable spatial resolution and their applicability to samples of complex shape. This is particularly worth emphasizing considering that the ease and economic viability of fabricating complicated shapes constitute a principal motivation for the use of 3D-printing.
The “double tower” prismatic sample shape is a good example of an “incremental” approach in the expansion of knowledge. This shape represents a step forward from a simple 3D prismatic element towards parts containing abrupt reductions of sample cross-section. Protruding shapes are commonly used in engineering design, especially in casings, guides and fitting parts, or actuators, making such objects relevant to practical engineering use.
The present authors recently studied the peculiarities of grain structure and mechanical performance of 3D-printed RS-333 Al-alloy parts [
28,
29] and considered the possible influence of the residual stresses on the variation of mechanical response. In the present article, we report a systematic comparative study of under-surface residual stresses in 3D-printed RS-300 series (AlSi10Mg) alloy samples using a number of macroscopic destructive techniques such as the contour method, hole drilling coupled with laser speckle interferometry, and microscopic Xe-ion pFIB-DIC ring-core drilling. Conventional X-ray diffraction (
) measurements were also carried out to complete the multi-technique characterization study. This approach was purposefully and systematically implemented to highlight the fundamental hierarchical character of RS at scaling dimensional levels with the Xe-FIB-DIC microscopic method to investigate the details, which were not captured with methods at the macroscopic level. To the best of authors’ knowledge, this approach has not been systematically applied to the majority of SLM 3D-printed metals and especially not to Al alloys, where RS are relatively small.
It has been experimentally found that the high levels of tensile and compressive residual stresses inherited after SLM 3D–printing vary in the range from 40 to 200 MPa (i.e., up to the yield stress) and remain unrelaxed for at least 6 months. All evaluation techniques return comparable estimates of residual stress values, in spite of the dramatically different dimensional scales, from millimeters for the contour method and laser speckle interferometry down to 70 µm for Xe pFIB-DIC ring-core drilling. In the concluding part of the manuscript, the authors address the subject of how the tuning of printing parameters may offer an approach to rational residual stress management to enhance both mechanical performance and service lifetime.
4. Conclusions
The residual stresses formed during additive manufacturing are dependent on the model geometry even under nominally identical 3D-printing conditions, albeit in indirect ways associated with the change of cross-section, the presence of supports, and the filling ratio, which strongly affect the thermal flux conditions and thermo-mechanical gradients. We believe that the conception of uneven cooling rates as a principal cause of RS is generally applicable for arbitrary shapes and models. Specific local values of RS may vary significantly depending on the sample geometry and printing conditions, which may be large enough to cause cracking.
The rational design of SLM 3D-printed parts is of great importance and must not be limited to geometry optimization. In the ultimate perspective, the design of a SLM 3D-printed part integrates geometrical modeling, thermo-mechanical numerical simulation, molding conditions, etc. The 3D mapping of RS must hold an important role in rational design for robustness and reliability.
As pointed out in the body of the article, the authors chose a particular geometry that combines simplicity with key features related to RS generation in 3D printing, but the path is open towards the consideration of a much wider range of sample shapes in connection with numerical process modeling, in order to extract key processing–structure–property relationships.
The systematic comparative study undertaken in this research provides evidence that multi-scale, multi-modal evaluation of RS supported by robust computer modeling delivers reliable mapping of RS distributions at a desirable spatial resolution and satisfactory precision. This approach can be readily expanded to arbitrary shapes and real engineering parts, e.g., elements of aerospace components, thereby forming a solid basis for future investigations.
The paper appears to be the first to report the results of multi-scale and multi-modal RS evaluation using several independent methods ranging from non-destructive XRD analysis to macroscopic sectioning to micro-scale ring-core FIB milling with digital image correlation analysis. The comparative study showed good agreement across dimensional scales from tens of micrometers to tens of millimeters. The plasma Xe-FIB-DIC method was used to obtain evaluations within material volumes of the order of 100 µm across. Significant tensile RS of up to +200 MPa was identified at the top of the upper tower, whilst moderate RS present in the lower block was compressive in all directions (hydrostatic) in the middle and tensile at the surface. The relationship between the cooling rate during 3D-printing, on the one hand, and the RS that persist in the sample as a consequence was put forward and justified.
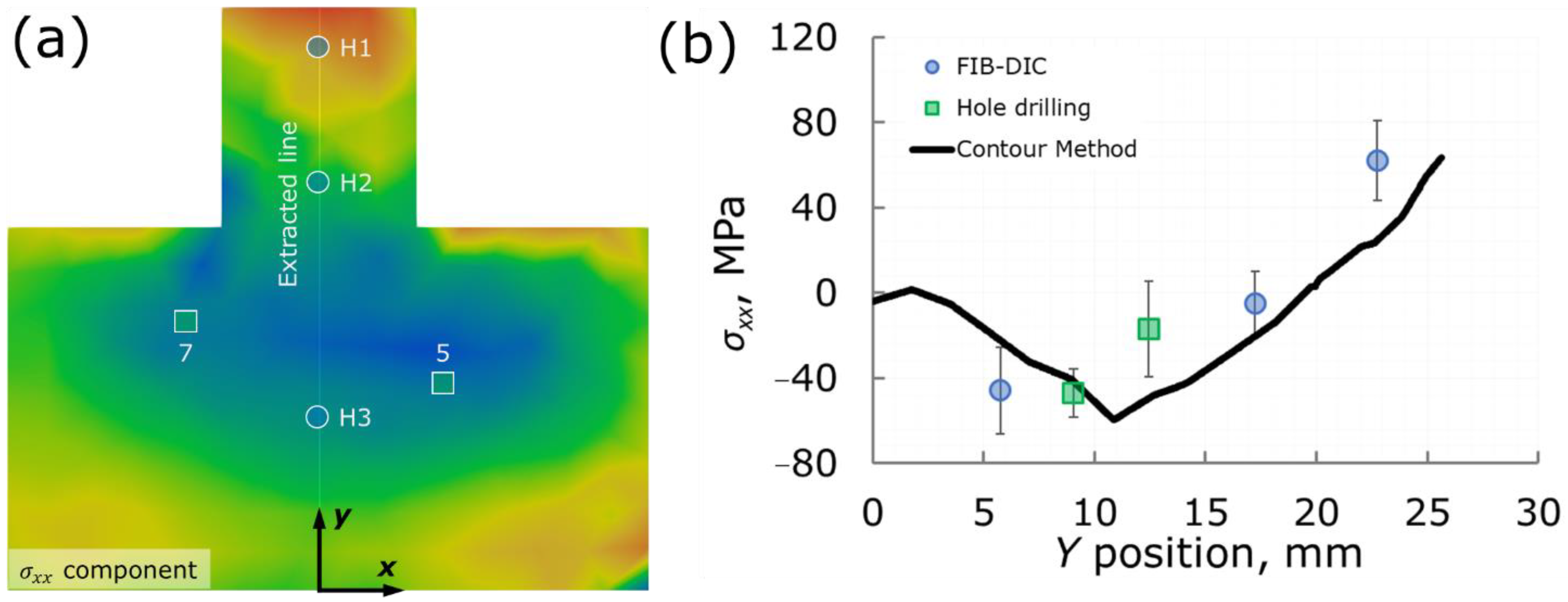
Figure 13 shows a comparison plot of all used methods. The results show that the calculations of the contour method solution provide a good match with FIB-DIC and hole drilling evaluations of the
xx-component of residual stress, but the quantity and quality of experimental measurements should be increased in order to state that all direct components of residual stress can be calculated reliably using the present approach.
The present paper opens up new avenues toward further systematic studies of RS in 3D-printed parts and components. In particular, the paper established clear ways to distinguish and evaluate Type I, II, and III residual stresses, and identified the approaches most suitable, in the authors’ opinion, for experimental assessment of the dependence of these parameters on the fabrication and processing conditions.
To sum up, residual stresses in SLM 3D-printed metal parts appearing as a result of complex thermal history are frequently discussed in respect to many aspects of their mechanical performance and operation service life. Although recovery annealing or various surface treatments (sand blasting, shot peening, etc.) are readily applicable, the efficiency of these measures can hardly be assessed without relevant and robust techniques for routine experimental measurements. The popular X-ray diffraction method, especially in a laboratory, has a number of disadvantages, with shallow probing and averaging over large lighted areas being the most obvious of them.
Today, a growing number of experimental investigations are still based on X-ray diffraction measurements, which deprives researchers of much valuable information. SLM 3D-printable Al-Si-Mg alloys seem to the least studied in comparison with printable steels and Ti and Ni alloys.
We deliberately undertook comparative residual stress evaluation using methods of contour measurements, mechanical drilling with speckle-pattern interferometry, X-ray diffraction, and Xe-pFIB ring-core drilling with DIC analysis. These destructive and non-destructive methods have spatial resolutions ranging from tens of millimeters for contour measurements to units of millimeters for speckle-pattern interferometry, and finally, down to 70 micrometers for Xe-pFIB ring-core drilling. All methods returned estimations of residual stresses in good agreement in terms of signs and values regardless of dramatically different spatial resolution.
The surface of SLM 3D-printed parts are residually extended, with stresses having values equal to and exceeding yield strength at the locations where the fastest cooling takes place: protrusions, slim cross-sections, and supports. The middle parts of large cross-sections are residually compressed (perhaps hydrostatically), with relatively weak stresses of about from ¼ to ⅓ of yield strength.
We believe that these findings rationally explain the anisotropy of mechanical responses for the parts printed with different orientations in respect to fast scanning and growth direction.
Author Contributions
A.M.K., A.I.S., V.S.P. and D.K.R.; methodology, E.S.S., Y.V.K., S.A.L., S.I.E., A.G.S., Y.V.M. and P.A.S.; software, E.S.S., F.U. and S.I.E.; validation, E.S.S. and F.U.; formal analysis, A.I.S. and E.S.S.; investigation, E.S.S., S.A.L. and F.U.; resources, A.I.S., E.S.S., F.U. and A.M.K.; data curation, E.S.S. and Y.V.K.; writing—original draft preparation, A.I.S. and E.S.S.; writing—review and editing, A.M.K.; visualization, E.S.S.; supervision, project administration, funding acquisition, A.I.S. and A.M.K. All authors have read and agreed to the published version of the manuscript.
Data Availability Statement
The data are available from the corresponding authors upon request.
Acknowledgments
This research was funded by the Russian Science Foundation, grant number 21-19-00791,
https://rscf.ru/en/project/21-19-00791/. The authors are grateful to the crew of the Fablab (Skoltech, Moscow, Russia) for their delicate and accurate sample preparations, and to Andrey Dyakov from CDMM (Skoltech, Moscow, Russia), who facilitated optical 3D scanning.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Barriobero-Vila, P.; Gussone, J.; Stark, A.; Schell, N.; Haubrich, J.; Requena, G. Peritectic Titanium Alloys for 3D Printing. Nat. Commun. 2018, 9, 3426. [Google Scholar] [CrossRef] [PubMed]
- Aboulkhair, N.T.; Simonelli, M.; Parry, L.; Ashcroft, I.; Tuck, C.; Hague, R. 3D Printing of Aluminium Alloys: Additive Manufacturing of Aluminium Alloys using Selective Laser Melting. Prog. Mater. Sci. 2019, 106, 100578. [Google Scholar] [CrossRef]
- Liu, Z.; He, B.; Lyu, T.; Zou, Y. A Review on Additive Manufacturing of Titanium Alloys for Aerospace Applications: Directed Energy Deposition and Beyond Ti-6Al-4V. JOM 2021, 73, 1804–1818. [Google Scholar] [CrossRef]
- Webster, G.A.; Ezeilo, A.N. Residual Stress Distributions and Their Influence on Fatigue Lifetimes. Int. J. Fatigue 2001, 23, 375–383. [Google Scholar] [CrossRef]
- Carter, T.J. Common Failures in Gas Turbine Blades. Eng. Fail. Anal. 2005, 12, 237–247. [Google Scholar] [CrossRef]
- Zerbst, U.; Bruno, G.; Buffiere, J.-Y.; Wegener, T.; Niendorf, T.; Wu, T.; Zhang, X.; Kashaev, N.; Meneghetti, G.; Hrabe, N.; et al. Damage Tolerant Design of Additively Manufactured Metallic Components Subjected to Cyclic Loading: State of the Art and Challenges. Prog. Mater. Sci. 2021, 121, 100786. [Google Scholar] [CrossRef] [PubMed]
- Song, X.; Zhai, W.; Huang, R.; Fu, J. Metal-Based 3D-Printed Micro Parts & Structures. In Reference Module in Materials Science and Materials Engineering; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Korsunsky, A.M.; Regino, G.M.; Nowell, D. Variational Eigenstrain Analysis of Residual Stresses in a Welded Plate. Int. J. Solids Struct. 2007, 44, 4574–4591. [Google Scholar] [CrossRef]
- Gibbons, D.W.; Serfontein, J.P.L.; van der Merwe, A.F. Mapping the path to certification of metal laser powder bed fusion for aerospace applications. Rapid Prototyp. J. 2021, 27, 355–361. [Google Scholar] [CrossRef]
- Mezghani, A.; Nassar, A.R.; Dickman, C.J.; Valdes, E.; Alvarado, R. Laser powder bed fusion additive manufacturing of copper wicking structures: Fabrication and capillary characterization. Rapid Prototyp. J. 2021, 27, 1181–1188. [Google Scholar] [CrossRef]
- Li, L.; Pan, T.; Zhang, X.; Chen, Y.; Cui, W.; Yan, L.; Liou, F. Deformations and stresses prediction of cantilever structures fabricated by selective laser melting process. Rapid Prototyp. J. 2021, 27, 453–464. [Google Scholar] [CrossRef]
- Zhang, B.; Han, X.; Chen, C.; Zhang, W.; Liao, H.; Chen, B. Effect of the strut size and tilt angle on the geometric characteristics of selective laser melting AlSi10Mg. Rapid Prototyp. J. 2021, 27, 879–889. [Google Scholar] [CrossRef]
- Guan, J.; Wang, Q.; Chen, C.; Xiao, J. Forming feasibility and interface microstructure of Al/Cu bimetallic structure fabricated by laser powder bed fusion. Rapid Prototyp. J. 2021, 27, 1337–1345. [Google Scholar] [CrossRef]
- Casavola, C.; Pappalettere, C.; Tursi, F. Residual Stress on AISI 300 Sintered Materials. In Experimental and Applied Mechanics; Conference Proceedings of the Society for Experimental Mechanics Series; Springer: New York, NY, USA, 2011; Volume 6, pp. 201–208. [Google Scholar]
- Bartlett, J.L.; Li, X. An Overview of Residual Stresses in Metal Powder Bed Fusion. Addit. Manuf. 2019, 27, 131–149. [Google Scholar] [CrossRef]
- Lopez, C.; Elias-Zuniga, A.; Jimenez, I.; Martinez-Romero, O.; Siller, H.R.; Diabb, J.M. Experimental Determination of Residual Stresses Generated by Single Point Incremental Forming of AlSi10Mg Sheets Produced using SLM Additive Manufacturing Process. Materials 2018, 11, 2542. [Google Scholar] [CrossRef]
- Karolus, M.; Maszybrocka, J.; Stwora, A.; Skrabalak, G. Residual Stresses of AlSi10Mg Fabricated by Selective Laser Melting. Arch. Metall. Mater. 2019, 64, 1011–1016. [Google Scholar]
- Colombo, C.; Biffi, C.A.; Fiocchi, J.; Tuissi, A.; Vergani, L.M. Effect of Optimized Heat Treatments on the Tensile Behavior and Residual Stresses of Selective Laser Melted AlSi10Mg Samples. Key Eng. Mater. 2019, 813, 364–369. [Google Scholar] [CrossRef]
- Xing, X.; Duan, X.; Sun, X.; Gong, H.; Wang, L.; Jiang, F. Modification of Residual Stresses in Laser Additive Manufactured AlSi10Mg Specimens using an Ultrasonic Peening Technique. Materials 2019, 12, 455. [Google Scholar] [CrossRef]
- Di Giovanni, M.T.; de Menezes, J.T.O.; Bolelli, G.; Cerri, E.; Castrodeza, E.M. Fatigue Crack Growth Behavior of a Selective Laser Melted AlSi10Mg. Eng. Fract. Mech. 2019, 217, 106564. [Google Scholar] [CrossRef]
- Mfusi, B.J.; Mathe, N.R.; Tshabalala, L.C.; Popoola, P.A.I. The Effect of Stress Relief on the Mechanical and Fatigue Properties of Additively Manufactured AlSi10Mg Parts. Metals 2019, 9, 1216. [Google Scholar] [CrossRef]
- Song, X.; Feih, S.; Zhai, W.; Sun, C.N.; Li, F.; Maiti, R.; Wei, J.; Yang, Y.; Oancea, V.; Romano Brandt, L.; et al. Advances in Additive Manufacturing Process Simulation: Residual Stresses and Distortion Predictions in Complex Metallic Components. Mater. Des. 2020, 193, 108779. [Google Scholar] [CrossRef]
- Beretta, S.; Gargourimotlagh, M.; Foletti, S.; du Plessis, A.; Riccio, M. Fatigue Strength Assessment of “as Built” AlSi10Mg Manufactured by SLM with Different Build Orientations. Int. J. Fatigue 2020, 139, 105737. [Google Scholar] [CrossRef]
- Amir, B.; Grinberg, E.; Gale, Y.; Sadot, O.; Samuha, S. Influences of Platform Heating and Post-processing Stress Relief Treatment on the Mechanical Properties and Microstructure of Selective-Laser-Melted AlSi10Mg Alloys. Mater. Sci. Eng. A 2021, 822, 141612. [Google Scholar] [CrossRef]
- Bhaduri, D.; Ghara, T.; Penchev, P.; Paul, S.; Pruncu, C.I.; Dimov, S.; Morgan, D. Pulsed Laser Polishing of Selective Laser Melted Aluminium Alloy Parts. Appl. Surf. Sci. 2021, 558, 149887. [Google Scholar] [CrossRef]
- Korsunsky, A.M.; Sebastiani, M.; Bemporad, E. Focused Ion Beam Ring Drilling for Residual Stress Evaluation. Mater. Lett. 2009, 63, 1961–1963. [Google Scholar] [CrossRef]
- Lord, J.; Cox, D.; Ratzke, A.; Sebastiani, M.; Korsunsky, A.; Mughal, M.; Salvati, E. A Good Practice Guide for Measuring Residual Stresses Using FIB-DIC; National Physical Laboratory: Teddington, UK, 2018. [Google Scholar]
- Statnik, E.S.; Nyaza, K.V.; Salimon, A.I.; Ryabov, D.; Korsunsky, A.M. In Situ SEM Study of the Micro-Mechanical Behaviour of 3D-Printed Aluminium Alloy. Technologies 2021, 9, 21. [Google Scholar] [CrossRef]
- Somov, P.A.; Statnik, E.S.; Malakhova, Y.V.; Nyaza, K.V.; Salimon, A.I.; Ryabov, D.K.; Korsunsky, A.M. On the Grain Microstructure-Mechanical Properties Relationships in Aluminium Alloy Parts Fabricated by Laser Powder Bed Fusion. Metals 2021, 11, 1175. [Google Scholar] [CrossRef]
- Uzun, F.; Korsunsky, A.M. On the Identification of Eigenstrain Sources of Welding Residual Stress in Bead-on-plate Inconel 740H Specimens. Int. J. Mech. Sci. 2018, 145, 231–245. [Google Scholar] [CrossRef]
- Kartal, M.E.; Kang, Y.H.; Korsunsky, A.M.; Cocks, A.C.F.F.; Bouchard, J.P. The Influence of Welding Procedure and Plate Geometry on Residual Stresses in Thick Components. Int. J. Solids Struct. 2016, 80, 420–429. [Google Scholar] [CrossRef]
- Sebastiani, M.; Sui, T.; Korsunsky, A.M. Residual Stress Evaluation at the Micro- and Nano-scale: Recent Advancements of Measurement Techniques, Validation through Modelling, and Future Challenges. Mater. Des. 2017, 118, 204–206. [Google Scholar] [CrossRef]
- Pisarev, V.S.; Odintsev, I.N.; Eleonsky, S.I.; Apalkov, A.A. Residual Stress Determination by Optical Interferometric Measurements of Hole Diameter Increments. Opt. Lasers Eng. 2018, 110, 437–456. [Google Scholar] [CrossRef]
- Everaerts, J.; Salvati, E.; Uzun, F.; Romano Brandt, L.; Zhang, H.; Korsunsky, A.M. Separating Macro-(Type I) and Micro-(Type II+III) Residual Stresses by Ring-Core FIB-DIC Milling and Eigenstrain Modelling of a Plastically Bent Titanium Alloy Bar. Acta Mater. 2018, 156, 43–51. [Google Scholar] [CrossRef]
- Winiarski, B.; Rue, C.; Withers, P.J. Plasma FIB Spin Milling for 3D Residual Stress Measurements. Microsc. Microanal. 2019, 25, 882–883. [Google Scholar] [CrossRef][Green Version]
- Senn, M. Digital Image Correlation and Tracking. In MATLAB Central File Exchange; 2021; Available online: https://www.mathworks.com/matlabcentral/fileexchange/50994-digital-image-correlation-and-tracking (accessed on 14 December 2021).
- Roy, M.J.; Stoyanov, N.; Moat, R.J.; Withers, P.J. pyCM: An Open-Source Computational Framework for Residual Stress Analysis Employing the Contour Method. SoftwareX 2020, 11, 100458. [Google Scholar] [CrossRef]
- Smith, M.; Levesque, J.B.; Bichler, L. Residual stress analysis in linear friction welded in-service Inconel 718 superalloy via neutron diffraction and contour method approaches. Mater. Sci. Eng. 2017, 691, 168–179. [Google Scholar] [CrossRef]
- Lunt, A.J.G.; Salvati, E.; Ma, L.; Dolbyna, I.P.; Neo, T.K.; Korsunsky, A.M. Full in-plane Strain Tensor Analysis using the Microscale Ring-Core FIB Milling and DIC Approach. J. Mech. Phys. Solids 2016, 94, 47–67. [Google Scholar] [CrossRef]
- Abboud, E.; Attia, H.; Shi, B.; Damir, A.; Thomson, V.; Mebrahtu, Y. Residual Stresses and Surface Integrity of Ti-alloys During Finish Turning—Guidelines for Compressive Residual Stresses. Procedia CIRP 2016, 45, 55–58. [Google Scholar] [CrossRef]
- Aboulkhair, N.T.; Maskery, I.; Tuck, C.; Ashcroft, I.; Everitt, N.M. The Microstructure and Mechanical Properties of Selectively Laser Melted AlSi10Mg: The Effect of a Conventional T6-like Heat Treatment. Mater. Sci. Eng. A 2016, 667, 139–146. [Google Scholar] [CrossRef]
- OpenCV Documentation. Inpainting. Available online: https://docs.opencv.org/4.x/d7/d8b/group__photo__inpaint.html (accessed on 14 December 2021).
- Telea, A. An image inpainting technique based on the fast marching method. J. Graph. Tools 2004, 9, 23–34. [Google Scholar] [CrossRef]
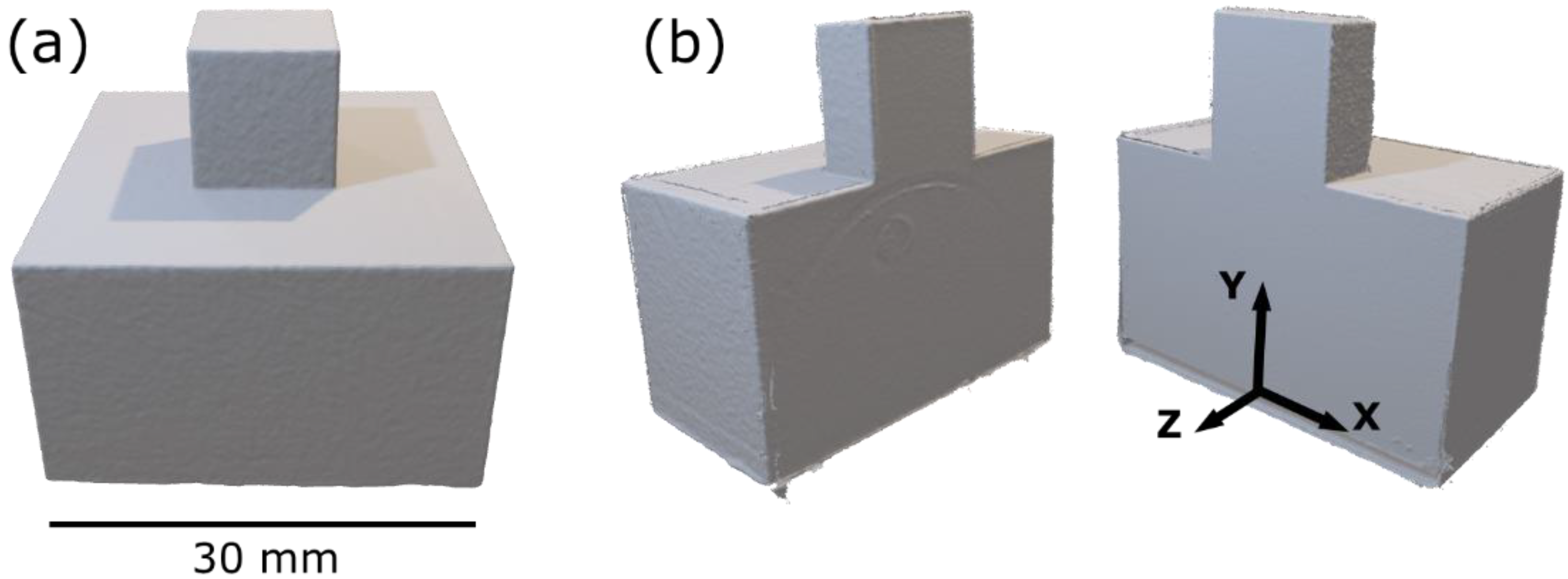
Figure 1.
The appearance of the double tower shape sample in the as-printed state: (a) front view, (b) side view, (c) dimensions.
Figure 2.
The appearance of the double tower sample (a) before and (b,c) after EDM cutting: (b) top view with the indicated cut plane (red line) and (c) sectional view.
Figure 3.
The appearance of double tower shaped sample as 3D models: (a) before and (b) after EDM cutting in half with the indicated primary coordinate system according to which all used methods are aligned.
Figure 4.
(a) general view of vertical outer face of the half-cut double tower perpendicular to the sectioning plane with the drill hole, and (b,c) interference fringe patterns obtained as a result of 1.9 mm diameter hole drilling: (b) the horizontal in-plane displacement component and (c) the vertical in-plane displacement component.
Figure 5.
Appearance of the polished half-cut double tower sample: (a) mounted in conductive resin for FIB-SEM studies, (b) fixed in the goniometer-like sample holder for X-ray diffraction measurements.
Figure 6.
Illustration of the distribution of the zz-component of residual stresses (a,c) and z-component of displacements (b,d) in the real (a,b) and continuously processed (c,d) geometry models, respectively.
Figure 7.
Illustration of distribution of xx- (a,c) and yy- (b,d) components of residual stresses in the real (a,b) and continuous (c,d) geometry models, respectively.
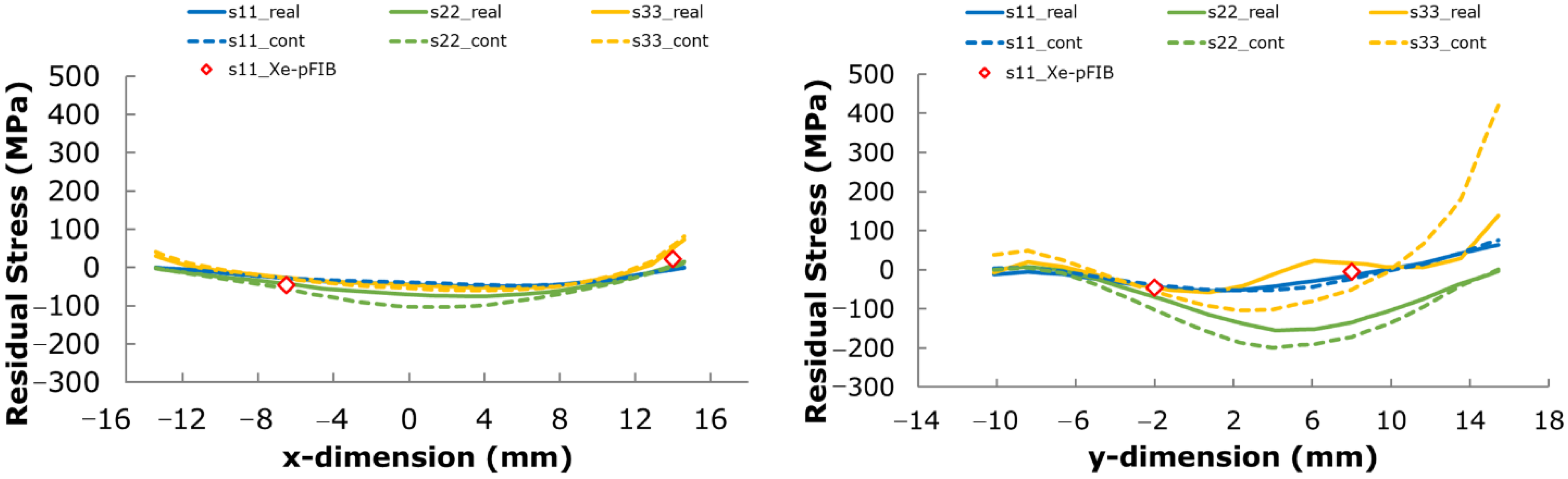
Figure 8.
Line plots of xx (s11), yy (s22), and zz (s33) components of residual stress along the (a) horizontal (x) and (b) vertical (y) lines illustrated by the dashed lines on the sectioned surface in Figure 12 below.
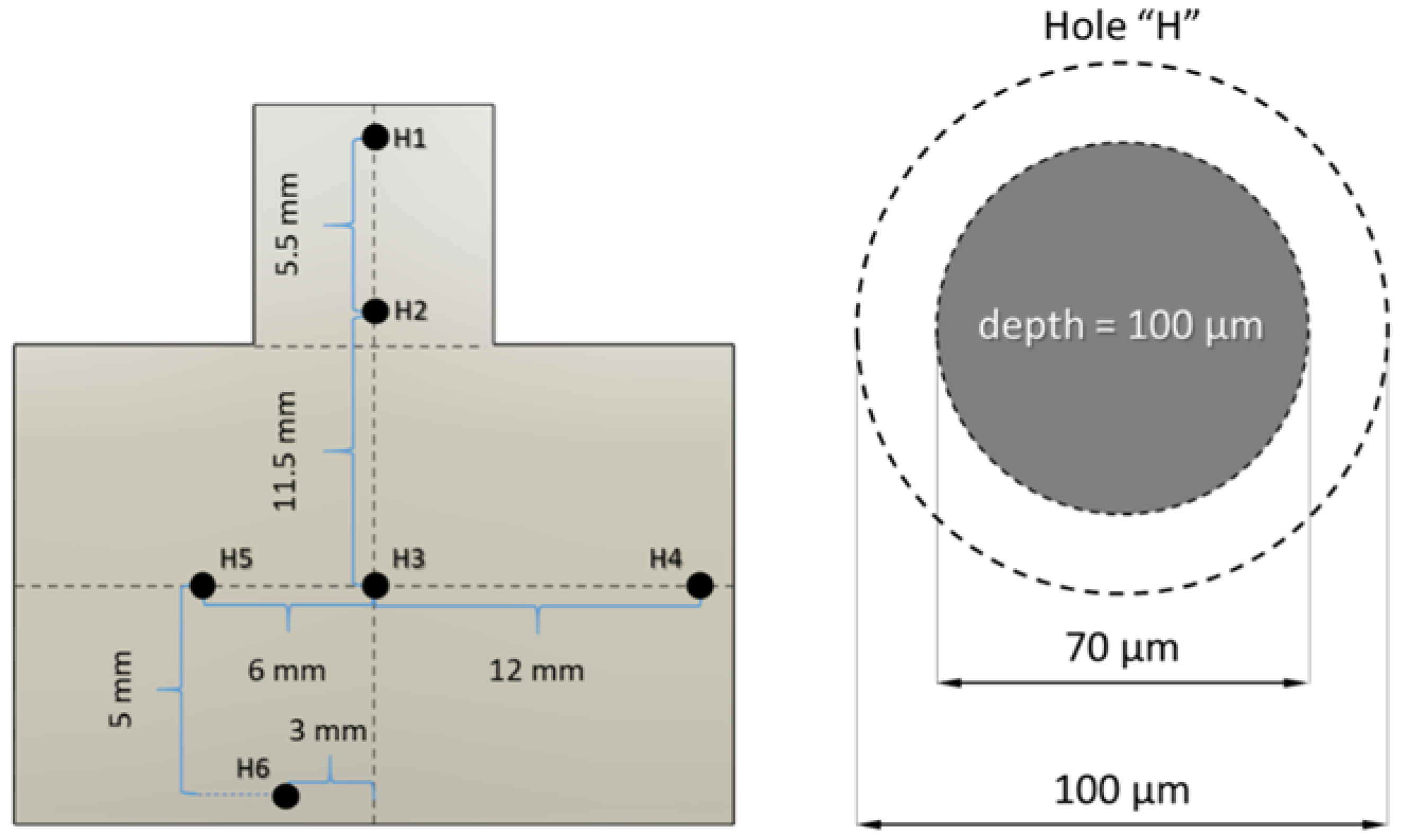
Figure 9.
Locations of holes for the hole drilling method with the indicated axis.
Figure 10.
Details of X-ray measurement of residual stresses at the cut plane: (a) measured plot for the specimen (highlighted red plane was selected for the next calculations); (b) plot.
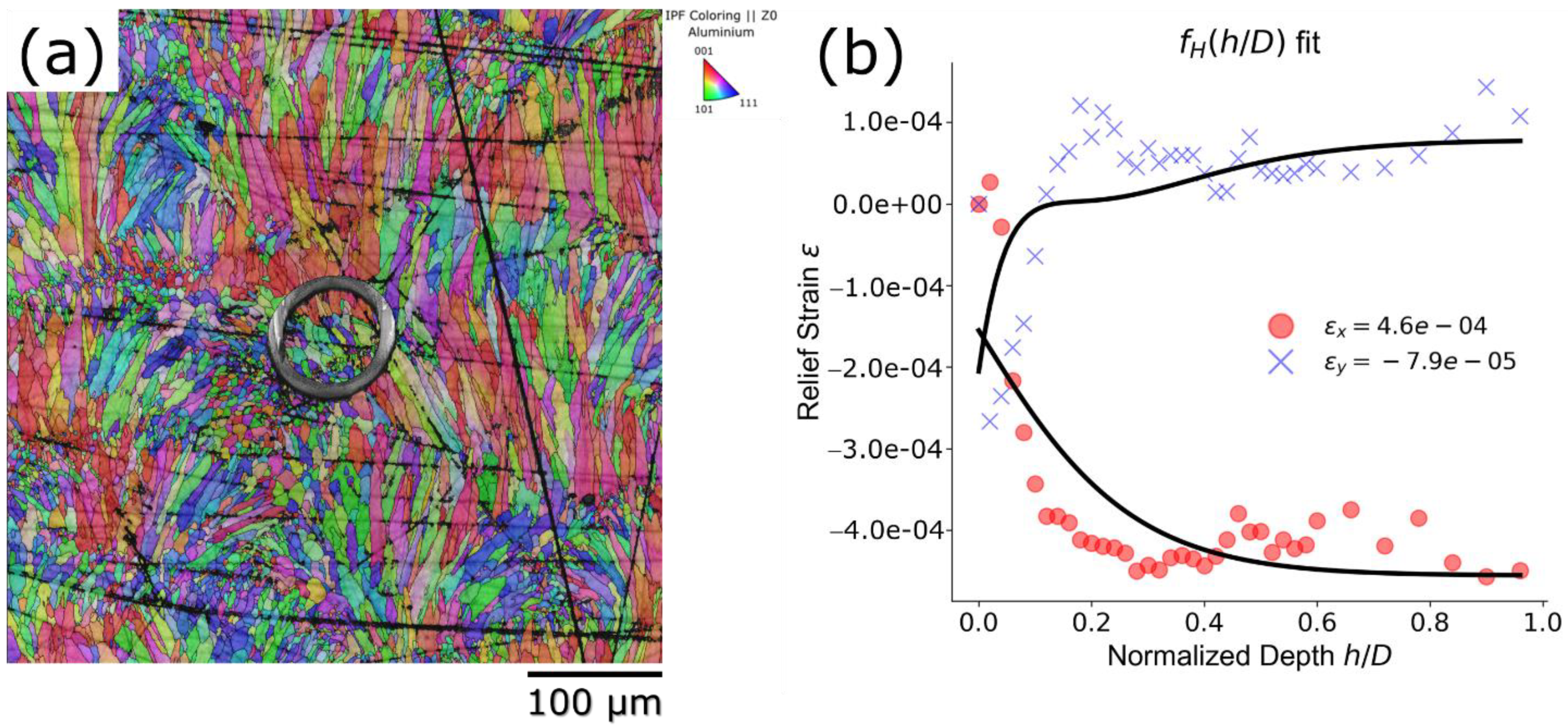
Figure 11.
Details of Xe-pFIB ring-core drilling measurements of residual stresses at the cut plane: (a) combined EBSD map with the Euler’ colors and milled ring, and (b) measured relief strains with the fitting curve.
Figure 12.
Mapping of residual stresses using Xe-pFIB ring-core drilling method.
Figure 13.
Comparison of all used methods: (a) the locations of the measured points and the plotting line, superimposed on the contour map of the horizontal stress component reconstructed by the contour method; (b) residual stress line plot.
Table 1.
Residual stresses at half-cut double tower sample faces.
| N | Description of Location | , MPa
|
|---|
| 1 | Vertical outer face parallel to the cut plane | ) |
| 2 | ) |
| 10 | ) |
| 3 | Vertical outer face perpendicular to the cut plane | ) |
| 5 | Cut plane | ) |
| 7 | ) |
| 9 | Bottom of the base | ) |
Table 2.
Residual stresses at faces and cut plane of half-cut double tower specimens.
| N | |
|---|
| H1 | 62.1 |
| H2 | −4.9 |
| H3 | −45.8 |
| H4 | 33.4 |
| H5 | 22.8 |
| H6 | −78.7 |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).