The Effect of Tin Content on the Strength of a Carbon Fiber/Al-Sn-Matrix Composite Wire
Abstract
1. Introduction
2. Selection of the Matrix Material
3. Materials and Methods
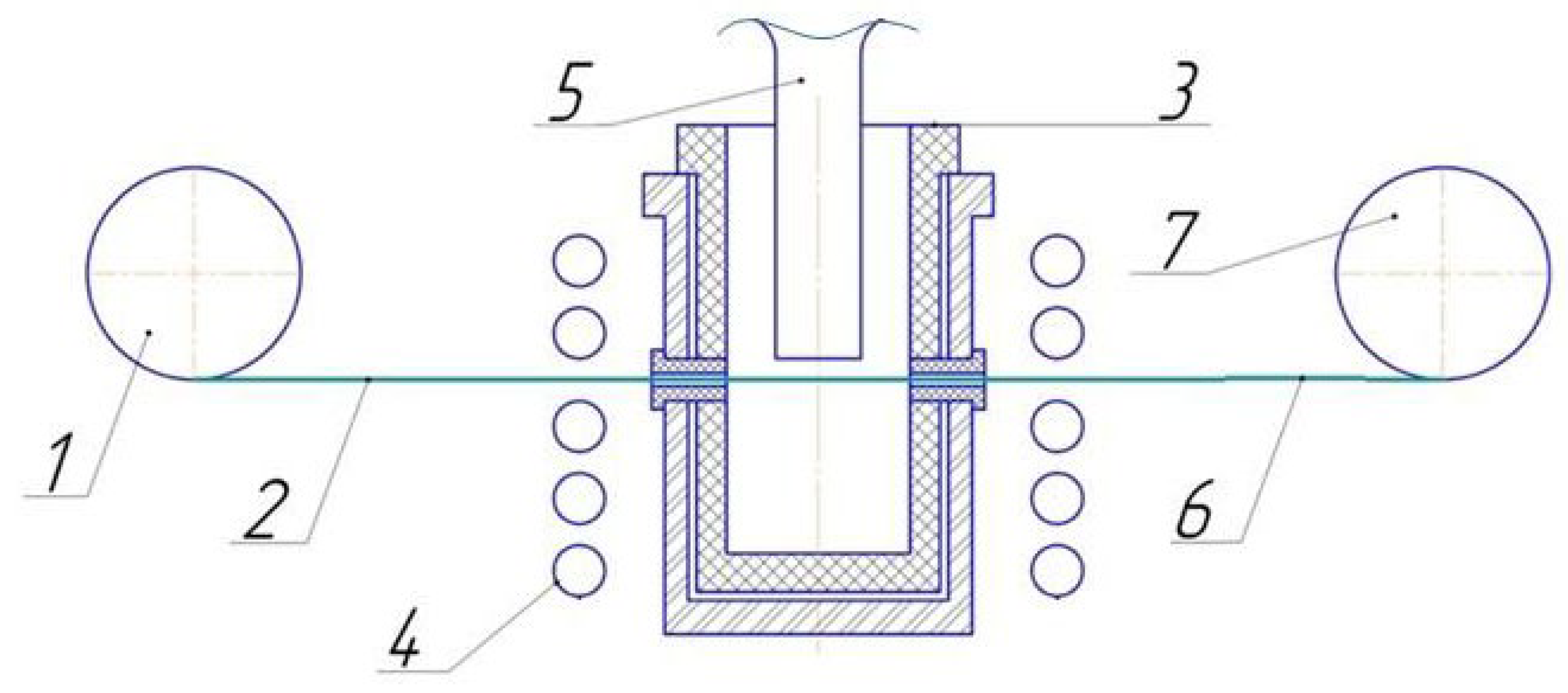
3.1. Composite Manufacturing
3.2. Characterization Methods
4. Results
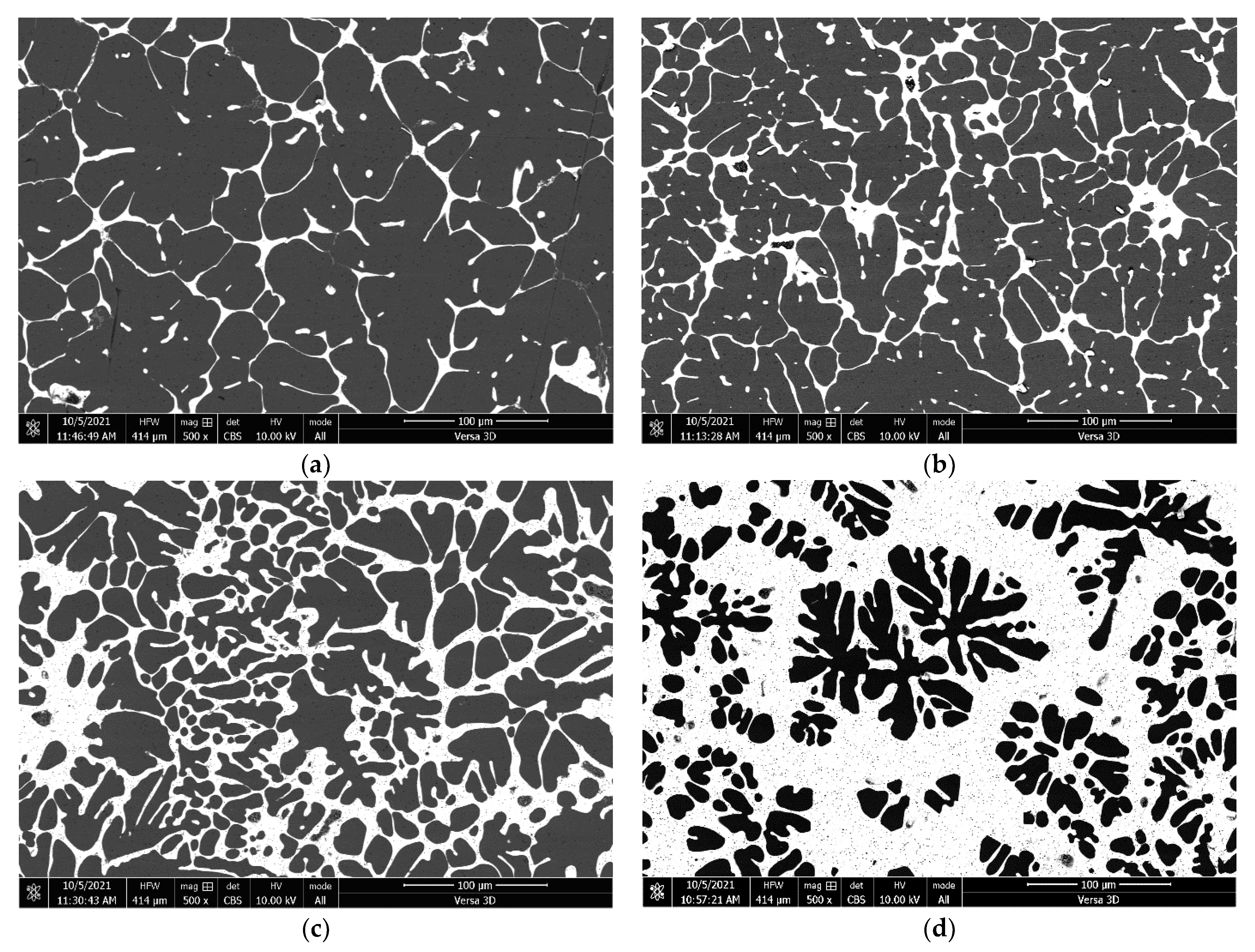
4.1. Microstructure of an Al-Sn Matrix Alloy
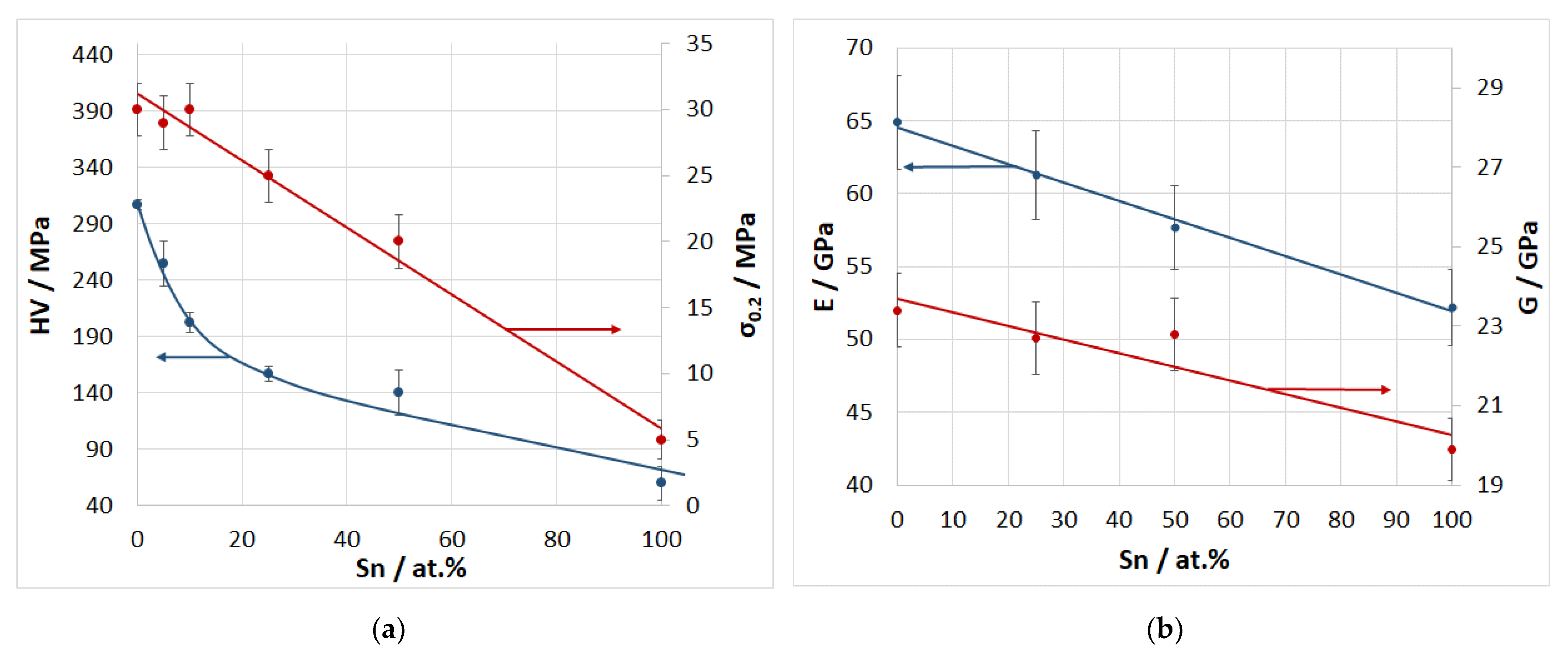
4.2. Conditional Yield Stress, Microhardness, Shear Modulus, and Young’s Modulus of the Matrix Alloy
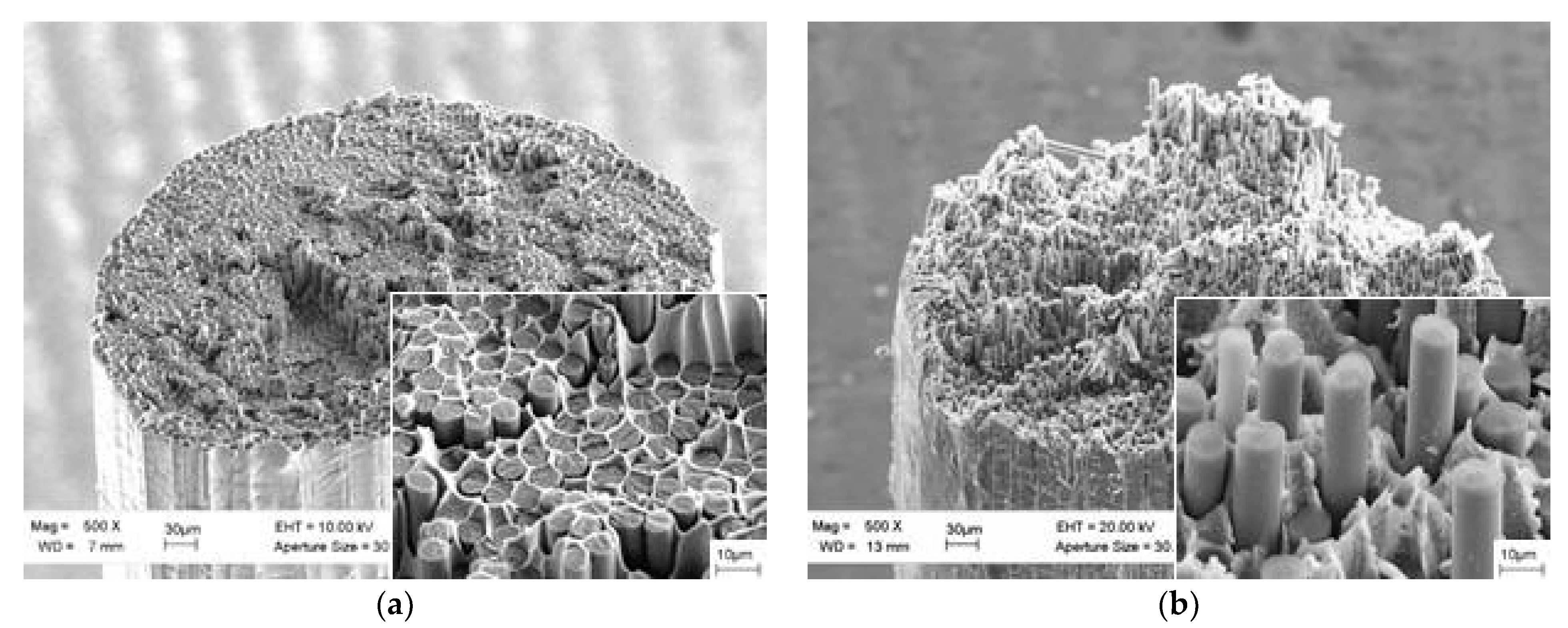
4.3. Fracture Surfaces of A CF/Al-Sn Wire
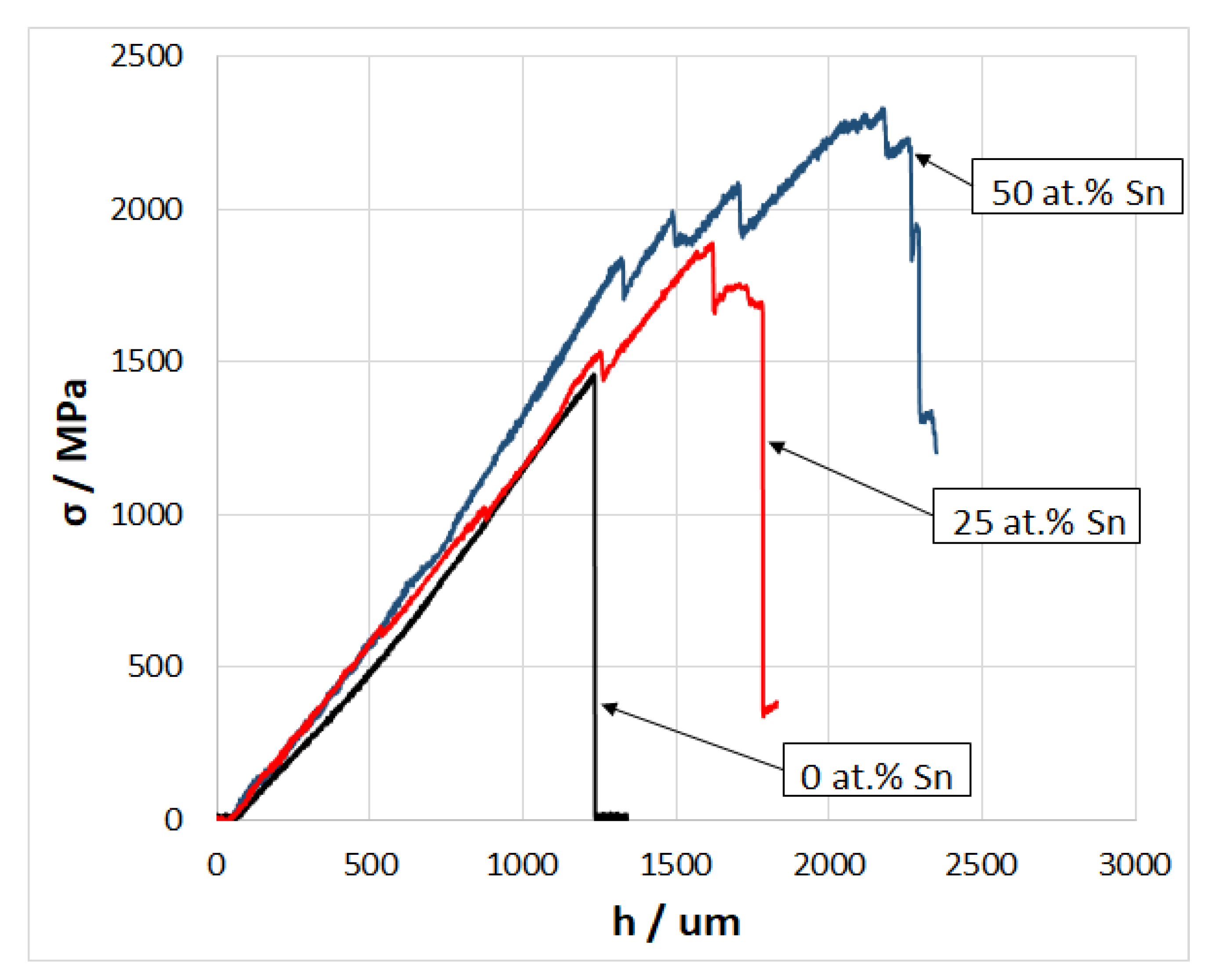
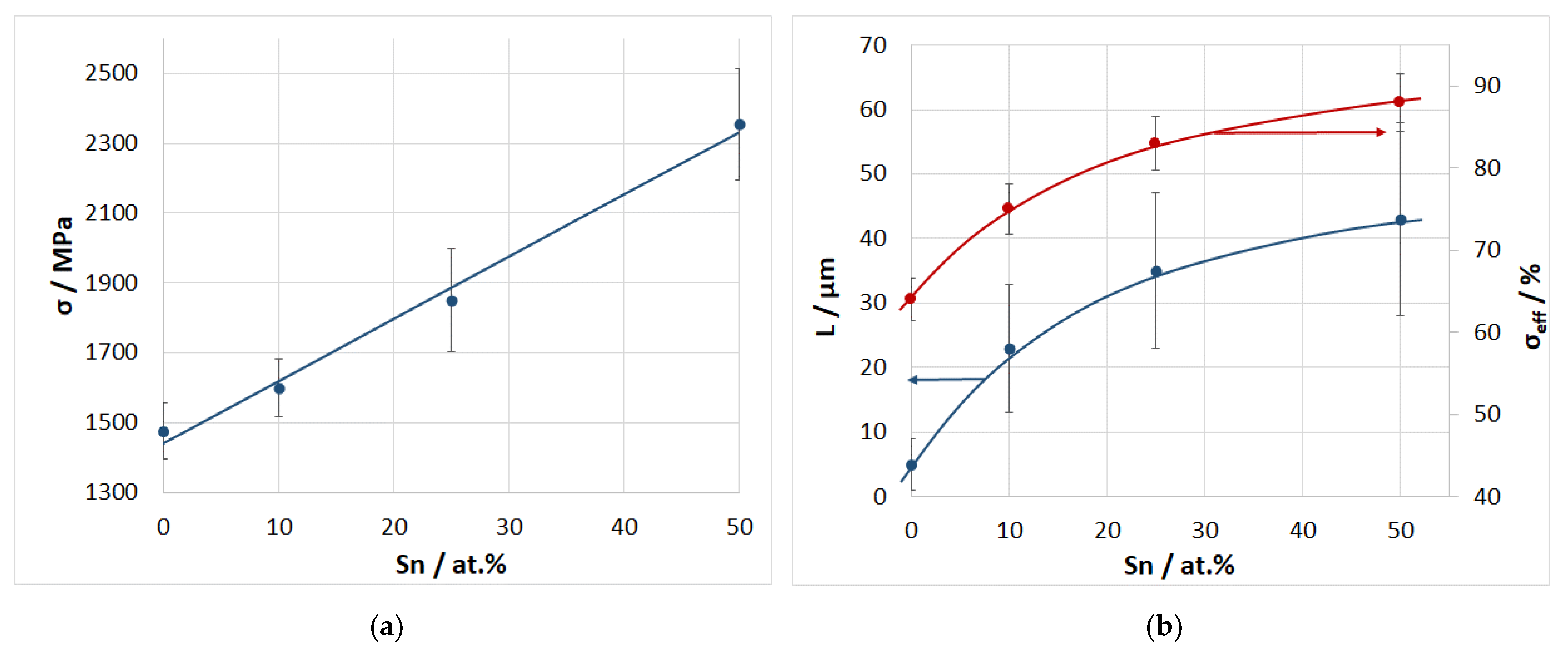
4.4. Strength of a CF/Al-Sn Wire and Effective Fiber Strength
4.5. Microstructure of a CF/Al-Sn Wire
5. Discussion
5.1. Matrix Alloy
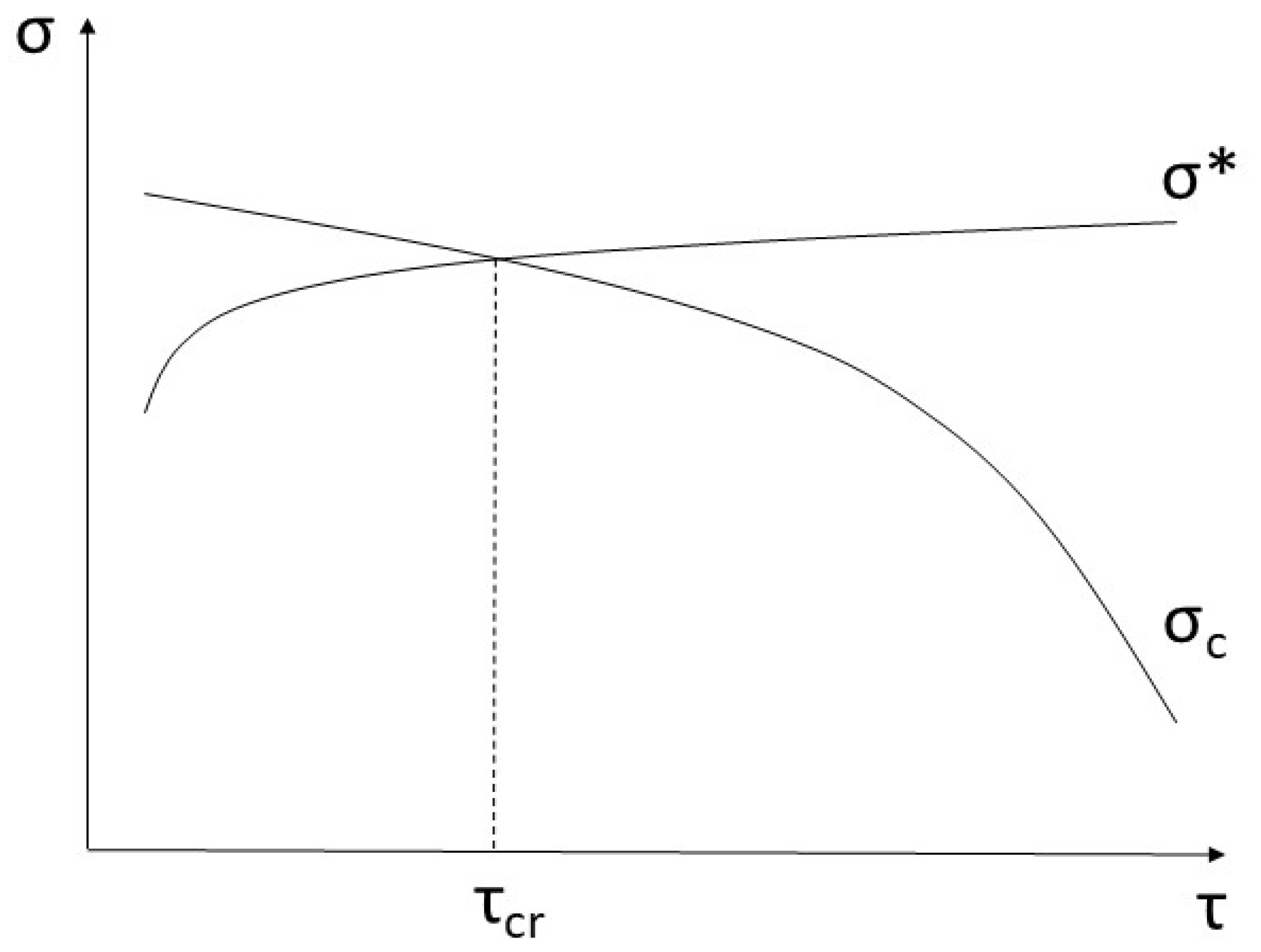
5.2. Composite CF/Al-Sn-Wire
6. Conclusions
- The effect of tin content in the Al-Sn alloy in the range from 0 to 100 at.% on its mechanical properties was studied. An increase in the tin content leads to a monotonic decrease in the microhardness and conditional yield stress of the Al-Sn alloy from 305 to 63 MPa and from 32 to 5 MPa, respectively. In addition, Young’s modulus and the shear modulus of the Al-Sn alloy decrease from 65 to 52 GPa and from 24 to 20 GPa, respectively. The change in these mechanical properties is almost linear, which is most likely due to an almost complete absence of mutual solubility and interaction between aluminum and tin.
- The effect of tin content in the Al-Sn matrix alloy in the range from 0 to 50 at.% on the strength of the CF/Al-Sn composite subjected to three-point bending was also investigated. Increasing tin content up to 50 at.% leads to a linear increase in the composite strength from 1450 to 2365 MPa, which is due to an increase in the effective fiber strength from 65 to 89%.
- The addition of tin up to 50 at.% to the matrix alloy leads to the formation of weak boundaries between the matrix and the fiber. This is most likely due to the suppression of the chemical reaction between aluminum and carbon and the fact that, in the composite structure, tin is predominantly located in the spaces between the fiber and aluminum grains. An increase in the composite strength is accompanied by an increase in the average length of the fibers pulled out at the fracture surface.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vidal-Sétif, M.; Lancin, M.; Marhic, C.; Valle, R.; Raviart, J.-L.; Daux, J.-C.; Rabinovitch, M. On the role of brittle interfacial phases on the mechanical properties of carbon fibre reinforced Al-based matrix composites. Mater. Sci. Eng. A 1999, 272, 321–333. [Google Scholar] [CrossRef]
- Yu, J.K.; Li, H.L.; Shang, B.L. A functionally gradient coating on carbon fibre for C/Al composites. J. Mater. Sci. 1994, 29, 2641–2647. [Google Scholar] [CrossRef]
- Matsunaga, T.; Matsuda, K.; Hatayama, T.; Shinozaki, K.; Yoshida, M. Fabrication of continuous carbon fiber-reinforced aluminum–magnesium alloy composite wires using ultrasonic infiltration method. Compos. Part A Appl. Sci. Manuf. 2007, 38, 1902–1911. [Google Scholar] [CrossRef]
- Mileiko, S.T. Metal and Ceramic Based Composites; Elsevier: Amsterdam, The Netherlands, 1997; ISBN 9780444828149. [Google Scholar]
- Sobczak, N.; Kudyba, A.; Siewiorek, A.; Homa, M.; Nowak, R.; Ruzda, G.; Sobczak, J.J.; Turalska, P.; Tchorz, A.; Andrzej, G.; et al. Textile Reinforced Carbon Fibre/Aluminium Matrix Composites for Lightweight Applications; Gude, M., Boczkowska, A., Eds.; Foundry Research Institute: Krakow, Poland, 2014; ISBN 9788388770975. [Google Scholar]
- Galyshev, S. On the Strength of the CF/Al-Wire Depending on the Fabrication Process Parameters: Melt Temperature, Time, Ultrasonic Power, and Thickness of Carbon Fiber Coating. Metals 2021, 11, 1006. [Google Scholar] [CrossRef]
- Deve, H.E.; McCullough, C. Continuous-fiber reinforced composites: A new generation. JOMA 1995, 47, 33–37. [Google Scholar] [CrossRef]
- Du, Z.-Z.; McMeeking, R.M. Control of strength anisotropy of metal matrix fiber composites. J. Comput.-Aided Mater. Des. 1994, 1, 243–264. [Google Scholar] [CrossRef]
- Oden, L.L.; Gokcen, N.A. Sn-C and Al-Sn-C phase diagrams and thermodynamic properties of C in the alloys: 1550 °C to 2300 °C. Metall. Trans. B 1993, 24, 53–58. [Google Scholar] [CrossRef]
- McAlister, A.J.; Kahan, D.J. The Al−Sn (Aluminum-Tin) System. Bull. Alloy Phase Diagr. 1983, 4, 410–414. [Google Scholar] [CrossRef]
- Son, K.S.; Park, T.E.; Kim, J.S.; Kang, S.M.; Kim, T.H.; Kim, D. Microstructural Control of Al-Sn Alloy with Addition of Cu and Si. Korean J. Met. Mater. 2010, 48, 248–255. [Google Scholar] [CrossRef][Green Version]
- Chikova, O.A.; Konstantinov, A.N.; Shishkina, E.V.; Chezganov, D.S. Influence of the microheterogeneity and crystallization conditions of the Al-50% Sn alloy on the mechanical properties of phase components of the ingot. Russ. J. Non-Ferr. Met. 2014, 55, 505–508. [Google Scholar] [CrossRef]
- Cruz, K.S.; Meza, E.S.; Fernandes, F.A.P.; Quaresma, J.M.V.; Casteletti, L.C.; Garcia, A. Dendritic Arm Spacing Affecting Mechanical Properties and Wear Behavior of Al-Sn and Al-Si Alloys Directionally Solidified under Unsteady-State Conditions. Metall. Mater. Trans. A 2010, 41, 972–984. [Google Scholar] [CrossRef]
- Galyshev, S.; Gomzin, A.; Gallyamova, R.; Khodos, I.; Musin, F. On the liquid-phase technology of carbon fiber/aluminum matrix composites. Int. J. Miner. Metall. Mater. 2019, 26, 1578–1584. [Google Scholar] [CrossRef]
- Kobelev, N.P.; Nikolaev, R.K.; Soifer, Y.M.; Khasanov, S.S. Elastic modules of monocrystalline C60. Solid State Phys. 1998, 40, 173. (In Russian) [Google Scholar] [CrossRef]
- Mileiko, S.T. Synergy in composites. Compos. Nanostruct. 2015, 7, 191–206. [Google Scholar]
- Mileiko, S.T.; Sarkissyan, N.S.; Kolchin, A.A.; Kiiko, V.M. Oxide fibres in a nickel-base matrix—Do they degrade or become stronger? Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2004, 218, 193–199. [Google Scholar] [CrossRef]
- Curtin, W.A. Ultimate strengths of fibre-reinforced ceramics and metals. Composites 1993, 24, 98–102. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galyshev, S.; Orlov, V.; Atanov, B.; Kolyvanov, E.; Averichev, O.; Akopdzhanyan, T. The Effect of Tin Content on the Strength of a Carbon Fiber/Al-Sn-Matrix Composite Wire. Metals 2021, 11, 2057. https://doi.org/10.3390/met11122057
Galyshev S, Orlov V, Atanov B, Kolyvanov E, Averichev O, Akopdzhanyan T. The Effect of Tin Content on the Strength of a Carbon Fiber/Al-Sn-Matrix Composite Wire. Metals. 2021; 11(12):2057. https://doi.org/10.3390/met11122057
Chicago/Turabian StyleGalyshev, Sergei, Valery Orlov, Bulat Atanov, Evgeniy Kolyvanov, Oleg Averichev, and Tigran Akopdzhanyan. 2021. "The Effect of Tin Content on the Strength of a Carbon Fiber/Al-Sn-Matrix Composite Wire" Metals 11, no. 12: 2057. https://doi.org/10.3390/met11122057
APA StyleGalyshev, S., Orlov, V., Atanov, B., Kolyvanov, E., Averichev, O., & Akopdzhanyan, T. (2021). The Effect of Tin Content on the Strength of a Carbon Fiber/Al-Sn-Matrix Composite Wire. Metals, 11(12), 2057. https://doi.org/10.3390/met11122057






