Review on Laser Interaction in Confined Regime: Discussion about the Plasma Source Term for Laser Shock Applications and Simulations
Abstract
1. Introduction
2. Fifty Years of Laser/Matter Interaction in Confined Regime: Plasma Generation, Significant Experimental Data, and Summary of Pressure Measurements
2.1. General Considerations about Confined Plasmas
2.2. Laser/Matter Interaction: Plasma Generation and Breakdown in Dielectric Medium
2.2.1. Main Plasma Generation
- At the beginning, when the laser pulse starts irradiating the metal target, only a small fraction of the energy is absorbed by the metal, the other part being reflected. The electrical current generated at the metal surface by the electromagnetic wave tends to heat it by joule heating, on a very small layer called the skin depth and given bywhere is the laser angular frequency, is the electrical conductivity of the metal, and is its permeability.Typical values of for aluminum at 1064 nm give a depth skin of 5 nm. This will be the initial size of the plasma, after the metal is vaporized and ionized by joule heating.This first step depends on the initial metal reflectivity, hence it depends on both the used metal and its surface state. However, at the high laser intensities used in the laser shock (>1 GW/cm2, far from the ablation threshold of metals typically of approximately 0.2 GW/cm2), losses associated with this mechanism have been shown to be negligible [40,41] and independent of the used metal. Furthermore, this step is considered to be almost instantaneous in the whole process.
- In a second step, the absorption of the laser energy by the plasma is assumed to be close to 100%. The main mechanism of absorption involved here is the inverse Bremsstrahlung (IB [42], as can be seen in Figure 3). IB is a collisional process involving three particles: a photon, an electron, and an ion. By conservation of the momentum, the photon’s energy is absorbed and the kinetic energy of both the ion and the electron are increased. Furthermore, electrons are accelerated in the electrical field of the laser and they transfer their energy to heavy particles by collision, leading to a global increase in plasma temperature.Thus, this mechanism is highly dependent on the frequency at which the electron and ion collide.This frequency may be obtained using Lorenz’s model [43,44]:where is the plasma electronic density, is the ionization state, and T is the temperature.Altogether, the optical index of the plasma is given bywhere is the permittivity of the plasma:where (in cm , with in nm: ) is the critical density of the plasma:As the absorption coefficient is related to the imaginary part of the refractive index:Thus, the absorption by IB is given bywhere is the laser wavelength.Finally, if we consider a linear variation of the electronic density from 0 (at the plasma outside surface) to (in the depth of the plasma) on a total length L, then we have:
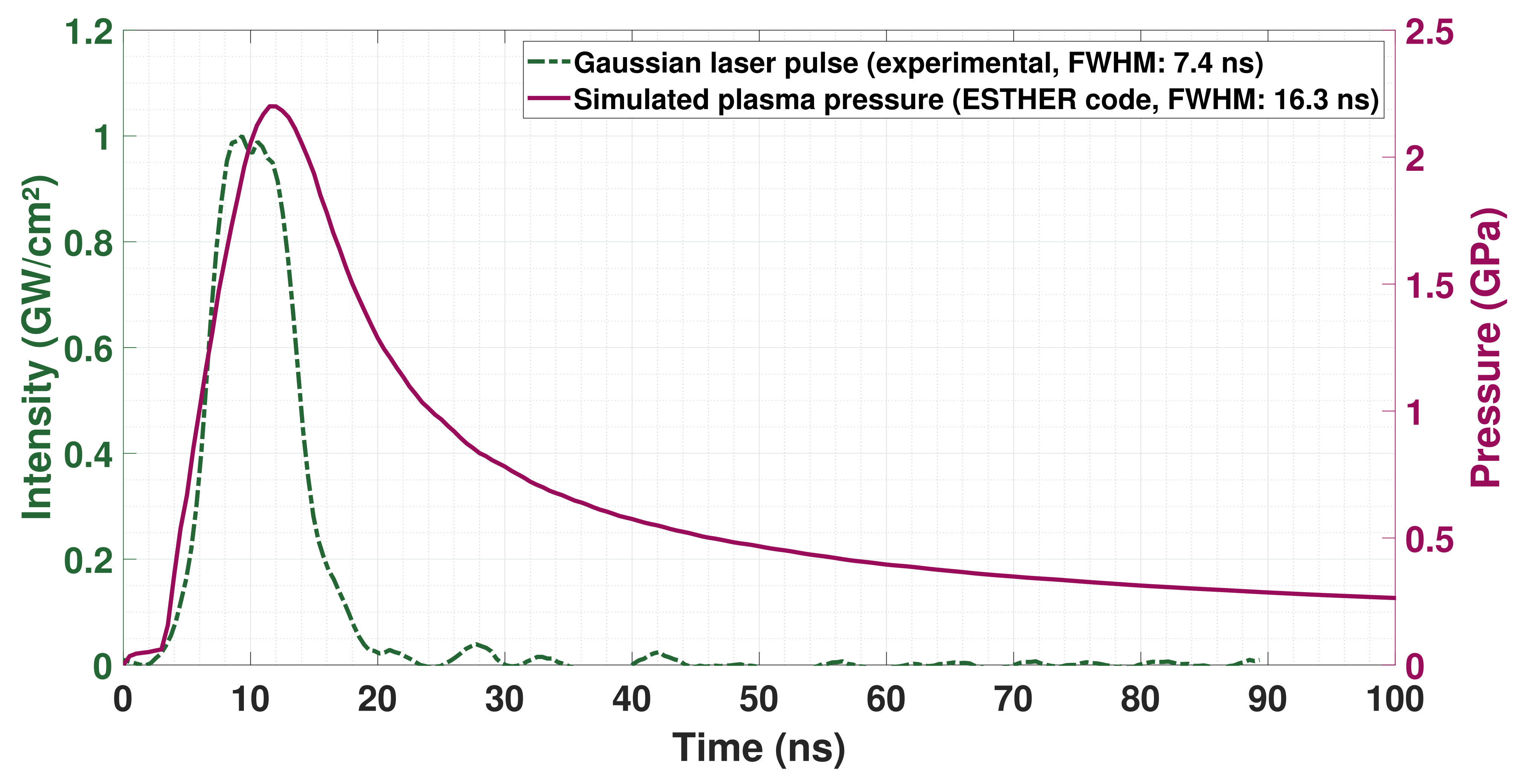
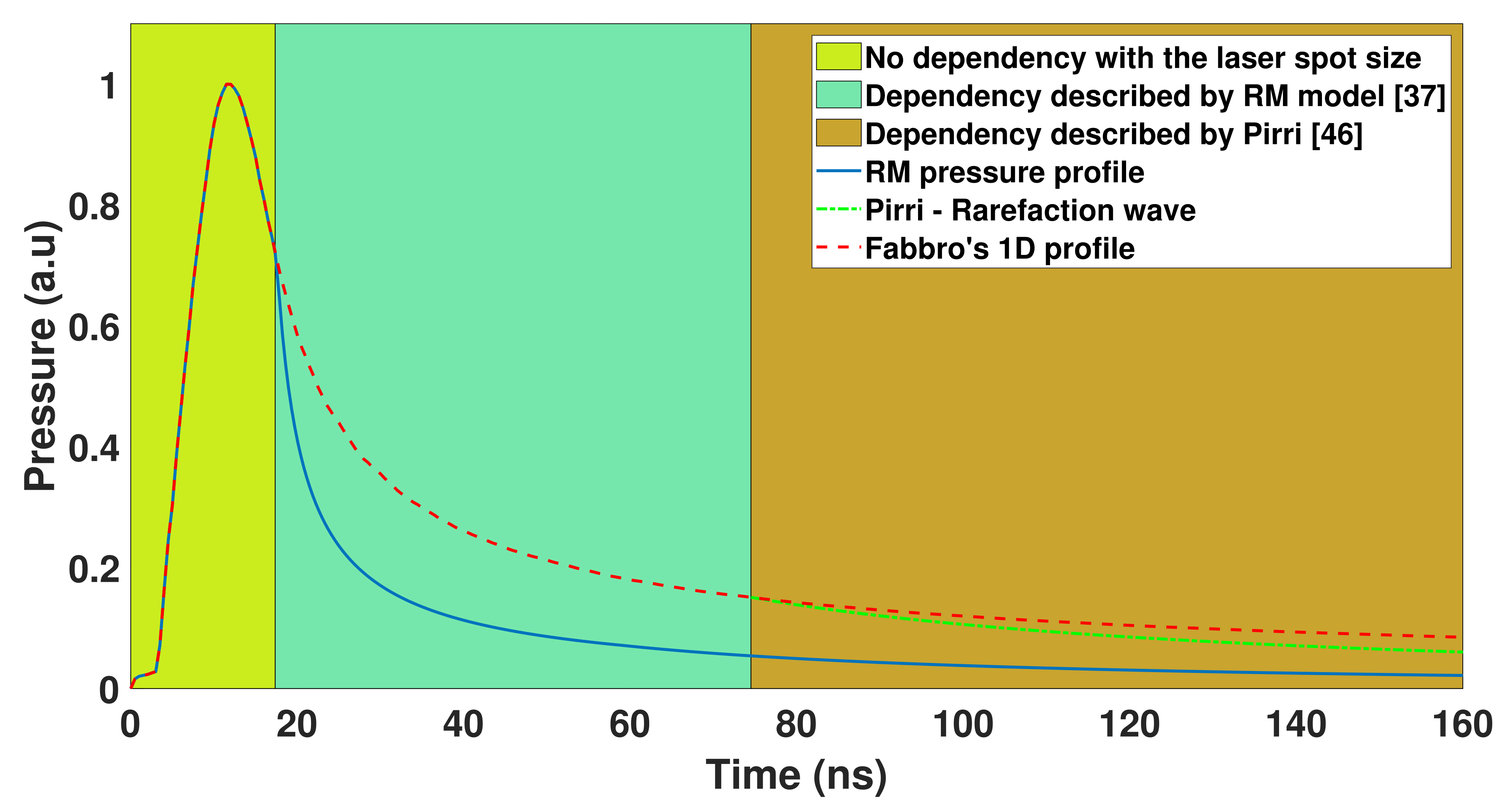
- The last step begins at the end of the laser pulse (, the laser pulse duration (FWHM)). The pressure of the plasma starts to decrease following an adiabatic law of Laplace:The pressure maintained in this last part is no longer useful for the shock process. However, the temperature is greatly important as the duration of this slow adiabatic release will mainly drive the thermally affected depth and thus whether the thermal protective coating shall be used.Indeed, a 1D thermal model (temperature applied during a duration ) gives the following depth that will be affected by the heating:where is the thermal diffusivity; typical values for range within a few micrometers in laser shock processes.To reduce the thermally affected depth , one should ensure that the duration of the plasma’s thermal loading is as short as possible.
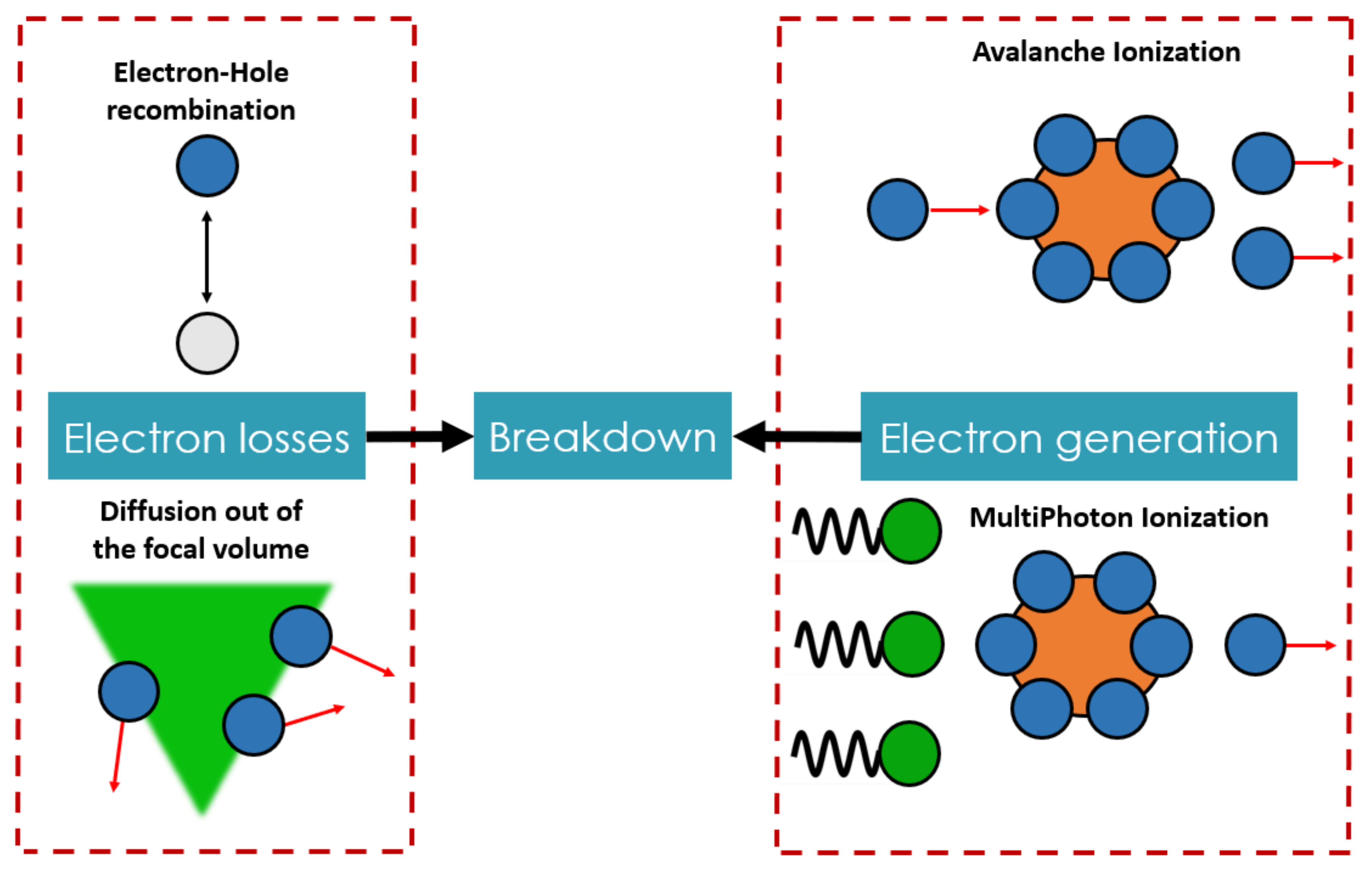
2.2.2. Breakdown Plasma Generation
- Avalanche ionization (AI)—here, electrons are accelerated by the electrical field of the laser pulse: their kinetic energy () increases and becomes sufficient to ionize an atom (, with being the ionization potential). This mechanism evolves exponentially: for one initial electron, and after n avalanche processes, there will be electrons created.If is the rate of AI per electron, then the density evolution is given by
- MultiPhotonIonization (MPI)—k (k an integer) photons are simultaneously absorbed by the atom (ionization) if the following condition is obtained:where h is the Planck constant, c is the speed of light, is the wavelength and is the ionization potential of the atom.As this is a quantum process, it can be shown that this mechanism is less effective with a higher value of k (thus a higher value of wavelength ).
- The electrons leaving out the focal volume by diffusion. If we use a rate of diffusion per electrons, the variation on the density is given by
- Losses by recombination: an electron–hole pair is recombined at a rate of per electron and hole. Then, the density variation is given by
- By measuring the pressure of the plasma (see the following part concerning the rear-free surface indirect determination of the plasma pressure)—when the breakdown threshold is reached, the pressure stops increasing with the laser intensity and fluctuates around a maximum value associated with the pressure value at the breakdown intensity threshold [23,25,26,27].
2.3. Experimental Data and Characterization of Confined Plasmas
- Fitting of a Planck-like distribution to the continuous background (this usually requires a plasma in thermodynamic equilibrium emitting a type of black body radiation);
- Excitation temperature obtained by comparing the relative intensities of the emission lines of an atomic system;
- Rotational and vibrational temperatures obtained by fitting the rovibrational spectrum of a well-defined electronic transition.
2.4. Development of Diagnostic Systems for Pressure Measurements
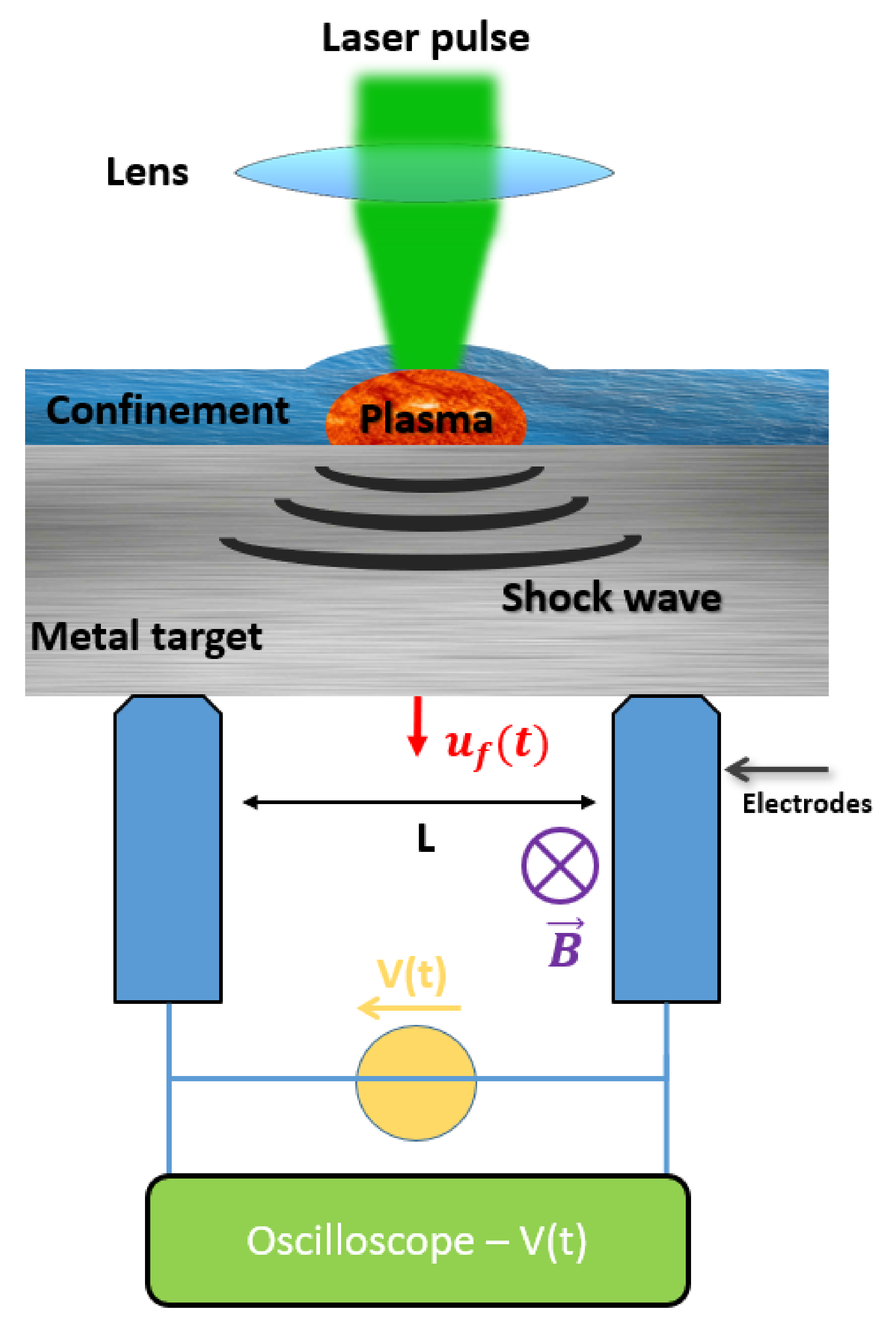
- Electromagnetic GaugeThis method uses the displacement of the metal induced by the shock wave when it arrives at the rear surface of the target [89,90,91].As shown in Figure 6, the target is placed in a constant magnetic field B (created by two magnets for example), and two metallic pins are connected to the target and separated by a distance L. Following Faraday’s law of induction, when the shock wave arrives at the rear surface and makes it accelerate, the created displacement in the magnetic field will induce a voltage , which corresponds to the variation in magnetic flux () through the wire loop.As, in this case, the rear surface is free, the measured rear free velocity is twice the material velocity u (reflection of the shock wave at the metal/air interface). Equation (22) then gives:This method has some advantages: it is an easy experimental setup to implement, and signals are directly related to the velocity without complicated treatments to be applied. Furthermore, a good temporal resolution is obtained, which is given by the speed of used oscilloscopes (typical resolution will be 0.3 ns with a 10 GS/s oscilloscope with a bandwidth of 2 GHz).However, there are a lot of possible uncertainties:
- −
- The magnetic field may vary during the process, mainly because of the perturbations induced by the plasma;
- −
- The distance between the two electrodes, which is constrained by the size of the laser spot size (a few mm) may also vary and be inaccurately measured. It may also be difficult to ensure that both electrodes are in contact with the target;
- −
- Typical values used for B (0.2 T) and L (1 mm) will give low voltage (40 mV for a maximum rear velocity of 200 m/s) and the signals may thus be noisy.
- PVDF Piezoelectric SystemA piezoelectric material, for which PVDF (polyvinylidene fluoride) is often chose, in laser shock experiments [91,92,93], is bonded on the rear-surface of the metal target. When the shock wave arrives at the interface between the metal and the PVDF, a part of the shock wave is transmitted and starts to propagate in the PVDF. As a result, it will undergo elastic deformation, and by a piezoelectric mechanism, a current will be generated. By measuring the electrical current generated between the front and back face of the PVDF, one can deduce the pressure of the shock wave. Thus, by taking into account the mismatch impedance between the metal and the piezoelectric material, the shock wave pressure at the rear surface of the metal can be deduced. Altogether, similarly to the previous measurement of the rear-surface by electromagnetic gauge, the pressure of the plasma is indirectly calculated.When the shock arrives at the interface, moving at a material velocity u, the intensity is given by: where is the thickness of the piezoelectric system and is the ferroelectric polarization.Though this system is quite easy to use and implement, there are a lot of drawbacks:
- −
- The material parameters of the piezoelectric medium must be precisely known, which is not often the case (calibration of );
- −
- At high pressure (>5 GPa), the material starts to respond non-linearly, making the pressure measurement inaccurate;
- −
- Some calculations have to be made to estimate the mismatch impedance in order to obtain the pressure at the rear surface of the metal target;
- −
- As with gauges, the electrical signal may be disturbed by the electromagnetic field of the plasma, especially at high laser intensity;
- PDVPhotonic doppler velocimetry (PDV) is based on the concept of heterodyning, but it has only recently been developed as a useful shock-physics diagnostic, thanks to the recent technological advances of the telecommunications industry [94,95]. In its simplest configuration (a light and compact system, with full optical beam transportation through fiber), PDV is a fiber-based Michelson interferometer in which laser light is divided among two paths: the first one containing the target and the other one a stationary reference mirror. The laser Doppler-shifted light coming back from the moving target is combined with the reference light and sent to an optical receiver. The optical interferences which are generated result in a beat frequency , where is the wavelength of the laser probe. At 1550 nm, which is the typical wavelength of most PDV systems, every km/s of velocity v requires 1.29 GHz of receiver/digitizer bandwidth. The velocity is finally extracted from the recorded signal through a time–frequency analysis, typically performed with short-time Fourier transforms (STFTs) [96]. The main advantages of PDV are its ease of use, its robustness, and its relatively low cost compared to other diagnostics such as VISAR. Moreover, because PDV tracks motion in a frequency-encoded temporal electro-optical signal, it is thus able to record multiple velocities simultaneously. However, like all other diagnostics, PDV also has some drawbacks:
- −
- The primary weakness of conventional PDV is its inability to resolve low-velocity transients;
- −
- Conventional PDV measurements are also directionally blind: motion toward and away from the probe lead to the same beat frequency;
- −
- Due to the use of time–frequency analysis to retrieve the velocity, the velocity resolution is inversely proportional to the time resolution. Thus, considering the fact that plasma-induced shock waves involve a short duration (in the nanosecond range), with a required resolution of approximately 1 ns, the resolution on velocities is then limited to approximately 50 m/s.
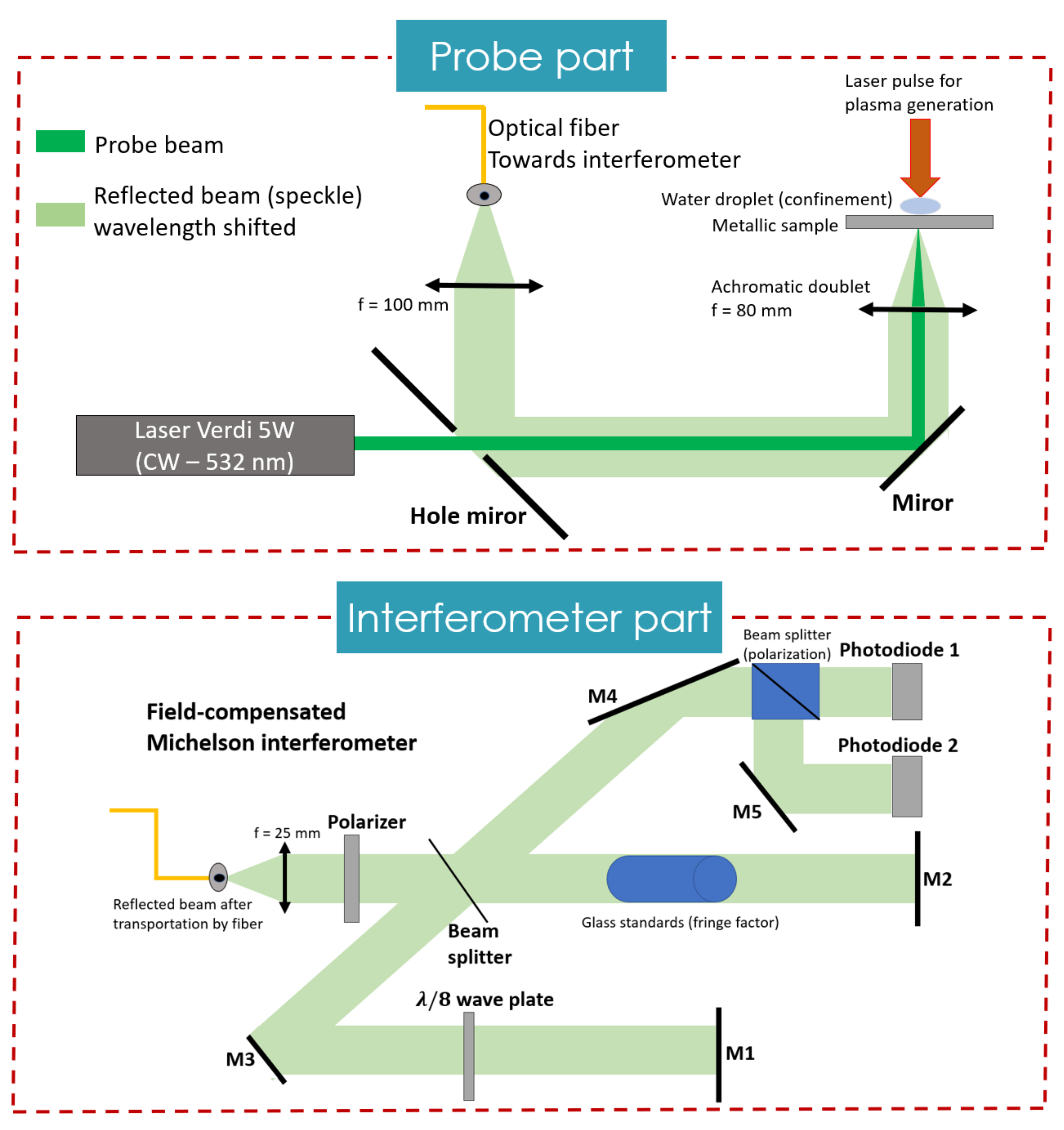
- VISAR Optical SystemThe Velocity Interferometer System for Any Reflector (VISAR), developed by Barker in 1972 [101]), is currently the most used system to measure plasma pressure: it also aims to measure the rear-free surface velocity of the target. An accurate optical measurement was performed.As shown in Figure 7, the VISAR is made of two parts (the probe part and the interferometer part):
- −
- The probe part—a single longitudinal mode ( with a narrow spectral width) collimated laser beam is focused on the rear surface of the metal target. The scattered reflection of the beam is then collected (using a short focal length) and directed towards the second part to be analyzed. This reflection is wavelength-shifted according to the Doppler–Fizeau effect as the surface is moving under a free velocity ().It may be preferable to use an unpolished sample to generate more scattered light compared to the specular reflection that could be deflected out of the interferometer if the sample is becoming excessively deformed (which often occurs for thin samples of ≈100 µm).
- −
- The interferometer part—this second part is a field-compensated Michelson-like interferometer. Calibrated glass enables to delay one arm of the interferometer from the other. This changes the initial path difference () in the interferometer, and hence the required velocity to move from one fringe to the next one is also changed: this is the velocity per fringe (VPF) factor. Then, the interference between the signal at a time t (wavelength ) and one at a time (wavelength ) is produced, and the interferogram’s intensity is acquired with a fast PhotoMultiplier (PM). Therefore, there is a translation of the interference fringes as soon as a wavelength-shift occurs. The time resolved measurement of the interference intensity enables one to obtain the corresponding velocity.
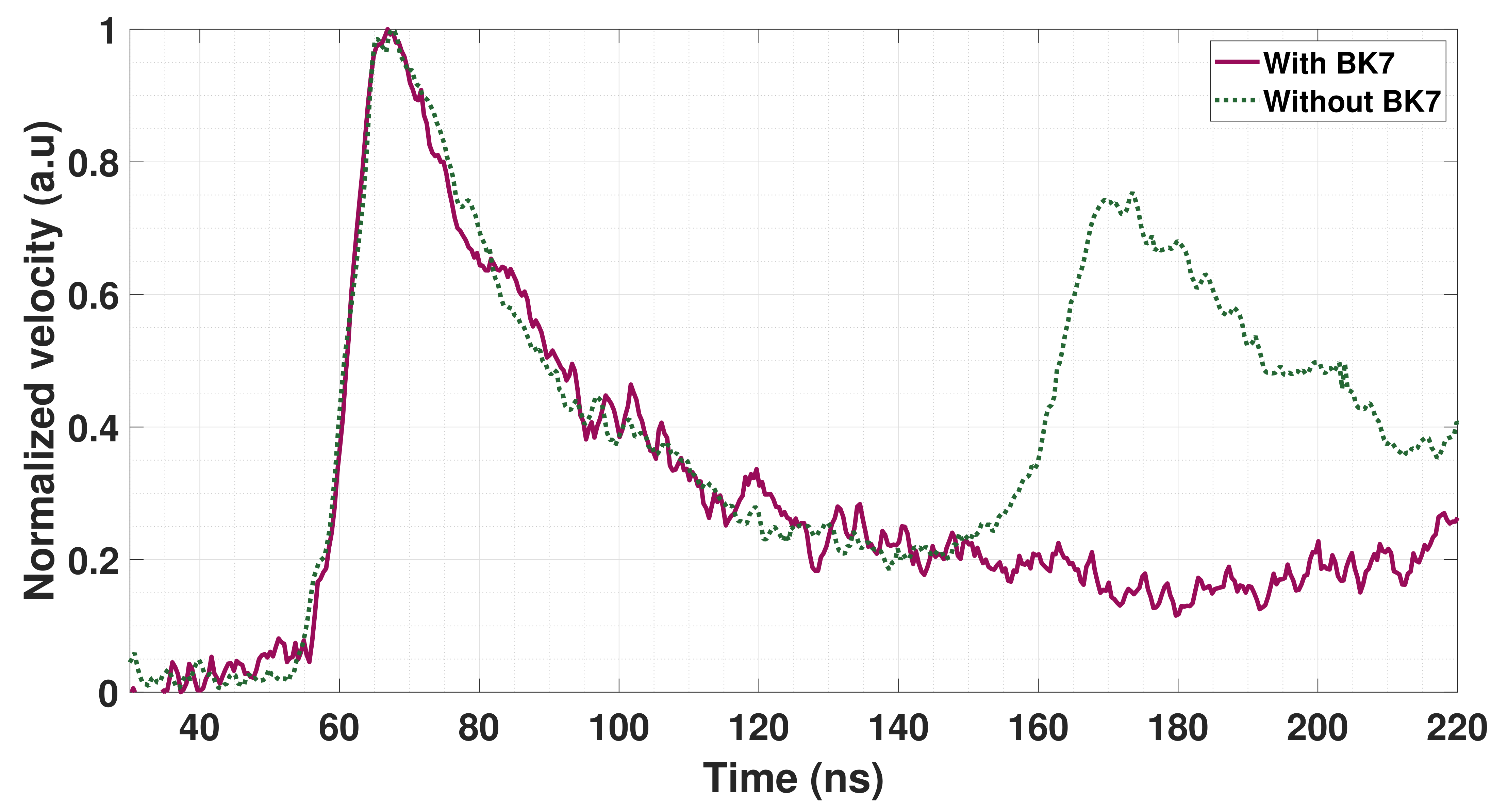
The intensity of the interferogram follows the following law: . Consequently, a simple code has to be used to analyze the intensity signals obtained on the PM in order to obtain the rear-free surface velocity . Thus, as for EM gauge, the plasma pressure is given byThe VISAR system is the most resilient and reliable means of plasma pressure measurement: it is without contact (and therefore not influenced by the process) and it can even be used at very high pressure. However, it is not the easiest system to implement as it must be carefully aligned. Indeed, both the probe laser beam (to be brought under the target) as well as the interferometer system (to analyse the wavelength shift) must be properly adjusted. Furthermore, a wise choice of calibrated glass length has to be made before the measurement beings, and some calculations must be performed to obtain the rear-free surface velocity.Finally, a great temporal resolution of less than 1 ns is achieved, only limited by the PM response-time. For all these reasons, we recommend using this system for pressure measurements as it offers the best compromise between assets and drawbacks. - Method to Measure the Plasma Pressure with VISARIt is important to measure the plasma pressure as accurately as possible as a function of the used laser parameters. Indeed, this will help perform simulations but also to use specific though not very well known material such as FSW materials which possess specific properties [102]. If one knows precisely, for a given laser configuration, the loading pressure term of the plasma, then it helps to more effectively extract the material parameters from a typical shock-wave measurement, as previously shown.First of all, we recommend using a well-known material, such as pure aluminum with a small thickness, to perform laser-induced shock-wave measurements. This will help prevent the dependency of the results with the material parameters or models.Secondly, we suggest using large laser spot sizes to prevent the interferences of complex phenomena such as edge effects (also called 2D effects) [103,104]. Keeping the shock wave as monodimensional as possible should be ensured whenever possible.Moreover, regarding VISAR optical measurements, one should use an unpolished target in order to avoid a loss of the optical signal.On the other hand, in the case of very thin samples which may become deformed under the shock (thus making the pressure measurement difficult to conduct), we recommend sticking a transparent glass window to the rear surface of the sample, such as a BK7 glass plate for aluminum (as performed in [37]). This window must have a mechanical impedance as close as possible to the target on which it will be stuck. Under these conditions, the shock wave is transmitted between the sample and the window without reflection and the full profile of the shock wave can be measured (as shown in Figure 5). One should note that in this case, the material velocity is measured and is half the value of the free surface velocity.
3. Improvements in Experimental Accuracy—Range of Plasma Pressure Data Obtained
3.1. Improvements in Optical Metrology and Better Understanding of Materials Behavior
3.2. Plasma Pressure in Confined Regime—Range of Pressures Obtained through Experiments and Simulations
4. A Review on Improvements in Analytical Models and Simulations
4.1. Analytical Models
- The first analytical expression developed to provide the maximum plasma pressure was given by Anderholm within their discovery of the confined regime [21]. The pressure was then given by
- This dependency was conceived in 1990 by Fabbro with a more detailed model, described in [28]. The main ideas of this model are as follows:
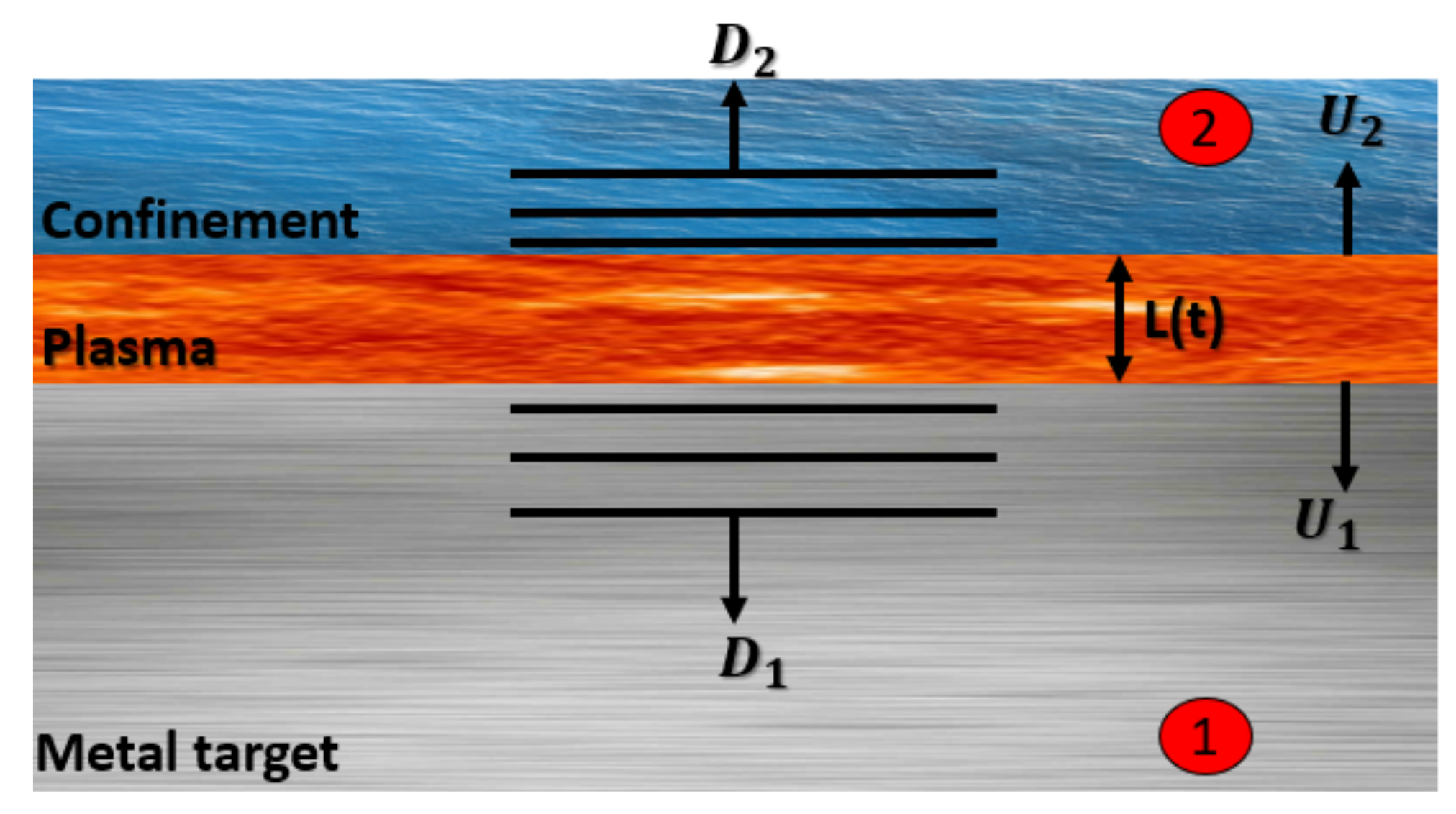
- The laser pulse is absorbed at the boundary between the confinement and the metal where the plasma is created. This plasma then extends in a 1D geometry (the model is said to be mono-dimensional) with two shock waves generated in both the metal and the confinement (see Figure 10).
- The melting and vaporization of the metal is instantaneous. Then, a plasma absorbs all the laser intensity. This plasma is assumed to behave as an ideal gas and a coefficient is introduced to determine how much of the internal energy of the ideal gas is converted into thermal energy () or devoted to ionization (). As no consideration of the plasma is made in this model, the coefficient must be experimentally determined (from Equation (30)).
- The absorbed laser energy by the ideal gas is assumed to be converted into two parts: the work of the pressure force (, L the thickness of the plasma), and the increase in the internal energy per volume V. ()The work of the pressure force is used to increase the plasma length by pushing both the confinement and the metal target (see Figure 10). Thus, the pressure will depend on the reduced acoustic impedance Z, given bywhere and are the acoustic impedance of the confinement and the metal, respectively.
- At the end of the laser pulse, the plasma/ideal gas will start to cool down, and the pressure will decrease. This was modeled as a slow adiabatic release which obeys the law of Laplace:where P is the plasma pressure, V is its volume and C is a given constant; is the adiabatic constant.
- In 2001, Zhang and Yao proposed a similar approach to Fabbro, with 5-layer geometry: the shocked confinement, the unaffected confinement, the plasma, the unaffected metal and the shocked metal [29,30]. A mass equation conservation was added to obtain the density of the plasma, and the mass flow from the metal and the confinement towards the plasma. Moreover, the rarefaction wave phenomenon described by Pirri [46] was also included in this model to take into account the drop in pressure due to the spherical blast wave generated during the laser pulse. Usually, this phenomenon should be considered over longer time (after the laser pulse), but Zhang was developing a model for micro-scale laser processes, thus resulting in an early apparition of this blast wave.
- In 2003, Sollier et al. proposed an extension of Fabbro’s model named ACCIC [31,36]. Similarly to Zhang and Yao [29,30], a mass conservation equation was included so that the whole involved system of equations can become self-closed. The evaporation of the protective coating layer is considered and calculated based on the Hertz–Knudsen theory. The Thomas–Fermi theory for electrons and Cowan’s theory for ions are applied as the equations of state for the confined plasma, and thermal losses to the work piece target and transparent overlay (water) are taken into account. The confined plasma is considered as a gas of neutrals from the target only, without any contribution from the confining overlay, and the laser absorption coefficient comes from experimental measurements. The rarefaction wave phenomena described by Pirri [46] were also included in this model to take into account the drop in pressure and temperature due to the spherical blast wave generated during the laser pulse. The ACCIC model has been used to compute the thermo-mechanical loading used as input conditions in FEM simulations of the LSP treatment [107].
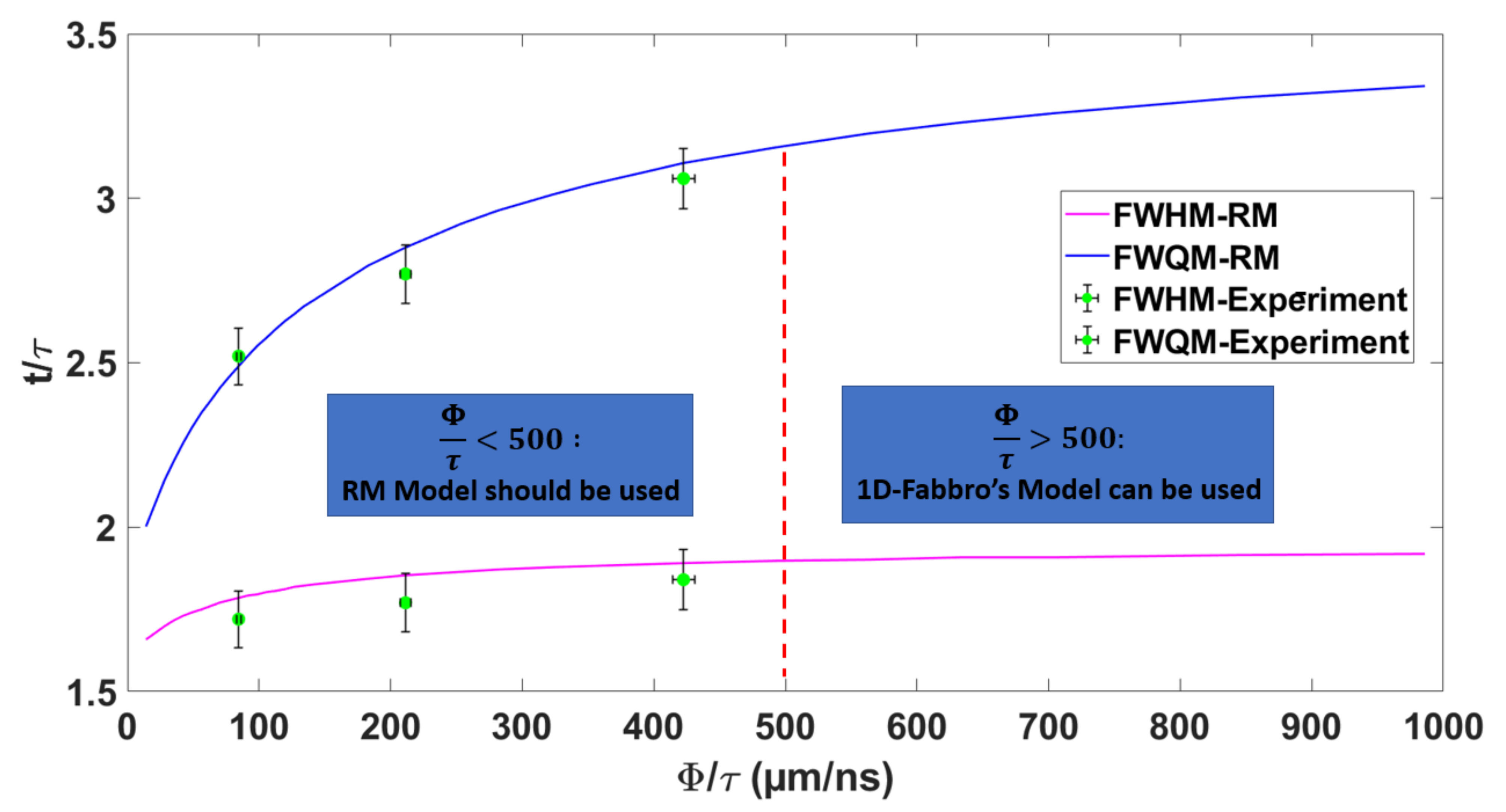
- More recently, it has been experimentally demonstrated that the plasma pressure release was shortened when using small laser spot sizes [37]. Hence, a new model, based on Fabbro’s model, has been proposed, as the previous one was under a mono-dimensional hypothesis which was only valid for large spot sizes. This radius-dependent model (RM) incorporates a plasma-leaking mechanism from the edges, leading to a shortening of the plasma pressure with smaller laser spot sizes. Indeed, this leaking will be proportionally more effective in increasing the plasma volume with small spot sizes, thus resulting in a faster drop of the pressure.
4.2. Numerical Models
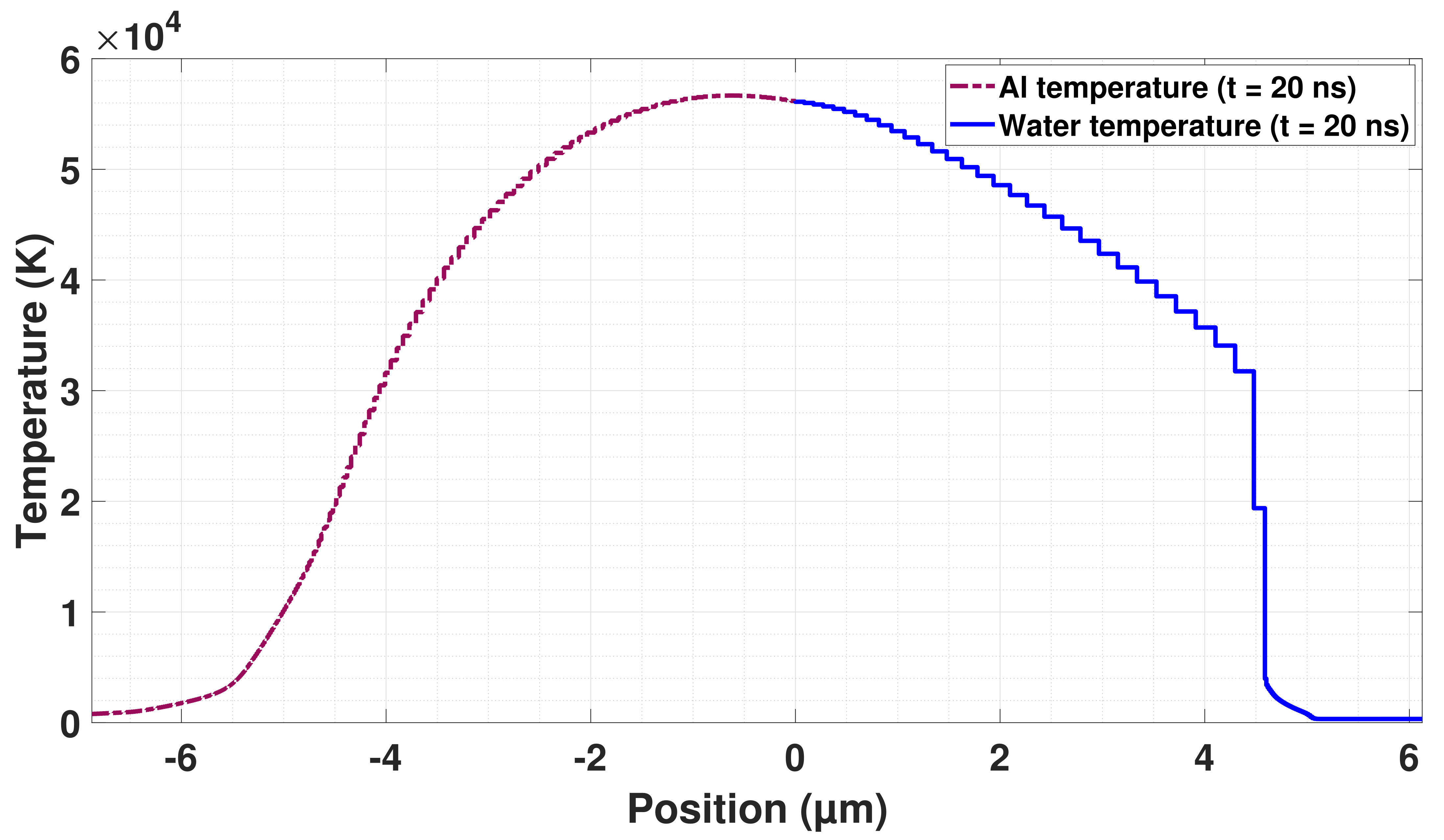
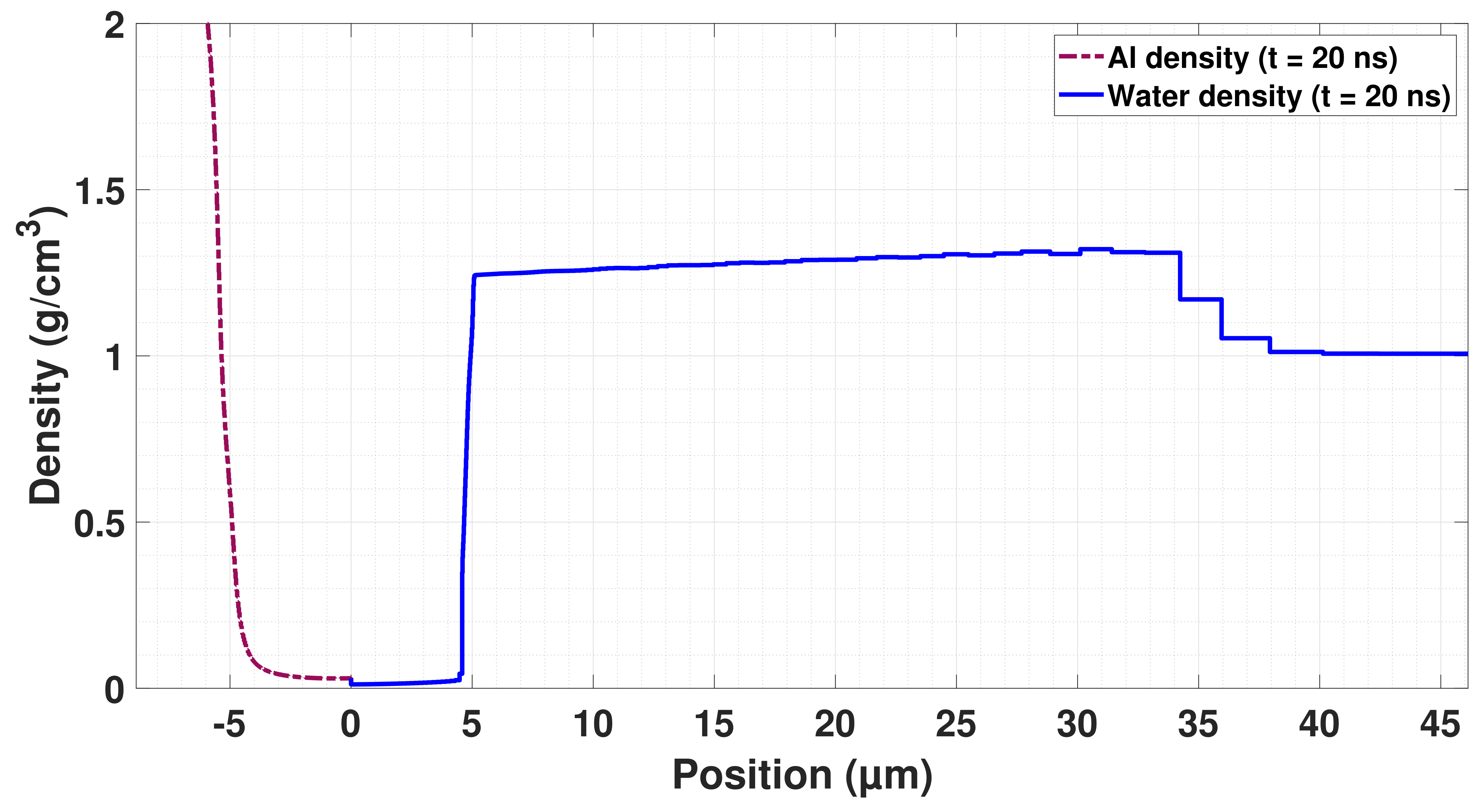
- A first numerical code was developed in the late 1970s by Clauer and their team [108,109,110,111], and was named LILA. This code is based on a finite difference method (FDM) resolution of the differential equations governing hydrodynamic phenomena in the plasma. The absorption of the laser light was calculated for both the cold dense metal and the plasma (through IB absorption). For simplification purposes, a unique equation of state (EOS) was used to describe both the metal and the plasma (taking into account thermal motion and thermal ionization).
- In 2003, Colvin et al. developed a model for low-intensity laser drives which was subsequently incorporated in the 2D radiation-hydrodynamics code LASNEX, in order to simulate the confined laser-matter interaction [112]. The elastic–plastic equations of stress wave propagation were treated in a Lagrangian formulation. The equation of state of all the materials was taken as the analytical quotidian equation of state (QEOS), which is reduces to a Gruneisen EOS at low temperatures. Radiation transport was calculated by multigroup diffusion, with opacities calculated from an average atom model. A ray tracing algorithm simulated laser light propagation through the matter, with inverse Bremsstrahlung absorption on free electrons. The authors also added several prescriptions for calculating:
- •
- The correct ionization state and electron densities for metals and insulators as a function of temperature;
- •
- The low-intensity absorption of the laser beam on a solid or liquid metal;
- •
- The photoionization absorption of the low-intensity laser beam in neutral vapor;
- •
- Collisional ionization, three-body recombination, and dielectric breakdown.
- From 2004 to 2009, Ocaña, Morales and their coworkers developed a simulation model named SHOCKLAS consisting of three principal modules, namely HELIOS, LSPSIM, and HARDSHOCK, which dealt with the main aspects of LSP modeling in a coupled way [113,114,115]. HELIOS is a 1-D radiation-magnetohydrodynamics code which is used to simulate the dynamic evolution of laser-created plasmas. HELIOS solves Lagrangian hydrodynamics equations for a single fluid in which electrons and ions are assumed to be co-moving. Energy transport in the plasma can be treated using either a one-temperature () model (for both electrons and ions) or a two-temperature () model. Both the electrons and ions are assumed to have Maxwellian distributions defined by their respective temperatures. Material EOS properties are based on either SESAME or PROPACEOS tables, whereas the opacities’ properties are based on tabulated multi-group PROPACEOS data, radiation emission, and absorption terms being coupled to the electron temperature equation. Laser energy deposition is computed using an inverse Bremsstrahlung model, with the restriction that no energy in the beam passes beyond the critical surface.
- In 2005, Wu and Shin from Purdue University brought significant improvement in 1D hydrodynamic numerical codes for confined laser-matter interaction [32,117]. Their code adopts a layer geometry (metal/plasma/confinement) to gain a better understanding of how the laser light is transmitted and reflected during the whole interaction. Altogether, the simulated absorption is more accurate. Furthermore, a model for the breakdown is also provided in order to take into account the saturation of intensity reaching the target when a breakdown plasma occurs.
- Most recently, Heya et al. also proposed a 1D code to simulate laser shock interaction [121]. This code, named the integrated simulation code for laser ablation peening (ISLAP), concentrates on the interaction of laser light with the metal target rather than simulating the whole laser shock process. There are three models used in this code: an atomic model, based on a screened hydrogenic model (SHM) and used to obtain the energy levels, population distributions, and ionization states of the metal target; an equation of state (EOS) model to calculate some parameters such as the pressure or the specific heat; and the Cowan model; a laser ablation peening code (LAPCO) to calculate the absorption of the laser light (inverse Bremsstrahlung and resonance absorption) during the process, and also to estimate energy transfers (heating and radiation).
5. Applications: Understanding of Laser Shock Generation and Propagation for Aluminum Alloys
6. Future Expectations and Improvements
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACCIC | Auto-Consistent Confinement Interaction Code |
| AI | Avalanche Ionization |
| CCD | Charge-Coupled Device |
| CRS | Compressive Residual Stress |
| CS | Cross-Section |
| DOE | Diffractive Optical Elements |
| EBSD | Electron BackScatter Diffraction |
| EOS | Equation of State |
| FDM | Finite Difference Method |
| FEM | Finite Element Method |
| FWHM | Full Width at Half-Maximum |
| FSW | Friction Stir Welding |
| HEL | Hugoniot Elastic Limit |
| IB | Inverse Bremsstrahlung |
| ICCD | Intensified Charge-Coupled Device |
| IP | In Plane |
| LAPCO | Laser Ablation Peening Code |
| LASAT | Laser Shock Adhesion Test |
| LIBS | Laser-Induced Breakdown Spectroscopy |
| LSA | Laser Shock Application |
| LSD | Laser-Supported Detonation Wave |
| LSP | Laser Shock Peening |
| LSPwC | Laser Shock Peening without Coating |
| LSR | Laser-Supported Radiation wave |
| MPI | MultiPhotonIonization |
| PDV | Photonic Doppler Velocimetry |
| PM | PhotoMultiplier |
| PVDF | Polyvinylidene Fluoride |
| QEOS | Quotidian Equation of State |
| RM | Radius-Dependent Model |
| RMS | Root Mean Square |
| SHM | Screened Hydrogenic Model |
| VISAR | Velocity Interferometer System for Any Reflector |
| VPF | Velocity per Fringe |
| WTC | Water Tank Configuration |
Symbols
| Thermal Efficiency Coefficient (Fabbro’s Model) | |
| Absorption Coefficient by IB | |
| Laplace Adiabatic Coefficient | |
| Plasma Coupling Coefficient | |
| Degenerate Plasma Coupling Coefficient | |
| Skin Depth | |
| Path Difference | |
| Shock Wave Attenuation | |
| Ionization Potential | |
| Vacuum Permittivity | |
| Plasma Permittivity | |
| Reference Plastic Strain | |
| AI Rate | |
| Electron Diffusion Rate | |
| Electron–Hole Recombination Rate | |
| Thermal Diffusivity | |
| Laser Wavelength | |
| De Broglie Length | |
| Permeability (Metal) | |
| Electron–Ion Collision Frequency | |
| Density | |
| Electrical Conduction (Metal) | |
| Elastic Limit | |
| Laser Pulse Duration (at FWHM) | |
| Magnetic Flux | |
| Angular Frequency | |
| Laplacian Differential Operator | |
| B | Magnetic Field |
| c | Speed of Light |
| C | Strain Rate Sensitivity |
| Bulk Sound Velocity | |
| e | Elementary Charge |
| E | Laser Energy (per Pulse) |
| Plasma Internal Energy | |
| Kinetic Energy | |
| Fermi Energy | |
| Potential Energy | |
| Electromagnetic Field | |
| f | Frequency |
| h | Planck Constant |
| I | Laser Intensity |
| Current Intensity | |
| K | Strain Hardening Modulus |
| Boltzmann Constant | |
| Electron Mass | |
| n | Optical Index |
| Strain Hardening Parameter | |
| Imaginary Part of the Optical Index | |
| Plasma Critical Density | |
| Electronic Density | |
| P | Plasma Pressure |
| Ferroelectric Polarization | |
| S | Hugoniot Constant |
| Laser Surface Spot Size | |
| t | Time |
| Electronic Temperature | |
| u | Material Velocity (under Shock) |
| Rear-Free Surface Velocity (under Shock) | |
| V | Plasma Volume |
| Voltage | |
| Z | Mechanical Impedance |
| Ionization State |
References
- Kearton, B.; Mattley, Y. Sparking New Applications. Nat. Photonics 2008, 2, 537–540. [Google Scholar] [CrossRef]
- Meijer, J. Laser beam machining (LBM), state ofthe art and new opportunities. J. Mater. Process. Technol. 2004, 149, 2–17. [Google Scholar] [CrossRef]
- Phipps, C.; Luke, J.; Helgeson, W. Laser space propulsion overview. Proc. SPIE 2007, 6606, 660602. [Google Scholar] [CrossRef]
- Jasim, H.; Demir, A.; Previtali, B.; Taha, Z. Process development and monitoring in stripping of a highly transparent polymeric paint with ns-pulsed fiber laser. Opt. Laser Technol. 2017, 93, 60–66. [Google Scholar] [CrossRef]
- Barletta, M.; Gisario, A.; Tagliaferri, V. Advance in paint stripping from aluminium subtrates. J. Mater. Process. Technol. 2006, 173, 232–239. [Google Scholar] [CrossRef]
- Berthe, L.; Arrigoni, M.; Boustie, M.; Cuq-Lelandais, J.; Broussillou, C.; Fabre, G.; Jeandin, M.; Guipond, V.; Nivard, M. State-of-the-art laser adhesion test (LASAT). Nondestruct. Test. Eval. 2011, 26, 303–317. [Google Scholar] [CrossRef]
- Sagnard, M.; Ecault, R.; Touchard, F.; Boustie, M.; Berthe, L. Development of the symmetrical laser shock test for weak bond inspection. Opt. Laser Technol. 2018, 111, 644–652. [Google Scholar] [CrossRef]
- Furfari, D. Laser Shock Peening to Repair, Design and Manufacture Current and Future Aircraft Structures by Residual Stress Engineering. Adv. Mater. Res. 2014, 891–892, 992–1000. [Google Scholar] [CrossRef]
- Pavan, M. Laser Shock Peening for Fatigue Life Enhancement of Aerospace Components. Ph.D. Thesis, Coventry University, Coventry, UK, 2017. [Google Scholar]
- Sano, Y.; Mukai, N.; Okazaki, K.; Obata, M. Residual stress improvement in metal surface by underwater laser irradiation. Nucl. Instrum. Methods Phys. Res. 1997, B121, 432–436. [Google Scholar] [CrossRef]
- Sano, Y.; Mukai, N.; Yoda, M.; Uehara, T.; Chida, I.; Obata, M. Development and Applications of Laser Peening without Coating as a Surface Enhancement Technology. Proc. SPIE 2006, 6343, 1–12. [Google Scholar] [CrossRef]
- Sano, Y. Quarter Century Development of Laser Peening without Coating. Metals 2020, 10, 152. [Google Scholar] [CrossRef]
- Tenaglia, R.; Lahrman, D. Shock tactics. Nat. Photonics 2009, 3, 267–270. [Google Scholar] [CrossRef]
- Ganesh, P.; Sundar, R.; Kumar, H.; Kaul, R.; Ranganathan, K.; Hedaoo, P.; Tiwari, P.; Kukreja, L.; Oak, S.; Dasari, S.; et al. Studies on laser peening of spring steel for automotive applications. Opt. Laser Eng. 2012, 50, 678–686. [Google Scholar] [CrossRef]
- Sonntag, R.; Reinders, J.; Gibmeier, J.; Kretzer, J. Fatigue Performance of Medical Ti6Al4V Alloy after Mechanical Surface Treatments. Mech. Surf. Treat. FüR Med 2015, 10, 1–15. [Google Scholar] [CrossRef]
- Peyre, P.; Fabbro, R.; Merrien, P.; Lieurade, H.P. Laser shock processing of aluminium alloys. Application to high cycle fatigue behaviour. Mater. Sci. Eng. 1996, A210, 102–113. [Google Scholar] [CrossRef]
- Sano, Y.; Masaki, K.; Gushi, T.; Sano, T. Improvement in fatigue performance of friction stir welded A6061-T6aluminum alloy by laser peening without coating. Mater. Des. 2012, 36, 809–814. [Google Scholar] [CrossRef]
- Kashaev, N.; Ventzke, V.; Horstmann, M.; Chupakhin, S.; Riekehr, S.; Falck, R.; Maawad, E.; Staron, P.; Schell, N.; Huber, N. Effects of laser shock peening on the microstructure and fatigue crack propagation behaviour of thin AA2024 specimens. Int. J. Fatigue 2017, 98, 223–233. [Google Scholar] [CrossRef]
- Peyre, P.; Carboni, C.; Forget, P.; Beranger, G.; Lemaitre, C.; Stuart, D. Influence of thermal and mechanical surface modifications induced by laser shock processing on the initiation of corrosion pits in 316L stainless steel. J. Mater. Sci. 2007, 42, 6866–6877. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Chen, J.; Zhou, J.; Ge, M.; Lu, Y.; Li, X. Effects of laser shock peening on stress corrosion behavior of 7075 aluminum alloy laser welded joints. Mater. Sci. Eng. A 2015, 647, 7–14. [Google Scholar] [CrossRef]
- Anderholm, N.C. Laser-generated stress waves. Appl. Phys. Lett. 1970, 16, 113–115. [Google Scholar] [CrossRef]
- Berthe, L.; Fabbro, R.; Peyre, P.; Tollier, L.; Bartnicki, E. Laser shock processing of materials: Study of laser-induced breakdown in water confinement regime. Proc. SPIE 1996, 2789, 246–253. [Google Scholar] [CrossRef]
- Berthe, L.; Fabbro, R.; Peyre, P.; Bartnicki, E. Laser shock processing of materials: Experimental study of breakdown plasma effects at the surface of confining water. Proc. SPIE 1997, 3097, 570–575. [Google Scholar] [CrossRef]
- Berthe, L.; Fabbro, R.; Peyre, P.; Bartnicki, E. Experimental study of the transmission of breakdown plasma generated during laser shock processing. Eur. Phys. J. Appl. Phys. 1998, 3, 215–218. [Google Scholar] [CrossRef]
- Berthe, L.; Fabbro, R.; Peyre, P.; Tollier, L.; Bartnicki, E. Shock waves from a water-confined laser-generated plasma. J. Appl. Phys. 1997, 82, 2826–2832. [Google Scholar] [CrossRef]
- Berthe, L.; Fabbro, R.; Peyre, P.; Bartnicki, E. Wavelength dependent of laser shock-wave generation in the water-confinement regime. J. Appl. Phys. 1999, 85, 7552–7555. [Google Scholar] [CrossRef]
- Berthe, L.; Sollier, A.; Peyre, P.; Fabbro, R.; Bartnicki, E. The generation of laser shock waves in a water-confinement regime with 50 ns and 150 ns XeCl excimer laser pulses. J. Phys. D Appl. Phys. 2000, 33, 2142–2145. [Google Scholar] [CrossRef]
- Fabbro, R.; Fournier, J.; Ballard, P.; Devaux, D.; Virmont, J. Physical study of laser-produced plasma in confined geometry. J. Appl. Phys. 1990, 68, 775–784. [Google Scholar] [CrossRef]
- Zhang, W.; Yao, Y. Microscale Laser Shock Processing—Modeling, Testing, and Microstructure Characterization. J. Manuf. Process. 2001, 3, 128–143. [Google Scholar] [CrossRef]
- Zhang, W.; Yao, Y. Modeling and simulation improvement in laser shock processing. ICALEO 2001, 2001, 59–68. [Google Scholar] [CrossRef]
- Sollier, A.; Berthe, L.; Peyre, P.; Bartnicki, E.; Fabbro, R. Laser-matter interaction in laser shock processing. Proc. SPIE 2003, 4831, 463–467. [Google Scholar] [CrossRef]
- Wu, B.; Shin, Y. A self-closed thermal model for laser shock peening under the water confinement regime configuration and comparisons to experiments. J. Appl. Phys. 2005, 97, 113517. [Google Scholar] [CrossRef]
- Bardy, S.; Aubert, B.; Bergara, T.; Berthe, L.; Combis, P.; Hébert, D.; Lescoute, E.; Rouchausse, Y.; Videau, L. Development of a numerical code for laser-induced shock waves applications. Opt. Laser Technol. 2020, 124, 1–12. [Google Scholar] [CrossRef]
- Peyre, P.; Sollier, A.; Chaieb, I.; Berthe, L.; Bartnicki, E.; Braham, C.; Fabbro, R. FEM simulation of residual stresses induced by laser Peening. Eur. Phys. J. Appl. Phys. 2003, 23, 83–88. [Google Scholar] [CrossRef]
- Hfaiedh, N.; Peyre, P.; Song, H.; Popa, I.; Ji, V.; Vignal, V. Finite element analysis of laser shock peening of 2050-T8 aluminum alloy. Int. J. Fatigue 2015, 70, 480–489. [Google Scholar] [CrossRef]
- Berthe, L.; Sollier, A.; Peyre, P.; Fabbro, R. Study of plasma induced by laser in water confinement regime: Application to laser shock processing with and without thermal protective coating. ICALEO 2003, 2003, 1502. [Google Scholar] [CrossRef]
- Rondepierre, A.; Unaldi, S.; Rouchausse, Y.; Videau, L.; Fabbro, R.; Casagrande, O.; Simon-Boisson, C.; Besaucèle, H.; Castelnau, O.; Berthe, L. Beam size dependency of a laser-induced plasma in confined regime: Shortening of the plasma release. Influence on pressure and thermal loading. Opt. Laser Technol. 2021, 135, 106689. [Google Scholar] [CrossRef]
- Sakka, T.; Takatani, K.; Ogata, Y.; Mabuchi, M. Laser ablation at the solid–liquid interface: Transient absorption of continuous spectral emission by ablated aluminium atoms. J. Phys. D Appl. Phys. 2001, 35, 65–73. [Google Scholar] [CrossRef]
- Kanitz, A.; Kalus, M.R.; Gurevich, E.; Ostendorf, A.; Barcikowski, S.; Amans, D. Review on experimental and theoretical investigations of the early stage, femtoseconds to microseconds processes during laser ablation in liquid-phase for the synthesis of colloidal nanoparticles. Plasma Sources Sci. Technol. 2019, 28, 103001. [Google Scholar] [CrossRef]
- Berthe, L.; Sollier, A.; Peyre, P.; Carboni, C.; Bartnicki, E.; Fabbro, R. Physics of shock-wave generation by laser plasma in water confinement regime. Proc. SPIE 2000, 4065, 511–520. [Google Scholar] [CrossRef]
- Berthe, L.; Sollier, A.; Courapied, D.; Bartnicki, E. Laser interaction in water confinement regime for laser shock processing (LSP): Absorption measurements. ICALEO 2014, 2014, 552–555. [Google Scholar] [CrossRef]
- Max, C. Theory of the coronal plasma in laser-fusion targets. Phys. Laser Fusion 1981, I, 1–78. [Google Scholar] [CrossRef][Green Version]
- Mora, P. Theoretical model of absorption of laser light by a plasma. Phys. Fluids 1982, 25, 1051–1056. [Google Scholar] [CrossRef]
- Spitzer, L.; Härm, R. Transport Phenomena in a Completely Ionized Gas. Phys. Rev. 1953, 89, 977–981. [Google Scholar] [CrossRef]
- Garban-Labaune, C.; Fabre, E.; Max, C.; Amiranoff, F.; Fabbro, R.; Virmont, J.; Mead, W. Experimental results and theoretical analysis of the effect of wavelength absorption and hot-electron generation in laser-plasma interaction. Phys. Fluids 1985, 28, 2580–2590. [Google Scholar] [CrossRef]
- Pirri, A. Theory for momentum transfer to a surface with a high-power laser. Phys. Fluids 1973, 16, 1435–1440. [Google Scholar] [CrossRef]
- Pirri, A.; Root, R.; Wu, P. Plasma Energy Transfer to Metal Surfaces Irradiated by Pulsed Lasers. AIAA J. 1978, 16, 1296–1304. [Google Scholar] [CrossRef]
- Sollier, A.; Berthe, L.; Fabbro, R. Numerical modeling of the transmission of breakdown plasma generated in water during laser shock processing. Eur. Phys. J. Appl. Phys. 2001, 16, 131–139. [Google Scholar] [CrossRef]
- Wu, B.; Shin, Y. Laser pulse transmission through the water breakdown plasma in laser shock peening. Appl. Phys. Lett. 2006, 88, 041116. [Google Scholar] [CrossRef]
- Kennedy, P. A fist-order model for computation of laser-induced breakdown thresholds in ocular and aqueous media: Part I—Theory. IEEE J. Quantum Electron. 1995, 31, 2241–2250. [Google Scholar] [CrossRef]
- Keldish, L. Ionization in the field of a strong electromagnetic wave. Sov. Phys. JETP 1965, 20, 1307–1314. [Google Scholar]
- Grey Morgan, C. Laser-induced breakdown of gases. Rep. Prog. Phys. 1975, 38, 621–665. [Google Scholar] [CrossRef]
- Scius-Bertrand, M.; Videau, L.; Rondepierre, A.; Lescoute, E.; Rouchausse, Y.; Kaufman, J.; Rostohar, D.; Brajer, J.; Berthe, L. Laser induced plasma characterization in direct and water confined regimes: New advances in experimental studies and numerical modelling. J. Phys. D Appl. Phys. 2020, 54, 055204. [Google Scholar] [CrossRef]
- Rondepierre, A.; Rouchausse, Y.; Videau, L.; Casagrande, O.; Castelnau, O.; Berthe, L. Laser interaction in a water tank configuration: Higher confinement breakdown threshold and greater generated pressures for laser shock peening. J. Laser Appl. 2021, 33. [Google Scholar] [CrossRef]
- Fabbro, R.; Peyre, P.; Berthe, L.; Scherpereel, X. Physics and applications of laser-shock processing. J. Laser Appl. 1998, 10, 265–279. [Google Scholar] [CrossRef]
- Peyre, P.; Carboni, C.; Sollier, A.; Berthe, B.; Richard, C.; de Los Rios, E.; Fabbro, R. New trends in laser shock wave physics and applications. Proc. SPIE 2002, 4760, 654–666. [Google Scholar] [CrossRef]
- Peyre, P. Laser Shock Processing on Metal. Metals 2017, 7, 409. [Google Scholar] [CrossRef]
- Clauer, A. Laser Shock Peening, the Path to Production. Metals 2019, 9, 626. [Google Scholar] [CrossRef]
- Zhang, D.; Gökce, B.; Barcikowski, S. Laser Synthesis and Processing of Colloids: Fundamentals and Applications. Chem. Rev. 2017, 117, 3990–4103. [Google Scholar] [CrossRef]
- Amans, D.; Cai, W.; Barcikowski, S. Status and demand of research to bring laser generation of nanoparticles in liquids to maturity. Appl. Surf. Sci. 2019, 488, 445–454. [Google Scholar] [CrossRef]
- Matsumoto, A.; Sakka, T. A review of underwater laser-induced breakdown spectroscopy of submerged solids. Anal. Sci. 2020, in press. [Google Scholar] [CrossRef]
- Nguyen, T.; Tanabe, R.; Ito, Y. Comparative study of the expansion dynamics of laser-driven plasma and shock wave in in-air and underwater ablation regimes. Opt. Laser Technol. 2018, 100, 21–26. [Google Scholar] [CrossRef]
- Saito, K.; Takatani, K.; Sakka, T.; Ogata, Y. Observation of the light emitting region produced by pulsed laser irradiation to a solid–liquid interface. Appl. Surf. Sci. 2002, 197–198, 56–60. [Google Scholar] [CrossRef]
- Oguchi, H.; Sakka, T.; Ogata, Y. Effects of pulse duration upon the plume formation by the laser ablation of Cu in water. J. Appl. Phys. 2007, 102, 023306. [Google Scholar] [CrossRef]
- Takada, N.; Nakano, T.; Sasaki, K. Influence of additional external pressure on optical emission intensity in liquid-phase laser ablation. Appl. Surf. Sci. 2009, 255, 9572–9575. [Google Scholar] [CrossRef]
- Dell’Aglio, M.; Santagata, A.; Valenza, G.; DeStradis, A.; DeGiacomo, A. Study of the effect of water pressure on plasma and cavitation bubble induced by pulsed laser ablation in liquid of silver and missed variations of observable nanoparticle features. ChemPhysChem 2017, 18, 1165–1174. [Google Scholar] [CrossRef]
- Ilyin, A.; Bukin, O.; Bulanov, A. Regimes of laser plasma expansion at optical breakdown in the normal atmosphere. Tech. Phys. 2008, 53, 693–696. [Google Scholar] [CrossRef]
- Raǐzer, Y.P. Heating of a Gas by a Powerful Light Pulse. Sov. Phys. JETP 1965, 21, 1009–1017. [Google Scholar]
- Sakka, T.; Iwanaga, S.; Ogata, Y.; Matsunawa, A.; Takemoto, T. Laser ablation at solid–liquid interfaces: An approach from optical emission spectra. J. Chem. Phys. 2000, 112, 8645–8653. [Google Scholar] [CrossRef]
- Sakka, T.; Saito, K.; Ogata, Y. Emission spectra of the species ablated from a solid target submerged in liquid: Vibrational temperature of C2 molecules in water-confined geometry. Appl. Surf. Sci. 2002, 197–198, 246–250. [Google Scholar] [CrossRef]
- Saito, K.; Sakka, T.; Ogata, Y. Rotational spectra and temperature evaluation of C2 molecules produced by pulsed laser irradiation to a graphite–water interface. J. Appl. Phys. 2003, 94, 5530–5536. [Google Scholar] [CrossRef]
- Sakka, T.; Saito, K.; Ogata, Y. Confinement effect of laser ablation plume in liquids probed by self-absorption of C2 Swan band emission. J. Appl. Phys. 2005, 97, 014902. [Google Scholar] [CrossRef]
- Sakka, T.; Oguchi, H.; Masai, S.; Hirata, K.; Ogata, Y.; Saeki, M.; Ohba, H. Use of a long-duration ns pulse for efficient emission of spectral lines from the laser ablation plume in water. Appl. Phys. Lett. 2006, 88, 061120. [Google Scholar] [CrossRef]
- Sakka, T.; Yamagata, H.; Oguchi, H.; Fukami, K.; Ogata, Y. Emission spectroscopy of laser ablation plume: Composition analysis of a target in water. Appl. Surf. Sci. 2009, 255, 9576–9580. [Google Scholar] [CrossRef]
- Sakka, T.; Masai, S.; Fukami, K.; Ogata, Y. Spectral profile of atomic emission lines and effects of pulse duration on laser ablation in liquid. Spectrochim. Acta Part B At. Spectrosc. 2009, 64, 981–985. [Google Scholar] [CrossRef]
- Tamura, A.; Matsumoto, A.; Fukami, K.; Nishi, N.; Sakka, T. Simultaneous observation of nascent plasma and bubble induced by laser ablation in water with various pulse durations. J. Appl. Phys. 2015, 117, 173304. [Google Scholar] [CrossRef]
- Matsumoto, A.; Tamura, A.; Honda, T.; Hirota, T.; Kobayashi, K.; Katakura, S.; Nishi, N.; Amano, K.; Fukami, K.; Sakka, T. Transfer of the Species Dissolved in a Liquid into Laser Ablation Plasma: An Approach Using Emission Spectroscopy. J. Phys. Chem. C 2015, 119, 26506–26511. [Google Scholar] [CrossRef]
- Lam, J.; Amans, D.; Chaput, F.; Diouf, M.; Ledoux, G.; Mary, N.; Masenelli-Varlot, K.; Motto-Ros, V.; Dujardin, C. γ-Al2O3 nanoparticles synthesised by pulsed laser ablation in liquids: A plasma analysis. Phys. Chem. Chem. Phys. 2014, 16, 963–973. [Google Scholar] [CrossRef]
- Amans, D.; Chenus, A.C.; Ledoux, G.; Dujardin, C.; Reynaud, C.; Sublemontier, O.; Masenelli-Varlot, K.; Guillois, O. Nanodiamond synthesis by pulsed laser ablation in liquids. Diam. Relat. Mater. 2009, 18, 177–180. [Google Scholar] [CrossRef]
- Kumar, B.; Thareja, R. Synthesis of nanoparticles in laser ablation of aluminum in liquid. J. Appl. Phys. 2010, 108, 064906. [Google Scholar] [CrossRef]
- Kumar, B.; Yadav, D.; Thareja, R. Growth dynamics of nanoparticles in laser produced plasma in liquid ambient. J. Appl. Phys. 2011, 110, 074903. [Google Scholar] [CrossRef]
- Kumar, B.; Thareja, R. Laser ablated copper plasmas in liquid and gas ambient. Phys. Plasmas 2013, 20, 053503. [Google Scholar] [CrossRef]
- De Giacomo, A.; Dell’Aglio, M.; Santagata, A.; Gaudiuso, R.; De Pascale, O.; Wagener, P.; Messina, G.C.; Compagnini, G.; Barcikowski, S. Cavitation dynamics of laser ablation of bulk and wire-shaped metals in water during nanoparticles production. Phys. Chem. Chem. Phys. 2013, 15, 3083–3092. [Google Scholar] [CrossRef] [PubMed]
- Dell’Aglio, M.; Gaudiuso, R.; DePascale, O.; DeGiacomo, A. Mechanisms and processes of pulsed laser ablation in liquids during nanoparticle production. Appl. Surf. Sci. 2015, 348, 4–9. [Google Scholar] [CrossRef]
- Amans, D.; Diouf, M.; Lam, J.; Ledoux, G.; Dujardin, C. Origin of the nano-carbon allotropes in pulsed laser ablation in liquids synthesis. J. Colloid Interface Sci. 2017, 489, 114–125. [Google Scholar] [CrossRef] [PubMed]
- Shih, C.Y.; Shugaev, M.; Wu, C.; Zhigilei, L. Generation of Subsurface Voids, Incubation Effect, and Formation of Nanoparticles in Short Pulse Laser Interactions with Bulk Metal Targets in Liquid: Molecular Dynamics Study. J. Phys. Chem. C 2017, 121, 16549–16567. [Google Scholar] [CrossRef] [PubMed]
- Shih, C.Y.; Wu, C.; Shugaev, M.; Zhigilei, L. Atomistic modeling of nanoparticle generation in short pulse laser ablation of thin metal films in water. J. Colloid Interface Sci. 2017, 489, 3–17. [Google Scholar] [CrossRef] [PubMed]
- Shugaev, M.; Shih, C.Y.; Karim, E.; Wu, C.; Zhigilei, L. Generation of nanocrystalline surface layer in short pulse laser processing of metal targets under conditions of spatial confinement by solid or liquid overlayer. Appl. Surf. Sci. 2017, 417, 54–63. [Google Scholar] [CrossRef]
- Romain, J.P.; Zagouri, D. Laser-shock studies using an electromagnetic gauge for particle velocity measurements. In Shock Compression of Condensed Matter–1991; Schmidt, S., Dick, R., Forbes, J., Tasker, D., Eds.; Elsevier: Amsterdam, The Netherlands, 1992; pp. 801–804. [Google Scholar] [CrossRef]
- Peyre, P.; Fabbro, R. Electromagnetic Gauge Study of Laser-Induced Shock Waves in Aluminium Alloys. J. Phys. III France 1995, 5, 1953–1964. [Google Scholar] [CrossRef]
- Peyre, P.; Berthe, L.; Fabbro, R.; Sollier, A. Experimental determination by PVDF and EMV techniques of shock amplitudes induced by 0.6–3 ns laser pulses in a confined regime with water. J. Phys. D Appl. Phys. 2000, 33, 498–503. [Google Scholar] [CrossRef]
- Romain, J.; Bauer, F.; Zagouri, D.; Boustie, M. Measurement of laser induced shock pressures using PVDF gauges. AIP Conf. Proc. 1994, 309, 1915–1918. [Google Scholar] [CrossRef]
- Boustie, M.; Couturier, S.; Zagouri, D.; Simonnet, H. Shock pressure and free surface velocity measurements in confined interaction—Response of new VF2/VF3 piezoelectric gauges. Laser Part. Beams 1996, 14, 171–179. [Google Scholar] [CrossRef]
- Strand, O.; Goosman, D.; Martinez, C.; Whitworth, T.; Kuhlow, W. Compact system for high-speed velocimetry using heterodyne techniques. Rev. Sci. Instruments 2006, 77, 083108. [Google Scholar] [CrossRef]
- Dolan, D. Extreme measurements with Photonic Doppler Velocimetry (PDV). Rev. Sci. Instruments 2020, 91, 051501. [Google Scholar] [CrossRef] [PubMed]
- Dolan, D. Accuracy and precision in photonic Doppler velocimetry. Rev. Sci. Instruments 2010, 81, 053905. [Google Scholar] [CrossRef]
- Valenzuela, A.; Rodriguez, G.; Clarke, S.; Thomas, K. Photonic Doppler Velocimetry of laser-ablated ultrathin metals. Rev. Sci. Instruments 2007, 78, 013101. [Google Scholar] [CrossRef]
- Mercier, P.; Bénier, J.; Frugier, P.; Sollier, A.; Le Gloahec, M.R.; Lescoute, E.; Cuq-Lelandais, J.P.; Boustie, M.; de Rességuier, T.; Claverie, A.; et al. PDV measurements of ns and fs laser driven shock experiments on solid targets. AIP Conf. Proc. 2009, 1195, 581–584. [Google Scholar] [CrossRef]
- Nissim, N.; Greenberg, E.; Werdiger, M.; Horowitz, Y.; Bakshi, L.; Ferber, Y.; Glam, B.; Fedotov-Gefen, A.; Perelmutter, L.; Eliezer, S. Free-surface velocity measurements of opaque materials in laser-driven shock-wave experiments using photonic Doppler velocimetry. Matter Radiat. Extrem. 2021, 6, 046902. [Google Scholar] [CrossRef]
- Bovid, S.; Clauer, A.; Kattoura, M.; Vivek, A.; Daehn, G.; Niezgoda, S. Measurement and characterization of nanosecond laser driven shockwaves utilizing photon Doppler velocimetry. J. Appl. Phys. 2021, 129, 205101. [Google Scholar] [CrossRef]
- Barker, L.; Hollenbach, R. Laser interferometer for measuring high velocities of any reflecting surface. J. Appl. Phys. 1972, 43, 4669–4675. [Google Scholar] [CrossRef]
- Thomas, W.; Threadgill, P.; Nicholas, E. Feasibility of friction stir welding steel. Sci. Technol. Weld. Join. 1999, 4, 365–372. [Google Scholar] [CrossRef]
- Boustie, M.; Cuq-Lelandais, J.; Berthe, L.; Bolis, C.; Barradas, S.; Arrigoni, M.; De Resseguier, T.; Jeandin, M. Damaging of material by bi-dimensional dynamic effects. AIP Conf. Proc. 2007, 955, 1323–1326. [Google Scholar] [CrossRef]
- Boustie, M.; Cuq-Lelandais, J.; Bolis, C.; Berthe, L.; Barradas, S.; Arrigoni, M.; de Resseguier, T.; Jeandin, M. Study of damage phenomena induced by edge effects into materials under laser driven shocks. J. Phys. D Appl. Phys. 2007, 40, 7103–7108. [Google Scholar] [CrossRef]
- Johnson, G.; Cook, W. A constitutive model and data for materials subjected to large strains, high-strain rates and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983; pp. 541–547. [Google Scholar]
- Radziejewska, J.; Strzelec, M.; Ostromski, R.; Sarzynski, A. Experimental investigation of shock wave pressure induced by a ns laser pulse under varying confined regimes. Opt. Laser Eng. 2019, 126. [Google Scholar] [CrossRef]
- Peyre, P.; Chaieb, I.; Braham, C. FEM calculation of residual stresses induced by laser shock processing in stainless steels. Model. Simul. Mater. Sci. Eng. 2007, 15, 205–221. [Google Scholar] [CrossRef]
- Fairand, B.; Clauer, A.; Jung, R.; Wilcox, B. Quantitative assessment of laser-induced stress waves generated at confined surfaces. Appl. Phys. Lett. 1974, 25, 431–433. [Google Scholar] [CrossRef]
- Fairand, B.; Clauer, A. Laser generation of high-amplitude stress waves in materials. J. Appl. Phys. 1979, 50, 1497–1502. [Google Scholar] [CrossRef]
- Fairand, B.; Clauer, A. Laser generated stress waves: Their characteristics and their effects to materials. AIP Conf. Proc. 1979, 50, 27–42. [Google Scholar] [CrossRef]
- Clauer, A.; Holbrook, J.; Fairand, B. Effects of Laser Induced Shock Waves on Metals. In Shock Waves and High-Strain-Rate Phenomena in Metals: Concepts and Applications; Springer: Boston, MA, USA, 1981; pp. 675–702. [Google Scholar] [CrossRef]
- Colvin, J.; Ault, E.; King, W.; Zimmerman, I. Computational model for a low-temperature laser-plasma driver for shock-processing of metals and comparison to experimental data. Phys. Plasmas 2003, 10, 2940–2947. [Google Scholar] [CrossRef]
- Ocaña, J.; Morales, M.; Molpeceres, C.; Torres, J. Numerical simulation of surface deformation and residual stresses fields in laser shock processing experiments. Appl. Surf. Sci. 2004, 238, 242–248. [Google Scholar] [CrossRef]
- Morales, M.; Ocaña, J.; Molpeceres, C.; Porro, J.; García-Beltrán, A. Model based optimization criteria for the generation of deep compressive residual stress fields in high elastic limit metallic alloys by ns-laser shock processing. Surf. Coatings Technol. 2008, 202, 2257–2262. [Google Scholar] [CrossRef]
- Morales, M.; Porro, J.; Blasco, M.; Molpeceres, C.; Ocaña, J. Numerical simulation of plasma dynamics in laser shock processing experiments. Appl. Surf. Sci. 2009, 255, 5181–5185. [Google Scholar] [CrossRef]
- Griffin, R.; Justus, B.; Campillo, A.; Goldberg, L. Interferometric studies of the pressure of a confined laser-heated plasma. J. Appl. Phys. 1986, 59, 1968–1971. [Google Scholar] [CrossRef]
- Wu, B.; Shin, Y. A one-dimensional hydrodynamic model for pressures induced near the coating-water interface during laser shock peening. J. Appl. Phys. 2007, 101, 023510. [Google Scholar] [CrossRef]
- Wu, B.; Shin, Y. Two dimensional hydrodynamic simulation of high pressures induced by high power nanosecond laser-matter interactions under water. J. Appl. Phys. 2007, 101, 103514. [Google Scholar] [CrossRef]
- Colombier, J.; Combis, P.; Bonneau, F.; Le Harzic, R.; Audouard, E. Hydrodynamic simulations of metal ablation by femtosecond laser irradiation. Phys. Rev. B 2005, 71, 165406. [Google Scholar] [CrossRef]
- Faussurier, G.; Blancard, C.; Combis, P.; Decoster, A.; Videau, L. Electronic transport coefficients in plasmas using an effective energy-dependent electron-ion collision-frequency. Phys. Plasmas 2017, 24. [Google Scholar] [CrossRef]
- Heya, M.; Furukawa, H.; Tsuyama, M.; Nakano, H. Simulations of the effects of laser wavelength, pulse duration, and power density on plume pressure generation using a one-dimensional simulation code for laser shock processing. J. Appl. Phys. 2021, 129, 1–21. [Google Scholar] [CrossRef]
- Ballard, P. Contraintes réSiduelles Induites par Impact Rapide. Application au Choc-Laser. Ph.D. Thesis, Ecole Polytechnique, Palaiseau, France, 1991. Available online: https://pastel.archives-ouvertes.fr/pastel-00001897 (accessed on 7 November 2021).
- Seddik, R.; Rondepierre, A.; Prabhakaran, S.; Morin, L.; Favier, V.; Palin-Luc, T.; Berthe, L. Identification of constitutive equations at very high strain rates using shock wave produced by laser. Eur. J. Mech. A Solids 2021, 92, 104432. [Google Scholar] [CrossRef]
- Ayad, M.; Rondepierre, A.; Lapostolle, L.; Le Bras, C.; Unaldi, S.; Trdan, U.; Rouchausse, Y.; Grassy, J.; Maillot, T.; Berthe, L. High Strain Rate Laser Shock Propagation through Aluminum Alloys. 2021; in press. [Google Scholar]
- Ayad, M.; Berthe, L.; Rondepierre, A.; Donik, C.; Klobcar, D.; Trdan, U. Material Model Characterization of Dissimilar 7075-2017 Friction stir Welded Aluminum Alloy Joint under High-Strain Rate Shock Loading. 2021; in press. [Google Scholar]


| Alloy | (MPa) | K (MPa) | C | ||
|---|---|---|---|---|---|
| Al-2024 | 1028 | 329 | 0.35 | 0.025 | 0.01 |
| Al-7175 | 920 | 0 | 0 | 0.01 | 0.01 |
| Alloy | (MPa) | K (MPa) | C | |
|---|---|---|---|---|
| Al-2024 | 369 | 329 | 0.35 | 0.025 |
| Al-2017 (CS/IP) | 260/270 | 700/350 | 0.6/0.3 | 0.035/0.03 |
| Al-7075 (CS/IP) | 400/473 | 800/210 | 0.45/0.38 | 0.05/0.033 |
| FSW (2017 + 7075) (CS/IP) | 285/340 | 500/200 | 0.35/0.2 | 0.033/0.017 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rondepierre, A.; Sollier, A.; Videau, L.; Berthe, L. Review on Laser Interaction in Confined Regime: Discussion about the Plasma Source Term for Laser Shock Applications and Simulations. Metals 2021, 11, 2032. https://doi.org/10.3390/met11122032
Rondepierre A, Sollier A, Videau L, Berthe L. Review on Laser Interaction in Confined Regime: Discussion about the Plasma Source Term for Laser Shock Applications and Simulations. Metals. 2021; 11(12):2032. https://doi.org/10.3390/met11122032
Chicago/Turabian StyleRondepierre, Alexandre, Arnaud Sollier, Laurent Videau, and Laurent Berthe. 2021. "Review on Laser Interaction in Confined Regime: Discussion about the Plasma Source Term for Laser Shock Applications and Simulations" Metals 11, no. 12: 2032. https://doi.org/10.3390/met11122032
APA StyleRondepierre, A., Sollier, A., Videau, L., & Berthe, L. (2021). Review on Laser Interaction in Confined Regime: Discussion about the Plasma Source Term for Laser Shock Applications and Simulations. Metals, 11(12), 2032. https://doi.org/10.3390/met11122032






