Mathematical Modelling for Furnace Design Refining Molten Aluminum
Abstract
:1. Introduction
2. Mathematical Modelling
2.1. Boundary Conditions
2.2. Discretization
2.2.1. Discretization for Momentum Equation
2.2.2. Discretization for Continuity Equation
3. Simulation-Based Design
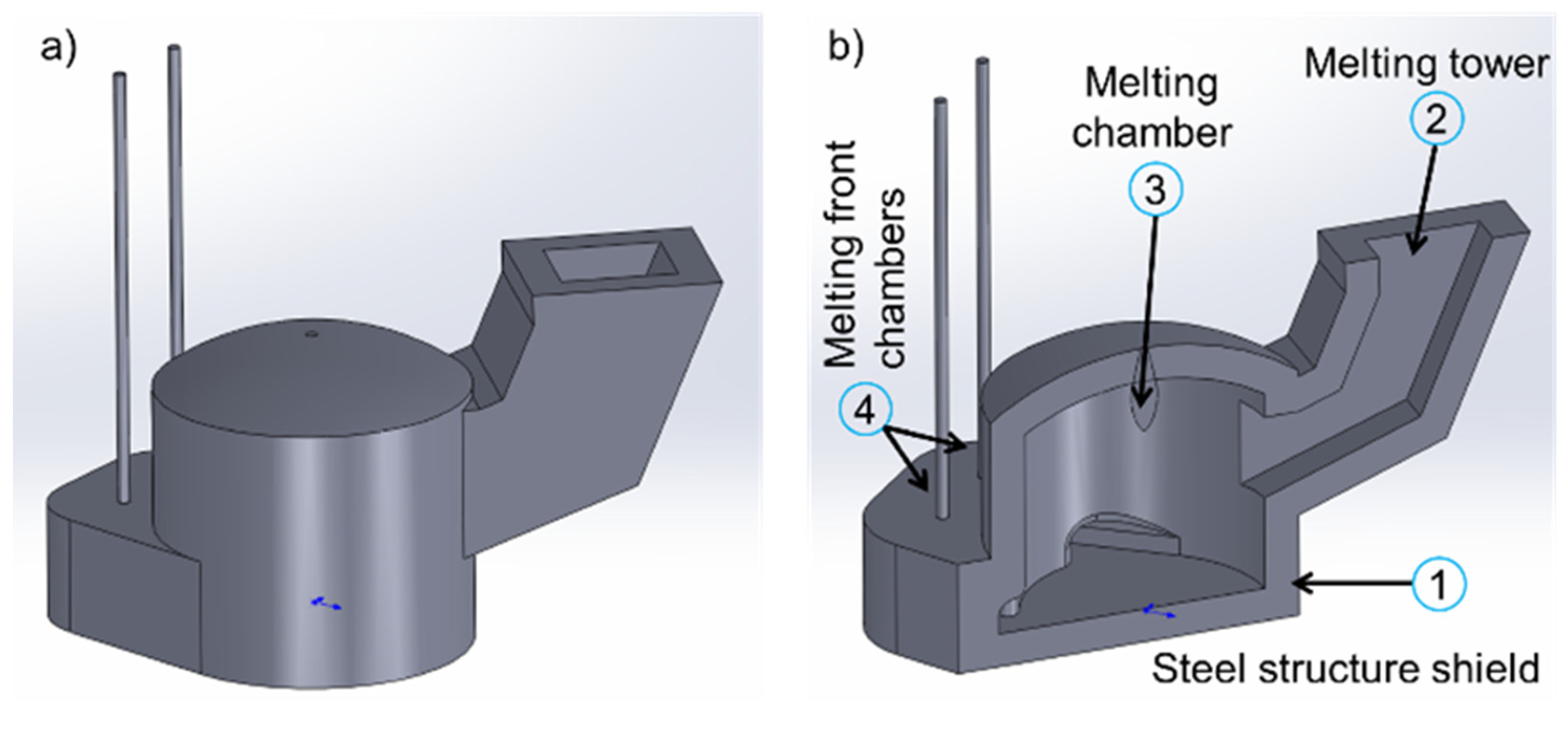
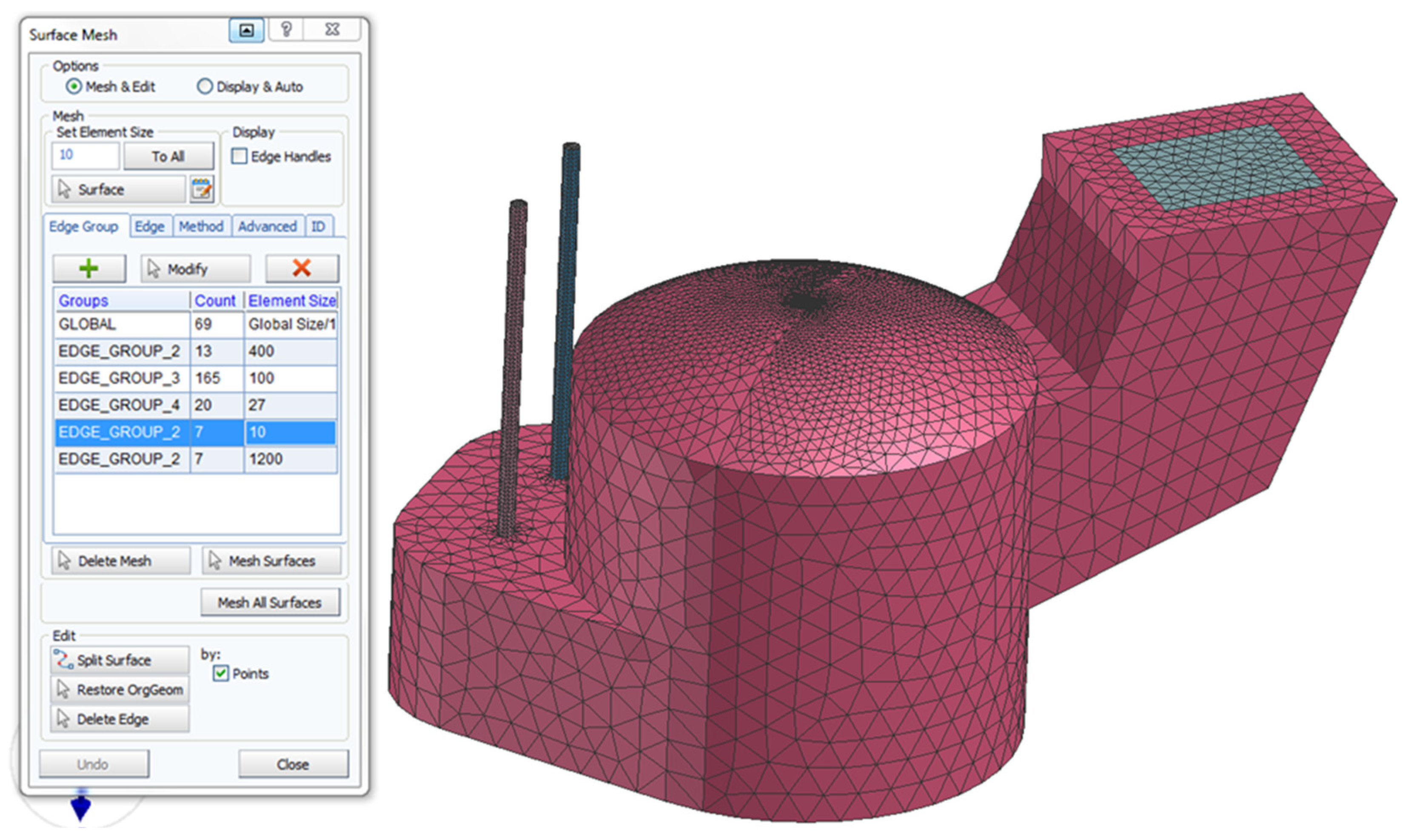
3.1. CFD Meshing for Simulations
3.2. Simulation-Based Design Settings
4. Analysis and Optimization
4.1. Energy Balance Analysis
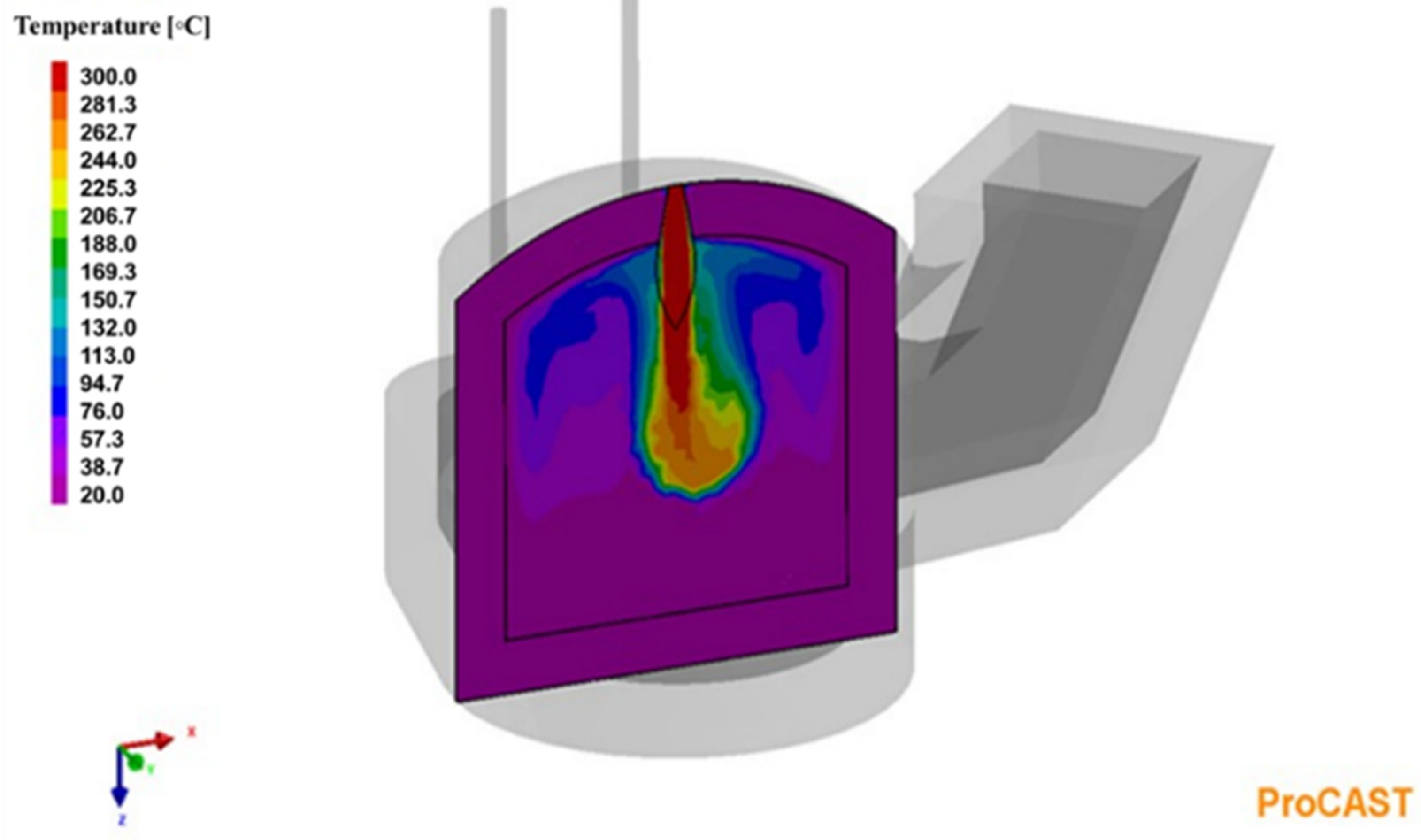
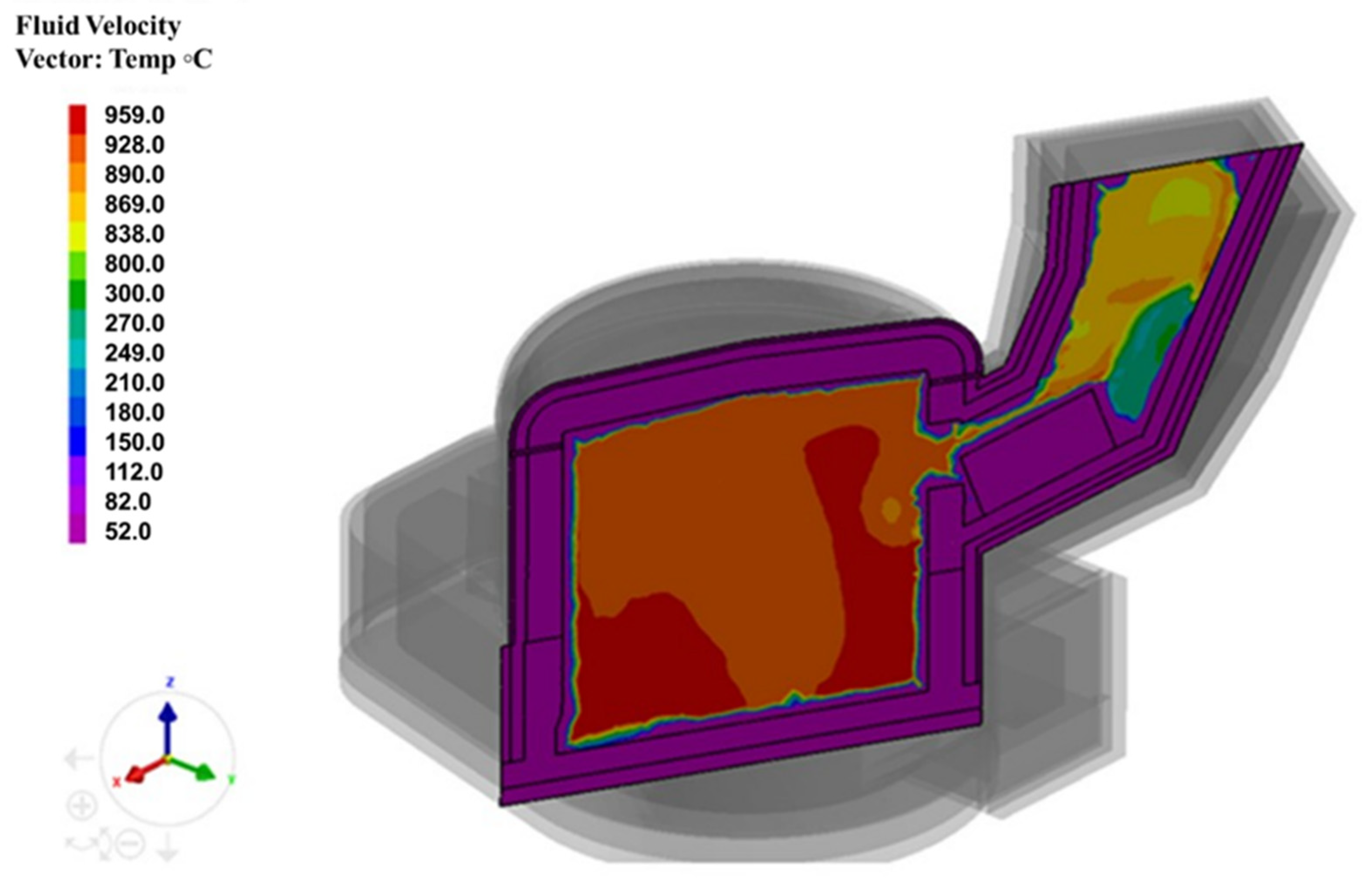
4.2. Temperature Profile
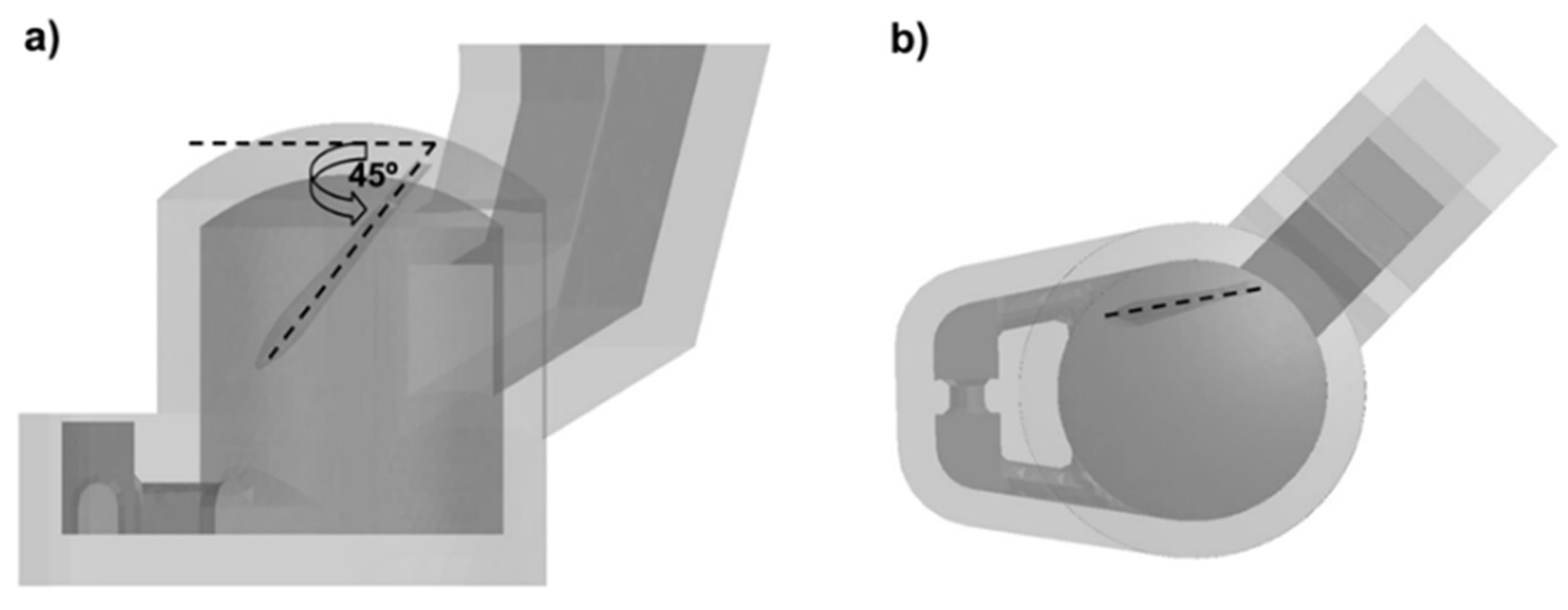
4.3. Optimization Conditions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Mathematical Expression | Equation Number | Description | Units |
| (1) | Fluid density | kg/m3 | |
| (1) | Time | s | |
| (1) | Flow velocity vector field | m/s | |
| (2) | Momentum per unit volume | kg⋅m/s | |
| (2) | gravitational force per unit volume | m/s2 | |
| (2) | Stress tensor | N/m2 | |
| (2) | Molecular viscosity | kg⋅m⋅s | |
| (2) | Bulk viscosity coefficient | kg⋅m⋅s | |
| (9) | Internal energy | kcal | |
| h | (9) | Enthalpy value | kJ/kg |
| (10) | Turbulent kinetic energy | m2/s2 | |
| (10) | Production of turbulence kinetic energy | m2/s3 | |
| (10) | Rate of turbulent kinetic energy dissipation | m2/s3 | |
| (11) | Concentration constant | ||
| (12) | Eddy viscosity | kg·m−1·s−1 | |
| (14) | FEM shape function i | ||
| (17) | Dynamic viscosity | kg/s·m | |
| (18) | Moment | kg·m2/s2 | |
| (18) | Deformation rate tensor | N/m2 | |
| (18) | Source term for gravity vector | ||
| (18) | Source term for density | ||
| (19) | Angle | ||
| (20) | Coefficient for continuity | ||
| (20) | Nodal velocities | m/s | |
| (20) | Tangential friction factor, generic variable | ||
| (24) | Source term for internal energy | ||
| (24) | Source term for density |
Appendix B
- Pressure gradients at continuous rate
- Furnace inner wall at an initial temperature of 950 °C
- Air inside the furnace at an initial temperature of 750 °C
- Room temperature 20 °C
- A boundary condition is selected of “air cooling” at a temperature of 20 °C
- Air properties were selected a temperature range of 20 to 1000 °C such as thermic conductivity (Wm/K), density (kg/m2), specific heat (KJ, Kg/Kg-K), and Newtonian viscosity (centipoise)
- The geometry of the processing aluminium chip used was spherical shape of 1 cm of diameter.
- The chemical composition of the aluminium chip used for the simulation was a homogeneous mix according to the AA390 norm.
References
- Qiu, L.; Feng, Y.; Chen, Z.; Li, Y.; Zhang, X. Numerical simulation and optimization of the melting process for the regenerative aluminum melting furnace. Appl. Therm. Eng. 2018, 145, 315–327. [Google Scholar] [CrossRef]
- Grachev, V. Aluminium Alloys Smelting in Shaft-Reverberatory Furnaces in a Liquid Bath Mode. Arch. Foundry Eng. 2017, 17, 183–189. [Google Scholar] [CrossRef]
- Heugenhauser, S.; Kaschnitz, E.; Schumacher, P. Development of an aluminum compound casting process—Experiments and numerical simulations. J. Mater. Process. Technol. 2020, 279, 116578. [Google Scholar] [CrossRef]
- Zhan, X.; Wang, Z.; Li, M.; Hu, Q.; Chen, J. Investigations on failure-to-fracture mechanism and prediction of forming limit for aluminum alloy incremental forming process. J. Mater. Process. Technol. 2020, 282, 116687. [Google Scholar] [CrossRef]
- Jepson, S.; Kim, H. Calculated Aluminum Oxidation Rates during Rotary Furnace Melting through Flue Gas Analysis—Part Two. In Light Metals 2016; Williams, E., Ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 767–771. [Google Scholar]
- Wei, X.; Wang, H.; Liu, C.; Cao, H.; Yan, P.; Sun, Z. A review on recycling of waste aluminum alloy. A review on recycling of waste/Chin. J. Process. Eng. 2019, 19, 45–54. [Google Scholar]
- Haraldsson, J.; Johansson, M.T. Review of measures for improved energy efficiency in production-related processes in the aluminium industry—From electrolysis to recycling. Renew. Sustain. Energy Rev. 2018, 93, 525–548. [Google Scholar] [CrossRef] [Green Version]
- Brimmo, A.T.; Hassan, M.I. Furnace Modeling for Efficient Combustion Gas Circulation. In Light Metals 2016; Williams, E., Ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 757–761. [Google Scholar]
- Wan, B.; Chen, W.; Mao, M.; Fu, Z.; Zhu, D. Numerical simulation of a stirring purifying technology for aluminum melt. J. Mater. Process. Technol. 2018, 251, 330–342. [Google Scholar] [CrossRef]
- Sviželová, J.; Tkadlečková, M.; Michalek, K.; Walek, J.; Saternus, M.; Pieprzyca, J.; Merder, T. Numerical Modelling Of Metal Melt Refining Process In Ladle With Rotating Impeller And Breakwaters. Arch. Metall. Mater. 2019, 64, 659–664. [Google Scholar]
- Brimmo, A.T.; Hassan, M.I.; Shatilla, Y. Transient heat transfer computational model for the stopped aluminium reduction pot —Cooling techniques evaluation. Appl. Therm. Eng. 2014, 73, 116–127. [Google Scholar] [CrossRef]
- Popa, M.; Sava, I.; Petre, M.; Ducu, C.; Moga, S.; Nicola, A.-V.; Drăghici, C.-N. Coupled Fluid Flow and Heat Transfer Analysis of Ageing Heat Furnace. In Book Coupled Fluid Flow and Heat Transfer Analysis of Ageing Heat Furnace; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 279–284. [Google Scholar]
- Hassan, M.I.; Brimmo, A.T. CFD Comparison of Immersed Heater and Open Fire Burner Designs for Casting Furnaces. In Light Metals 2015; Hyland, M., Ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 915–920. [Google Scholar]
- Niehoff, T.; Viyyuri, S. Oxyfuel Optimization using CFD Modeling. In Light Metals 2011; Lindsay, S.J., Ed.; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 1185–1187. [Google Scholar]
- Walter, G.; Kiss, L.; Charette, A.; Goutière, V. Flame Object Heat Transfer using Different Burner Types and Orientations. TMS Light Met. 2006, 2006, 741–746. [Google Scholar]
- Li, T.X.; Hassan, M.; Kuwana, K.; Saito, K.; Viswanathan, S.; Han, Q.; King, P. Thermodynamic analyses of energy utilization and pollutant formation control in secondary aluminum melting furnaces. In Proceedings of the Technical Sessions Presented by the Materials Processing and Manufacturing Division of TMS, San Diego, CA, USA, 2–6 March 2003. [Google Scholar]
- Golchert, B.; Ridenour, P.; Walker, W.; Selvarasu, N.K.; Gu, M.; Zhou, C.Q. Effect of Nitrogen and Oxygen Concentration on NOx Emissions in an Aluminum Furnace. In Effect of Nitrogen and Oxygen Concentration on NOx Emissions in an Aluminum Furnace; ASME: New York, NY, USA, 2006; pp. 323–333. [Google Scholar]
- Juárez, R.; Flores, A.; Macias, E.; Reyes, N. Análisis del comportamiento de flujo de fluidos en un horno de reverbero agitado con diferentes impulsores, mediante la modelación física y numérica. Rev. De Metal. 2009, 45, 384–396. [Google Scholar] [CrossRef]
- Viswanath, A.; Manu, M.V.; Savithri, S.; Pillai, U.T.S. Numerical simulation and experimental validation of free surface flows during low pressure casting process. J. Mater. Process. Technol. 2017, 244, 320–330. [Google Scholar] [CrossRef]
- Humphreys, N.J.; McBride, D.; Shevchenko, D.M.; Croft, T.N.; Withey, P.; Green, N.R.; Cross, M. Modelling and validation: Casting of Al and TiAl alloys in gravity and centrifugal casting processes. Appl. Math. Model. 2013, 37, 7633–7643. [Google Scholar] [CrossRef]
- Malikov, Z.M. Mathematical model of turbulent heat transfer based on the dynamics of two fluids. Appl. Math. Model. 2021, 91, 186–213. [Google Scholar] [CrossRef]
- Patankar, S.V. Computational modeling of flow and heat transfer in industrial applications. Int. J. Heat Fluid Flow 2002, 23, 222–231. [Google Scholar] [CrossRef]
- Wang, Z.H.; Wang, J.; Yu, L.B.; Wu, J.; Wang, M.; Su, B. Numerical Simulation and Process Optimization of Vacuum Investment Casting for Be–Al Alloys. Int. J. Met. 2019, 13, 74–81. [Google Scholar] [CrossRef]
- Ragab, K.A.; Bouaicha, A.; Bouazara, M. Optimization of Casting Design Parameters on Fabrication of Reliable Semi-Solid Aluminum Suspension Control Arm. J. Mater. Eng. Perform. 2017, 26, 4450–4461. [Google Scholar] [CrossRef]
- Bazhenov, V.E.; Koltygin, A.V.; Fadeev, A.V. The use of the ProCast software to simulate the process of investment casting of alloy based on titanium aluminide TNM-B1 into ceramic molds. Russ. J. Non-Ferr. Met. 2014, 55, 15–19. [Google Scholar] [CrossRef]
- Skripalenko, M.M.; Bazhenov, V.E.; Romantsev, B.A.; Skripalenko, M.N.; Huy, T.B.; Gladkov, Y.A. Mannesmann piercing of ingots by plugs of different shapes. Mater. Sci. Technol. 2016, 32, 1712–1720. [Google Scholar] [CrossRef]
- Skripalenko, M.M.; Romantsev, B.A.; Bazhenov, V.E.; Tran, B.H.; Skripalenko, M.N.; Galkin, S.P.; Savonkin, M.B.; Gladkov, Y.A. Computer Simulation of Mannesmann Piercing of Aluminium Alloy Ingots. Russ. J. Non-Ferr. Met. 2019, 60, 27–34. [Google Scholar] [CrossRef]
- Hassan, M.I.; Al Kindi, R. Feasibility Study of Regenerative Burners in Aluminum Holding Furnaces. JOM 2014, 66, 1603–1611. [Google Scholar] [CrossRef]

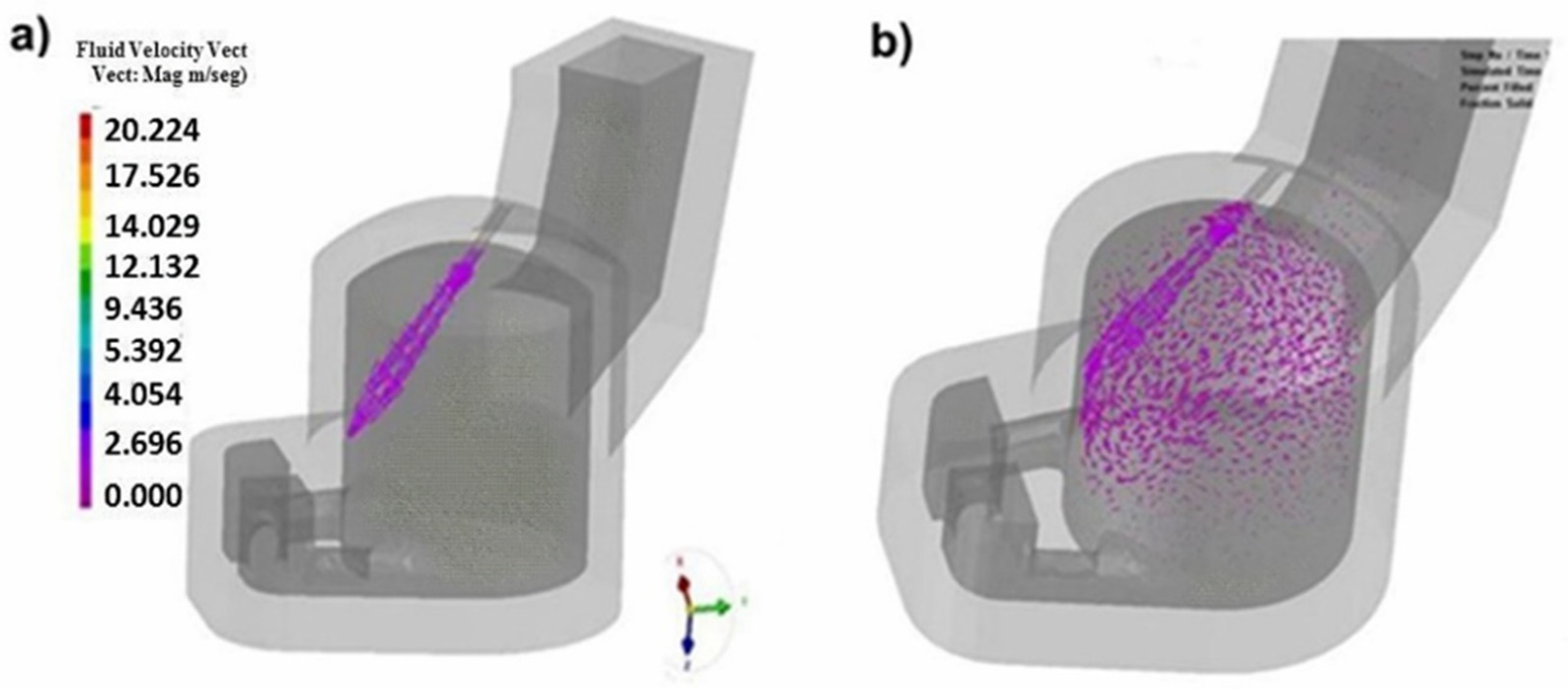
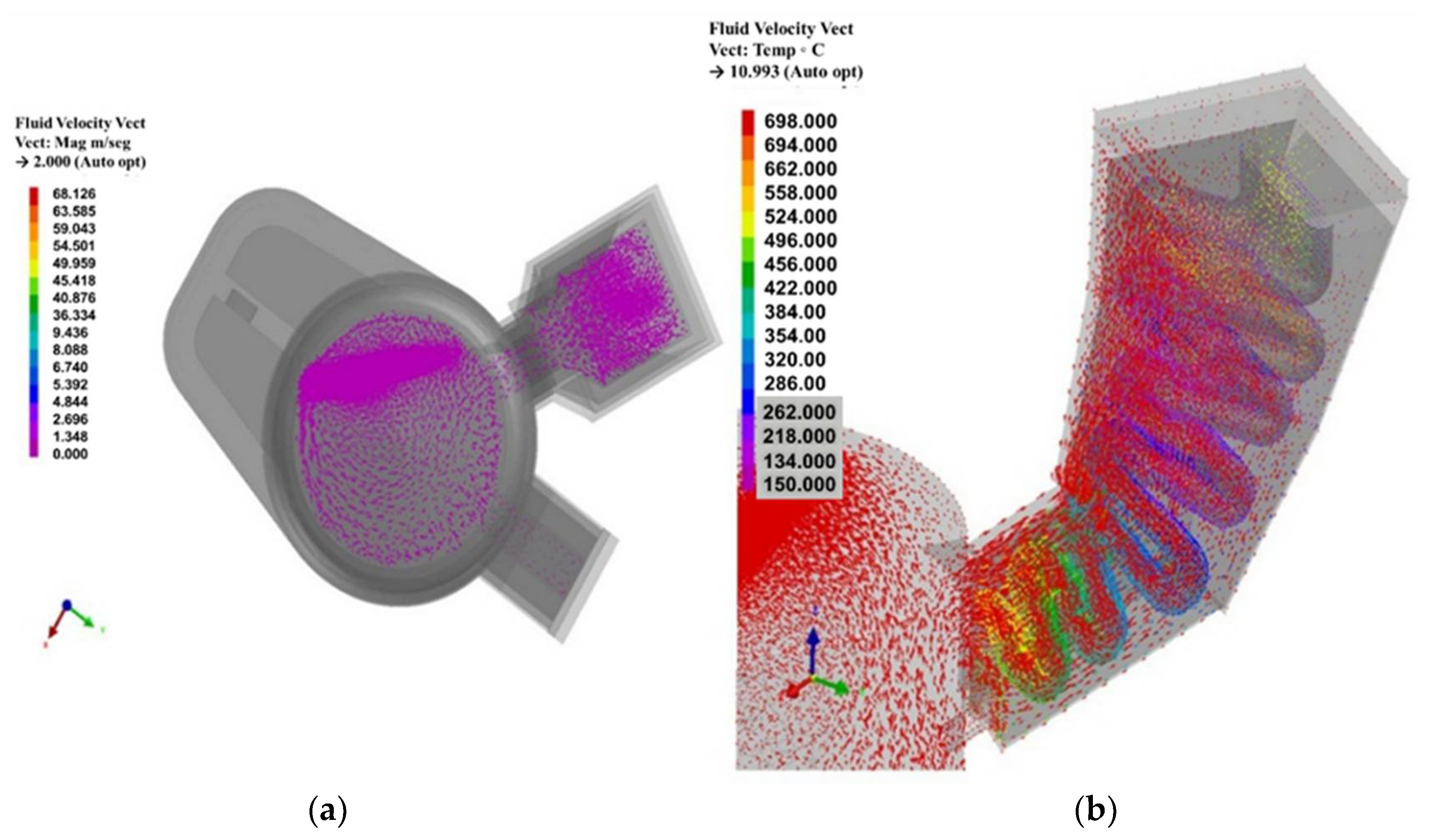
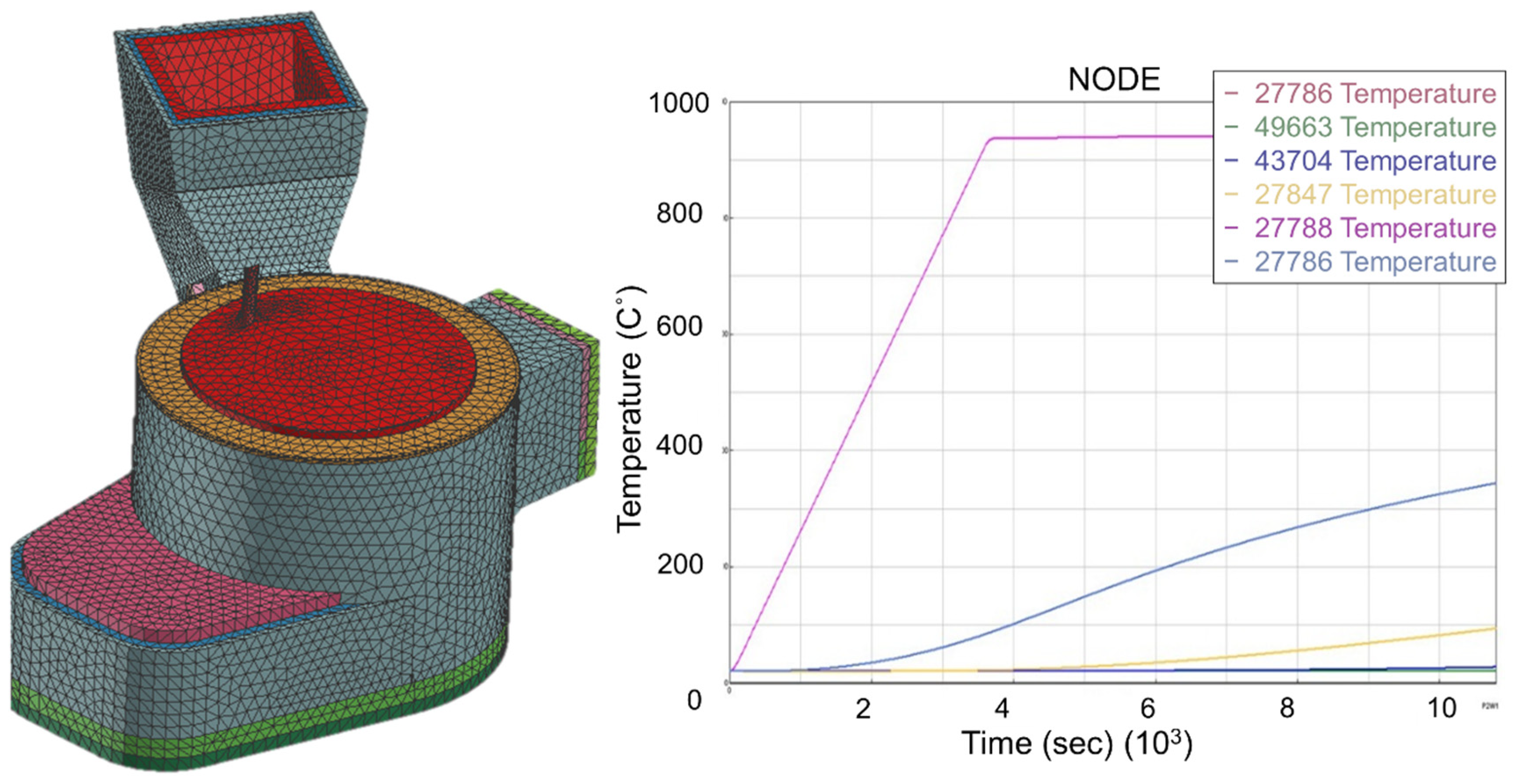
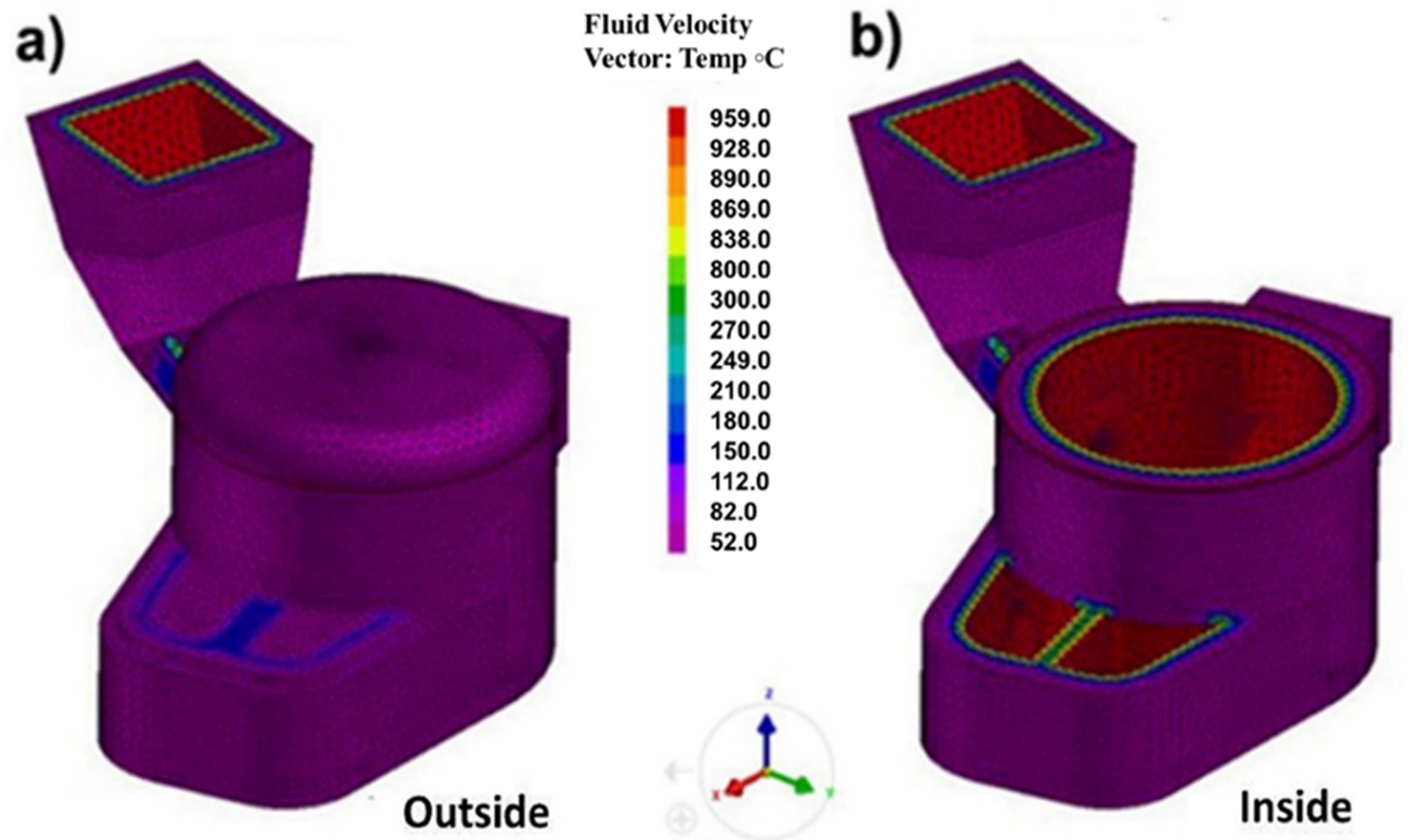

| Castable Materials | Thermal Conductivity (W/m K) | Specific Heat (KJ/kg K) | Density (kg/m3) |
|---|---|---|---|
| Refractory concrete | 1.3–1.5 | 0.96 | 2250–2270 |
| Insulating concrete | 0.22–0.22 | 1.22 | 900–1000 |
| Refractory blanket | 0.06–1.19 | 1.22 | 128 |
| Simulation Setting | Parameter Values |
|---|---|
| Timing for iteration | 0.1 s |
| Iteration Limit solver | 50 |
| Linear Convergence limit solver | 10−6 |
| Iteration limit for pressure equations solvers | 250 |
| Solver for linear convergence limit | 10−6 |
| Solver type | Conjugate gradient |
| Energy absorbed by the refractory | QCR = 252,212 kcal/h |
| Energy required for melting 1000 kg | Q1 = 5,520,945 kcal/h |
| Energy required to produce a phase change | Q2 = 95,600 kcal/h |
| Furnace Processing Features | Furnace without Modifications | Furnace with Modifications |
|---|---|---|
| Aluminium chip 0.5 cm2 (ton/h) | 0.3–0.5 | 0.8–1.2 |
| Aluminium chip thick 10–30 cross section (ton/h) | 0.3–0.5 | 0.4–0.6 |
| Average production (ton/day) | 6.5–7.5 | 12–16 |
| Weight Mg percentage after 100 min of treatment | 0.26 | 0.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flores Saldívar, A.A.; Juárez Martínez, R.; Flores Valdés, A.; Torres, J.T.; Ochoa Palacios, R.M.; Li, Y. Mathematical Modelling for Furnace Design Refining Molten Aluminum. Metals 2021, 11, 1798. https://doi.org/10.3390/met11111798
Flores Saldívar AA, Juárez Martínez R, Flores Valdés A, Torres JT, Ochoa Palacios RM, Li Y. Mathematical Modelling for Furnace Design Refining Molten Aluminum. Metals. 2021; 11(11):1798. https://doi.org/10.3390/met11111798
Chicago/Turabian StyleFlores Saldívar, Alfredo Alan, Rodrigo Juárez Martínez, Alfredo Flores Valdés, Jesús Torres Torres, Rocío Maricela Ochoa Palacios, and Yun Li. 2021. "Mathematical Modelling for Furnace Design Refining Molten Aluminum" Metals 11, no. 11: 1798. https://doi.org/10.3390/met11111798






