1. Introduction
There are various solutions for storing products and merchandise throughout the production process, with industrial storage racks being an alternative commonly used today by industry worldwide, and the selective type rack being the most widely used of them [
1]. The structural configuration of the pallet racks consists of the combination of orthogonal frame systems, running parallel to the aisles, and frames are braced in a perpendicular direction to the aisles [
2]. The bracing is used perpendicularly for practical reasons because it can affect storage capacity [
3].
Industrial storage racks are structures that support operating much greater loads than their own weight [
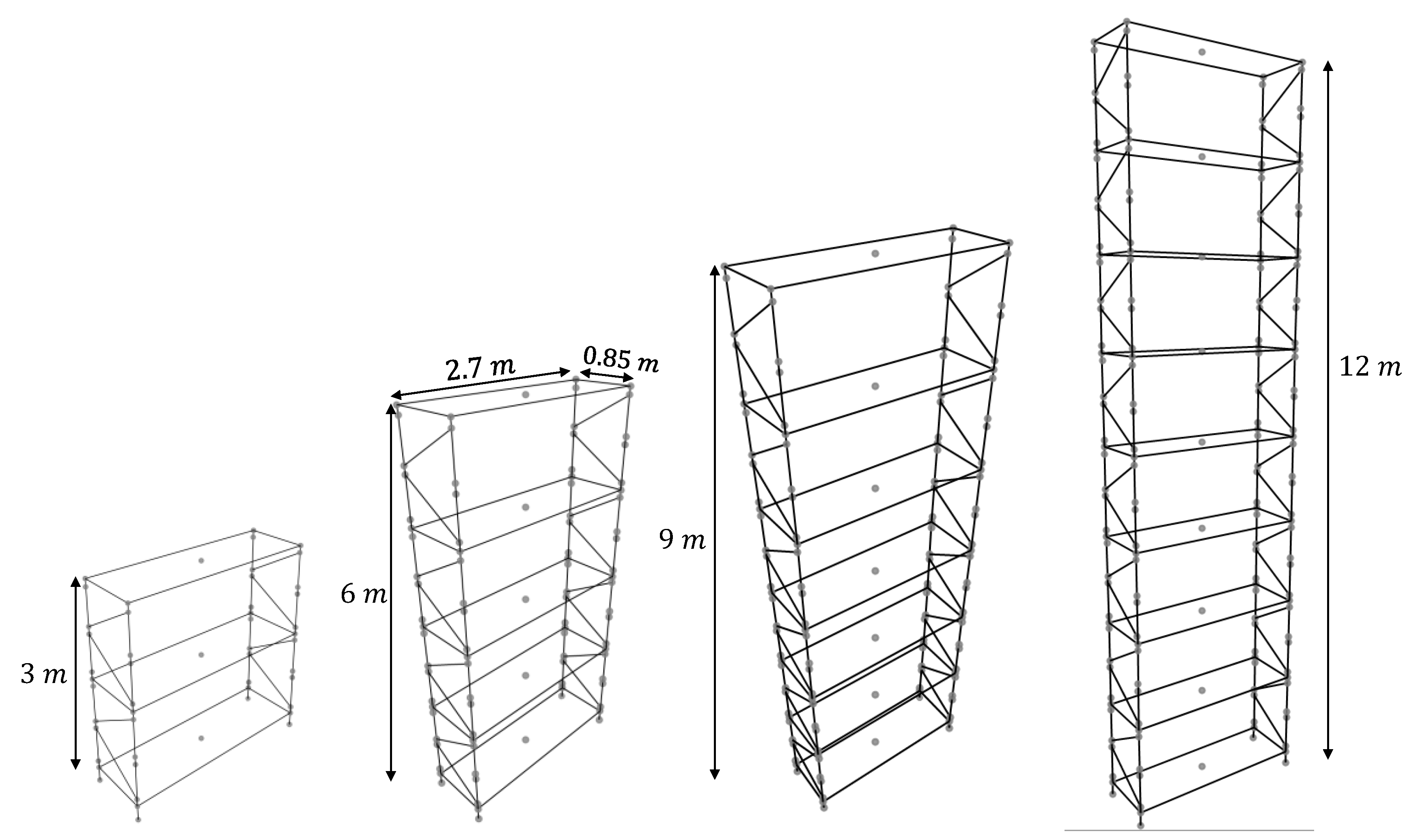
4]. The elements used to design these structures are cold-formed thin-walled steel elements. The columns are manufactured from open sections with perforations at standard intervals so that the beam and diagonals of the lattice system can be connected in a modular way. The material commonly used is carbon steel according to ASTM-A36. The beams have a generally rectangular closed section, composed of two C-sections with stiffened wings with discontinuous welded joints between them in the longitudinal direction [
5,
6,
7,
8]. These structures are designed to be narrow perpendicular to the aisles, while they are longer in a parallel direction to them [
3]. Industrial storage racks can reach heights that exceed 10 m with a high vertical load, reaching very large slendernesses —height/width ratio—[
9]. All of the above leads to the racks being vulnerable to seismic action, as well as their content [
10,
11], being a risk for people who regularly walk near them [
12].
In the last decade, research in relation to steel racks has focused on reducing design uncertainty by refining analysis methodologies and characterizing earthquake-resistant components and their connections [
13,
14,
15,
16]. It has been determined that the uncertainty in the designs is because racks, particularly tall and slender ones, are affected by global, local and distortionary instability, due to the slenderness of their elements [
13]. These structures have a high probability of inelastic incursion in beam-column connections [
14] and column-base connection [
15]. Kwarteng et al. [
16] performed characterization tests of the moment-rotation relationship in beam-column connections of racks in order to reduce uncertainties in the design of racks. They proposed a model of characteristic curves of the moment-rotation relationship for seismic analysis, which they applied numerically to a frame under different seismic actions.
An alternative to address the problems of rack instability in the face of seismic action is the use of seismic protection systems. In this sense, Gutelius et al. [
17] developed a device designed to protect racks for storage of sensitive electronic equipment such as computers and servers. Later, Pellegrino et al. [
18] patented a specific base isolation system for palletized industrial storage racks. This solution allows the rack to be isolated seismically only in the direction transverse to the aisle, with no effect in the longitudinal direction [
19]. In such a device, the uplift resistance is provided through a vertical displacement restriction mechanism, which shows a composite of elastomer sheets working in compression. The elastomer also helps restore the undeformed position, existing friction dissipated due to sliding at the base and inelastic behavior of the elastomer [
19].
Kilar et al. [
20], evaluated the economic feasibility of implementing an elastomeric seismic isolation system in industrial storage racks. The cost of the isolation implementation turned out to be comparable with the cost of the repairs of structural elements, the halt to productive activity and losses of products in the face of the action of a severe earthquake. However, other aspects, such as workers and customers who transit in areas near the industrial storage racks’ safety, have not been evaluated. In Chile, research on industrial steel storage systems with seismic protection systems subjected to Chilean earthquakes is limited. Furthermore, the current standard NCh2369 [
21] does not contemplate the implementation of these types of seismic protection systems in racks. NCh2745 “Analysis and design of buildings with basal insulation” [
22] can only be considered as a reference, as it is not applicable to storage rack structures.
The effect of local instability on capacity of steel beams exposed to fire was conducted by Kodur et al. [
23]. In this numerical study, the behavior of fire exposed steel beams taking into consideration temperature-induced instabilities was performed. The results show that shear capacity in steel beams can degrade higher than moment capacity. These considerations can be important when steel storage racks are used. Finally, the effect of nonuniform bending on the lateral torsional buckling of steel beams with slender cross-section at elevated temperatures was studied by Couto et al. [
24]. In this research, the influence of fire in local buckling using a numerical model obtained a new factor for design procedure according to Eurocode 3.
In this research, the seismic behavior of base isolated racks is studied using a roller-type device with tensile strength [
25,
26]. This device is connected at the base of the structure by means of a flexible cable attached to a post-tensioned element inside the device, which gives it lateral stiffness. The device can dissipate energy due to work between rotation and friction on the ball joint of the isolation bearing. In addition, the rotation with respect to its support allows the uncoupling of the superstructure from the ground. The device is vertically very rigid, and its lateral stiffness is controlled by the tension of a post-tensioned element inside it. The evaluated device offers baseline isolation in both directions of analysis [
25]. The main objective of this research is to evaluate the effectiveness of the use of base isolation in reducing seismic demand, through a numerical study of racks with both fixed and isolated bases subjected to Chilean earthquakes.
4. Results and Discussion
The seismic performance of the entire set of racks analyzed was evaluated employing three responses of interest that allow all cases to be objectively compared. These responses were: average in levels and maximum in time for floor drift (drift); average in levels and maximum in time for absolute acceleration (üabs); and maximum in time for basal shear load relative to the seismic weight (Q0/Ps). The maximum values of üabs and Q0/Ps were obtained by imposing the seismic force perpendicularly to the direction of the aisles of racks. This is consistent with the fact that in this direction, the structure is more rigid due to stiffer braced axes that provide lateral resistance. The maximum drift was obtained by imposing the seismic force parallel to the direction of the aisles of racks since it is the most flexible direction of the structure where the resistant axes are flexible frames.
The average maximum floor drift (drift) was first calculated as the sum of the drift of each level in all time, and then the maximum value was calculated throughout the duration of the analysis. The basal shear load Q0 was divided by the seismic weight Ps to be able to compare this response in racks of different heights and weights. To determine the average maximum absolute floor acceleration üabs, the average value of the absolute floor accelerations was first determined for all levels, obtaining a single value for each analysis instance. Then, the maximum of said average acceleration was determined throughout the duration of the analysis in order to soften the maximum response obtained, eliminating specific peak values of very short duration, since the effect of absolute acceleration is reflected in practice in the overturning of stored pallets. However, acceleration peaks of very short duration fail to generate this effect, since, by rapidly reversing its direction, the pallet stabilizes again on the rack. This effect is shown graphically relative to the acceleration of gravity in Figure 11.
Table 4 shows the first three natural periods of the fixed racks in its analyzed base, depending on the number of levels. It is observed that the slenderer the structure is, it becomes more flexible, that is, its natural periods lengthen.
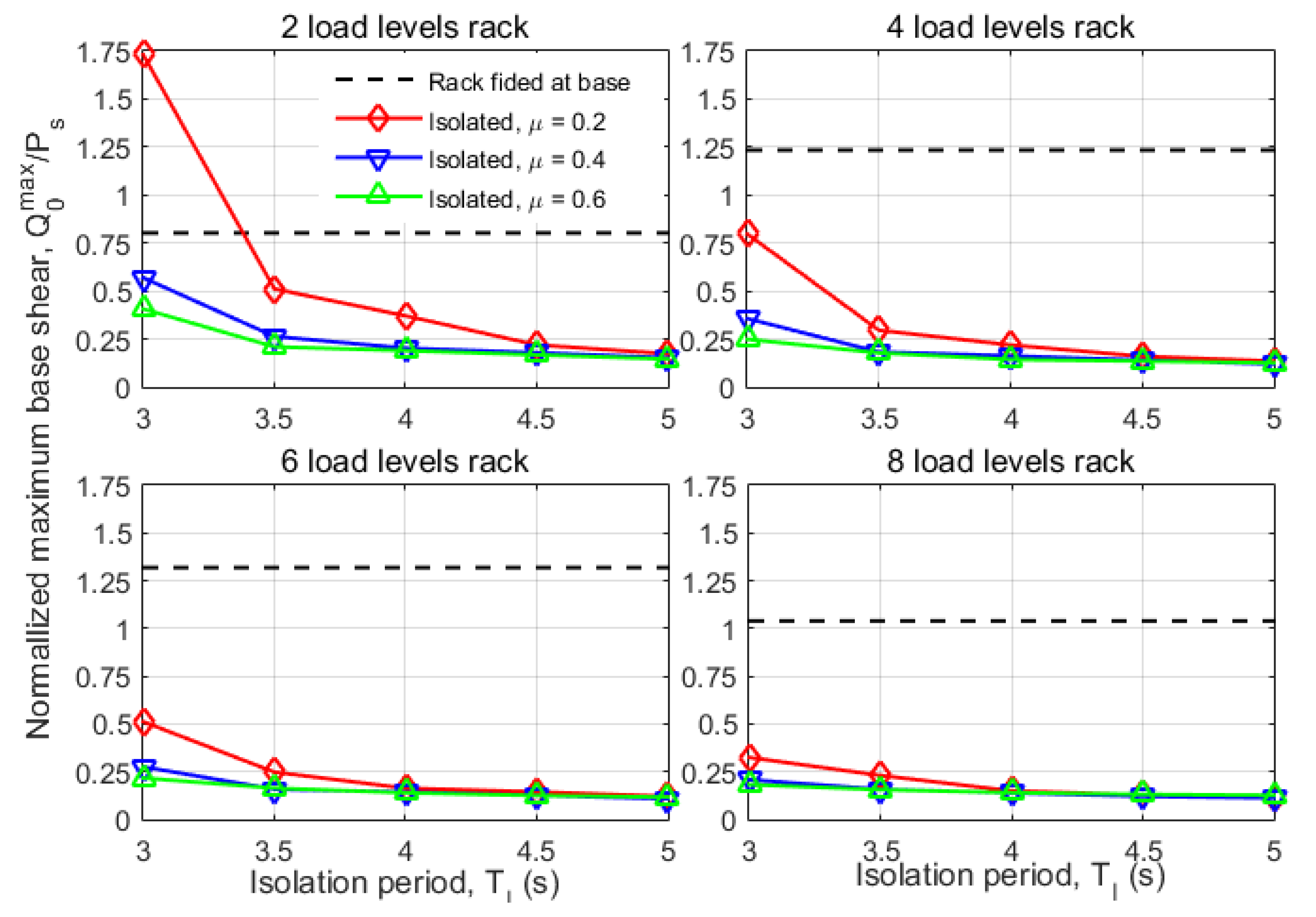
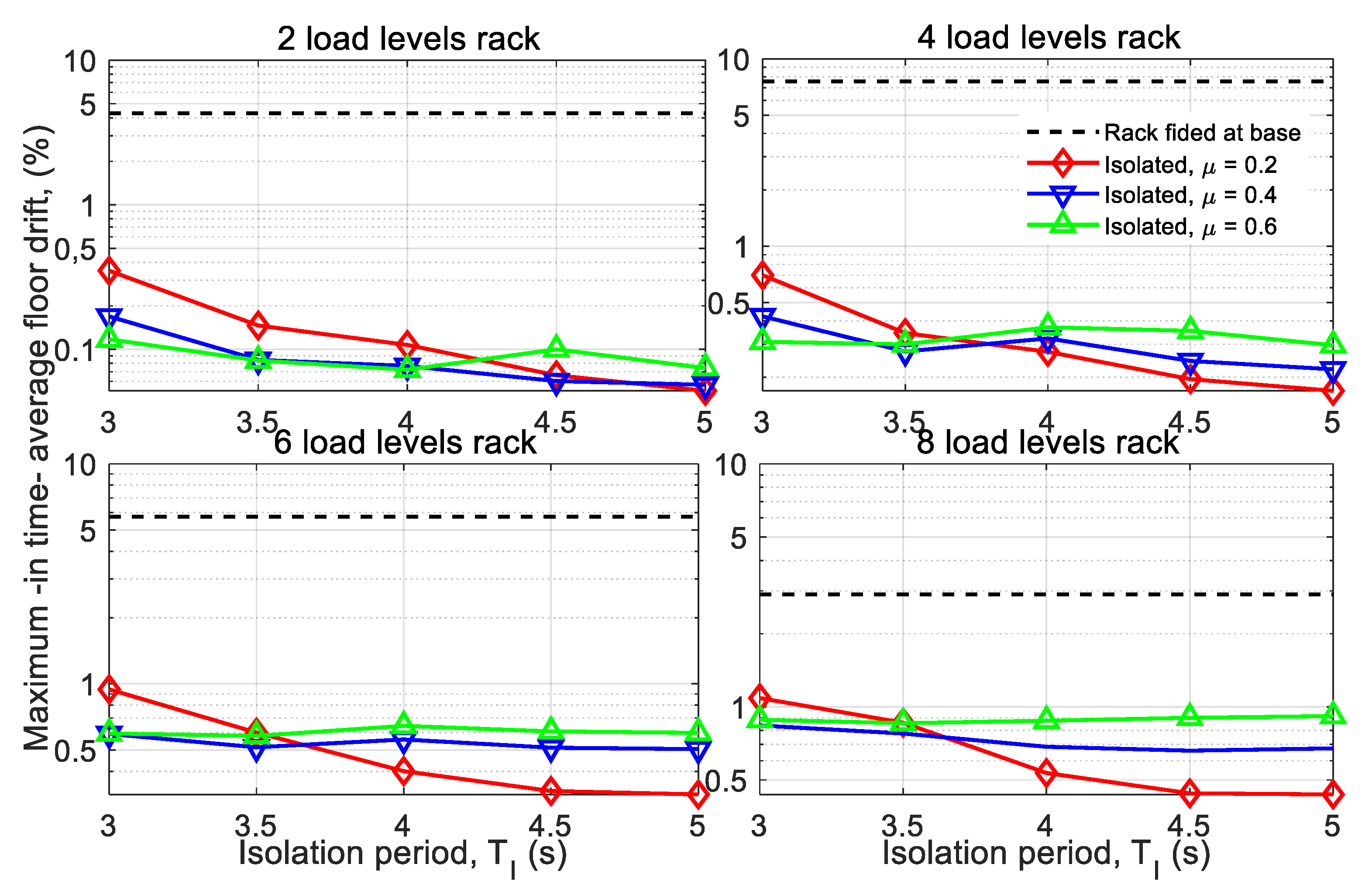
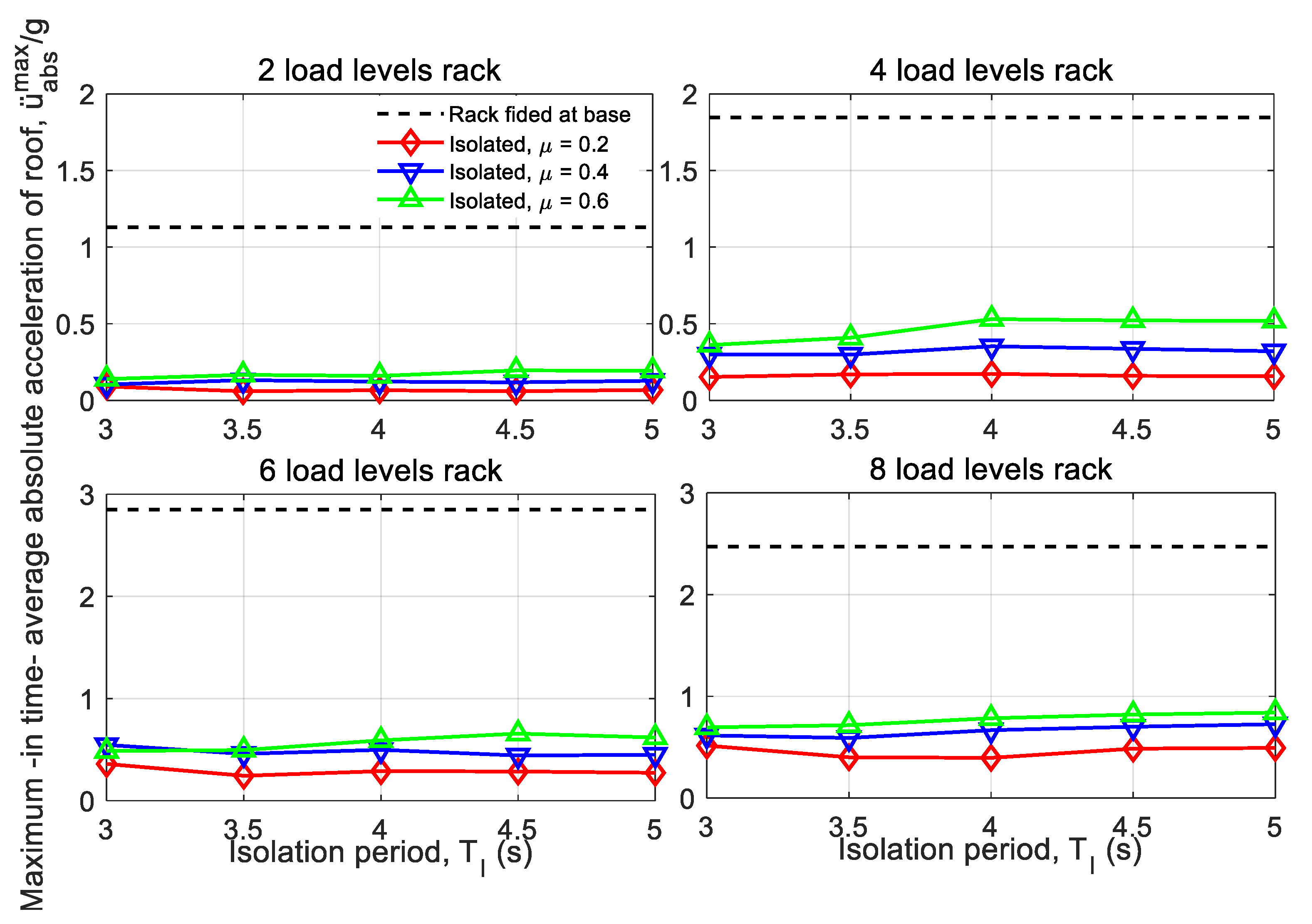
Figure 8,
Figure 9 and
Figure 10 show the three maximum target responses obtained for the base isolation racks considering different friction coefficients on the ball joint at the base of the isolator (
μ), isolation periods (
TI) and load levels. In order to verify the effectiveness of the use of the base isolation and show the decrease of the target responses, the corresponding maximum response of the fixed base rack is included.
In all the cases shown in
Figure 8,
Figure 9 and
Figure 10, except one, the three maximum target responses of base isolated racks were found to be lower than those of the corresponding fixed rack at its base. The anomalous case corresponds to the 3-level rack with isolation period
TI = 3 s, friction coefficient in the ball joint
μ = 0.2 and its diameter
d = 10 cm, according to
Table 1.
Regarding the basal shear load, it is observed that the longer the isolation period
TI, the response decreases consistently, independent of the value of the friction coefficient
μ and the load levels of the rack. The effect of modifying the friction coefficient
μ shows a clear trend, the higher it, the lower the basal shear load, regardless of the number of rack levels. However, the reduction in this response is greater in racks with higher load levels. As shown in
Table 1, the more load levels the rack has, the greater the diameter d assigned to the ball joint of the base support of the isolators. According to the analysis of Equation (3) in
Section 2.2, the energy dissipation provided by the isolation system as a whole is proportional to the product
d∙μ. This explains why the maximum basal shear load in racks with base isolation is lower in racks with more load levels, for the same
TI and
μ values; because the greater the number of levels, the greater the diameter d of the ball joint at the base (
Table 1).
Unlike the maximum basal shear load that decreases when increasing the number of load levels in the racks, the drift increases in higher racks, as shown in
Figure 9. This increase occurs because, in higher and heavier racks, less decoupling of the ground movement is achieved for the same period of isolation
TI.
Table 4 shows that the natural periods of the rack fixed at its base are longer when it has more load levels. The closer the period of isolation is to the fundamental period of the fixed rack at its base, the less the effect of the basal isolation in decoupling the movement of the structure from the ground. This phenomenon explains why the maximum drifts are larger in racks with more load levels with basal isolation of the same
TI period and the same friction coefficient
μ on the isolator ball joint. However, in all cases with base isolation, the maximum drift is below 1%, complying with the requirement of NCh2369, which establishes 1.5% as the desired limit.
It is observed in
Figure 9 that the effect of the friction coefficient on the maximum drift response does not follow a single trend. The response curves for
μ = 0.2, 0.4 and 0.6 intersect for
TI isolation period values that differ depending on the number of rack levels. For low isolation periods, an increase in
μ leads to a reduction in the maximum drift. On the other hand, for high
TI values, the trend is the opposite. The
TI value for which the trend is reversed is lower the more load levels the rack has. In general, either the higher the rack, the longer its isolation period
TI, or both, the more convenient it is to have a lower value of the friction coefficient
μ to reduce the rack’s maximum floor drift.
It can be seen from
Figure 10 that all the racks with a fixed support at the base exceed the critical acceleration defined by Equation (12). This indicator suggests that in the racks with fixed basal supports analyzed, the stored pallets could overturn under the action of a severe earthquake that equals the most severe design expectations of NCh2745. With the implementation of base isolation and using the same criteria, in practically all analyzed structures, it is suggested that no pallet overturning would occur. An exception to the above is the 8-level rack with isolation periods
TI = 4, 4.5 and 5 s and friction coefficient in the ball joint
μ = 0.6, where the critical acceleration is slightly exceeded. This value is consistent, since the friction dissipation acts as a brake, increasing the absolute accelerations, although the basal shear load is reduced. However, this problem is solved by reducing the dissipation capacity in the isolation system by decreasing the friction coefficient
μ or the diameter of the ball joint at the base of the isolation devices d.
The maximum absolute acceleration was considered a response of interest since it is related to the overturning of the products stored in the rack.
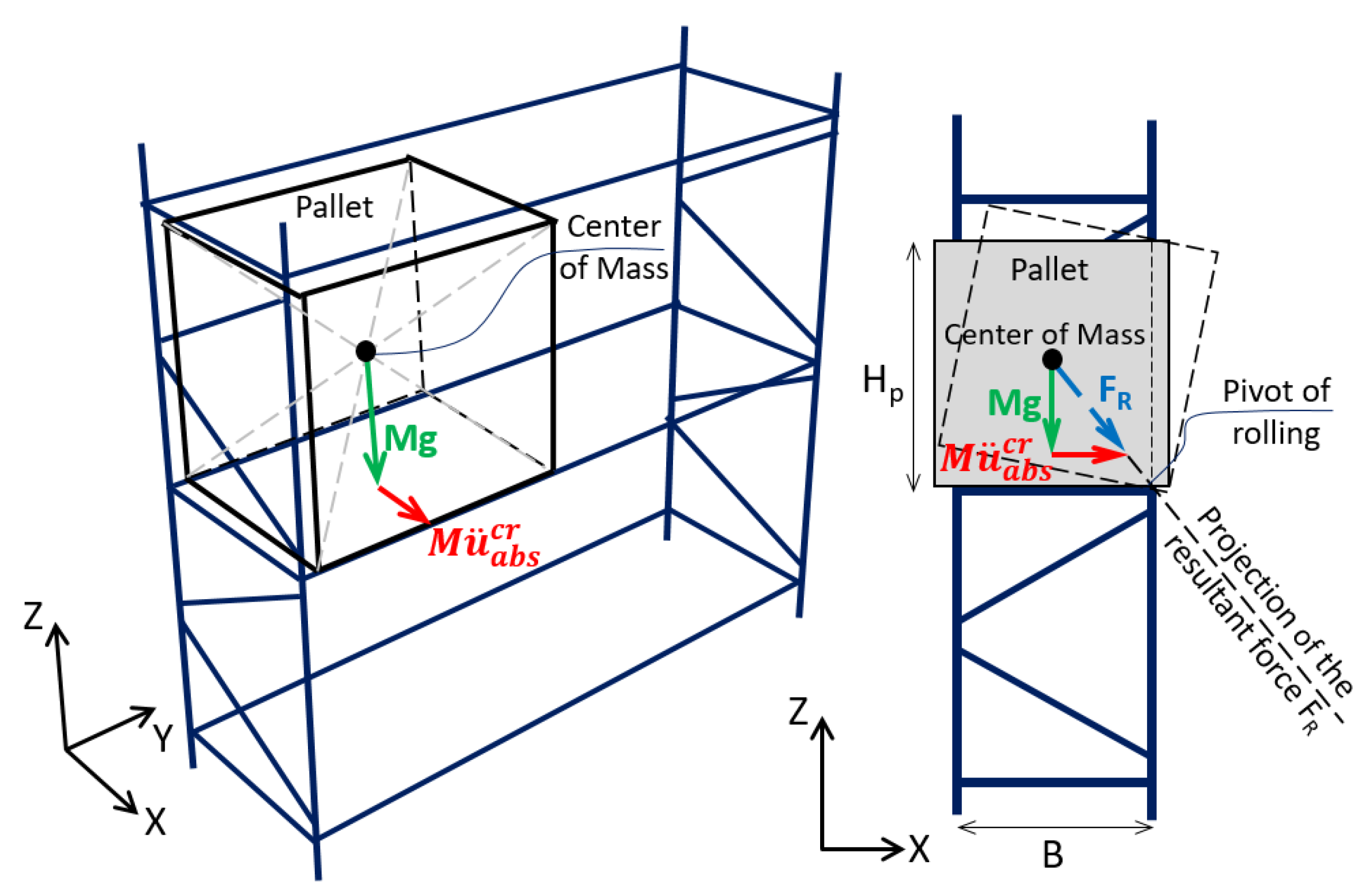
Figure 11 shows a diagram of the stored pallet, with height
Hp = 1.35 m and width between support beams
B = 0.85 m. This figure illustrates the horizontal acceleration condition considered critical for overturning effects. This condition is defined by the state in which the projection of the force resulting from the seismic action and the acceleration of gravity cuts the basal edge of the pallet (pivot rolling in
Figure 11). This effect corresponds to an unstable equilibrium condition, since a horizontal acceleration greater than that illustrated in
Figure 11 and defined analytically by Equation (12), will cause the stored pallet to overturn. In the illustrated condition, if the absolute horizontal acceleration is greater than 0.63∙g, the pallets will overturn.
Figure 12 shows the maximum lateral displacement of each level considering 8-level racks with a friction coefficient in the ball joint at the base of the isolator
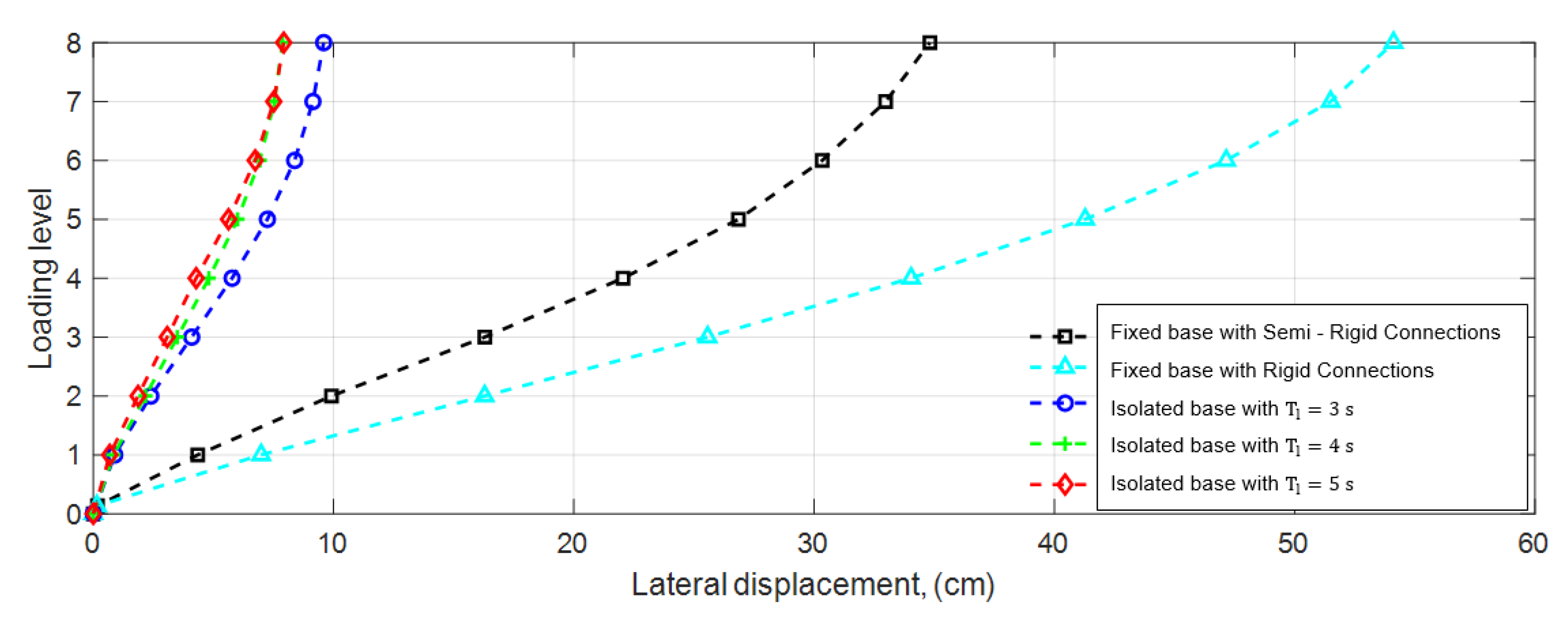
µ = 0.4, corresponding to steel against steel. In the figure, results are superimposed for different conditions: (1) rack with a fixed support at the base and rigid connections, (2) rack with a fixed support at the base and semi-rigid connections and (3) racks with base isolation and period of isolation
TI = 3, 4 and 5 s. It is observed that there is a reduction in the lateral displacements of the base isolated rack (models 3) with respect to the models (1) and (2) of racks fixed at its base. In storage level 8, a reduction of 46.2 cm is observed between rack (3) with
TI = 5 s and rack (1); such reduction is 26.9 cm when compared to the rack (2). Furthermore, the lateral displacements in level 8 are 9.6 and 7.9 cm, for the racks with an isolation period of 3 and 5 s, respectively. The displacement of the racks with isolation periods of 4 s and 5 s are practically the same. It is inferred that the longer the period of isolation the structure will have a greater reduction in the target response of floor drift. It is also observed that the maximum floor displacements of the rack with semi-rigid connections are less than those of the rack with rigid connections. Although the former is more flexible than the latter, the energy dissipation capacity provided by the semi-rigid connections contributed to reducing lateral displacement, achieving better performance in terms of maximum drift.
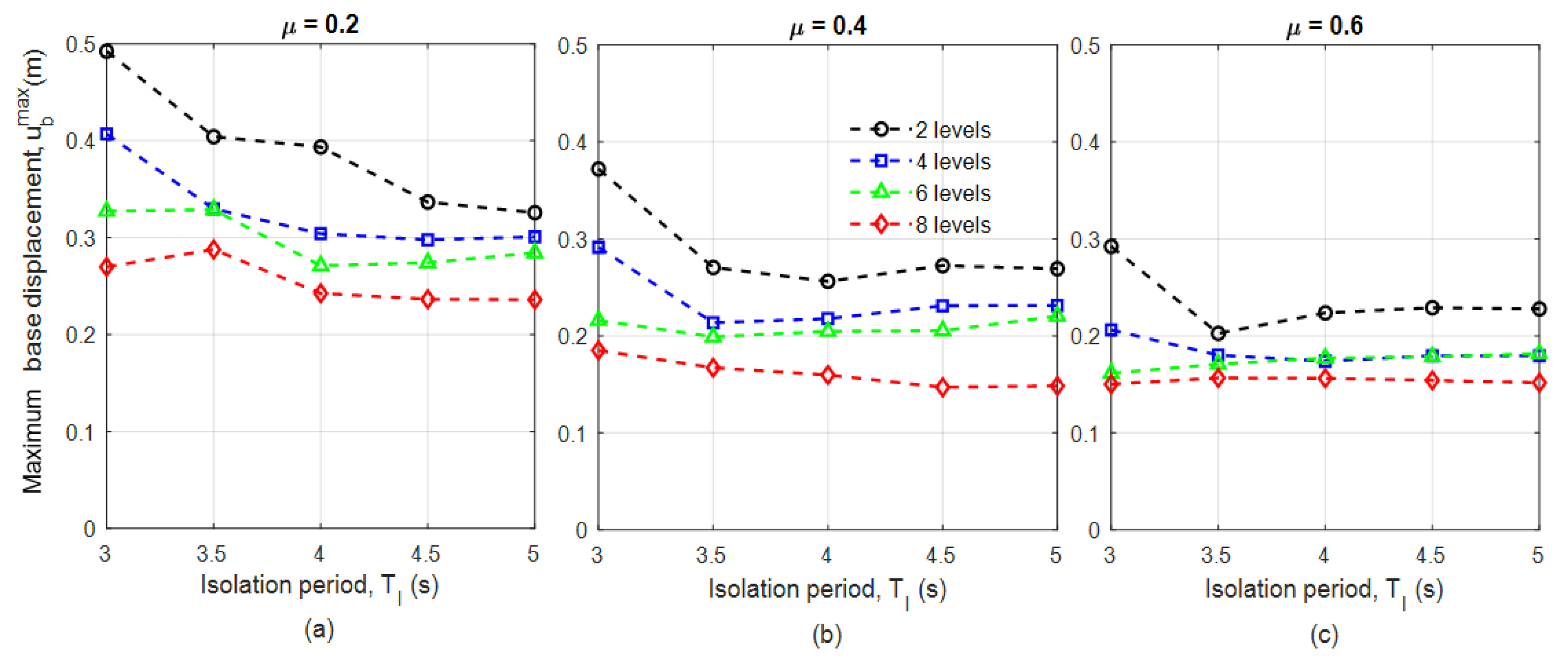
Figure 13 shows the maximum displacement of the isolation level for racks with different load levels, friction coefficient on the ball joint at the base of the insulator (
μ) and isolation period
TI. It is observed that the greater the magnitude of
μ, the maximum displacement in the base becomes less and less, due to the greater dissipation of energy. It is also observed that the less slender the structure—fewer load levels—the greater the maximum displacement achieved at the base, compared to more slender structures. This relation makes sense since the structure becomes more flexible as it is more slender, that is, its fundamental period increases, having a lower acceleration in the design spectrum (
Figure 6).
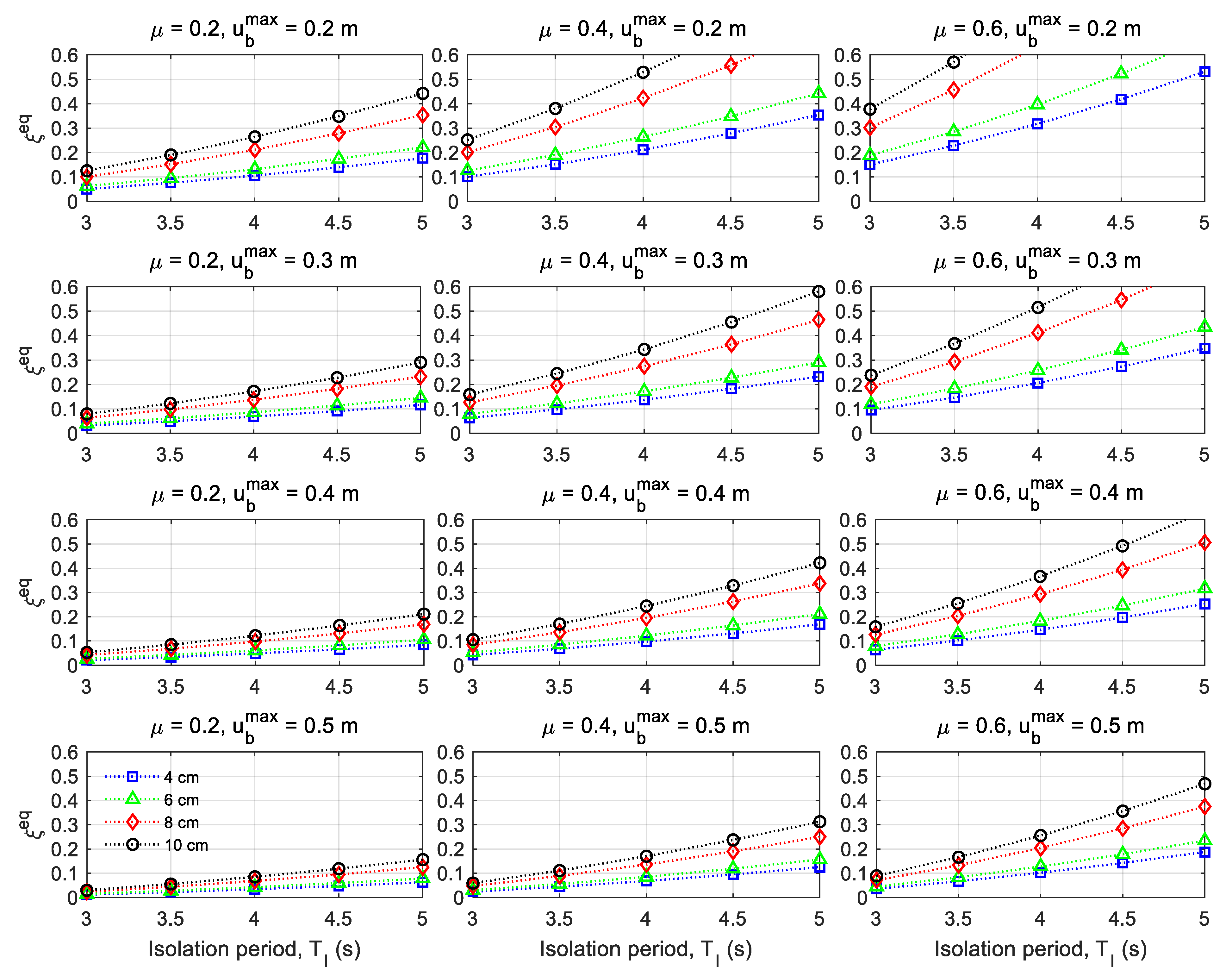
Figure 14 shows the equivalent damping ratio (
) of the isolation system considering different coefficients of friction in the ball joint at the base of the isolator
μ = 0.2, 0.4 and 0.6. The calculation of
was performed by matching the dissipated energy of two 1 degree of freedom systems, one of them being linear elastic and the other governed by Equation (3). Both are subjected to a harmonic basal displacement force of the type
, where
ωI = 2
π/TI is the isolation frequency (rad/s). The energy dissipated by a linear dynamic system in an imposed displacement cycle is given by [
25]:
For the case of the nonlinear dynamic system that uses the roller type isolator,
is calculated with Equation (3), assuming
Rn = mt∙g and performing the calculations, the following is obtained:
For the case of the linear dynamic system, we have that
, so by performing the calculations we obtain:
Equating the dissipated energies and solving for
we have:
For the calculation of
, maximum displacements at the level of the isolation system
= 20, 30, 40 and 50 cm were considered. In addition, the different isolator ball diameters are considered:
d = 5, 7.5, 8.5 and 10 cm, which are related to racks with 2, 4, 6 and 8 load levels, respectively (
Table 1). The results are shown in
Figure 14.
Figure 14 explains why high maximum displacements at basal level (
) occur in some rack analysis cases. For example,
~ is obtained, considering
μ = 0.2,
TI = 3 s and a rack with 2 load levels (
Figure 13a). This value is due to the fact that the equivalent damping is very low,
1.2% in this case, as shown in
Figure 14. However, when the displacement is less than 30 cm, there is a greater
. This is exemplified when
μ = 0.2, a rack with 4 load levels and
TI = 4, 4.5 and 5 s is considered, obtaining
= 8.5, 11.4 and 14.5%, respectively (
Figure 14).
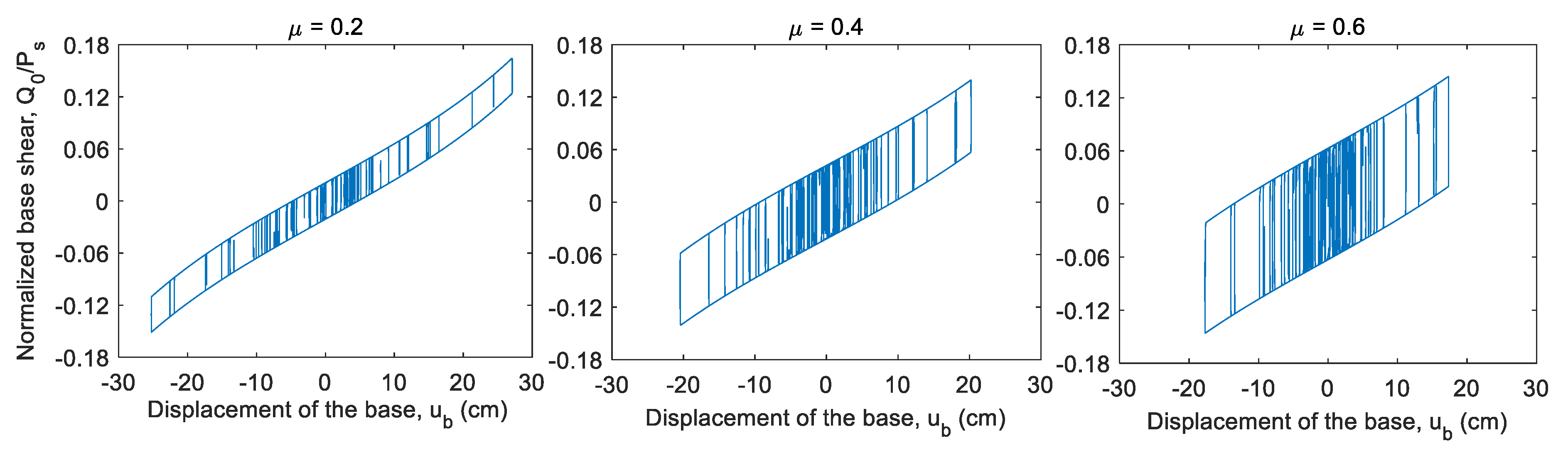
Figure 15 shows the hysterical cycle of the base isolation system in terms of normalized basal shear load versus the displacement of the center of the mass of the basal level. The results are shown with different coefficients of friction in the ball joint at the isolator base (
μ) of a 6-level rack and isolation period
TI = 4 s. It is observed that the greater the magnitude
μ, the band of the hysterical cycle becomes wider, so there is a greater dissipation of energy; the same is observed in the equivalent damping ratio (
Figure 14). The effectiveness of energy dissipation can be seen when the magnitudes of the maximum displacement of the isolation level (
Figure 15) decrease with increasing
μ for racks with the same number of levels.
Figure 16 shows the ratio between the maximum axial load—tension—or minimum axial load—compression—on the isolators, and the initial tension of the cable (
T0), considering the seismic input acting in cross the aisles direction of the rack. While in
Figure 17, the seismic input is considered to be acting in the longitudinal direction. If the quotient is greater than 1 there is lifting in the isolator, otherwise, the isolator is compressed and works stably.
In many of the cases analyzed, the racks suffer uplift at the isolation interface when the seismic input acts in the transverse direction of the rack (
Figure 16). The cases where lifting is foreseen are the racks with 6 and 8 load levels. In racks with 2 and 4 load levels, lifting can be avoided by considering adequate values for the isolation period and coefficient of friction in the ball joint.
From
Figure 16 it can be seen that when considering a coefficient of friction in the ball joint at the base of the isolator
μ = 0.2, a reduction in the tensile load on the isolators is achieved either by increasing the isolation period or by increasing the number of rack load levels. However, this trend is not maintained in the highest racks when considering
μ = 0.4 and 0.6; in such cases, the slimmer the rack, the more traction on the insulators. From the above, it follows that increasing the frictional dissipation capacity of the insulation system is inefficient and even detrimental for slimmer racks with six or more levels.
When considering the earthquake acting in the longitudinal direction, no uplift is observed in any isolator (
Figure 17). This is due to greater separation between the compressed and tensile isolators by seismic load—2.7 m compared to 0.85 m when considering the earthquake transversely. In this way, the seismic turning moment can be resisted with much lower dynamic load induced on the isolators. This condition is exemplified in
Figure 18 and the reactions are determined by Equation (17):