Cyclic Behavior of Hollow Section Beam–Column Moment Connection: Experimental and Numerical Study
Abstract
1. Introduction
2. Hollow Structural Section (HSS) Moment Connection
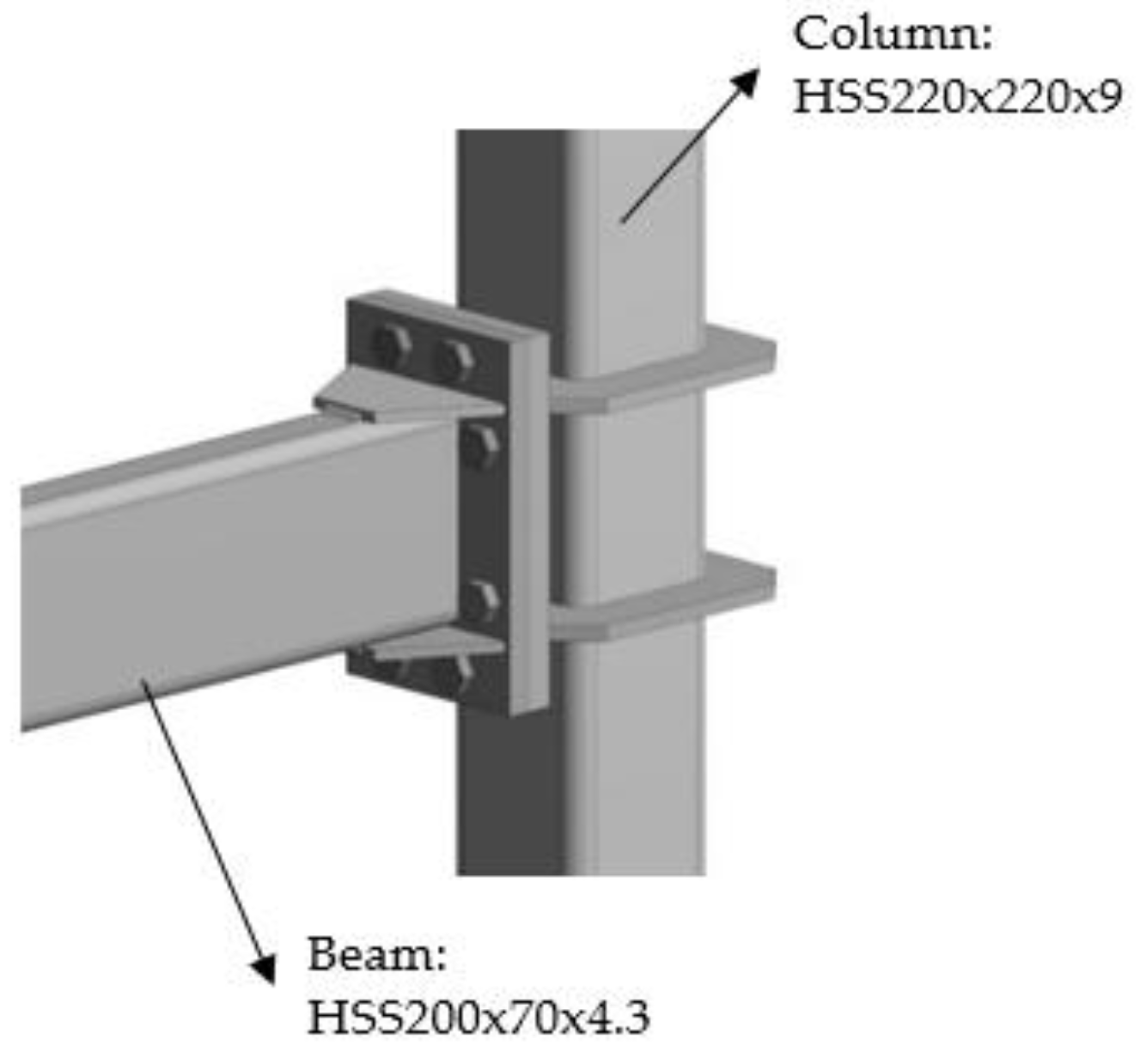
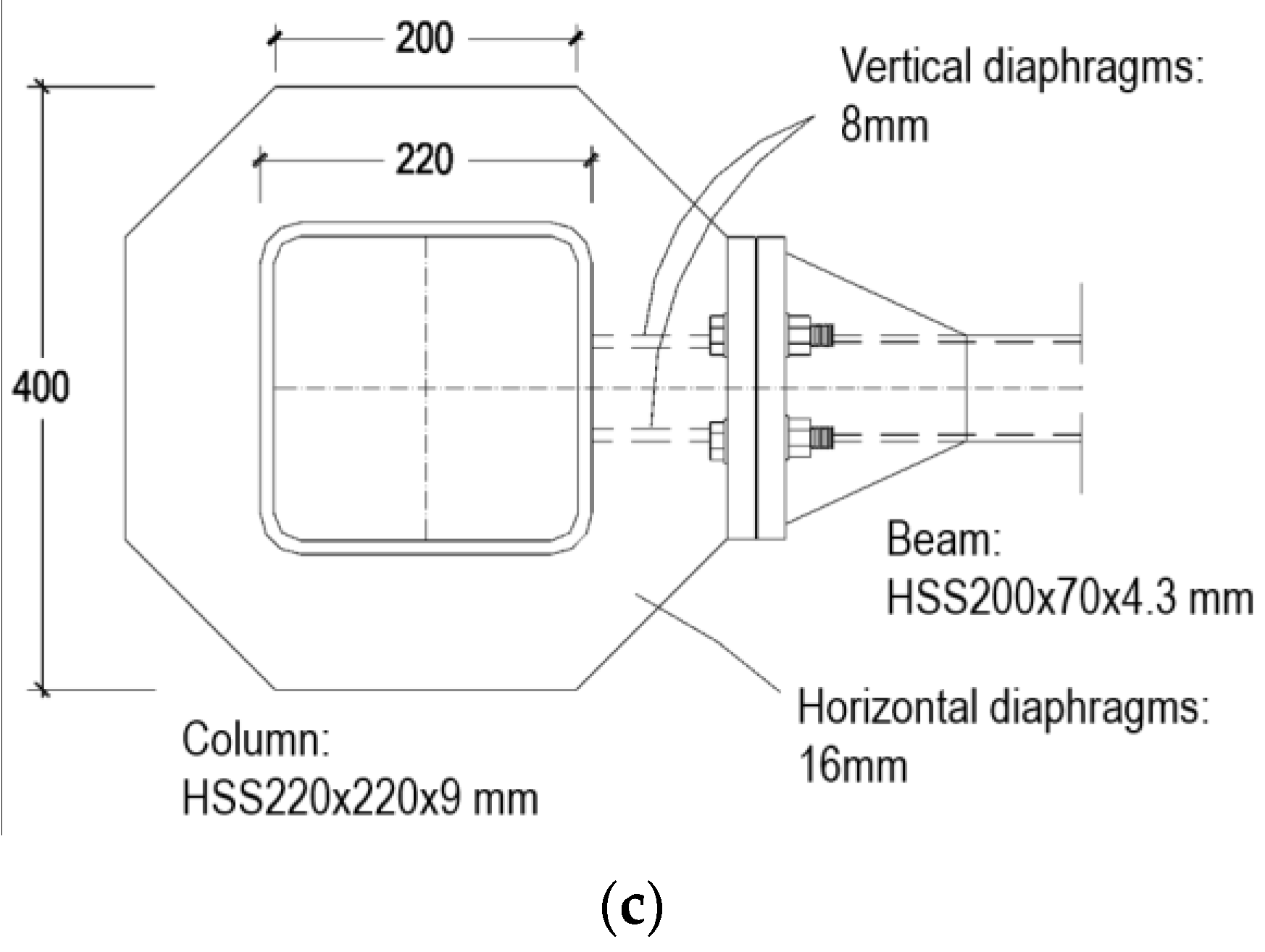
2.1. Description of HSS Moment Connection
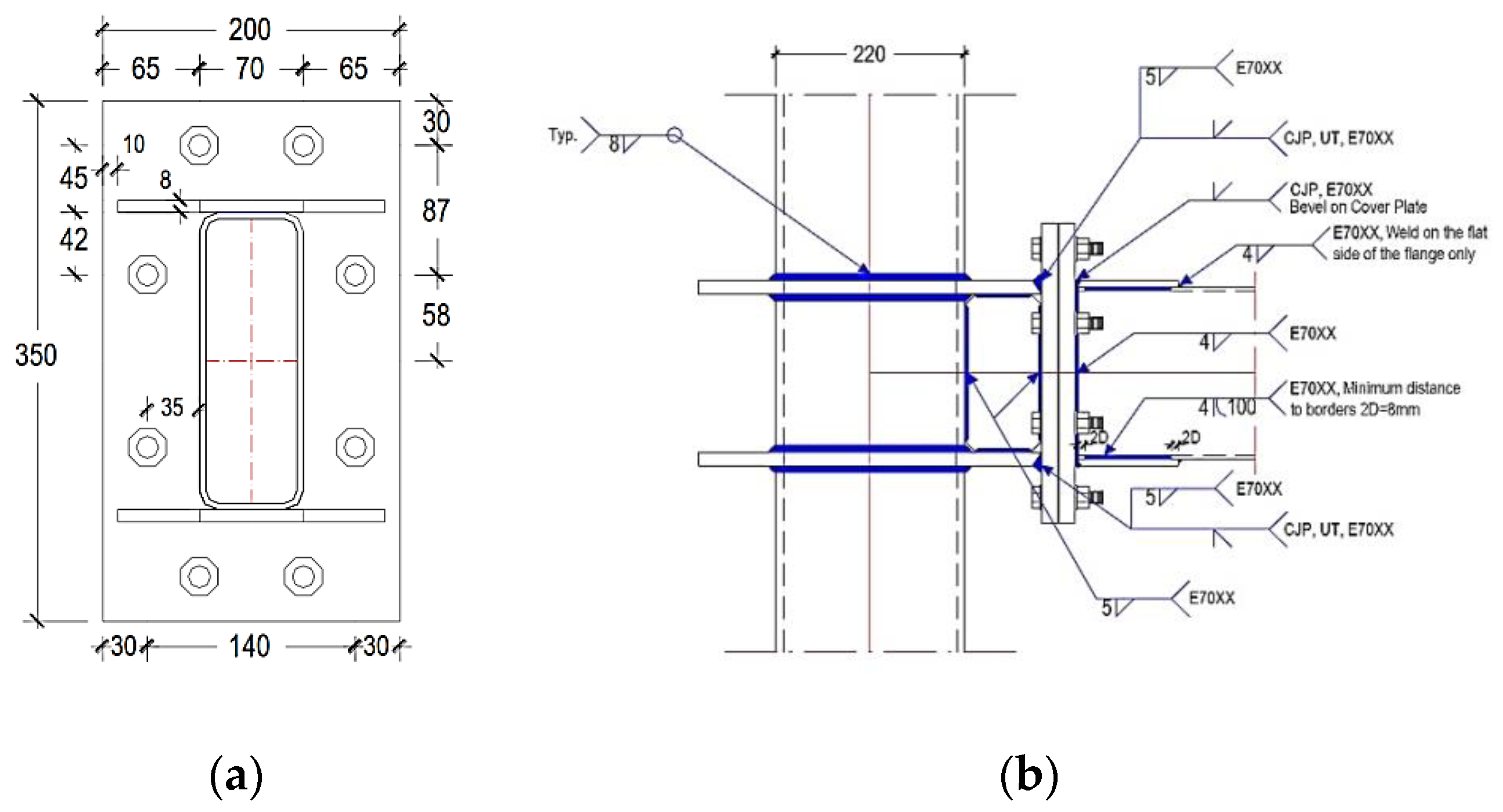
2.2. Proposed End-Plate Design
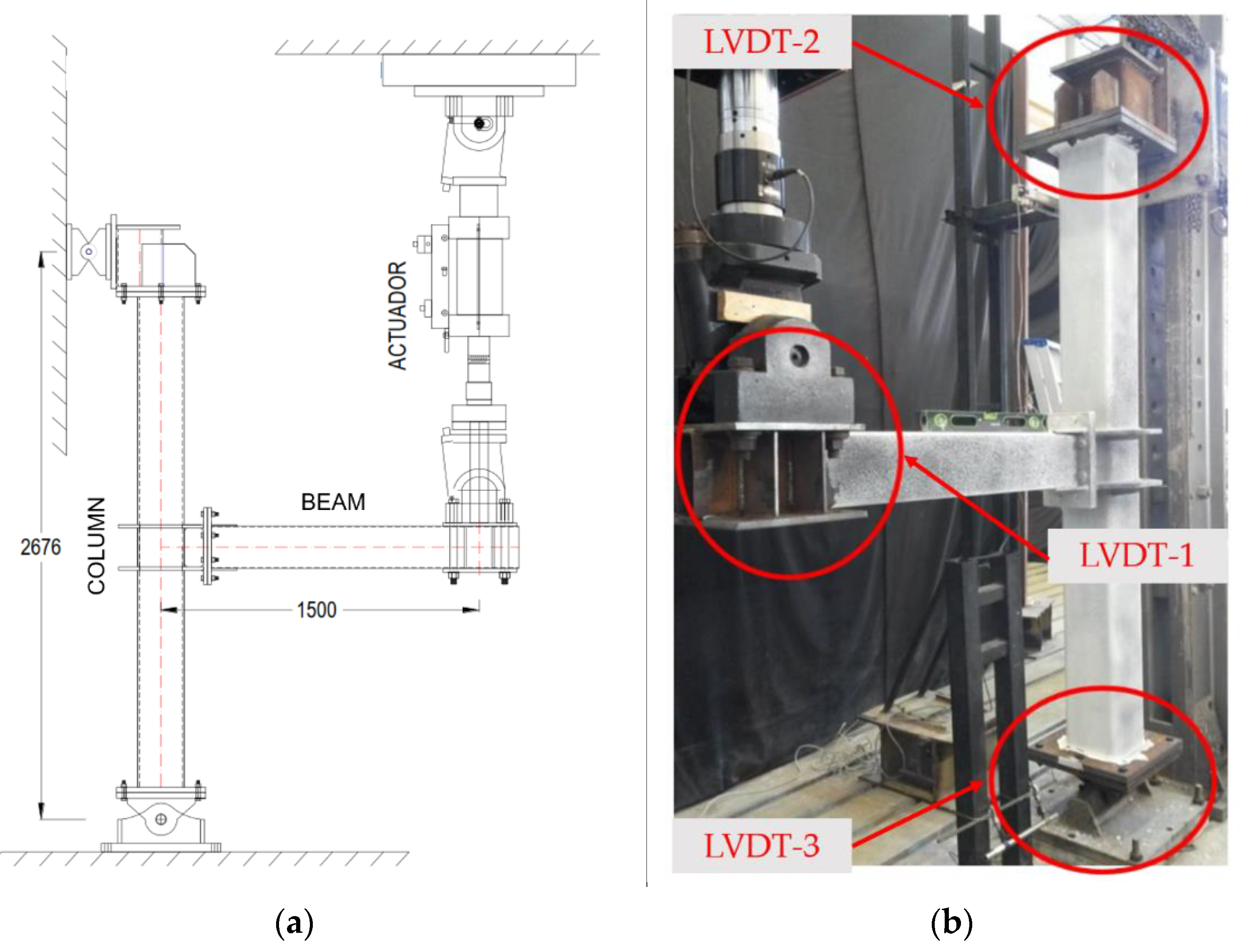
3. Experimental Study
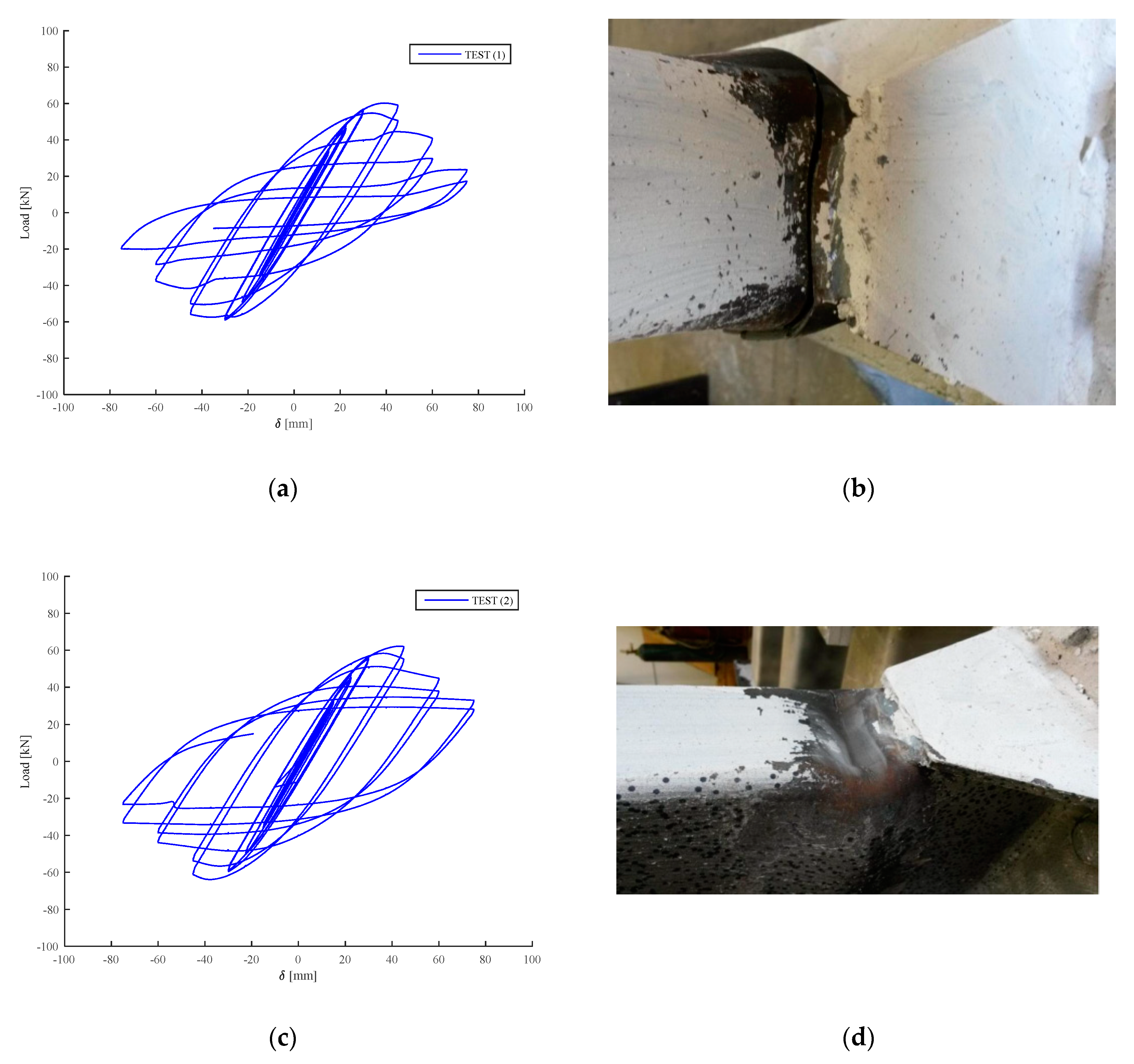
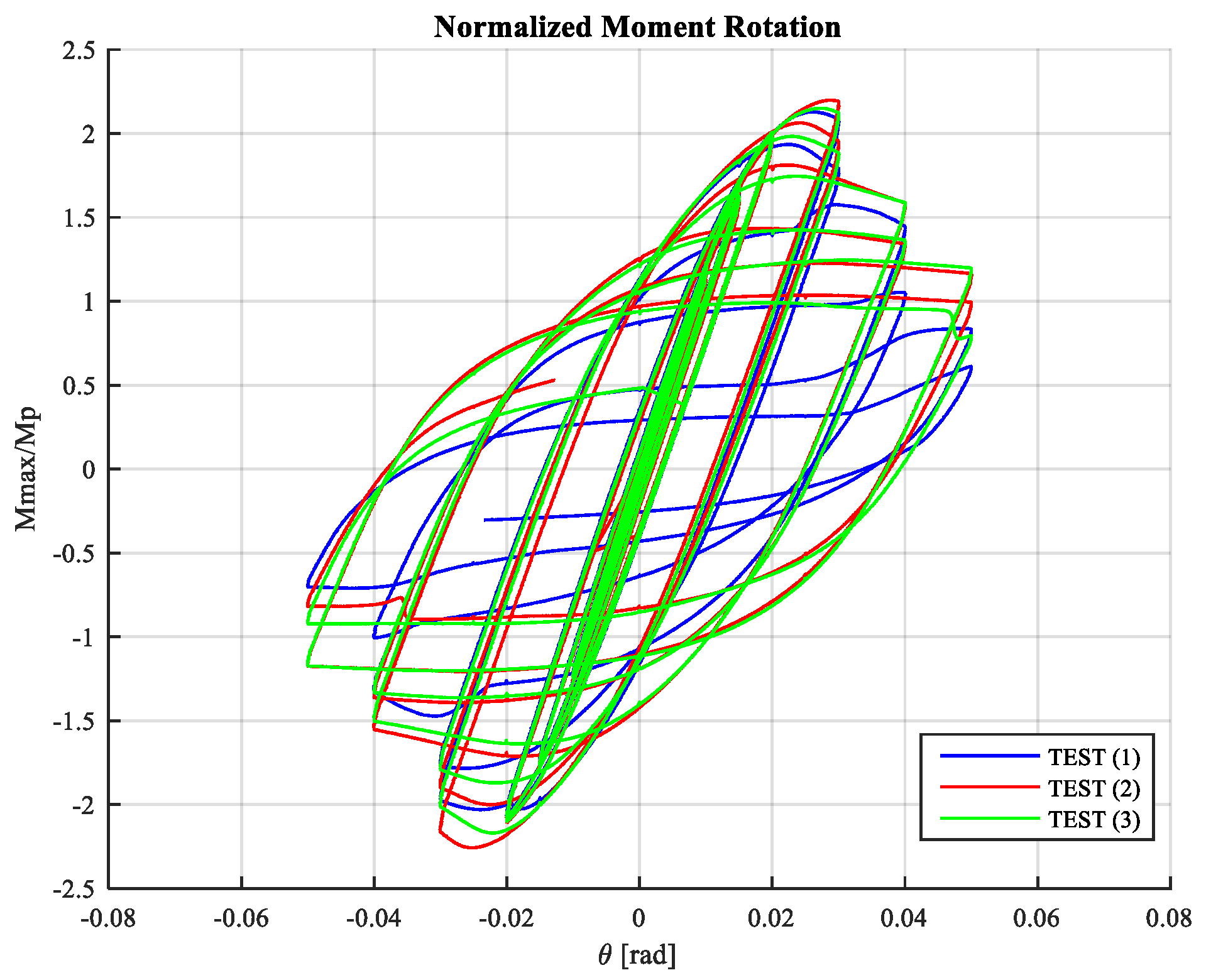
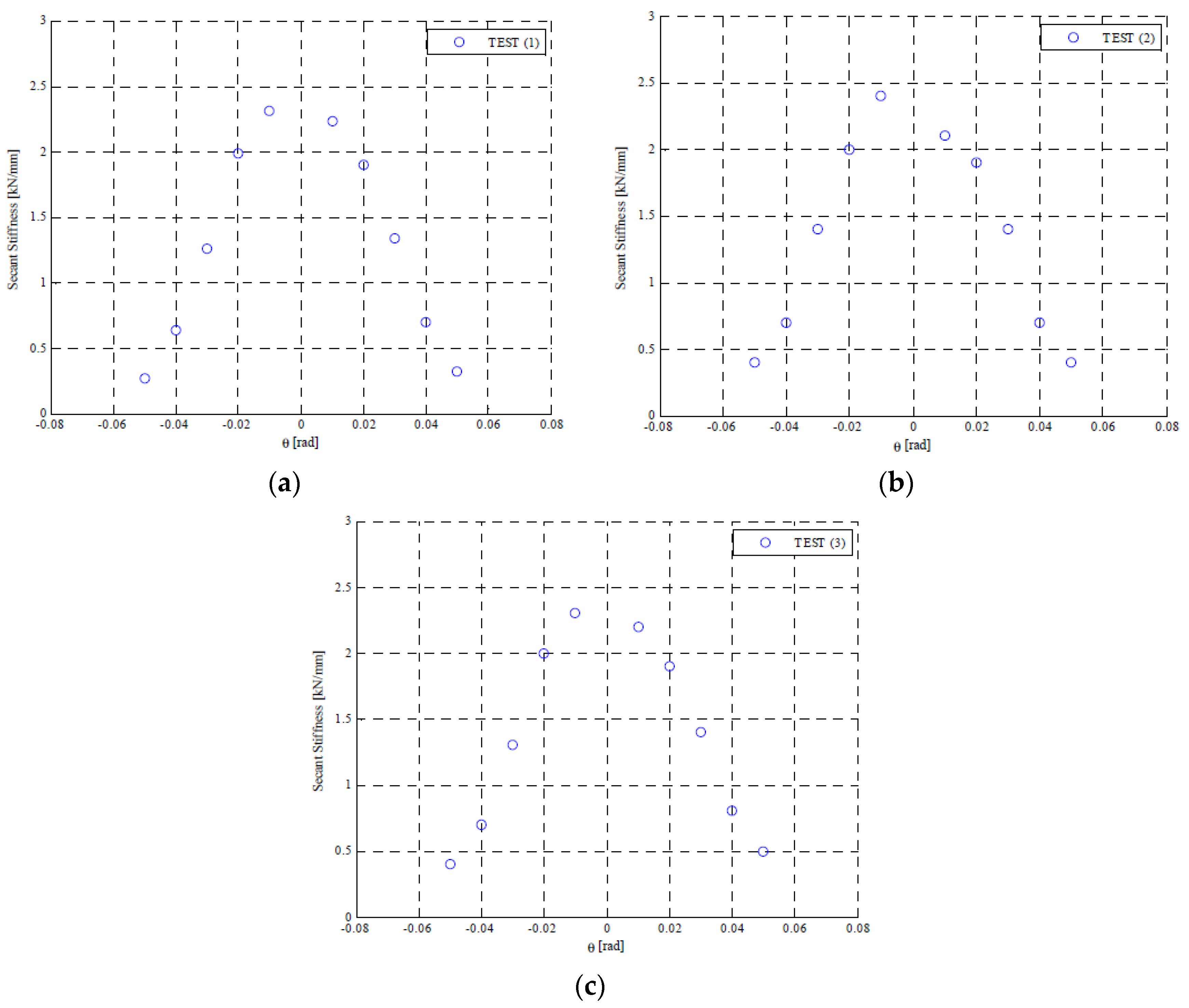
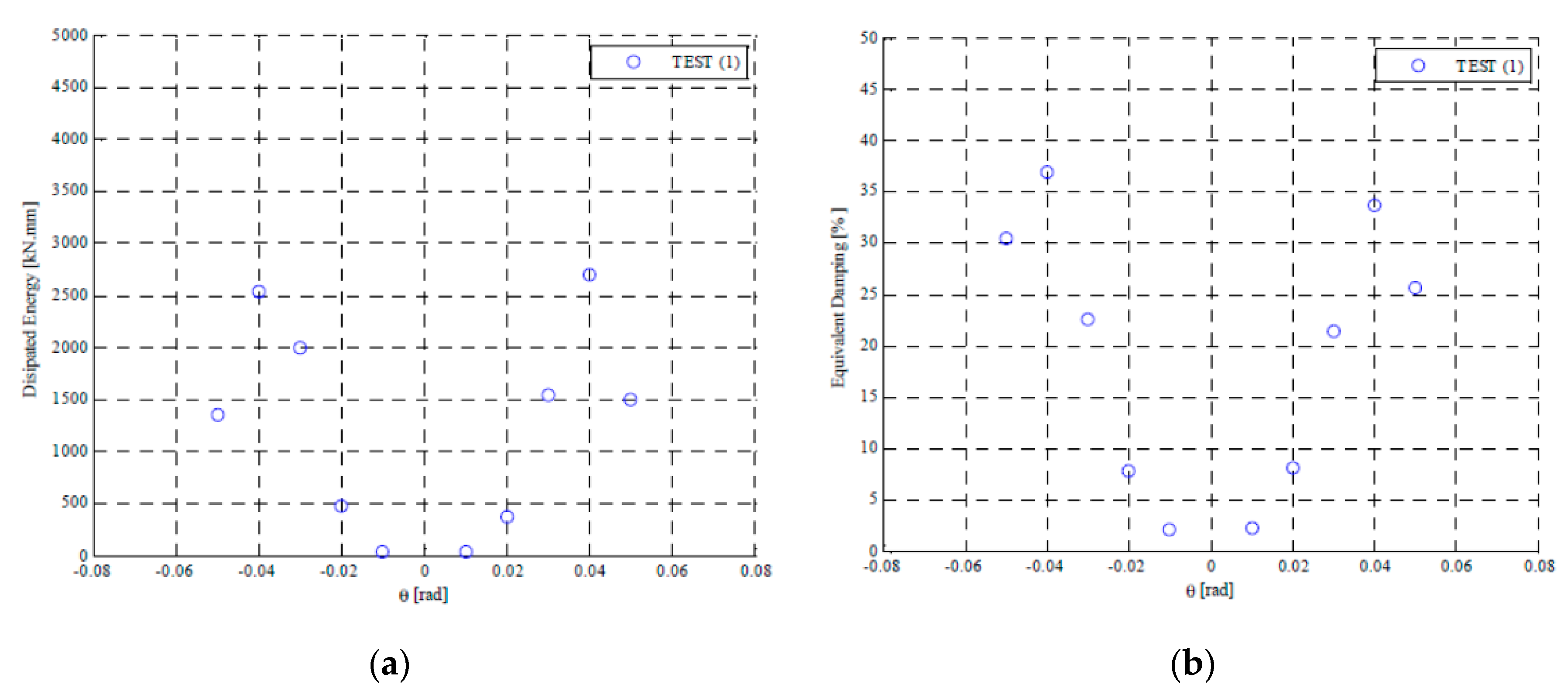
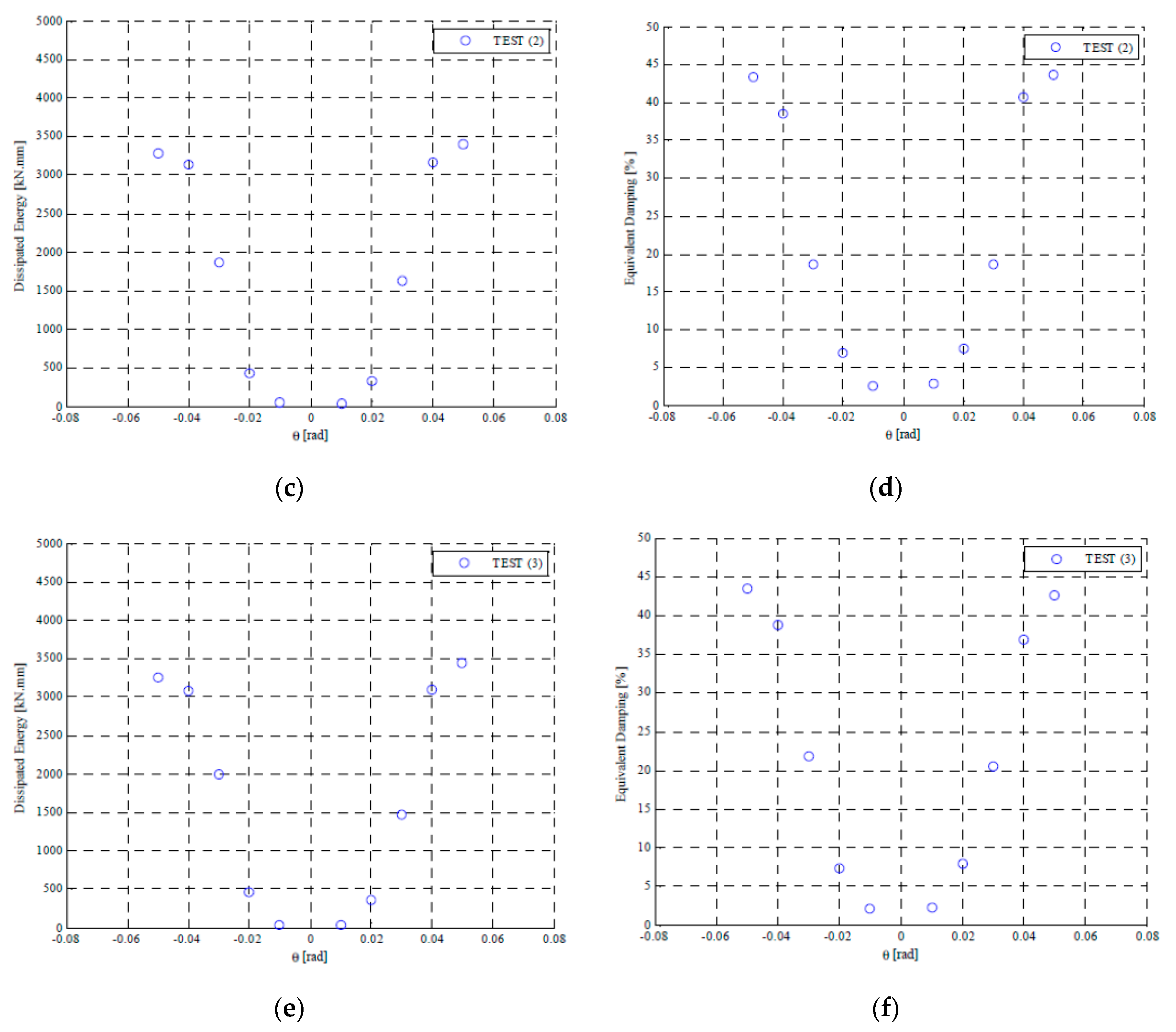
Experimental Results
4. Numerical Study
4.1. General Characteristics of the Numerical Model
- Length of the column is equal to inflection points at mid-height of each story.
- Washers are not included in the model for simplicity, considering that inelastic incursion is manifesting in the beam exclusively [16].
- Diameter of the bolt holes is assumed to be equal to the diameter of the bolts, avoiding rigid body movements that could affect the convergence of the model [16].
4.2. Element Type and Mesh
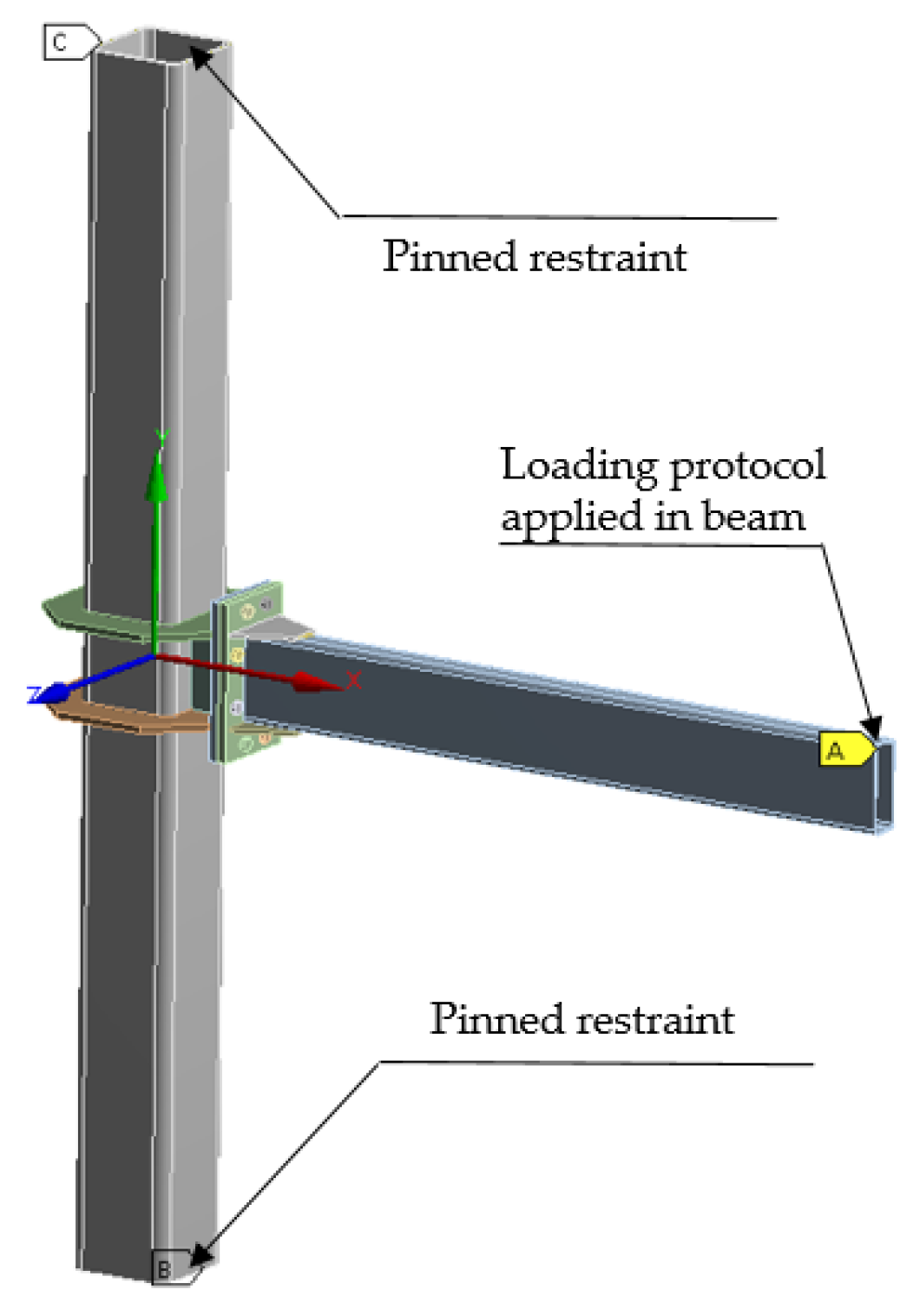
4.3. Boundary Conditions and Loading
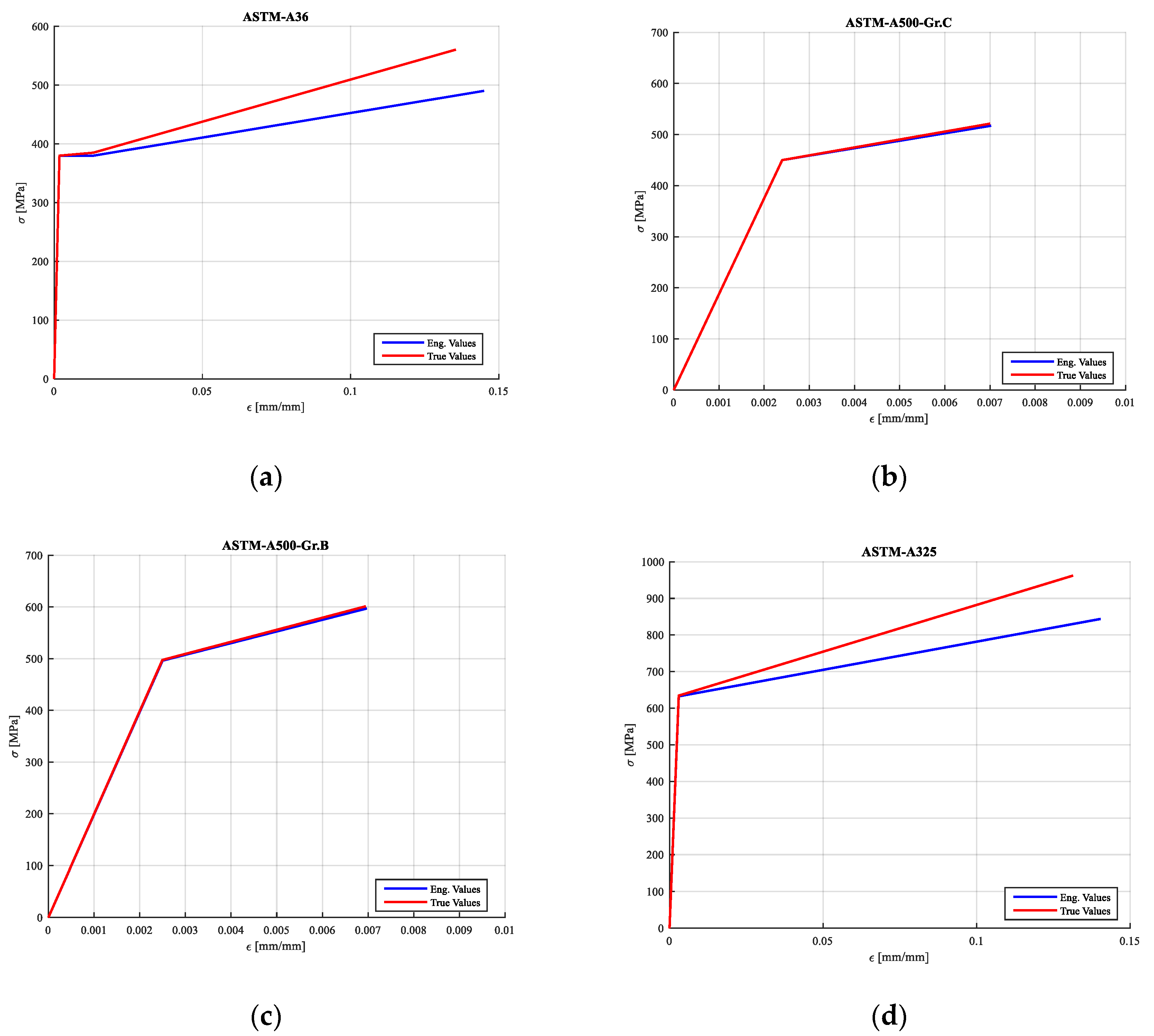
4.4. Material Modeling
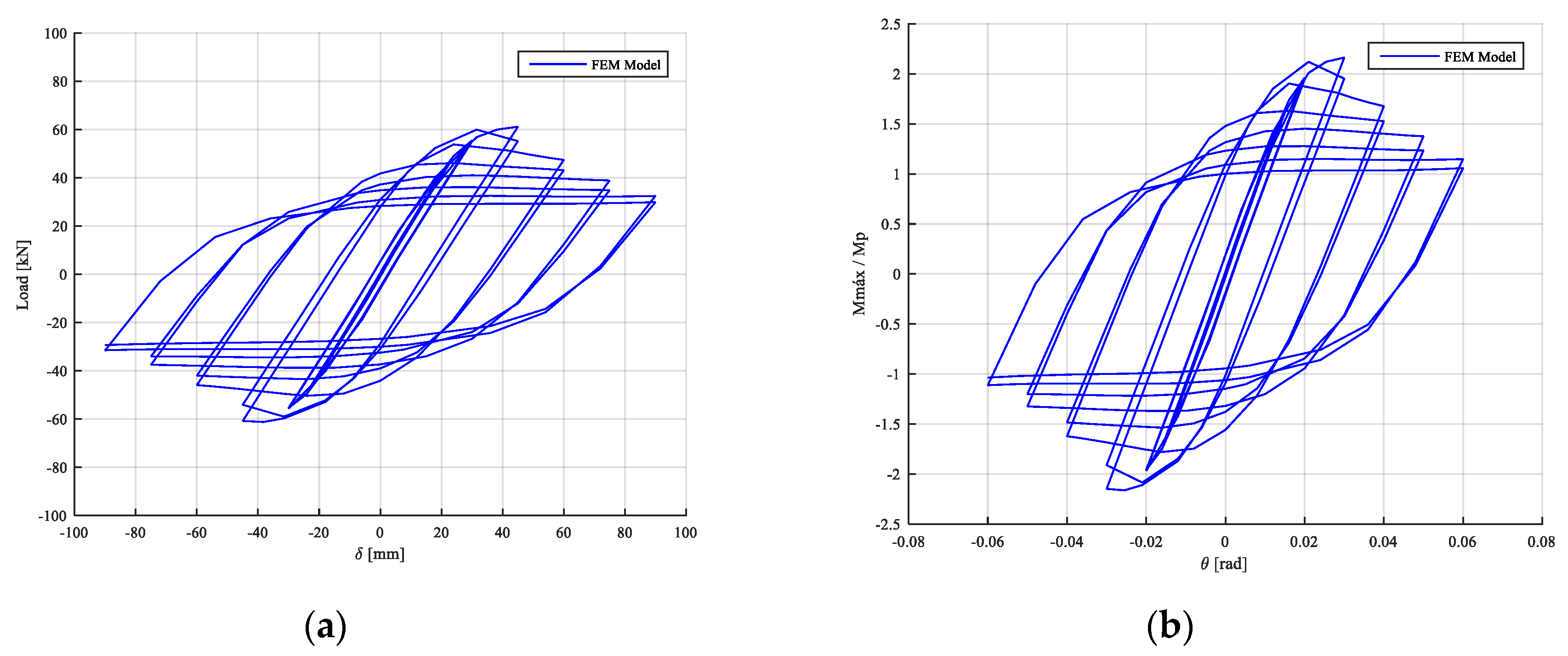
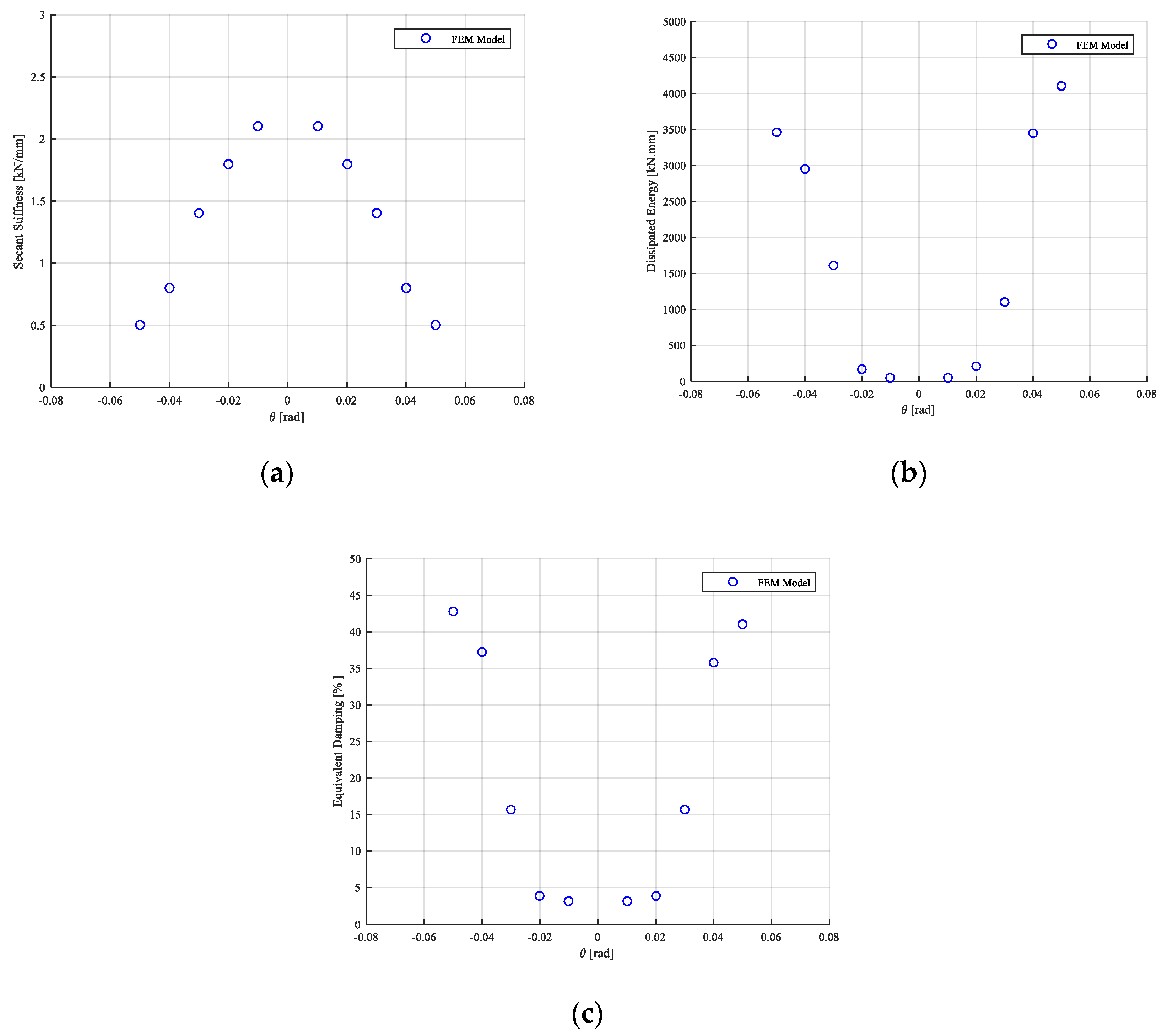
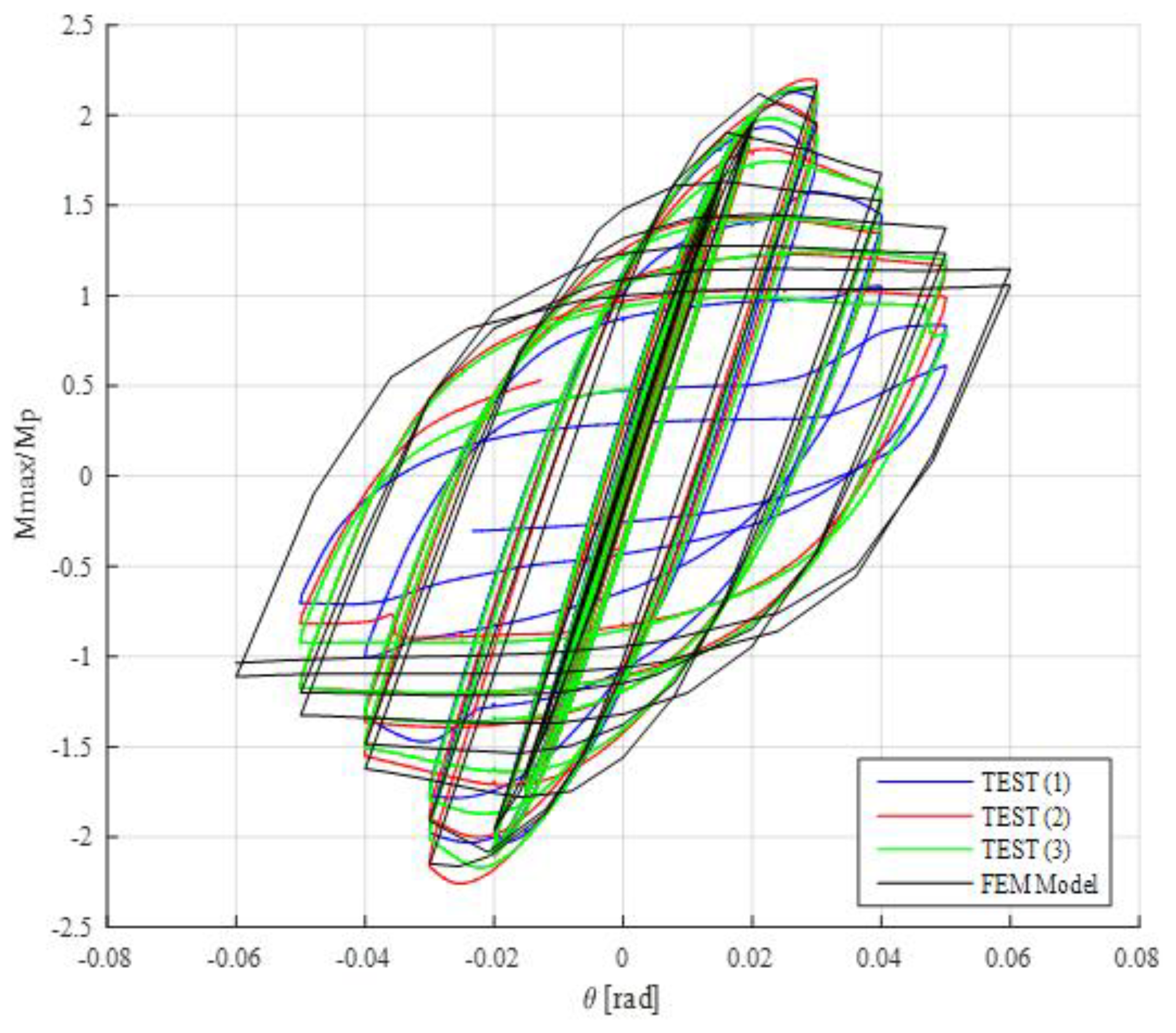
4.5. Results of Numerical Model
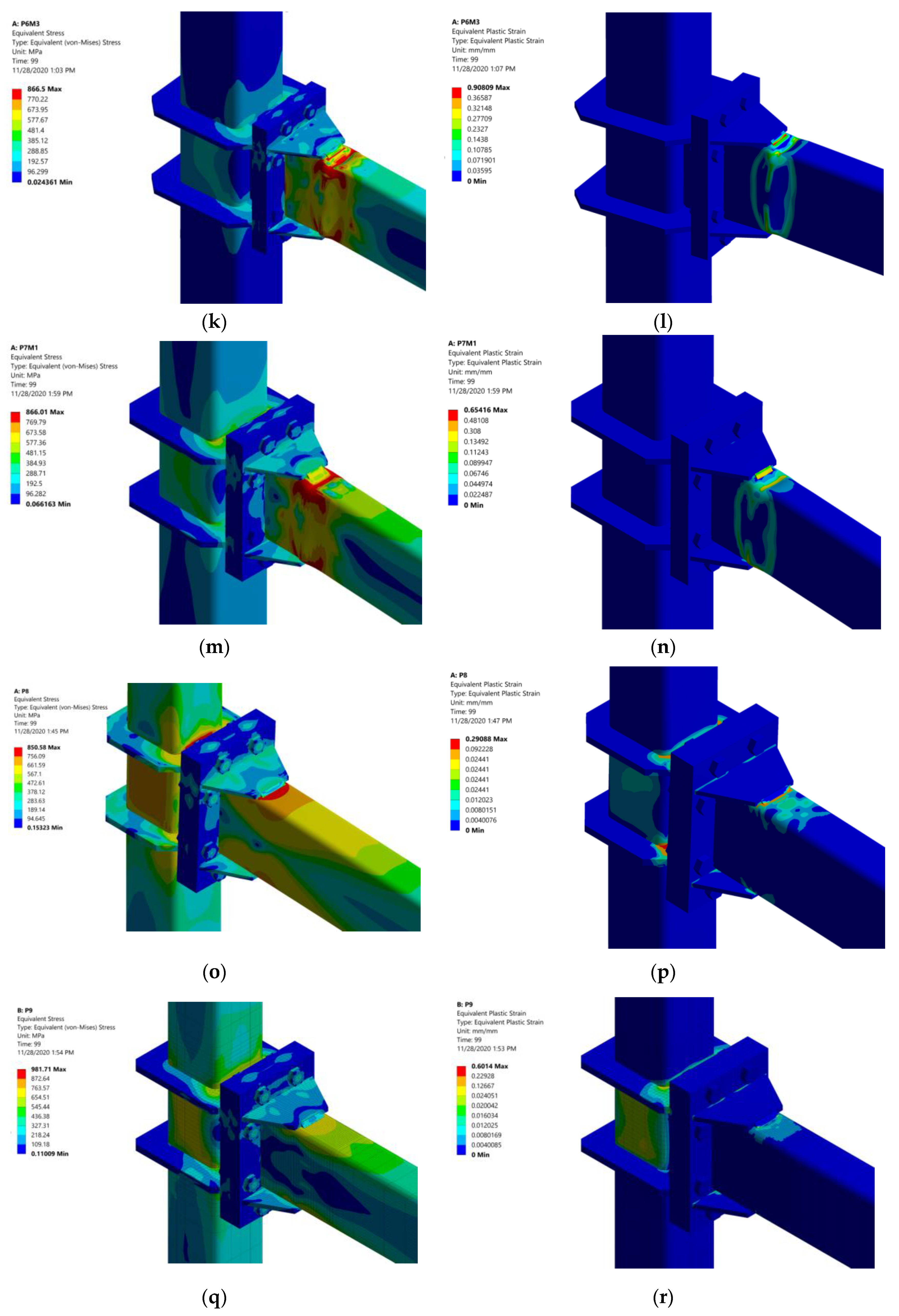
5. Cyclic Response of HSS Moment Connection with Other Configurations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbol | Definition |
| bf | Flange width of the beam |
| bp | Width of end-plate |
| d | Overall depth of beam |
| de | Column bolt edge distance |
| Fy | Specified minimum yield stress of the yielding element |
| g1 | Horizontal distance (gage) between fastener lines |
| g2 | Horizontal distance (gage) between fastener lines below cover plate |
| hi | Distance from centerline of compression flange to the centerline of the ith tension bolt row |
| ho | Distance from centerline of compression flange to the tension-side outer bolt row in EP-HSS moment connection |
| li | length of yield line |
| mp | plastic momento of beam |
| mpi | plastic moment internal of beam |
| M | Moment obtained |
| Mf | Probable maximum moment at face of column |
| Mn | Nominal flexural strength of beam |
| Mp | Plastic moment of beam |
| pfi | Vertical distance from inside of a beam tension flange to nearest inside bolt row |
| pfo | Vertical distance from inside of a beam tension flange to nearest outside bolt row |
| s | Distance from centerline of most inside or most outside tension bolt row to the edge of a yield line pattern |
| tp | Thickness of end-plate |
| WE | External work |
| Wi | Internal work |
| Yp | End-plate yield line mechanism parameter |
| δ1 | Virtual displacement for yield line 2 |
| δ2 | Virtual displacement for yield line 5 |
| δ3 | Virtual displacement for yield line 3, 7 and 8 |
| εu | Ultimate deformation |
| εy | Yielding deformation |
| ϕd | Resistance factor for ductile limit states |
| θ | Rotation angle due to moment of beam |
| θi | Rotation internal |
| σu | Ultimate stress |
| σy | Yielding stress |
References
- Sherman, D.R. Designing with structural tubing. Eng. J. AISC 1996, 33, 101–109. [Google Scholar]
- FEMA-355D. State of the Art Report on Connection Performance; Federal Emergency Management Agency: Washington, DC, USA, 2000.
- Wheeler, A.; Clarke, M.; Hancock, G.; Murray, T. Design model for bolted moment end-plate connections using rectangular hollow sections. In Report of Centre for Advanced Structural Engineering; Department of Civil Engineering, University of Sydney: Sydney, Australia, 1997. [Google Scholar]
- Guerrero, N.; Marante, M.E.; Picón, R.; Flórez-López, J. Model of local buckling in steel hollow structural elements subjected to biaxial bending. J. Constr. Steel Res. 2007, 63, 779–790. [Google Scholar] [CrossRef]
- Marante, M.; Picón, R.; Guerrero, N.; Flórez-López, J. Local buckling in tridimensional frames: Experimentation and simplified analysis. Lat. Am. J. Solids Struct. 2012, 9, 691–712. [Google Scholar]
- Fadden, M. Cyclic Bending Behavior of Hollow Structural Sections and Their Application in Seismic Moment Frame Systems. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2013. [Google Scholar]
- Fadden, M.; McCormick, J. Finite element model of the cyclic bending behavior of hollow structural section beam members. J. Constr. Steel Res. 2014, 94, 64–75. [Google Scholar] [CrossRef]
- Fadden, M.; McCormick, J. HSS-to-HSS seismic moment connection performance and design. J. Constr. Steel Res. 2014, 101, 373–384. [Google Scholar] [CrossRef]
- Esfandyary, R.; Razzaghi, M. and Eslami, A. A parametric investigation on the hysteretic behavior of CFT column to steel beam connections. Struct. Eng. Mech. 2015, 55, 205–228. [Google Scholar] [CrossRef]
- Faridmehr, I.; Osman, M.H.; Tahir, M.B.M.; Nejad, A.F.; Hodjati, R. Seismic and progressive collapse assessment of SidePlate moment connection system. Struct. Eng. Mech. 2015, 54, 35–54. [Google Scholar] [CrossRef]
- Ataollahi, S.; Banan, M.-R.; Banan, M.-R. Numerical cyclic behavior of T-RBS: A new steel moment connection. Steel Compos. Struct. 2016, 21, 1251–1264. [Google Scholar] [CrossRef]
- Saleh, A.; Zahrai, S.M.; Mirghaderi, S.R. Experimental study on innovative tubular web RBS connections in steel MRFs with typical shallow beams. Struct. Eng. Mech. 2016, 57, 785–808. [Google Scholar] [CrossRef][Green Version]
- Yang, C.; Yang, J.F.; Su, M.S.; Liu, C.Z. Numerical study on seismic behaviors of ConXtech® ConXLTM biaxial moment connection. J. Constr. Steel Res. 2016, 121, 185–201. [Google Scholar] [CrossRef]
- ANSI/AISC 358-16. Prequalified Connections for Special and Intermediate Steel Moment Frames for Seismic Applications; ANSI: Washington, DC, USA, 2016. [Google Scholar]
- Liu, X.-C.; Yang, Z.; Wang, H.; Zhang, A.; Pu, S.; Chai, S.; Wu, L. Seismic performance of H-section beam to HSS column connection in prefabricated structures. J. Constr. Steel Res. 2017, 138, 1–16. [Google Scholar] [CrossRef]
- Nuñez, E.; Torres, R.; Herrera, R. Seismic performance of moment connections in steel moment frames with HSS columns. Steel Compos. Struct. 2017, 25, 271–286. [Google Scholar]
- Tahir, M.M.; Mohammadhosseini, H.; Poi-Ngian, S.; Effendi, M.K. I-beam to square hollow column blind bolted moment connection: Experimental and numerical study. J. Constr. Steel Res. 2018, 148, 383–398. [Google Scholar] [CrossRef]
- Wang, J.; Lü, J.; Zhang, H.; Zhao, C. Experimental investigation on seismic performance of endplate composite joints to CFST columns. J. Constr. Steel Res. 2018, 145, 352–367. [Google Scholar] [CrossRef]
- Ali, A.M.; Masmoudi, R. Experimental and analytical investigation of new concrete filled FRP tube beam-column connections. Eng. Struct. 2019, 191, 311–322. [Google Scholar] [CrossRef]
- Eslami, M.; Namba, H.; Kodur, V.; Mahamid, M.; Morovat, M.A. Seismic behavior of composite beam connected to HSS column with large width-to-thickness ratio. Eng. Struct. 2019, 183, 423–442. [Google Scholar] [CrossRef]
- Kishiki, S.; Lee, D.-S.; Yamada, S.; Ishida, T.; Jiao, Y. Low-cycle fatigue performance assessment of current Japanese steel beam-to-column connections determined by ductile fracture. Eng. Struct. 2019, 182, 241–250. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y.; Yang, F.; An, Q. Influence of weld details on fracture behavior of connections using high-strength steel. J. Constr. Steel Res. 2019, 153, 578–587. [Google Scholar] [CrossRef]
- Jiang, J.; Chen, S. Experimental and numerical study of double-through plate connections to CFST column. J. Constr. Steel Res. 2019, 153, 385–394. [Google Scholar] [CrossRef]
- Ye, J.; Mojtabaei, S.M.; Hajirasouliha, I. Seismic performance of cold-formed steel bolted moment connections with bolting friction-slip mechanism. J. Constr. Steel Res. 2019, 156, 122–136. [Google Scholar] [CrossRef]
- Liu, X.-C.; Cui, F.Y.; Zhan, X.X.; Yu, C.; Jiang, Z.Q. Seismic performance of bolted connection of H-beam to HSS-column with web end-plate. J. Constr. Steel Res. 2019, 156, 167–181. [Google Scholar] [CrossRef]
- ANSI/AISC 341-16. Seismic Provisions for Structural Steel Buildings; American Institute of Steel Construction: Chicago, IL, USA, 2016. [Google Scholar]
- Johansen, K.W. Brudlinieteorier; Gjellerup Forlag: Copenhagen, Denmark, 1943. [Google Scholar]
- ANSI/AISC 360-16. Specification for Structural Steel Buildings; American Institute of Steel Construction: Chicago, IL, USA, 2016. [Google Scholar]
- Chopra, A.K. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Prentice-Hall: Englewood Cliffs, NJ, USA, 2007. [Google Scholar]
- ANSYS. Multiphysics version 17.2; ANSYS Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Díaz, C. Diseño de Uniones Semirrígidas Mediante Simulación Numérica y Modelos Kriging. Ph.D. Thesis, Universidad Politécnica de Cartagena, Cartagena, Spain, 12 April 2010. (In Spanish). [Google Scholar]
- Kim, T.S.; Kuwamura, H. Finite element modeling of bolted connections in thin-walled stainless steel plates under static shear. Thin Walled Struct. 2007, 45, 407–421. [Google Scholar] [CrossRef]
- Diaz, C.; Victoria, M.; Martí, P.; Querin, O.M.; Martí, P. FE model of beam-to-column extended end-plate joints. J. Constr. Steel Res. 2011, 67, 1578–1590. [Google Scholar] [CrossRef]
- Bravo, M.A.; Herrera, R. Performance under cyclic load of built-up T-stubs for Double T moment connections. J. Constr. Steel Res. 2014, 103, 117–130. [Google Scholar] [CrossRef]
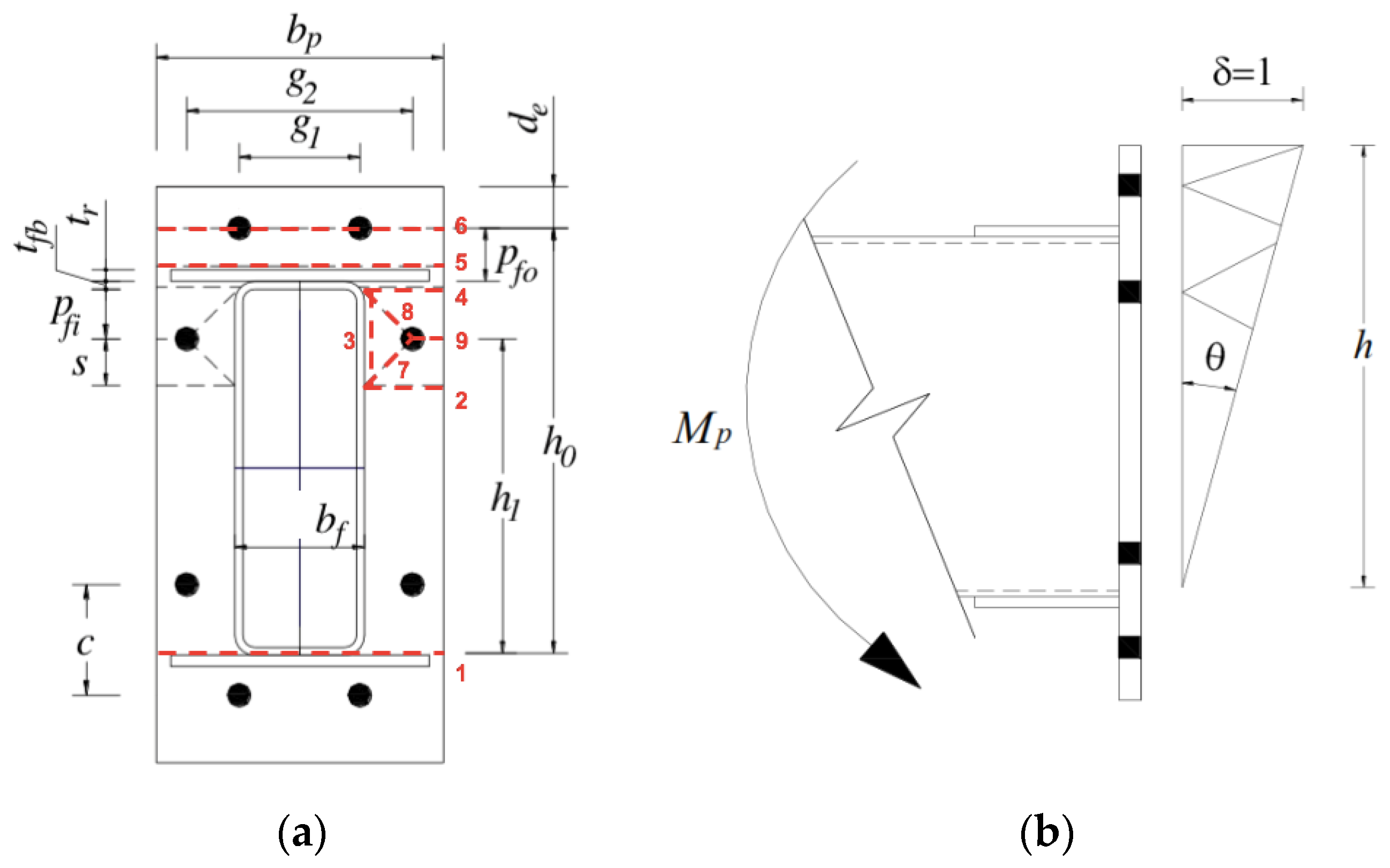








| Yield Line | Length (li) | Rotation (θi) |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 |
| Element | Designation | Σy [MPa] | εy | σu [MPa] | εu |
|---|---|---|---|---|---|
| Stiffeners, End-plates | ASTM-A-36 | 380 | 0.0018 | 575 | 0.20 |
| Beam 200 × 70 × 4.3 | ASTM-A-500 Gr. C | 450 | 0.0024 | 517 | 0.007 |
| Column 220 × 220 × 9 | ASTM-A-500 Gr. B | 496 | 0.0025 | 597 | 0.01 |
| Bolt | ASTM-A-325 | 634 | 0.0036 | 848 | 0.14 |
| No. | No. of Cycles | Drift Angle (θ) [rad] |
|---|---|---|
| 1 | 6 | 0.00375 |
| 2 | 6 | 0.005 |
| 3 | 6 | 0.0075 |
| 4 | 4 | 0.01 |
| 5 | 2 | 0.015 |
| 6 | 2 | 0.02 |
| 7 | 2 | 0.03 |
| 8 | 2 | 0.04 |
| Specimen | Lmax [kN] | Dmax [mm] | M/Mp | Mmax [kN.m] | Rmax [rad] |
|---|---|---|---|---|---|
| Test 1 | 60.24 | 75.17 | 2.12 | 90.35 | 0.05 |
| Test 2 | 62.25 | 75.18 | 2.20 | 93.37 | 0.05 |
| Test 3 | 60.86 | 75.17 | 2.15 | 91.30 | 0.05 |
| Component | Number of Elements | Number of Nodes |
|---|---|---|
| End-plates | 4600 | 24,975 |
| Column | 2960 | 19,128 |
| Beam | 6264 | 43,411 |
| Bolts | 10,619 | 18,948 |
| Vertical Stiffener | 132 | 1042 |
| Horizontal Stiffener | 2250 | 13,444 |
| Elements Connection | Contact | Movement in Normal Direction | Movement in Tangential Direction |
|---|---|---|---|
| Column-Horizontal Stiffeners | Bonded | No separation | No slip |
| Column-Vertical Stiffeners | Bonded | No separation | No slip |
| Vertical Stiffeners-Horizontal Stiffeners | Bonded | No separation | No slip |
| End-plate-Horizontal Stiffeners | Bonded | No separation | No slip |
| End-plate-Vertical Stiffeners | Bonded | No separation | No slip |
| End-plate-End-plate | Frictional | Separation allowed | Slip allowed |
| Beam-End-plate, Bolt-Nut | Bonded | No separation | No slip |
| Bolt- End-plate, Nut-End-plate | Frictionless | Separation allowed | Slip allowed |
| Specimen | Lmax [kN] | Dmax [mm] | M/Mp | Mmax [kN.m] | Rmax [rad] |
|---|---|---|---|---|---|
| Test S-01 | 60.24 | 75.17 | 2.12 | 90.35 | 0.05 |
| Test S-02 | 62.25 | 75.18 | 2.20 | 93.37 | 0.05 |
| Test S-03 | 60.86 | 75.17 | 2.15 | 91.30 | 0.05 |
| FEM Model | 61.18 | 90 | 2.16 | 91.77 | 0.06 |
| Numerical Model | Dimension of Column [mm] | Dimension of Beam [mm] |
|---|---|---|
| P0 | 220 × 220 × 9 | 200 × 70 × 4.3 |
| P1 | 220 × 220 × 9 | 180 × 65 × 4 |
| P2 | 220 × 220 × 9 | 220 × 90 × 4.5 |
| P3 | 220 × 220 × 9 | 260 × 90 × 5.5 |
| P4 | 220 × 220 × 9 | 300 × 100 × 5.5 |
| P5 | 220 × 220 × 9 | 300 × 100 × 7 |
| P6 | 260 × 260 × 11 | 320 × 120 × 7 |
| P7 | 260 × 260 × 11 | 320 × 120 × 9 |
| P8 | 260 × 260 × 11 | 350 × 170 × 9 |
| P9 | 260 × 260 × 11 | 350 × 170 × 11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nuñez, E.; Boainy, N.; González, F.; Torres, R.; Picón, R.; Guerrero, N. Cyclic Behavior of Hollow Section Beam–Column Moment Connection: Experimental and Numerical Study. Metals 2020, 10, 1608. https://doi.org/10.3390/met10121608
Nuñez E, Boainy N, González F, Torres R, Picón R, Guerrero N. Cyclic Behavior of Hollow Section Beam–Column Moment Connection: Experimental and Numerical Study. Metals. 2020; 10(12):1608. https://doi.org/10.3390/met10121608
Chicago/Turabian StyleNuñez, Eduardo, Nwar Boainy, Freddy González, Ronald Torres, Ricardo Picón, and Néstor Guerrero. 2020. "Cyclic Behavior of Hollow Section Beam–Column Moment Connection: Experimental and Numerical Study" Metals 10, no. 12: 1608. https://doi.org/10.3390/met10121608
APA StyleNuñez, E., Boainy, N., González, F., Torres, R., Picón, R., & Guerrero, N. (2020). Cyclic Behavior of Hollow Section Beam–Column Moment Connection: Experimental and Numerical Study. Metals, 10(12), 1608. https://doi.org/10.3390/met10121608







