A Vision-Based Fuzzy Control to Adjust Compression Speed for a Semi-Dieless Bellows-Forming
Abstract
1. Introduction
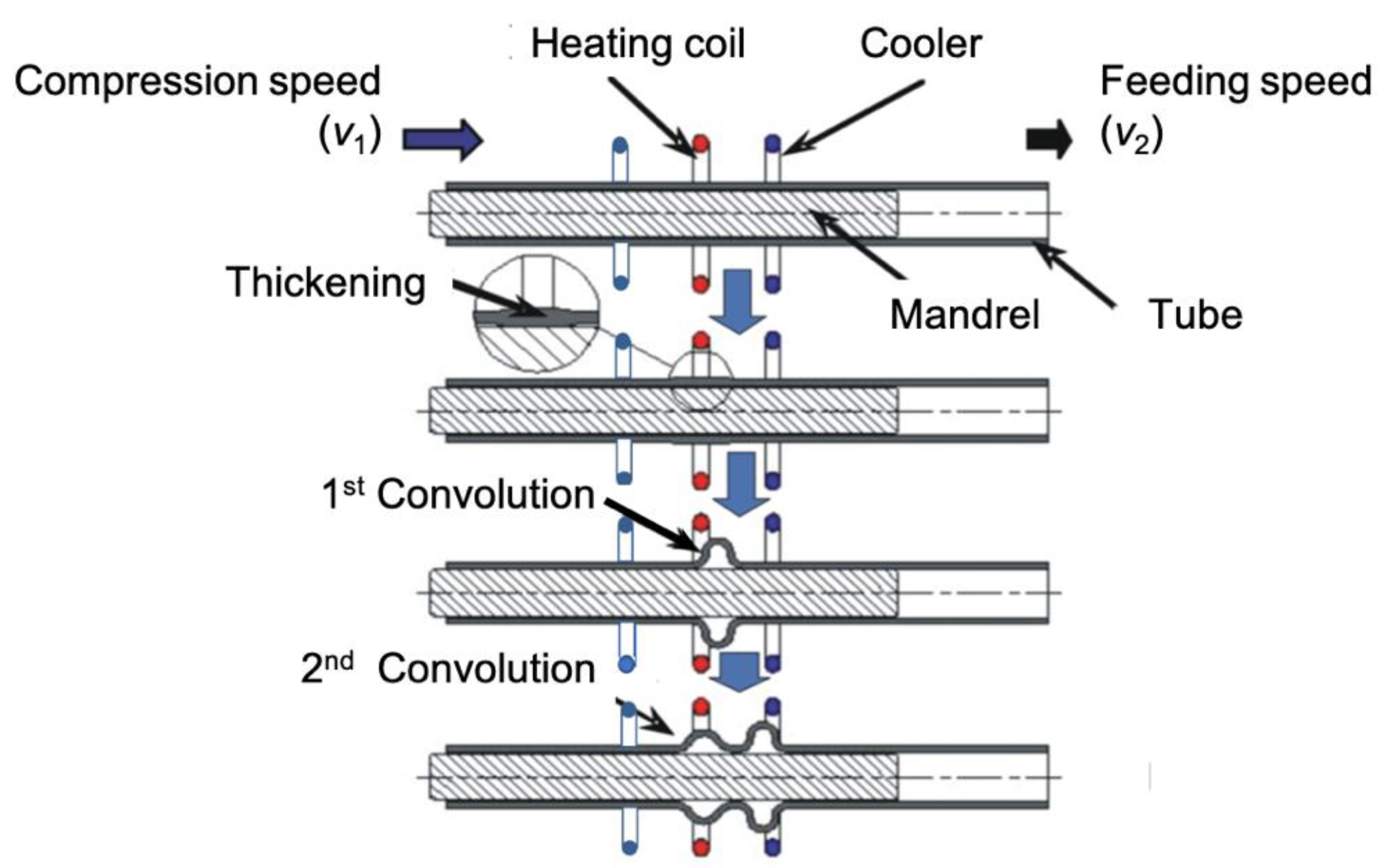
2. The Principle of Semi-Dieless Bellows Forming through Local Heating
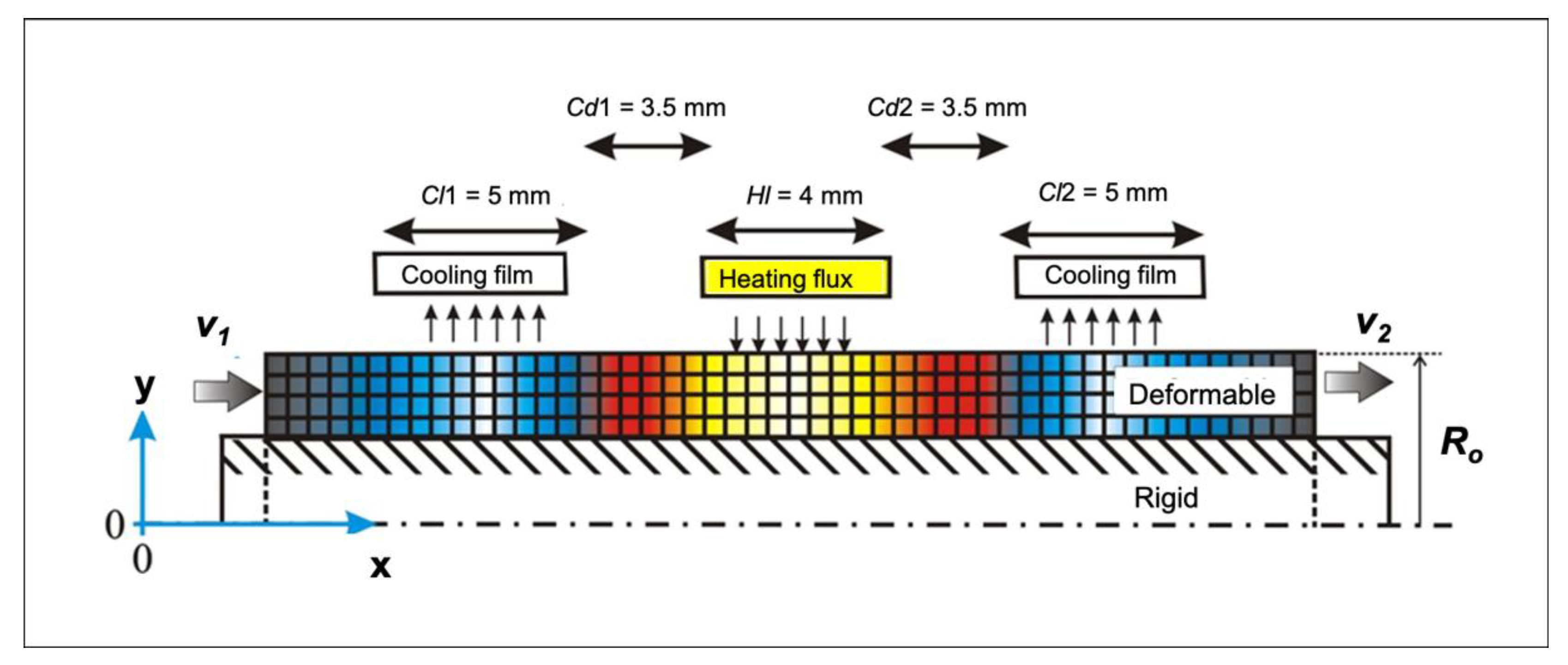
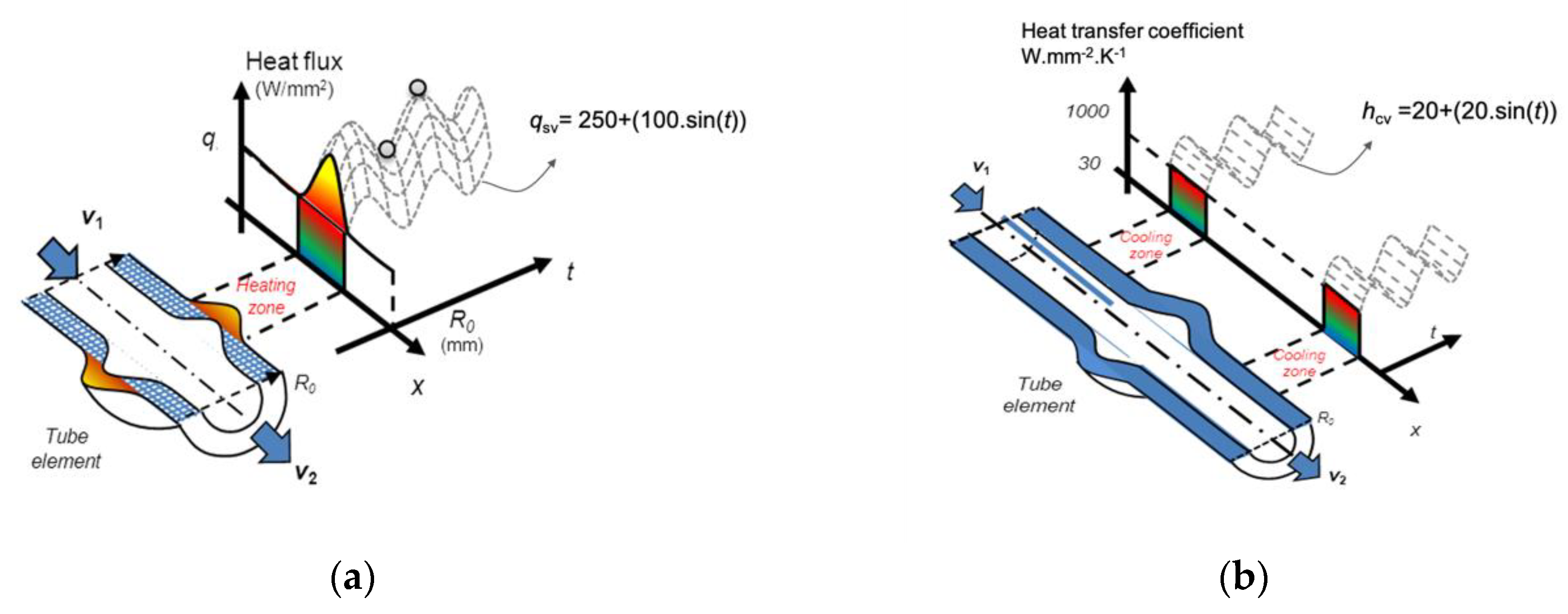
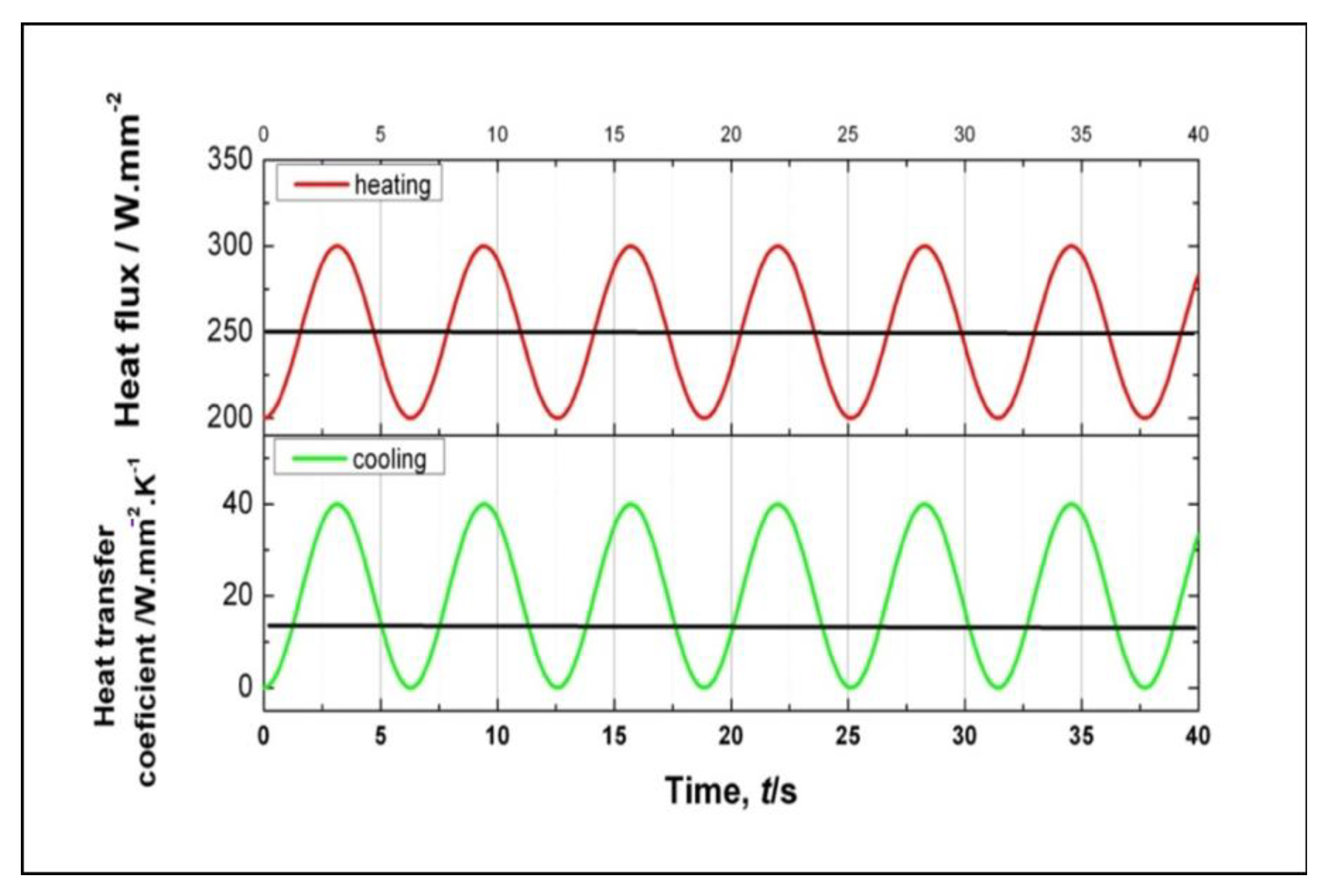
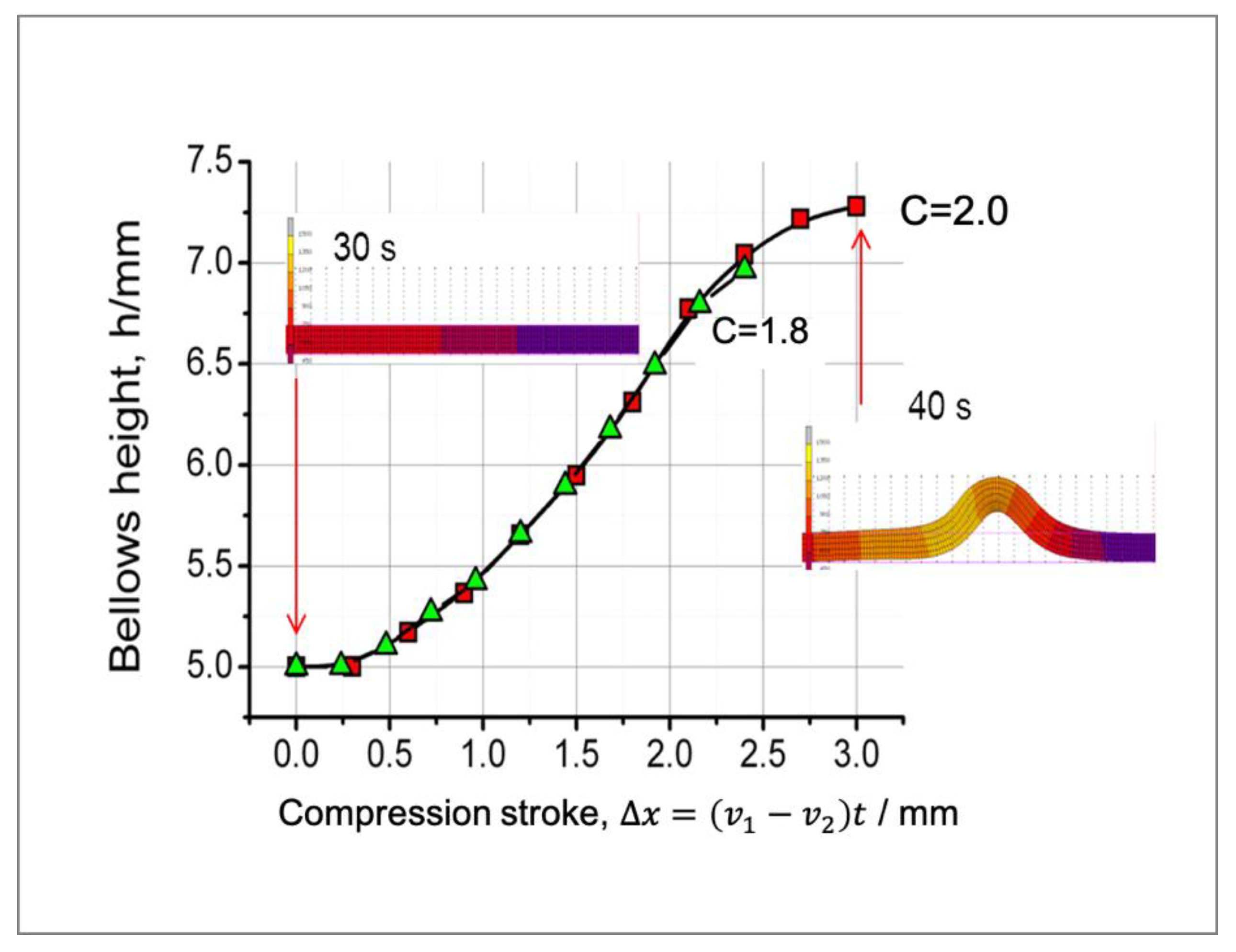
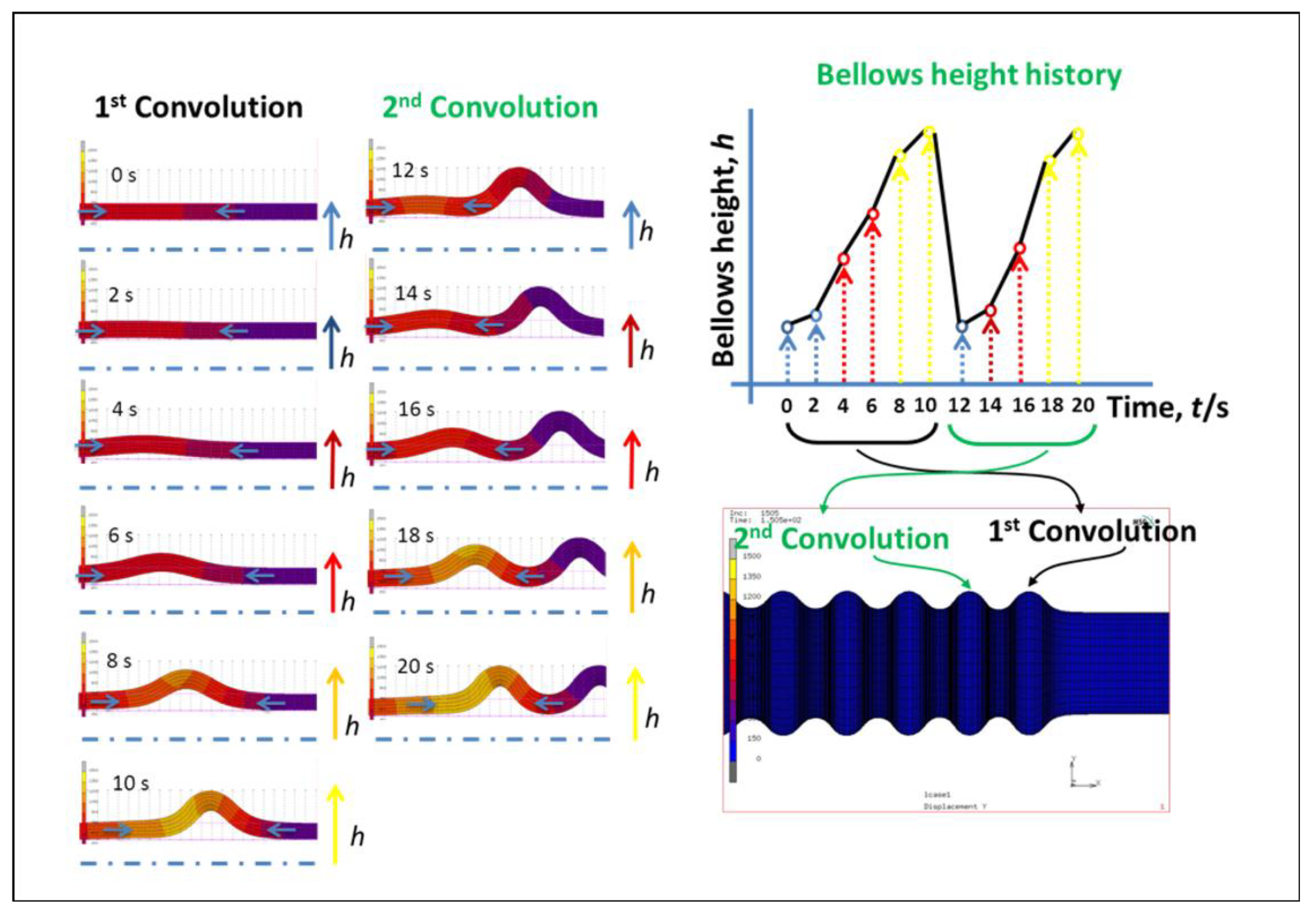
3. Finite Element Analysis (FEA)
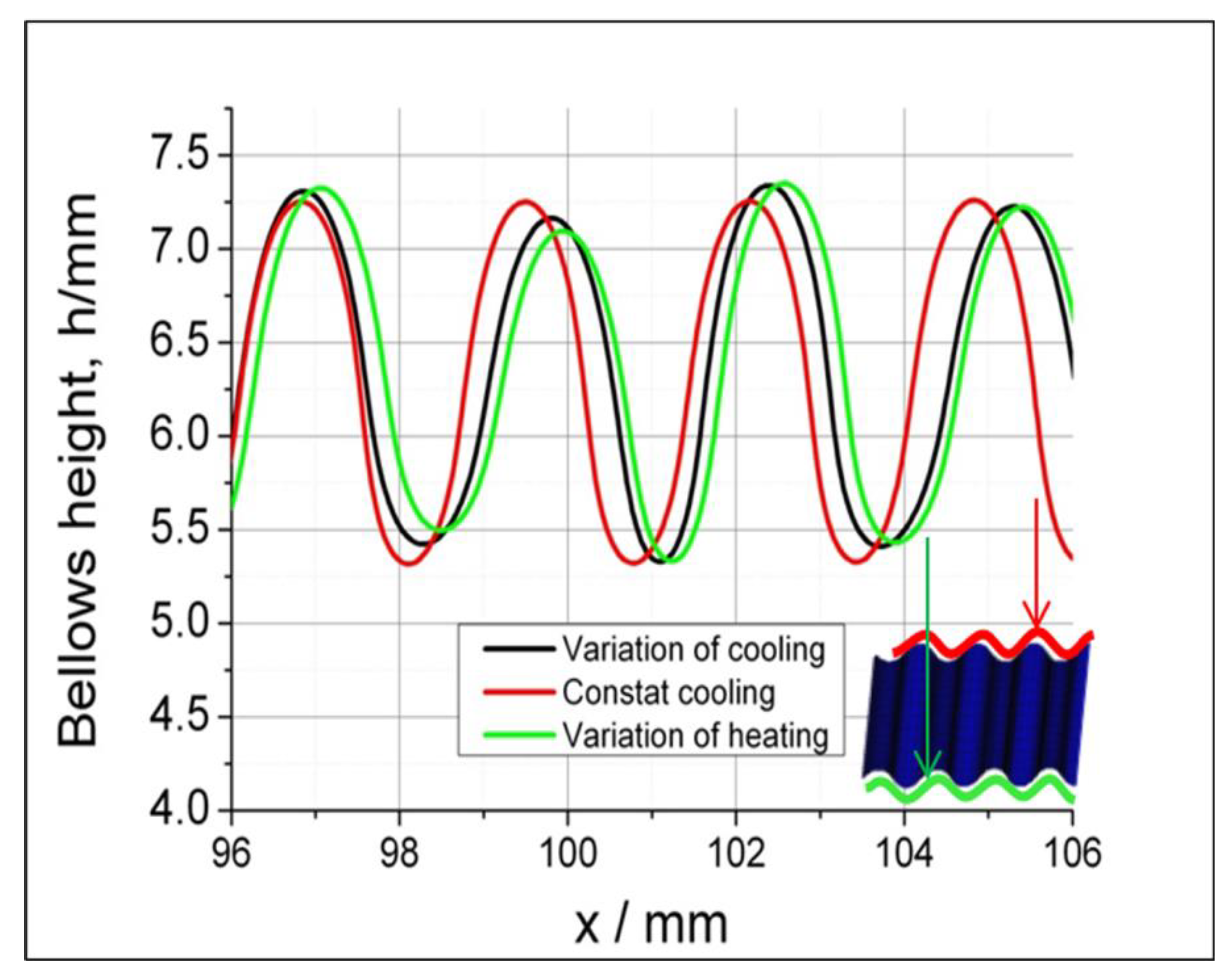
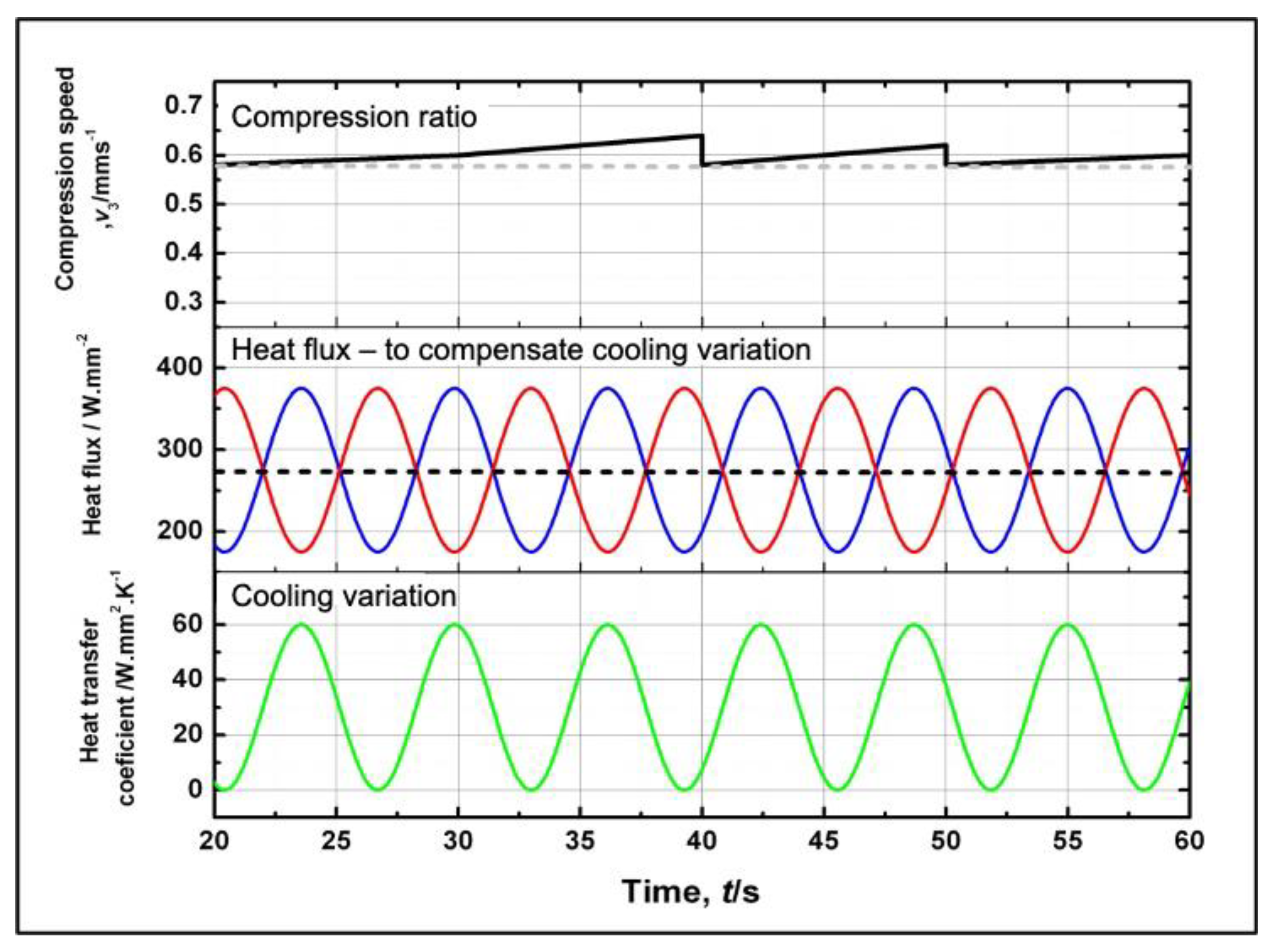
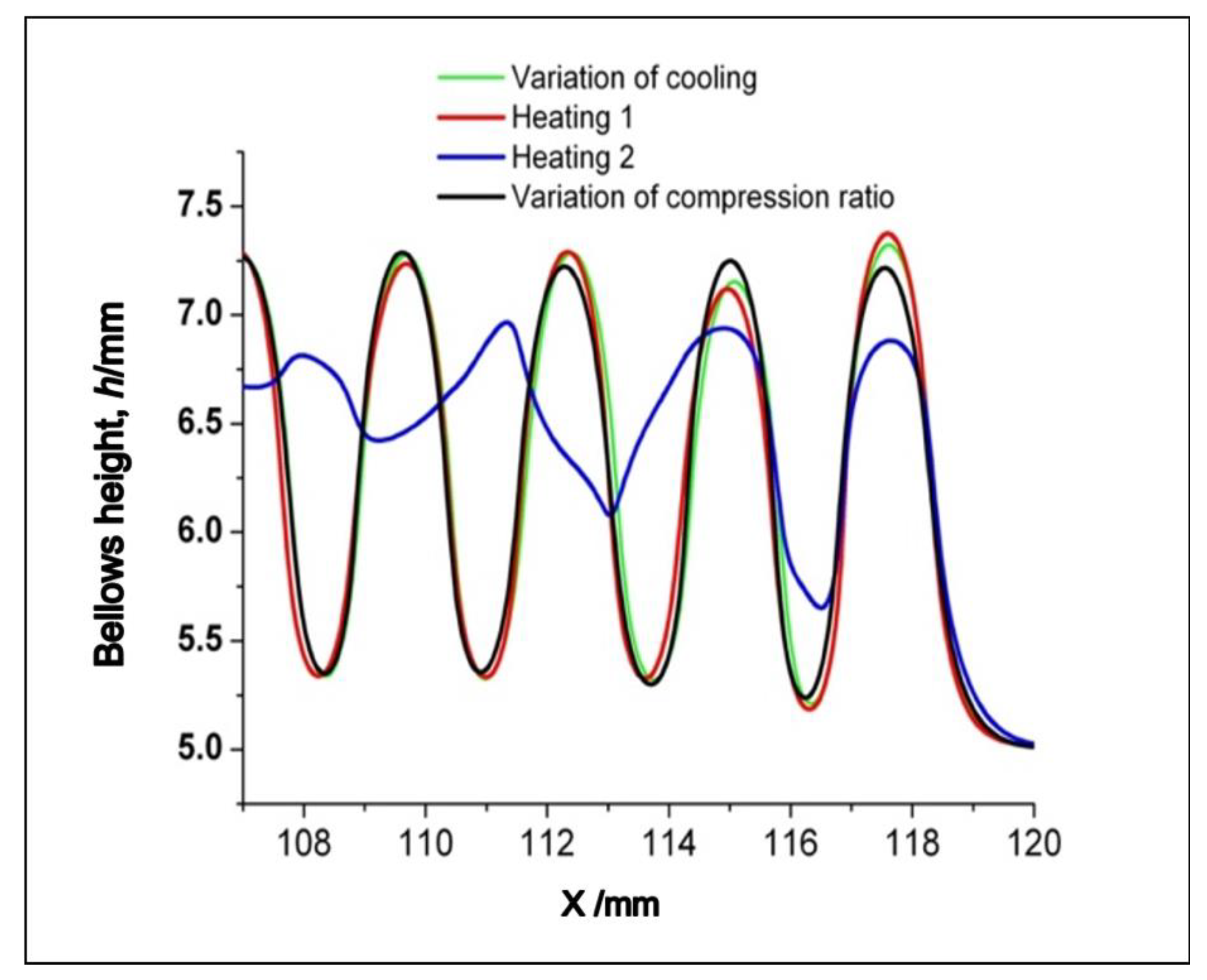
4. Selecting the Compensation Method for the Unstable Deformation Promoted by a Variety of Temperatures
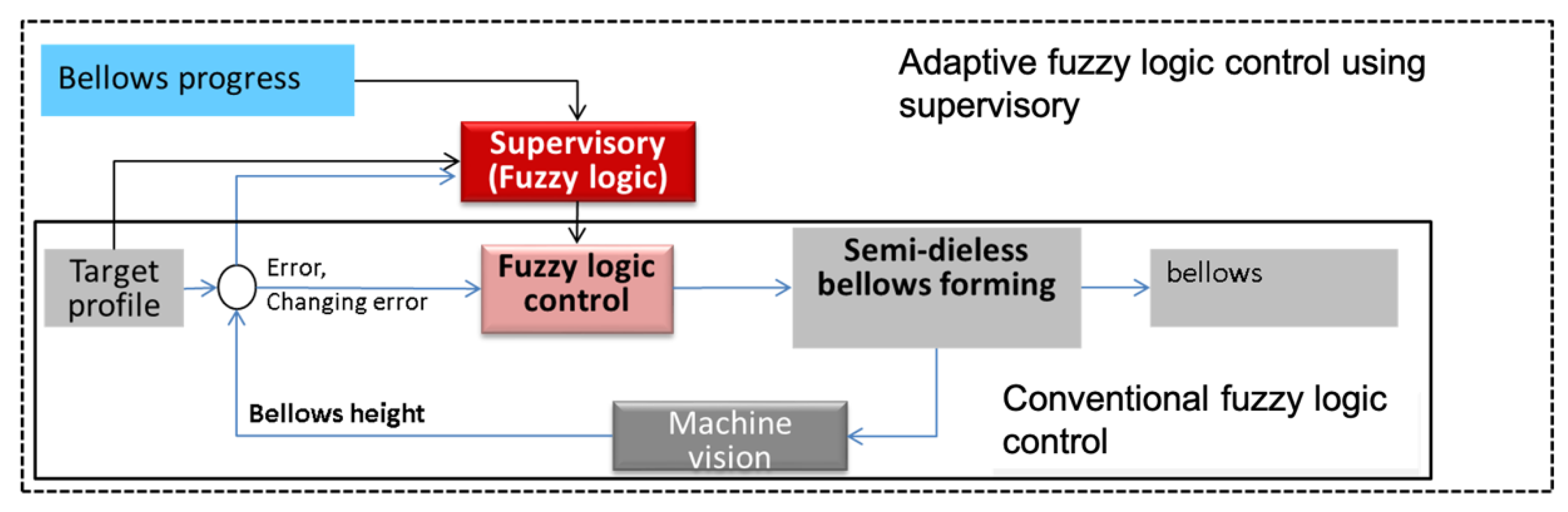
5. Improving the Dieless Bellows Forming Process with the Application of a Feedback Control System
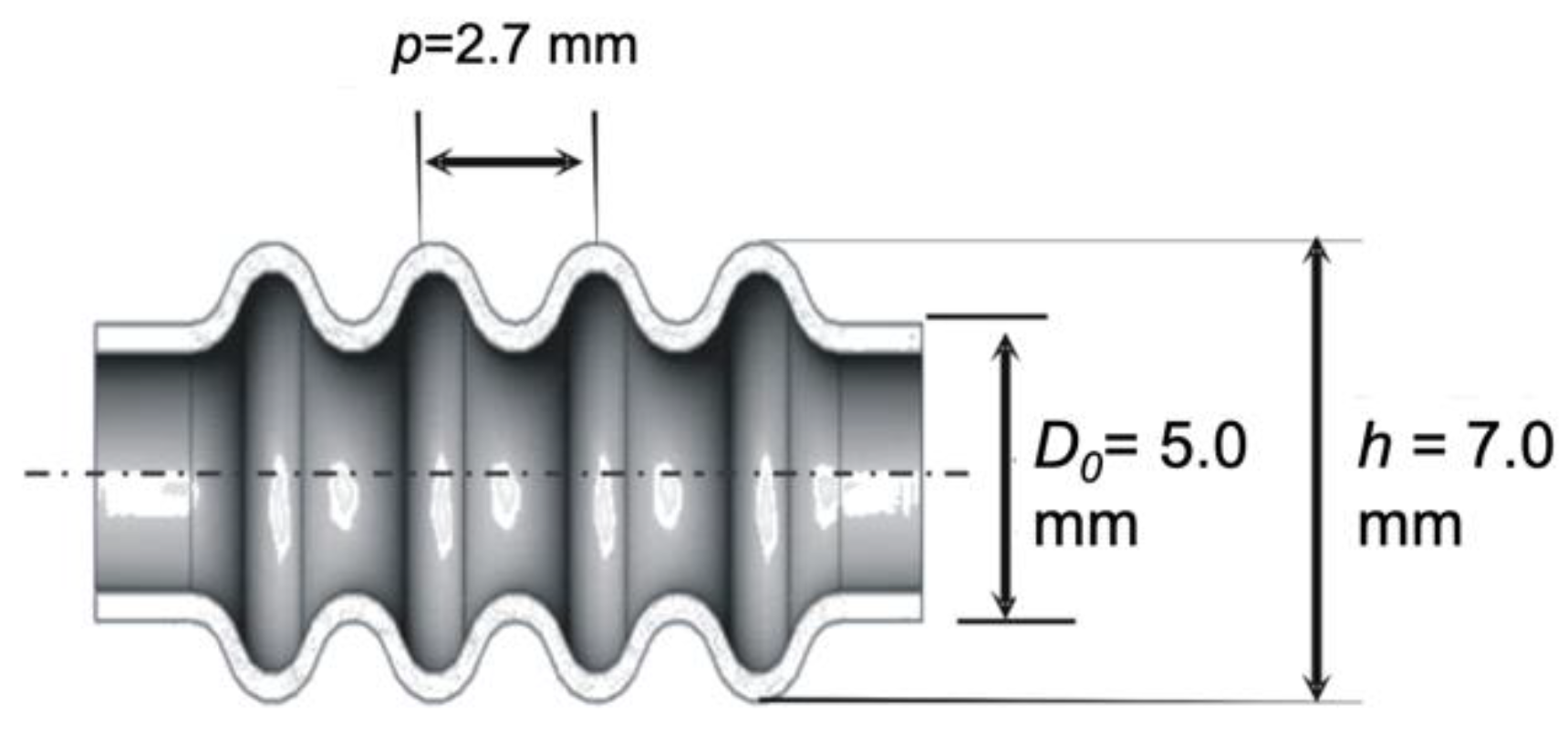
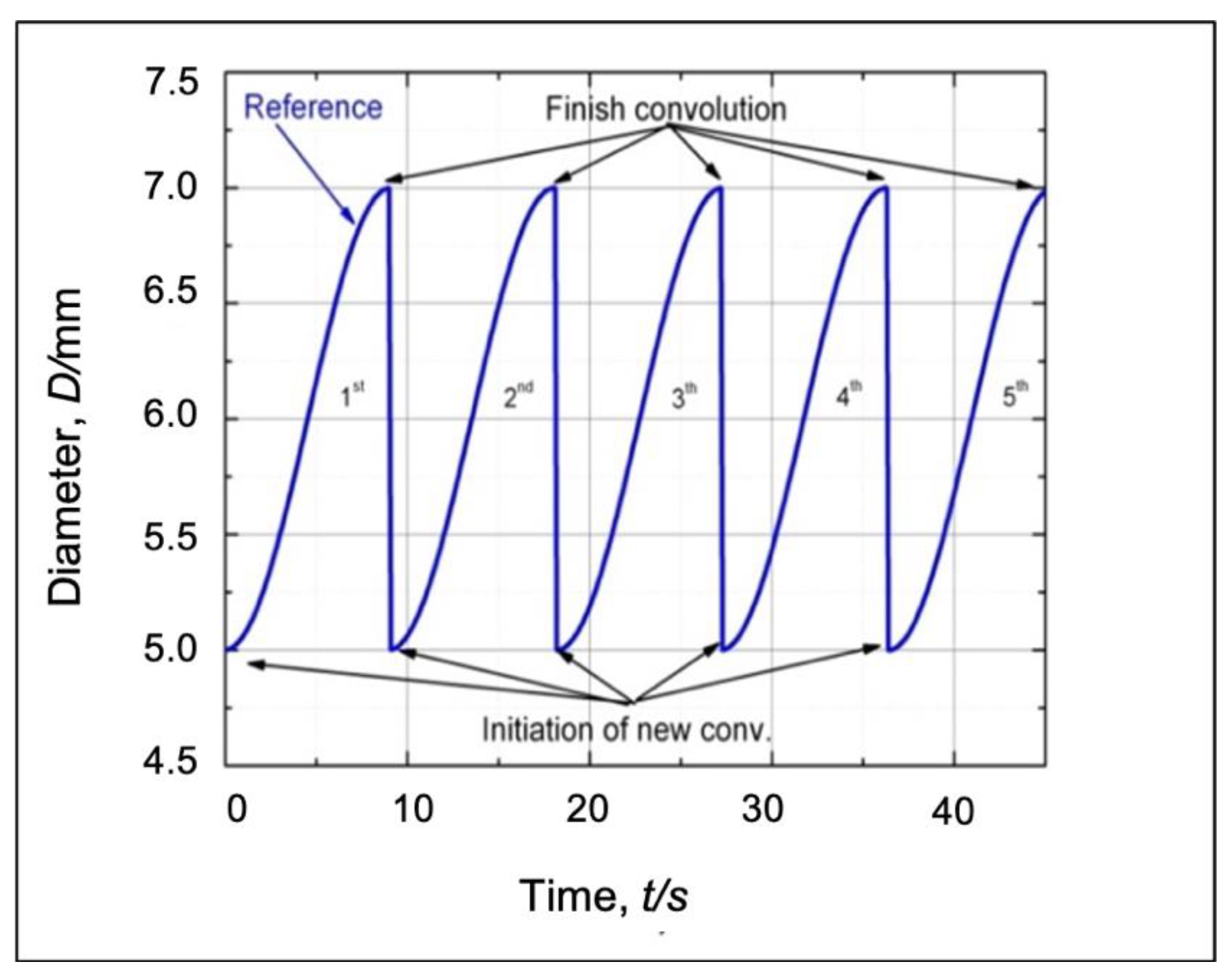
5.1. Deformation Reference
5.2. A Vision-Based Feedback Control
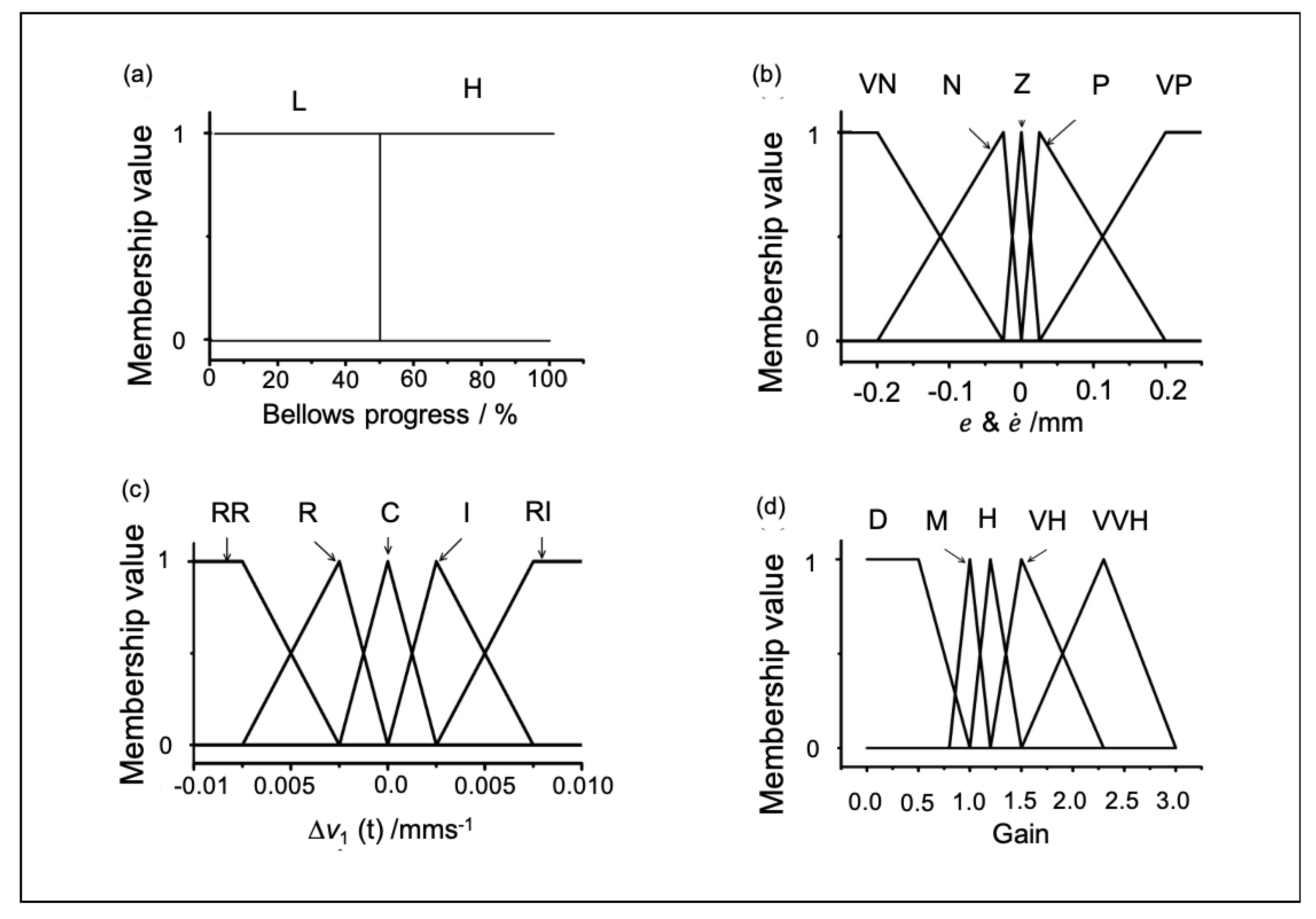
5.3. Establishing a Control System
6. Experimental Method
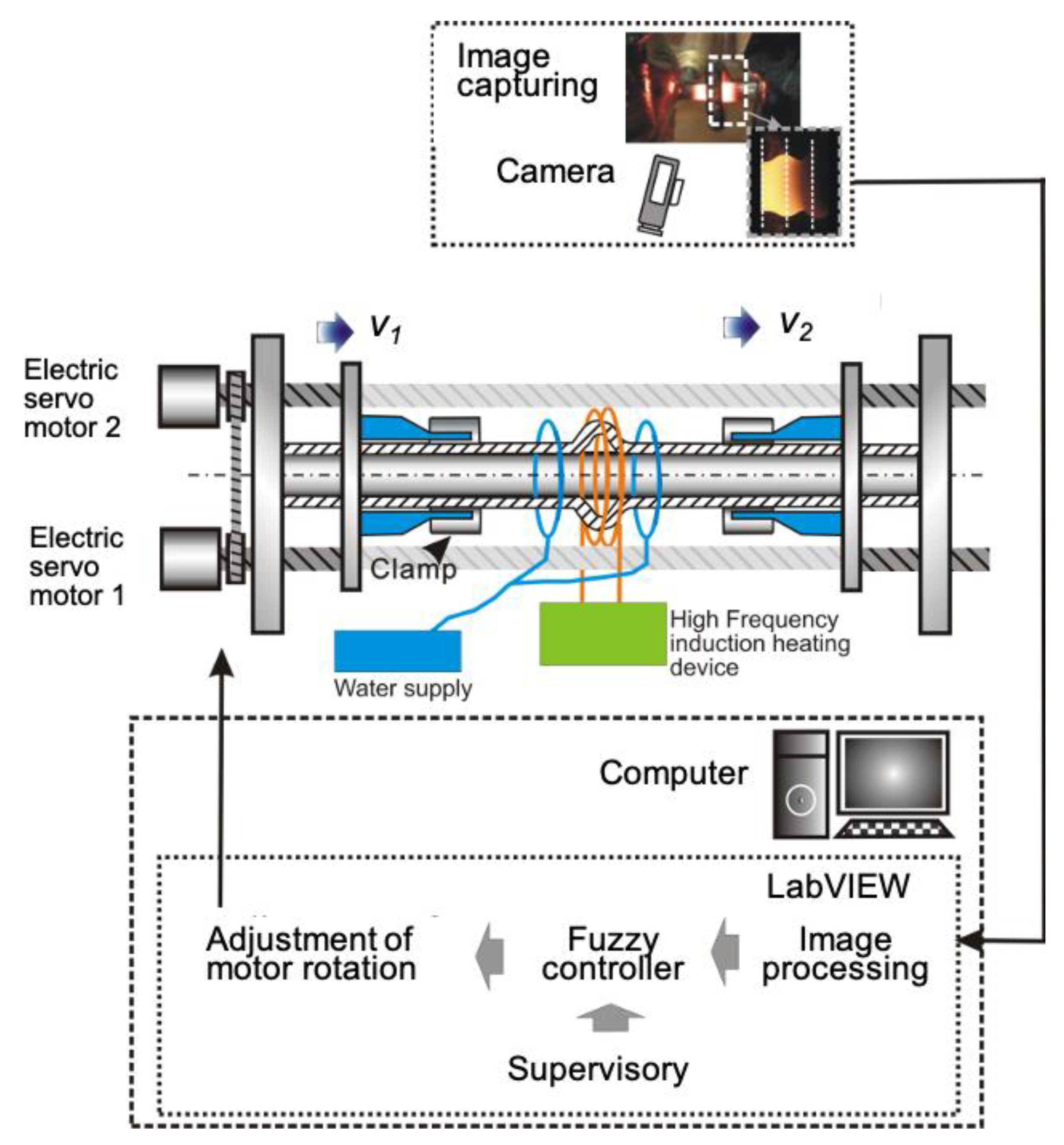
6.1. Experimental Equipment
6.2. Materials and Experimental Conditions
7. Results and Discussion
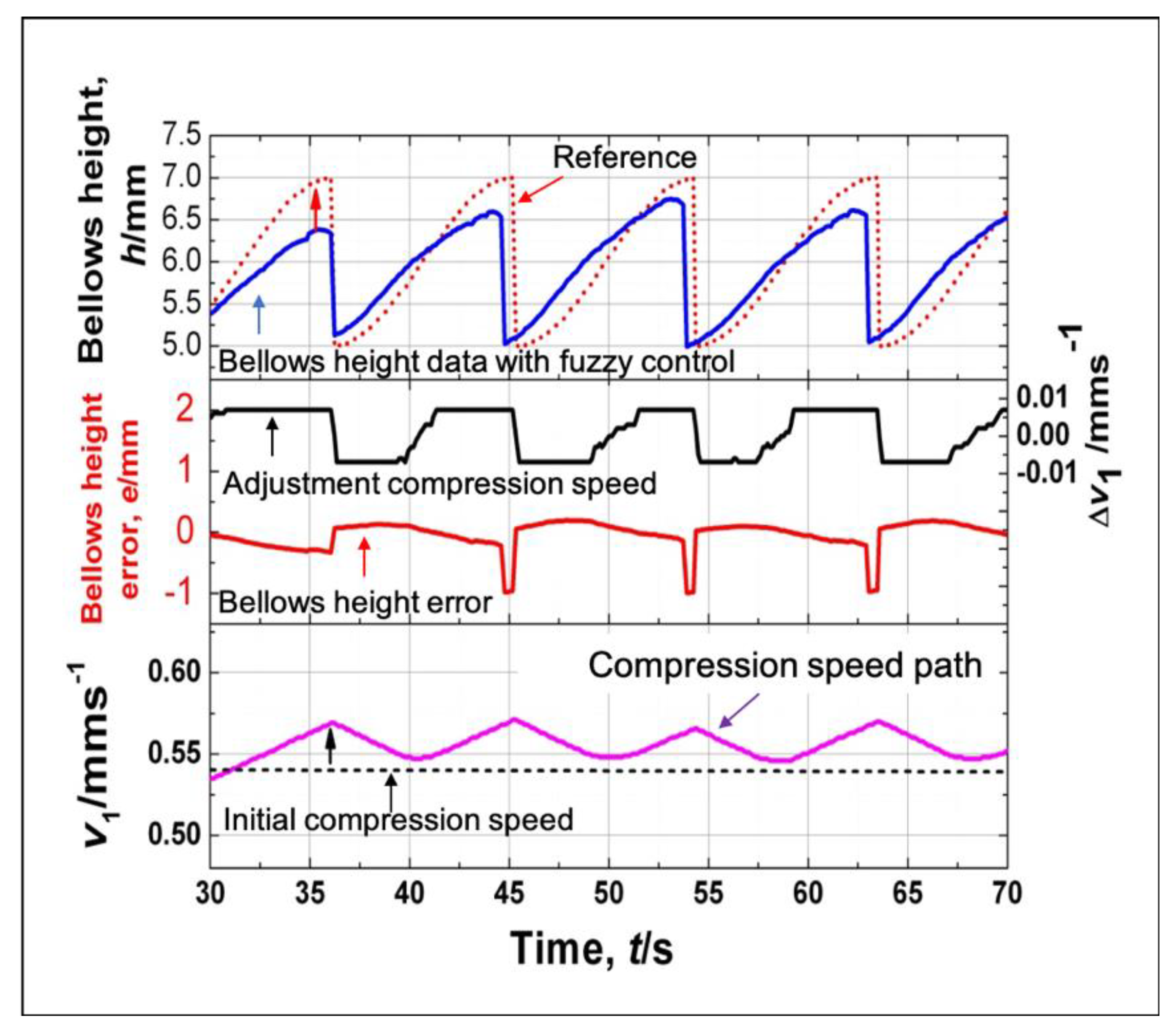
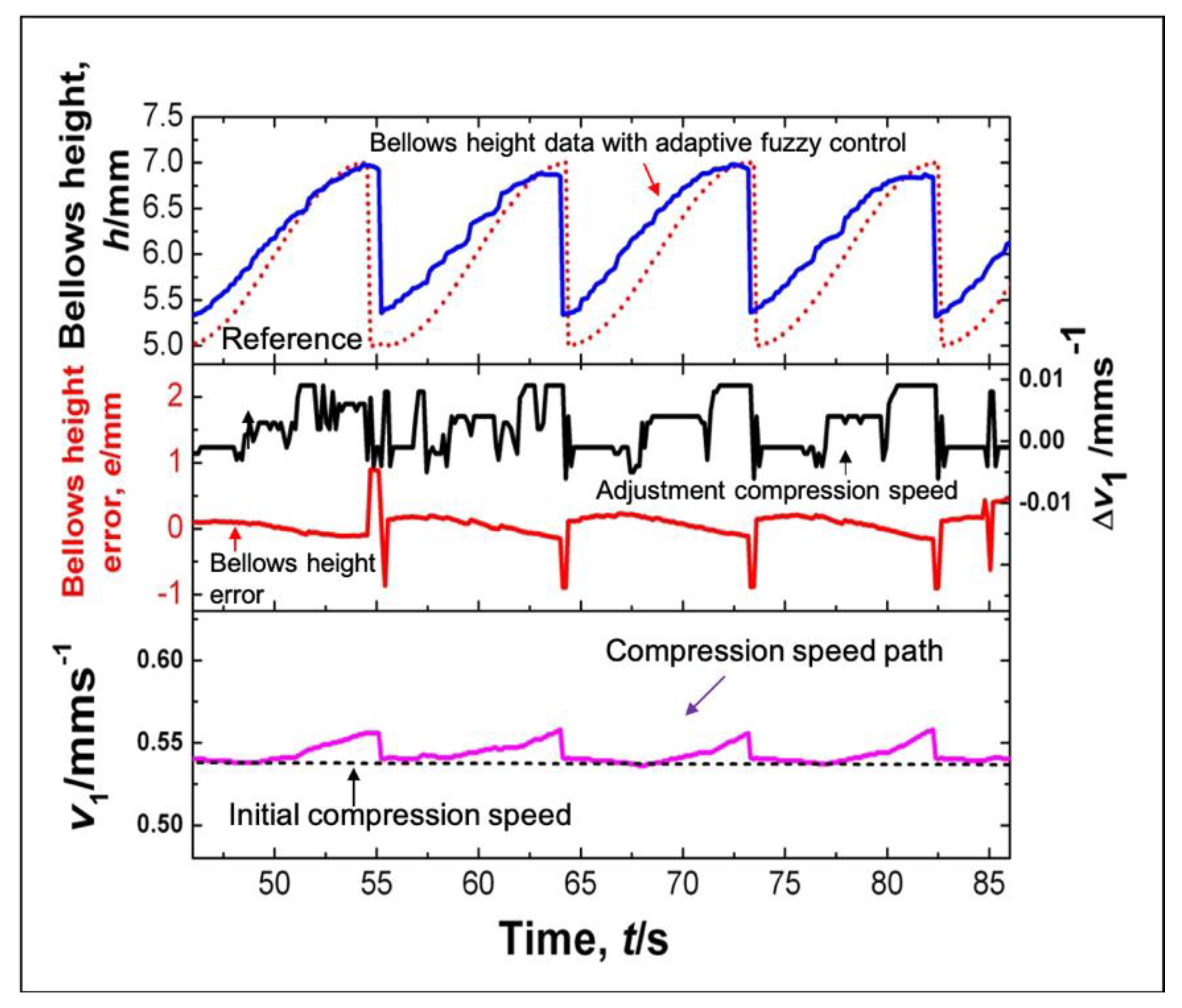
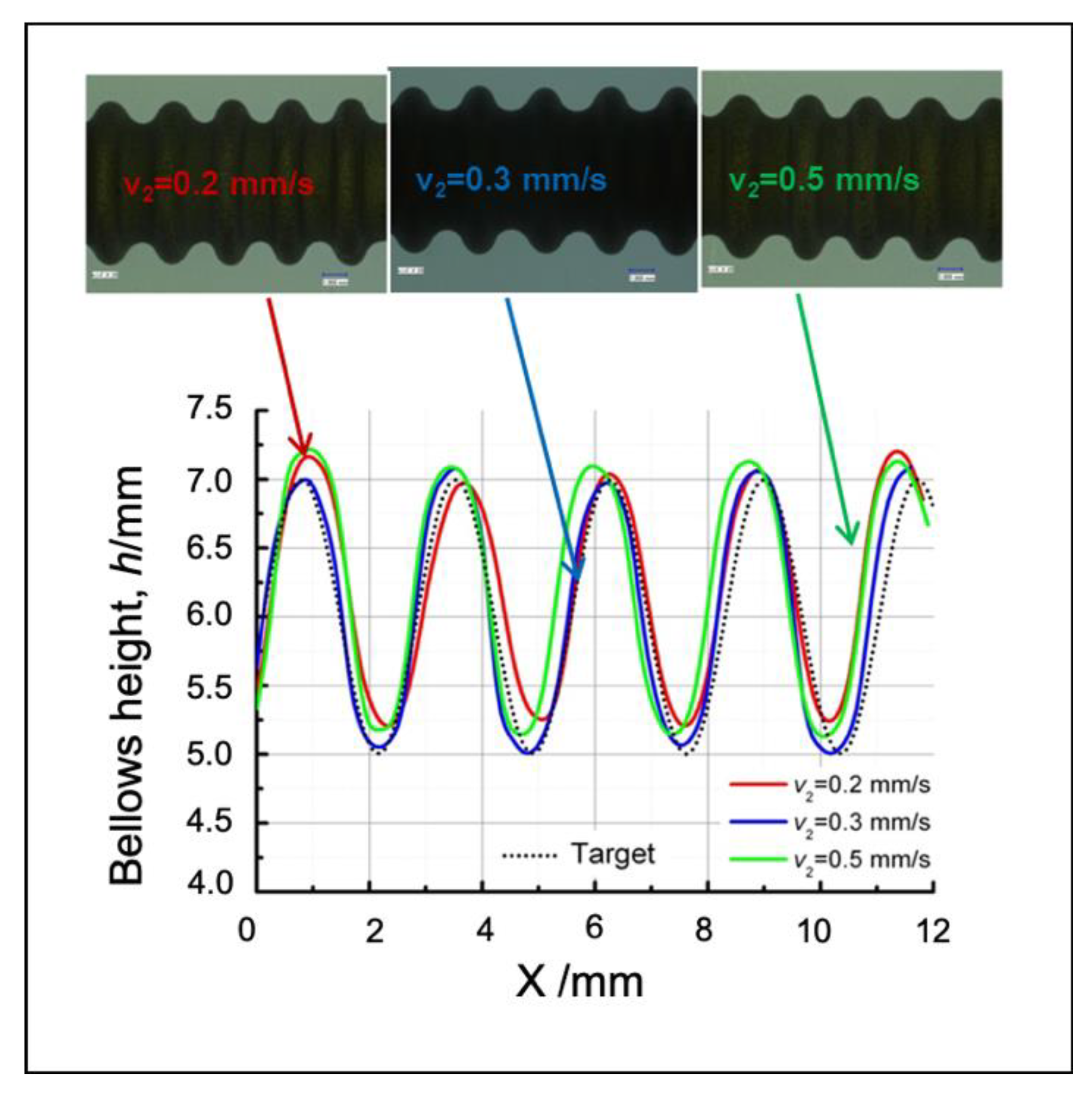
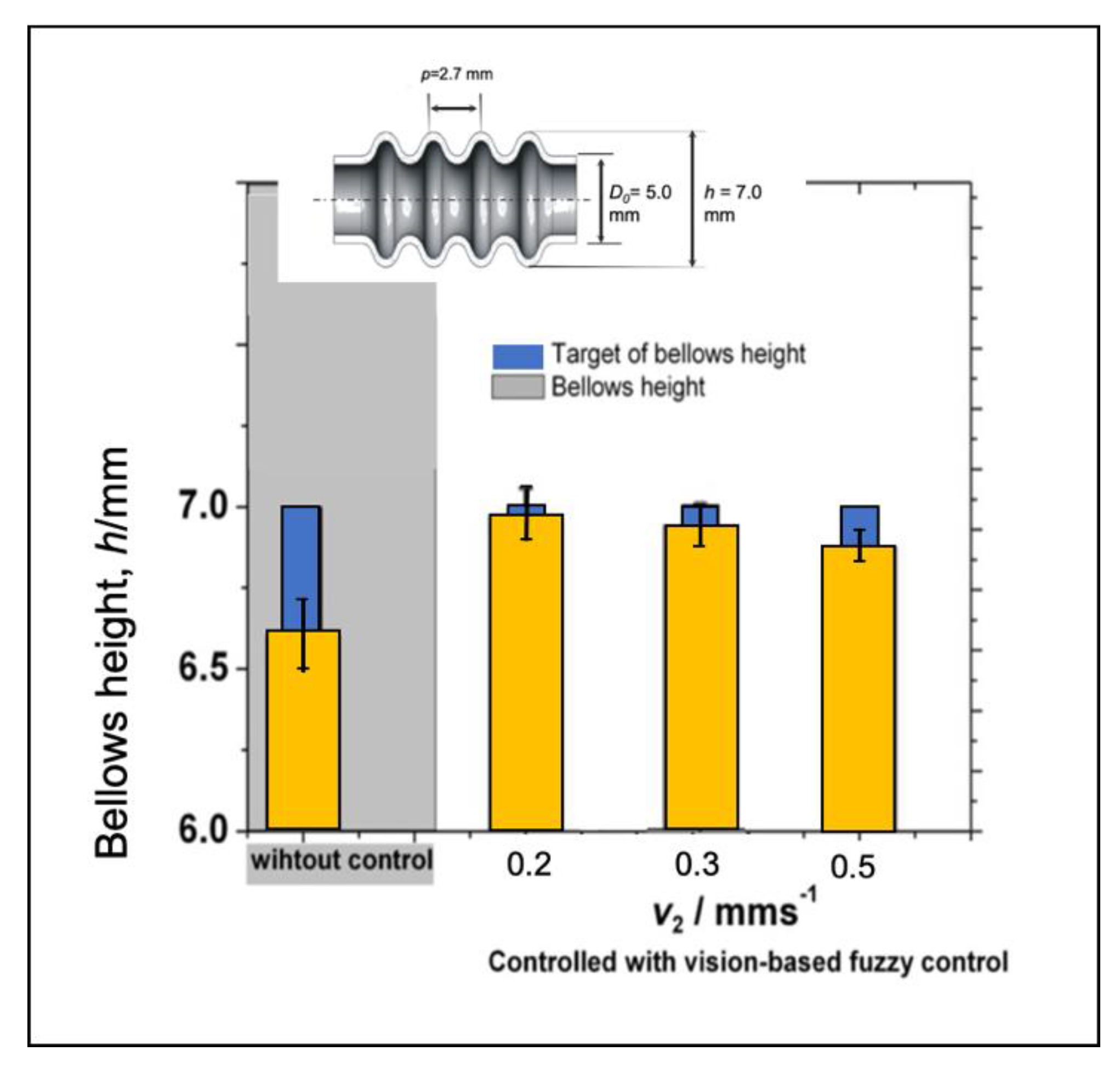
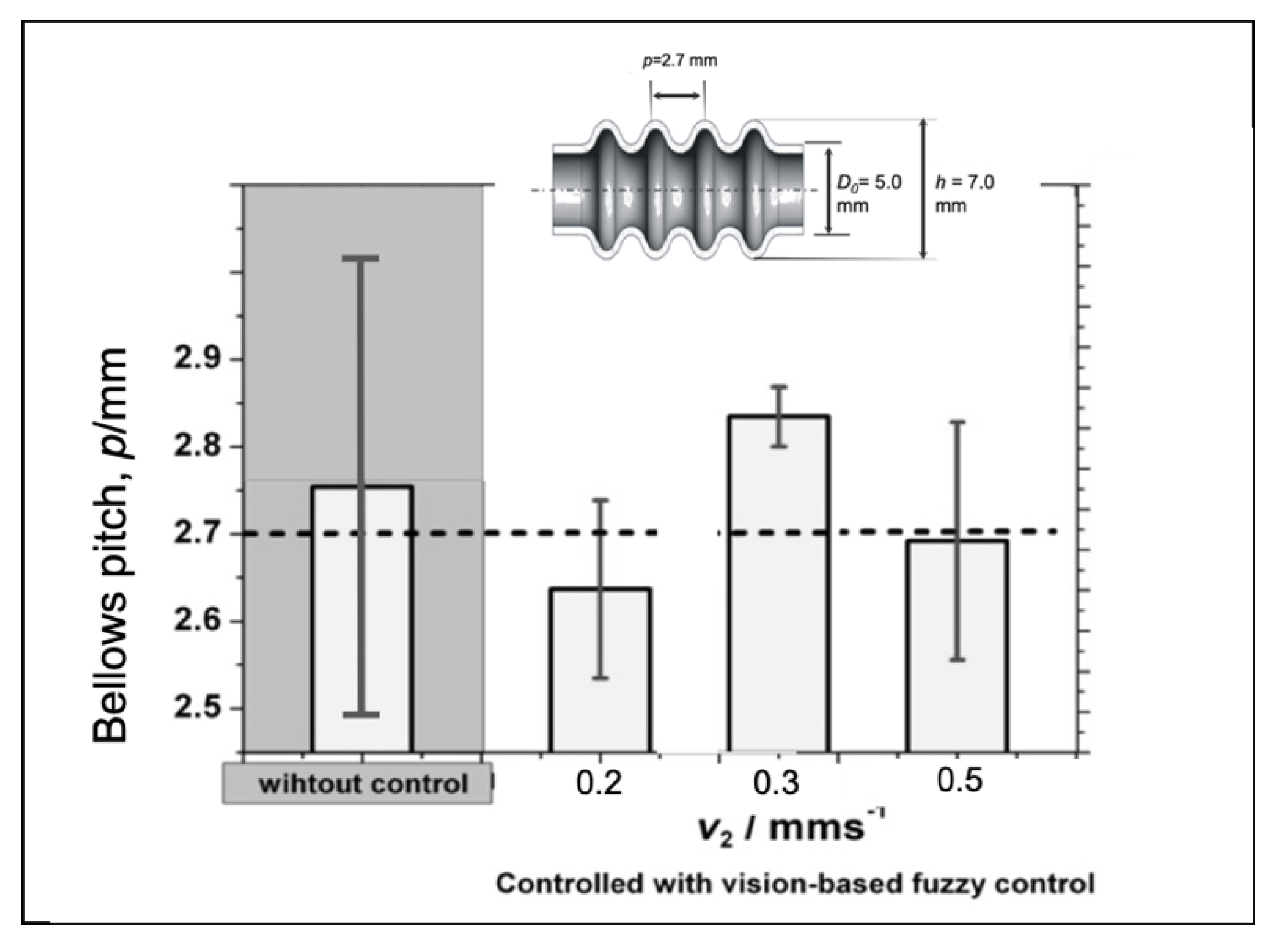
7.1. Verification of the Proposed Control System for the Semi-Dieless Bellows Forming under Various Feeding Speeds
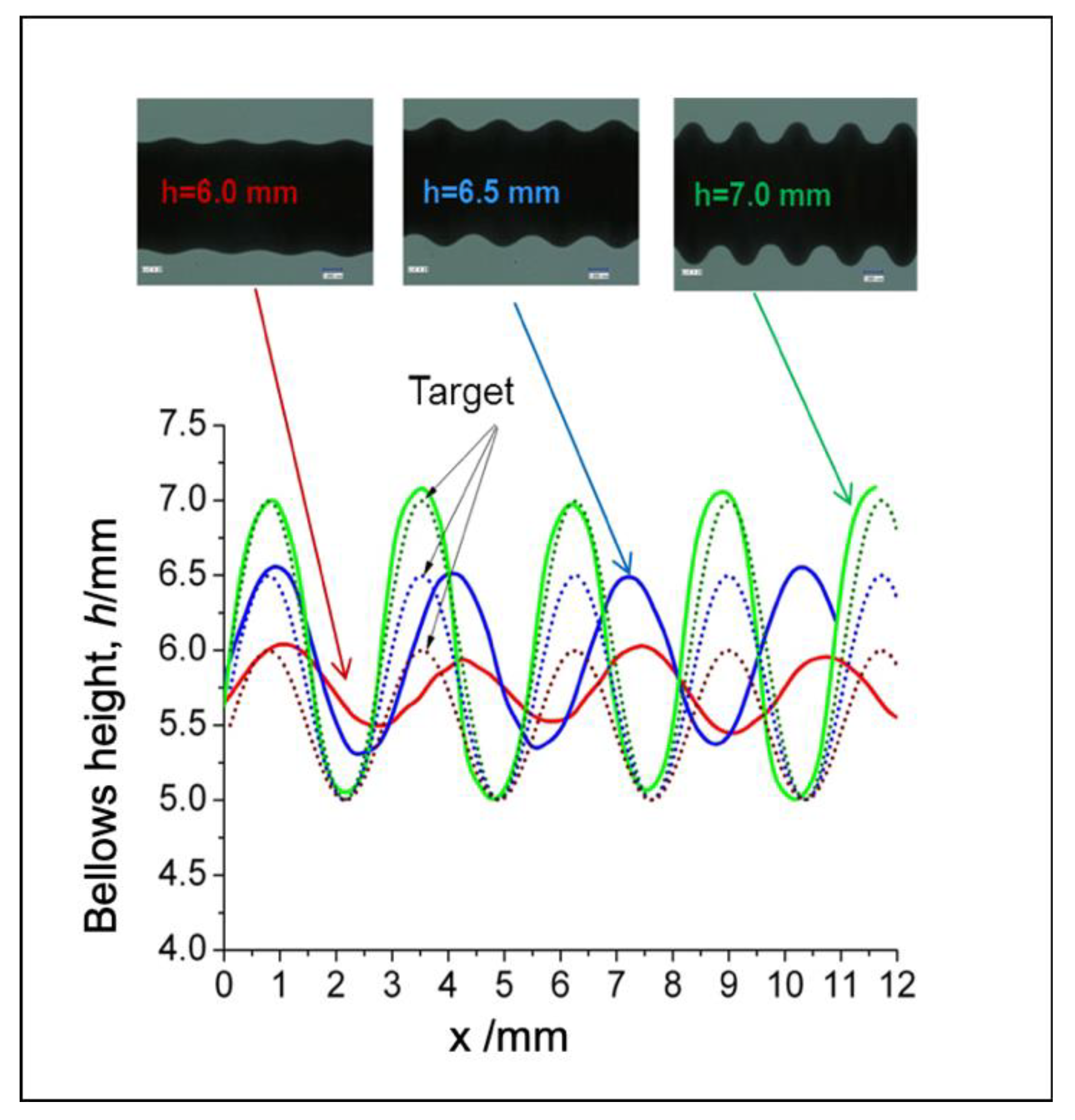
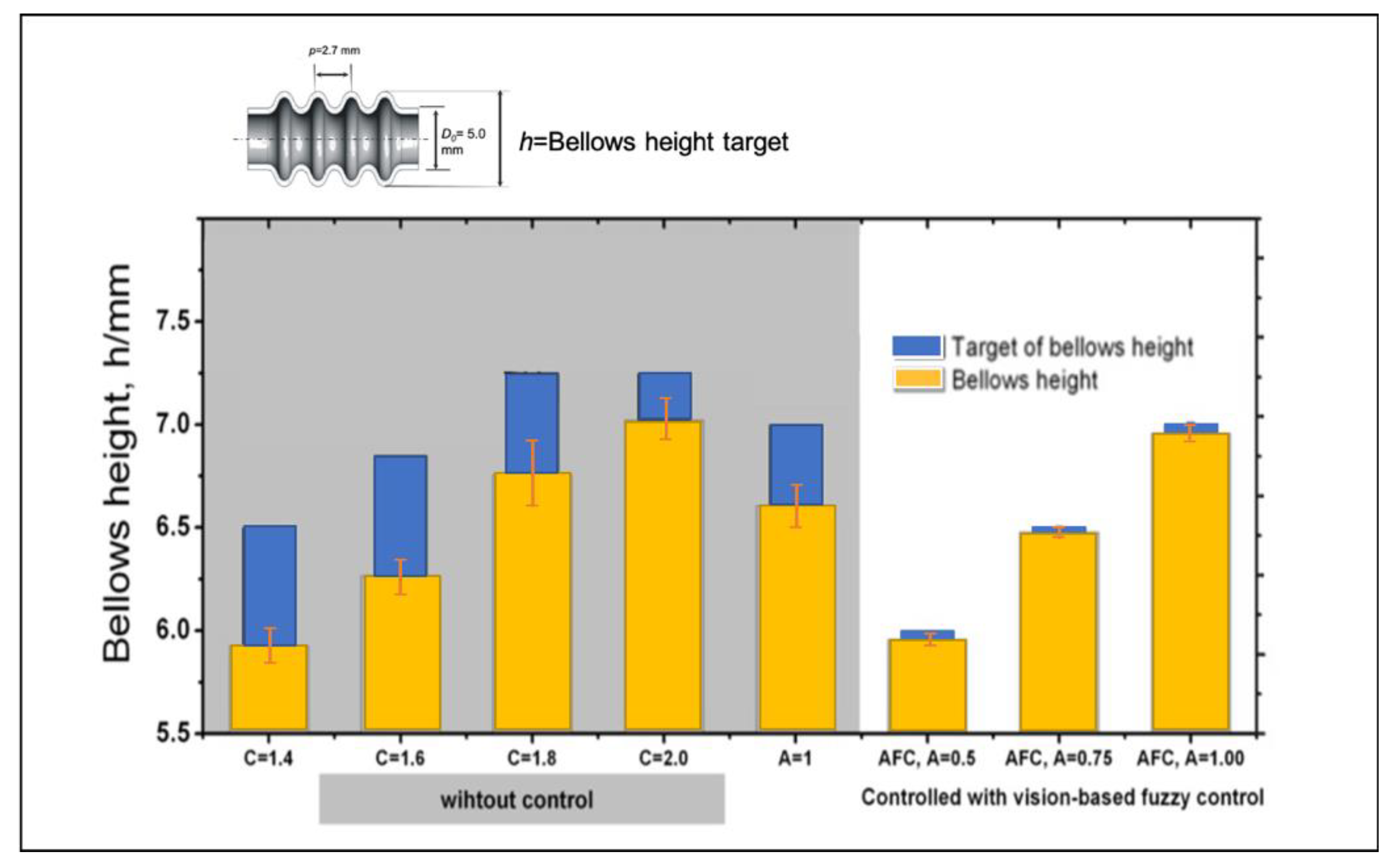
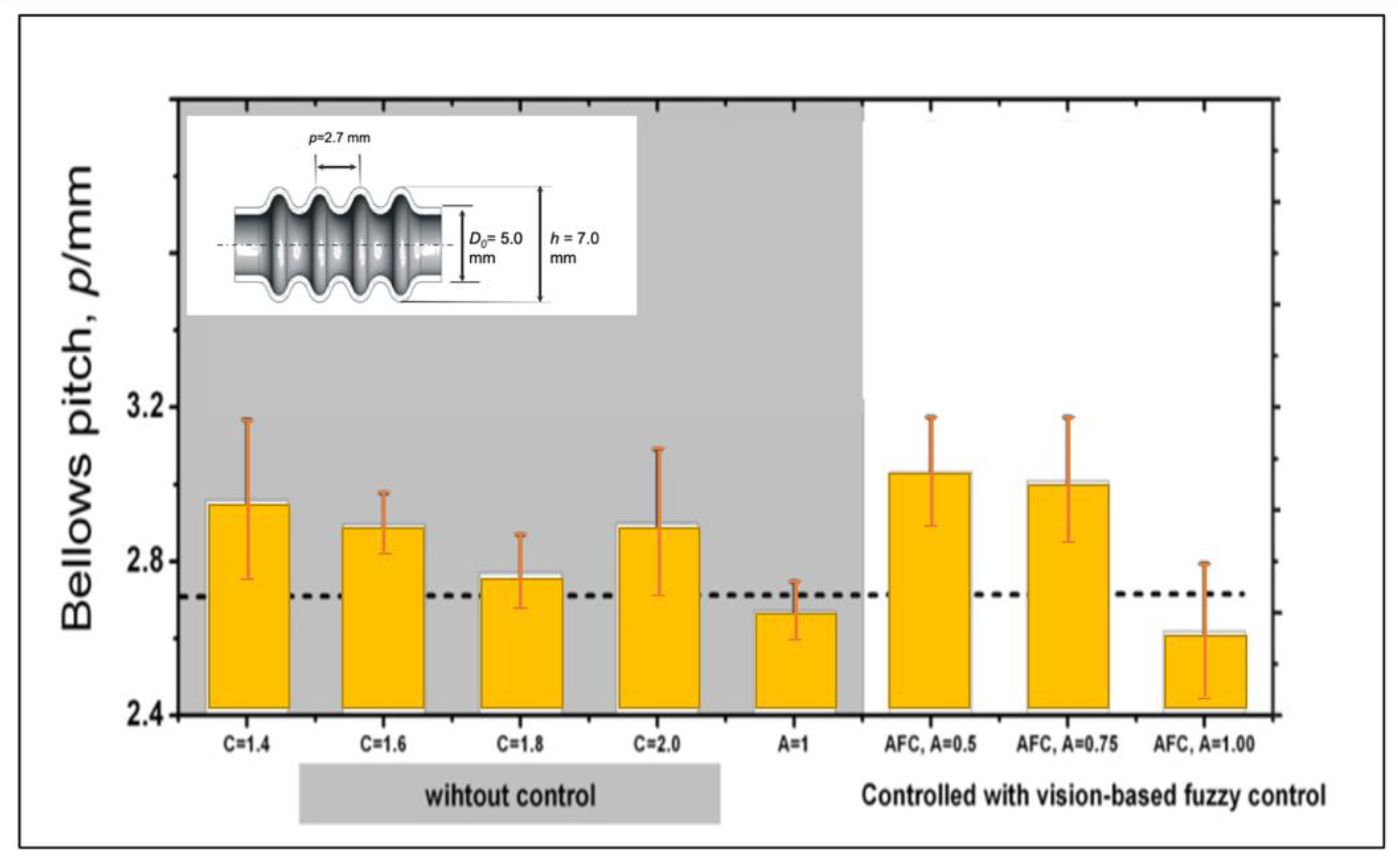
7.2. Verification of the Proposed Control System for the Semi-Dieless Bellows Forming under Various Bellows Targets
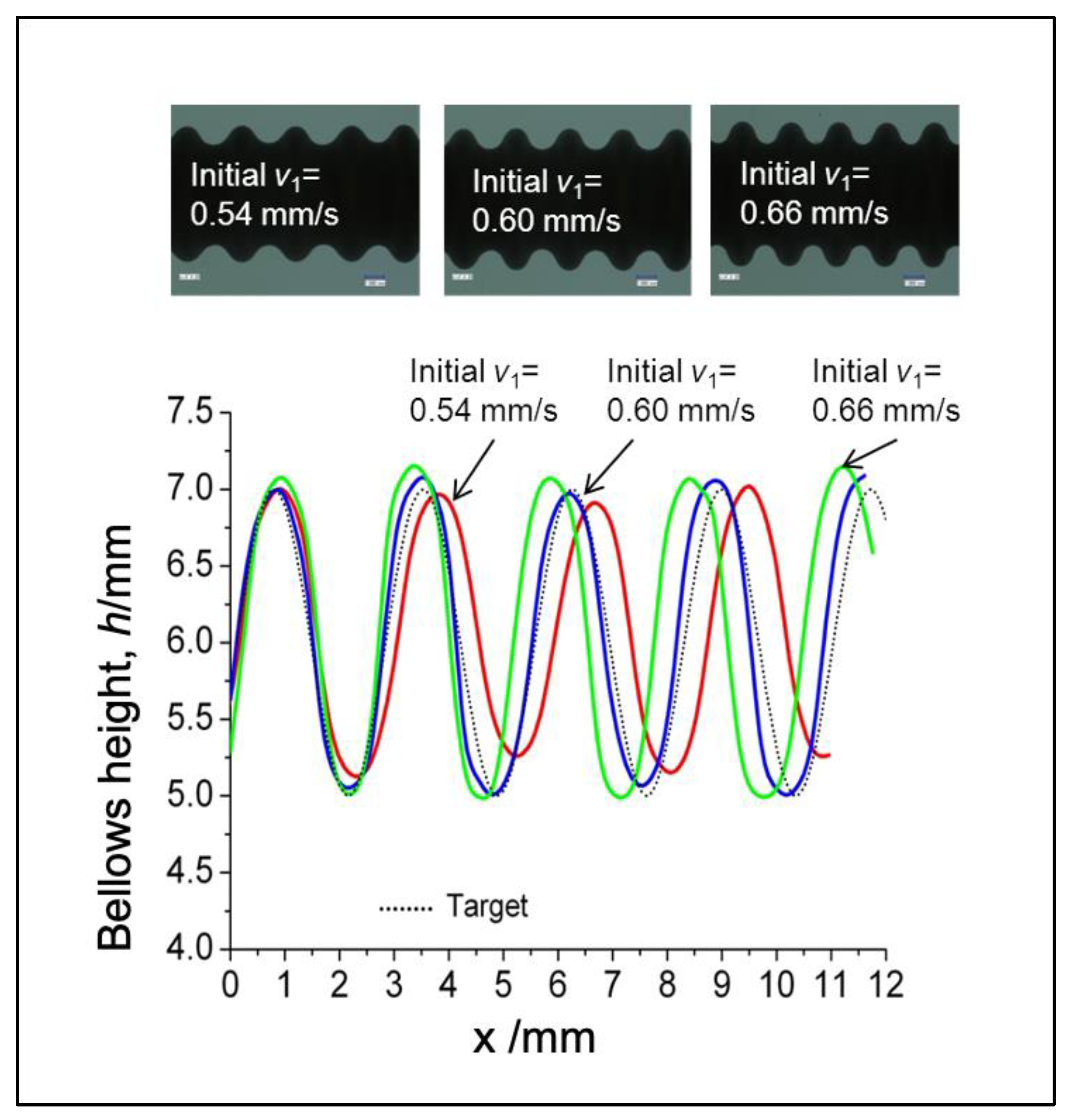
7.3. Verification of the Proposed Control System for the Semi-Dieless Bellows Forming under Various Initial Compression Speeds
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| : Initial cross section area of tube, mm2 | |
| Amp | : Amplitude, mm |
| a | : Constanta for increasing heat quantity, W⋅mm−2 |
| Cd | : Cooling distance, mm |
| Cl | : Cooling zone, mm |
| c | : Heat capacity, J⋅Kg−1⋅K−1 |
| D | : Diameter, mm |
| : Initial diameter, mm | |
| : Bellows height error, mm | |
| : Increment of bellows height error, mm | |
| : Average bellows height error, mm | |
| G | : Gain |
| h | : Bellows height |
| ha | : Heat transfer coefficient of radiation to air, W.mm−2⋅K−1 |
| hc | : Heat transfer coefficient of cooling, W⋅mm−2⋅K−1 |
| Hl | : Heating length, mm |
| K | : Strength coefficient, MPa |
| n | : Strain hardening index |
| m | : Strain rate sensitivity |
| : Reference bellows height, mm | |
| : Progress of bellows height, % | |
| q | : Heat flux quantity, W⋅mm−2 |
| : Initial heat flux quantity, W⋅mm−2 | |
| p | : Pitch, mm |
| t | : Time, s |
| X | : Elongation, mm |
| : Time to produce one bellows, s | |
| : Compression speed, mm.s−1 | |
| : Feeding speed, mm⋅s−1 | |
| y | : Position of node in y axis in global position, mm |
| σ | : Flow stress, MPa |
| ε | : Strain |
| : Strain rate, s−1 | |
| ω | : Frequency, Hz |
| ϕ | : Phase, rad |
| λ | : Thermal conductivity, W⋅mm−1⋅K−1 |
| : Standard deviation of error, mm | |
| : Changing of compression speed, mm⋅s−1 | |
| : Changing of feeding speed, mm⋅s−1 | |
| : Compression stroke |
References
- Wang, G.; Zhang, K.F.; Wu, D.Z.; Wang, J.Z.; Yu, Y.D. Superplastic forming of bellows expansion joints made of titanium alloys. J. Mater. Process. Technol. 2006, 178, 24–28. [Google Scholar] [CrossRef]
- Faraji, G.; Mashhadi, M.M.; Norouzifard, V. Evaluation of effective parameters in metal bellows forming process. J. Mater. Process. Technol. 2009, 209, 3431–3437. [Google Scholar] [CrossRef]
- Kang, B.H.; Lee, M.Y.; Shon, S.M.; Moon, Y.H. Forming various shapes of tubular bellows using a single-step hydroforming process. J. Mater. Process. Technol. 2007, 194, 1–6. [Google Scholar] [CrossRef]
- Furushima, T.; Hung, N.Q.; Manabe, K.; Sasaki, O. Development of Semi-dieless Metal Bellows Forming Process. J. Jpn. Soc. Technol. Plast. 2012, 53, 251–255. [Google Scholar] [CrossRef]
- Supriadi, S.; Hung, N.Q.; Furushima, T.; Manabe, K. A Novel Dieless Bellows Forming Process Using Local Heating Technique. Steel Res. Int. 2011, 950–955. [Google Scholar]
- Furushima, T.; Suzuki, Y.; Manabe, K.; Sasaki, O. Convolution Formation Behavior of Semi-dieless Bellows Forming Process for Metal Tubes. In Proceedings of the 6th International Conference on Tube Hydroforming (TUBEHYDRO 2013), Jeju, Korea, 25–28 August 2013; pp. 268–274. [Google Scholar]
- Sekiguchi, H.; Kobatake, K.; Osakada, K.A. Fundamental Study on Dieless Drawing. In Proceedings of the 15th MTDR Conference, Birmingham, UK; 1974; pp. 539–544. [Google Scholar]
- Sekiguchi, H.; Kobatake, K.; Osakada, K. Dieless Drawing Process. J. Jpn. Soc. Technol. Plast. 1976, 70, 67–71. [Google Scholar]
- Milenin, A.; Kustra, P.; Furushima, T.; Du, P.; Němeček, J. Design of the laser dieless drawing process of tubes from magnesium alloy using FEM model. J. Mater. Process. Technol. 2018, 262, 65–74. [Google Scholar] [CrossRef]
- Kustra, P.; Milenin, A.; Płonka, B.; Furushima, T. Production Process of Biocompatible Magnesium Alloy Tubes Using Extrusion and Dieless Drawing Processes. J. Mater. Eng. Perform. 2016, 25, 2528–2535. [Google Scholar] [CrossRef]
- Furushima, T.; Manabe, K. A novel superplastic dieless drawing process of ceramic tubes. CIRP Ann. Manuf. Technol. 2017, 66, 265–268. [Google Scholar] [CrossRef]
- Furushima, T.; Manabe, K. Large reduction die-less mandrel drawing of magnesium alloy micro-tubes. CIRP Ann. Manuf. Technol. 2018, 67, 309–312. [Google Scholar] [CrossRef]
- Zhang, Z.; Manabe, K.; Furushima, T.; Tada, K.; Sasaki, O. Deformation behavior of aluminum alloy tube in semi-dieless metal bellows forming process with local heating technique. Adv. Mater. Res. 2014, 936, 1742–1746. [Google Scholar] [CrossRef]
- Zhang, Z.; Furushima, T.; Manabe, K.; Tada, K.; Sasaki, O. Development of dieless metal bellows forming process with local heating technique. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2015, 229, 664–669. [Google Scholar] [CrossRef]
- Hashizume, S. Resistance to plastic deformation of metals (stainless steel). J. Jpn. Soc. Technol. Plast. 1965, 6, 71–75. [Google Scholar]
- Supriadi, S.; Manabe, K. Enhancement of dimensional accuracy of dieless tube-drawing process with vision-based fuzzy control. J. Mater. Process. Technol. 2013, 213, 905–912. [Google Scholar] [CrossRef]
- Dworkin, S.B.; Nye, T.J. Image processing for machine vision measurement of hot formed parts. J. Mater. Process. Technol. 2006, 174, 1–6. [Google Scholar] [CrossRef]
- Kurada, S.; Bradley, C. A machine vision system for tool wear assessment. Tribol. Int. 1997, 30, 295–304. [Google Scholar] [CrossRef]
- Kurada, S.; Bradley, C. A review of machine vision sensors for tool condition monitoring. Comput. Ind. 1997, 34, 55–72. [Google Scholar] [CrossRef]
- Supriadi, S.; Furushima, T.; Manabe, K. Real-time Monitoring System of Dieless Bellows Forming using Machine Vision. Adv. Mater. Res. 2013, 789, 429–435. [Google Scholar] [CrossRef]
- Rahman, S.M.; Ratrout, N.T. Review of the Fuzzy Logic Based Approach in Traffic Signal Control: Prospects in Saudi Arabia. J. Transp. Syst. Eng. Inf. Technol. 2009, 9, 58–70. [Google Scholar] [CrossRef]




| Boundary Conditions | |
|---|---|
| Heating quantity, q (W·mm−2) | Equation (1) |
| Heating temperature (°C) | 1100 |
| Heating length, Hl (mm) | 5 |
| Cooling Length, Cl (mm) | 5 |
| Heat transfer coefficient of cooling, hc (W·mm−2·K−1) | 1000 |
| Heat transfer coefficient of radiation to air, ha (W·mm−2·K−1) | 30 |
| Thermal conductivity, λ (W·mm−1·K−1) | 0.0163 |
| Specific heat (J·g−1·K−1) | 0.502 |
| Mass density,ρ (g·mm−3) | 0.008 |
| Input | Output | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| VN* | N* | Z* | P* | VP* | ||||||||
| Input 1: Bellows height error (eh) | VP* | Δv1 | I | I | R | R | RR | |||||
| P* | Δv1 | I | C | C | R | R | ||||||
| Z* | Δv1 | I | C | C | R | R | ||||||
| N* | Δv1 | I | C | C | C | I | ||||||
| VN* | Δv1 | RI | I | R | I | I | ||||||
| Input | Output | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| VN* | N* | Z* | P* | VP* | ||||||||
| Input 1: Bellows height error (eh) | VP* | Δv1/gain | RI | /H | I | /M | I | /M | /M | C | R | /H |
| P* | Δv1/gain | RI | /M | C | /M | C | /M | C | /M | C | /M | |
| Z* | Δv1/gain | C | /M | C | /M | C | /M | C | /M | R | /M | |
| N* | Δv1/gain | C | /M | C | /M | C | /M | I | /M | RI | /H | |
| VN* | Δv1/gain | R | /H | C | /M | I | /M | I | /M | RI | /VH | |
| Input | Output | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| VN* | N* | Z* | P* | VP* | ||||||||
| Input 1: Bellows height error (eh) | VP* | Δv1/gain | I | /H | I | /M | R | /M | R | /H | RR | /H |
| P* | Δv1/gain | I | /H | C | /M | C | /M | R | /M | R | /H | |
| Z* | Δv1/gain | I | /M | C | /M | C | /M | R | /M | R | /H | |
| N* | Δv1/gain | I | /M | C | /M | C | /M | C | /M | I | /M | |
| VN* | Δv1/gain | RI | /H | I | /M | R | /M | I | /M | I | /H | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Supriadi, S.; Furushima, T.; Manabe, K.-i. A Vision-Based Fuzzy Control to Adjust Compression Speed for a Semi-Dieless Bellows-Forming. Metals 2020, 10, 720. https://doi.org/10.3390/met10060720
Supriadi S, Furushima T, Manabe K-i. A Vision-Based Fuzzy Control to Adjust Compression Speed for a Semi-Dieless Bellows-Forming. Metals. 2020; 10(6):720. https://doi.org/10.3390/met10060720
Chicago/Turabian StyleSupriadi, Sugeng, Tsuyoshi Furushima, and Ken-ichi Manabe. 2020. "A Vision-Based Fuzzy Control to Adjust Compression Speed for a Semi-Dieless Bellows-Forming" Metals 10, no. 6: 720. https://doi.org/10.3390/met10060720
APA StyleSupriadi, S., Furushima, T., & Manabe, K.-i. (2020). A Vision-Based Fuzzy Control to Adjust Compression Speed for a Semi-Dieless Bellows-Forming. Metals, 10(6), 720. https://doi.org/10.3390/met10060720






