Effects of Testing Temperature on the Serration Behavior of an Al–Zn–Mg–Cu Alloy with Natural and Artificial Aging in Sharp Indentation
Abstract
1. Introduction
2. Materials and Methods
2.1. Specimen
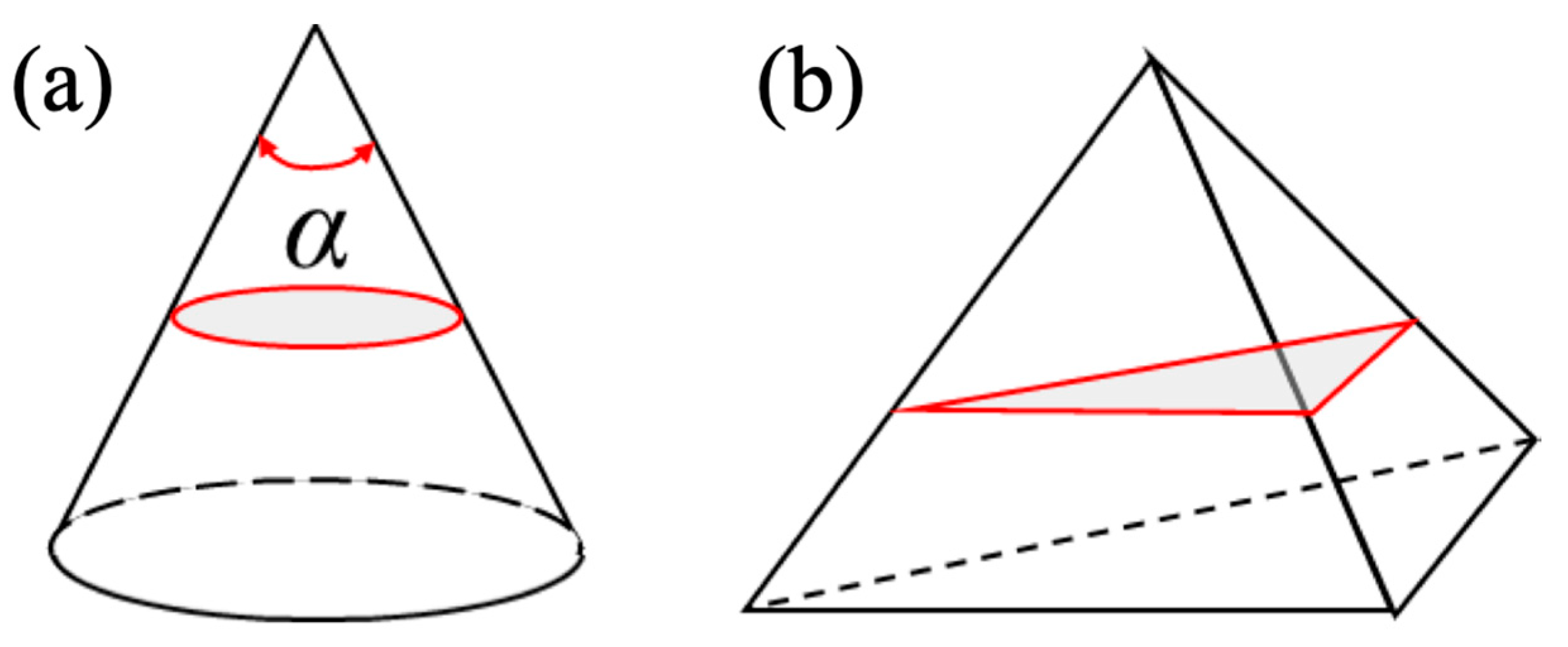
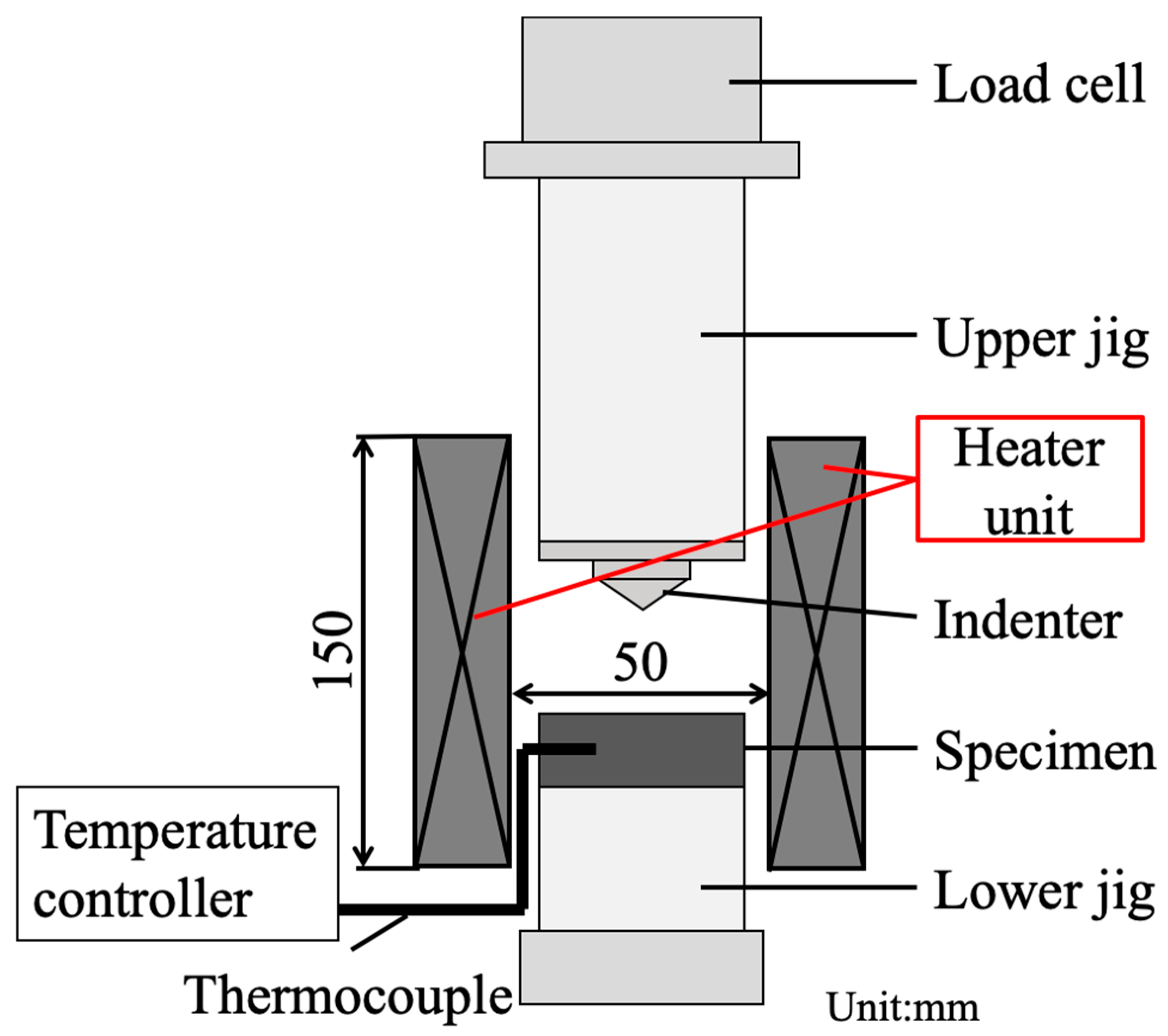
2.2. Indentation
2.2.1. Testing Conditions
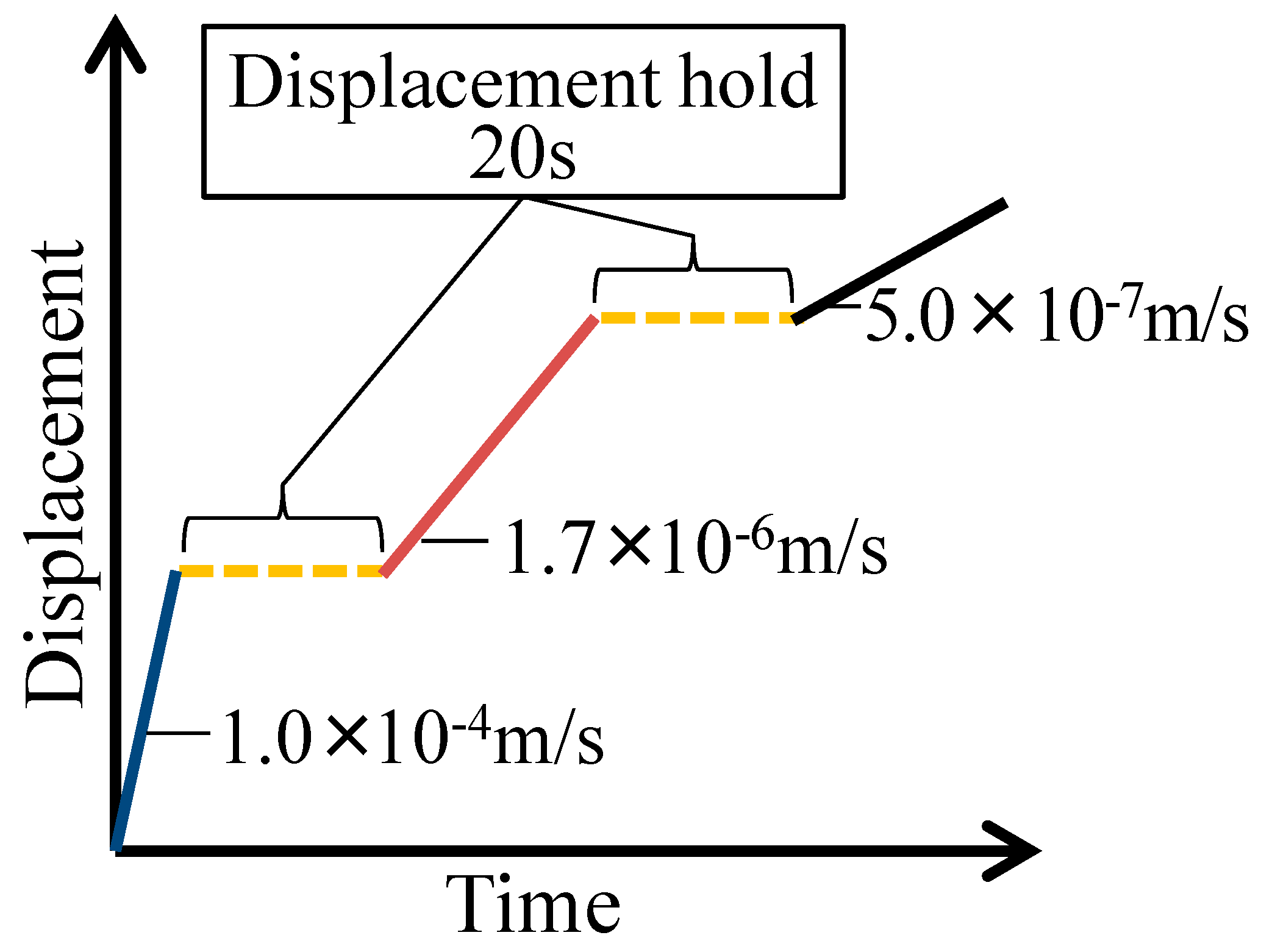
2.2.2. Indenter Control
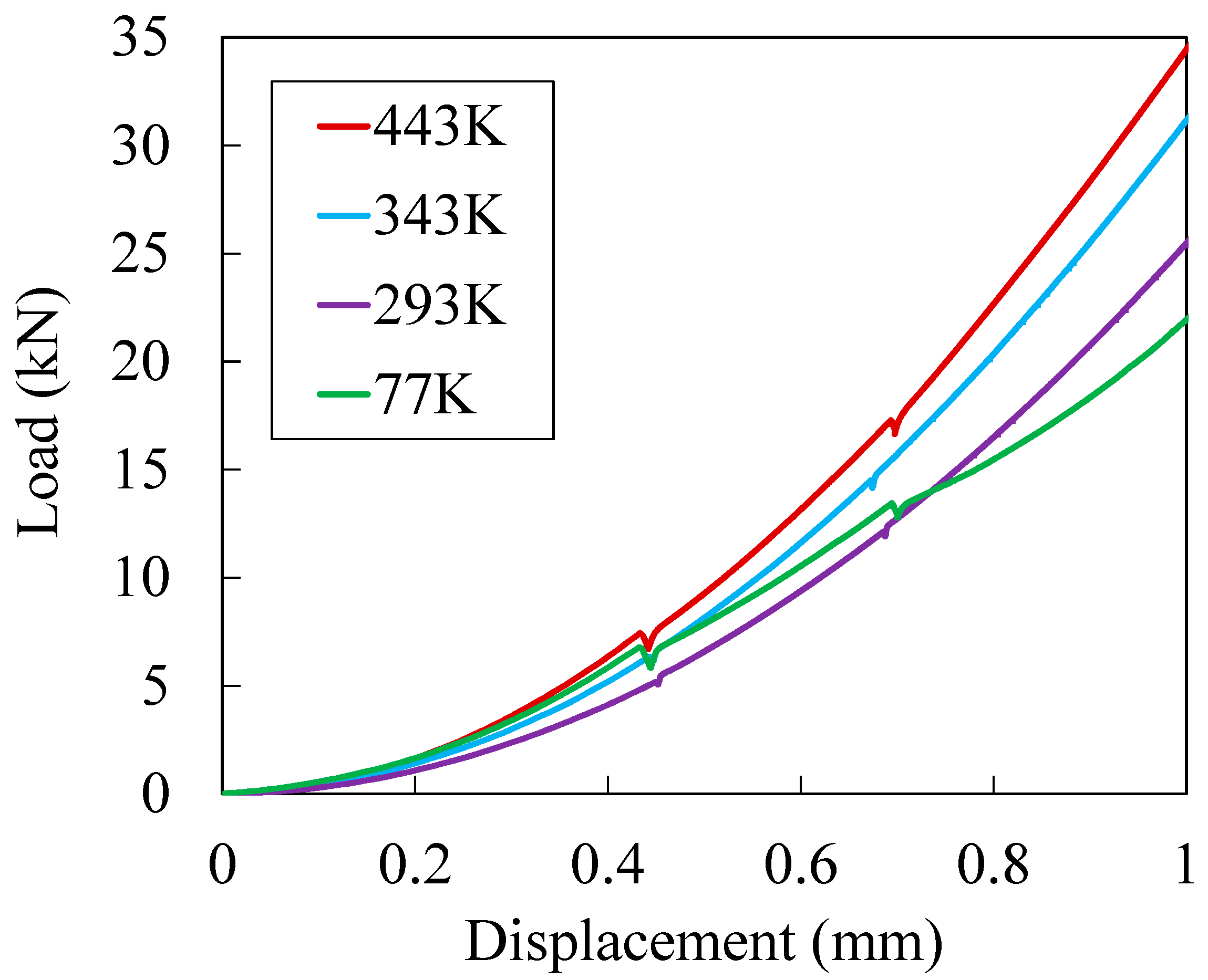
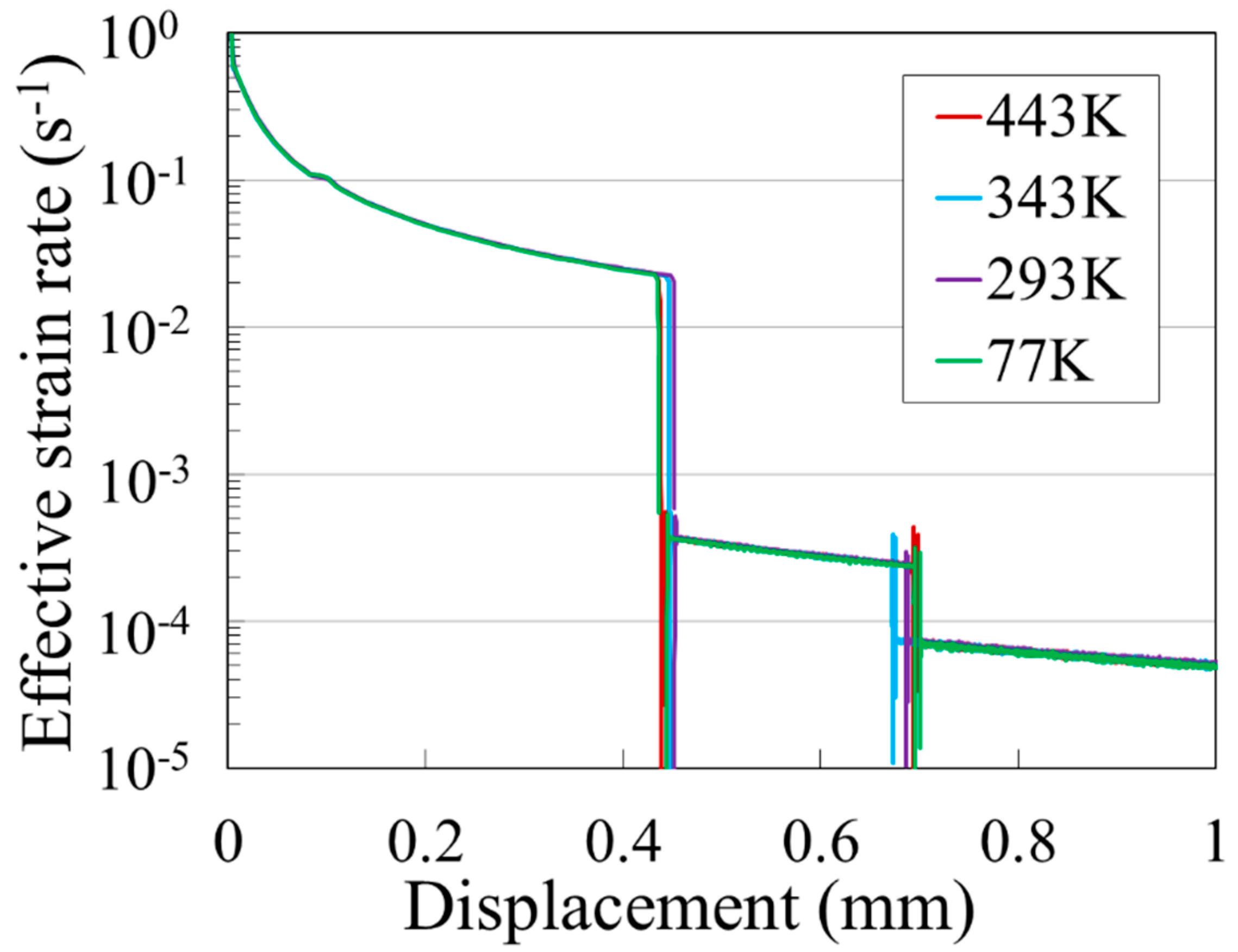
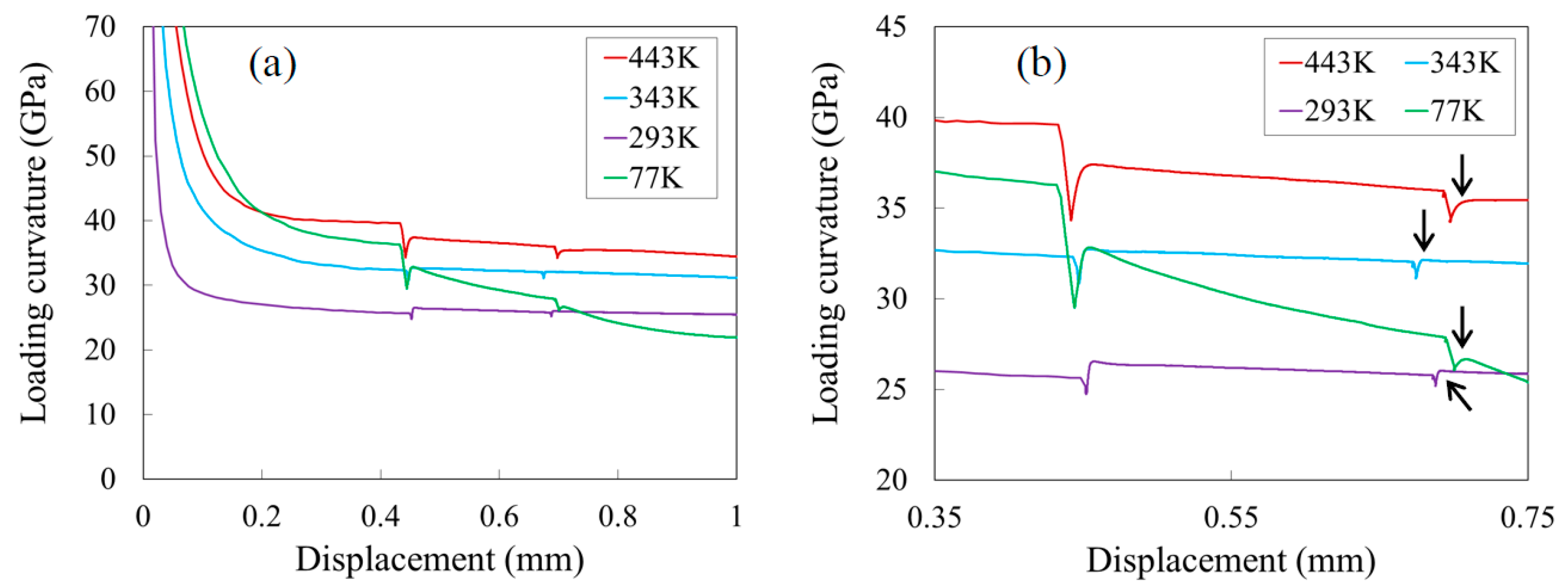
3. Results
4. Discussion
4.1. Effect of Aging on the Material Strength
4.1.1. Temperature of 77 K
4.1.2. Temperature of 293 and 343 K
4.1.3. Temperature of 443 K
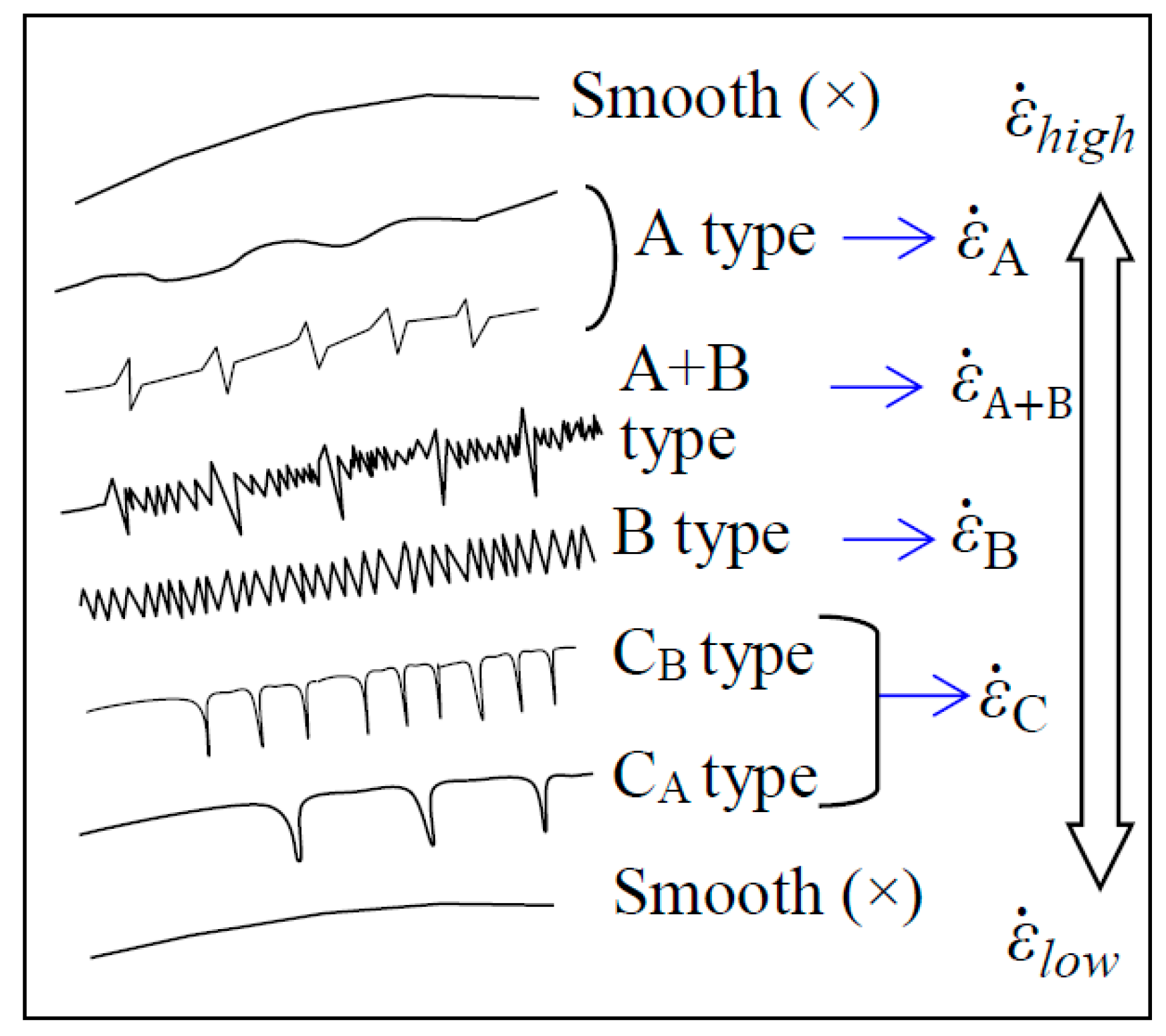
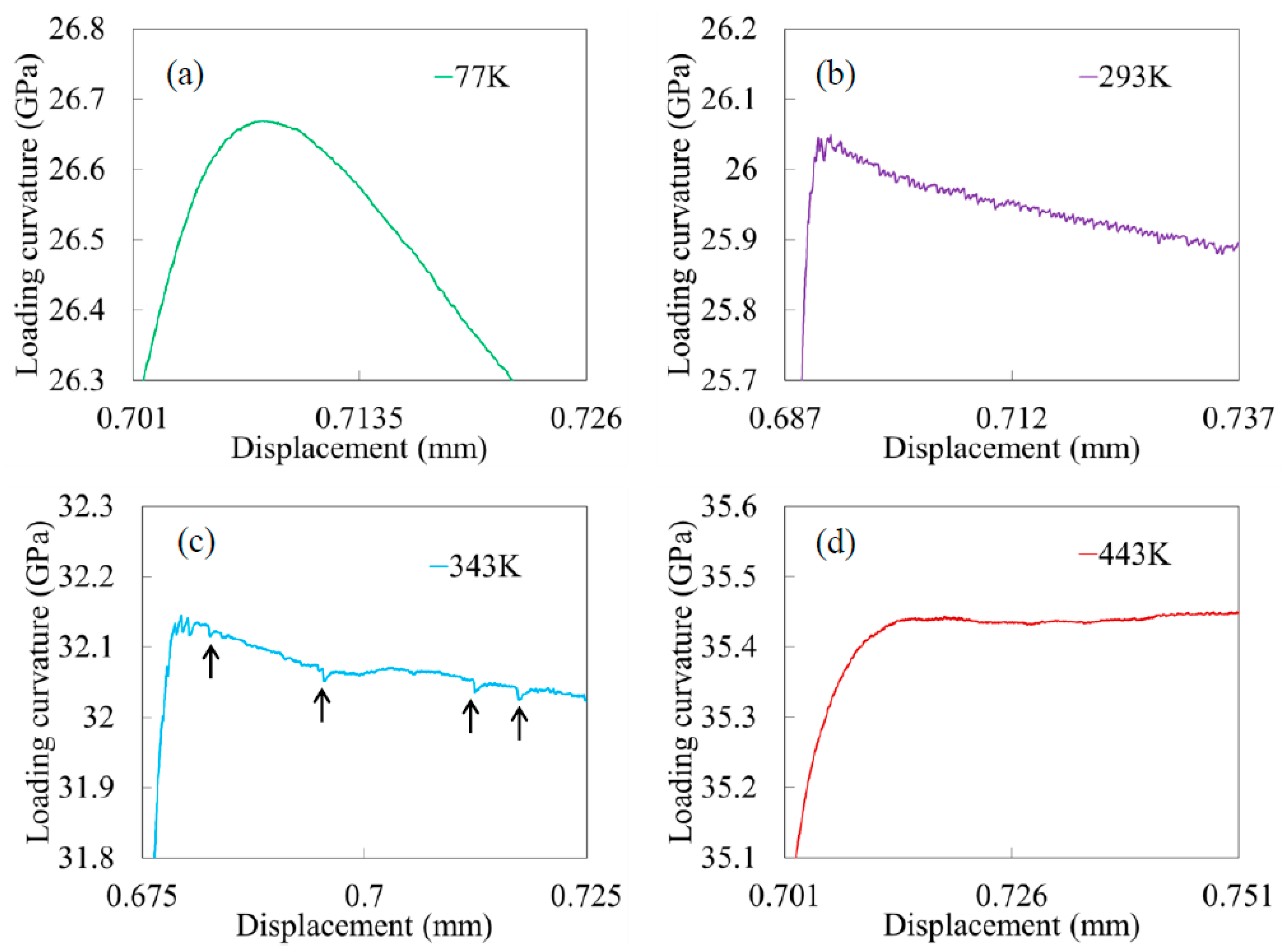
4.2. Effect of Testing Temperature on the Serration Behavior
4.2.1. Temperature of 77 K
4.2.2. Temperature of 293 K
4.2.3. Temperature of 343 K
4.2.4. Temperature of 443 K
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pink, E.; Grinberg, A. Stress drops in serrated flow curves of Al5Mg. Acta Metall. 1982, 30, 2153–2160. [Google Scholar] [CrossRef]
- Pink, E.; Webernig, W.M. Precipitation during serrated flow in AlZn5Mg1. Acta Metall. 1987, 35, 127–132. [Google Scholar] [CrossRef]
- Abbadi, M.; Hähner, P.; Zeghloul, A. On the characteristics of Portevin–Le Chatelier bands in aluminum alloy 5182 under stress-controlled and strain-controlled tensile testing. Mater. Sci. Eng. A 2002, 337, 194–201. [Google Scholar] [CrossRef]
- Picu, R.C.; Vincze, G.; Ozturk, F.; Gracio, J.J.; Barlat, F.; Maniatty, A.M. Strain rate sensitivity of the commercial aluminum alloy AA5182-O. Mater. Sci. Eng. A. 2005, 390, 334–343. [Google Scholar] [CrossRef]
- McCormick, P.G. A model for the Portevin-Le Chatelier effect in substitutional alloys. Acta Metall. 1972, 20, 351–354. [Google Scholar] [CrossRef]
- Estrin, Y.; Kubin, L.P.; Aifantis, E.C. Introductory remarks to the viewpoint set on propagative plastic instabilities. Scr. Metall. Mater. 1993, 29, 1147–1150. [Google Scholar] [CrossRef]
- Robinson, J.M.; Shaw, M.P. Microstructural and mechanical influences on dynamic strain aging phenomena. Int. Mater. Rev. 1994, 39, 113–122. [Google Scholar] [CrossRef]
- Kami, T.; Yamada, H.; Ogasawara, N. Effect of strain rate on serrated load of indentation in Al-Mg alloy. Trans. JSME 2017, 83, 17–261. [Google Scholar]
- Fischer-Cripps, A.C. Nanoindentation, 3rd ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Doerner, M.F.; Nix, W.D. A method for interpreting the data from depth-sensing indentation instruments. J. Mater. Res. 1986, 1, 601–609. [Google Scholar] [CrossRef]
- Cheng, Y.T.; Cheng, C.M. Scaling approach to conical indentation in elastic-plastic solids with work hardening. J. Appl. Phys. 1998, 84, 1284–1291. [Google Scholar] [CrossRef]
- Dao, M.; Chollacoop, N.; Van Vliet, K.J.; Venkatesh, T.A.; Suresh, S. Computational modeling of the forward and reverse problems in instrumented sharp indentation. Acta Mater. 2001, 49, 3899–3918. [Google Scholar] [CrossRef]
- Ogasawara, N.; Chiba, N.; Zhao, M.; Chen, X. Measuring material plastic properties with optimized representative strain-based indentation technique. J. Solid Mech. Mater. Eng. 2007, 1, 895–906. [Google Scholar] [CrossRef]
- Kami, T.; Yamada, H.; Ogasawara, N.; Chen, X. Strain rate behavior of pure aluminum in conical indentation with different indenter control methods. Int. J. Comput. Methods Exp. Meas. 2017, 6, 515–526. [Google Scholar] [CrossRef]
- Wei, B.C.; Zhang, L.C.; Zhang, T.H.; Xing, D.M.; Das, J.; Eckert, J. Strain rate dependence of plastic flow in Ce-based bulk metallic glass during nanoindentation. J. Mater. Res. 2007, 22, 258–263. [Google Scholar] [CrossRef]
- Su, C.; Herbert, E.G.; Sohn, S.; LaManna, J.A.; Oliver, W.C.; Pharr, G.M. Measurement of power-law creep parameters by instrumented indentation methods. J. Mech. Phys. Solids. 2013, 61, 517–536. [Google Scholar] [CrossRef]
- Sudharshan Phani, P.; Oliver, W. Ultra high strain rate nanoindentation testing. Materials 2017, 10, 663. [Google Scholar] [CrossRef]
- Kami, T.; Yamada, H.; Ogasawara, N. Critical strain of the sharp indentation through serration behavior with strain rate. Inter. J. Mech. Sci. 2019, 152, 512–523. [Google Scholar] [CrossRef]
- Liu, L.; Ogasawara, N.; Chiba, N.; Chen, X. Can indentation technique measure unique elastoplastic properties? J. Mater. Res. 2008, 24, 784–800. [Google Scholar] [CrossRef]
- Thevenet, D.; Mliha-Touati, M.; Zeghloul, A. The effect of precipitation on the Portevin-Le Chatelier effect in an Al–Zn–Mg–Cu alloy. Mater. Sci. Eng. A. 1999, 266, 175–182. [Google Scholar] [CrossRef]
- Xue, Z.; Huang, Y.; Hwang, K.C.; Li, M. The influence of indenter tip radius on the micro-indentation hardness. J. Eng. Mater. Tech. 2002, 124, 371–379. [Google Scholar] [CrossRef]
- Ferragut, R.; Somoza, A.; Tolley, A.; Torriani, I. Precipitation kinetics in Al-Zn-Mg commercial alloys. J. Mater. Process Technol. 2003, 141, 35–40. [Google Scholar] [CrossRef]
- Riley, D.M.; McCormick, P.G. The effect of precipitation hardening on the Portevin–Le Chatelier effect in an Al-Mg-Si alloy. Acta Metall. 1977, 25, 181–185. [Google Scholar] [CrossRef]
- Saha, G.G.; McCormick, P.G.; Rama Rao, P. Portevin–Le Chatelier effect in an Al–Mn Alloy I: Serration characteristics. Mater. Sci. Eng. 1984, 62, 187–196. [Google Scholar] [CrossRef]
- Ikeno, S.; Watanabe, T.; Tada, S. On the serration in Al-Mg alloys at elevated temperatures. J. Jpn. Inst. Met. 1983, 47, 231–236. [Google Scholar] [CrossRef][Green Version]
- Nakayama, Y. Effects of Mg concentration, test temperature and strain rate on serration of Al-Mg system alloys and cause of its generation. J. Jpn. Inst. Met. 2000, 64, 1257–1262. [Google Scholar] [CrossRef][Green Version]
- Fujikawa, S.; Hirano, K. Diffusion of 65Zn in aluminum and Al–Zn–Mg alloy over a wide range of temperature. Trans. JIM 1976, 17, 809–818. [Google Scholar] [CrossRef]
- Fujikawa, S.; Hirano, K. Diffusion of 28Mg in aluminum. Mater. Sci. Eng. 1977, 27, 25–33. [Google Scholar] [CrossRef]
- Anand, M.S.; Murarka, S.P.; Agarwala, R.P. Diffusion of copper in nickel and aluminum. J. Appl. Phys. 1965, 36, 3860–3862. [Google Scholar] [CrossRef]
- Park, W.S.; Chun, M.S.; Han, M.S.; Kim, M.H.; Lee, J.M. Comparative study on mechanical behavior of low temperature application materials for ships and offshore structures: Part I—Experimental investigations. Mater. Sci. Eng. A 2011, 528, 5790–5803. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, Z. Dynamic compressive behavior of selected aluminum alloy at low temperature. Mater. Sci. Eng. A 2012, 553, 176–180. [Google Scholar] [CrossRef]
- Sha, G.; Cerezo, A. Early-stage precipitation in Al–Zn–Mg–Cu alloy (7050). Acta Mater. 2004, 52, 4503–4516. [Google Scholar] [CrossRef]
- Buha, J.; Lumley, R.N.; Crosky, A.G. Secondary ageing in an aluminium alloy 7050. Mater. Sci. Eng. A. 2008, 492, 1–10. [Google Scholar] [CrossRef]
- Cao, C.; Zhang, D.; Zhuang, L.; Zhang, J. Improved age-hardening response and altered precipitation behavior of Al-5.2Mg-0.45Cu-2.0Zn (wt%) alloy with pre-aging treatment. J. Alloys Compd. 2017, 691, 40–43. [Google Scholar] [CrossRef]
| Alloy | Si | Fe | Cu | Mn | Mg | Cr | Zn | Ti | Al |
|---|---|---|---|---|---|---|---|---|---|
| 7075 | 0.09 | 0.19 | 1.6 | 0.04 | 2.6 | 0.20 | 5.6 | 0.02 | Bal. |
| Solute Atom | D0 (m2/s) | Q (kcal/mol) | Testing Temperature (K) | D (m2/s) | Reference |
|---|---|---|---|---|---|
| Zn | 1.77 × 10−5 | 28.0 | 77 | 7.74 × 10−85 | [27] |
| 293 | 2.47 × 10−26 | ||||
| 343 | 2.71 × 10−23 | ||||
| 443 | 2.85 × 10−19 | ||||
| Mg | 6.23 × 10−6 | 27.5 | 77 | 7.11 × 10−84 | [28] |
| 293 | 2.05 × 10−26 | ||||
| 343 | 1.98 × 10−23 | ||||
| 443 | 1.77 × 10−19 | ||||
| Cu | 1.5 × 10−5 | 30.2 | 77 | 3.81 × 10−91 | [29] |
| 293 | 4.81 × 10−28 | ||||
| 343 | 9.14 × 10−25 | ||||
| 443 | 1.99 × 10−20 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamada, H.; Kami, T.; Ogasawara, N. Effects of Testing Temperature on the Serration Behavior of an Al–Zn–Mg–Cu Alloy with Natural and Artificial Aging in Sharp Indentation. Metals 2020, 10, 597. https://doi.org/10.3390/met10050597
Yamada H, Kami T, Ogasawara N. Effects of Testing Temperature on the Serration Behavior of an Al–Zn–Mg–Cu Alloy with Natural and Artificial Aging in Sharp Indentation. Metals. 2020; 10(5):597. https://doi.org/10.3390/met10050597
Chicago/Turabian StyleYamada, Hiroyuki, Tsuyoshi Kami, and Nagahisa Ogasawara. 2020. "Effects of Testing Temperature on the Serration Behavior of an Al–Zn–Mg–Cu Alloy with Natural and Artificial Aging in Sharp Indentation" Metals 10, no. 5: 597. https://doi.org/10.3390/met10050597
APA StyleYamada, H., Kami, T., & Ogasawara, N. (2020). Effects of Testing Temperature on the Serration Behavior of an Al–Zn–Mg–Cu Alloy with Natural and Artificial Aging in Sharp Indentation. Metals, 10(5), 597. https://doi.org/10.3390/met10050597





