Comparative Study on the Uniaxial Behaviour of Topology-Optimised and Crystal-Inspired Lattice Materials
Abstract
1. Introduction
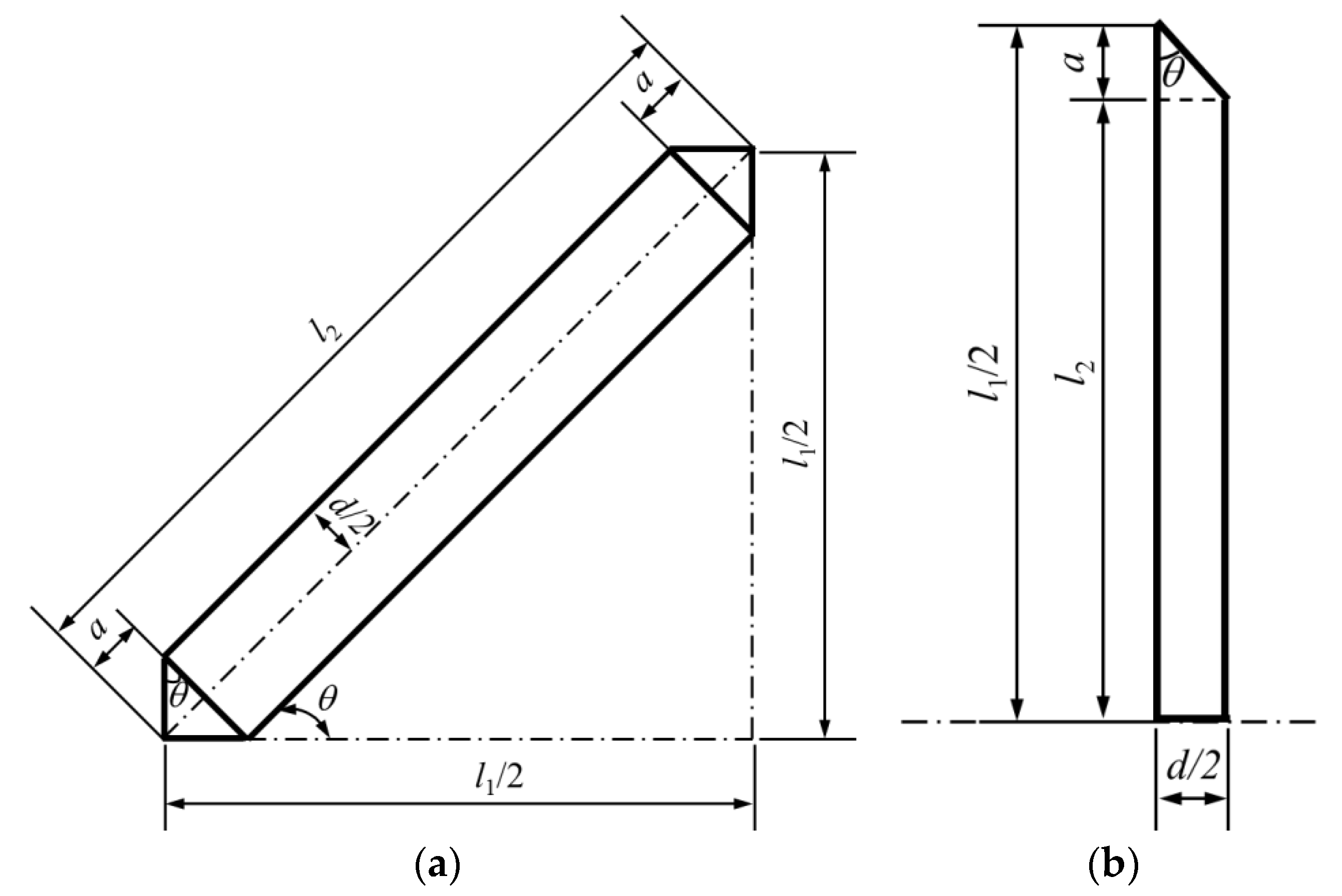
2. Cell Architecture Design
2.1. Topology Optimisation Problem
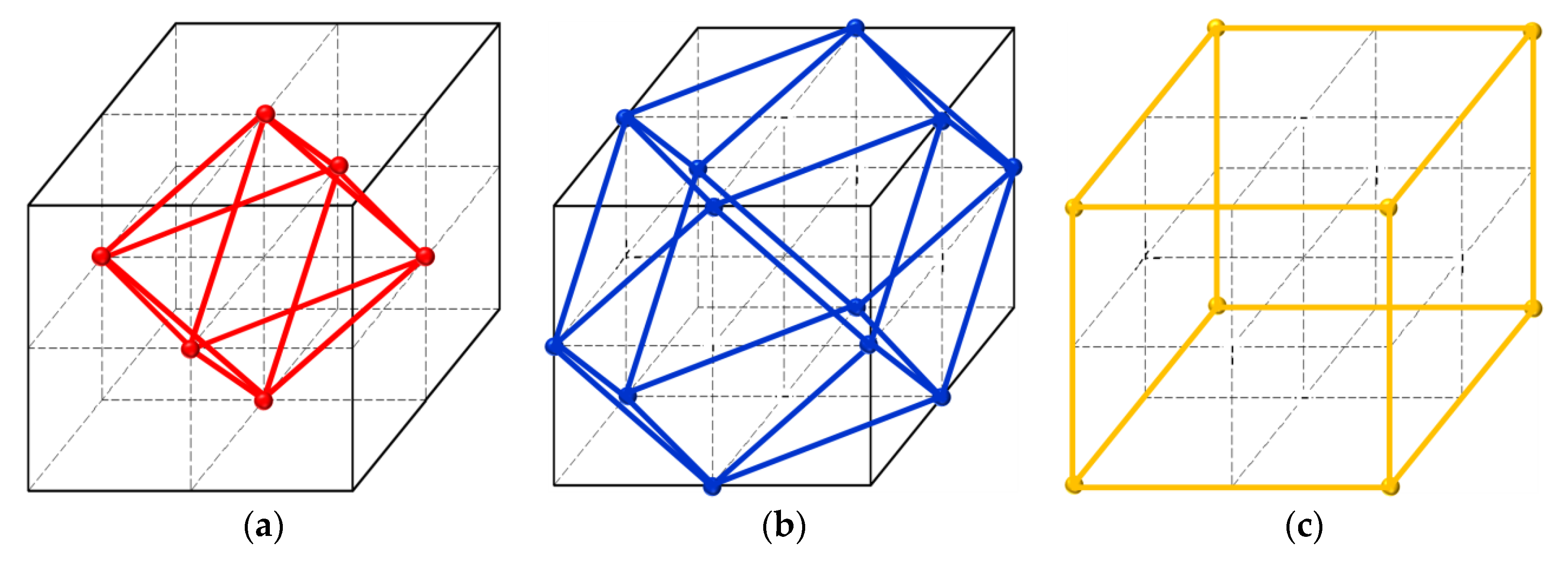
2.2. Analogy with Crystal Structures
2.3. Numerical Results
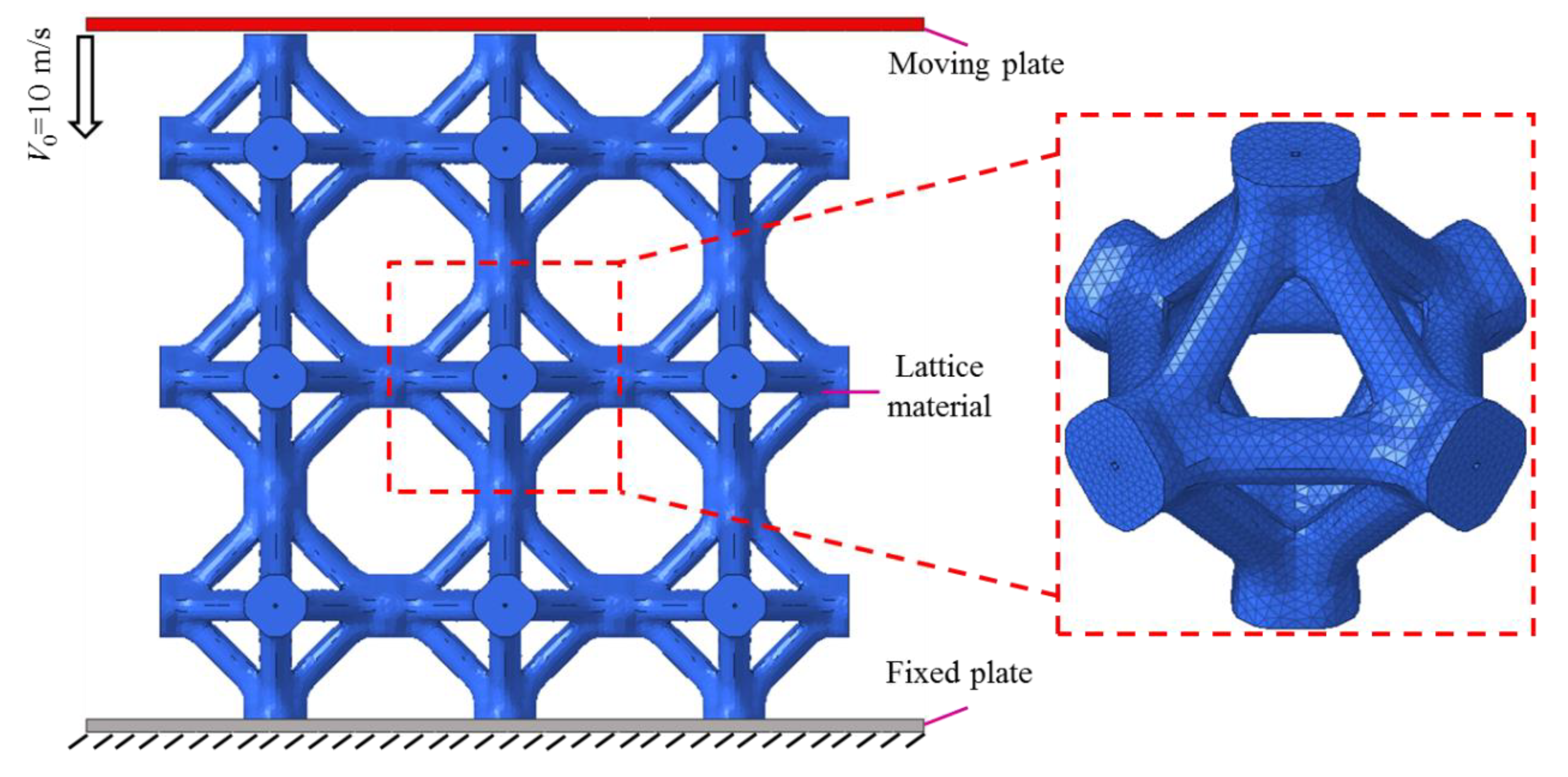
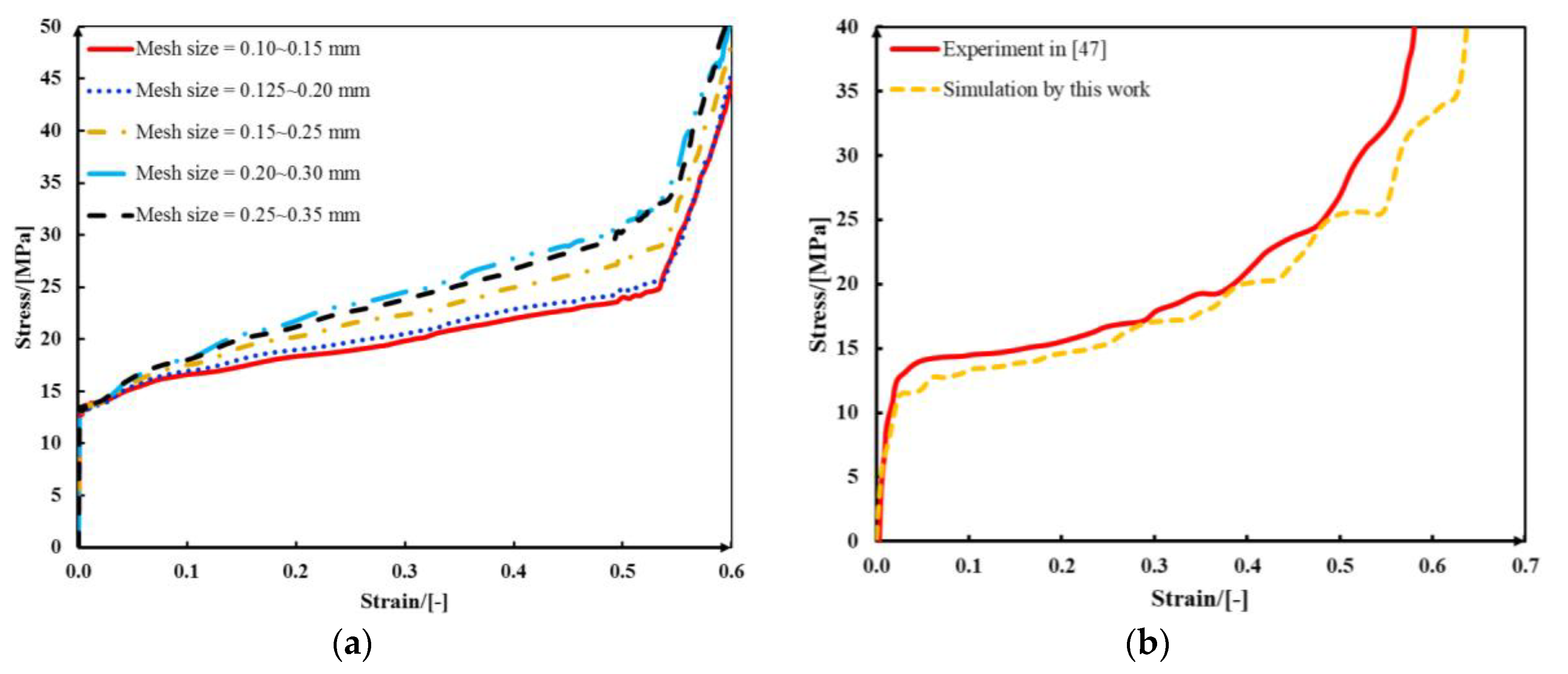
3. Finite Element Modelling
4. Results and Discussion
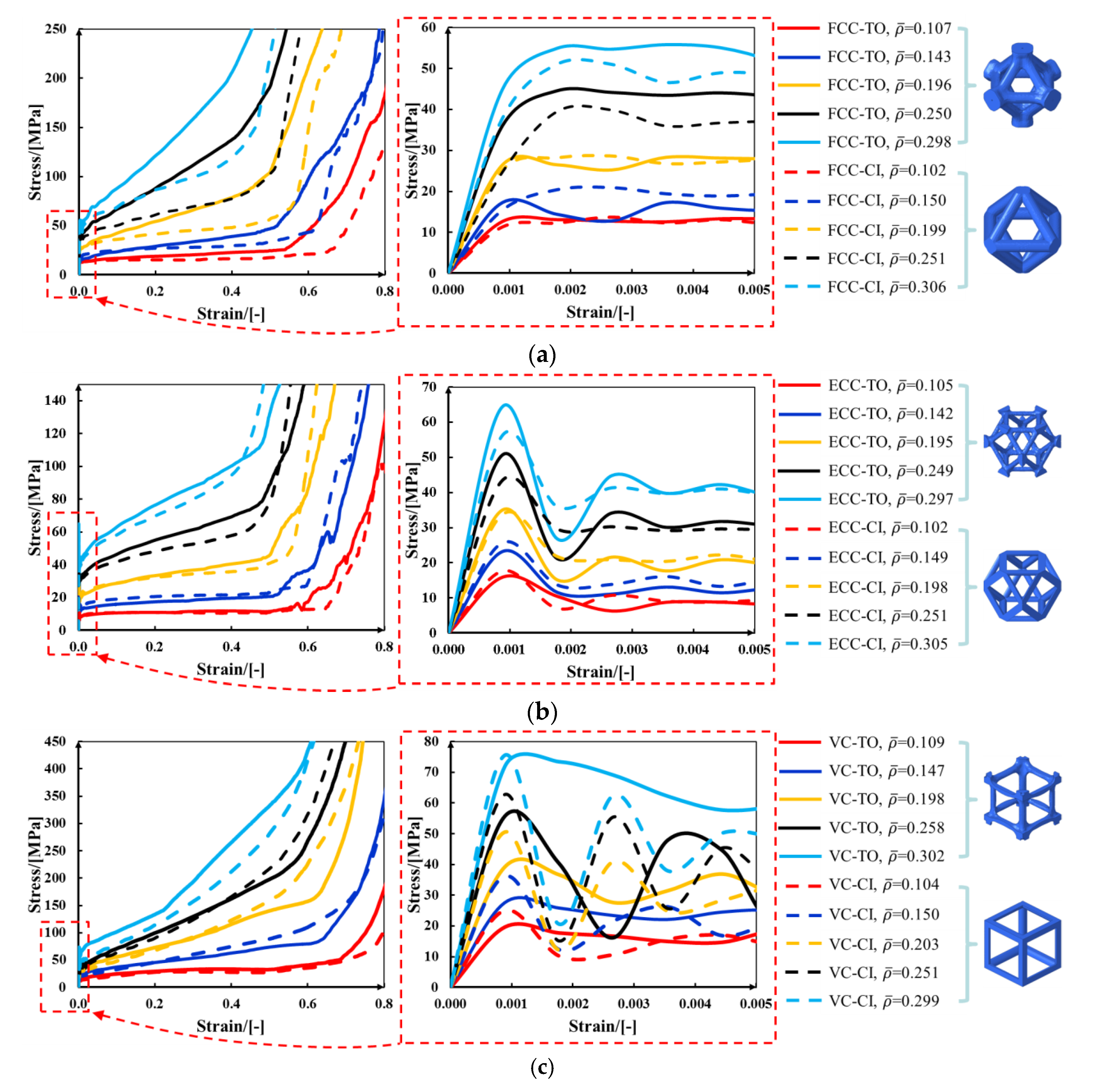
4.1. Deformation Modes
4.2. Stress-Strain Curves
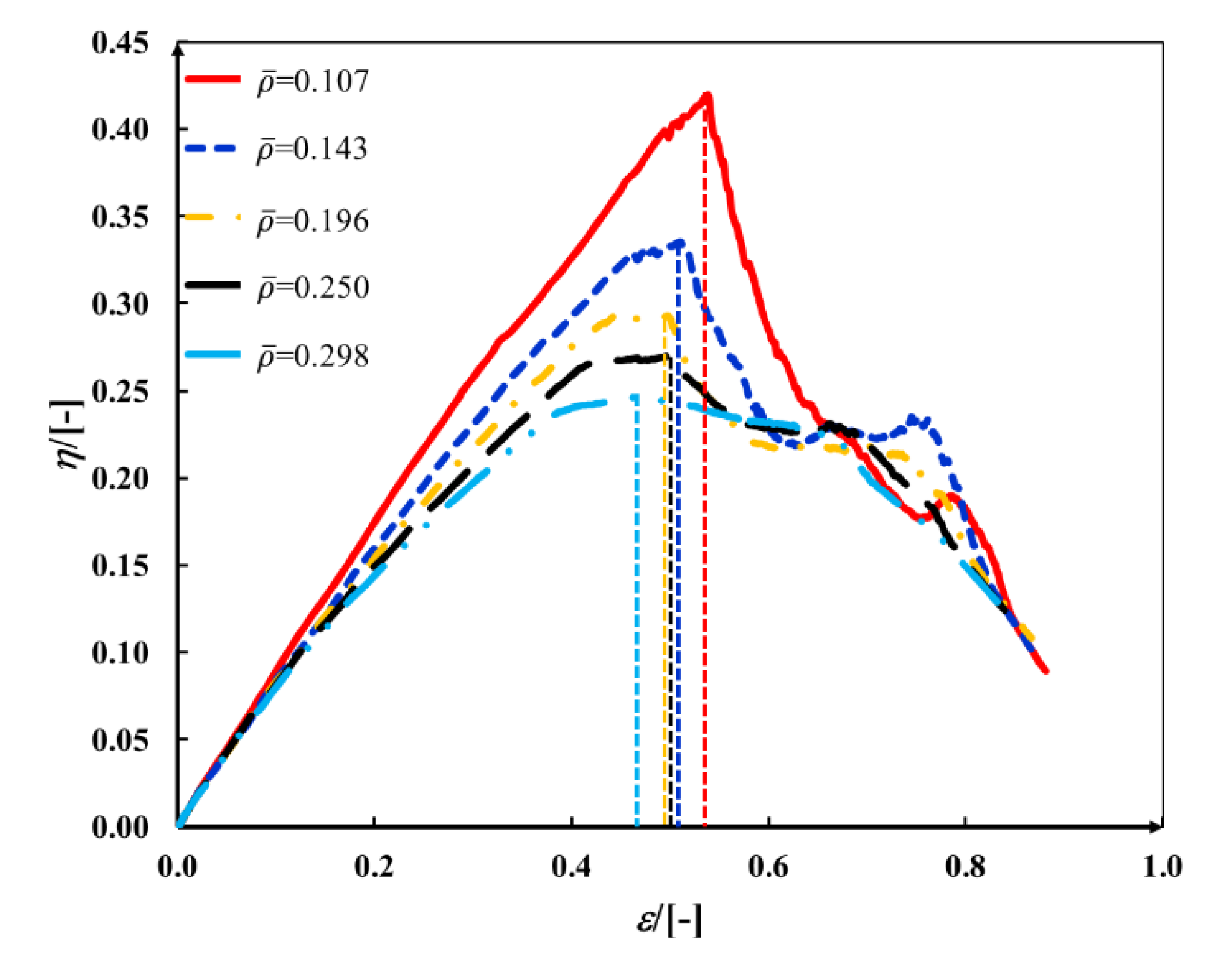
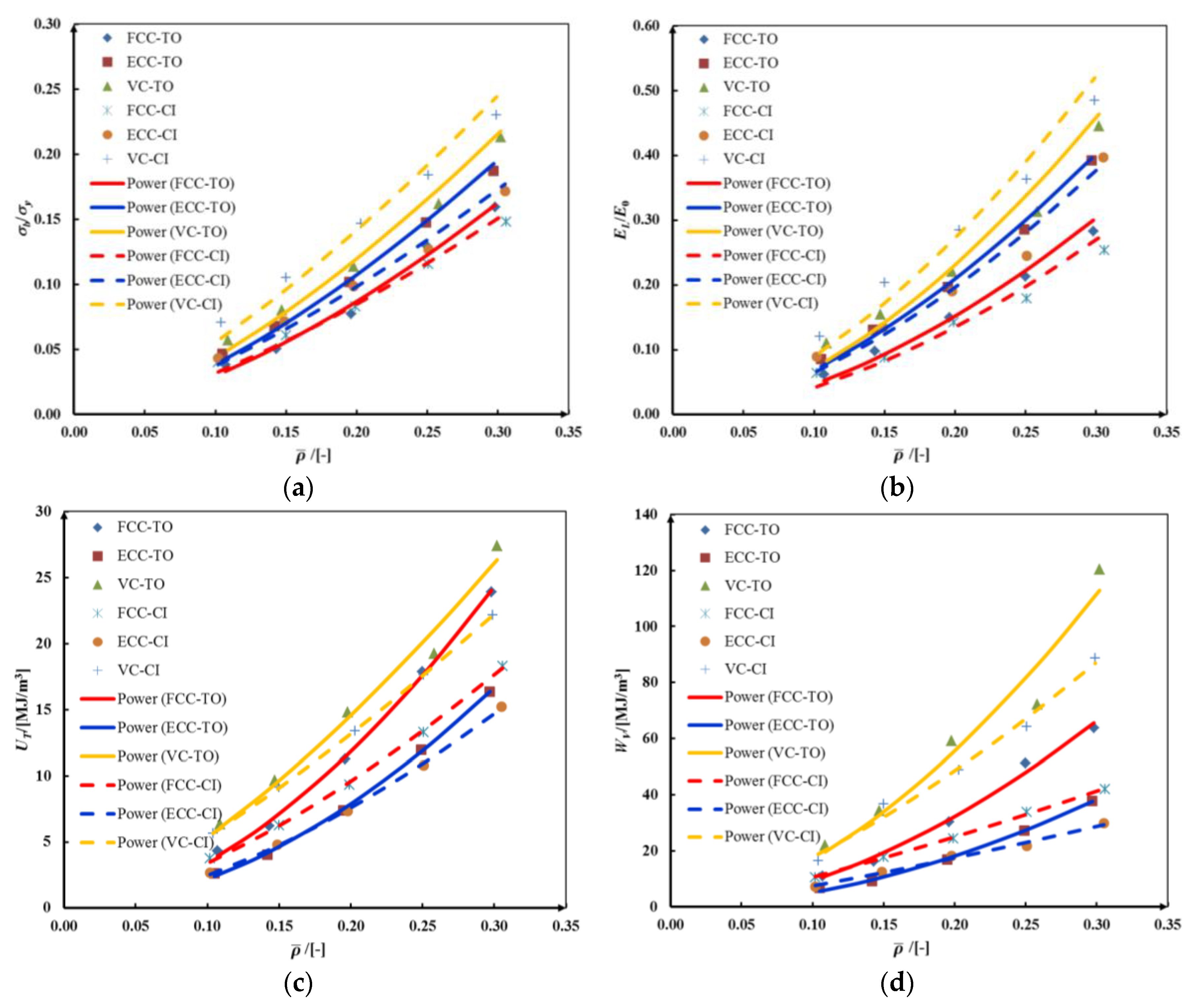
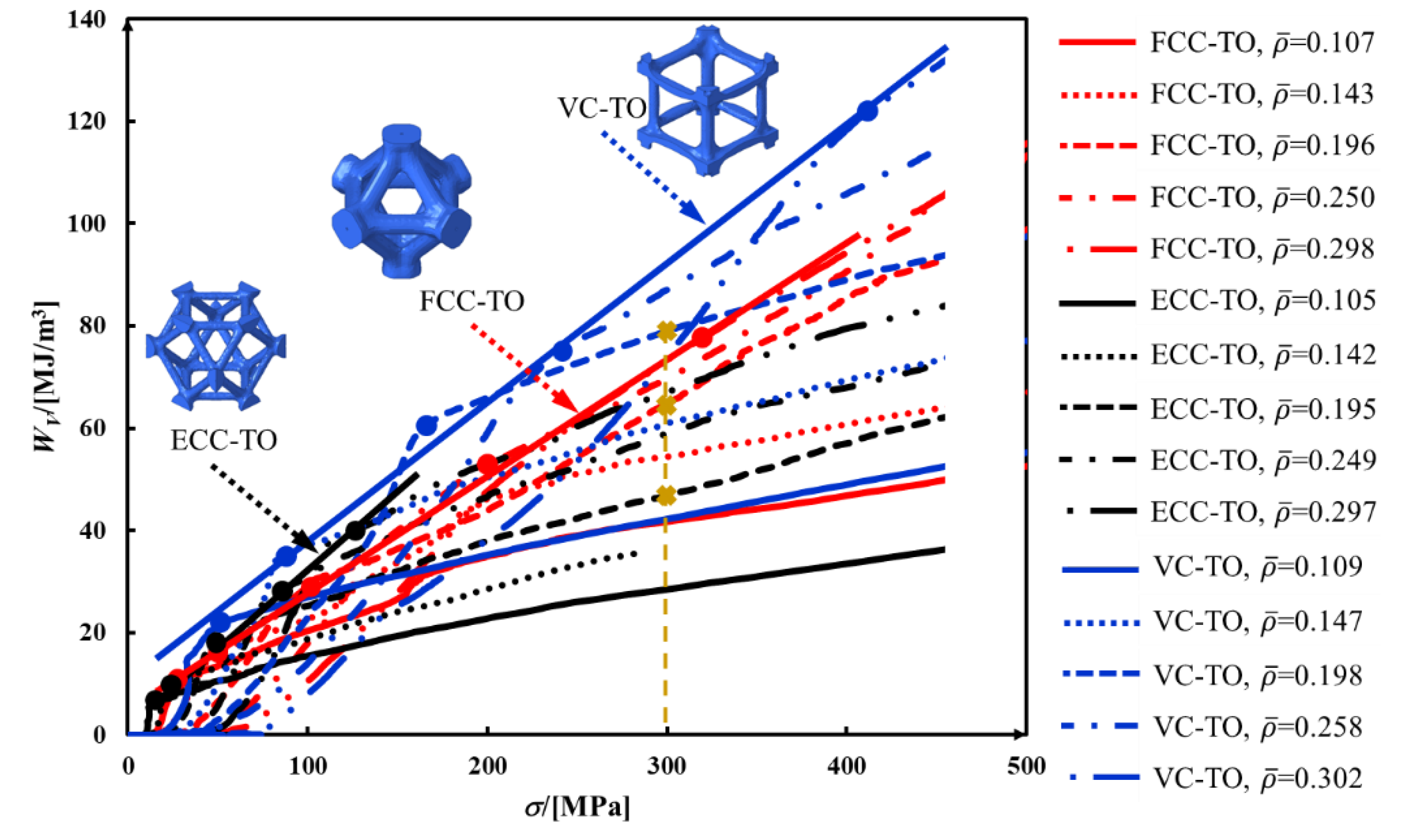
4.3. Mechanical Properties and Energy Absorption
5. Conclusions
- a)
- Topology optimisation-guided lattice materials are highly similar to the corresponding crystal-inspired lattice materials, especially at a low relative density. The topology optimisation-guided lattice materials are generally non-uniform in terms of strut thickness and joints shape, while the crystal-inspired cells are uniform.
- b)
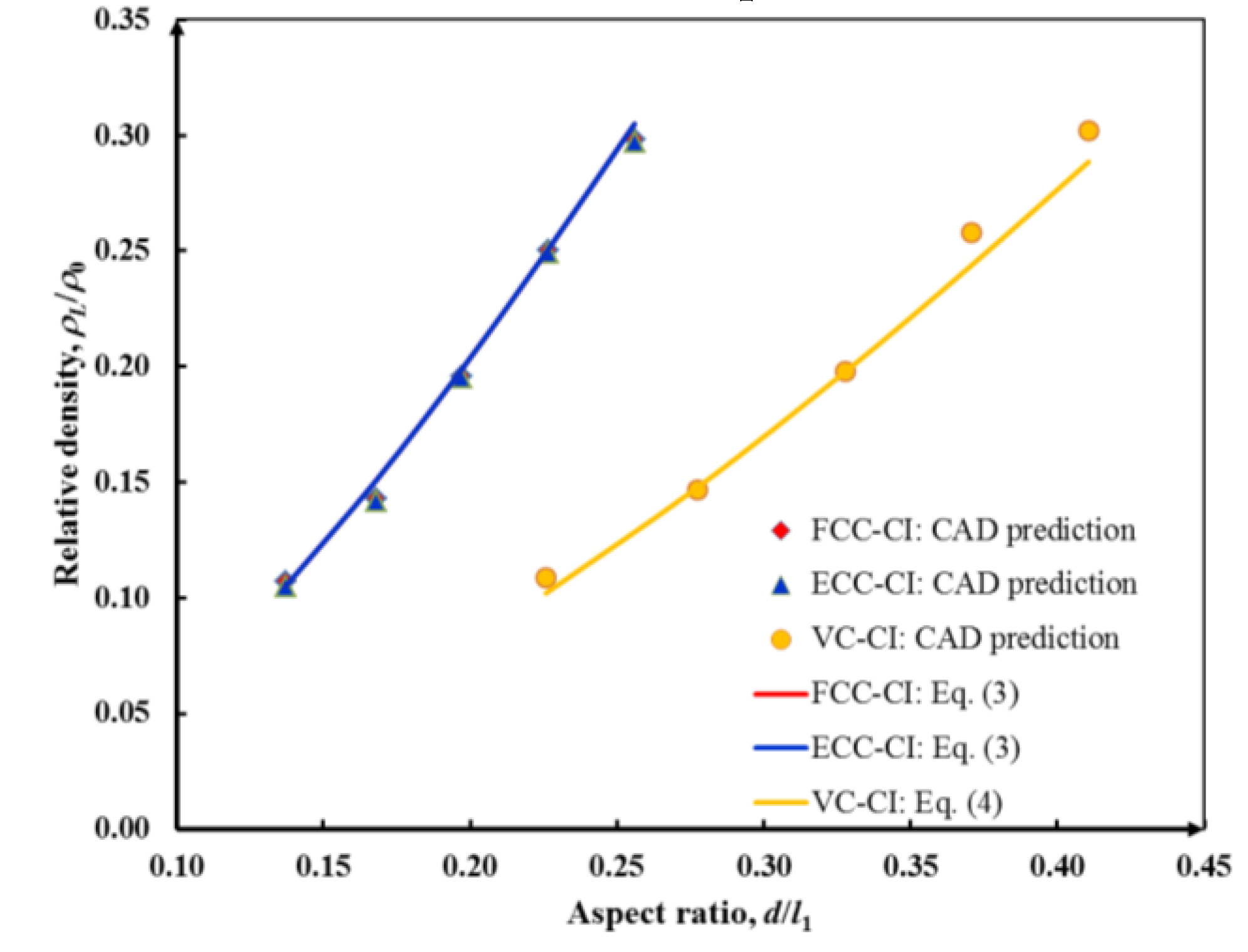
- Formulae relating the relative density () and aspect ratio (d/l1) of crystal-inspired lattices are presented, which has been well validated by CAD predictions.
- c)
- Comparing the topology-guided and manually generated structures, FCC-TO and ECC-TO exhibit a highly similar bending-dominated deformation mode to FCC-CI and ECC-CI, respectively. However, differences are found between VC-TO and VC-CI lattices. Shear band is observed in VC-CI structures at a low relative density while the VC-TO lattice deforms stably.
- d)
- In terms of collapse strength and elastic modulus, the VC lattice is stronger than the FCC and ECC lattices because its struts are arranged along the loading direction. On the other hand, topology-generated lattices outperform the corresponding crystal-guided lattices in aspects of toughness and energy absorption per unit volume.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xiao, Z.; Yang, Y.; Xiao, R.; Bai, Y.; Song, C.; Wang, D. Evaluation of topology-optimized lattice structures manufactured via selective laser melting. Mater. Des. 2018, 143, 27–37. [Google Scholar] [CrossRef]
- Mei, H.; Zhao, R.; Xia, Y.; Du, J.; Wang, X.; Cheng, L. Ultrahigh strength printed ceramic lattices. J. Alloys Compd. 2019, 797, 786–796. [Google Scholar] [CrossRef]
- Kadic, M.; Milton, G.; van Hecke, M.; Wegener, M. 3D metamaterials. Nat. Rev. Phys. 2019, 1, 198–210. [Google Scholar] [CrossRef]
- Peng, C.; Tran, P.; Nguyen-Xuan, H.; Ferreira, A.J.M. Mechanical performance and fatigue life prediction of lattice structures: Parametric computational approach. Compos. Struct. 2020, 235, 111821. [Google Scholar] [CrossRef]
- Helou, M.; Kara, S. Design, analysis and manufacturing of lattice structures: An overview. Int. J. Comput. Integr. Manuf. 2017, 31, 243–261. [Google Scholar] [CrossRef]
- Daynes, S.; Feih, S.; Lu, W.; Wei, J. Design concepts for generating optimised lattice structures aligned with strain trajectories. Comput. Methods Appl. Mech. Eng. 2019, 354, 689–705. [Google Scholar] [CrossRef]
- Hazeli, K.; Babamiri, B.; Indeck, J.; Minor, A.; Askari, H. Microstructure-topology relationship effects on the quasi-static and dynamic behavior of additively manufactured lattice structures. Mater. Des. 2019, 176, 107826. [Google Scholar] [CrossRef]
- Alaña, M.; Lopez-Arancibia, A.; Pradera-Mallabiabarrena, A.; Ruiz de Galarreta, S. Analytical model of the elastic behavior of a modified face-centered cubic lattice structure. J. Mech. Behav. Biomed. Mater. 2019, 98, 357–368. [Google Scholar] [CrossRef]
- Leary, M.; Mazur, M.; Elambasseril, J.; McMillan, M.; Chirent, T.; Sun, Y.; Qian, M.; Easton, M.; Brandt, M. Selective laser melting (SLM) of AlSi12Mg lattice structures. Mater. Des. 2016, 98, 344–357. [Google Scholar] [CrossRef]
- Sienkiewicz, J.; Płatek, P.; Jiang, F.; Sun, X.; Rusinek, A. Investigations on the Mechanical Response of Gradient Lattice Structures Manufactured via SLM. Metals 2020, 10, 213. [Google Scholar] [CrossRef]
- Gautam, R.; Idapalapati, S. Compressive Properties of Additively Manufactured Functionally Graded Kagome Lattice Structure. Metals 2019, 9, 517. [Google Scholar] [CrossRef]
- Al-Saedi, D.; Masood, S.; Faizan-Ur-Rab, M.; Alomarah, A.; Ponnusamy, P. Mechanical properties and energy absorption capability of functionally graded F2BCC lattice fabricated by SLM. Mater. Des. 2018, 144, 32–44. [Google Scholar] [CrossRef]
- Gross, A.; Pantidis, P.; Bertoldi, K.; Gerasimidis, S. Correlation between topology and elastic properties of imperfect truss-lattice materials. J. Mech. Phys. Solids 2019, 124, 577–598. [Google Scholar] [CrossRef]
- Deshpande, V.; Fleck, N.; Ashby, M. Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids 2001, 49, 1747–1769. [Google Scholar] [CrossRef]
- Nguyen, D.S.; Tran, T.T.; Le, D.K.; Le, V.T. Creation of Lattice Structures for Additive Manufacturing in CAD Environment. In Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bangkok, Thailand, 16–19 December 2018; pp. 396–400. [Google Scholar]
- Hedayati, R.; Sadighi, M.; Mohammadi-Aghdam, M.; Zadpoor, A. Analytical relationships for the mechanical properties of additively manufactured porous biomaterials based on octahedral unit cells. Appl. Math. Model. 2017, 46, 408–422. [Google Scholar] [CrossRef]
- Bonatti, C.; Mohr, D. Mechanical performance of additively-manufactured anisotropic and isotropic smooth shell-lattice materials: Simulations & experiments. J. Mech. Phys. Solids 2019, 122, 1–26. [Google Scholar]
- Ling, C.; Cernicchi, A.; Gilchrist, M.; Cardiff, P. Mechanical behaviour of additively-manufactured polymeric octet-truss lattice structures under quasi-static and dynamic compressive loading. Mater. Des. 2019, 162, 106–118. [Google Scholar] [CrossRef]
- Lozanovski, B.; Downing, D.; Tran, P.; Shidid, D.; Qian, M.; Choong, P.; Brandt, M.; Leary, M. A Monte Carlo simulation-based approach to realistic modelling of additively manufactured lattice structures. Addit. Manuf. 2020, 32, 101092. [Google Scholar] [CrossRef]
- Lozanovski, B.; Leary, M.; Tran, P.; Shidid, D.; Qian, M.; Choong, P.; Brandt, M. Computational modelling of strut defects in SLM manufactured lattice structures. Mater. Des. 2019, 171, 107671. [Google Scholar] [CrossRef]
- Peng, C.; Tran, P. Bioinspired functionally graded gyroid sandwich panel subjected to impulsive loadings. Compos. Part B Eng. 2020, 188, 107773. [Google Scholar] [CrossRef]
- Tran, P.; Peng, C. Triply periodic minimal surfaces sandwich structures subjected to shock impact. J. Sandw. Struct. Mater. 2020, 1–30. [Google Scholar] [CrossRef]
- Bai, L.; Zhang, J.; Chen, X.; Yi, C.; Chen, R.; Zhang, Z. Configuration optimization design of Ti6Al4V lattice structure formed by SLM. Materials 2018, 11, 1856. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Gadipudi, V.; Salem, D. Topology Optimization of Lightweight Lattice Structural Composites Inspired by Cuttlefish Bone. Appl. Compos. Mater. 2018, 26, 15–27. [Google Scholar] [CrossRef]
- Chiandussi, G. On the solution of a minimum compliance topology optimisation problem by optimality criteria without a priori volume constraint specification. Comput. Mech. 2005, 38, 77–99. [Google Scholar] [CrossRef]
- Zhang, W.; Li, D.; Kang, P.; Guo, X.; Youn, S.-K. Explicit topology optimization using IGA-based moving morphable void (MMV) approach. Comput. Methods Appl. Mech. Eng. 2020, 360, 112685. [Google Scholar] [CrossRef]
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications, 2nd ed.; Springer Science & Business Media: Berlin, Germany, 2004. [Google Scholar]
- Sigmund, O.; Maute, K. Topology optimization approaches. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Kentli, A. Topology optimization applications on engineering structures. In Truss and Frames-Recent Advances and New Perspectives; IntechOpen: London, UK, 2019. [Google Scholar]
- Zhang, X.; Ramos, A.S.; Paulino, G.H. Material nonlinear topology optimization using the ground structure method with a discrete filtering scheme. Struct. Multidiscip. Optim. 2017, 55, 2045–2072. [Google Scholar] [CrossRef]
- Costa, G.; Montemurro, M.; Pailhès, J. A 2D topology optimisation algorithm in NURBS framework with geometric constraints. Int. J. Mech. Mater. Des. 2018, 14, 669–696. [Google Scholar] [CrossRef]
- Costa, G.; Montemurro, M.; Pailhès, J. Minimum length scale control in a NURBS-based SIMP method. Comput. Methods Appl. Mech. Eng. 2019, 354, 963–989. [Google Scholar] [CrossRef]
- Costa, G.; Montemurro, M.; Pailhès, J. NURBS hyper-surfaces for 3D topology optimization problems. Mech. Adv. Mater. Struct. 2019, 1582826, 1–20. [Google Scholar] [CrossRef]
- Lazarov, B.S.; Wang, F.; Sigmund, O. Length scale and manufacturability in density-based topology optimization. Arch. Appl. Mech. 2016, 86, 189–218. [Google Scholar] [CrossRef]
- Geoffroy-Donders, P.; Allaire, G.; Pantz, O. 3-d topology optimization of modulated and oriented periodic microstructures by the homogenization method. J. Comput. Phys. 2020, 401, 108994. [Google Scholar] [CrossRef]
- Da, D.; Xia, L.; Li, G.; Huang, X. Evolutionary topology optimization of continuum structures with smooth boundary representation. Struct. Multidiscip. Optim. 2017, 57, 2143–2159. [Google Scholar] [CrossRef]
- Allaire, G.; Jouve, F.; Toader, A.-M. Structural optimization using sensitivity analysis and a level-set method. J. Comput. Phys. 2004, 194, 363–393. [Google Scholar] [CrossRef]
- Yamada, T.; Izui, K.; Nishiwaki, S.; Takezawa, A. A topology optimization method based on the level set method incorporating a fictitious interface energy. Comput. Methods Appl. Mech. Eng. 2010, 199, 2876–2891. [Google Scholar] [CrossRef]
- Afrousheh, M.; Marzbanrad, J.; Göhlich, D. Topology optimization of energy absorbers under crashworthiness using modified hybrid cellular automata (MHCA) algorithm. Struct. Multidiscip. Optim. 2019, 60, 1021–1034. [Google Scholar] [CrossRef]
- Yang, C.; Xu, P.; Xie, S.; Yao, S. Mechanical performances of four lattice materials guided by topology optimisation. Scr. Mater. 2020, 178, 339–345. [Google Scholar] [CrossRef]
- Yang, C.; Xu, P.; Yao, S.; Xie, S.; Li, Q.; Peng, Y. Optimization of honeycomb strength assignment for a composite energy-absorbing structure. Thin-Walled Struct. 2018, 127, 741–755. [Google Scholar] [CrossRef]
- Tovar, A. Bone Remodelling as a Hybrid Cellular Automaton Optimization Process. Ph.D. Thesis, University of Notre Dame, Cotabato City, Philippines, 2004. [Google Scholar]
- LS-TaSC™. Theory Manual (Version 4.0) of Topology and Shape Computations; Livermore Software Technology Corporation: Livermore, CA, USA, 2018. [Google Scholar]
- Tro, N.J. Chemistry: A Molecular Approach, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Yuan, S.; Chua, C.; Zhou, K. 3D-Printed Mechanical Metamaterials with High Energy Absorption. Adv. Mater. Technol. 2019, 4, 1800419. [Google Scholar] [CrossRef]
- Montemayor, L.; Greer, J. Mechanical Response of Hollow Metallic Nanolattices: Combining Structural and Material Size Effects. J. Appl. Mech. 2015, 82, 071012. [Google Scholar] [CrossRef]
- Maskery, I.; Aremu, A.O.; Parry, L.; Wildman, R.D.; Tuck, C.J.; Ashcroft, I.A. Effective design and simulation of surface-based lattice structures featuring volume fraction and cell type grading. Mater. Des. 2018, 155, 220–232. [Google Scholar] [CrossRef]
- Ls-dyna. Keyword User’s Manual Volume I (Version 971 R8.0); Livermore Software Technology Corporation: Livermore, CA, USA, 2015. [Google Scholar]
- Zhang, L.; Feih, S.; Daynes, S.; Chang, S.; Wang, M.; Wei, J.; Lu, W. Energy absorption characteristics of metallic triply periodic minimal surface sheet structures under compressive loading. Addit. Manuf. 2018, 23, 505–515. [Google Scholar] [CrossRef]
- Al-Ketan, O.; Rowshan, R.; Abu Al-Rub, R. Topology-mechanical property relationship of 3D printed strut, skeletal, and sheet based periodic metallic cellular materials. Addit. Manuf. 2018, 19, 167–183. [Google Scholar] [CrossRef]
- Liu, Y.; Li, S.; Zhang, L.; Hao, Y.; Sercombe, T. Early plastic deformation behaviour and energy absorption in porous β-type biomedical titanium produced by selective laser melting. Scr. Mater. 2018, 153, 99–103. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Q.M. Dynamic compressive behaviour of cellular materials: A review of phenomenon, mechanism and modelling. Int. J. Impact Eng. 2018, 112, 74–115. [Google Scholar] [CrossRef]
- Yang, L.; Mertens, R.; Ferrucci, M.; Yan, C.; Shi, Y.; Yang, S. Continuous graded Gyroid cellular structures fabricated by selective laser melting: Design, manufacturing and mechanical properties. Mater. Des. 2019, 162, 394–404. [Google Scholar] [CrossRef]
- ISO 13314. Mechanical Testing of Metals-Ductility Testing-Compression Test for Porous and Cellular Metals; International Organization for Standardization: Geneva, Switzerland, 2011. [Google Scholar]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Yu, S.; Sun, J.; Bai, J. Investigation of functionally graded TPMS structures fabricated by additive manufacturing. Mater. Des. 2019, 182, 108021. [Google Scholar] [CrossRef]
| Density, ρ0/(kg·m−3) | Young’s Modulus, E0/GPa | Poisson’s Ratio, μ | Tangent Modulus, Etan/MPa | Yield Strength, σy/MPa | Ultimate Strength σu/MPa |
|---|---|---|---|---|---|
| 7850 | 206 | 0.26 | 517 | 382 | 482 |
| Lattice Material | |||||
|---|---|---|---|---|---|
FCC-TO |  |  |  |  |  |
ECC-TO |  |  |  |  |  |
VC-TO |  |  |  |  |  |
| FCC-CI |  |  |  |  |  |
| ECC-CI |  |  |  |  |  |
| VC-CI |  |  |  |  |  |
| Lattice Materials | ||||
|---|---|---|---|---|
| FCC-TO |  | 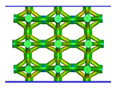 | 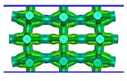 | 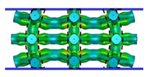 |
| FCC-CI | 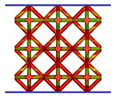 | 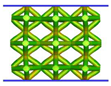 |  |  |
| ECC-TO | 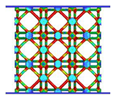 | 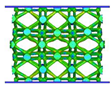 | 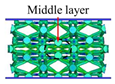 |  |
| ECC-CI |  |  | 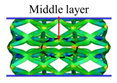 |  |
| VC-TO | 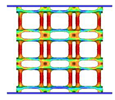 | 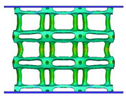 | 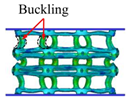 | 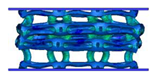 |
| VC-CI |  | 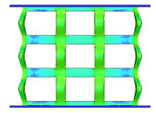 | 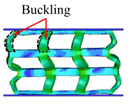 | 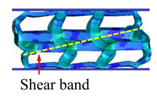 |
| Lattice Materials | ||||
|---|---|---|---|---|
| FCC-TO | 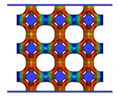 | 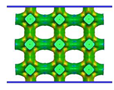 | 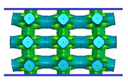 | 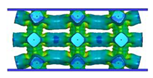 |
| FCC-CI | 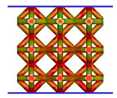 | 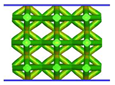 |  |  |
| ECC-TO | 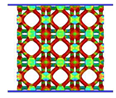 | 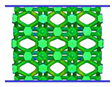 |  |  |
| ECC-CI |  |  |  |  |
| VC-TO | 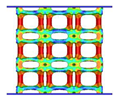 | 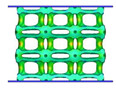 | 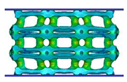 | 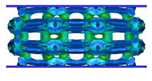 |
| VC-CI | 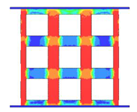 |  | 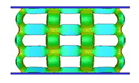 | 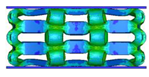 |
| [-] | FCC-TO | FCC-CI | Difference | ECC-TO | ECC-CI | Difference | VC-TO | VC-CI | Difference |
|---|---|---|---|---|---|---|---|---|---|
| 0.10 | 20.63 | 15.59 | 32.33% | 11.43 | 10.70 | 6.78% | 32.19 | 28.36 | 13.49% |
| 0.15 | 33.69 | 28.08 | 19.98% | 18.45 | 21.24 | −13.13% | 52.96 | 60.08 | −11.84% |
| 0.20 | 65.43 | 45.05 | 45.24% | 36.76 | 34.16 | 7.63% | 90.26 | 93.16 | −3.12% |
| 0.25 | 110.53 | 69.13 | 59.89% | 61.00 | 52.64 | 15.89% | 127.66 | 124.92 | 2.19% |
| 0.30 | 156.75 | 100.09 | 56.60% | 86.66 | 80.37 | 7.82% | 190.38 | 158.42 | 20.18% |
| Lattice Material | Collapse Strength, σb [MPa] | Elastic Modulus, EL [GPa] | Toughness, UT [MJ/m3] | Strain Energy, WV [MJ/m3] | ||||
|---|---|---|---|---|---|---|---|---|
| C1 | n1 | C2 | n2 | C3 | n3 | C4 | n4 | |
| FCC-TO | 1.048 | 1.548 | 2.369 | 1.707 | 205.554 | 1.773 | 566.801 | 1.782 |
| ECC-TO | 1.165 | 1.482 | 2.807 | 1.611 | 154.456 | 1.849 | 354.951 | 1.849 |
| VC-TO | 1.242 | 1.453 | 3.512 | 1.691 | 147.402 | 1.438 | 884.025 | 1.719 |
| FCC-CI | 0.830 | 1.418 | 2.106 | 1.705 | 107.533 | 1.502 | 183.828 | 1.241 |
| ECC-CI | 0.935 | 1.397 | 2.613 | 1.603 | 103.767 | 1.625 | 126.143 | 1.230 |
| VC-CI | 1.250 | 1.353 | 3.614 | 1.608 | 105.342 | 1.292 | 499.610 | 1.449 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Xu, K.; Xie, S. Comparative Study on the Uniaxial Behaviour of Topology-Optimised and Crystal-Inspired Lattice Materials. Metals 2020, 10, 491. https://doi.org/10.3390/met10040491
Yang C, Xu K, Xie S. Comparative Study on the Uniaxial Behaviour of Topology-Optimised and Crystal-Inspired Lattice Materials. Metals. 2020; 10(4):491. https://doi.org/10.3390/met10040491
Chicago/Turabian StyleYang, Chengxing, Kai Xu, and Suchao Xie. 2020. "Comparative Study on the Uniaxial Behaviour of Topology-Optimised and Crystal-Inspired Lattice Materials" Metals 10, no. 4: 491. https://doi.org/10.3390/met10040491
APA StyleYang, C., Xu, K., & Xie, S. (2020). Comparative Study on the Uniaxial Behaviour of Topology-Optimised and Crystal-Inspired Lattice Materials. Metals, 10(4), 491. https://doi.org/10.3390/met10040491






