Deformation Behavior of C15E + C Steel under Different Uniaxial Stress Tests
Abstract
1. Introduction
2. The Main Determinants of Research
3. Research Results
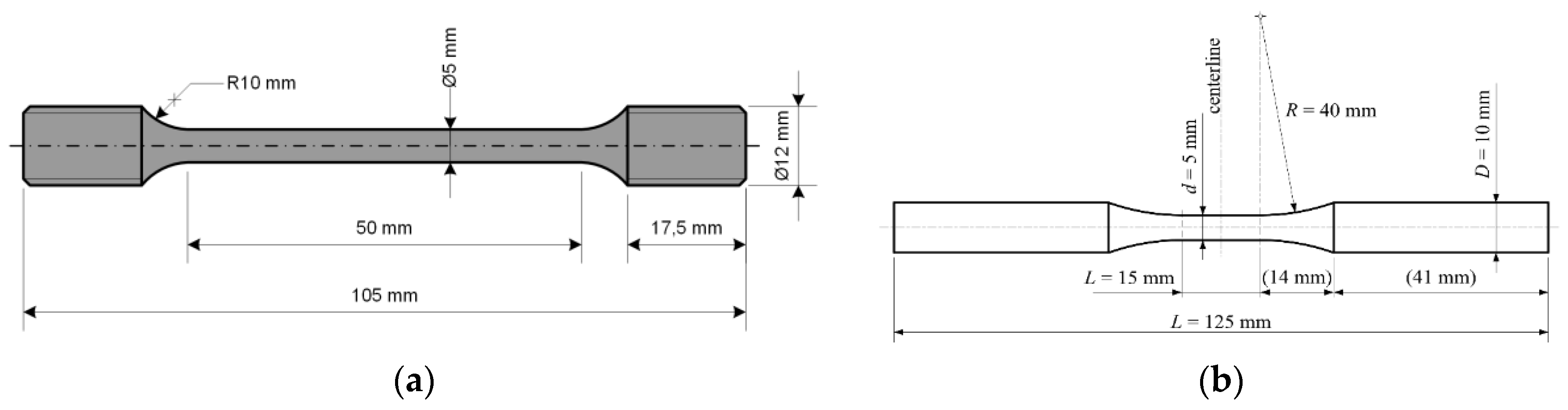
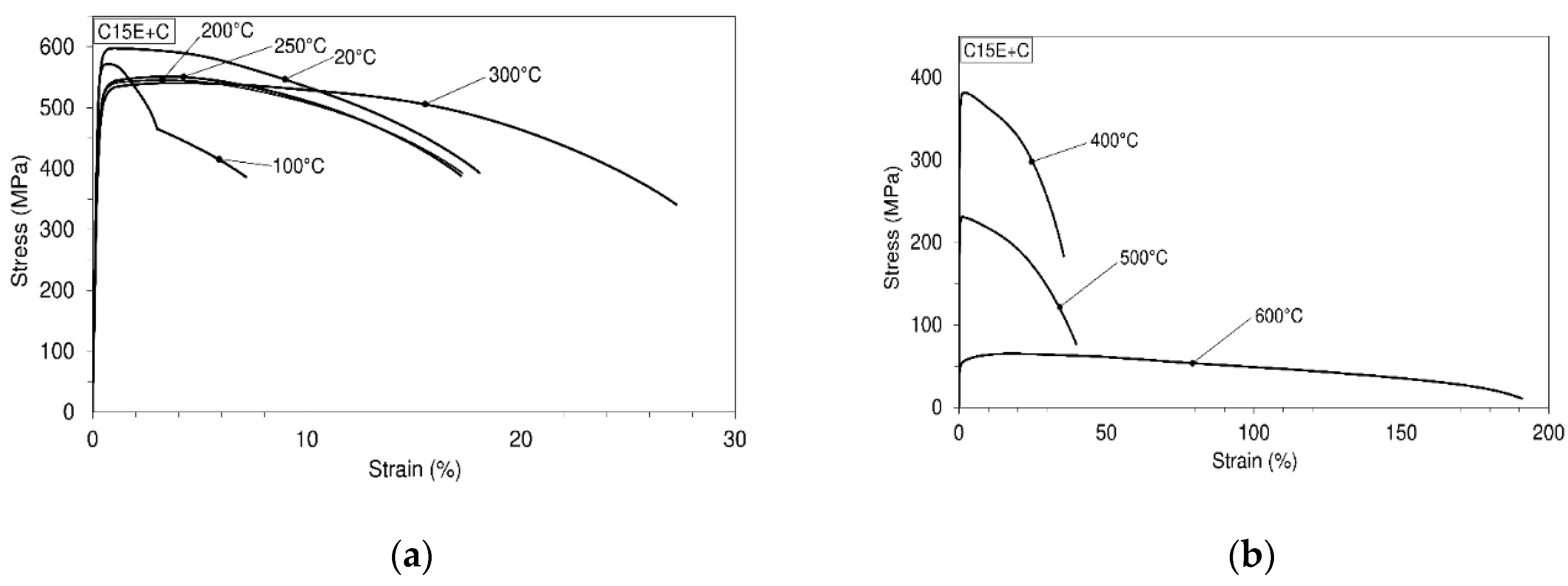
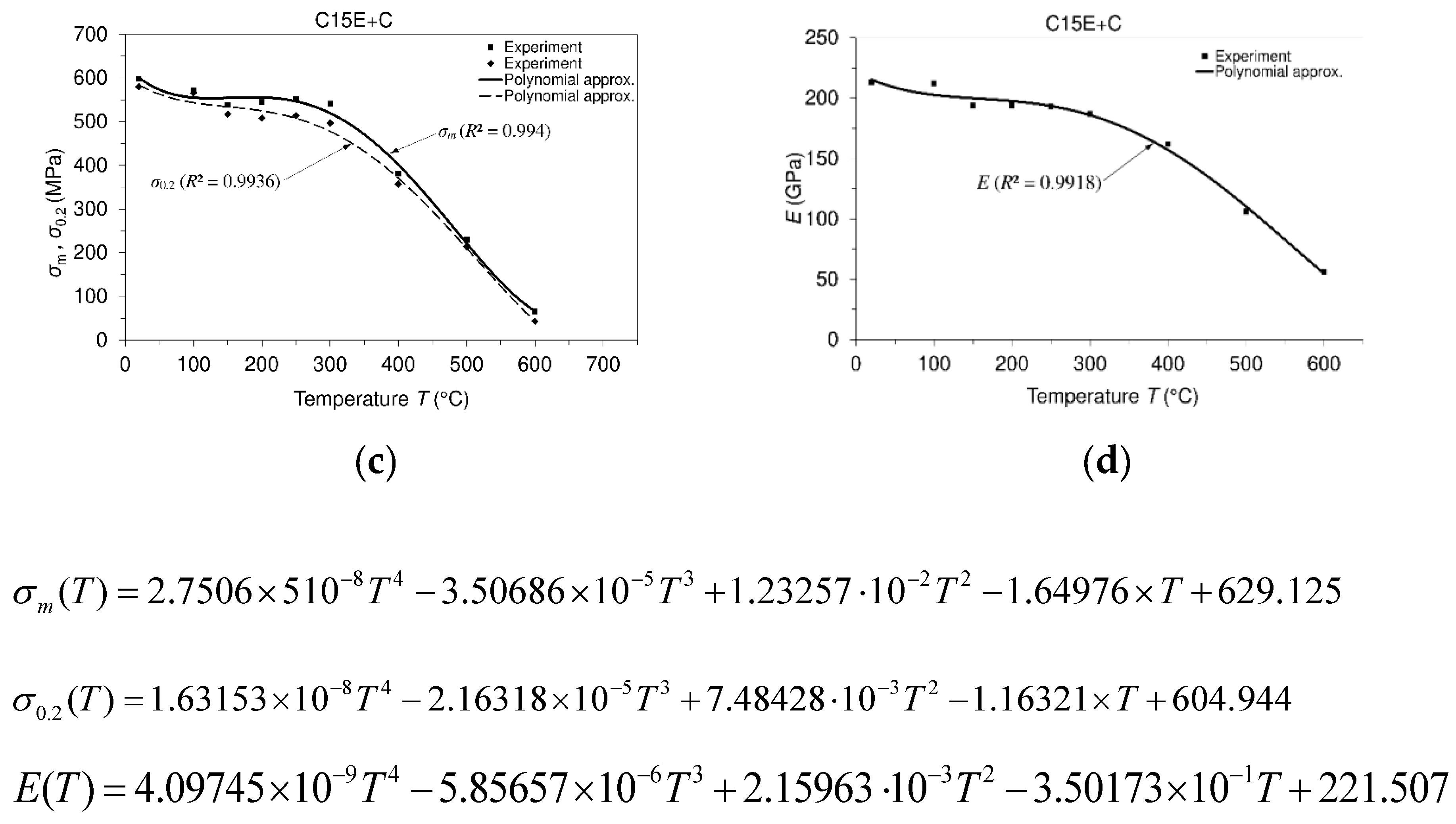
3.1. Mechanical Behavior of Material at Different Temperatures
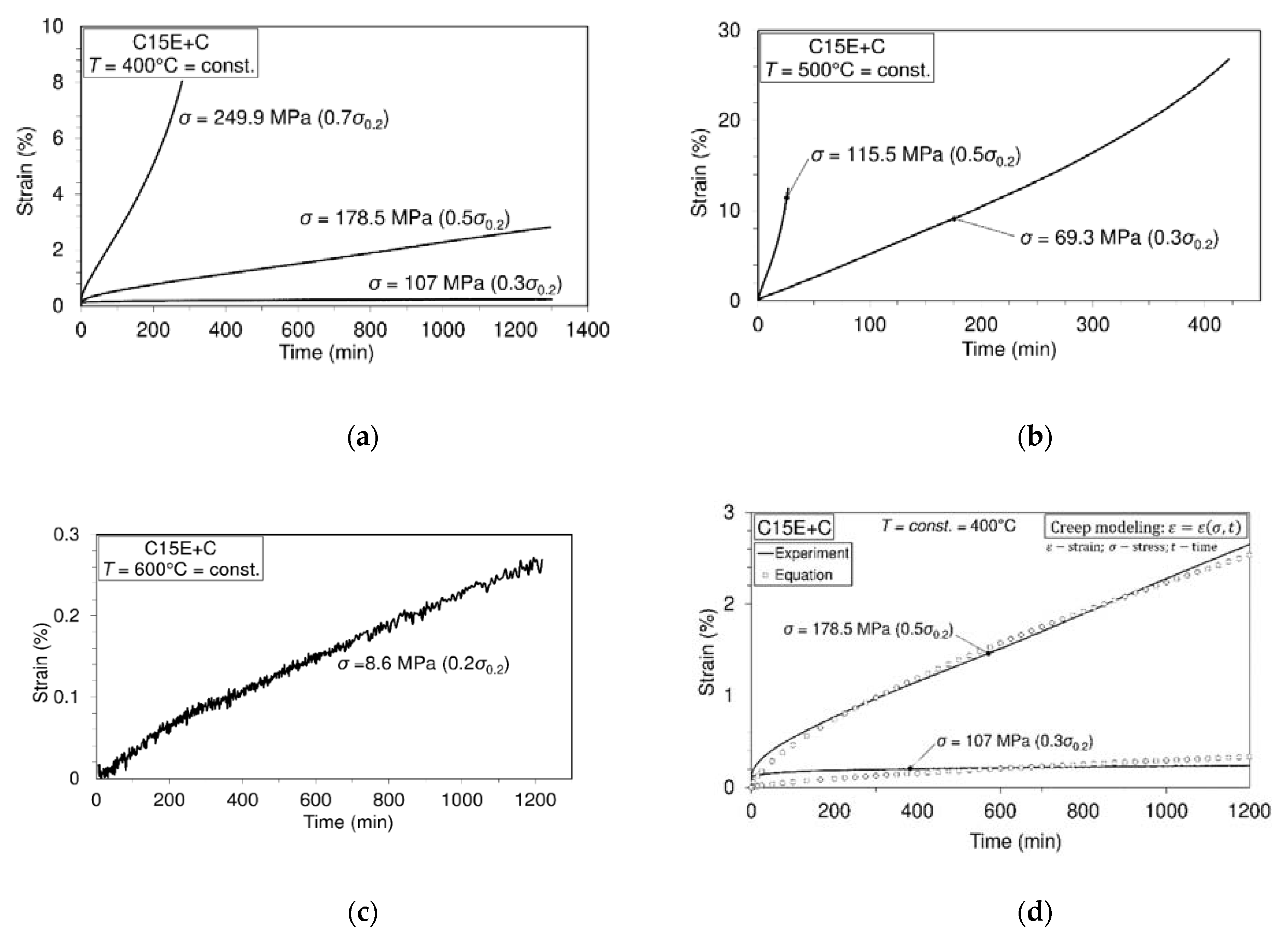
3.2. Short-Time Creep Tests and Creep Simulation
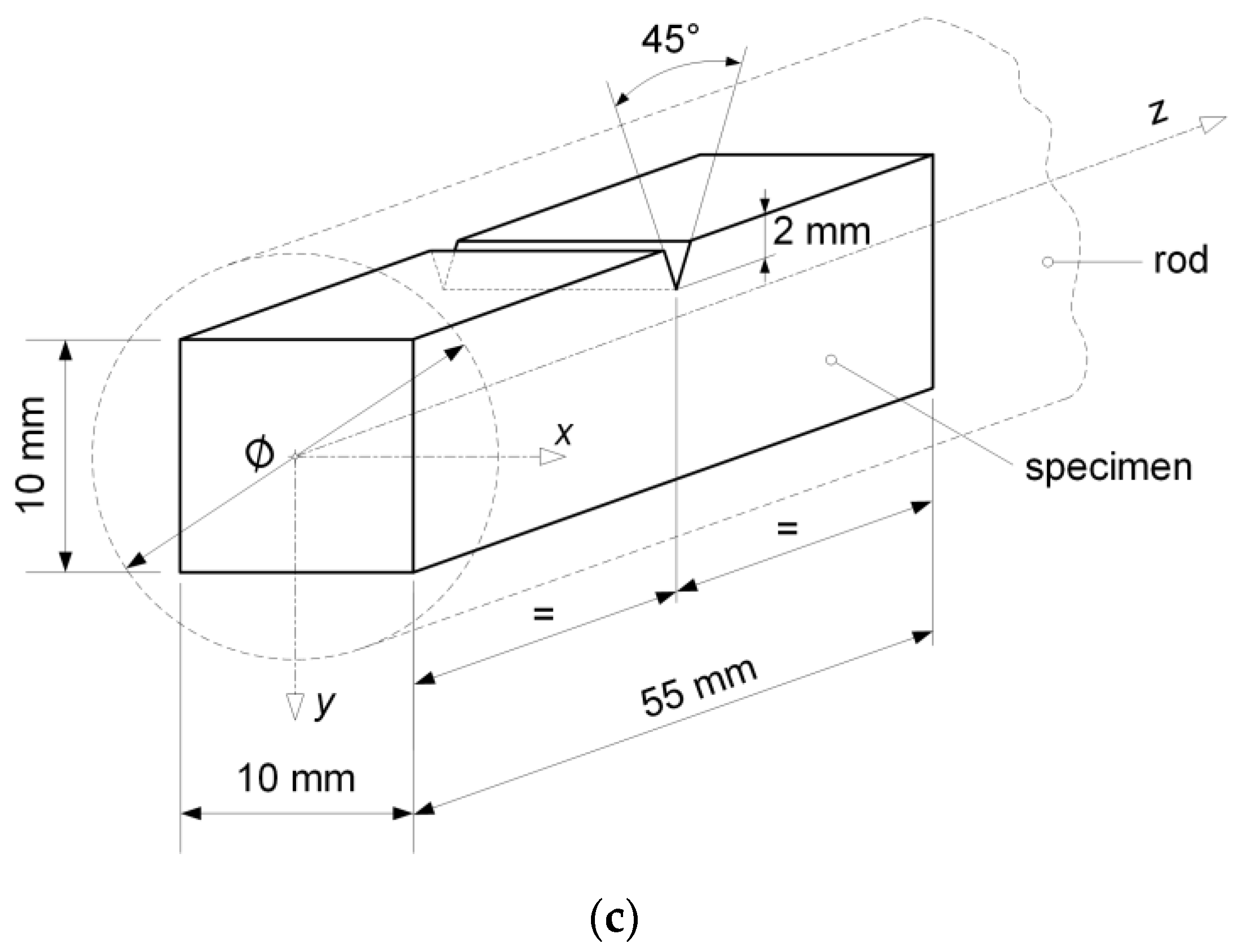
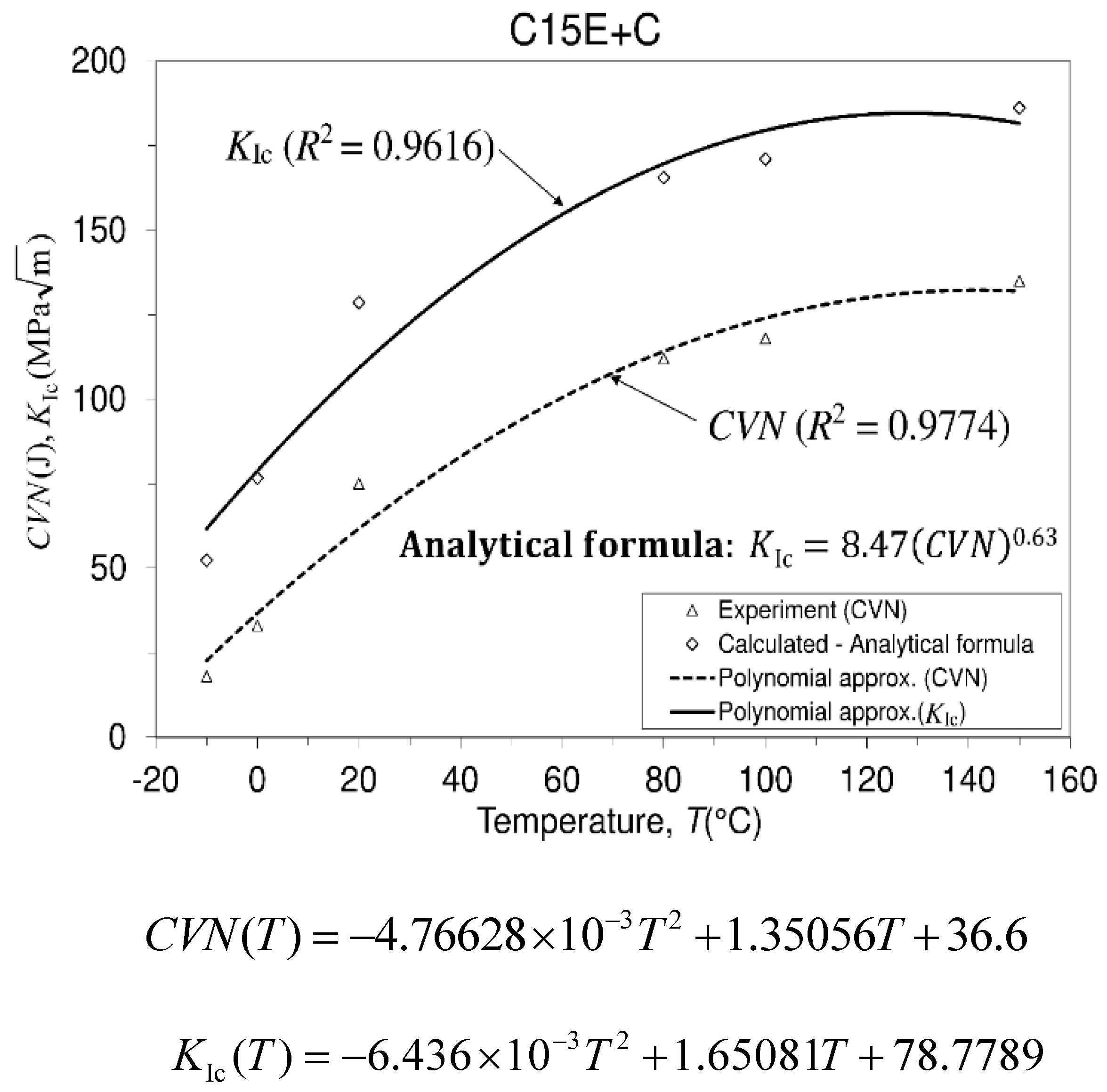
3.3. Testing the Energy of Impact Fracture of a Material and Fracture Toughness Assessment
3.4. Uniaxial Fully Reversed Mechanical Fatigue of the Material
3.4.1. Different Types of Material Fatigue
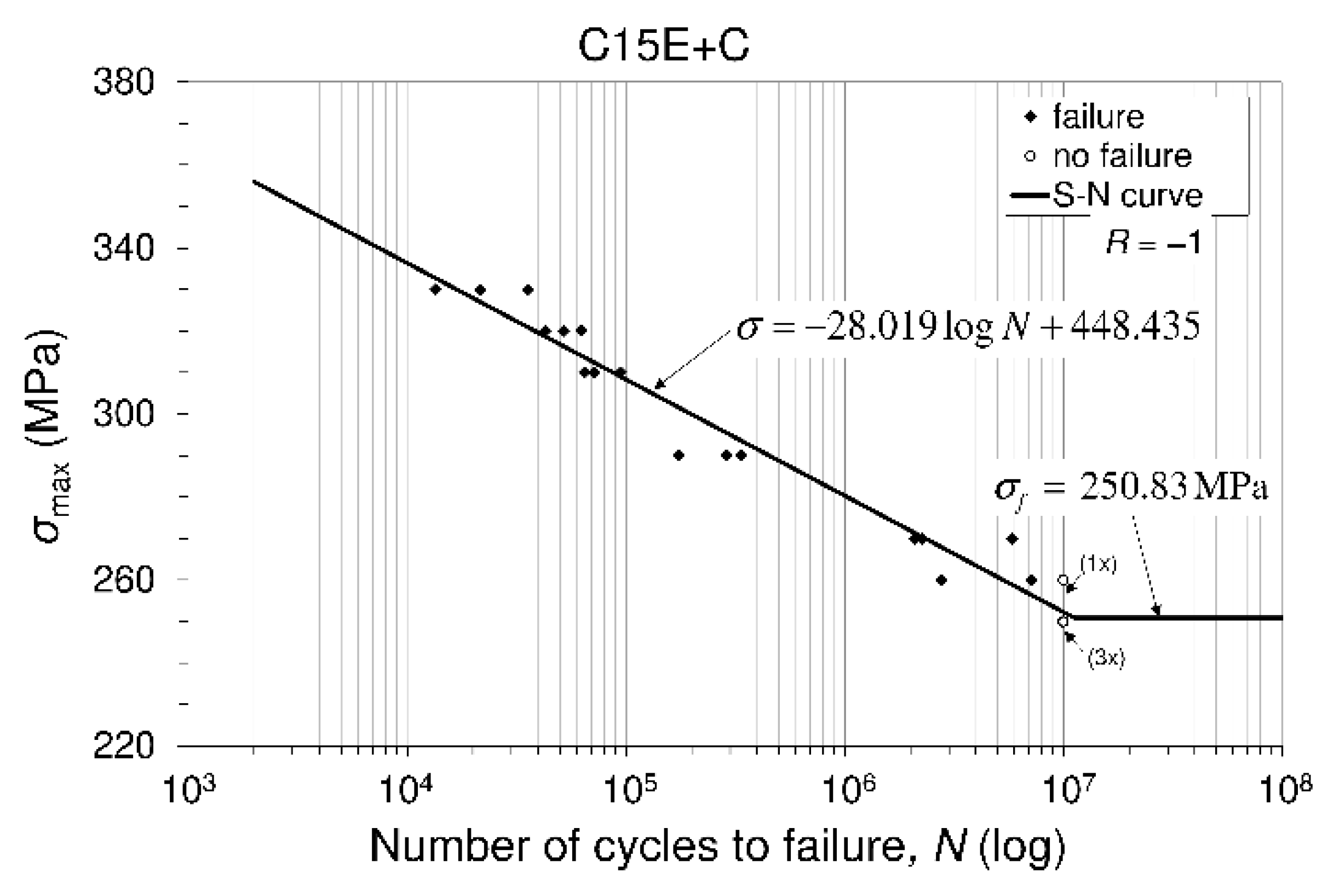
3.4.2. Fatigue-Life (S-N) Diagram Based on Fully Reversed Mechanical Fatigue Tests
3.4.3. Determination of Fatigue Limit Based on Modified Staircase Method
- , the coefficient for the one-sided tolerance limit for a normal distribution, and
- , the estimated standard deviation of the fatigue strength that can be calculated as:
- for = 250 + 10 (8/5 − 1/2) = 261 MPa,or, this can be obtained as (Table 3):for = (250 + 260 + 270 + 260 + 270 + 260 + 270)/7 = 262.86 MPa, whose amount is similar to previously obtained ones.
- for = 1.62 (0.24 + 0.029) = 4.36 MPa.
- for = 261 –2.333 4.36 = 250.83 MPa.
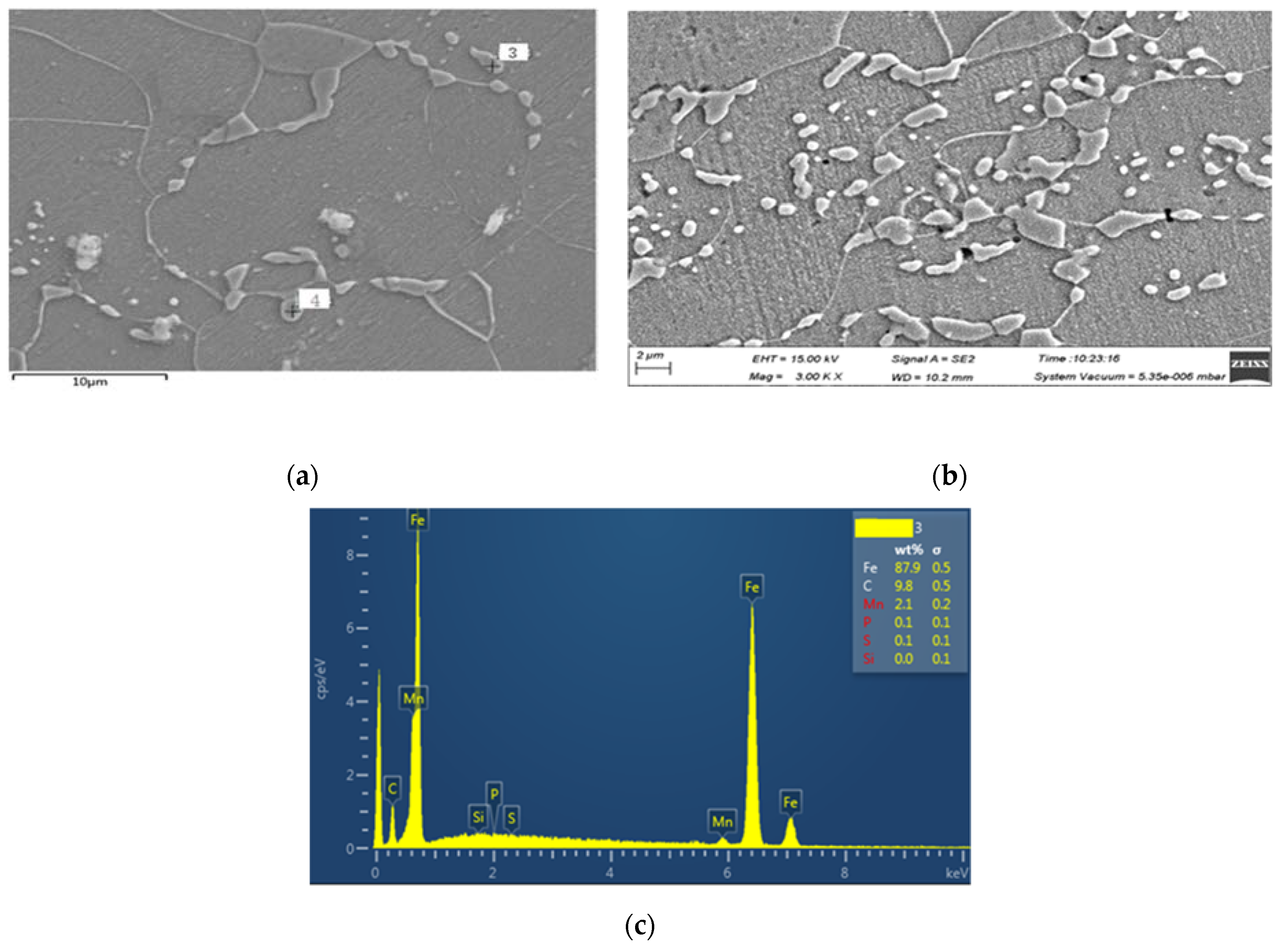
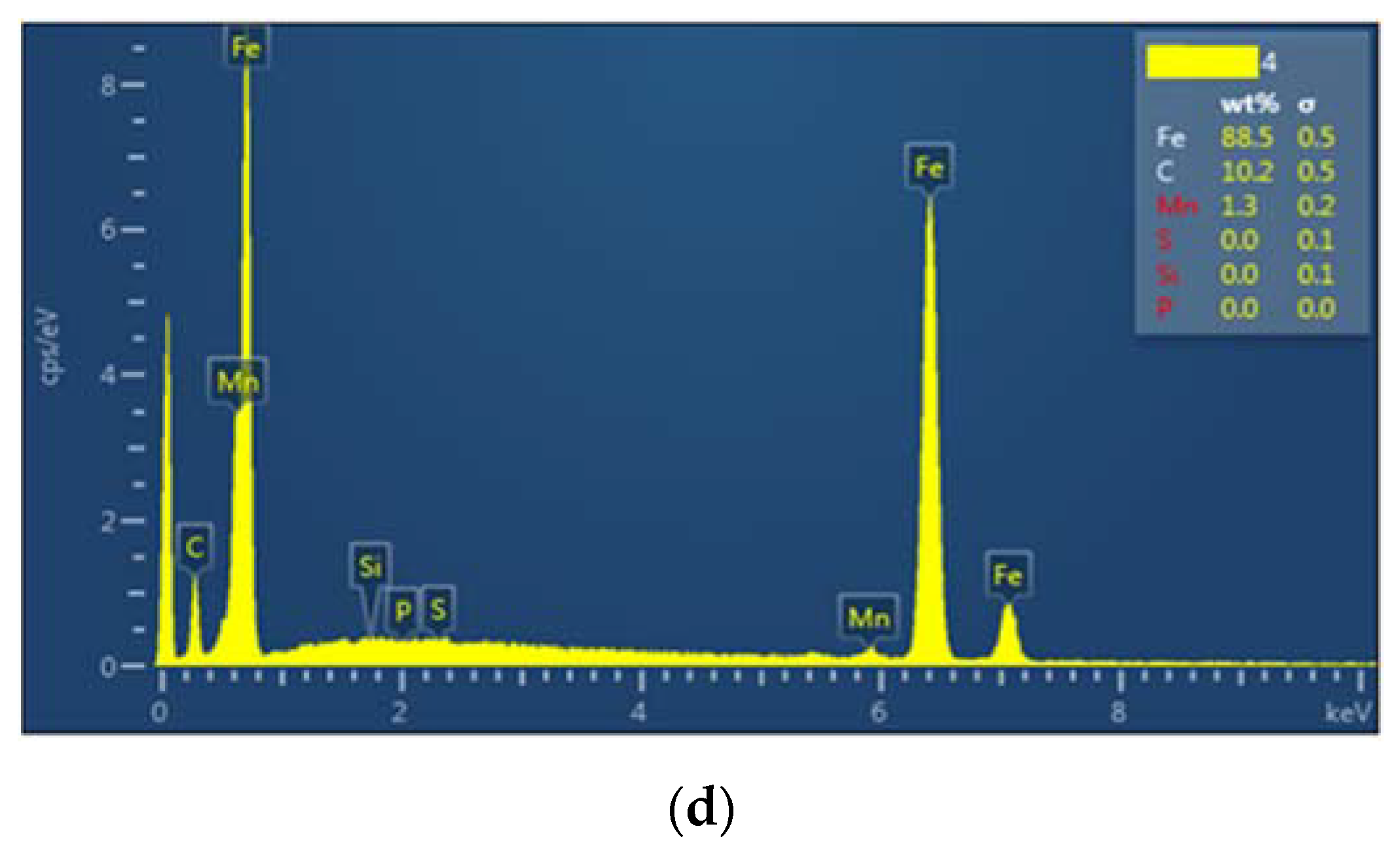
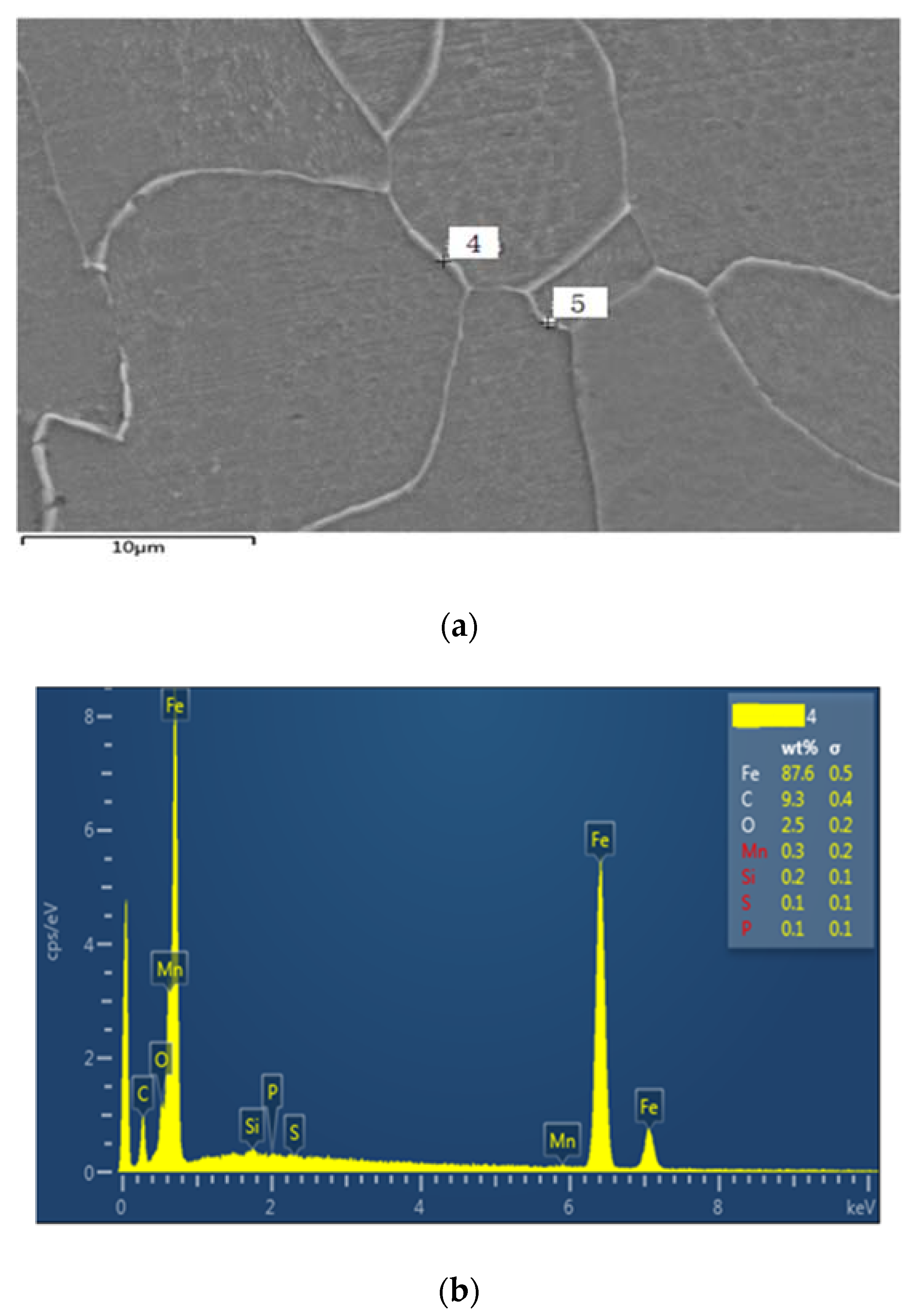
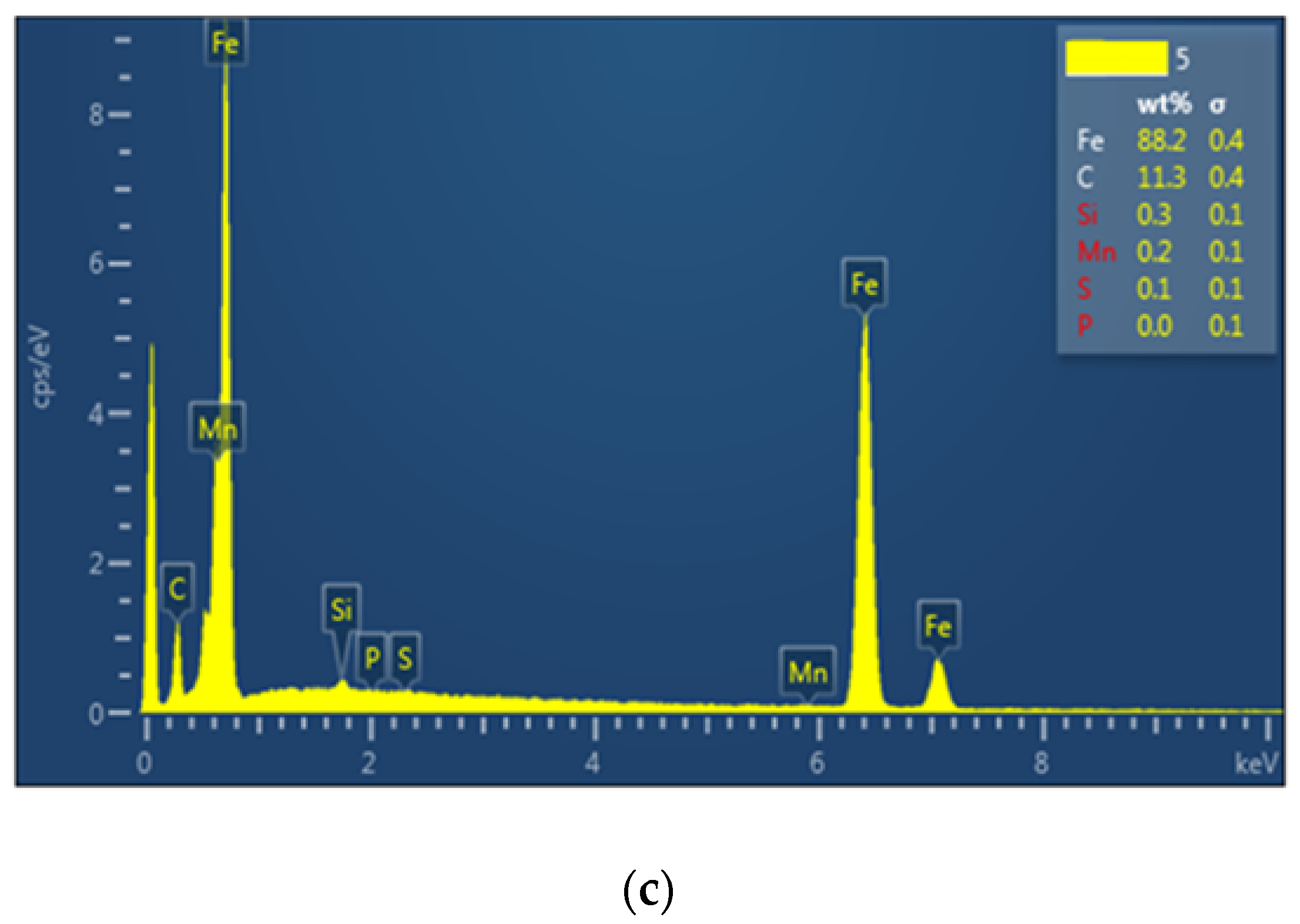
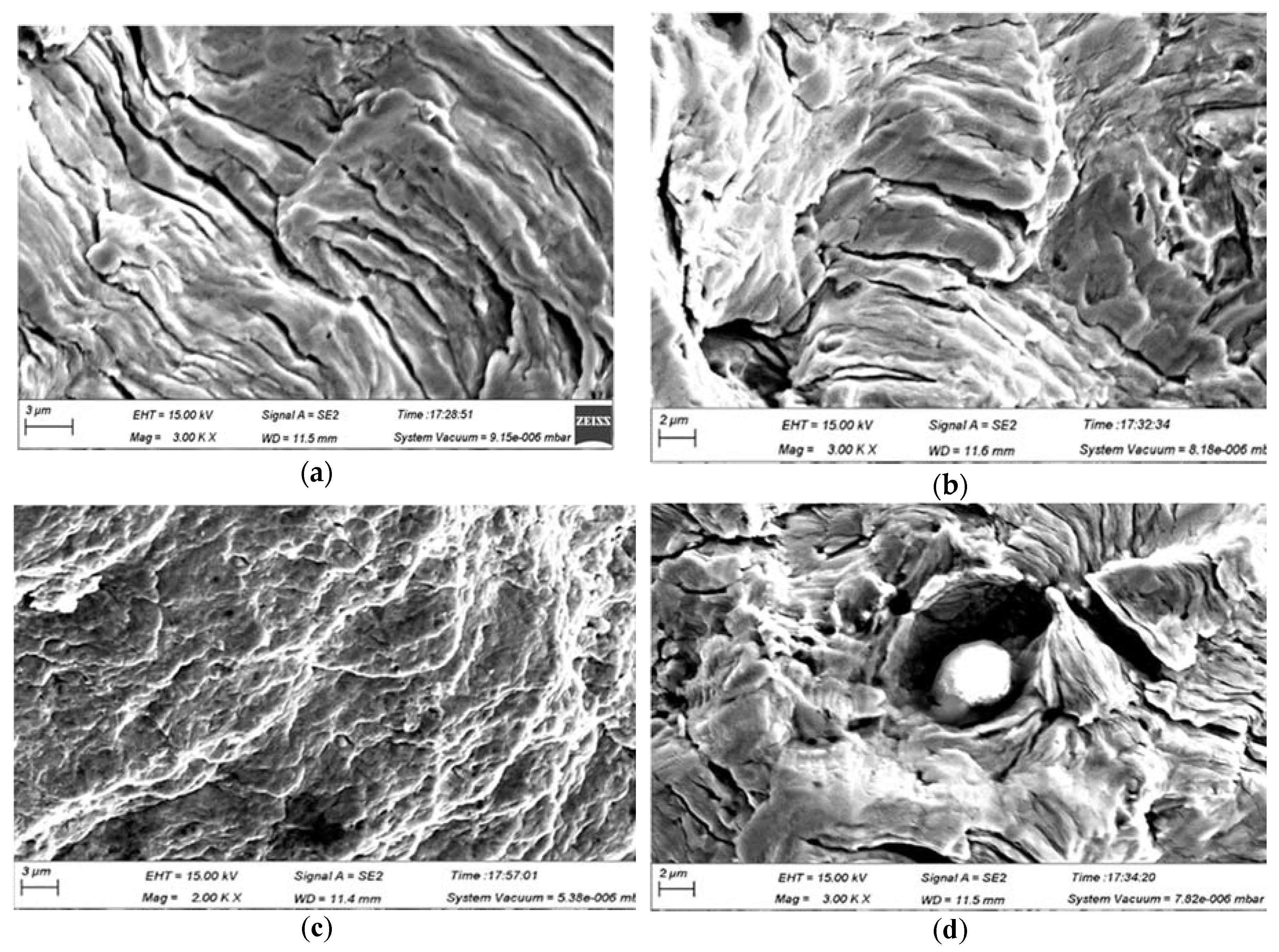
3.5. A Brief Analysis of the Microstructure of Material in State: As-Received, Previously Subjected to Creep, after Fracture Due to Fatigue
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stephens, R.I.; Fatemi, A.; Stephens, R.R.; Fuchs, H.O. Metal Fatigue in Engineering, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2001; pp. 1–3. [Google Scholar]
- Brooks, C.; Choudhury, A. Failure Analysis of Engineering Materials; McGraw-Hill: New York, NY, USA, 2002; pp. 2–7. [Google Scholar]
- Collins, J.A. Failure of Materials in Mechanical Design, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1993; pp. 6–15. [Google Scholar]
- Brnic, J. Analysis of Engineering Structures and Material Behavior; Wiley & Sons: Chichester, UK, 2018; pp. 209–222. [Google Scholar]
- Brnic, J.; Turkalj, G.; Niu, J.; Canadija, M.; Lanc, D. Analysis of experimental data on the behavior of steel S275JR—Reliability of modern design. Mater. Des. 2013, 47, 497–504. [Google Scholar] [CrossRef]
- Findley, W.N.; James, S.L.; Ksif, O. Creep and Relaxation of Nonlinear Viscoelastic Materials; Dover Publications, Inc.: New York, NY, USA, 1989; pp. 3–7. [Google Scholar]
- Gariboldi, E.; Spigarelli, S. Creep and high-temperature deformation of metals and alloys. Metals 2019, 9, 1087. [Google Scholar] [CrossRef]
- Raghavan, V. Materials Science and Engineering—A First Course, 6th ed.; PHI Learning, Private Limited: New Delhi, India, 2015; pp. 287–297. [Google Scholar]
- Boresi, A.P.; Schmidt, R.J.; Sidebottom, O.M. Advanced Mechanics of Material, 4th ed.; John Wiley & Sons: New York, NY, USA, 1993; pp. 655–691. [Google Scholar]
- Essa, K.; Kacmarcik, I.; Hartley, P.; Plancak, M.; Vilotic, D. Upsetting of bi-metallic ring billets. J. Mater. Process. Tech. 2013, 212, 817–824. [Google Scholar] [CrossRef]
- Brezinová, J.; Guzanová, A.; Draganovská, D.; Egri, M. Assessment tribological properties of coatings applied by HVOF technology. Acta Mech. Autom. 2013, 7, 135–139. [Google Scholar] [CrossRef][Green Version]
- Zettl, B.; Mayer, H.; Ede, C.; Tschegg, S.S. Very high cycle fatigue of normalized carbon steels. Int. J. Fatigue 2006, 28, 1583–1589. [Google Scholar] [CrossRef]
- Bach, J.; Göken, M.; Höppel, H.W. Fatigue of low-alloyed carbon steels in the HCF/VHCF-regimes. In Fatigue of Materials at Very High Numbers of Loading Cycles; Christ, H.J., Ed.; Springer Fachmedien Wiesbaden GmbH: Wiesbaden, Germany, 2018; pp. 1–23. [Google Scholar]
- Bach, J.; Göken, M.; Höppel, H.W. Stages of fatigue damage of plain carbon steels at the transition from the high cycle fatigue to the very high cycle fatigue regime. In Proceedings of the VHCF7-Seventh International Conference on Very High Cycle Fatigue, Dresden, Germany, 3–5 July 2017; Zimmermann, M., Christ, H.J., Eds.; University Siegen: Dresden, Germany, 2017; pp. 154–159. [Google Scholar]
- Nonaka, I.; Setowaki, S.; Ichikawa, Y. Effect of load frequency on high cycle fatigue strength of bullet train axle steel. Int. J. Fatigue 2014, 60, 43–47. [Google Scholar] [CrossRef]
- Brnic, J.; Turkalj, G.; Canadija, M. Mechanical testing of the behavior of steel 1.7147 at different temperatures. Steel Compos. Struct. 2014, 17, 549. [Google Scholar] [CrossRef]
- Brnic, J.; Canadija, M.; Turkalj, G.; Krscanski, S.; Lanc, D.; Brcic, M.; Gao, Z. Short-time creep, fatigue and mechanical properties of 42CrMo4-low alloy structural steel. Steel Compos. Struct. 2016, 22, 875. [Google Scholar] [CrossRef]
- Krewerth, D.; Weidner, A.; Biermann, H. Investigation of the damage behavior of cast steel 42CrMo4 during ultrasonic fatigue by combination of thermography and fractography. Adv. Eng. Mater. 2013, 15, 1251–1259. [Google Scholar] [CrossRef]
- Torizuka, S.; Kuntz, M.; Furuya, Y.; Bacher-Hoechst, M. Effect of tensile strength and microstructure on notch-fatigue properties of ultrafine-grained steels. ISIJ Int. 2012, 52, 910. [Google Scholar] [CrossRef][Green Version]
- Pantazopoulos, G.A. Short review on fracture mechanisms of mechanical components operated under industrial process conditions: Fractographic analysis and selected prevention strategies. Metals 2019, 8, 148. [Google Scholar] [CrossRef]
- Mayer, H. Fatigue damage of low amplitude cycles in low carbon steel. J. Mater. Sci. 2009, 44, 4919. [Google Scholar] [CrossRef]
- Cai, Y.; Young, B. Experimental investigation of carbon steel and stainless steel bolted connections at different strain rates. Steel Compos. Struct. 2019, 30, 551. [Google Scholar] [CrossRef]
- Annual Book of ASTM Standards, Metals-Mechanical Testing; Elevated and Low-Temperature Tests; Metallography; ASTM International: Baltimore, MD, USA, 2015; Volume 03.01.
- ISO 12107:2012 (E) (2012), Metallic Materials—Fatigue Testing—Statistical Planning and Analysis of Data; ISO: Geneva, Switzerland, 2012.
- Rawlings, J.O.; Pantula, S.G.; Dickey, D.A. Applied Regression Analysis—A Research Tool, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1998; pp. 220–222. [Google Scholar]
- Horňák, P.; KyzioL, D.; Kyzioł, K.; Trebuňová, M.; Majerníková, J.; Kaczmarek, Ł.; Trebuňa, J.; Hašuľ, J.; Paľo, M. Microstructure and Mechanical Properties of Annealed WC/C PECVD Coatings Deposited Using Hexacarbonyl of W with Different Gases. Materials 2020, 13, 3576. [Google Scholar] [CrossRef]
- Huang, T.; Song, Z.; Chen, F.; Guo, J.; Pei, Y.; Xing, B.; Xiang, N.; Song, K. Influence of the anisotropy on the microstructure and mechanical properties of Ti/Al laminated composites. Materials 2020, 13, 3556. [Google Scholar] [CrossRef]
- Christopher, J.; Choudhary, B.K. Modeling creep deformation and damage behavior of tempered martensitic steel in the framework of additive creep rate formulation. J. Press. Vessel Technol. 2018, 140, 051401. [Google Scholar] [CrossRef]
- Li, C.Q.; Fu, G.; Yang, W.; Yang, S. Derivation of elastic fracture toughness for ductile metal pipes with circumferential external cracks under combined tension and bending. Eng. Fract. Mech. 2017, 178, 39–49. [Google Scholar] [CrossRef]
- Roberts, R.; Newton, C. Interpretive report on small-scale test correlation with KIc data. Weld. Res. Counc. Bull. 1981, 65, 1–16. [Google Scholar]
- Brnic, J.; Turkalj, G.; Lanc, D.; Canadija, M.; Brcic, M.; Vukelic, G. Comparison of material properties: Steel 20MnCr5 and similar steels, J. Constr. Steel Res. 2014, 95, 81–89. [Google Scholar] [CrossRef]
- Suresh, S. Fatigue of Materials, 2nd ed.; Cambridge University Press: Cambridge, UK, 2003; pp. 1–35. [Google Scholar]
- Brnic, J.; Krscanski, S.; Brcic, M.; Geng, L.; Niu, J.; Ding, B. Reliable experimental data as a key factor for design of mechanical structures. Struct. Eng. Mech. 2019, 72, 245–256. [Google Scholar] [CrossRef]
- Farahmand, B.; Bockrath, G.; Glassco, J. Fatigue and Fracture Mechanics of High Risk Parts; Chapman & Hall: New York, NY, USA, 1997; pp. 13–102. [Google Scholar]
- Barson, J.M.; Rolf, S.T. Fracture and Fatigue Control in Structures, 3rd ed.; Butterworth-Heinemann: Philadelphia, PA, USA, 1999; pp. 163–181. [Google Scholar]
- Feng, L.; Qian, X. Rapid S-N type life estimation for low cycle fatigue of high-strength steels at a low ambient temperature. Steel Compos. Struct. 2019, 33, 777–792. [Google Scholar] [CrossRef]
- Papuga, J.; Fojtík, F. Multiaxial fatigue strength of common structural steel and the response of some estimation methods. Int. J. Fatigue 2017, 104, 27–42. [Google Scholar] [CrossRef]
- Brnić, J.; Brčić, M.; Kršćanski, S.; Lanc, D.; Niu, J.; Wang, P. Steel 51CrV4 under high temperatures, short-time creep and high cycle fatigue. J. Constr. Steel Res. 2018, 147, 468–476. [Google Scholar] [CrossRef]
- Christou, G.; Hegger, J.; Classen, M. Fatigue of clothoid shaped rib shear connectors. J. Constr. Steel Res. 2020, 171, 106133. [Google Scholar] [CrossRef]


| Material: C15E + C Steel (Special Nonalloyed-Case Hardening Steel) | |||||||
|---|---|---|---|---|---|---|---|
| Designation | |||||||
| Steel name (type, grade, and quality)/i.e., letter mark of steel in accordance with the norm (country code): (EN, DIN, and other norms) | Steel number (Mat. No, W. Nr, and Mat. code)/i.e., numerical designation of steel | ||||||
| (EN)/(DIN): (10084 (2008))/(17210 (1986)): C15E/C15, Ck15 England/ BS 080M15; France/AFNOR XC15; USA/AISI-ESA 1015 In accordance with above given norms that define technical delivery conditions, this steel belongs to the material group classified (named) as case hardening nonalloy special steels, which is confirmed by the below given chemical composition. | 1.1141 | ||||||
| Chemical composition, Mass (%) | |||||||
| C | Si | Mn | P | S | Cr | Ni | |
| 0.135 | 0.233 | 0.38 | 0.01 | 0.009 | 0.084 | 0.06 | |
| Mo | Cu | Al | W | Sn | Rest | ||
| 0.019 | 0.027 | 0.035 | 0.006 | 0.007 | 98.99 | ||
| Material | C15E + C (1.1141) | |
|---|---|---|
| Time–Stress Dependence Model: ; | ||
| Equation | ||
| and Time (min) = 1200 | ||
| Creep processes were carried out at temperature and stresses listed below | ||
| Constant temperature/°C | 400 | |
| Applied constant stress level | 107 | 178.5 |
| Parameters (according to Equation) | Parameters valid for | |
| x = 0.3–0.5 | ||
| D | 1.21913163202914 | |
| p | 3.96411487762191 | |
| r | 0.686440947878887 | |
Failed (◆), Unfailed (○) | |||||||
|---|---|---|---|---|---|---|---|
| Stress max (MPa) | Specimen | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 270 | ♦ | ♦ | ♦ | ||||
| 260 | ♦ | ♦ | ○ | ||||
| 250 | ○ | ||||||
Room Temperature | ||||
|---|---|---|---|---|
| Stress /MPa | Stress level, i | fi | ifi | i2fi |
| 270 | 2 | 3 | 6 | 12 |
| 260 | 1 | 2 | 2 | 2 |
| 250 | 0 | 0 | 0 | 0 |
| 5 | 8 | 14 | ||
| Formula | Material: C15E + C (1.1141) |
| 8 | |
| 14 | |
| 5 | |
| 0.24 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brnic, J.; Brcic, M.; Krscanski, S.; Niu, J.; Chen, S.; Gao, Z. Deformation Behavior of C15E + C Steel under Different Uniaxial Stress Tests. Metals 2020, 10, 1445. https://doi.org/10.3390/met10111445
Brnic J, Brcic M, Krscanski S, Niu J, Chen S, Gao Z. Deformation Behavior of C15E + C Steel under Different Uniaxial Stress Tests. Metals. 2020; 10(11):1445. https://doi.org/10.3390/met10111445
Chicago/Turabian StyleBrnic, Josip, Marino Brcic, Sanjin Krscanski, Jitai Niu, Sijie Chen, and Zeng Gao. 2020. "Deformation Behavior of C15E + C Steel under Different Uniaxial Stress Tests" Metals 10, no. 11: 1445. https://doi.org/10.3390/met10111445
APA StyleBrnic, J., Brcic, M., Krscanski, S., Niu, J., Chen, S., & Gao, Z. (2020). Deformation Behavior of C15E + C Steel under Different Uniaxial Stress Tests. Metals, 10(11), 1445. https://doi.org/10.3390/met10111445


.JPG)




