Softening of Shear Elastic Coefficients in Shape Memory Alloys Near the Martensitic Transition: A Study by Laser-Based Resonant Ultrasound Spectroscopy
Abstract
:1. Introduction
2. Materials and Methods
- a Cu-Al-Ni single crystal (sample dimensions in austenite 3.05 × 2.03 × 1.29 mm , sample orientation in austenite approximately , mass density 6.78 g·cm ). This sample was characterized with cooling from 330 K towards the martensite start temperature (, 299 K). To discern sufficient details of the behavior near the transition temperature, the measurement was done with a 0.5 K step (temperature control ±0.01 K) and the internal friction parameter was evaluated at each temperature. Six lowest resonant modes were used for the determination of and the analysis of the internal friction;
- a Ni-Mn-Ga single crystal (sample dimensions in austenite 3.41 × 2.80 × 0.92 mm at 335 K, sample orientation in austenite approximately , mass density 8.12 g·cm ). This sample was characterized with cooling from above the Curie temperature (, 372 K) towards K, where the sample transformed into 10 M modulated martensite [26] (a thermally induced mixture of variants). Afterwards, an external magnetic field was used for martensite reorientation [27,28], and the sample was set in a single (tetragonal) variant state with the axis that was oriented along the shortest edge. Note that the 10 M martensite is slightly monoclinic, so this state was still a mixture of monoclinic variants sharing a common axis, but such a microstructure can be understood as a single variant in the tetragonal approximation [29]. The sample in this condition was then characterized with heating from 289 K until the sample transformed back to austenite (austenite start temperature, ). This procedure was repeated second time, with the axis set along the longest edge of the sample. For the sample in austenite, ten lowest resonant modes were used for determination. However, for temperatures that were below , the strong internal friction in 10 M martensite did not allow for reliable detection and identification of more than two or three resonant modes. This was insufficient for the reliable determination of any of the elastic coefficients of the (effectively tetragonal) mixture of monoclinic martensites. Hence, instead, we analyzed the RUS data assuming again cubic symmetry, which resulted in some effective for the martensite. Although this effective elastic constant has no direct relation to any shearing mode of the 10 M modulated lattice, its temperature evolution provides a qualitative information on the shear instability in martensite (see e.g., [30,31] for similar approaches);
- another Ni-Mn-Ga single crystal (dimensions in martensite 4.92 × 4.65 × 3.40 mm , sample orientation approximately for the dominant variant, mass density 8.12 g·cm ). At the room temperature, this sample was in tetragonal non-modulated (NM) martensite phase, consisting of a mixture of all three variants with one orientation being dominant. The sample was characterized with heating from the room temperature over the reverse transition temperature K. In this case, the temperature was above the Curie point (373 K), i.e., the transition occurred in the paramagnetic state. Similarly as in the case of sample No.2, an effective coefficient was used for characterizing the shear softening in non-modulated martensite below ; and,
- a Ni-Ti sample (sample dimensions in austenite 3.48 × 3.16 × 2.78 mm , sample orientation in austenite approximately , mass density 6.50 g·cm ). This sample was characterized with cooling from 293 K towards the vicinity of the austenite→R-phase transition temperature K. Twenty lowest resonant modes were traced in the measured temperature interval. Unlike samples Nos. 1, 2, and 3, the Ni-Ti sample was heterogeneous, consisting of a Ni-Ti matrix with finely dispersed precipitates. This means that the observed behavior (the elastic constants, the transformation temperatures, etc.) resulted from an interplay between the lattice (phonon mediated) instability of the matrix and the local stress fields that come from the precipitates. The discussion of such phenomena falls beyond the scope of this paper; here we will treat the measured elastic coefficients and their temperature dependencies as sufficiently representing the studied material at the macro-scale.
3. Results and Discussion
3.1. Cu-Al-Ni
3.2. Ni-Mn-Ga
3.3. Ni-Ti
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Delaey, L. Diffusionless transformations. In Phase Transformations in Materials; Kostorz, G., Ed.; Wiley-VCH: Weinheim, Germany, 2001; pp. 583–654. [Google Scholar]
- Nakanishi, N. Elastic constants as they relate to lattice properties and martensite formation. Prog. Mater. Sci. 1980, 24, 143–265. [Google Scholar] [CrossRef]
- Lüthi, B. Physical Acoustics in the Solid State; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Otsuka, K.; Ren, X. Physical metallurgy of Ti-Ni-based shape memory alloys. Prog. Mater. Sci. 2005, 50, 511–678. [Google Scholar] [CrossRef]
- Chernenko, V.A.; Pons, J.; Seguí, C.; Cesari, E. Premartensitic phenomena and other phase transformations in Ni-Mn-Ga alloys studied by dynamical mechanical analysis and electron diffraction. Acta Mater. 2002, 50, 53–60. [Google Scholar] [CrossRef]
- Muto, S.; Oshima, R.; Fujita, F.E. Elastic softening and elastic strain energy consideration in the f.c.c.-f.c.t. transformation of FePd alloys. Acta Metall. Mater. 1990, 38, 685–694. [Google Scholar] [CrossRef]
- Stipcich, M.; Mañosa, L.; Planes, A.; Morin, M.; Zarestky, J.; Lograsso, T.; Stassis, C. Elastic constants of Ni-Mn-Ga magnetic shape memory alloys. Phys. Rev. B Condens. Matter Mater. Phys. 2004, 70, 054115. [Google Scholar] [CrossRef] [Green Version]
- Worgull, J.; Petti, E.; Trivisonno, J. Behavior of the elastic properties near an intermediate phase transition in Ni2MnGa. Phys. Rev. B Condens. Matter Mater. Phys. 1996, 54, 15695–15699. [Google Scholar] [CrossRef]
- Musgrave, M.J.P. Crystal Acoustics; Holden Day: San Francisco, CA, USA, 1965. [Google Scholar]
- Ledbetter, H.M. Sound velocities and elastic-constant averaging for polycrystalline copper. J. Phys. D Appl. Phys. 1980, 13, 1879–1884. [Google Scholar] [CrossRef]
- Seiner, H.; Kopeček, J.; Sedlák, P.; Bodnárová, L.; Landa, M.; Sedmák, P.; Heczko, O. Microstructure, martensitic transformation and anomalies in c′-softening in Co-Ni-Al ferromagnetic shape memory alloys. Acta Mater. 2013, 61, 5869–5876. [Google Scholar] [CrossRef]
- Zoubková, K. Elastic Response of Ferromagnetic Shape Memory Alloys in the Vicinity of the Critical Point. Master’s Thesis, Czech Technical University, Prague, Czech Republic, 2018. [Google Scholar]
- Papadakis, E.P.; Lerch, T.P. Pulse superposition, pulse-echo overlap and related techniques. In Handbook of Elastic Properties of Solids, Liquids and Gases, 1–4; Levy, M., Bass, H., Stern, R., Eds.; Academic Press: San Diego, CA, USA, 2001; pp. 39–66. [Google Scholar]
- Migliori, A.; Sarrao, J.L.; Visscher, W.M.; Bell, T.M.; Lei, M.; Fisk, Z.; Leisure, R.G. Resonant ultrasound spectroscopic techniques for measurement of the elastic moduli of solids. Phys. B Phys. Condens. Matter 1993, 183, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Leisure, R.G.; Willis, F.A. Resonant ultrasound spectroscopy. J. Phys. Condens. Matter 1997, 9, 6001–6029. [Google Scholar] [CrossRef]
- Hirao, M.; Ogi, H. EMATs for Science and Industry: Noncontacting Ultrasonic Measurements; Kluwer Academic Publishers: London, UK, 2003. [Google Scholar]
- Vasil’ev, A.N.; Kokorin, V.V.; Savchenko, Y.I.; Chernenko, V.A. The magnetoelastic properties of a Ni2MnGa single crystal. Sov. Phys. JETP 1990, 71, 803–805. [Google Scholar]
- Landa, M.; Sedlák, P.; Seiner, H.; Heller, L.; Bicanová, L.; Šittner, P.; Novák, V. Modal resonant ultrasound spectroscopy for ferroelastics. Appl. Phys. A Mater. Sci. Process. 2009, 96, 557–567. [Google Scholar] [CrossRef]
- Hurley, D.H.; Reese, S.J.; Park, S.K.; Utegulov, Z.; Kennedy, J.R.; Telschow, K.L. In situ laser-based resonant ultrasound measurements of microstructure mediated mechanical property evolution. J. Appl. Phys. 2010, 107, 063510. [Google Scholar] [CrossRef] [Green Version]
- Wolfe, J.P. Imaging Phonons (Acoustic Wave Propagation in Solids); Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Sedlák, P.; Seiner, H.; Zídek, J.; Janovská, M.; Landa, M. Determination of All 21 Independent Elastic Coefficients of Generally Anisotropic Solids by Resonant Ultrasound Spectroscopy: Benchmark Examples. Exp. Mech. 2014, 54, 1073–1085. [Google Scholar] [CrossRef]
- Sato, S.; Inakagi, K.; Gusev, V.E.; Wright, O.B. Resonant ultrasound spectroscopy using optical excitation and detection. AIP Conf. Proc. 1999, 463, 424–426. [Google Scholar]
- Zadler, B.J.; Le Rousseau, J.H.L.; Scales, J.A.; Smith, M.L. Resonant ultrasound spectroscopy: Theory and application. Geophys. J. Int. 2004, 156, 154–169. [Google Scholar] [CrossRef]
- Sumino, Y.; Ohno, I.; Goto, T.; Kumazawa, M. Measurement of elastic constants and internal frictions on single-crystal mgo by rectangular parallelepiped resonance. J. Phys. Earth 1976, 24, 263–273. [Google Scholar] [CrossRef] [Green Version]
- Seiner, H.; Sedlák, P.; Koller, M.; Landa, M.; Ramírez, C.; Osendi, M.I.; Belmonte, M. Anisotropic elastic moduli and internal friction of graphene nanoplatelets/silicon nitride composites. Compos. Sci. Technol. 2013, 75, 93–97. [Google Scholar] [CrossRef]
- Straka, L.; Drahokoupil, J.; Pacherová, O.; Fabiánová, K.; Kopecký, V.; Seiner, H.; Hänninen, H.; Heczko, O. The relation between lattice parameters and very low twinning stress in Ni50Mn25+xGa25-x magnetic shape memory alloys. Smart Mater. Struct. 2016, 25, 025001. [Google Scholar] [CrossRef] [Green Version]
- Sozinov, A.; Likhachev, A.A.; Lanska, N.; Söderberg, O.; Ullakko, K.; Lindroos, V.K. Stress- and magnetic-field-induced variant rearrangement in Ni-Mn-Ga single crystals with seven-layered martensitic structure. Mater. Sci. Eng. A 2004, 378, 399–402. [Google Scholar] [CrossRef]
- Scheerbaum, N.; Heczko, O.; Liu, J.; Hinz, D.; Schultz, L.; Gutfleisch, O. Magnetic field-induced twin boundary motion in polycrystalline Ni-Mn-Ga fibres. New J. Phys. 2008, 10, 073002. [Google Scholar] [CrossRef] [Green Version]
- Straka, L.; Heczko, O.; Seiner, H.; Lanska, N.; Drahokoupil, J.; Soroka, A.; Fähler, S.; Hänninen, H.; Sozinov, A. Highly mobile twinned interface in 10 M modulated Ni-Mn-Ga martensite: Analysis beyond the tetragonal approximation of lattice. Acta Mater. 2011, 59, 7450–7463. [Google Scholar] [CrossRef]
- Zhao, P.; Dai, L.; Cullen, J.; Wuttig, M. Magnetic and elastic properties of Ni49.0Mn23.5 Ga27.5 premartensite. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2007, 38, 745–751. [Google Scholar] [CrossRef]
- Dai, L.; Cui, J.; Wuttig, M. Elasticity of Austenitic and Martensitic NiMnGa. Proc. SPIE Int. Soc. Opt. Eng. 2003, 5053, 595–602. [Google Scholar]
- Ogi, H.; Sato, K.; Asada, T.; Hirao, M. Complete mode identification for resonance ultrasound spectroscopy. J. Acoust. Soc. Am. 2002, 112, 2553–2557. [Google Scholar] [CrossRef]
- Recarte, V.; Pérez-Landazábal, J.I.; Nó, M.L.; San Juan, J. Study by resonant ultrasound spectroscopy of the elastic constants of the β phase in Cu-Al-Ni shape memory alloys. Mater. Sci. Eng. A 2004, 370, 488–491. [Google Scholar] [CrossRef]
- Landa, M.; Sedlák, P.; Šittner, P.; Seiner, H.; Heller, L. On the evaluation of temperature dependence of elastic constants of martensitic phases in shape memory alloys from resonant ultrasound spectroscopy studies. Mater. Sci. Eng. A 2008, 481–482, 567–573. [Google Scholar] [CrossRef]
- Landa, M.; Sedlák, P.; Šittner, P.; Seiner, H.; Novák, V. Temperature dependence of elastic properties of cubic and orthorhombic phases in Cu-Al-Ni shape memory alloy near their stability limits. Mater. Sci. Eng. A 2007, 462, 320–324. [Google Scholar] [CrossRef]
- Sugimoto, K.; Mori, T.; Otsuka, K.; Shimizu, K. Simultaneous measurements of internal friction, young’s modulus and shape change associated with thermoelastic martensite transformation in CuAlNi single crystals. Scr. Metall. 1974, 8, 1341–1348. [Google Scholar] [CrossRef]
- Sedlák, P.; Seiner, H.; Landa, M.; Novák, V.; Šittner, P.; Mañosa, L. Elastic constants of bcc austenite and 2H orthorhombic martensite in CuAlNi shape memory alloy. Acta Mater. 2005, 53, 3643–3661. [Google Scholar] [CrossRef]
- Seiner, H.; Sedlak, P.; Landa, M. Shape recovery mechanism observed in single crystals of Cu-Al-Ni shape memory alloy. Phase Transitions 2008, 81, 537–551. [Google Scholar] [CrossRef]
- Vronka, M.; Seiner, H.; Heczko, O. Temperature dependence of twinning stress–Analogy between Cu–Ni–Al and Ni–Mn–Ga shape memory single crystals. Philos. Mag. 2017, 97, 1479–1497. [Google Scholar] [CrossRef]
- Seiner, H.; Heczko, O.; Sedlák, P.; Bodnárová, L.; Novotný, M.; Kopeček, J.; Landa, M. Combined effect of structural softening and magneto-elastic coupling on elastic coefficients of NiMnGa austenite. J. Alloy. Compd. 2013, 577, S131–S135. [Google Scholar] [CrossRef]
- Seiner, H.; Sedlák, P.; Bodnárová, L.; Drahokoupil, J.; Kopecký, V.; Kopeček, J.; Landa, M.; Heczko, O. The effect of antiphase boundaries on the elastic properties of Ni-Mn-Ga austenite and premartensite. J. Phys. Condens. Matter 2013, 25, 425402. [Google Scholar] [CrossRef] [PubMed]
- Söderberg, O.; Straka, L.; Novák, V.; Heczko, O.; Hannula, S.-P.; Lindroos, V.K. Tensile/compressive behaviour of non-layered tetragonal Ni52.8Mn25.7Ga21.5 alloy. Mater. Sci. Eng. A 2004, 386, 27–33. [Google Scholar] [CrossRef]
- Sozinov, A.; Lanska, N.; Soroka, A.; Zou, W. 12% magnetic field-induced strain in Ni-Mn-Ga-based non-modulated martensite. Appl. Phys. Lett. 2013, 102, 021902. [Google Scholar] [CrossRef]
- Bodnárová, L.; Zelený, M.; Sedlák, P.; Straka, L.; Heczko, O.; Sozinov, A.; Seiner, H. Switching the soft shearing mode orientation in Ni-Mn-Ga non-modulated martensite by Co and Cu doping. Smart Mater. Struct. 2020, 29, 045022. [Google Scholar] [CrossRef]
- Heczko, O.; Seiner, H.; Sedlák, P.; Kopeček, J.; Kopecký, V.; Landa, M. Resonant ultrasound spectroscopy—A tool to probe magneto-elastic properties of ferromagnetic shape memory alloys. Eur. Phys. J. B 2013, 86, 62. [Google Scholar] [CrossRef]
- James, R.D.; Zhang, Z. A Way to Search for Multiferroic Materials with “Unlikely” Combinations of Physical Properties. Springer Ser. Mater. Sci. 2005, 79, 159–175. [Google Scholar]
- Cui, J.; Chu, Y.S.; Famodu, O.O.; Furuya, Y.; Hattrick-Simpers, J.; James, R.D.; Ludwig, A.; Thienhaus, S.; Wuttig, M.; Zhang, Z.; et al. Combinatorial search of thermoelastic shape-memory alloys with extremely small hysteresis width. Nat. Mater. 2006, 5, 286–290. [Google Scholar] [CrossRef]
- Seiner, H.; Kopecký, V.; Landa, M.; Heczko, O. Elasticity and magnetism of Ni2MnGa premartensitic tweed. Phys. Status Solidi (B) Basic Res. 2014, 251, 2097–2103. [Google Scholar] [CrossRef]
- Ren, X.; Miura, N.; Zhang, J.; Otsuka, K.; Tanaka, K.; Koiwa, M.; Suzuki, T.; Chumlyakov, Y.I.; Asai, M. A comparative study of elastic constants of Ti-Ni based alloys prior to martensitic transformation. Mater. Sci. Eng. A 2001, 312, 196–206. [Google Scholar] [CrossRef]
- Brill, T.M.; Mittelbach, S.; Assmus, W.; Mullner, M.; Luthi, B. Elastic properties of NiTi. J. Phys. Condens. Matter 1991, 3, 9621–9627. [Google Scholar] [CrossRef]
- Mercier, O.; Melton, K.N.; Gremaud, G.; Hägi, J. Single-crystal elastic constants of the equiatomic NiTi alloy near the martensitic transformation. J. Appl. Phys. 1980, 51, 1833–1834. [Google Scholar] [CrossRef]
- Ren, X.; Otsuka, K. The role of softening in elastic constant c44 in martensitic transformation. Scr. Mater. 1998, 38, 1669–1675. [Google Scholar] [CrossRef]
- Šittner, P.; Landa, M.; Lukáš, P.; Novák, V. R-phase transformation phenomena in thermomechanically loaded NiTi polycrystals. Mech. Mater. 2006, 38, 475–492. [Google Scholar] [CrossRef]
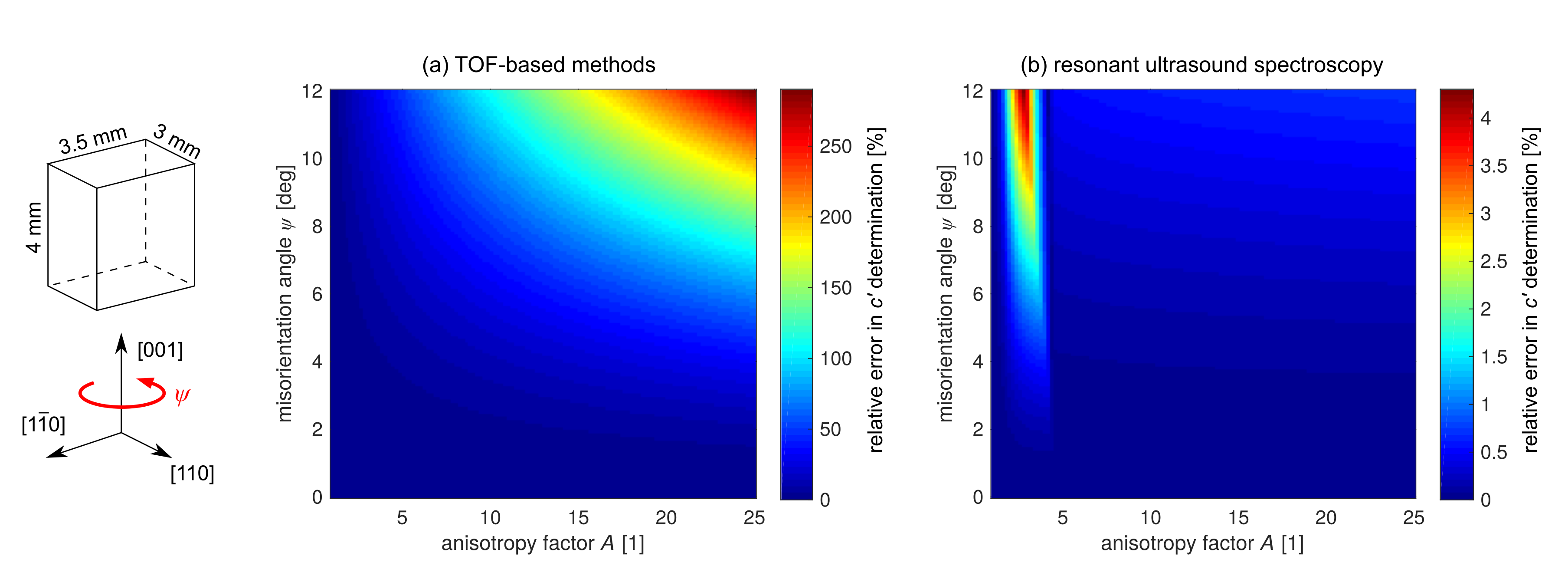
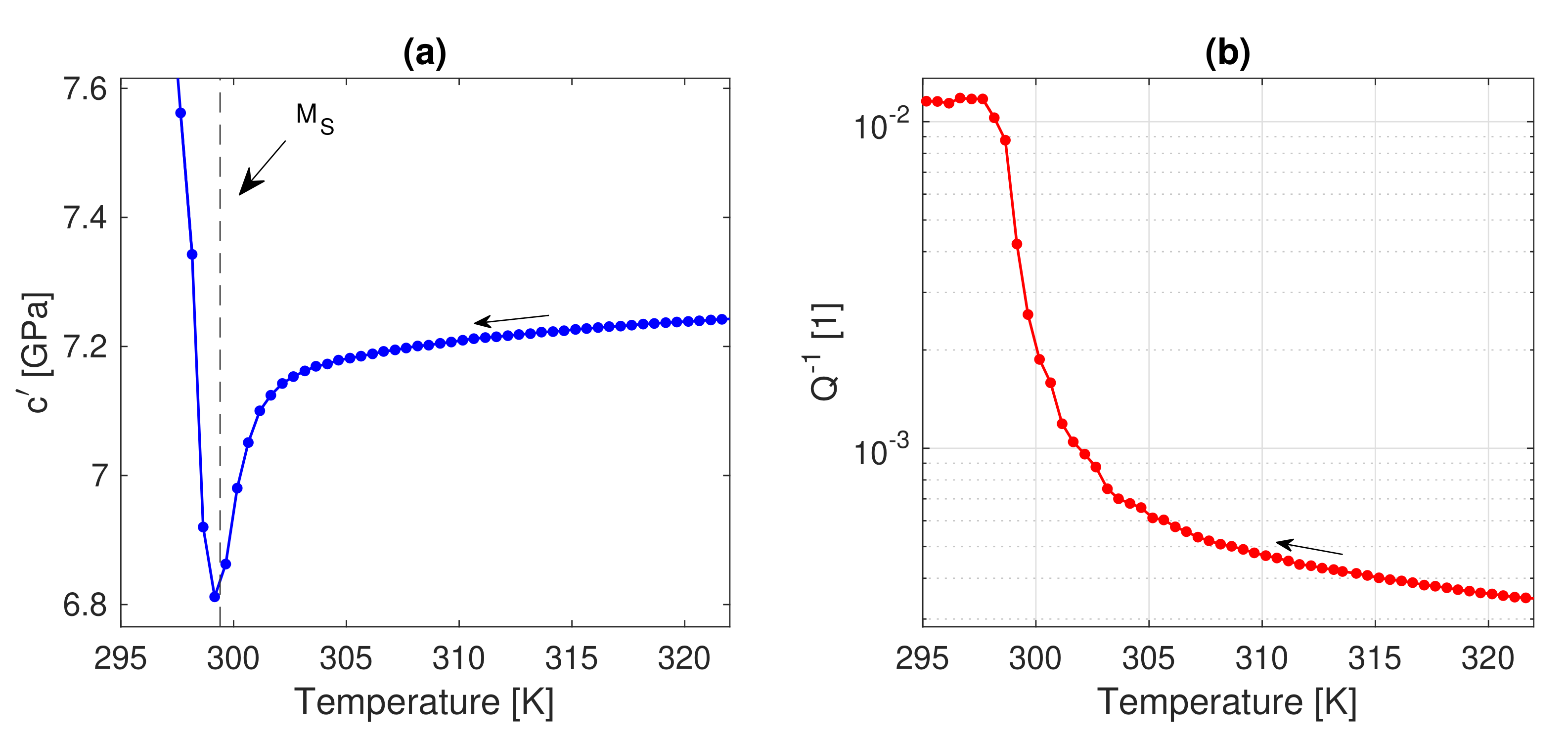
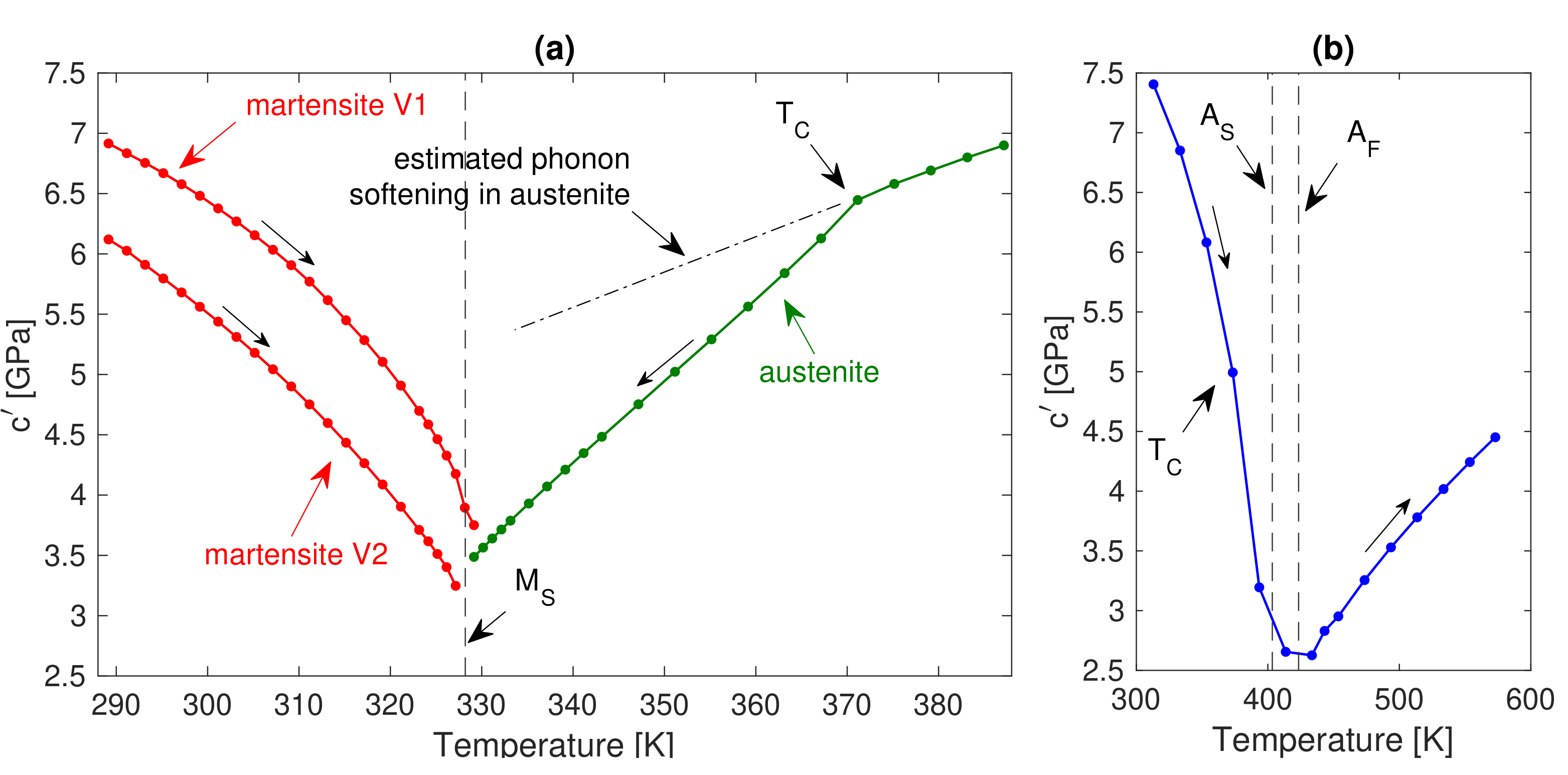
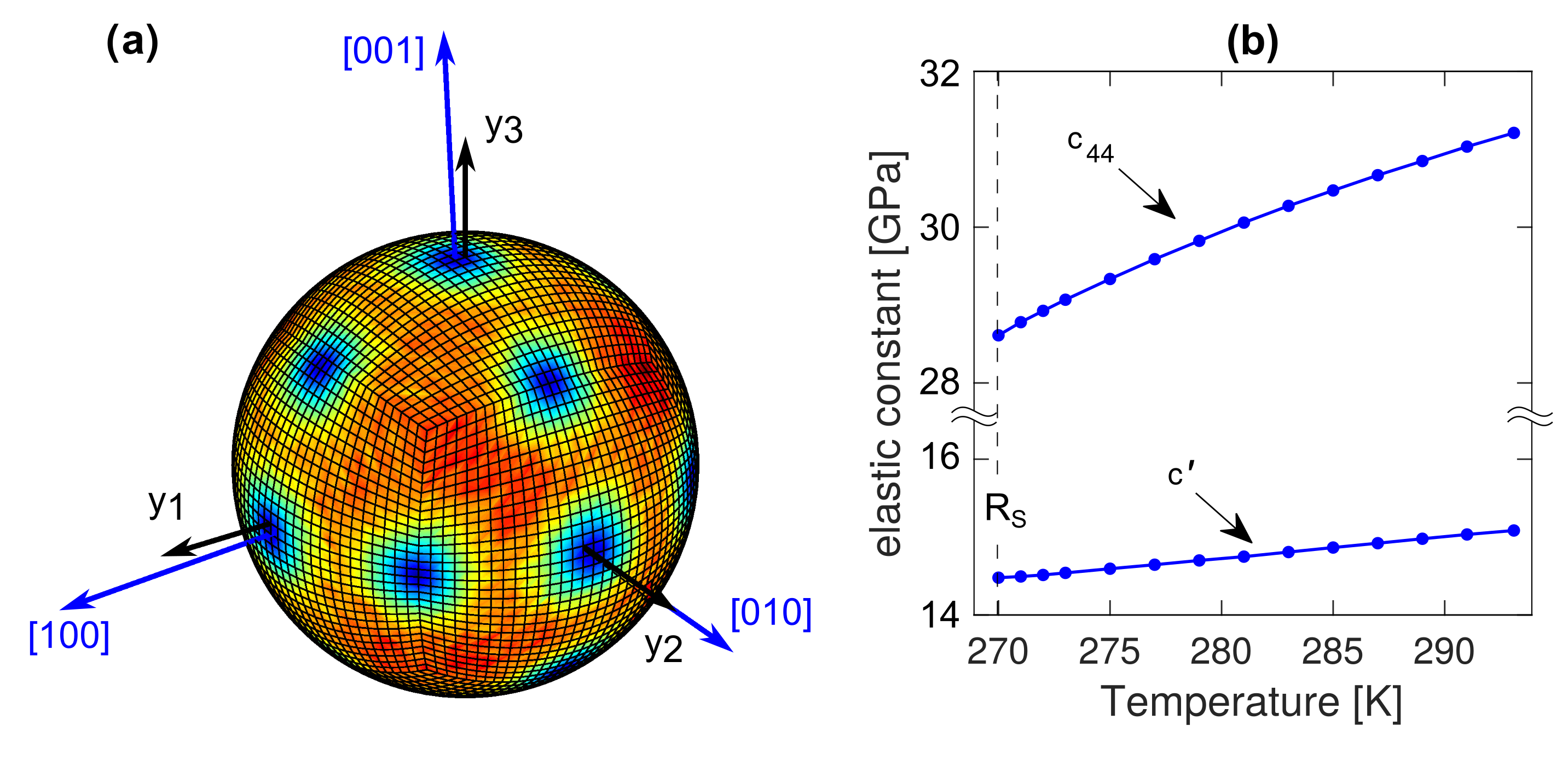
| Sample No. | Alloy | Composition (at.%) | [K] | [K] | [K] | [K] | [K] | [K] |
|---|---|---|---|---|---|---|---|---|
| 1 | Cu-Al-Ni | Cu Al Ni | 395 | 314 | 299 | 284 | - | - |
| 2 | Ni-Mn-Ga | Ni Mn Ga | 328 | 329 | 328 | 326 | - | - |
| 3 | Ni-Mn-Ga | Ni Mn Ga | 400 | 420 | - | - | - | - |
| 4 | Ni-Ti | multiphase | 240 | 286 | 232 | 226 | ∼270 | 245 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sedlák, P.; Janovská, M.; Bodnárová, L.; Heczko, O.; Seiner, H. Softening of Shear Elastic Coefficients in Shape Memory Alloys Near the Martensitic Transition: A Study by Laser-Based Resonant Ultrasound Spectroscopy. Metals 2020, 10, 1383. https://doi.org/10.3390/met10101383
Sedlák P, Janovská M, Bodnárová L, Heczko O, Seiner H. Softening of Shear Elastic Coefficients in Shape Memory Alloys Near the Martensitic Transition: A Study by Laser-Based Resonant Ultrasound Spectroscopy. Metals. 2020; 10(10):1383. https://doi.org/10.3390/met10101383
Chicago/Turabian StyleSedlák, Petr, Michaela Janovská, Lucie Bodnárová, Oleg Heczko, and Hanuš Seiner. 2020. "Softening of Shear Elastic Coefficients in Shape Memory Alloys Near the Martensitic Transition: A Study by Laser-Based Resonant Ultrasound Spectroscopy" Metals 10, no. 10: 1383. https://doi.org/10.3390/met10101383
APA StyleSedlák, P., Janovská, M., Bodnárová, L., Heczko, O., & Seiner, H. (2020). Softening of Shear Elastic Coefficients in Shape Memory Alloys Near the Martensitic Transition: A Study by Laser-Based Resonant Ultrasound Spectroscopy. Metals, 10(10), 1383. https://doi.org/10.3390/met10101383





