Magnetic Properties in Finemet-Type Soft Magnetic Toroidal Cores Annealed under Radial Stresses
Abstract
1. Introduction
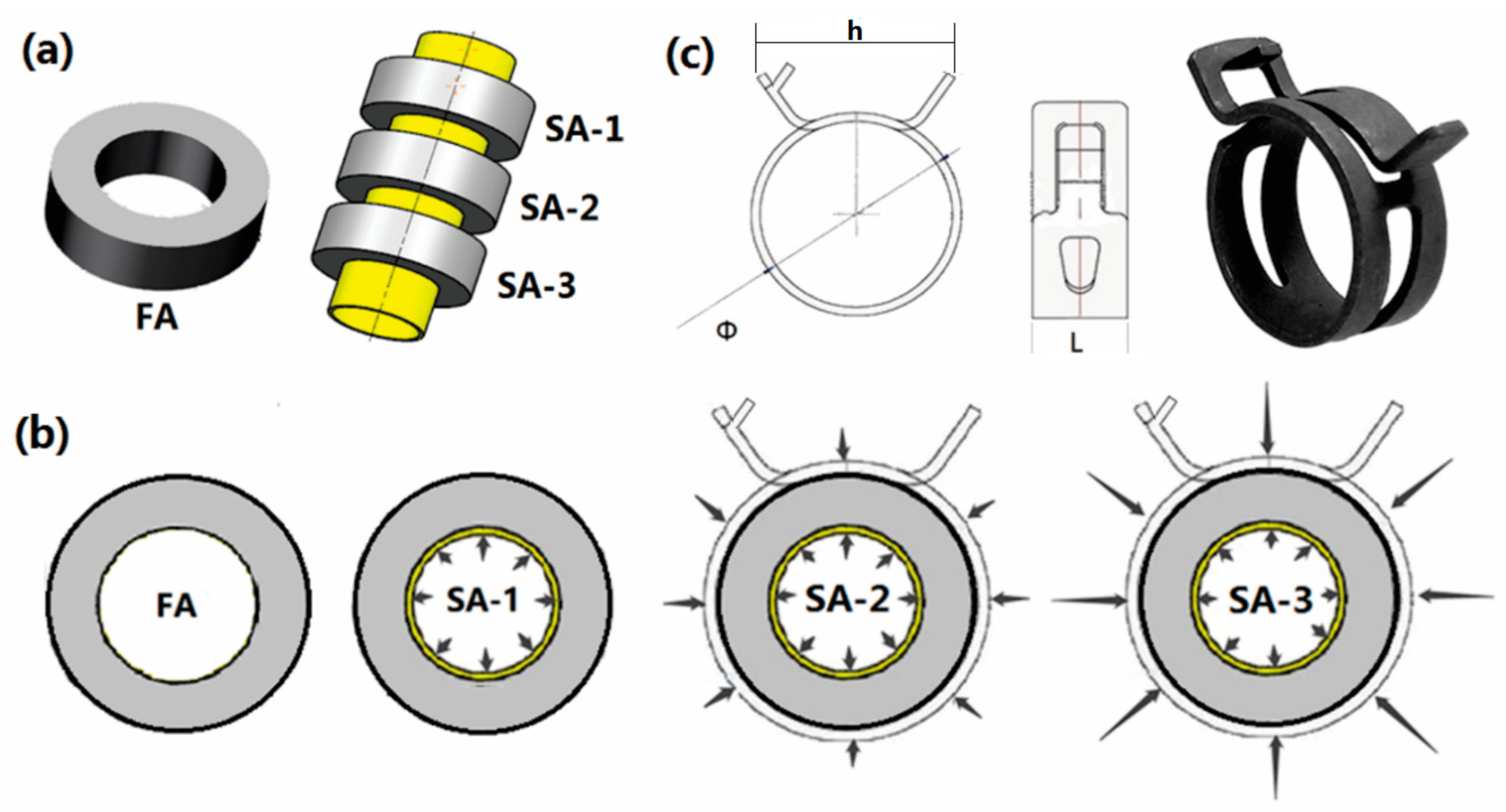
2. Material and Methods
3. Result and Discussion
3.1. Analysis of Strain in Stress-Annealed Samples
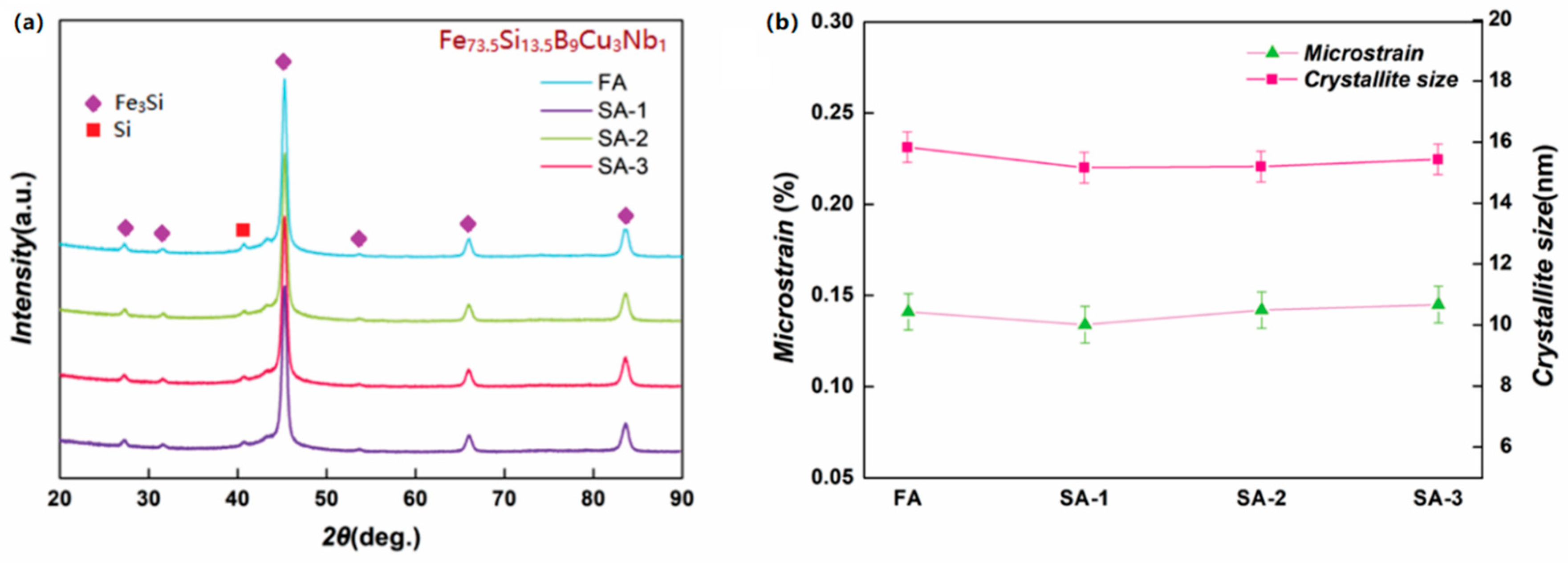
3.2. Structural Characterizations
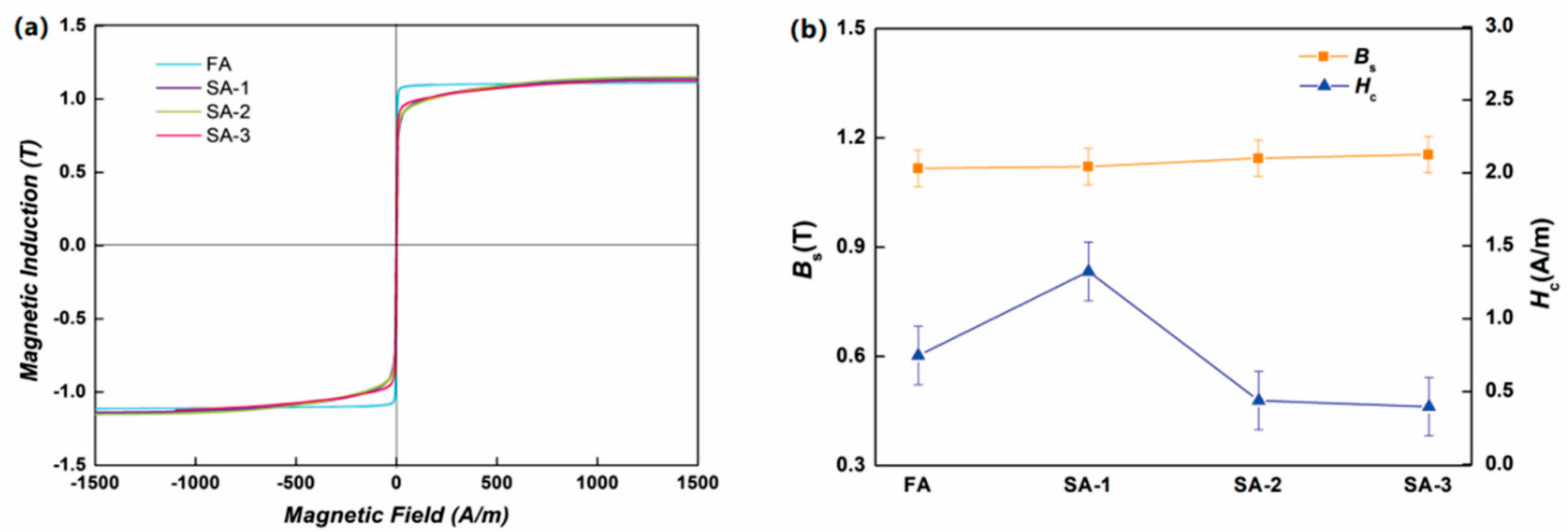
3.3. DC B–H Hysteresis Loops
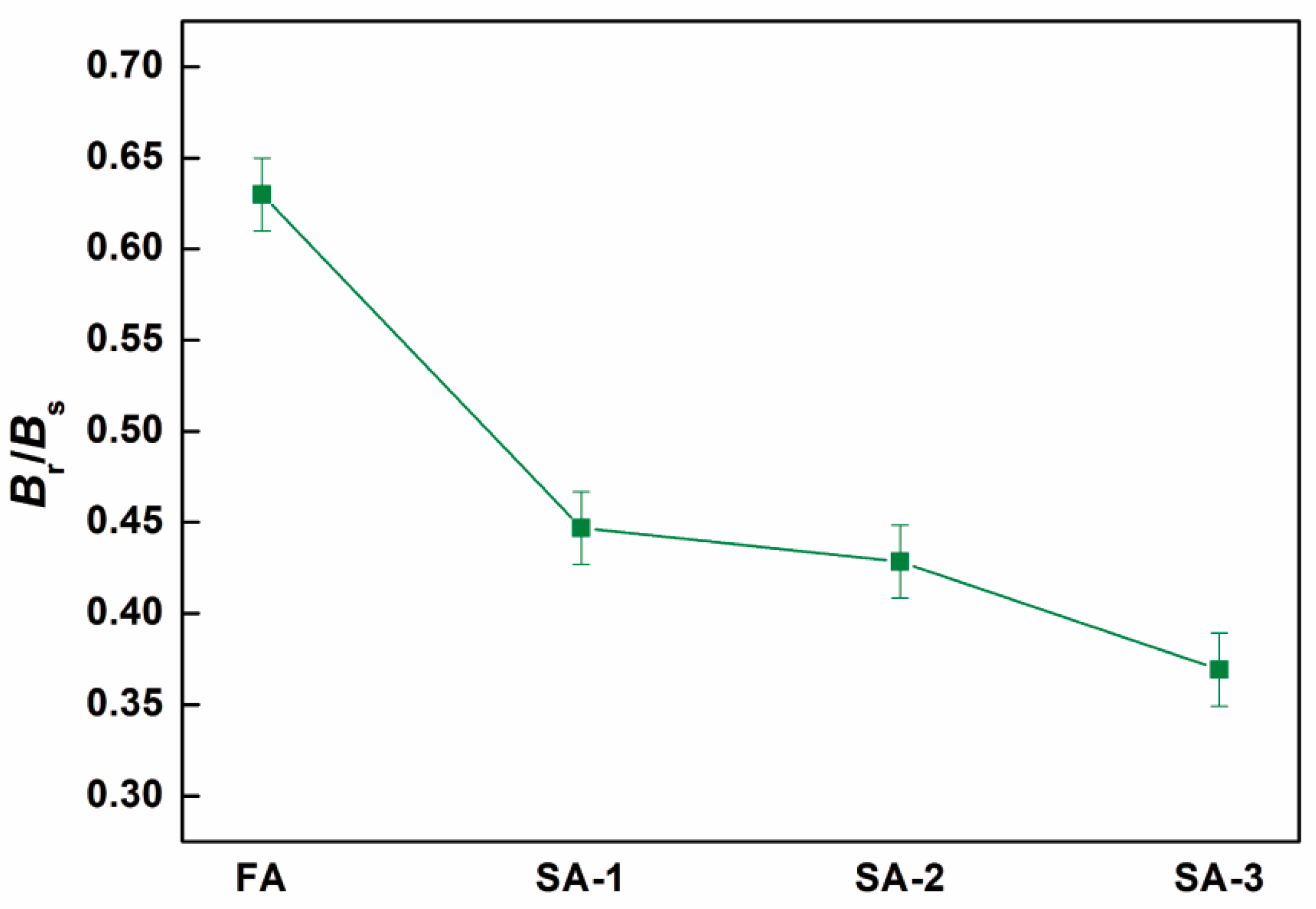
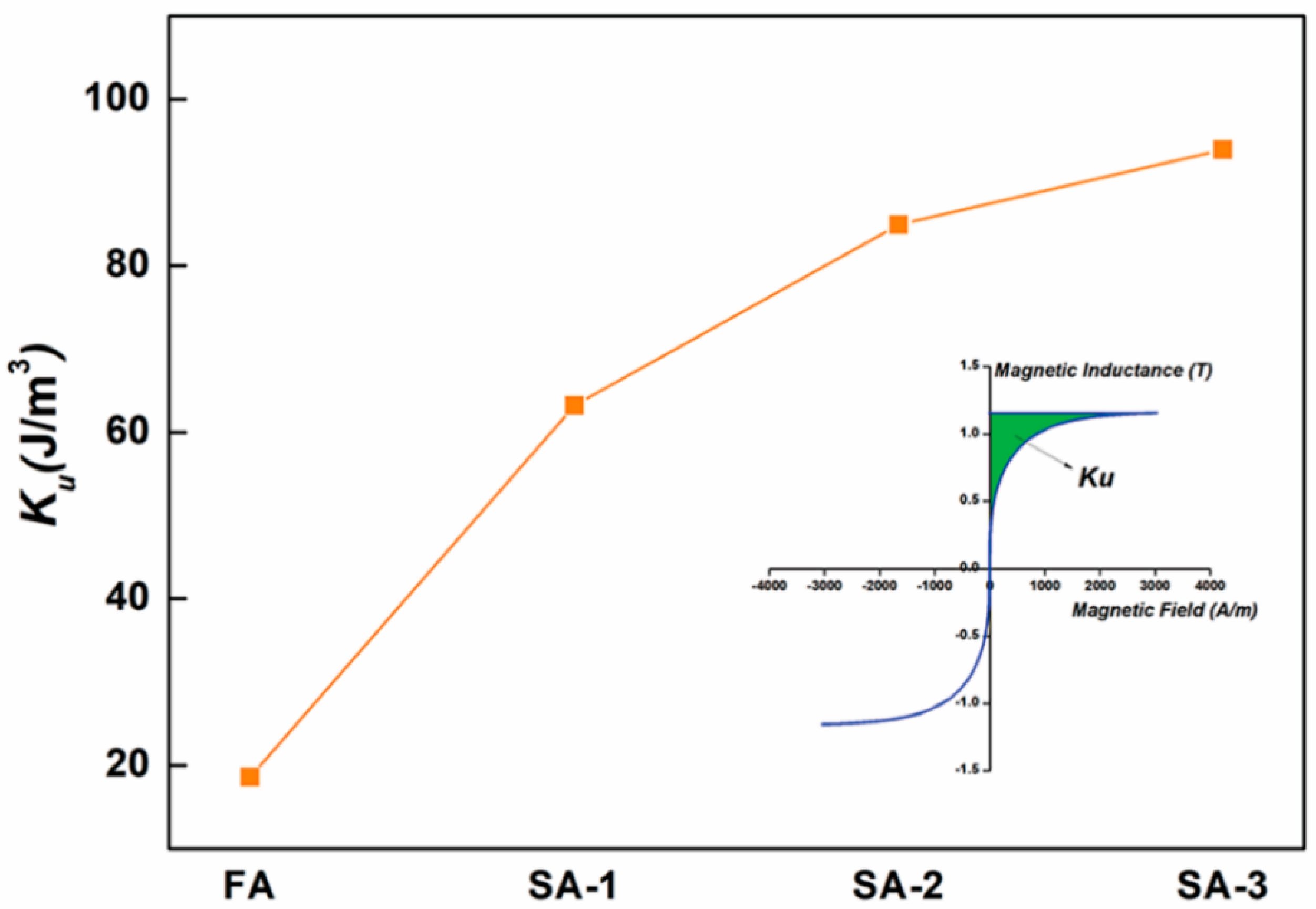
3.4. Induced Anisotropy
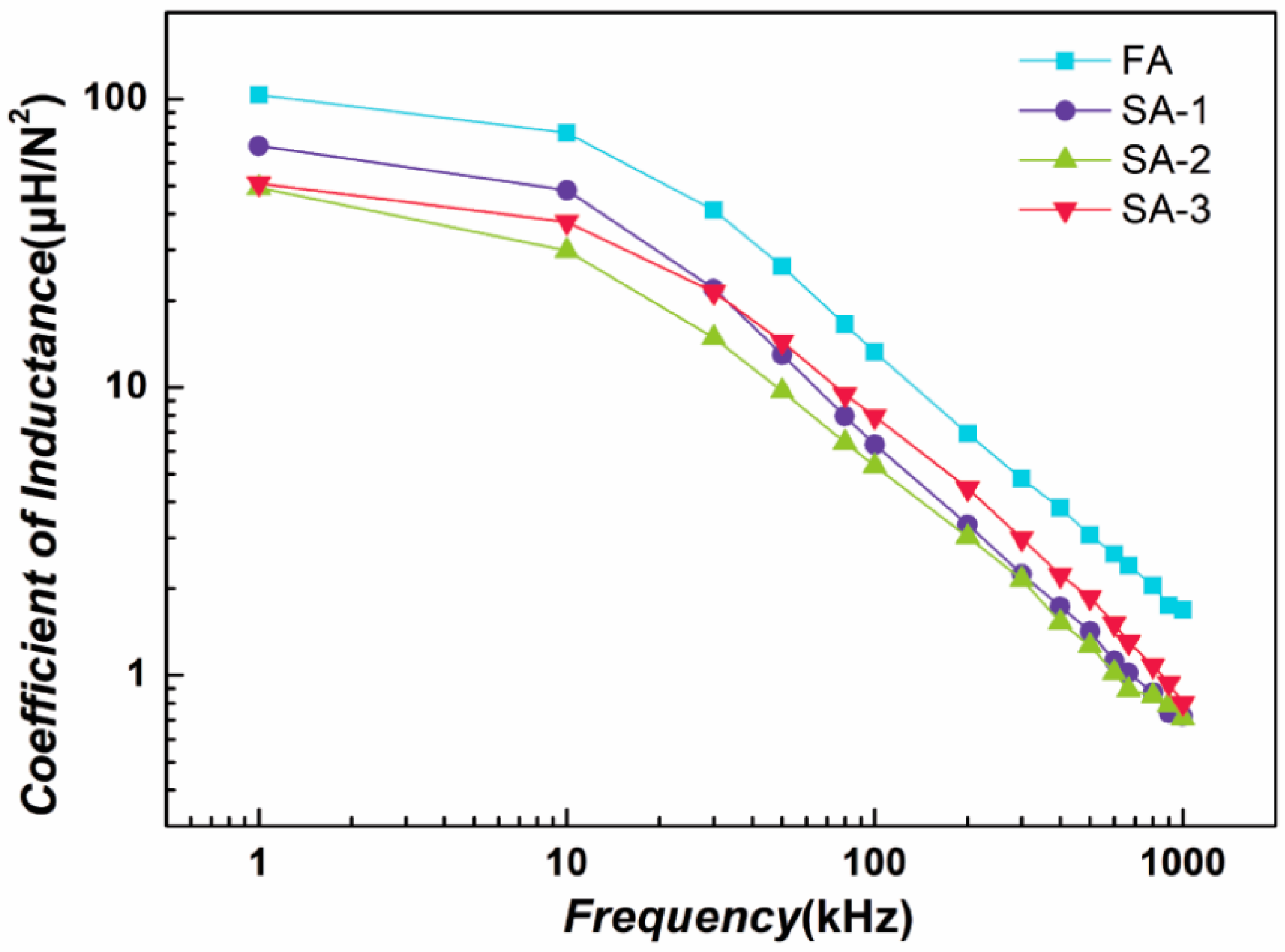
3.5. Coefficient of Inductance (Effective Permeability)
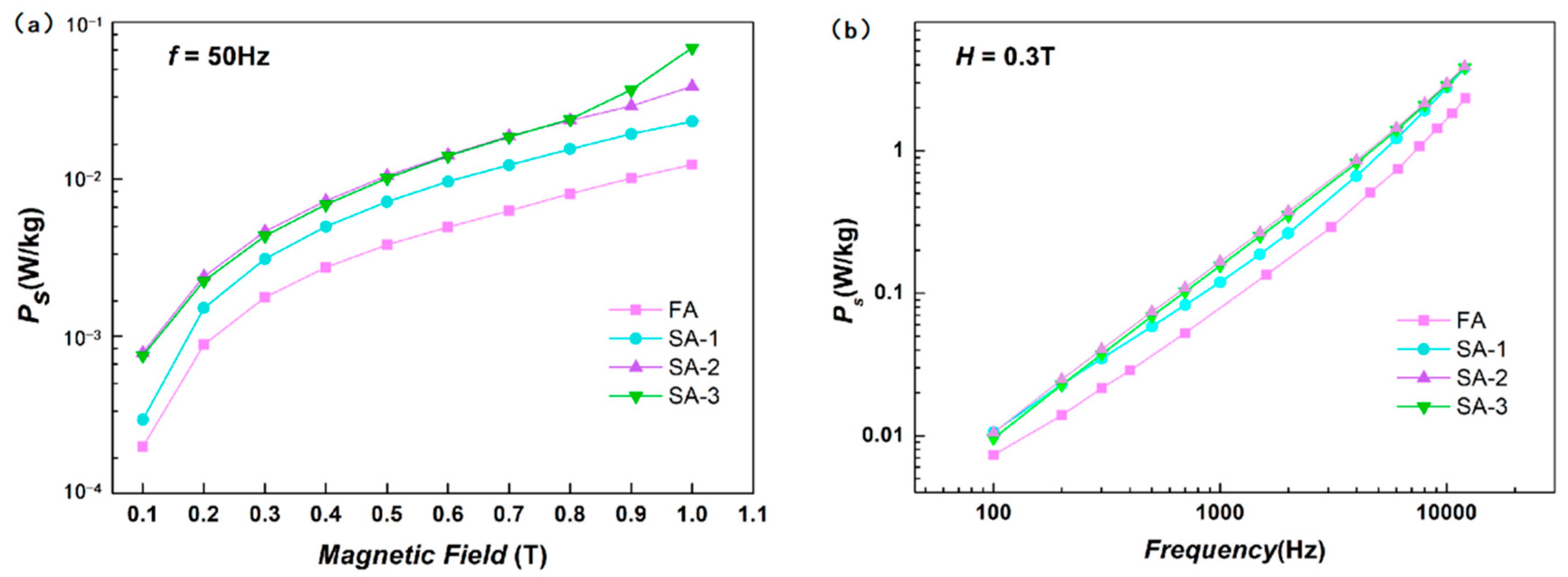
3.6. Core Losses in Treated Samples
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Willard, M.A.; Daniil, M. Nanocrystalline Soft Magnetic Alloys Two Decades of Progress. In Handbook of Magnetic Materials; Buschow, K.H.J., Ed.; Elsevier: Amsterdam, The Netherlands, 2013; Volume 21, pp. 173–342. [Google Scholar]
- Huang, B.; Yang, Y.; Wang, A.D.; Wang, Q.; Liu, C.T. Saturated magnetization and glass forming ability of soft magnetic Fe-based metallic glasses. Intermetallics 2017, 84, 74–81. [Google Scholar] [CrossRef]
- Inoue, A.; Shen, B. Soft magnetic bulk glassy Fe-B-Si-Nb alloys with high saturation magnetization above 1.5T. Mater. Trans. 2002, 42, 766–769. [Google Scholar] [CrossRef]
- Wang, F.; Inoue, A.; Han, Y.; Kong, F.L.; Zhu, S.L.; Shalaan, E. Excellent soft magnetic Fe-Co-B-based amorphous alloys with extremely high saturation magnetization above 1.85 T and low coercivity below 3 A/m. J. Alloy. Compd. 2017, 711, 132–142. [Google Scholar] [CrossRef]
- Luborsky, F.; Becker, J.; Walter, J.; Martin, D. The Fe-B-C ternary amorphous alloy. IEEE Trans. Magn. 1980, 166, 521–525. [Google Scholar] [CrossRef]
- Hasegawa, R. Advances in amorphous and nanocrystalline magnetic materials. J. Magn. Magn. Mater. 2006, 304, 187–191. [Google Scholar] [CrossRef]
- Willard, M.R.; Daniil, M. Nanostructured soft magnetic materials. In Nanoscale Magnetic Materials and Applications; Liu, J.P., Fullerton, E., Gutfleisch, O., Sellmyer, D.J., Eds.; Springer Science: New York, NY, USA, 2009. [Google Scholar]
- McHenry, M.E.; Willard, M.A.; Laughlin, D.E. Amorphous and nanocrystalline materials for applications as soft magnets. Prog. Mater. Sci. 1999, 44, 291–433. [Google Scholar] [CrossRef]
- Ramin, D.; Riehemann, W. Dependence of magnetic properties of finemet on nanocrystallisation conditions. Nanostruct. Mater. 1999, 12, 867–869. [Google Scholar] [CrossRef]
- Ito, N.; Suzuki, K. Improvement of magnetic softness in nanocrystalline soft magnetic materials by rotating magnetic field annealing. J. Appl. Phys. 2005, 97, 10F503. [Google Scholar] [CrossRef]
- Allia, P.; Baricco, M.; Knobel, M.; Tiberto, P.; Vinai, F. Nanocrystalline Fe73.5 Cu1Nb3Si13.5B9 obtained by direct-current Joule heating. Magnetic and mechanical properties. Philos. Mag. B Phys. Condens. Matter 1993, 68, 853–860. [Google Scholar] [CrossRef]
- Yoshizawa, Y.; Yamauchi, K. Effects of magnetic field annealing on magnetic properties in ultrafine crystalline Fe-Cu-Nb-Si-B alloys. IEEE Trans. Magn. 1989, 25, 3324–3326. [Google Scholar] [CrossRef]
- Herzer, G. Creep induced magnetic anisotropy in nanocrystalline Fe-Cu-Nb-Si-B alloys. IEEE Trans. Magn. 1994, 30, 4800–4802. [Google Scholar] [CrossRef]
- Hofmann, B.; Kronmüller, H. Stress-induced magnetic anisotropy in nanocrystalline FeCuNbSiB alloy. J. Magn. Magn. Mater. 1996, 152, 91–98. [Google Scholar] [CrossRef]
- Yanai, T.; Shimada, A.; Takahashi, K.; Nakano, M.; Yoshizawa, Y.; Fukunaga, H. Magnetic properties of Fe-based ribbons and toroidal cores prepared by continuous Joule heating under tensile stress. IEEE Trans. Magn. 2006, 42, 2781–2783. [Google Scholar] [CrossRef][Green Version]
- Csizmadia, E.; Varga, L.K.; Palánki, Z.; Zámborszky, F. Creep or tensile stress induced anisotropy in FINEMET-type ribbons? J. Magn. Magn. Mater. 2015, 374, 587–590. [Google Scholar] [CrossRef]
- Rietveld, H. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 1969, 2, 65–71. [Google Scholar] [CrossRef]
- Günther, W. Stress annealing process suitable for the production of low permeable nanocrystalline tape wound cores. J. Magn. Magn. Mater. 2005, 290, 1483–1486. [Google Scholar] [CrossRef]
- Herzer, G. Grain structure and magnetism of nanocrystalline ferromagnets. IEEE Trans. Magn. 1989, 25, 3327–3329. [Google Scholar] [CrossRef]
- Kulik, T.; Żuberek, R.; Hernando, A. Magnetic properties of nanocrystalline Fe73.5Cu1Nb3Si16.5B6. J. Magn. Magn. Mater. 1995, 140, 433–434. [Google Scholar] [CrossRef]
- Ri, M.C.; Sun, Y.H.; Xue, Z.Y.; Ding, D.W.; Wang, W.H. Determination of internal residual strain induced by cryogenic thermal cycling in partially-crystalized Fe-based metallic glasses. J. Alloy. Compd. 2018, 781, 357–361. [Google Scholar] [CrossRef]
- Nutor, R.K.; Fan, X.; He, X.; Xu, X.; Lu, X.; Jiang, J.; Fang, Y. Formation mechanism of stress-induced anisotropy in stress-annealed Fe-based nanocrystalline ribbon alloys. J. Alloy. Compd. 2019, 774, 1243–1249. [Google Scholar] [CrossRef]
- Fan, X.Z.; He, X.W.; Nutor, R.K.; Pan, R.M.; Zheng, J.J.; Ye, H.Q.; Wu, F.M.; Jiang, J.Z.; Fang, Y.Z. Effect of stress on crystallization behavior in a Fe-based amorphous ribbon: An in situ synchrotron radiation X-ray diffraction study. J. Magn. Magn. Mater. 2019, 469, 349–353. [Google Scholar] [CrossRef]
- Herzer, G.; Budinsky, V.; Polak, C. Magnetic properties of FeCuNbSiB nanocrystallized by flash annealing under high tensile stress. Phys. Status Solidi B 2011, 248, 2382–2388. [Google Scholar] [CrossRef]
- Williams, R.; Egami, T. Effects of deformation and annealing on magnetic amorphous alloys. IEEE Trans. Magn. 2003, 12, 927–929. [Google Scholar] [CrossRef]
- Herzer, G. Magnetic field-induced anisotropy in nanocrystalline Fe-Cu-Nb-Si-B alloys. J. Magn. Magn. Mater. 1994, 133, 248–250. [Google Scholar] [CrossRef]
- Shuvaeva, E.; Kaloshkin, S.; Churyukanova, M.; Perminov, A.; Khriplivets, I.; Mitra, A.; Panda, A.K.; Roy, R.K.; Premkumar, V.; Zhukova, A. The impact of bending stress on magnetic properties of Finemet type microwires and ribbons. J. Alloy. Compd. 2018, 743, 388–393. [Google Scholar] [CrossRef]
- Fuchs, E.F.; Masoum, M.A.S. Magnetic circuits: Inductors and permanent magnets. In Power Conversion of Renewable Energy Systems; Springer: Boston, MA, USA, 2011; pp. 217–287. [Google Scholar]
- Wu, Y.Q.; Bitoh, T.; Hono, K.; Makino, A.; Inoue, A. Microstructure and properties of nanocrystalline Fe-Zr-Nb-B soft magnetic alloys with low magnetostriction. Acta Mater. 2001, 49, 4069–4077. [Google Scholar] [CrossRef]
- Fukunaga, H.; Tanaka, H.; Yanai, T.; Nakano, M.; Takahashi, K.; Yoshizawa, Y. High performance nanostructured cores for chock coils prepared by using creep-induced anisotropy. J. Magn. Magn. Mater. 2002, 242, 279–281. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, Z.; Li, X.; Sohrabi, S.; Ren, Y.; Wang, W. Magnetic Properties in Finemet-Type Soft Magnetic Toroidal Cores Annealed under Radial Stresses. Metals 2020, 10, 122. https://doi.org/10.3390/met10010122
Xue Z, Li X, Sohrabi S, Ren Y, Wang W. Magnetic Properties in Finemet-Type Soft Magnetic Toroidal Cores Annealed under Radial Stresses. Metals. 2020; 10(1):122. https://doi.org/10.3390/met10010122
Chicago/Turabian StyleXue, Zhiyong, Xuesong Li, Sajad Sohrabi, Yu Ren, and Weihua Wang. 2020. "Magnetic Properties in Finemet-Type Soft Magnetic Toroidal Cores Annealed under Radial Stresses" Metals 10, no. 1: 122. https://doi.org/10.3390/met10010122
APA StyleXue, Z., Li, X., Sohrabi, S., Ren, Y., & Wang, W. (2020). Magnetic Properties in Finemet-Type Soft Magnetic Toroidal Cores Annealed under Radial Stresses. Metals, 10(1), 122. https://doi.org/10.3390/met10010122




