Mechanical Properties Characterization of Welded Automotive Steels
Abstract
:1. Introduction
2. Experimental Analysis
2.1. Material Characterization
2.2. Resistance Spot Welding
2.3. Laser Beam Welding
2.4. Tensile Specimen
2.5. Indentation Test
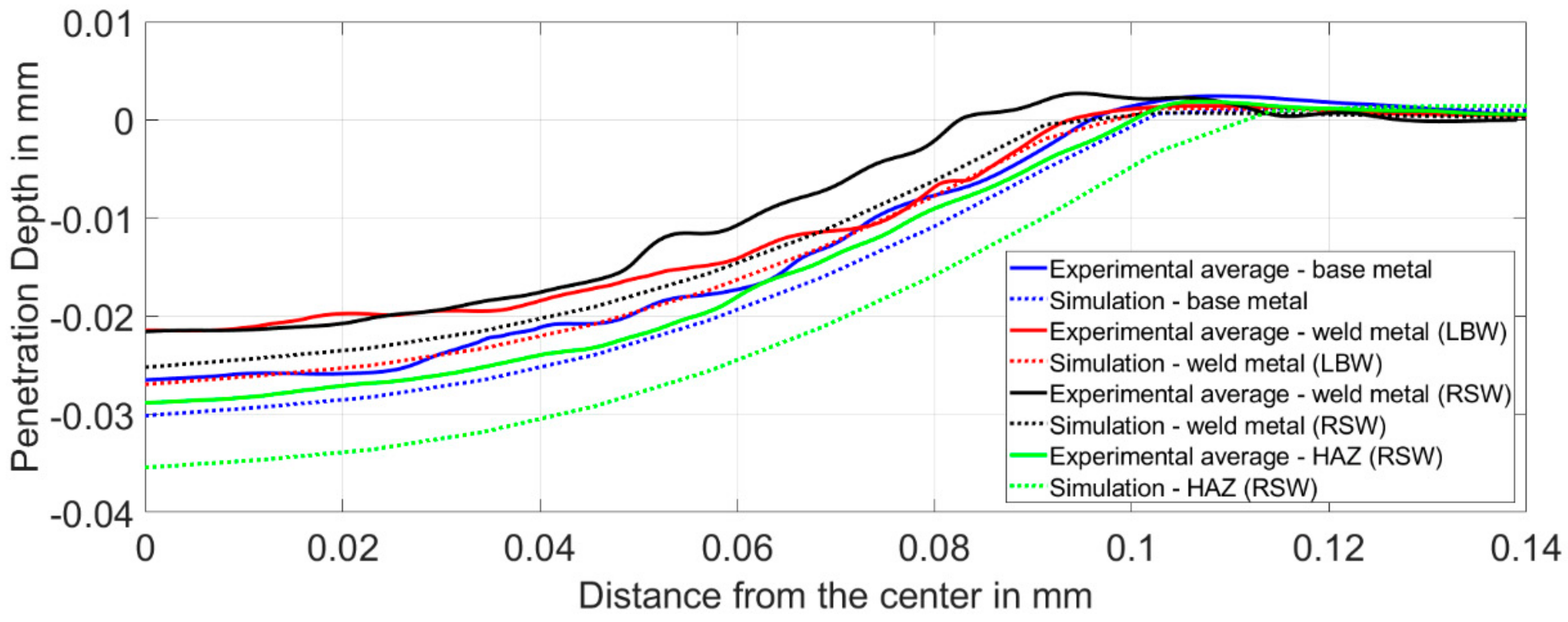
2.6. Analysis of the Penetration Profile
3. Numerical Approach
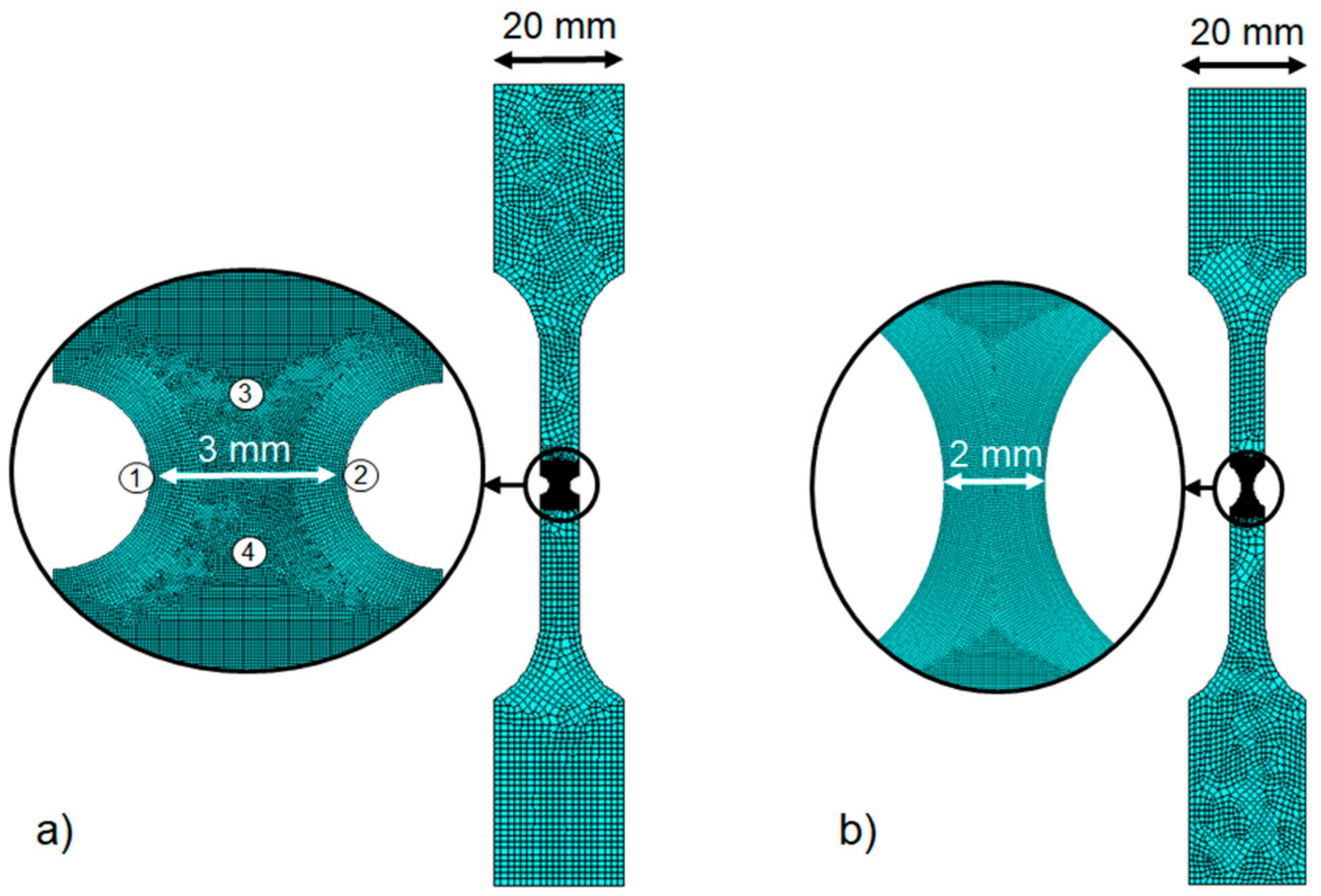
3.1. Tensile Test
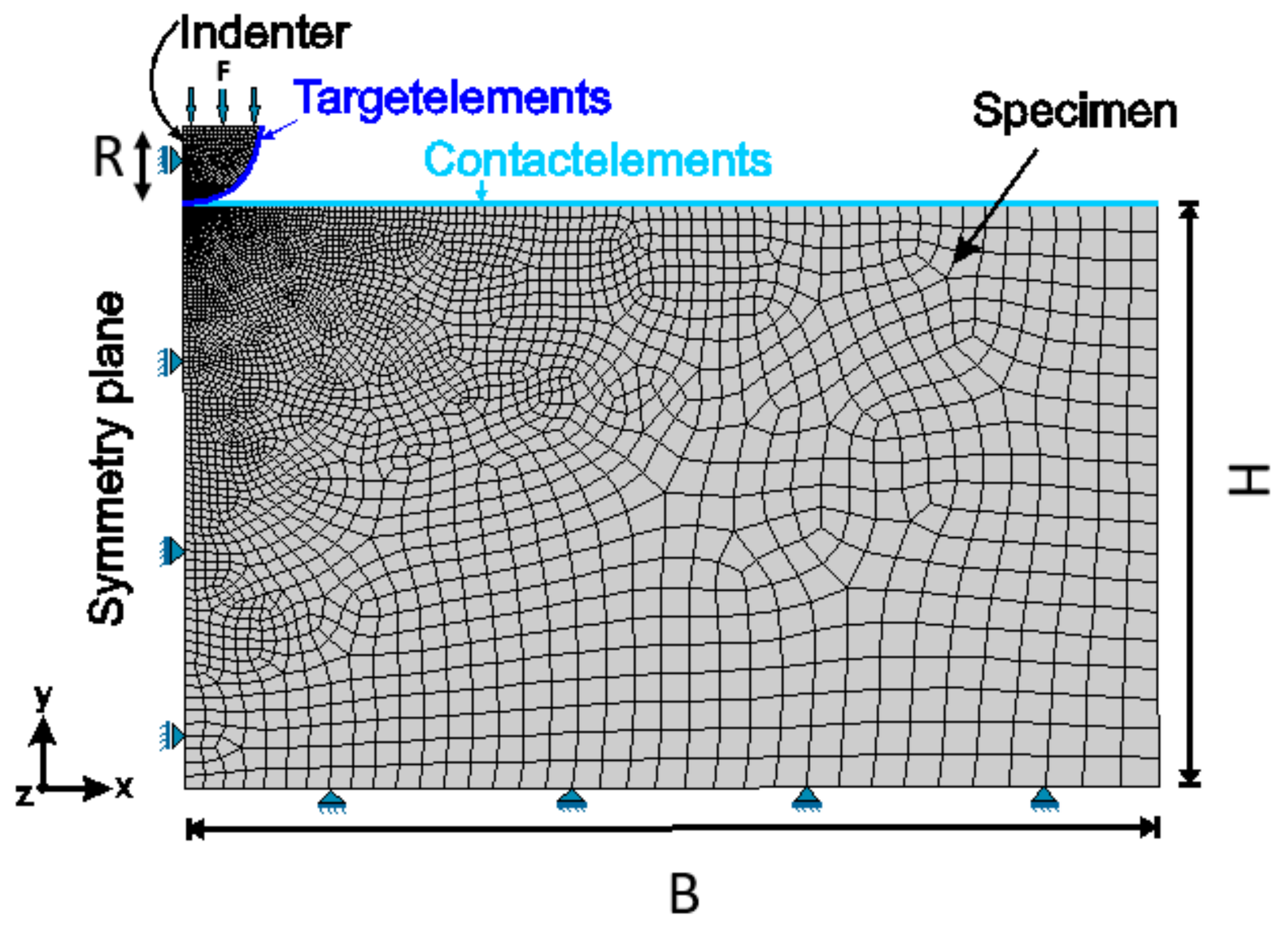
3.2. Indentation Test
4. Results and Discussion
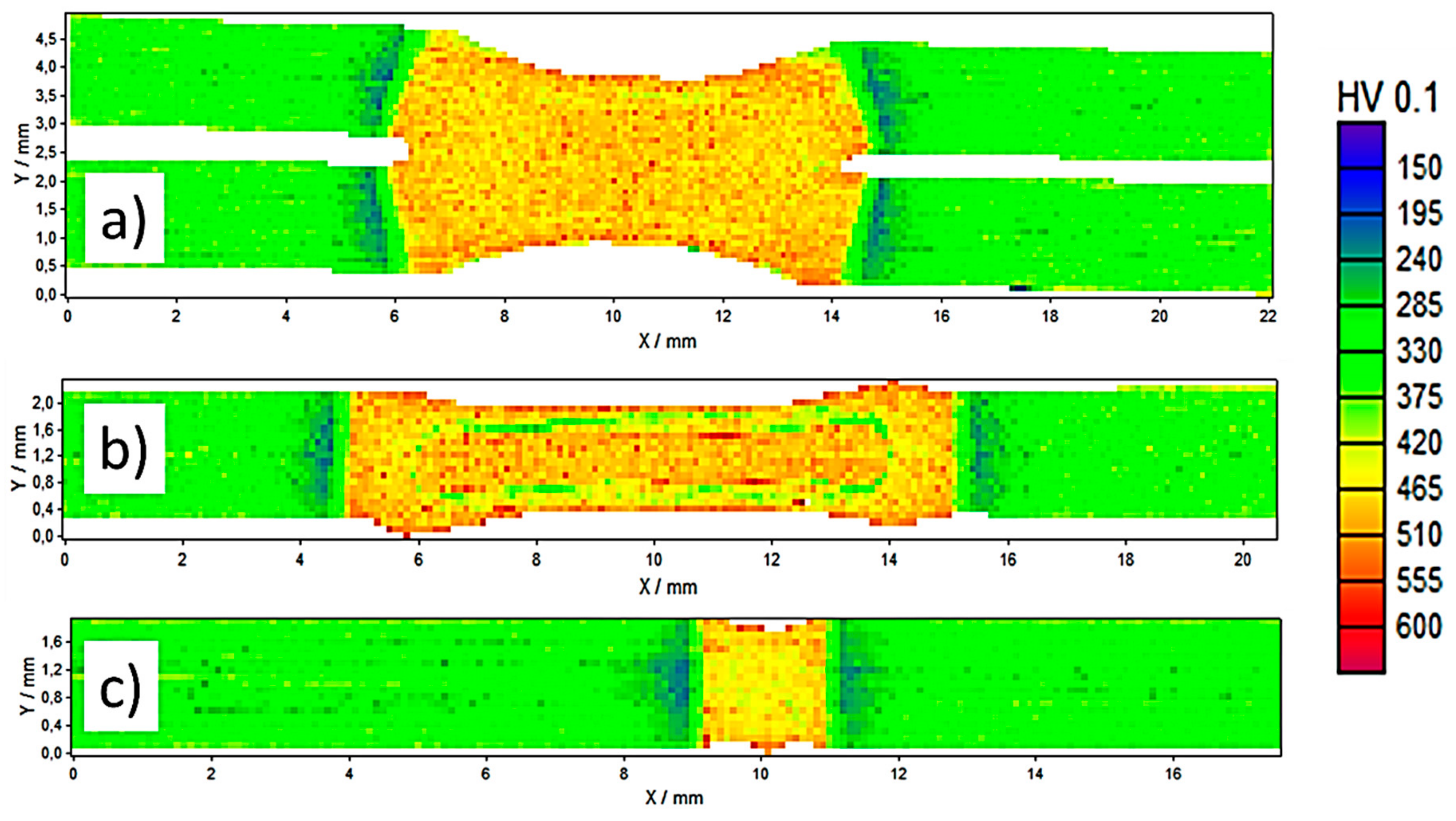
4.1. Metallographic Analysis
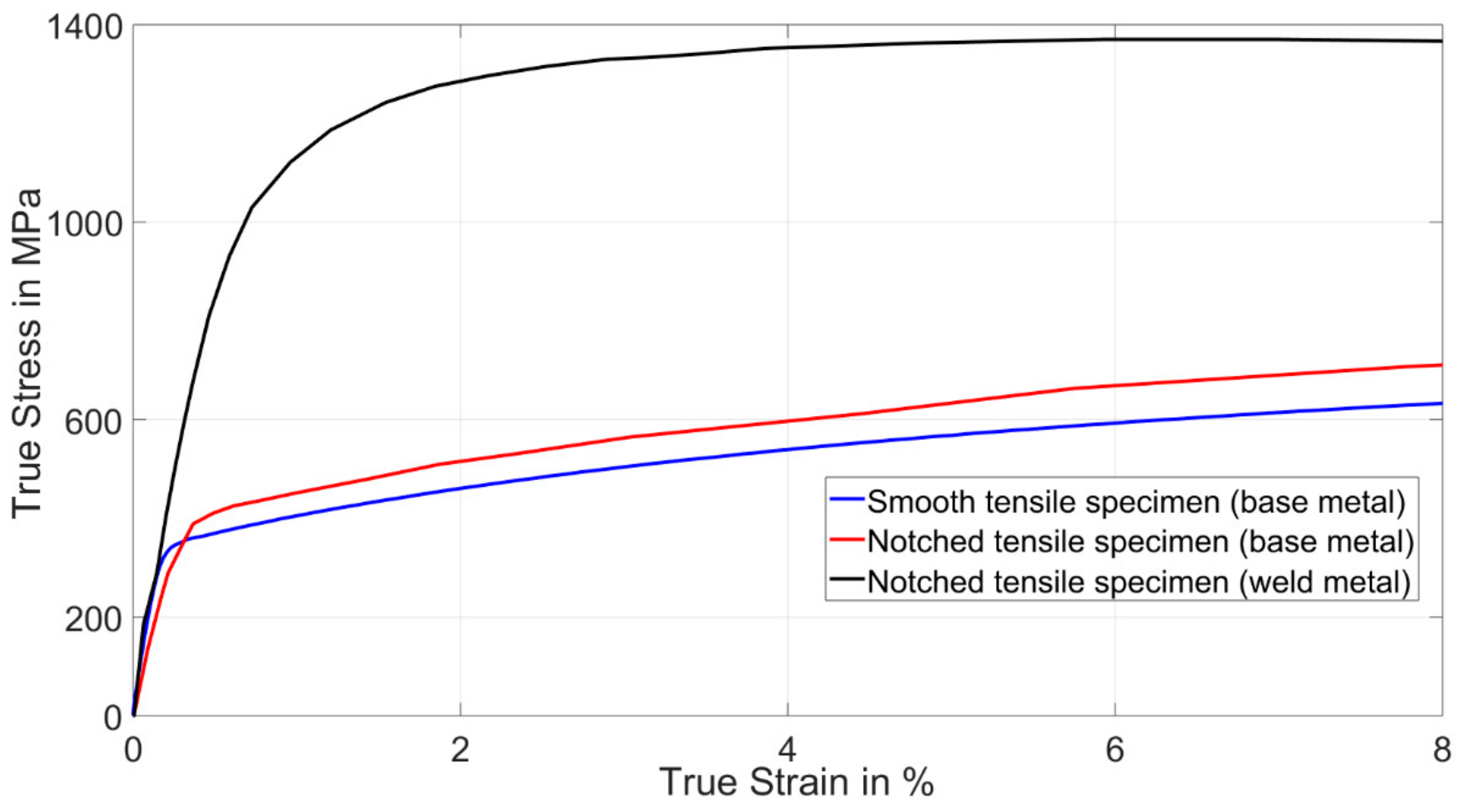
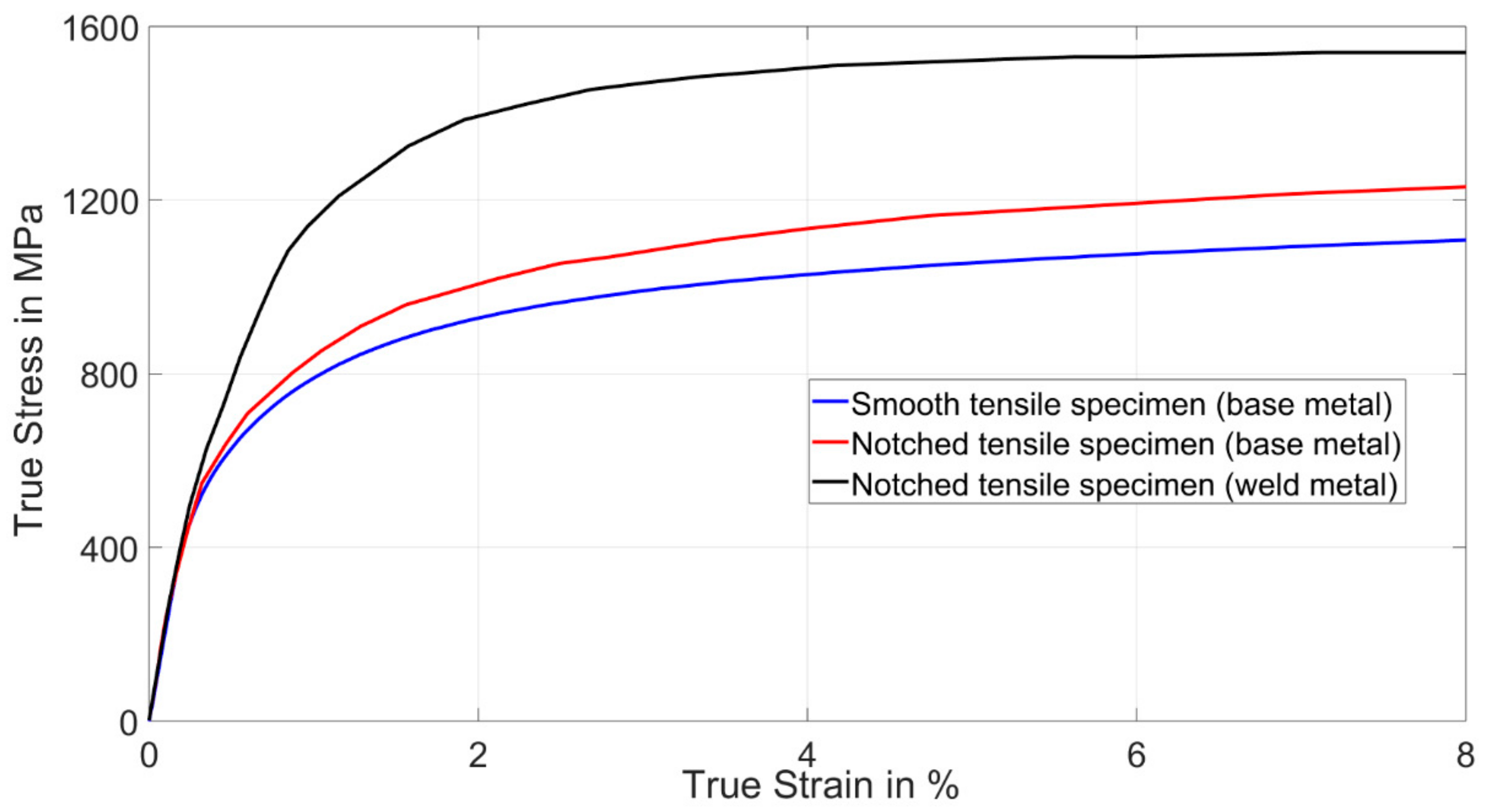
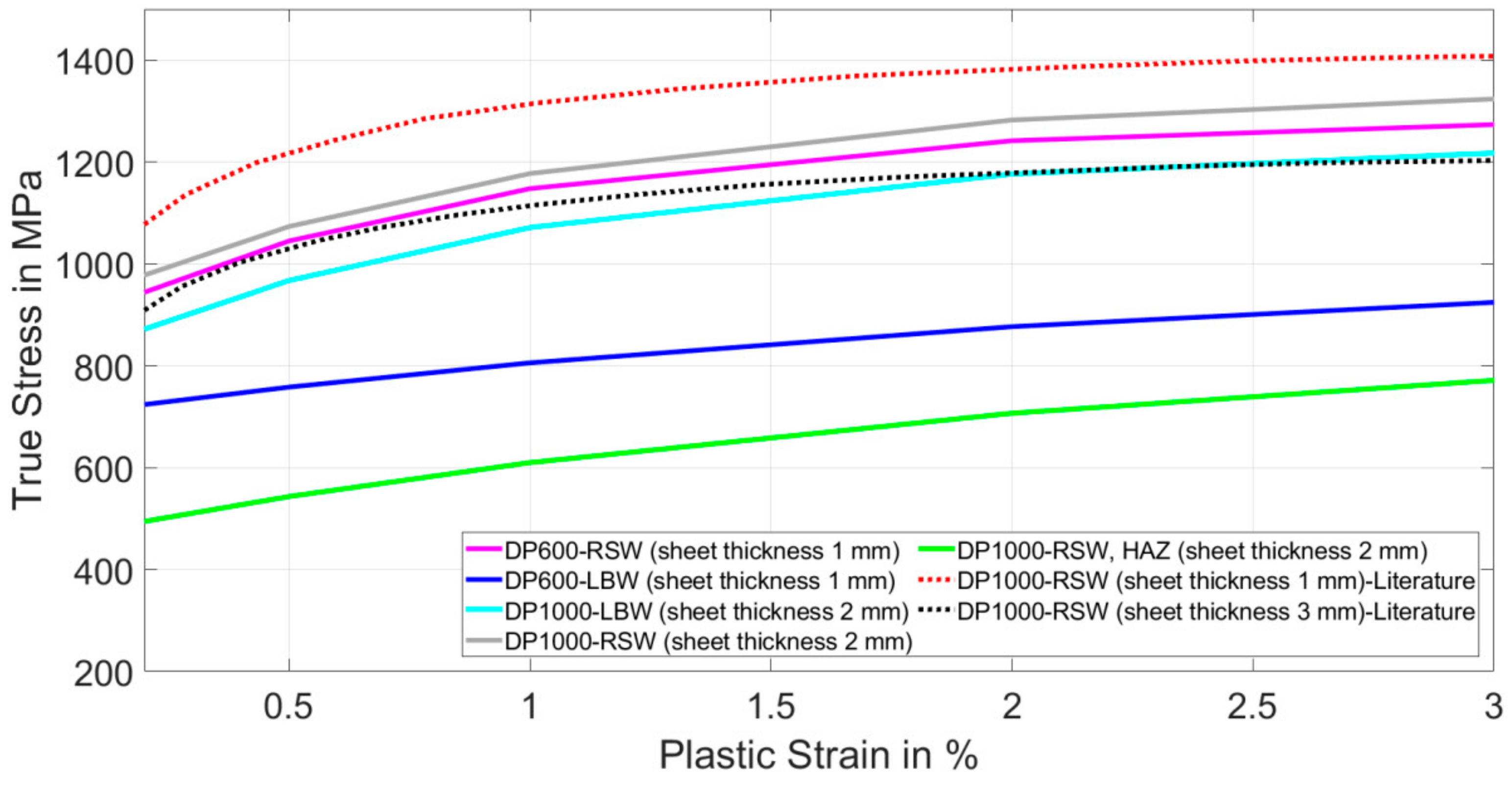
4.2. Tensile Test
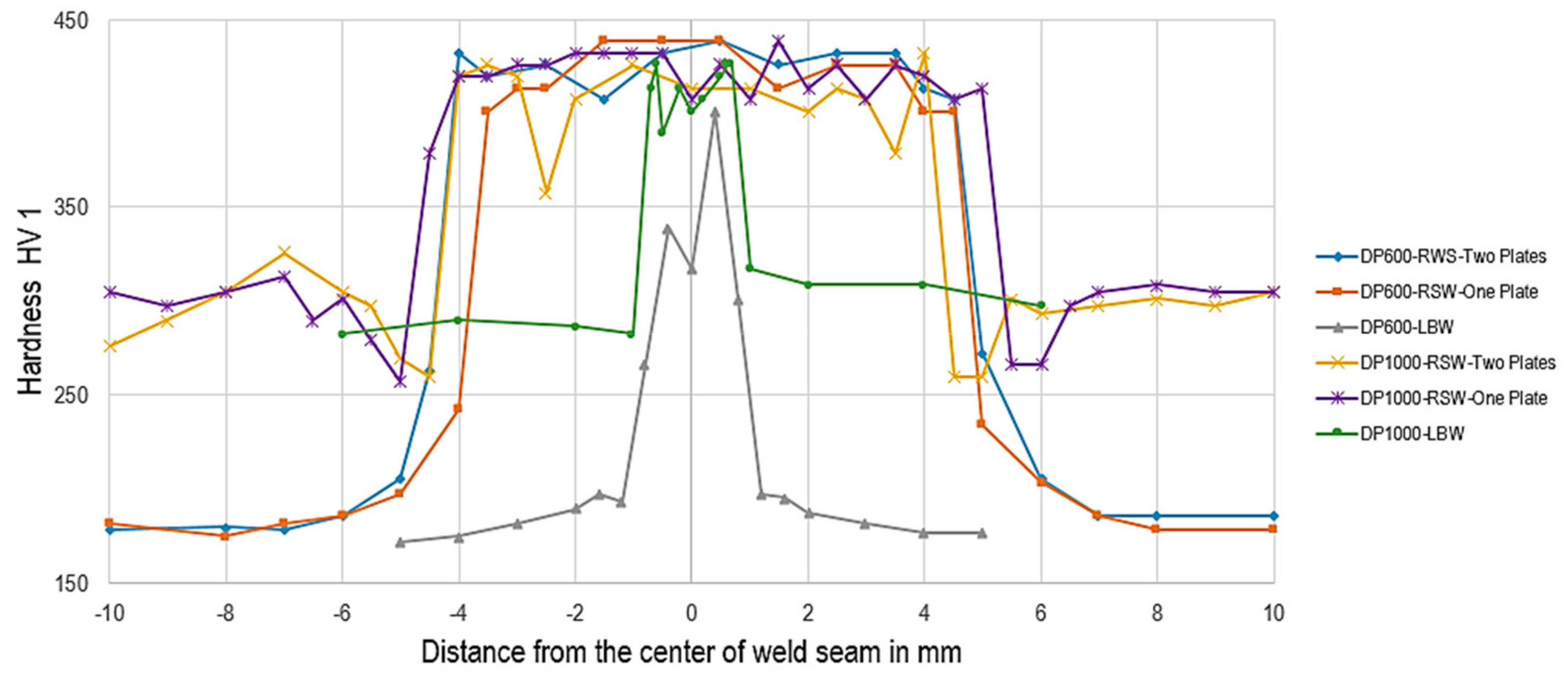
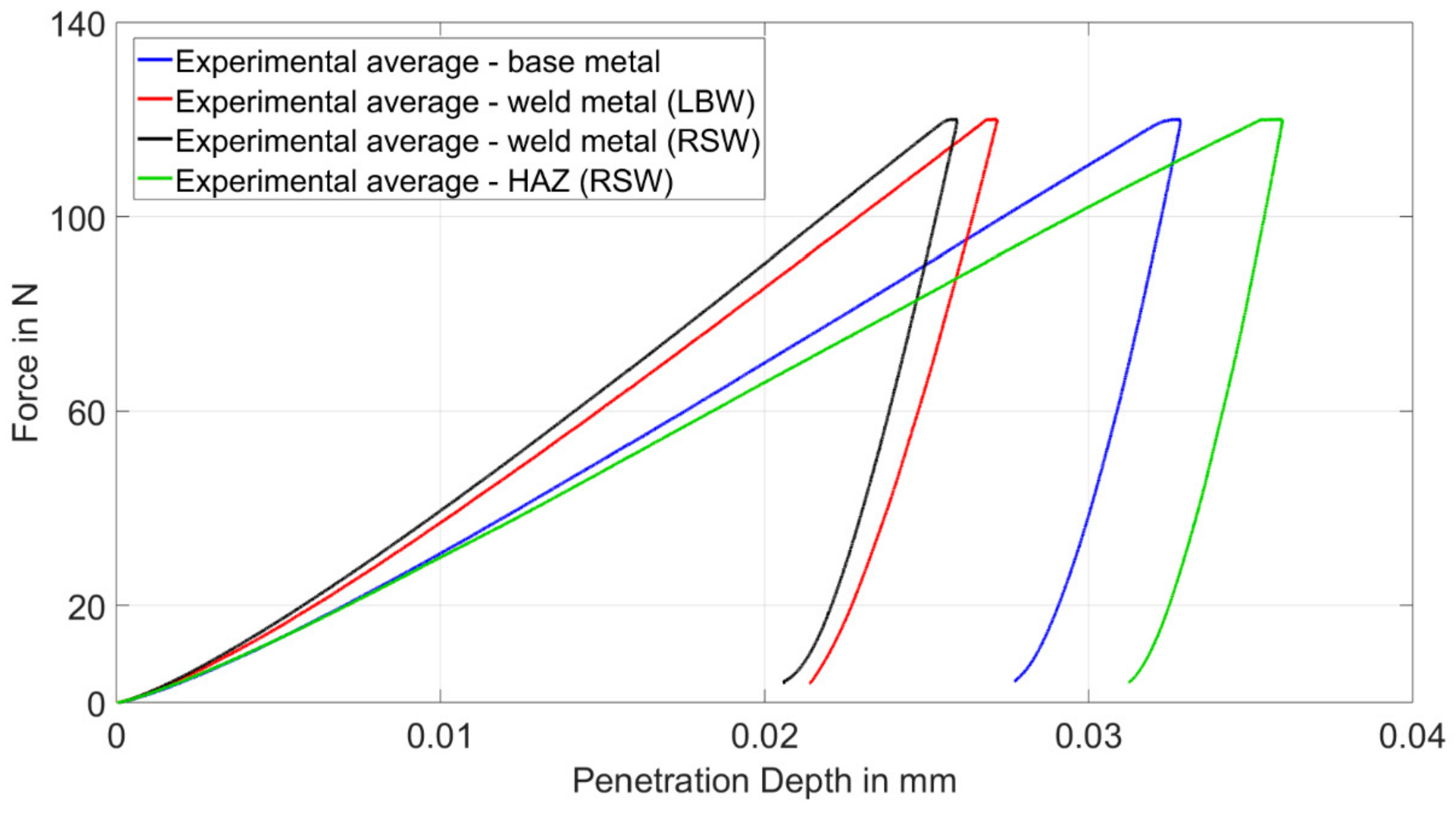
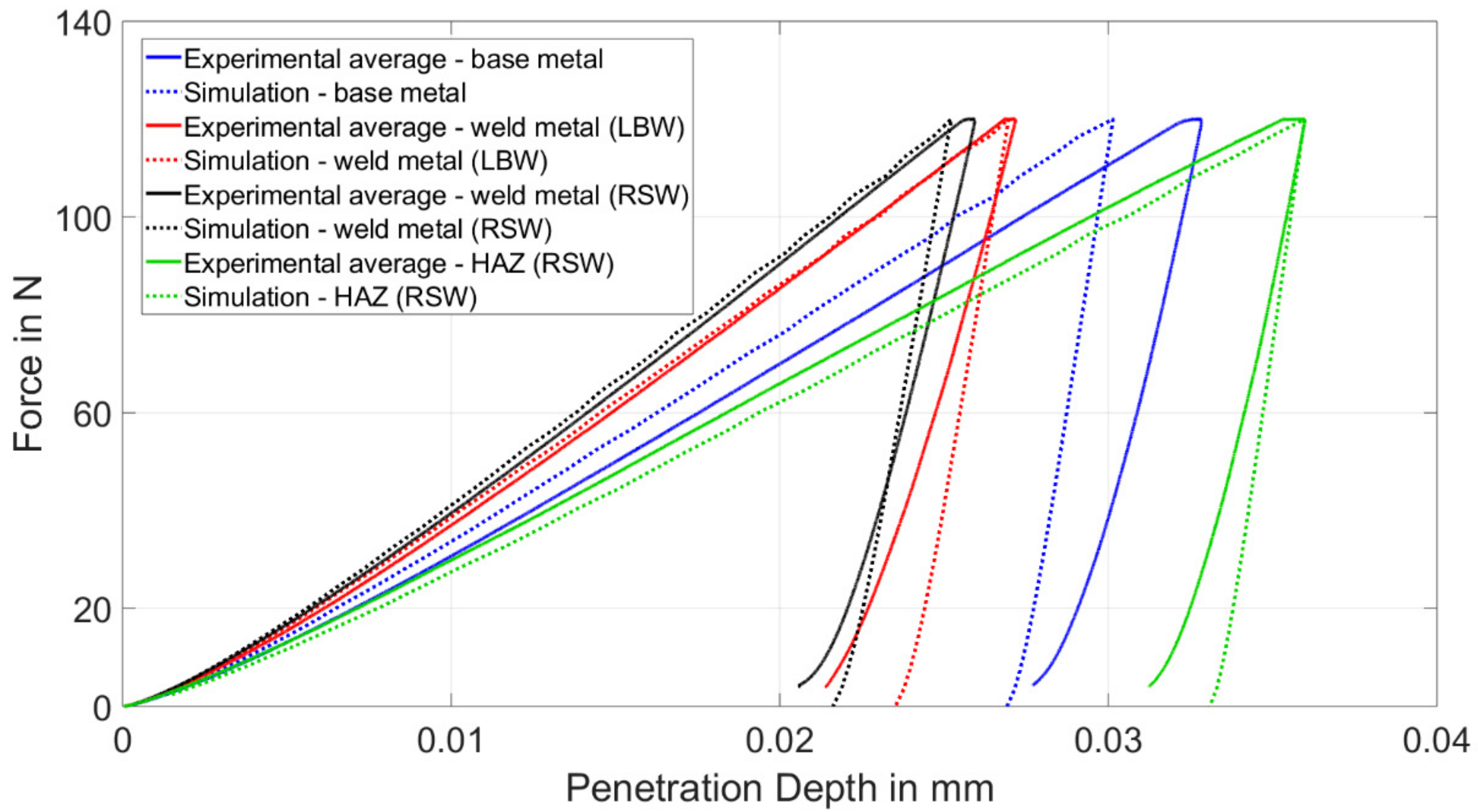
4.3. Indentation Test
4.4. Numerical Analysis
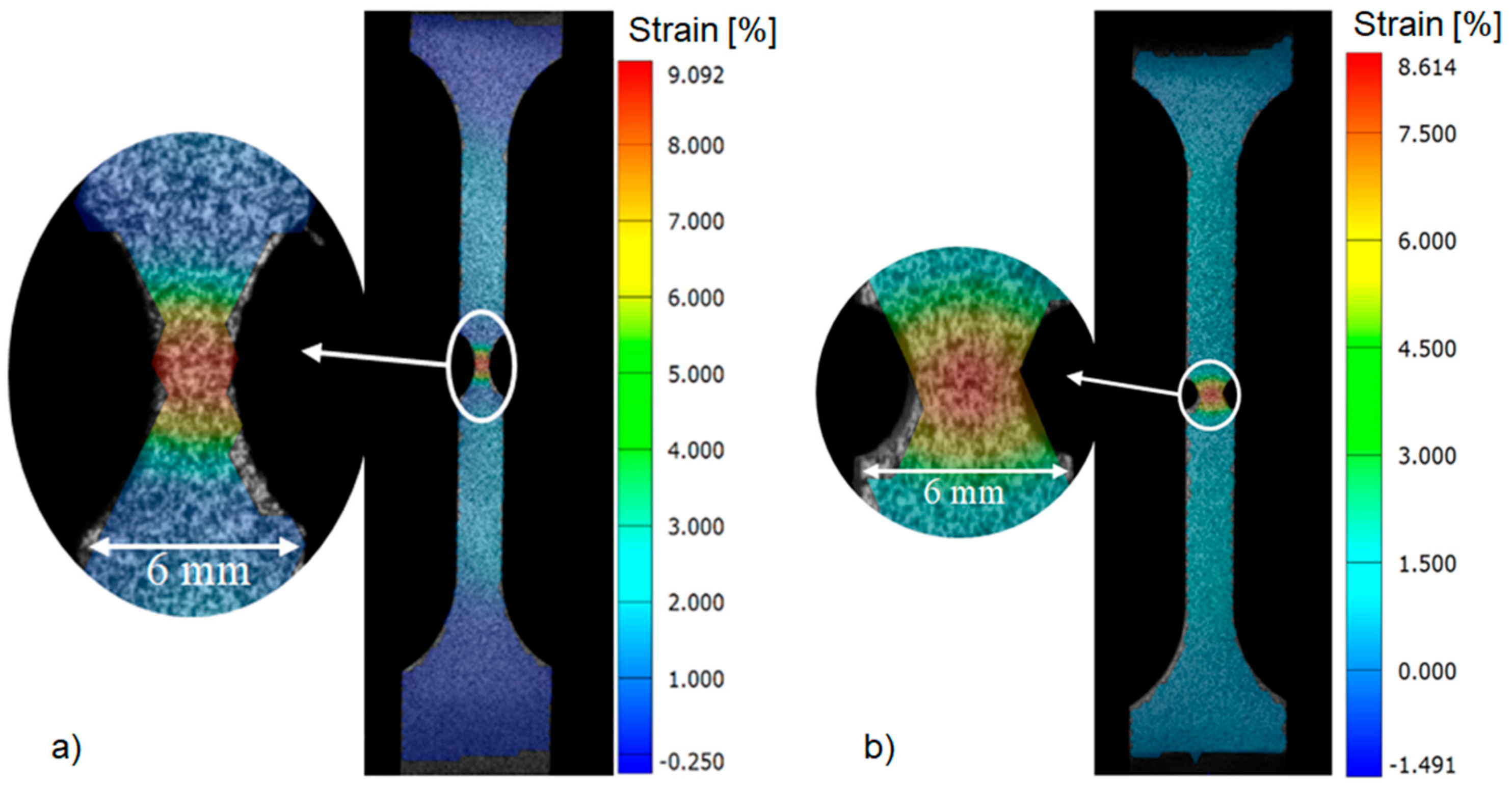
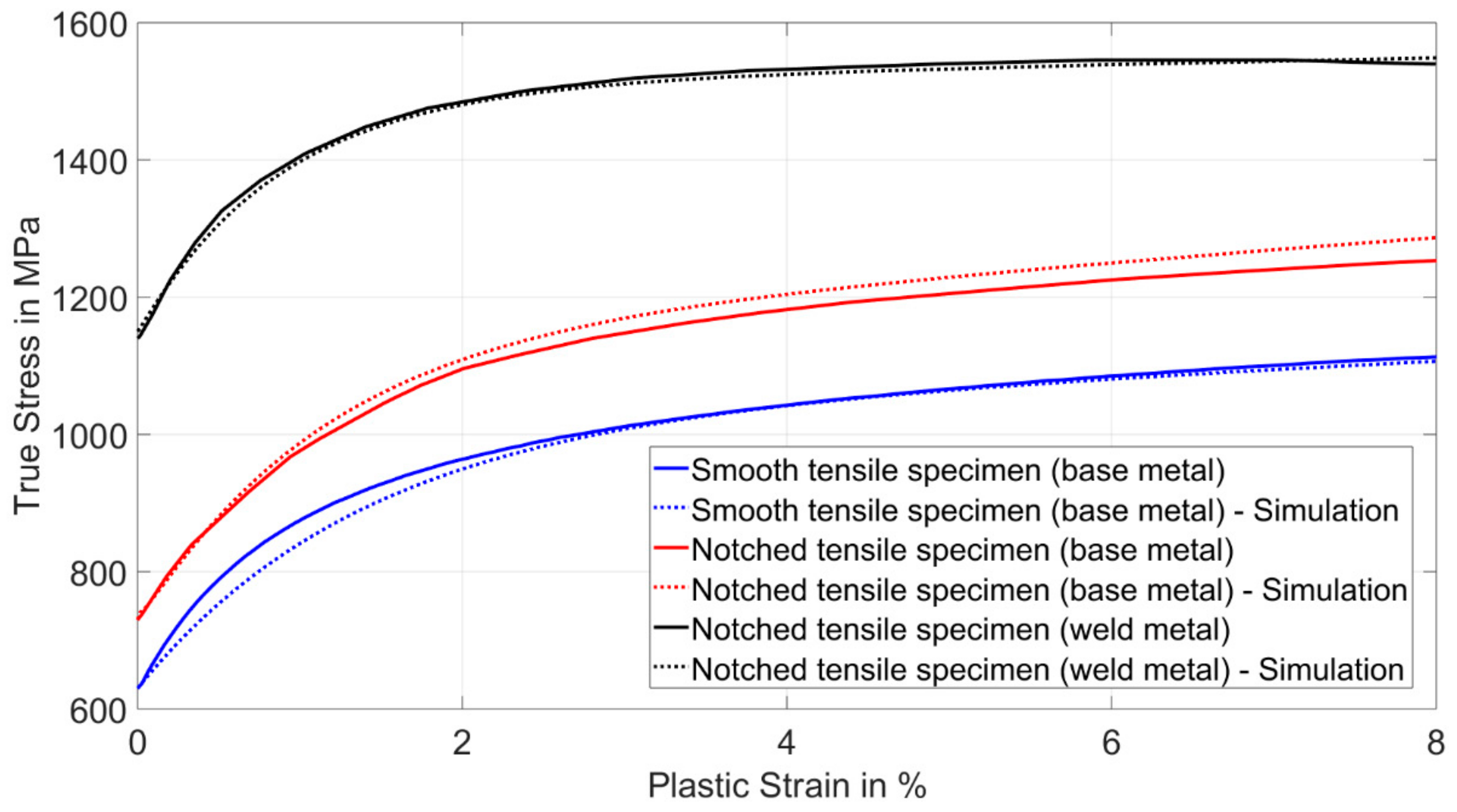
4.4.1. Numerical Simulation of the Tensile Tests
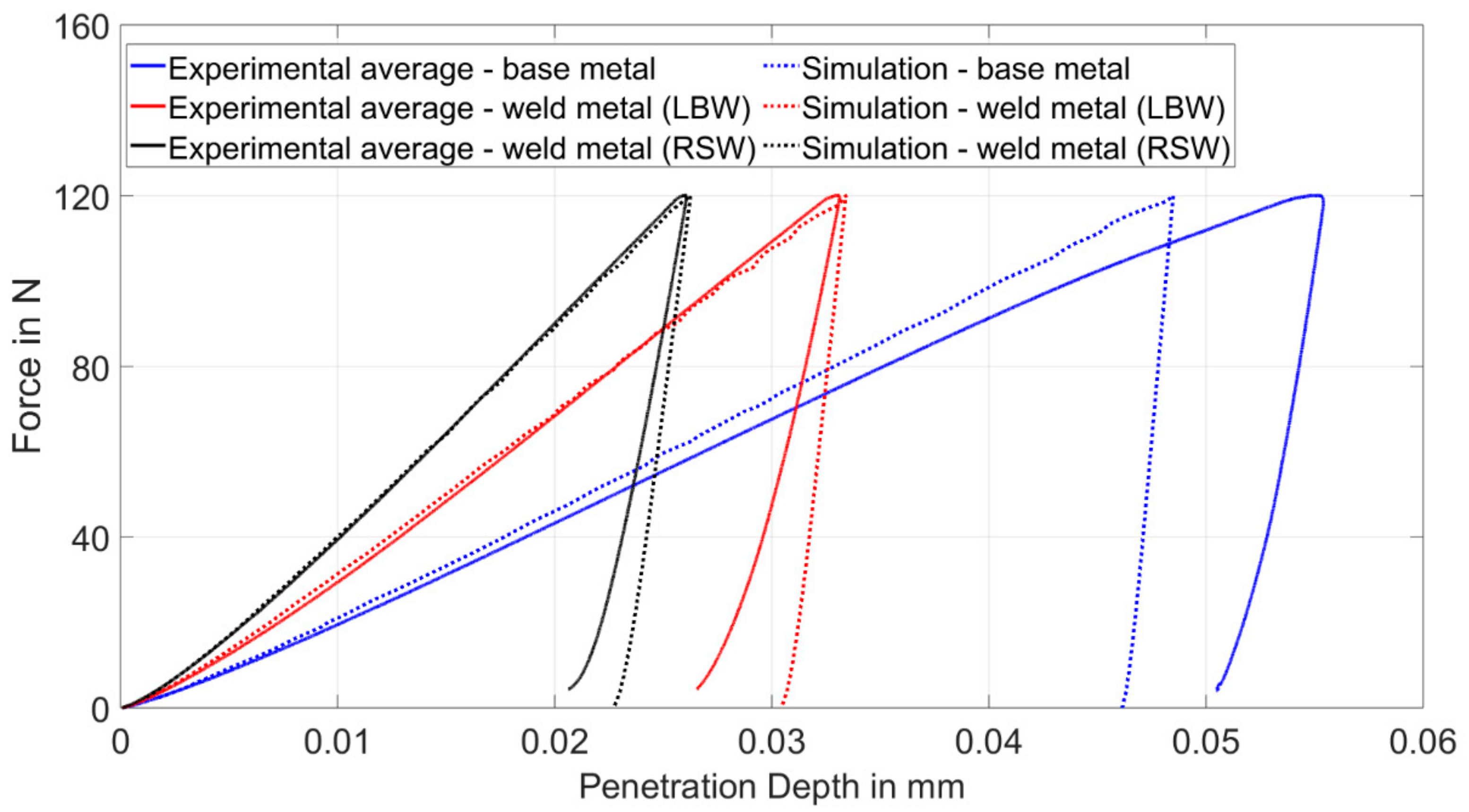
4.4.2. Numerical Simulation of the Indentation Tests
4.5. Method Validation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ramazani, A.; Mukherjee, K.; Abdurakhmanov, A.; Abbasi, M.; Prahl, U. Characterization of Microstructure and Mechanical Properties of Resistance Spot Welded DP600 Steel. Metals 2015, 5, 1704–1716. [Google Scholar] [CrossRef] [Green Version]
- Ramazani, A.; Mukherjee, K.; Prahl, U.; Bleck, W. Modelling the effect of microstructural banding on the flow curve behaviour of dual-phase (DP) steels. Comput. Mater. Sci. 2012, 52, 46–54. [Google Scholar] [CrossRef]
- Ramazania, A.; Ebrahimib, Z.; Prahl, U. Study the effect of martensite banding on the failure initiation in dual-phase steel. Comput. Mater. Sci. 2014, 87, 241–247. [Google Scholar] [CrossRef]
- Cornette, D.; Hourman, T.; Hudin, O.; Laurent, J.; Reynaert, A. High Strength Steels for Automotive Safety Parts. SAE Tech. Pap. 2001. [Google Scholar] [CrossRef]
- Davies, G. Materials for Automobile Bodies; Elsevier Butterworth–Heinemann: Oxford, UK, 2003. [Google Scholar]
- Nanda, T.; Singh, V.; Chakraborty, A.; Sharma, S. Third generation of advanced high-strength steels: Processing routes and properties. Proc. Inst. Mech. Eng. Part L 2016, 233, 209–238. [Google Scholar] [CrossRef]
- Nikoosohbat, F.; Kheirandish, S.; Goodarzi, M.; Marashi, P. Microstructure and failure behaviour of resistance spot welded DP980 dual phase steel. Mater. Sci. Technol. 2010, 26, 738–744. [Google Scholar] [CrossRef]
- Manladan, S.; Abdullahi, I.; Hamza, M. A Review on the Application of Resistance Spot Welding of Automotive. J. Eng. Tech. 2015, 10, 20–37. [Google Scholar]
- Pouranvari, M.; Asgari, H.; Mosavizadch, S.; Marashi, P.; Goodarzi, M. Effect of weld nugget size on overload failure mode of resistance spot welds. Sci. Technol. Weld. Joining 2013, 12, 217–225. [Google Scholar] [CrossRef]
- Weber, G.; Brauser, S.; Gaul, H.; Rethmeier, M. Study of Fatigue Behavior for Spot Welded Tensile Shear Specimens of Advanced High Strength Steels. Steel Res. Int. 2012, 83, 988–994. [Google Scholar] [CrossRef]
- Nayah, S.; Biro, E. Resistance Spot Welding of Dual-phase Steels: Heat affected zone softening and tensile properties. In Proceedings of the 9th International Conference (ASM International): Trends in Welding Research, Chicago, IL, USA, 4–8 June 2012. [Google Scholar]
- Pouranvari, M.; Marashi, S.; Mousavizadeh, S. Failure mode transition and mechanical properties of similar and dissimilar resistance spot welds of DP600 and low carbon steels. Sci. Technol. Weld. Joining 2010, 15, 625–631. [Google Scholar] [CrossRef]
- Dancette, S.; Massardier-Jourdan, V.; Fabrègue, D.; Merlin, J.; Dupuy, T.; Bouzekri, M. HAZ Microstructures and Local Mechanical Properties of High Strength Steels Resistance Spot Welds. ISIJ Int. 2011, 51, 99–107. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Choi, J. Overload analysis and fatigue life prediction of spot-welded specimens using an effective J-integral. Mech. Mater. 2005, 37, 19–32. [Google Scholar] [CrossRef]
- Kong, X.; Yang, Q.; Li, B.; Rothwell, G.; English, R.; Ren, X.J. Numerical study of strengths of spot-welded joints of steel. Mater. Des. 2008, 29, 1554–1561. [Google Scholar] [CrossRef]
- Yang, Y.; Babu, S.; Peterson, W. Integrated computational model to predict mechanical behaviour of spot weld. Sci. Technol. Weld. Joining 2008, 13, 232–239. [Google Scholar] [CrossRef]
- Ghosh, S.; Pal, T.; Mukherjee, S. Comparative study of heat-affected zone with weld and base material after post-weld heat treatment of HSLA steel using ball indentation technique. J. Mater. Sci. 2008, 43, 5474–5482. [Google Scholar] [CrossRef]
- Murty, K.; Miraglia, P.; Mathew, M.; Shah, V.; Haggag, F. Characterization of gradients in mechanical properties of SA-533B steel welds using ball indentation. Int. J. Press. Vessels Pip. 1999, 76, 361–369. [Google Scholar] [CrossRef]
- Javaheri, E.; Pittner, A.; Graf, B.; Rethmeier, M. Mechanical properties characterization of resistance spot welded DP1000 Steel under uniaxial tensile test. Mater. Test. 2019, 61, 527–532. [Google Scholar] [CrossRef]
- Lemaitre, J.; Chaboche, J.L. Mechanics of Solid Materials; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Lee, H.; Lee, J.; Pharr, M. A numerical approach to spherical indentation techniques for material property evaluation. J. Mech. Phys. Solids 2005, 53, 2037–2069. [Google Scholar] [CrossRef]
- Zhong, N.; Liao, X.; Wang, M.; Wu, Y.; Rong, Y. Improvement of microstructures and mechanical properites of resistance spot welded DP600 steel by double pulse technology. Mater. Trans. 2011, 52, 2143–2150. [Google Scholar] [CrossRef] [Green Version]
- DIN EN ISO 6507-1:2018-07: Metallische Werkstoffe-Härteprüfung nach Vickers-Teil 1: Prüfverfahren (ISO 6507-1:2018); Beuth Verlag: Berlin, Germany, 2018.
- Tang, Z.; Guo, Y.; Jia, Z.; Li, Y.; Wei, Q. Examining the Effect of Pileup on the Accuracy of Sharp Indentation Testing. Adv. Mater. Sci. Eng. 2015. [Google Scholar] [CrossRef] [Green Version]
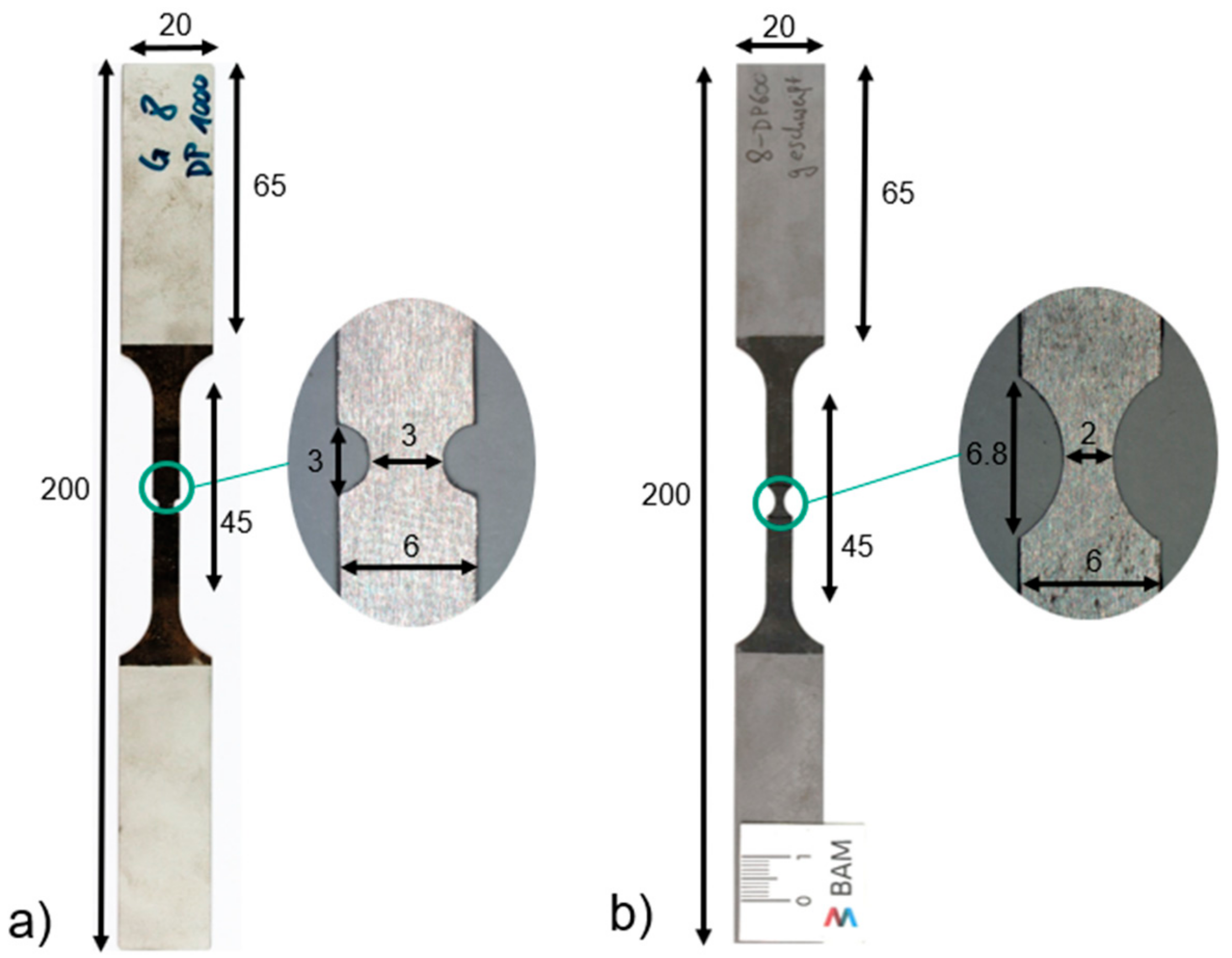








| Material | C | Si | Mn | Cr | Mo | Al | Fe |
|---|---|---|---|---|---|---|---|
| DP1000 | 0.11 | 0.5 | 2.14 | 0.03 | 0.002 | 0.04 | balance |
| DP600+ZE75/75 | 0.1 | 0.14 | 1.4 | 0.16 | 0.18 | 0.02 | balance |
| Material | Force in kN | Hold Time in ms | Current in kA | Electrode Cape |
|---|---|---|---|---|
| DP600 | 5 | 600 | 16 | A16 |
| DP1000 | 5 | 600 | 13.5 | A16 |
| Material | Power in kW | Focusing in mm | Speed in m/min |
|---|---|---|---|
| DP600 | 1.6 | 0 | 1.8 |
| DP1000 | 2.4 | 0 | 1.8 |
| Geometry | Abbreviation | Dimension [mm] |
|---|---|---|
| Radius of the indenter | R | 0.2 |
| Width of the specimen | B | 2.5 |
| Height of the specimen | H | 1.5 |
| Material | Yield Strength in MPa | Tensile Strength in MPa | Strain Hardening Exponent | Total Elongation at Maximum Force in % | |
|---|---|---|---|---|---|
| DP600 | Smooth sample | 360 ± 1.73 | 633 ± 2 | 0.216 ± 0.002 | 18.7 ± 1.1 |
| Notched sample | 430 ± 10.07 | 698 ± 2 | 0.124 ± 0.009 | 15.8 ± 1.37 | |
| Notched-welded sample (RSW) | 1036 ± 3.06 | 1304 ± 10.82 | 0.049 ± 0.008 | 4.18 ± 0.26 | |
| DP1000 | Smooth sample | 630 ± 2.08 | 1025 ± 1.53 | 0.096 ± 0.002 | 8.3 ± 0.036 |
| Notched sample | 800 ± 36.3 | 1145 ± 8.08 | 0.104 ± 0.003 | 8.7 ± 0.376 | |
| Notched-welded sample (RSW) | 1150 ± 20.5 | 1460 ± 13.44 | 0.057 ± 0.008 | 4.3 ± 0.25 | |
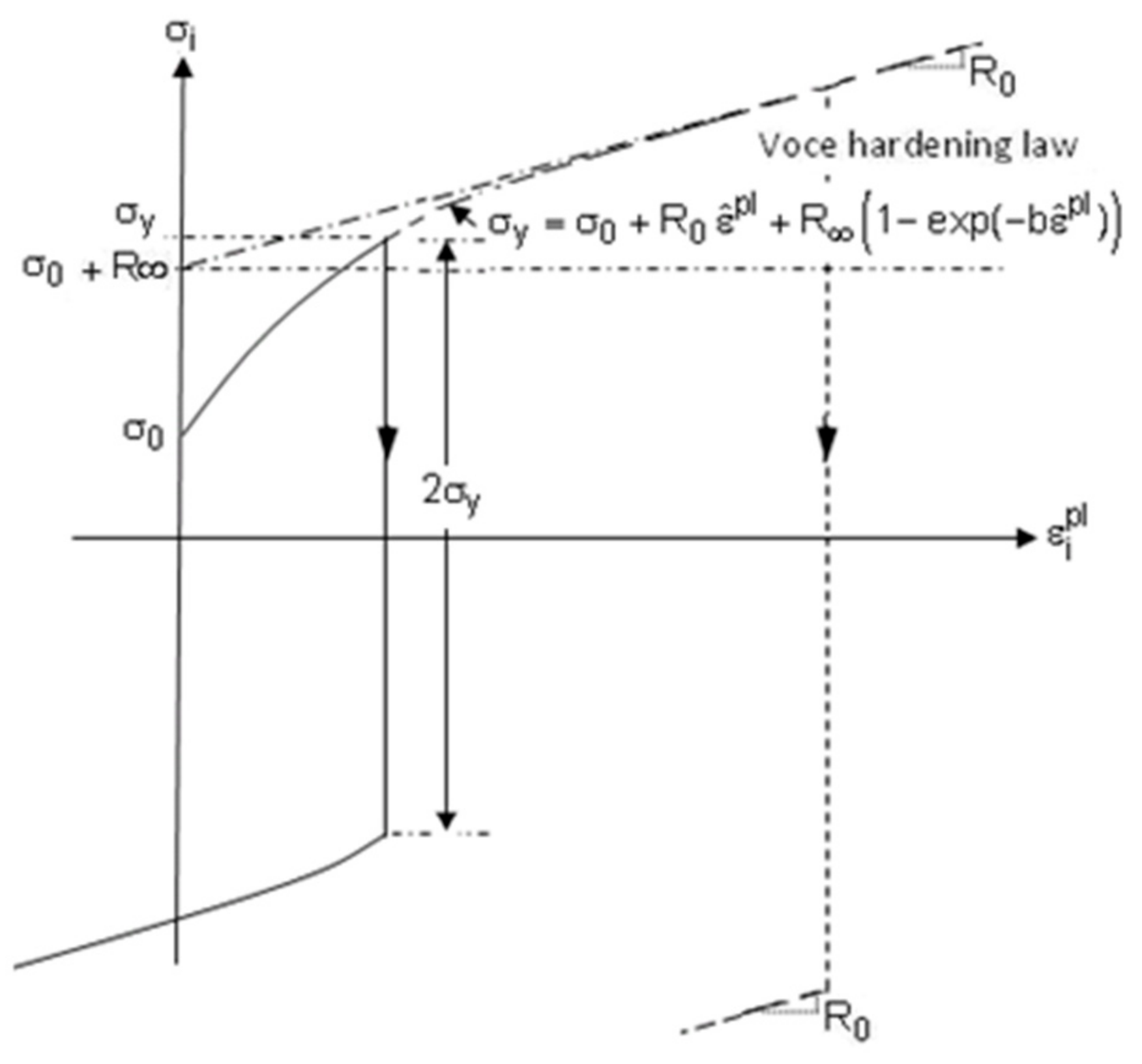
| Material | in MPa | R0 in MPa | Rinf in MPa | b | |
|---|---|---|---|---|---|
| DP600 | Smooth sample | 360 | 710 | 268 | 22 |
| Notched sample | 430 | 1300 | 207 | 25 | |
| Resulting geometric factors for DP600 | 1.19 | 1.83 | 0.77 | 1.14 | |
| DP1000 | Smooth sample | 630 | 1100 | 390 | 72 |
| Notched sample | 800 | 1250 | 340 | 75 | |
| Resulting geometric factors for DP1000 | 1.27 | 1.14 | 0.87 | 1.04 | |
| Material | in MPa | R0 in MPa | Rinf in MPa | b | |
|---|---|---|---|---|---|
| DP600 | Smooth-welded sample | 867 | 65 | 420 | 110 |
| Notched-welded sample | 1036 | 120 | 325 | 125 | |
| DP1000 | Smooth-welded sample | 906 | 175 | 437 | 96 |
| Notched-welded sample | 1150 | 200 | 380 | 100 | |
| Material | in MPa | R0 in MPa | Rinf in MPa | b | |
|---|---|---|---|---|---|
| DP600 | LBW-Weldment | 700 | 30 | 320 | 40 |
| DP1000 | RSW-HAZ | 460 | 1500 | 343 | 50 |
| LBW-Weldment | 800 | 175 | 437 | 96 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Javaheri, E.; Lubritz, J.; Graf, B.; Rethmeier, M. Mechanical Properties Characterization of Welded Automotive Steels. Metals 2020, 10, 1. https://doi.org/10.3390/met10010001
Javaheri E, Lubritz J, Graf B, Rethmeier M. Mechanical Properties Characterization of Welded Automotive Steels. Metals. 2020; 10(1):1. https://doi.org/10.3390/met10010001
Chicago/Turabian StyleJavaheri, Ehsan, Janot Lubritz, Benjamin Graf, and Michael Rethmeier. 2020. "Mechanical Properties Characterization of Welded Automotive Steels" Metals 10, no. 1: 1. https://doi.org/10.3390/met10010001
APA StyleJavaheri, E., Lubritz, J., Graf, B., & Rethmeier, M. (2020). Mechanical Properties Characterization of Welded Automotive Steels. Metals, 10(1), 1. https://doi.org/10.3390/met10010001






