Bilateral Deficit and Bilateral Performance: Relationship with Sprinting and Change of Direction in Elite Youth Soccer Players
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design
2.2. Participants
2.3. Procedures
2.4. Squat Jump Test (SJ)
2.5. Horizontal Countermovement Jump (HCMJ)
2.6. Horizontal Countermovement Jump Single Leg (HCMJL and HCMJR)
2.7. Bilateral Deficit (BLD)
2.8. Sprint Assessment (10, 20, 30 and 40 m)
2.9. Change of Direction Assessment (COD-90°)
- T COD-90° = Time in COD-90° test
- T 20 m = Time in maximal 20 m sprinting test
2.10. Data Analysis
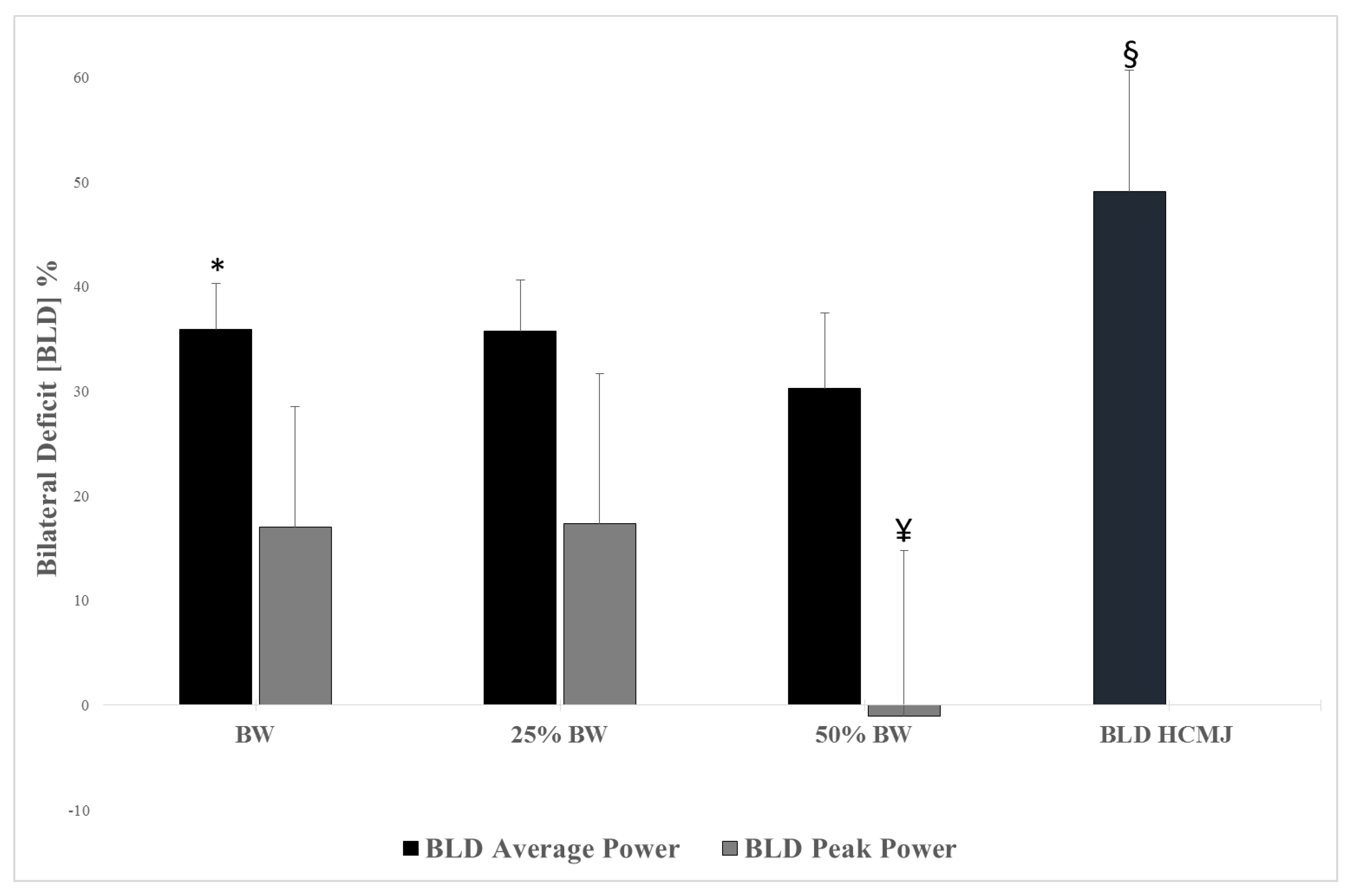
3. Results
4. Discussion
Limitations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jakobi, J.M.; Chilibeck, P.D. Bilateral and unilateral contractions: Possible differences in maximal voluntary force. Can. J. Appl. Physiol. 2001, 26, 12–33. [Google Scholar] [CrossRef]
- Bogdanis, G.C.; Tsoukos, A.; Kaloheri, O.; Terzis, G.; Veligekas, P.; Brown, L.E. Comparison Between Unilateral and Bilateral Plyometric Training on Single- and Double-Leg Jumping Performance and Strength. J. Strength Cond. Res. 2019, 33, 633–640. [Google Scholar] [CrossRef] [PubMed]
- Botton, C.E.; Radaelli, R.; Wilhelm, E.N.; Silva, B.G.C.; Brown, L.E.; Pinto, R.S. Bilateral deficit between concentric and isometric muscle actions. Isokinet. Exerc. Sci. 2013, 21, 161–165. [Google Scholar] [CrossRef]
- Brown, L.; Whitehurst, M.; Gilbert, R.; Findley, B.; Buchalter, D. Effect of velocity on the bilateral deficit during dynamic knee extension and flexion exercise in females. Isokinet. Exerc. Sci. 1994, 4, 153–159. [Google Scholar] [CrossRef]
- Dickin, D.C.; Too, D. Effects of movement velocity and maximal concentric and eccentric actions on the bilateral deficit. Res. Q. Exerc. Sport 2006, 77, 296–303. [Google Scholar] [CrossRef] [PubMed]
- Botton, C.E.; Wilhelm, E.N.; Brown, L.E.; Pinto, R.S. Neuromuscular Adaptations to Unilateral vs. Bilateral Strength Training in Women. J. Strength Cond. Res. 2016, 30, 1924–1932. [Google Scholar] [CrossRef] [PubMed]
- Challis, J.H. An investigation of bilateral deficit on human jumping. Hum. Mov. Sci. 1998, 17, 307–325. [Google Scholar] [CrossRef]
- Howard, J.D.; Enoka, R.M. Maximum bilateral contractions are modified by neurally mediated interlimb effects. J. Appl. Physiol. 1991, 70, 306–316. [Google Scholar] [CrossRef]
- Dickin, D.C.; Sandow, R.; Dolny, D.G. Bilateral deficit in power production during multi joint leg extension. Eur. J. Sport Sci. 2011, 11, 437–445. [Google Scholar] [CrossRef]
- Bobbert, M.F.; de Graaf, W.W.; Jonk, J.N.; Casius, L.J. Explanation of the bilateral deficit in human vertical squat jumping. J. Appl. Physiol. 2006, 100, 493–499. [Google Scholar] [CrossRef]
- Sado, N.; Yoshioka, S.; Fukashiro, S. Free-leg side elevation of pelvis in single-leg jump is a substantial advantage over double-leg jump for jumping height generation. J. Biomech. 2020, 104, 109751. [Google Scholar] [CrossRef]
- Skarabot, J.; Cronin, N.; Strojnik, V.; Avela, J. Bilateral deficit in maximal force production. Eur. J. Appl. Physiol. 2016, 116, 2057–2084. [Google Scholar] [CrossRef] [PubMed]
- Ebben, W.P.; Flanagan, E.; Jensen, R.L. Bilateral facilitation and laterality during the countermovement jump. Percept. Mot. Ski. 2009, 108, 251–258. [Google Scholar] [CrossRef] [PubMed]
- Bishop, C.; Berney, J.; Lake, J.; Loturco, I.; Blagrove, R.; Turner, A.; Read, P. Bilateral Deficit During Jumping Tasks: Relationship With Speed and Change of Direction Speed Performance. J. Strength Cond. Res. 2019. [Google Scholar] [CrossRef] [PubMed]
- Bracic, M.; Supej, M.; Peharec, S.; Bacic, P.; Coh, M. An investigation of the influence of bilateral deficit on the counter movement jump performance in elite sprinters. Kinesiology 2010, 1, 71–81. [Google Scholar]
- Hoff, J.; Helgerud, J. Endurance and strength training for soccer players: Physiological considerations. Sports Med. 2004, 34, 165–180. [Google Scholar] [CrossRef]
- Helgerud, J.; Rodas, G.; Kemi, O.J.; Hoff, J. Strength and endurance in elite football players. Int. J. Sports Med. 2011, 32, 677–682. [Google Scholar] [CrossRef]
- Silva, J.R.; Nassis, G.P.; Rebelo, A. Strength training in soccer with a specific focus on highly trained players. Sports Med. Open 2015, 1, 17. [Google Scholar] [CrossRef]
- Chaouachi, A.; Manzi, V.; Chaalali, A.; Wong del, P.; Chamari, K.; Castagna, C. Determinants analysis of change-of-direction ability in elite soccer players. J. Strength Cond. Res. 2012, 26, 2667–2676. [Google Scholar] [CrossRef]
- Bangsbo, J.; Mohr, M.; Krustrup, P. Physical and metabolic demands of training and match-play in the elite football player. J. Sports Sci. 2006, 24, 665–674. [Google Scholar] [CrossRef]
- Ruscello, B.; Esposito, M.; Partipilo, F.; Di Cicco, D.; Filetti, C.; Pantanella, L.; D’Ottavio, S. Exercise-to-rest ratios in repeated sprint ability training in women’s soccer. J. Sports Med. Phys. Fit. 2018, 58, 1790–1799. [Google Scholar] [CrossRef] [PubMed]
- Ruscello, B.; Partipilo, F.; Pantanella, L.; Esposito, M.; D’Ottavio, S. The optimal exercise to rest ratios in repeated sprint ability training in youth soccer players. J. Sports Med. Phys. Fit. 2016, 56, 1465–1475. [Google Scholar]
- Ruscello, B.; Esposito, M.; Fusco, C.; Ceccarelli, C.; Pomponi, S.; Filetti, C.; Pantanella, L.; Gabrielli, P.; D’Ottavio, S. Acute effects of two different initial heart rates on testing the repeated sprint ability in elite women’s soccer players. J. Sports Med. Phys. Fit. 2020. [Google Scholar] [CrossRef] [PubMed]
- Faude, O.; Koch, T.; Meyer, T. Straight sprinting is the most frequent action in goal situations in professional football. J. Sports Sci. 2012, 30, 625–631. [Google Scholar] [CrossRef] [PubMed]
- Barr, M.J.; Sheppard, J.M.; Agar-Newman, D.J.; Newton, R.U. Transfer effect of strength and power training to the sprinting kinematics of international rugby players. J. Strength Cond. Res. 2014, 28, 2585–2596. [Google Scholar] [CrossRef]
- López-Segovia, M.; Marques, M.C.; van den Tillaar, R.; González-Badillo, J.J. Relationships between vertical jump and full squat power outputs with sprint times in u21 soccer players. J. Hum. Kinet. 2011, 30, 135–144. [Google Scholar] [CrossRef]
- Wisløff, U.; Castagna, C.; Helgerud, J.; Jones, R.; Hoff, J. Strong correlation of maximal squat strength with sprint performance and vertical jump height in elite soccer players. Br. J. Sports Med. 2004, 38, 285–288. [Google Scholar] [CrossRef]
- Hamilton, R.T.; Shultz, S.J.; Schmitz, R.J.; Perrin, D.H. Triple-hop distance as a valid predictor of lower limb strength and power. J. Athl. Train. 2008, 43, 144–151. [Google Scholar] [CrossRef]
- Barker, D.; Nance, S. The Relation between Strength and Power in Professional Rugby League Players. J. Strength Cond. Res. 1999, 13, 224–229. [Google Scholar]
- Cronin, J.B.; Hansen, K.T. Strength and power predictors of sports speed. J. Strength Cond. Res. 2005, 19, 349–357. [Google Scholar] [CrossRef]
- Hewit, J.K.; Cronin, J.B.; Hume, P.A. Kinematic factors affecting fast and slow straight and change-of-direction acceleration times. J. Strength Cond. Res. 2013, 27, 69–75. [Google Scholar] [CrossRef]
- Suarez-Arrones, L.; Gonzalo-Skok, O.; Carrasquilla, I.; Asian-Clemente, J.; Santalla, A.; Lara-Lopez, P.; Nunez, F.J. Relationships between Change of Direction, Sprint, Jump, and Squat Power Performance. Sports 2020, 8, 38. [Google Scholar] [CrossRef] [PubMed]
- Ben Abdelkrim, N.; Chaouachi, A.; Chamari, K.; Chtara, M.; Castagna, C. Positional role and competitive-level differences in elite-level men’s basketball players. J. Strength Cond. Res. 2010, 24, 1346–1355. [Google Scholar] [CrossRef] [PubMed]
- Jones, P.A.; Thomas, C.; Dos’Santos, T.; McMahon, J.J.; Graham-Smith, P. The Role of Eccentric Strength in 180 degrees Turns in Female Soccer Players. Sports 2017, 5, 42. [Google Scholar] [CrossRef] [PubMed]
- Tous-Fajardo, J.; Gonzalo-Skok, O.; Arjol-Serrano, J.L.; Tesch, P. Enhancing Change-of-Direction Speed in Soccer Players by Functional Inertial Eccentric Overload and Vibration Training. Int. J. Sports Physiol. Perform. 2016, 11, 66–73. [Google Scholar] [CrossRef] [PubMed]
- Dos’Santos, T.; Thomas, C.; Jones, P.A.; Comfort, P. Assessing Asymmetries in Change of Direction Speed Performance: Application of Change of Direction Deficit. J. Strength Cond. Res. 2019, 33, 2953–2961. [Google Scholar] [CrossRef] [PubMed]
- Brughelli, M.; Cronin, J.; Levin, G.; Chaouachi, A. Understanding change of direction ability in sport: A review of resistance training studies. Sports Med. 2008, 38, 1045–1063. [Google Scholar] [CrossRef]
- Spiteri, T.; Nimphius, S.; Hart, N.H.; Specos, C.; Sheppard, J.M.; Newton, R.U. Contribution of strength characteristics to change of direction and agility performance in female basketball athletes. J. Strength Cond. Res. 2014, 28, 2415–2423. [Google Scholar] [CrossRef]
- Nunez, F.J.; Santalla, A.; Carrasquila, I.; Asian, J.A.; Reina, J.I.; Suarez-Arrones, L.J. The effects of unilateral and bilateral eccentric overload training on hypertrophy, muscle power and COD performance, and its determinants, in team sport players. PLoS ONE 2018, 13, e0193841. [Google Scholar] [CrossRef]
- Lockie, R.G.; Callaghan, S.J.; Berry, S.P.; Cooke, K.R.A. Relationship between unilateral jumping ability and asymmetry on multidirectional speed in team sport athletes. J. Strength Cond. Res. 2014, 28, 3557–3566. [Google Scholar] [CrossRef]
- Ramirez-Campillo, R.; Burgos, C.H.; Henriquez-Olguin, C.; Andrade, D.C.; Martinez, C.; Alvarez, C.; Castro-Sepulveda, M.; Marques, M.C.; Izquierdo, M. Effect of unilateral, bilateral, and combined plyometric training on explosive and endurance performance of young soccer players. J. Strength Cond. Res. 2015, 29, 1317–1328. [Google Scholar] [CrossRef] [PubMed]
- Ramirez-Campillo, R.; Sanchez-Sanchez, J.; Gonzalo-Skok, O.; Rodriguez-Fernandez, A.; Carretero, M.; Nakamura, F.Y. Specific Changes in Young Soccer Player’s Fitness After Traditional Bilateral vs. Unilateral Combined Strength and Plyometric Training. Front. Physiol. 2018, 9, 265. [Google Scholar] [CrossRef] [PubMed]
- Gonzalo-Skok, O.; Tous-Fajardo, J.; Valero-Campo, C.; Berzosa, C.; Bataller, A.V.; Arjol-Serrano, J.L.; Moras, G.; Mendez-Villanueva, A. Eccentric-Overload Training in Team-Sport Functional Performance: Constant Bilateral Vertical Versus Variable Unilateral Multidirectional Movements. Int. J. Sports Physiol. Perform. 2017, 12, 951–958. [Google Scholar] [CrossRef] [PubMed]
- Gonzalo-Skok, O.; Tous-Fajardo, J.; Suarez-Arrones, L.; Arjol-Serrano, J.L.; Casajús, J.A.; Mendez-Villanueva, A. Single-Leg Power Output and Between-Limbs Imbalances in Team-Sport Players: Unilateral Versus Bilateral Combined Resistance Training. Int. J. Sports Physiol. Perform. 2017, 12, 106–114. [Google Scholar] [CrossRef] [PubMed]
- Padulo, J.; Tiloca, A.; Powell, D.; Granatelli, G.; Bianco, A.; Paoli, A. EMG amplitude of the biceps femoris during jumping compared to landing movements. SpringerPlus 2013, 2, 520. [Google Scholar] [CrossRef]
- McCurdy, K.W.; Langford, G.A.; Doscher, M.W.; Wiley, L.P.; Mallard, K.G. The effects of short-term unilateral and bilateral lower-body resistance training on measures of strength and power. J. Strength Cond. Res. 2005, 19, 9–15. [Google Scholar] [CrossRef]
- McCurdy, K.; O’Kelley, E.; Kutz, M.; Langford, G.; Ernest, J.; Torres, M. Comparison of Lower Extremity EMG Between the 2-Leg Squat and Modified Single-Leg Squat in Female Athletes. J. Sport Rehabil. 2010, 19, 57–70. [Google Scholar] [CrossRef]
- Tagesson, S.K.; Kvist, J. Intra- and interrater reliability of the establishment of one repetition maximum on squat and seated knee extension. J. Strength Cond. Res. 2007, 21, 801–807. [Google Scholar] [CrossRef]
- Jidovtseff, B.; Harris, N.K.; Crielaard, J.-M.; Cronin, J.B. Using the load-velocity relationship for 1RM prediction. J. Strength Cond. Res. 2011, 25, 267–270. [Google Scholar] [CrossRef]
- Pareja-Blanco, F.; Rodríguez-Rosell, D.; Sánchez-Medina, L.; Sanchis-Moysi, J.; Dorado, C.; Mora-Custodio, R.; Yáñez-García, J.M.; Morales-Alamo, D.; Pérez-Suárez, I.; Calbet, J.A.L.; et al. Effects of velocity loss during resistance training on athletic performance, strength gains and muscle adaptations. Scand. J. Med. Sci. Sports 2017, 27, 724–735. [Google Scholar] [CrossRef]
- Maulder, P.; Cronin, J. Horizontal and vertical jump assessment: Reliability, symmetry, discriminative and predictive ability. Phys. Ther. Sport 2005, 6, 74–82. [Google Scholar] [CrossRef]
- Meylan, C.; McMaster, T.; Cronin, J.; Mohammad, N.I.; Rogers, C.; Deklerk, M. Single-leg lateral, horizontal, and vertical jump assessment: Reliability, interrelationships, and ability to predict sprint and change-of-direction performance. J. Strength Cond. Res. 2009, 23, 1140–1147. [Google Scholar] [CrossRef] [PubMed]
- Buchheit, M.; Simpson, B.M.; Peltola, E.; Mendez-Villanueva, A. Assessing maximal sprinting speed in highly trained young soccer players. Int. J. Sports Physiol. Perform. 2012, 7, 76–78. [Google Scholar] [CrossRef] [PubMed]
- Brown, T.D.; Vescovi, J.D.; VanHeest, J.L. Assessment of linear sprinting performance: A theoretical paradigm. J. Sports Sci. Med. 2004, 3, 203. [Google Scholar]
- Hopkins, W.G.; Marshall, S.W.; Batterham, A.M.; Hanin, J. Progressive Statistics for Studies in Sports Medicine and Exercise Science. Med. Sci. Sports Exerc. 2009, 41, 3–12. [Google Scholar] [CrossRef]
- Psycharakis, S.G.; Eagle, S.R.; Moir, G.L.; Rawcliffe, A.; McKenzie, C.; Graham, S.M.; Lamont, H.S.; Connaboy, C. Effects of Additional Load on the Occurrence of Bilateral Deficit in Counter-Movement and Squat Jumps. Res. Q. Exerc. Sport 2019, 90, 461–469. [Google Scholar] [CrossRef]
| Variables | Mean ± SD | Range | |
|---|---|---|---|
| Max | Min | ||
| BL Average Power (W) | |||
| BW | 937.9 ± 114.2 ** | 1157.7 | 728.9 |
| 25%BW | 992.6 ± 159.7 ** | 1529.6 | 798.1 |
| 50%BW | 1064.4 ± 170.7 ** | 1593.1 | 838 |
| UL Average power (W) | |||
| BW | 749.7 ± 92.3 | 978.1 | 587.1 |
| 25%BW | 772.5 ± 107.3 | 1107.7 | 617.1 |
| 50%BW | 755.9 ± 99.3 | 955.6 | 578.7 |
| UR Average power (W) | |||
| BW | 715.4 ± 86.7 | 917.2 | 547.3 |
| 25%BW | 765.1 ± 94.8 | 971.8 | 647.7 |
| 50%BW | 768.5 ± 105.2 | 987.7 | 585.1 |
| BL Peak power (W) | |||
| BW | 2921.9 ± 366.2 ** | 4382 | 1265 |
| 25%BW | 2962.6 ± 533.6 ** | 4814 | 2310 |
| 50%BW | 3042.1 ± 534.4 ** | 4686 | 2333 |
| UL Peak power (W) | |||
| BW | 1845.9 ± 329.9 | 2551.4 | 1348.2 |
| 25%BW | 1834.1 ± 352.1 | 2731 | 1399.7 |
| 50%BW | 1730.1 ± 356.9 | 2384 | 1024.4 |
| UR Peak power (W) | |||
| BW | 1712.5 ± 295.9 | 2370.4 | 1209 |
| 25%BW | 1766.8 ± 289.3 | 2524.3 | 1163.9 |
| 50%BW | 1761.9 ± 362.8 | 2652.2 | 883.7 |
| Variables | Mean ± SD | Range | |
|---|---|---|---|
| Max | Min | ||
| Sprinting (s) | |||
| 10 m | 1.67 ± 0.06 | 1.84 | 1.53 |
| 20 m | 2.91 ± 0.01 | 3.14 | 2.69 |
| 30 m | 4.05 ± 0.12 | 4.37 | 3.77 |
| 40 m | 5.19 ± 0.16 | 5.61 | 4.89 |
| COD-90° (s) | |||
| COD-Left | 4.10 ± 0.11 | 4.30 | 3.89 |
| COD-Right | 4.14 ± 0.17 | 4.46 | 3.82 |
| COD-DEC (%) | |||
| Left | 41.5 ± 3.8 | 49.1 | 54.3 |
| Right | 42.9 ± 5.4 | 33.4 | 35.5 |
| HCMJ (cm) | |||
| HCMJ-Bilateral | 235.1 ± 12.9 ** | 271 | 208 |
| HCMJ-Left | 212.6 ± 7.8 | 232 | 190 |
| HCMJ-Right | 212.6 ± 11.2 | 239 | 189 |
| Variables | Sprinting 10 m (s) | Sprinting 40 m (s) | ||||
|---|---|---|---|---|---|---|
| Fast (n = 18) | Slow (n = 9) | ES | Fast (n = 17) | Slow (n = 10) | ES | |
| BPAvg Power (W) | ||||||
| BW | 966.1 ± 101.4 | 863.4 ± 102.8 * | −0.87 ± 0.69↓↓ | 980.9 ± 89.7 | 846.8 ± 95.3 ** | −1.39 ± 0.70↓↓ |
| 25%BW | 1010.8 ± 182.6 | 957.2 ± 99.8 | −0.35 ± 0.62 | 1039.3 ± 176.3 | 909.4 ± 83.5 * | −0.90 ± 0.61↓↓ |
| 50%BW | 1101.5 ± 179.5 | 958.4 ± 59.1 ** | −1.03 ± 0.58↓↓ | 1116.2 ± 171.9 | 946.7 ± 74.2 ** | −1.23 ± 0.60↓↓ |
| BPPeak Power (W) | ||||||
| BW | 2904.1 ± 598.2 | 2705.2 ± 284.8 | −0.41 ± 0.61 | 2936.8 ± 607.1 | 2065.5 ± 260.4 | −0.55 ± 0.60↓ |
| 25%BW | 3052.5 ± 619.9 | 2846.3 ± 377.8 | −0.39 ± 0.64 | 3159.1 ± 598.4 | 2667.8 ± 277.9 ** | −1.01 ± 0.61↓↓ |
| 50%BW | 3088.3 ± 750.8 | 2675.3 ± 220.3 * | −0.71 ± 0.57↓↓ | 3108.6 ± 764.1 | 2682.8 ± 238.4 * | −0.72 ± 0.58↓↓ |
| Jump (cm) | ||||||
| HCMJ | 237.8 ± 12.9 | 227.5 ± 11.0** | −0.83 ± 0.70↓↓ | 238.1 ± 12.8 | 228.6 ± 12.5 ** | −0.73 ± 0.71↓ |
| COD 90° | ||||||
| Left | 4.08 ± 0.13 | 4.14 ± 0.09 | 0.50 ± 0.70 | 4.07 ± 0.12 | 4.17 ± 0.09 | 0.86 ± 0.73↓ |
| Right | 4.12 ± 0.18 | 4.17 ± 0.17 | 0.29 ± 0.72 | 4.10 ± 0.18 | 4.23 ± 0.12 | 0.77 ± 0.71↓ |
| COD-DEC (%) | ||||||
| Left | 42.7 ± 3.4 | 38.2 ± 3.1 ** | −1.30 ± 0.80↓↓ | 42.6 ± 3.5 | 39.1 ± 3.5 ** | −0.91 ± 0.78↓↓ |
| Right | 44.3 ± 5.6 | 39.2 ± 2.5 ** | −1.16 ± 0.66↓↓ | 43.7 ± 5.6 | 41.6 ± 4.9 | −0.46 ± 0.75 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ascenzi, G.; Ruscello, B.; Filetti, C.; Bonanno, D.; Di Salvo, V.; Nuñez, F.J.; Mendez-Villanueva, A.; Suarez-Arrones, L. Bilateral Deficit and Bilateral Performance: Relationship with Sprinting and Change of Direction in Elite Youth Soccer Players. Sports 2020, 8, 82. https://doi.org/10.3390/sports8060082
Ascenzi G, Ruscello B, Filetti C, Bonanno D, Di Salvo V, Nuñez FJ, Mendez-Villanueva A, Suarez-Arrones L. Bilateral Deficit and Bilateral Performance: Relationship with Sprinting and Change of Direction in Elite Youth Soccer Players. Sports. 2020; 8(6):82. https://doi.org/10.3390/sports8060082
Chicago/Turabian StyleAscenzi, Giampiero, Bruno Ruscello, Cristoforo Filetti, Daniele Bonanno, Valter Di Salvo, F. Javier Nuñez, Alberto Mendez-Villanueva, and Luis Suarez-Arrones. 2020. "Bilateral Deficit and Bilateral Performance: Relationship with Sprinting and Change of Direction in Elite Youth Soccer Players" Sports 8, no. 6: 82. https://doi.org/10.3390/sports8060082
APA StyleAscenzi, G., Ruscello, B., Filetti, C., Bonanno, D., Di Salvo, V., Nuñez, F. J., Mendez-Villanueva, A., & Suarez-Arrones, L. (2020). Bilateral Deficit and Bilateral Performance: Relationship with Sprinting and Change of Direction in Elite Youth Soccer Players. Sports, 8(6), 82. https://doi.org/10.3390/sports8060082






