1. Introduction
Winning one or two games during a Major League Baseball (MLB) season is often the difference between a team advancing to post-season play or “waiting until next year”. There is strong economic incentive to win; the estimated total market for U.S. spectator sports is in somewhere in the
range [
1]. Winning on the field produces a positive feedback effect on future sales of tickets, merchandising and advertising revenues.
Prior to each game or series, statistical metrics and scouting reports on opposing teams are compiled and are used to inform the design of lineups and strategies. Technology advances have made it feasible to augment this historical data with a dynamic statistical view of a game as it unfolds in real time. Forward thinking MLB teams may have already begun building large computing infrastructure for analysis and prediction using unstructured data [
2]. When combined with observations made by managers, coaches and players during a game, complex queries of data and predictions on opponents’ actions are possible.
Our hypothesis is that teams may gain a competitive edge by using real-time statistical decision support during a game.
Proposed here is an approach to exploit such data; a central element of this approach is machine learning. Prediction of the next pitch type is selected as a prototypical case study for real-time baseball analytics. The pitcher controls the pace and flow of the game. The time interval between pitches can be used to incrementally compute new statistics and make predictions according to the current game situation. In particular, the ability to improve the guess of the next pitch from the pitcher’s repertoire would represent a fundamental advantage to the offensive team. For pitchers, increasing deception by changing selection and sequencing of pitches in certain game situations can improve outcomes [
3].
Previous investigators [
4] applied support vector machine classifiers to predict the type of next pitch. They framed the machine learning problem as a binary decision,
i.e., predicting whether or not the next pitch is a fastball. Average overall accuracy for the “fastball, no fastball” prediction was reported as 70%. Linear predictive models were used, in order to analyze the importance of attributes contributing to correct prediction [
4].
A second hypothesis addressed in this study is that predictability of a player’s pitch sequences may be used to project his performance over a longer term. Such a capability would reduce risk faced by management in evaluation of potential trades, or to scouts assessing unproven emerging talent. We use classical regression analysis to demonstrate a relationship between pitch sequence complexity and both Earned Run Average (ERA) and Fielding Independent Pitching (FIP) statistics. To our knowledge, a predictive model relating pitch-wise complexity and long-term performance appears to be novel.
3. Results
3.1. Overall Predictability
The overall predictability of next pitch type using the current method is
. Predictive accuracy is averaged over all players in the sample
, each pitcher’s most frequently thrown four pitches, and all batters and game situations from the 2011–2013 regular MLB seasons. This rate of correct prediction compares favorably with other investigations, where an overall accuracy of
was obtained when classifying only “fastball/not fastball” as the next pitch [
4].
The top and bottom fifteen pitchers ranked in decreasing order of their associated predictability index π are listed in
Table 2. The most predictable player based on this statistic is Trevor Rosenthal; the least deterministic in terms of pitch selection is Adam Ottavino.
Table 2.
Most and least predictable pitchers, according to overall predictability.
Table 2.
Most and least predictable pitchers, according to overall predictability.
| Top 15: Pitcher | | Last 15: Pitcher | |
|---|
| Trevor Rosenthal | 92.4 | Tom Wilhelmsen | 64.7 |
| Tony Cingrani | 92.1 | Steve Cishek | 64.6 |
| Joe Kelly | 90.2 | Greg Holland | 64.5 |
| J.J. Hoover | 89.7 | Jesse Crain | 64.3 |
| Michael Wacha | 89.2 | Troy Patton | 64.1 |
| Sean Doolittle | 88.4 | Matt Lindstrom | 64.0 |
| Brad Peacock | 88.1 | Boone Logan | 63.9 |
| Junichi Tazawa | 87.8 | Antonio Bastardo | 63.8 |
| Aaron Cook | 87.5 | Manuel Corpas | 63.2 |
| Aroldis Chapman | 86.4 | Michael Gonzalez | 62.9 |
| Edward Mujica | 86.1 | Ervin Santana | 62.9 |
| Bryan Shaw | 86.0 | George Kontos | 62.6 |
| Jake Westbrook | 85.8 | Shawn Camp | 62.5 |
| Ronald Belisario | 85.8 | Bryan Morris | 58.0 |
| Pat Neshek | 85.6 | Adam Ottavino | 54.9 |
3.2. Predictability by Pitch Count
The ten most (and least) predictable pitchers for each pitch count scenario studied are summarized in
Table 3 and
Table 4. The sample size for this study was reduced slightly
as our procedure enforced the requirement that all four distinct pitch-predictor models converged to a feasible solution during training, and that a sufficient number of samples in each category were available.
It is observed from
Table 3 that several pitchers remain near amongst the most predictable in terms of pitch selection without regard to pitch count. These include Trevor Rosenthal, Joe Kelly, J.J. Hoover and Brad Peacock. An interesting observation is made by comparing
Table 3 with the results for the least predictable pitchers in
Table 4. Joel Hanrahan’s pitch selection is highly predictable when the batter is ahead in the count, but when the batter is behind, Hanrahan becomes very unpredictable. Contrast this with Luke Gregerson, whose selection is easy to predict when the batter is behind in the count, yet much less deterministic when pitching at a count disadvantage.
Table 3.
Most predictable pitchers, for batter ahead, behind and even in pitch count.
Table 3.
Most predictable pitchers, for batter ahead, behind and even in pitch count.
| Pitcher | | Pitcher | | Pitcher | |
|---|
| (Batter ahead) | | (Batter behind) | | (Even Count) | |
|---|
| Tony Cingrani | 97.7 | Trevor Rosenthal | 89.4 | Trevor Rosenthal | 93.7 |
| Aroldis Chapman | 95.9 | Edward Mujica | 88.5 | Tony Cingrani | 93.0 |
| Trevor Rosenthal | 95.2 | J.J. Hoover | 87.4 | Joe Kelly | 90.0 |
| Joel Hanrahan | 95.1 | Luke Gregerson | 86.2 | J.J. Hoover | 89.0 |
| Brad Peacock | 94.7 | Brandon League | 85.8 | Jake Westbrook | 87.5 |
| Joe Kelly | 94.5 | Joe Kelly | 85.7 | Phil Hughes | 87.1 |
| J.J. Hoover | 93.9 | Pat Neshek | 84.8 | Brad Peacock | 86.8 |
| Aaron Loup | 93.1 | Heath Bell | 83.5 | Aroldis Chapman | 86.7 |
| Brandon League | 91.8 | Wei-Yin Chen | 83.3 | Aaron Loup | 86.1 |
| Jake Westbrook | 91.6 | Brad Peacock | 83.0 | Heath Bell | 85.9 |
Table 4.
Least predictable pitchers, for batter ahead, behind and even in pitch count.
Table 4.
Least predictable pitchers, for batter ahead, behind and even in pitch count.
| Pitcher | | Pitcher | | Pitcher | |
|---|
| (Batter ahead) | | (Batter behind) | | (Even Count) | |
|---|
| Alfredo Aceves | 67.1 | Anthony Bass | 61.9 | Brandon McCarthy | 65.2 |
| Jamey Wright | 67.1 | Edwin Jackson | 61.7 | Ervin Santana | 64.9 |
| Louis Coleman | 66.9 | Tony Sipp | 61.5 | Rafael Soriano | 64.8 |
| Jesse Chavez | 66.8 | Kevin Jepsen | 60.3 | Aaron Crow | 64.8 |
| Luke Gregerson | 66.6 | Ervin Santana | 59.9 | Tony Sipp | 64.0 |
| Koji Uehara | 66.5 | Jonny Venters | 59.5 | Scott Atchison | 63.5 |
| Brandon McCarthy | 63.2 | Jose Mijares | 59.3 | Michael Gonzalez | 62.4 |
| Dan Haren | 62.9 | Daniel Bard | 58.4 | Jesse Crain | 62.2 |
| Scott Atchison | 62.7 | Rex Brothers | 56.2 | Guillermo Moscoso | 59.5 |
| Michael Gonzalez | 59.6 | Joel Hanrahan | 56.1 | Carlos Carrasco | 57.0 |
3.3. Predictability by Platoon
When batter and pitcher are of like-handedness, we observed an aggregated mean predictability of . In the case of the batter’s platoon advantage, overall predictability was . This increased degree of predictability may contribute to a hitter’s presumed advantage in such situations.
Numerical results obtained from predictive modeling of pitch selection under platooning based on handedness are presented in
Table 5 and
Table 6. These tables distill results for the top and bottom ten players ranked by predictability index π. In the most predictable list (
Table 5), several pitchers appearing consistently across all analyses are seen. Trevor Rosenthal, Tony Cingrani, Junichi Tazawa and Brad Peacock are very predictable, regardless of whether the batter is right- or left-handed. Similarly unaffected by platooning are Aaron Crow and Antonio Bastardo, as seen in the least predictable set in
Table 6.
Table 5.
Most predictable pitchers, for same and opposite handedness relative to the batter.
Table 5.
Most predictable pitchers, for same and opposite handedness relative to the batter.
| Pitcher | | Pitcher | |
|---|
| (Same Handedness) | | (Opposite Handedness) | |
|---|
| Trevor Rosenthal | 93.4 | Tony Cingrani | 94.0 |
| Charlie Morton | 89.5 | Brad Peacock | 91.7 |
| Jake Westbrook | 86.7 | Aaron Cook | 91.3 |
| Tony Cingrani | 86.4 | Junichi Tazawa | 91.2 |
| Will Harris | 85.7 | Trevor Rosenthal | 91.0 |
| Junichi Tazawa | 85.5 | Aaron Loup | 88.0 |
| Steve Delabar | 85.4 | Aroldis Chapman | 87.8 |
| Brad Peacock | 84.1 | Robbie Ross | 87.7 |
| Roy Oswalt | 83.2 | Matt Albers | 87.5 |
| Phil Hughes | 83.0 | Michael Wacha | 86.7 |
Table 6.
Least predictable pitchers, for same and opposite handedness relative to the batter.
Table 6.
Least predictable pitchers, for same and opposite handedness relative to the batter.
| Pitcher | | Pitcher | |
|---|
| (Same Handedness) | | (Opposite Handedness) | |
|---|
| Bud Norris | 63.3 | Justin Grimm | 69.0 |
| Mike Dunn | 63.2 | Aaron Crow | 68.1 |
| Alexi Ogando | 63.2 | Antonio Bastardo | 68.0 |
| Nick Vincent | 63.1 | Chris Tillman | 67.8 |
| Aaron Crow | 62.3 | David Huff | 67.7 |
| Grant Balfour | 62.3 | Jesse Crain | 67.7 |
| P.J. Walters | 62.2 | Luke Gregerson | 67.6 |
| Everett Teaford | 62.1 | Alex Burnett | 65.7 |
| Jon Rauch | 61.6 | Koji Uehara | 51.5 |
| Antonio Bastardo | 57.1 | Steve Delabar | 43.2 |
3.4. Out-of-Sample Test
In-sample cross-validation tests are commonly used for estimating generalization performance, and may in fact have greater statistical power in some cases [
13]. Nonetheless, it is important to assess the predictive performance of classifiers in out-of-sample mode. One inspiration for the current research is to inform an analytics platform that provides continuously-updated models, based on new input data, to predict the next behavior made by the opponent during a game. Results presented in earlier sections were focused on experiments to optimize pitch-specific predictors, and integrate their outputs in order to gain insight into the relative predictability of different pitchers’ selections, within different game situations.
For in-game application, with new input data
x, the outputs from each model must be combined to declare the next pitch type. The final decision
on pitch type prediction is made according to the (most positive) magnitude of the decision function output
from each classifier, or
[
14].
Results from out-of-sample predictions on previously unseen data from the 2013 World Series between the Boston Red Sox and the St. Louis Cardinals are summarized in
Table 7. On this limited sample of pitchers
, predictive accuracy upon combining all four pitch models is seen to range from 50% to nearly 70%. Also shown in the table are the number of batters faced (
) and the pitcher’s recorded earned run average (
).
Note that there is no obvious correlation between high predictability and performance as indicated by . The most predictable pitcher in this sample was Clay Buchholz, whose in the 2013 Series was 0.00. Similarly, Jon Lester was very predictable, yet his was outstanding at 0.590. Several pitchers previously identified during this research appear in the table. Jake Peavy’s pitch selection pattern was more difficult to decipher, but his was elevated at 4.50.
Table 7.
Out-of-sample predictive accuracy for pitchers appearing in the 2013 World Series.
Table 7.
Out-of-sample predictive accuracy for pitchers appearing in the 2013 World Series.
| Pitcher | | BF | ERA |
|---|
| Clay Buchholz | 69.8 | 18 | 0.00 |
| Jon Lester | 66.8 | 54 | 0.59 |
| Joe Kelly | 65.8 | 21 | 3.38 |
| Junichi Tazawa | 65.6 | 9 | 3.16 |
| Michael Wacha | 65.5 | 45 | 7.45 |
| Ryan Dempster | 65.4 | 5 | 9.00 |
| Adam Wainwright | 63.7 | 52 | 4.50 |
| Lance Lynn | 61.1 | 25 | 4.76 |
| John Lackey | 60.1 | 60 | 2.57 |
| Trevor Rosenthal | 57.4 | 16 | 0.00 |
| Felix Doubront | 55.5 | 17 | 1.93 |
| Craig Breslow | 54.7 | 7 | 54.00 |
| Koji Uehara | 51.2 | 15 | 0.00 |
| Jake Peavy | 50.2 | 19 | 4.50 |
3.5. Long-Term ERA and FIP Forecasting
An interesting question is whether the output from the machine learning method for prediction of pitches within a game situation could be used to estimate a pitcher’s future statistical performance.
The sample size represented in
Table 7 is insufficient for inference on a relationship between pitch selection predictability and
ERA, a fundamental metric of pitcher performance. We carried out linear regression analysis on the entire sample population
(from the original sample
, four
ERA values had data quality issues and were not included in the analysis) to determine if there was a meaningful statistical relationship between these variables, further including analysis of
FIP as a function of predictability index π. The dependent variables were constructed as the mean values of
ERA and
FIP recorded for each pitcher during the seasons in question.
Regression analysis on the entire sample did not uncover significant relationships between either π and ERA, or π and FIP.
Considering next only the third quartile of values
of the independent variable
, we calculated a regression equation for a player’s
ERA from his pitch selection predictability π as follows:
The coefficient for the predictor π is significant at the level . Standard error estimates for the intercept and coefficient are and , respectively. Plotting the residuals suggested an unbiased and random distribution throughout the range of fitted response values.
Similarly, a regression equation to predict
FIP was computed for this sample, applicable over the same range of the independent variable. This relationship is expressed as
which was also found significant at
(
; s.e.
and
for intercept and coefficient).
These results suggest that reducing complexity in selection of pitches (a proxy for increased predictability) is correlated with higher values of both FIP and ERA.
At predictability index scores
, the linear relationships break down.
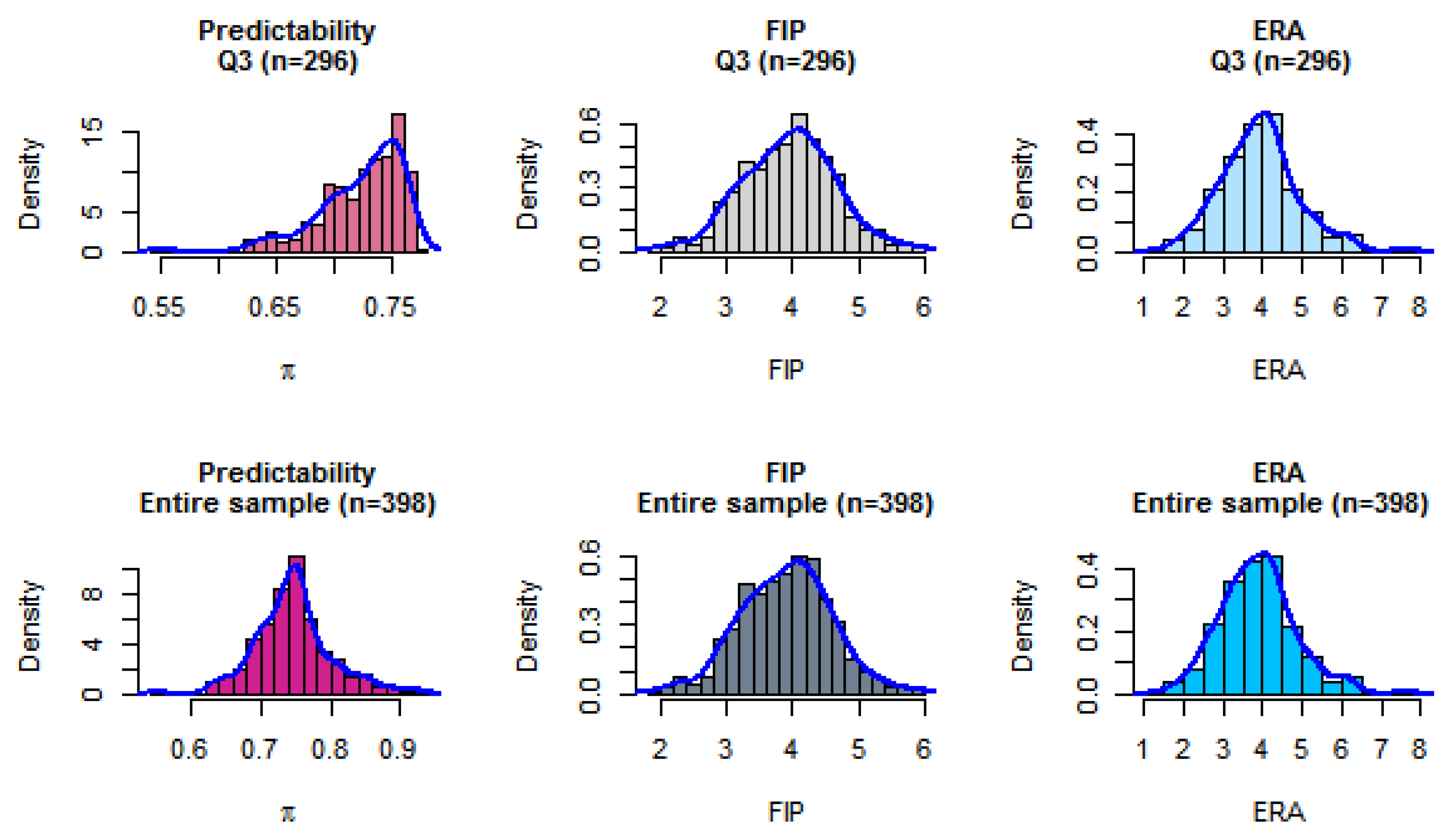
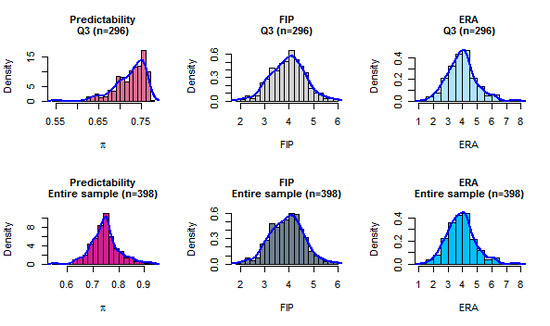
Figure 1 plots probability densities of the independent and explanatory variables subject to regression analysis. The top row in the figure represents the
distributions: computed predictability, and recorded
FIP and
ERA in that order. In the bottom row, the corresponding quantities for the entire sample are depicted.
It is noteworthy that the coefficient of determination for each regression model is low (ERA: ; FIP: ), clearly indicating that other factors contribute to the response variables beyond the predictability index considered in this preliminary analysis. The determination of such factors is left for future research.
The low p-values imply that changes in the predictor variable relate to changes in the response, however inadequate model precision. The value of these regression equations may rest in estimating a player’s potential performance with respect to his peers, when evaluating young athletes within a given level of competition.
For reference, the distribution of scores computed from the entire experimental sample is summarized in
Table 8.
Figure 1.
Densities of predictability , FIP and ERA for valid range of π in the regression equations (top row) and for the entire sample (bottom row).
Figure 1.
Densities of predictability , FIP and ERA for valid range of π in the regression equations (top row) and for the entire sample (bottom row).
Table 8.
Quartiles of all predictability index scores .
Table 8.
Quartiles of all predictability index scores .
| Min. | Q1 | Median | Q3 | Max. |
|---|
| 54.88 | 71.39 | 74.58 | 77.03 | 92.38 |
4. Discussion
It is hypothesized that baseball teams may gain a competitive edge by using real-time statistical decision support during a game. Technology advances now enable a potential pitch-wise dynamic statistical view of a game. Certain MLB teams are said to have built computing infrastructures for analysis and prediction using unstructured data [
2]. When combined with observations made by managers, coaches and players during a game, complex queries of data and predictions on opponents’ actions are possible.
We have presented a methodology to predict the next type of pitch anticipated from a pitcher, based on a machine learning model that includes historical data and game context as inputs. The time interval between pitches can be used to incrementally compute new statistics and make predictions according to the current game situation. The strategic value of the model outlined herein may be improved significantly by including relevant data such as scouting notes, text and voice annotations of player and coaching observations during the game.
Essentially, this is a method to dynamically predict player behavior. Both pitchers and batters can benefit from this approach. The batter might improve his guess as to the next pitch in a certain situation. The pitcher in turn could use knowledge of his predictability to confound the hitter by intermittent deviation from his statistical tendencies. Some non-cooperative game theoretic strategizing comes into play, assuming this type of information is applied in a game [
15]. We recognize and appreciate that being presented with this information during an at-bat may be confounding to certain players, who may choose to ignore it.
Sequence complexity and errors predicting the next value in that sequence are not simply related [
11,
16]. Many of the pitchers whose selection was found to be more deterministic in our experiments remain hard to hit. Knowing in advance that Aroldis Chapman is going to deliver a slider or a fastball does not make the task of hitting either pitch any easier.
The data contain many examples of statistically effective pitchers with a high predictability index (Trevor Rosenthal, ; Aroldis Chapman: ). Likewise, a number of pitchers with low predictability yet high ERA and/or FIP (Daisuke Matsuzaka, ; Everett Teaford: can be identified.
We observed that out-of-sample results were not as accurate upon prediction as those obtained from in-sample cross-validation testing. In-sample cross-validation tests are often used for estimating generalization performance. A common assumption is such tests are biased. However, it was noted in [
13] that in-sample tests may in fact have greater statistical power. This is especially true for cases where the sample size in the out-of-sample test is small, as the test may fail to detect predictability that exists in the population [
13].
For combining pitch-specific binary classifiers into a single decision, a number of schemes have been described in the literature [
14,
17]. Greater accuracy in prediction may be achieved by the introduction of more sophisticated voting mechanisms, e.g., [
18].
The main statistic used for evaluation of predictive performance in this research is accuracy. It is well known that accuracy as a statistical metric is counter-indicated in cases where costs of misclassification are unequal [
19]. In the present case, a misclassification equates to a wrong pitch type prediction. The cost of a wrong prediction is identical to that incurred when the batter’s guess is incorrect, which happens routinely.
Predictive results obtained in this study are good, in comparison with previous research [
4]. The cited study cast the prediction objective into terms of predicting “fastball, no fastball” for the next pitch, and observed an average rate of accuracy of 70%. In the present investigation, the predictability of the next pitch type here was found to be
. Here, we predict one of four pitches for each player, a somewhat more difficult induction objective. Results for certain pitches, players and game situations were observed often in high
even to
accuracy range, upon cross-validation.
The experimental sample used in this study was limited to pitchers recording at least 1000 pitches over the course of the three seasons considered. This subsetting of the population of all pitchers omits players with less than three years’ experience. Middle-relief pitchers and closers who do not throw as many total pitches as do starters are also generally excluded from this sample.
Linear regression analysis to explain ERA using an individual’s pitch sequence complexity suggests a simple relationship, given by the expression
This model was significant at the level . Reducing complexity in selection of pitches (increasing predictability) is correlated with higher values of ERA for the players represented in the sample. At values of π greater than the 75th percentile of all sample scores, the relationship is not statistically significant.
A regression equation to predict
FIP over the third quartile of predictability indices was found. This expression is written as
, and is likewise significant at
with a smaller
p value (
). Sabermetricians have stated that
FIP is a better predictor of future performance than measuring the present (e.g., using
ERA), owing to observed fluctuations in small samples [
20]. In terms of our hypothesis that predictability of pitch sequences may help project longer term pitching performance, the articulation of a linear relationship between predictability and
FIP is an important result.
A large proportion of the variances in FIP and ERA are not explained by these models, based on low values of determination coefficient for the model fits. Other explanatory variables must be included to explain the variance in response variables for precise forecasts for specific players.
A short list of variables that may impact observed pitching performance includes specific pitcher–batter matchups [
21], a catcher’s skills in pitch framing [
22], or even the effect of the umpire on called strikes [
23].
The investigation of these and other predictors is left to further research. Nonetheless, we can still infer that changes in the predictor (π), a measure of the “learnability” of pitch sequence patterns, are directly associated with changes in a player’s FIP and ERA over a longer term of performance.
This observation is valuable for management evaluation of hypothetical trades, or to scouts assessing pitching potential of undeveloped players.