Physiological Correspondence Between Different Indexes of High-Intensity Endurance Exercise in Young Male Runners
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Experimental Design
2.3. Maximal Incremental Test
2.4. Critical Speed (CS) Determination
2.5. Statistical Analysis
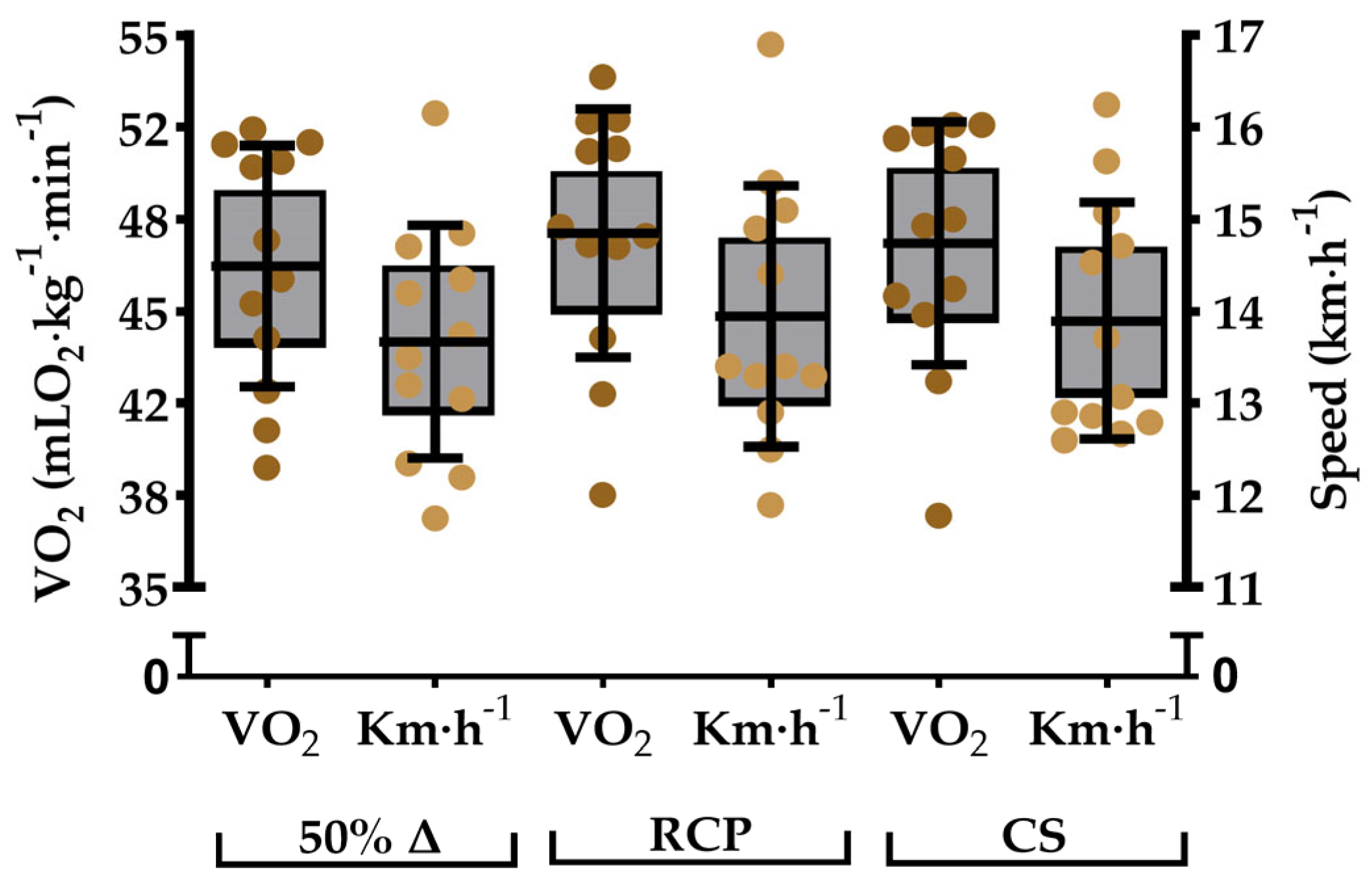
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| VO2 | Oxygen uptake |
| VO2max | Maximal oxygen uptake |
| vVO2max | Speed corresponding to the VO2max in the incremental test |
| VCO2 | Carbon dioxide |
| H+ | Hydrogen ion |
| Pi | Inorganic phosphate |
| [La-] | Blood lactate concentration |
| GET | Gas exchange threshold |
| vGET | Speed corresponding to the GET in incremental test |
| 50%Δ | Middle point of the difference GET and VO2max |
| v50%Δ | Speed corresponding to 50%Δ in the incremental test |
| LT | Lactate threshold |
| VT1 | First ventilatory threshold |
| MLSS | Maximal lactate steady state |
| VE | Pulmonary ventilation |
| RCP | Respiratory compensation point |
| vRCP | Speed corresponding to the RCP in the incremental test |
| VT2 | Second ventilatory threshold |
| LTP | Lactate turn point |
| CS | Critical speed |
| tLim | Time limit |
| v-tLim | Time-limited model for the assessment of CS using trials with different velocities |
| d-tLim | Distance-limited model for the assessment of CS using trials with different distances |
References
- Burnley, M.; Jones, A.M. Power–duration relationship: Physiology, fatigue, and the limits of human performance. Eur. J. Sport Sci. 2018, 18, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Jones, A.M.; Burnley, M.; Black, M.I.; Poole, D.C.; Vanhatalo, A. The maximal metabolic steady state: Redefining the ‘gold standard’. Physiol. Rep. 2019, 7, e14098. [Google Scholar] [CrossRef] [PubMed]
- Jones, A.M.; Wilkerson, D.P.; DiMenna, F.; Fulford, J.; Poole, D.C. Muscle metabolic responses to exercise above and below the “critical power” assessed using 31P-MRS. Am. J. Physiol. Regul. Integr. Comp. Physiol. 2008, 294, 585–593. [Google Scholar] [CrossRef] [PubMed]
- Sietsema, K.E.; Rossiter, H.B. Exercise physiology and cardiopulmonary exercise testing. Semin. Respir. Crit. Care Med. 2023, 44, 661–680. [Google Scholar] [CrossRef]
- Whipp, B.J. Physiological mechanisms dissociating pulmonary CO2 and O2 exchange dynamics during exercise in humans. Exp. Physiol. 2007, 92, 347–355. [Google Scholar] [CrossRef]
- Broxterman, R.M.; Ade, C.J.; Craig, J.C.; Wilcox, S.L.; Schlup, S.J.; Barstow, T.J. The relationship between critical speed and the respiratory compensation point: Coincidence or equivalence. Eur. J. Sport Sci. 2015, 15, 631–639. [Google Scholar] [CrossRef]
- Jones, A.M.; Kirby, B.S.; Clark, I.E.; Rice, H.M.; Fulkerson, E.; Wylie, L.J.; Wilkerson, D.P.; Vanhatalo, A.; Wilkins, B.W. Physiological demands of running at 2-hour marathon race pace. J. Appl. Physiol. 2021, 130, 369–379. [Google Scholar] [CrossRef]
- Poole, D.C.; Burnley, M.; Vanhatalo, A.; Rossiter, H.B.; Jones, A.M. Critical power: An important fatigue threshold in exercise physiology. Med. Sci. Sports Exerc. 2016, 48, 2320–2334. [Google Scholar] [CrossRef]
- Vanhatalo, A.; Fulford, J.; DiMenna, F.J.; Jones, A.M. Influence of hyperoxia on muscle metabolic responses and the power-duration relationship during severe-intensity exercise in humans: A 31P magnetic resonance spectroscopy study. Exp. Physiol. 2010, 95, 528–540. [Google Scholar] [CrossRef]
- Zoladz, J.A.; Majerczak, J.; Grassi, B.; Szkutnik, Z.; Korostyński, M.; Gołda, S.; Grandys, M.; Jarmuszkiewicz, W.; Kilarski, W.; Karasinski, J.; et al. Mechanisms of attenuation of pulmonary VO2 slow component in humans after prolonged endurance training. PLoS ONE 2016, 11, e0154135. [Google Scholar] [CrossRef]
- Massini, D.A.; Pessôa Filho, D.M.; Caritá, R.A.C.; Denadai, B.S. Physiological and perceptual response at critical speed and respiratory compensation point. Braz. J. Sports Med. 2016, 22, 439–444. [Google Scholar] [CrossRef][Green Version]
- Souza, K.M.; Lucas, R.D.; Salvador, P.C.N.; Helal, L.C.A.S.; Guglielmo, L.G.A.; Greco, C.C.; Denadai, B.S. Agreement analysis between critical power and intensity corresponding to 50% in cycling exercise. Braz. J. Kinanthropom Hum. Perform. 2016, 18, 197–206. [Google Scholar] [CrossRef]
- Sitko, S.; Ciper-Sastre, R.; Corbi, F.; López-Laval, I. Relationship between functional threshold power, ventilatory threshold and respiratory compensation point in road cycling. J. Sports Med. Phys. Fit. 2022, 62, 626–632. [Google Scholar] [CrossRef]
- Pringle, J.S.M.; Doust, J.H.; Carter, H.; Tolfrey, K.; Campbell, I.T.; Jones, A.M. Oxygen uptake kinetics during moderate, heavy and severe intensity “submaximal” exercise in humans: The influence of muscle fibre type and capillarisation. Eur. J. Appl. Physiol. 2003, 89, 289–300. [Google Scholar] [CrossRef]
- Caputo, F.; Denadai, B.S. Does 75% of the difference between VO2 at lactate threshold and VO2max lie at the severe-intensity domain in well-trained cyclists? Sci. Sports 2009, 24, 257–261. [Google Scholar] [CrossRef]
- Caritá, R.A.C.; Caputo, F.; Greco, C.C.; Denadai, B.S. Aerobic fitness and amplitude of the exercise intensity domains during cycling. Braz. J. Sports Med. 2013, 19, 271–274. [Google Scholar] [CrossRef]
- Denadai, B.S.; Greco, C.C. Can the critical power model explain the increased peak speed/power during incremental test after concurrent strength and endurance training? J. Strength Cond. Res. 2017, 31, 2319–2323. [Google Scholar] [CrossRef]
- Rossiter, H.B. Exercise: Kinetic considerations for gas exchange. Compr. Physiol. 2011, 1, 203–244. [Google Scholar] [CrossRef]
- Lansley, K.E.; DiMenna, F.J.; Bailey, S.J.; Jones, A.M. A ‘new’ method to normalise exercise intensity. Int. J. Sports Med. 2011, 32, 535–541. [Google Scholar] [CrossRef]
- Carter, H.; Pringle, J.S.; Jones, A.M.; Doust, J.H. Oxygen uptake kinetics during treadmill running across exercise intensity domains. Eur. J. Appl. Physiol. 2002, 86, 347–354. [Google Scholar] [CrossRef]
- Burnley, M.; Davison, G.; Baker, J.R. Effects of Priming exercise on VO2 Kinetics and the power-duration relationship. Med. Sci. Sports Exerc. 2011, 43, 2171–2179. [Google Scholar] [CrossRef]
- Dekerle, J.; Baron, B.; Dupont, L.; Vanvelcenaher, J.; Pelayo, P. Maximal lactate steady state, respiratory compensation threshold and critical power. Eur. J. Appl. Physiol. 2003, 89, 281–288. [Google Scholar] [CrossRef]
- Pessôa Filho, D.M.; Alves, F.; Reis, J.; Greco, C.; Denadai, B.S. VO2 kinetics during heavy and severe exercise in swimming. Int. J. Sports Med. 2012, 33, 744–748. [Google Scholar] [CrossRef]
- Almeida, T.A.F.; Espada, M.C.; Massini, D.A.; Macedo, A.G.; Castro, E.A.; Ferreira, C.C.; Reis, J.F.; Pessôa Filho, D.M. Stroke and physiological relationships during the incremental front crawl test: Outcomes for planning and pacing aerobic training. Front. Physiol. 2023, 14, 1241948. [Google Scholar] [CrossRef]
- Massini, D.A.; Espada, M.C.; Macedo, A.G.; Santos, F.J.; Castro, E.A.; Ferreira, C.C.; Robalo, R.A.M.; Dias, A.A.P.; Almeida, T.A.F.; Pessôa Filho, D.M. Oxygen uptake kinetics and time limit at maximal aerobic workload in tethered swimming. Metabolites 2023, 13, 773. [Google Scholar] [CrossRef]
- Broxterman, R.M.; Ade, C.J.; Barker, T.; Barstow, T.J. Influence of pedal cadence on the respiratory compensation point and its relation to critical power. Respir. Physiol. Neurobiol. 2015, 208, 1–7. [Google Scholar] [CrossRef]
- Harriss, D.J.; Jones, C.; MacSween, A. Ethical standards in sport and exercise science research: 2022 update. Int. J. Sports Med. 2022, 43, 1065–1070. [Google Scholar] [CrossRef]
- Vucetić, V.; Sentija, D.; Sporis, G.; Trajković, N.; Milanović, Z. Comparison of ventilation threshold and heart rate deflection point in fast and standard treadmill test protocols. Acta Clin. Croat 2014, 52, 190–203. [Google Scholar]
- Scheuermann, B.W.; Kowalchuk, J.M. Attenuated respiratory compensation during rapidly incremented ramp exercise. Respir. Physiol. 1998, 114, 227–238. [Google Scholar] [CrossRef]
- Massini, D.A.; Caritá, R.A.C.; Siqueira, L.O.; Simionato, A.R.; Denadai, B.S.; Pessôa Filho, D.M. Assessment of critical speed in track and treadmill: Physiological profiles and relationship with 3000-meter performance. Braz. J. Kinanthropom Hum. Perform. 2018, 20, 432–444. [Google Scholar] [CrossRef][Green Version]
- Díaz, S.P.; Fernández, S.P. Determinación del tamaño muestral para calcular la significación del coeficiente de correlación lineal. Cad. Aten. Primaria 2002, 9, 209–211. [Google Scholar]
- Bland, J.M.; Altman, D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Ferguson, C.J. An effect size primer: A guide for clinicians and researchers. Prof. Psychol. Res. 2009, 40, 532–538. [Google Scholar] [CrossRef]
- Vanhatalo, A.; Black, M.I.; DiMenna, F.J.; Blackwell, J.R.; Schmidt, J.F.; Thompson, C.; Wylie, L.J.; Mohr, M.; Bangsbo, J.; Krustrup, P.; et al. The mechanistic bases of the power-time relationship: Muscle metabolic responses and relationships to muscle fibre type. J. Physiol. 2016, 594, 4407–4423. [Google Scholar] [CrossRef]
- Murgatroyd, S.R.; Wylde, L.A.; Cannon, D.T.; Ward, S.A.; Rossiter, H.B. A ‘ramp-sprint’ protocol to characterise indices of aerobic function and exercise intensity domains in a single laboratory test. Eur. J. Appl. Physiol. 2014, 114, 1863–1874. [Google Scholar] [CrossRef]
- Philp, A.; Macdonald, A.; Carter, H.; Watt, P.; Pringle, J. Maximal lactate steady state as a training stimulus. Int. J. Sports Med. 2008, 29, 475–479. [Google Scholar] [CrossRef]
- Neder, J.A.; Jones, P.W.; Nery, L.E.; Whipp, B.J. The effect of age on the power/duration relationship and the intensity-domain limits in sedentary men. Eur. J. Appl. Physiol. 2000, 82, 326–332. [Google Scholar] [CrossRef]
- Busso, T.; Chatagnon, M. Modelling of aerobic and anaerobic energy production in middle-distance running. Eur. J. Appl. Physiol. 2006, 97, 745–754. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Massini, D.A.; Caritá, R.A.C.; Almeida, T.A.F.; Macedo, A.G.; Hernández-Beltrán, V.; Gamonales, J.M.; Espada, M.C.; Pessôa Filho, D.M. Physiological Correspondence Between Different Indexes of High-Intensity Endurance Exercise in Young Male Runners. Sports 2025, 13, 167. https://doi.org/10.3390/sports13060167
Massini DA, Caritá RAC, Almeida TAF, Macedo AG, Hernández-Beltrán V, Gamonales JM, Espada MC, Pessôa Filho DM. Physiological Correspondence Between Different Indexes of High-Intensity Endurance Exercise in Young Male Runners. Sports. 2025; 13(6):167. https://doi.org/10.3390/sports13060167
Chicago/Turabian StyleMassini, Danilo A., Renato A. C. Caritá, Tiago A. F. Almeida, Anderson G. Macedo, Víctor Hernández-Beltrán, José M. Gamonales, Mário C. Espada, and Dalton M. Pessôa Filho. 2025. "Physiological Correspondence Between Different Indexes of High-Intensity Endurance Exercise in Young Male Runners" Sports 13, no. 6: 167. https://doi.org/10.3390/sports13060167
APA StyleMassini, D. A., Caritá, R. A. C., Almeida, T. A. F., Macedo, A. G., Hernández-Beltrán, V., Gamonales, J. M., Espada, M. C., & Pessôa Filho, D. M. (2025). Physiological Correspondence Between Different Indexes of High-Intensity Endurance Exercise in Young Male Runners. Sports, 13(6), 167. https://doi.org/10.3390/sports13060167











