Relationship between Longitudinal Upper Body Rotation and Energy Cost of Running in Junior Elite Long-Distance Runners
Abstract
:1. Introduction
2. Materials and Methods
2.1. Subjects
2.2. Test Design and Protocol
2.3. Data Acquisition and Pre-Processing
2.4. Data Analysis
3. Results
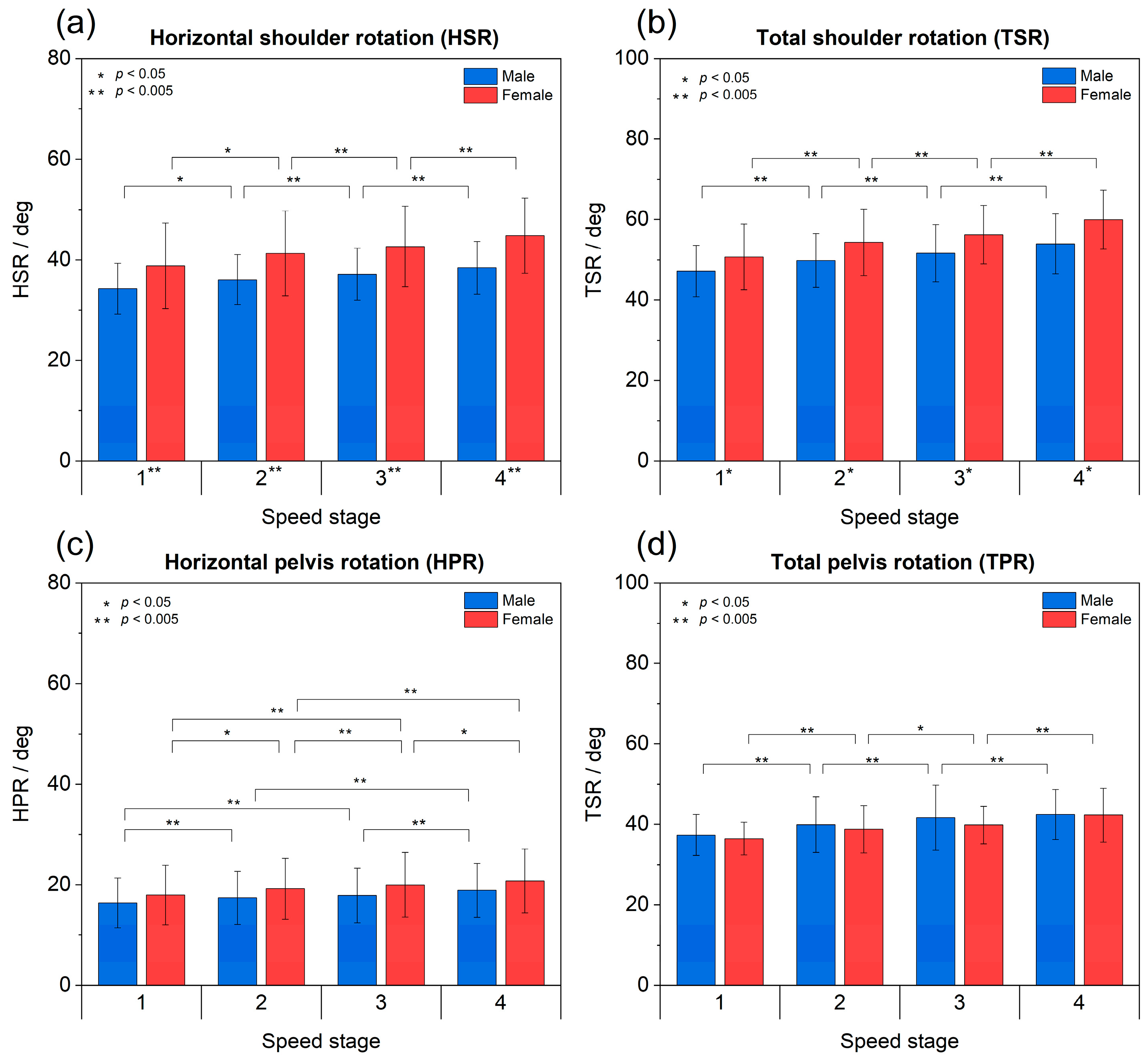
3.1. Shoulder Rotation
3.2. Pelvis Rotation
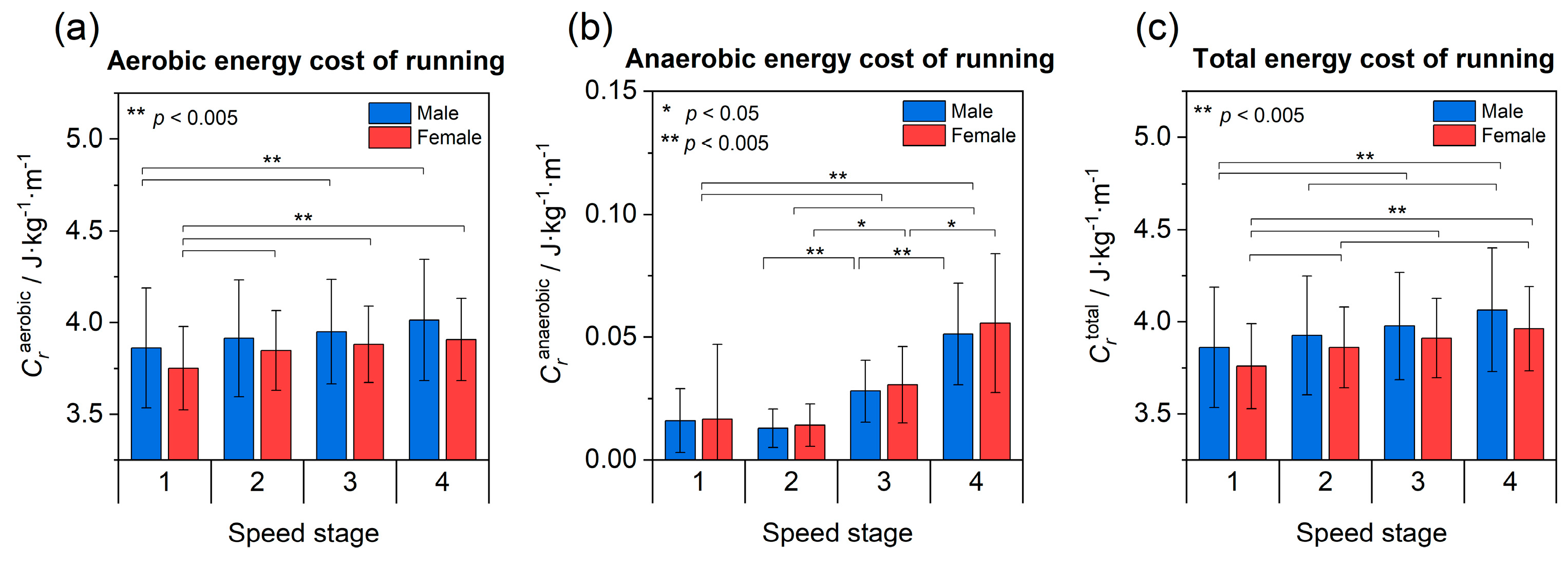
3.3. Energy Cost of Running
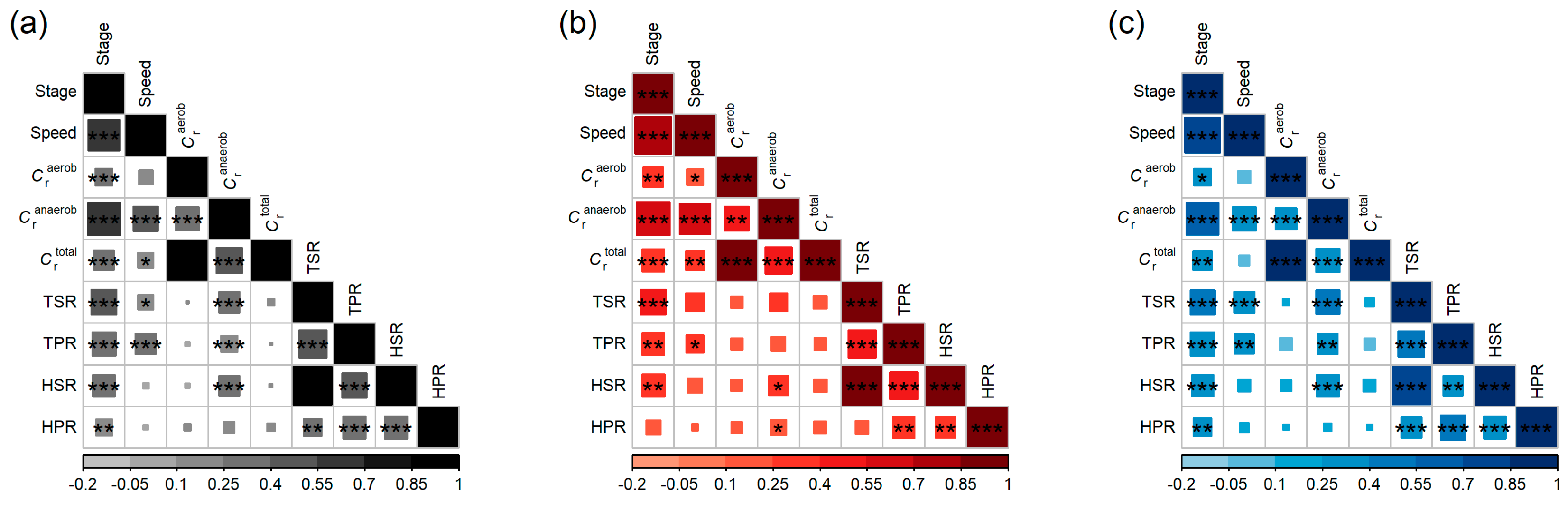
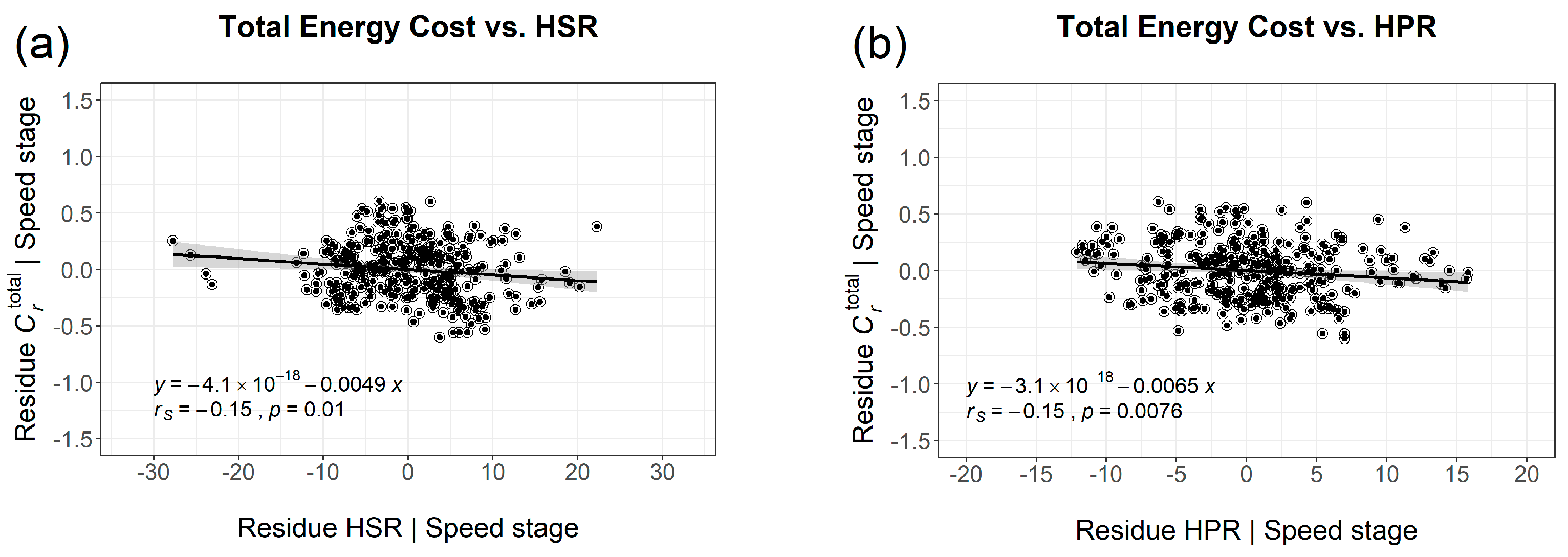
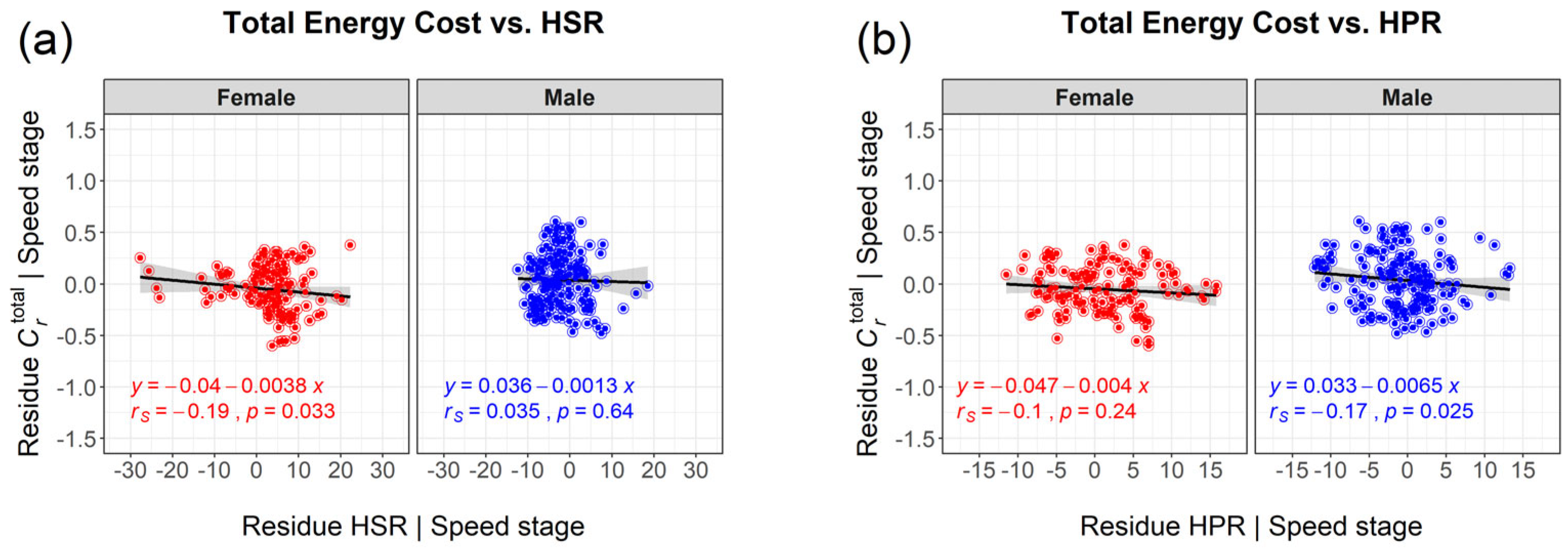
3.4. Relations between Trunk Rotation and Running Economy
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 13 | 15.9 ± 1.2 | 15.9 ± 1.2 | 15.9 ± 1.2 | 15.9 ± 1.2 | |
| 2 (3.50/3.75 m/s) | male | n = 11 | 17.6 ± 1.0 | 17.6 ± 1.0 | 17.6 ± 1.0 | 17.6 ± 1.0 |
| female | n = 22 | 17.6 ± 2.4 | 17.6 ± 2.4 | 17.6 ± 2.4 | 17.6 ± 2.4 | |
| 3 (4.00/4.25 m/s) | male | n = 33 | 17.4 ± 1.1 | 17.4 ± 1.1 | 17.4 ± 1.1 | 17.4 ± 1.1 |
| female | n = 2 | 17.0 ± 0.0 | 17.0 ± 0.0 | 17.0 ± 0.0 | 17.0 ± 0.0 | |
| 4 (4.50/4.75 m/s) | male | n = 5 | 22.6 ± 5.1 | 22.6 ± 5.1 | 22.6 ± 5.1 | 22.6 ± 5.1 |
| female | - | - | - | - | - | |
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 13 | 52.0 ± 5.7 | 52.0 ± 5.7 | 52.0 ± 5.7 | 52.0 ± 5.7 | |
| 2 (3.50/3.75 m/s) | male | n = 11 | 70.3 ± 7.9 | 70.3 ± 7.9 | 70.3 ± 7.9 | 70.3 ± 7.9 |
| female | n = 22 | 52.2 ± 4.6 | 52.2 ± 4.6 | 52.2 ± 4.6 | 52.2 ± 4.6 | |
| 3 (4.00/4.25 m/s) | male | n = 33 | 66.2 ± 6.1 | 66.2 ± 6.1 | 66.2 ± 6.1 | 66.2 ± 6.1 |
| female | n = 2 | 53.6 ± 13.6 | 53.6 ± 13.6 | 53.6 ± 13.6 | 53.6 ± 13.6 | |
| 4 (4.50/4.75 m/s) | male | n = 5 | 65.3 ± 3.4 | 65.3 ± 3.4 | 65.3 ± 3.4 | 65.3 ± 3.4 |
| female | - | - | - | - | - | |
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 13 | 169.6 ± 6.2 | 169.6 ± 6.2 | 169.6 ± 6.2 | 169.6 ± 6.2 | |
| 2 (3.50/3.75 m/s) | male | n = 11 | 183.6 ± 6.4 | 183.6 ± 6.4 | 183.6 ± 6.4 | 183.6 ± 6.4 |
| female | n = 22 | 169.5 ± 5.3 | 169.5 ± 5.3 | 169.5 ± 5.3 | 169.5 ± 5.3 | |
| 3 (4.00/4.25 m/s) | male | n = 33 | 180.9 ± 5.1 | 180.9 ± 5.1 | 180.9 ± 5.1 | 180.9 ± 5.1 |
| female | n = 2 | 166.1 ± 0.2 | 166.1 ± 0.2 | 166.1 ± 0.2 | 166.1 ± 0.2 | |
| 4 (4.50/4.75 m/s) | male | n = 5 | 184.2 ± 5.8 | 184.2 ± 5.8 | 184.2 ± 5.8 | 184.2 ± 5.8 |
| female | - | - | - | - | - | |
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 13 | 2.82 ± 0.09 | 2.83 ± 0.11 | 2.85 ± 0.11 | 2.88 ± 0.12 | |
| 2 (3.50/3.75 m/s) | male | n = 11 | 2.70 ± 0.09 | 2.71 ± 0.08 | 2.73 ± 0.09 | 2.75 ± 0.10 |
| female | n = 22 | 2.82 ± 0.13 | 2.85 ± 0.14 | 2.88 ± 0.14 | 2.91 ± 0.14 | |
| 3 (4.00/4.25 m/s) | male | n = 33 | 2.73 ± 0.10 | 2.76 ± 1.10 | 2.80 ± 0.11 | 2.83 ± 0.12 |
| female | n = 2 | 2.95 ± 0.05 | 2.98 ± 0.06 | 3.02 ± 0.03 | 3.05 * | |
| 4 (4.50/4.75 m/s) | male | n = 5 | 2.77 ± 0.15 | 2.78 ± 0.17 | 2.81 ± 0.19 | 2.86 ± 0.19 |
| female | - | - | - | - | - | |
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 13 | 169.2 ± 5.4 | 169.8 ± 6.6 | 171± 6.6 | 172.8 ± 7.2 | |
| 2 (3.50/3.75 m/s) | male | n = 11 | 162 ± 5.4 | 162.6 ± 4.8 | 163.8 ± 5.4 | 165 ± 6 |
| female | n = 22 | 169.2 ± 7.8 | 171 ± 8.4 | 172.8 ± 8.4 | 174.6 ± 8.4 | |
| 3 (4.00/4.25 m/s) | male | n = 33 | 163.8 ± 6 | 165.6 ± 6.6 | 168 ± 6.6 | 169.8 ± 7.2 |
| female | n = 2 | 177 ± 3 | 178.8 ± 3.6 | 181.2 ± 1.8 | 183 * | |
| 4 (4.50/4.75 m/s) | male | n = 5 | 166.2 ± 9 | 166.8 ± 10.2 | 168.6 ± 11.4 | 171.6 ± 11.4 |
| female | - | - | - | - | - | |
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 11 | 195 ± 9 | 190 ± 9 | 184 ± 8 | 178 ± 8 | |
| 2 (3.50/3.75 m/s) | male | n = 9 | 194 ± 15 | 188 ± 14 | 182 ± 14 | 177 ± 14 |
| female | n = 16 | 186 ± 14 | 180 ± 14 | 174 ± 14 | 169 ± 14 | |
| 3 (4.00/4.25 m/s) | male | n = 31 | 182 ± 12 | 178 ± 12 | 173 ± 11 | 168 ± 11 |
| female | n = 2 | 176 ± 4 | 173 ± 5 | 167 ± 4 | 166 * | |
| 4 (4.50/4.75 m/s) | male | n = 2 | 176 ± 14 | 171 ± 14 | 167 ± 16 | 163 ± 17 |
| female | - | - | - | - | - | |
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 11 | 161 ± 10 | 166 ± 12 | 170 ± 11 | 173 ± 10 | |
| 2 (3.50/3.75 m/s) | male | n = 9 | 177 ± 13 | 182 ± 13 | 185 ± 15 | 188 ± 17 |
| female | n = 16 | 168 ± 17 | 171 ± 18 | 171 ± 17 | 174 ± 18 | |
| 3 (4.00/4.25 m/s) | male | n = 31 | 185 ± 11 | 186 ±11 | 186 ± 11 | 187 ± 11 |
| female | n = 2 | 162 ± 2 | 162 ± 2 | 163 ± 0.5 | 162 * | |
| 4 (4.50/4.75 m/s) | male | n = 2 | 201 ± 28 | 202 ± 29 | 203 ± 30 | 200 ± 30 |
| female | - | - | - | - | - | |
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 8 | 9.6 ± 0.9 | 9.6 ± 1.1 | 9.4 ± 1.3 | 9.4 ± 1.4 | |
| 2 (3.50/3.75 m/s) | male | n = 11 | 11.0 ± 1.1 | 10.9 ± 0.9 | 10.9 ± 1.1 | 10.8 ± 1.1 |
| female | n = 21 | 9.9 ± 1.2 | 9.7 ± 1.1 | 9.5 ± 1.0 | 9.3 ± 1.0 | |
| 3 (4.00/4.25 m/s) | male | n = 27 | 10.8 ± 1.1 | 10.5 ± 1.1 | 10.2 ± 1.0 | 9.9 ± 1.1 |
| female | n = 2 | 8.8 ± 0.5 | 8.7 ± 0.6 | 8.4 ± 0.5 | 4.2 ± 5.9 | |
| 4 (4.50/4.75 m/s) | male | n = 5 | 10.5 ± 1.9 | 10.5 ± 2.0 | 10.1 ± 2.1 | 9.8 ± 1.8 |
| female | - | - | - | - | - | |
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 11 | 3.2 ± 0.4 | 3.4 ± 0.5 | 3.5 ± 0.5 | 3.7 ± 0.4 | |
| 2 (3.50/3.75 m/s) | male | n = 9 | 3.9 ± 0.6 | 4.1 ± 0.6 | 4.2 ± 0.7 | 4.3 ± 0.8 |
| female | n = 16 | 3.5 ± 0.7 | 3.6 ± 0.8 | 3.6 ± 0.7 | 3.7 ± 0.8 | |
| 3 (4.00/4.25 m/s) | male | n = 31 | 4.2 ± 0.5 | 4.2 ± 0.5 | 4.3 ± 0.5 | 4.3 ± 5.2 |
| female | n = 2 | 3.2 ± 0.1 | 3.2 ± 0.1 | 3.3 ± 0.0 | 3.2 * | |
| 4 (4.50/4.75 m/s) | male | n = 2 | 5.0 ± 1.4 | 5.1 ± 1.4 | 6.2 | 5.0 ± 1.5 |
| female | - | - | - | - | - | |
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 13 | 115 ± 5 | 123 ± 6 | 131 ± 6 | 138 ± 7 | |
| 2 (3.50/3.75 m/s) | male | n = 11 | 139 ± 7 | 147 ± 6 | 155 ± 6 | 163 ± 7 |
| female | n = 22 | 128 ± 7 | 134 ± 7 | 142 ± 8 | 149 ± 8 | |
| 3 (4.00/4.25 m/s) | male | n = 33 | 152 ± 6 | 159 ± 6 | 166 ± 6 | 173 ± 7 |
| female | n = 2 | 135 ± 2 | 142 ± 3 | 149 ± 2 | 156 * | |
| 4 (4.50/4.75 m/s) | male | n = 5 | 166 ± 7 | 175 ± 8 | 182 ± 9 | 188 ± 10 |
| female | - | - | - | - | - | |
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 13 | 39.2 ± 2.6 | 42.8 ± 2.6 | 45.5 ± 2.5 | 48.2 ± 1.1 | |
| 2 (3.50/3.75 m/s) | male | n = 11 | 47.4 ± 3.6 | 50.4 ± 3.6 | 53.2 ± 3.7 | 55.8 ± 3.4 |
| female | n = 22 | 43.1 ± 2.7 | 46.8 ± 2.8 | 49.8 ± 2.9 | 52.8 ± 1.2 | |
| 3 (4.00/4.25 m/s) | male | n = 33 | 50.0 ± 3.2 | 53.5 ± 3.4 | 56.7 ± 3.2 | 60.3 ± 5.7 |
| female | n = 2 | 46.8 ± 0.5 | 50.8 ± 0.1 | 55.0 ± 0.3 | 57.4 * | |
| 4 (4.50/4.75 m/s) | male | n = 5 | 51.5 ± 8.3 * | 55.4 ± 8.5 * | 58.3 ± 6.6 | 63.6 ± 3.9 |
| female | - | - | - | - | - | |
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 13 | 1.32 ± 0.36 | 1.70 ± 0.63 | 2.62 ± 1.04 | 4.22 ± 2.04 | |
| 2 (3.50/3.75 m/s) | male | n = 11 | 1.75 ± 0.48 | 2.34 ± 0.65 | 3.53 ± 1.03 | 5.50 ± 1.61 |
| female | n = 22 | 1.22 ± 0.38 | 1.68 ± 0.44 | 2.65 ± 0.87 | 4.48 ± 1.51 | |
| 3 (4.00/4.25 m/s) | male | n = 33 | 1.49 ± 0.52 | 1.90 ± 0.59 | 2.83 ± 0.80 | 4.54 ± 1.25 |
| female | n = 2 | 1.34 ± 0.21 | 2.05 ± 0.44 | 3.64 ± 1.04 | 4.86 * | |
| 4 (4.50/4.75 m/s) | male | n = 5 | 1.17 ± 0.42 | 1.55 ± 0.54 | 2.40 ± 0.78 | 4.38 ± 1.38 |
| female | - | - | - | - | - | |
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 13 | 3.76 ± 0.24 | 3.86 ± 0.24 | 3.85 ± 0.21 | 3.87 ± 0.17 | |
| 2 (3.50/3.75 m/s) | male | n = 11 | 4.01 ± 0.29 | 4.05 ± 0.30 | 4.06 ± 0.30 | 4.03 ± 0.25 |
| female | n = 22 | 3.75 ± 0.23 | 3.84 ± 0.22 | 3.90 ± 0.22 | 3.93 ± 0.26 | |
| 3 (4.00/4.25 m/s) | male | n = 33 | 3.83 ± 0.23 | 3.90 ± 0.24 | 3.95 ± 0.22 | 4.03 ± 0.37 |
| female | n = 2 | 3.69 ± 0.04 | 3.82 ± 0.02 | 3.95 ± 0.03 | 3.93 * | |
| 4 (4.50/4.75 m/s) | male | n = 5 | 3.51 ± 0.73 | 3.62 ± 0.72 | 3.70 ± 0.51 | 3.90 ± 0.27 |
| female | - | - | - | - | - | |
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 13 | 0.037 ± 0.06 | 0.013 ± 0.01 | 0.029 ± 0.02 | 0.051 ± 0.03 | |
| 2 (3.50/3.75 m/s) | male | n = 11 | 0.018 ± 0.01 | 0.018 ± 0.01 | 0.037 ± 0.01 | 0.063 ± 0.03 |
| female | n = 22 | 0.010 ± 0.01 | 0.014 ± 0.01 | 0.031 ± 0.01 | 0.058 ± 0.02 | |
| 3 (4.00/4.25 m/s) | male | n = 33 | 0.015 ± 0.01 | 0.011 ± 0.00 | 0.026 ± 0.01 | 0.048 ± 0.02 |
| female | n = 2 | 0.010 ± 0.00 | 0.018 ± 0.00 | 0.040 ± 0.00 | 0.06 * | |
| 4 (4.50/4.75 m/s) | male | n = 5 | 0.014 ± 0.01 | 0.010 ± 0.00 | 0.021 ± 0.01 | 0.049 ± 0.02 |
| female | - | - | - | - | - | |
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 13 | 3.77 ± 0.25 | 3.87 ± 0.25 | 3.88 ± 0.22 | 3.92 ± 0.17 | |
| 2 (3.50/3.75 m/s) | male | n = 11 | 4.03 ± 0.29 | 4.06 ± 0.30 | 4.09 ± 0.30 | 4.09 ± 0.27 |
| female | n = 22 | 3.76 ± 0.23 | 3.86 ± 0.22 | 3.92 ± 0.22 | 3.99 ± 2.64 | |
| 3 (4.00/4.25 m/s) | male | n = 33 | 3.85 ± 0.24 | 3.92 ± 0.24 | 3.98 ± 0.20 | 4.06 ± 0.37 |
| female | n = 2 | 3.70 ± 0.04 | 3.84 ± 0.02 | 3.99 ± 0.04 | 3.99 * | |
| 4 (4.50/4.75 m/s) | male | n = 5 | 3.51 ± 0.72 | 3.63 ± 0.72 | 3.72 ± 0.52 | 3.95 ± 0.29 |
| female | - | - | - | - | - | |
References
- Videbæk, S.; Bueno, A.M.; Nielsen, R.O.; Rasmussen, S. Incidence of running-related injuries per 1000 h of running in different types of runners: A systematic review and meta-analysis. Sports Med. 2015, 45, 1017–1026. [Google Scholar] [CrossRef] [PubMed]
- Shipway, R.; Holloway, I. Running free: Embracing a healthy lifestyle through distance running. Perspect. Public Health 2010, 130, 270–276. [Google Scholar] [CrossRef] [PubMed]
- Hreljac, A. Etiology, prevention, and early intervention of overuse injuries in runners: A biomechanical perspective. Phys. Med. Rehabil. Clin. N. Am. 2005, 16, 651–667. [Google Scholar] [CrossRef] [PubMed]
- van Mechelen, W. Running injuries. A review of the epidemiological literature. Sports Med. 1992, 14, 320–335. [Google Scholar] [CrossRef]
- Ueberschär, O.; Fleckenstein, D.; Warschun, F.; Kränzler, S.; Walter, N.; Hoppe, M.W. Measuring biomechanical loads and asymmetries in junior elite long-distance runners through triaxial inertial sensors. Sports Orthop. Traumatol. 2019, 35, 296–308. [Google Scholar] [CrossRef]
- Goss, D.L.; Lewek, M.; Yu, B.; Ware, W.B.; Teyhen, D.S.; Gross, M.T. Lower extremity biomechanics and self-reported foot-strike patterns among runners in traditional and minimalist shoes. J. Athl. Train. 2015, 50, 603–611. [Google Scholar] [CrossRef]
- Taunton, J.E.; Ryan, M.B.; Clement, D.B.; McKenzie, D.C.; Lloyd-Smith, D.R.; Zumbo, B.D. A retrospective case-control analysis of 2002 running injuries. Br. J. Sports Med. 2002, 36, 95–101. [Google Scholar] [CrossRef]
- Ferber, R.; Hreljac, A.; Kendall, K.D. Suspected mechanisms in the cause of overuse running injuries: A clinical review. Sports Health 2009, 1, 242–246. [Google Scholar] [CrossRef]
- Gruber, A.H.; Boyer, K.A.; Derrick, T.R.; Hamill, J. Impact shock frequency components and attenuation in rearfoot and forefoot running. J. Sport Health Sci. 2014, 3, 113–121. [Google Scholar] [CrossRef]
- Sheerin, K.R.; Reid, D.; Besier, T.F. The measurement of tibial acceleration in runners—A review of the factors that can affect tibial acceleration during running and evidence-based guidelines for its use. Gait Posture 2019, 67, 12–24. [Google Scholar] [CrossRef]
- Saunders, P.U.; Pyne, D.B.; Telford, R.D.; Hawley, J.A. Factors affecting running economy in trained distance runners. Sports Med. 2004, 34, 465–485. [Google Scholar] [CrossRef]
- Tartaruga, M.P.; Brisswalter, J.; Peyré-Tartaruga, L.A.; Ávila, A.O.V.; Alberton, C.L.; Coertjens, M.; Cadore, E.L.; Tiggemann, C.L.; Silva, E.M.; Kruel, L.F.M. The relationship between running economy and biomechanical variables in distance runners. Res. Q. Exerc. Sport 2012, 83, 367–375. [Google Scholar] [CrossRef]
- Folland, J.P.; Allen, S.J.; Black, M.I.; Handsaker, J.C.; Forrester, S.E. Running technique is an important component of running economy and performance. Med. Sci. Sports Exerc. 2017, 49, 1412. [Google Scholar] [CrossRef] [PubMed]
- Tjelta, L.I.; Shalfawi, S.A. Physiological factors affecting performance in elite distance runners. Acta Kinesiol. Univ. Tartu. 2016, 22, 7–19. [Google Scholar] [CrossRef]
- Moore, I.S. Is there an economical running technique? A review of modifiable biomechanical factors affecting running economy. Sports Med. 2016, 46, 793–807. [Google Scholar] [CrossRef]
- Saunders, S.W.; Schache, A.; Rath, D.; Hodges, P.W. Changes in three dimensional lumbo-pelvic kinematics and trunk muscle activity with speed and mode of locomotion. Clin. Biomech. 2005, 20, 784–793. [Google Scholar] [CrossRef] [PubMed]
- Hunter, I.; McLeod, A.; Valentine, D.; Low, T.; Ward, J.; Hager, R. Running economy, mechanics, and marathon racing shoes. J. Sports Sci. 2019, 37, 2367–2373. [Google Scholar] [CrossRef]
- Van Oeveren, B.T.; de Ruiter, C.J.; Beek, P.J.; van Dieën, J.H. The biomechanics of running and running styles: A synthesis. Sports Biomech. 2021, 1–39. [Google Scholar] [CrossRef] [PubMed]
- Kuindersma, S.; Deits, R.; Fallon, M.; Valenzuela, A.; Dai, H.; Permenter, F.; Koolen, T.; Marion, P.; Tedrake, R. Optimization-based locomotion planning, estimation, and control design for the atlas humanoid robot. Auton. Robot. 2016, 40, 429–455. [Google Scholar] [CrossRef]
- Mikolajczyk, T.; Mikołajewska, E.; Al-Shuka, H.F.N.; Malinowski, T.; Kłodowski, A.; Pimenov, D.Y.; Paczkowski, T.; Hu, F.; Giasin, K.; Mikołajewski, D.; et al. Recent Advances in Bipedal Walking Robots: Review of Gait, Drive, Sensors and Control Systems. Sensors 2022, 22, 4440. [Google Scholar] [CrossRef]
- Hinrichs, R.N.; Cavanagh, P.R.; Williams, K.R. Upper extremity function in running. I: Center of mass and propulsion considerations. J. Appl. Biomech. 1987, 3, 222–241. [Google Scholar] [CrossRef]
- Arellano, C.J.; Kram, R. The effects of step width and arm swing on energetic cost and lateral balance during running. J. Biomech. 2011, 44, 1291–1295. [Google Scholar] [CrossRef]
- Arellano, C.J.; Kram, R. The metabolic cost of human running: Is swinging the arms worth it? J. Exp. Biol. 2014, 217, 2456–2461. [Google Scholar] [CrossRef]
- Camomilla, V.; Bergamini, E.; Fantozzi, S.; Vannozzi, G. Trends supporting the in-field use of wearable inertial sensors for sport performance evaluation: A systematic review. Sensors 2018, 18, 873. [Google Scholar] [CrossRef] [PubMed]
- Arrese, A.L.; Izquierdo, D.M.; Urdiales, D. A review of the maximal oxygen uptake values necessary for different running performance levels. New Stud. Athl. 2005, 20, 7. [Google Scholar]
- Reiss, M.; Gohlitz, D. Schlüsselprobleme der Leistungsdiagnostik im Hochleistungstraining der Ausdauersportarten dargestellt am Beispiel der leichtathletischen Lauf-und Gehdisziplinen. [Elektronische Version]. Schriftenreihe Zur Angew. Trainingswissenschaft Heft 1994, 1, 30–48. [Google Scholar]
- Meyer, T. Der Respiratorische Quotient (RQ). Dtsch. Z. Für Sportmed. 2003, 54, 29–30. [Google Scholar]
- Heck, H.; Schulz, H. Methoden der anaeroben Leistungsdiagnostik. Dtsch. Z. Für Sportmed. 2002, 53, 8. [Google Scholar]
- Ueberschär, O.; Fleckenstein, D.; Warschun, F.; Walter, N.; Wüstenfeld, J.; Wolfarth, B.; Hoppe, M. Energy cost of running under hypogravity in well-trained runners and triathletes: A biomechanical perspective. Int. J. Comput. Sci. Sport 2019, 18, 60–80. [Google Scholar] [CrossRef]
- Spss, I. IBM SPSS Statistics for Windows; Version 23.0; IBM Corp: Armonk, NY, USA, 2015. [Google Scholar]
- Fritz, C.O.; Morris, P.E.; Richler, J.J. Effect size estimates: Current use, calculations, and interpretation. J. Exp. Psychol. Gen. 2012, 141, 2–18. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Hillsdale Educational Publishers: Hillsdale, MI, USA, 1988. [Google Scholar]
- RStudio Posit. Integrated Development Environment for R. Posit Software. 2023. Available online: https://posit.co/ (accessed on 3 September 2023).
- Scafoglieri, A.; Tresignie, J.; Provyn, S.; Marfell-Jones, M.; Reilly, T.; Bautmans, I.; Clarys, J.P. Prediction of segmental lean mass using anthropometric variables in young adults. J. Sports Sci. 2012, 30, 777–785. [Google Scholar] [CrossRef] [PubMed]
- Etnyre, B.R.; Lee, E.J. Chronic and acute flexibility of men and women using three different stretching techniques. Res. Q. Exerc. Sport 1988, 59, 222–228. [Google Scholar] [CrossRef]
- Anderson, T. Biomechanics and running economy. Sports Med. 1996, 22, 76–89. [Google Scholar] [CrossRef] [PubMed]
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 13 | 37.4 ± 12 | 41.0 ± 12.2 | 41.7 ± 11.1 | 42.3 ± 10.5 | |
| 2 (3.50/3.75 m/s) | male | n = 11 | 32.3 ± 3.9 | 34.4 ± 4.7 | 35.5 ± 5.0 | 36.2 ± 3.6 |
| female | n = 21 | 40.3 ± 5.0 | 41.9 ± 4.9 | 43.7 ± 4.9 | 45.8 ± 5.2 | |
| 3 (4.00/4.25 m/s) | male | n = 31 | 34.9 ± 5.3 | 36.6 ± 5.1 | 37.7 ± 5.3 | 39.1 ± 5.6 |
| female | n = 2 | 32.3 ± 12.1 | 35.5 ± 14.3 | 37.1 ± 15.1 | 52.3 * | |
| 4 (4.50/4.75 m/s) | male | n = 5 | 34.4 ± 5.5 | 36.1 ± 5.0 | 37.3 ± 5.7 | 38.4 ± 5.1 |
| female | - | - | - | - | - | |
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 13 | 49.7 ± 11.0 | 54.0 ± 11.3 | 55.3 ± 9.5 | 58.1 ± 10.2 | |
| 2 (3.50/3.75 m/s) | male | n = 11 | 43.3 ± 4.6 | 45.9 ± 5.5 | 48.7 ± 6.0 | 51.5 ± 6.1 |
| female | n = 21 | 51.9 ± 5.6 | 55.2 ± 5.7 | 57.4 ± 5.2 | 60.7 ± 5.5 | |
| 3 (4.00/4.25 m/s) | male | n = 31 | 47.6 ± 6.3 | 50.3 ± 6.6 | 51.8 ± 7.1 | 54.1 ± 7.8 |
| female | n = 2 | 43.7 ± 9.5 | 47.4 ± 11.3 | 50.0 ± 11.6 | 63.5 * | |
| 4 (4.50/4.75 m/s) | male | n = 5 | 52.9 ± 5.6 | 55.3 ± 5.7 | 57.1 ± 6.2 | 58.7 ± 7.0 |
| female | - | - | - | - | - | |
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 13 | 18.4 ± 7.7 | 20.0 ± 7.8 | 20.9 ± 8.3 | 21.6 ± 8.1 | |
| 2 (3.50/3.75 m/s) | male | n = 11 | 16.6 ± 5.0 | 17.4 ± 5.3 | 18.0 ± 5.0 | 19.5 ± 3.3 |
| female | n = 21 | 17.7 ± 5.1 | 18.7 ± 5.0 | 19.5 ± 5.5 | 20.1 ± 5.4 | |
| 3 (4.00/4.25 m/s) | male | n = 31 | 16.3 ± 5.3 | 17.3 ± 5.6 | 17.8 ± 5.9 | 18.6 ± 6.1 |
| female | n = 2 | 17.5 ± 4.9 | 18.9 ± 5.4 | 19.6 ± 5.3 | 24.0 * | |
| 4 (4.50/4.75 m/s) | male | n = 5 | 16.4 ± 3.8 | 17.5 ± 4.2 | 18.0 ± 3.7 | 19.1 ± 3.0 |
| female | - | - | - | - | - | |
| Performance Group (Starting Speed) | Sex | Speed Stage | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 1 (3.00/3.25 m/s) | male | - | - | - | - | - |
| female | n = 13 | 36.9 ± 4.3 | 39.0 ± 5.0 | 40.2 ± 5.3 | 42.2 ± 6.1 | |
| 2 (3.50/3.75 m/s) | male | n = 11 | 34.9 ± 4.4 | 36.7 ± 4.3 | 38.7 ± 4.5 | 40.3 ± 4.5 |
| female | n = 21 | 36.3 ± 4.0 | 38.8 ± 6.6 | 39.8 ± 4.5 | 42.2 ± 7.3 | |
| 3 (4.00/4.25 m/s) | male | n = 31 | 37.6 ± 4.9 | 40.4 ± 7.0 | 42.0 ± 8.6 | 42.6 ± 6.2 |
| female | n = 2 | 34.6 ± 4.2 | 37.1 ± 5.3 | 38.7 ± 5.3 | 44.0 * | |
| 4 (4.50/4.75 m/s) | male | n = 5 | 40.7 ± 6.1 | 43.6 ± 9.2 | 45.5 ± 10.1 | 45.9 ± 8.5 |
| female | - | - | - | - | - | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lang, C.; Schleichardt, A.; Warschun, F.; Walter, N.; Fleckenstein, D.; Berkel, F.; Ueberschär, O. Relationship between Longitudinal Upper Body Rotation and Energy Cost of Running in Junior Elite Long-Distance Runners. Sports 2023, 11, 204. https://doi.org/10.3390/sports11100204
Lang C, Schleichardt A, Warschun F, Walter N, Fleckenstein D, Berkel F, Ueberschär O. Relationship between Longitudinal Upper Body Rotation and Energy Cost of Running in Junior Elite Long-Distance Runners. Sports. 2023; 11(10):204. https://doi.org/10.3390/sports11100204
Chicago/Turabian StyleLang, Charlotte, Axel Schleichardt, Frank Warschun, Nico Walter, Daniel Fleckenstein, Fides Berkel, and Olaf Ueberschär. 2023. "Relationship between Longitudinal Upper Body Rotation and Energy Cost of Running in Junior Elite Long-Distance Runners" Sports 11, no. 10: 204. https://doi.org/10.3390/sports11100204
APA StyleLang, C., Schleichardt, A., Warschun, F., Walter, N., Fleckenstein, D., Berkel, F., & Ueberschär, O. (2023). Relationship between Longitudinal Upper Body Rotation and Energy Cost of Running in Junior Elite Long-Distance Runners. Sports, 11(10), 204. https://doi.org/10.3390/sports11100204






