Unexpected Frictional Behavior of Laser-Textured Hydrophobic Surfaces
Abstract
1. Introduction
2. Materials and Methods
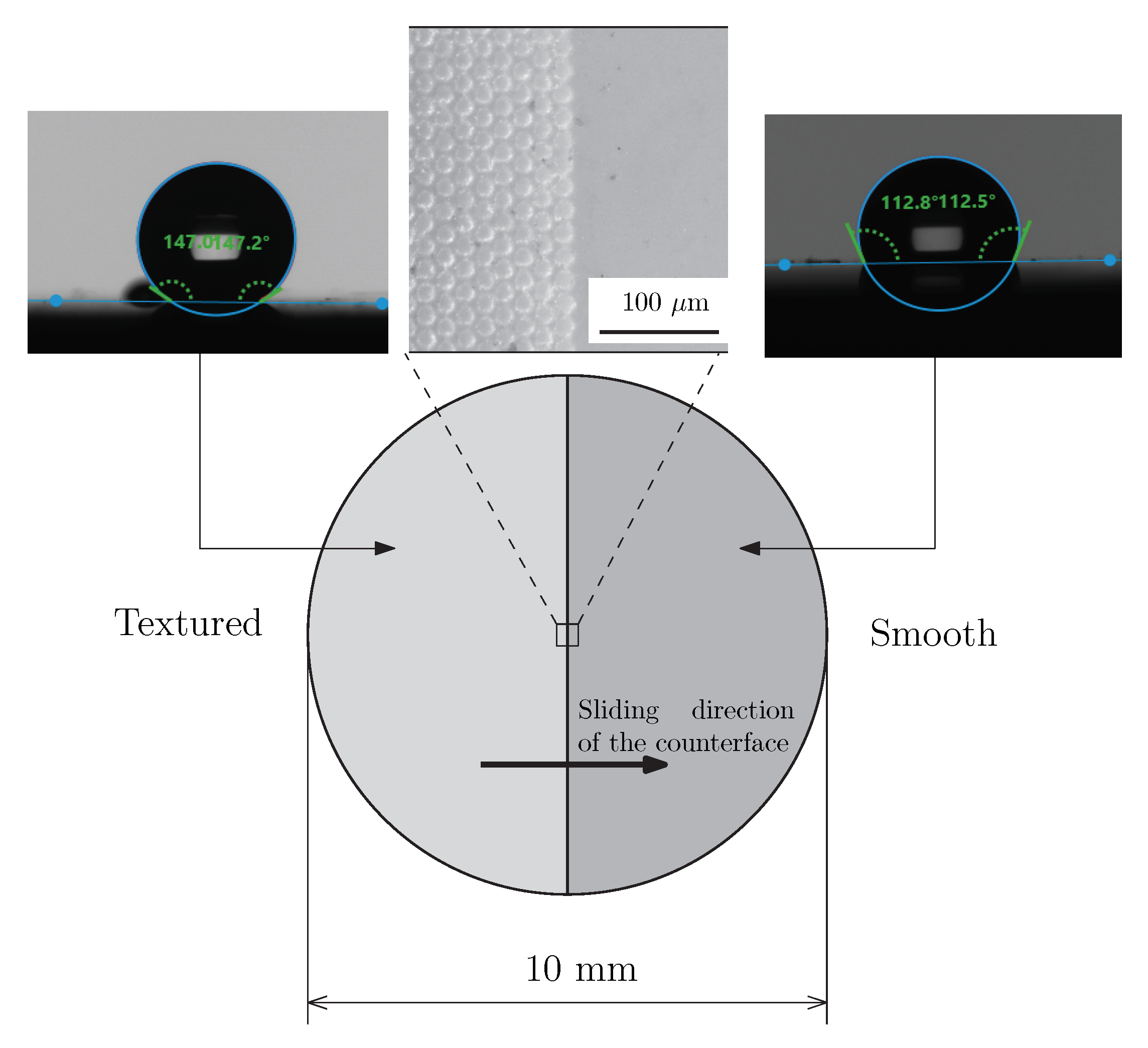
2.1. Samples
2.2. Surface Texturing
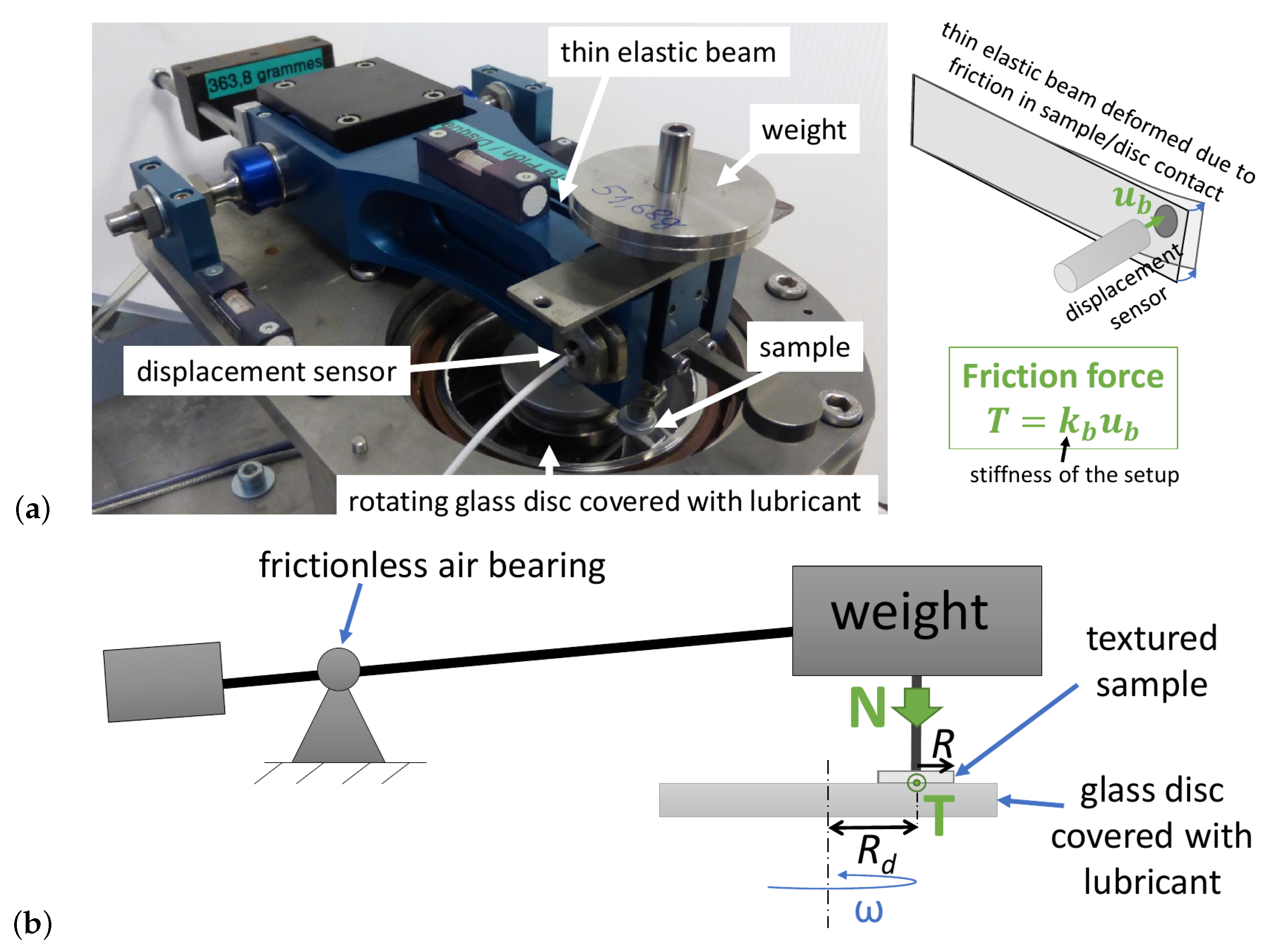
2.3. Test Rig and Experimental Conditions
2.4. Simulation Tool
3. Results
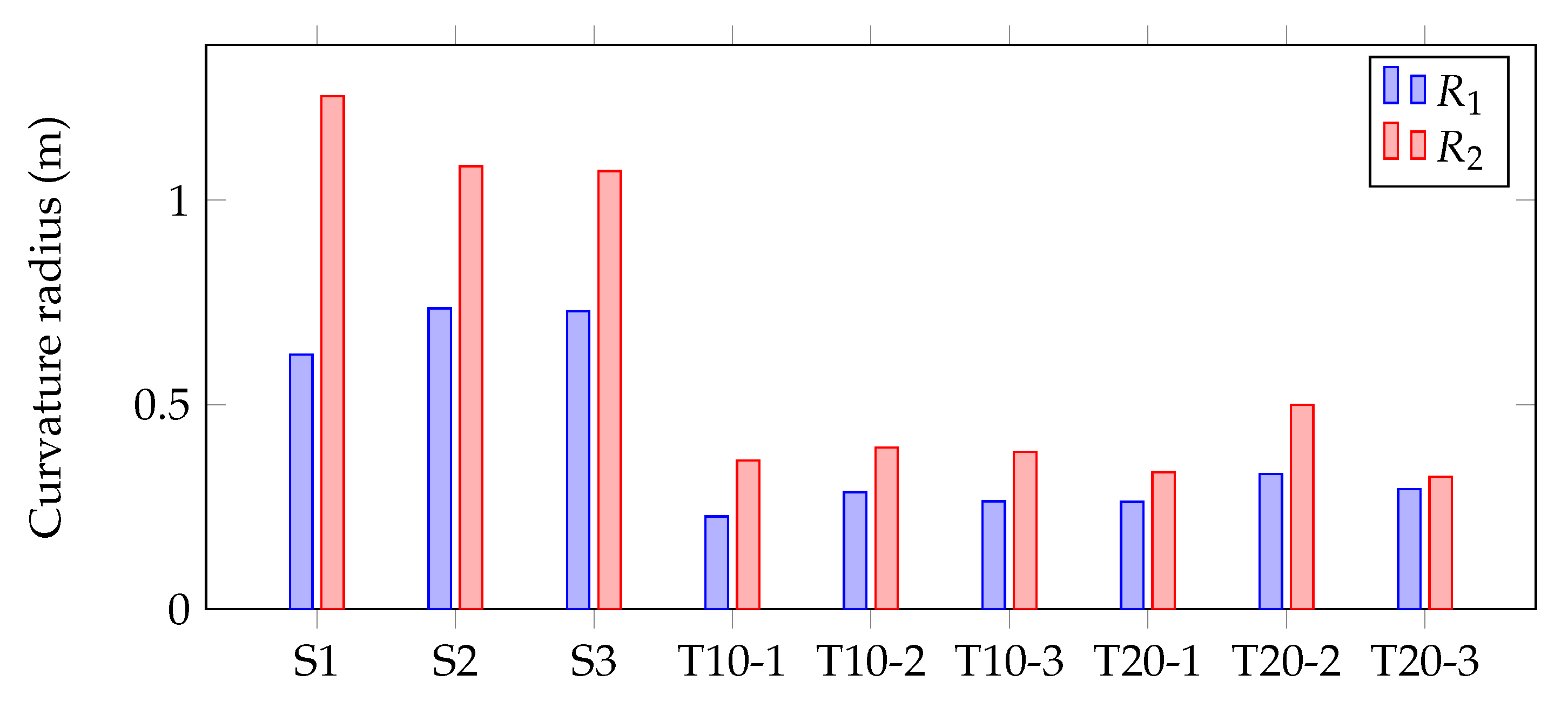
3.1. Sample Characterization
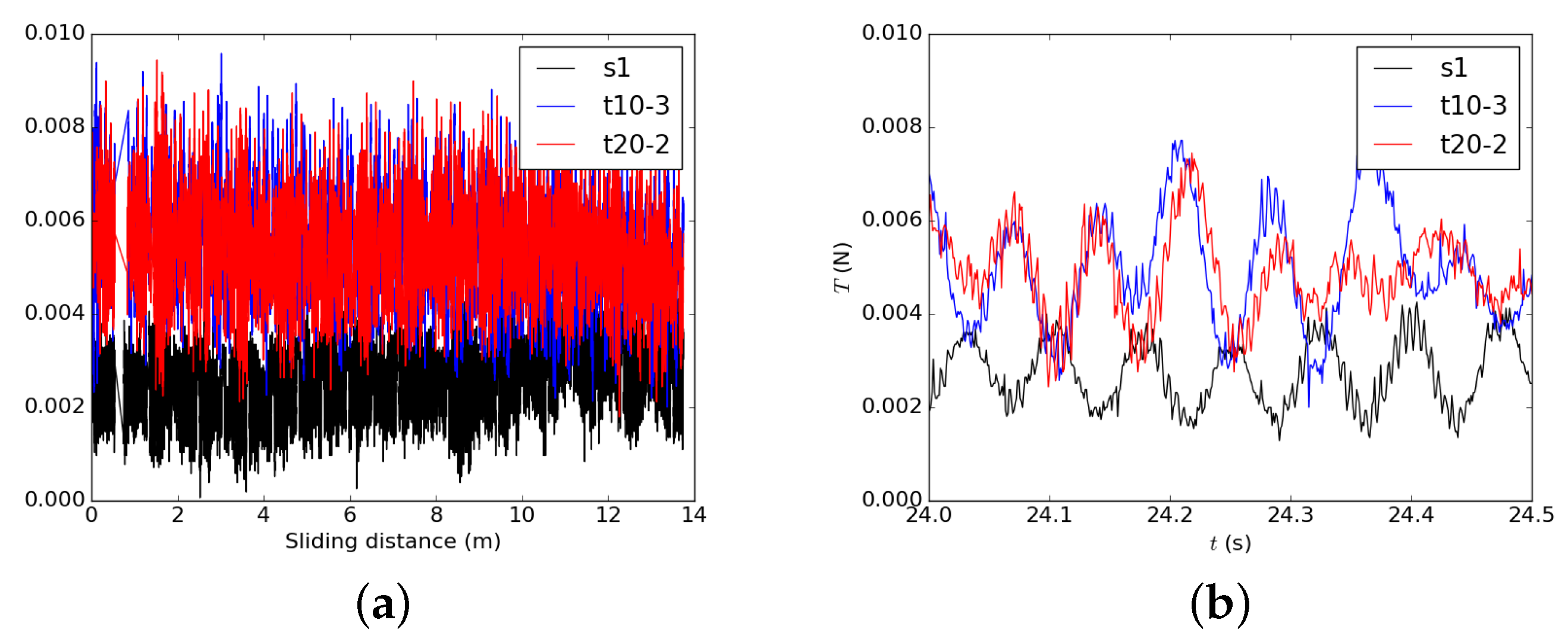
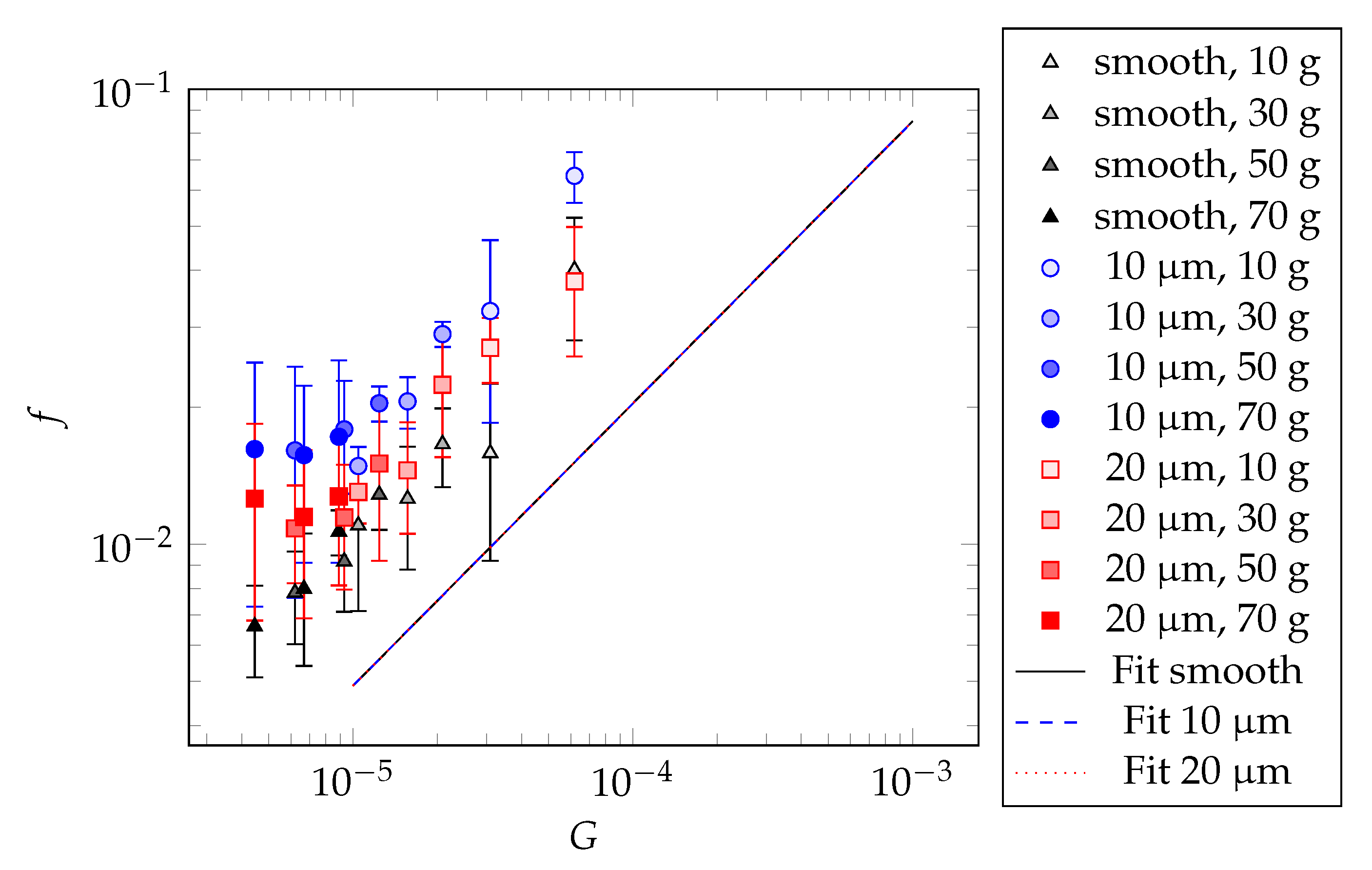
3.2. Friction Tests
4. Discussion
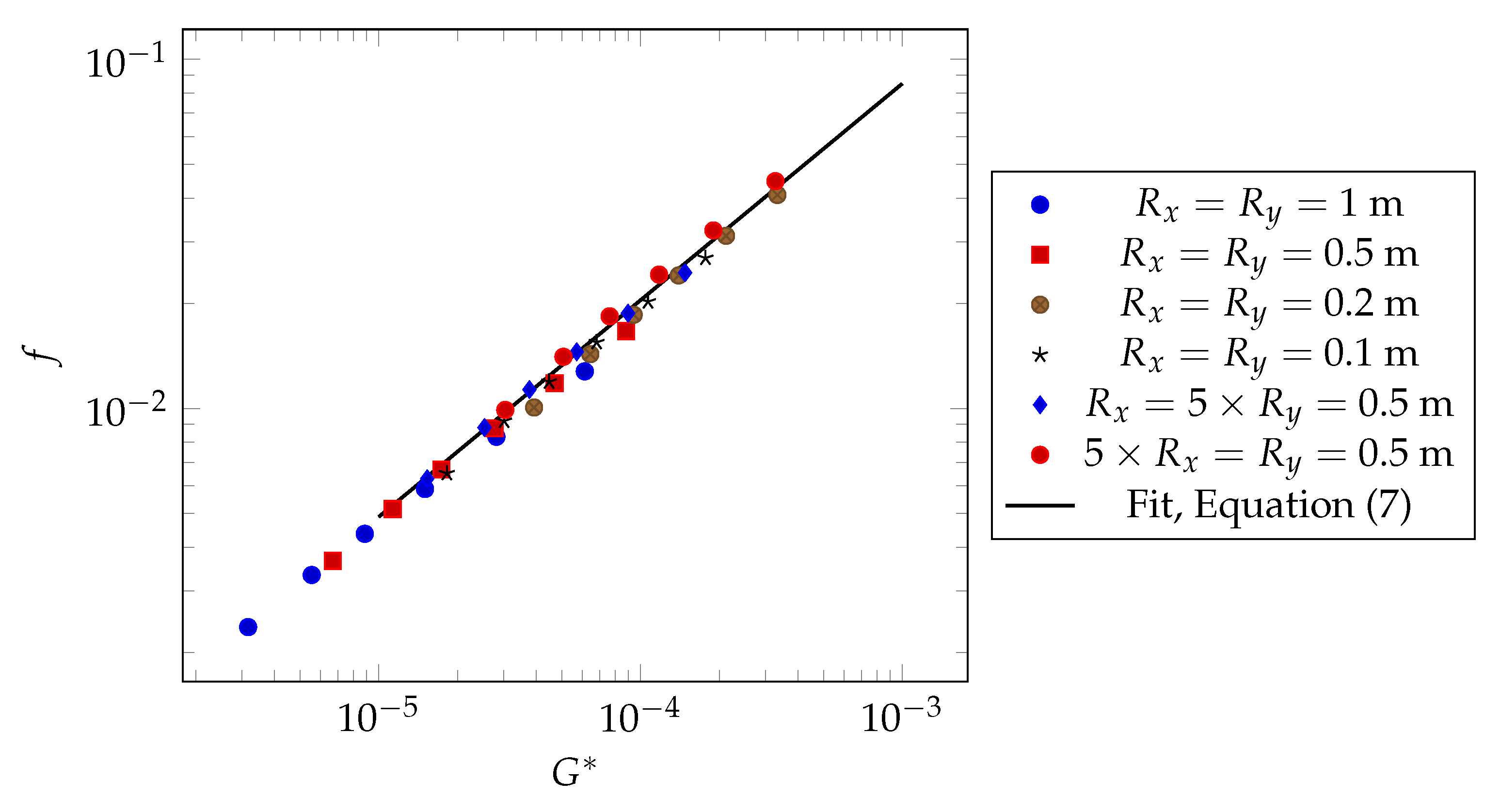
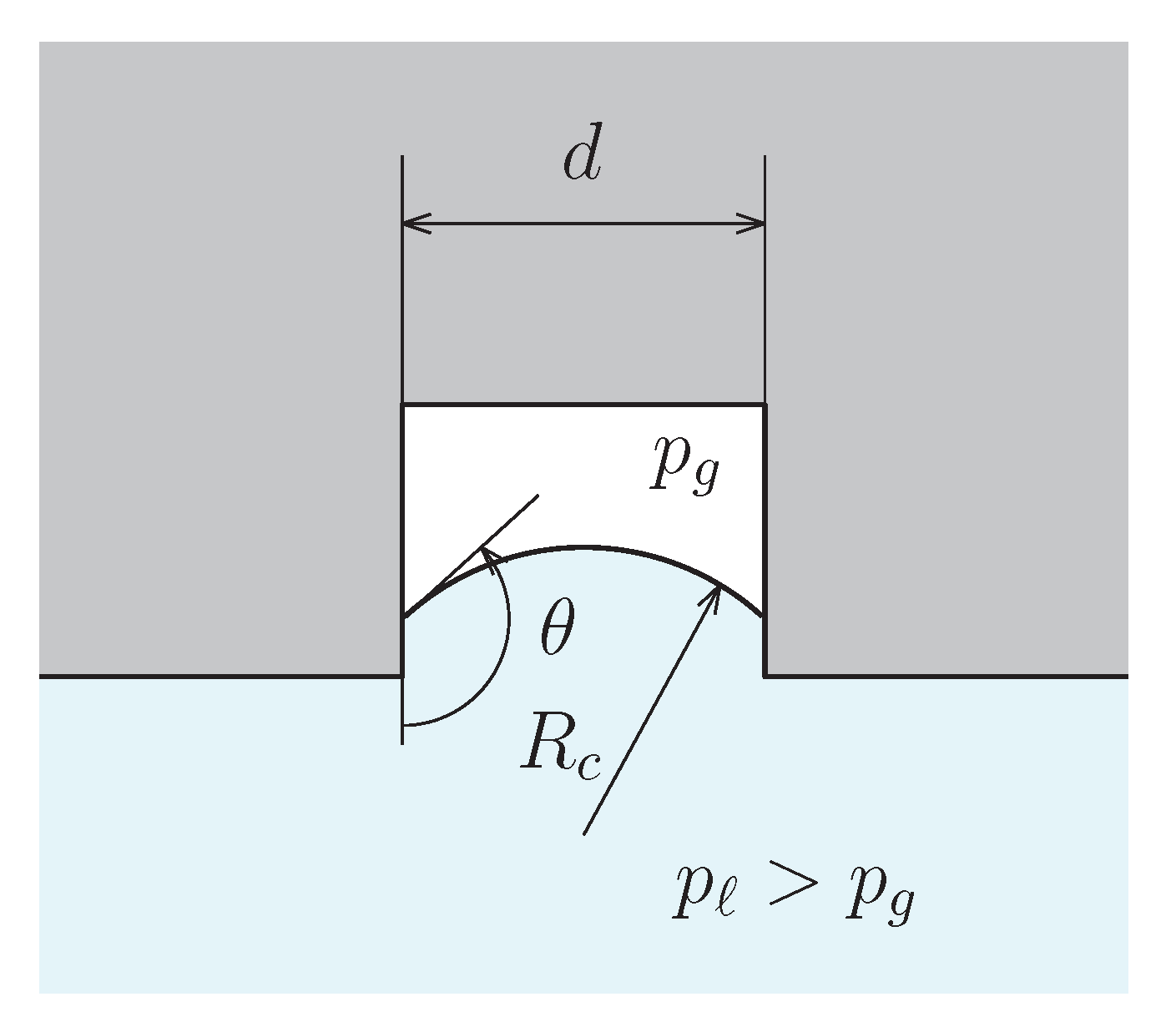
4.1. Simulation of the Effect of Surface Curvature
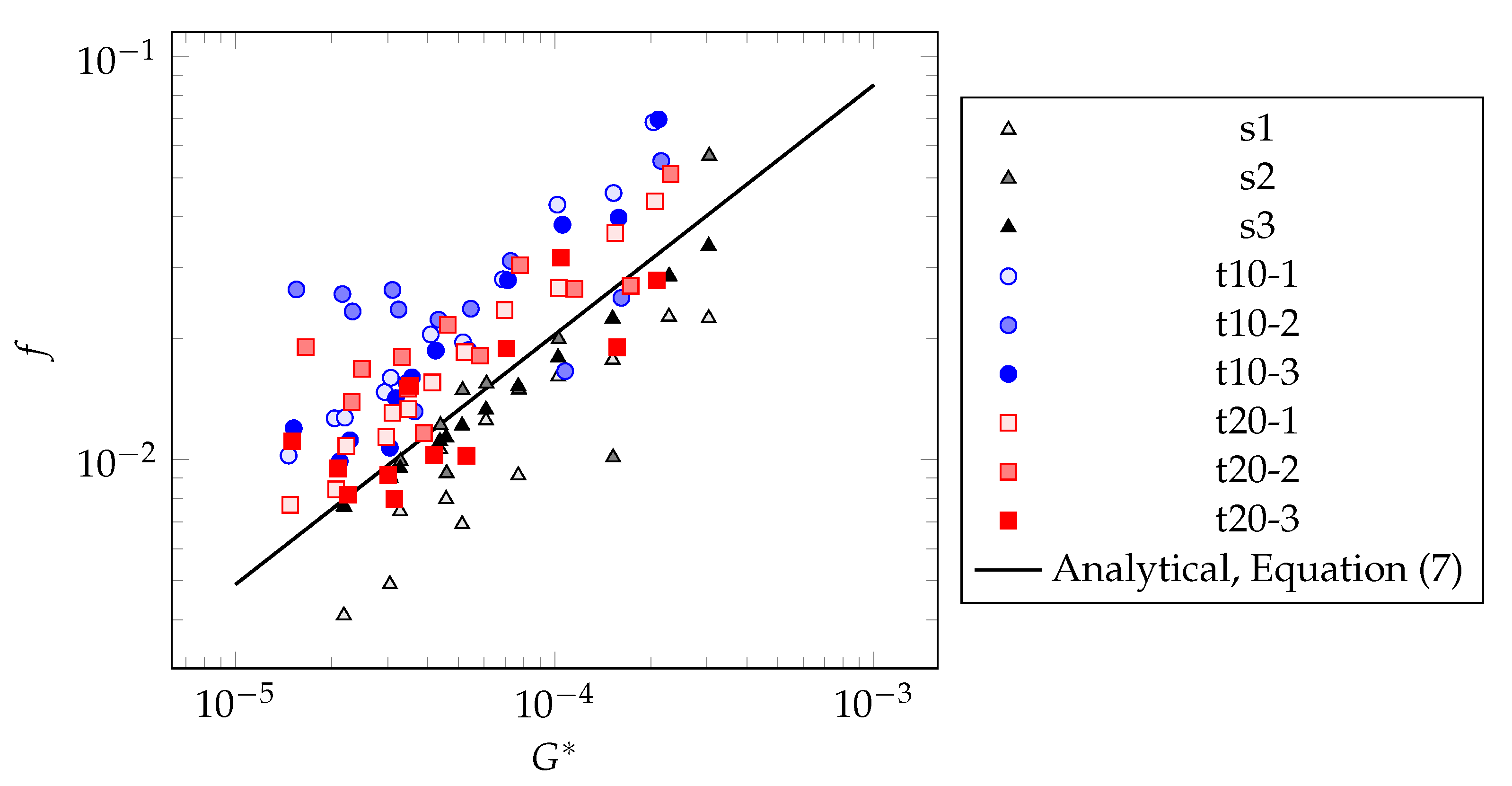
4.2. Discussion of the Experimental Friction Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PTFE | PolyTetreFluoroEthylene |
References
- Holmberg, K.; Erdemir, A. Influence of tribology on global energy consumption, costs and emissions. Friction 2017, 5, 263–284. [Google Scholar] [CrossRef]
- Gropper, D.; Wang, L.; Harvey, T.J. Hydrodynamic lubrication of textured surfaces: A review of modeling techniques and key findings. Tribol. Int. 2016, 94, 509–529. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Grützmacher, P.G.; Gachot, C.; Costa, H.L. Surface Texturing in Machine Elements—A Critical Discussion for Rolling and Sliding Contacts. Adv. Eng. Mater. 2019, 21, 1900194. [Google Scholar] [CrossRef]
- Etsion, I.; Halperin, G. A Laser Surface Textured Hydrostatic Mechanical Seal. Tribol. Trans. 2002, 45, 430–434. [Google Scholar] [CrossRef]
- Dingui, K.; Brunetière, N.; Bouyer, J.; Adjemout, M. Surface Texturing to Reduce Temperature in Mechanical Seals. Tribol. Online 2020, 15, 222–229. [Google Scholar] [CrossRef]
- Spikes, H. The Half-wetted Bearing. Part 2: Potential Application in Low Load Contacts. IMechE Part J J. Eng. Tribol. 2003, 217, 15–26. [Google Scholar] [CrossRef]
- Spikes, H. The Half-wetted Bearing. Part 1: Extended Reynolds Equation. IMechE Part J J. Eng. Tribol. 2003, 217, 1–14. [Google Scholar] [CrossRef]
- Salant, R.; Fortier, A. Numerical Analysis of a Slider Bearing with a Heterogeneous Slip/No-Slip Surface. Tribol. Trans. 2004, 47, 328–334. [Google Scholar] [CrossRef]
- Wu, C.; Ma, G.; Zhou, P.; Wu, C. Low friction and high load support capacity of slider bearing with a mixed slip surface. J. Tribol. 2006, 128, 904–907. [Google Scholar] [CrossRef]
- Fatu, A.; Maspeyrot, P.; Hajjam, M. Wall slip effects in (elasto) hydrodynamic journal bearings. Tribol. Int. 2011, 44, 868–877. [Google Scholar] [CrossRef]
- Zhu, Y.; Granick, S. Limits of the Hydrodynamic No-Slip Boundary Condition. Phys. Rev. Lett. 2002, 88, 106102. [Google Scholar] [CrossRef] [PubMed]
- Schnell, E. Slippage of water over nonwettable surfaces. J. Appl. Phys. 1956, 27, 1149–1152. [Google Scholar] [CrossRef]
- Kunert, C.; Harting, J. Roughness Induced Boundary Slip in Microchannel Flows. Phys. Rev. Lett. 2007, 99, 176001. [Google Scholar] [CrossRef]
- Huang, D.M.; Sendner, C.; Horinek, D.; Netz, R.R.; Bocquet, L. Water Slippage versus Contact Angle: A Quasiuniversal Relationship. Phys. Rev. Lett. 2008, 101, 226101. [Google Scholar] [CrossRef]
- Choo, J.; Spikes, H.; Ratoi, M.; Glovnea, R.; Forrest, A. Friction reduction in low-load hydrodynamic lubrication with a hydrophobic surface. Tribol. Int. 2007, 40, 154–159. [Google Scholar] [CrossRef]
- Guo, L.; Wong, P.; Guo, F. Correlation of contact angle hysteresis and hydrodynamic lubrication. Tribol. Lett. 2015, 58, 45. [Google Scholar] [CrossRef]
- Guo, L.; Wong, P.; Guo, F. Identifying the optimal interfacial parameter correlated with hydrodynamic lubrication. Friction 2016, 4, 347–358. [Google Scholar] [CrossRef]
- Lin, W.; Klein, J. Control of surface forces through hydrated boundary layers. Curr. Opin. Colloid Interface Sci. 2019, 44, 94–106. [Google Scholar] [CrossRef]
- Rosenhek-Goldian, I.; Kampf, N.; Klein, J. Trapped Aqueous Films Lubricate Highly Hydrophobic Surfaces. ACS Nano 2018, 12, 10075–10083. [Google Scholar] [CrossRef] [PubMed]
- Bhushan, B. Biomimetics: Lessons from Nature - An Overview. Philos. Trans. R. Soc. A 2009, 367, 1445–1486. [Google Scholar] [CrossRef] [PubMed]
- Law, K.Y.; Zhao, H. Surface Wetting-Characterization, Contact Angle, and Fundamentals; Springer: London, UK, 2016. [Google Scholar]
- Ou, J.; Perot, B.; Rothstein, J.P. Laminar drag reduction in microchannels using ultrahydrophobic surfaces. Phys. Fluids 2004, 16, 4635–4643. [Google Scholar] [CrossRef]
- Choi, C.H.; Kim, C.J. Large Slip of Aqueous Liquid Flow over a Nanoengineered Superhydrophobic Surface. Phys. Rev. Lett. 2006, 96, 066001. [Google Scholar] [CrossRef]
- Srinivasan, S.; Choi, W.; Park, K.C.; Chhatre, S.S.; Cohen, R.E.; McKinley, G.H. Drag reduction for viscous laminar flow on spray-coated non-wetting surfaces. Soft Matter 2013, 9, 5691–5702. [Google Scholar] [CrossRef]
- Solomon, B.R.; Khalil, K.S.; Varanasi, K.K. Drag reduction using lubricant-impregnated surfaces in viscous laminar flow. Langmuir 2014, 30, 10970–10976. [Google Scholar] [CrossRef]
- Küper, S.; Stuke, M. Ablation of polytetrafluoroethylene (Teflon) with femtosecond UV excimer laser pulses. Appl. Phys. Lett. 1989, 54, 4–6. [Google Scholar] [CrossRef]
- Dann, J. Forces involved in the adhesive process: I. Critical surface tensions of polymeric solids as determined with polar liquids. J. Colloid Interface Sci. 1970, 32, 302–320. [Google Scholar] [CrossRef]
- Bittoun, E.; Marmur, A. Optimizing Super-Hydrophobic Surfaces: Criteria for Comparison of Surface Topographies. J. Adhes. Sci. Technol. 2009, 23, 401–411. [Google Scholar] [CrossRef]
- Payvar, P.; Salant, R. A Computational Method for Cavitation in a Wavy Mechanical Seal. J. Tribol. 1992, 114, 199–204. [Google Scholar] [CrossRef]
- Mateescu, G.; Ribbens, C.J.; Watson, L.T.; Wang, C.Y. Effect of a sawtooth boundary on Couette flow. Comput. Fluids 1999, 28, 801–813. [Google Scholar] [CrossRef]
- Arghir, M.; Roucou, N.; Helene, M.; Frene, J. Theoretical Analysis of the Incompressible Laminar Flow in a Macro-Roughness Cell. J. Tribol. 2003, 125, 309–318. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Sample material | PTFE |
| Rotating disk material | Glass |
| Lubricant | Water at 20 °C |
| Rotational speed (rpm) | 100, 150, 200 |
| Applied mass (g) | 10, 30, 50, 70 |
| Corresponding averaged pressure (kPa) | 1.3, 3.8, 6.4, 9.0 |
| Sample | Spacing | Static Angle |
|---|---|---|
| T10-1 | 10 μm | 133 ± 1 |
| T10-2 | 10 μm | 143 ± 2 |
| T10-3 | 10 μm | 145 ± 2 |
| T20-1 | 20 μm | 147 ± 2 |
| T20-2 | 20 μm | 142 ± 2 |
| T20-3 | 20 μm | 153 ± 3 |
| Parameter | Value |
|---|---|
| Viscosity μ (Pa·s) | 0.001 |
| Averaged sliding speed V (m·s) | 1 |
| Sample radius R (m) | 0.005 |
| Curvature radius (m) | 0.1–1 |
| Curvature radius (m) | 0.1–1 |
| Domain size (m) | 0.012 |
| Number of nodes | 256 × 256 |
| Cavitation pressure (Pa) | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jendoubi, H.; Smerdova, O.; Brunetière, N. Unexpected Frictional Behavior of Laser-Textured Hydrophobic Surfaces. Lubricants 2021, 9, 31. https://doi.org/10.3390/lubricants9030031
Jendoubi H, Smerdova O, Brunetière N. Unexpected Frictional Behavior of Laser-Textured Hydrophobic Surfaces. Lubricants. 2021; 9(3):31. https://doi.org/10.3390/lubricants9030031
Chicago/Turabian StyleJendoubi, Hiba, Olga Smerdova, and Noël Brunetière. 2021. "Unexpected Frictional Behavior of Laser-Textured Hydrophobic Surfaces" Lubricants 9, no. 3: 31. https://doi.org/10.3390/lubricants9030031
APA StyleJendoubi, H., Smerdova, O., & Brunetière, N. (2021). Unexpected Frictional Behavior of Laser-Textured Hydrophobic Surfaces. Lubricants, 9(3), 31. https://doi.org/10.3390/lubricants9030031







